Efficient Surrogate-Based Optimization of Prefractionation Column Using Self-Adaptive Kriging Model with Modified Firefly Algorithm
Abstract
1. Introduction
- The integrated SAK-MFA framework is successfully applied to the economic optimization of an industrial prefractionation column. It is demonstrated to significantly reduce computational costs compared to high-fidelity simulation-based optimization while identifying superior operating points, thus providing a practical and efficient tool for real-world process optimization.
- A SAK model is implemented, featuring an automated Bayesian optimization approach for hyperparameter tuning. This eliminates the need for manual, expert-driven selection and enhances the predictive accuracy of the model for the complex behaviour of prefractionation columns.
- A MFA is applied to solve the optimization problem defined by the SAK surrogate efficiently. The MFA is specifically structured to balance global exploration and local exploitation, enabling a more effective search for optimal operating conditions.
2. Problem Statement
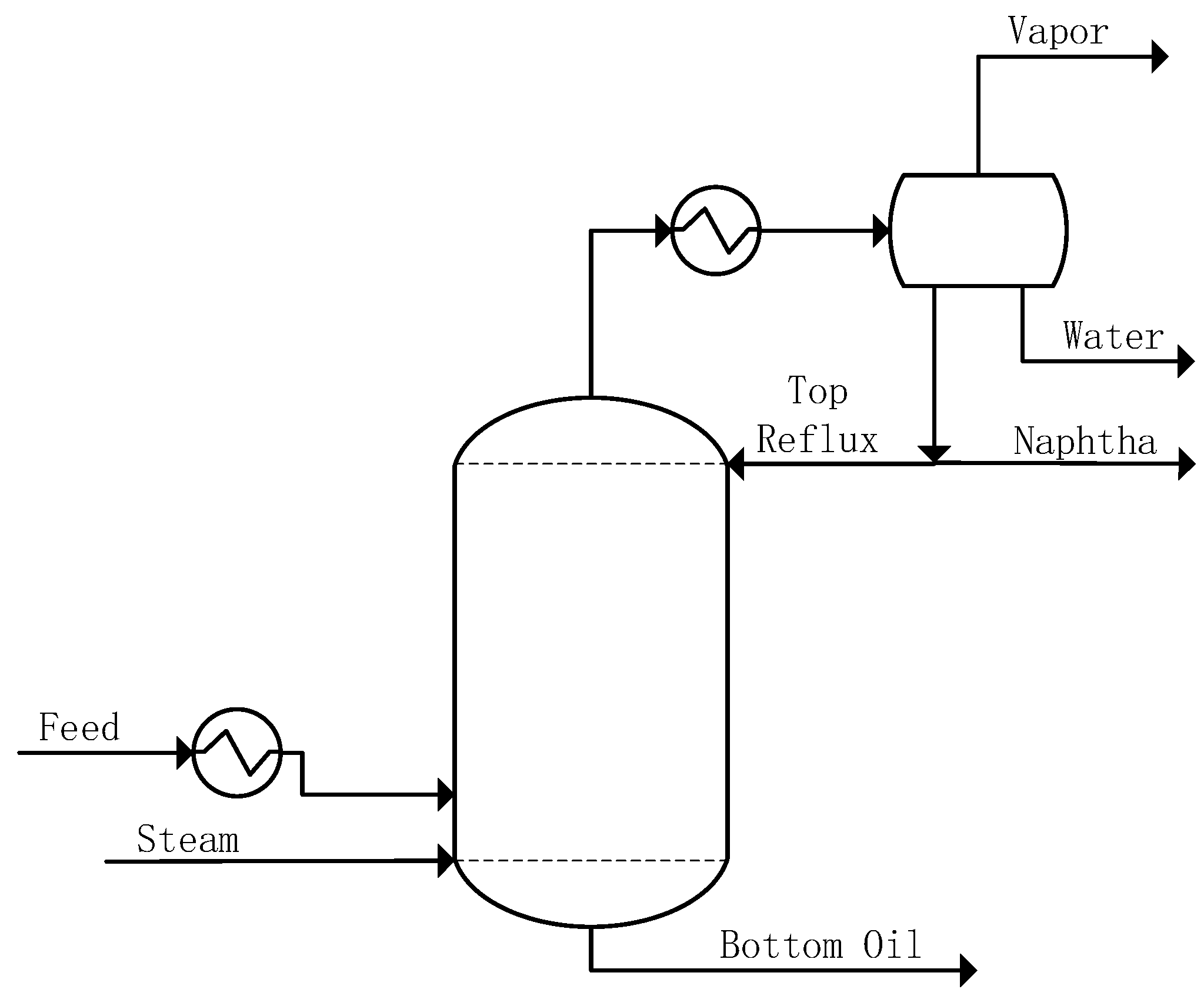
2.1. Prefractionation Column Description
2.2. Optimization Problem Formulation
3. Surrogate-Aided Optimization Strategy
3.1. Surrogate Modeling Modular
3.2. Bayesian Hyperparameter Optimizer
3.3. Modified Firefly Algorithm
3.4. Integration Framework
- Inner Loop: SAK Hyperparameter Optimization. This loop ensures the surrogate model’s adaptability. The hyperparameters of the SAK model (e.g., the correlation function parameter ) are automatically tuned using Bayesian optimization. The objective is to minimize the cross-validation error (CV-MSE) of the model based on the currently available training data. This inner loop ensures the surrogate provides the most accurate possible representation of the actual process behaviour given the data.
- Outer Loop: Process Economic Optimization. This loop performs the primary optimization task. The MFA searches for optimal operating conditions by iteratively evaluating candidate solutions using the fast, accurate SAK model built by the inner loop, rather than the computationally expensive high-fidelity simulator. The objective is to maximize the economic profit, subject to operational constraints. Within this outer loop, a critical model management strategy is employed to maintain and improve surrogate accuracy throughout the search. Candidate solutions identified by MFA on the surrogate are periodically selected for validation using the high-fidelity process simulator (e.g., Aspen Plus, detailed for our case study in Section 4.2). The simulator provides accurate output data for these points, enabling reliable economic profit calculations and validating the surrogate’s predictions in promising regions. These validated high-fidelity input-output data pairs are then added back to the training dataset used by the SAK model. The SAK model is periodically updated (retrained and hyperparameters potentially re-optimized, as per Algorithm 1) using this dynamically enriched dataset, ensuring its fidelity improves as the optimization progresses towards the optimum.
| Algorithm 1: Surrogate-based Optimization using SAK and MFA with Two-Tiered Model Update. |
 |
4. Results and Discussion
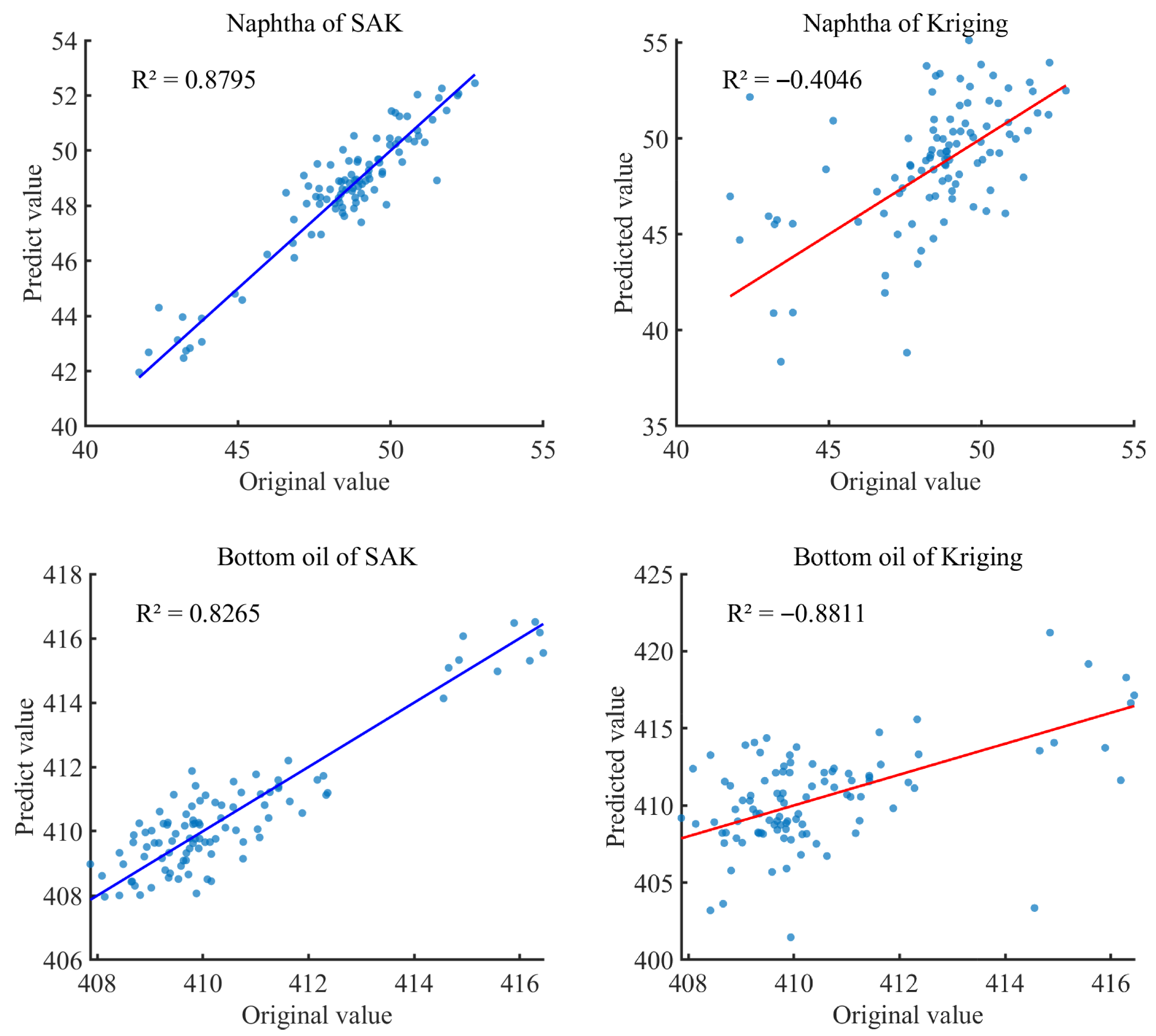
4.1. Surrogate Model Improvement
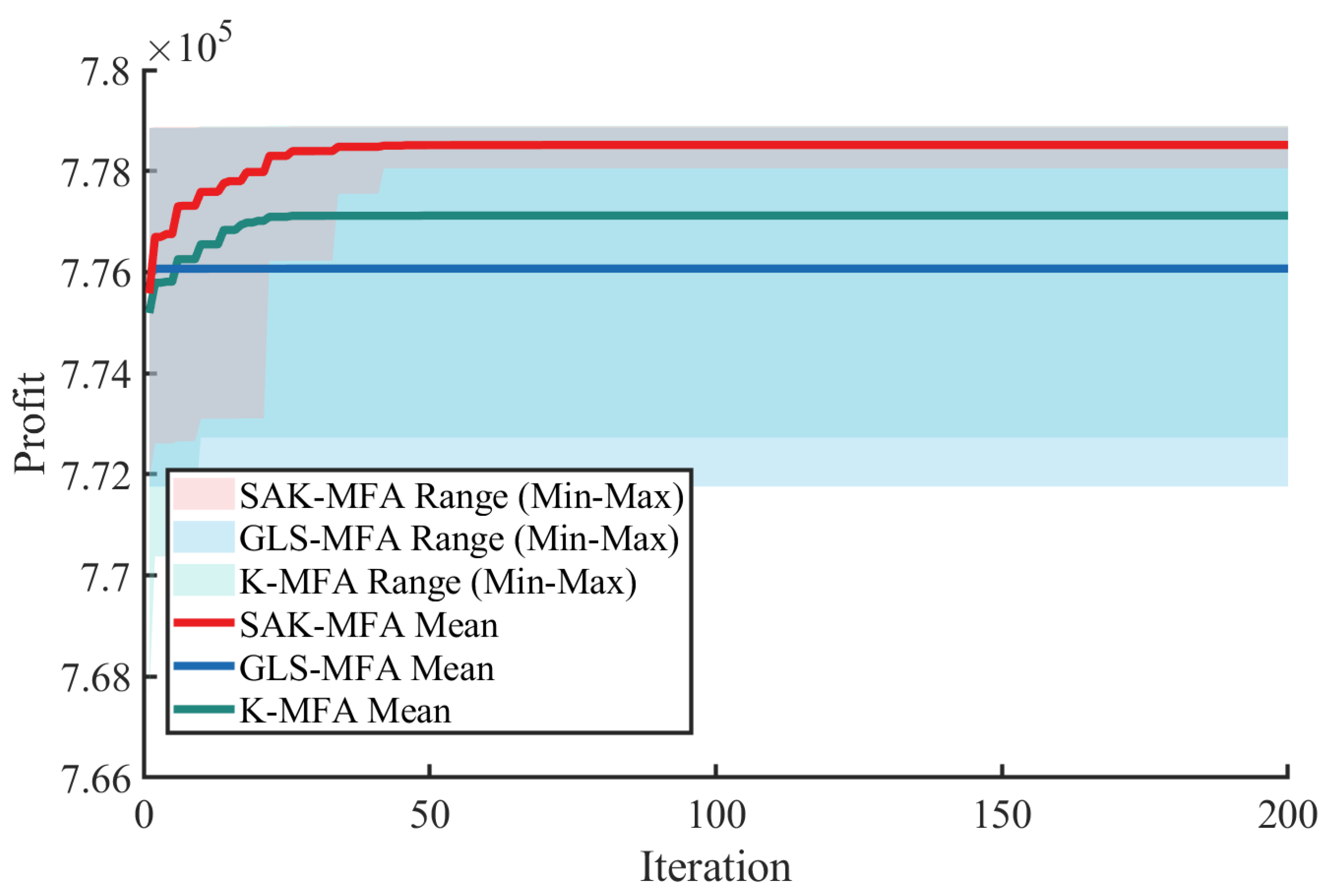
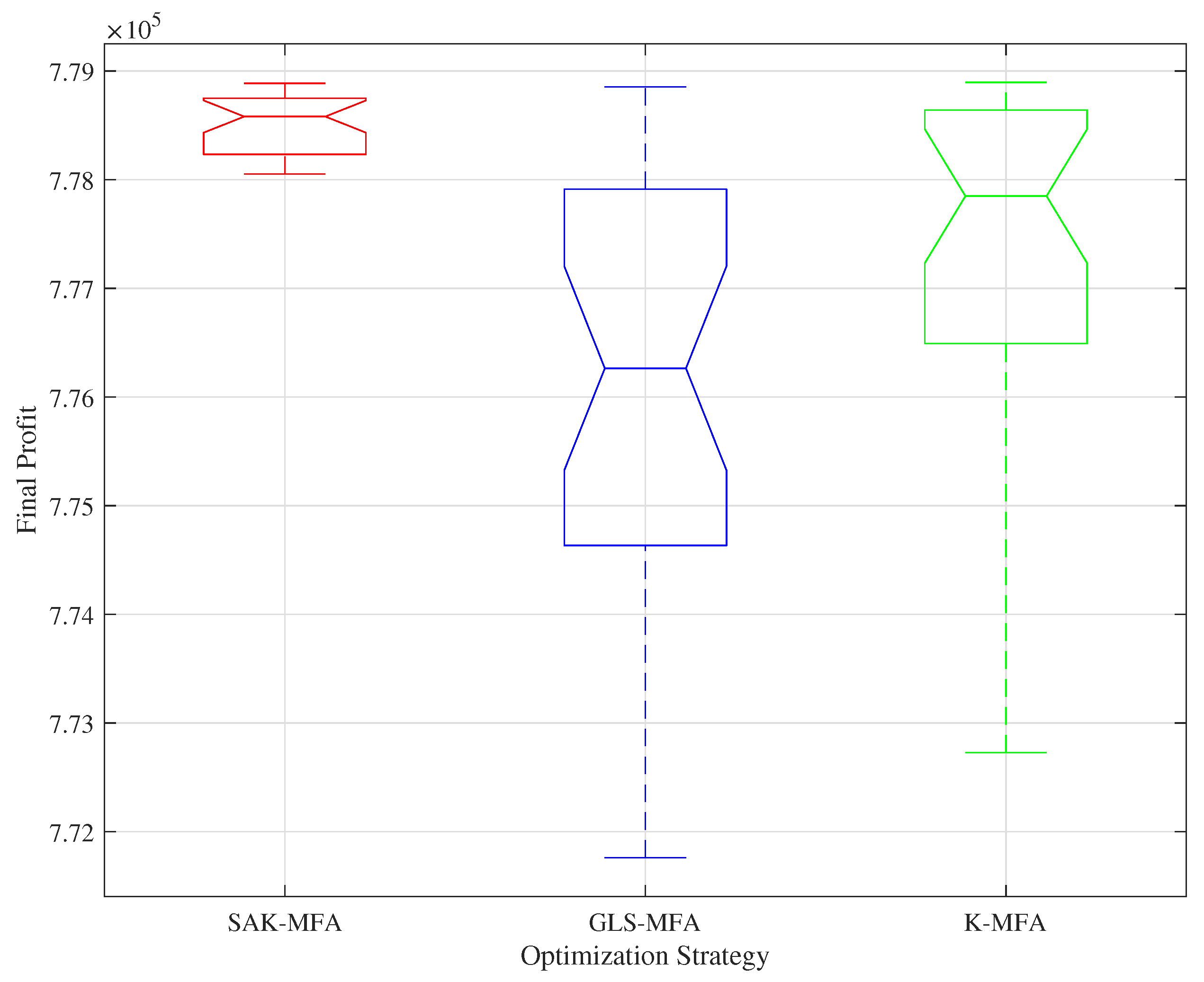
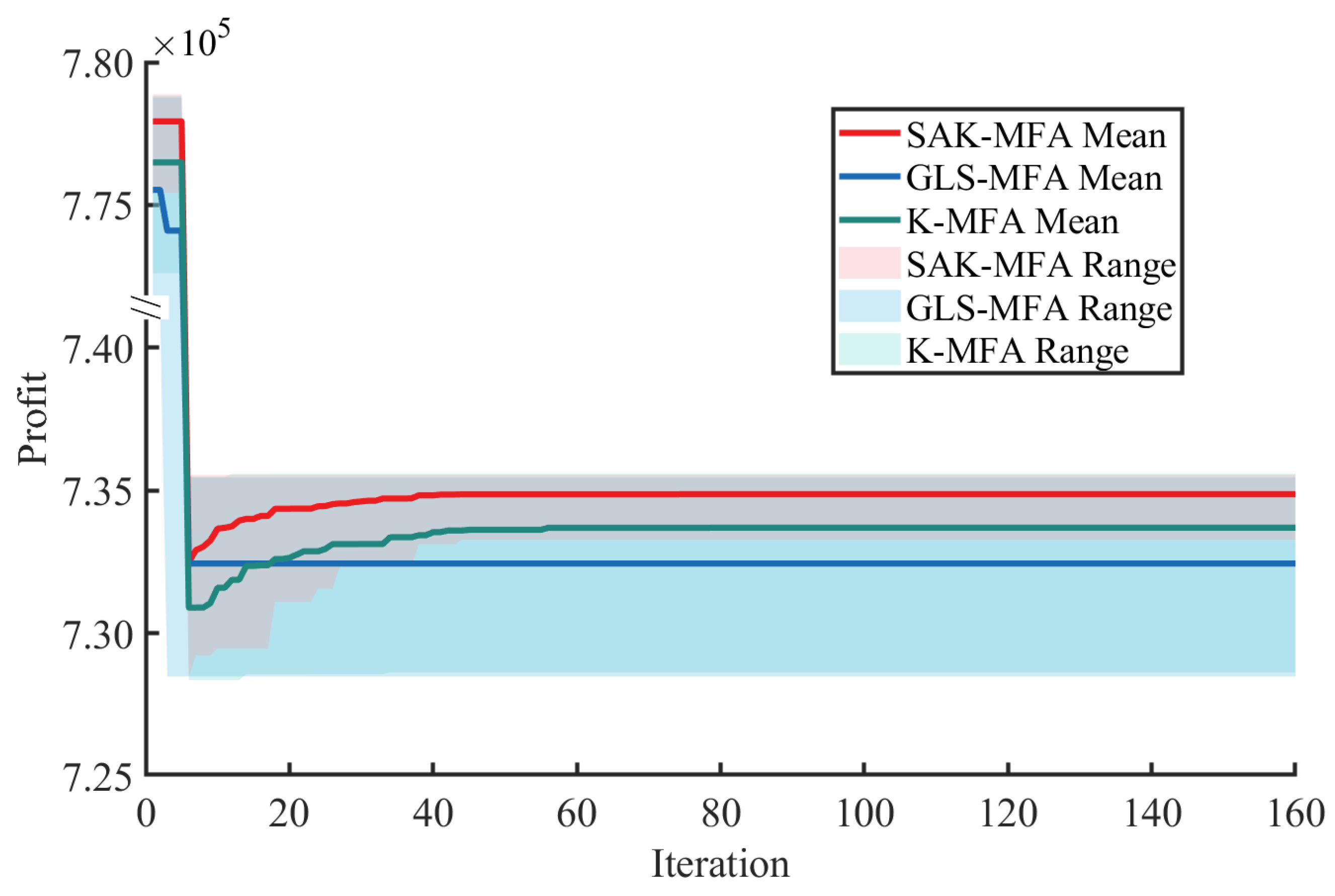
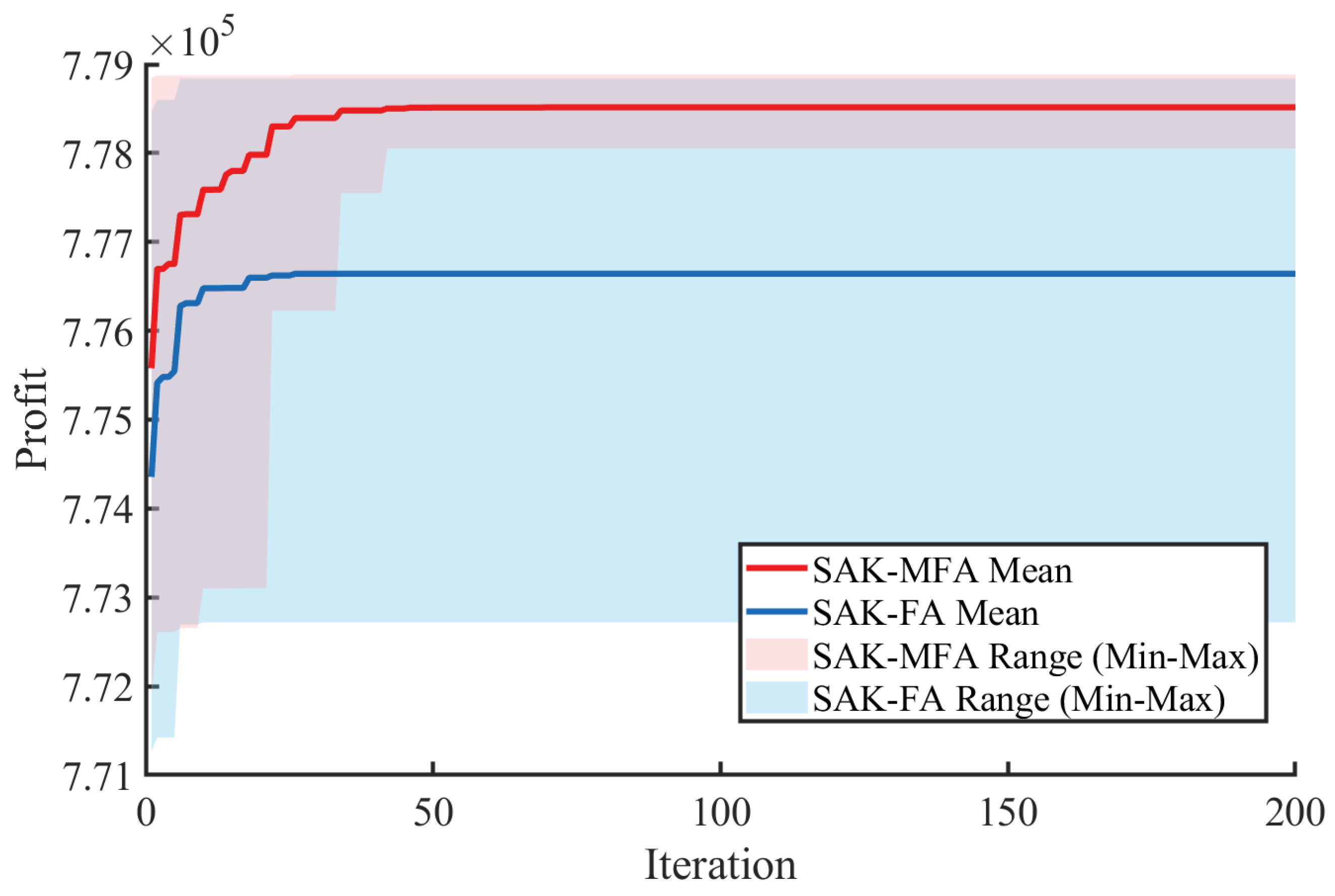
4.2. Surrogate-Based Optimization Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Crude oil feed flow rate (tonne/h) | Expected Improvement acquisition function | ||
| Crude oil feed temperature (°C) | Exploration-exploitation trade-off parameter | ||
| Reflux flow rate (tonne/h) | Standard normal Cumulative Distribution Function (CDF) | ||
| Reflux temperature (°C) | Standard normal Probability Density Function (PDF) | ||
| Reflux accumulator feeding temp. (°C) | Std. deviation of Gaussian Process prediction | ||
| Column top section temperature (°C) | n | Population size of fireflies | |
| Column top section pressure (kPa) | n-dimensional uniform distribution vector | ||
| Column feeding section (stage 27) temp. (°C) | Position of firefly i | ||
| Column bottom (stage 28) temp. (°C) | Position of the best firefly (brightest) | ||
| Set of product streams {vapor, naphtha, bo} | Position of the worst firefly (dimmest) | ||
| s | Index for a product stream, | I | Light intensity of a firefly |
| Flow rate of product stream s (tonne/h) | Original (base) light intensity | ||
| Operational profit (unit/h) | Light absorption coefficient | ||
| Unit price of product stream s (unit/tonne) | Spatial distance between firefly i and j | ||
| Unit price of crude oil (unit/tonne) | Attractiveness of a firefly (FA) | ||
| Lower and upper bounds of the feasible region | Base attractiveness coefficient | ||
| x | Input vector of decision variables | Step size factor (dynamic in MFA) | |
| Kriging model prediction at point x | Percentage of re-initialized fireflies | ||
| Trend component (polynomial) of Kriging model | Input and output training datasets | ||
| Stochastic process (deviation) component | Initial sampled data subset for training | ||
| Variance of the stochastic process | t | Iteration counter | |
| Correlation function | Stopping criterion (number of stable iterations) | ||
| Vector of correlation hyperparameters | Profit by high-fidelity simulation (unit/h) | ||
| j-th correlation hyperparameter | Kriging model for the j-th output |
References
- Ye, L.; Zhang, N.; Li, G.; Gu, D.; Lu, J.; Lou, Y. Intelligent Optimization Design of Distillation Columns Using Surrogate Models Based on GA-BP. Processes 2023, 11, 2386. [Google Scholar] [CrossRef]
- Xue, F.; Liu, L.; Chen, X.; Shi, X.; IEEE. Crude Oil Distillation Optimization Using Surrogate-aided Constrained Evolutionary Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1118–1125. [Google Scholar]
- Ibrahim, D.; Jobson, M.; Li, J.; Guillén-Gosálbez, G. Optimization-Based Design of Crude Oil Distillation Units Using Surrogate Column Models and a Support Vector Machine. Chem. Eng. Res. Des. 2018, 134, 212–225. [Google Scholar] [CrossRef]
- Keßler, T.; Kunde, C.; Mertens, N.; Michaels, D.; Kienle, A. Global Optimization of Distillation Columns Using Surrogate Models. SN Appl. Sci. 2019, 1, 11. [Google Scholar] [CrossRef] [PubMed]
- Franzoi, R.E.; Menezes, B.C.; Kelly, J.D.; Gut, J.A.W.; Grossmann, I.E. Cutpoint Temperature Surrogate Modeling for Distillation Yields and Properties. Ind. Eng. Chem. Res. 2020, 59, 18616–18628. [Google Scholar] [CrossRef]
- Ma, K.; Sahinidis, N.V.; Bindlish, R.; Bury, S.J.; Haghpanah, R.; Rajagopalan, S. Data-Driven Strategies for Extractive Distillation Unit Optimization. Comput. Chem. Eng. 2022, 167, 107970. [Google Scholar] [CrossRef]
- Zhu, X.; Li, X.; Pei, Y.; Ren, H.; Choi, J.H. An Efficient Surrogate Model-Based Method for Deep-Towed Seismic System Optimization. Ocean. Eng. 2023, 268, 113463. [Google Scholar] [CrossRef]
- Guo, D.; Wang, X.; Gao, K.; Jin, Y.; Ding, J.; Chai, T. Evolutionary Optimization of High-Dimensional Multiobjective and Many-Objective Expensive Problems Assisted by a Dropout Neural Network. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 2084–2097. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Q.; Gielen, G.G.E. A Gaussian Process Surrogate Model Assisted Evolutionary Algorithm for Medium Scale Expensive Optimization Problems. IEEE Trans. Evol. Computat. 2014, 18, 180–192. [Google Scholar] [CrossRef]
- Ferreira, J.; Pedemonte, M.; Tories, A.I. A Genetic Programming Approach for Construction of Surrogate Models. Comput. Aided Chem. Eng. 2019, 47, 451–456. [Google Scholar]
- McBride, K.; Sanchez Medina, E.I.; Sundmacher, K. Hybrid Semi-parametric Modeling in Separation Processes: A Review. Chem. Ing. Tech. 2020, 92, 842–855. [Google Scholar] [CrossRef]
- Quirante, N.; Javaloyes, J.; Caballero, J.A. Rigorous Design of Distillation Columns Using Surrogate Models Based on Kriging Interpolation. AIChE J. 2015, 61, 2169–2187. [Google Scholar] [CrossRef]
- Carranza-Abaid, A.; Jakobsen, J.P. Neural Network Programming: Integrating First Principles into Machine Learning Models. Comput. Chem. Eng. 2022, 163, 107858. [Google Scholar] [CrossRef]
- Mandis, M.; Baratti, R.; Chebeir, J.; Tronci, S.; Romagnoli, J.A. Exploring Nontraditional LSTM Architectures for Modeling Demethanizer Column Operations. Comput. Chem. Eng. 2024, 183, 108591. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Q.; Zhang, Z.; Tang, J.; Cui, M.; Chen, X.; Liu, Q.; Fei, Z.; Qiao, X. Surrogate Modeling-Based Multi-Objective Optimization for the Integrated Distillation Processes. Chem. Eng. Process. Process Intensif. 2021, 159, 108224. [Google Scholar] [CrossRef]
- Koksal, E.S.; Aydin, E. Physics Informed Piecewise Linear Neural Networks for Process Optimization. Comput. Chem. Eng. 2023, 174, 108244. [Google Scholar] [CrossRef]
- Osuolale, F.N.; Zhang, J. Energy Efficiency Optimisation for Distillation Column Using Artificial Neural Network Models. Energy 2016, 106, 562–578. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Minh, L.Q.; Duong, P.L.T.; Lee, M. Global Sensitivity Analysis and Uncertainty Quantification of Crude Distillation Unit Using Surrogate Model Based on Gaussian Process Regression. Ind. Eng. Chem. Res. 2018, 57, 5035–5044. [Google Scholar] [CrossRef]
- Quirante, N.; Javaloyes, J.; Ruiz-Femenia, R.; Caballero, J.A. Optimization of Chemical Processes Using Surrogate Models Based on a Kriging Interpolation. Comput. Aided Chem. Eng. 2015, 37, 179–184. [Google Scholar]
- Liu, K.; Tang, Q.Q.; He, C.; Chen, Q.L.; Zhang, B.J. Hybrid Modelling for Combined Design Optimization of CO2 Removal and Compression in Raw Natural Gas Treatment Complexes. Chem. Eng. Res. Des. 2021, 173, 170–182. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhao, Z.; Liu, F. Developing New Products with Kernel Partial Least Squares Model Inversion. Comput. Chem. Eng. 2021, 155, 107537. [Google Scholar] [CrossRef]
- Qi, M.; Jang, K.; Cui, C.; Moon, I. Novel Control-Aware Fault Detection Approach for Non-Stationary Processes via Deep Learning-Based Dynamic Surrogate Modeling. Process Saf. Environ. Prot. 2023, 172, 379–394. [Google Scholar] [CrossRef]
- Lee, K.D.; Kim, K.Y. Objective Function Proposed for Optimization of Convective Heat Transfer Devices. Int. J. Heat Mass Transf. 2012, 55, 2792–2799. [Google Scholar] [CrossRef]
- Liu, Z.; Mei, J.; Wang, D.; Guo, Y.; Wu, L. A Novel Damage Identification Method for Steel Catenary Risers Based on a Novel CNN-GRU Model Optimized by PSO. J. Mar. Sci. Eng. 2023, 11, 200. [Google Scholar] [CrossRef]
- Xiong, Y.; Shi, X.; Ma, Y.; Chen, Y. Optimization Design of Crude Oil Distillation Unit Using Bi-Level Surrogate Model. Front. Control Eng. 2023, 4, 1162318. [Google Scholar] [CrossRef]
- Wang, Z.; Long, Z.; Luo, J.; He, Z.; Li, X. Data Driven State Monitoring of Maglev System With Experimental Analysis. IEEE Access 2020, 8, 79104–79113. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Wu, X.; Hou, Y.; Zhang, K. Optimal Control Approach for Nonlinear Chemical Processes with Uncertainty and Application to a Continuous Stirred-Tank Reactor Problem. Arab. J. Chem. 2022, 15, 104257. [Google Scholar] [CrossRef]
- Jian, J.; Liu, P.; Yin, J.; Zhang, C.; Chao, M. A QCQP-based Splitting SQP Algorithm for Two-Block Nonconvex Constrained Optimization Problems with Application. J. Comput. Appl. Math. 2021, 390, 113368. [Google Scholar] [CrossRef]
- Burke, J.V.; Curtis, F.E.; Wang, H.; Wang, J. Inexact Sequential Quadratic Optimization with Penalty Parameter Updates within the QP Solver. SIAM J. Optim. 2020, 30, 1822–1849. [Google Scholar] [CrossRef]
- Fister, I.; Fister, I.; Yang, X.S.; Brest, J. A Comprehensive Review of Firefly Algorithms. Swarm Evol. Comput. 2013, 13, 34–46. [Google Scholar] [CrossRef]
- Zitouni, F.; Harous, S.; Maamri, R. A Novel Quantum Firefly Algorithm for Global Optimization. Arab. J. Sci. Eng. 2021, 46, 8741–8759. [Google Scholar] [CrossRef]
- Tilahun, S.L.; Ngnotchouye, J.M.T. Firefly Algorithm for Discrete Optimization Problems: A Survey. KSCE J. Civ. Eng. 2017, 21, 535–545. [Google Scholar] [CrossRef]
- Çimen, M.E.; Yalçın, Y. A Novel Hybrid Firefly–Whale Optimization Algorithm and Its Application to Optimization of MPC Parameters. Soft Comput. 2022, 26, 1845–1872. [Google Scholar] [CrossRef]
- Gandomi, A.; Yang, X.S.; Talatahari, S.; Alavi, A. Firefly Algorithm with Chaos. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 89–98. [Google Scholar] [CrossRef]
- Ibrahim, D.; Jobson, M.; Li, J.; Guillén-Gosálbez, G. Optimal Design of Flexible Heat-Integrated Crude Oil Distillation Units Using Surrogate Models. Chem. Eng. Res. Des. 2021, 165, 280–297. [Google Scholar] [CrossRef]
- Stein, M. Large Sample Properties of Simulations Using Latin Hypercube Sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Saves, P.; Lafage, R.; Bartoli, N.; Diouane, Y.; Bussemaker, J.; Lefebvre, T.; Hwang, J.T.; Morlier, J.; Martins, J.R. SMT 2.0: A Surrogate Modeling Toolbox with a Focus on Hierarchical and Mixed Variables Gaussian Processes. Adv. Eng. Softw. 2024, 188, 103571. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Firefly Algorithm: Recent Advances and Applications. Int. J. Swarm Intell. 2013, 1, 36–50. [Google Scholar] [CrossRef]
| Product | Model | MAE | RMSE | |
|---|---|---|---|---|
| Naphtha | SAK | 0.6035 | 0.8019 | 0.8795 |
| Kriging | 2.0317 | 2.7374 | −0.4046 | |
| RBF | 45.8285 | 46.3210 | −401.2060 | |
| ANN | 2.6513 | 3.6103 | −1.4433 | |
| Bottom oil | SAK | 0.6807 | 0.8173 | 0.8265 |
| Kriging | 1.9817 | 2.6913 | −0.8811 | |
| RBF | 391.4664 | 394.0707 | −40331.2 | |
| ANN | 32.9843 | 39.3541 | −401.2390 |
| Decision variables | Ranges | Unit |
|---|---|---|
| Feed rate | 878–949 | tonne/h |
| Feed temperature | 180–256 | °C |
| Reflux rate | 25–47 | tonne/h |
| Reflux temperature | 30–49 | °C |
| Stage 1 temperature | 120–159 | °C |
| Stage 1 pressure | 220–384 | kPa |
| Stage 27 temperature | 200–258 | °C |
| Stage 28 temperature | 200–258 | °C |
| Parameters | Value | Description |
|---|---|---|
| n | 30 | Population size |
| 1.0 | Base attractiveness coefficient | |
| 1.0 | Light absorption coefficient | |
| 10% | Percentage of reinitialized fireflies |
| Variables | Unit | SAK-MFA | GLS-MFA | K-MFA |
|---|---|---|---|---|
| Feed rate | tonne/h | 878.95 | 878.95 | 878.95 |
| Feed temperature | °C | 236.02 | 218.76 | 228.63 |
| Reflux rate | tonne/h | 41.90 | 28.74 | 25.90 |
| Reflux temperature | °C | 47.28 | 37.66 | 44.27 |
| Stage 1 temperature | °C | 153.95 | 153.95 | 153.95 |
| Stage 1 pressure | kPa | 379.08 | 379.08 | 379.08 |
| Stage 27 temperature | °C | 235.99 | 218.70 | 228.60 |
| Stage 28 temperature | °C | 236.04 | 218.74 | 228.64 |
| Profit | unit/h | 778,530.200 | 776,142.144 | 777,209.980 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Jin, Q.; Wang, B. Efficient Surrogate-Based Optimization of Prefractionation Column Using Self-Adaptive Kriging Model with Modified Firefly Algorithm. Appl. Sci. 2025, 15, 11962. https://doi.org/10.3390/app152211962
Huang Y, Jin Q, Wang B. Efficient Surrogate-Based Optimization of Prefractionation Column Using Self-Adaptive Kriging Model with Modified Firefly Algorithm. Applied Sciences. 2025; 15(22):11962. https://doi.org/10.3390/app152211962
Chicago/Turabian StyleHuang, Yifan, Qibing Jin, and Bin Wang. 2025. "Efficient Surrogate-Based Optimization of Prefractionation Column Using Self-Adaptive Kriging Model with Modified Firefly Algorithm" Applied Sciences 15, no. 22: 11962. https://doi.org/10.3390/app152211962
APA StyleHuang, Y., Jin, Q., & Wang, B. (2025). Efficient Surrogate-Based Optimization of Prefractionation Column Using Self-Adaptive Kriging Model with Modified Firefly Algorithm. Applied Sciences, 15(22), 11962. https://doi.org/10.3390/app152211962






