Three-Phase Powerline Energy Harvesting Circuit with Maximum Power Point Tracking and Cold Start-Up
Abstract
1. Introduction
2. Introduced Energy Harvester
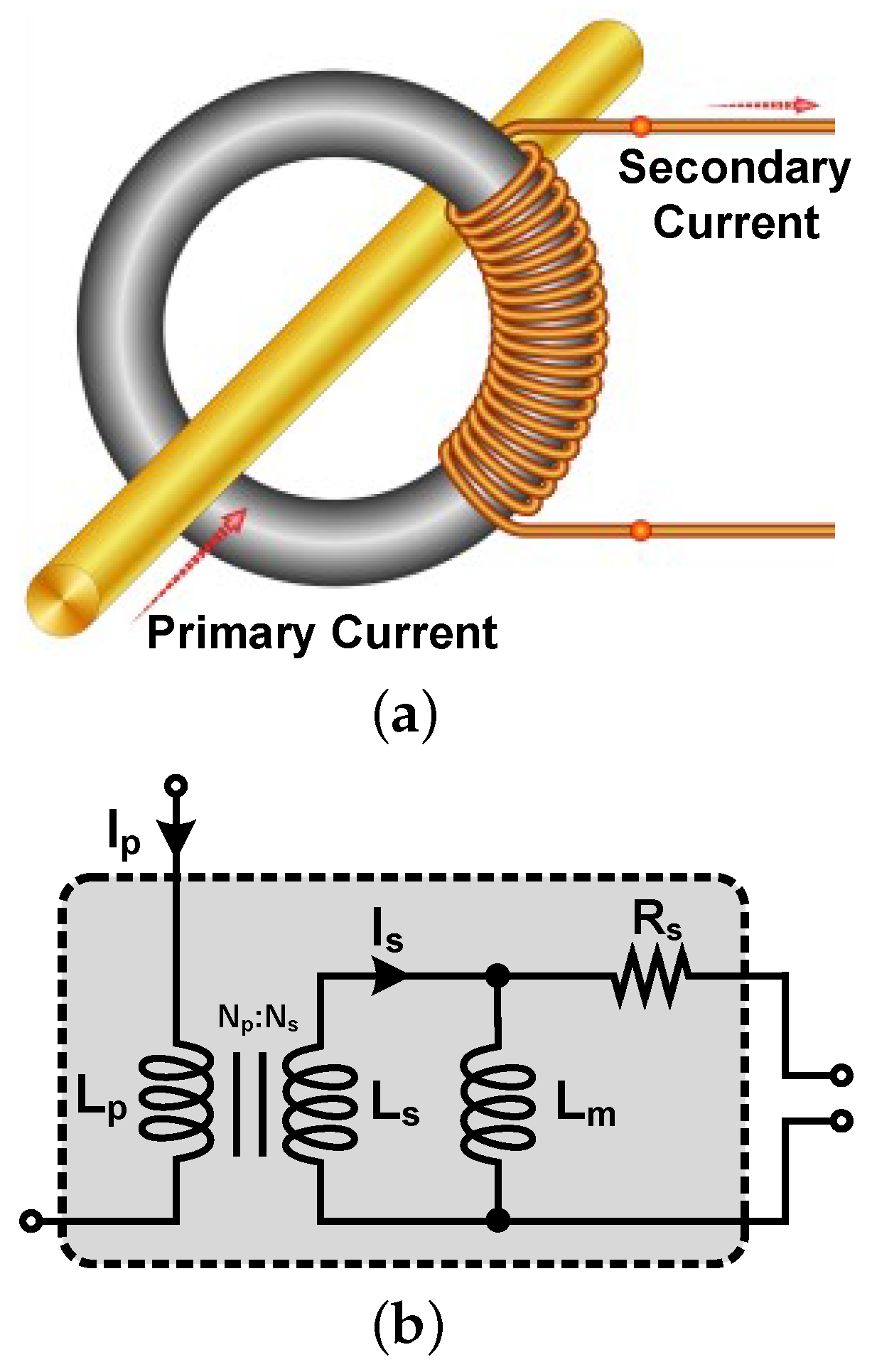
2.1. Single-Phase Energy Harvester
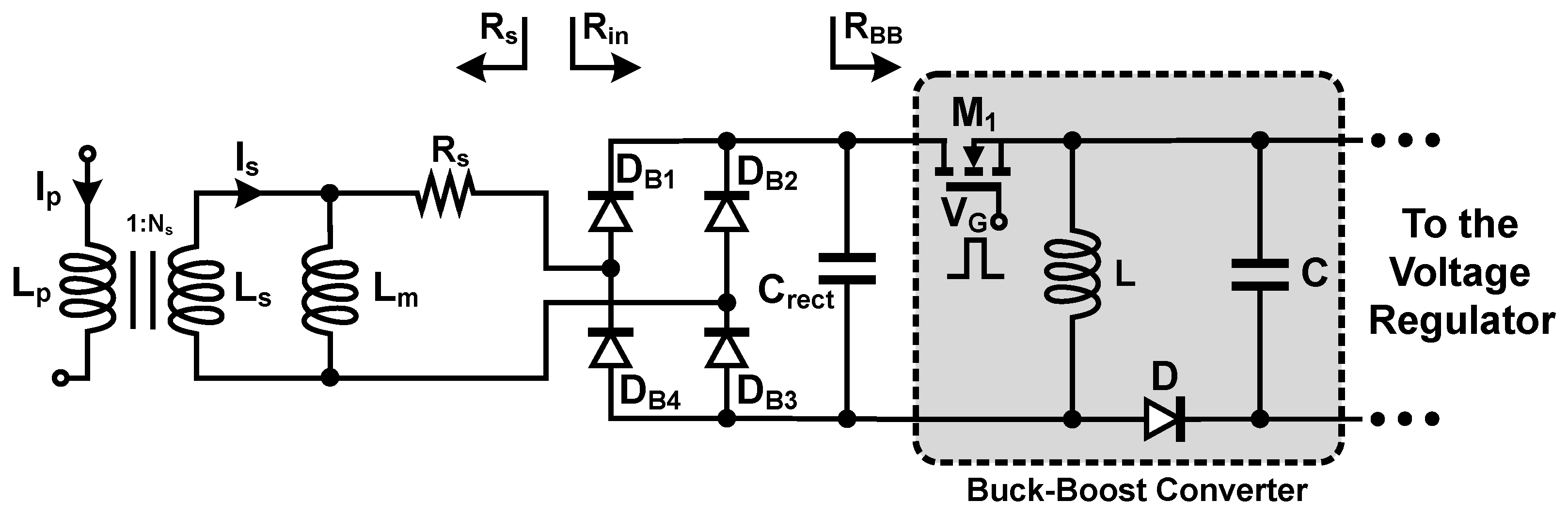
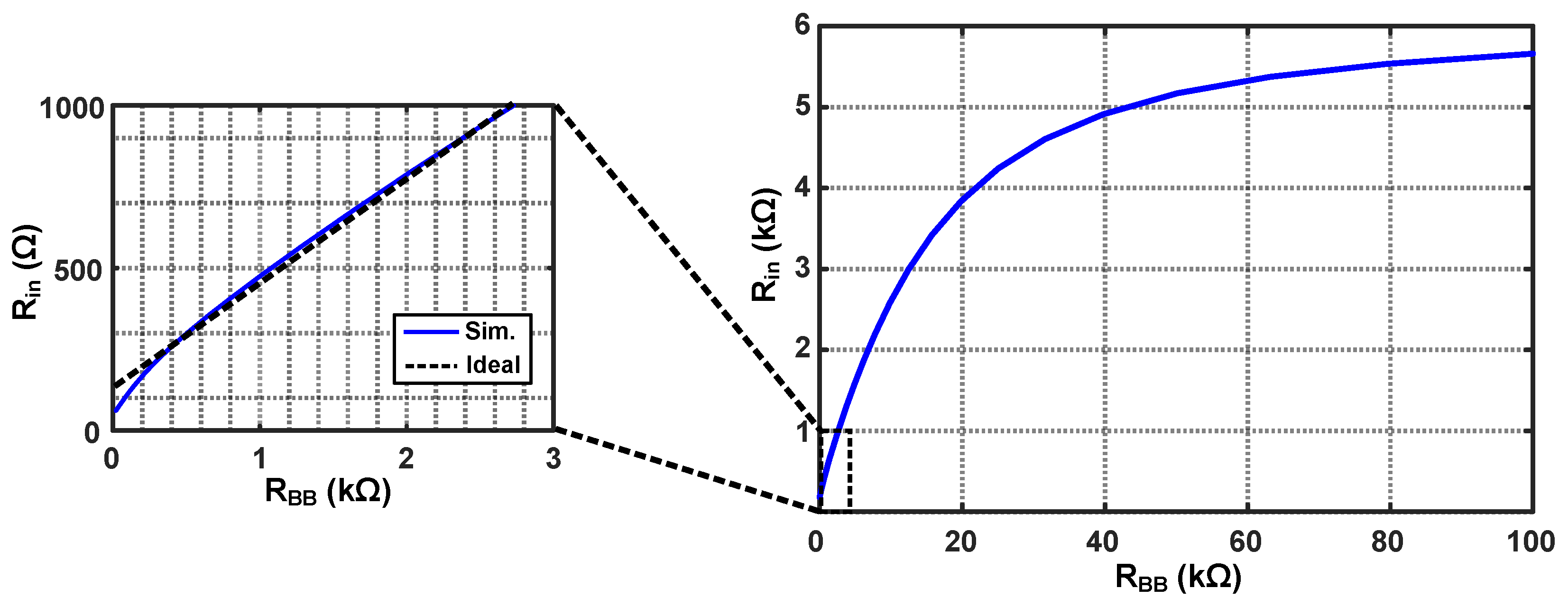
2.1.1. Source Impedance Matching
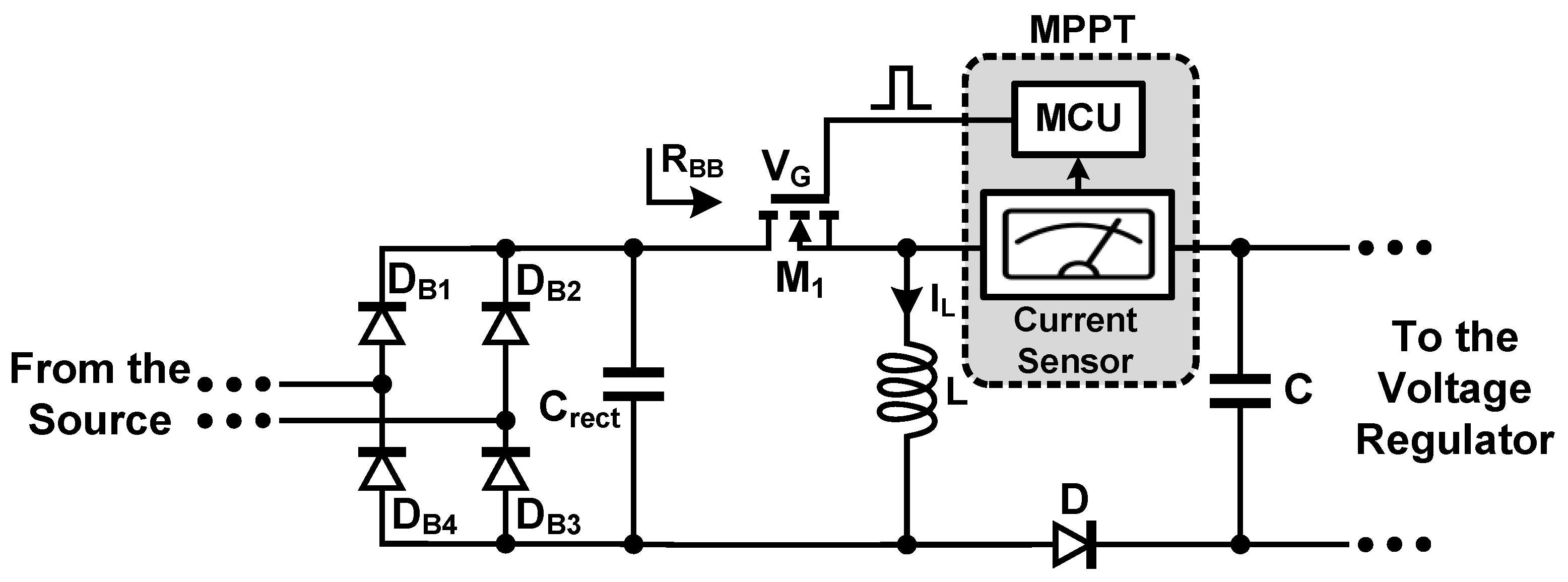
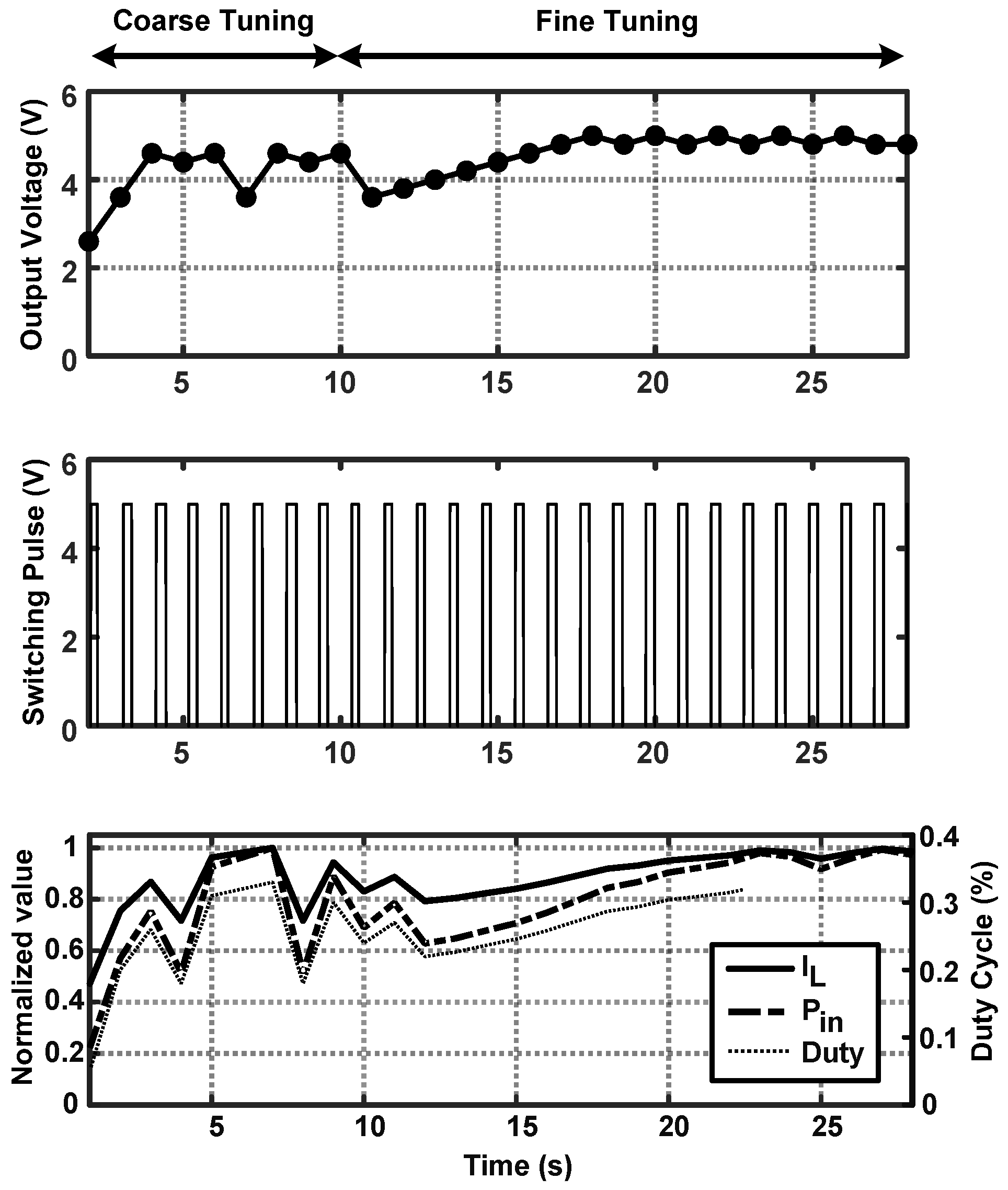
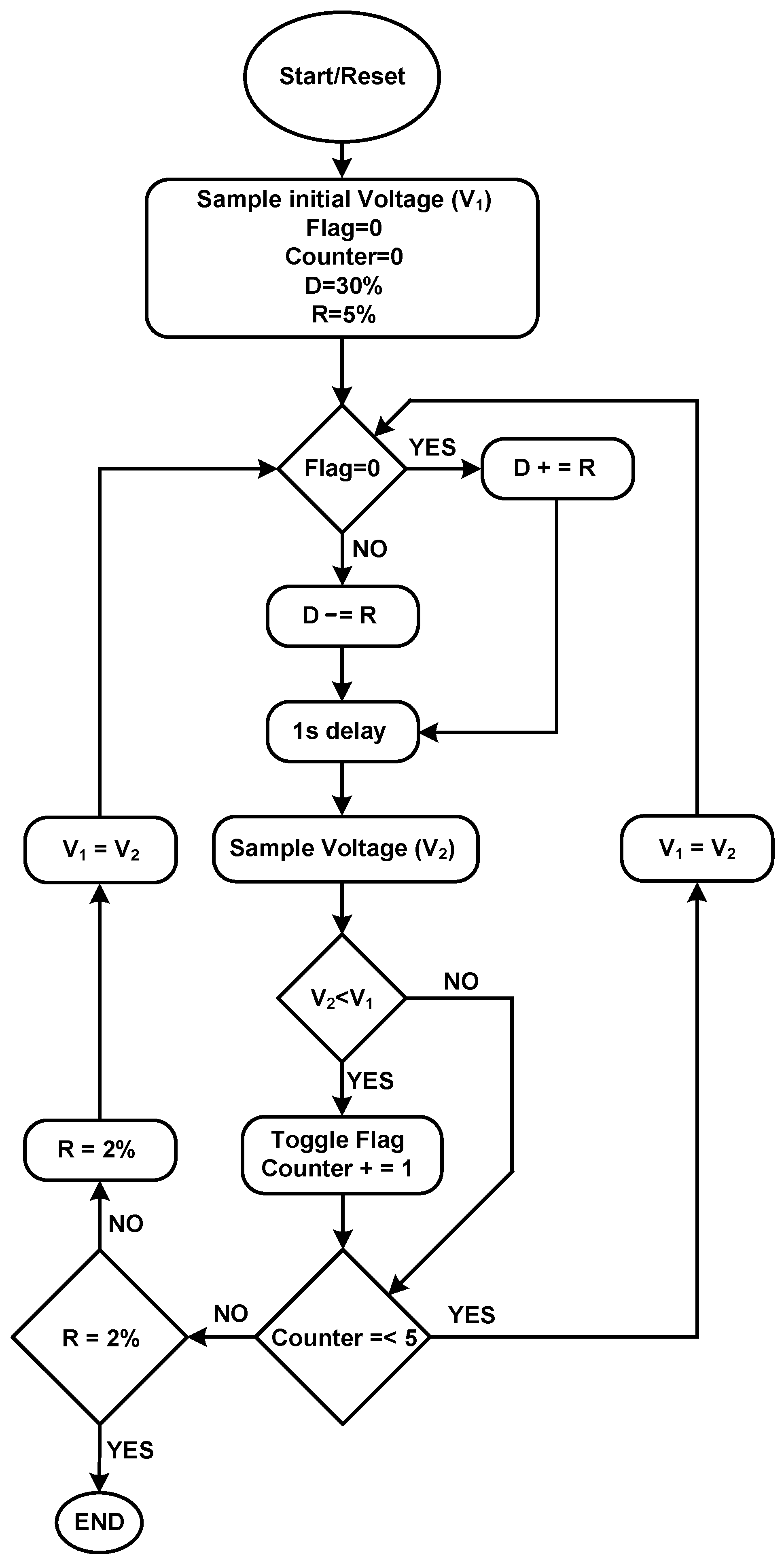
2.1.2. Maximum Power Point Tracking (MPPT)
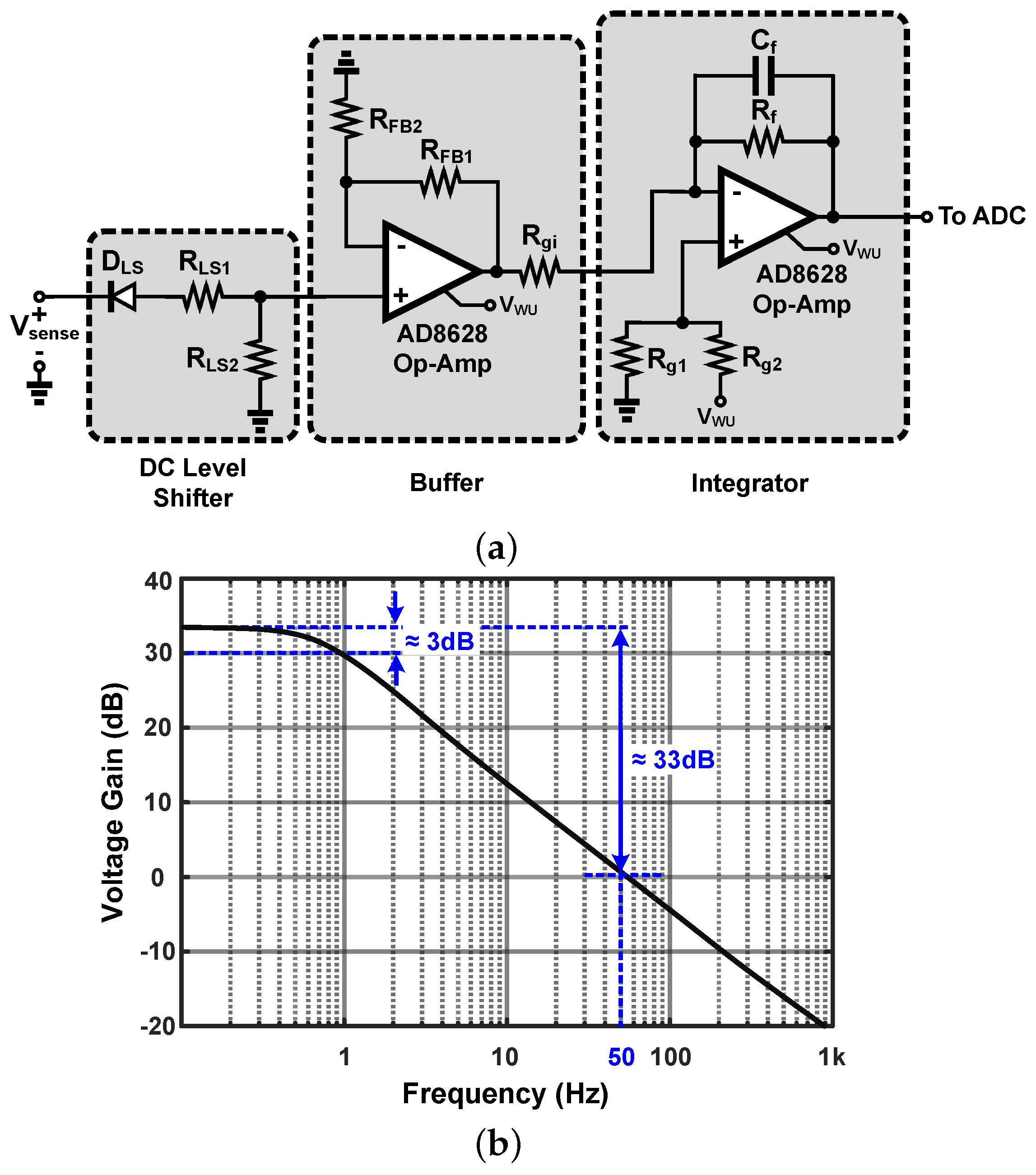
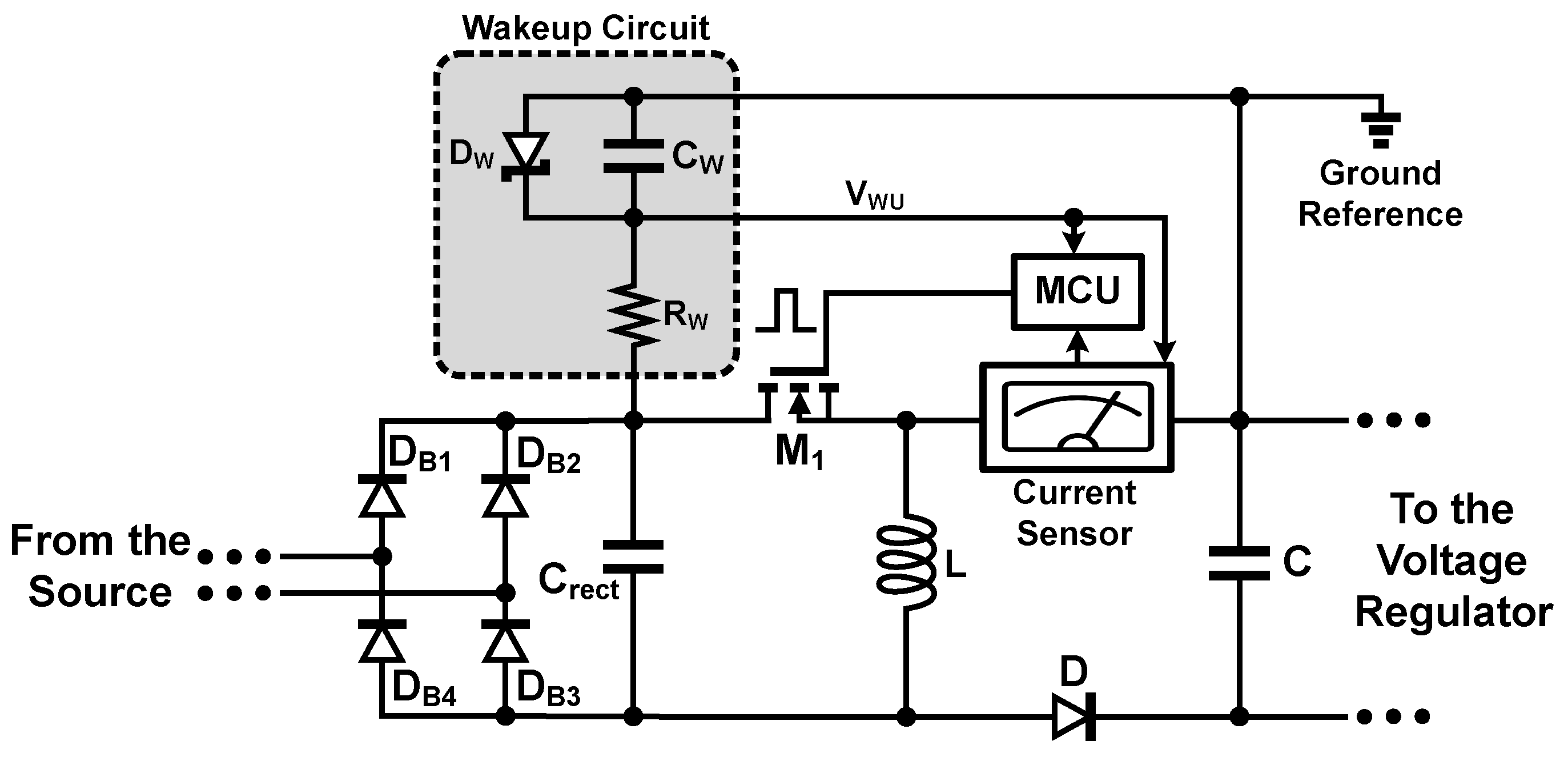
2.1.3. Current Sensor
2.1.4. Cold Start-Up
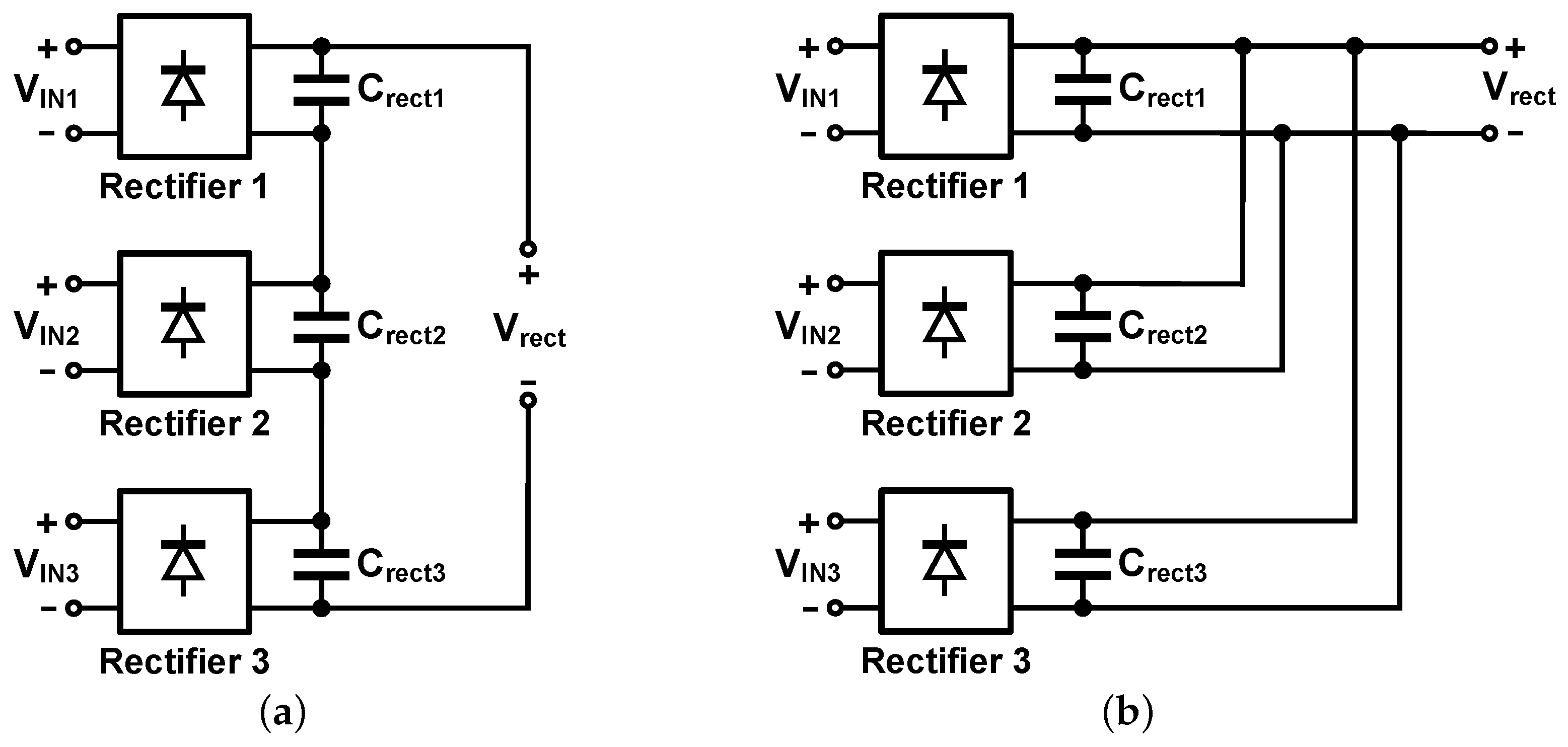
2.2. Extension from Single-Phase Input to Three-Phase Input
3. Measurement Results and Discussion
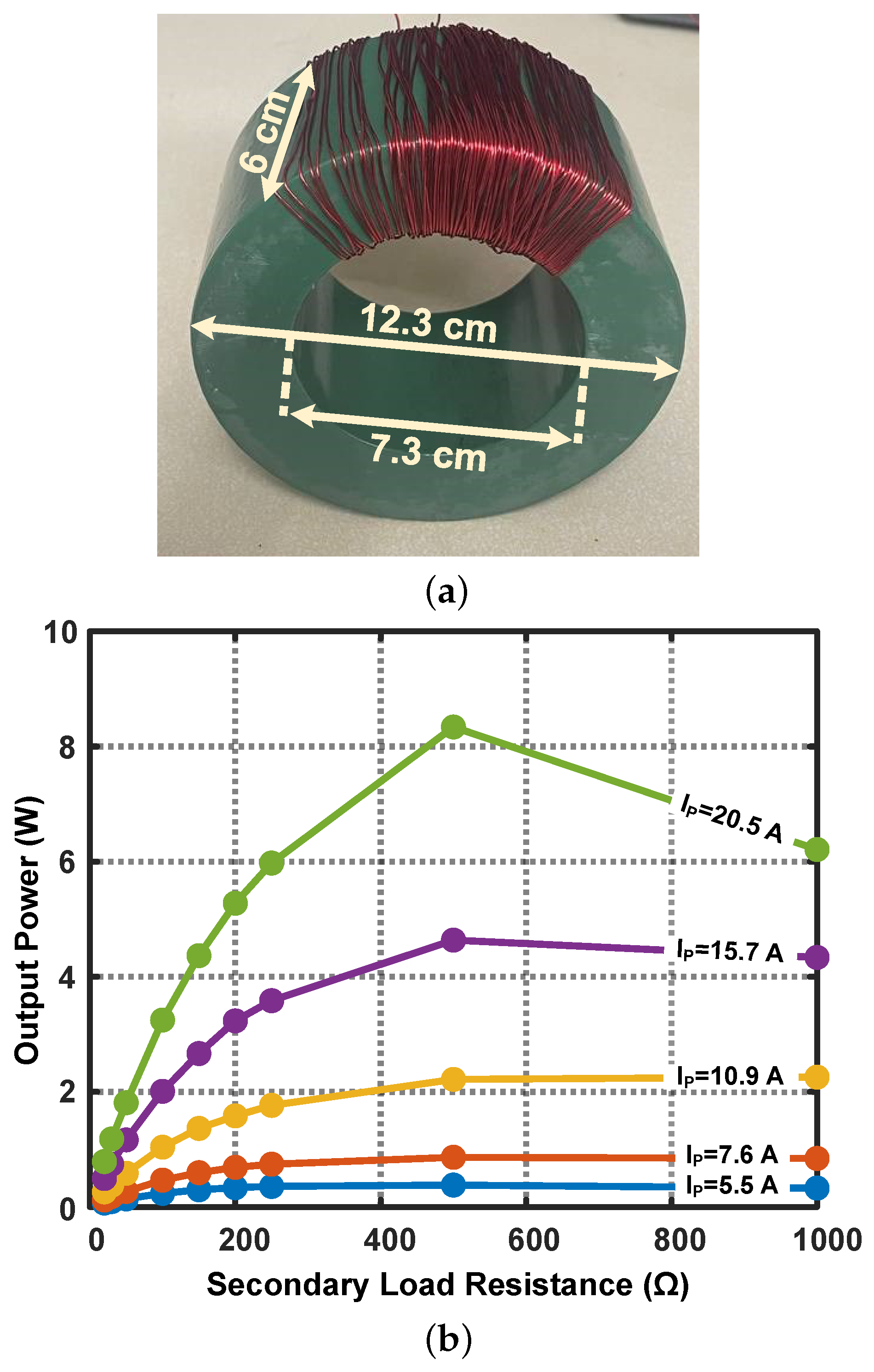
3.1. Magnetic Core
3.2. Current Sensor
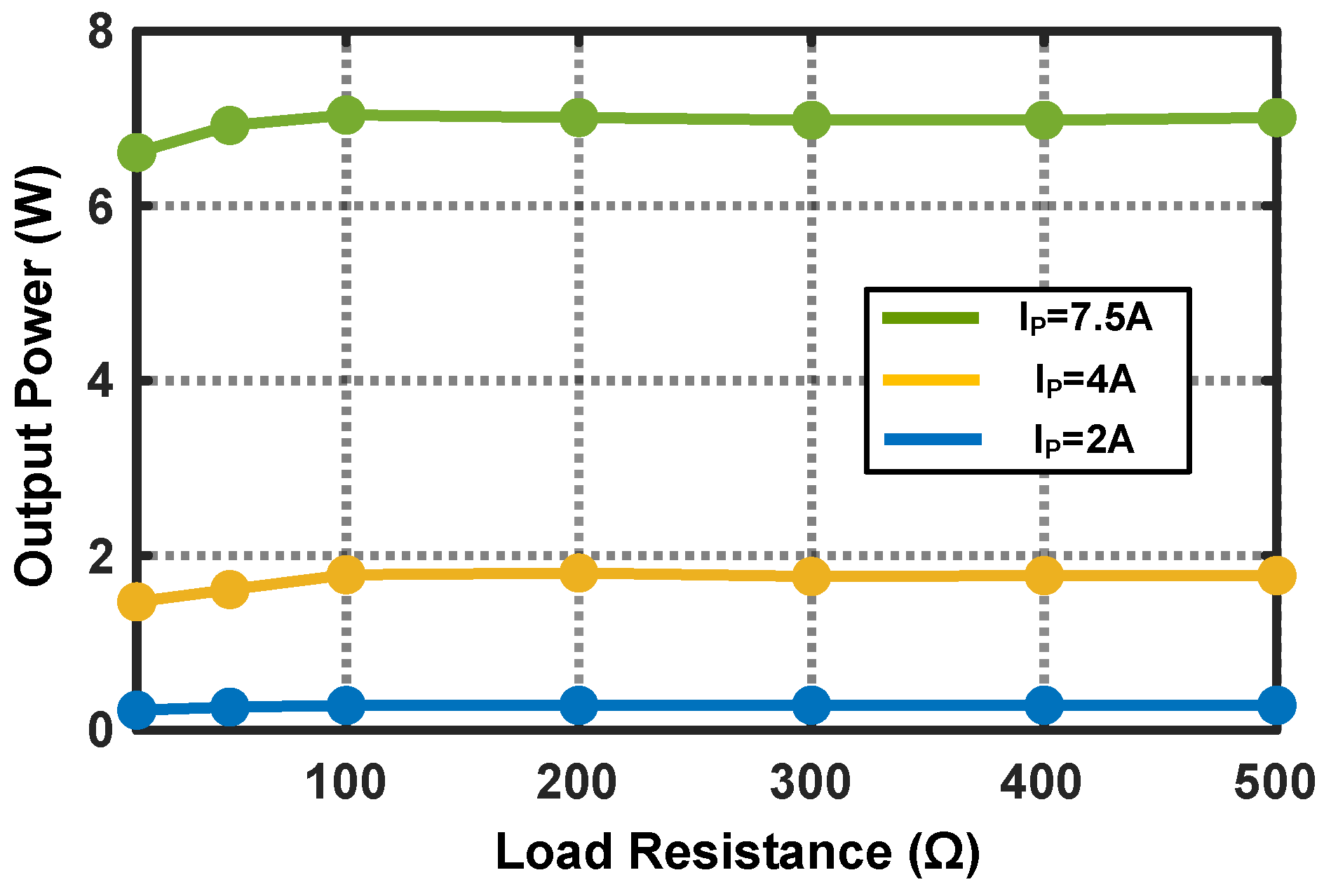
3.3. Three-Phase Energy Harvester
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Williams, A.J.; Torquato, M.F.; Cameron, I.M.; Fahmy, A.A.; Sienz, J. Survey of energy harvesting technologies for wireless sensor networks. IEEE Access 2021, 9, 77493–77510. [Google Scholar] [CrossRef]
- Akin-Ponnle, A.E.; Carvalho, N.B. Energy harvesting mechanisms in a smart city—A review. Smart Cities 2021, 4, 476–498. [Google Scholar] [CrossRef]
- Bhatt, K.; Kumar, S.; Kumar, S.; Sharma, S.; Singh, V. A review on energy harvesting technologies: Comparison between non-conventional and conceptual approaches. Energy Rep. 2024, 12, 4717–4740. [Google Scholar] [CrossRef]
- Sudevalayam, S.; Kulkarni, P. Energy harvesting sensor nodes: Survey and implications. IEEE Commun. Surv. Tutor. 2010, 13, 443–461. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Z.; Ji, J.; Hu, M. Research and application of wireless sensor network technology in power transmission and distribution system. Intell. Converg. Netw. 2020, 1, 199–220. [Google Scholar] [CrossRef]
- Mushtaq, M.U.; Venter, H.S.; Singh, A.; Owais, M. Advances in energy harvesting for sustainable wireless sensor networks: Challenges and opportunities. Hardware 2025, 3, 1. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Greer, J.; Pour, F.L.; Ha, D.S. Powerline Energy Harvesting with Maximum Power Point Tracking for a Wide Current Range. In Proceedings of the 2023 IEEE International Symposium on Circuits and Systems (ISCAS), Monterey, CA, USA, 21–25 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, J.; Kim, J.; Ha, D.S. Powerline energy harvesting circuit with a desaturation controller for a magnetic core. In Proceedings of the IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Lansing, MI, USA, 9–11 August 2021; pp. 220–223. [Google Scholar] [CrossRef]
- Zhuang, Y.; Xu, C.; Yuan, S.; He, C.; Chen, A.; Lee, W.W.; Zhou, J.; Huang, Y. An improved energy harvesting system on power transmission lines. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Li, P.; Wen, Y.; Zhang, Z.; Pan, S. A high-efficiency management circuit using multiwinding upconversion current transformer for power-line energy harvesting. IEEE Trans. Ind. Electron. 2015, 62, 6327–6335. [Google Scholar] [CrossRef]
- Yuan, S.; Huang, Y.; Zhou, J.; Xu, Q.; Song, C.; Thompson, P. Magnetic field energy harvesting under overhead power lines. IEEE Trans. Power Electron. 2015, 30, 6191–6202. [Google Scholar] [CrossRef]
- Wang, W.; Huang, X.; Tan, L.; Guo, J.; Liu, H. Optimization design of an inductive energy harvesting device for wireless power supply system overhead high-voltage power lines. Energies 2016, 9, 242. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X.; Li, J.; Yan, D. A novel electromagnetic energy harvester based on double-ring core for power line energy harvesting. J. Circuits Syst. Comput. 2020, 29, 2050265. [Google Scholar] [CrossRef]
- Xu, C.; Wang, W.; Su, W.; Duan, M.; Hu, M. Anti-saturation and power decoupling control of multiwinding energy harvester based on magnetomotive force compensation. IEEE Trans. Ind. Inf. 2023, 19, 10555–10563. [Google Scholar] [CrossRef]
- Jung, S.; Kim, S.; Cho, W.; Lee, K. Development of highly efficient energy harvester based on magnetic field emanating from a household power line and its autonomous interface electronics. IEEE Sens. J. 2023, 23, 6607–6615. [Google Scholar] [CrossRef]
- Andres, C.; Fritsch, M.; Wolter, M. Inductive energy harvester with saturation-controlled maximum power point tracking. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Seattle, WA, USA, 21–25 July 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Duan, N.; Liu, Z.; Hu, J.; He, Z. Impedance-matching-based maximum power tracking for magnetic field energy harvesters using active rectifiers. IEEE Trans. Ind. Electron. 2022, 70, 10730–10739. [Google Scholar] [CrossRef]
- Yablokov, A.A.; Panashchatenko, A.V.; Tychkin, A.R. Determining the characteristics of current transformers required for correct operation of relay protection devices. In Proceedings of the 6th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 29 February–2 March 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Huang, X.; Wang, H.; Li, Q.; Yang, N.; Ren, T.; Peng, Y.; Li, H. Electrical characteristics of new three-phase traction power supply system for rail transit. Railw. Eng. Sci. 2022, 31, 75–88. [Google Scholar] [CrossRef]
- Kim, J.; Kwon, I. Design of a high-efficiency DC-DC boost converter for RF energy harvesting IoT sensors. Sensors 2022, 22, 10007. [Google Scholar] [CrossRef]
- Kong, N.; Ha, D.S.; Erturk, A.; Inman, D.J. Resistive impedance matching circuit for piezoelectric energy harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1293–1302. [Google Scholar] [CrossRef]
- Pande, J.; Nasikkar, P.; Kotecha, K.; Varadarajan, V. A review of maximum power point tracking algorithms for wind energy conversion systems. J. Mar. Sci. Eng. 2021, 9, 1187. [Google Scholar] [CrossRef]
- Jackson, H.W. Introduction to Electronic Circuits; Prentice-Hall: Englewood Cliffs, NJ, USA, 1959. [Google Scholar]
- Brufau-Penella, J.; Puig-Vidal, M. Piezoelectric energy harvesting improvement with complex conjugate impedance matching. J. Intell. Mater. Syst. Struct. 2009, 20, 597–608. [Google Scholar] [CrossRef]
- De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; de Azevedo e Melo, G.; Canesin, C.A. Evaluation of the main MPPT techniques for photovoltaic applications. IEEE Trans. Ind. Electron. 2012, 60, 1156–1167. [Google Scholar] [CrossRef]
- Shi, X.; Cai, M.; Jiang, Y. Key role of cold-start circuits in low-power energy harvesting systems: A research review. J. Low Power Electron. Appl. 2024, 14, 55. [Google Scholar] [CrossRef]



| Component | Model | Key Parameters |
|---|---|---|
| Schottky Diodes | RB068L150DDTE25 | V @ , A @ V |
| Zener Diode | CZ5338B TR PBFREE | V @ mA, , mA |
| Switching Transistor | IPP110N20NAAKSA1 | mΩ, V @ , |
| MCU | PIC16F15313 | mA @ V, MHz, nA |
| Operational Amplifiers | AD8628 | V @ Hz, dB, mA @ V |
| Voltage Regulators | LM338T | @ , @ V V |
| Wake-up Capacitor | F | |
| Rectifier Capacitor | mF | |
| Output capacitor | C | mF |
| Buck–Boost Inductor | L | H |
| Input Current (A) | Output Power (W) | Efficiency (%) | MOSFET Loss (%) | Rectifier Loss (%) | Control Circuit (%) | Other a (%) |
|---|---|---|---|---|---|---|
| 7.5 | 7.00 | 84.0 | 9.0 | 5.0 | 1.5 | 0.5 |
| 4.0 | 1.80 | 80.0 | 7.0 | 6.0 | 3.5 | 3.5 |
| 2.0 | 0.29 | 74.3 | 5.5 | 6.5 | 7.0 | 6.7 |
| Reference | [7] | [8] | [16] | [17] | This Work |
|---|---|---|---|---|---|
| Scheme | MC 1/Rect./DCM Conv./Output Reg. | MC/Rect./Mag. Desat. | MC/Rect./DC-DC Conv./Output Reg. | MC/Rect./MPPT | MC/Rect./DCM Conv./Output Reg. |
| Impedance Matching | Yes | No | Yes | Yes | Yes |
| Cold Start-up | No | No | No | No | Yes |
| Line Current (RMS) | 20 A | 25 A | 100 A | 80 A | 7.5 A/3-Phases |
| Line Frequency | 60 Hz | 50 Hz | 50 Hz | 50 Hz | 50 Hz |
| Load Voltage or Resistance | 250 | 1.1 kΩ | NA 2 | 800 | 5 V/5.7 V |
| Harvested Power | 7 W | 65 mW | 1 W | 2.5 W | 7 W |
| Efficiency 3 | 70% | 64% | NA | 97.5% | 84% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lohrabi Pour, F.; Hong, S.K.; Lee, J.; Sohani Darban, M.; Kim, J.M.; Ha, D.S. Three-Phase Powerline Energy Harvesting Circuit with Maximum Power Point Tracking and Cold Start-Up. Appl. Sci. 2025, 15, 11954. https://doi.org/10.3390/app152211954
Lohrabi Pour F, Hong SK, Lee J, Sohani Darban M, Kim JM, Ha DS. Three-Phase Powerline Energy Harvesting Circuit with Maximum Power Point Tracking and Cold Start-Up. Applied Sciences. 2025; 15(22):11954. https://doi.org/10.3390/app152211954
Chicago/Turabian StyleLohrabi Pour, Fariborz, Seong Kwang Hong, Jaeyun Lee, Meysam Sohani Darban, Jaehoon Matthias Kim, and Dong Sam Ha. 2025. "Three-Phase Powerline Energy Harvesting Circuit with Maximum Power Point Tracking and Cold Start-Up" Applied Sciences 15, no. 22: 11954. https://doi.org/10.3390/app152211954
APA StyleLohrabi Pour, F., Hong, S. K., Lee, J., Sohani Darban, M., Kim, J. M., & Ha, D. S. (2025). Three-Phase Powerline Energy Harvesting Circuit with Maximum Power Point Tracking and Cold Start-Up. Applied Sciences, 15(22), 11954. https://doi.org/10.3390/app152211954






