Analysis of Wind-Induced Effects and Vibration Control of a Cable-Supported Bridge with a Steel Truss Girder in Strong Marine Wind Environments

Abstract

This study aims to analyze the wind-induced effects and vibration control of a long-span cable-stayed bridge with a steel truss girder under strong marine wind conditions during its maximum single-cantilever state. During the cantilever construction stage of cable-stayed bridges, the reduction in structural stiffness and damping may lead to excessive wind-induced responses, affecting construction accuracy and safety. Focusing on a newly constructed sea-crossing railway cable-stayed bridge with a steel truss girder and a main span of 364 m, this research utilizes field-measured data and finite element simulations to analyze the buffeting responses of the bridge in the maximum single-cantilever state during construction. The vibration suppression effects of different wind-resistant measures are compared, and we propose an economical and efficient vibration mitigation solution. The results indicate that using the turbulent field parameters and unit aerodynamic admittance function recommended in JTG/T 3360-01—2018 Wind-resistant Design Specification for Highway Bridges leads to conservative in predictions regarding the buffeting responses, and this approach can be used in the preliminary design of large-span bridges. The measured turbulent field parameters can effectively estimate the bridge buffeting responses, especially in the transverse direction. Measuring wind speeds at the bridge site is crucial for the rational design and construction of cable-stayed bridges in strong marine wind environments. The effectiveness of vibration reduction decreases in the order of temporary piers, inclined struts, tuned mass dampers, and wind-resistant cables. The inclined strut scheme achieved vibration reductions of 84.45% in the transverse direction and 68.17% in the vertical direction, slightly lower than those of the auxiliary pier scheme (89.04% and 85.47%). However, the installation of temporary piers during the construction of a sea-crossing bridge would significantly increase construction costs, whereas the inclined strut scheme requires only temporary steel structures near the main tower and piers without substantially increasing the construction workload. Therefore, the inclined strut scheme is recommended as an effective and economical vibration control measure for large-span sea-crossing cable-stayed bridges.

1. Introduction

The bridge wind-induced vibrations can be categorized into fluttering, buffeting, galloping, and vortex-induced resonance, in which fluttering and galloping are types of divergent vibrations while buffeting and vortex-induced resonance belong to bounded vibrations [1]. Although buffeting is considered a bounded vibration, its amplitude tends to increase super-linearly with the span of the bridge. During the construction of cable-stayed bridges, where the main girder is often constructed with a cantilever, its structural stiffness is significantly lower than that in the completed bridge state, resulting in lower natural frequencies of vibration and damping ratios. Consequently, the main girder is prone to excessive buffeting displacements and acceleration responses, which can compromise the precise installation of bridge components and the overall construction quality. Since high-speed railway bridges with large spans need to meet rigorous stability requirements for the smooth operation of high-speed trains, it imposes even more rigorous accuracy demands on the installation of steel girder cantilevers during construction. Based on recent studies on the non-stationary and turbulence characteristics of typhoon winds [2,3], wind loads have become a dominant, and in some cases controlling, factor in the structural design and construction of large-span bridges. In marine strong wind environments, bridges are susceptible to wind-induced vibration effects during the maximum cantilever construction stage, which can compromise structural stability and the precision of component installation. Therefore, it is necessary to investigate the wind-induced effects and vibration control of large-span railway bridges during cantilever erection under strong wind conditions.

The wind-induced effects on large-span bridges under wind loading primarily manifest as vibrations in the main girder, which will further change the surrounding flow field and the aerodynamic forces acting on the main girder, thus creating a coupling effect between the wind loading and the structure. When such a coupling effect is weak, the aerodynamic forces acting on the main girder will induce structural bounded vibrations, including buffeting and vortex-induced vibration. Vortex-induced vibration (VIV) is a coupled resonance phenomenon between the wind and the structure, which occurs when the incoming flow causes periodic vortex shedding alternately from both sides of the bridge, forming a Kármán vortex street. When the vortex shedding frequency synchronizes with the natural frequency of the structure, resonance may be excited, as exemplified by the 2020 vortex-induced vibration event of the Humen Bridge in Guangdong, China [4]. Under this synchronization mechanism, once the system enters the so-called “lock-in” region, the vortex shedding frequency becomes governed by the structural vibration rather than by the wind speed, exhibiting the characteristics of self-excited vibration. For vortex-induced vibration effects, it can be effectively suppressed by optimizing the aerodynamic shape of the components’ cross-sections during the bridge’s design. However, for the buffeting induced by pulsating winds, as the bridge’s span increases, the stiffness decreases, especially in areas featuring strong winds such as the areas over the sea and deep-cut valleys. In this sense, the buffeting analysis and vibration control during construction become increasingly prominent.

The key to suppressing wind-induced vibrations lies in: during the design phase, selecting an appropriate bridge structural system and aerodynamic configuration of components based on factors such as the wind environment at the bridge site, bridge type, and span length; when the wind resistance performance of the structure fails to meet the design requirements for the ultimate limit state or serviceability limit state, measures such as optimizing the aerodynamic shape of components, adding aerodynamic measures, installing damping devices, or modifying the structural system or stiffness should be implemented to enhance structural stiffness and damping ratio, thereby reducing wind-induced vibration responses; the selection of wind-induced vibration control measures should comprehensively consider factors such as wind resistance performance, economic efficiency, and durability over the entire life cycle of the bridge. The buffeting analysis methods proposed in References [5,6] have established a framework for the classic frequency domain analysis of wind-induced bridge buffeting. Building upon this framework, References [7,8,9,10] have systematically considered factors such as aerodynamic nonlinearity, structural nonlinearity, and aerodynamic admittance, etc., proposing the time domain analysis methods for buffeting. References [10,11] have conducted studies on buffeting and vibration control during the construction of large-span bridges using diversified methods and mitigation measures. It has been found that cable-stayed bridges exhibit significant buffeting responses during the construction of cantilever, necessitating the implementation of such measures as wind-resistant cables, temporary supports, or tuned mass dampers (TMDs) for vibration reduction.

Although considerable research has been devoted to wind-induced vibrations of completed cable-stayed bridges, studies focusing on construction stages under strong marine wind conditions remain relatively limited. Most current investigations rely on idealized stationary wind field models and often overlook the inherent non-stationary turbulence characteristics of typhoon environments. There is also a notable lack of systematic validation of the effectiveness of wind-induced vibration control measures based on field monitoring data during construction phases. To address these research gaps, this study integrates field monitoring with finite element analysis to investigate the wind-induced responses of a newly constructed sea-crossing cable-stayed railway bridge with a 364 m main steel truss girder span during its maximum single-cantilever state in the construction phase. The effectiveness of various wind-resistant measures in suppressing wind-induced vibrations is comprehensively compared, providing critical references for formulating vibration mitigation strategies for long-span railway bridges in strong marine wind environments.

2. Project Background

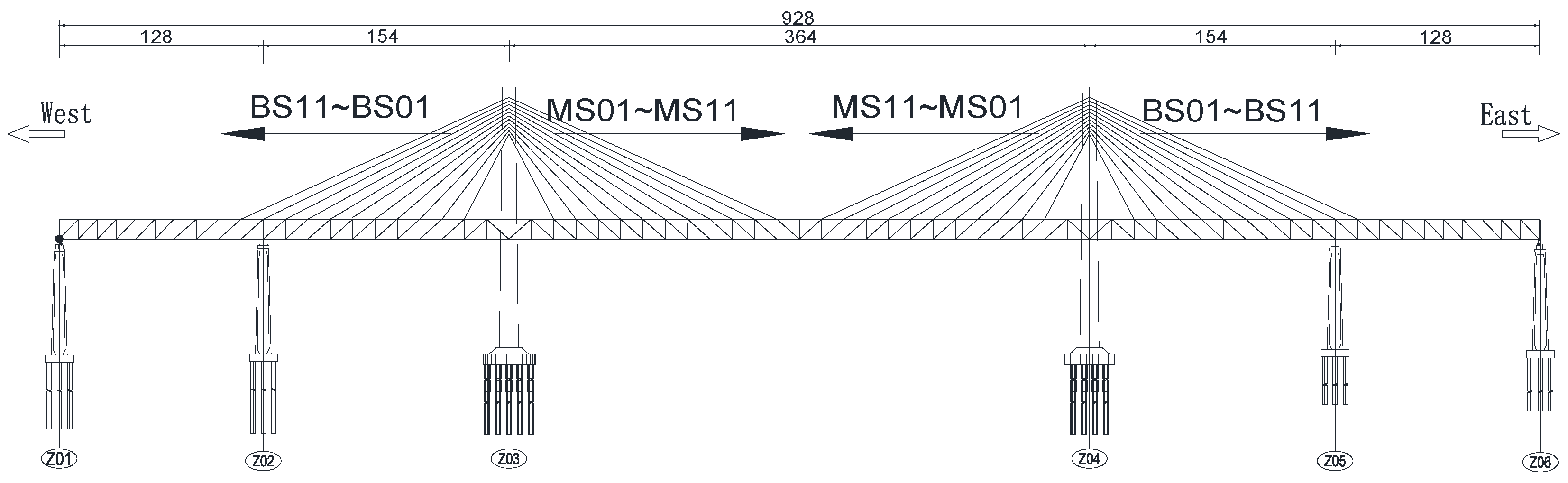
The Pingtan Straits Rail-cum-Road Bridge is a crucial control project connecting the Fuzhou-to-Pingtan Railway and the Changle-to-Pingtan Expressway. It serves as an extension of the Hefei-Fuzhou Railway and an essential component of the Beijing-Fuzhou transportation corridor. It acts as a rapid passage linking Changle’s sub-center city to the Pingtan Comprehensive Experimental Zone. With a total length of 16.34 km, the railway portion was designed to meet the standards of a double-track Grade I railway with a speed of 200 km/h, while the highway portion was designed as a six-lane expressway with a speed of 100 km/h. It is the world’s longest and also China’s first rail-cum-road bridge over the strait.

This bridge is located at the northern entrance of Haitan Strait, characterized by pronounced monsoon features and high extreme wind speeds, representing a typical strong wind marine environment. The proportions of days with strong winds above Level 6 (10.8 m/s) based on daily maximum wind speed (10 min interval) and daily extreme wind speed (3 s interval) were 40% and 62%, respectively. Due to the influence of a tropical depression near the bridge site on 24 August 2018, the monthly maximum wind speed (10 min interval) and extreme wind speed (3 s interval) reached as high as 16.71 m/s and 24.52 m/s, respectively. The strong wind contains significant pulsating wind, which will lead to structural responses such as buffeting in the steel truss girder, thus imposing higher requirements on the wind resistance performance of the structure and the installation accuracy during the erection of the main girder [12,13]. The bridge spans three navigational channels from north to south in order, namely, Yuanhong Channel, Guyu Gate Channel, and Daixiaolian Island Channel. The main bridge over the Guyu Gate Channel adopts a double-tower double-cable-plane steel truss cable-stayed bridge with a main span of 364 m, spanning a total length of 928 m. The bridge span is arranged as (128 + 154 + 364 + 154 + 128) meters, respectively, as shown in Figure 1.

The main girder adopts a plate–truss composite steel truss girder structure with auxiliary trusses. The upper and lower decks are of unequal widths. The center-to-center spacing between the main trusses is 15.0 m, and the distance between the top and bottom centerlines of the upper chord members of the auxiliary trusses is 35.7 m. The truss height is 13.5 m, with panel lengths of 14.0 m and 12.0 m. The main tower adopts an “H”-shaped reinforced concrete structure. For the Z03# main tower, the elevations at the tower top and bottom are +164.0 m and +6.0 m, respectively, with a total height of 158 m. The stay cables are arranged in a spatial double-cable-plane configuration with a fan-shaped layout. The longitudinal and transverse spacings of the cables on the girder are 14.0 m and 35.6 m, respectively, while the vertical and transverse spacings on the tower are 2.5 m and 44.0 m, respectively. The steel truss girder is erected using the cantilever method. After the stay cables are tensioned, the structure reaches the maximum single cantilevered state, as shown in Figure 2.

Wind speed data were measured using WindMaster Pro three-axis ultrasonic anemometers, with their technical specifications detailed in

Table 1. Technical specifications of the WindMaster Pro three-axis ultrasonic anemometer.

Parameter	Measurement Range	Resolution	Accuracy
Wind speed	0–65 m/s	0.01 m/s or 0.001 m/s	±1.5%RMS @ 12 m/s
Wind direction	0–359.9°	1° or 0.1°	2°@ 12 m/s

. During the single cantilever construction stage of the steel truss girder, two WindMaster Pro three-axis ultrasonic anemometers (numbered 001# and 002#) were installed on a vertical pole (length 2.50 m) at the location of the first upper cross-member in the seventh girder segment. The installation site was 83.2 m from Pier Z01# (198.8 m from the main tower Z01#), with an elevation of 76.30 m for the anemometers. Specifically, anemometer 001# was positioned on the right side of the main girder (from Z01# to Z03#), and anemometer 002# was on the left side (from Z01# to Z03#). The detailed arrangement is as shown in Figure 2. For the daily average wind speed and daily maximum wind speed, a step size of 1 min and a time interval of 10 min are used; for the daily extreme wind speed, a step size of 1 s and a time interval of 3 s are used. The wind environment parameters are calculated by performing a sliding average calculation on the wind speed data.

3. Finite Element Model

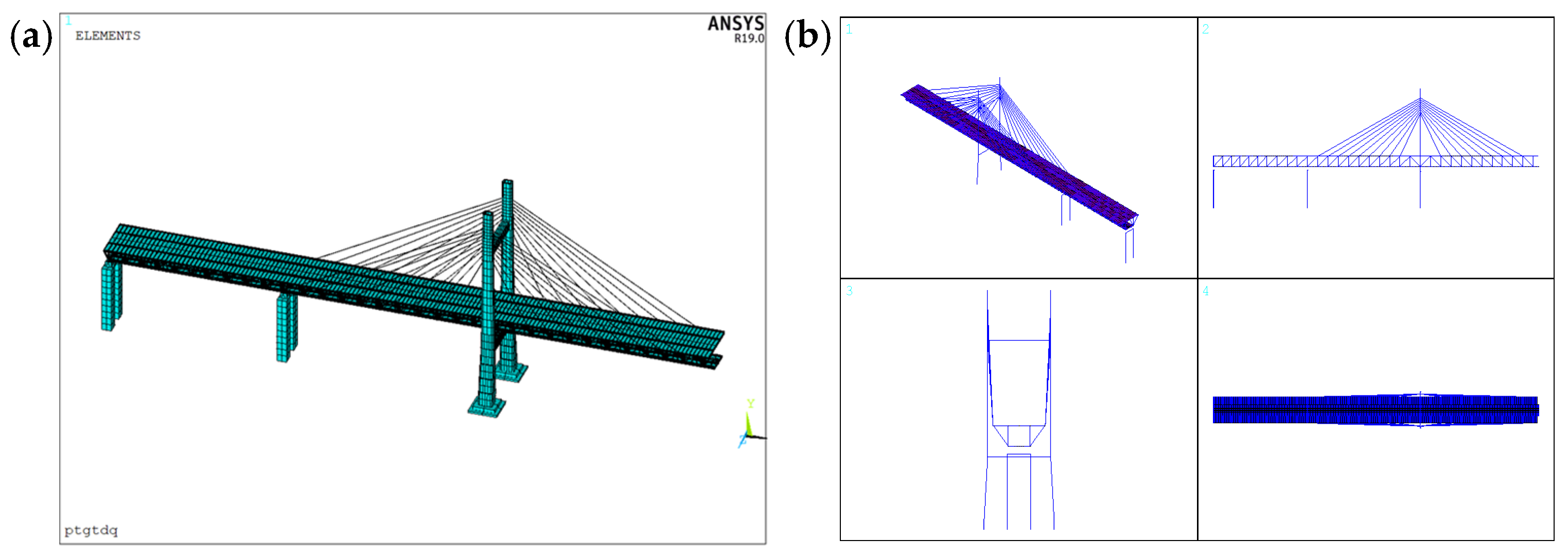
Based on design drawings and field data, a refined finite element model of the Guyu Gate Channel Bridge during the cantilever erection process was established, as shown in Figure 3. The structural dynamic characteristics under wind load in the maximum single-cantilever state of the main girder were calculated and analyzed, providing a foundation for wind-induced vibration analysis. The main girder is a plate-truss combined structure. Considering the influence of the deck slabs on the force distribution of the main truss, BEAM188 beam elements were used to model the plate–truss combined stiffening-girder members, and SHELL63 shell elements were used to model the concrete and steel deck slabs. The towers were modeled with BEAM188 elements and treated as segmented variable cross-sections; the stay cables were modeled with LINK10 elements, with corrections applied to account for the sag effect on the cables’ effective elastic modulus; rigid trans-verse beams were modeled with BEAM4 elements to connect the main truss to the upper and lower deck systems. Considering factors such as bolted and welded Gusset plates, which would increase the weight of the main girder, the density of the main girder steel material has been increased by 15%, resulting in a density of 9027.5 kg/m³ (7850 × 1.15). Element types and material properties used in the finite element model is provided in

Table 2. Material properties and element types of finite element model.

Component	Density/(kg·m−3)	Elasticity Modulus/MPa	Poisson’s Ratio	Finite Element
Main girder	9027.5	2.06 × 105	0.3	BEAM188
Bridge tower	2625	3.45 × 104	0.2	BEAM188
Stayed cable	7850	1.95 × 105	0.3	LINK10
Concrete deck slab	2625	3.55 × 104	0.3	SHELL63
Steel deck slab	7850	2.06 × 105	0.3	SHELL63
Rigid cross girder	0	1.0 × 109	0.3	BEAM4

.

Define the x-axis as the longitudinal direction of the bridge, the y-axis as the transverse direction, and the z-axis as the vertical direction. The main tower, the side piers, and the auxiliary piers are all rigidly supported at their bases. At the main tower, the tower girder constrains the main girder’s linear displacements in the vertical, transverse, and longitudinal directions. In contrast, at the auxiliary piers and side piers, the tower girder constrains the main girder’s linear displacements in the vertical and transverse directions.

The bridge adopts the cantilever construction method, with its maximum single-cantilever state serving as a critical construction phase, corresponding to the structural stress system upon completion of the unilateral cantilever hoisting of the steel truss girder. Dynamic characteristic analysis reveals that under this state, the first three vibration modes of the structure are, in order, lateral bending of the bridge tower (0.4769 Hz), first-order vertical bending of the main girder (0.4776 Hz), and first-order lateral bending of the main girder (0.5426 Hz), as illustrated in

Table 3. Dynamic characteristic analysis of the Guyu Gate Channel Bridge.

Mode	Frequency (Hz)	Mode of Vibration
1	0.4769	Lateral bending of the bridge tower
2	0.4776	First-order vertical bending of the main girder
3	0.5426	First-order lateral bending of the main girder
4	0.8772	Second-order vertical bending of the main girder
5	1.0132	Lateral bending of the side span
6	1.1017	First-order torsion of the main girder

. These modal characteristics provide a reliable theoretical foundation for buffeting response analysis and vibration control during the construction stage of the bridge in strong marine wind environments.

4. Impacts of Strong Marine Wind on the Construction of Cable-Stayed Bridges with a Steel Truss Girder

The serviceability criteria for displacement and deformation under wind load (e.g., peak acceleration ≤ 1.1 m/s², Dickmann indicator K < 10, etc.) serve as the cornerstone for ensuring the safety, comfort, and durability of railway bridges. To this end, in-depth research is required on the structural response under natural wind action, where internal forces primarily comprise two components: the static response induced by the mean wind component and the buffeting response triggered by the fluctuating wind component. To quantify the impact of mean wind on the construction of railway steel truss girder cable-stayed bridges in strong marine wind environments, static wind loads are applied to the model in combination with measured data. This analysis examines the structural displacement, internal force distribution, and variations in stay cable tension caused by mean wind, thereby providing a basis for design control.

4.1. Static Wind Load

Under the action of static wind loads, the static wind resistance force (F_H), the lift force (F_V), and the torsional moment (M) per unit length of the bridge section are represented as follows [14]:

$$F_H={\displaystyle \frac{1}{2}}\rho U^{2}H{C}_H$$

(1)

$$F_V={\displaystyle \frac{1}{2}}\rho U^{2}B{C}_V$$

(2)

$$M={\displaystyle \frac{1}{2}}\rho U^2{B}^2{C}_M$$

(3)

where ρ represents the air density (taken as 1.225 kg/m³), U denotes the mean wind speed, H stands for the girder height (taken as 15.3 m), B represents the girder width (taken as 36.8 m), and C_H, C_V, and C_M respectively denote the resistance coefficient, the lift coefficient, and the torsional moment coefficient of the main girder, which can be obtained through wind tunnel experiments.

According to the wind tunnel experiment research reports, the main girder’s resistance coefficient, lift coefficient, and moment coefficient are 0.6452, 0.0308, and 0.1065, respectively, at a wind attack angle of 0°. For components such as bridge towers and cables, only the effects of resistance are considered in the calculation. When calculating the wind loads on bridge towers and cables, the wind speed at different heights is considered according to the variation in the wind profile. The resistance coefficient C_D is taken from the value specified in JTG/T 3360-01—2018 [15] Wind-resistant Design Specification for Highway Bridges [16], that is,

$$F_D={\displaystyle \frac{1}{2}}\rho U^{2}D{C}_D$$

(4)

where F_D refers to the wind loads in the horizontal direction and D refers to the pillar width or the cable’s outer diameter.

4.2. Displacement Response Under Wind Loads

Based on the aerodynamic parameters obtained from wind tunnel tests, the static wind load is calculated, and the structural displacement caused by the average wind is studied [17]. During the construction of the Guyu Gate Channel Bridge in the maximum single-cantilever state, under the condition of a designed wind speed of 51.4 m/s and a current wind attack angle of 0°, the static wind displacements at the cantilever end of the main girder and the top of the bridge tower are listed in

Table 4. Static wind displacement of the main section (mm).

Section Location	Longitudinal Displacement	Vertical Displacement	Lateral Displacement
Mid-span cantilever end	−0.1	5.1	79.7
Tower top on the windward side	3.0	−0.0	68.7
Tower top on the leeward side	0	0.5	68.6

. Under the action of wind in the transverse direction, the vertical and lateral displacements at the cantilever end of the main girder in the maximum single-cantilever state are 5.1 mm and 79.7 mm, respectively. Assuming the resistance coefficients on the windward and leeward sides of the main tower and the main girder are the same, the windward and leeward sides of the main girder experience increased lateral deformation, resulting in lateral displacements much larger than vertical displacements.

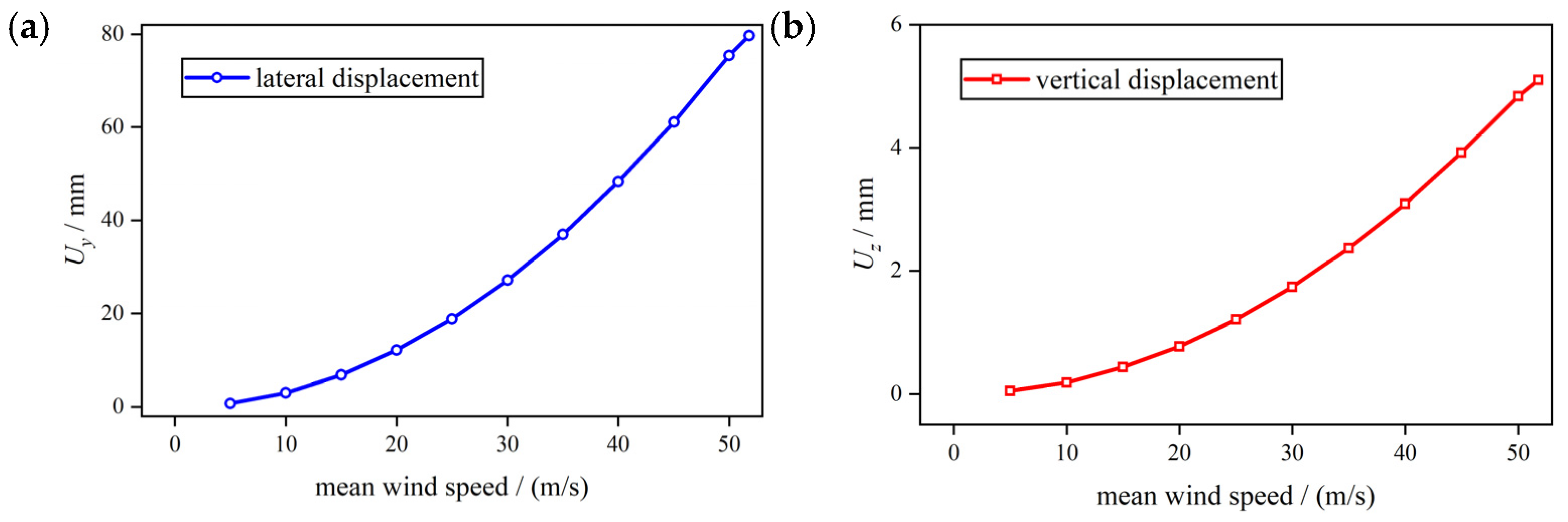
During the construction of railway steel truss cable-stayed bridges, particular attention is paid to the influence of displacements at the cantilever end of the main girder. The static wind displacements of the main span at the cantilever end under wind speeds ranging from 5.0 to 51.4 m/s are depicted in Figure 4. It can be observed that the static wind displacements at the cantilever end of the main girder increase nonlinearly with increasing wind speed, with lateral displacements being predominant. construction activities should be avoided under high wind speed, and combined thermal–wind effects should also be considered for safe erection [18,19].

4.3. Cable Tensions Under Static Wind Loads

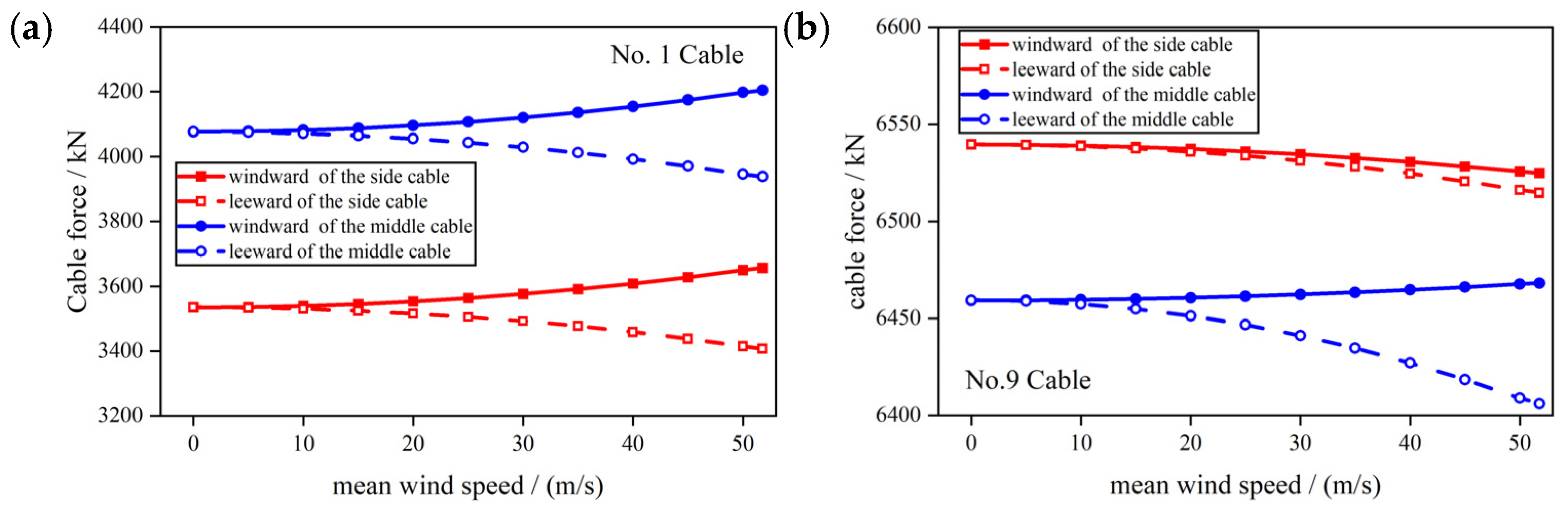
During the construction of steel truss girders, the erection of segments and the tensioning of stay cables can induce stress relaxation in previously tensioned cables, requiring secondary tensioning upon bridge completion to optimize cable forces and align them with design values. However, during the construction phase, variations in cable forces may still result in vertical displacement of the steel truss girder. During the construction of railway cable-stayed bridges, in order to ensure structural safety and control the alignment of the main girder, it is necessary to calculate the cable tensions under average wind loads at each construction stage, as a basis for secondary cable tensioning after closure. The cable tensions under different wind speeds are depicted in Figure 5.

From Figure 5, it can be observed that for stay cables near the main tower (BS01 and MS01) and the middle cable away from the main tower (MS09), the cable tension on the windward side increases with the increase in average wind speed, while the cable tension on the leeward side decreases with the increase in average wind speed. The cable tensions of the lateral cable (BS09) away from the main tower tend to decrease with increasing wind speed, but the magnitude differs between the windward and leeward sides, with a larger magnitude on the leeward side. This phenomenon is related to the aerodynamic torsional moment of the main girder. Therefore, during cable tensioning construction, it is necessary to control the cable tensions near the main tower to prevent excessive variations in tension, which may lead to relaxation. For cables further away from the main tower, where tensions are higher, attention should be paid to ensure tensioning accuracy.

The vibration monitoring system consisted of six 941B vibration pickups arranged in pairs (H and V) at the left side of the main girder cantilever end, specifically at the locations of stay cables #6, #8, and #10 from Z01# to Z03# tower, at distances of 98 m, 126 m, and 154 m from the Z03# main tower, respectively. During data acquisition, construction interferences (such as the movement of beam erection cranes) were excluded, and the raw signals were processed with band-pass filtering (0.25–2 Hz) to ensure data accuracy. When the tensioning of the No. 9 stayed cable at Tower Z03 is completed, the corresponding state is that of the maximum single cantilever. At this point, a comparison can be made between the measured cable tension values and the values obtained from finite element analysis. The measured cable tension corresponds to weather conditions with wind speed at Beaufort scale 8. According to JTG/T 3360-01, the wind speed at a height of 10 m above the ground (U_s10) ranges from 17.2 to 20.7 m/s. On this basis, the designed wind speed (U_sd) for the construction of the main girder can be determined as [20]:

$$U_{sd}=k_{sf}{\left({\displaystyle \frac{Z}{10}}\right)}^{{\alpha }_0}{U}_{s_{10}}$$

(5)

where k_sf represents the wind risk coefficient during construction, which can be obtained based on the reference wind speed at 10 m above the ground and the construction period. For this bridge, it is taken as 0.92; Z denotes the elevation of the main girder.

According to Equation (5), the wind speed at the bridge deck is calculated as 19.72–23.7 m/s. For conservative estimation, the stayed-cable tensions are compared with the measured results at an average wind speed of 25 m/s, as shown in

Table 5. Comparison between stayed-cable tensions and calculated results (kN).

Location	BS09		Error/(%)	MS09		Error/(%)
	Measured Values	Calculated Values		Measured Values	Calculated Values
Windward side	6481	6536.1	0.85	6458	6461.4	0.05
Leeward side	6314	6533.8	3.48	6157	6446.8	4.71

. It can be observed that there are discrepancies between the finite element calculated values and the measured values, with smaller errors on the windward side and larger errors on the leeward side. This is attributed to the susceptibility of the side span’s mid-span and the cantilever end of the main span to construction disturbances, which can affect the vibration and consequently the tension of the stayed cables. Based on field measurements and finite element analysis results, the error in stay cable tensions on the windward and leeward sides during the construction phase should be controlled within 1% and 5%, respectively. In the maximum single-cantilever state, the structural stiffness of the main girder is relatively low. If the cable tension deviation exceeds ±5%, it will have a significant impact on the alignment control of the main girder and structural safety: it may cause changes in the vertical displacement of the main girder, affecting the accuracy and smoothness of the track elevation and requiring adjustments through measures such as secondary tensioning; it can lead to uneven stress distribution in the stay cables, potentially inducing fatigue damage at anchor points or weld cracks, thereby shortening the structural lifespan; the cable tension error can alter the dynamic characteristics of the structure, amplify buffeting effects, and reduce overall stability; and it is detrimental to long-term durability and construction comfort.

5. Buffeting Response Prediction

The primary factor affecting construction safety is the buffeting response at the cantilever end of the steel truss girder induced by fluctuating wind. It is necessary to conduct field measurements of this response and adopt certain vibration control measures to mitigate the buffeting response. Based on field wind data and finite element models, frequency-domain methods (such as the Complete Quadratic Combination, CQC method) are used to calculate displacement and acceleration responses, predicting the buffeting response of the bridge under fluctuating wind.

5.1. Calculation Conditions

The Complete Quadratic Combination (CQC) method [21] was applied to calculate the acceleration response at the cantilever end of the main girder under different wind speeds at the maximum single cantilever stage. According to wind tunnel test data, the first-order derivatives of the resistance, the lift force, and the moment coefficients (C_D’, C_L’, and C_M’) at a wind attack angle of 0° are 0.3266, 4.3144, and 0.6088, respectively. The Oresund Bridge is a long-span cross-sea cable-stayed bridge situated in a strong marine wind environment. It exhibits similar structural dimensions and aerodynamic characteristics to the steel truss girder of the Guyu Gate Channel Bridge [22]. Therefore, in the simulation of self-excited forces, the aerodynamic derivatives in the horizontal direction are calculated based on quasi-steady theory, while those in other directions are adopted from results of analogous bridges (e.g., the Oresund Bridge), ensuring the rationality of the wind-induced vibration response analysis. 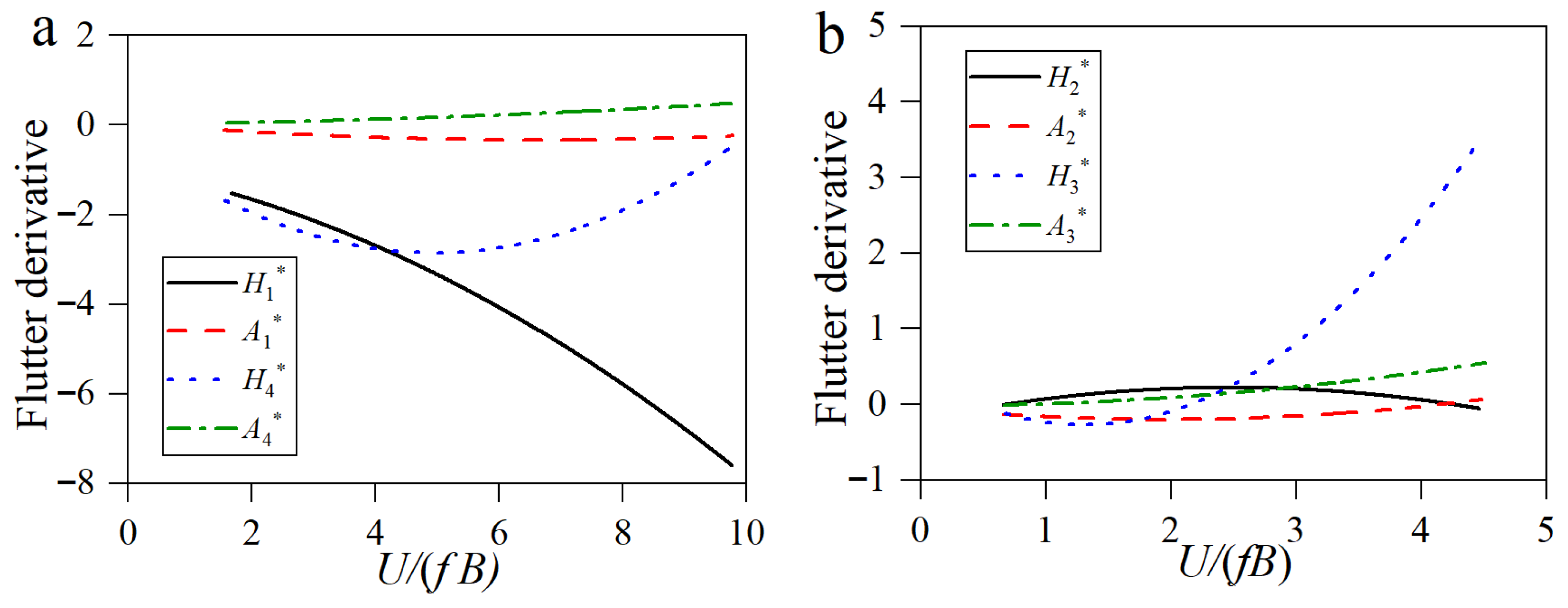The sectional aerodynamic derivatives are presented in Figure 6. In the figure, H_i* and A_i* (i = 1, 2, 3, 4) are the flutter derivatives of the bridge section, all of which are functions of the reduced frequency U/(fB) [21], where f represents the structural vibration frequency of the bridge (Hz), B is the width of the main girder (m), and U is the average wind speed (m/s).

The structural damping ratio was assumed to be 0.005 according to JTG/T 3360-01 for steel truss girder structures. The buffeting response analysis considered the first 10 natural modes, with a frequency interval of approximately 0.001 within the range of 0.001 to 2 H_z. Davenport’s along-wind and vertical turbulence velocity spectra were adopted along with span coherence models, with a decay coefficient assumed to be 7 [23]. The aerodynamic admittance functions of the main girder were assumed to be either 1 (the unit function) or the Sears function.

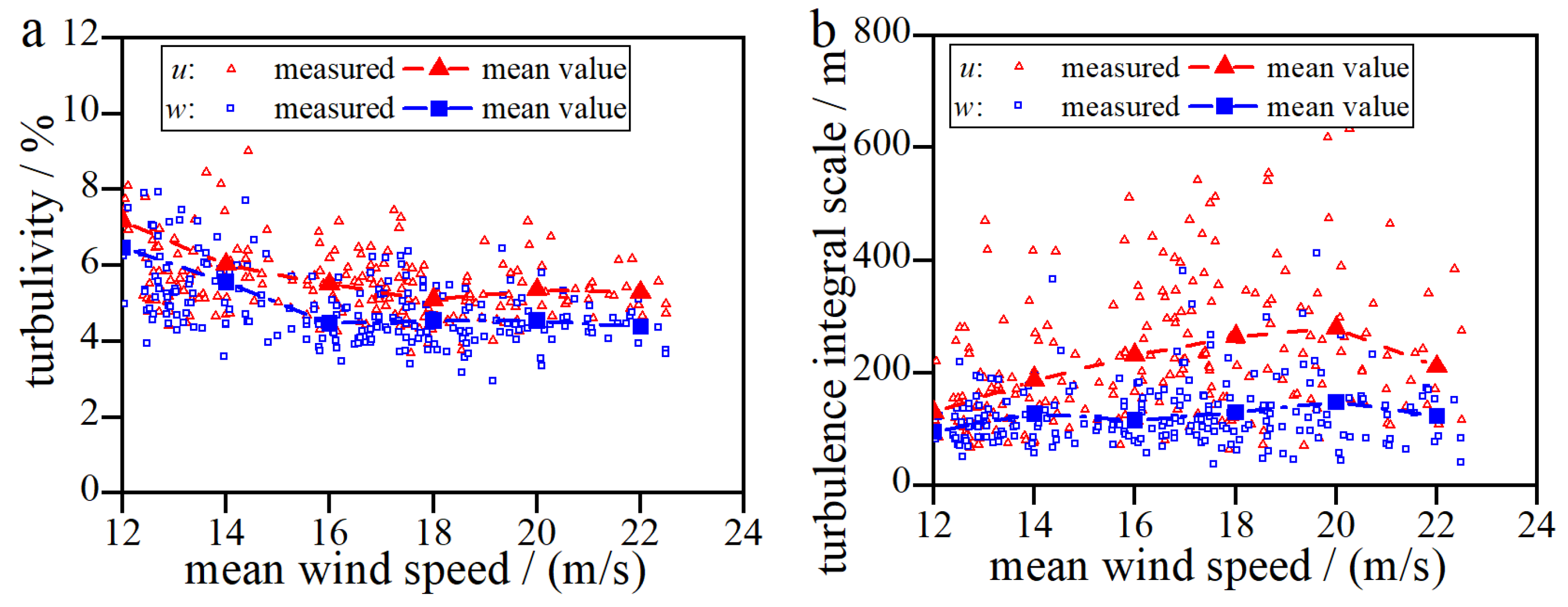
Three scenarios (as shown in

Table 6. Buffeting analysis scenarios.

Scenario	Turbulence Parameters	Aerodynamic Admittance of the Main Girder
1	Wind spectrum, turbulence intensity, and turbulence integral scale specified in JTG/T 3360-01Specification	Unit function
2	Von Karman spectrum along with measured turbulence intensity and turbulence integral scale	Unit function
3	Von Karman spectrum along with measured turbulence intensity and turbulence integral scale	Sears function

) were designed for buffeting analysis. The relationship among the measured along-wind and vertical turbulence intensity, the turbulence integral scale, and the average wind speed is depicted in Figure 7. As shown in Figure 7, the turbulence intensity decreases with increasing average wind speed, while the turbulence integral scale increases with increasing average wind speed, and the growth of the along-wind turbulence integral scale is greater than that of the vertical direction. When the average wind speed is the same, both the along-wind turbulence intensity and the turbulence integral scale are higher than those in the vertical direction. For Scenarios 1 and 2, the turbulence parameters recommended in the Wind-resistant Design Specification for Highway Bridges and those measured at the site were adopted, respectively. In both scenarios, the aerodynamic admittance functions of the main girder adopted the unit function (equal to 1 for the entire frequency range). In Scenario 3, the same turbulence parameters as Scenario 2 were utilized, while the aerodynamic admittance function adopted the Sears empirical function.

5.2. Result Analysis

The comparison between measured and numerical values of buffeting response under Scenario 1 and Scenario 2 is illustrated in Figure 8. The measured standard deviation of acceleration is generally lower than the numerical solutions, suggesting that the results obtained using the specified standard turbulence parameters may overestimate the structural buffeting response. The reliability of buffeting response prediction is highly dependent on the accuracy of turbulence parameters (including turbulence intensity, integral length scale, and spectral energy distribution). Field-measured parameters can significantly improve prediction accuracy. Therefore, in marine wind environments, it is recommended to use measured turbulence parameters for calculating structural buffeting responses to ensure prediction reliability and structural safety, which is consistent with recent findings on non-Gaussian turbulence and typhoon–hurricane field measurements [24,25].

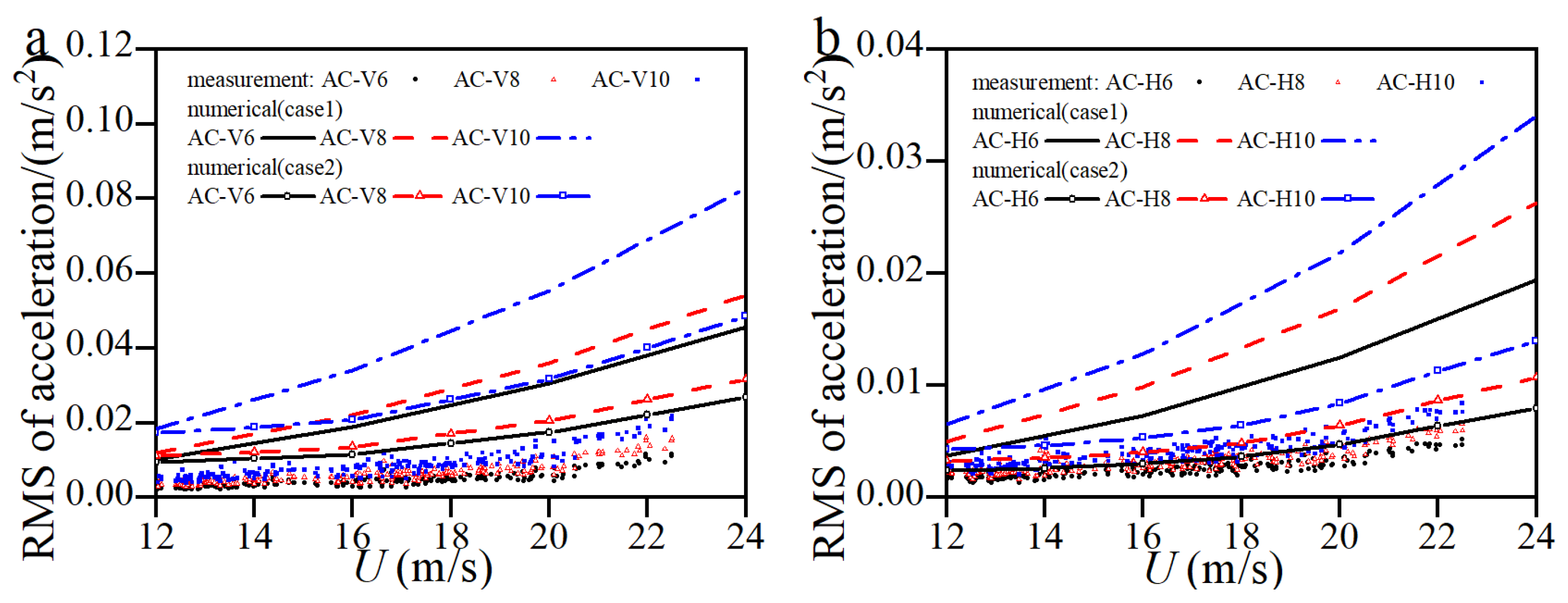
Figure 9 illustrates the standard deviation of acceleration response obtained through field measurements and numerical analysis under Scenario 2 and Scenario 3 conditions. It is observed that the standard deviation of the calculated acceleration based on the Sears aerodynamic admittance is approximately 10–20% lower than the measured values, indicating that using the Sears function may considerably underestimate the buffeting response of the main girder. In contrast, when the aerodynamic admittance is assumed to be a unity function, the numerically predicted buffeting responses agree more closely with the field measurements, particularly in the transverse direction. The discrepancies between the measured and calculated acceleration standard deviations in Working Conditions 2 and 3 are likely attributable to the different forms of aerodynamic admittance adopted for the main girder section. This suggests that wind tunnel tests should be conducted to identify a more appropriate admittance function for the actual girder profile. From the perspective of construction safety, adopting a unity aerodynamic admittance yields a more conservative estimation of vibration levels, thereby reducing the allowable wind speed for lifting and welding operations. In contrast, using the Sears function may overestimate the safe wind speed threshold by approximately 2–3 m/s, which could pose potential risks under strong marine wind conditions. Therefore, the unity admittance is adopted in this study to ensure safety during the cantilever construction stage.

According to Article 6.0.2 and related provisions in GB 50868-2013 Standard for Allowable Vibration of Building Engineering [26], it is stipulated that in vibrating work environments, the vibration limit at which the attention of operators shifts and work efficiency decreases be defined as the fatigue-work efficiency reduction limit, while the vibration limit that maintains the physiological and psychological comfort of the human body be defined as the comfort reduction limit. The vertical and transverse accelerations of the main girder are determined using the 1/3 octave method. The fatigue-work efficiency reduction limits for vertical (112 dB) and horizontal (107 dB) accelerations are considered as the general operation limits for activities such as welding, with an exposure time of 8 h. The comfort reduction limits for vertical (109 dB) and horizontal (104 dB) accelerations, with an exposure time of 2.5 h, are considered special operation limits. Therefore, by inversely deducing the wind speed from the acceleration under buffeting effects, suggested wind speeds that are unsuitable for lifting operations and welding operations are obtained, respectively, as 12.3 m/s and 10.6 m/s.

6. Measures for Vibration Control in the Maximum Single-Cantilever State

The purpose of this chapter is to evaluate and implement effective vibration control measures to suppress the buffeting response of the steel truss girder during the maximum single cantilever construction stage, ensuring structural safety and smooth construction progress. To control the vertical and horizontal buffeting responses at the cantilever end of the Guyu Gate Channel Bridge during the maximum single cantilever construction, four damping measures including the addition of inclined struts, auxiliary piers, temporary wind cables, and Tuned Mass Dampers (TMDs) were analyzed using the buffeting time-domain method. A comparison was also made with the buffeting response of the original structure (without measures). By solving the root mean square values of buffeting responses at the cantilever end of the main girder and the top of the main tower before and after the adoption of damping measures, the effectiveness of different wind-resistant measures in reducing the root mean square of vertical, longitudinal, and transverse buffeting displacements at the cantilever end of the main girder and the top of the tower can be determined. 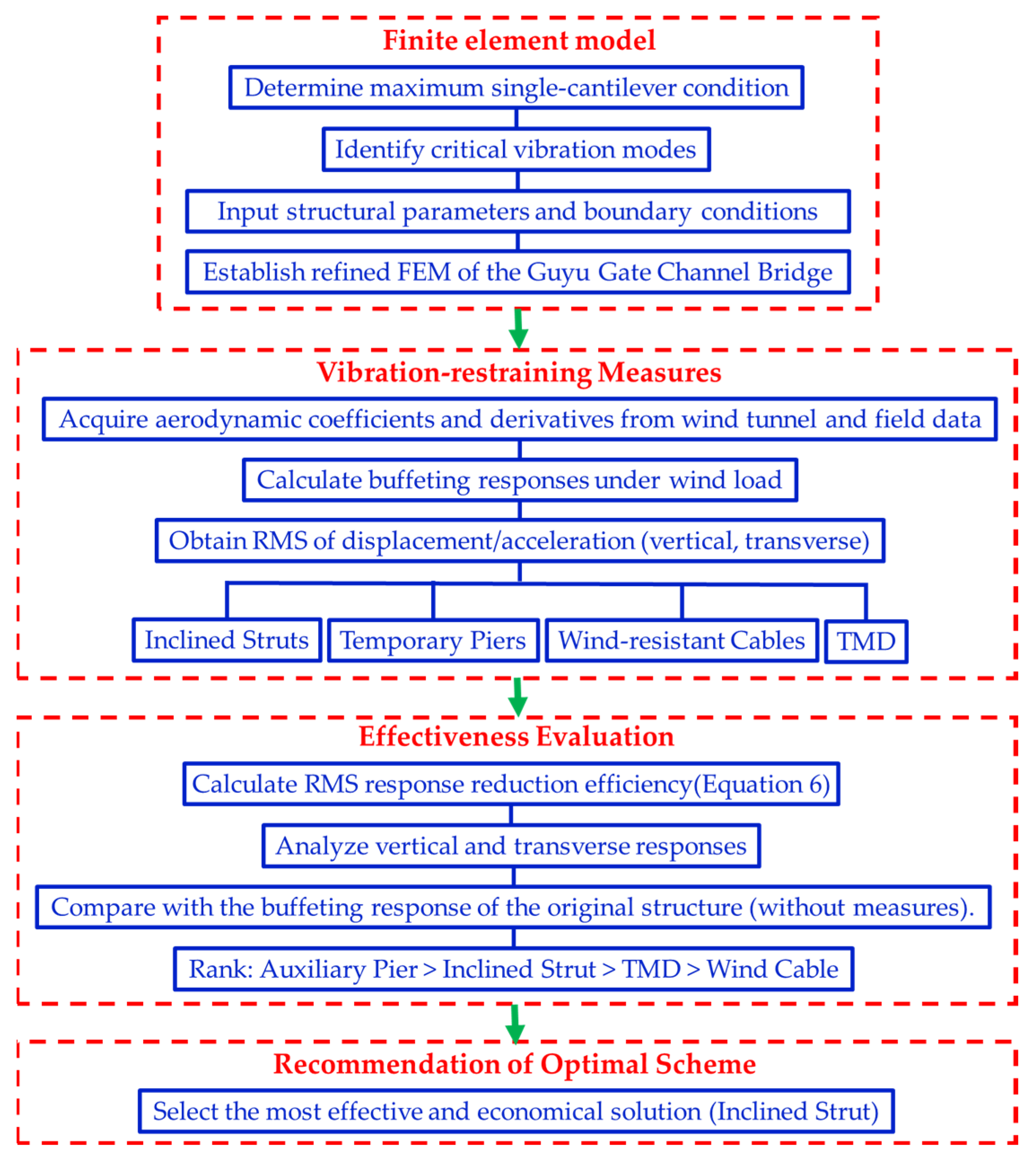Figure 10 is the flow chart of the proposed method in this paper. This has provided a basis for the formulation of buffeting control measures during the construction of large-span cable-stayed bridges across the sea.

6.1. Model Scenarios Without Wind-Resistant Measures

Table 7. Working conditions of wind-resistant measures for the Guyu Gate Channel Bridge in the maximum single-cantilever state.

Scenario	Vibration-Restraining Measures
1	Original structure (without measure)
2	Inclined strut
3	Temporary pier
4	Wind-resistant cable
5	TMD

shows the models and their working conditions of different wind-resistant measures for the Guyu Gate Channel Bridge in the maximum single-cantilever state. It should be noted that in Scenario 2, the inclined strut scheme adopts inclined struts to constrain the degrees of freedom of the abutments, the auxiliary piers, and the main girder at the main tower, firmly securing the inclined struts to the main girder. Moreover, assuming that the inclined struts have very high rigidity, the displacements at the main girder anchorage can be ignored. In Scenario 3, the temporary pier scheme involves setting up a temporary pier at the midpoint of the maximum cantilever end of the main girder, anchoring the main girder to the temporary pier vertically and horizontally. In Scenario 4, the wind-resistant cable scheme uses four symmetrical wind cables connected to both sides of the bridge tower, with one end fixed to the top surface of the main tower pedestal and the other end fixed to the anchorage point of the main girder and the stayed cable. Thus, these wind-resistant cables can be temporarily anchored symmetrically at the No. 4 cable of the main girder, with the main girder’s anchorage point 56 m away from the centerline of the bridge tower, and the angle between the wind-resistant cable and the vertical direction of the main beam being 43.25°. Considering that the steel strand cables have significant damping, 42-strand 15.2 mm steel strand cables (with an area of 5814 mm²) have been applied as wind-resistant cables, with a stress of 150 MPa and a length of 85.78 m. In Scenario 5, the TMD scheme involves the addition of vertical and horizontal TMDs at the cantilever end of the main girder.

Inclined struts were modeled using BEAM188 elements; auxiliary piers adopted the same section properties and material parameters as the side piers; wind-resistant cables were simulated with LINK10 rod elements; the TMD stiffness and damping system was modeled with COMBIN14 elements, and the TMD mass was simulated using MASS21 elements. The finite element model of the Guyu Gate Channel Bridge in the maximum single-cantilever state with these four vibration suppression measures implemented is as shown in Figure 11.

To reasonably obtain a Tuned Mass Damper (TMD) suitable for construction applications, the mass ratio μ is adjusted based on the optimal frequency ratio and optimal damping ratio. Due to the substantial mass of the TMD, employing an excessively large mass ratio μ is not advisable, as it would induce excessive stress at the main girder where the TMD is installed. Therefore, a TMD device with a mass ratio μ of 0.01 is typically utilized. The specific coefficients of the TMD, including stiffness and damping parameters, are detailed in

Table 8. Parameters of TMDs in different directions.

Scenario	Vertical	Horizontal
TMD Mass Ratio	0.01	0.01
TMD Mass (t)	29.21	19.93
$\text{TMD Stiffness }{k}_{\mathrm{T}\mathrm{M}\mathrm{D}}$$/\left({\displaystyle \frac{\mathrm{N}}{\mathrm{m}}}\right)$	282,440	228,075
$\text{TMD Damping }{c}_{\mathrm{T}\mathrm{M}\mathrm{D}}$$/(\mathrm{N}·\mathrm{s}/\mathrm{m}$)	11,063.1	8211.8
$\text{Optimal Frequency Ratio }{\alpha }_{opt}$	0.9901	0.9901
$\text{Optimal Damping Ratio }{\xi }_{opt}$	0.0609	0.0609
$\text{Equivalent Damping Ratio }{\xi }_e$	0.0284	0.0284

.

The analysis of the buffeting response for the original structure of the Guyu Gate Channel Bridge in the maximum single-cantilever state and after implementing various wind-resistant measures indicates that each anti-wind scheme has distinct effects on the structural dynamic characteristics. Specifically, the use of inclined struts increased the natural frequencies of the main tower lateral bending, main girder first vertical bending, and first lateral bending to 0.5051 Hz, 0.9960 Hz, and 1.4110 Hz, respectively, demonstrating that this measure effectively enhances the vertical and lateral stiffness of the main girder. After installing auxiliary piers, the main tower lateral bending frequency rose to 0.4834 Hz, the main girder first vertical bending frequency significantly increased to 1.5556 Hz, and the lateral bending frequency improved to 1.2976 Hz, with a longitudinal floating mode appearing before the vertical bending mode, indicating that auxiliary piers also substantially boost the vertical and lateral stiffness of the main girder. When employing wind-resistant cables, the first ten modal shapes of the structure remained largely unchanged, the main tower lateral bending frequency stabilized at 0.4706 Hz, while the main girder vertical and lateral bending frequencies slightly increased to 0.5041 Hz and 0.5472 Hz, suggesting a moderate improvement in girder stiffness. In contrast, horizontal and vertical Tuned Mass Damper (TMD) measures primarily suppress vibrations by adding mass and increasing the damping ratio, with minimal impact on stiffness; the horizontal TMD barely altered the girder stiffness, and the vertical TMD only slightly raised the vertical bending frequency. Both induced local TMD vibrations before the first lateral bending mode, with frequencies of 0.5168 Hz and 0.4738 Hz, respectively. Overall, the different wind-resistant measures effectively improved the structure’s anti-buffeting performance by either enhancing stiffness or adjusting damping characteristics.

6.2. Vibration Control Analysis

The buffeting response analysis was conducted for the original structure of the Guyu Gate Channel Bridge at its maximum single-cantilever state and for the structure after the adoption of various wind-resistant measures. The analysis considered a wind attack angle of 0° and a wind yaw angle of 0° during the construction of the main girder. Under a wind attack angle of 0°, the static force coefficients and their derivatives for the main girder’s section are as follows: C_D = 0.6452, C_L = 0.0308, C_M = 0.1065, C_D’ = 0.3266, C_L’ = 4.3144, and C_M’ = 0.6088, respectively.

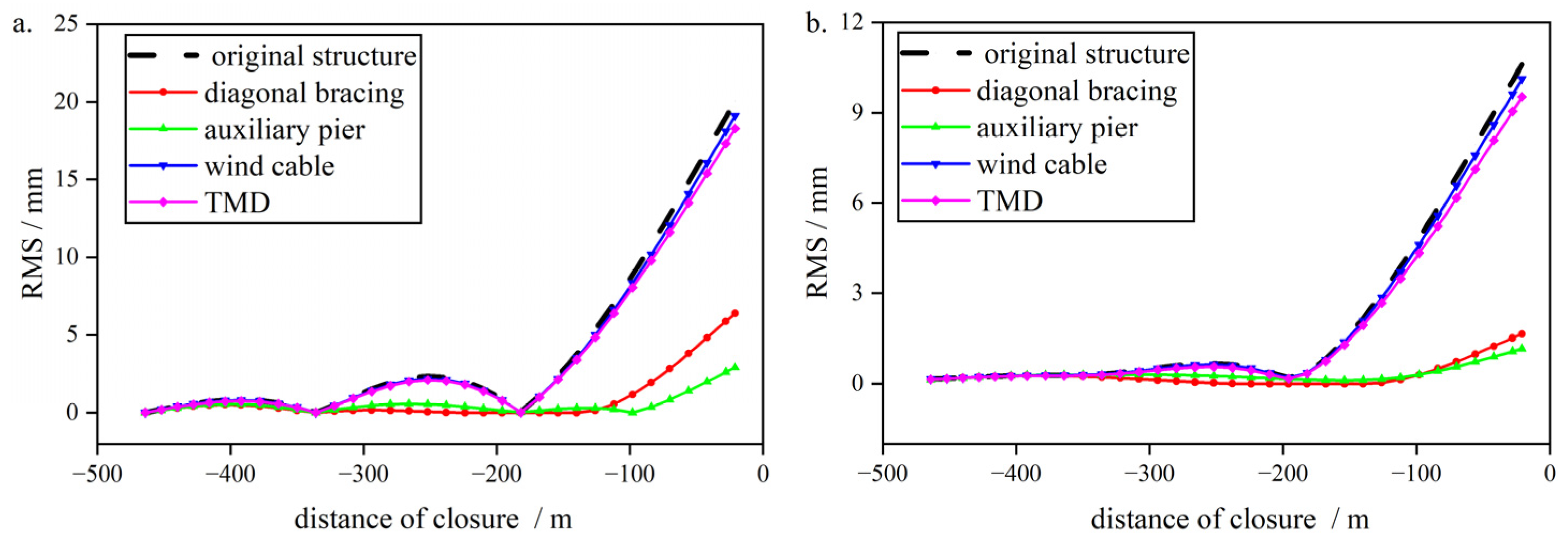
To evaluate the weakening effect of wind-resistant measures on the buffeting response at the cantilever end of the main girder, the RMS statistic in buffeting analysis is adopted to reflect the magnitude of the buffeting displacement response. Here, RMS/mm denotes the root mean square of the buffeting displacement response at the cantilever end (mm), while distance of closure/m indicates the distance from the main girder to the closure point (m). The coupled buffeting analysis was applied to calculate the root mean square (RMS) of the transverse and vertical vibration responses at the cantilever end of the main girder for the five scenarios. To evaluate the damping effect of the Tuned Mass Damper (TMD) scheme, the first 20-order damping ratios involved in the calculation were set as equivalent damping ratios correspondingly.

The RMS values of the vertical and transverse displacements of the main girder under different wind-resistant measures (U = 51.8 m/s) are shown in Figure 12. It can be observed that the adoption of inclined struts and auxiliary piers can effectively reduce the transverse and vertical displacements of the main girder’s cantilever end, while the measures of wind-resistant cables and TMD have shown poorer control effects on the buffeting response.

To further investigate the damping effect of different wind-resistant measures on the buffering response of the main girder, the root mean square (RMS) values of the transverse and vertical displacement buffeting responses of the main girder at the cantilever end were compared, with the results shown in

Table 9. Efficiency of wind-resistant damping measures in the maximum cantilever state.

Condition	RMS transverse/mm	η/%	RMS vertical/mm	η/%
1	10.6		20.1
2	1.6	84.5	6.4	68.2
3	1.2	89.0	3.0	85.5
4	10.1	4.4	19.1	4.7
5	9.5	10.1	18.3	8.9

. Here, η represents the effectiveness of the wind-resistant measures, defined as [27]:

$$\eta ={\displaystyle \frac{{\sigma }_b-{\sigma }_c}{{\sigma }_b}}\times 100\%$$

(6)

where σc refers to the root mean square (RMS) of the vibration response at the main girder’s cantilever end without any damping measures, and σb refers to the RMS of the vibration response at the main girder’s cantilever end with damping measures.

Table 9 indicates that the reduction in vertical and transverse buffeting response at the main girder’s cantilever end is most significant with the use of inclined struts and auxiliary piers, while the damping effect of wind-resistant cables is minimal, which is attributed to the positioning of the wind-resistant cables. In the wind-resistant cable scheme, one end of the cable can only be anchored to the base of the main tower, and the angle with the vertical direction is relatively large, resulting in limited damping effectiveness. The damping effect of the TMD scheme is not very ideal, ranging from 8% to 10%, which is attributed to the structural vibration mode in the maximum cantilever state during construction, where there is no vertical or transverse sway of the main girder, resulting in limited damping effect when the TMD acts on the cantilever end. This highlights the importance of integrating real-time monitoring technologies, such as satellite-based displacement monitoring, to support vibration control and ensure construction safety [28].

Overall speaking, the auxiliary piers have exhibited the best damping efficiency. However, it costs more to construct submerged piers while increasing construction complexity and workload for sea-crossing bridge projects. On the contrary, the inclined strut scheme involves only setting up temporary steel structural inclined struts near the main tower and piers, without significantly increasing construction difficulty or workload. For sea-crossing railway bridges or bridges with even larger spans, the latter scheme stands out.

7. Conclusions

This study integrated high-precision field monitoring data with a refined finite element model to comprehensively investigate the wind-induced responses and vibration control of a steel truss girder cable-stayed bridge during construction in strong marine wind environments. By combining field-measured turbulence parameters with frequency-domain buffeting analysis, the study achieved accurate prediction of wind-induced responses under the most unfavorable single-cantilever state. Numerical models considering various wind-resistant measures, including inclined struts, auxiliary piers, wind-resistant cables, and TMDs, were developed to systematically compare their vibration reduction efficiencies. On this basis, an economical, and effective buffeting control scheme was proposed, providing practical guidance for the wind-resistant design and construction of long-span cross-sea cable-stayed bridges. The main conclusions are as follows:

(1)

The predictions of the buffeting responses based on the recommended turbulence field parameters and unit aerodynamic admittance function specified in (JTG/T 3360-01-2018) Wind-resistant Design Specification for Highway Bridges tend to be conservative, making them suitable for the preliminary design of long-span bridges.

(2)

The measured turbulence field parameters may estimate the bridge buffeting responses well, especially in the transverse direction. Measuring wind speeds at bridge sites is of great significance for the rational design and construction of cable-stayed bridges in strong marine wind environments.

(3)

The vertical and transverse accelerations of the main girder are determined using the 1/3 octave method. The vertical and horizontal limits for on-site welding and other general operations are based on the 8 h fatigue–effectiveness reduction limit, while the vertical and horizontal limits for special operations are based on the 2.5 h comfort–effectiveness reduction limit.

(4)

The damping effects of temporary piers, inclined struts, TMD, and wind-resistant cables decrease in order. Therefore, since the addition of temporary piers during the construction of a sea-crossing bridge significantly increases construction costs, while the inclined strut scheme only requires the installation of temporary steel struts near the main tower and piers without significantly increasing the construction workload, the inclined strut scheme is recommended.

(5)

The limitations of this study mainly stem from the uncertainty of the bridge aerodynamic admittance function, the prediction errors caused by idealized assumptions in the model, and the lack of field validation data for vibration control measures. Future work should involve precise identification of the aerodynamic admittance function through wind tunnel experiments, correction of model parameters, and enhancement of real bridge test validation to optimize the vibration reduction efficiency and design parameters of vibration control measures, and to identify wind-induced vibration reduction measures that are more effective and economical.