Optimal Planning and Investment Return Analysis of Grid-Side Energy Storage System Addressing Multi-Dimensional Grid Security Requirements

Abstract

To address the challenges posed to the secure and reliable operation of the power grid under the “dual-carbon” goals, an optimal planning and investment return analysis method for grid-side energy storage system (GSESS) is proposed, with multi-dimensional grid security requirements being considered. By this method, a decision-making framework for the scientific planning of GSESS is provided, through which both technical and economic viability are balanced. Firstly, an evaluation indicator system for GSESS demand is established, in which loading stress, voltage quality, and renewable energy accommodation capacity are comprehensively considered. The candidate sites are then prioritized by a hybrid subjective-objective weighting method combined with the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS). Subsequently, the top 10% most severe scenarios are identified from historical operational data, and a set of typical extreme scenarios is extracted using an improved K-means clustering algorithm. Based on these scenarios, an optimal capacity planning model incorporating multi-dimensional security constraints is formulated, and the final planning scheme is thereby determined. Furthermore, with the objective of maximizing net revenue from multiple application scenarios, an optimal operational model for GSESS is established. The life-cycle costs and benefits are quantified, and a comprehensive investment return analysis is conducted accordingly. Finally, the proposed methodology is validated through a case study based on the 220 kV substations in QZ City of China. It is demonstrated by the results that through the application of the derived planning scheme, the operational security of the power grid is significantly enhanced, and a promising outlook for investment returns is also exhibited.

1. Introduction

With the deepening implementation of China’s “dual-carbon” strategy, the large-scale integration of clean energy has become a primary direction for the transformation of the nation’s energy structure [1]. However, the inherent intermittency and volatility of such energy sources pose severe challenges to the secure and stable operation of the power grid. These challenges are mainly manifested in altered power flow characteristics, increased difficulty in nodal voltage control, exacerbated system load fluctuations, and insufficient system rotational inertia [2,3]. Against this background, energy storage systems (ESS), by virtue of their flexible and controllable charging and discharging characteristics, have emerged as a critical technology for enhancing the regulation capability and operational stability of the new-type power system [4,5,6]. Consequently, the scientific planning of ESS on the grid side has become particularly important [7].

In recent years, extensive research has been conducted by scholars worldwide on the planning and investment return of the grid-side energy storage system (GSESS). A cloud energy storage configuration method was proposed in [8], which integrates adjustable time-of-use (TOU) pricing with an improved multi-objective optimization algorithm. In [9], demonstration projects in typical Chinese provinces were analyzed, and business models and planning concepts suitable for the corresponding policy environments and application scenarios were proposed. For multi-regional integrated energy systems, a bi-level programming method was employed in [10] to coordinate capacity sharing and benefit allocation among multiple regional ESS. In [11], typical scenarios were extracted through deep clustering, and a joint planning method for long-term and short-term ESS was proposed, which accounted for both long-term energy balancing and short-term power regulation. A bi-level planning model for ESS in hybrid AC/DC distribution networks was presented in [12], where a flexibility evaluation index was constructed, and the siting and sizing of ESS were realized using a combination of K-means and genetic algorithms. The Markov fault transmission model was introduced in [13] to quantify the resilience enhancement benefits provided by ESS in extreme scenarios, thereby effectively strengthening system resilience. In [14], a three-stage collaborative planning model for source-grid-load-storage, which included mobile ESS from electric vehicles, was put forward. A siting and sizing model for grid-side ESS based on a bi-level optimization framework was proposed in [15], where market arbitrage, ancillary services, life-cycle costs, and grid losses were comprehensively considered. In [16], a three-stage stochastic programming model from microgrid to main grid was constructed, integrating Vehicle-to-Grid (V2G) and ESS to improve voltage quality and optimize network congestion control. The cost composition of user-side ESS was quantified in [17], and effective cost reduction paths were identified. It was found in [18] that centralized, independently shared ESS offers greater cost advantages. The impact of tariff mechanisms on ESS costs was investigated in [19]. A method for evaluating the optimal investment scale and profitability of shared ESS was explored in [20]. Through a comparative analysis of revenue results from various models, it was found in [21] that higher returns can be obtained from either combined frequency regulation and peak shaving services or direct participation in frequency regulation markets. It was pointed out in [22] that security assurance fees should also be regarded as a significant cost component for investors.

Nevertheless, certain gaps can be identified in the existing literature. Firstly, most planning methodologies are formulated with a focus on a single or a limited set of technical objectives. As a result, the complex operational requirements of the power grid, which span multiple dimensions including security, stability, and economy, cannot be fully addressed. Secondly, the cost–benefit analysis in the majority of studies is often limited to simplified static estimations. The investment return of a proposed scheme under realistic market conditions is not typically validated through detailed operational simulations, leading to a lack of robust data support for the economic feasibility of the planning schemes.

Therefore, an optimal planning and investment return analysis method for grid-side ESS is proposed in this paper to address the multi-dimensional security requirements of the power grid. Firstly, a comprehensive demand indicator system is constructed, encompassing load rate, voltage quality, and renewable energy accommodation capacity. The candidate sites are then prioritized by a hybrid subjective-objective weighting method and the Technique for Order of Preference by Similarity to an Ideal Solution (TOPSIS). Subsequently, based on typical severe scenarios obtained through screening and clustering, an optimal capacity planning model that incorporates multi-dimensional security indicator constraints is established to determine the planning scheme. Finally, an operational model for GSESS is established with the objective of maximizing net revenue. The costs and benefits of the ESS under multiple application scenarios are quantified, and its investment return is comprehensively analyzed to provide a decision-support framework for ESS planning that balances both technical effectiveness and economic feasibility.

2. Priority Evaluation Method for Grid-Side Energy Storage System Demand

2.1. Evaluation Indicator System for Grid-Side Energy Storage System Demand

To facilitate a comprehensive evaluation of the priority of GSESS demand at substations, a multi-dimensional evaluation indicator system is established in this section in accordance with the following principles [23,24]:

(1)

Comprehensiveness: The indicator system is required to cover the primary application scenarios of ESS and reflect the multifaceted characteristics of the substations. This ensures that the evaluation results can comprehensively represent the demand for ESS configuration at each site.

(2)

Quantifiability: All indicators should be directly calculable from the operational data of the power grid. This approach facilitates objective evaluation and precludes biases that could be introduced by subjective judgment.

(3)

Differentiability: The selected indicators are intended to effectively differentiate the ESS demand characteristics among various substations, thereby highlighting the sites with high potential value.

(4)

Practicality: The design of the indicators is required to be closely aligned with the actual operational needs of the QZ power grid and the technical characteristics of ESS technology, ensuring that the methodology possesses practical engineering guidance value.

2.1.1. Structure of the Evaluation Indicator System

In accordance with the principles outlined above, an evaluation system comprising six core indicators has been constructed. It is divided into five evaluation indicators and one security constraint, as detailed in Table 1.

Table 1. Evaluation Indicator System for GSESS Demand.

Demand Dimension	Evaluation Indicator	Symbol
Congestion Mitigation	1. High Load Concentration	dpeak
	2. Peak-to-Valley Difference in Load Rate	dLD
Voltage Quality Improvement	3. Power Factor Deviation	dPF
	4. Reactive Power Fluctuation Range	dRF
Renewable Energy Accommodation	5. Reverse Power Flow Concentration	drev
Equipment Security Constraint	6. Short-Circuit Capacity Margin	MSC

Specifically, the indicators of high load concentration and peak-to-valley difference in load rate are utilized to identify sites with the highest potential value for peak shaving and valley filling. Meanwhile, the indicators for power factor deviation and reactive power fluctuation range are designed to address the increasingly prominent voltage quality issues associated with the large-scale integration of renewables. Through these indicators, substations with substandard power factors, which lead to increased line losses and voltage instability, are effectively identified; precise reactive power compensation for such issues can be provided by the ESS by virtue of its rapid response characteristics. The reverse power flow concentration indicator is primarily included to account for the reverse power flow problems caused by the rapid growth of photovoltaic (PV) installations in the QZ region; this indicator allows for the localization of sites where the accommodation of renewable energy is constrained. The short-circuit capacity margin is introduced as a security constraint to ensure that the integration of ESS does not result in the short-circuit capacity limit being exceeded. A fundamental safeguard for the secure and stable operation of the system is thereby provided. Collectively, these indicators constitute a comprehensive, scientific, and practical evaluation system, which is intended to guide the optimal planning of ESS resources in the QZ region.

2.1.2. Description and Formulation of the Evaluation Indicators

(1)

High Load Concentration

The d_peak is formulated to identify critical substations that experience significant loading stress and urgently require peak shaving by ESS for congestion relief. The assessment is achieved by synthetically considering both the maximum daily load rate during peak hours and the duration for which the high load is sustained.

$$d_{\mathrm{peak}}={\displaystyle \frac{t_{\mathrm{heavy},\mathrm{sub}}}{24}}\underset{t\in T_{\mathrm{peak}}}{\max }\left({\displaystyle \frac{p_{t,\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}\cos {\phi }_{t,\mathrm{sub}}}}\right)$$

(1)

where $t_{\mathrm{heavy},\mathrm{sub}}$ represents the duration of sustained high-load operation, which is statistically determined based on a predefined high-load threshold (e.g., a load rate ≥ 50.0%); $T_{\mathrm{peak}}$ is the set of daily peak-load hours during which the ESS is available for effective discharge, with periods of unavailability such as scheduled charging being excluded; $p_{t,\mathrm{sub}}$ is the total active power load of the substation at time interval t; $S_{\mathrm{sub}}^{\mathrm{rated}}$ is the rated apparent power of the substation; $\cos {\phi }_{t,\mathrm{sub}}$ is the power factor of the substation at time interval t.

(2)

Peak-to-Valley Difference in Load Rate

The d_LD is utilized to identify the optimal candidate sites for ESS-based peak-shaving and valley-filling. This indicator is determined by calculating the difference between the load rate observed during daily peak-load hours and that during off-peak hours.

$$d_{\mathrm{LD}}={\displaystyle \frac{1}{\left|T_{\mathrm{peak}}\right|}}{\displaystyle \sum _{t\in T_{\mathrm{peak}}}\frac{p_{t,\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}\cos {\phi }_{t,\mathrm{sub}}}}-{\displaystyle \frac{1}{\left|T_{\mathrm{valley}}\right|}}{\displaystyle \sum _{t\in T_{\mathrm{valley}}}\frac{p_{t,\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}\cos {\phi }_{t,\mathrm{sub}}}}$$

(2)

where $T_{\mathrm{valley}}$ is the set of off-peak hours available for effective charging. This period is determined based on the net load profile to accurately reflect the grid’s supply-demand dynamics in the presence of distributed renewables, thereby ensuring the charging strategy is aligned with practical grid off-peak conditions.

(3)

Power Factor Deviation

The d_PF is utilized to identify substations with poor voltage quality by calculating the deviation of their power factor from a specified standard.

$$d_{\mathrm{PF}}=\underset{t\in T_{\mathrm{key}}}{\max }\left|{\displaystyle \frac{p_{t,\mathrm{sub}}}{\sqrt{p_{t,\mathrm{sub}}^2+q_{t,\mathrm{sub}}^2}}}-\cos {\phi }_{\mathrm{rated}}\right|$$

(3)

where $T_{\mathrm{key}}$ represents the set of schedulable hours during which the ESS is available for effective charge and discharge, $q_{t,\mathrm{sub}}$ is the total active power load of the substation at time interval t, and $\cos {\phi }_{\mathrm{rated}}$ is the rated power factor.

(4)

Reactive Power Fluctuation Range

The d_RF is an indicator utilized to identify substations characterized by wide reactive power variations.

$$d_{\mathrm{RF}}=\underset{t\in T_{\mathrm{key}}}{\max }\left({\displaystyle \frac{q_{t,\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}\right)-\underset{t\in T_{\mathrm{key}}}{\min }\left({\displaystyle \frac{q_{t,\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}\right)$$

(4)

(5)

Reverse Power Flow Concentration

The d_rev is utilized to identify substations experiencing severe reverse power flow by comprehensively accounting for both its peak magnitude and duration.

$$d_{\mathrm{rev}}={\displaystyle \frac{t_{\mathrm{rev},\mathrm{sub}}}{24}}\underset{t\in T_{\mathrm{key}}}{\max }\left({\displaystyle \frac{p_{\mathrm{rev},t,\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}\cos {\phi }_{t,\mathrm{sub}}}}\right)$$

(5)

where $t_{\mathrm{rev},\mathrm{sub}}$ is the duration of reverse power flow, determined based on a threshold (e.g., load rate ≤ 0) that is scientifically calibrated to the actual operational characteristics of the local grid; and $p_{\mathrm{rev},t,\mathrm{sub}}$ is the total reverse active power at the substation at time interval t.

(6)

Short-Circuit Capacity Margin

The M_SC is defined as the difference between the maximum permissible and the actual short-circuit capacity of a site; this margin is required to be greater than zero for the integration of ESS.

$$M_{\mathrm{SC}}=S_{\mathrm{SC},\max }-\left[\underset{t\in T}{\max }\left(S_{\mathrm{SC},t}\right)+\mathrm{\Delta }{S}_{\mathrm{ES}}\right]$$

(6)

where $S_{\mathrm{SC},\max }$ is the maximum permissible short-circuit capacity limit specified for the substation’s voltage level; T represents the set of all time intervals within a 24 h period; $S_{\mathrm{SC},t}$ represents the site’s baseline short-circuit capacity at time interval t prior to the integration of ESS; and $\mathrm{\Delta }{S}_{\mathrm{ES}}$ quantifies the incremental short-circuit capacity contributed by the ESS upon its connection.

2.2. Priority Evaluation of Regional GSESS Demand in QZ Based on a Hybrid Subjective-Objective Weighting Method and TOPSIS

Subsequent to the establishment of the evaluation indicator system, a multi-criteria decision-making approach is employed for the priority ranking of GSESS demand across all substations in the QZ region. This approach integrates a hybrid subjective-objective weighting method [25] with the TOPSIS [26,27]. By fusing expert knowledge with intrinsic data patterns, the bias associated with single-method weighting is effectively mitigated. Moreover, the core TOPSIS algorithm intuitively quantifies the relative proximity of each site to an ideal solution, a calculation that is unaffected by the dimensional heterogeneity of the indicators. This attribute renders the method particularly well-suited for complex evaluation problems involving multi-dimensional, heterogeneous metrics, as is typical for power systems. Furthermore, a contribution analysis is conducted to reveal the impact weight of each demand indicator on the final ranking, thereby providing a scientific basis for decision-making regarding the subsequent functional positioning and precise allocation of ESS resources.

2.2.1. Hybrid Subjective-Objective Weighting Based on the Analytic Hierarchy Process and the Entropy Method

The Analytic Hierarchy Process (AHP) is adopted as the subjective weighting method [28], while the Entropy Method (EM) is used to determine the objective weights [29]. A comprehensive set of weights is then formulated by systematically integrating these two weighting schemes through an adjustable proportion coefficient.

(1)

Subjective Weighting via the AHP Method

The AHP is a method wherein a complex decision-making problem is decomposed into a hierarchical structure to determine the relative importance of each indicator. The specific calculation procedure is as follows:

Based on expert knowledge and system requirements, a pairwise comparison judgment matrix A is constructed for the indicators as follows:

$$\mathit{A}={[a_{i,j}]}_{i,j\in N_{\mathrm{ind}}}$$

(7)

where the matrix element $a_{i,j}$ denotes the relative importance of indicator i over indicator j, and $N_{\mathrm{ind}}$ is the set of indicators, ordered as d_peak, d_LD, d_PF, d_RF, and d_rev. The eigenvector W is then calculated from the judgment matrix A as follows:

$$(\mathit{A}-\lambda \mathit{I})\mathit{W}=0$$

(8)

where λ is the eigenvalue and $\mathit{W}={[w_i]}_{i\in N_{\mathrm{ind}}}$ is the corresponding eigenvector. Upon passing a consistency check, the eigenvector associated with the maximum eigenvalue ${\lambda }_{\max }$ is then normalized to obtain the weight ${\omega }_j^{\mathrm{AHP}}$ for the j-th indicator:

$${\omega }_j^{\mathrm{AHP}}=w_j/{\displaystyle \sum _{i\in N_{\mathrm{ind}}}{w}_i}$$

(9)

(2)

Objective Weighting via the EM

The EM is an objective weighting technique derived from information theory, by which indicator weights are automatically determined based on the degree of data dispersion. The specific calculation procedure is as follows:

The raw data matrix is normalized to eliminate the influence of different physical dimensions, as follows:

$$x_{s,j}^{*}={\displaystyle \frac{x_{s,j}-\underset{s\in N_{\mathrm{sub}}}{\min }(x_{s,j})}{\underset{s\in N_{\mathrm{sub}}}{\max }(x_{s,j})-\underset{s\in N_{\mathrm{sub}}}{\min }(x_{s,j})}}$$

(10)

where $x_{s,j}^{*}$ and $x_{s,j}$ represent the normalized and original values, respectively, of the j-th indicator for the s-th substation, and $N_{\mathrm{sub}}$ is the set of all substations. The information entropy, $e_j$, for the j-th indicator is then calculated as follows:

$$e_j=-{\displaystyle \frac{1}{\ln (|N_{\mathrm{sub}}|)}}{\displaystyle \sum _{s\in N_{\mathrm{sub}}}\left[\frac{x_{s,j}^{*}}{{\displaystyle \sum _{s\in N_{\mathrm{sub}}}{x}_{s,j}^{*}}}\ln \left(\frac{x_{s,j}^{*}}{{\displaystyle \sum _{s\in N_{\mathrm{sub}}}{x}_{s,j}^{*}}}\right)\right]}$$

(11)

where the weight ${\omega }_j^{\mathrm{EM}}$ for the j-th indicator is obtained through normalization, recognizing that a smaller information entropy value signifies a greater contribution of effective information and thus warrants a larger weight:

$${\omega }_j^{\mathrm{EM}}=(1-e_j)/{\displaystyle \sum _{i\in N_{\mathrm{ind}}}(1-e_i)}$$

(12)

(3)

Calculation of the Comprehensive Weights

To effectively balance the subjective and objective weighting methods, the comprehensive weight for the j-th indicator, ${\omega }_j^{\mathrm{com}}$, is determined via a linear combination as follows:

$${\omega }_j^{\mathrm{com}}=\alpha \cdot {\omega }_j^{\mathrm{AHP}}+(1-\alpha )\cdot {\omega }_j^{\mathrm{EM}}$$

(13)

where $\alpha$ is the subjective weighting coefficient, which ranges from 0 to 1 and is set to 0.5 by default. For substations at different voltage levels, the entropy weights are calculated independently while the AHP weights are held constant, thereby generating voltage-level-specific comprehensive weights.

2.2.2. TOPSIS-Based Prioritization of Regional GSESS Demand in QZ

A priority ranking of GSESS demand for all sites across the QZ region is generated using the TOPSIS, a multi-criteria decision-making method in which the relative merit of each site is evaluated by calculating its distance from both a positive and a negative ideal solution. The specific calculation procedure is as follows:

The weighted normalized decision matrix is then constructed by applying the comprehensive weights to the normalized indicator data as follows:

$$v_{s,j}=x_{s,j}^{*}\cdot {\omega }_j^{\mathrm{com}}$$

(14)

where $v_{s,j}$ is the weighted normalized value for the j-th indicator of the s-th substation, from which the positive ideal solution, ${\mathit{A}}^{+}={[v_j^{+}]}_{j\in N_{\mathrm{ind}}}$, and the negative ideal solution, ${\mathit{A}}^{-}={[v_j^{-}]}_{j\in N_{\mathrm{ind}}}$, are, respectively, determined by identifying the best and worst values for each indicator across all sites:

$$v_j^{+}=\underset{s\in N_{\mathrm{sub}}}{\max }{v}_{s,j}$$

(15)

$$v_j^{-}=\underset{s\in N_{\mathrm{sub}}}{\min }{v}_{s,j}$$

(16)

The relative closeness of the s-th substation to the positive ideal solution, $c_s$, is then determined by calculating its distances to both the positive and negative ideal solutions as follows:

$$c_s={\displaystyle \frac{d_s^{-}}{d_s^{+}+d_s^{-}}}={\displaystyle \frac{\sqrt{{\displaystyle \sum _{j\in N_{\mathrm{ind}}}{(v_{s,j}-v_j^{-})}^2}}}{\sqrt{{\displaystyle \sum _{j\in N_{\mathrm{ind}}}{(v_{s,j}-v_j^{+})}^2}}+\sqrt{{\displaystyle \sum _{j\in N_{\mathrm{ind}}}{(v_{s,j}-v_j^{-})}^2}}}}$$

(17)

where $d_s^{+}$ and $d_s^{-}$ are the Euclidean distances of the s-th substation from the positive and negative ideal solutions, respectively. A larger value for $c_s$ signifies a higher overall score, which is interpreted as a greater demand at the site for services including congestion mitigation, voltage quality improvement, and renewable energy accommodation. Consequently, substations with higher $c_s$ values are identified as priority candidates for the deployment of ESS.

To identify the key indicators that most significantly influence the final score, and thereby provide targeted guidance for the functional optimization of the corresponding ESS, the contribution of the j-th indicator for the s-th substation is calculated as:

$$p_{s,j}^{\mathrm{con}}={\displaystyle \frac{|v_{s,j}-v_j^{-}|/(|v_{s,j}-v_j^{+}|+|v_{s,j}-v_j^{-}|)}{{\displaystyle \sum _{j\in N_{\mathrm{ind}}}|v_{s,j}-v_j^{-}|/(|v_{s,j}-v_j^{+}|+|v_{s,j}-v_j^{-}|)}}}\times c_s$$

(18)

Based on the methodology described, all substations are first screened to ensure they satisfy the security constraint M_SC > 0. To preclude biases from direct cross-voltage-level comparisons, a priority ranking is then performed independently for each voltage group. Within each voltage level group, the GSESS demand priority rank, $r_s$, for each substation is determined by sorting the sites in descending order of their relative closeness to the ideal solution, $c_s$:

$$r_s=1+{\displaystyle \sum _{s^{\prime }\in N_{s,\mathrm{sub},\mathrm{vol}}}I(c_{s^{\prime }}>c_s)}$$

(19)

where $I(c_{s^{\prime }}>c_s)$ is an indicator function that equals 1 if the condition is met $c_{s^{\prime }}>c_s$ and 0 otherwise; $N_{s,\mathrm{sub},\mathrm{vol}}$ is the set of all substations that share the same voltage level as substation s.

3. Optimal Capacity Planning Methodology for GSESS Incorporating Multi-Dimensional Operational Security Constraints

3.1. Data-Driven Generation of a Severe Scenario Set Considering Multi-Dimensional Security Indicators

The GSESS planning methodology presented in this paper prioritizes system operational security. To this end, a data-driven method for generating a severe operating scenario set is proposed based on multi-dimensional security indicators. From the site’s annual historical operational data, the top 10% most severe daily scenarios are first screened for each individual indicator. Subsequently, an improved K-means algorithm, which incorporates the selection of an optimal number of clusters, is employed to categorize these screened scenarios, thereby forming the final severe scenario set [30,31,32]. The underlying premise is that if a planning scheme can satisfy the security constraint for a given indicator within this severe set, its operational security for that indicator throughout the year is also considered to be ensured. The historical data used in this study has a time resolution of 15 min. Taking the d_peak as an example, if the set of all historical daily scenarios for a year is denoted by $S$, where the i-th daily scenario is $s_i$ with an indicator value of $d_i^{\mathrm{peak}}$, then the set of the top 10% most severe daily scenarios can be obtained as follows:

$$s_{10\%\mathrm{wst}}^{\mathrm{peak}}=\left\{s_i|d_i^{\mathrm{peak}}\ge d_{10\%}^{\mathrm{peak}},s_i\in S\right\}$$

(20)

where $d_{10\%}^{\mathrm{peak}}$ represents the 90th percentile of all annual values for the high load concentration indicator.

This screening process is similarly applied to generate severe scenario sets for the remaining indicators, including peak-to-valley difference, power factor deviation, reactive power fluctuation, and reverse power flow concentration. Subsequently, these large sets are reduced using an improved K-means clustering algorithm to yield a representative set of typical scenarios for security verification in the planning model. The clustering is performed based on features that include active power, reactive power, peak-to-valley difference, and the average daily load rate. To overcome the limitation of conventional K-means, which relies on empirically setting the number of clusters, an iterative approach is adopted here. The optimal number of clusters is determined by evaluating a composite metric that incorporates the inertia score (from the Elbow Method), the silhouette coefficient, and a specifically introduced constraint satisfaction rate, with the well-established calculation methods for the former two being omitted for brevity.

3.2. Optimal Capacity Planning Model for GSESS Incorporating Multi-Dimensional Operational Security Constraints

3.2.1. Objective Function

The objective function is formulated to minimize the total configuration cost $C^{\mathrm{inv}}$ for a target site A, while ensuring all fundamental and multi-dimensional security constraints are met over the subsequent one-year period, as expressed below:

$$\min C^{\mathrm{inv}}=c^{\mathrm{e}}{E}^{\mathrm{inv}}+c^p{P}^{\mathrm{inv}}+c^q{Q}^{\mathrm{inv}}$$

(21)

$${(S^{\mathrm{inv}})}^2={(P^{\mathrm{inv}})}^2+{(Q^{\mathrm{inv}})}^2$$

(22)

where $E^{\mathrm{inv}}$, $P^{\mathrm{inv}}$, $Q^{\mathrm{inv}}$, and $S^{\mathrm{inv}}$ are the configured capacities for energy, active power, reactive power, and apparent power, respectively, with the apparent power capacity being calculated from the active and reactive power capacities; and $c^{\mathrm{e}}$, $c^p$, and $c^q$ are the respective unit costs for energy capacity, active power capacity, and reactive power capacity.

3.2.2. Constraints Incorporating Multi-Dimensional Operational Security Controls

• ESS Investment and Construction Constraints

$$0\le E^{\mathrm{inv}}\le E^{\max }$$

(23)

$$0\le P^{\mathrm{inv}}\le P^{\max }$$

(24)

$$0\le Q^{\mathrm{inv}}\le Q^{\max }$$

(25)

where $E^{\max }$, $P^{\max }$, and $Q^{\max }$ are the maximum permissible installed capacities for energy, active power, and reactive power at the site, respectively.

2.

ESS Operational Constraints within the Severe Scenario Set

To ensure the derived configuration satisfies the operational security constraints under the most adverse conditions, the system’s operation is simulated within each severe scenario $s$ from the set $S_{\mathrm{wst}}$. The specific operational constraints for any given scenario are formulated as follows:

$$b_{s,t}^{\mathrm{d}}+b_{s,t}^{\mathrm{c}}\le 1$$

(26)

$$0\le P_{s,t}^{\mathrm{d}}\le b_{s,t}^{\mathrm{d}}{P}^{\max }$$

(27)

$$0\le P_{s,t}^{\mathrm{c}}\le b_{s,t}^{\mathrm{c}}{P}^{\max }$$

(28)

$$0\le Q_{s,t}^{\mathrm{d}}\le b_{s,t}^{\mathrm{d}}{Q}^{\max }$$

(29)

$$0\le Q_{s,t}^{\mathrm{c}}\le b_{s,t}^{\mathrm{c}}{Q}^{\max }$$

(30)

$$S_{\mathrm{oc}}^{\min }{E}^{\max }\le E_{s,t}\le S_{\mathrm{oc}}^{\max }{E}^{\max }$$

(31)

$$E_{s,t+1}=E_{s,t}+{\eta }^{\mathrm{c}}{P}_{s,t}^{\mathrm{c}}\mathrm{\Delta }t-{\displaystyle \frac{P_{s,t}^{\mathrm{d}}\mathrm{\Delta }t}{{\eta }^{\mathrm{d}}}}$$

(32)

$$E_{s,0}=E_{s,T}=E^{\max }{S}_{\mathrm{oc}}^{\mathrm{ini}}$$

(33)

where $\mathrm{\Delta }t$ is the duration of each time step; $b_{s,t}^{\mathrm{d}}$ and $b_{s,t}^{\mathrm{c}}$ are binary variables representing the discharging and charging states, respectively, during time step t of scenario s, where a value of 1 indicates the active state; $P_{s,t}^{\mathrm{c}}$, $P_{s,t}^{\mathrm{d}}$, $Q_{s,t}^{\mathrm{c}}$, and $Q_{s,t}^{\mathrm{d}}$ are the active and reactive power values for discharging and charging; $E_{s,t}$ is the remaining energy capacity of the ESS; $S_{\mathrm{oc}}^{\max }$, $S_{\mathrm{oc}}^{\min }$, and $S_{\mathrm{oc}}^{\mathrm{ini}}$ represent the upper limit, lower limit, and initial value for the SOC during secure operation; and ${\eta }^{\mathrm{c}}$ and ${\eta }^{\mathrm{d}}$ are the charging and discharging efficiencies, respectively.

3.

Multi-dimensional Operational Security Constraints

For any given severe operating scenario, the satisfaction of all security indicators is enforced through the following constraints. These correspond, respectively, to the control limits for $d_s^{\mathrm{peak}}$, $d_s^{\mathrm{LD}}$, $d_s^{\mathrm{PF}}$, $d_s^{\mathrm{RF}}$ and $d_s^{\mathrm{rev}}$, with the calculation of each indicator being as previously described. It should be noted that the majority of these constraints are inherently nonlinear and are subsequently linearized to ensure the computational tractability of the model.

$$P_{s,t}^{\mathrm{sub}}=P_{s,t}^{\mathrm{load}}+P_{s,t}^{\mathrm{d}}-P_{s,t}^{\mathrm{c}}$$

(34)

$$Q_{s,t}^{\mathrm{sub}}=Q_{s,t}^{\mathrm{load}}+Q_{s,t}^{\mathrm{d}}-Q_{s,t}^{\mathrm{c}}$$

(35)

$$d_s^{\mathrm{peak}}={\displaystyle \frac{t_s^{\mathrm{heavy}}}{24}}\underset{t\in T}{\max }({\displaystyle \frac{\sqrt{{(P_{s,t}^{\mathrm{sub}})}^2+{(Q_{s,t}^{\mathrm{sub}})}^2}}{S_{\mathrm{sub}}^{\mathrm{rated}}}})\le d_{\mathrm{acc}}^{\mathrm{peak}}$$

(36)

$$d_s^{\mathrm{LD}}={\displaystyle \frac{1}{\left|T_s^{\mathrm{peak}}\right|}}{\displaystyle \sum _{t\in T_s^{\mathrm{peak}}}\frac{\sqrt{{(P_{s,t}^{\mathrm{sub}})}^2+{(Q_{s,t}^{\mathrm{sub}})}^2}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}-{\displaystyle \frac{1}{\left|T_s^{\mathrm{valley}}\right|}}{\displaystyle \sum _{t\in T_x^{\mathrm{valley}}}\frac{\sqrt{{(P_{s,t}^{\mathrm{sub}})}^2+{(Q_{s,t}^{\mathrm{sub}})}^2}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}\le d_{\mathrm{acc}}^{\mathrm{LD}}$$

(37)

$$d_s^{\mathrm{PF}}=\underset{t\in T}{\max }\left|{\displaystyle \frac{P_{s,t}^{\mathrm{sub}}}{\sqrt{{(P_{s,t}^{\mathrm{sub}})}^2+{(Q_{s,t}^{\mathrm{sub}})}^2}}}-\cos {\phi }_{\mathrm{rated}}\right|\le d_{\mathrm{acc}}^{\mathrm{PF}}$$

(38)

$$d_s^{\mathrm{RF}}=\underset{t\in T}{\max }\left({\displaystyle \frac{Q_{s,t}^{\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}\right)-\underset{t\in T}{\min }\left({\displaystyle \frac{Q_{s,t}^{\mathrm{sub}}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}\right)\le d_{\mathrm{acc}}^{\mathrm{RF}}$$

(39)

$$d_s^{\mathrm{rev}}={\displaystyle \frac{t_s^{\mathrm{rev}}}{24}}\underset{t\in T_s^{\mathrm{rev}}}{\max }\left({\displaystyle \frac{\sqrt{{(P_{s,t}^{\mathrm{sub}})}^2+{(Q_{s,t}^{\mathrm{sub}})}^2}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}\right)\le d_{\mathrm{acc}}^{\mathrm{rev}}$$

(40)

where $P_{s,t}^{\mathrm{sub}}$ and $Q_{s,t}^{\mathrm{sub}}$ are the net active and reactive loads of the substation with ESS, while $P_{s,t}^{\mathrm{load}}$ and $Q_{s,t}^{\mathrm{load}}$ are the corresponding baseline loads without ESS; $t_s^{\mathrm{heavy}}$ is the duration of high-load operation, determined based on a predefined threshold (e.g., load rate ≥ 50.0%); $T_s^{\mathrm{peak}}$ is the set of peak-load hours within scenario s available for effective discharging; $S_{\mathrm{sub}}^{\mathrm{rated}}$ is the rated apparent power of the substation; $d_{\mathrm{acc}}^{\mathrm{peak}}$, $d_{\mathrm{acc}}^{\mathrm{LD}}$, $d_{\mathrm{acc}}^{\mathrm{PF}}$, $d_{\mathrm{acc}}^{\mathrm{RF}}$, and $d_{\mathrm{acc}}^{\mathrm{rev}}$ are the acceptable thresholds for their respective indicators; $T_s^{\mathrm{valley}}$ is the set of off-peak hours available for effective charging; $\cos {\phi }_{\mathrm{rated}}$ is the rated power factor; $t_s^{\mathrm{rev}}$ is the duration of reverse power flow, determined based on a predefined threshold (e.g., reverse load rate ≤ −0.0%); $T_s^{\mathrm{rev}}$ is the set of time intervals during which reverse power flow occurs.

3.2.3. Linearization

The planning model is solved using the Gurobi commercial solver, which is capable of handling mixed-integer problems with certain nonlinearities, including quadratic terms and maximum functions. Consequently, these specific terms are not linearized. The following linearization techniques are applied only to those nonlinear constraints that fall outside the native capabilities of Gurobi.

For the calculation of $t_s^{\mathrm{heavy}}$, a binary indicator variable, $b_{s,t}^{\mathrm{heavy}}$, is first defined. Its value is set to 1 if the substation’s load rate at time t is greater than or equal to 50.0%, and 0 otherwise. $t_s^{\mathrm{heavy}}$ can then be expressed as follows:

$$t_s^{\mathrm{heavy}}={\displaystyle \sum _{t=1}^T{b}_{s,t}^{\mathrm{heavy}}\mathrm{\Delta }t}$$

(41)

$$\left\{\begin{array}{c}{b}_{s,t}^{\mathrm{heavy}}=1,{\displaystyle \frac{S_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}\ge 0.5\\ b_{s,t}^{\mathrm{heavy}}=0,{\displaystyle \frac{S_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}<0.5\end{array}\right.$$

(42)

$$S_{s,t}=\sqrt{{(P_{s,t}^{\mathrm{sub}})}^2+{(Q_{s,t}^{\mathrm{sub}})}^2}$$

(43)

where $S_{s,t}$ represents the apparent power of the substation during time step t of scenarios.

Noting that Equation (42) is a conditional constraint, it is linearized into the following set of inequalities by employing the Big-M method.

$${\displaystyle \frac{S_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}-0.5\ge -M(1-b_{s,t}^{\mathrm{heavy}})$$

(44)

$${\displaystyle \frac{S_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}}}-0.5\le -\epsilon +M{b}_{s,t}^{\mathrm{heavy}}$$

(45)

where $\epsilon$ is a sufficiently small positive number and M is a sufficiently large positive number.

The linearization for $t_s^{\mathrm{rev}}$ and $T_s^{\mathrm{rev}}$ follows a similar logic to that used for $t_s^{\mathrm{heavy}}$. For practical computation, the peak-to-valley load rate difference, as expressed in Equation (37), is simplified by directly defining it as the difference between the daily maximum and minimum load rates. This simplification precludes the need for numerous auxiliary sorting variables and is formulated as follows:

$$d_s^{\mathrm{LD}}=\underset{t\in T}{\max }({\displaystyle \frac{S_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}}})-\underset{t\in T}{\min }({\displaystyle \frac{S_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}}})\le d_{\mathrm{acc}}^{\mathrm{LD}}$$

(46)

3.2.4. Calculation of the Upper Bound for ESS Planning

The solution obtained from the previously described optimization model represents the minimum required capacity for GSESS, i.e., the lower bound necessary to ensure secure operation of the power system. Although a larger capacity is generally preferable from a security perspective, physical limitations at the substation, such as available feeder bays and transformer capacity, impose an upper bound on the practical planning. Specifically, the total load, comprising the baseline load plus the ESS’s (dis)charging power, should not exceed the main transformer’s capacity. From this principle, the upper limit for the storage power rating is derived as follows:

$$P_{\max }^{\mathrm{inv}}=\min (0.8S_{\mathrm{tr}}^{\mathrm{rated}}-\underset{t\in A}{\min }({\displaystyle \frac{P_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}\cos {\phi }_{s,t}}})S_{tr}^{\mathrm{rated}},\underset{t\in A}{\max }({\displaystyle \frac{P_{s,t}}{S_{\mathrm{sub}}^{\mathrm{rated}}\cos {\phi }_{s,t}}})S_{tr}^{\mathrm{rated}}+0.8S_{tr}^{\mathrm{rated}})$$

(47)

where $S_{\mathrm{tr}}^{\mathrm{rated}}$ is the capacity of a single main transformer, and $\cos {\phi }_{s,t}$ is the power factor angle of the substation during time step t of scenario s.

4. Investment Return Analysis of GSESS for Multiple Application Scenarios

While the preceding sections have determined the optimal siting and sizing of GSESS based on multi-dimensional security requirements, the economic viability of such a project is a decisive factor in its actual implementation. Therefore, an optimal operational model for GSESS is established with the objective of maximizing net revenue over its entire lifecycle. This model simulates the optimal charging and discharging strategies across multiple application scenarios, including price arbitrage and ancillary services, while accounting for market prices and battery degradation. By quantifying the annual cost and revenue cash flows, a comprehensive investment return analysis is then conducted using key financial metrics such as the payback period and internal rate of return (IRR), thereby evaluating the economic feasibility of the proposed planning scheme.

4.1. Optimal Operation Model of GSESS for Multiple Application Scenarios

4.1.1. Objective Function

The objective function of the optimal operational model is formulated to maximize the Net Present Value (NPV) of the GSESS over its entire lifecycle, as expressed by:

$$\max C_{\mathrm{NPV}}=R_{\mathrm{ARB}}+R_{\mathrm{AS}}-C_{\mathrm{LCC}}$$

(48)

$$R_{\mathrm{AS}}=R_{\mathrm{p}}+R_{\mathrm{fc}}+R_{\mathrm{fm}}$$

(49)

$$C_{\mathrm{LCC}}=C_{\mathrm{INV}}+C_{\mathrm{OMC}}+C_{\mathrm{RC}}+C_{\mathrm{CH}}-C_{\mathrm{DC}}$$

(50)

where $C_{\mathrm{NPV}}$ is the net revenue over the entire lifecycle; $R_{\mathrm{ARB}}$ and $R_{\mathrm{AS}}$ are the lifecycle revenues from TOU arbitrage [33] and ancillary services [34], respectively; $C_{\mathrm{LCC}}$ is the total lifecycle cost; $R_{\mathrm{p}}$, $R_{\mathrm{fc}}$, and $R_{\mathrm{fm}}$ represent the revenues from peak regulation, frequency regulation capacity, and frequency regulation mileage; and $C_{\mathrm{INV}}$, $C_{\mathrm{OMC}}$, $C_{\mathrm{RC}}$, $C_{\mathrm{CH}}$, and $C_{\mathrm{DC}}$ denote the initial investment, operation and maintenance, replacement, charging, and salvage costs. It is important to note that all cost and revenue components in the above formulation are present values, discounted to account for the time value of money, with their detailed quantification provided in Appendix A.1.

4.1.2. Constraints

• TOU Price Arbitrage Constraints

$$0\le P_{\mathrm{a},t}^{\mathrm{ch}}\le P_{\mathrm{a},\max }\cdot {\delta }_{\mathrm{a},t}^{\mathrm{ch}}$$

(51)

$$0\le P_{\mathrm{a},t}^{\mathrm{dis}}\le P_{\mathrm{a},\max }\cdot {\delta }_{\mathrm{a},t}^{\mathrm{dis}}$$

(52)

$${\delta }_{\mathrm{a},t}^{\mathrm{ch}}+{\delta }_{\mathrm{a},t}^{\mathrm{dis}}\le 1$$

(53)

$$E_{\mathrm{a},t}=E_{\mathrm{a},t-1}+(P_{\mathrm{a},t}^{\mathrm{ch}}\cdot {\eta }^{\mathrm{c}}-P_{\mathrm{a},t}^{\mathrm{dis}}/{\eta }^{\mathrm{d}})\mathrm{\Delta }t$$

(54)

$$0\le E_{\mathrm{a},t}\le E_{\mathrm{a},\max }$$

(55)

where $P_{\mathrm{a},t}^{\mathrm{ch}}$ and $P_{\mathrm{a},t}^{\mathrm{dis}}$ are the charging and discharging power, respectively, for TOU arbitrage during time step t; $P_{\mathrm{a},\max }$ is the power capacity allocated for this service; ${\delta }_{\mathrm{a},t}^{\mathrm{ch}}$ and ${\delta }_{\mathrm{a},t}^{\mathrm{dis}}$ are binary variables representing the charging and discharging states for TOU arbitrage, where a value of 1 denotes the active state; $E_{\mathrm{a},t}$ is the state of charge for the capacity allocated to TOU arbitrage; $E_{\mathrm{a},\max }$ is the total energy capacity allocated for this service.

2.

Peak Regulation Ancillary Service Constraints

$$0\le P_{\mathrm{p},t}^{\mathrm{up}}\le P_{\mathrm{p},\max }\cdot {\delta }_{\mathrm{p},t}^{\mathrm{up}}$$

(56)

$$0\le P_{\mathrm{p},t}^{\mathrm{down}}\le P_{\mathrm{p},\max }\cdot {\delta }_{\mathrm{p},t}^{\mathrm{down}}$$

(57)

$$P_{\mathrm{p},\max }\ge {\mathrm{P}}_{\mathrm{pm}}$$

(58)

$${\delta }_{\mathrm{p},t}^{\mathrm{up}}+{\delta }_{\mathrm{p},t}^{\mathrm{down}}\le 1$$

(59)

$$E_{\mathrm{p},t}=E_{\mathrm{p},t-1}+(P_{\mathrm{p},t}^{\mathrm{up}}-P_{\mathrm{p},t}^{\mathrm{down}})\mathrm{\Delta }t$$

(60)

$$-E_{\mathrm{p},\max }\le E_{\mathrm{p},t}\le E_{\mathrm{p},\max }$$

(61)

$$E_{\mathrm{p},\max }\ge {\mathrm{E}}_{\mathrm{pm}}$$

(62)

where $P_{\mathrm{p},t}^{\mathrm{up}}$ and $P_{\mathrm{p},t}^{\mathrm{down}}$ are the upward and downward peak regulation power provided by the ESS at time step t, respectively; $P_{\mathrm{p},\max }$ is the maximum charge/discharge power allocated for this service; ${\delta }_{\mathrm{p},t}^{\mathrm{up}}$ and ${\delta }_{\mathrm{p},t}^{\mathrm{down}}$ are the binary state variables for upward and downward regulation; $E_{\mathrm{p},t}$ is the state of charge of the capacity allocated for peak regulation; $E_{\mathrm{p},\max }$ is the total energy capacity reserved for this service; Equation (58) enforces the market entry requirement that the regulating power must be no less than ${\mathrm{P}}_{\mathrm{pm}}$ MW; and Equation (62) enforces the market requirement that the energy capacity participating in peak regulation should be at least ${\mathrm{E}}_{\mathrm{pm}}$ MWh.

3.

Frequency Regulation Ancillary Service Constraints

$$0\le P_{\mathrm{f},t}^{\mathrm{up}}\le P_{\mathrm{f},\max }\cdot {\delta }_{\mathrm{f},t}^{\mathrm{up}}$$

(63)

$$0\le P_{\mathrm{f},t}^{\mathrm{down}}\le P_{\mathrm{f},\max }\cdot {\delta }_{\mathrm{f},t}^{\mathrm{down}}$$

(64)

$$P_{\mathrm{f},\max }\ge {\mathrm{P}}_{\mathrm{fm}}$$

(65)

$${\delta }_{\mathrm{f},t}^{\mathrm{up}}+{\delta }_{\mathrm{f},t}^{\mathrm{down}}\le 1$$

(66)

$$E_{\mathrm{f},t}=E_{\mathrm{f},t-1}+(P_{\mathrm{f},t}^{\mathrm{up}}-P_{\mathrm{f},t}^{\mathrm{down}})\mathrm{\Delta }t$$

(67)

$$0\le E_{\mathrm{f},t}\le E_{\mathrm{f},\max }$$

(68)

where $P_{\mathrm{f},t}^{\mathrm{up}}$ and $P_{\mathrm{f},t}^{\mathrm{down}}$ are the upward and downward frequency regulation power provided by the ESS at time step t, respectively; $P_{\mathrm{f},\max }$ is the maximum charge/discharge power allocated for this service; ${\delta }_{\mathrm{f},t}^{\mathrm{up}}$ and ${\delta }_{\mathrm{f},t}^{\mathrm{down}}$ are the binary state variables for upward and downward regulation; $E_{\mathrm{f},t}$ is the state of charge of the capacity allocated for frequency regulation; $E_{\mathrm{f},\max }$ represents the total energy capacity reserved for this service; and Equation (65) enforces the market entry requirement that the regulating power should be no less than ${\mathrm{P}}_{\mathrm{fm}}$ MW.

4.

Coupling Constraints for Multiple Scenarios

To ensure that the total dispatched power and energy do not exceed the system’s limits, the capacities declared by the ESS in each distinct market must be appropriately coupled and coordinated.

$$P_{\mathrm{ESD}}^{t,\mathrm{cha}}=P_{\mathrm{a},t}^{\mathrm{ch}}+P_{\mathrm{r},t}^{\mathrm{ch}}+P_{\mathrm{p},t}^{\mathrm{up}}+P_{\mathrm{f},t}^{\mathrm{up}}$$

(69)

$$P_{\mathrm{ESD}}^{t,\mathrm{dis}}=P_{\mathrm{a},t}^{\mathrm{dis}}+P_{\mathrm{p},t}^{\mathrm{down}}+P_{\mathrm{f},t}^{\mathrm{down}}$$

(70)

$${\delta }_{\mathrm{a},t}^{\mathrm{ch}}\le B_{\mathrm{ESD}}^{t,\mathrm{cha}},{\delta }_{\mathrm{a},t}^{\mathrm{dis}}\le B_{\mathrm{ESD}}^{t,\mathrm{dis}}$$

(71)

$${\delta }_{\mathrm{p},t}^{\mathrm{up}}\le B_{\mathrm{ESD}}^{t,\mathrm{cha}}, {\delta }_{\mathrm{p},t}^{\mathrm{down}}\le B_{\mathrm{ESD}}^{t,\mathrm{dis}}$$

(72)

$${\delta }_{\mathrm{f},t}^{\mathrm{up}}\le B_{\mathrm{ESD}}^{t,\mathrm{cha}},{\delta }_{\mathrm{f},t}^{\mathrm{down}}\le B_{\mathrm{ESD}}^{t,\mathrm{dis}}$$

(73)

$$E_{\mathrm{p},\max }({\delta }_{\mathrm{p},t}^{\mathrm{up}}+{\delta }_{\mathrm{p},t}^{\mathrm{down}})+E_{\mathrm{f},\max }({\delta }_{\mathrm{f},t}^{\mathrm{up}}+{\delta }_{\mathrm{f},t}^{\mathrm{down}})+E_{\mathrm{a},\max }({\delta }_{\mathrm{a},t}^{\mathrm{ch}}+{\delta }_{\mathrm{a},t}^{\mathrm{dis}})\le E_{\mathrm{ESS}}$$

(74)

where $P_{\mathrm{ESD}}^{t,\mathrm{cha}}$ and $P_{\mathrm{ESD}}^{t,\mathrm{dis}}$ are the total charging and discharging power of the ESS at time step t, respectively, and $E_{\mathrm{ESS}}$ is its total energy capacity. The fundamental operational constraints for the ESS are detailed in Appendix A.2.

4.1.3. Lifetime Degradation Model Based on the Rainflow Counting Method

To ensure that economic gains are pursued without causing the premature retirement of the ESS due to excessive use, a battery degradation model based on the rainflow counting method [35,36] is incorporated into the formulation, as expressed in Equations (75)–(80). The detailed modeling procedure for this degradation model is provided in Appendix A.3.

$${\displaystyle \sum _{t=1}^T{\displaystyle \sum _{k=1}^K(K_{\mathrm{seg}}^k{d}_{\mathrm{DOD}}^{t,k}+B_{\mathrm{seg}}^k{g}^{t,k})}}\le N_{\mathrm{day}}^{\max }$$

(75)

$$d_{\mathrm{DOD}}^{k,\min }{g}^{t,k}\le d_{\mathrm{DOD}}^{t,k}\le d_{\mathrm{DOD}}^{k,\max }{g}^{t,k}$$

(76)

$$N_{\mathrm{day}}^{\max }=N_0/N_{\mathrm{Life}}^{\mathrm{EXP}}$$

(77)

$${\displaystyle \sum _{k=1}^K{g}^{t,k}}=B_{\mathrm{cyc}}^t$$

(78)

$$0\le d_{\mathrm{DOD}}^t\le 1-S_{\mathrm{ESD}}^{t-1}$$

(79)

$$(1-S_{\mathrm{ESD}}^{t-1})-M(1-B_{\mathrm{cyc}}^t)\le d_{\mathrm{DOD}}^t\le M{B}_{\mathrm{cyc}}^t$$

(80)

$$B_{\mathrm{ESD}}^{t,\mathrm{cha}}-B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}\le B_{\mathrm{cyc}}^t\le \min \left\{B_{\mathrm{ESD}}^{t,\mathrm{cha}},1-B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}\right\}$$

(81)

where $d_{DOD}^t$ is the battery’s depth of discharge (DoD) at time step t; K is the number of piecewise linear segments; $K_{\mathrm{seg}}^k$ and $B_{\mathrm{seg}}^k$ are the slope and intercept of each linear segment, respectively; $g^{t,k}$ is an auxiliary binary variable; $N_{\mathrm{day}}^{\max }$ is the maximum average daily cycle count, derived from the expected battery lifetime; $N_0$ is the maximum cycle count at a 100% depth of discharge; $N_{\mathrm{Life}}^{\mathrm{EXP}}$ is the expected lifetime of the ESS; $d_{\mathrm{DOD}}^{k,\max }$ and $d_{\mathrm{DOD}}^{k,\min }$ are the lower and upper bounds of the DoD for the k-th segment; $B_{\mathrm{cyc}}^t$ is a binary variable indicating the cycle state at time t, where a value of 1 signifies that a cycle has occurred; $B_{\mathrm{ESD}}^{t,\mathrm{cha}}$ and $B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}$ are binary variables representing the charging state at time steps t and t-1, respectively, with a cycle being completed if and only if the system transitions from discharging to charging (i.e., $B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}=0$ and $B_{\mathrm{ESD}}^{t,\mathrm{cha}}=1$); $S_{\mathrm{ESD}}^t$ and $S_{\mathrm{ESD}}^{t-1}$ are the SOC values at their respective time steps.

4.2. Economic Assessment of GSESS

Based on the annual cost and revenue cash flows obtained from the optimal operational model presented in Section 4.1, a comprehensive investment return analysis of the planning scheme is conducted in this section, encompassing both a cost assessment and a project economic evaluation.

4.2.1. Life-Cycle Cost Assessment Metrics

• Levelized Cost of Storage (LCOS)

The LCOS represents the average discounted cost per unit of electricity stored and subsequently discharged by the ESS over its entire lifetime [37]. By comprehensively accounting for all expenditures—including initial investment, operation and maintenance, and replacement costs—relative to the total lifetime discharge throughput, this metric serves as a core indicator for evaluating the unit cost of stored energy.

$$C_{\mathrm{LCOS}}=C_{\mathrm{LCC}}/{\displaystyle \sum _{i=1}^I\frac{E_{\mathrm{dis},i}}{{\left(1+r_{\mathrm{d}}\right)}^i}}$$

(82)

where $E_{\mathrm{dis},i}$ is the total energy discharged by the ESS in year i, and $r_{\mathrm{d}}$ is the discount rate.

2.

Average Annualized Cost (AAC)

The AAC is the annualized equivalent of the total life-cycle cost [38], a metric designed to provide an intuitive assessment of the project’s annual financial burden.

$$C_{\mathrm{AAC}}=C_{\mathrm{LCC}}{\displaystyle \frac{r_{\mathrm{d}}{\left(1+r_{\mathrm{d}}\right)}^I}{{\left(1+r_{\mathrm{d}}\right)}^I-1}}$$

(83)

4.2.2. Economic Evaluation Methods

The investment value of the ESS project is comprehensively evaluated in this paper using the NPV, payback period, and IRR methods [39,40]. The formulation for NPV has been previously defined as the objective function in Equation (48).

• Dynamic Payback Period (DPP)

The DPP is the time required to recoup the total initial investment, with the time value of money being taken into account. This metric, which is used to evaluate the project’s capital recovery speed and risk exposure, is considered more favorable when shorter. Its calculation is expressed as follows:

$${\displaystyle {\sum }_{t=1}^{T_{\mathrm{DPP}}}\frac{NC{F}_t}{{(1+r)}^t}}=I_0$$

(84)

where $T_{\mathrm{DPP}}$ is the DPP; $I_0$ is the initial investment; $\overline{NCF}$ is the average annual net cash flow; and $NC{F}_t$ is the net cash flow in year $t$.

2.

Internal Rate of Return

The IRR is defined as the discount rate at which the NPV of a project equals zero [41], thereby reflecting the project’s intrinsic rate of return. The project is considered economically feasible if the IRR exceeds a predefined benchmark rate. Its calculation is expressed as follows:

$${\displaystyle {\sum }_{t=0}^n\frac{C{I}_t-C{O}_t}{{(1+IRR)}^t}}=0$$

(85)

where $C{I}_t$ and $C{O}_t$ are the cash inflow and outflow in year $t$, respectively. This equation is typically solved using numerical methods, such as interpolation; the specific solution process is detailed in Appendix A.4.

5. Case Studies

To validate the effectiveness and practicality of the proposed evaluation methodology, a case study is conducted using actual data from the 220 kV substations within the QZ power grid. The dataset comprises multi-period operational records for the years 2024 and 2025, including active power (MW), reactive power (MVar), and the total rated apparent power (MVA) for each substation, with a time resolution of 15 min. The data preprocessing procedure is as follows:

(1)

Site Feasibility Screening: A screening process is performed to ensure that candidate substations possess the necessary physical conditions for ESS deployment, such as the presence of 110 kV or 35 kV busbars with available or expandable feeder bays.

(2)

Data Integrity Verification: The completeness of the data records is verified. Minor missing values are imputed using the average of adjacent time steps, while significant outliers (e.g., instantaneous power spikes beyond a reasonable range) are identified and corrected through statistical methods.

(3)

Time-Series Alignment: All timestamps are unified to ensure temporal consistency across the dataset, thereby facilitating cross-site comparisons.

(4)

Data Normalization: Data is converted into a standardized format to eliminate the influence of varying substation capacities, which allows for uniform processing.

(5)

Load Rate Calculation: For each time interval, the load rate is calculated based on the active power, reactive power, and the rated apparent power.

5.1. Results of Energy Storage Demand Assessment for Substations

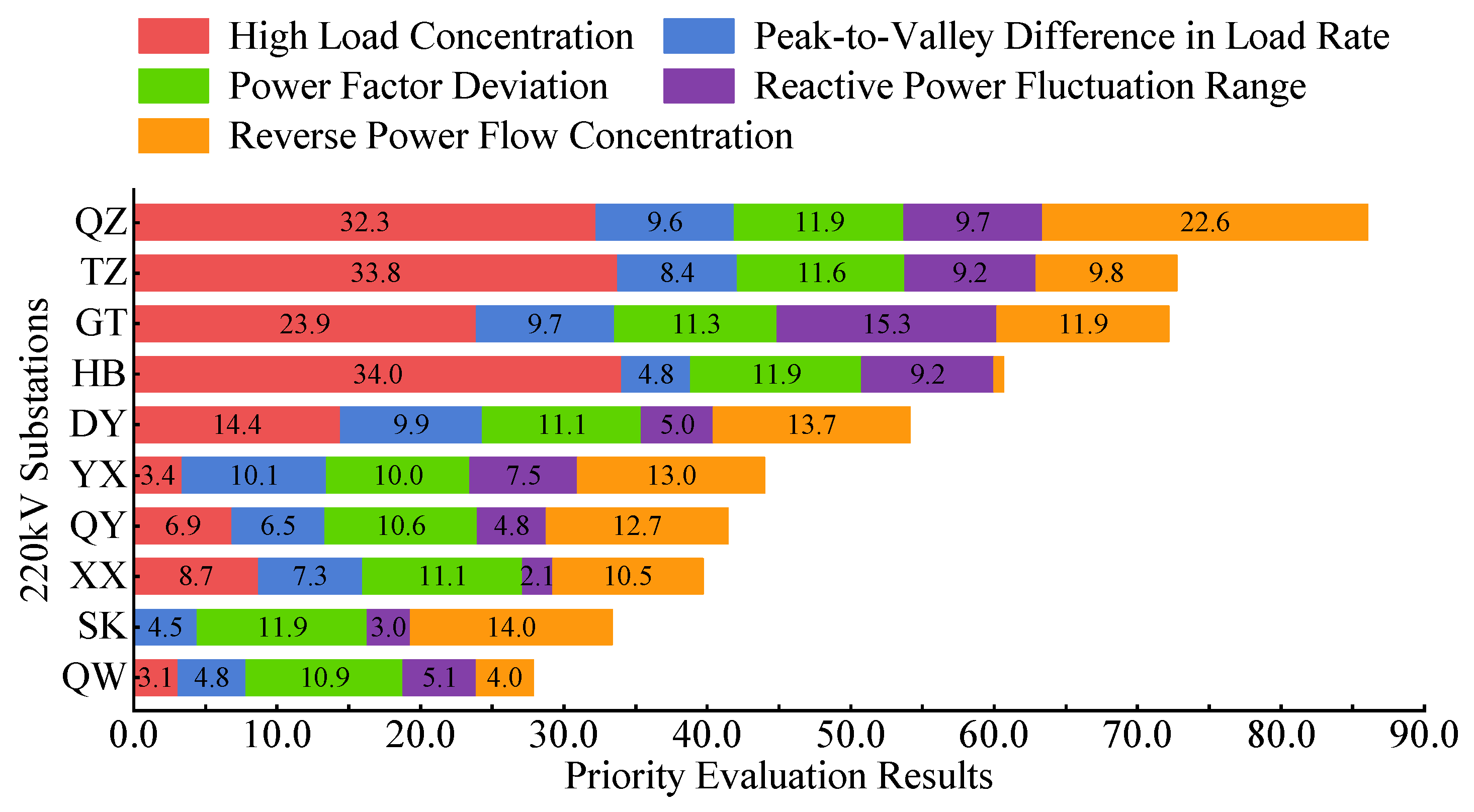
Following data preprocessing, an assessment of the 15 220 kV substations within the QZ power grid was performed. The comprehensive evaluation results, including the final rankings, normalized indicator values, and composite scores for all substations, are presented in Table 2.

Table 2. Evaluation of Energy Storage Demand Priority for 220 kV Substations in QZ.

Rank	Substation	dpeak	dLD	dPF	dRF	drev	Score
1	QZ	0.688	0.577	0.949	0.188	0.153	86.0
2	TZ	0.729	0.523	0.945	0.183	0.067	72.8
3	QT	0.533	0.600	0.949	0.259	0.084	72.2
4	HB	0.720	0.349	0.947	0.182	0.005	60.7
5	DY	0.330	0.623	0.949	0.139	0.099	54.1
6	YX	0.087	0.688	0.949	0.180	0.105	44.0
7	QY	0.161	0.459	0.941	0.138	0.094	41.5
8	XX	0.198	0.488	0.948	0.104	0.075	39.7
9	SK	0.000	0.335	0.949	0.113	0.095	33.4
10	QW	0.070	0.361	0.938	0.139	0.029	27.9
11	NZ	0.097	0.302	0.948	0.088	0.037	27.2
12	SY	0.000	0.323	0.915	0.079	0.044	24.3
13	LF	0.000	0.214	0.948	0.088	0.031	23.2
14	CW	0.000	0.125	0.911	0.101	0.000	19.7
15	CK	0.000	0.213	0.495	0.136	0.000	10.7

As shown in the table, the QZ, TZ, and GT substations are ranked as the top three candidates, with high composite scores of 86.0, 72.8, and 72.2, respectively. A high-priority demand for ESS deployment is thereby indicated for these sites. A detailed analysis of the individual demand drivers, based on the specific indicators in Table 2, is provided below.

In terms of high load concentration, the highest values are exhibited by the TZ, HB, and QZ substations. These sites are distinguished by maximum load rates exceeding 70% and sustained high-load durations of over 22 h, from which significant loading stress is indicated. Consequently, they are positioned as primary candidates for peak-shaving via ESS. Conversely, a high load concentration of zero was recorded for the substations ranked 11–15, signifying that these sites are currently operated under low-load conditions and are not affected by significant high-load issues.

Regarding the peak-to-valley difference in load rate, the YX, DY, and GT substations were ranked as the top three. Notably, the maximum difference of 0.688 was observed at the YX substation on 28 May 2024, characterized by significant reverse power flow (−24.5%) during off-peak hours. It is noteworthy that at most of the top-ranked sites, the load minimums were observed during midday, a pattern highly consistent with the temporal characteristics of PV generation. This indicates that the integration of renewable energy sources is a primary driver for the widening peak-valley difference. These sites are therefore well-suited for the deployment of ESS to enhance system flexibility.

In terms of power factor deviation, the largest deviations were recorded for the QZ, YX, and SK substations, all occurring during midday hours where the power factor was extremely low (approaching zero). This finding suggests the presence of severe reactive power issues, likely attributable to near-zero active power from PV generation coexisting with significant reactive power demand. The deployment of ESS with reactive power compensation capabilities can effectively address these issues.

With respect to the reactive power fluctuation range, the widest was observed at the GT substation, where a rapid drop in reactive power from a peak of 26.5% to 0.5% was recorded within a single day—a fluctuation corresponding to a magnitude of 0.259—which signifies severe reactive power volatility at the site. The QZ and TZ substations followed, with ranges also exceeding 0.180. It is noteworthy that the maximum reactive power fluctuations for multiple substations were recorded on the same date, i.e., 2 February 2024, suggesting the occurrence of a potential system-wide reactive power event.

In terms of reverse power flow, the highest concentration was recorded at the QZ substation, where a continuous duration of 17.75 h of reverse flow was observed on 9 June 2024, reaching a maximum reverse load rate of −20.7%. The YX and DY substations were ranked second and third, with both sites experiencing maximum reverse load rates exceeding −30%. The majority of these reverse flow incidents were concentrated during midday hours (11:30–14:15), a pattern highly consistent with peak PV generation periods. Simultaneous reverse flows were also observed across multiple substations in February (particularly on 11–12 February), which can likely be attributed to a specific combination of meteorological conditions and electricity demand patterns at the time. These sites are therefore identified as primary targets for the deployment of ESS to enhance renewable energy accommodation.

Based on the evaluation results, the comprehensive subjective-objective weights were obtained using AHP and the entropy method, as presented in Table 3. The subjective weights from AHP assign the highest importance to high load concentration and reverse power flow concentration (both at 0.270), reflecting the expert view that mitigating grid congestion and facilitating renewable energy accommodation are the most critical applications. Conversely, in the objective weights, a value of 0.436 was assigned to high load concentration, indicating it has the highest distinguishing power in the dataset. The final comprehensive weights thus preserve the expert-driven rationale while incorporating objective data characteristics, providing a more balanced reflection of each indicator’s relative importance.

Table 3. Comprehensive Subjective-Objective Weights for the Evaluation Indicators.

Weight Type	dpeak	dLD	dPF	dRF	drev
Subjective (AHP)	0.270	0.125	0.202	0.132	0.270
Objective (EM)	0.436	0.122	0.044	0.200	0.198
Comprehensive	0.353	0.124	0.123	0.166	0.234

Based on the aforementioned evaluation results and the comprehensive weights, the indicator values and final rankings for the 10 220 kV substations are presented in Figure 1. The QZ substation is ranked first with a comprehensive score of 86.0, with its ESS demand being primarily driven by high-load mitigation (37.5% contribution) and renewable energy accommodation (26.3% contribution). The TZ and GT substations are ranked second and third, respectively, and are both predominantly driven by high load concentration. A clear dominant demand driver was identified for each of the top five substations, which facilitates the determination of the primary functional role for the corresponding ESS.

Figure 1. Priority Ranking of Energy Storage Demand for the 15 220 kV Substations in QZ (Top 10).

From the perspective of application scenarios, the 15 substations can be categorized into three types:

(1)

Dominated by grid congestion mitigation: QZ, TZ, GT, HB, and DY.

(2)

Dominated by renewable energy accommodation: QZ, DY, YX, QY, and XX.

(3)

Dominated by voltage quality improvement: GT, DY, YX, QY, and XX.

This classification highlights that, to achieve an optimal return on investment, the functionalities of the configured ESS should be specifically tailored to the dominant needs of each substation type.

5.2. Results of Optimal ESS Planning

To validate the effectiveness of the proposed optimal capacity planning model, the top-ranked substations from the demand assessment are selected. For these sites, the economically optimal planning that satisfies the multi-dimensional operational security constraints is determined. The planning horizon is set to one year with a single planning stage. Based on historical data from 2024, the most severe daily operating scenarios for each indicator are screened. The corresponding load for these scenarios in 2025 is then forecasted by applying an annual load growth rate, and these forecasted scenarios are utilized for the operational security verification. Based on the official statistical yearbooks, an average annual load growth rate of 8.5% was calculated and adopted for this study. In accordance with the local dispatch requirements, the peak-load hours are defined as 08:00–11:00 and 13:00–24:00, while the off-peak hours are 00:00–08:00 and 11:00–13:00. The key parameters for the planning model are set as detailed in Table 4.

Table 4. Parameter Settings for the Planning Model.

Parameter	Value	Parameter	Value
Annual Load Growth Rate	8.5%	Time Step Duration	0.25 h
SOC Lower Limit	0.1	SOC Upper Limit	0.9
Initial Daily SOC	0.5	Charging Efficiency	0.95
Discharging Efficiency	0.95	High Load Threshold	0.5
Reverse Power Flow Threshold	0	Rated Power Factor	0.95
Maximum Load Rate Limit	0.8	Unit Energy Capacity Cost	1200 CNY/kWh
Unit Active Power Capacity Cost	750 CNY/kW	Unit Reactive Power Capacity Cost	200 CNY/kVar
Security Threshold for High Load Concentration	0.6	Security Threshold for Peak-to-Valley Difference	0.4
Security Threshold for Power Factor Deviation	0.05	Security Threshold for Reactive Power Fluctuation	0.4
Security Threshold for Reverse Power Flow Concentration	0.3

It is noteworthy that, although the energy-to-power ratio was not strictly constrained to 2:1 within the optimization model—a ratio commonly observed in practice—the final results presented are adjusted to reflect this standard. Specifically, the greater of the two optimized values (energy capacity or power rating) is taken as the baseline, and the other quantity is subsequently adjusted to maintain the 2:1 ratio.

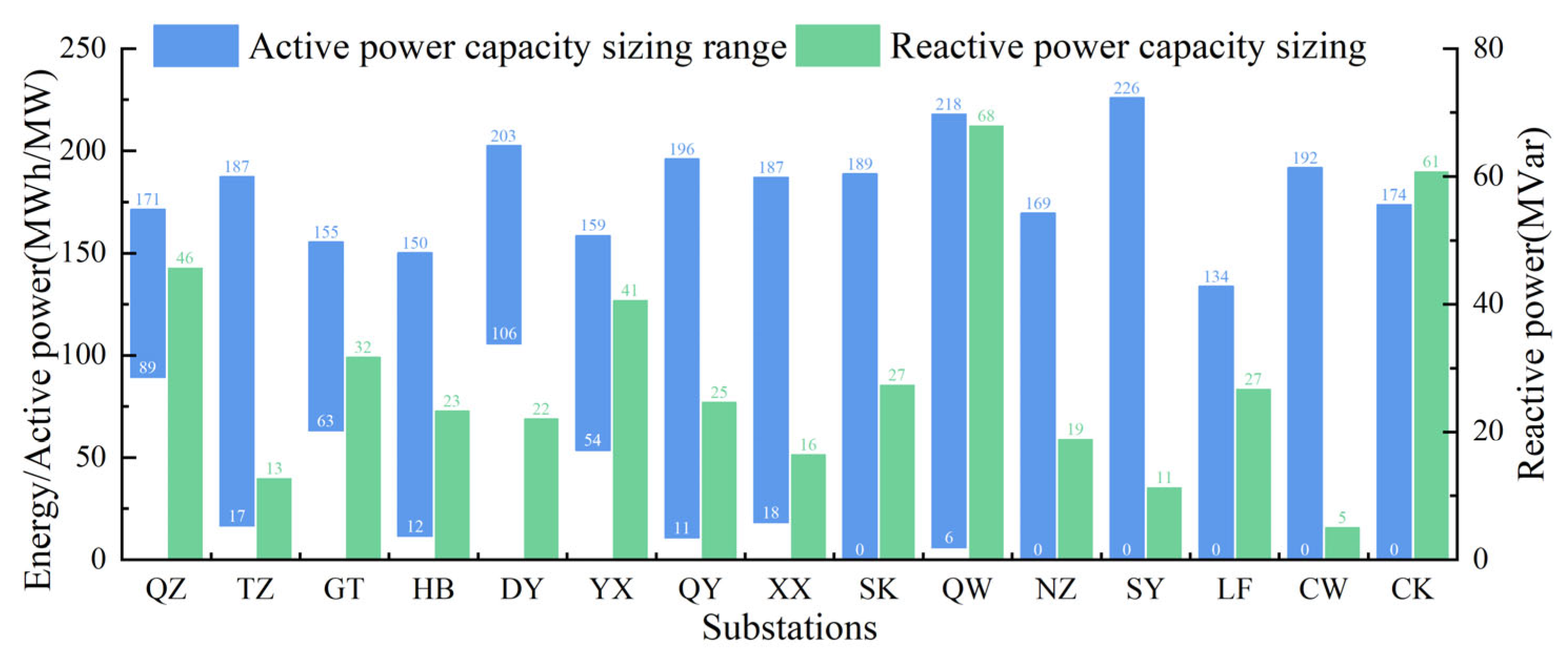
Using the Gurobi commercial solver, the optimal capacity planning model was solved for the screened severe scenario sets. The resulting planning for the 220 kV substations, as illustrated in Figure 2, exhibits significant differentiation, which reflects the model’s ability to tailor allocations to the specific characteristics of each site. A strong correlation between the demand ranking and the allocated capacity was observed: the top 40% of substations account for 90.17% of the total minimum configured active power, whereas the lowest-ranked sites were assigned a minimum capacity of zero. This disparity validates the effectiveness of the proposed priority assessment method in accurately distinguishing site-specific needs. Notably, the largest minimum active power capacity (106 MW) was assigned to the DY substation.

Figure 2. Results of Optimal ESS Planning for the 220 kV Substations.

It is also noteworthy that reactive power allocations vary significantly among the sites. The two substations receiving the largest reactive power capacities, QW (68 MVar) and CK (61 MVar), were ranked lower in the overall demand assessment. This is attributed to two factors: firstly, the indicators correlated with reactive power were assigned lower weights in the comprehensive ranking; secondly, the unit cost of reactive power is substantially lower, causing the model to preferentially deploy it when operational security can be met without active power. The allocation of reactive power capacity to all substations indicates that such issues are prevalent system-wide and that, in addition to active power regulation, many sites face significant voltage stability challenges.

In terms of the active power configuration range, the largest interval (226 MW) was identified for the SY substation, while the smallest (only 82 MW) was attributed to the QZ substation. This narrow range signifies a severe configuration bottleneck at the QZ site, highlighting the urgent need for alternative solutions to be explored. Overall, these planning results embody the principle of a site-specific and precisely targeted allocation strategy, thereby providing a scientific basis for the efficient utilization of the grid’s ESS resources.

To visually demonstrate the technical benefits of the proposed method, the DY substation, which has the highest requirement for active power configuration (i.e., the largest lower bound), is selected as a case study. A comparative analysis of the improvement in key security indicators before and after the deployment of an ESS is conducted.

The indicator values before and after deployment, along with their respective improvement rates under different typical severe scenarios, are presented in Table 5 and Table 6. Specifically: Regarding the d_LD: The most significant improvement for this indicator is observed in ‘Scenario 2’ of the corresponding severe scenario set. After ESS deployment, the indicator value for this scenario is optimized from 0.579 (which exceeded the safety threshold) to 0.4, corresponding to an improvement rate of 30.91%. The issue of an excessive peak-to-valley difference is thereby effectively mitigated. Regarding the d_PF: For this indicator, an improvement rate exceeding 90% is achieved in most of the severe scenarios. It is thereby strongly confirmed that a low power factor is a prevalent and critical bottleneck issue at the DY substation, for which an extremely effective solution is provided by the deployment of ESS, particularly through its reactive power compensation capabilities.

Table 5. Before-and-After Comparison of the d_LD Indicator for the Severe Scenario Set at the 220 kV DY Substation.

Indicator	Scenario 1			Scenario 2			Scenario 3
	Before	After	Improvement (%)	Before	After	Improvement (%)	Before	After	Improvement (%)
dpeak	0.2768	0.2872	−3.75	0.3366	0.3446	−2.38	0.2399	0.2357	1.75
dLD	0.551	0.4	27.41	0.579	0.4	30.91	0.5254	0.4	23.87
dPF	0.9399	0.05	94.68	0.664	0.05	92.47	0.9461	0.05	94.72
dRF	0.0697	0.1108	−59.04	0.0613	0.0823	−34.32	0.0753	0.0802	−6.44
drev	0.0025	0.0131	−423.89	0	0.0156	0	0.0254	0.0652	−156.68

Table 6. Before-and-After Comparison of the d_PF Indicator for the Severe Scenario Set at the 220 kV DY Substation.

Indicator	Scenario 1			Scenario 2			Scenario 3
	Before	After	Improvement (%)	Before	After	Improvement (%)	Before	After	Improvement (%)
dpeak	0	0	0	0	0	0	0	0	0
dLD	0.2661	0.4	−50.3	0.1839	0.4	−117.52	0.351	0.4	−13.97
dPF	0.8812	0.05	94.33	0.9281	0.05	94.61	0.8978	0.05	94.43
dRF	0.0495	0.0635	−28.34	0.0948	0.0865	8.79	0.0587	0.072	−22.82
drev	0.0378	0.0673	−78.19	0.047	0.0635	−35.33	0.0078	0.0297	−280.73

5.3. Analysis of Investment Return on ESS

Based on the preceding evaluation results, an investment return analysis was conducted for the QZ substation, which was identified as the highest-priority site. In accordance with the capacity configuration results, a 100 MW/200 MWh Lithium Iron Phosphate (LFP) ESS was modeled for the site; the associated cost and operational parameters are detailed in Appendix A.5.

The life-cycle cost and benefit composition for this project is presented in Table 7. It is observed that the total cost is dominated by the initial investment of 179 million CNY, which constitutes 66% of the life-cycle expenditure. On the revenue side, TOU price arbitrage is the primary income source, generating 492 million CNY (86.7%), while frequency regulation services provide a significant secondary revenue stream (13.3%). It is noteworthy that revenue from dedicated peak regulation was found to be negligible, as the marginal returns from TOU arbitrage far exceed the compensation offered in the peak regulation market. Ultimately, a total net revenue of 299 million CNY is realized over the project’s lifetime.

Table 7. Life-Cycle Cost and Benefit Composition for the QZ Substation ESS Project.

Category	Item	Value (104 CNY)
Cost Composition	Initial Investment	17,930.40
	O&M Cost	9357.42
	Charging Cost	/
	Replacement Cost	0
	Salvage Value	385.27
	Total Life-Cycle Cost	26,902.55
Benefit Composition	TOU Arbitrage Revenue	49,211.02
	Peak Regulation Revenue	0.53
	Frequency Regulation Revenue	7542.35
	Net Revenue	29,851.35

The economic evaluation metrics for the QZ ESS project are presented in Table 8. The project’s robust profitability is demonstrated by an achieved IRR of 32.28%, a value substantially exceeding the 5% benchmark rate. Concurrently, a DPP of only 3.24 years and a static payback period (SPP) of 2.92 years were determined; a duration significantly shorter than the 10-year design lifetime, indicating that the initial investment can be rapidly recouped before the project enters its long-term profitability phase. Furthermore, the calculated LCOS of 0.3236 CNY/kWh is markedly lower than the local peak and critical-peak tariffs, which constitutes the core competitive advantage of the business model.

Table 8. Economic Evaluation Results for the QZ Substation ESS Project.

Evaluation Metric	220 kV QZ Substation	Acceptance Criterion
LCOS	0.3236 CNY/kWh	≤Peak/Critical-Peak Tariff
AAC	3484 Million CNY/year	/
SPP	2.92 years	≤Design Lifetime (10 years)
DPP	3.24 years	≤Design Lifetime (10 years)
IRR	32.28%	>Benchmark Rate (5%)
Evaluation Metric	220 kV QZ Substation	Acceptance Criterion

To investigate the project’s sensitivity to key techno-economic parameters, a sensitivity analysis was conducted on the impact of fluctuations in the initial investment cost and the peak-to-valley price differential on the IRR, LCOS, and DPP. These two core variables were independently varied by ±10% and ±20% from their baseline values, with the results presented in Table 9. It was found that for every 10% decrease in initial investment cost, the IRR is increased by more than four percentage points, and the DPP is shortened by approximately 0.4 years. A similar effect was observed for the price differential, where a 10% increase improves the IRR by nearly four percentage points and reduces the DPP by a comparable duration. The LCOS was observed to be sensitive only to investment cost and is unaffected by the market price spread. Notably, even under a 20% adverse fluctuation in either variable, the project’s IRR is maintained above 20%, which demonstrates that the project possesses both high return potential and significant robustness against financial risks.

Table 9. Results of Single-Factor Sensitivity Analysis for Key Parameters.

Sensitivity Factor	Variation	IRR (%)	DPP (years)	LCOS (CNY/kWh)
Initial Investment Cost	+20%	21.98	4.53	0.3994
	+10%	24.99	4.07	0.3713
	0%	28.53	3.63	0.3433
	−10%	32.73	3.20	0.3152
	−20%	37.87	2.79	0.2871
Peak-to-Valley Price Differential	+20%	35.85	2.94	0.3433
	+10%	32.23	3.25	0.3433
	0%	28.53	3.63	0.3433
	−10%	24.74	4.10	0.3433
	−20%	20.82	4.73	0.3433

6. Conclusions

In this paper, an optimal siting and sizing methodology for GSESS, which considers multi-dimensional demand indicators, was proposed and validated through a case study on the 220 kV substations in QZ City of China. The main conclusions are as follows:

(1)

A generally high demand for ESS was observed across the 220 kV substations in QZ, with 33% of the sites achieving scores above 0.5. The demand is characterized by a relatively balanced distribution, dominated by the needs for high-load mitigation and voltage quality improvement. Furthermore, peak loads are temporally dispersed throughout the year, indicating that the configuration of large-capacity, multi-functional ESS is advisable, primarily to address high-loading and voltage quality issues.

(2)

At the 220 kV voltage level, the largest minimum active power configuration is required at the DY substation (104 MW), while the largest reactive power configuration is found at the QW substation (68 MVar).

(3)

The investment return analysis, conducted for the QZ substation as a case study, demonstrates that under an operational model leveraging multiple application scenarios, an IRR as high as 28.53% and a DPP of only 3.63 years are achieved. These results indicate a promising investment outlook for the project.

Appendix A.1. Quantification of Life-Cycle Costs and Benefits

The Life-Cycle Cost is defined as the total expenditure incurred throughout the entire lifespan of an ESS, encompassing construction, operation, maintenance, and decommissioning.

(1)

Initial Investment Cost

$$C_{\mathrm{INV}}=C_{\mathrm{ESS}}+C_{\mathrm{PCS}}+C_{\mathrm{BOP}}=C_{\mathrm{E}}{E}_{\mathrm{rat}}+C_{\mathrm{P}}{P}_{\mathrm{rat}}+C_{\mathrm{B}}{E}_{\mathrm{rat}}$$

(A1)

where $C_{\mathrm{INV}}$ is the initial investment cost; $C_{\mathrm{ESS}}$, $C_{\mathrm{PCS}}$, and $C_{\mathrm{BOP}}$ are the costs of the battery system, the Power Conversion System (PCS), and the Balance of Plant (BOP), respectively; $C_{\mathrm{E}}$ is the unit cost of the battery system per unit of energy capacity; $E_{\mathrm{rat}}$ and $P_{\mathrm{rat}}$ are the rated energy and power capacities; $C_{\mathrm{P}}$ is the unit cost of the PCS per unit of power; and $C_{\mathrm{B}}$ is the unit energy cost for the BOP.

(2)

Operation and Maintenance (O&M) Cost

$$C_{\mathrm{OMC}}={\displaystyle \sum _{i=1}^I\frac{C_{\mathrm{INV}}\times r_{\mathrm{OM}}+c_{\mathrm{OM}}\times E_{\mathrm{all},i}}{{\left(1+r_{\mathrm{d}}\right)}^i}}$$

(A2)

where $C_{\mathrm{OMC}}$ is the total present value of the annual O&M costs; $r_{\mathrm{OM}}$ is the fixed maintenance cost rate; $c_{\mathrm{OM}}$ is the variable maintenance cost per unit of energy throughput; $E_{\mathrm{all},i}$ is the total energy throughput in year i; I is the operational lifetime of the ESS; and $r_{\mathrm{d}}$ is the discount rate.

(3)

Replacement Cost

$$C_{\mathrm{RC}}={\displaystyle \sum _{j=1}^J\frac{r_{\mathrm{rep}}\times C_{\mathrm{ESS}}}{{\left(1+r_{\mathrm{d}}\right)}^j}}$$

(A3)

where $C_{\mathrm{RC}}$ is the total present value of the replacement costs; $r_{\mathrm{rep}}$ is the proportion of the battery capacity that requires replacement; and j is the year in which the replacement occurs.

(4)

Charging Cost

$$C_{\mathrm{CH}}={\displaystyle \sum _{i=1}^I\frac{{\displaystyle \sum _t{C}_{\mathrm{el}}\times E_{\mathrm{ch},t,i}}}{{\left(1+r_{\mathrm{d}}\right)}^i}}$$

(A4)

where $C_{\mathrm{CH}}$ is the total present value of the charging costs; $C_{\mathrm{el}}$ is the unit cost of charging per kWh; and $E_{\mathrm{ch},t,i}$ is the actual energy charged during time step t of year i.

(5)

Decommissioning and Salvage Cost

$$C_{\mathrm{DC}}={\displaystyle \frac{r_{\mathrm{EOL}}\cdot C_{\mathrm{INV}}}{{\left(1+r_{\mathrm{d}}\right)}^I}}$$

(A5)

where $r_{\mathrm{EOL}}$ is the salvage cost rate.

The revenue streams for GSESS comprise the TOU price arbitrage, peak regulation services, and frequency regulation services.

(1)

TOU Price Arbitrage

$$R_{\mathrm{ARB}}={\displaystyle \sum _{i=1}^I\frac{{\displaystyle \sum _t(E_{\mathrm{dis},t,i}-E_{\mathrm{ch},t,i})C_t}}{{\left(1+r_{\mathrm{d}}\right)}^i}}$$

(A6)

where $R_{\mathrm{ARB}}$ is the total present value of the revenue from TOU arbitrage; $E_{\mathrm{dis},t,i}$ and $E_{\mathrm{ch},t,i}$ are the energy discharged and charged, respectively, during time interval t of year i; and $C_t$ is the electricity price at time t.

(2)

Peak Regulation Revenue

$$R_{\mathrm{p}}={\displaystyle \sum _{i=1}^I\frac{{\displaystyle \sum _t{P}_{\mathrm{p},t}\times {\rho }_{\mathrm{p}}\times \mathrm{\Delta }t}}{{\left(1+r_{\mathrm{d}}\right)}^i}}$$

(A7)

where $R_{\mathrm{p}}$ is the total present value of the revenue from peak regulation ancillary services; ${\rho }_{\mathrm{p}}$ is the daily tariff for peak regulation; $P_{\mathrm{p},t}$ is the daily regulation power.

(3)

Frequency Regulation Revenue

$$R_{\mathrm{fc}}={\displaystyle \sum _{i=1}^I\frac{{\displaystyle \sum _t{E}_{\mathrm{f},t}\times {\rho }_{\mathrm{fc}}\times \mathrm{\Delta }t}}{{\left(1+r_{\mathrm{d}}\right)}^i}}$$

(A8)

where $R_{\mathrm{fc}}$ is the total present value of the revenue from frequency regulation capacity compensation; $E_{\mathrm{f},t}$ is the regulation capacity dispatched at time interval t; and ${\rho }_{\mathrm{fc}}$ is the compensation price for frequency regulation capacity.

The compensation for frequency regulation mileage is calculated as follows:

$$R_{\mathrm{fm}}={\displaystyle \sum _{i=1}^I\frac{{\displaystyle \sum _t{P}_{\mathrm{f},t}\times {\rho }_{\mathrm{fc}}\times \mathrm{\Delta }t}}{{\left(1+r_{\mathrm{d}}\right)}^i}}$$

(A9)

where $R_{\mathrm{fm}}$ is the total present value of the revenue from mileage compensation; $P_{\mathrm{f},t}$ is the actual regulation power delivered; and ${\rho }_{\mathrm{fc}}$ is the compensation price for regulation mileage.

Appendix A.2. Fundamental Operational Constraints for ESS

$$S_{\mathrm{ESD}}^t=(1-{\gamma }_{\mathrm{ESD}}^{\mathrm{los}})S_{\mathrm{ESD}}^{t-1}+(P_{\mathrm{ESD}}^{t,\mathrm{cha}}{\gamma }_{\mathrm{ESD}}^{\mathrm{cha}}-{\displaystyle \frac{P_{\mathrm{ESD}}^{t,\mathrm{dis}}}{{\gamma }_{\mathrm{ESD}}^{\mathrm{dis}}}})\mathrm{\Delta }t$$

(A10)

$$S_{\mathrm{ESD}}^0=S_{\mathrm{ESD}}^T$$

(A11)

$$S_{\mathrm{ESD},\min }\le S_{\mathrm{ESD}}^t\le S_{\mathrm{ESD},\max }$$

(A12)

$$0\le P_{\mathrm{ESD}}^{t,\mathrm{cha}}\le P_{\mathrm{ESD},\max }^{\mathrm{cha}}{B}_{\mathrm{ESD}}^{t,\mathrm{cha}}$$

(A13)

$$0\le P_{\mathrm{ESD}}^{t,\mathrm{dis}}\le P_{\mathrm{ESD},\max }^{\mathrm{dis}}{B}_{\mathrm{ESD}}^{t,\mathrm{dis}}$$

(A14)

$$B_{\mathrm{ESD}}^{t,\mathrm{cha}}+B_{\mathrm{ESD}}^{t,\mathrm{dis}}\le 1$$

(A15)

where $S_{\mathrm{ESD}}^t$ and $S_{\mathrm{ESD}}^{t-1}$ are the state-of-charge(SOC) at time steps t and t-1, respectively; $P_{\mathrm{ESD}}^{t,\mathrm{cha}}$ and $P_{\mathrm{ESD}}^{t,\mathrm{dis}}$ are the charging and discharging power of the ESS; ${\gamma }_{\mathrm{ESD}}^{\mathrm{los}}$, ${\gamma }_{\mathrm{ESD}}^{\mathrm{cha}}$, and ${\gamma }_{\mathrm{ESD}}^{\mathrm{dis}}$ are the self-discharge, charging, and discharging loss coefficients; $S_{\mathrm{ESD}}^0$ and $S_{\mathrm{ESD}}^T$ are the SOC values at the beginning and end of the dispatch cycle; T is the total number of dispatch intervals; $S_{\mathrm{ESD},\max }$ and $S_{\mathrm{ESD},\min }$ are the upper and lower limits for the SOC; $P_{\mathrm{ESD},\max }^{\mathrm{cha}}$ and $P_{\mathrm{ESD},\max }^{\mathrm{dis}}$ are the maximum charging and discharging power ratings; and $B_{\mathrm{ESD}}^{t,\mathrm{cha}}$ and $B_{\mathrm{ESD}}^{t,\mathrm{dis}}$ are auxiliary binary variables indicating the charge/discharge state at time step t.

Appendix A.3. ESS Lifetime Degradation Model Based on the Rainflow Counting Method

Firstly, a power function is used to model the relationship between the ESS’s cycle life and its depth of discharge (DoD), with the function being fitted to industry-standard test data that correlates the maximum number of charge/discharge cycles to the corresponding DoD:

$$N_{\mathrm{Life}}^t=N_0{(d_{\mathrm{DOD}}^t)}^{-k_p}$$

(A16)

where $d_{DOD}^t$ is the ESS’s DoD at time step t; $N_{\mathrm{Life}}^t$ is the maximum number of cycles the ESS can withstand at that specific DoD; $N_0$ is the maximum cycle count at 100% DoD; and $k_p$ is a fitting parameter.

Subsequently, $N_{\mathrm{Life}}^t$ is converted into an equivalent cycle count normalized to a 100% depth of discharge:

$$N_{\mathrm{eq}}^t={\displaystyle \frac{N_0}{N_{\mathrm{Life}}^t}}{(d_{\mathrm{DOD}}^t)}^{-k_p}$$

(A17)

To incorporate the non-convex, non-linear relationship presented in Equation (A17) into a linear optimization framework, a piecewise linearization method is employed. This transforms the variable $N_{\mathrm{eq}}^t$ into the form shown in Equation (A18), subject to the additional constraints specified in Equations (A19) and (A20):

$$N_{\mathrm{eq}}^t={(d_{\mathrm{DOD}}^t)}^{-k_p}={({\displaystyle \sum _{k=1}^K{d}_{\mathrm{DOD}}^{t,k}})}^{-k_p}\approx {\displaystyle \sum _{k=1}^K[(K_{\mathrm{seg}}^k{d}_{\mathrm{DOD}}^{t,k}+B_{\mathrm{seg}}^k)g^{t,k}]}$$

(A18)

$$d_{\mathrm{DOD}}^{k,\min }{g}^{t,k}\le d_{\mathrm{DOD}}^{t,k}\le d_{\mathrm{DOD}}^{k,\max }{g}^{t,k}$$

(A19)

$${\displaystyle \sum _{k=1}^K{g}^{t,k}}=B_{\mathrm{cyc}}^t$$

(A20)

where K is the number of linear segments; $K_{\mathrm{seg}}^k$ and $B_{\mathrm{seg}}^k$ are the slope and intercept of each segment, respectively; $g^{t,k}$ is an auxiliary binary variable, which equals 1 if the DoD at time t falls within the k-th segment (in which case $d_{\mathrm{DOD}}^{t,k}=d_{\mathrm{DOD}}^t$) and 0 otherwise (in which case $d_{\mathrm{DOD}}^{t,k}=0$); $d_{\mathrm{DOD}}^{k,\max }$ and $d_{\mathrm{DOD}}^{k,\min }$ are the lower and upper bounds of the DoD for the k-th segment; and $B_{\mathrm{cyc}}^t$ is a binary variable indicating the cycle state, where a value of 1 signifies that a charge/discharge cycle has occurred at time t.

Building upon this, a constraint is imposed via Equation (A21) to limit the cumulative degradation within a permissible daily average threshold, thereby ensuring the ESS achieves its designed lifetime. Furthermore, as the $d_{\mathrm{DOD}}^t$ is a decision variable dependent on the charge/discharge strategy, its relationship with the SOC and the cycling state is defined by the constraints presented in Equations (A22) and (A23).

$${\displaystyle \sum _{t=1}^T{N}_{\mathrm{eq}}^t}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{k=1}^K[(K_{\mathrm{seg}}^k{d}_{\mathrm{DOD}}^{t,k}+B_{\mathrm{seg}}^k)g^{t,k}]}}\le N_{\mathrm{day}}^{\max }$$

(A21)

$$d_{\mathrm{DOD}}^t=(1-S_{\mathrm{ESD}}^{t-1})B_{\mathrm{cyc}}^t$$

(A22)

$$B_{\mathrm{ESD}}^{t,\mathrm{cha}}-B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}\le B_{\mathrm{cyc}}^t\le \min \left\{B_{\mathrm{ESD}}^{t,\mathrm{cha}},1-B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}\right\}$$

(A23)

where $N_{\mathrm{day}}^{\max }$ is the maximum average daily cycle count, which is derived from the expected lifetime of the ESS, $N_{\mathrm{day}}^{\max }=N_0/N_{\mathrm{Life}}^{\mathrm{EXP}}$, $N_{\mathrm{Life}}^{\mathrm{EXP}}$ is the expected lifetime of the ESS; and $B_{\mathrm{ESD}}^{t,\mathrm{cha}}$ and $B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}$ are auxiliary binary variables representing the charging state at time steps t and t − 1, respectively. A charge/discharge cycle is considered complete if, and only if, the system transitions from a discharging to a charging state, i.e., when $B_{\mathrm{ESD}}^{t-1,\mathrm{cha}}=0$ and $B_{\mathrm{ESD}}^{t,\mathrm{cha}}=1$. It is noted that both Equations (A21) and (A22) contain non-convex, non-linear terms arising from the product of binary and continuous variables, which precludes their direct use in a linear optimization model and thus necessitates linearization. Specifically, based on the conditions established in Equation (A19), it is known that when $g^{t,k}=0$, $d_{\mathrm{DOD}}^{t,k}=0$, and when $g^{t,k}=1$, $d_{\mathrm{DOD}}^{t,k}{g}^{t,k}=d_{\mathrm{DOD}}^{t,k}$. Consequently, Equation (A21) can be equivalently relaxed into the form presented in Equation (A24). Subsequently, Equation (A22) is linearized into the constraints shown in Equations (A25) and (A26) by employing the Big-M method.

$${\displaystyle \sum _{t=1}^T{\displaystyle \sum _{k=1}^K(K_{\mathrm{seg}}^k{d}_{\mathrm{DOD}}^{t,k}+B_{\mathrm{seg}}^k{g}^{t,k})}}\le N_{\mathrm{day}}^{\max }$$

(A24)

$$0\le d_{\mathrm{DOD}}^t\le 1-S_{\mathrm{ESD}}^{t-1}$$

(A25)

$$(1-S_{\mathrm{ESD}}^{t-1})-M(1-B_{\mathrm{cyc}}^t)\le d_{\mathrm{DOD}}^t\le M{B}_{\mathrm{cyc}}^t$$

(A26)

where M is a sufficiently large positive number. The complete linearized ESS degradation model, based on the rainflow counting method, thus comprises the constraints presented in Equations (A19) and (A20) and Equations (A23) and (A26).

Appendix A.4. Calculation Methodology for the Internal Rate of Return

As the direct analytical solution of the high-order univariate equation for the IRR, given in Equation (A27), is generally infeasible, an approximate solution is typically obtained using the linear interpolation method. This procedure is initiated by estimating two distinct discount rates, $i_1$ and $i_2$, such that their corresponding Net Present Values, ${\mathrm{NPV}}_1$ and ${\mathrm{NPV}}_2$, bracket a value of zero (i.e., ${\mathrm{NPV}}_1$ > 0 and ${\mathrm{NPV}}_2$ < 0). The approximate value of the IRR is then determined from these points via the formulation in Equation (A28).

$${\displaystyle {\sum }_{t=0}^n\frac{C{I}_t-C{O}_t}{{(1+IRR)}^t}}=0$$

(A27)

$$IRR=i_1+{\displaystyle \frac{\left|{\mathrm{NPV}}_1\right|}{\left|{\mathrm{NPV}}_1\right|+\left|{\mathrm{NPV}}_2\right|}}(i_2-i_1)$$

(A28)

Appendix A.5. Parameters of the LFP Battery ESS

For a 100 MW/200 MWh LFP ESS, an EPC (Engineering, Procurement, and Construction) cost of 0.964 CNY/Wh is assumed. Based on this unit price and typical industry cost breakdowns—where the PCS and BOP account for approximately 14% and 25%, respectively—the costs for the battery system itself, the PCS, and the BOP are calculated to be 58.804 million CNY, 13.496 million CNY, and 24.10 million CNY, respectively. The corresponding unit costs are thus derived as 588.04 CNY/kWh, 269.92 CNY/kW, and 241 CNY/kWh. These cost parameters, along with other key technical specifications, are detailed in Table A1. The TOU pricing mechanism adopted for the economic analysis is based on the official policy of Zhejiang Province, with the peak and off-peak periods defined as shown in Table A2.

Table A1. Parameters of the 100 MW/200 MWh LFP Battery ESS.

Parameter	Value	Parameter	Value
$\mathrm{Unit} \mathrm{Energy} \mathrm{Capacity} \mathrm{Cos}\mathrm{t} C_{\mathrm{E}}$	588.04 CNY/kWh	$\mathrm{Discount} \mathrm{Rate} r_{\mathrm{d}}$	5%
$\mathrm{Unit} \mathrm{Power} \mathrm{Capacity} \mathrm{Cos}\mathrm{t} C_{\mathrm{P}}$	269.92 CNY/kW	$\mathrm{Fixed} \mathrm{O}\&\mathrm{M} \mathrm{Rate} r_{\mathrm{OM}}$	3%
$\mathrm{Unit} \mathrm{Energy} \mathrm{Cos}\mathrm{t} \mathrm{for} \mathrm{BOP} C_{\mathrm{B}}$	241 CNY/kWh	$\mathrm{Variable} \mathrm{O}\&\mathrm{M} \mathrm{Cos}\mathrm{t} c_{\mathrm{OM}}$	0.03 CNY/kWh
$\mathrm{Salvage} \mathrm{Cos}\mathrm{t} \mathrm{Rate} r_{\mathrm{EOL}}$	3.5%	$\mathrm{Maximum} \mathrm{Cycle} \mathrm{Count} N_0$	6000
Round-Trip Efficiency	90%	Design Lifetime	10 years

Table A1. Parameters of the 100 MW/200 MWh LFP Battery ESS.

Parameter	Value	Parameter	Value
$\mathrm{Unit} \mathrm{Energy} \mathrm{Capacity} \mathrm{Cos}\mathrm{t} C_{\mathrm{E}}$	588.04 CNY/kWh	$\mathrm{Discount} \mathrm{Rate} r_{\mathrm{d}}$	5%
$\mathrm{Unit} \mathrm{Power} \mathrm{Capacity} \mathrm{Cos}\mathrm{t} C_{\mathrm{P}}$	269.92 CNY/kW	$\mathrm{Fixed} \mathrm{O}\&\mathrm{M} \mathrm{Rate} r_{\mathrm{OM}}$	3%
$\mathrm{Unit} \mathrm{Energy} \mathrm{Cos}\mathrm{t} \mathrm{for} \mathrm{BOP} C_{\mathrm{B}}$	241 CNY/kWh	$\mathrm{Variable} \mathrm{O}\&\mathrm{M} \mathrm{Cos}\mathrm{t} c_{\mathrm{OM}}$	0.03 CNY/kWh
$\mathrm{Salvage} \mathrm{Cos}\mathrm{t} \mathrm{Rate} r_{\mathrm{EOL}}$	3.5%	$\mathrm{Maximum} \mathrm{Cycle} \mathrm{Count} N_0$	6000
Round-Trip Efficiency	90%	Design Lifetime	10 years

Table A2. Definition of TOU Periods in Zhejiang Province.

Season	Period	Time
Spring/Autumn (February–June, September–November)	Peak	8:00–11:00, 13:00–17:00
	Shoulder	17:00–24:00
	Off-Peak	0:00–8:00, 11:00–13:00
Summer/Winter (January, July, August, December)	Critical-Peak	9:00–11:00, 15:00–17:00
	Peak	8:00–9:00, 17:00–23:00
	Shoulder	13:00–15:00, 23:00–24:00
	Off-Peak	0:00–8:00, 11:00–13:00

Table A2. Definition of TOU Periods in Zhejiang Province.

Season	Period	Time
Spring/Autumn (February–June, September–November)	Peak	8:00–11:00, 13:00–17:00
	Shoulder	17:00–24:00
	Off-Peak	0:00–8:00, 11:00–13:00
Summer/Winter (January, July, August, December)	Critical-Peak	9:00–11:00, 15:00–17:00
	Peak	8:00–9:00, 17:00–23:00
	Shoulder	13:00–15:00, 23:00–24:00
	Off-Peak	0:00–8:00, 11:00–13:00