Development of Two-Wrinkled Tubes Using an Electrostatic Structural Analysis
Abstract
1. Introduction
1.1. Tube Deformation Processes
1.2. Numerical Study Applied to Electromagnetic Tube Forming
1.3. State of the Art: Wrinkled Tube in Metal Sheets by Forming
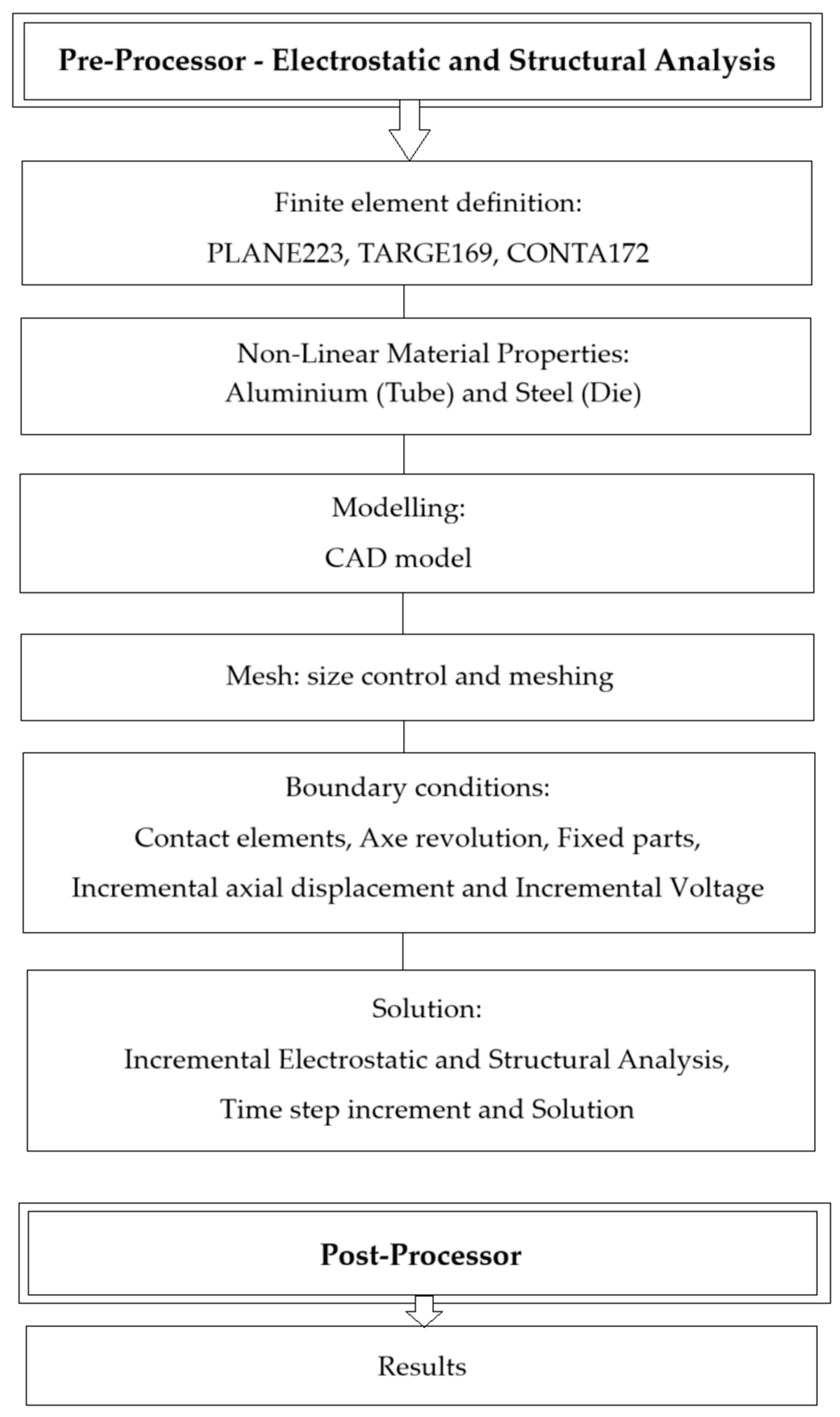
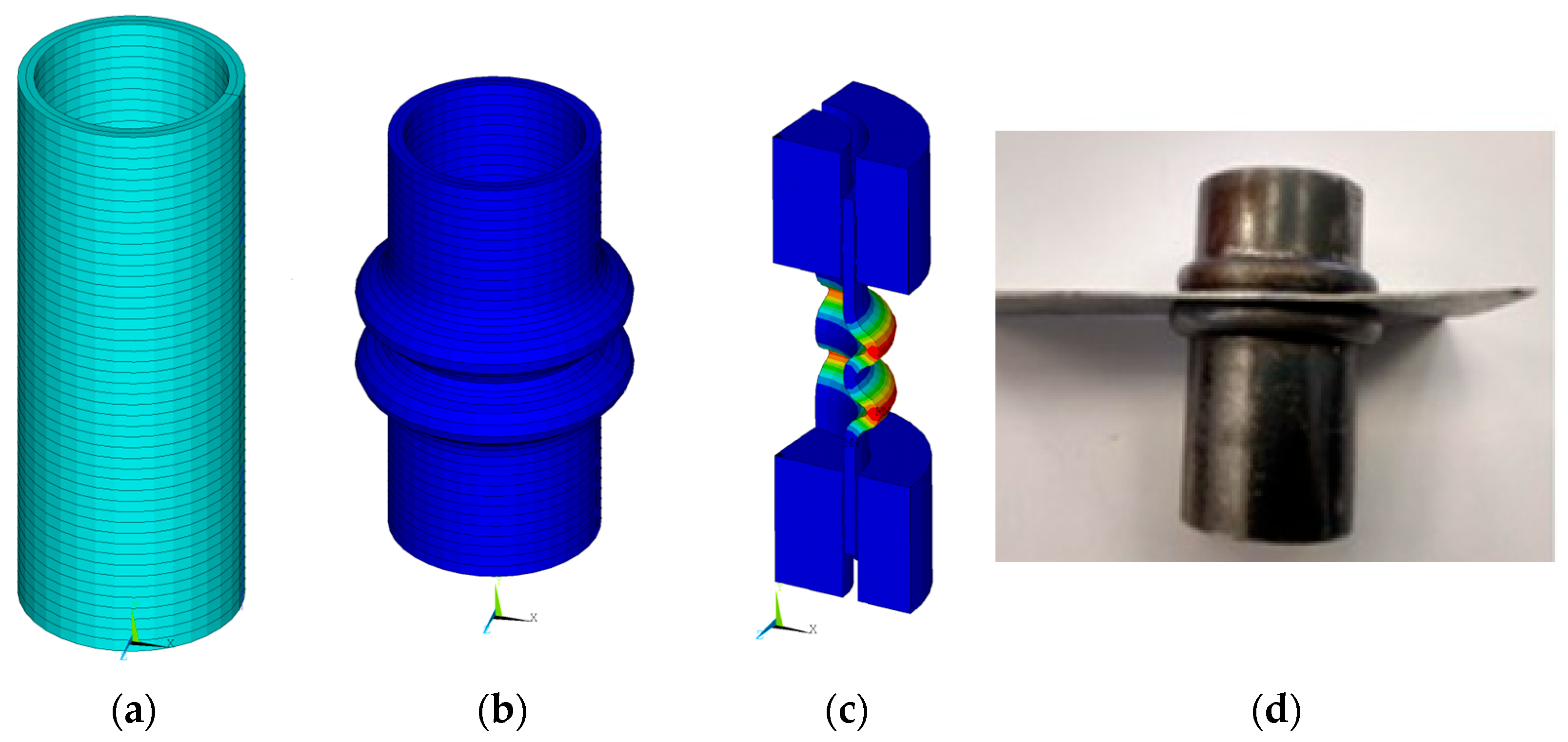
2. Materials and Methods
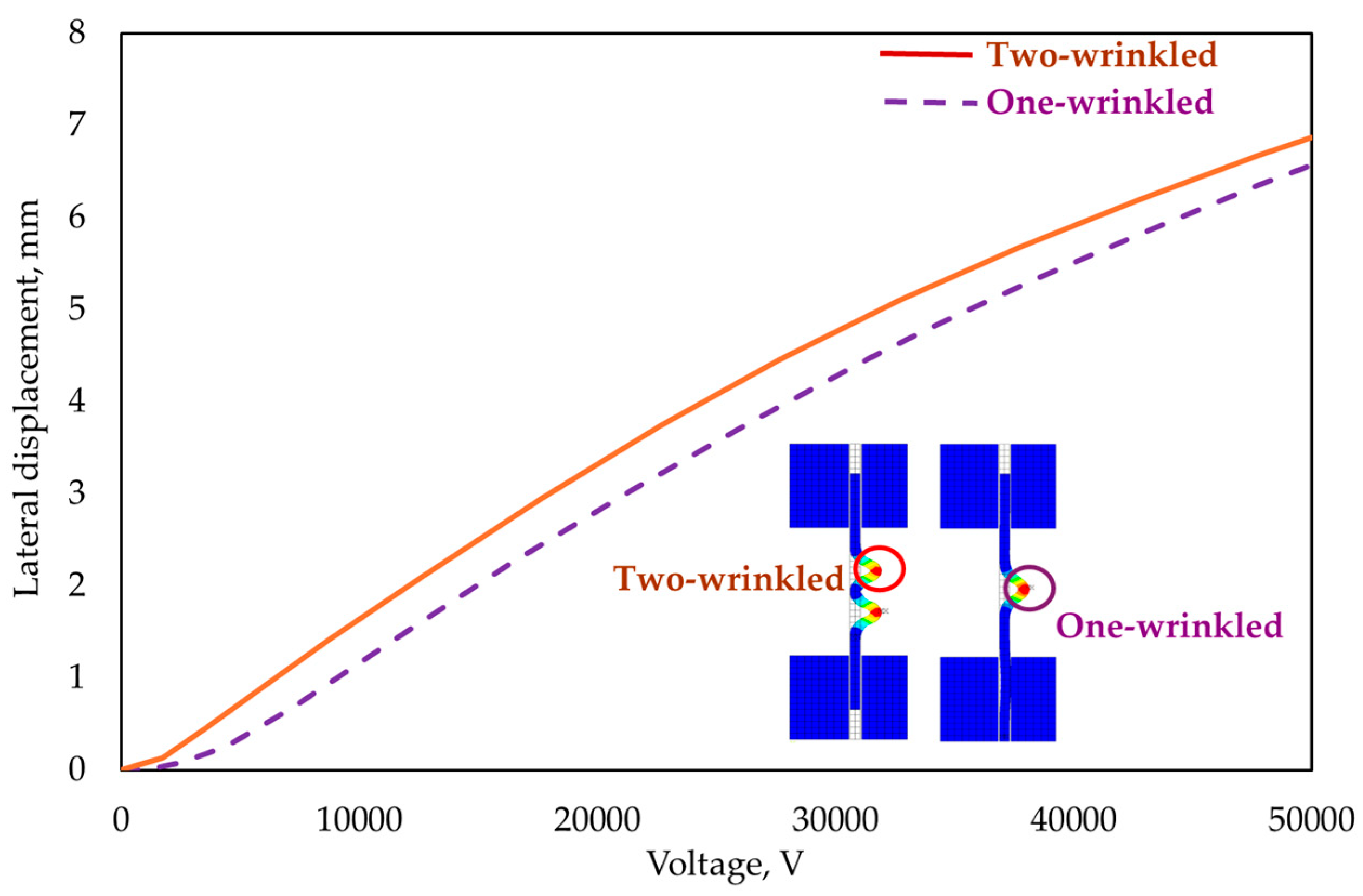
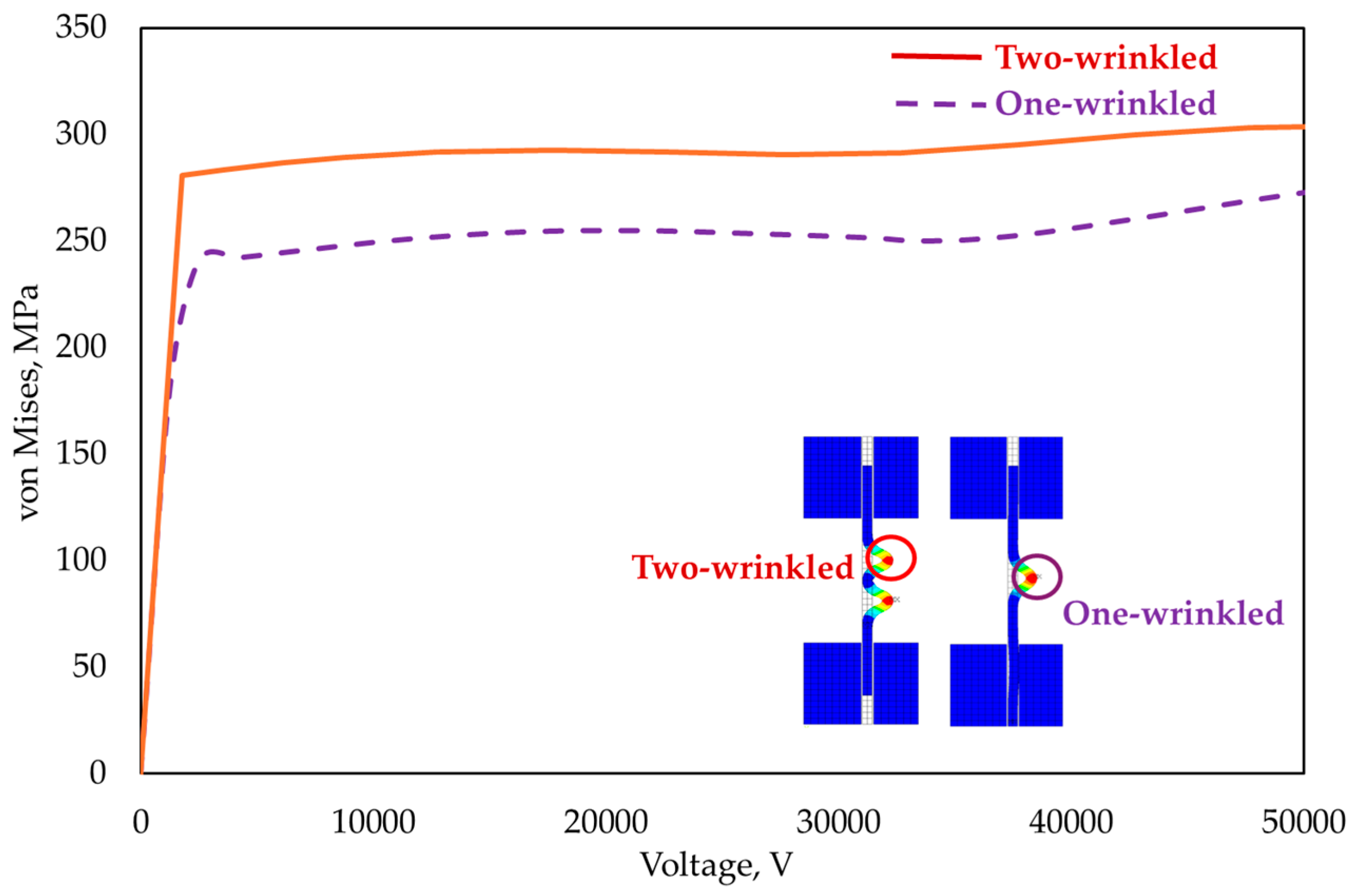
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.; Zhu, Y.; Chen, W.; Yuan, C.; Wang, L. Advanced Bending and Forming Technologies for Bimetallic Composite Pipes. Materials 2025, 18, 111. [Google Scholar] [CrossRef]
- Hwang, Y.-M.; Lin, S.L.; Xu, Z.Z. Finite Element Analysis of Tube End Forming and Process Design. Key Eng. Mater. 2020, 830, 69–76. [Google Scholar] [CrossRef]
- Nikhare, C.P. Fundamentals in Sheet and Tube Forming: Material Characterization, Conventional and Novel Processes and Involved Mechanics; Springer: Cham, Switzerland, 2020; pp. 1–39. [Google Scholar] [CrossRef]
- Cheng, C.; Guo, J.; El-Aty, A.A.; Tao, J.; Guo, X. Approach Based on Response-Surface Method to Optimize Lining of Dies Used in 3D Free-Bending Forming Technology. Chin. J. Mech. Eng. 2024, 37, 110. [Google Scholar] [CrossRef]
- Fadodun, O.; Olokuntoye, B.; Layeni, P.; Akinola, A. Finite Electroelastic Deformation of Dielectric Semilinear Hyperelastic Tubes. In Advanced Topics in Mechanics of Materials, Structures and Construction; Materials Research Proceedings; Materials Research Forum LLC: Millersville, PA, USA, 2023; Volume 31, pp. 336–346. [Google Scholar] [CrossRef]
- Melnikov, A.; Ogden, R.W. Finite Deformations of an Electroelastic Circular Cylindrical Tube. Z. Angew. Math. Phys. 2016, 67, 140. [Google Scholar] [CrossRef]
- Chen, C.-S.; Ou, J.-H.; Hsu, C.-J. Simulation Analysis of Shell Aluminum Alloy Tube for Neck-In Spinning Process. WSEAS Trans. Syst. 2012, 11, 385–397. [Google Scholar]
- Dorfmann, L.; Ogden, R.W. Waves and Vibrations in a Finitely Deformed Electroelastic Circular Cylindrical Tube. Proc. R. Soc. A 2020, 476, 20190701. [Google Scholar] [CrossRef]
- Soares, S.C.R.; Silva, G.C.; Fonseca, E.M.M. Computational Methodology for the Development of Wrinkled Tubes by Plastic Deformation. Appl. Sci. 2024, 14, 11126. [Google Scholar] [CrossRef]
- Bell, C.; Corney, J.; Zuelli, N.; Savings, D. A State-of-the-Art Review of Hydroforming Technology. Int. J. Mater. Form. 2020, 13, 789–828. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, X.; Wang, W.; Yu, T. An Improved Two-Arcs Deformational Theoretical Model of the Expansion Tubes. Int. J. Mech. Sci. 2017, 133, 240–250. [Google Scholar] [CrossRef]
- Silva, G.C.; Soares, S.C.R.; Vieira, A.L. Pipe Joining by Mechanical Conformation in Thin Sheets with Rotary Locking via a Notch. Eng. Struct. 2021, 249, 113151. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.; He, Z. Formability Assessment of Plastic Joining by Compression Instability for Thin-Walled Tubes. Int. J. Adv. Manuf. Technol. 2018, 97, 3423–3430. [Google Scholar] [CrossRef]
- Islam, M.R.; Wang, M. Digital Twin of Tube Hydroforming Press and Process. Int. J. Eng. Res. Appl. 2024, 14, 24–29. [Google Scholar]
- Bhujangrao, T.; Veiga, F.; Penalva, M.; Costas, A.; Ruiz, C. Three-Dimensional Finite Element Modelling of Sheet Metal Forming for the Manufacture of Pipe Components: Symmetry Considerations. Symmetry 2022, 14, 228. [Google Scholar] [CrossRef]
- Simonetto, E.; Wang, Q.; Ghiotti, A.; Bruschi, S. Forming Quality Indices for Tube Roll Forming: Definition and Modelling. In Proceedings of the International Conference on Manufacturing; Springer: Cham, Switzerland, 2023; pp. 569–576. [Google Scholar]
- Liu, Y.; Zhang, R.; Guo, Z.; Cheng, H. Research Overview on Rectangular Tube Cross-Section Deformation in Rotary-Draw Bending Process. J. Phys. Conf. Ser. 2024, 2706, 012069. [Google Scholar] [CrossRef]
- Volgin, V.M.; Kukhar, V.D.; Kireeva, A.E. Multiphysics Simulation of Electromagnetic Forming of Aluminum Alloy Tubes. In Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2018; pp. 1855–1866. [Google Scholar]
- Wang, D.; Zhu, Z.; Pan, F.; Sun, X.; Cui, X.; Fang, J. Numerical Simulation and Experimental Study on Axial Compression Electromagnetic Bulging of Aluminum Alloy Tube. Int. J. Adv. Manuf. Technol. 2024, 133, 3477–3493. [Google Scholar] [CrossRef]
- Savadkoohian, H.; Arezoodar, A.F.; Arezoo, B. Analytical and Experimental Study of Wrinkling in Electromagnetic Tube Compression. Int. J. Adv. Manuf. Technol. 2017, 93, 901–914. [Google Scholar] [CrossRef]
- Baines, K.; Duncan, J.L.; Johnson, W. Electromagnetic Metal Forming. Proc. Inst. Mech. Eng. 1965, 180, 93–110. [Google Scholar] [CrossRef]
- Hosseini, S.V.; Hatami, S.; Darvizeh, A.; Chizari, M. Analytical Modelling of Electromagnetic Bulging of Thin Metallic Tubes. In Recent Trends in Manufacturing and Materials Towards Industry 4.0; Springer: Singapore, 2021; pp. 791–803. [Google Scholar]
- Pawar, S.; Kore, S.D.; Nandy, A. Recent Advancement in Electromagnetic Forming Processes. In Recent Advances in Manufacturing Processes; Springer: Singapore, 2021; pp. 147–155. [Google Scholar]
- Pawar, S.; Kore, S.D.; Nandy, A. Magnetic Pulse Forming and Punching of Al Tubes—A Novel Technique for Forming and Perforation of Tubes. In Advances in Material Forming and Joining; Springer: Singapore, 2019; pp. 67–77. [Google Scholar]
- Xiong, Q.; Li, Z.; Tang, J.; Zhou, H.; Yang, M.; Song, X. A Flexible and Economical Method for Electromagnetic Flanging of Tubes with Field Shapers. Int. J. Adv. Manuf. Technol. 2021, 116, 1169–1177. [Google Scholar] [CrossRef]
- Xiong, Q.; Yang, M.; Tang, H.; Huang, H.; Song, X.; Qiu, L.; Yu, K.; Cao, Q. Flaring Forming of Small Tube Based on Electromagnetic Attraction. IEEE Access 2020, 8, 104753–104761. [Google Scholar] [CrossRef]
- Park, H.; Lee, J.; Kim, S.-J.; Lee, Y.; Kim, D. Form-Fit Joining Behavior Between an Aluminium Tube and Sheet Using Electromagnetic Forming. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012115. [Google Scholar] [CrossRef]
- Qiu, L.; Yu, Y.; Nie, X.; Yang, Y.; Su, P. Study on Material Deformation Performance and Electromagnetic Force Loading in Electromagnetic Tube Expansion Process. Trans. Chin. Electrotech. Soc. 2019, 34, 212–218. [Google Scholar] [CrossRef]
- Boutana, I.; Mekideche, M.R.; Bali, H. Analysis Model and Numerical Investigation of Electromagnetic Tube Expansion with Field Concentrator. In Proceedings of the 2023 International Conference on Systems, Signals and Devices, Mahdia, Tunisia, 20–23 February 2023; IEEE: Sousse, Tunisia, 2023; pp. 294–298. [Google Scholar]
- Xiong, Q.; Huang, H.; Xia, L.; Tang, H.; Qiu, L. A Research Based on Advance Dual-Coil Electromagnetic Forming Method on Flanging of Small-Size Tubes. Int. J. Adv. Manuf. Technol. 2019, 102, 4087–4094. [Google Scholar] [CrossRef]
- Geier, M.; Paese, E.; Rossi, R.; Rosa, P.A.R.; Homrich, R.P. Experimental Analysis of Interference-Fit Joining of Aluminum Tubes by Electromagnetic Forming. IEEE Trans. Appl. Supercond. 2020, 30, 1–6. [Google Scholar] [CrossRef]
- ASM International. Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; ASM Handbook; ASM International: Materials Park, OH, USA, 1990; Volume 2. [Google Scholar]
- Davis, J.R. Aluminum and Aluminum Alloys; ASM Specialty Handbook; ASM International: Materials Park, OH, USA, 1993. [Google Scholar]
- Marciniak, Z.; Duncan, J.L.; Hu, J. Mechanics of Sheet Metal Forming, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2002; ISBN 978-0-7506-4796-7. [Google Scholar]
- Altan, T.; Tekkaya, A.E. (Eds.) Metal Forming: Fundamentals and Applications; ASM International: Metals Park, OH, USA, 1983; ISBN 0-87170-155-7. [Google Scholar]
- Groover, M.P. Fundamentals of Modern Manufacturing: Materials, Processes, and Systems, 6th ed.; Wiley: Hoboken, NJ, USA, 2015; ISBN 978-1-118-97233-6. [Google Scholar]
- Capelli, F.; Riba, J.; Sanllehí, J. Finite Element Analysis to Predict Temperature Rise Tests in High-Capacity Substation Connectors. IET Gener. Transm. Distrib. 2017, 11, 2283–2291. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soares, S.C.R.; Silva, G.C.; Fonseca, E.M.M. Development of Two-Wrinkled Tubes Using an Electrostatic Structural Analysis. Appl. Sci. 2025, 15, 11912. https://doi.org/10.3390/app152211912
Soares SCR, Silva GC, Fonseca EMM. Development of Two-Wrinkled Tubes Using an Electrostatic Structural Analysis. Applied Sciences. 2025; 15(22):11912. https://doi.org/10.3390/app152211912
Chicago/Turabian StyleSoares, Samara C. R., Gilmar C. Silva, and Elza M. M. Fonseca. 2025. "Development of Two-Wrinkled Tubes Using an Electrostatic Structural Analysis" Applied Sciences 15, no. 22: 11912. https://doi.org/10.3390/app152211912
APA StyleSoares, S. C. R., Silva, G. C., & Fonseca, E. M. M. (2025). Development of Two-Wrinkled Tubes Using an Electrostatic Structural Analysis. Applied Sciences, 15(22), 11912. https://doi.org/10.3390/app152211912






