Next Article in Journal
Synergistic Regulation of Soil Water–Salt Transport by Irrigation Quality, Quota, and Texture
Next Article in Special Issue
Data-Driven and Structure-Based Modelling for the Discovery of Human DNMT1 Inhibitors: A Pathway to Structure–Activity Relationships
Previous Article in Journal
Revealing the Potential Use of Macro and Microalgae Compounds in Skin Barrier Repair
Previous Article in Special Issue
XANES Absorption Spectra of Penta-Graphene and Penta-SiC2 with Different Terminations: A Computational Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 22
10.3390/app152211898
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

DFT-Computation-Assisted EPR Study on Oxalate Anion-Radicals, Generated in γ-Irradiated Polycrystallites of H2C2O4·2H2O, Cs2C2O4, and K2C2O4·H2O

by
Jarosław Sadło
* and
Dariusz Pogocki
*
Centre for Radiation Research and Technology, Institute of Nuclear Chemistry and Technology, 16 Dorodna St., 03-195 Warsaw, Poland
*
Authors to whom correspondence should be addressed.
Appl. Sci. 2025, 15(22), 11898; https://doi.org/10.3390/app152211898
Submission received: 19 September 2025 / Revised: 5 November 2025 / Accepted: 7 November 2025 / Published: 8 November 2025
(This article belongs to the Special Issue Development and Application of Computational Chemistry Methods)
Browse Figures
Versions Notes

Abstract

This report focuses on the oxalate anion radical (C2O4●−) formed during γ-radiolysis of polycrystalline oxalates: protonated oxalic acid (H2C2O4·2H2O), caesium oxalate (Cs2C2O4), and potassium oxalate monohydrate (K2C2O4·H2O). Irradiation at 77 K generates stable radical species, revealed by EPR spectroscopy and supported by DFT calculations. In H2C2O4·2H2O, the primary axial signal (gavg = 2.0035) is shown to arise from the structural relaxation of the HC2O4∙ radical into the intrinsically stable non-planar (D2d) conformation, resolving the symmetry conflict with the planar crystal precursor. Numerical deconvolution confirmed the co-existence of this radical with the secondary HCO2● species, exhibiting distinct relaxation characteristics. In Cs2C2O4, the broad isotropic signal (g ≈ 2.008) is attributed to the D2d form. Quantitative analysis proved a sharp, thermodynamically driven structural conversion (D2d→D2h) upon annealing above 220 K, where the D2h conformer (gavg ≈ 2.011) becomes the dominant species (≈73%). In K2C2O4·H2O, the C2O4●− radical undergoes rapid decomposition into the CO2●− radical (gavg ≈ 2.0007) due to the kinetic instability of the primary species in that matrix. Our findings underscore the crucial role of computational assistance and quantitative numerical fitting in EPR studies: DFT provided crucial assistance and yielded satisfactory agreement in most cases, while clarifying the structural and kinetic stability governed by the local cationic environment. The stability of the most resistant radical forms persists up to 430 K in the caesium salt.

1. Introduction

The oxalate anion radical (C2O4•−) and the hydrogen oxalate radical (HC2O4•) are important but under-characterised species that arise as transient intermediates in a variety of redox and photochemical processes involving oxalate. Although their formation has been proposed in systems ranging from the radiolysis of aqueous solutions to metal–oxalate photoreduction, direct spectroscopic evidence—particularly from electron paramagnetic resonance (EPR) [1,2,3,4] and complementary methods [5,6,7,8,9,10]—remains relatively scarce.
The investigation of the oxalate radical is warranted not only by the broader interest in carbon-centred and carboxylate-based radicals and its potential role in oxidative biological pathways [11], but also by its environmental relevance, including its involvement in the reduction of carbon dioxide (CO2) to oxalate (C2O42−). For example, its transient formation during the reductive conversion of CO2 to C2O42− by hydrated electrons (eaq−) on the surface of gold (Au) catalysts [12] has been postulated [13].
The C2O4•− radical is also a strong reducing agent, with a calculated redox potential for the C2O42−/C2O4•− couple of approximately 1.5–2.0 V vs. SHE in aqueous solution [14,15]. Notably, when generated from oxalate in photocatalytic processes [15,16,17,18,19,20], C2O4•− can be applied to the reductive defluorination of persistent organic pollutants, particularly perfluoroalkyl and polyfluoroalkyl substances (PFAS) [21,22,23,24].
This study focuses on the oxalate anion radical formed during γ-radiolysis, the chemical decomposition induced by γ-radiation, of polycrystalline oxalates: K2C2O4·H2O, Cs2C2O4, and H2C2O4·2H2O. A central issue is the need to distinguish the C2O4•− radical of D2h symmetry from that of D2d symmetry, as well as from related species such as the carbon dioxide radical anion (CO2•−) and the hydroxyformyl radical (HOCO•) [3].
We hypothesise that the structure, stability, and EPR characteristics of C2O4•− depend on the conformation of its precursor, the C2O42− anion. The oxalate dianion can adopt both planar (D2h symmetry) and non-planar (D2d symmetry, with O–C–C–O dihedral angles approaching 90°) conformations [25,26]. In metal complexes, oxalate typically adopts the planar D2h conformation [27,28].
The conformational preferences of the oxalate dianion are governed by several key factors: (i) electron distribution and conjugation [29,30]; (ii) electrostatic repulsion; (iii) molecular symmetry [31,32,33]; (iv) environmental effects such as solvation, metal coordination, or crystal packing; and (v) energetic conditions, including temperature and photoexcitation [27,28]. In some salts, however, deviations are observed—for example, in caesium oxalate (Cs2C2O4), the O–C–C–O dihedral angle is ca. 81°, approaching D2d symmetry and reflecting a staggered arrangement of the carboxylate groups [34]. Interestingly, rubidium oxalate (Rb2C2O4) has been reported in both planar and staggered forms [34,35].
Given the short lifetime and complex electronic structure of C2O4•−, EPR spectroscopy combined with density functional theory (DFT) calculations provides a powerful approach for probing its spin distribution, g-values, and hyperfine interactions. Such insights not only elucidate the radical’s electronic structure and reactivity, but also contribute to understanding ligand-centred radical formation in metal–oxalate complexes, which are increasingly studied for their redox activity and photoreactivity.

2. Materials and Methods

Polycrystalline materials of the highest available purity were used. Caesium oxalate (Cs2C2O4) was purchased from Sigma-Aldrich (St. Louis, MI, USA), potassium oxalate monohydrate (K2C2O4·H2O) from Aktyn (Poznań, Poland), and oxalic acid dihydrate (H2C2O4·2H2O) from Chempur (Piekary Śląskie, Poland). All samples were sealed in quartz tubes and irradiated at liquid nitrogen temperature using a 60Co Gamma Chamber 5000 source (BRIT, Bombay, India) with a total dose of 10 kGy and a dose rate of 1.25 kGy·h−1.
Electron paramagnetic resonance (EPR) spectra were recorded with an X-band continuous-wave spectrometer (EMXplus, Bruker, Portland, OR, USA) equipped with a Teslameter, an EPR 4131VT temperature controller, and a nitrogen-flow cryostat. The measurement parameters were as follows: field modulation frequency 100 kHz, modulation amplitude 0.1 mT, conversion time 11.44 ms, time constant 1.28 ms, sweep time 40 s, field sweep 35 mT, microwave power range 0.01–10 mW, and spectral resolution of 3500 points. Temperature-dependent measurements of the γ-irradiated materials were carried out in 30 K steps from 100 K up to room temperature.
The EPR spectra obtained in these experiments were interpreted on the basis of the Zeeman g-tensor [36], whose values were calculated using quantum-chemical density functional theory (DFT).
The g-tensor calculations were performed for model clusters of oxalates corresponding to the geometries of the crystal lattices of H2C2O4·2H2O (CSD code 7104409 [37]), Cs2C2O4 (CSD code 192182 [34]), K2C2O4·H2O (CSD code 1199898 [38]), and K2C2O4 (CSD code 192180 [34]). The clusters are shown in Figure 1a–d and are hereafter referred to as M1, M2, M3, and M4. Their Cartesian coordinates are provided in the Supplementary Materials. The crystal structure data for K2C2O4 and Cs2C2O4 were obtained from the CSD/CCDC, while that for H2C2O4·2H2O was retrieved from the COD database.
The crystal-derived geometries were optimised in the local cationic environment using the B3LYP hybrid functional [39] and the def2-TZVP [40] basis set.
The single-point computations of the g-tensor and the hyperfine coupling tensor A were performed using the B3LYP [39], PBE0 [41,42], and RI-B2PLYP [43,44] double-hybrid functionals. These functionals were combined with the Weigend–Ahlrichs basis sets def2-TZVP, def2-TZVPD, def2-QZVPP (with auxiliary basis def2-QZVPP/C), and def2-TZVPP (with auxiliary basis def2-TZVPP/C) [40,45,46,47], as well as with the EPR-III basis set of Barone [47]. Hereafter, ℜ will refer to the g-tensor calculations at the RI-B2PLYP/def2-QZVPP (aux. def2-QZVPP/C) level of theory, and ℜ1 to those at the RI-B2PLYP/def2-TZVPP (aux. def2-TZVPP/C) level.
The electronic energy, electron density distribution, and dependence of the EPR signal on radical geometry for C2O42− and C2O4•− were investigated using potential energy surface (PES) scans at the B3LYP/def2-SVPD level of theory [48]. All computations were carried out with the ORCA 6.0.1 quantum chemistry package [49,50,51,52,53,54,55,56,57,58]. Importantly, to avoid confusion, we adopted the common convention of ordering g-values as gx > gy > gz when discussing experimental results, while in Tables S1–S7 (Supplementary Materials) the g-factors are presented in the reverse order, as reported in the ORCA output. Löwdin spin populations and hyperfine coupling constants A (in MHz) for atoms with |A| > 1 MHz, calculated at the ℜ and ℜ1 levels in models M1–M4, are summarised in Table S8. For direct comparison between experimental and calculated results, the hyperfine coupling constants A obtained in MHz were converted into mT. For protons, the standard conversion factor of 1 mT ≈ 28.024 MHz was used. For other nuclei, the corresponding nuclear gyromagnetic ratios (γ/2π) were applied, yielding the following conversion factors: 13C (I = ½), 1 mT ≈ 10.705 MHz; 17O (I = 5/2), 1 mT ≈ 1.772 MHz; and 133Cs (I = 7/2), 1 mT ≈ 3.498 MHz [36,59].

3. Results

3.1. Validation of DFT Calculations

Among the radicals observed in this work, the CO2•− radical is the one most extensively described in the literature. Its nature has been examined in detail by EPR and computational techniques in Ref. [60] and in numerous studies cited therein. In all reported cases, the experimental gavg value lies in the range 2.0005–2.0009. The gavg of CO2•− can, therefore, to some extent serve as a reference for validating the level of DFT calculations: regardless of the functional used with the Weigend–Ahlrichs basis sets [40], the calculated gavg value for the CO2•− radical falls within the narrow range of 2.00074–2.00075.
For instance, the g-tensor values reported for CO2•− (gx = 2.0029, gy = 2.0017, gz = 1.9974, gavg ≈ 2.00067), in Ref. [61] and cited in Ref. [36], are very well reproduced at the ℜ level of theory, which yields gx = 2.00318, gy = 2.00167, gz = 1.99739, with gavg ≈ 2.00074. Calculations employing the EPR-III basis set of Barone [47] result in a slightly higher, though still acceptable, value of gavg ≈ 2.00084.
The detailed results of the DFT g-tensor calculations are provided in Tables S1–S9 of the Supplementary Materials. Selected results obtained at the ℜ and ℜ1 levels will be used in the discussion of the experimental EPR data in the following sections.
The reliability of the computational assignments across different levels of theory was evaluated by performing a comparative analysis of the calculated g-tensor components using the RI-B2PLYP (double-hybrid), B3LYP (hybrid), and PBE0 (hybrid) functionals.
The results, summarised in Table 1, demonstrate that while absolute gavg values vary slightly between methods, the qualitative assignments and overall conclusions remain robust. For instance, the calculated gavg for the protonated oxalate (M1) is highly stable across all three functionals (gavg ≈ 2.0036 ± 0.0001), confirming the reliability of the HC2O4 identity. Similarly, the calculation of the decomposition product CO2•− shows near-perfect consistency across all tested levels (gavg ≈ 2.00074).
Crucially, this comparison reinforces the justification for selecting RI-B2PLYP as the primary functional: In both the H2C2O4 (M1) and Cs2C2O4 (M2) systems, the RI-B2PLYP functional yields the best quantitative agreement with the experimental gavg values, supporting its use for the final structural assignments. Furthermore, the failure to reproduce the experimental gavg value in the K2C2O4 model (M4) is consistently observed across all three functionals (Δg > 1 × 10−2), validating the conclusion that the discrepancy is structural/kinetic (decomposition) and not an artefact of the chosen functional.
The complex and overlapping EPR spectra of polycrystalline oxalates (H2C2O4·2H2O, Cs2C2O4, and K2C2O4·H2O) were analysed using numerical deconvolution. This procedure modelled the experimental first-derivative curves as the sum of individual Gaussian derivative functions, with g-tensor components fixed to the computed ℜ and ℜ1 levels. The full methodology, including the quantitative criteria for r2 (Coefficient of Determination) evaluation, analysis of power/temperature dependence, and the specific parameters used for each radical component, is detailed in the Supplementary Materials.

3.2. The EPR Experiment and Numerical Correlation with DFT Calculations

All samples before irradiation are EPR silent, which means no paramagnetic centres in non-irradiated polycrystalline powders. The results for irradiated samples are discussed below:
H2C2O4·2H2O. At low temperature, the spectrum is complex and consists of at least two singlet signals (Figure 2).
To accurately characterise co-existing species and demonstrate the reliability of the DFT parameters, the experimental spectra recorded across varying microwave powers (0.01 mW to 10.8 mW) were subjected to rigorous numerical deconvolution (fitting). The best fit (r2 up to 0.904 at 0.1 mW) confirmed the co-existence of two distinct radical populations (see Table 2):
The first signal, dominant at low power (0.01 mW) and associated with the protonated oxalate radical (HC2O4•), was successfully modelled with an axial g-tensor (g⊥ = 2.0053, g∥ = 1.9999), yielding gavg = 2.0035. This average value is in excellent agreement with the ℜ level DFT calculation for the planar model (M1: gavg ≈ 2.0036, see Table S1) and the literature assignment [2]. The numerical analysis of the power dependence (Table 1) confirms that the HC2O4• signal is characterised by rapid spin-lattice relaxation (T1), as evidenced by its dominant contribution (79.0% at 0.01 mW).
The second signal, more prominent at 10 mW, was assigned to the hydroxyformyl radical (HCO2•). It was modelled with an orthorhombic g-tensor (gx = 2.0084, gy = 2.0020, gz = 1.9973), yielding gavg ≈ 2.0026. This average value is in good agreement with our ℜ level DFT calculations for HCO2• (gavg ≈ 2.0023, see Table S5), suggesting it is a product of HC2O4• decarboxylation. The observed high anisotropy of this signal is attributed to the severe geometric constraints imposed by the rigid crystal lattice on the HCO2• radical.
The axial symmetry of Signal A is highly characteristic of the non-planar (D2d) conformation of the oxalate radical. Our initial ℜ level calculations for the planar (D2h) model (M1) yielded an orthorhombic g-tensor (gx ≈ 2.00482, gy ≈ 2.00389, gz ≈ 2.00212) which is structurally inconsistent with the experimental axial symmetry.
The inconsistency between the calculated orthorhombic tensor and the experimental axial symmetry is resolved by considering post-radiolysis structural relaxation: The planar D2h structure of the parent oxalic acid is enforced by strong hydrogen bonds. Radiolytically induced loss of stabilising H+ cations allows for the nascent radical to relax into its intrinsically more stable, non-planar (D2d) conformation (as shown by our PES analysis, see bellow). This structural relaxation leads to the observed axial symmetry of the HC2O4• radical trapped in the lattice.
In addition, hyperfine couplings calculated for the nearest protons (H18, H19) in the M1 model at the ℜ level are A ≈ 0.18 mT, with Löwdin spin densities [62] of only ∼0.007. Such proton hyperfine couplings are confirmed to be significantly smaller than the intrinsic experimental line-widths (ΔBpp = 0.3–0.4 mT) and the broader spectral features. This quantitative disparity confirms that the small couplings are indeed unresolved in the powder spectrum and contribute primarily to line broadening, rather than distinct splitting.
Thermal Stability and Dynamical Effects: The numerical deconvolution across varying temperatures (Table 3) demonstrates the stability limits and dynamical changes in the trapped radicals. We selected the data measured at 10 mW and 0.01 mW as they represent the highest and lowest powers presented in the spectral analysis (Figure 3a,b).
While both species persist up to 310 K (Figure 3a,b), the quality of the numerical fit (r2) drops sharply above 190 K (becoming negative from 220 K onwards, as shown in Table 2). This demonstrates that the static g-tensor model is not valid above 190 K. This drop suggests that the trapped radicals are no longer rigid, but are undergoing molecular motion (e.g., librational or hindered rotation) within the lattice. This dynamic effect partially averages the g-tensor anisotropy, leading to spectra that can no longer be accurately modelled by static g-tensors (the D2d and orthorhombic models), indicating the limitations of the DFT static geometry approach in predicting g-values at higher temperatures.
Upon annealing, no significant changes are observed, and both signals persist up to 310 K under microwave powers of 10 mW and 0.01 mW (Figure 3a,b).
Cs2C2O4. Following γ-irradiation at 77 K, an intense, broad, and almost isotropic signal (g ≈ 2.008, ΔBpp = 4.9 mT) was detected (Figure 4).
This signal is attributed to the C2O4•− radical of D2d symmetry, consistent with the non-planar geometry found in the precursor crystal structure [34]. Our DFT calculations for the D2d model (M2, gavg ≈ 2.0056, see Table S2) yield satisfactory agreement with the experimental average value.
Upon heating to 130 K, this signal transformed into a singlet with axial symmetry, characterised by g⊥ = 2.021 and g‖ = 1.992 (gavg = 2.011) and ΔBpp = 2.8 mT. This value is quantitatively close to our DFT calculations for the planar D2h model (M3/M4, gavg ≈ 2.0118).
To provide rigorous quantitative insight into this structural conversion, the experimental spectra were analysed using numerical deconvolution with a three-component model (Table 4).
Quantitative Analysis of Thermal Conversion: The numerical deconvolution (Table 4) provides direct quantitative evidence for a structural transition:
Below 220 K: The fit quality is excellent (r2 > 0.9), and the primary C2O4•− radical exists predominantly in the D2d conformation (≈50−70%), with the planar D2h component being negligible (≈0%).
Structural Conversion: Upon annealing to 250 K, the D2h component (gavg ≈ 2.0118) rapidly grows, becoming the dominant radical (72.7%). This sharp, quantifiable transition strongly supports the assignment of a thermodynamically driven structural conversion (D2d→D2h) upon heating, confirming that the stability of the oxalate radical is critically governed by its local crystalline geometry.
The hyperfine analysis, based on the ℜ1 level calculation, shows that the unpaired spin density is mainly localised on the oxalate fragment. Oxygen nuclei carry the largest spin populations, resulting in hyperfine couplings up to ca. −0.77 mT for O1, −0.67 mT for O2, and 0.40 mT for O3. Carbon atoms contribute smaller couplings: −4.01 mT for C1 and −0.87 mT for C2. All caesium nuclei show essentially no hyperfine interaction. These results confirm that the experimental spectrum appears as a broadened singlet, with no resolved hyperfine structure from Cs, and that the radical is centred on the oxalate moiety while the Cs cations provide structural stabilisation.
K2C2O4·H2O. Immediately after irradiation, during measurement at 100 K, an anisotropic singlet with orthorhombic symmetry and g-factor values gx = 2.005, gy = 2.0009, and gz = 1.998 (gavg ≈ 2.0013) and ΔBpp = 0.34 mT was recorded (Figure 5a,b).
Our initial DFT calculations for the primary C2O4•− radical (D2h symmetry, M3/M4) yielded significantly higher gavg ≈ 2.01178 (Tables S3 and S4). This quantitative failure was investigated using rigorous numerical deconvolution with a five-component model, including all expected decay (CO2•−) and protonation (HC2O4•) products (see Table 5 for key results).
Analysis of the Numerical Deconvolution (Table 5): The failure of the primary DFT model (M3/M4) is primarily an indication of the kinetic instability of the C2O4•− radical in this lattice. The highly unstable D2h C2O4•− species (calculated gavg ≈ 2.0118) rapidly decays or is heavily overlapped. Instead, the experimental signal observed at 100 K is strongly dominated by products with low gavg, specifically the C2O4•− EXP component (gavg ≈ 2.0013) and the CO2•− component (gavg ≈ 2.0007). The gavg ≈ 2.0013 signal is thus assigned to a structurally constrained CO2•− radical (or similar decay product), which is highly characteristic of irradiated oxalates.
The presence of the CO2•− component is therefore strong quantitative evidence for the rapid and spontaneous decomposition of the primary oxalate radical in the potassium matrix, confirming the structural and kinetic predictions suggested by our PES analysis.
Thermal and Dynamical Limitations: The high thermal stability is confirmed as the spectral signals persist up to 310 K (Figure 5a,b). However, the quality of the numerical fit (r2) severely deteriorates above 160 K and becomes negative at higher temperatures. This sharp decline demonstrates the limitations of the static g-tensor model above 160 K, as the trapped radicals begin undergoing molecular motion (e.g., hindered rotation), partially averaging the g-tensor anisotropy. This renders static DFT calculations insufficient for accurately predicting g-values in the mobile phase.
The hyperfine analysis, based on the ℜ and ℜ levels calculation, further supports this assignment. In both models, the unpaired spin density is strongly localised on the oxalate unit, with negligible delocalization onto surrounding potassium ions. In M3, the oxygen atoms give rise to hyperfine couplings up to –0.79 mT, and the carbon atoms contribute smaller couplings, up to –0.21 mT. In M4, a very similar picture emerges: the largest interactions are again on oxygen (up to –0.61 mT), while carbons contribute weakly (~0.036 mT). Potassium nuclei show essentially no measurable hyperfine interaction. These results indicate that the orthorhombic signal observed experimentally originates from oxalate-centred radicals, with alkali cations providing structural stabilisation, but remaining magnetically silent.
This signal is visible over a wide microwave power range (10 mW–0.01 mW).
Upon heating, when measured at a power of 10 mW, an almost isotropic signal with gavg = 2.0007 and a peak-to-peak width of 0.85 mT appears, and from 250 K it begins to dominate. Such a signal is characteristic of the CO2•− radical, which has been observed in many irradiated systems (see above). For example, a similar signal in irradiated white coral [63] was assigned to tumbling CO2•− located in occluded water.
At lower microwave powers, the isotropic signal is almost invisible, while the orthorhombic signal continues to dominate.

4. Discussion

The γ-radiolysis of polycrystalline oxalates at 77 K involves the interaction of high-energy γ-photons (from 60Co, ca. 1.25 MeV), with their energy being deposited in the crystal lattice. At 77 K, where molecular mobility is greatly restricted, primary radiolytic processes prevail [64]. The deposited energy ionises and excites molecules within the lattice, as represented in Reactions (1) and (2).
C 2 O 4 2 − → γ ( C 2 O 4 2 − ) ⊕ + e − ,
An oxalate dianion loses an electron, forming a hole h+ = (C2O42−)⊕, which is equivalent to the oxalate anion radical C2O4●−.
C 2 O 4 2 − → γ ( C 2 O 4 2 − ) * ,
In a rigid crystal lattice at 77 K, electrons may be trapped at cation vacancies or other lattice defects, while holes may be stabilised on oxalate dianions, leading to the formation of radical species: the oxalate radical anion (C2O4●−) and the carbon dioxide radical anion (CO2●−). The latter results from decarboxylation of excited or ionised oxalate groups, as shown in Reactions (3) and (4) [65].
( C 2 O 4 2 − ) * → CO 2 • − + CO 2 ,
( C 2 O 4 2 − ) ⊕ → CO 2 • − + CO 2 ,
Computational studies on oxalate decarboxylase (OxDC) [30] have shown that, within the CPCM continuum solvation model [66] mimicking an aqueous environment, the oxalate radical anion (C2O4●−) undergoes C–C bond cleavage to yield CO2 and CO2●−. At the CCSD(T) level of theory [67,68], the calculated free energy barrier for this process is ~80–120 kJ mol−1. This barrier is almost an order of magnitude lower than that for the closed-shell oxalate dianion (C2O42−), since in the radical species part of the unpaired electron density is delocalized into the C–C antibonding (σ*) orbital, thereby facilitating β-cleavage-type decarboxylation [69,70,71].
Our PES calculations show a difference of almost 8 kJ mol−1 between the D2h and D2d conformations of C2O4●− (see Figure 6).
These energy values indicate that the D2h conformation of C2O4●− is considerably less stable than the D2d conformation. However, in a rigid, cation-rich environment such as a polycrystalline matrix, the C2O4●− radical is expected to be stabilised. This is particularly true for the D2h form, where interaction with cations reduces the electron density on oxygen atoms and partially compensates for the repulsive interactions between carboxyl groups. In this case, withdrawal of excess electron density toward adjacent cations stabilises the radical.
The interplay between the radical’s intrinsic structural preference (D2d) and external lattice constraint (D2h) is key to interpreting the EPR data: As demonstrated by the structural relaxation observed in H2C2O4·2H2O, the C2O4●− radical adopts the energetically favoured D2d geometry upon loss of stabilising counter-ions. Conversely, the sharp thermal transition observed in Cs2C2O4 from the primary D2d radical to the D2h conformer at 250 K confirms that D2h is a kinetically accessible intermediate. This D2h geometry, despite being highly strained and possessing lower thermodynamic stability than the D2d form, is a key step towards bond cleavage. The concentration peak of the D2h species immediately precedes the rapid disappearance of the CO2●− product, strongly suggesting that the conversion D2d→D2h acts as a structural prerequisite that initiates the overall decarboxylation process.
Supporting evidence comes from studies on the instability of oxalate radicals via CO2 production. Gas analyses performed in the early 1960s after γ-irradiation (0.1–2000 kGy) of various oxalate salts demonstrated a pronounced dependence of the decarboxylation radiation-chemical yield (G(CO2), µmol J−1) on the cationic environment: anhydrous oxalic acid (H2C2O4), G(CO2) ≈ 0.74; oxalic acid dihydrate ≈ 0.47; Li2C2O4 ≈ 0.016; Na2C2O4 ≈ 0.006; K2C2O4·H2O ≈ 0.082 [65]. These data indicate that Reactions (3) and (4) proceed far less efficiently in salts than in anhydrous oxalic acid. Consequently, in polycrystalline oxalate salts, the probability of detecting primary, intact C2O4●− radicals is substantially higher.
Our results are therefore in excellent agreement with this general scheme: in the EPR measurements, we detect all radical products arising from Reactions (1)–(4). Importantly, owing to calculations performed for simplified molecular models (M1–M4), we were able to quantitatively characterise the EPR signal of oxalate radicals with D2h and D2d symmetry, which, combined with numerical deconvolution, provided the necessary rigour to identify the co-existing species and structural conversions in all systems.

5. Conclusions

This work highlights the crucial role of computational assistance combined with quantitative numerical analysis in deciphering the complex EPR spectra of microcrystalline oxalate salts. Radiation-induced radicals are stabilised by alkali cations.
The DFT calculations provided crucial assistance and yielded satisfactory quantitative agreement in most cases, confirming the identity of the primary radical and providing the physical justification (structural relaxation) needed to resolve experimental/theoretical symmetry discrepancies (H2C2O4). The significant discrepancy observed in the K2C2O4 system successfully established the kinetic instability of the primary radical, leading to its rapid decomposition into CO2●−.
Furthermore, the combined DFT and numerical kinetic analysis allowed for the quantitative identification of molecular motion limitations in the static model at elevated temperatures, indicating the clear boundaries of its predictive power. Only the synergy between EPR spectroscopy and quantum chemical methods provides a comprehensive picture of these processes.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/app152211898/s1. Cartesian coordinates of model systems M1–M4; Table S1: DFT-calculated g-tensors for M1, [C2H14O10]●−; Table S2: DFT- calculated g-tensors for M2, [Cs11C2O4]●10+; Table S3: DFT-calculated g-tensors for M3; [K14C2H4O6]●13+, Table S4: DFT-calculated g-tensors for M4; [K12C2O4]●11+, Table S5: DFT-calculated g-tensors for CO2●−, K-CO2●, Cs-CO2●, H-CO2●, Cs-C2O4●, K-C2O4●, Table S6: DFT-calculated g-tensors for H-C2O4●, Table S7: DFT-calculated g-tensors for H-C2O4●-H2O; Table S8. Löwdin spin populations and hyperfine coupling constants (A, MHz) for atoms with |A| > 1 MHz in models M1–M4. The full methodology of spectra numerical deconvolution and analysis of power/temperature dependence.

Author Contributions

Conceptualisation, D.P. and J.S.; writing—original draft preparation, D.P. and J.S.; writing—review and editing, D.P.; supervision, D.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding authors. The custom-written Python 3.8 script used for the numerical deconvolution and kinetic analysis is available upon request from the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CSDThe Cambridge Structural Database
CCDCThe Cambridge Crystallographic Data Centre, http://www.ccdc.cam.ac.uk/
CODThe Crystallography Open Database, http://www.crystallography.net/
PubChemThe open chemistry database, https://pubchem.ncbi.nlm.nih.gov/
DFTDensity Functional Theory
EPRElectron Paramagnetic Resonance

References

  1. Köseoğlu, R.; Köseoğlu, E.; Köksal, F.; Başaran, E.; Demirci, D. EPR of Some Irradiated Renal Stones. Radiat. Meas. 2005, 40, 65–68. [Google Scholar] [CrossRef]
  2. Sosulin, I.S.; Lisouskaya, A. Structure and Kinetics of Organic Acid Radicals Formed in Reaction with •OH Radicals. J. Phys. Chem. A 2024, 128, 7558–7567. [Google Scholar] [CrossRef] [PubMed]
  3. Imaram, W.; Saylor, B.T.; Centonze, C.P.; Richards, N.G.; Angerhofer, A. EPR Spin Trapping of an Oxalate-Derived Free Radical in the Oxalate Decarboxylase Reaction. Free Radic. Biol. Med. 2011, 50, 1009–1015. [Google Scholar] [CrossRef] [PubMed]
  4. Reddy, M.V.V.S.; Lingam, K.V.; Gundu Rao, T.K. Studies of Radicals in Oxalate Systems. Mol. Phys. 1980, 41, 1493–1500. [Google Scholar] [CrossRef]
  5. Steffan, C.R.; Bakac, A.; Espenson, J.H. Quenching of the Doublet Excited State of Tris(Polypyridine) Chromium(III) Ions by Oxalate Ions: An Example of Irreversible Electron Transfer. Inorg. Chem. 1989, 28, 2992–2995. [Google Scholar] [CrossRef]
  6. Mulazzani, Q.G.; D’Angelantonio, M.; Venturi, M.; Hoffman, M.Z.; Rodgers, M.A.J. Interaction of Formate and Oxalate Ions with Radiation-Generated Radicals in Aqueous Solution. Methylviologen as a Mechanistic Probe. J. Phys. Chem. 1986, 90, 5347–5352. [Google Scholar] [CrossRef]
  7. Kai, T.; Zhou, M.; Johnson, S.; Ahn, H.S.; Bard, A.J. Direct Observation of C2O4•− and CO2•− by Oxidation of Oxalate within Nanogap of Scanning Electrochemical Microscope. J. Am. Chem. Soc. 2018, 140, 16178–16183. [Google Scholar] [CrossRef]
  8. Billing, R.; Rehorek, D.; Hennig, H. Photoinduced Electron Transfer in Ion Pairs R. In Photoinduced Electron Transfer II; Topics of Current Chemistry; Springer: Berlin/Heidelberg, Germany, 1990; Volume 2, pp. 151–200. ISBN 3-540-52568-X. [Google Scholar]
  9. Huie, R.E.; Clifton, C.L. Kinetics of the Reaction of the Sulfate Radical with the Oxalate Anion. Int. J. Chem. Kinet. 1996, 28, 195–199. [Google Scholar] [CrossRef]
  10. Zhou, M.; Andrews, L. Infrared Spectra of the C2O4+ Cation and C2O4− Anion Isolated in Solid Neon. J. Chem. Phys. 1999, 110, 6820–6826. [Google Scholar] [CrossRef]
  11. Zan, X.; Yan, Y.; Chen, G.; Sun, L.; Wang, L.; Wen, Y.; Xu, Y.; Zhang, Z.; Li, X.; Yang, Y.; et al. Recent Advances of Oxalate Decarboxylase: Biochemical Characteristics, Catalysis Mechanisms, and Gene Expression and Regulation. J. Agric. Food Chem. 2024, 72, 10163–10178. [Google Scholar] [CrossRef]
  12. Prinsen, P.; Luque, R. (Eds.) Introduction to Nanocatalysts. In Nanoparticle Design and Characterization for Catalytic Applications in Sustainable Chemistry; The Royal Society of Chemistry: London, UK, 2019; pp. 1–36. ISBN 978-1-78801-490-8. [Google Scholar]
  13. Jiang, Z.; Clavaguéra, C.; Hu, C.; Denisov, S.A.; Shen, S.; Hu, F.; Ma, J.; Mostafavi, M. Direct Time-Resolved Observation of Surface-Bound Carbon Dioxide Radical Anions on Metallic Nanocatalysts. Nat. Commun. 2023, 14, 7116. [Google Scholar] [CrossRef] [PubMed]
  14. Dooley, M.R.; Vyas, S. Role of Explicit Solvation and Level of Theory in Predicting the Aqueous Reduction Potential of Carbonate Radical Anion by DFT. Phys. Chem. Chem. Phys. 2025, 27, 6867–6874. [Google Scholar] [CrossRef]
  15. Russo, C.; Volpe, C.; Giustiniano, M. The Multiple Facets of Oxalate Dianion in Photochemistry. ChemPhotoChem 2025, 9, e202400407. [Google Scholar] [CrossRef]
  16. Li, Y.; Wasgestian, F. Photocatalytic Reduction of Nitrate Ions on TiO2 by Oxalic Acid. J. Photochem. Photobiol. A 1998, 112, 255–259. [Google Scholar] [CrossRef]
  17. Wang, Y.; Zhang, P. Photocatalytic Decomposition of Perfluorooctanoic Acid (PFOA) by TiO2 in the Presence of Oxalic Acid. J. Hazard. Mater. 2011, 192, 1869–1875. [Google Scholar] [CrossRef]
  18. Herrmann, J.-M.; Mozzanega, M.-N.; Pichat, P. Oxidation of Oxalic Acid in Aqueous Suspensions of Semiconductors Illuminated with UV or Visible Light. J. Photochem. 1983, 22, 333–343. [Google Scholar] [CrossRef]
  19. Sun, T.; Wang, Y.; Zhang, H.; Liu, P.; Zhao, H. Adsorption and Oxidation of Oxalic Acid on Anatase TiO2 (001) Surface: A Density Functional Theory Study. J. Colloid Interface Sci. 2015, 454, 180–186. [Google Scholar] [CrossRef] [PubMed]
  20. Luong, N.T.; Hanna, K.; Boily, J.-F. Water Film-Mediated Photocatalytic Oxidation of Oxalate on TiO2. J. Catal. 2024, 432, 115425. [Google Scholar] [CrossRef]
  21. Buck, R.C.; Franklin, J.; Berger, U.; Conder, J.M.; Cousins, I.T.; de Voogt, P.; Jensen, A.A.; Kannan, K.; Mabury, S.A.; van Leeuwen, S.P. Perfluoroalkyl and Polyfluoroalkyl Substances in the Environment: Terminology, Classification, and Origins. Integr. Environ. Assess. Manag. 2011, 7, 513–541. [Google Scholar] [CrossRef]
  22. Patlewicz, G.; Richard, A.M.; Williams, A.J.; Grulke, C.M.; Sams, R.; Lambert, J.; Noyes, P.D.; DeVito, M.J.; Hines, R.N.; Strynar, M.; et al. A Chemical Category-Based Prioritization Approach for Selecting 75 Per- and Polyfluoroalkyl Substances (PFAS) for Tiered Toxicity and Toxicokinetic Testing. Environ. Health Perspect. 2019, 127, 14501. [Google Scholar] [CrossRef]
  23. Kisała, J.; Goclon, J.; Pogocki, D. Reductive Dehalogenation—Challenges of Perfluorinated Organics. J. Photocat. 2021, 2, 244–251. [Google Scholar] [CrossRef]
  24. Pogocki, D.; Kisała, J.; Bankiewicz, B.; Goclon, J.; Kolek, P.; Szreder, T. Reduction Potentials of Perfluorinated Organic Acids in Alkaline Polar Solvents. Computational Thermodynamic Insight into the Electron-Attachment Induced Defluorination. J. Mol. Liq. 2024, 397, 123929. [Google Scholar] [CrossRef]
  25. Clark, T.; Von Ragué Schleyer, P. Conformational Preferences of 34 Valence Electron A2X4 Molecules: An Ab Initio Study of B2F4, B2Cl4, N2O4, and C2O. J. Comp. Chem. 1981, 2, 20–29. [Google Scholar] [CrossRef]
  26. Dewar, M.J.S.; Zheng, Y.-J. Structure of the Oxalate Ion. J. Mol. Struct. THEOCHEM 1990, 209, 157–162. [Google Scholar] [CrossRef]
  27. Beagley, B.; Small, R.W.H. The Structure of Lithium Oxalate. Acta Crystallogr. 1964, 17, 783–788. [Google Scholar] [CrossRef]
  28. Reed, D.A.; Olmstead, M.M. Sodium Oxalate Structure Refinement. Acta Crystallogr. Sect. B 1981, 37, 938–939. [Google Scholar] [CrossRef]
  29. Jestilä, J.S.; Denton, J.K.; Perez, E.H.; Khuu, T.; Aprà, E.; Xantheas, S.S.; Johnson, M.A.; Uggerud, E. Characterization of the Alkali Metal Oxalates (MC2O4−) and Their Formation by CO2 Reduction via the Alkali Metal Carbonites (MCO2−). Phys. Chem. Chem. Phys. 2020, 22, 7460–7473. [Google Scholar] [CrossRef]
  30. Molt, R.W., Jr.; Lecher, A.M.; Clark, T.; Bartlett, R.J.; Richards, N.G.J. Facile Csp2–Csp2 Bond Cleavage in Oxalic Acid-Derived Radicals. J. Am. Chem. Soc. 2015, 137, 3248–3252. [Google Scholar] [CrossRef]
  31. Dean, P.A.W. The Oxalate Dianion, C2O42−: Planar or Nonplanar? J. Chem. Educ. 2012, 89, 417–418. [Google Scholar] [CrossRef]
  32. Peterson, K.I.; Pullman, D.P. Determining the Structure of Oxalate Anion Using Infrared and Raman Spectroscopy Coupled with Gaussian Calculations. J. Chem. Educ. 2016, 93, 1130–1133. [Google Scholar] [CrossRef]
  33. Longetti, L.; Barillot, T.R.; Puppin, M.; Ojeda, J.; Poletto, L.; van Mourik, F.; Arrell, C.A.; Chergui, M. Ultrafast Photoelectron Spectroscopy of Photoexcited Aqueous Ferrioxalate. Phys. Chem. Chem. Phys. 2021, 23, 25308–25316. [Google Scholar] [CrossRef]
  34. Dinnebier, R.E.; Vensky, S.; Panthöfer, M.; Jansen, M. Crystal and Molecular Structures of Alkali Oxalates:  First Proof of a Staggered Oxalate Anion in the Solid State. Inorg. Chem. 2003, 42, 1499–1507. [Google Scholar] [CrossRef]
  35. Echigo, T.; Kimata, M. The Common Role of Water Molecule and Lone Electron Pair as a Bond-Valence Mediator in Oxalate Complexes: The Crystal Structures of Rb2(C2O4) H2O and Tl2(C2O4). Z. Krist.-Cryst. Mater. 2006, 221, 762–769. [Google Scholar] [CrossRef]
  36. Weil, J.A.; Bolton, J.R. Electron Paramagnetic Resonance. Elementary Theory and Practical Applications; Wiley-Interscience: Hoboken, NJ, USA, 2007; ISBN 978-0-471-75496-1. [Google Scholar]
  37. Casati, N.; Macchi, P.; Sironi, A. Hydrogen Migration in Oxalic Acid Di-Hydrate at High Pressure? Chem. Commun. 2009, 2679–2681. [Google Scholar] [CrossRef] [PubMed]
  38. Chidambaram, R.; Sequeira, A.; Sikka, S.K. Neutron-Diffraction Study of the Structure of Potassium Oxalate Monohydrate: Lone-Pair Coordination of the Hydrogen-Bonded Water Molecule in Crystals. J. Chem. Phys. 1964, 41, 3616–3622. [Google Scholar] [CrossRef]
  39. Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  40. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for h to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
  41. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
  42. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  43. Grimme, S. Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
  44. Mardirossian, N.; Head-Gordon, M. Survival of the Most Transferable at the Top of Jacob’s Ladder: Defining and Testing the ωB97M(2) Double Hybrid Density Functional. J. Chem. Phys. 2018, 148, 241736. [Google Scholar] [CrossRef]
  45. Tran, V.A.; Neese, F. Double-Hybrid Density Functional Theory for g-Tensor Calculations Using Gauge Including Atomic Orbitals. J. Chem. Phys. 2020, 153, 054105. [Google Scholar] [CrossRef] [PubMed]
  46. Hellweg, A.; Rappoport, D. Development of New Auxiliary Basis Functions of the Karlsruhe Segmented Contracted Basis Sets Including Diffuse Basis Functions (Def2-SVPD, Def2-TZVPPD, and Def2-QVPPD) for RI-MP2 and RI-CC Calculations. Phys. Chem. Chem. Phys. 2015, 17, 1010–1017. [Google Scholar] [CrossRef]
  47. Barone, V. Structure, Magnetic Properties and Reactivities of Open-Shell Species from Density Functional and Self-Consistent Hybrid Methods. In Recent Advances in Density Functional Methods, Part I; Chong, D.P., Ed.; World Scientific Publ. Co.: Singapore, 1996. [Google Scholar]
  48. Rappoport, D.; Furche, F. Property-Optimized Gaussian Basis Sets for Molecular Response Calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef]
  49. Neese, F. The ORCA Program System. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  50. Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
  51. Neese, F. Software Update: The ORCA Program System-Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
  52. Neese, F. Prediction of Electron Paramagnetic Resonance g Values Using Coupled Perturbed Hartree-Fock and Kohn-Sham Theory. J. Chem. Phys. 2001, 115, 11080–11096. [Google Scholar] [CrossRef]
  53. Neese, F. An Improvement of the Resolution of the Identity Approximation for the Formation of the Coulomb Matrix. J. Comp. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef]
  54. Helmich-Paris, B. A Trust-Region Augmented Hessian Implementation for Restricted and Unrestricted Hartree–Fock and Kohn–Sham Methods. J. Chem. Phys. 2021, 154, 164104. [Google Scholar] [CrossRef]
  55. Neese, F. Efficient and Accurate Approximations to the Molecular Spin-Orbit Coupling Operator and Their Use in Molecular g-Tensor Calculations. J. Chem. Phys. 2005, 122, 034107. [Google Scholar] [CrossRef]
  56. Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, Approximate and Parallel Hartree-Fock and Hybrid DFT Calculations. A “chain-of-Spheres” Algorithm for the Hartree-Fock Exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
  57. Helmich-Paris, B.; de Souza, B.; Neese, F.; Izsák, R. An Improved Chain of Spheres for Exchange Algorithm. J. Chem. Phys. 2021, 155, 104109. [Google Scholar] [CrossRef]
  58. Neese, F. The SHARK Integral Generation and Digestion System. J. Comp. Chem. 2022, 44, 381–396. [Google Scholar] [CrossRef]
  59. Brustolon, M. Electron Paramagnetic Resonance: A Practitioner’s Toolkit; John Wiley & Son: Hoboken, NJ, USA, 2009; ISBN 978-0-470-43222-8. [Google Scholar]
  60. Bhide, M.; Kadam, R.M.; Babu, Y.; Natarajan, V.; Sastry, M. EPR and ENDOR Studies of Self (α) -Irradiation Effects in Pu(VI) Oxalate: Evidence for Participation of 5f Electrons of 239Pu in Chemical Bonding with CO2−. Chem. Phys. Lett. 2000, 332, 98–104. [Google Scholar] [CrossRef]
  61. Lunsford, J.H.; Jayne, J.P. Formation of CO2− Radical Ions When CO2 Is Adsorbed on Irradiated Magnesium Oxide. J. Phys. Chem. 1965, 69, 2182–2184. [Google Scholar] [CrossRef]
  62. Jacob, C.R.; Reiher, M. Spin in Density-Functional Theory. Int. J. Quantum Chem. 2012, 112, 3661–3684. [Google Scholar] [CrossRef]
  63. Debuyst, R.; Dejehet, F.; Idrissi, S. Isotropic CO3 and CO2 Radicals in Gamma Irradiated Monohydrocalcite. Radiat. Prot. Dosim. 1993, 47, 659–664. [Google Scholar] [CrossRef]
  64. Kroh, J. Elektrony w Chemii Radiacyjnej Układów Skondensowanych. [Electrons in Radiation Chemistry of Condensed Systems]; Ossolineum: Wrocław, Poland, 1980; ISBN 83-04-00222-1. [Google Scholar]
  65. Dougherty, P.L.; Gottschall, W.C. Gamma Radiolysis of Oxalic Acid and Selected Metal Oxalates. Radiat. Res. 1976, 68, 229–233. [Google Scholar] [CrossRef]
  66. Takano, Y.; Houk, K.N. Benchmarking the Conductor-like Polarizable Continuum Model (CPCM) for Aqueous Solvation Free Energies of Neutral and Ionic Organic Molecules. J. Chem. Theory Comput. 2004, 1, 70–77. [Google Scholar] [CrossRef] [PubMed]
  67. Parkinson, C.J.; Mayer, P.M.; Radom, L. An Assessment of Theoretical Procedures for the Calculation of Reliable Radical Stabilization Energies. J. Chem. Soc. Perkin Trans. 2 1999, 2305–2313. [Google Scholar] [CrossRef]
  68. Jurečka, P.; Šponer, J.; Černý, J.; Hobza, P. Benchmark Database of Accurate (MP2 and CCSD(T) Complete Basis Set Limit) Interaction Energies of Small Model Complexes, DNA Base Pairs, and Amino Acid Pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985. [Google Scholar] [CrossRef] [PubMed]
  69. Chanon, M.; Rajzmann, M.; Chanon, F. One Electron More, One Electron Less. What Does It Change? Activations Induced by Electron Transfer. The Electron, an Activating Messenger. Tetrahedron 1990, 46, 6193–6299. [Google Scholar] [CrossRef]
  70. Beckwith, A.L.J. Regio-Selectivity and Stereo-Selectivity in Radical Reactions. Tetrahedron 1981, 37, 3073–3100. [Google Scholar] [CrossRef]
  71. Fossey, J.; Lefort, D.; Sorba, J. Free Radicals in Organic Chemistry; Willey & Sons: New York, NY, USA, 1995. [Google Scholar]
Applsci 15 11898 g001
Figure 1. DFT-investigated model clusters of oxalates with counterions: (a) M1, D2h symmetry, two H+ and five water molecules (based on H2C2O4·2H2O, CSD code 7104409); (b) M2, D2d symmetry, eleven Cs+ cations (based on Cs2C2O4, CSD code 192182); (c) M3, D2h symmetry, fourteen K+ cations and two water molecules (based on K2C2O4·H2O, CSD code 1199898); (d) M4, D2h symmetry, twelve K+ cations (based on K2C2O4, CSD code 192180).
Figure 1. DFT-investigated model clusters of oxalates with counterions: (a) M1, D2h symmetry, two H+ and five water molecules (based on H2C2O4·2H2O, CSD code 7104409); (b) M2, D2d symmetry, eleven Cs+ cations (based on Cs2C2O4, CSD code 192182); (c) M3, D2h symmetry, fourteen K+ cations and two water molecules (based on K2C2O4·H2O, CSD code 1199898); (d) M4, D2h symmetry, twelve K+ cations (based on K2C2O4, CSD code 192180).
Applsci 15 11898 g001
Applsci 15 11898 g002
Figure 2. EPR spectra of H2C2O4·2H2O irradiated with a 10 kGy dose at 77 K and recorded at 100 K under different microwave powers. The blue line represents the original, unresolved EPR spectrum recorded at the 0.01 mW power, where the HC2O4● radical is dominant (data extracted from this specific 0.01 mW spectrum are denoted with an asterisk (*) in Table 2 and Table 3) (a); the deconvolution model, showing the breakdown of this complex (b) spectrum into its individual fitted components (b).
Figure 2. EPR spectra of H2C2O4·2H2O irradiated with a 10 kGy dose at 77 K and recorded at 100 K under different microwave powers. The blue line represents the original, unresolved EPR spectrum recorded at the 0.01 mW power, where the HC2O4● radical is dominant (data extracted from this specific 0.01 mW spectrum are denoted with an asterisk (*) in Table 2 and Table 3) (a); the deconvolution model, showing the breakdown of this complex (b) spectrum into its individual fitted components (b).
Applsci 15 11898 g002
Applsci 15 11898 g003
Figure 3. EPR spectra of H2C2O4·2H2O irradiated with a 10 kGy dose at 77 K and recorded at different temperatures with microwave powers of 10 mW (a) and 0.01 mW (b).
Figure 3. EPR spectra of H2C2O4·2H2O irradiated with a 10 kGy dose at 77 K and recorded at different temperatures with microwave powers of 10 mW (a) and 0.01 mW (b).
Applsci 15 11898 g003
Applsci 15 11898 g004
Figure 4. EPR spectra of Cs2C2O4 irradiated with a 10 kGy dose at 77 K and recorded at different temperatures with a microwave power of 10 mW.
Figure 4. EPR spectra of Cs2C2O4 irradiated with a 10 kGy dose at 77 K and recorded at different temperatures with a microwave power of 10 mW.
Applsci 15 11898 g004
Applsci 15 11898 g005
Figure 5. EPR spectra of K2C2O4·H2O irradiated with a 10 kGy dose at 77 K and recorded at different temperatures with microwave powers of 10 mW (a) and 0.1 mW (b).
Figure 5. EPR spectra of K2C2O4·H2O irradiated with a 10 kGy dose at 77 K and recorded at different temperatures with microwave powers of 10 mW (a) and 0.1 mW (b).
Applsci 15 11898 g005
Applsci 15 11898 g006
Figure 6. Relative energies of oxalate radical anion (C2O4●−) conformers obtained from a potential energy scan (PES) along the dihedral angle (O–C–O–C) coordinate at the B3LYP/def2-SVPD level of theory.
Figure 6. Relative energies of oxalate radical anion (C2O4●−) conformers obtained from a potential energy scan (PES) along the dihedral angle (O–C–O–C) coordinate at the B3LYP/def2-SVPD level of theory.
Applsci 15 11898 g006
Table 1. Comparative analysis of gavg values for key radical species and crystal models calculated using different DFT functionals (data derived from Tables S1–S5).
Table 1. Comparative analysis of gavg values for key radical species and crystal models calculated using different DFT functionals (data derived from Tables S1–S5).
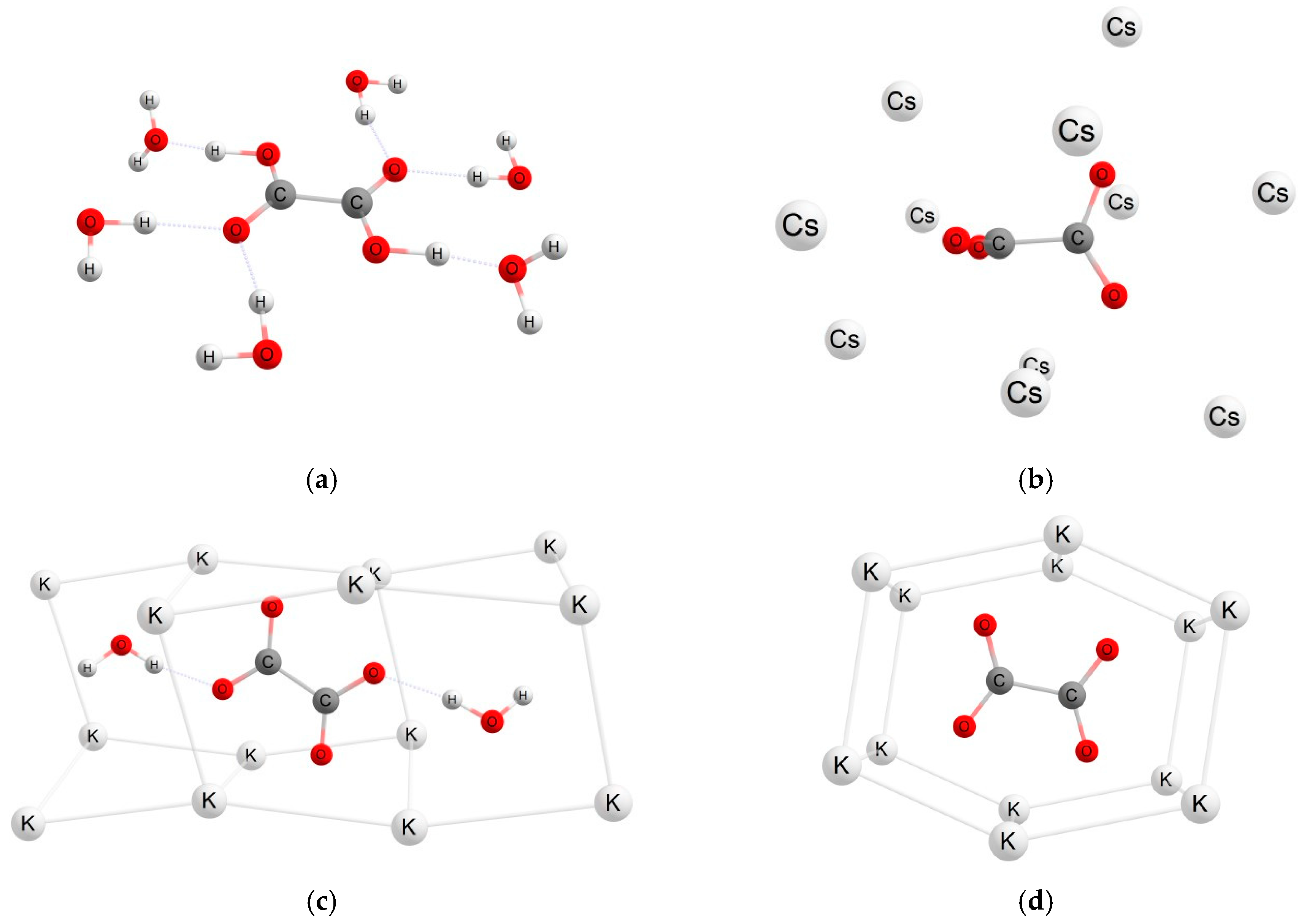
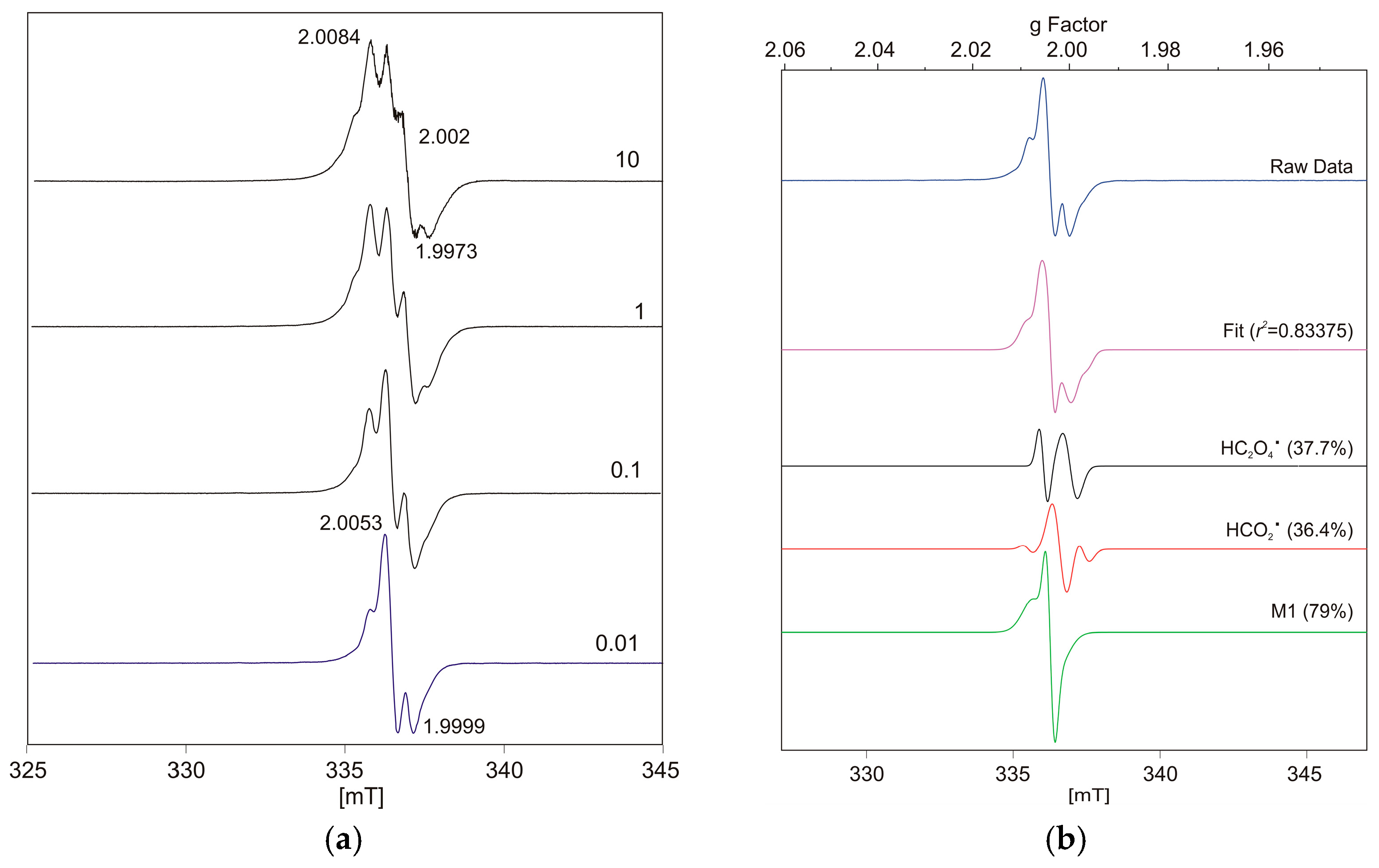
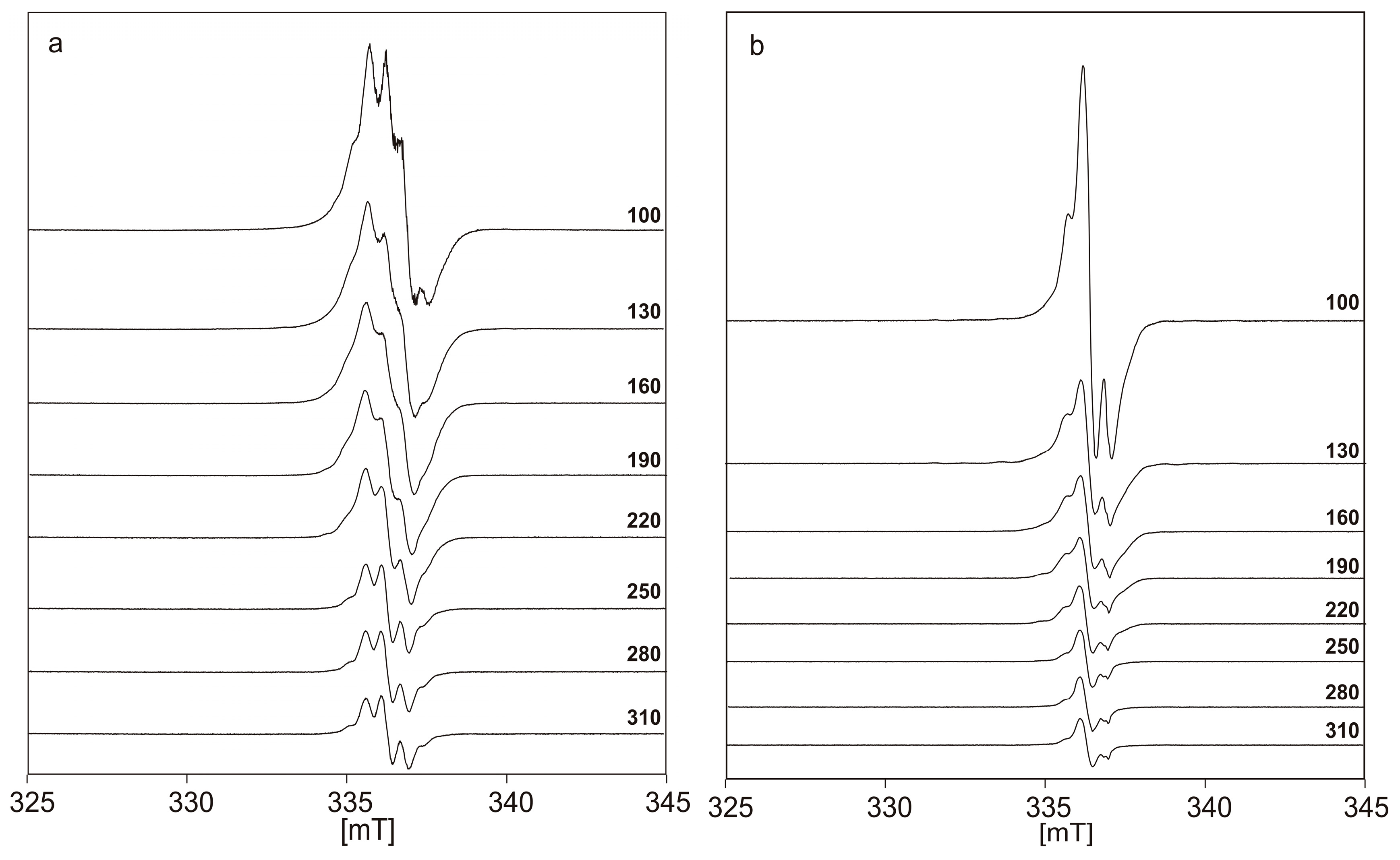
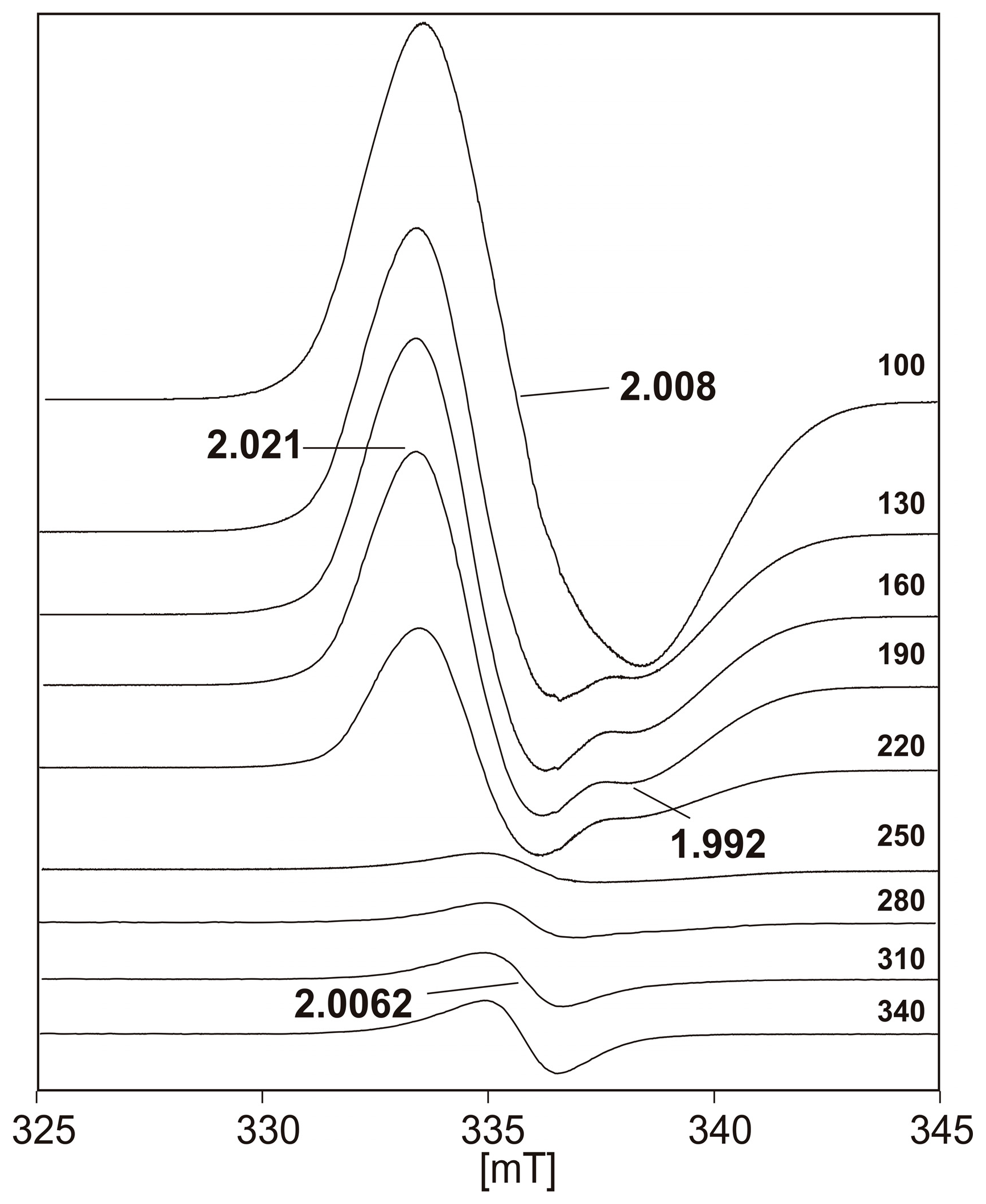
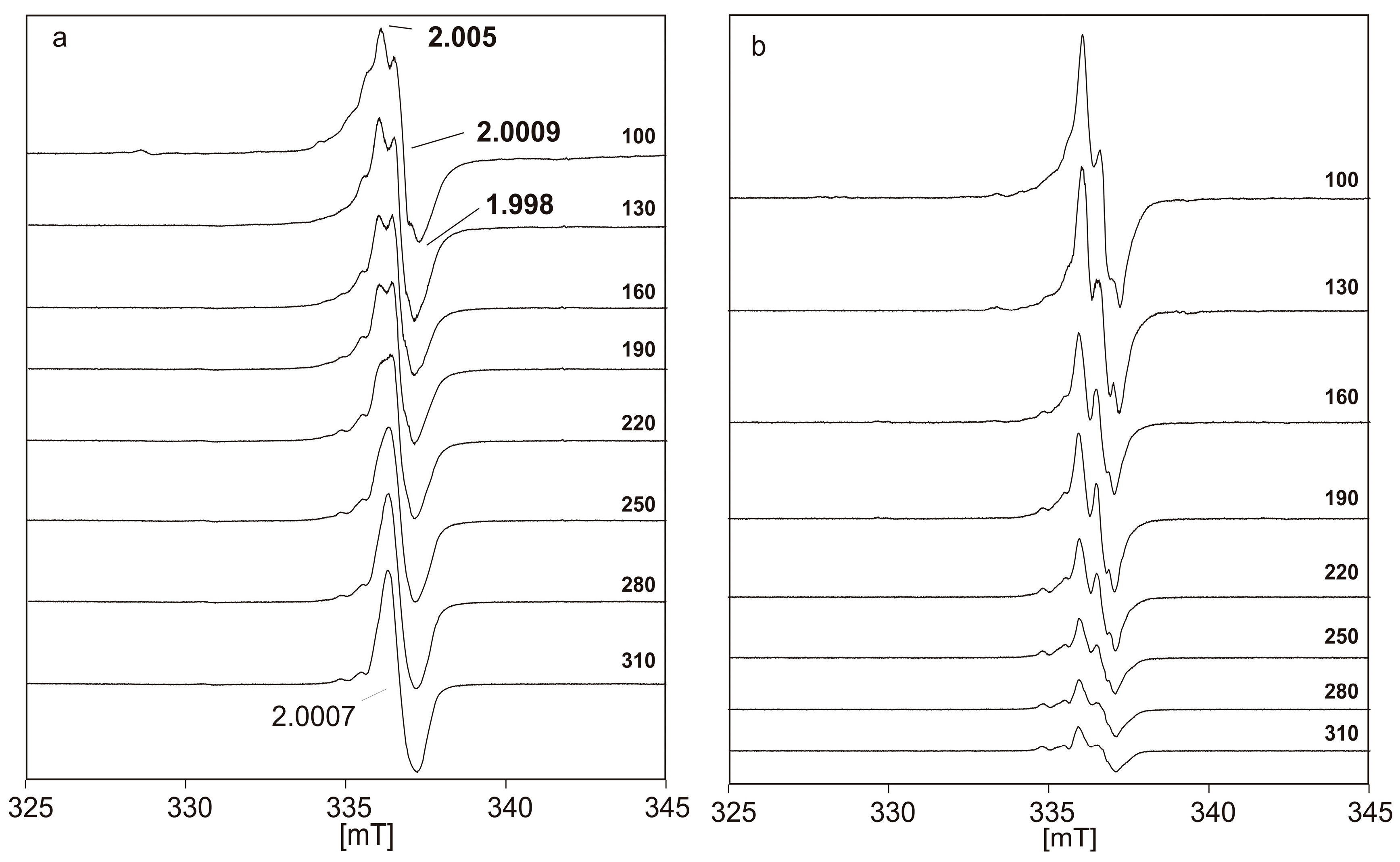
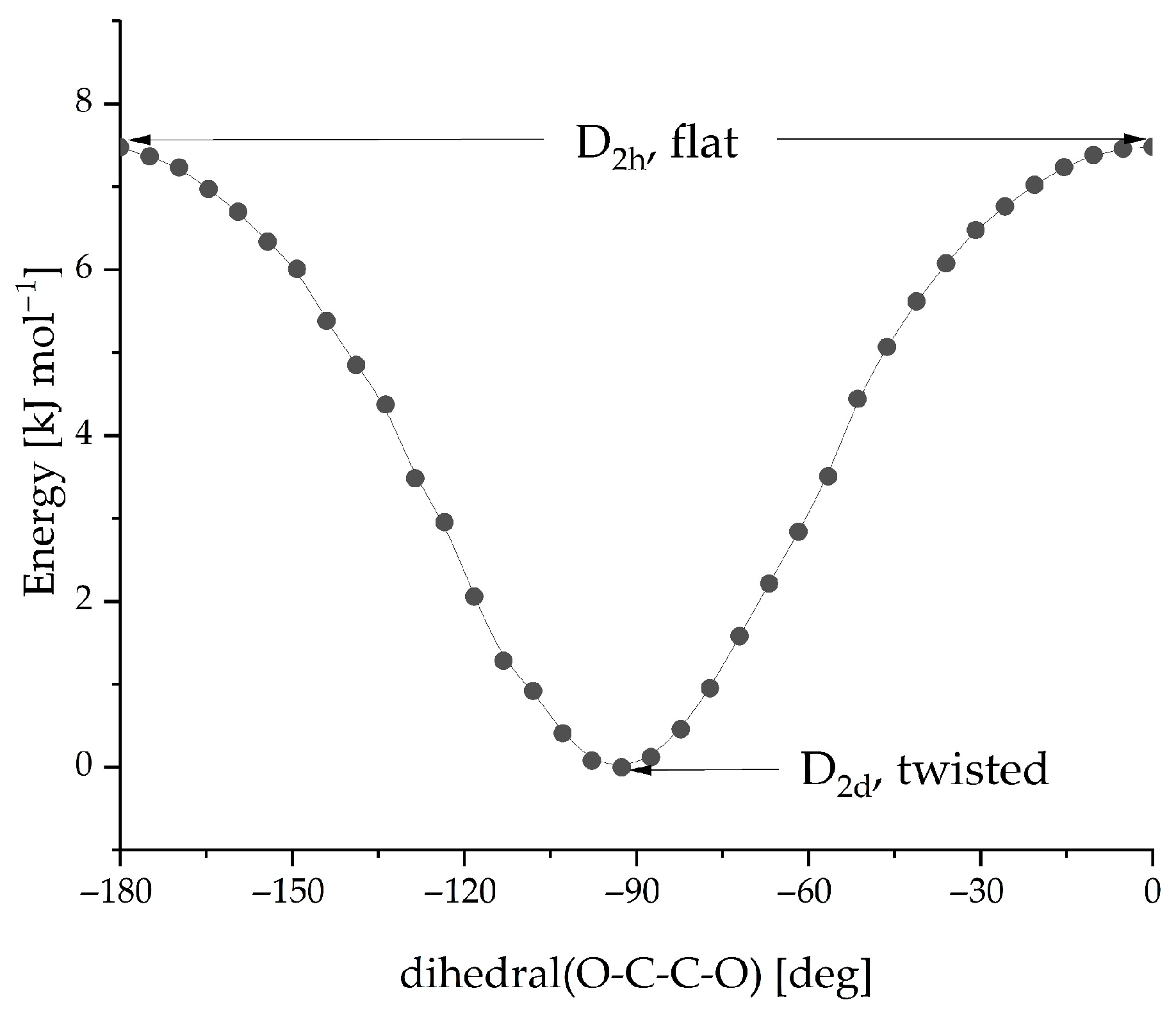
Radical System
(M Model)		DFT FunctionalBasis Setgavg
(Calculated)		gavg
(Experiment)		Δg (×103)
HC2O4• (M1)RI-B2PLYPdef2-QZVPP2.003612.00350.11
(H2C2O4)PBE0def2-TZVPD2.00356 0.06
B3LYPdef2-QZVPD2.00372 0.22
C2O4•− (M2)RI-B2PLYPdef2-QZVPP2.005622.0082.38
(Cs2C2O4)PBE0def2-QZVPD2.00694 1.06
B3LYPdef2-QZVPD2.0075 0.5
C2O4•− (M4)RI-B2PLYPdef2-QZVPP2.011792.001310.49
(K2C2O4)PBE0def2-TZVP2.01505 13.75
B3LYPdef2-TZVP2.01821 16.91
CO2•− (Gas Phase)RI-B2PLYPdef2-QZVPP2.00074
PBE0def2-QZVPD2.00074
B3LYPdef2-QZVPD2.00074
Table 2. Percentage contributions of the main radical species in H2C2O4·2H2O obtained from numerical deconvolution of the EPR spectra as a function of microwave power. Temperature of measurement (Tmeas = 100 K).
Table 2. Percentage contributions of the main radical species in H2C2O4·2H2O obtained from numerical deconvolution of the EPR spectra as a function of microwave power. Temperature of measurement (Tmeas = 100 K).
Dominant
Signal		HCO2• Contribution
(Orthorhombic,
gavg ≈ 2.0026)		HC2O4• Contribution
(Axial, gavg ≈ 2.0035)		r2
(Fit Quality)		ν
[GHz]		Power (P) [mW]
Balance44.2%44.4%0.7969.4379010.81
HCO2•55.4%52.3%0.8799.438201.045
HC2O4•21.3%51.3%0.9049.437830.1027
HC2O4• (M1)36.4%37.7%0.8349.437860.01016 *
Table 3. Quality of the numerical deconvolution (r2) versus temperature of measurement (Tmeas) for the two-component static g-tensor model at the two extreme microwave powers.
Table 3. Quality of the numerical deconvolution (r2) versus temperature of measurement (Tmeas) for the two-component static g-tensor model at the two extreme microwave powers.
Tmeas [K]r2 (p ≈ 0.01 mW)r2 (p ≈ 10.7 mW)
1000.8337 *0.7959
130−0.01950.6978
160−0.99540.5477
190−2.85360.2775
220−4.7217−0.1297
250−9.6869−1.7954
280−10.4314−2.5426
310−14.8533−3.6690
Table 4. Contributions of the primary (D2d) and annealed (D2h) oxalate radical conformers derived from numerical deconvolution.
Table 4. Contributions of the primary (D2d) and annealed (D2h) oxalate radical conformers derived from numerical deconvolution.
CO2•−
(gavg = 2.0007)		C2O4•−
(D2h, gavg = 2.0118)		C2O4•−
(D2d, gavg = 2.0056)		r2
(Fit Quality)		p [mW]Tmeas [K]
42.0%0.0%58.0%0.99410.78100
28.1%0.0%71.9%0.97510.76130
0.7%72.7%26.6%−1.53710.78250
10.0%26.8%63.2%−0.13310.71310
Table 5. Selected results of the five-component numerical deconvolution for K2C2O4·H2O showing the contributions of the primary radical models and decomposition products.
Table 5. Selected results of the five-component numerical deconvolution for K2C2O4·H2O showing the contributions of the primary radical models and decomposition products.
C2O4•− EXP
(gavg ≈ 2.0013)		CO2•−
(gavg ≈ 2.0007)		C2O4•− DFT
(gavg ≈ 2.0118)		r2
(Fit Quality)		p [mW]Tmeas [K]
23.6%12.4%44.6%0.57281.039100
65.3%11.7%5.4%0.49751.038130
21.4%8.8%53.8%−0.409710.71190
24.1%7.7%57.3%−1.15471.054250
26.8%8.6%58.5%−1.133910.78310
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sadło, J.; Pogocki, D. DFT-Computation-Assisted EPR Study on Oxalate Anion-Radicals, Generated in γ-Irradiated Polycrystallites of H2C2O4·2H2O, Cs2C2O4, and K2C2O4·H2O. Appl. Sci. 2025, 15, 11898. https://doi.org/10.3390/app152211898

AMA Style

Sadło J, Pogocki D. DFT-Computation-Assisted EPR Study on Oxalate Anion-Radicals, Generated in γ-Irradiated Polycrystallites of H2C2O4·2H2O, Cs2C2O4, and K2C2O4·H2O. Applied Sciences. 2025; 15(22):11898. https://doi.org/10.3390/app152211898

Chicago/Turabian Style

Sadło, Jarosław, and Dariusz Pogocki. 2025. "DFT-Computation-Assisted EPR Study on Oxalate Anion-Radicals, Generated in γ-Irradiated Polycrystallites of H2C2O4·2H2O, Cs2C2O4, and K2C2O4·H2O" Applied Sciences 15, no. 22: 11898. https://doi.org/10.3390/app152211898

APA Style

Sadło, J., & Pogocki, D. (2025). DFT-Computation-Assisted EPR Study on Oxalate Anion-Radicals, Generated in γ-Irradiated Polycrystallites of H2C2O4·2H2O, Cs2C2O4, and K2C2O4·H2O. Applied Sciences, 15(22), 11898. https://doi.org/10.3390/app152211898

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop