Comparative Evaluation of Parallel and Sequential Hybrid CNN–ViT Models for Wrist X-Ray Anomaly Detection

Abstract

Medical anomaly detection is challenged by limited labeled data and domain shifts, which reduce the performance and generalization of deep learning (DL) models. Hybrid convolutional neural network–Vision Transformer (CNN–ViT) architectures have shown promise, but they often rely on large datasets. Multistage transfer learning (MTL) provides a practical strategy to address this limitation. In this study, we evaluated parallel hybrids, where convolutional neural network (CNN) and Vision Transformer (ViT) features are fused after independent extraction, and sequential hybrids, where CNN features are passed through the ViT for integrated processing. Models were pretrained on non-wrist musculoskeletal radiographs (MURA), fine-tuned on the MURA wrist subset, and evaluated for cross-domain generalization on an external wrist X-ray dataset from the Al-Huda Digital X-ray Laboratory. Parallel hybrids (Xception–DeiT, a data-efficient image transformer) achieved the strongest internal performance (accuracy 88%), while sequential DenseNet–ViT generalized best in zero-shot transfer. After light fine-tuning, parallel hybrids achieved near-perfect accuracy (98%) and recall (1.00). Statistical analyses showed no significant difference between the parallel and sequential models (McNemar’s test), while backbone selection played a key role in performance. The Wilcoxon test found no significant difference in recall and F1-score between image and patient-level evaluations, suggesting balanced performance across both levels. Sequential hybrids achieved up to 7× faster inference than parallel models on the MURA test set while maintaining similar GPU memory usage (3.7 GB). Both fusion strategies produced clinically meaningful saliency maps that highlighted relevant wrist regions. These findings present the first systematic comparison of CNN–ViT fusion strategies for wrist anomaly detection, clarifying trade-offs between accuracy, generalization, interpretability, and efficiency in clinical AI.

1. Introduction

X-ray medical images are useful in detecting musculoskeletal conditions. The advancement of DL has improved diagnostic capability, yet challenges including limited data availability, black-box algorithms, cross-domain adaptability, and the necessity for thorough validation in actual clinical environments remain [1,2]. Musculoskeletal disorders represent a significant global health issue, affecting 1.7 billion individuals and leading to disabilities; they limit mobility and impact work life [3]. The wrist has a complicated structure consisting of numerous small bones and associated soft-tissue components, which reduces the effectiveness of radiologic study [4]. Thus, wrist pathology is one of the most common reasons for emergency settings [5].

Given this clinical motivation, studies have explored DL methods or computer-aided detection and analysis of anomalies on wrist musculoskeletal radiographs. Convolutional neural networks (CNNs) dominate the field in wrist X-ray anomaly detection, but important limitations remain. Several single-center wrist X-ray studies have reported strong CNN performance 98% accuracy with DenseNet-201 and U-Net [6]; accuracies up to 86.9% (Cohen’s kappa($\kappa$) = 0.728) across 11 architectures [7]; 99.3% accuracy, and 98.7% sensitivity with an ensemble of EfficientNet-B2 to EfficientNet-B5 model [8]. Data augmentation was applied to expand small training sets and still achieved 97–98% accuracy [9,10,11], yet their limited data diversity raises concerns about unrealistic performance estimates. However, all of these studies relied on small, single-source datasets and omitted external validation, leaving their robustness to diverse anomalies untested. A recent systematic review confirms that CNNs now rival clinical experts for fracture detection, but reviews emphasize persistent challenges: small or unrepresentative test sets, lack of external validation, and limited focus on non-fracture wrist anomalies [12].

Hybrid DL approaches that combine multiple CNN architectures, or CNN with other networks, have shown notable gains in wrist anomaly detection. For example, Bhangare et al. [13] developed an ensemble that fuses DenseNet, MobileNet, and a custom CNN using a Least Entropy Combiner (LEC), achieving 97% accuracy. Similarly, Duan et al. [14] combined ResNet-50, DenseNet-121, and a human-designed module in a decision-level hybrid, reporting 90.7% recall. Some studies explore sequential architectures, including Dilated CNN linked with a bidirectional Long Short-Term Memory (LSTM) for sequential feature extraction, achieving 88.2% accuracy and 92.2% recall [15]. However, as models grow more complex, their computational demands increase significantly. These results show that hybridization consistently improves diagnostic performance, motivating the exploration of more advanced combinations such as CNN–ViT hybrids.

Recently, interest has shifted toward Vision Transformers (ViTs), which use self-attention rather than convolution. Direct comparisons between CNNs and ViTs on musculoskeletal radiographs generally reveal only minor performance gaps. DenseNet-201 outperformed a ViT by just 1.3 percentage points in accuracy [16], and DenseNet-121 was similarly close to the data-efficient image transformer-base (DeiT-B) on the MURA wrist subset [17]. Building on these findings, Selvaraj et al. [18] showed that ViT-only models can outperform CNNs for bone fracture detection, yet their sequential CNN–ViT hybrid achieved the best results (recall 92.4%, Area Under the Curve (AUC) 94.8%). In contrast, the parallel fusion strategy, where CNN and ViT pipelines operate simultaneously, remains largely unexplored, and its advantages over sequential fusion are still unclear in radiological image analysis [19].

Beyond musculoskeletal imaging, several studies have explored hybrid CNN–ViT architectures in other medical domains. Rahman [20] and Zeynali et al. [21] implemented parallel fusion on the BreakHis and invasive ductal carcinoma (IDC) histopathology datasets, respectively. In Rahman [20], CNN and ViT outputs were concatenated before classification, while Zeynali et al. [21] combined Xception and a custom CNN whose features were passed to a ViT and later merged for prediction. Hadhoud et al. [22] and Yulvina et al. [23] extended these hybrids to chest radiographs, applying parallel and sequential fusion strategies, respectively, for tuberculosis-related disease detection. These works confirm the growing utility of hybrid CNN–ViT architectures in medical imaging, yet their evaluations remain limited to single-domain, image-level settings.

A key challenge in transfer learning (TL) is the domain shift problem performance drops that occur when models are deployed on data that differ from their training distributions [2]. MTL, in which models are sequentially trained on related medical datasets before fine-tuning on the target task, has been shown to mitigate domain shift and yield better results [24]. For example, Hadhoud et al. [22] demonstrated an implicit multistage TL process by first training a CNN–ViT hybrid for tuberculosis detection and then fine-tuning the same model to distinguish tuberculosis from pneumonia, achieving improved generalization across related chest X-ray tasks. Similarly, models pretrained on X-rays from other anatomical regions and then fine-tuned on the wrist achieve higher accuracy, recall, and Cohen’s kappa than those using only ImageNet weights [1,25]. In wrist X-ray classification, fine-tuning an Xception model on non-wrist MURA images first improved accuracy from 69.1% to 84.1%, recall from 64.3% to 73.6%, and Cohen’s kappa from 0.38 to 0.68 compared to ImageNet-only pretraining [1]. Comparable improvements were observed in shoulder X-rays, highlighting the value of MTL for musculoskeletal radiography [25]. However, few studies have explored MTL specifically for wrist-to-wrist transfer across different clinical groups or hospitals.

Interpretability is increasingly recognized as essential in medical imaging, as clinicians require transparency to trust DL models. Several approaches have been explored: Alammar et al. [1] applied gradient-based class activation heatmap (Grad-CAM), activation visualization, and locally interpretable model-independent explanations (LIME) [26] to explain predictions, while Harris et al. [16] found, with input from radiologists, that Grad-CAM produced more clinically meaningful localizations than LIME for wrist X-rays. Other studies highlight how architecture affects explanation quality. Murphy et al. [17] reported that attention maps from DeiT-B offered sharper localization of abnormalities, whereas Grad-CAM on DenseNet-121 gave broader, less specific regions. In related hybrid studies, Rahman [20] applied Grad-CAM on the CNN and Attention Rollout [27] on the ViT branch, illustrating the complementary interpretability of parallel attention mechanisms. These results show that both the interpretability method and model type influence clinical usefulness. Despite progress, explainable AI remains underused in wrist radiograph analysis [28]. This study addresses that gap by applying LayerCAM [29] and Attention Rollout to hybrid CNN–ViT models, aiming to provide clearer and more clinically relevant explanations.

Despite recent advances, several limitations remain in existing wrist anomaly detection research:

(1)

Although CNN and ViT models have been used individually in musculoskeletal imaging, hybrid CNN–ViT architectures remain underexplored for wrist abnormality detection, and the effect of different fusion strategies (parallel vs. sequential) on performance and robustness has not been systematically investigated.

(2)

Existing studies are mostly restricted to in-domain evaluation, with limited validation on external or cross-institutional datasets, leaving real-world generalization underexamined.

(3)

Prior work predominantly reports image-level metrics, which do not fully capture patient-level diagnostic reliability or clinical interpretability.

(4)

The potential of MTL for mitigating domain shift across wrist datasets remains insufficiently explored.

(5)

Explainability methods are inconsistently applied, with most wrist studies relying on Grad-CAM, while more advanced techniques such as LayerCAM and Attention Rollout are rarely explored despite their potential for finer, layer-specific localization.

To address these gaps, this study makes the following contributions:

(1)

It presents the systematic evaluation of parallel and sequential hybrid CNN–ViT architectures for wrist anomaly detection.

(2)

It extends evaluation to external datasets, enabling a robust assessment of cross-domain generalization.

(3)

It introduces patient-level evaluation, demonstrating its clinical value compared with image-level reporting.

(4)

It applies a wrist-to-wrist MTL framework to reduce domain shift and improve transfer performance.

(5)

It enhances model interpretability by employing LayerCAM and Attention Rollout to provide clinically meaningful visual explanations.

Collectively, these contributions establish a foundation for developing robust, interpretable hybrid architectures for real-world radiology support.

The remainder of this paper is organized as follows: Section 2 describes the datasets, preprocessing steps, hybrid model architectures, and training procedures. Section 3 presents the experimental results, including classification performance, robustness validation, statistical analyses, interpretability assessments, and computational efficiency. Section 4 discusses the main findings, limitations, and potential directions for future work.

2. Materials and Methods

2.1. Datasets

The primary dataset used in this study is the MURA dataset, a large-scale collection of musculoskeletal radiographs [30]. MURA includes X-ray images from seven anatomical regions: elbow, finger, forearm, hand, humerus, shoulder, and wrist. Each region is categorized into normal and abnormal classes. The dataset was originally compiled from the Picture Archiving and Communication System (PACS) of Stanford Hospital, with DICOM images acquired between 2001 and 2012 and labeled by board-certified radiologists using 3-megapixel medical-grade displays (maximum luminance 400 cd/m², minimum luminance 1 cd/m², pixel size 0.2 mm, and native resolution 1500 × 2000 pixels) [30]. However, the publicly released version contains only de-identified PNG images and does not include DICOM metadata such as imaging equipment or acquisition parameters.

The wrist subset contains 10,411 images from 3514 patients. All non-wrist categories in MURA were used as the source domain for transfer learning, while wrist images served as the target domain. To avoid overlap of imaging studies across subsets, splits were created using the GroupShuffleSplit method with the patient study identifier (study_key) as the grouping variable and a fixed random seed (random_state = 42). Approximately 5% of studies were assigned to the test set and 5% to the validation set, ensuring that each study_key appeared in only one subset. This 90/5/5 study-level split is fully reproducible and produced patient-consistent validation and test sets, while 84 patients with both normal and abnormal wrist studies remained only in the training set.

To evaluate cross-domain generalization, an external wrist fracture dataset collected from the Al-Huda Digital X-ray Laboratory was also utilized [31]. This dataset comprises 193 wrist X-ray images from unique patients. Each patient is assigned a single binary label (fracture vs. normal), and patients with mixed labels are explicitly rejected to avoid ambiguous ground truth. The dataset is then split at the patient level using a fixed random seed (random_state = 42) to ensure reproducibility. First, patients are stratified by label and divided into a held-out test cohort (35%). The remaining patients are again stratified and split into a training set and a validation set such that approximately 50% of all patients are used for training, 15% for validation, and 35% for testing. Patients do not appear in more than one split. This procedure preserves class balance at the patient level and matches the deployment setting in which models classify previously unseen patients. The detailed patient and image distributions across the internal (MURA) and external (Al-Huda) datasets are summarized in

Table 1. Patient and image distribution across internal (MURA) and external (Al-Huda) datasets. “Neg” and “Pos” refer to normal and abnormal cases, respectively.

Dataset	Split	Patients (Neg–Pos)	Total Patients	Images (Neg–Pos)	Total Images
MURA (Internal)	Train	1888–1256	3144	5513–3835	9348
	Validation	112–73	185	305–229	534
	Test	112–73	185	311–218	529
Al-Huda (External)	Train	41–28	69	41–55	96
	Validation	12–9	21	12–17	29
	Test	29–20	49	29–39	68

Counts correspond to the final splits used for experimentation.

.

For the MTL stage, we additionally used the non-wrist MURA regions (elbow, finger, forearm, hand, humerus, shoulder) to learn general musculoskeletal representations before wrist-specific fine-tuning. The per-region distribution is reported separately in

Table 2. Non-wrist MURA data used for the multi-task learning stage. “Neg” and “Pos” refer to normal and abnormal cases, respectively.

Region	Training Set			Validation Set
	Images (Neg–Pos)	Total	Patients	Images (Neg–Pos)	Total	Patients
ELBOW	2642–1792	4434	1544	283–214	497	176
FINGER	2809–1775	4584	1680	329–193	522	194
FOREARM	1049–580	1629	781	115–81	196	88
HAND	3631–1363	4994	1756	428–121	549	202
HUMERUS	602–544	1146	527	71–55	126	60
SHOULDER	3801–3753	7554	2438	410–415	825	281
Total	14,534–9807	24,341	8726	1636–1079	2715	1001

Non-wrist regions were split at the study level (90% training, 10% validation) with random_state = 42.

to enable reproductions that match the original regional proportions.

2.2. Preprocessing

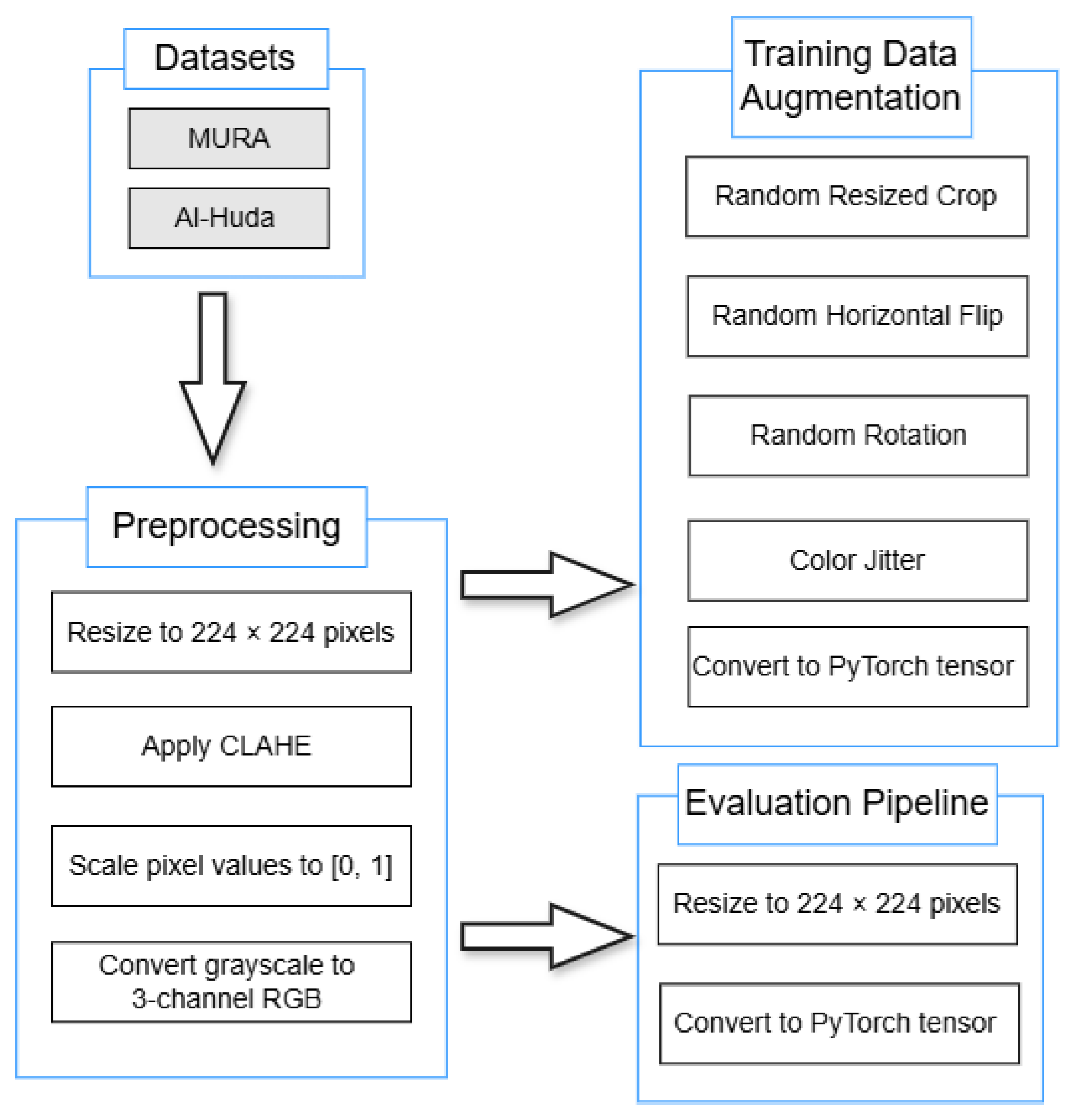
Figure 1 illustrates the complete preprocessing and augmentation pipeline, showing the order of operations adopted in this study.

All images were resized to $224\times 224$ pixels, enhanced using Contrast Limited Adaptive Histogram Equalisation (CLAHE, clipLimit = 5.0, tileGridSize = 8 × 8) to improve local contrast, rescaled to the $[0,1]$ range, and converted from single-channel grayscale to three-channel RGB $(224\times 224\times 3)$ to meet CNN/ViT input requirements. During training, random augmentations were applied sequentially, including random resized cropping (scale = [0.8, 1.0], aspect_ratio = [0.9, 1.1]), horizontal flipping ($p=0.5$), small-angle rotations of ±10°, and color jitter (brightness = 0.2, contrast = 0.2, saturation = 0.2, hue = 0.02). The evaluation pipeline used the same preprocessing steps (including CLAHE) but excluded all random transformations. All preprocessing and augmentation operations were implemented in OpenCV and PyTorch and applied consistently to both the MURA and Al-Huda wrist datasets. Unless otherwise stated, parameters not explicitly listed (e.g., default kernel sizes or interpolation modes) used the standard default values provided by their respective libraries.

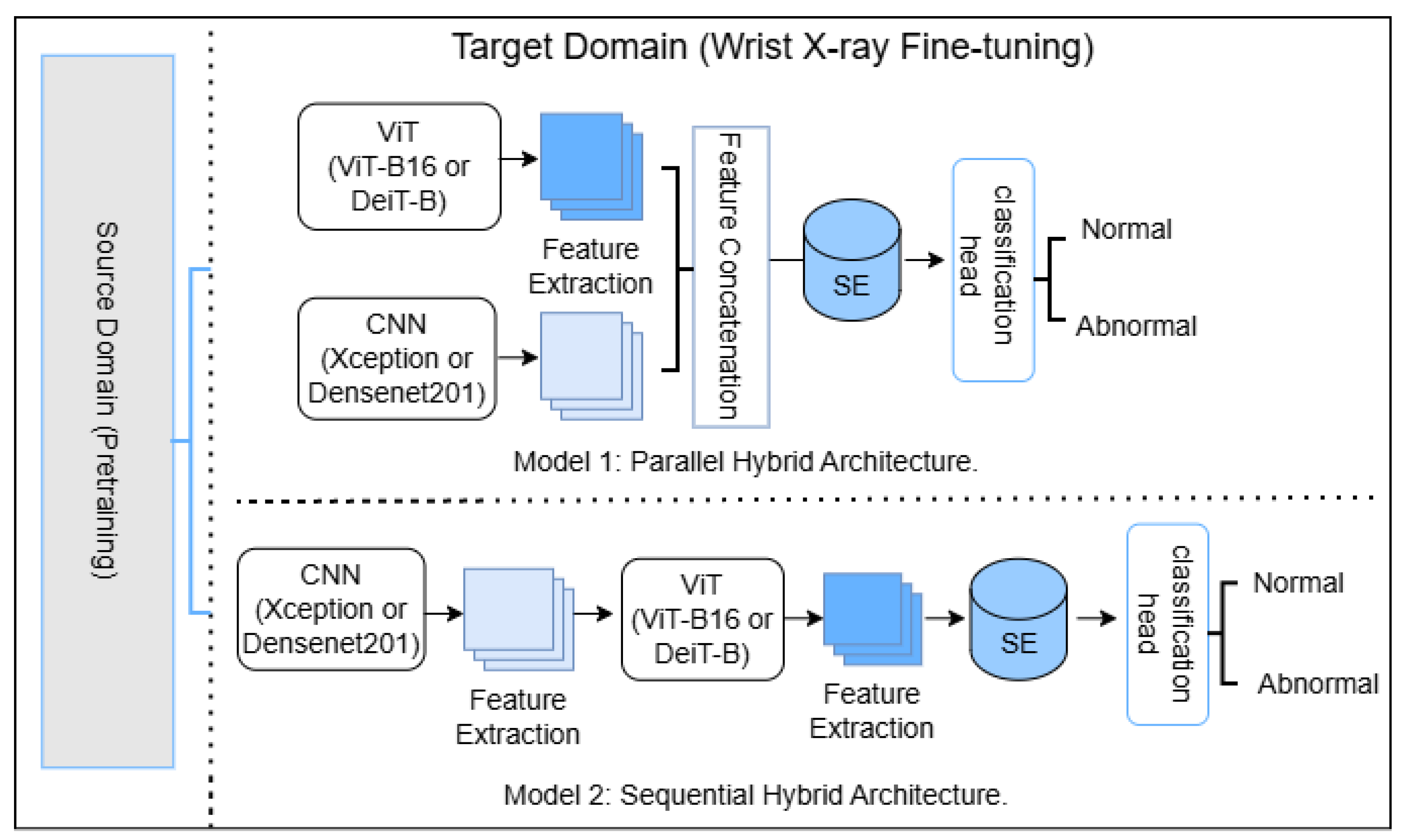
2.3. Model Architectures

This study investigates two hybrid integration strategies for combining CNNs and ViTs in wrist X-ray anomaly detection: parallel fusion and sequential fusion. The objective is to evaluate which architecture better leverages both local (CNN) and global (ViT) feature representations. The complete implementation, including preprocessing, training, and evaluation scripts for all experimental stages, as well as model definitions, utilities, and interpretability modules, is publicly available at https://github.com/Brianmahlatse/wrist-anomaly-hybrids (accessed on 31 October 2025). The repository also provides example training scripts for each stage (Stage 1–4) under the scripts/ directory to ensure the full reproducibility of the results. The overall designs of both hybrid configurations are illustrated in Figure 2.

In the parallel configuration, an input image is processed simultaneously by two independent feature extractors: a CNN (DenseNet201 or Xception) and a ViT (Vision Transformer Base-16 (ViT-B16) or the distilled data-efficient image transformer-base (DeiT-B)). The resulting feature vectors, $f_{\mathrm{cnn}}\in {\mathbb{R}}^{C_c}$ and $f_{\mathrm{vit}}\in {\mathbb{R}}^{C_v}$, are concatenated to form a unified representation $x=[f_{\mathrm{cnn}};f_{\mathrm{vit}}]\in {\mathbb{R}}^C$, where $C=C_c+C_v$. A Squeeze-and-Excitation (SE) block then adaptively recalibrates the channel dependencies of x to emphasize task-relevant features. The reweighted vector $\tilde{x}$ is passed through a dense classification head comprising two fully connected layers with Batch Normalization, Dropout ($p=0.3$), and a final sigmoid output for binary classification.

In the sequential configuration, the image is first processed by a CNN to extract intermediate feature maps. These maps are linearly projected to 1024 dimensions, reshaped into a $32\times 32$ single-channel map, and upsampled to $224\times 224$. A $1\times 1$ convolution converts this into a three-channel input for the ViT. The transformer encodes the input into a sequence, and the embedding corresponding to the learnable classification ([CLS]) token ($f_{\mathrm{cls}}\in {\mathbb{R}}^{C_v}$) is selected as the fused representation. The SE block operates on this vector using the same reduction ratio ($r=8$), and the reweighted output is fed into the same classification head used in the parallel model.

Integration of Squeeze-and-Excitation Modules

Both hybrid configurations employ a standard two-layer SE block [32] to adaptively recalibrate channel responses. Each SE module performs global average pooling followed by two fully connected layers with ReLU and sigmoid activations, using a reduction ratio of $r=8$ and hidden dimension $max(1,\lfloor C/8\rfloor )$. No Batch Normalization or Layer Normalization is applied inside the SE block; feature scaling is handled by the Batch Normalization layers in the classifier head. The detailed computation of the SE block is summarized in Algorithm 1.

In the parallel model, feature vectors from the CNN and ViT backbones are concatenated to form $x=[f_{\mathrm{cnn}};f_{\mathrm{vit}}]\in {\mathbb{R}}^{B\times C}$, where $C=C_{\mathrm{cnn}}+C_{\mathrm{vit}}$ with $C_{\mathrm{cnn}}\in \{1920,2048\}$ (DenseNet201 or Xception) and $C_{\mathrm{vit}}=768$ (ViT-B/16 or DeiT-B). The SE block refines this fused representation before classification.

In the sequential model, the CNN output (1920 or 2048-D) is projected to 1024 dimensions, reshaped to a $32\times 32$ map, upsampled to $224\times 224$, converted to three channels by a $1\times 1$ convolution, and processed by the ViT backbone. The resulting 768-D ViT embedding is passed through the same SE block prior to the classifier head.

Algorithm 1: Squeeze-and-Excitation block.

Input: $x\in {\mathbb{R}}^{B\times C}$

Parameters: reduction ratio $r=8$

Output: $\tilde{x}=w\odot x$

$z\leftarrow \mathrm{GAP}\left(x\right)$;

$h\leftarrow \mathrm{ReLU}\left(W_{1}z\right)$, where   $W_1\in {\mathbb{R}}^{\lfloor C/r\rfloor \times C}$;

$w\leftarrow \sigma \left(W_{2}h\right)$, where   $W_2\in {\mathbb{R}}^{C\times \lfloor C/r\rfloor }$;

return $\tilde{x}$;

2.4. Rationale for Selecting Only Four Backbones

This study focused on four representative backbones: Xception and DenseNet201 for CNNs, and ViT-B16 and DeiT-B for Vision Transformers. The selection was guided by computational feasibility and prior evidence of strong performance on musculoskeletal radiographs, including wrist studies based on the MURA dataset. DenseNet201 and Xception have been frequently employed for X-ray abnormality detection [1,7,28], while DeiT-B and ViT-B16 have shown competitive results in radiograph classification [17]. ViT-B16 was further chosen to balance DeiT-B at the model scale (≈86 M parameters). Other mainstream backbones such as ResNet or Swin Transformer were not included due to resource constraints, but the selected models cover two distinct CNN and ViT paradigms, providing a balanced foundation for evaluating CNN–ViT fusion strategies.

2.5. Multistage Transfer Learning Framework

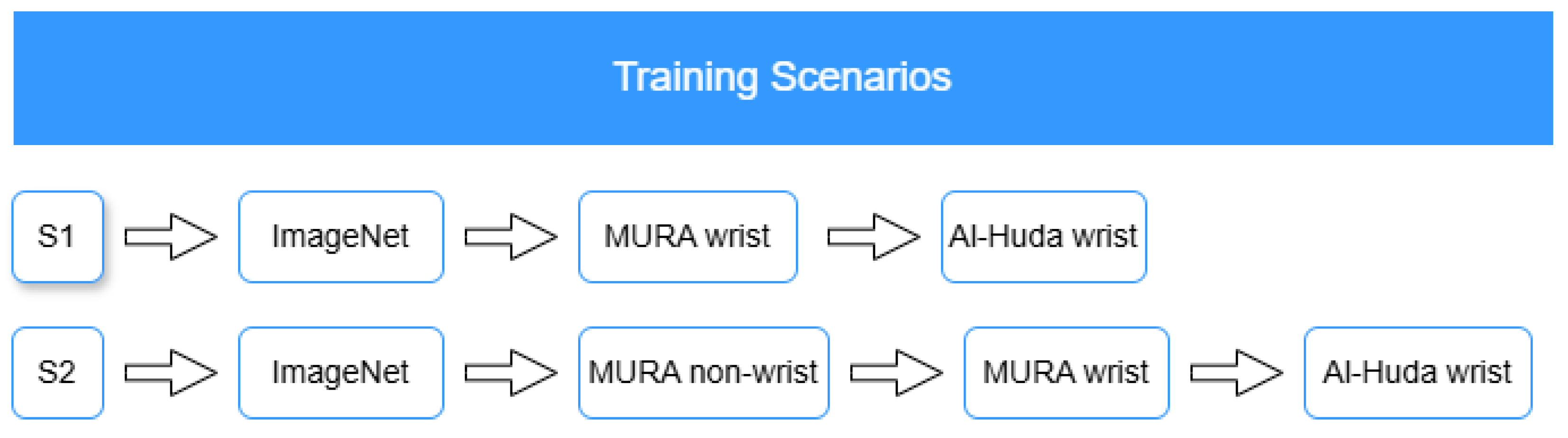
To illustrate the complete four-stage MTL process, Figure 3 summarizes the general (S1) and proposed wrist-to-wrist (S2) strategies adopted in this study, corresponding to sequential stages of pretraining, wrist fine-tuning, hybrid training, and external fine-tuning.

2.5.1. General MTL Strategy

Transfer learning enables a model to reuse knowledge gained from a large, general dataset and apply it to a smaller, task-specific one. A common source for TL is a pretrained model developed on the ImageNet dataset, which contains over one million color images categorized into 1000 object classes. Such models provide rich feature representations that can be fine-tuned for specialized tasks, mitigating the issue of limited data availability [1].

In the general MTL setup (S1), models were initialized with ImageNet weights, fine-tuned directly on the MURA wrist subset, and subsequently adapted to the external Al-Huda wrist fracture dataset. This sequential adaptation represents a standard multistage transfer process that captures domain-relevant wrist features but does not explicitly leverage non-wrist musculoskeletal information. The approach serves as a baseline to assess the benefits of the proposed strategy.

2.5.2. Proposed Wrist-to-Wrist MTL Strategy

Machine learning models in medical imaging often suffer from the domain shift problem, where performance declines when models are applied to data drawn from distributions different from those used for training [2]. To address this limitation, the proposed wrist-to-wrist MTL (S2) introduces an intermediate in-domain adaptation step using non-wrist musculoskeletal radiographs from the MURA dataset before fine-tuning on the wrist subset. This step allows the model to first learn generic musculoskeletal features, which serve as a bridge between the general ImageNet domain and the target wrist domain, thereby enhancing robustness to domain shifts [24].

The complete MTL pipeline follows four progressive stages:

• Stage 1: Pretraining on MURA non-wrist data to capture general musculoskeletal representations.
• Stage 2: Fine-tuning on the MURA wrist subset, where standalone CNN and transformer models (DenseNet201, Xception, ViT-B16, and DeiT-B) are refined.
• Stage 3: Construction and training of hybrid CNN–ViT models (DenseNet–ViT and Xception–DeiT) using the fine-tuned standalone weights as backbones.
• Stage 4: Final fine-tuning on the external Al-Huda wrist dataset to validate model generalization under a wrist-to-wrist transfer setting.

This progressive design leverages the structural and visual similarity across musculoskeletal regions to enable smoother knowledge transfer from internal (MURA wrist) to external (Al-Huda wrist) domains, thereby supporting the final wrist-to-wrist adaptation stage.

2.6. Training Environment and Hyperparameter Summary

2.6.1. Hardware and Software

All experiments were conducted in Google Colab Pro+ using an NVIDIA (NVIDIA Corporation, Santa Clara, CA, USA) A100 GPU with 40 GB VRAM, 83.5 GB system memory, and 235.7 GB available disk space. Mixed-precision (FP16) training and inference were enabled on GPU to reduce memory usage and accelerate training. The software environment and library versions used throughout the experiments are summarized in

Table 3. Software environment and library versions used in experiments.

Component	Version	Purpose/Description
Python	3.12.12	Runtime environment
PyTorch	2.8.0+cu126	Core deep learning framework
CUDA (torch)	12.6	GPU backend for PyTorch
torchvision	0.23.0+cu126	Vision utilities and transforms
timm	1.0.21	CNN and ViT backbone library
Transformers	4.57.1	Hugging Face implementation of ViT and DeiT
NumPy	2.0.2	Array operations and numerical computations
pandas	2.2.2	Data manipulation and tabular storage
Pillow	11.3.0	Image I/O and preprocessing for datasets
scikit-learn	1.6.1	Evaluation metrics and classification reports
SciPy	1.16.3	Statistical tests (e.g., Wilcoxon)
statsmodels	0.14.5	Exact McNemar’s test and statistical validation
OpenCV	4.12.0	Image preprocessing (CLAHE enhancement, resizing)
matplotlib	3.10.0	Visualization of results and interpretability maps

.

2.6.2. Stage-Wise Hyperparameters and Model Selection

The reported trainable fractions (for example, 5%, 20%, or 70%) were computed based on the relative count of architectural blocks unfrozen within each backbone, rather than exact parameter proportions. Each model defines its internal structure differently, so the resulting parameter ratio may slightly deviate from the nominal percentage. For instance, Xception consists of 26 depth-wise-separable convolutional blocks, DenseNet has 11 dense blocks, and ViT/DeiT have 12 transformer layers. Because some blocks differ greatly in parameter density, unfreezing a certain number of final blocks (e.g., 1 of 26 or 2 of 12) may correspond to 4–8% of parameters rather than the exact numeric fraction. The percentages therefore indicate relative training depth, not a precise parametric ratio, ensuring a consistent comparison across architectures and stages. In all cases, the unfrozen layers correspond to the final blocks of each backbone (e.g., the last convolutional or transformer layers), ensuring that fine-tuning targets the most task-relevant high-level features while lower-level representations remain frozen. The detailed hyperparameter settings and training configurations for each stage of the MTL process are summarized in

Table 4. Stage 1: Pretraining on MURA non-wrist regions.

Item	Configuration
Models	ViT-B16, DeiT-B, Xception, DenseNet201
Trainable fraction	100% of layers (Xception 26 of 26, DenseNet 11 of 11, ViT/DeiT 12 of 12)
Batch size	256
Learning rate	DeiT/ViT $2\times {10}^{-5}$, Xception $1\times {10}^{-3}$, DenseNet $2\times {10}^{-5}$
Weight decay	0.01 (DeiT/ViT/Xception), 0.03 (DenseNet)
Epochs	ViT = 20, DeiT = 20, Xception = 50, DenseNet201 = 50
Scheduler	Cosine annealing with 10% step-based warm-up (final learning rate (LR) = 0)
Loss	Binary cross-entropy with logits (BCEWithLogits), no class weights
Initialization	ImageNet-pretrained weights
Model selection	Highest validation recall
Early stopping	Enabled (patience = 5)

,

Table 5. Stage 2: Fine-tuning on the MURA wrist subset.

Item	Configuration
Models	Same as Stage 1; initialized from Stage 1 checkpoints
Trainable fraction	Approximately 70% (Xception 18 of 26, DenseNet 8 of 11, ViT/DeiT 8 of 12)
Batch size	64
Learning rate	Xception $2\times {10}^{-5}$, DeiT $2\times {10}^{-4}$, ViT/DenseNet $2\times {10}^{-5}$
Weight decay	0.03
Epochs	50
Scheduler	Cosine annealing with 10% step-based warm-up (final LR = 0)
Loss	BCEWithLogits, no class weights
Model selection	Highest validation recall
Early stopping	Enabled (patience = 5)

,

Table 6. Stage 3: Hybrid CNN–ViT training on the MURA wrist dataset.

Item	Configuration
Hybrids	DenseNet–ViT and Xception–DeiT (parallel and sequential)
Initialization	Backbones from Stage 2; fusion and classification heads randomly initialized (Xavier uniform)
Trainable fraction	Parallel: CNN 40% (DenseNet 4 of 11, Xception 10 of 26), ViT 20% (2 of 12); Sequential: CNN 20% (2 of 11 / 2 of 26), ViT 20% (2 of 12)
Batch size	64
Learning rate	$2\times {10}^{-4}$
Weight decay	0.03
Epochs	50
Scheduler	Cosine annealing with 10% step-based warm-up (final LR = 0)
Loss	BCEWithLogits, no class weights
Model selection	Highest validation recall
Early stopping	Enabled (patience = 5)

and

Table 7. Stage 4: External fine-tuning on the Al-Huda wrist dataset.

Item	Configuration
Hybrids	Same as Stage 3
Trainable fraction	Final 5% of each backbone (DenseNet 1 of 11, ViT/DeiT 1 of 12, Xception 1 of 26 *)
Batch size	32
Learning rate	Parallel $1\times {10}^{-3}$, Sequential $1\times {10}^{-4}$
Weight decay	0.01 (parallel), 0.02 (sequential)
Epochs	50
Scheduler	Cosine annealing with 10% step-based warm-up (final LR = 0)
Loss	BCEWithLogits, no class weights
Model selection	Lowest validation loss
Early stopping	Enabled (patience = 5)

* The final Xception block (block12) contains no trainable convolutional parameters, leaving the backbone effectively frozen.

.

2.7. Experimental Evaluation

2.7.1. Classification Performance

Model performance was evaluated using accuracy, recall, F1-score, Cohen’s kappa, and AUC, which are standard metrics in musculoskeletal imaging studies [1,7]. Metrics were computed from true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) on the test set. Model performance was primarily reported at the patient level to reflect real-world clinical decision-making, where diagnosis is assigned per patient rather than per image. Image-level metrics were computed only for statistical comparison using the Wilcoxon signed-rank test (Section 2.7.2). This ensured that patient-level reporting remained the basis of all quantitative and clinical interpretations, while image-level analysis served solely to validate consistency across evaluation scales.

For patient-level evaluation, predictions from all images belonging to the same patient were aggregated using strict majority voting: a patient was classified as abnormal if more than half of their images were predicted abnormal. In cases of a tie (e.g., an equal number of normal and abnormal predictions), the mean abnormal probability across the patient’s images was used as a tie-breaker, with abnormal assigned if this mean exceeded the decision threshold of 0.5. The same rule was applied to derive the patient-level ground truth label. Patient-level AUC was then computed using these per-patient mean probabilities as continuous scores, ensuring one AUC value per patient rather than per image. This procedure ensures methodological consistency between the patient-level evaluation metrics and the aggregation logic used to generate them, allowing all reported performance values to be computed reproducibly from the defined protocol. The evaluation metrics are summarized in

Table 8. Evaluation metrics reported in this study, with their primary purpose being to assess model performance.

Metric	Purpose
Accuracy	Overall correctness of predictions
Recall	Sensitivity to fractures (true positive rate)
F1-score	Harmonic mean of recall and precision
AUC	Discrimination between classes across all thresholds
Cohen’s kappa	Agreement adjusted for chance

.

2.7.2. Wilcoxon Signed-Rank Test

The Wilcoxon signed-rank test was employed to assess whether statistically significant differences existed between paired evaluation settings. This non-parametric alternative to the paired t-test does not assume normality of differences and is well suited for comparing paired observations [33]. Specifically, it was applied (i) to compare image- and patient-level evaluations, and (ii) to compare the general MTL and proposed MTL configurations across equivalent models and datasets.

The null hypothesis in each case was that the paired evaluations yield equivalent results, while the alternative was that systematic differences exist.

Let $d_i$ denote the difference between the paired values for the i-th comparison, with $i=1,\dots ,n$. The absolute differences $|d_i|$ are ranked, and the sums of ranks for positive and negative differences are defined as

$$R^{+}=\sum _{d_i>0}rank(|d_i|),R^{-}=\sum _{d_i<0}rank(|d_i|).$$

The test statistic is

$$T=min\{R^{+},R^{-}\},$$

(1)

where $R^{+}$ and $R^{-}$ represent the sums of ranks for positive and negative differences, respectively. For sufficiently large n, T can be standardized as

$$z={\displaystyle \frac{T-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}},$$

(2)

which follows an approximate normal distribution under the null hypothesis.

2.7.3. McNemar’s Test for Classifier Comparison

To statistically compare the parallel and sequential hybrid models, we used McNemar’s test, which evaluates differences between paired classifiers on the same test data [34]. The test focuses on discordant predictions (instances classified correctly by one model but not the other). A ${\chi }^2$ approximation was used when the number of discordant pairs exceeded 25; otherwise, an exact binomial test was applied [35].

The McNemar test statistic is defined as

$${\chi }^2={\displaystyle \frac{{\left(\right|b-c|-1)}^2}{b+c}},$$

(3)

where b is the number of cases misclassified by the sequential model but correctly classified by the parallel model, and c is the number of cases misclassified by the parallel model but correctly classified by the sequential model.

2.8. Interpretability Methods for Deep Learning Models

To enhance transparency and provide insight into model reasoning, we applied two complementary interpretability techniques. These methods generate visual explanations of model decisions, highlighting whether predictions are based on clinically relevant regions.

2.8.1. LayerCAM

LayerCAM [29] an extension of Grad-CAM [26], was applied to the CNN backbone of each hybrid model. Following the original formulation, activation maps from the last three convolutional layers were aggregated to produce class activation maps, which highlight spatial regions most influential for predictions.

For each target class c, the weighted activation at spatial location $(i,j)$ in channel k is defined as

$${\widehat{A}}_{ij}^k=\mathrm{ReLU}\left({\displaystyle \frac{\partial y^c}{\partial A_{ij}^k}}\right)·A_{ij}^k,$$

(4)

where $y^c$ is the class score and $A_{ij}^k$ is the activation at $(i,j)$ in the k-th feature map.

The final class activation map is then obtained as

$$M_c=\mathrm{ReLU}\left(\sum _k{\widehat{A}}^k\right).$$

(5)

2.8.2. Attention Rollout

For the transformer backbone, we applied Attention Rollout [27] to trace how information flows from image patches to the classification ([CLS]) token. By recursively combining attention matrices across layers, this method produces 2D heatmaps, indicating which patches contributed most strongly to the final decision.

Formally, for layers $L_i$ to $L_j$ ($j\ge i$), the rollout attention is defined as

$$\tilde{A}\left(L_j\right)=\left\{\begin{array}{cc}A\left(L_j\right)·\tilde{A}\left(L_{j-1}\right),\hfill & j>i\hfill \\ A\left(L_j\right),\hfill & j=i,\hfill \end{array}\right.$$

(6)

where $\tilde{A}\left(L_j\right)$ denotes the aggregated rollout attention at layer $L_j$, and $A\left(L_j\right)$ is the raw attention matrix at that layer.

This formulation propagates attention through successive layers, enabling the visualization of how information flows from local patches to the [CLS] token. Together with LayerCAM, these interpretability techniques allow for the qualitative assessment of whether the hybrid models attend to clinically relevant wrist regions or rely on spurious features, thereby strengthening trust in model predictions and helping identify potential sources of error or bias.

3. Results

3.1. Classification Performance

After fine-tuning, the eight hybrid models were evaluated on the in-domain MURA test set and the out-of-domain Al-Huda wrist test set. For clarity and clinical relevance, only patient-level results are reported in the tables. Image-level results were also computed and used in the Wilcoxon signed-rank test to evaluate systematic differences between the two evaluation levels, but these are not shown here to avoid redundancy.

On the MURA wrist set, Xception–DeiT (P) outperformed its sequential counterpart and both DenseNet–ViT hybrids in accuracy, recall, F1-score, and Cohen’s kappa, while tying with them on AUC. The sequential Xception–DeiT (S) also outperformed both DenseNet–ViT hybrids across most metrics (

Table 9. Classification performance on the MURA wrist dataset. P = parallel fusion; S = sequential fusion.

Model	Accuracy	F1-Score	Recall	Kappa	AUC
DenseNet–ViT (P)	0.86	0.82	0.78	0.71	0.91
DenseNet–ViT (S)	0.86	0.80	0.71	0.69	0.91
Xception–DeiT (P)	0.88	0.84	0.85	0.74	0.91
Xception–DeiT (S)	0.87	0.83	0.79	0.72	0.91

Bold values indicate the best performance per metric; ties are not bolded.

).

Table 10. External Al-Huda wrist fracture dataset results (zero-shot, ZS).

Model	Accuracy	F1-Score	Recall	Kappa	AUC
DenseNet–ViT (P)	0.73	0.70	0.75	0.46	0.88
DenseNet–ViT (S)	0.80	0.78	0.90	0.60	0.85
Xception–DeiT (P)	0.76	0.67	0.60	0.48	0.86
Xception–DeiT (S)	0.78	0.67	0.55	0.51	0.85

Bold values indicate the best performance per metric; ties are not bolded.

shows the zero-shot performance of the four hybrids on the external dataset. DenseNet–ViT (S) demonstrated the strongest generalization, maintaining high recall (0.90), balanced accuracy (0.80), and acceptable discrimination (AUC = 0.85). DenseNet–ViT (P) achieved the highest AUC (0.88) but suffered a recall drop to 0.75, indicating moderate sensitivity. In contrast, both Xception–DeiT hybrids showed a substantial decline in recall (0.60), reflecting poor anomaly detection under domain shift. These findings suggest that DenseNet-based hybrids, particularly the sequential variant, transfer more robustly to unseen external data than their Xception-based counterparts. However, all hybrids fell short of moderate radiologist agreement ($\kappa \le 0.60$) and performed worse than on the in-domain set, motivating fine-tuning on a small external subset.

After fine-tuning, all hybrids improved, with parallel variants showing the largest overall gains (

Table 11. External Al-Huda wrist fracture dataset results (fine-tuned, FT).

Model	Accuracy	F1-Score	Recall	Kappa	AUC
DenseNet–ViT (P)	0.96	0.95	0.95	0.92	0.99
DenseNet–ViT (S)	0.88	0.87	1.00	0.76	0.92
Xception–DeiT (P)	0.98	0.98	1.00	0.96	0.99
Xception–DeiT (S)	0.88	0.85	0.85	0.75	0.92

Bold values indicate the best performance per metric; ties are not bolded.

). Xception–DeiT (P) achieved the strongest performance across all metrics, reaching the highest accuracy (0.98), F1-score (0.98), Cohen’s kappa (0.96), and AUC (0.99), alongside perfect recall. DenseNet–ViT (P) also performed strongly, with high accuracy (0.96), kappa (0.92), and AUC (0.99). DenseNet–ViT (S) achieved perfect recall (1.00) but lagged on other metrics, while Xception–DeiT (S) showed the weakest overall performance. Notably, Cohen’s kappa increased by more than 90% in both parallel hybrids, raising agreement from moderate in the zero-shot setting to almost perfect agreement after fine-tuning. These results indicate that backbone choice sets the baseline on familiar data, whereas fusion strategy influences robustness under domain shift, with parallel fusion enabling more effective recovery of performance through light domain adaptation.

3.2. Robustness Validation Under Alternative Optimizers

For a fair comparison, all optimizers were evaluated under consistent training settings, including the same initial learning rate, weight decay, and experimental protocol. Backbone fine-tuning was applied uniformly across experiments, and the same overall training strategy was maintained for each optimizer. The main results under AdamW are reported in Table 9, while

Table 12. Optimizer performance evaluation.

Model	Optimizer	Accuracy	F1-Score	Recall	Kappa	AUC
DenseNet–ViT (P)	AdaBoB	0.85	0.78	0.68	0.67	0.92
DenseNet–ViT (P)	RMSprop	0.83	0.75	0.64	0.63	0.89
DenseNet–ViT (S)	AdaBoB	0.86	0.80	0.73	0.70	0.90
DenseNet–ViT (S)	RMSprop	0.85	0.78	0.67	0.67	0.92
Xception–DeiT (P)	AdaBoB	0.86	0.81	0.71	0.71	0.92
Xception–DeiT (P)	RMSprop	0.88	0.83	0.75	0.73	0.91
Xception–DeiT (S)	AdaBoB	0.86	0.81	0.74	0.70	0.90
Xception–DeiT (S)	RMSprop	0.87	0.82	0.74	0.72	0.91

presents the performance of the proposed hybrid models when trained with alternative optimizers, namely AdaBoB [36] and RMSprop. AdaBoB, a recently introduced dynamic bound adaptive gradient method with belief in observed gradients, was included to test whether the observed performance improvements were optimizer-dependent or inherent to the model architectures.

On the MURA wrist dataset, DenseNet–ViT (S) trained with AdaBoB achieved the same accuracy (0.86) as under the AdamW baseline, while DenseNet–ViT (P) and DenseNet–ViT (S) with AdaBoB and RMSprop remained within one percentage point of that baseline (0.85). Similarly, Xception–DeiT (P) and Xception–DeiT (S) with RMSprop matched their AdamW accuracies of 0.88 and 0.87, respectively, with the corresponding AdaBoB variants trailing by only one to two percentage points. Models trained with AdamW exhibited slightly better performance on critical metrics such as recall and Cohen’s kappa, with the lowest recall and kappa under AdamW being 0.71 and 0.69 (DenseNet–ViT (S)), compared to the highest recall (0.75) and kappa (0.73) achieved under RMSprop (Xception–DeiT (P)). Despite these minor differences, models optimized with AdaBoB and RMSprop achieved comparable accuracy and consistently high AUC values, further supporting that the proposed architectures retain strong performance across different optimization strategies.

3.3. Statistical Analysis

3.3.1. Wilcoxon Signed-Rank Test

To investigate differences between evaluation levels, we applied the Wilcoxon signed-rank test to paired samples, where each pair consisted of performance values computed at both the image and patient levels for the same model and dataset. The paired differences were defined as

$$d_i=\text{Patient-level}\mathrm{value}-\text{Image-level}\mathrm{value}.$$

Each experimental setting contributed four paired comparisons (DenseNet–ViT and Xception–DeiT, in both parallel and sequential configurations), yielding a total of 12 pairs across three evaluation contexts:

• Internal (MURA): Hybrids trained and evaluated on the MURA wrist dataset.
• Zero-shot transfer: MURA-trained hybrids evaluated directly on the Al-Huda wrist dataset without fine-tuning.
• External (fine-tuned): Hybrids fine-tuned on the Al-Huda wrist dataset and evaluated on its test split.

The results are presented in

Table 13. Wilcoxon signed-rank test comparing image-level and patient-level evaluations across all models and datasets. T denotes Wilcoxon test statistic.

Metric	Median Diff	Mean Diff	T	z	p-Value	Effect Size r
Accuracy	0.0292	0.0304	6.0	−2.589	0.0068	0.7473
AUC	0.0334	0.0311	3.0	−2.824	0.0024	0.8152
F1-score	0.0099	−0.0001	28.0	−0.863	0.4238	0.2491
Kappa	0.0554	0.0513	7.0	−2.510	0.0093	0.7247
Recall	0.0248	0.0355	16.0	−1.804	0.0771	0.5208

. Accuracy, AUC, and Cohen’s kappa showed significant differences between image- and patient-level evaluation ($p<0.05$), with large effect sizes ($r>0.5$). Recall and F1-score did not differ significantly. Therefore, all analyses are reported at the patient level, supported by statistical evidence and the clinical relevance of patient-level assessment.

3.3.2. McNemar’s Test

To determine whether the performance differences between the parallel and sequential hybrid models were statistically significant, McNemar’s test was applied to their patient-level binary predictions on the MURA wrist test set and the externally fine-tuned Al-Huda wrist test set. Patient-level evaluation was used because it reflects the study’s clinical objective of classifying patients rather than individual images, while still providing enough paired samples for a valid exact test.

Table 14. Exact McNemar’s test comparing parallel and sequential CNN–ViT hybrids on internal (MURA) and external wrist datasets. B and C denote discordant pairs.

Model Pair	Dataset	B	C	Statistic	p-Value
DenseNet–ViT	MURA	6	5	5.00	1.00
Xception–DeiT	MURA	7	6	6.00	1.00
DenseNet–ViT	External	5	1	1.00	0.22
Xception–DeiT	External	5	0	0.00	0.06

presents the results of McNemar’s exact test comparing the binary predictions of parallel and sequential CNN–ViT hybrids on both the internal (MURA) and external wrist datasets. Columns B and C represent the number of discordant pairs, i.e., cases correctly classified by one model but misclassified by the other. The McNemar statistic quantifies whether these discordant counts differ significantly. On the MURA dataset, p > 0.05 for both hybrid pairs (DenseNet–ViT and Xception–DeiT), indicating no statistically significant difference in their predictions. On the external set, the Xception–DeiT pair showed a marginal trend (p = 0.06), while DenseNet–ViT remained non-significant (p = 0.22), suggesting comparable decision behavior between fusion strategies.

3.4. Comparative Evaluation of General and Proposed MTL Models

Table 15. Classification performance on the MURA wrist dataset.

Model	Accuracy	F1-Score	Recall	Kappa	AUC
DenseNet–ViT (P)	0.88	0.83	0.78	0.73	0.92
DenseNet–ViT (S)	0.86	0.83	0.88	0.71	0.93
Xception–DeiT (P)	0.80	0.75	0.78	0.59	0.89
Xception–DeiT (S)	0.83	0.77	0.70	0.64	0.90

and

Table 16. External Al-Huda wrist fracture dataset results (fine-tuned).

Model	Accuracy	F1-Score	Recall	Kappa	AUC
DenseNet–ViT (P)	0.88	0.87	1.00	0.76	0.99
DenseNet–ViT (S)	0.86	0.84	0.95	0.72	0.97
Xception–DeiT (P)	65	0.69	0.95	0.36	0.87
Xception–DeiT (S)	0.78	0.76	0.85	0.55	0.90

present the performance of the hybrid models under the general MTL setup, while Table 9 and Table 11 report the results under the proposed MTL framework.

On the MURA wrist dataset, DenseNet–ViT hybrids show notable improvements across all metrics under the general MTL approach, with DenseNet–ViT (S) achieving the most substantial gain in recall (from 0.71 to 0.88). In contrast, Xception–DeiT hybrids exhibit a significant performance drop compared to their results under the proposed MTL. After fine-tuning on the external wrist fracture dataset, DenseNet–ViT hybrids maintain strong performance, with further gains in F1-score, recall, Cohen’s kappa, and AUC. However, Xception–DeiT models decline further, with DenseNet–ViT (P) achieving performance comparable to DenseNet–ViT (S) under the proposed MTL.

These observations suggest that the proposed MTL’s intermediate pretraining stage facilitates more effective domain adaptation. In contrast, general MTL may favor hybrids by enabling faster convergence on the wrist domain but at the expense of cross-domain generalization.

The Wilcoxon signed-rank test (

Table 17. Wilcoxon signed-rank test comparing general and proposed MTL evaluations across all models and datasets.

Metric	Median Diff	Mean Diff	T	z	p-Value	Effect Size r
Accuracy	0.075	0.0808	4.5	2.471	0.0112	0.7133
AUC	0.015	0.0308	17.5	1.294	0.1656	0.3737
F1-score	0.065	0.0592	15.0	1.883	0.0592	0.5435
Kappa	0.115	0.1417	9.0	2.353	0.0185	0.6794
Recall	0.000	−0.0258	19.5	−0.745	0.4133	0.2151

) shows that accuracy and Cohen’s kappa differ significantly (p < 0.05) with large effect sizes, indicating that the proposed MTL substantially improves model reliability and agreement. Meanwhile, F1-score, AUC, and recall do not show significant differences, suggesting that the main benefit of the proposed approach lies in improving classification consistency rather than sensitivity or ranking.

Overall, these findings validate the effectiveness of the proposed MTL framework. By introducing an intermediate non-wrist pretraining stage, it achieves balanced performance across hybrid architectures and enhances domain adaptation, whereas the general MTL tends to favor specific architectures and exhibits limited generalization.

3.5. Model Interpretability

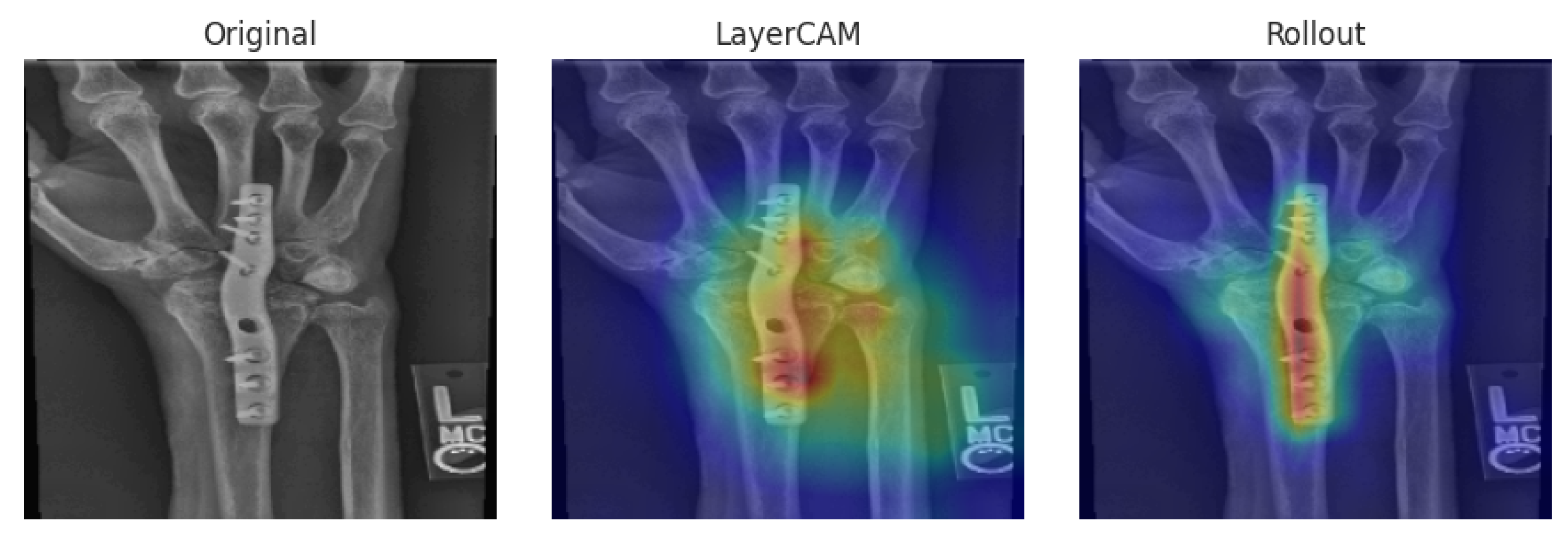
For interpretability analysis, LayerCAM [29] and Attention Rollout were applied to the Xception–DeiT hybrid models. The Xception backbone comprises 36 convolutional layers, of which the last three within the exit flow stage (Conv2d(728, 728), Conv2d(1024, 1024), and Conv2d(1536, 1536)) were used to generate the LayerCAM maps, capturing the highest-level spatial features. For the DeiT component, Attention Rollout was computed across all twelve transformer encoder layers using equal layer weights (1/12), producing attention maps that reflect the cumulative focus of the network across depths. These visualizations provide insight into how each hybrid attends to discriminative wrist regions associated with abnormality detection.

3.5.1. MURA

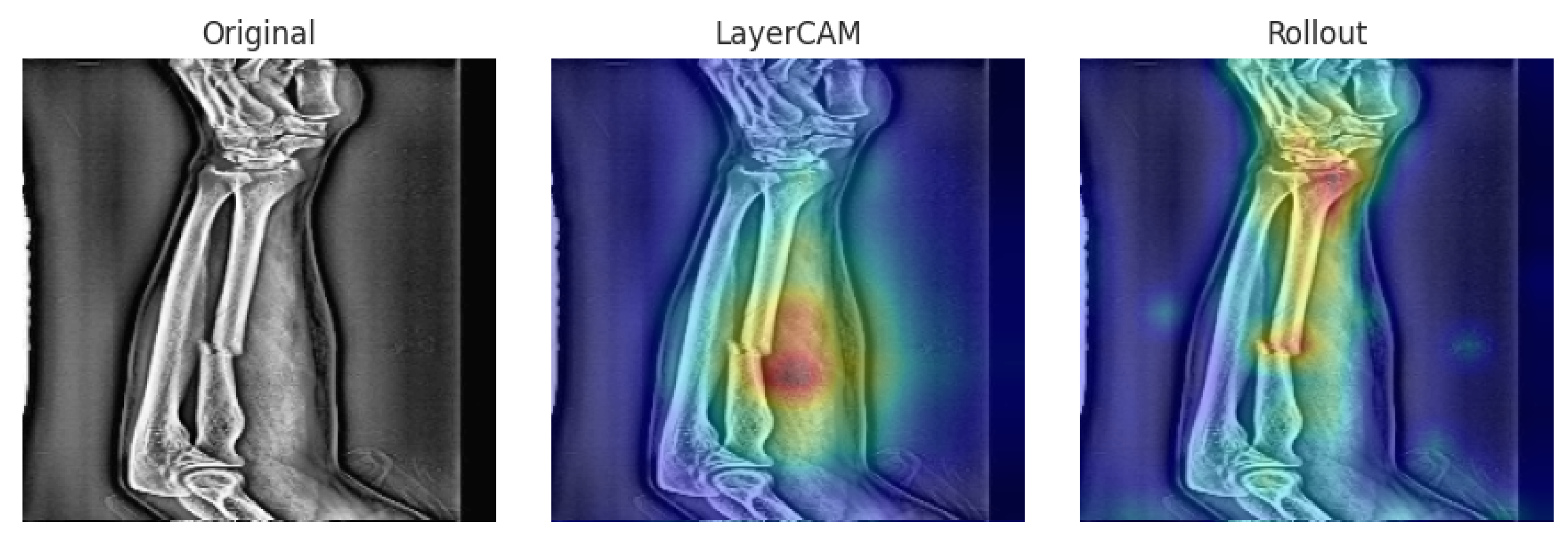
We present representative interpretability cases from the MURA wrist X-ray dataset, covering a TP, FP, and FN example. These cases provide a basis for analyzing how the models attend to different regions of interest.

Representative cases from the MURA wrist set are shown in Figure 4, Figure 5 and Figure 6. In the true positive example (Figure 4), both hybrids localized the abnormal area, correctly classifying the case as abnormal. In the false positive case (Figure 5), attention was drawn to a low-contrast region in a normal wrist, leading to misclassification. The false negative case (Figure 6) shows how attention focused too narrowly on a metallic feature while neglecting other relevant regions can result in a missed anomaly.

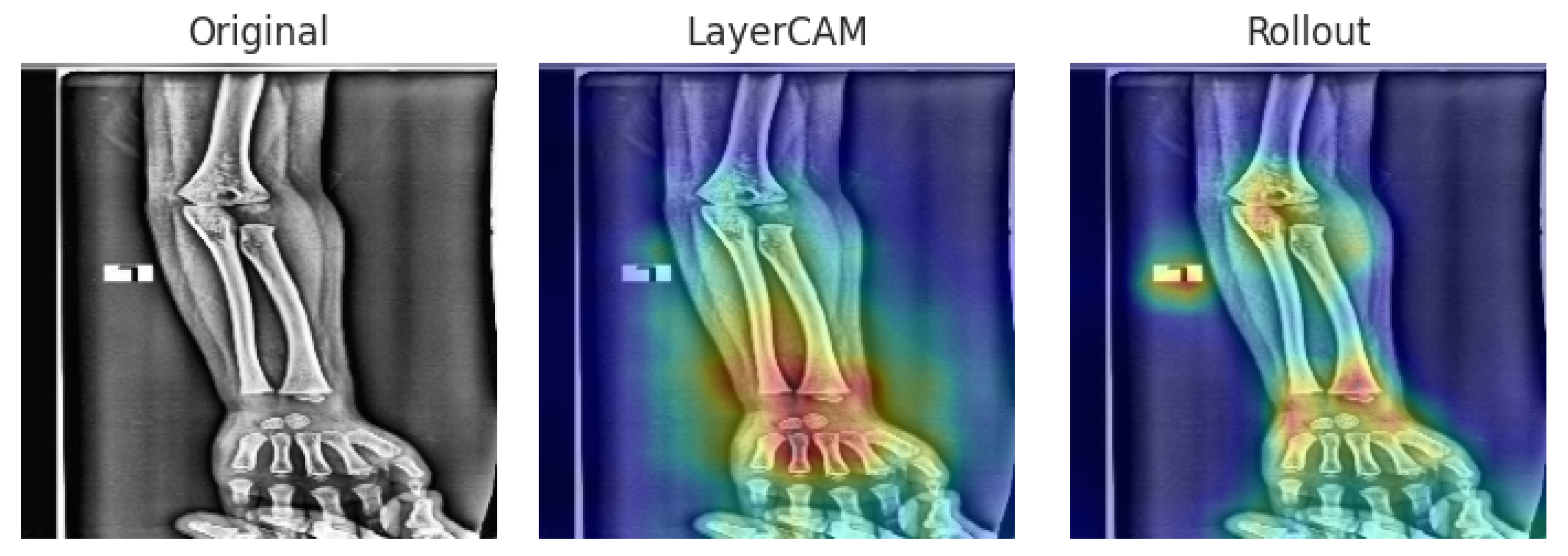
3.5.2. External

To further assess generalization beyond the internal dataset, we analyzed interpretability cases from the external wrist X-ray dataset. These examples allow us to evaluate whether the hybrid models maintain consistent attention patterns across datasets and to identify potential challenges when confronted with images acquired under different conditions. Representative TP and FP cases are presented below.

Figure 7 and Figure 8 illustrate interpretability on the external dataset. In the true positive case, both hybrids attended precisely to the fracture site. In the false positive case, subtle bone texture was incorrectly highlighted, producing an erroneous abnormal prediction.

Overall, the Xception–DeiT hybrids consistently focused on clinically relevant wrist regions, and even in misclassified cases, the heatmaps revealed cues that could assist clinicians in reviewing ambiguous findings.

3.6. Computational Efficiency

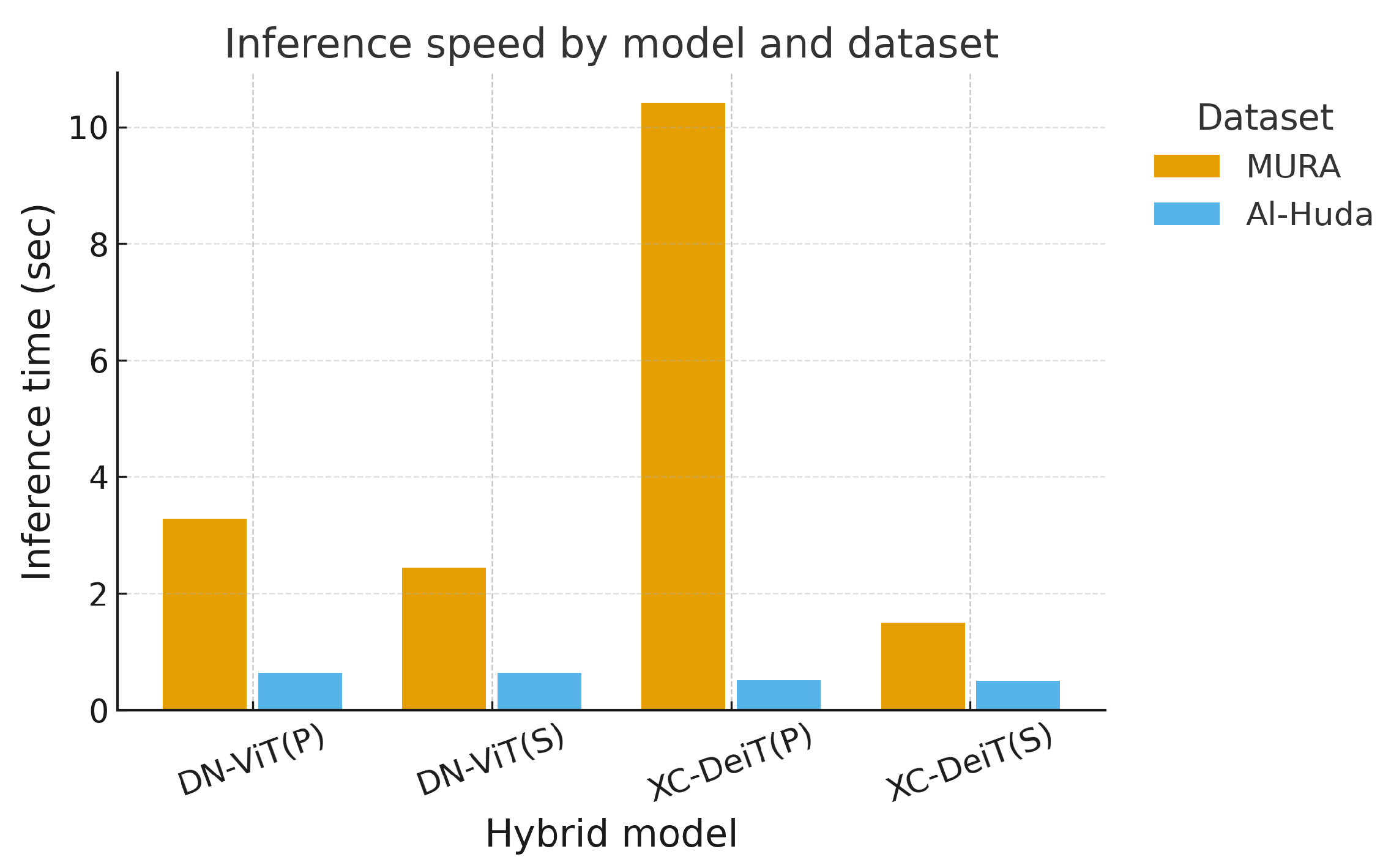
To complement the performance evaluation, we further examined the computational efficiency of the hybrid models in terms of inference speed and parameter count. These factors are critical for practical deployment in clinical and research settings.

Figure 9 reports the total inference time required to evaluate each full test set, rather than per-image latency. On the internal MURA test set (529 images), Xception–DeiT(P) required approximately 10.4 s end-to-end, while DenseNet–ViT(P) and DenseNet–ViT(S) completed in about 3.3 s and 2.4 s, respectively. Xception–DeiT(S) was the fastest, completing inference in 1.5 s, approximately 7× faster than its parallel counterpart. On the external Al-Huda test set (68 images), all models processed the dataset in under 1 s. These results confirm that all architectures achieve near-real-time throughput suitable for batch-level clinical screening.

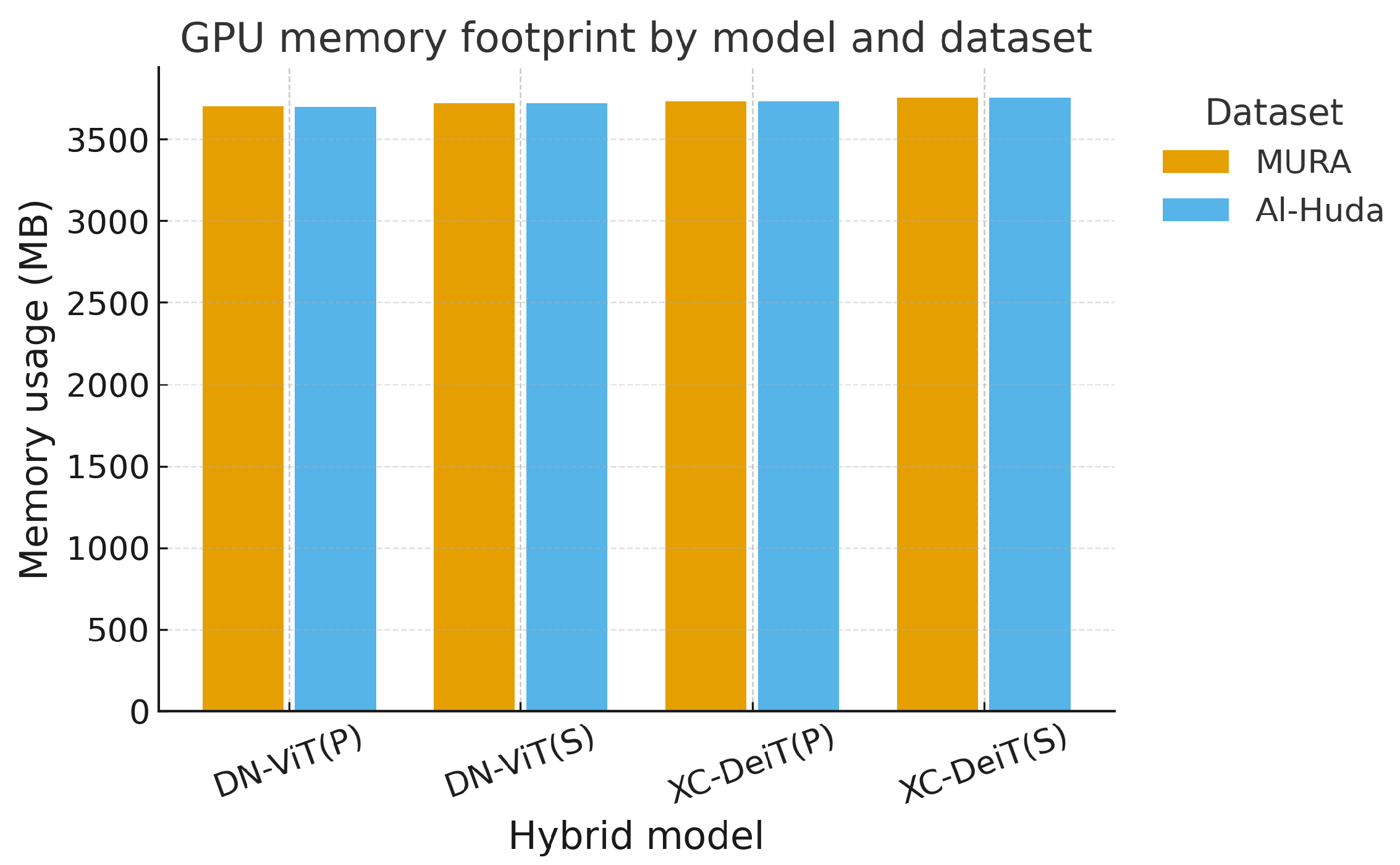
As shown in Figure 10 and

Table 18. Exact inference time and GPU memory usage for hybrid models on internal (MURA) and external (Al-Huda) wrist test sets. Inference time is the total time to process the full test split (529 images for MURA, 68 images for Al-Huda).

Model	Dataset	Inference Time (s)	GPU Memory (MB)
DN–ViT (P)	MURA	3.28	3701.6
DN–ViT (S)	MURA	2.44	3722.3
XC–DeiT (P)	MURA	10.41	3732.3
XC–DeiT (S)	MURA	1.50	3754.1
DN–ViT (P)	Al-Huda	0.64	3700.5
DN–ViT (S)	Al-Huda	0.64	3721.9
XC–DeiT (P)	Al-Huda	0.51	3732.3
XC–DeiT (S)	Al-Huda	0.50	3754.1

, all models required approximately 3.7 GB of GPU memory on both datasets. The differences were negligible, indicating that neither backbone nor integration type affected memory footprint. This suggests that memory is not a limiting factor for deployment, as all hybrids operate within typical GPU capacities available in research and hospital settings.

Overall, memory demands were stable across architectures, but inference efficiency was model-dependent. Sequential hybrids, particularly Xception–DeiT(S), offered the best trade-off between speed and accuracy, making them attractive for deployment in resource-sensitive environments.

3.7. Analysis of Model Complexity Using Parameter Quantity Shifting–Fitting Performance Framework

To enable a controlled analysis of architectural complexity, the classifier heads in

Table 19. Classifier head configurations used in the hybrid models. Width is the number of hidden units per fully connected (FC) block. Depth refers to the number of stacked FC blocks before the final output. The SE ratio controls the reduction factor in the squeeze–excitation module, where a smaller ratio indicates stronger channel recalibration.

Variant	Width	Depth	SE ratio
S (Small)	128	1	32
M (Medium)	512	2	16
L (Large)	1024	3	8

Note: The designations S, M, and L stand for Small, Medium, and Large classifier heads, respectively. They indicate increasing model capacity, with larger heads having more hidden units (width), deeper architectures (depth), and stronger channel recalibration (smaller SE ratio).

were used to generate scaled variants (Small, Medium, Large) across both hybrid fusion strategies. These head definitions differ from those used in the main evaluation models; here, the intent was not to retrain the best-performing architectures, but to systematically vary head capacity while keeping the CNN and ViT backbones fixed. This controlled setup enabled us to examine how increasing parameter count and head depth influence model fitting behavior and validation performance. The analysis followed the Parameter Quantity Shifting–Fitting Performance (PQS–FP) framework originally introduced by Xiang et al. [37] and complemented by Pareto analyses, providing a principled means of assessing the relationship between model scale, parameter efficiency, and generalization capacity in hybrid architectures.

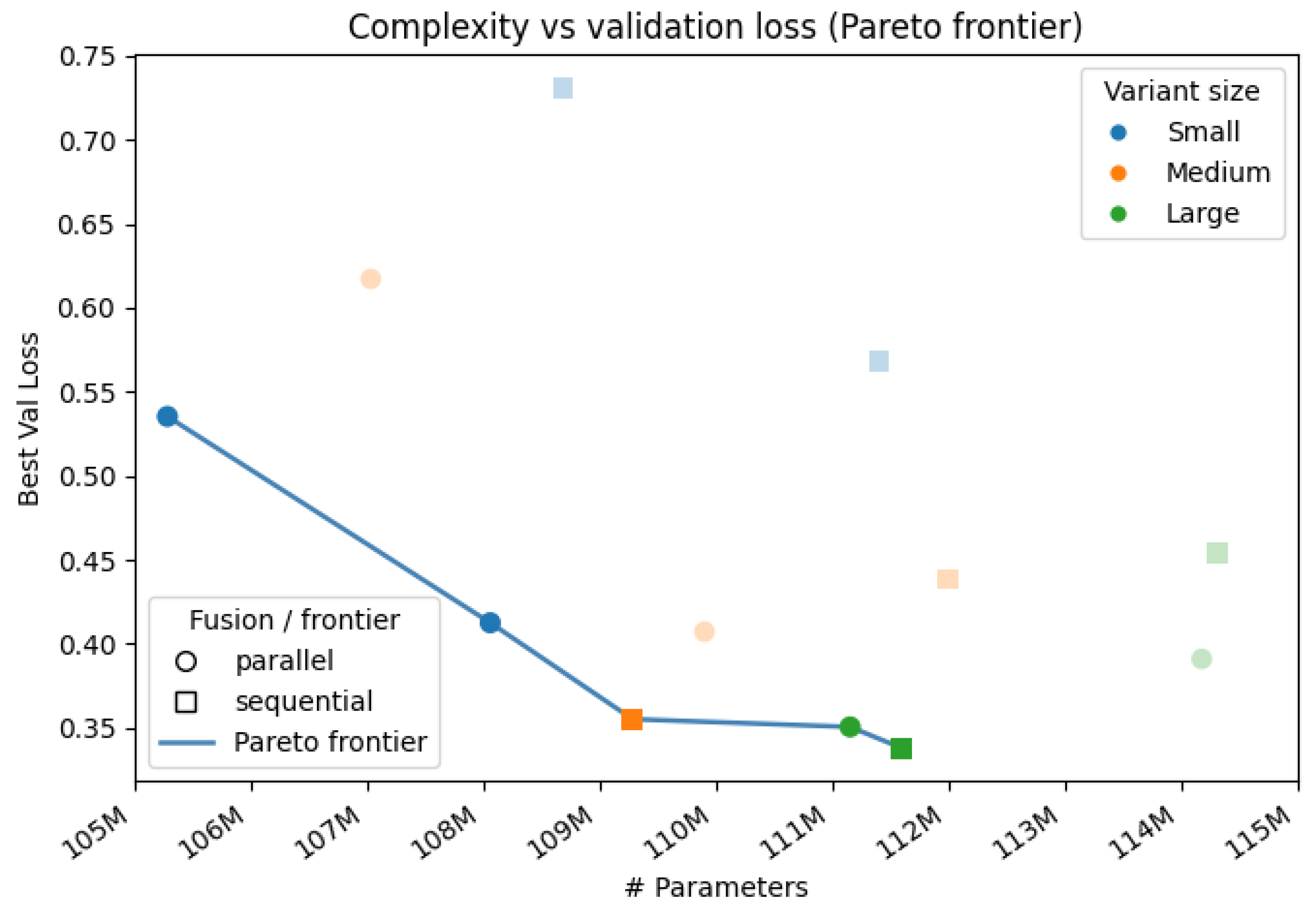
As shown in Figure 11, models with more trainable parameters generally achieve lower validation loss along the Pareto frontier. In particular, Pareto-efficient configurations transition from the smallest DenseNet–ViT (P) [S] through Xception–DeiT (P) [S] and DenseNet–ViT (S) [M] to the largest DenseNet–ViT (P) [L] and DenseNet–ViT (S) [L] (

Table 20. PQS–FP summary for all twelve hybrid configurations. PQS is computed relative to the smallest model. Fitting Performance (FP) is the difference between validation (Val) and training loss at the best validation epoch.

Model	# Params	PQS	Best Val Loss	Train Loss @ Best Val	FP	Quadrant (Predict)
DenseNet–ViT (P) [S]	105,281,109	+0.000	0.5400	0.4900	+0.0500	Q2 (Over-fitting & Efficient)
DenseNet–ViT (P) [M]	107,030,185	+0.017	0.6200	0.6000	+0.0200	Q2 (Over-fitting & Efficient)
Xception–DeiT (P) [S]	108,057,217	+0.026	0.4100	0.3200	+0.0900	Q2 (Over-fitting & Efficient)
DenseNet–ViT (S) [S]	108,683,935	+0.032	0.7300	0.6500	+0.0800	Q2 (Over-fitting & Efficient)
DenseNet–ViT (S) [M]	109,280,951	+0.038	0.3600	0.2200	+0.1400	Q2 (Over-fitting & Efficient)
Xception–DeiT (P) [M]	109,899,481	+0.044	0.4100	0.2800	+0.1300	Q2 (Over-fitting & Efficient)
DenseNet–ViT (P) [L]	111,151,441	+0.056	0.3500	0.2500	+0.1000	Q2 (Over-fitting & Efficient)
Xception–DeiT (S) [S]	111,399,495	+0.058	0.5600	0.4200	+0.1400	Q2 (Over-fitting & Efficient)
DenseNet–ViT (S) [L]	111,589,607	+0.060	0.3400	0.2500	+0.0900	Q2 (Over-fitting & Efficient)
Xception–DeiT (S) [M]	111,996,511	+0.064	0.4400	0.1700	+0.2700	Q2 (Over-fitting & Efficient)
Xception–DeiT (P) [L]	114,174,345	+0.084	0.3900	0.3000	+0.0900	Q2 (Over-fitting & Efficient)
Xception–DeiT (S) [L]	114,305,167	+0.086	0.4500	0.1200	+0.3300	Q2 (Over-fitting & Efficient)

Bold rows indicate Pareto-efficient configurations that minimize validation loss relative to their parameter budget. These models define the efficiency frontier used in the complexity analysis (Figure 11 and Figure 12). [S], [M], and [L] denote models with Small, Medium, and Large classifier heads, respectively.

). This indicates that increasing capacity can improve validation performance without requiring a disproportionate increase in parameters, up to a point.

Table 20 supports this trend within architecture families. For DenseNet–ViT (S), the best validation loss improves from 0.73 in the Small variant [S] to 0.36 in the Medium variant [M] and 0.34 in the Large variant [L]. A similar effect is visible across backbones: replacing DenseNet with Xception and replacing ViT with DeiT leads to a reduction in validation loss at comparable scales. For example, switching from DenseNet–ViT (P) [S] to Xception–DeiT (P) [S] lowers the best validation loss from 0.54 to 0.41 with only a modest parameter increase. This suggests that backbone choice is as important as fusion strategy or head width.

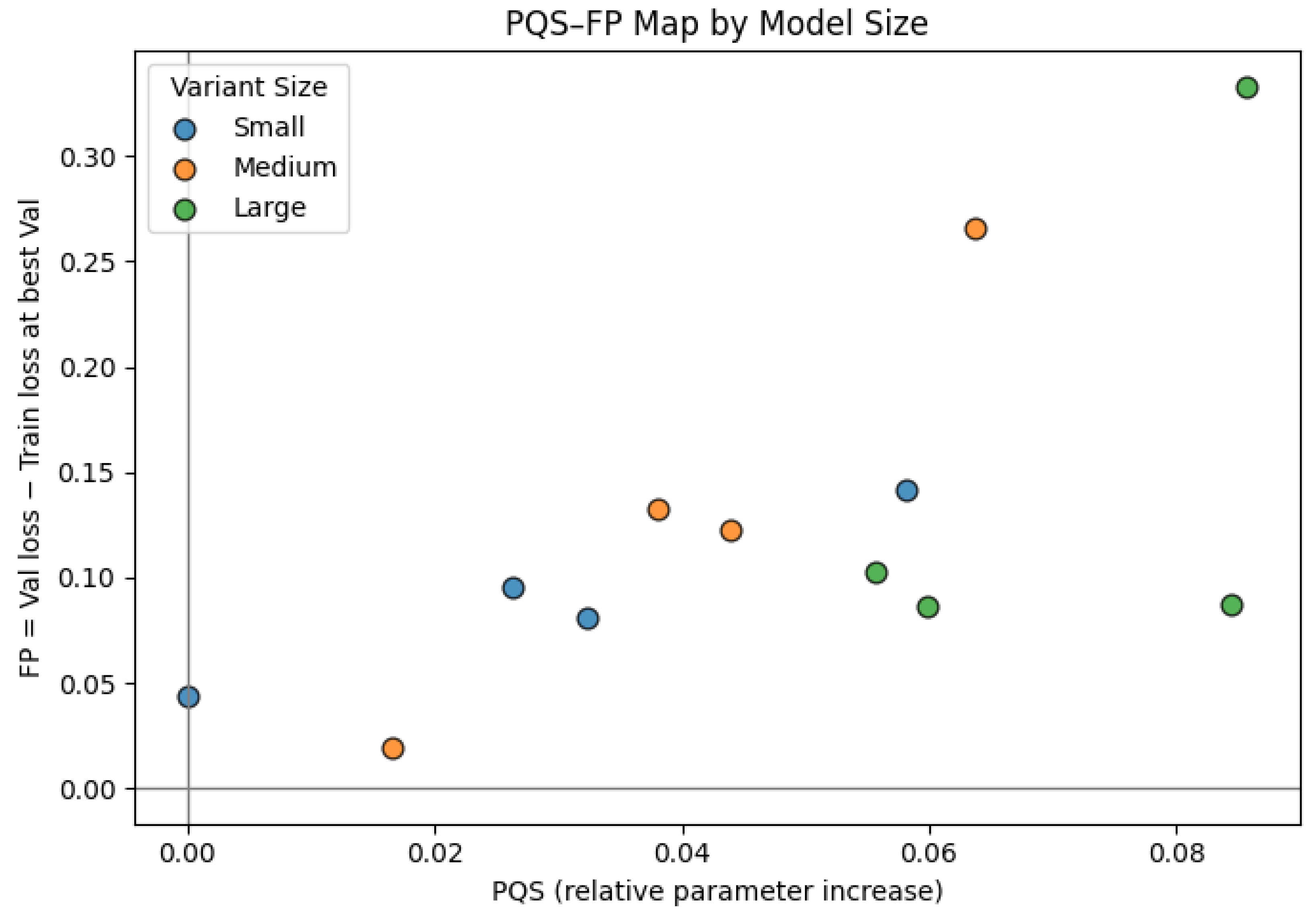
Figure 12 shows how these gains are achieved. Parameter Quantity Shift (PQS, x axis) measures how far each model sits from the smallest configuration in terms of parameter count. Fitting Performance (FP, y axis) is the validation minus training loss at the best validation epoch. Larger models (high PQS) tend to have higher FP, which indicates stronger overfitting pressure. In other words, models that achieve the best validation loss are also the ones that exhibit the largest gap between training and validation loss.

All models fall in Quadrant Q2 of the PQS–FP map. Q2 corresponds to high-capacity regimes that reduce loss effectively but do so by fitting the data very tightly. This means that while higher-capacity hybrids are efficient at driving down validation loss for their size budget, they also carry increased generalization risk and would likely require stronger regularization or data augmentation to remain robust.

3.8. Comparison with State-of-the-Art

Most existing studies on the MURA and Al-Huda wrist datasets report results at the image level, making direct numerical comparison with our patient-level evaluation inappropriate. Nevertheless,

Table 21. Representative state-of-the-art wrist anomaly detection models on the MURA dataset.

Model	Accuracy (%)	AUC	Kappa	Human Input
Xception–DeiT  (P)	88	0.91	0.74	No
Human–ResNet50–DenseNet121 [14]	87	0.94	0.77	Yes
Xception–InceptionResNetV2–KNN [1]	86	–	0.70	No

and

Table 22. Comparison of classification performance on the external wrist dataset with state-of-the-art models.

Model	Accuracy (%)	Kappa
Xception–DeiT (P)	98	0.96
DenseNet–ViT (P)	96	0.92
DCNN–LSTM [15]	88	0.76

summarize representative image-level state-of-the-art (SOTA) methods for contextual reference.

3.8.1. Internal Dataset

Recent parallel-fusion hybrid CNN-based approaches have reported accuracies of approximately 86–87%. Our hybrid CNN–ViT model, Xception–DeiT (P), achieves 88% accuracy and 0.91 AUC under patient-level evaluation, indicating comparable performance with SOTA image-level methods while requiring no human input. This underscores the potential of hybrid architectures for reliable and fully automated wrist anomaly detection.

3.8.2. External Dataset

The DCNN–LSTM model by Rashid et al. [15], which links a dilated CNN with a LSTM network in a sequential architecture, achieved 88% accuracy and a kappa of 0.76. In contrast, our hybrid CNN–ViT models achieved 96–98% accuracy and kappa values above 0.90, demonstrating substantially better performance and stronger cross-domain generalization. These results suggest that the proposed CNN–ViT hybrids generalize effectively across domains and demonstrate strong robustness under distribution shift. While direct comparison with image-level DCNN–LSTM results Rashid et al. [15] is not strictly equivalent, the consistently higher patient-level performance of our hybrids indicates their strong potential for reliable clinical deployment.

4. Discussion

4.1. Experimental Findings

This study evaluated hybrid CNN–ViT architectures for wrist X-ray anomaly detection, emphasizing classification performance, generalization, interpretability, computational efficiency, and transfer learning under both general and proposed wrist-to-wrist MTL frameworks. On the internal MURA wrist dataset, backbone architecture had the greatest impact, with Xception–DeiT (P) achieving the best overall performance (accuracy = 0.88, recall = 0.85, $\kappa$ = 0.74). DenseNet-based hybrids, especially the sequential variant, demonstrated stronger zero-shot transfer to the external domain. After fine-tuning, all models improved substantially, with Xception–DeiT (P) reaching near-perfect results (accuracy = 0.98, F1-score = 0.98, $\kappa$ = 0.96, AUC = 0.99). Parallel fusion generally outperformed sequential fusion, confirming that dual-path feature integration yields complementary visual and contextual cues.

The proposed hybrids achieve results comparable to those reported in recent wrist anomaly detection studies. For instance, Xception–InceptionResNetV2–KNN achieved 0.86 accuracy [1], and Human–ResNet50–DenseNet121 reported 0.87 accuracy and 0.94 AUC [14] when evaluated on the MURA wrist dataset with human input. Similarly, DCNN–LSTM achieved 0.88 accuracy and 0.76 Cohen’s kappa [15] on the Al-Huda wrist dataset. On the internal MURA wrist dataset, the proposed Xception–DeiT (P) attained performance comparable to these MURA-based methods, while on the external Al-Huda wrist dataset, the proposed DenseNet–ViT (P) and Xception–DeiT (P) achieved markedly higher results (accuracy = 0.96–0.98, $\kappa$ = 0.92–0.96, AUC = 0.99). Although differences in dataset composition and evaluation protocols (image- vs. patient-level) make direct comparison conservative, these outcomes demonstrate that hybrid CNN–ViT fusion effectively combines local texture and global contextual reasoning, offering a robust alternative to conventional CNN-only approaches.

The comparison between the general MTL and the proposed wrist-to-wrist MTL frameworks shows that the latter enhances robustness and generalization. DenseNet–ViT hybrids maintained stable accuracy across both frameworks, but Xception–DeiT hybrids degraded sharply under general MTL, especially on the Al-Huda dataset (accuracy drop from 0.98 to 0.65). The proposed MTL’s progressive pretraining on non-wrist musculoskeletal regions followed by targeted adaptation to wrist radiographs improved both in-domain and cross-domain generalization, demonstrating the value of anatomy-specific pretraining. Wilcoxon signed-rank analysis confirmed statistically significant differences in accuracy and Cohen’s kappa, validating the superiority of the proposed MTL in achieving stable, reproducible gains across architectures and domains.

Parameter–performance analysis (PQS–FP) revealed that larger hybrids achieved lower validation losses along the Pareto frontier, with diminishing returns beyond medium-scale variants. All configurations resided in Quadrant Q2, indicating increased overfitting risk at higher capacity but proportional improvements in validation performance. Despite their complexity, memory usage remained modest at approximately 3.7 GB and inference was fast; the slowest model processed 529 images in 10.4 s, while the fastest completed the same workload in approximately 1.5 s. These results confirm that the proposed hybrids are efficient enough for clinical batch-level or near-real-time deployment.

Saliency and attention maps highlighted radiologically meaningful wrist regions, such as the distal radius and carpal joints, aligning with areas commonly assessed for Colles’ or Smith fractures. These consistent focus regions across correctly and incorrectly classified cases suggest that the models’ decision logic partially mirrors expert reasoning. In clinical practice, this interpretability supports the model’s role as an assistive diagnostic tool, as it can flag suspicious regions for radiologist review, reduce diagnostic fatigue, and improve workflow throughput. Moreover, the proposed MTL framework, by enhancing generalization across institutions, increases potential clinical portability to varied imaging environments without retraining from scratch.

4.2. Limitations and Future Work

This study has several limitations. Only two CNN backbones (Xception and DenseNet201) and two Transformer backbones (DeiT-B and ViT-B16) were evaluated in parallel and sequential fusion; other backbone combinations were excluded due to computational constraints and may yield different results. The external dataset used to assess domain shift contained only 193 wrist images, limiting statistical power and preventing subgroup analyses. Patient-level outcomes were computed using a simple aggregation rule (majority voting with mean probability as a tie-breaker). The results are also based on single training runs without repeated seeds or error bars, limiting the assessment of variability. Moreover, both the MURA and Al-Huda datasets lack essential metadata such as imaging equipment details, acquisition parameters, and patient demographics, hindering the evaluation of device bias, domain shift, and real-world generalizability.

Future work should include variance reporting for reproducibility, explore larger and more diverse datasets to better capture domain shift effects, benchmark additional CNN and Transformer backbones, and incorporate richer metadata to enable clinically meaningful validation across diverse imaging environments.

Overall, this study demonstrates that hybrid CNN–ViT models, supported by multistage transfer learning, can deliver robust and interpretable wrist anomaly detection. Patient-level evaluation provides clinically meaningful insights, while parallel fusion shows greater adaptability under domain shift. The models achieve near real-time inference with moderate memory requirements, suggesting feasibility for clinical deployment. Saliency and attention visualizations align with radiologist focus areas, improving transparency and trust. These attributes collectively advance the clinical applicability of deep learning systems in radiology, bridging diagnostic accuracy, efficiency, and interpretability.