Abstract
Slope instability in mountainous regions poses serious challenges to infrastructure resilience, particularly under anthropogenic pressures and climatic variability. This study evaluates the mechanical reinforcement provided by Vetiver (Chrysopogon zizanioides) to stabilize slopes in seven representative soils of the Quillollaco Formation, southern Ecuador. Direct shear tests on soil–root composites were used to quantify root-induced improvements in cohesion (c′) and internal friction angle (ϕ′), and slope stability was analyzed with the Spencer limit equilibrium method for heights of 5, 10, and 15 m under dry conditions. Results demonstrated significant reinforcement effects, with Vetiver increasing shear strength parameters at all depths and maintaining safety factors above 1.10 in every scenario. The highest gains, up to 16%, were observed in high-plasticity soils (CH and MH). Sensitivity and inferential statistical analyses confirmed the robustness of these improvements, with over 95% of paired t-tests yielding p < 0.05. These findings highlight Vetiver as a reliable nature-based solution for slope stabilization in tropical mountain environments, offering a sustainable and transferable alternative to conventional geotechnical methods.
1. Introduction
Nature-based solutions are increasingly adopted for shallow slope stabilization because plant roots can enhance near-surface shear resistance and, under certain climates, modify suction and infiltration. Recent syntheses clarify that vegetation affects stability through two interlinked pathways—mechanical reinforcement by roots and hydrological modulation through evapotranspiration and rainfall partitioning—yet the magnitude and persistence of these effects depend on species, root architecture, and climate forcing. To avoid conflating mechanisms, the present work deliberately isolates the mechanical pathway under dry conditions, while acknowledging the coupled context established by recent reviews [1,2]. Throughout this study, “dry conditions” mean that the laboratory direct-shear tests used specimens at field-representative dry-season water contents reported in Table 1, without measuring or imposing suction, and the slope-stability analyses, using the limit-equilibrium method, assumed zero pore-water pressure along candidate slip surfaces and did not model matric suction, infiltration, or evapotranspiration. No phreatic surface was observed during the dry-season campaign.

Table 1.
Geotechnical properties of the studied soils under bare-soil conditions.
Under dry states, laboratory and field-oriented studies consistently show that roots primarily increase the equivalent cohesion of the root–soil composite, with smaller or soil-dependent changes in friction angle; this behaviour can be captured with Mohr–Coulomb parameters for use in limit-equilibrium design. Mechanistically, changes in friction angle arise from interlocking at rough root–soil interfaces and dilation, and remain modest in fines-dominated matrices, whereas cohesion increases more systematically with depth. Direct-shear programs on rooted soils report systematic cohesion gains across growth stages and species, whereas the friction angle shows weaker trends, supporting a mechanics-only parameterization for dry-season assessments. These findings provide the empirical basis for treating root effects as an equivalent increase in shear strength parameters when hydrological transients are negligible [3,4,5].
Three-dimensional formulations that encode root architectures and planting patterns couple root water uptake, suction, and effective stress. In contrast, plasticity-based limit analyses represent the tensile reinforcement provided by roots. Reliability-based frameworks propagate spatial variability of root traits and soils into stability metrics. These developments are essential for wet-season or rainfall-driven problems. By contrast, the present study is intentionally restricted to dry conditions and to the mechanical contribution of roots; it does not model root water uptake or suction transients and provides depth-resolved equivalent parameters directly usable in limit-equilibrium analyses [6,7,8,9].
A practical gap remains for design in data-scarce contexts: design practice relies on depth-resolved Mohr–Coulomb parameters with quantified uncertainty for root-reinforced soils across different textures, for use in limit-equilibrium methods (e.g., Spencer), particularly under dry-season conditions. Comprehensive parameterizations that (i) span multiple soil groups, (ii) resolve rooting depth, and (iii) translate laboratory direct-shear measurements into design-ready envelopes remain limited relative to the growing body of coupled simulations and reliability-based frameworks that propagate spatial variability in root traits and soils into stability metrics. This motivates a mechanics-focused, dry-condition characterization that is transparent, transferable, and aligned with routine geotechnical practice [1,2,6,9].
This study addresses that need by assembling a depth-resolved laboratory dataset of equivalent cohesion and friction angle for rooted soils typical of the study area in Loja, Ecuador, and by interpreting these mechanical gains under dry conditions within the bounds suggested by recent numerical insights. The contributions are a coherent set of design-level parameters for root-reinforced soils across several USCS classes and depths; a discussion of variability with depth to inform conservative envelopes for shallow translational failures; and an explicit statement of scope and applicability—dry mechanical reinforcement—so that extrapolation to wet seasons rightly defers to coupled hydro-mechanical frameworks.
2. Materials and Methods
2.1. Methodological Framework and Fieldwork
This study adopts a hypothesis-led, mechanics-only framework under dry states, operationalized through the methodological workflow summarized in Figure 1. It is hypothesized that roots increase the equivalent cohesion of the root–soil composite across soil textures and depth strata, while changes in friction angle are modest and soil-dependent; and these depth-resolved parameter shifts yield higher factors of safety for representative slope heights when propagated with Spencer’s limit-equilibrium method. To evaluate these hypotheses, undisturbed specimens were sampled by depth from vegetated and adjacent bare soils during the dry season; direct-shear tests were performed at field-representative water contents without measuring or imposing suction to obtain effective cohesion and friction angle. The resulting depth-resolved Mohr–Coulomb parameters were assembled into design envelopes and applied in limit-equilibrium analyses to compare slope stability with and without roots, explicitly excluding hydrological transients.
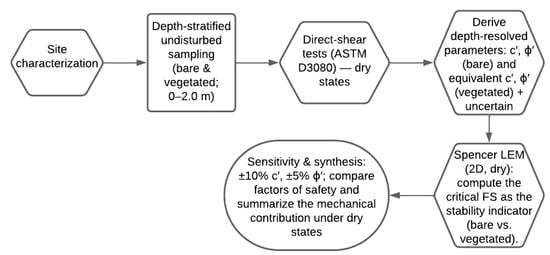
Figure 1.
Methodological workflow for dry-state slope-stability assessment with vegetation analysis.
Fieldwork was carried out on cultivated hillslopes within the Quillollaco Formation in Loja, Ecuador, where slopes commonly range between 30° and 60°. Seven sampling locations spanning lithological and geomorphic variability were selected along Ángel Felicísimo Rojas Avenue. Undisturbed specimens were extracted at 0.00–0.50 m, 0.50–1.50 m, and 1.50–2.00 m to capture the rooting horizon after approximately eighteen months of establishment.
2.2. Regional Setting and Site Characteristics
The research was conducted in Loja, southern Ecuador, within the Quillollaco Formation, a Miocene fluvio-alluvial unit composed of conglomerates, sandstones, and laminated silts. The terrain includes cultivated hillslopes with sustained inclinations commonly between 30 and 60 degrees, with local cut slopes where infrastructure intersects weathered horizons [10,11] A general overview of the regional and local setting is presented in Figure 2.
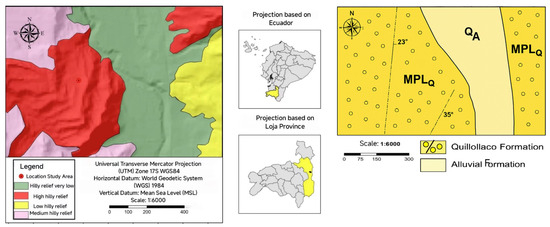
Figure 2.
Geological setting of the study area showing the Quillollaco Formation (MPLQ) and Quaternary alluvial deposits (QA).
2.3. Vegetation Selection, Nursery Preparation, and Field Conditions
Vegetation relied exclusively on rainfall for establishment, and minimal intervention was carried out apart from occasional manual weeding. A 18-month growth period was allowed to ensure root maturity before soil sampling [12]. Figure 3 illustrates the established vegetation cover at one of the monitored sites.

Figure 3.
Field establishment of Vetiver at the slope monitoring site.
2.4. Experimental Investigation
Seven representative soil types were sampled and classified according to the Unified Soil Classification System (USCS) [13]. Laboratory tests were performed under ASTM standards, including Grain Size Analysis (ASTM D422) [14], Natural Moisture Content (ASTM D2216) [15], Atterberg Limits (ASTM D4318) [16], and Direct Shear Tests (ASTM D3080M–11) [17].
Sampling was conducted at seven locations distributed along Ángel Felicísimo Rojas Avenue, within the coordinate corridor bounded by SW: 4°03′01.07″ S, 79°14′14.10″ W; SE: 4°03′01.07″ S, 79°11′55.58″ W; NW: 3°58′09.07″ S, 79°14′14.73″ W; NE: 3°58′09.07″ S, 79°11′56.22″ W, to capture representative variation in slope gradient, lithology, and vegetation cover. Undisturbed samples were collected at 0.00–0.50 m, 0.50–1.50 m, and 1.50–2.00 m—corresponding, respectively, to the root-dense surface mat, the intermediate zone where structural Vetiver roots persist, and the lower-density deep zone—consistent with the depthwise root distribution illustrated in Figure 4 (high near-surface concentration tapering with depth to ~2 m). These intervals reflect the short-term horizon of the study (approximately eighteen months), during which root systems had not yet fully penetrated deeper strata, and align with the depth range of the most probable failure mechanisms in the area.
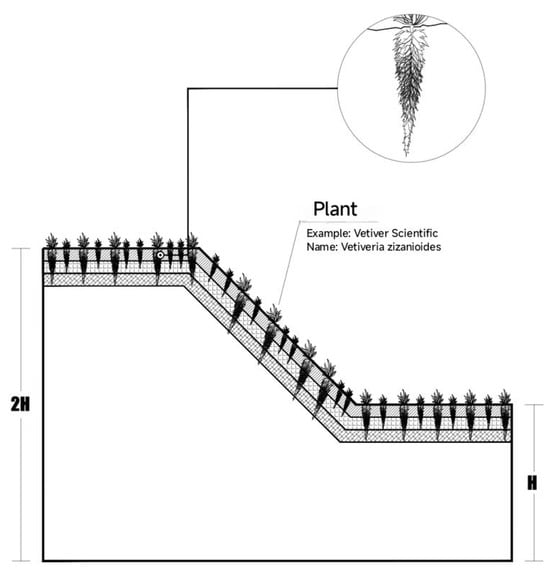
Figure 4.
Schematic comparing Vetiver root distribution.
Direct shear tests (American Society for Testing and Materials (ASTM) D3080M–11) [17]) used normal stresses of 50 and 100 kPa to represent shallow confinement for slopes of 30–60 degrees and depths up to two meters, with 200 kPa included as an upper bound to span the shear-strength envelope. Specimens were consolidated at the target stress and sheared at 1 mm/min. These tests provided effective cohesion (c′) and internal friction angle (ϕ′) for both bare and root-reinforced soils. For each soil–depth cell and condition (bare vs. vegetated), the shear envelope τ = c′ + σ′ tan ϕ′ was estimated to obtain the equivalent parameters c′ and ϕ′ used in subsequent stability analyses.
Roots were isolated from bulk soil by wet sieving with a 0.25-mm screen and oven-dried at 60 °C. The dry-root percentage (relative to total sample mass) is reported only as a depthwise presence indicator—used solely for mechanical root–soil separation, not for soil gradation or as a proxy for reinforcement—and it underrepresents fine roots thinner than 0.25 mm.
2.5. Slope Stability Analysis
All stability analyses were conducted under dry conditions to isolate mechanical reinforcement. Pore-water pressure along candidate slip surfaces was set to zero (no infiltration, evapotranspiration, or suction). Slice unit weights and shear-strength parameters were assigned from laboratory measurements for each soil–depth cell. No surcharge loads or seismic actions were considered. The analysis targeted shallow translational failures; accordingly, the slip-surface search was confined to 0–2 m depth.
Spencer’s limit-equilibrium method was adopted because the analysis targets shallow, quasi-two-dimensional translational slip surfaces within the upper 0–2 m under dry states, using depth-resolved Mohr–Coulomb parameters from laboratory tests. In this regime, a 2D formulation that satisfies overall force and moment equilibrium provides stable, design-ready factors of safety for section-scale assessments.
The factor of safety (FS) was computed with Spencer’s limit-equilibrium method, which satisfies overall force and moment equilibrium for a system of slices with a constant interslice force inclination [18]. For slice i the available shear resistance along the base is
and the factor of safety is defined implicitly as
where is the mobilized shear demand obtained from the simultaneous solution of overall force and moment equilibrium with constant interslice force inclination . In the present dry-state analyses, pore-water pressure along the slip surface was set to zero, so .
Nomenclature: = effective cohesion; = effective friction angle; = slice-base length; = effective normal force; = mobilized base shear; = constant interslice force inclination. (If referenced later: = slice weight; = base inclination.)
Two scenarios were evaluated for each slope and soil–depth cell: bare soil (baseline) using depth-resolved parameters and , and vegetated using the equivalent parameters and obtained from direct-shear tests on root–soil composites. Root reinforcement primarily increases the equivalent cohesion and may also induce small, soil-dependent changes in friction angle; both effects enter the resistance term . For each scenario, the critical slip surface is the one that yields the minimum within the 0–2 m search domain; results are then compared to quantify the net mechanical contribution of vegetation. Partially wet and fully wet scenarios were not simulated. The field campaign and laboratory program were conducted during the dry season, when pore-water pressure along candidate slip surfaces is effectively zero; restricting the analysis to this state allows isolation of root-induced mechanical effects (tensile reinforcement and interfacial interlocking) without the additional assumptions and data requirements of coupled unsaturated-flow modeling (soil–water retention, hydraulic conductivity, rainfall/ET forcing).
2.6. Sensitivity Analysis
A local (one-factor-at-a-time) sensitivity analysis was performed to emulate laboratory repeatability of consolidated–drained direct-shear parameters [19,20]. Cohesion (c′) was perturbed by ±10% and friction angle (ϕ′) by ±5%, adopting a priori bounds from reported precision/repeatability for consolidated–drained direct shear [16,21]. These ranges were subsequently checked against the dispersion of the replicate tests in this study, without further calibration. For each soil–depth cell, and for both bare and vegetated scenarios, parameters were perturbed independently and propagated through the limit-equilibrium analysis to quantify the resulting variation in factor of safety. For each soil–depth cell and for both scenarios (bare soil and vegetated), c′ and ϕ′ were varied independently with other inputs held fixed, and the factor of safety was recomputed using the Spencer formulation [19]. To evaluate the vegetation effect, paired-sample t-tests (α = 0.05) were applied to the differences between vegetated and bare-soil scenarios, and 95% confidence intervals were reported [20]. As a dispersion diagnostic, the coefficient of variation (CV%) for the factor of safety and for laboratory-derived parameters is provided in Appendix B [20,21]. A comprehensive probabilistic reliability analysis employing input COVs and parameter correlations lies beyond the present dry, mechanics-only scope and is identified for future work [19,20].
2.7. Outlier Detection Methodology
Values exceeding ±10% deviation from baseline parameters were classified as outliers and excluded to maintain dataset robustness. This threshold is consistent with geotechnical practices for handling experimental uncertainty.
3. Results
3.1. Bare-Soil Geotechnical Characterization
Seven representative soils were classified under the Unified Soil Classification System (USCS), ranging from low-plasticity silts (ML, CL-ML) to high-plasticity clays (CH) and organic silts (OH, OL). Laboratory analyses conducted under ASTM standards (ASTM D2216, D4318, D3080M–11) provided the geotechnical baseline presented in Table 1. Cohesion-prone soils such as CH exhibited high liquid limits (53.29%) and plastic indices (34.27), while OL soils presented very low cohesion potential, with a plastic index of 12.68. These results reflect the heterogeneity of the Quillollaco Formation, where fine-grained soils (CH, MH) pose greater stability challenges compared to coarse silts (CL-ML, ML).
The direct shear results for bare soils are summarized in Table 2, which reports cohesion (c′) and internal friction angle (ϕ′). Cohesion ranged from 2.69 kPa in OL to 50.70 kPa in CH, while friction angles varied between 14.57° (CH) and 29.49° (OL). These values are consistent with expected ranges for each USCS classification, confirming the reliability of the experimental dataset. Notably, CH soils combined high cohesion with very low friction angles, whereas OL soils showed the opposite trend, highlighting the contrasting failure mechanisms that may arise in the absence of vegetation reinforcement.

Table 2.
Shear strength parameters of the studied soils under bare-soil conditions.
3.2. Root Content and Distribution Assessment
Vetiver roots were concentrated in the upper 0–0.5 m layer, with decreasing percentages at depth (Table 3). CL-ML and MH soils exhibited the highest root densities near the surface, while OH and OL soils showed the lowest. This distribution ensured representative sampling for soil–root composites.

Table 3.
Root distribution percentages of vetiver at different soil depths.
3.3. Effect of Vetiver on Shear Strength Parameters
Direct shear tests confirmed that Vetiver improved both cohesion (c′) and internal friction angle (ϕ′) across all soils (Table 4). The most notable gains were observed in CH (+10% in cohesion, +20% in ϕ′) and CL-ML (+15% in cohesion, +17% in ϕ′). In OL soils, cohesion doubled from 2.7 to 5.4 kPa, indicating substantial reinforcement even in low-strength materials. These results demonstrate the depth-dependent mechanical contribution of Vetiver roots, particularly through increased anchorage in cohesive profiles.

Table 4.
Shear strength parameters of the studied soils reinforced with vetiver roots.
3.4. Impact of Vegetation on Slope Stability
The slope stability analysis established clear differences between bare and Vetiver-reinforced soils. Under bare-soil conditions, safety factors (FS) consistently decreased with slope height across all soil types (Table 5). For instance, in High-Plasticity Clay (CH), FS declined from 1.28 at 10 m to 1.01 at 15 m, approaching critical thresholds. A similar trend was observed in Elastic Silt (MH), where FS dropped from 1.40 to 1.20.

Table 5.
Safety factors of the studied soils under bare-soil conditions.
These results highlight the vulnerability of fine-grained soils under steep geometries. The representative simulations in Figure 5 illustrate this instability pattern.
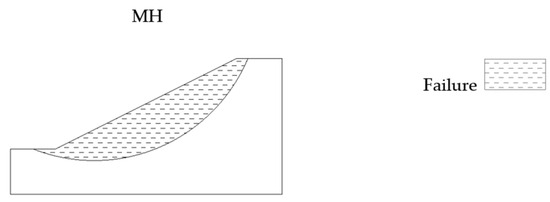
Figure 5.
Slope stability simulation under bare soil conditions for different soil types.
When Vetiver roots were incorporated, all soils exhibited increased FS values across the three slope heights (Table 6). For example, in CL-ML soil, FS improved from 1.48 to 1.58 at 5 m (+6.7%), while in CH soil, FS increased from 1.01 to 1.10 at 15 m (+10%). These improvements were particularly notable in cohesive soils, where the deep and fibrous root system of Vetiver provided enhanced anchorage and shear resistance.

Table 6.
Safety factors of the studied soils reinforced with vetiver roots.
Representative simulations in Figure 6 confirm the stabilizing effect of Vetiver across soil types.
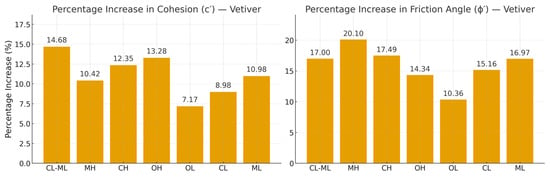
Figure 6.
Slope stability simulation under Vetiver conditions for different soil types.
3.5. Effect on Shear Strength Parameters
Laboratory direct shear tests confirmed significant improvements in cohesion (c′) and internal friction angle (ϕ′) when Vetiver roots were present. Cohesion increased up to +14.7% in CL-ML soils, while the highest gain in friction angle was recorded in CH soils (+20.1%). Detailed results are shown in Table 7, with percentage gains summarized. These enhancements are attributed to Vetiver’s vertically oriented root system, which increases interparticle interlocking and shear resistance.

Table 7.
Mean shear strength parameters (cohesion c′ and friction angle ϕ′) of bare and Vetiver-reinforced soils, with percentage increase relative to bare-soil conditions, and SE (Standard erro).
These increases in effective cohesion and effective friction angle are consistent with tensile load transfer (root bridging/dowel action), pull-out resistance, and interface interlocking/dilation documented for root–soil composites under dry conditions [22]. The percentage increase in shear strength parameters (c′ and ϕ′) due to Vetiver reinforcement across different soil types is illustrated in Figure 7, highlighting the consistent improvement in both cohesion and friction angle.
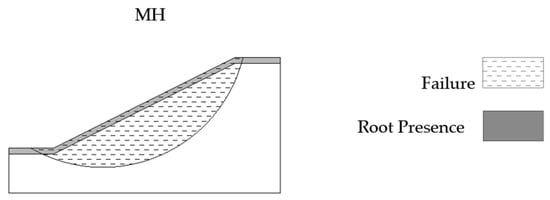
Figure 7.
Comparative increase (%) in cohesion (c′) and internal friction angle (ϕ′) for Vetiver across different soil types.
3.6. Synthesis Across Soil Types and Heights
Vetiver reinforcement demonstrated consistently strong performance across most soil types and slope configurations. CL-ML and MH soils were classified as Very Good, showing robust improvements across all slope heights (5–15 m). CH and OL soils were rated as Good, with reinforcement effects more dependent on slope geometry and depth. In OH soils, performance was considered Moderate, suggesting sensitivity to potential saturation. CL and ML soils were also classified as Good, although slight variability was observed at greater depths. Overall, Vetiver provided reliable and effective mechanical reinforcement across a wide range of geotechnical contexts, confirming its suitability for slopes requiring deep root penetration and enhanced shear resistance.
3.7. Robustness and Statistical Reliability
The sensitivity analysis demonstrated that unreinforced slopes were highly vulnerable to parameter variation. For example, in CL-ML soil, ±10% changes in cohesion or friction angle resulted in up to 11.5% variation in FS (Appendix A). With Vetiver reinforcement, FS values remained consistently above 1.10, even under adverse parameter changes, confirming its stabilizing role.
Statistical analyses further reinforced these findings. Mean FS values increased across all soils and slope heights with Vetiver, while coefficients of variation (CV%) remained below 9%, ensuring consistency. Paired t-tests confirmed significant differences (p < 0.05) in over 95% of cases. Confidence intervals narrowed under reinforced conditions; for instance, in CL-ML soil at 5 m, FS ranged from 1.51 to 1.65, compared with wider intervals in bare soil (Appendix B and Appendix C). Together, these results validate the robustness of Vetiver reinforcement against both mechanical variability and statistical uncertainty.
3.8. Comparative Reinforcement Performance
The overall comparative assessment (Table 8) shows that Vetiver consistently increased FS across all soils and slope heights, with maximum gains in cohesive soils (CH, OH, CL). At 15 m slope height, FS improved by +16.1% in ML soils and +10.2% in CL-ML soils.

Table 8.
Safety factors (FS) for soils—bare and vetiver-reinforced—across slope heights and their standard error (SE).
To provide a clearer visualization of the improvements induced by Vetiver reinforcement, Figure 8 summarizes the percentage increase in Safety Factor (FS) across the three slope heights (5 m, 10 m, and 15 m). This figure highlights the consistent gains in stability observed in cohesive soils, particularly CH, OH, and CL, where Vetiver’s deep root architecture provided the greatest reinforcement effect.
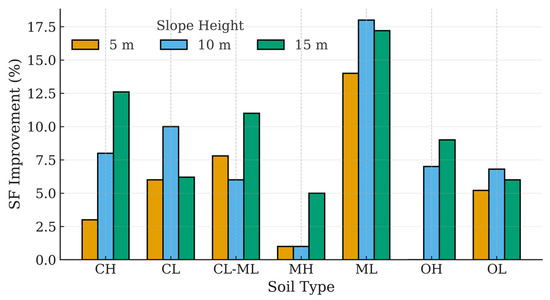
Figure 8.
Percentage Increase in Safety Factor (FS) with Vetiver Reinforcement at 5 m, 10 m, and 15 m slope heights.
4. Discussion
Using a parameterized limit-equilibrium framework under dry conditions (Spencer method), the study quantifies changes in safety factor between vegetated and bare slopes. Results show a consistent mechanical contribution from Vetiver, driven primarily by gains in equivalent cohesion and accompanied by smaller, context-dependent changes in equivalent friction angle. These findings align with prior work on deep-rooted vegetation in cohesive soils and corroborate the role of root–soil interactions in enhancing shear strength and overall slope resistance [19,20,21].
4.1. Root Distribution and Geomechanical Enhancement by Depth
The reinforcement provided by vegetation is governed by root architecture and mechanical properties—diameter distribution, tensile capacity, orientation, and connectivity—rather than bulk biomass alone. Depth-resolved observations indicate that Vetiver maintains structural roots well below one meter, consistent with a vertically biased system capable of mobilizing interfacial pull-out and tensile bridging under dry states [23,24]. However, the direct-shear tests were not instrumented to distinguish in-shear root breakage from interfacial pull-out; therefore, dominance between these mechanisms cannot be resolved from the present dataset. The measured response—systematic increases in equivalent cohesion with only modest changes in friction angle—is compatible with interfacial dowel action and root–soil interlocking as principal contributors. Prior work likewise shows that, although root area ratio and tensile strength may decrease with depth, thicker, lignified structural roots continue to contribute disproportionately to shear resistance through dowel action and interlocking [25,26,27].
In the present study, structural roots remained evident between 0.50 and 1.50 m and, despite lower density at depth, were associated with measurable improvements in the composite shear response (see Table 4 for depth-specific parameters). These patterns reinforce the need to evaluate root diameter and mechanical properties—such as tensile strength and stiffness—when assessing geotechnical reinforcement, rather than relying on biomass as a proxy.
Moreover, Vetiver displayed a pronounced reduction in root percentage from surface to depth, particularly in CL–ML soil (0–0.5 m: 0.95%; 0.5–1.0 m: 0.23%; 1.0–1.5 m: 0.14%). In parallel, bare-soil strength parameters typically increase with depth due to confinement; when roots are present, the composite response reflects this baseline plus a reinforcement increment. In the CL–ML profile, the vegetated composite showed increases in cohesion (26.78→29.55 kPa) and a modest rise in friction angle (27.41°→28.47°) with depth. This depth-wise trend reflects two components: the confinement-driven strengthening of the bare matrix and a positive root-reinforcement increment that persists at depth, sustained by thicker, lignified structural roots intersecting the shear plane and mobilizing interfacial interlocking, dowel action, and pull-out [28,29].
Similar results were obtained in CH soil, where cohesion rose from 51.7 kPa (upper) to 56.01 kPa (deep), and friction angle increased from 16.43° to 17.5°, despite reduced root mass. This confirms the mechanical importance of deeper roots in resisting shear stresses [30].
4.2. Mechanical Reinforcement and Root–Soil Interaction
The mechanical reinforcement provided by Vetiver was evident in consistent increases in both cohesion and internal friction angle across tested soils. Its vertically oriented and fibrous root system enhances slope stability by anchoring the soil and improving interparticle friction. These observations are supported by Schwarz et al. [22], who emphasized root–soil bonding as a critical factor for shear resistance, and by Kuriakose et al. [31], who highlighted tensile strength and root arrangement as key reinforcement parameters.
Vetiver’s contribution was particularly effective in cohesive soils (CH, OH), where root penetration increased equivalent cohesion and friction angle, aligning with findings of Fan and Su [32]. Wu et al. [33] further corroborated that the magnitude of reinforcement is influenced by root stiffness and distribution, especially in high-plasticity soils, a trend confirmed by the results of this study. While no axial root tensile tests were performed in this study, the measured stress–displacement response of undisturbed, root-bearing composites under multiple normal stresses supports tensile bridging and interfacial pull-out as the dominant mechanisms. This interpretation is consistent with published tensile/root-strength evidence and root area-ratio effects reported for Vetiver and other species.
4.3. Mechanistic Basis for the Observed Gains in Effective Cohesion and Effective Friction Angle (Dry Conditions)
Under dry conditions, roots intersecting the potential shear plane mobilize tensile load transfer and dowel action. This load transfer across soil–root interfaces increases the effective cohesion of the root–soil composite, with larger gains where fine-grained matrices promote root–soil bonding [34]. Pull-out and bundle experiments further show that mobilized resistance scales with root diameter, length, and surface roughness; therefore, deeper structural roots—although less abundant—can still raise effective cohesion, consistent with the depth-resolved trends measured here [35]. Increases in effective friction angle are typically smaller and soil-dependent, arising from interparticle interlocking at rough root–soil interfaces and dilation-induced shear; large-scale direct-shear studies on root-permeated soils report such modest but consistent frictional gains under low water contents [36]. These mechanisms explain the pattern observed in our data: larger increases in effective cohesion in cohesive profiles, and modest, depth-sensitive increases in effective friction angle where interlocking and confinement are activated.
4.4. Influence of Vetiver on Slope Stability Compared to Bare Soil Conditions
Vetiver roots consistently improved slope stability across all soil types and slope heights. For example, in CL-ML soil at 15 m, the safety factor (FS) increased from 1.280 (bare) to 1.401 (+9.45%). In CH soil, the FS rose from 1.300 to 1.430 (+10.0%), and in OL soil at 10 m, it improved from 1.310 to 1.401 (+6.95%). These improvements are consistent with findings from Badhon [37], who reported ~13% gains in clayey slopes reinforced with Vetiver, and Mickovski et al. [38], who demonstrated that Vetiver roots enhance layered slope stability under varying saturation.
The reinforcement capacity of Vetiver can be attributed to its tensile resistance, dense fibrous structure, and deep penetration, which jointly increase shear strength and reduce deformation along potential slip surfaces. This confirms the suitability of Vetiver for ecological engineering strategies targeting deep-seated slope instabilities [34]. Safety factors are model-based quantities that reflect measured shear-strength parameters, slope geometry, and method assumptions. Accordingly, reinforcement is interpreted as a change in safety factor with 95 percent confidence intervals and reported replication. Sensitivity analyses to plausible laboratory variability (plus or minus ten percent on cohesion and plus or minus five percent on friction angle) indicate that the direction of the safety-factor change remains positive for the tested cases. These bounds delimit the practical significance of the reinforcement under dry conditions.
4.5. Failure Mechanisms and Short-Term Effectiveness
Under short-term dry-season establishment (~18 months), Vetiver rooting is largely confined to the upper ~2 m; therefore, reinforcement is most relevant to shallow, translational failures with critical slip surfaces within this depth. In this regime, roots intersecting the failure plane mobilize tensile bridging and pull-out that chiefly increase the equivalent cohesion of the root–soil composite, while frictional gains are modest and depth-sensitive as interlocking and confinement evolve [34].
For deep-seated failures with slip surfaces well below ~2 m, the direct mechanical contribution from the vegetated horizon is limited; larger effects would require longer establishment (deeper rooting) or complementary engineered measures. Sudden, infiltration-triggered failures fall outside the dry-condition scope considered here and warrant coupled hydro-mechanical assessment to capture pore-pressure transients and unsaturated flow effects [39,40].
Under wet-season infiltration, the reduction in matric suction and the rise in pore-water pressure reduce effective stress and could offset part of the root-induced gains observed under dry conditions [41,42]. Shallow translational mechanisms remain plausible where roots intercept the critical surface, but in fines-dominated profiles rapid pore-pressure transients can dominate the stability response [42], while root-reinforcement efficacy depends on root–soil interaction (tensile bridging, interfacial pull-out) and the depth at which roots intersect the potential slip plane [43].
From an implementation standpoint, these findings should be interpreted over an early establishment horizon in which root systems are initially shallow. Near-surface protection may still be required during the first months, with progressive gains as finer roots develop at depth. While bulk root biomass is a proxy for abundance and architecture—and does not map one-to-one onto cohesive or frictional components—the stratified results indicate that layers dominated by finer roots at greater depths, despite lower biomass, still provide measurable reinforcement via increased soil–root interface area and pull-out resistance, yielding modest Δc′ and depth-sensitive Δϕ′. Accordingly, the reported benefits pertain primarily to shallow translational mechanisms within a two-meter rooting depth over an ~18-month horizon, and should be regarded as a conservative representation of early-stage dry-season establishment [44,45].
Under rainy-season conditions, reduced matric suction and increased pore-water pressures lower effective stress and may diminish the mechanical gains reported here under dry conditions. This study did not simulate infiltration or transients; thus, wet-season performance should be expected to differ, particularly where perched groundwater or rapid infiltration occurs [46,47,48].
4.6. Sensitivity and Data Consistency
Sensitivity analysis demonstrated that bare slopes exhibited high vulnerability to parameter variations, with FS fluctuations up to ±11.5%. Vetiver reinforcement substantially reduced this variability, maintaining FS above 1.10 even under ±10% cohesion and ±5% friction angle variations. For instance, in CH soils, FS values ranged between 1.35 and 1.65, showing consistent reinforcement effectiveness.
Outlier analysis revealed localized increases beyond expected thresholds, with cohesion rising up to +16% and friction angle +13% in highly plastic soils such as CH and OH. These anomalies likely reflect concentrated reinforcement in shallow layers or measurement variability. Their exclusion ensured methodological rigor, while the overall dataset confirmed Vetiver’s stabilizing influence across soil types.
Finally, to reflect variability in root establishment and growth under dry-season conditions, the reliability interpretation was anchored in the observed depth-dependent dispersion of root traits and their translated mechanical effects (Δc′, Δϕ′). While biomass quantifies the proportion and abundance of roots, it does not map directly onto cohesive or frictional components. Nevertheless, layers dominated by finer roots at greater depths—despite lower biomass—exhibited measurable reinforcement through increased soil–root interface and pull-out contributions, expressed as modest Δc′ and depth-sensitive Δϕ′. Carrying this biological variability through the stability evaluation alongside the ±10% (c′) and ±5% (ϕ′) perturbations widens FS bounds with depth, particularly beyond ~1.5 m, yet the net stabilizing effect of vegetation remains evident. This framing links the observed heterogeneity in root traits to the spread of geotechnical outcomes and provides a conservative reliability perspective for early-stage, dry-season establishment.
4.7. Limitations and Future Directions
This work is confined to dry states documented during the field campaign and to a mechanics-only representation of root effects. Analyses did not simulate infiltration or pore-pressure transients—processes critical to long-term slope behavior—so results should not be extrapolated to partially or fully wet conditions. Accordingly, wet-season scenarios and topography-controlled 3D failures require coupled hydro-mechanical modeling that resolves unsaturated flow and pore-pressure dynamics [34,35]. The present assessment targets shallow translational slips in 2D only, The evaluation covers short-term reinforcement (eighteen months of growth), with rooting depths confined to about two meters; long-term processes such as root decay, seasonal variability, and soil creep were not considered and should be incorporated to improve predictive reliability [38,39].
Accordingly, the reported improvements primarily apply to shallow, translational mechanisms with critical surfaces within approximately two meters; deep-seated or infiltration-triggered sudden failures require longer establishment, complementary measures, and coupled analyses. Accordingly, the dry-season results should not be extrapolated to wet-season performance without coupled hydro-mechanical assessment informed by unsaturated soil mechanics and rainfall-induced instability studies already cited in this work. Future studies should incorporate unsaturated flow coupling [8] and random-field representations of root traits to propagate spatial variability into safety-factor uncertainty. Sensitivity analyses targeting hydromechanical parameters (soil–water retention, hydraulic conductivity, and root tensile properties under varying water contents) are recommended to quantify how wet–dry cycles modulate net reinforcement. Finally, mixed-species reinforcement systems warrant investigation to explore potential synergies.
4.8. Implications for Ecological Engineering and NbS
The findings confirm Vetiver as a robust nature-based solution (NbS) for slope stabilization, especially in cohesive and steep soils. Its deep, vertically structured roots provide reliable reinforcement, making it a cost-effective and environmentally sustainable alternative to conventional stabilization methods [49]. The methodological framework developed—root–soil composite testing, depth-specific reinforcement modeling, and sensitivity analysis—offers a replicable strategy for ecological engineering in urban and mountainous environments such as Loja.
5. Conclusions
This study indicates that Vetiver (Chrysopogon zizanioides) provides measurable mechanical reinforcement under dry conditions, reflected in higher safety factors (FS) than bare-soil cases within the tested range of soils and slope heights. For illustration, in CH soil at a 15-m slope height, the FS increased from 1.300 (bare) to 1.430 with Vetiver, an improvement of about 10%.
Stress–displacement responses from direct-shear tests on undisturbed, root-bearing specimens under multiple normal stresses exhibited higher peak shear and a steeper initial response than bare soil, with similar or reduced displacement at peak. This pattern is consistent with tensile bridging and root–soil interfacial interlocking/pull-out as the dominant mechanisms, which primarily elevate the apparent cohesion (Δc′) and produce modest, depth-sensitive changes in friction (Δϕ′). Depth-resolved results further show that layers dominated by finer roots at greater depths—despite lower biomass—contribute measurable, though moderate, reinforcement via increased interface area and pull-out resistance.
The applicability of these findings is bounded by short-term, dry-season establishment (~18 months) with rooting largely confined to the upper ~2 m; consequently, the reported gains are most relevant to shallow translational failures with likely slip surfaces within this depth range. Within this domain, paired comparisons between bare and reinforced conditions were generally significant (p < 0.05), and variability remained controlled (CV typically below ~9%). When depth-dependent root traits and strength-parameter variability are reflected in the reliability interpretation, the spread of FS widens with depth as roots become sparser, yet the net stabilizing effect persists within the tested range.
These conclusions represent a conservative view of early-stage establishment under dry conditions. They do not extend to coupled hydro-mechanical processes, long-term root system evolution, or economic/life-cycle considerations. Deep-seated or infiltration-triggered failures lie outside the present scope and would require longer establishment and/or complementary engineered measures. Within the stated limits and for settings comparable to those tested, Vetiver is supported as an effective nature-based measure for enhancing shallow slope stability.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, writing—review and editing, visualization, supervision, project administration, and funding acquisition were performed by J.L.C.T., T.F., K.Z. and S.K. contributed to the review and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This appendix documents the perturbation scheme applied to cohesion (c′) and internal friction angle (ϕ′), considering independent variations of ±5% and ±10% relative to baseline values. A representative sensitivity matrix for bare soil is shown in Table A1 while the corresponding matrices for Vetiver-reinforced soils at different depths are summarized in Table A2. Compact changes in the computed safety factor (FS) by soil type and slope height are presented in Table A3. These results allow a concise evaluation of parameter variability and its influence on slope stability.
Appendix A.1

Table A1.
Sensitivity matrix—Bare Soil, ±5%, ±10% cohesion (kPa) and friction (∘).
Table A1.
Sensitivity matrix—Bare Soil, ±5%, ±10% cohesion (kPa) and friction (∘).
| Soil Type | c′Base | c′ + 5% | c′ − 5% | c′ + 10% | c′ − 10% | ϕ′Base | ϕ′ + 5% | ϕ′ − 5% | ϕ′ + 10% | ϕ′ − 10% |
|---|---|---|---|---|---|---|---|---|---|---|
| CL-ML | 25.77 | 27.06 | 24.48 | 28.35 | 23.19 | 24.34 | 25.56 | 23.12 | 26.77 | 21.91 |
| MH | 31.07 | 32.62 | 29.52 | 34.18 | 27.96 | 21.48 | 22.55 | 20.41 | 23.63 | 19.33 |
| CH | 50.7 | 53.24 | 48.16 | 55.77 | 45.63 | 14.57 | 15.3 | 13.84 | 16.03 | 13.11 |
| OH | 18.53 | 19.46 | 17.6 | 20.38 | 16.68 | 14.87 | 15.61 | 14.13 | 16.36 | 13.38 |
| OL | 2.69 | 2.82 | 2.56 | 2.96 | 2.42 | 29.49 | 30.96 | 28.02 | 32.44 | 26.54 |
| CL | 6.82 | 7.16 | 6.48 | 7.5 | 6.14 | 27.82 | 29.21 | 26.43 | 30.6 | 25.04 |
| ML | 16.96 | 17.81 | 16.11 | 18.66 | 15.26 | 26.1 | 27.41 | 24.8 | 28.71 | 23.49 |
Appendix A.2

Table A2.
Sensitivity matrix—Vetiver-Reinforced Soil (±5%, ±10% c′ and ϕ′ by depth, cohesion (kPa) and friction angle (∘)).
Table A2.
Sensitivity matrix—Vetiver-Reinforced Soil (±5%, ±10% c′ and ϕ′ by depth, cohesion (kPa) and friction angle (∘)).
| Soil Type | Layer (m) | c′Base | c′ + 5% | c′ − 5% | c′ + 10% | c′ − 10% | ϕ′Base | ϕ′ + 5% | ϕ′ − 5% | ϕ′ + 10% | ϕ′ − 10% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CL-ML | 0.5 | 26.78 | 28.12 | 25.44 | 29.46 | 24.1 | 27.41 | 28.78 | 26.04 | 30.15 | 24.67 |
| CL-ML | 1 | 27.78 | 29.17 | 26.39 | 30.56 | 25 | 28.31 | 29.73 | 26.89 | 31.14 | 25.48 |
| CL-ML | 1.5 | 29.55 | 31.03 | 28.07 | 32.51 | 26.6 | 28.47 | 29.89 | 27.05 | 31.32 | 25.62 |
| MH | 0.5 | 34.33 | 36.05 | 32.61 | 37.76 | 30.9 | 22.33 | 23.45 | 21.21 | 24.56 | 20.1 |
| MH | 1 | 34.83 | 36.57 | 33.09 | 38.31 | 31.35 | 23.65 | 24.83 | 22.47 | 26.02 | 21.29 |
| MH | 1.5 | 36.34 | 38.16 | 34.52 | 39.97 | 32.71 | 24 | 25.2 | 22.8 | 26.4 | 21.6 |
| CH | 0.5 | 51.7 | 54.29 | 49.12 | 56.87 | 46.53 | 16.43 | 17.25 | 15.61 | 18.07 | 14.79 |
| CH | 1 | 52.96 | 55.61 | 50.31 | 58.26 | 47.66 | 17.33 | 18.2 | 16.46 | 19.06 | 15.6 |
| CH | 1.5 | 56.01 | 58.81 | 53.21 | 61.61 | 50.41 | 17.5 | 18.38 | 16.62 | 19.25 | 15.75 |
| OH | 0.5 | 19.23 | 20.19 | 18.27 | 21.15 | 17.31 | 15.4 | 16.17 | 14.63 | 16.94 | 13.86 |
| OH | 1 | 19.33 | 20.3 | 18.36 | 21.26 | 17.4 | 15.91 | 16.71 | 15.11 | 17.5 | 14.32 |
| OH | 1.5 | 19.98 | 20.98 | 18.98 | 21.98 | 17.98 | 16.66 | 17.49 | 15.83 | 18.33 | 14.99 |
| OL | 0.5 | 4.13 | 4.34 | 3.92 | 4.54 | 3.72 | 30.01 | 31.51 | 28.51 | 33.01 | 27.01 |
| OL | 1 | 5.12 | 5.38 | 4.86 | 5.63 | 4.61 | 30.13 | 31.64 | 28.62 | 33.14 | 27.12 |
| OL | 1.5 | 5.38 | 5.65 | 5.11 | 5.92 | 4.84 | 30.22 | 31.73 | 28.71 | 33.24 | 27.2 |
| CL | 0.5 | 8.15 | 8.56 | 7.74 | 8.97 | 7.34 | 28.88 | 30.32 | 27.44 | 31.77 | 25.99 |
| CL | 1 | 8.66 | 9.09 | 8.23 | 9.53 | 7.79 | 28.94 | 30.39 | 27.49 | 31.83 | 26.05 |
| CL | 1.5 | 8.91 | 9.36 | 8.46 | 9.8 | 8.02 | 29.67 | 31.15 | 28.19 | 32.64 | 26.7 |
| ML | 0.5 | 20.49 | 21.51 | 19.47 | 22.54 | 18.44 | 27.31 | 28.68 | 25.94 | 30.04 | 24.58 |
| ML | 1 | 21 | 22.05 | 19.95 | 23.1 | 18.9 | 27.5 | 28.88 | 26.12 | 30.25 | 24.75 |
| ML | 1.5 | 22.25 | 23.36 | 21.14 | 24.48 | 20.03 | 27.85 | 29.24 | 26.46 | 30.64 | 25.07 |
Appendix A.3

Table A3.
Sensitivity analysis results for factor of safety (FS) Vetiver-reinforced slopes.
Table A3.
Sensitivity analysis results for factor of safety (FS) Vetiver-reinforced slopes.
| Soil Type | Height (m) | FS c′Base | FSc′ + 5% | FSc′ − 5% | FSc′ + 10% | FSc′ − 10% | FSϕ′ + 5% | FSϕ′ − 5% | FSϕ′ + 10% | FSϕ′ − 10% |
|---|---|---|---|---|---|---|---|---|---|---|
| CL-ML | 5 | 1.58 | 1.66 | 1.50 | 1.74 | 1.42 | 1.68 | 1.49 | 1.77 | 1.39 |
| CL-ML | 10 | 1.46 | 1.53 | 1.39 | 1.61 | 1.31 | 1.55 | 1.37 | 1.64 | 1.29 |
| CL-ML | 15 | 1.40 | 1.47 | 1.33 | 1.54 | 1.26 | 1.49 | 1.32 | 1.57 | 1.23 |
| MH | 5 | 1.24 | 1.30 | 1.18 | 1.36 | 1.12 | 1.31 | 1.17 | 1.39 | 1.09 |
| MH | 10 | 1.30 | 1.37 | 1.24 | 1.43 | 1.17 | 1.38 | 1.22 | 1.46 | 1.15 |
| MH | 15 | 1.32 | 1.39 | 1.25 | 1.45 | 1.19 | 1.40 | 1.24 | 1.48 | 1.16 |
| CH | 5 | 1.50 | 1.58 | 1.43 | 1.65 | 1.35 | 1.59 | 1.41 | 1.68 | 1.32 |
| CH | 10 | 1.50 | 1.58 | 1.43 | 1.65 | 1.35 | 1.59 | 1.41 | 1.68 | 1.32 |
| CH | 15 | 1.43 | 1.50 | 1.36 | 1.57 | 1.29 | 1.52 | 1.35 | 1.60 | 1.26 |
| OH | 5 | 1.35 | 1.42 | 1.28 | 1.49 | 1.22 | 1.43 | 1.27 | 1.51 | 1.19 |
| OH | 10 | 1.20 | 1.26 | 1.14 | 1.32 | 1.08 | 1.27 | 1.13 | 1.35 | 1.06 |
| OH | 15 | 1.20 | 1.26 | 1.14 | 1.32 | 1.08 | 1.27 | 1.13 | 1.35 | 1.06 |
| OL | 5 | 1.25 | 1.31 | 1.19 | 1.38 | 1.13 | 1.33 | 1.18 | 1.40 | 1.10 |
| OL | 10 | 1.40 | 1.47 | 1.33 | 1.54 | 1.26 | 1.48 | 1.32 | 1.57 | 1.23 |
| OL | 15 | 1.38 | 1.45 | 1.31 | 1.52 | 1.24 | 1.46 | 1.30 | 1.55 | 1.22 |
| CL | 5 | 1.25 | 1.31 | 1.19 | 1.38 | 1.13 | 1.33 | 1.18 | 1.40 | 1.10 |
| CL | 10 | 1.10 | 1.16 | 1.05 | 1.21 | 0.99 | 1.17 | 1.03 | 1.23 | 0.97 |
| CL | 15 | 1.13 | 1.19 | 1.07 | 1.24 | 1.02 | 1.20 | 1.06 | 1.27 | 1.00 |
| ML | 5 | 1.12 | 1.18 | 1.06 | 1.23 | 1.01 | 1.19 | 1.05 | 1.26 | 0.99 |
| ML | 10 | 1.17 | 1.23 | 1.11 | 1.29 | 1.05 | 1.24 | 1.10 | 1.31 | 1.03 |
| ML | 15 | 1.30 | 1.37 | 1.24 | 1.43 | 1.17 | 1.38 | 1.22 | 1.46 | 1.15 |
Appendix B
The tables report the mean safety factors FS), standard deviations (SD), coefficients of variation (CV%), standard error (SE), and 95% confidence intervals (CI) for each soil type and slope height under Vetiver-reinforced conditions. These descriptors were critical for quantifying the central tendency, dispersion, and variability of slope stability outcomes. The statistical summaries also served as the basis for paired Student’s t-tests used to assess the significance of differences between scenarios.

Table A4.
Statistical summary of safety factors for Vetiver-reinforced slopes.
Table A4.
Statistical summary of safety factors for Vetiver-reinforced slopes.
| Soil Type | Height | Mean FS | Standard Deviation (SD) | Coefficient of Variation (CV%) | CI Lower | CI Upper | Standard Error (SE) |
|---|---|---|---|---|---|---|---|
| CL-ML | 5 | 1.58 | 0.14 | 8.73 | 1.24 | 1.92 | 0.1 |
| CL-ML | 10 | 1.46 | 0.13 | 8.72 | 1.15 | 1.78 | 0.09 |
| CL-ML | 15 | 1.40 | 0.12 | 8.74 | 1.10 | 1.70 | 0.08 |
| MH | 5 | 1.24 | 0.11 | 8.74 | 0.97 | 1.51 | 0.08 |
| MH | 10 | 1.30 | 0.11 | 8.72 | 1.02 | 1.58 | 0.08 |
| MH | 15 | 1.32 | 0.12 | 8.74 | 1.03 | 1.61 | 0.08 |
| CH | 5 | 1.50 | 0.13 | 8.72 | 1.18 | 1.83 | 0.09 |
| CH | 10 | 1.50 | 0.13 | 8.72 | 1.18 | 1.83 | 0.09 |
| CH | 15 | 1.43 | 0.13 | 8.73 | 1.12 | 1.74 | 0.09 |
| OH | 5 | 1.35 | 0.12 | 8.73 | 1.06 | 1.64 | 0.08 |
| OH | 10 | 1.20 | 0.11 | 8.74 | 0.94 | 1.46 | 0.08 |
| OH | 15 | 1.20 | 0.11 | 8.72 | 0.94 | 1.46 | 0.08 |
| OL | 5 | 1.25 | 0.11 | 8.74 | 0.98 | 1.52 | 0.08 |
| OL | 10 | 1.40 | 0.12 | 8.72 | 1.10 | 1.70 | 0.08 |
| OL | 15 | 1.38 | 0.12 | 8.72 | 1.08 | 1.68 | 0.08 |
| CL | 5 | 1.25 | 0.11 | 8.72 | 0.98 | 1.52 | 0.08 |
| CL | 10 | 1.10 | 0.10 | 8.74 | 0.86 | 1.34 | 0.07 |
| CL | 15 | 1.13 | 0.10 | 8.74 | 0.88 | 1.38 | 0.07 |
| ML | 5 | 1.12 | 0.10 | 8.73 | 0.88 | 1.36 | 0.07 |
| ML | 10 | 1.17 | 0.10 | 8.74 | 0.92 | 1.42 | 0.07 |
| ML | 15 | 1.30 | 0.11 | 8.72 | 1.02 | 1.58 | 0.08 |
Appendix C
This appendix reports the outlier values detected during the sensitivity analysis for Vetiver-reinforced soils. A ± 10% threshold relative to baseline parameters was applied to both cohesion (c′) and internal friction angle (ϕ′). Observations exceeding this threshold were excluded from inferential analyses. The consolidated results are shown in Table A5.

Table A5.
Outlier Values—Vetiver-Reinforced Soil (Exceeding + 10% Threshold), cohesion (kPa) and friction (∘).
Table A5.
Outlier Values—Vetiver-Reinforced Soil (Exceeding + 10% Threshold), cohesion (kPa) and friction (∘).
| Soil Type | Depth Layer (m) | c′ Base (kPa) | Outlier c′ (kPa) | Δc′ (%) | ϕ′ Base (°) | Outlier ϕ′ (°) | Δϕ′ (%) |
|---|---|---|---|---|---|---|---|
| CL-ML | 1.5 | 29.55 | 33.25 | +12.5% | 28.47 | 32.05 | +12.6% |
| MH | 1.5 | 36.34 | 40.40 | +11.2% | 24.00 | 27.60 | +15.0% |
| CH | 0.5 | 51.70 | 59.75 | +15.6% | 16.43 | 18.95 | +15.3% |
| OH | 0.5 | 19.23 | 21.80 | +13.4% | 15.40 | 17.90 | +16.2% |
| ML | 1.5 | 22.25 | 25.30 | +13.7% | 27.85 | 31.20 | +12.0% |
References
- Lann, T.; Bao, H.; Lan, H.; Zheng, H.; Yan, C.; Peng, J. Hydro-mechanical effects of vegetation on slope stability: A review. Sci. Total Environ. 2024, 926, 171691. [Google Scholar] [CrossRef] [PubMed]
- DiBiagio, A.; Capobianco, V.; Oen, A.; Tallaksen, L.M. State-of-the-art: Parametrization of hydrological and mechanical reinforcement effects of vegetation in slope stability models for shallow landslides. Landslides 2024, 21, 2417–2446. [Google Scholar] [CrossRef]
- Eab, K.H.; Likitlersuang, S.; Takahashi, A. Laboratory and modelling investigation of root-reinforced system for slope stabilisation. Soils Found. 2015, 55, 1270–1281. [Google Scholar] [CrossRef]
- Valizade, N.; Tabarsa, A. Laboratory investigation of plant root reinforcement on the mechanical behaviour and collapse potential of loess soil. Eur. J. Environ. Civ. Eng. 2022, 26, 1475–1491. [Google Scholar] [CrossRef]
- Zhou, X.; Fu, D.; Wan, J.; Xiao, H.; He, X.; Li, Z.; Deng, Q. The Shear Strength of Root–Soil Composites in Different Growth Periods and Their Effects on Slope Stability. Appl. Sci. 2023, 13, 11116. [Google Scholar] [CrossRef]
- Ng, C.W.; Zhang, Q.; Ni, J.; Li, Z. A new three-dimensional theoretical model for analysing the stability of vegetated slopes with different root architectures and planting patterns. Comput. Geotech. 2021, 130, 103912. [Google Scholar] [CrossRef]
- Guo, H.; Ng, C.W.W.; Zhang, Q. Three-dimensional numerical analysis of plant-soil hydraulic interactions on pore water pressure of vegetated slope under different rainfall patterns. J. Rock Mech. Geotech. Eng. 2024, 16, 3696–3706. [Google Scholar] [CrossRef]
- Cheng, P.; Wu, L.; Zhang, H.; Zhou, J. Inclusion of root water absorption and reinforcement in upper bound limit stability analysis of vegetated slopes. Comput. Geotech. 2024, 169, 106227. [Google Scholar] [CrossRef]
- Guo, H.; Qu, C.; Liu, L.; Zhang, Q.; Liu, Y. Reliability analysis of vegetated slope considering spatial variability of soil and root properties. Comput. Geotech. 2024, 169, 106257. [Google Scholar] [CrossRef]
- Oñate-Valdivieso, F.; Fries, A.; Mendoza, K.; Gonzalez-Jaramillo, V.; Pucha-Cofrep, F.; Rollenbeck, R.; Bendix, J. Temporal and spatial analysis of precipitation patterns in an Andean region of southern Ecuador using LAWR weather radar. Meteorol. Atmos. Phys. 2018, 130, 473–484. [Google Scholar] [CrossRef]
- Granda, J.V.T.; Arcentales, H.R.A. Estudio Geológico-Estructural e Inventario de Deslizamientos del Área 3 de la Cuenca de Loja. 2015. Available online: http://dspace.utpl.edu.ec/handle/123456789/11433 (accessed on 25 August 2025).
- Cazzuffi, D.; Crippa, E. Contribution of Vegetation to Slope Stability: An Overview of Experimental Studies Carried Out on Different Types of Plants. In Erosion of Soils and Scour of Foundations; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 1–12. [Google Scholar] [CrossRef]
- ASTM D2487-17e1; Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM: West Conshohocken, PA, USA, December 2017. [CrossRef]
- ASTM E112-13; Test Methods for Determining Average Grain Size. ASTM: West Conshohocken, PA, USA, September 2021. [CrossRef]
- ASTM D2488-17e1; Practice for Description and Identification of Soils (Visual-Manual Procedures). ASTM: West Conshohocken, PA, USA, July 2017. [CrossRef]
- ASTM D4318-17e1; Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM: West Conshohocken, PA, USA, June 2017. [CrossRef]
- ASTM D3080/D3080M-23; Test Method for Direct Shear Test of Soils Under Consolidated Drained Conditions. ASTM: West Conshohocken, PA, USA, November 2023. [CrossRef]
- Spencer, E. A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Duncan, J.M. Factors of Safety and Reliability in Geotechnical Engineering. J. Geotech. Geoenviron. Eng. 2000, 126, 307–316. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering. 2005; p. 619. Available online: https://www.wiley.com/en-us/Reliability+and+Statistics+in+Geotechnical+Engineering-p-9780470871256 (accessed on 10 October 2025).
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 2011, 36, 612–624. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. Earth Surf. 2010, 115, 4035. [Google Scholar] [CrossRef]
- Chiaradia, E.A.; Vergani, C.; Bischetti, G.B. Evaluation of the effects of three European forest types on slope stability by field and probabilistic analyses and their implications for forest management. For. Ecol. Manag. 2016, 370, 114–129. [Google Scholar] [CrossRef]
- Chen, B.; Shui, W.; Liu, Y.; Deng, R. Analysis of Slope Stability with Different Vegetation Types under the Influence of Rainfall. Forests 2023, 14, 1865. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Chiaradia, E.A.; Simonato, T.; Speziali, B.; Vitali, B.; Vullo, P.; Zocco, A. Root strength and root area ratio of forest species in lombardy (Northern Italy). Plant Soil 2005, 278, 11–22. [Google Scholar] [CrossRef]
- Stokes, A.; Atger, C.; Bengough, A.G.; Fourcaud, T.; Sidle, R.C. Desirable plant root traits for protecting natural and engineered slopes against landslides. Plant Soil 2009, 324, 1–30. [Google Scholar] [CrossRef]
- Kim, J.H.; Fourcaud, T.; Jourdan, C.; Maeght, J.; Mao, Z.; Metayer, J.; Meylan, L.; Pierret, A.; Rapidel, B.; Roupsard, O.; et al. Vegetation as a driver of temporal variations in slope stability: The impact of hydrological processes. Geophys. Res. Lett. 2017, 44, 4897–4907. [Google Scholar] [CrossRef]
- Saim, N.M.; Kasa, A. Comparative Analysis of Slope Stability using Finite Element Method (FEM) and Limit Equilibrium Method (LEM). In Proceedings of the 2023 IEEE 14th Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 5 August 2023; pp. 224–229. [Google Scholar] [CrossRef]
- Yang, Y.; Li, S.; Li, C.; Wu, L.; Yang, L.; Zhang, P.; Huang, T. Comprehensive Laboratory Evaluations and a Proposed Mix Design Procedure for Cement-Stabilized Cohesive and Granular Soils. Front. Mater. 2020, 7, 239. [Google Scholar] [CrossRef]
- Teerawattanasuk, C.; Maneecharoen, J.; Bergado, D.T.; Voottipruex, P.; Le, G.L. Root Strength Measurements of Vetiver and Ruzi Grasses. Lowl. Technol. Int. 2014, 16, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Dade, W.; Renshaw, C.; Magilligan, F. Sediment transport constraints on river response to regulation. Geomorphology 2011, 126, 245–251. [Google Scholar] [CrossRef]
- Zurita, F.; Belmont, M.; De Anda, J.; Cervantes-Martinez, J. Stress detection by laser-induced fluorescence in Zantedeschia aethiopica planted in subsurface-flow treatment wetlands. Ecol. Eng. 2008, 33, 110–118. [Google Scholar] [CrossRef]
- Wu, T.H.; McKinnell, W.P., III; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Masi, E.B.; Segoni, S.; Tofani, V. Root Reinforcement in Slope Stability Models: A Review. Geosciences 2021, 11, 212. [Google Scholar] [CrossRef]
- Lin, W.; Fan, W.; Liu, H.; Xu, Y.; Wu, J. Classification of Handheld Laser Scanning Tree Point Cloud Based on Different KNN Algorithms and Random Forest Algorithm. Forests 2021, 12, 292. [Google Scholar] [CrossRef]
- Tengbeh, G. The effect of grass roots on shear strength variations with moisture content. Soil Technol. 1993, 6, 287–295. [Google Scholar] [CrossRef]
- Badhon, F.F.; Islam, M.S.; Islam, A. Contribution of Vetiver Root on the Improvement of Slope Stability. Indian Geotech. J. 2021, 51, 829–840. [Google Scholar] [CrossRef]
- Mickovski, S.; Bengough, A.; Bransby, M.; Davies, M.; Hallett, P.; Sonnenberg, R. The effect of roots on soil reinforcement. J. Biomech. 2006, 39, S353. [Google Scholar] [CrossRef]
- Kong, K.; Deng, Z.; Chen, F.; Wang, Z.; Chen, Y. Numerical analysis of the effect of vegetation root reinforcement on the rainfall-induced instability of loess slopes. Sci. Rep. 2025, 15, 23233. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Hales, T.C. Modelling biome-scale root reinforcement and slope stability. Earth Surf. Processes Landforms 2018, 43, 2157–2166. [Google Scholar] [CrossRef]
- Zhang, Q.; Luo, Z.; Chen, Y.; Wang, Z. Physical Model Experiments on Failure Mechanism on Slopes of Weathered Basalt Soils during Heavy Rainfall Events. Materials 2023, 16, 832. [Google Scholar] [CrossRef]
- Song, H.; Huang, J.; Zhang, Z.; Jiang, Q.; Liu, L.; He, C.; Zhou, Y. Analysis of Water Migration and Spoil Slope Stability under the Coupled Effects of Rainfall and Root Reinforcement Based on the Unsaturated Soil Theory. Forests 2024, 15, 640. [Google Scholar] [CrossRef]
- Lopez, G.; Gaiser, T.; Ewert, F.; Srivastava, A. Effects of Recent Climate Change on Maize Yield in Southwest Ecuador. Atmosphere 2021, 12, 299. [Google Scholar] [CrossRef]
- Asima, H.; Niedzinski, V.; O’donnell, F.C.; Montgomery, J. Comparison of Vegetation Types for Prevention of Erosion and Shallow Slope Failure on Steep Slopes in the Southeastern USA. Land 2022, 11, 1739. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, M.; Meng, X.; Chen, G.; Zeng, R.; Yang, Q.; Liu, Y.; Wang, B. Evaluation of the Effects of Forest on Slope Stability and Its Implications for Forest Management: A Case Study of Bailong River Basin, China. Sustainability 2020, 12, 6655. [Google Scholar] [CrossRef]
- Machado, L.; Holanda, F.S.R.; da Silva, V.S.; Maranduba, A.I.A.; Lino, J.B. Contribution of the root system of vetiver grass towards slope stabilization of the São Francisco River. Semin. Agrar. 2015, 36, 2453. [Google Scholar] [CrossRef][Green Version]
- Lal, R. Restoring Soil Quality to Mitigate Soil Degradation. Sustainability 2015, 7, 5875–5895. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).