Analysis on Wind-Induced Fatigue Life of Steel Tall Buildings Based on Wind Tunnel Test and Time-Domain Analysis
Abstract
1. Introduction
2. Prototype Buildings and Wind Tunnel Test
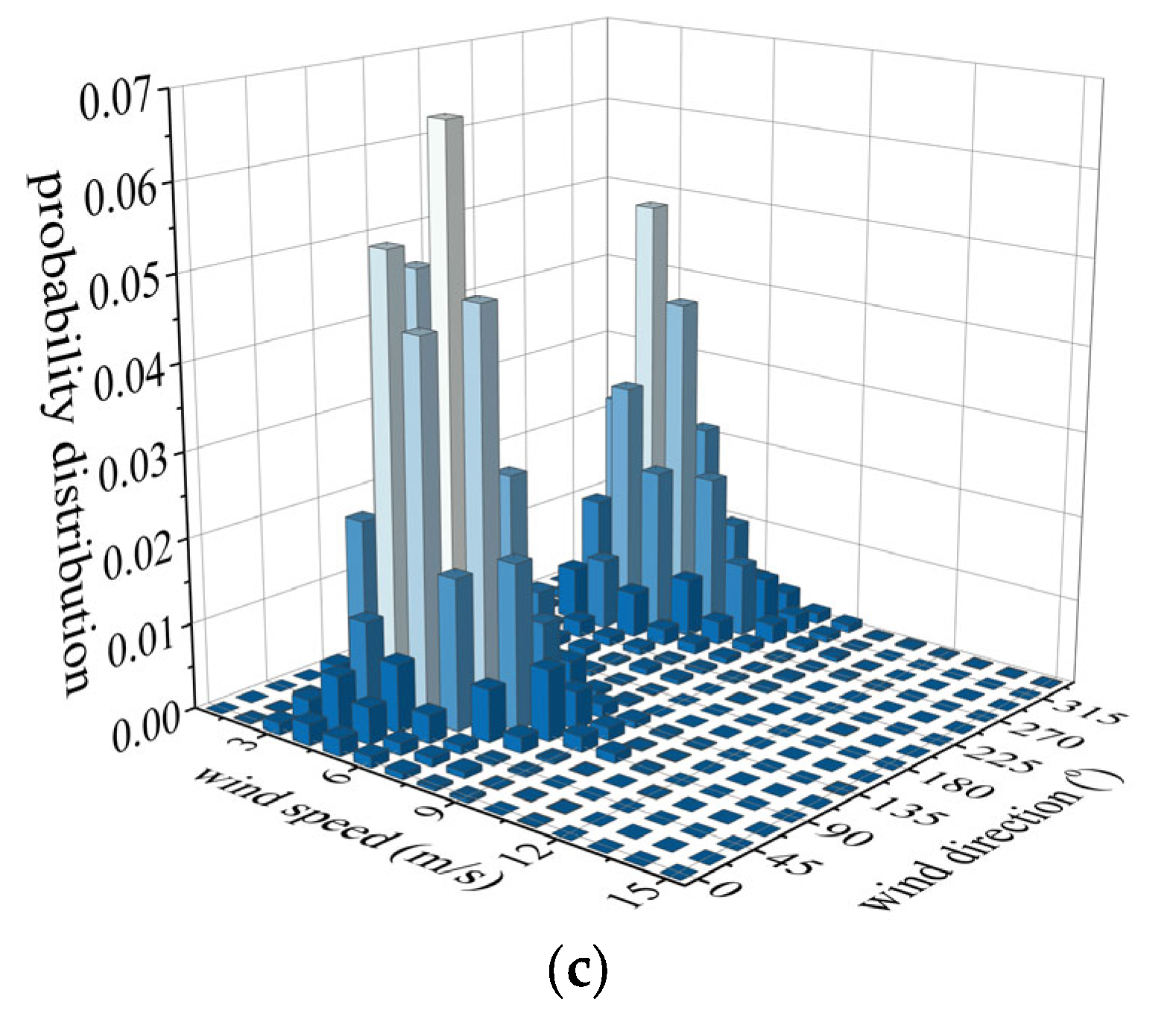
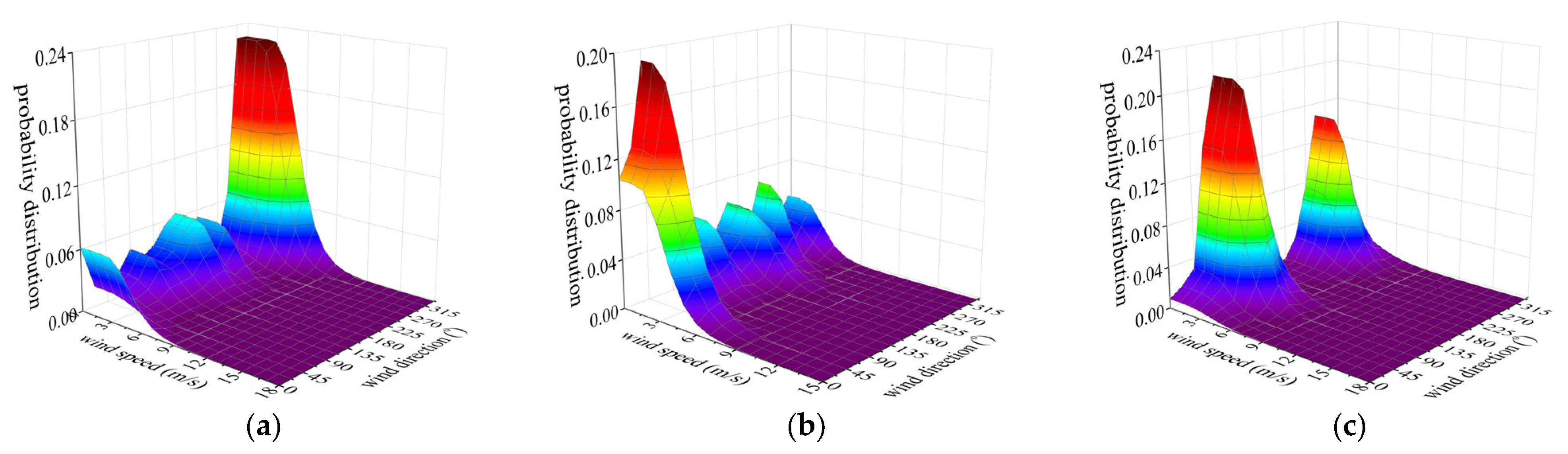
3. Probability Distribution of Wind Speed and Direction
4. Calculation of Wind-Induced Response
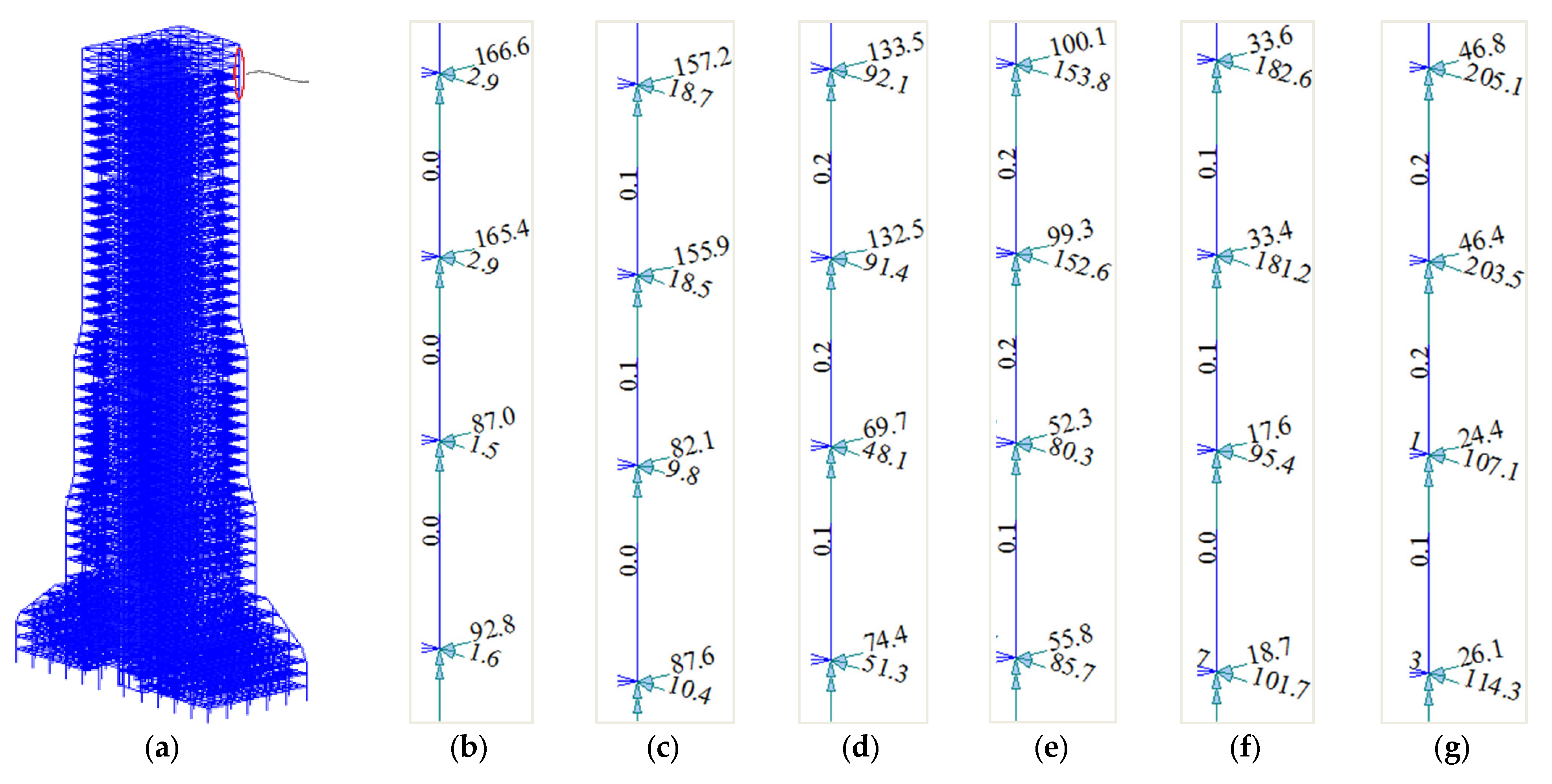
4.1. Static Wind-Induced Response
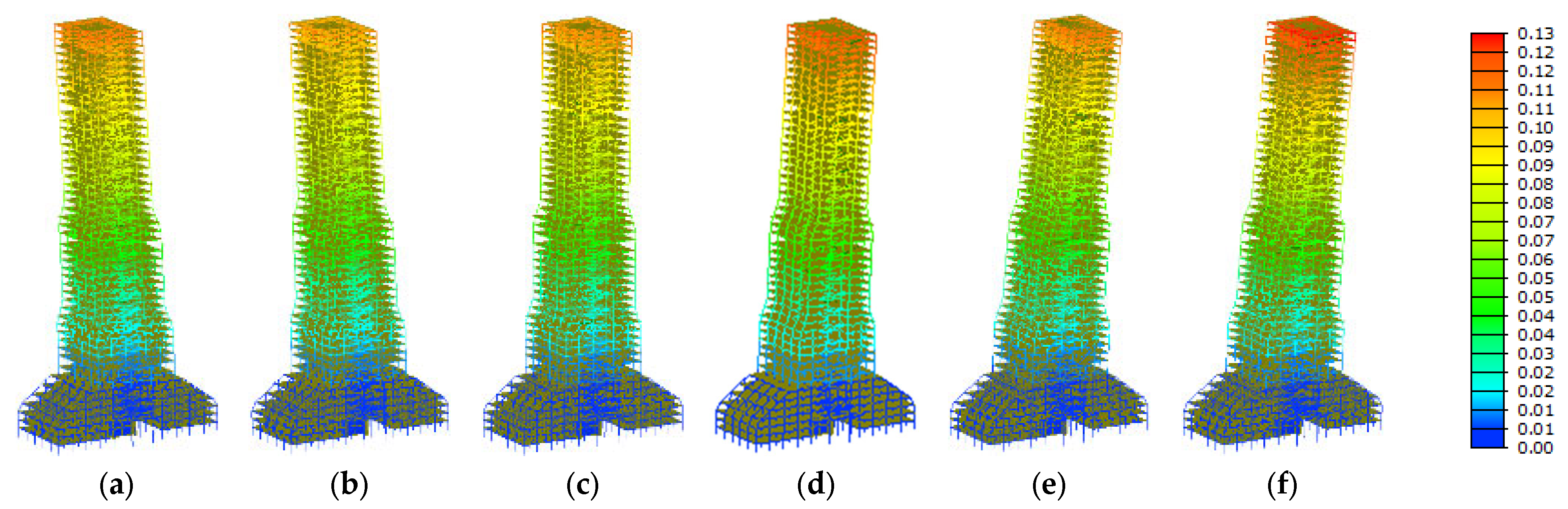
4.2. Dynamic Wind-Induced Response
5. Calculation and Analysis of Fatigue Life
5.1. Calculation Method
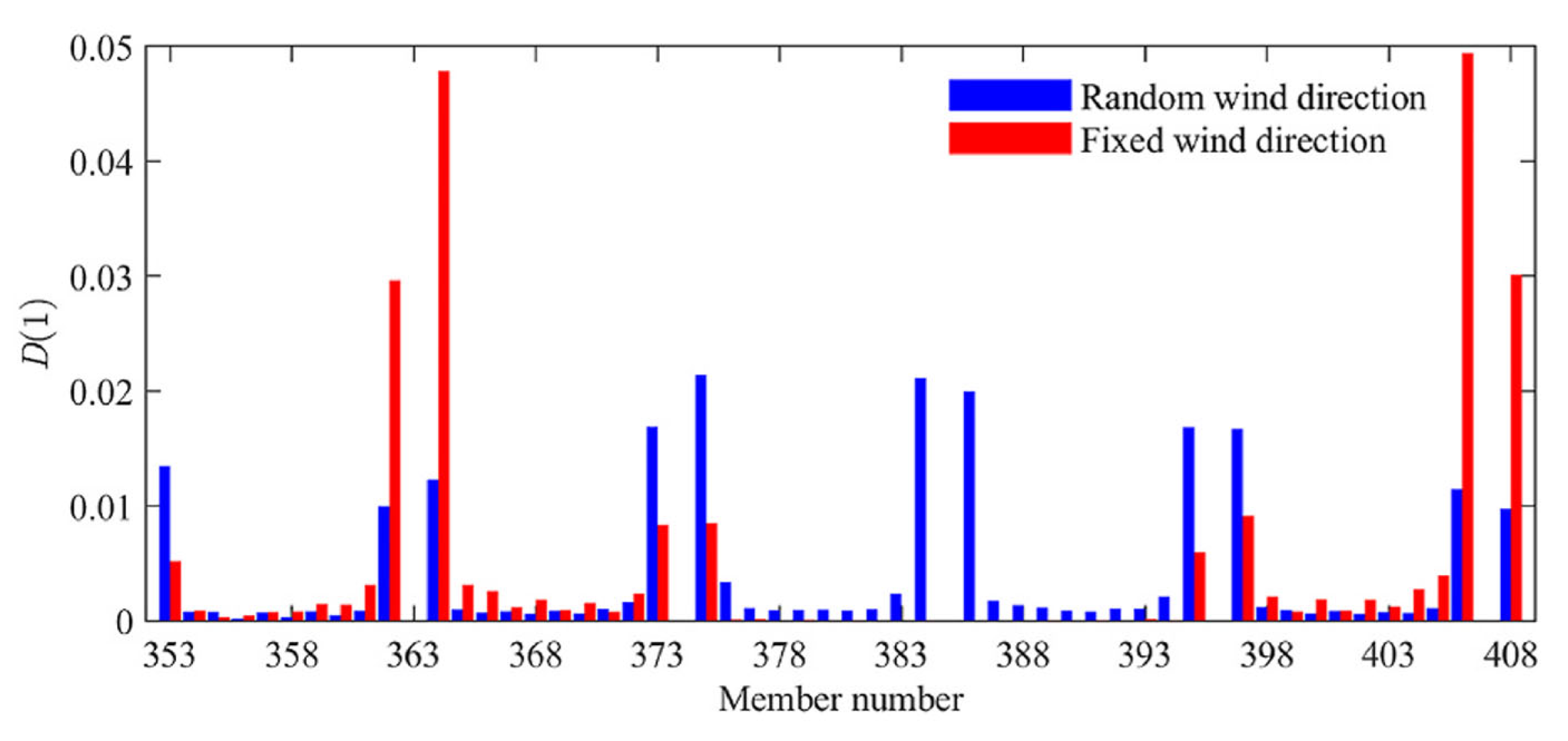
5.2. Calculation Results and Analysis
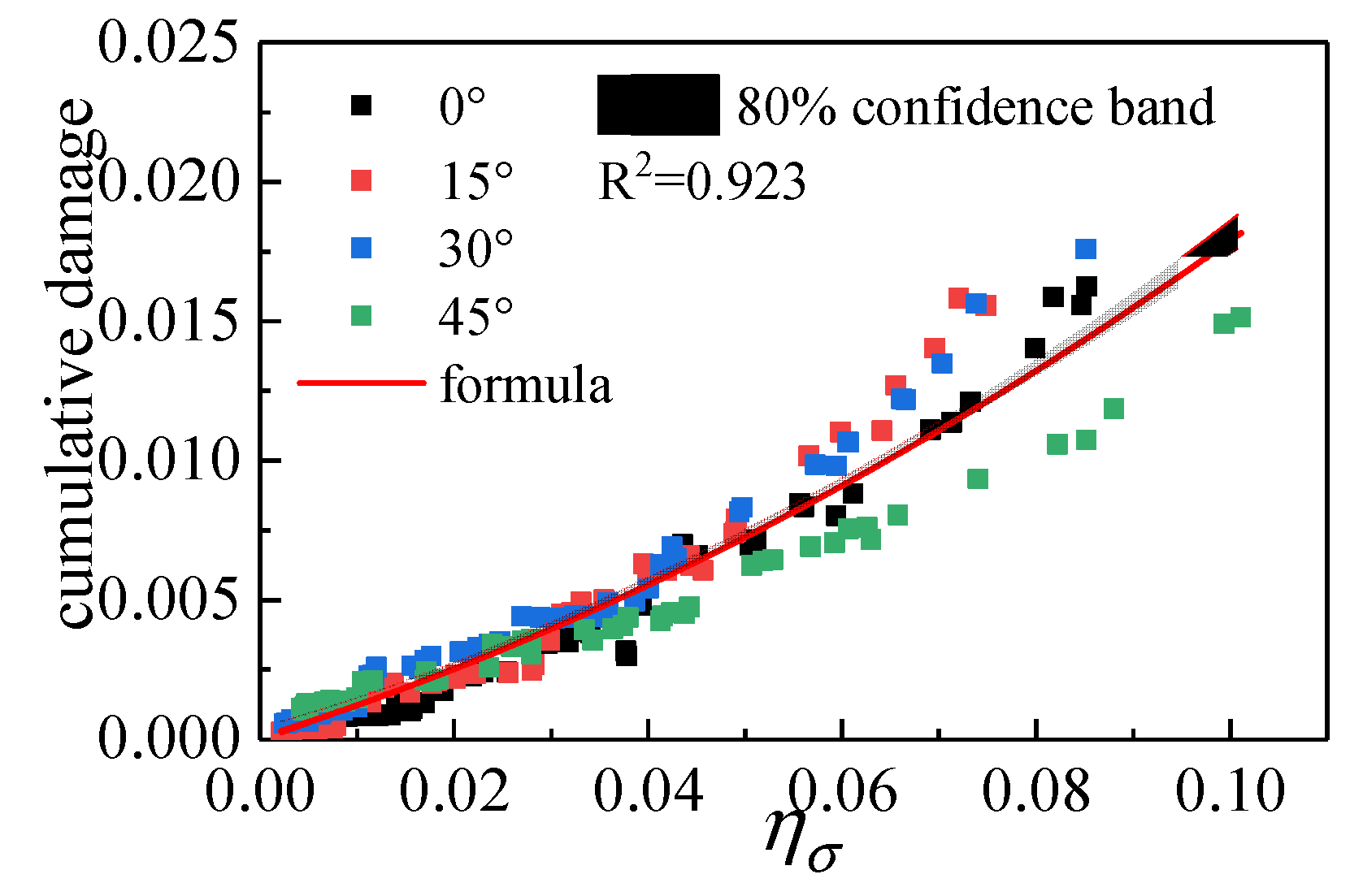
5.3. Approximate Method to Estimate Fatigue Life
5.4. About the Application of This Research in Practical Engineering
6. Limitations in This Study and Future Research Prospects
7. Conclusions and Prospect
- (1)
- Under the current normal design conditions, both the element stresses and fatigue life of steel tall buildings exhibit significant safety margins. The fatigue life is approximately over 400 years, indicating that wind-induced fatigue failure will not occur within the design life.
- (2)
- When the ratio of the RMS stress to the ultimate tensile strength reaches 0.125–0.164, the fatigue life of the critical elements will be shorter than the design life. In such cases, it is necessary to consider the potential for fatigue failure of the structure. Designers should take preventive measures to avoid the occurrence of such scenarios.
- (3)
- Under extreme conditions where the prevailing wind predominantly acts in the most hazardous direction, the fatigue life of critical elements will be shorter than the design life when the stress ratio reaches 0.085–0.118, also necessitating consideration of potential fatigue damage of the steel tall building.
- (4)
- This paper proposes an approximate estimation formula for the fatigue life of steel structure tall buildings. This approximate formula can assist designers in making preliminary estimations of the wind-induced fatigue life for tall steel buildings. A procedure based on the RMS stress ratio is proposed to preliminarily assess whether structural fatigue life needs to be considered. When the estimation results indicate that the fatigue life is close to the design life, further precise calculations of fatigue life should be conducted.
- (5)
- It should be mentioned is that this study discusses only six engineering cases; the approximate estimation formula and the proposed RMS stress ratio threshold are derived from only six case studies and may not generalize to all tall building configurations since the design parameters such as structure form, building shape, vibration frequency, building height, design wind speed, and ground roughness will affect structure vibrations and fatigue life. In addition, the simplified approach does not explicitly incorporate directional variability or non-Gaussian turbulence effects. These factors are likely to compromise the accuracy of this empirical formula. Therefore, if a more precise relationship between these design parameters, random parameters of structures, and wind loads and fatigue life could be established, it would provide more accurate guidance for practical engineering applications. If necessary, this work requires more engineering cases and theoretical research in the future.
- (6)
- With the deepening of studies on the impact of multiple hazards on structural safety, the effects of multi-hazard coupling on fatigue damage and dynamic response of tall steel buildings should become a key focus of future investigations, such as those into wind–earthquake interaction and rain–wind interaction. Additionally, the exploration of advanced technical approaches, such as machine learning-based fatigue estimators trained on larger datasets, could also be pursued to enhance predictive generalization in wind-induced fatigue analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wöhler, A. Versuche zur Ermittlung der auf die Eisenbahnwagenachsen einwirkenden Kräfte und die Widerstandsfähigkeit der Wagen-Achsen. Z. Bauwes. 1960, 10, 583–614. [Google Scholar]
- Dowling, N.E. Fatigue failure prediction for complicated stress strain histories. J. Mater. 1972, 7, 71–87. [Google Scholar]
- Miner, M. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Matsuiski, M.; Endo, T. Fatigue of metals subjected to varying stress. Jpn. Soc. Mech. Eng. 1968, 68, 37–40. [Google Scholar]
- De Fazio, N.; Placidi, L.; Tomassi, A.; Fraddosio, A.; Castellano, A.; Paparella, F. Different mechanical models for the study of ultrasonic wave dispersion for mechanical characterization of construction materials. Int. J. Solids Struct. 2025, 315, 113352. [Google Scholar] [CrossRef]
- Caracoglia, L.; Jones, N.P. Wind-induced failures of highway light poles during winter storms. In Proceedings of the ASME Pressure Vessels and Piping Division Conference, Vancouver, BC, Canada, 23–27 July 2006. [Google Scholar]
- Repetto, M.P.; Solari, G. Wind-induced fatigue collapse of real slender structures. Eng. Struct. 2010, 32, 3888–3898. [Google Scholar] [CrossRef]
- Ribeiro, D.; Bragana, C.; Montenegro, P.A.; Carvalho, H.; Costa, B.; Marques, F. Wind-induced fatigue analysis of high-rise guyed lattice steel towers. Structures 2022, 36, 719–734. [Google Scholar] [CrossRef]
- Huo, T.; Tong, L. An approach to wind-induced fatigue analysis of wind turbine tubular towers. J. Constr. Steel Res. 2020, 166, 105917. [Google Scholar] [CrossRef]
- Banday, Z.Z.; Fenerci, A.; Lystad, T.M.; Øiseth, O.A. Buffeting induced fatigue damage assessment of long-span bridge decks under uncertain turbulence conditions. Eng. Struct. 2025, 323, 119292. [Google Scholar] [CrossRef]
- Rong, K.; Tian, L.; Luo, J.; Wang, L. Study on wind-induced fatigue performance of large-span transmission tower-line system considering the combined distribution probability of wind direction and speed. Eng. Fail. Anal. 2024, 156, 107785. [Google Scholar] [CrossRef]
- Li, C.; Pan, H.; Tian, L.; Bi, W. Lifetime multi-hazard fragility analysis of transmission towers under earthquake and wind considering wind-induced fatigue effect. Struct. Saf. 2022, 99, 102266. [Google Scholar] [CrossRef]
- Wang, L.; Fan, X.-Y. Failure cases of high chimneys: A review. Eng. Fail. Anal. 2019, 105, 1107–1117. [Google Scholar] [CrossRef]
- Repetto, M.P.; Solari, G. Directional Wind-Induced Fatigue of Slender Vertical Structures. J. Struct. Eng. 2004, 130, 1032–1040. [Google Scholar] [CrossRef]
- Barle, J.; Grubisic, V.; Radica, D. Service strength validation of wind-sensitive structures, including fatigue life evaluation. Eng. Struct. 2010, 32, 2767–2775. [Google Scholar] [CrossRef]
- Petrini, F.; Bontempi, F. Estimation of fatigue life for long span suspension bridge hangers under wind action and train transit. Struct. Infrastruct. Eng. 2011, 7, 491–507. [Google Scholar] [CrossRef]
- Hosomi, M.; Kobayashi, H.; Nitta, Y. Fatigue strength design for vortex-induced oscillation and buffeting of a bridge. J. Wind Eng. Ind. Aerodyn. 1997, 67, 227–237. [Google Scholar] [CrossRef]
- Klinger, C.; Michael, T.; Bettge, D. Fatigue cracks in railway bridge hangers due to wind induced vibrations–Failure analysis, measures and remaining service life estimation. Eng. Fail. Anal. 2014, 43, 232–252. [Google Scholar] [CrossRef]
- Song, J.; Qu, J.; Huo, L. Lifetime seismic fragility analysis of long-span spatial structures considering the wind-induced fatigue effect. J. Build. Eng. 2024, 87, 109032. [Google Scholar] [CrossRef]
- Huang, M.-F.; Ye, H.-K.; Lou, W.-J.; Sun, X.-T.; Ye, J.-Y. Wind-induced vibration and fatigue analysis of long span lattice structures considering distribution of wind speed and direction. J. Zhejiang Univ. (Eng. Sci.) 2019, 53, 1916–1926. [Google Scholar]
- Kim, S.H.; Shin, H.K.; Joo, Y.C.; Kim, K.H. A study of the wake effects on the wind characteristics and fatigue loads for the turbines in a wind farm. Renew. Energy 2015, 74, 536–543. [Google Scholar] [CrossRef]
- Qing, M.F.; Shi, W.; Chai, W.; Fu, X.; Li, L.; Li, X. Extreme structural response prediction and fatigue damage evaluation for large-scale monopile offshore wind turbines subject to typhoon conditions. Renew. Energy 2023, 208, 450–464. [Google Scholar] [CrossRef]
- Chen, T.; Li, W.; Deng, R.; Zuo, H. Fatigue analysis of offshore wind turbines with soil-structure interaction and various pile types. Ocean Eng. 2024, 314, 119786. [Google Scholar] [CrossRef]
- Fu, B.; Zhao, J.; Li, B.; Yao, J.; Teifouet, A.R.M.; Sun, L.; Wang, Z. Fatigue reliability analysis of wind turbine tower under random wind load. Struct. Saf. 2020, 87, 101982. [Google Scholar] [CrossRef]
- Kumar, K.S. Prediction of wind-induced fatigue on claddings of low buildings. Comput. Struct. 2000, 75, 31–44. [Google Scholar] [CrossRef]
- Xhelaj, A.; Orlando, A.; Pagnini, L.; Tubino, F.; Repetto, M.P. Fatigue life assessment of a slender lightning rod due to wind excited vibrations. Procedia Struct. Integr. 2024, 57, 754–761. [Google Scholar] [CrossRef]
- Merarda, H.; Toumi, M.; Boutelhig, A. Analysis of heliostat fatigue: Impact of wind speed distribution, studied over six regions of Algeria. Sol. Energy 2024, 278, 112776. [Google Scholar] [CrossRef]
- Tan, J.; Tan, P.; Wu, J.; Feng, D. Evaluation of wind-induced fragility and cumulative fatigue damage on seismically isolated high-rise building. J. Wind Eng. Ind. Aerodyn. 2024, 254, 105915. [Google Scholar] [CrossRef]
- Palmeri, A.; Ricciardelli, F. Fatigue analyses of buildings with viscoelastic dampers. J. Wind Eng. Ind. Aerodyn. 2006, 94, 377–395. [Google Scholar] [CrossRef]
- Arul, M.; Kareem, A.; Kwon, D.K. Identification of Vortex-Induced Vibration of Tall Building Pinnacle Using Cluster Analysis for Fatigue Evaluation: Application to Burj Khalifa. J. Struct. Eng. 2020, 146, 04020234. [Google Scholar] [CrossRef]
- Okajima, A. Strouhal numbers of rectangular cylinders. J. Fluid Mech. 1982, 123, 379–398. [Google Scholar] [CrossRef]
- Sohankar, A.; Norberg, C.; Davidson, L. Low-Reynolds-number flow around a square cylinder at incidence: Study of blockage, onset of vortex shedding and outlet boundary condition. Int. J. Numer. Methods Fluids 2015, 26, 39–56. [Google Scholar] [CrossRef]
- Coles, S.G.; Walshaw, D. Directional modeling of extreme wind speeds. J. R. Stat. Soeiety Appl. Stat. 1994, 43, 139–157. [Google Scholar]
- GB 50017-2003; Code for Design of Steel Structures. Progress in Steel Building Structures: Beijing, China, 2010.
- AISC 360-22; Specification for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2022.
- Asgarkhani, N.; Kazemi, F.; Jankowski, R. Machine-learning based tool for seismic response assessment of steel structures including masonry infill walls and soil-foundation-structure interaction. Comput. Struct. 2025, 317, 107918. [Google Scholar] [CrossRef]





| Building | Location | Height | First Three Modes | First Three Frequencies | Designed Group |
|---|---|---|---|---|---|
| 1# | Changsha | 347 m |  | 0.17 Hz | Hunan Provincial Architectural Design Institute Group Co., Ltd. Changsha, China. |
| 0.18 Hz | |||||
| 0.34 Hz | |||||
| 2# | Wuhan | 187 m |  | 0.23 Hz | Wong Tung Group. Hongkong, China. |
| 0.29 Hz | |||||
| 0.35 Hz | |||||
| 3# | Wuhan | 157 m |  | 0.27 Hz | Wong Tung Group. Hongkong, China. |
| 0.33 Hz | |||||
| 0.40 Hz | |||||
| 4# | Wuhan | 242 m |  | 0.18 Hz | CITIC Architectural Design & Research Institute Co., Ltd. Wuhan, China. |
| 0.20 Hz | |||||
| 0.28 Hz | |||||
| 5# | Wuhan | 248 m |  | 0.16 Hz | Central-South Architectural Design and Research Institute Co., Ltd. Wuhan, China. |
| 0.21 Hz | |||||
| 0.26 Hz | |||||
| 6# | Huangshi | 92 m |  | 0.39 Hz | Central-South Architectural Design and Research Institute Co., Ltd. Wuhan, China. |
| 0.43 Hz | |||||
| 0.46 Hz |
| Building | Ground Roughness Category | Geometric Scale Ratio | Wind Direction | Pressure Point Number |
|---|---|---|---|---|
| 1# | C | 1:400 | 0–350°, interval 10° | 360 |
| 2# | B | 1:200 | 0–345°, interval 15° | 582 |
| 3# | B | 1:200 | 0–345°, interval 15° | 574 |
| 4# | C | 1:250 | 0–345°, interval 15° | 510 |
| 5# | C | 1:300 | 0–345°, interval 15° | 499 |
| 6# | B | 1:200 | 0–345°, interval 15° | 402 |
| Building 1# | Building 2# | Building 3# | Building 4# | Building 5# | Building 6# | |
|---|---|---|---|---|---|---|
| structural height | 347 m | 187 m | 157 m | 242 m | 248 m | 92 m |
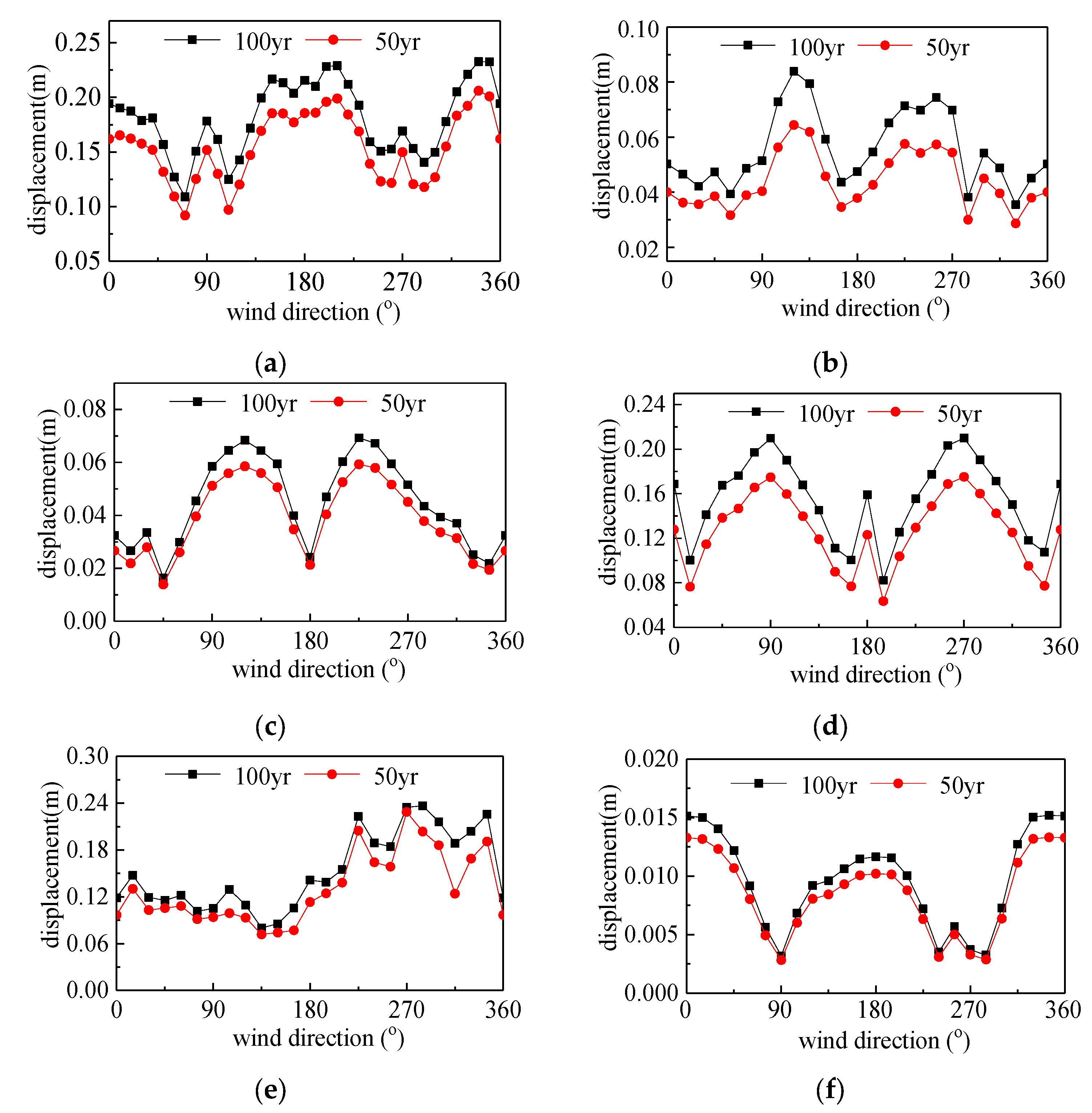
| lateral displacement | 0.23 m | 0.084 m | 0.068 m | 0.21 m | 0.24 m | 0.015 m |
| displacement ratio | 1/1510 | 1/2230 | 1/2310 | 1/1150 | 1/1030 | 1/6133 |
| Building | Material | Fatigue Life T1 | Fatigue Life T2 |
|---|---|---|---|
| 1# | Q345 | 533.97 years | 391.98 years |
| 2# | Q345 | 647.63 years | 468.67 years |
| 3# | Q235 | 681.87 years | 569.87 years |
| 4# | Q345 | 732.66 years | 582.93 years |
| 5# | Q345 | 714.72 years | 611.14 years |
| 6# | Q345 | 645.24 years | 502.90 years |
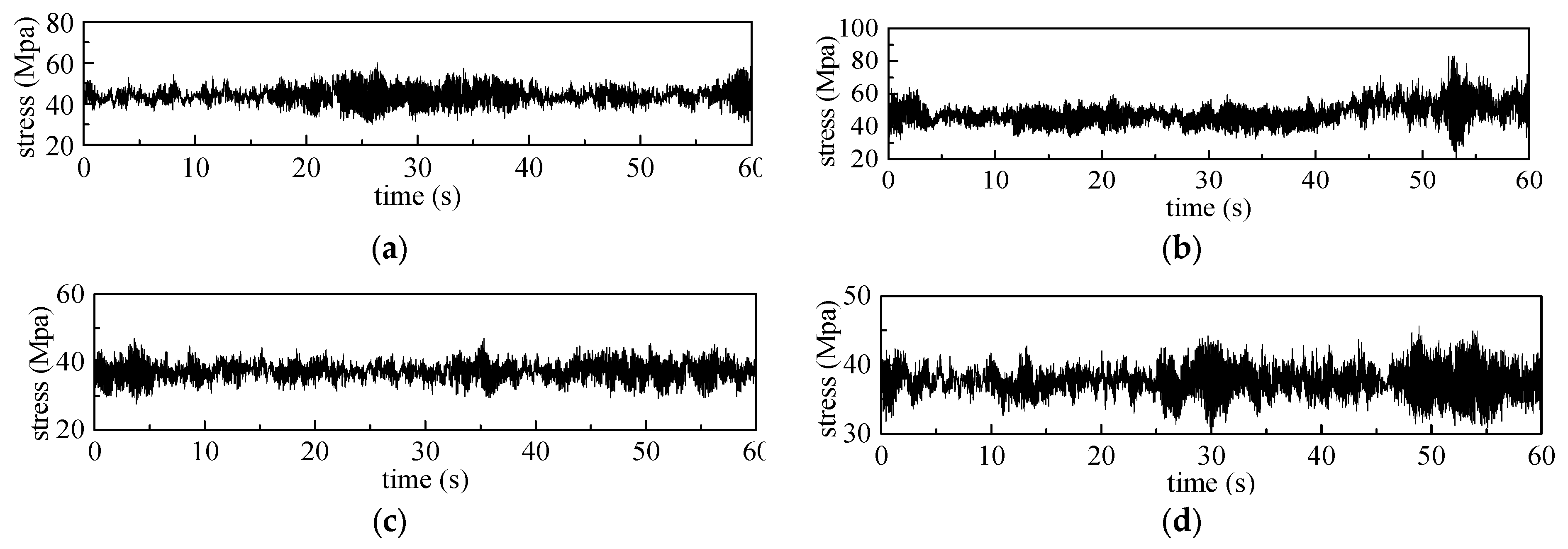
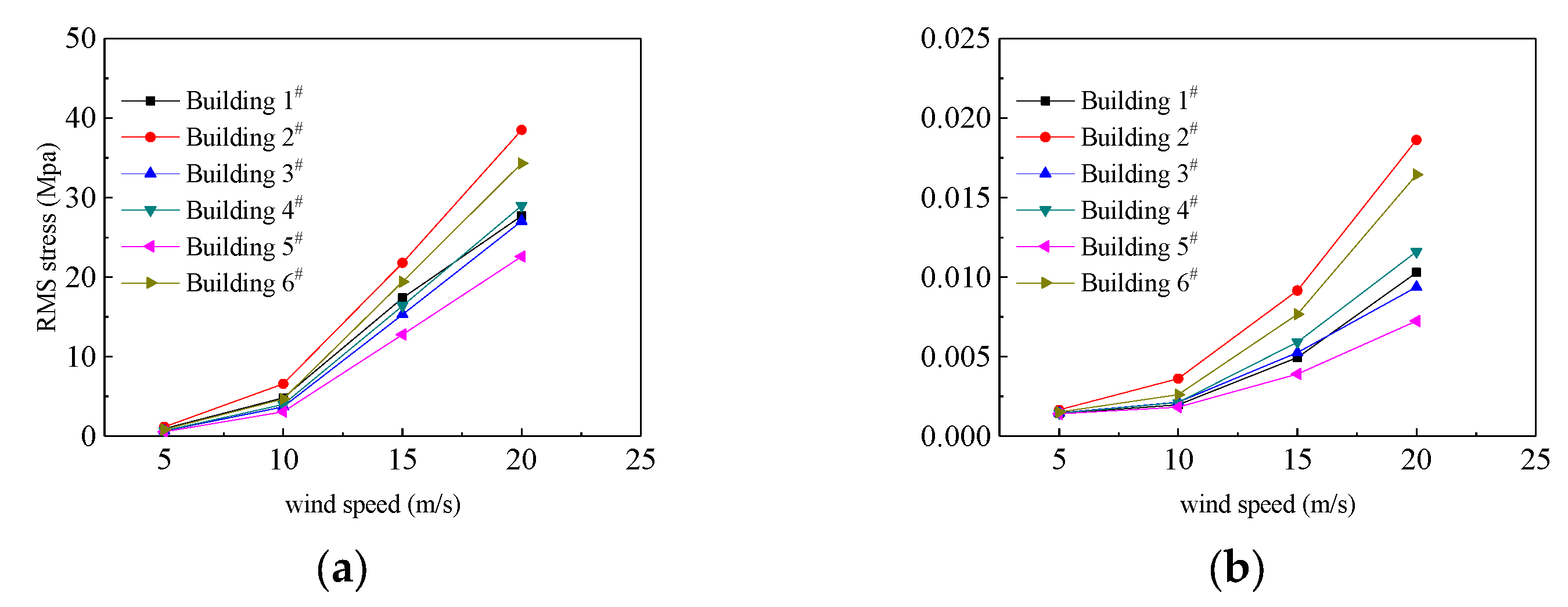
| Building | RMS Stress | Stress Ratio ησ | RMS Stress in Extreme Conditions | ησ in Extreme Conditions |
|---|---|---|---|---|
| 1# | 71.0 MPa | 0.145 | 41.8 Mpa | 0.085 |
| 2# | 61.0 MPa | 0.125 | 41.9 Mpa | 0.086 |
| 3# | 61.8 MPa | 0.164 | 44.3 Mpa | 0.118 |
| 4# | 77.8 MPa | 0.159 | 45.1 Mpa | 0.092 |
| 5# | 62.2 MPa | 0.127 | 45.8 Mpa | 0.093 |
| 6# | 66.8 MPa | 0.136 | 49.6 Mpa | 0.101 |
| Building | Calculated Fatigue Life | Estimated Cumulative Damage by Equation (8) | Estimated Fatigue Life |
|---|---|---|---|
| 1# | 533.97 years | 0.00199 | 500.68 years |
| 2# | 647.63 years | 0.00182 | 548.19 years |
| 3# | 681.87 years | 0.00167 | 599.25 years |
| 4# | 732.66 years | 0.00155 | 644.49 years |
| 5# | 714.72 years | 0.00159 | 627.19 years |
| 6# | 645.24 years | 0.00179 | 558.41 years |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.-K.; Gao, R.-F.; Wang, L. Analysis on Wind-Induced Fatigue Life of Steel Tall Buildings Based on Wind Tunnel Test and Time-Domain Analysis. Appl. Sci. 2025, 15, 11736. https://doi.org/10.3390/app152111736
Wang Z-K, Gao R-F, Wang L. Analysis on Wind-Induced Fatigue Life of Steel Tall Buildings Based on Wind Tunnel Test and Time-Domain Analysis. Applied Sciences. 2025; 15(21):11736. https://doi.org/10.3390/app152111736
Chicago/Turabian StyleWang, Ze-Kang, Rui-Fang Gao, and Lei Wang. 2025. "Analysis on Wind-Induced Fatigue Life of Steel Tall Buildings Based on Wind Tunnel Test and Time-Domain Analysis" Applied Sciences 15, no. 21: 11736. https://doi.org/10.3390/app152111736
APA StyleWang, Z.-K., Gao, R.-F., & Wang, L. (2025). Analysis on Wind-Induced Fatigue Life of Steel Tall Buildings Based on Wind Tunnel Test and Time-Domain Analysis. Applied Sciences, 15(21), 11736. https://doi.org/10.3390/app152111736





