Abstract
The complex structures and diverse object categories in indoor environments pose significant challenges for point cloud semantic segmentation. To address the insufficient capability of extracting local features in complex scenes, this paper proposes a point cloud segmentation network based on neighborhood feature enhancement termed PKA-Net. First, to obtain richer and more discriminative feature representations, we design a local feature encoding module that extracts geometric features, color information, and spatial information from local regions of the point cloud for joint feature encoding. Furthermore, we enhance the hierarchical feature extraction by integrating Kolmogorov–Arnold Networks (KAN) to form the SAPK module, improving the network’s ability to fit complex geometric structures. A residual structure is also adopted to optimize feature propagation and alleviate the problem of gradient vanishing. Finally, we propose the dual attention mechanism C-MSCA, which dynamically selects and strengthens key features through the synergistic action of channel and spatial attention, enhancing the network’s perception of local details and global structure. To evaluate the performance of the proposed PKA-Net, extensive experiments were conducted on the S3DIS dataset. Experimental results demonstrate that PKA-Net improves OA by 2.1%, mAcc by 2.9%, and mIoU by 4% compared to the baseline model. It outperforms other mainstream models, delivering enhanced overall segmentation performance.
1. Introduction
With the rapid advancement of three-dimensional (3D) sensor technologies, the acquisition and processing of 3D data have found extensive applications in autonomous driving [1,2], 3D reconstruction [3], and smart city development [4,5]. 3D point clouds consist of vast spatial coordinate data acquired through various sensors such as laser scanning, structured light, and radar, directly reflecting an object’s geometric form and surface characteristics. Semantic segmentation of 3D point cloud [6] serves as a critical step in processing point cloud data. It aims to divide complex point cloud data into meaningful subsets or objects, with each subset corresponding to an independent object or surface within the scene. This process plays a foundational role for subsequent tasks such as object recognition, tracking, and environmental modeling. Effective segmentation significantly enhances data processing efficiency and accuracy, providing more structured information inputs for advanced applications.
Traditional point cloud segmentation primarily employs machine learning methods [7,8], first extracting manually designed geometric or statistical features from point cloud data and then training classifiers such as Support Vector Machines (SVM) on these features. Sampath et al. [9] employed the K-means algorithm, Biosca et al. [10] utilized fuzzy clustering, and Zhang et al. [11] employed the Mean-shift algorithm. They utilized Euclidean distance as a similarity metric to partition point cloud data into distinct categories, thereby achieving segmentation. Mills et al. [12] proposed a two-stage semantic segmentation framework that identifies boundaries through edge detection, followed by grouping points within regions. They innovatively utilize local surface property gradients and compare them against preset thresholds to determine edge points, subsequently connecting these points to form segmentation boundaries. Christoph et al. [13] proposed a region-growing-based supervoxel segmentation algorithm. This approach determines initial growth regions by generating supervoxels corresponding to seed points, and then employs a similarity algorithm to expand regions based on their concavity and convexity. Overall, these methods heavily rely on manually designed features, and their segmentation performance is often constrained by their limited expressiveness, making it difficult to achieve satisfactory results in complex scenes.
In recent years, with the rise of deep learning [14], semantic segmentation techniques for 3D point cloud scenes have undergone a significant shift from manual feature-based methods to data-driven approaches, achieving remarkable progress. However, semantic segmentation of point clouds in indoor scenes still presents numerous challenges. Indoor objects are diverse in type and complex in geometry, with similar shapes and textures between different objects, making it difficult to delineate their boundaries. Furthermore, the semantic distinctions between structural elements and decorative items in the environment are subtle. This demands that segmentation algorithms not only possess global semantic understanding capabilities but also capture fine-grained local features to achieve precise segmentation of object edges and details. In this context, this paper proposes a point cloud segmentation network based on neighborhood feature enhancement, aiming to enhance detection performance. The main contributions of this paper are as follows:
- A local feature encoding module PFE is designed to extract geometric features from local regions of the point cloud, including normal vectors and curvature, and then jointly encoded with color and spatial information to obtain richer and more discriminative feature representations.
- An enhanced hierarchical feature extraction module, SAPK, is proposed by integrating the KAN [15] network, using learnable spline functions to better model complex geometries. A residual structure is also adopted to improve feature propagation and reduce gradient vanishing.
- A dual attention mechanism, C-MSCA, is proposed by combining the Multi-Scale Convolutional Attention (MSCA) [16] to dynamically enhance key features and improve perception of local details and global structures.
2. Related Work
2.1. Point-Based Semantic Segmentation
To reduce feature loss during point cloud preprocessing, Qi et al. from Stanford University proposed deep learning methods capable of directly processing raw point cloud data, with the most representative being PointNet [17] and PointNet++ [18]. PointNet takes raw point cloud data as input and uses shared Multilayer Perceptrons (MLPs) to extract features for each point, followed by a symmetric aggregation function to obtain global features. However, PointNet mainly focuses on global feature learning and ignores local relationships between points, which limits its performance in fine-grained segmentation tasks. To address this limitation, PointNet++ was introduced. It incorporates a hierarchical structure, applying PointNet within local regions to extract detailed features. By combining local and global feature extraction, PointNet++ enhances the network’s ability to capture both fine-grained and high-level information.
In 2018, Li et al. [19] proposed PointCNN, which learns a transformation matrix from the input to reorder the unordered point cloud into a structured format, allowing the direct application of conventional convolution operations. Later, Thomas et al. [20] introduced KPConv, which constructs kernel point distributions via linear interpolation to compute transformation matrices for point features and employs 2D CNNs to extract features. Zhao et al. [21] proposed PointWeb, which incorporates an Adaptive Feature Adjustment (AFA) module. AFA learns the influence between each pair of points, effectively integrating neighborhood context into point features and enhancing their local representational ability. To improve computational efficiency, Hu et al. [22] proposed RandLA-Net, which utilizes a random sampling strategy. RandLA-Net also introduces a Local Feature Aggregation module that gradually enlarges the receptive field of each point, effectively preserving geometric details and compensating for the potential information loss caused by random sampling. In 2021, Zhao et al. [23] introduced Point Transformer, which employs a local–global attention mechanism to capture spatial and structural relationships among points. It also introduces the SortNet module to learn permutation-invariant point orderings, improving model robustness. In 2022, Qian et al. [24] proposed PointNeXt based on PointNet++, incorporating inverted residual bottlenecks and separable MLPs to achieve efficient model scaling. They further enhanced generalization through a richer set of data augmentation techniques. Building on Point Transformer, Wu et al. [25] proposed Point Transformer V3, which emphasizes simplicity and efficiency by replacing exact neighborhood search with efficient serialized neighborhood mapping, significantly improving both processing speed and model performance.
2.2. Feature Extraction
Due to the unstructured nature of 3D point cloud data, processing point cloud information relies on effective feature extraction to comprehend and analyze the data. Global feature extraction is primarily used to extract features representing overall shapes or structures from the entire point cloud. It provides a fundamental description of the entire dataset, aids in understanding the general morphology and distribution of point cloud data, and typically offers high computational efficiency. After the feature extraction stage in PointNet [17], each point possesses a high-dimensional feature vector. Through max pooling operations, the maximum values across each dimension of these feature vectors are selected, thereby forming a global feature vector. KPConv [20] employs kernel point convolution to perform convolutional operations on point clouds of arbitrary density, subsequently using global pooling to obtain global features. Point Cloud Transformer (PCT) [26] extracts global features by combining global pooling with average pooling to support subsequent classification and segmentation tasks.
Local feature extraction primarily focuses on capturing the characteristic representation of each point or point cluster, which enables the detailed capture of local geometric details within the point cloud. In point clouds containing complex shapes or variable geometric structures, local features can more effectively process information such as object surfaces, boundaries, and sharp corners. This makes them particularly well-suited for handling three-dimensional objects with complex topological structures. Compared to global features, local features offer greater flexibility in adapting to variations in geometric detail. PointNet++ [18] employs a spherical query mechanism to organize neighboring points into clusters, utilizing a shared MLP encoding and max-pooling method to capture local features. Furthermore, refs. [27,28] propose distinct mechanisms to optimize local feature extraction, enabling the model to efficiently capture meaningful local features across diverse scenarios. Global features capture the overall structure and shape of the entire point cloud, while local features extract details and local geometric information. By fusing global and local features, the model can simultaneously understand both the overall layout and intricate local details of a scene, thereby enhancing performance in complex environments. Point-Voxel Transformer (PVT) [29] aggregates local features and global features through separate voxel and point branches, finally fusing the output features from both branches. Point-BERT [30] integrates local geometric details and global understanding of point cloud data using local point embeddings and a class token.
3. Methods
3.1. Overall Framework
The overall architecture of PKA-Net is shown in Figure 1. It followed the classic encoder and decoder architecture of PointNet++. Specifically, the input unordered 3D point cloud first passes through an MLP layer to ensure consistency in feature dimensions. Subsequently, downsampling and multi-level feature extraction operations are performed sequentially. The SAP module does not use the KAN module, while the SAPK module incorporates the KAN module to enhance the learning capability of local geometric features. In the decoder, we adopt the Feature Propagation (FP) module from PointNet++ to perform upsampling operations, effectively achieving the propagation of features from low to high resolution.
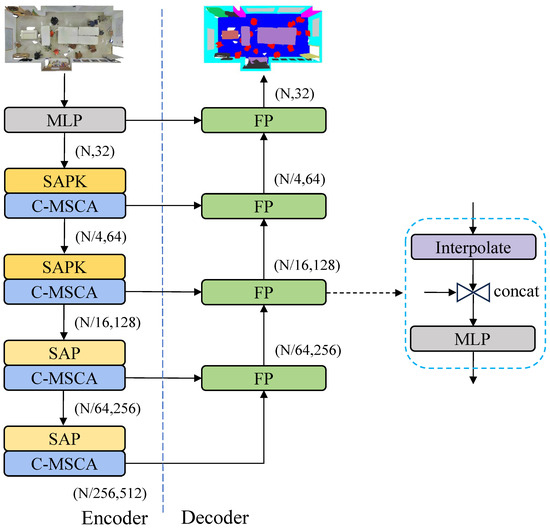
Figure 1.
The architecture of PKA-Net.
3.2. Point Features Encoding
The Point Feature Encoding module (PFE) aims to encode the spatial geometry and color information of the point cloud to simultaneously learn geometric structures and color variations, thereby enhancing the model’s perception of local point cloud information. The architecture of PFE is shown in Figure 2. This module jointly encodes geometric features such as normal vectors and curvature extracted from the local neighborhood, along with the point cloud’s coordinate information, color information, and additional attributes, achieving a unified modeling of local geometric structures and color differences.
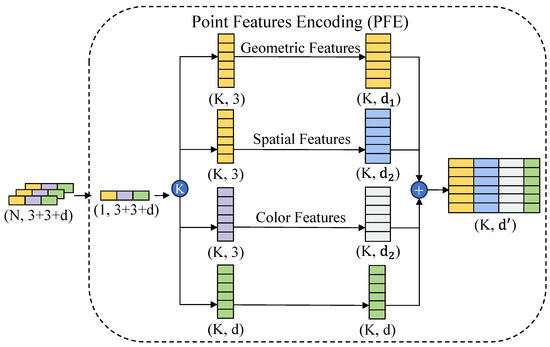
Figure 2.
The architecture of Point Feature Encoding module.
In the feature encoding process of PFE, we first analyze the local information at each point and construct the local neighborhood. For each center point in the point cloud, a spherical neighborhood is formed using Ball Query. Within this spherical region, the KNN algorithm is applied to select the k closest points, forming the neighborhood point set for the center point. If the number of points in the spherical region is less than k, the nearest point to the center is duplicated to fill the neighborhood set, ensuring the completeness of the feature representation. Let denote the current center point, and the neighborhood point set of point is defined as follows:
where r is the radius of the spherical neighborhood, and the neighborhood point is defined by computing the Euclidean distance.
Inspired by RandLA-Net, PFE concatenates the absolute coordinates of the center point and its neighboring points , the relative distances , and the Euclidean distances to form the spatial coordinate encoding, as shown in Equation (2):
Similar to the encoding of spatial coordinate information, PFE concatenates the color information of the center point , the color information of its neighboring points , the relative color difference , and the absolute color difference , forming the color information encoding as shown in Equation (3):
where is calculated by converting the RGB colors to grayscale values, its definition is
where , and represent the RGB values of a pixel in the original image. In the geometric feature encoding stage, PFE selects the normal vectors and curvatures of the neighboring points as core features to describe the local geometric properties of the point cloud. The normal vectors are obtained by performing Principal Component Analysis (PCA) on the local neighborhood points. Specifically, the centroid of the neighborhood points is first calculated, then the neighborhood points are centralized by subtracting the centroid coordinates, and a distance-weighted covariance matrix is constructed. The distance weights follow a Gaussian function, where points farther away receive smaller weights. The eigenvector corresponding to the smallest eigenvalue of the covariance matrix is taken as the normal vector. The curvature is computed from the eigenvalues of the covariance matrix. A smaller smallest eigenvalue indicates a flatter local surface, while a larger one implies higher curvature. The definition of the curvature feature is
where , , and are the eigenvalues of the covariance matrix, satisfying . is the smallest eigenvalue, representing the variation of neighborhood points along the normal vector direction.
Finally, PFE concatenates the normal vectors and curvature into the geometric feature encoding, which is then concatenated with the spatial coordinate encoding, color encoding, and additional information to form the final feature representation.
3.3. Improvement of Set Abstraction
To enhance the model’s ability to represent complex geometric structures, this paper proposes an SAPK module, which followed the classical SA layer in Point++. The module fully utilizes the learnable spline function in KAN to effectively capture complex nonlinear relationships by dynamically fitting the local geometric patterns of the point cloud.
KAN is a novel neural network architecture, as shown in Figure 3. Compared to traditional MLPs with fixed activation functions, KAN’s spline functions can adaptively adjust local feature mappings, offering greater flexibility and expressive power during the modeling process.
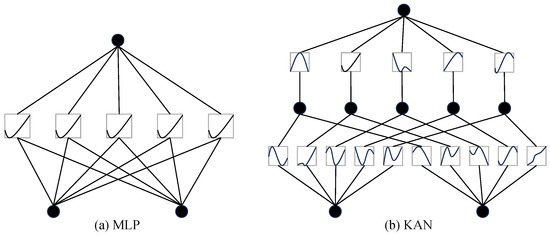
Figure 3.
The structural comparison of MLP and KAN.
The structure of the SAPK module is illustrated in Figure 4. Specifically, the point cloud is first divided into multiple local regions by farthest point sampling and spherical neighborhood grouping. Within each region, the PFE module is directly applied to encode geometric, spatial, and color information, enabling comprehensive capture of local point cloud features.
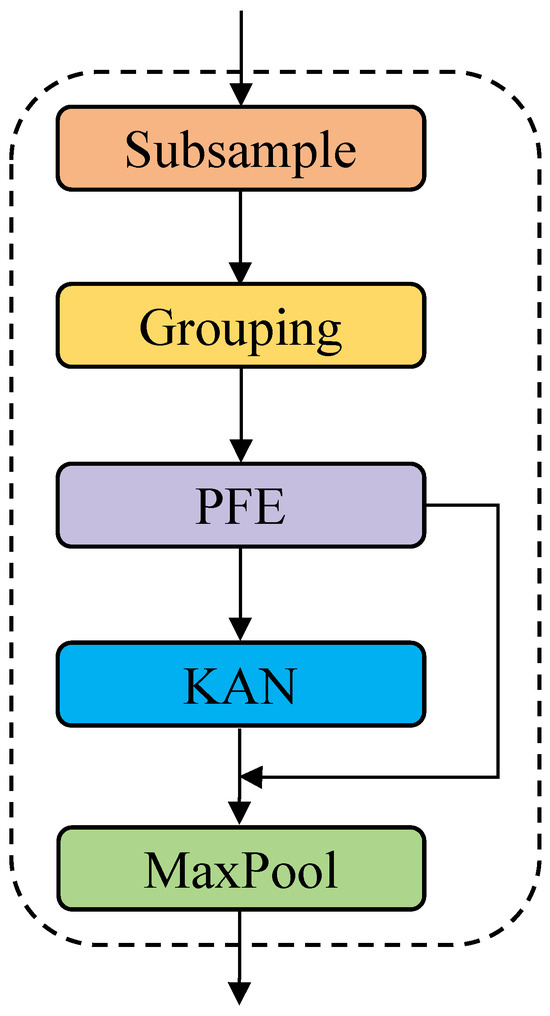
Figure 4.
The architecture of SAPK.
In the feature extraction stage, SAPK replaces traditional MLPs with KAN modules, which dynamically capture geometric patterns within local regions through learnable spline functions, enabling efficient and accurate feature extraction. In addition, a residual structure is employed to fuse the original grouped input with the local features extracted by the KAN module. This design effectively mitigates potential gradient vanishing issues in deep networks and enhances the stability of feature propagation and overall performance. Finally, max pooling is applied to aggregate the most significant features within each local region.
3.4. C-MSCA Mechanism
Local features extracted from point clouds may contain redundant information or details that are irrelevant to the task, which can adversely affect the accuracy and robustness of point cloud segmentation. To address this issue, this paper proposes a dual-attention module named C-MSCA, which integrates both channel attention and spatial attention. By incorporating the MSCA mechanism, the C-MSCA module enhances the model’s ability to focus on task-relevant features more effectively. As shown in Figure 5, the C-MSCA module dynamically adjusts channel and spatial weights, thereby improving segmentation accuracy and robustness.
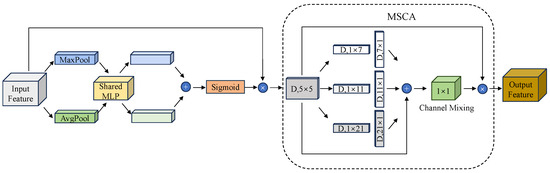
Figure 5.
The architecture of C-MSCA.
The channel attention mechanism learns inter-channel dependencies to highlight important features and suppress irrelevant ones. Specifically, global average pooling and global max pooling are applied to the input feature map to generate two feature descriptors, which are then passed through a shared MLP. The outputs are summed and normalized using the Sigmoid function to produce the channel attention weights , as shown in Equation (6):
where , represent feature representations generated by performing global average pooling and global max pooling operations on the input feature matrix, respectively. Finally, the channel attention weights are multiplied with the original features in a channel-wise manner to obtain the enhanced feature representation , as given in Equation (7):
where is the original feature matrix. For spatial attention, we introduced the MSCA module. It computes spatial attention maps independently for each channel using multi-scale strip convolutions, which effectively capture both local and global spatial information. Compared to traditional pooling operations, strip convolutions better preserve fine-grained details while being more computationally efficient.
MSCA first applies a standard convolution to extract initial features, followed by multiple strip convolution branches of different scales to model multi-scale context. Compared to traditional convolution, strip convolution reduces computational complexity from to . By replacing the structure with a combination of and operations, strip convolution can effectively model large-scale spatial relationships while reducing the computational load. Each convolutional branch operates independently to capture spatial information at specific scales. Through these branches, both local details and global contextual information can be efficiently captured. The outputs of these branches are then fused using a convolution to generate the spatial attention weights , as defined in (8):
where DWConv denotes deep convolution, and denotes the i-th convolution branch. Finally, the spatial attention weights are applied to the enhanced feature representation via element-wise multiplication to obtain the final enhanced feature representation, as shown in (9):
4. Experiments and Discussion
4.1. Dataset
S3DIS [31] is a large-scale 3D indoor scene dataset created by researchers at Stanford University. The dataset covers 11 types of indoor environments, comprising a total of 6 large areas, as shown in Figure 6. Each area contains multiple rooms, with a total of 271 rooms. All rooms are annotated with detailed semantic labels, covering 13 categories including ceiling, floor, wall, beam, column, window, door, table, chair, sofa, bookshelf, board, and clutter. Each point in the dataset is associated not only with its 3D coordinates but also with RGB color information and a semantic label from the 13 categories.
Figure 6.
Sample images of the S3DIS Dataset.
4.2. Evaluation Metrics
The performance evaluation of point cloud semantic segmentation tasks typically uses the following three metrics: Overall Accuracy (OA), Mean Accuracy (mAcc), and Mean Intersection over Union (mIoU).
OA is the ratio of correctly predicted samples to the total number of samples, reflecting the overall classification accuracy. Although it is simple to calculate, OA may overlook poor performance on minority classes in imbalanced datasets. Therefore, it should be used together with other metrics like mIoU for a comprehensive evaluation. The formula for calculating OA is shown in Equation (10):
mAcc is an important metric for evaluating multi-class classification tasks. It calculates the accuracy for each class individually and then averages these accuracies across all classes. The formulas for accuracy and mAcc are shown in Equations (11) and (12):
mIoU is a key metric for evaluating semantic segmentation models. It calculates the IoU for each class, which is the ratio of the intersection to the union between predicted results and ground truth, then averages these values across all classes. A higher mIoU indicates better segmentation performance across categories. The formulas for IoU and mIoU are shown in Equations (13) and (14):
4.3. Experiment Settings
The experimental environment configuration for this study is shown in Table 1. For training parameter settings, the batch size is set to 16. The optimizer used is AdamW, with a momentum parameter of 0.9 and a weight decay of 0.0001. The initial learning rate is set to 0.01, and a cosine decay learning rate schedule is applied to dynamically adjust the learning rate. The maximum number of training epochs is set to 100 to ensure sufficient model convergence. The baseline model is the PointNet++.

Table 1.
Experimental settings.
4.4. Results and Analysis
To better evaluate the performance of the proposed algorithm, this paper selects several mainstream networks [17,18,19,21,22,24] in the field of semantic segmentation. All experiments are conducted under the same environment settings on the S3DIS Area 5 dataset. The experimental results are shown in Table 2.

Table 2.
The comparative results with classic models on the S3DIS dataset.
The experimental results indicate that PKA-Net outperforms other comparative networks, mainly due to its effective extraction of neighborhood features. Compared to the PointNet++, PKA-Net achieves significant improvements across multiple evaluation metrics: OA increases by 2.1%, mAcc increases by 2.9%, and mIoU increases by 4%.
Table 3 presents the quantitative segmentation results of PKA-Net on the 13 categories of the S3DIS dataset, compared with various state-of-the-art methods. The experimental results show that our proposed model outperforms the PointNet++ method in all categories, with particularly significant improvements in the categories of windows, tables, sofas, and clutter, where the IoU increases by 6.3%, 9.7%, 6.7%, and 7.9%.

Table 3.
The comparative results of IoU for each class on the S3DIS dataset.
Compared with existing advanced networks, PKA-Net shows better performance in most categories. For example, in the chair category, PKA-Net achieves a 6.2% higher IoU than the high-performing PointNeXt-B, thanks to the local feature encoding module that enhances the recognition of key regions. However, the recognition accuracy for columns and beams is low across all methods, mainly due to the high imbalance in the S3DIS dataset, with fewer points and less distinguishable features in these categories. Nevertheless, PKA-Net still achieves the highest accuracy for columns. For the floor category, PKA-Net performs slightly worse than PointWeb, as PointWeb models point relationships through a point relation network, effectively integrating long-range context and improving global structure recovery. These comparative and quantitative results validate the effectiveness of the proposed PKA-Net.
To better evaluate the generalization performance of PKA-Net, we conducted generalization experiments on the ScanNet dataset. ScanNet comprises 1513 real-world indoor scenes, covering 20 categories of indoor objects and scene types. The experimental results of PKA-Net and other classical methods [18,19,20,22,32] on the ScanNet dataset are shown in Table 4. Experimental results demonstrate that compared to existing classical methods, PKA-Net achieves superior segmentation performance on the ScanNet dataset, with a mIoU of 69. 0%. This outcome fully validates the robust generalization capability of the network.

Table 4.
The comparative results with classic models on the ScanNet dataset.
Table 5 presents the segmentation results of PKA-Net and several classical methods across 20 categories on the ScanNet dataset. Experimental results indicate that different networks exhibit varying performance across categories, while PKA-Net demonstrates high segmentation accuracy in most categories. For categories such as walls, floors, beds, chairs, sofas, sinks, toilets, counters, and windows, PKA-Net achieves segmentation results that are superior to or comparable with other methods, primarily due to its strengths in local feature extraction. However, for categories such as tables, doors, bathtubs and shower curtains, KPConv or PointASNL demonstrated certain advantages. For instance, KPConv achieved IoU values of 84.7% and 80.5% on bathtubs and shower curtains, respectively. This may be attributed to the relatively regular geometric shapes of these categories, which are better suited for processing by convolutional-based feature extraction methods. Overall, PKA-Net demonstrates strong expressive capabilities in complex scenes and detail-rich categories, fully validating its effectiveness and generalization in point cloud semantic segmentation tasks.

Table 5.
The comparative results of IoU for each class on the ScanNet dataset.
4.5. Ablation Study
To verify the performance gains brought by the three improvements, a series of ablation experiments were designed. The experimental results are shown in Table 6.

Table 6.
The ablation results on S3DIS dataset.
The experimental results indicate that adding the PFE module improves the network’s ability to model geometric, spatial, and color features of point clouds, increasing OA by 1.1%, mAcc by 1.6%, and mIoU by 2.1%. Using only the SAPK module in the first two layers raises OA by 1.3%, mAcc by 2.1%, and mIoU by 2.5%, indicating that SAPK with KAN better fits complex feature distributions, and its residual structure enhances feature propagation and representation. After adding the C-MSCA mechanism, OA increases by 0.8%, mAcc by 1.2%, and mIoU by 1.1%, which demonstrates that C-MSCA focuses on key features, suppresses irrelevant information, and improves segmentation accuracy. Finally, when SAPK and C-MSCA are combined as PKA-Net, the best performance is achieved. C-MSCA dynamically focuses on critical features extracted by SAPK, strengthening their representation and jointly enhancing network performance and robustness.
In addition, we show representative visualization results in Figure 7 to more intuitively demonstrate the outstanding performance of PKA-Net. Each column corresponds to the same room, displaying from top to bottom: the original point cloud, the manually annotated reference semantic segmentation, the segmentation result of the PointNet++, and the segmentation result of PKA-Net.
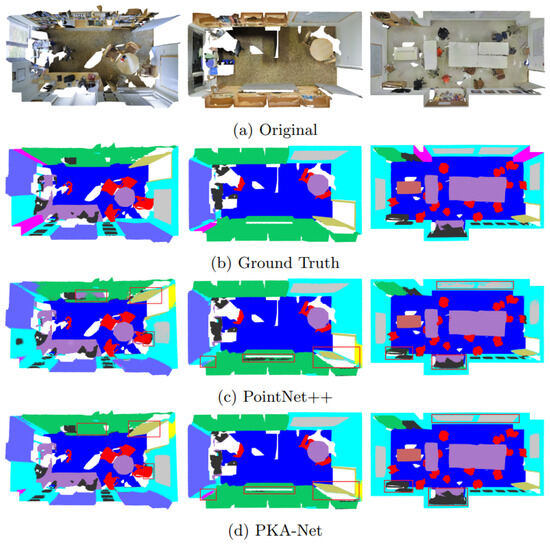
Figure 7.
The visual comparison results on S3DIS Dataset.
The visualization results clearly demonstrate that PKA-Net outperforms PointNet++ in segmentation accuracy. In the first scene, the baseline model exhibits noticeable misclassifications: the central region of the bookshelf is incorrectly labeled as a window, the outer edges of the door appear incomplete and blurry, and several scattered misclassified points can be observed around the chair area. In contrast, our proposed model demonstrates a stronger semantic understanding, accurately identifying the bookshelf, improving door segmentation, and almost completely eliminating errors on the chairs, thereby highlighting its superior ability to capture local details. In the second scenario, PointNet++ performs poorly in column segmentation, failing to capture the complete geometric structure. Although PKA-Net still faces some challenges, its segmentation results are noticeably better. Nevertheless, PKA-Net occasionally misclassifies certain points as clutter on bookshelves, and the boundary segmentation among bookshelves, walls, and windows remains somewhat unclear. In the third, more complex scene, cluttered objects with irregular shapes and overlapping boundaries make accurate geometric capture difficult. The baseline frequently confuses boards with walls due to spatial overlap, whereas PKA-Net achieves more precise differentiation. These improvements can be attributed to the local feature encoding module, which effectively models geometric, spatial, and color relationships among points, thereby enhancing the perception of irregular objects. Furthermore, the improved hierarchical feature extraction with dynamic nonlinear mapping enables better modeling of complex shapes.
5. Conclusions
As an important branch of point cloud technology, point cloud semantic segmentation for indoor scenes has many practical applications. To address the insufficient feature extraction capability, loss of local details, and limited feature expression capabilities in complex scenes, we proposed the PKA-Net based on neighborhood feature enhancement, which followed the classic encoder–decoder architecture of PointNet++. In the network, we designed a local feature encoding module, PFE, to encode geometric, spatial, and color information of local regions, obtaining richer and more discriminative feature representations. Additionally, we proposed an effective hierarchical feature extraction module, SAPK. It introduces a novel neural network, KAN, which utilizes its learnable spline functions to effectively fit the complex geometric structures of point clouds. Through a residual structure, it optimizes feature propagation, enhancing the network’s ability to capture fine-grained geometric details. We also designed a C-MSCA module based on MSCA, enabling the network to focus more on task-relevant key features while effectively suppressing irrelevant information, thereby improving the network’s overall segmentation performance. Extensive experimental results on the S3DIS dataset indicate that PKA-Net achieves improvements in overall classification accuracy, average classification accuracy, and average intersection-over-union ratio. Compared to the baseline model, it achieves a 2.1% increase in OA, a 2.9% increase in mAcc, and a 4% increase in mIoU, and it outperforms other mainstream point cloud segmentation algorithms.
In future research, we will integrate 2D images with 3D point cloud data, leveraging the rich texture and color information in 2D images to optimize point cloud segmentation results, thereby advancing the application of point cloud segmentation technology in more complex scenarios. Additionally, while the proposed modules enhance segmentation performance, they increase the overall number of parameters and computational overhead. We aim to reduce the number of parameters in the model to make it more efficient.
Author Contributions
Conceptualization, S.H. and X.L.; methodology, S.H. and X.L.; software, S.H.; validation, S.H. and X.L.; formal analysis, S.H.; investigation, S.H.; resources, X.L.; data curation, S.H. and X.L.; writing—original draft preparation, S.H.; writing—review and editing, S.H. and X.L.; visualization, S.H.; supervision, X.L.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Acknowledgments
We sincerely express our gratitude to all those who have supported our research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gong, R.; Sun, R.; Chen, W. Series Active Disturbance Rejection Autopilot Design for Hyper Velocity Projectiles. IEEE Access 2020, 8, 149447–149455. [Google Scholar] [CrossRef]
- Zhou, W.; Berrio, J.S.; Worrall, S.; Nebot, E. Automated Evaluation of Semantic Segmentation Robustness for Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1951–1963. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Li, J.; Tian, M.; Dai, W.; Zhong, R. Automated Reconstruction of Building LoDs from Airborne LiDAR Point Clouds Using an Improved Morphological Scale Space. Remote Sens. 2017, 9, 14. [Google Scholar] [CrossRef]
- Chew, A.W.Z.; Ji, A.; Zhang, L. Large-scale 3D point-cloud semantic segmentation of urban and rural scenes using data volume decomposition coupled with pipeline parallelism. Autom. Constr. 2022, 133, 103995–104013. [Google Scholar] [CrossRef]
- Merkle, D.; Reiterer, A. Overview of 3D point cloud annotation and segmentation techniques for smart city applications. In Remote Sensing Technologies and Applications in Urban Environments VII; International Society for Optics and Photonics: Bellingham, WA, USA, 2022; pp. 10–18. [Google Scholar]
- Zhang, J.; Zhao, X.; Chen, Z.; Lu, Z. A review of deep learning-based semantic segmentation for point cloud. IEEE Access 2019, 7, 179118–179133. [Google Scholar] [CrossRef]
- Papon, J.; Abramov, A.; Schoeler, M.; Worgotter, F. Voxel Cloud Connectivity Segmentation—Supervoxels for Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 25–27 June 2013; pp. 2027–2034. [Google Scholar]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L. 3D segmentation of forest structure using a mean-shift based algorithm. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, 26–29 September 2010; pp. 1413–1416. [Google Scholar]
- Sampath, A.; Shan, J. Segmentation and Reconstruction of Polyhedral Building Roofs From Aerial Lidar Point Clouds. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1554–1567. [Google Scholar] [CrossRef]
- Biosca, J.M.; Lerma, J.L. Unsupervised robust planar segmentation of terrestrial laser scanner point clouds based on fuzzy clustering methods. ISPRS J. Photogramm. Remote Sens. 2008, 63, 84–98. [Google Scholar] [CrossRef]
- Zhang, X.; Li, G.; Xiong, Y.; He, F. 3D Mesh Segmentation Using Mean-Shifted Curvature. In Proceedings of the 5th International Conference on Geometric Modeling and Processing, Hangzhou, China, 23–25 April 2008; pp. 465–474. [Google Scholar]
- Rabbani, T.; Van Den Heuvel, F.; Vosselmann, G. Segmentation of Point Clouds Using Smoothness Constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Christoph Stein, S.; Schoeler, M.; Papon, J.; Worgotter, F. Object Partitioning using Local Convexity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 304–311. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.H.; Lu, C.Z.; Hou, Q.; Liu, Z.; Cheng, M.M.; Hu, S.M. SegNeXt: Rethinking Convolutional Attention Design for Semantic Segmentation. Adv. Neural Inf. Process. Syst. 2022, 35, 1140–1156. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution On X-Transformed Points. Adv. Neural Inf. Process. Syst. 2018, 31, 828–838. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Zhao, H.; Jiang, L.; Fu, C.W.; Jia, J. PointWeb: Enhancing Local Neighborhood Features for Point Cloud Processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 July 2019; pp. 5565–5573. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11108–11117. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Virtual, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. PointNeXt: Revisiting PointNet++ with Improved Training and Scaling Strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Wu, X.; Jiang, L.; Wang, P.S.; Liu, Z.; Liu, X.; Qiao, Y.; Ouyang, W.; He, T.; Zhao, H. Point Transformer V3: Simpler Faster Stronger. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–18 June 2024; pp. 4840–4851. [Google Scholar]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. Pct: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Meng, G.; Lu, J.; Xiang, S.; Pan, C. Densepoint: Learning densely contextual representation for efficient point cloud processing. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5239–5248. [Google Scholar]
- Xu, M.; Ding, R.; Zhao, H.; Qi, X. Paconv: Position adaptive convolution with dynamic kernel assembling on point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 3173–3182. [Google Scholar]
- Zhang, C.; Wan, H.; Shen, X.; Wu, Z. PVT: Point-voxel transformer for point cloud learning. Int. J. Intell. Syst. 2022, 37, 11985–12008. [Google Scholar] [CrossRef]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-bert: Pre-training 3D point cloud transformers with masked point modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 19313–19322. [Google Scholar]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Yan, X.; Zheng, C.; Li, Z.; Wang, S.; Cui, S. PointASNL: Robust Point Clouds Processing Using Nonlocal Neural Networks With Adaptive Sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 5589–5598. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).