Dual Intelligent Prediction of Strength and Energy Absorption Performance of Rubber-Modified Concrete via Machine Learning and Metaheuristic Optimization Algorithms
Abstract
1. Introduction
2. Materials
3. Methodologies
3.1. ANN Model
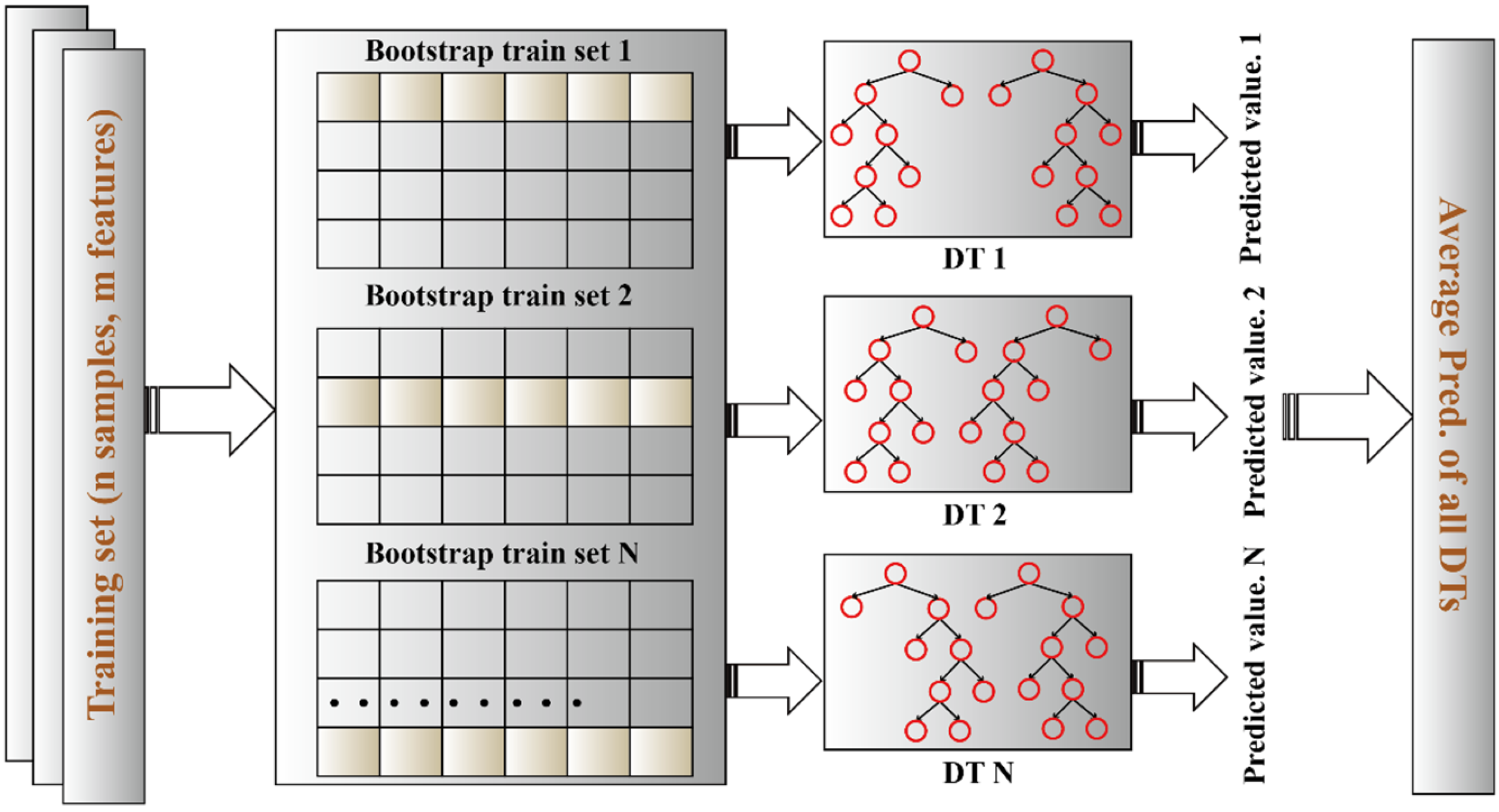
3.2. RF Model
3.3. Metaheuristic Optimization Algorithms
3.3.1. Dream Optimization Algorithm
- (1)
- Initialization phase
- (2)
- Exploration phase
- (3)
- Exploitation phase
3.3.2. Football Optimization Algorithm
- (1)
- Initialization phase
- (2)
- Exploration phase
- (3)
- Exploitation phase
3.3.3. Hiking Optimization Algorithm
- (1)
- Initialization phase
- (2)
- Exploration phase
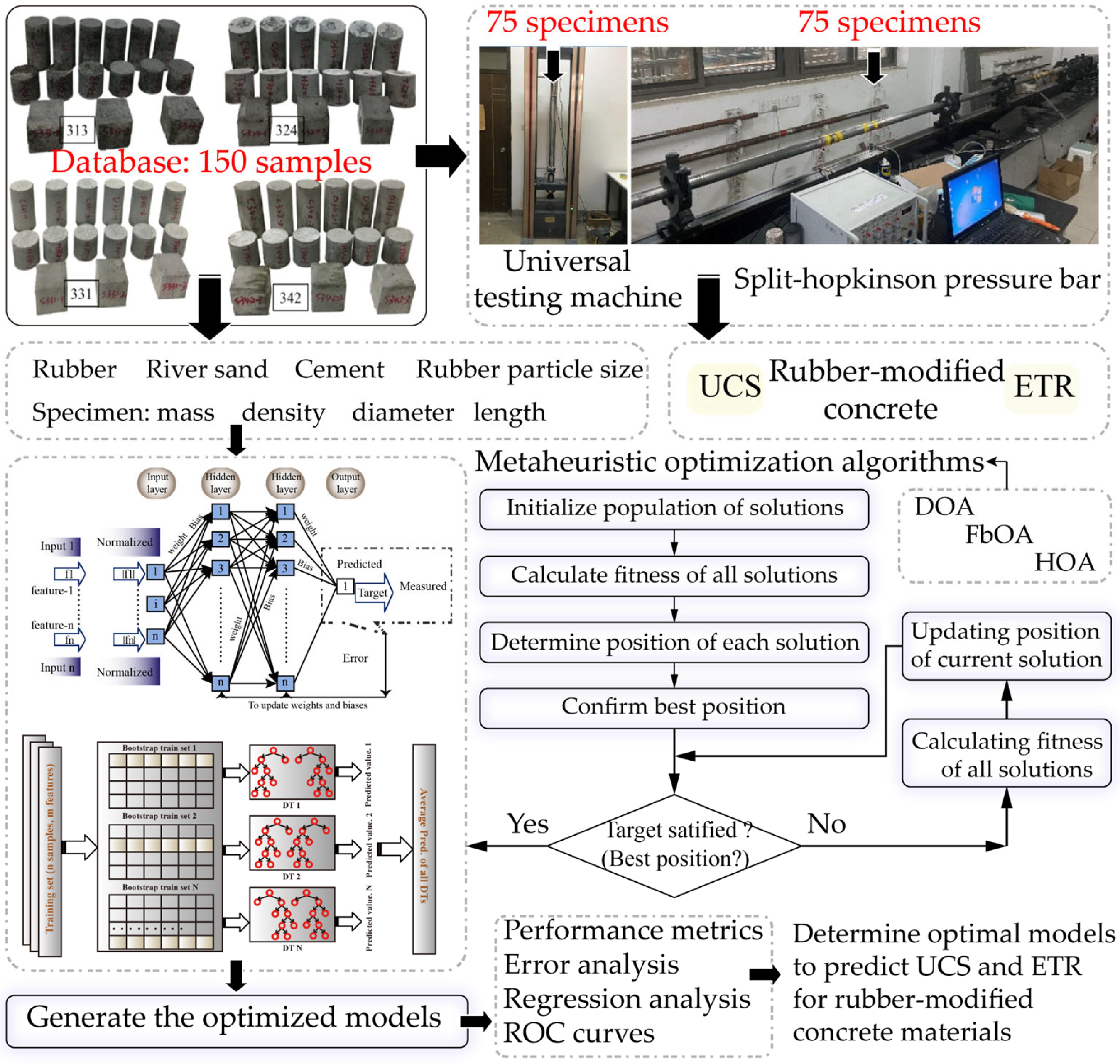
4. Development of Prediction Models
- (a)
- Database generation: As mentioned in Section 2, 75 samples were used to predict the UCS of rubber-modified concrete material, and another 75 samples were used to predict ETR. Based on similar studies [18,19], the ratio of training set to test set was set equal to 80%:20%. To avoid performance anomalies in the model caused by differences in feature scales, all features are normalized to the range of −1 to 1.
- (b)
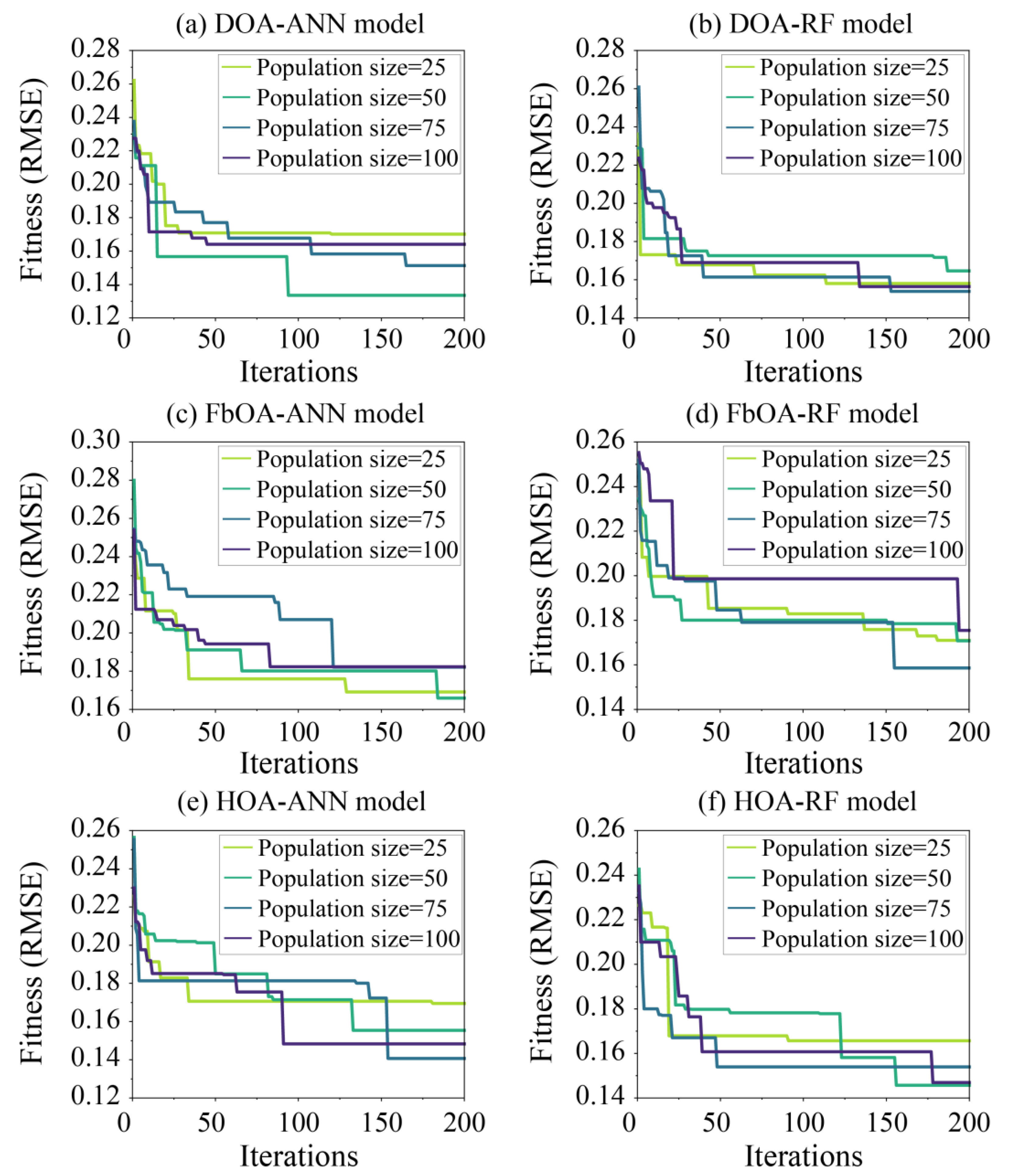
- Model construction: In this work, DOA, FbOA, and HOA were combined with ANN and RF models to generate different prediction models, i.e., DOA-ANN, DOA-RF, FbOA-ANN, FbOA-RF, HOA-ANN, and HOA-RF. For the ANN mode, the range of Nh and Nn are [1, 3] and [1, 10], respectively. For the RF model, the ranges of Nt and Md are [1, 100] and [1, 10], respectively. On the other hand, for optimization algorithms, the settings of population size and iteration count significantly affect optimization performance. A larger population size helps increase the coverage of the search space and improves the probability of finding the global optimal solution, but it also raises computational cost [32]. In contrast, a smaller population size tends to localize the search process, making it more likely to converge to a local optimum. On the other hand, the number of iterations is positively correlated with the probability of finding the optimal solution. However, excessive iterations may lead to overfitting, thus increasing computation time. In the preliminary experiments, increasing the population size beyond 100 (e.g., to 125 or 150) did not necessarily improve the model’s predictive accuracy or fitness value (R2 or RMSE), while computational time increased significantly (more than double in some cases) [18]. Therefore, the population sizes were set as 25, 50, 75, and 100 to search for the optimal solutions during 200 iterations. Moreover, the hybrid fitness function established by statistical index and cross-validation was used to evaluate optimization performance. In this paper, the root mean square error (RMSE) without absolute values was adopted as a statistical metric, and five-fold cross-validation was employed to prevent overfitting. The definition of the developed fitness function is expressed using Equation (12).
- (c)
- Performance evaluation: To quantitatively assess model performance in predicting the UCS and ETR of the novel aseismic concrete, four statistical indicators were employed. R2, commonly referred to as the goodness-of-fit index, quantifies the proportion of variance in the observed data that is explained by the model predictions. An R2 value approaching unity indicates nearly perfect agreement between estimated and actual values. The variance accounted for (VAF) is another metric used to evaluate how effectively the model captures the variability present in the target dataset. RMSE provides a robust measure of prediction accuracy by penalizing large deviations between actual and predicted values. Complementarily, the mean absolute error (MAE) offers an intuitive understanding of average prediction error without emphasizing outliers. Together, these metrics provide a comprehensive framework for evaluating the regression capability of different predictive approaches [32,33,34,35,36,37,38,39,40].
5. Results and Discussion
5.1. Model Optimization
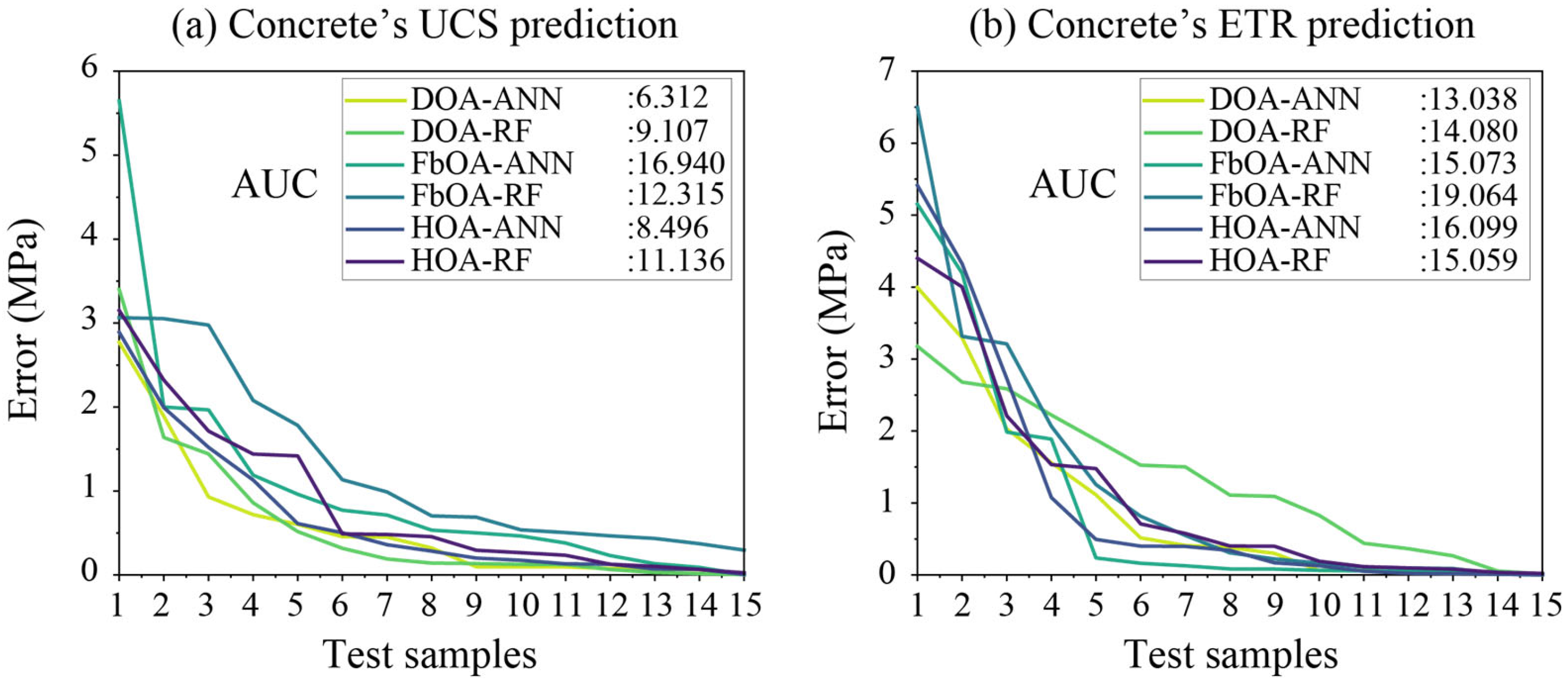
5.2. Model Evaluation
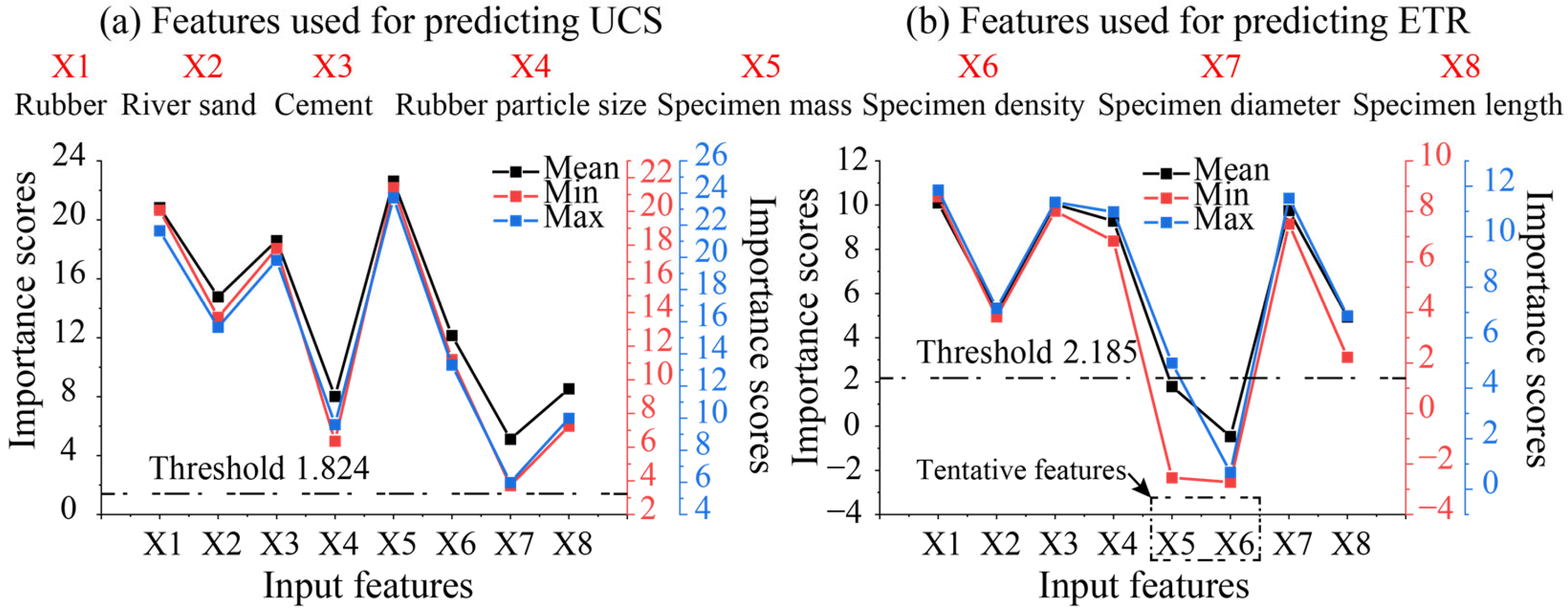
5.3. Sensitivity Analysis
5.4. Prediction Visual
6. Conclusions
- (1)
- The DOA-ANN model achieved the best predictive capability for both UCS and ETR, surpassing other optimized ANN, RF, and benchmark ML models. These results indicate the ANN’s superior ability to capture nonlinear and coupled relationships between input variables and target properties compared with RF and other ML models. The model effectively balances generalization and precision, confirming its robustness in predicting both the material’s strength and energy absorption performance.
- (2)
- SHAP analysis revealed cement and specimen mass as dominant predictors for ETR and UCS, respectively, while rubber content significantly influenced both properties, demonstrating a trade-off between strength and energy absorption.
- (3)
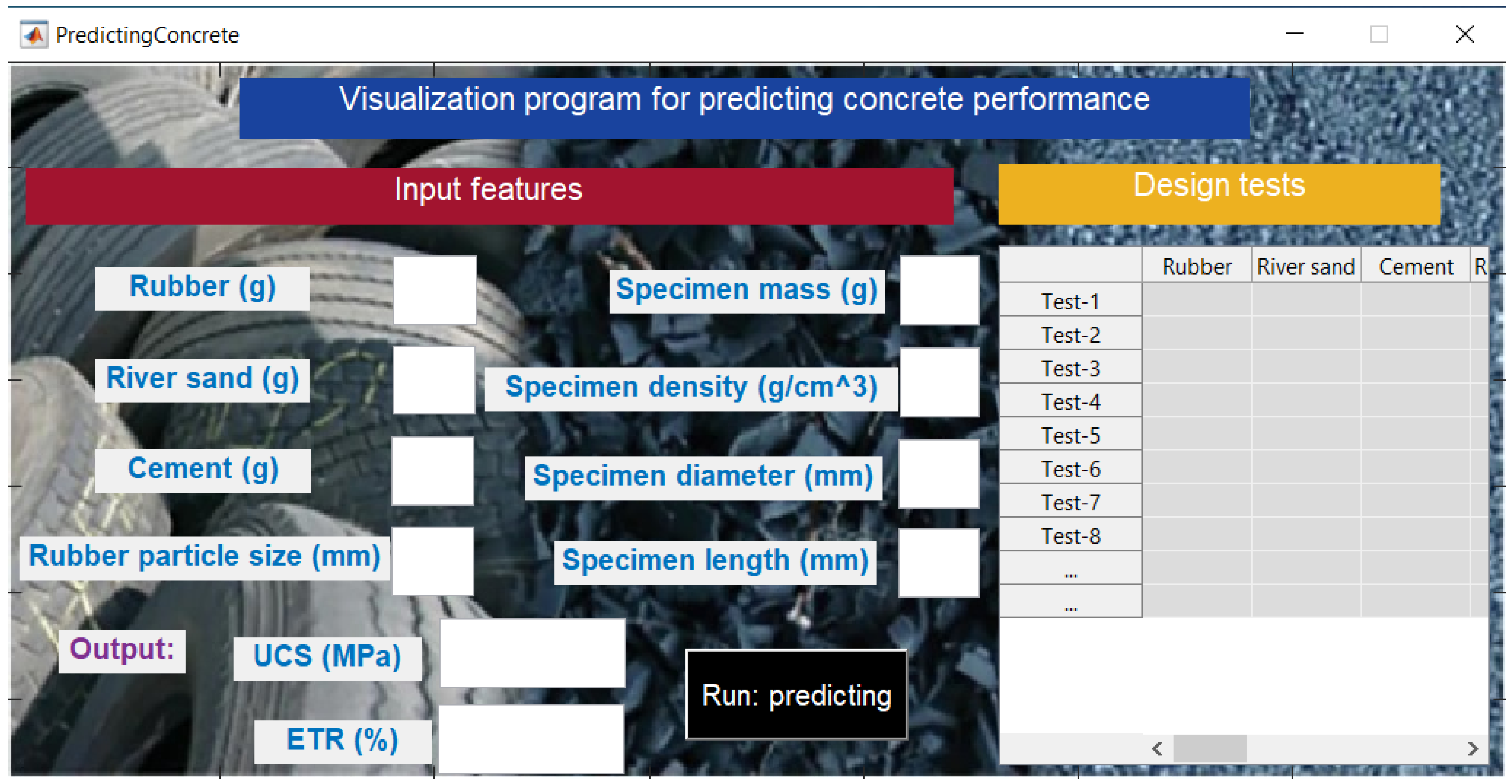
- To enhance practical applicability, a visualization interface embedding the optimized DOA-ANN model was developed. This tool allows engineers to input mix parameters, instantly predict mechanical performance, and iteratively adjust designs in real time. The system bridges model computation with practical engineering design, significantly improving design efficiency and facilitating performance-driven mix proportioning for aseismic and sustainable concrete structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roy, N.; Sarkar, R. A review of seismic damage of mountain tunnels and probable failure mechanisms. Geotech. Geol. Eng. 2017, 35, 1–28. [Google Scholar] [CrossRef]
- Bird, J.F.; Bommer, J.J. Earthquake losses due to ground failure. Eng. Geol. 2004, 75, 147–179. [Google Scholar] [CrossRef]
- Lai, J.; He, S.; Qiu, J.; Chen, J.; Wang, L.; Wang, K.; Wang, J. Characteristics of seismic disasters and aseismic measures of tunnels in Wenchuan earthquake. Environ. Earth Sci. 2017, 76, 94. [Google Scholar] [CrossRef]
- Saad, A.G.; Sakr, M.A.; Khalifa, T.M.; Darwish, E.A. Structural performance of concrete reinforced with crumb rubber: A review of current research. Iran. J. Sci. Technol. Trans. Civ. Eng. 2025, 49, 3211–3254. [Google Scholar] [CrossRef]
- Mei, X.C.; Ding, C.D.; Zhang, J.M.; Li, C.Q.; Cui, Z.; Sheng, Q.; Chen, J. Application of optimized random forest regressors in predicting maximum principal stress of aseismic tunnel lining. J. Cent. South Univ. 2024, 31, 3900–3913. [Google Scholar] [CrossRef]
- Mei, X.; Li, J.; Zhang, J.; Cui, Z.; Zhou, J.; Li, C. Predicting energy absorption characteristic of rubber concrete materials. Constr. Build. Mater. 2025, 465, 140248. [Google Scholar] [CrossRef]
- Sathiparan, N.; Jeyananthan, P. Predicting compressive strength of cement-stabilized earth blocks using machine learning models incorporating cement content, ultrasonic pulse velocity, and electrical resistivity. Nondestruct. Test. Eval. 2024, 39, 1045–1069. [Google Scholar] [CrossRef]
- Khan, M.M.; Iqbal, M.A. Dynamic increase factor of concrete subjected to compression and tension by using split Hopkinson pressure bar setup: Overview. Mech. Solids 2023, 58, 2115–2131. [Google Scholar] [CrossRef]
- Hussain, A.; Sakhaei, A.H.; Shafiee, M. Machine learning-based constitutive modelling for material non-linearity: A review. Mech. Adv. Mater. Struct. 2024, 1–19. [Google Scholar] [CrossRef]
- Hong, Y.; Hou, B.; Jiang, H.; Zhang, J. Machine learning and artificial neural network accelerated computational discoveries in materials science. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1450. [Google Scholar] [CrossRef]
- Garg, A.; Zheng, W.; Raman, R.; Li, L. Machine Learning in Functionally Graded Materials and Nano FGMs: A Comprehensive Review of Predictive Modeling for Mechanical Behavior. Arch. Comput. Methods Eng. 2025, 1–43. [Google Scholar] [CrossRef]
- Khawaja, L.; Asif, U.; Onyelowe, K.; Al Asmari, A.F.; Khan, D.; Javed, M.F.; Alabduljabbar, H. Development of machine learning models for forecasting the strength of resilient modulus of subgrade soil: Genetic and artificial neural network approaches. Sci. Rep. 2024, 14, 18244. [Google Scholar] [CrossRef] [PubMed]
- Atici, U. Prediction of the strength of mineral admixture concrete using multivariable regression analysis and an artificial neural network. Expert Syst. Appl. 2011, 38, 9609–9618. [Google Scholar] [CrossRef]
- Kostić, S.; Vasović, D. Prediction model for compressive strength of basic concrete mixture using artificial neural networks. Neural Comput. Appl. 2015, 26, 1005–1024. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H.; Song, C.; Wang, Z. Predicting compressive strength of manufactured-sand concrete using conventional and metaheuristic-tuned artificial neural network. Measurement 2022, 194, 110993. [Google Scholar] [CrossRef]
- Dadashi, F.; Naderpour, H.; Mirrashid, M. Mechanical Property Prediction in Silica Fume and Crumb Rubber–Modified Concrete: Soft Computing and Experimental Approach. Pract. Period. Struct. Des. Constr. 2024, 29, 04024049. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Y.; Sun, J.; Tang, Y.; Wu, D.; Jiang, Z.; Wang, J.; Wang, X. Prediction of thermo-mechanical properties of rubber-modified recycled aggregate concrete. Constr. Build. Mater. 2022, 318, 125970. [Google Scholar] [CrossRef]
- Mei, X.; Li, C.; Sheng, Q.; Cui, Z.; Zhou, J.; Dias, D. Development of a hybrid artificial intelligence model to predict the uniaxial compressive strength of a new aseismic layer made of rubber-sand concrete. Mech. Adv. Mater. Struct. 2023, 30, 2185–2202. [Google Scholar] [CrossRef]
- Mei, X.; Cui, Z.; Sheng, Q.; Zhou, J.; Li, C. Application of the improved POA-RF model in predicting the strength and energy absorption property of a novel aseismic rubber-concrete material. Materials 2023, 16, 1286. [Google Scholar] [CrossRef]
- Nematzadeh, S.; Kiani, F.; Torkamanian-Afshar, M.; Aydin, N. Tuning hyperparameters of machine learning algorithms and deep neural networks using metaheuristics: A bioinformatics study on biomedical and biological cases. Comput. Biol. Chem. 2022, 97, 107619. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D.; Akay, R. A comprehensive survey on optimizing deep learning models by metaheuristics. Artif. Intell. Rev. 2022, 55, 829–894. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Optimizing convolutional neural network hyperparameters by enhanced swarm intelligence metaheuristics. Algorithms 2020, 13, 67. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Umar, A.M.; Linus, O.U.; Arshad, H.; Kazaure, A.A.; Gana, U.; Kiru, M.U. Comprehensive review of artificial neural network applications to pattern recognition. IEEE Access 2019, 7, 158820–158846. [Google Scholar] [CrossRef]
- Badini, S.; Regondi, S.; Pugliese, R. Unleashing the power of artificial intelligence in materials design. Materials 2023, 16, 5927. [Google Scholar] [CrossRef]
- Ng, W.L.; Goh, G.L.; Goh, G.D.; Ten, J.S.J.; Yeong, W.Y. Progress and opportunities for machine learning in materials and processes of additive manufacturing. Adv. Mater. 2024, 36, 2310006. [Google Scholar] [CrossRef]
- Salman, H.A.; Kalakech, A.; Steiti, A. Random forest algorithm overview. Babylon. J. Mach. Learn. 2024, 2024, 69–79. [Google Scholar] [CrossRef]
- Halabaku, E.; Bytyçi, E. Overfitting in Machine Learning: A Comparative Analysis of Decision Trees and Random Forests. Intell. Autom. Soft Comput. 2024, 39, 987–1006. [Google Scholar] [CrossRef]
- Lang, Y.; Gao, Y. Dream Optimization Algorithm (DOA): A novel metaheuristic optimization algorithm inspired by human dreams and its applications to real-world engineering problems. Comput. Methods Appl. Mech. Eng. 2025, 436, 117718. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Rizk, F.H.; Zaki, A.M.; Mohamed, M.E.; Ibrahim, A.; Abdelhamid, A.A.; Khodadadi, N.; Almetwally, E.M.; Eid, M.M. Football optimization algorithm (FbOA): A novel metaheuristic inspired by team strategy dynamics. J. Artif. Intell. Metaheuristics 2024, 8, 21–38. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Ahmad, W.; Ahmad, A.; Ostrowski, K.A.; Aslam, F.; Joyklad, P.; Zajdel, P. Application of advanced machine learning approaches to predict the compressive strength of concrete containing supplementary cementitious materials. Materials 2021, 14, 5762. [Google Scholar] [CrossRef]
- Huynh, A.T.; Nguyen, Q.D.; Xuan, Q.L.; Magee, B.; Chung, T.; Tran, K.T.; Nguyen, K.T. A machine learning-assisted numerical predictor for compressive strength of geopolymer concrete based on experimental data and sensitivity analysis. Appl. Sci. 2020, 10, 7726. [Google Scholar] [CrossRef]
- Dai, L.; Zhao, X.; Pan, Y.; Luo, H.; Gao, Y.; Wang, A.; Ding, L.; Li, P. Microseismic criterion for dynamic risk assessment and warning of roadway rockburst induced by coal mine seismicity. Eng. Geol. 2025, 357, 108324. [Google Scholar] [CrossRef]
- Du, K.; Yang, C.; Su, R.; Tao, M.; Wang, S. Failure properties of cubic granite, marble, and sandstone specimens under true triaxial stress. Int. J. Rock Mech. Min. Sci. 2020, 130, 104309. [Google Scholar] [CrossRef]
- Shang, M.; Li, H.; Ahmad, A.; Ahmad, W.; Ostrowski, K.A.; Aslam, F.; Joyklad, P.; Majka, T.M.; Majka, T.M. Predicting the mechanical properties of RCA-based concrete using supervised machine learning algorithms. Materials 2022, 15, 647. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Zhao, J.; Ostrowski, K.A.; Javed, M.F.; Ahmad, A.; Khan, M.I.; Aslam, F.; Kinasz, R.; Kinasz, R. Prediction of compressive strength of fly-ash-based concrete using ensemble and non-ensemble supervised machine-learning approaches. Appl. Sci. 2021, 12, 361. [Google Scholar] [CrossRef]
- Vargas, J.F.; Oviedo, A.I.; Ortega, N.A.; Orozco, E.; Gómez, A.; Londoño, J.M. Machine-learning-based predictive models for compressive strength, flexural strength, and slump of concrete. Appl. Sci. 2024, 14, 4426. [Google Scholar] [CrossRef]
- Al-Kahtani, M.S.M.; Zhu, H.; Ibrahim, Y.E.; Haruna, S.I.; Al-Qahtani, S.S.M. Study on the mechanical properties of polyurethane-cement mortar containing nanosilica: RSM and machine learning approach. Appl. Sci. 2023, 13, 13348. [Google Scholar] [CrossRef]
- Jing, W.; Yin, S.; Li, J. Using a machine learning method with novel optimization algorithms in estimating compressive strength rates in ultra-high performance concrete. Int. J. Knowl. -Based Intell. Eng. Syst. 2025, 29, 171–187. [Google Scholar] [CrossRef]




| Variables | Sign | Unit | Min | Max | Mean | Median | St. D |
|---|---|---|---|---|---|---|---|
| Rubber | Ru | g | 0.00 | 106.50 | 60.68 | 65.55 | 25.65 |
| River sand | RS | g | 0.00 | 249.00 | 96.52 | 74.90 | 61.58 |
| Cement | Ce | g | 54.00 | 235.80 | 128.25 | 129.75 | 47.18 |
| Rubber particle size | RPS | mm | 0.16 | 1.50 | 0.55 | 0.38 | 0.49 |
| Specimen mass | M | g | 169.50 | 415.00 | 285.46 | 279.50 | 67.95 |
| Specimen density | r | g/cm3 | 0.93 | 50.59 | 13.83 | 1.64 | 21.32 |
| Specimen diameter | D | mm | 49.17 | 50.59 | 50.11 | 50.15 | 0.29 |
| Specimen length | L | mm | 95.57 | 102.67 | 98.97 | 99.15 | 1.26 |
| Uniaxial compressive strength | UCS | MPa | 0.50 | 31.10 | 6.43 | 4.39 | 6.54 |
| Variables | Sign | Unit | Min | Max | Mean | Median | St. D |
|---|---|---|---|---|---|---|---|
| Rubber | Ru | g | 0.00 | 48.06 | 28.88 | 30.66 | 12.19 |
| River sand | RS | g | 0.00 | 120.90 | 45.95 | 36.78 | 29.24 |
| Cement | Ce | g | 24.36 | 109.14 | 61.02 | 60.40 | 22.31 |
| Rubber particle size | RPS | mm | 0.16 | 1.50 | 0.55 | 0.38 | 0.49 |
| Specimen mass | M | g | 78.70 | 201.50 | 135.86 | 137.90 | 32.22 |
| Specimen density | r | g/cm3 | 0.89 | 2.15 | 1.45 | 1.46 | 0.33 |
| Specimen diameter | D | mm | 48.47 | 49.98 | 49.44 | 49.41 | 0.31 |
| Specimen length | L | mm | 46.28 | 50.15 | 48.63 | 48.83 | 0.80 |
| Energy transmission rate | ETR | % | 0.00 | 36.43 | 1.89 | 0.13 | 5.59 |
| Population | Fitness (RMSE) | |||||
| UCS | ||||||
| DOA-ANN | DOA-RF | FbOA-ANN | FbOA-RF | HOA-ANN | HOA-RF | |
| 25 | 0.1701 | 0.1335 | 0.1513 | 0.1641 | 0.1701 | 0.1335 |
| 50 | 0.1580 | 0.1646 | 0.1539 | 0.1564 | 0.1580 | 0.1646 |
| 75 | 0.1692 | 0.1660 | 0.1822 | 0.1823 | 0.1692 | 0.1660 |
| 100 | 0.1710 | 0.1708 | 0.1586 | 0.1754 | 0.1710 | 0.1708 |
| Best hyperparameters combination | ||||||
| Nh | 2 | / | 2 | / | 1 | / |
| Nn | 4; 2 | / | 4; 3 | / | 5 | / |
| Nt | / | 58 | / | 49 | / | 52 |
| Md | / | 1 | / | 1 | / | 1 |
| Population | Fitness (RMSE) | |||||
| ETR | ||||||
| DOA-ANN | DOA-RF | FbOA-ANN | FbOA-RF | HOA-ANN | HOA-RF | |
| 25 | 0.1976 | 0.1834 | 0.1682 | 0.1701 | 0.1976 | 0.1834 |
| 50 | 0.2017 | 0.1807 | 0.1973 | 0.2081 | 0.2017 | 0.1807 |
| 75 | 0.2397 | 0.2441 | 0.2351 | 0.2550 | 0.2397 | 0.2441 |
| 100 | 0.3152 | 0.3052 | 0.3001 | 0.3070 | 0.3152 | 0.3052 |
| Best hyperparameters combination | ||||||
| Nh | 2 | / | 1 | / | 1 | / |
| Nn | 4; 2 | / | 6 | / | 4 | / |
| Nt | / | 44 | / | 37 | / | 49 |
| Md | / | 1 | / | 7 | / | 1 |
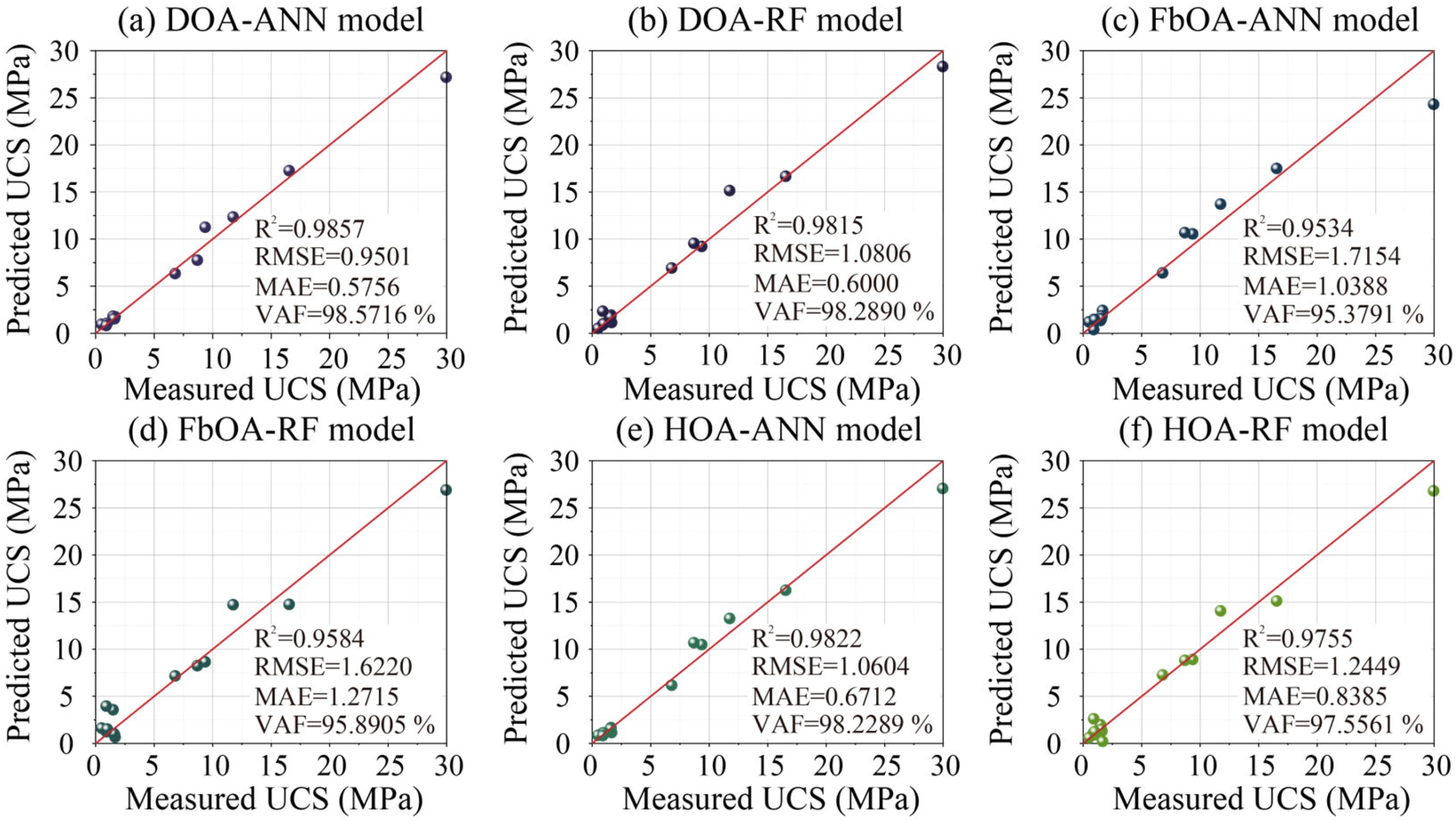
| Models | UCS prediction | |||
| R2 | RMSE | MAE | VAF (%) | |
| DOA-ANN | 0.9857 | 0.9501 | 0.5756 | 98.5716 |
| DOA-RF | 0.9815 | 1.0806 | 0.6000 | 98.2890 |
| FbOA-ANN | 0.9534 | 1.7154 | 1.0388 | 95.3791 |
| FbOA-RF | 0.9584 | 1.6220 | 1.2715 | 95.8905 |
| HOA-ANN | 0.9822 | 1.0604 | 0.6712 | 98.2289 |
| HOA-RF | 0.9755 | 1.2449 | 0.8385 | 97.5561 |
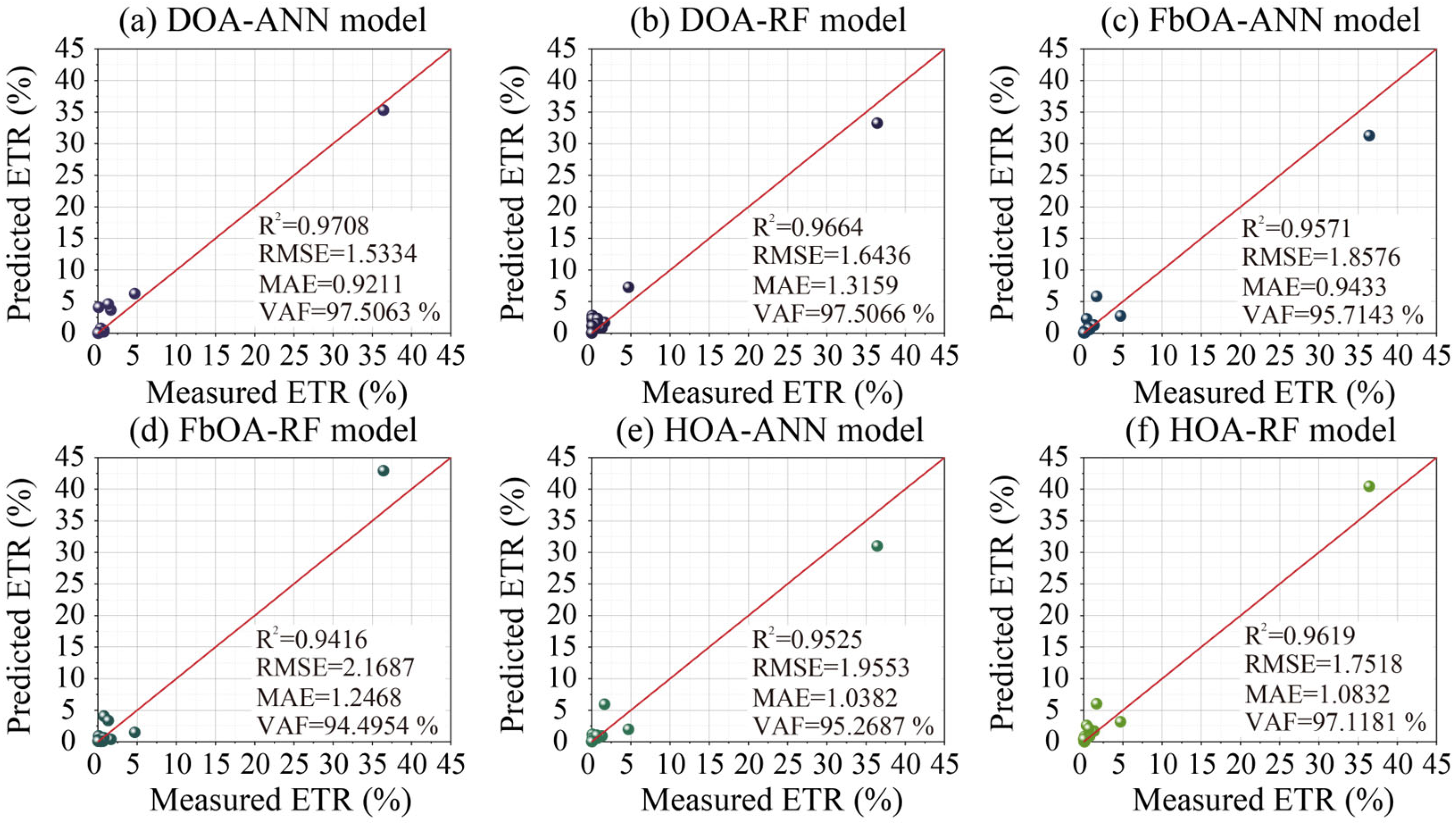
| Models | ETR prediction | |||
| R2 | RMSE | MAE | VAF (%) | |
| DOA-ANN | 0.9708 | 1.5334 | 0.9211 | 97.5063 |
| DOA-RF | 0.9664 | 1.6436 | 1.3159 | 97.5066 |
| FbOA-ANN | 0.9571 | 1.8576 | 0.9433 | 95.7143 |
| FbOA-RF | 0.9416 | 2.1687 | 1.2468 | 94.4954 |
| HOA-ANN | 0.9525 | 1.9553 | 1.0382 | 95.2687 |
| HOA-RF | 0.9619 | 1.7518 | 1.0832 | 97.1181 |
| Reference | Datasets | Target | Models | R2 |
|---|---|---|---|---|
| This paper | 75 samples | UCS | DOA-ANN | 0.9857 |
| UCS | HOA-ANN | 0.9822 | ||
| UCS | FbOA-RF | 0.9584 | ||
| Mei et al. [18] | 81 samples | UCS | PSO-BPNN | 0.8898 |
| UCS | FOA-BPNN | 0.9011 | ||
| UCS | LSO-BPNN | 0.9165 | ||
| UCS | SSA-BPNN | 0.8129 | ||
| Mei et al. [19] | 70 samples | UCS | POA-RF | 0.9663 |
| UCS | LHSPOA-RF | 0.9857 | ||
| UCS | CMPOA-RF | 0.9726 | ||
| This paper | 75 samples | ETR | DOA-ANN | 0.9708 |
| ETR | HOA-RF | 0.9619 | ||
| ETR | FbOA-ANN | 0.9571 | ||
| Mei et al. [6] | 80 samples | ETR | GOA-RF | 0.9342 |
| Mei et al. [19] | 70 samples | ETR | POA-RF | 0.8790 |
| ETR | LHSPOA-RF | 0.9065 | ||
| ETR | CMPOA-RF | 0.9047 |
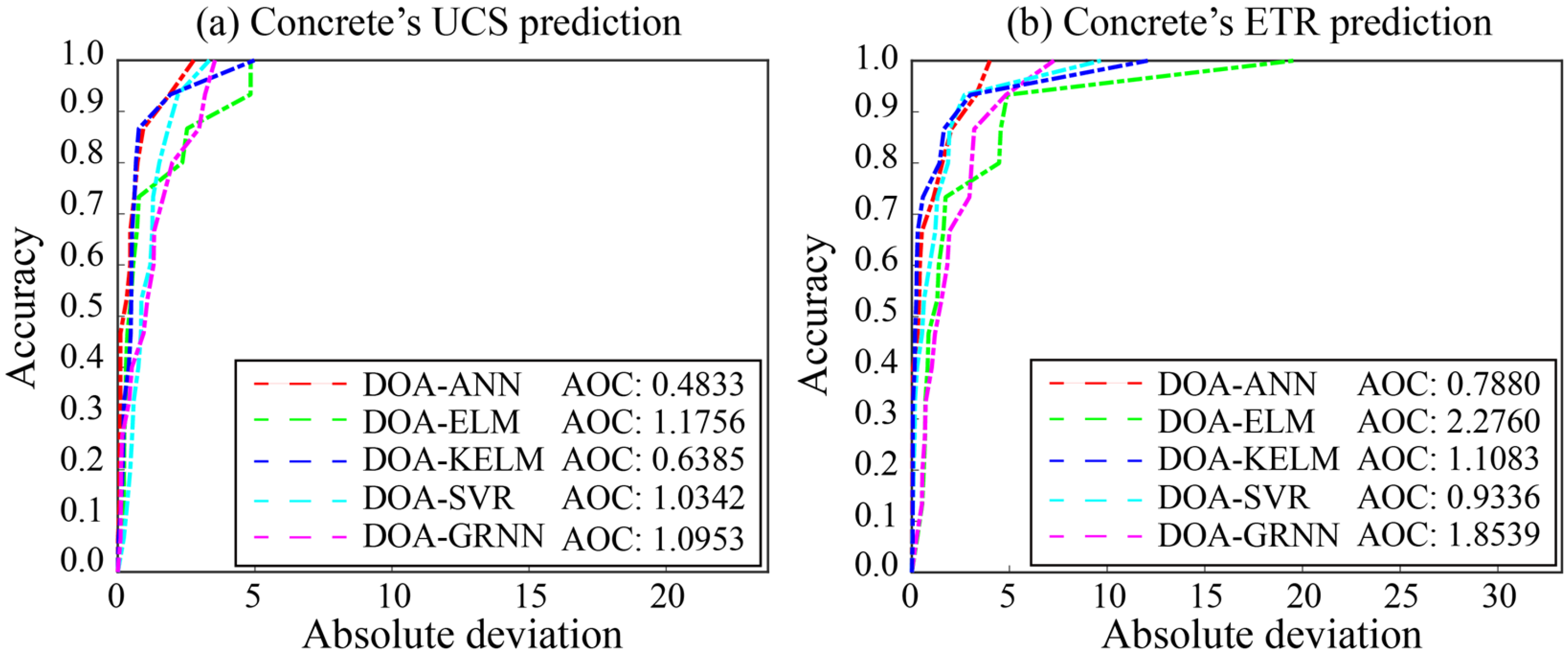
| Models DOA- | UCS prediction | Hyperparameter | |||
| Performance indices | |||||
| R2 | RMSE | MAE | VAF (%) | ||
| ELM | 0.9357 | 2.0160 | 1.2568 | 93.7914 | Nn = 110 |
| KELM | 0.9691 | 1.3972 | 1.1456 | 97.3872 | Rc = 142.3; k1 = 0.44 |
| SVR | 0.9671 | 1.4414 | 0.8045 | 96.7133 | Rc = 108.9; k2 = 0.26 |
| GRNN | 0.9534 | 1.7163 | 1.2937 | 96.3714 | Sf = 0.3 |
| Models DOA- | ETR prediction | ||||
| Performance indices | |||||
| R2 | RMSE | MAE | VAF (%) | ||
| ELM | 0.6205 | 5.5260 | 2.9269 | 62.1447 | Nn = 65 |
| KELM | 0.9024 | 2.8026 | 2.0965 | 91.6196 | Rc = 125.6; k1 = 0.56 |
| SVR | 0.9065 | 2.7428 | 1.4308 | 90.6531 | Rc = 174.8; k2 = 0.74 |
| GRNN | 0.8674 | 3.2667 | 1.3361 | 87.4631 | Sf = 0.2 |
| Variables | No. 1 | No. 2 |
|---|---|---|
| Rubber (g) | 22.2 | 7.3 |
| River sand (g) | 199.8 | 65.5 |
| Cement (g) | 148.0 | 109.1 |
| Rubber particle size (mm) | 0.2 | 0.2 |
| Specimen mass (g) | 370.0 | / |
| Specimen density (g/cm3) | 1.9 | / |
| Specimen diameter (mm) | 50.3 | 50.0 |
| Specimen length (mm) | 99.1 | 48.0 |
| UCS (MPa) | 16.1 | / |
| ETR (%) | / | 36.4 |
| Variables | No. 1 | No. 2 | ||||
|---|---|---|---|---|---|---|
| Rubber (g) | 18.9 | 15.0 | 10.0 | 15 | 25 | 35 |
| River sand (g) | 203.1 | 199.8 | 199.8 | 65.5 | 65.5 | 40 |
| Cement (g) | 148 | 155.2 | 160.2 | 101.4 | 91.4 | 106.9 |
| Rubber particle size (mm) | 0.2 | 0.2 | 0.15 | 0.2 | 0.2 | 0.2 |
| Specimen mass (g) | 370 | 370 | 370 | / | / | / |
| Specimen density (g/cm3) | 1.9 | 1.9 | 1.9 | / | / | / |
| Specimen diameter (mm) | 50.3 | 50.3 | 50.3 | 50 | 50 | 50 |
| Specimen length (mm) | 99.1 | 99.1 | 99.1 | 48 | 48 | 48 |
| UCS (MPa) | 18.4 | 21.8 | 24.7 | / | / | / |
| ETR (%) | / | / | / | 35.3 | 34.8 | 22.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wang, P.; Zhou, J.; Mei, X. Dual Intelligent Prediction of Strength and Energy Absorption Performance of Rubber-Modified Concrete via Machine Learning and Metaheuristic Optimization Algorithms. Appl. Sci. 2025, 15, 11680. https://doi.org/10.3390/app152111680
Li C, Wang P, Zhou J, Mei X. Dual Intelligent Prediction of Strength and Energy Absorption Performance of Rubber-Modified Concrete via Machine Learning and Metaheuristic Optimization Algorithms. Applied Sciences. 2025; 15(21):11680. https://doi.org/10.3390/app152111680
Chicago/Turabian StyleLi, Chuanqi, Pu Wang, Jian Zhou, and Xiancheng Mei. 2025. "Dual Intelligent Prediction of Strength and Energy Absorption Performance of Rubber-Modified Concrete via Machine Learning and Metaheuristic Optimization Algorithms" Applied Sciences 15, no. 21: 11680. https://doi.org/10.3390/app152111680
APA StyleLi, C., Wang, P., Zhou, J., & Mei, X. (2025). Dual Intelligent Prediction of Strength and Energy Absorption Performance of Rubber-Modified Concrete via Machine Learning and Metaheuristic Optimization Algorithms. Applied Sciences, 15(21), 11680. https://doi.org/10.3390/app152111680







