Advancing Machine Learning-Based Streamflow Prediction Through Event Greedy Selection, Asymmetric Loss Function, and Rainfall Forecasting Uncertainty
Abstract
1. Introduction
2. Hydrological Model
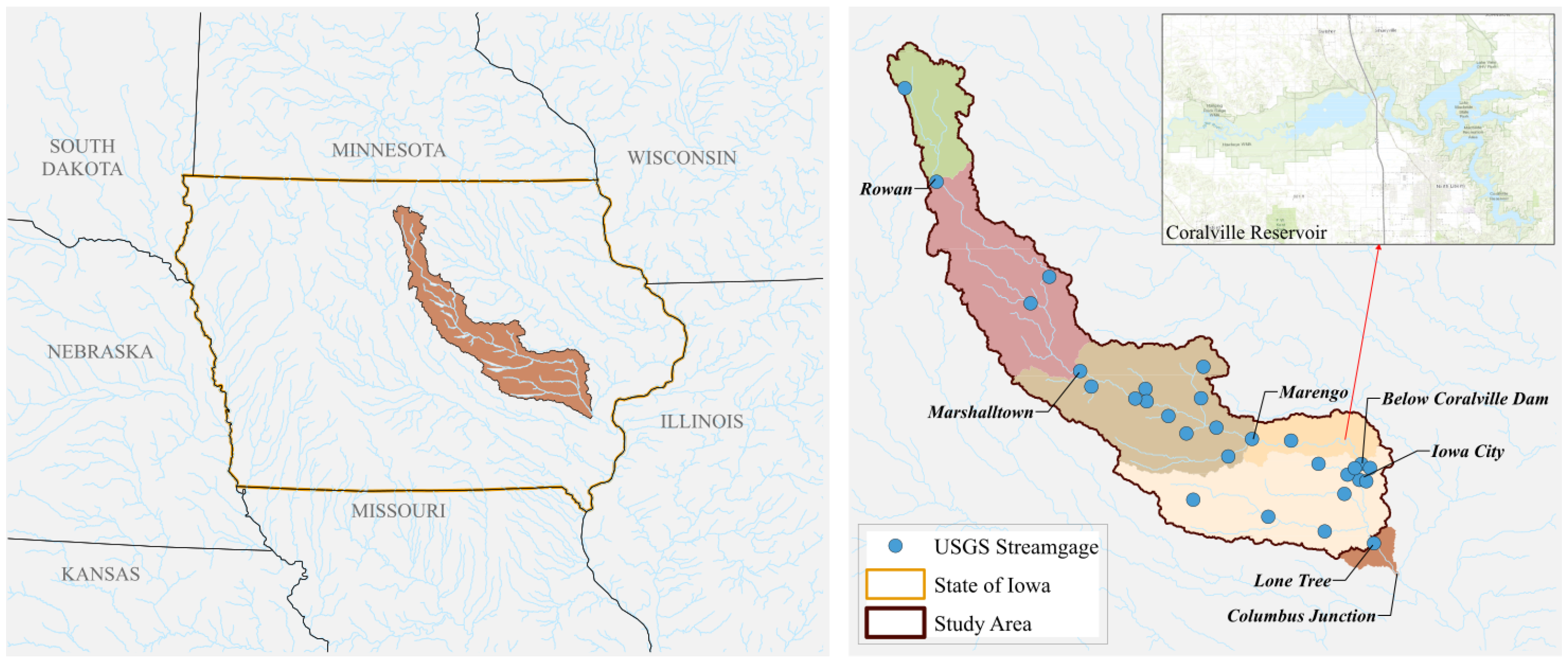
2.1. Iowa River Basin
2.2. Semi-Distributed HEC-HMS Hydrological Model
2.3. Model Calibration
3. Data Generation
3.1. Rainfall Event Generation
3.2. Greedy Event Selection
3.3. Data Generation Process
4. Streamflow Prediction
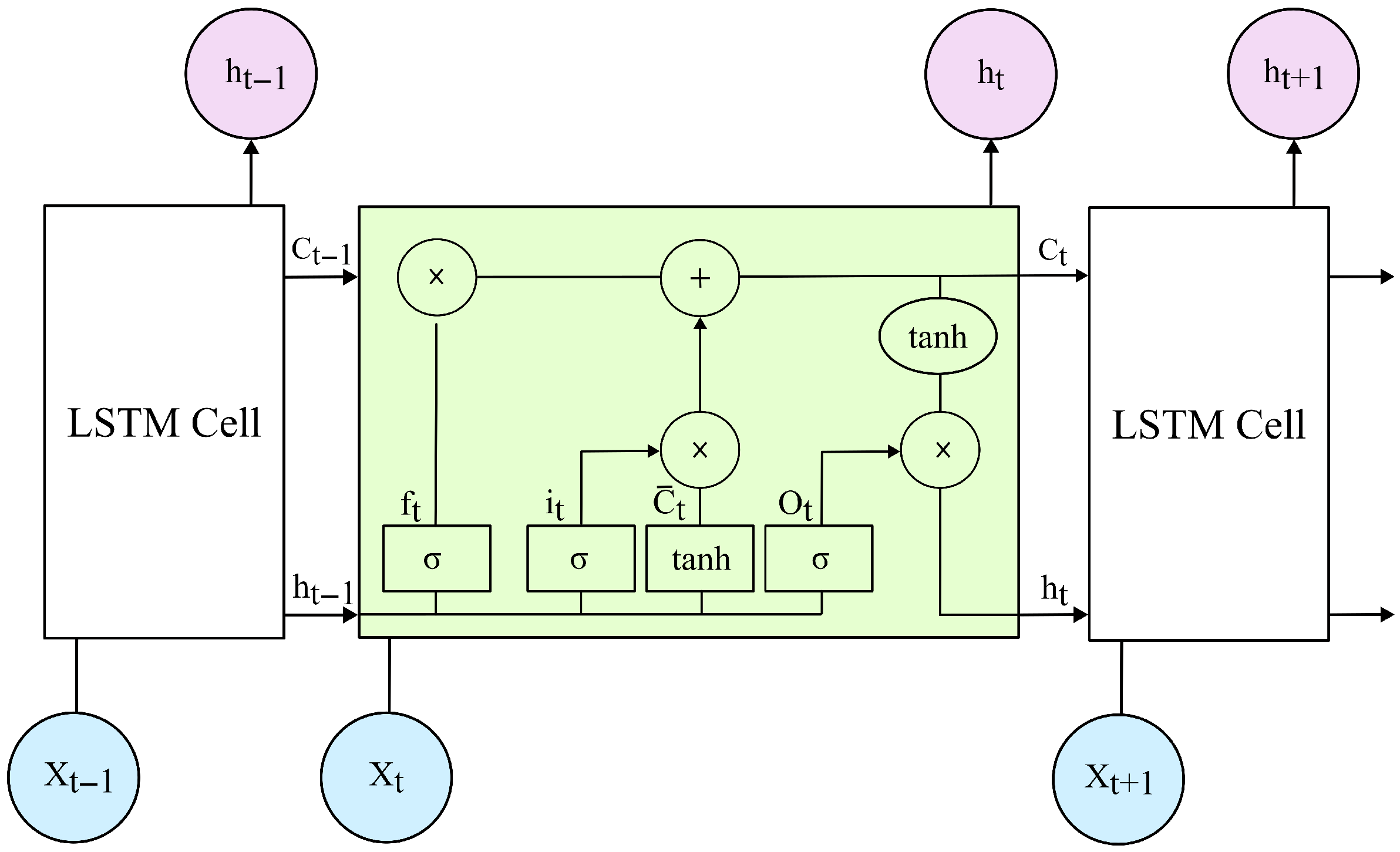
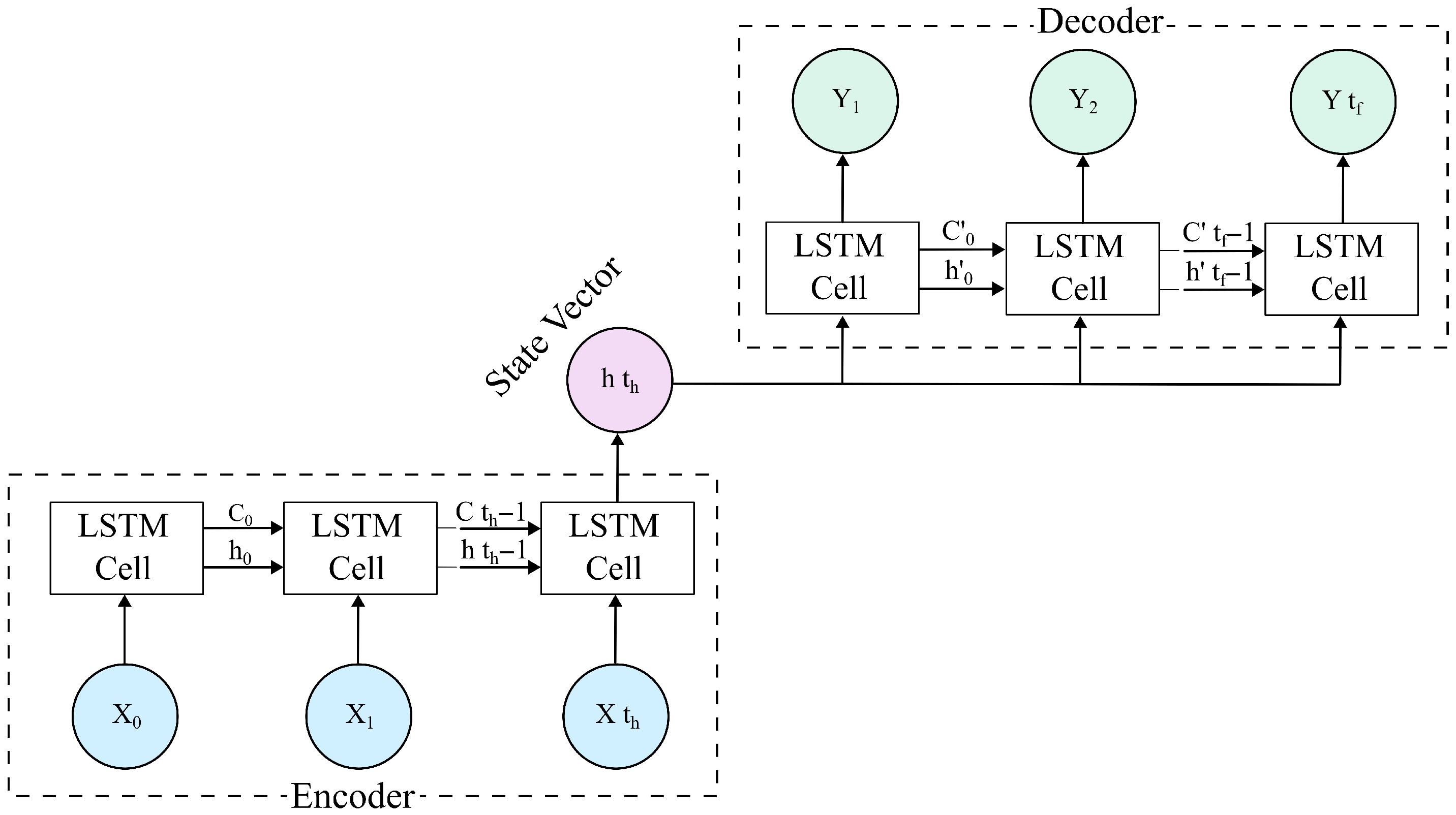
4.1. LSTM-Based Encoder–Decoder
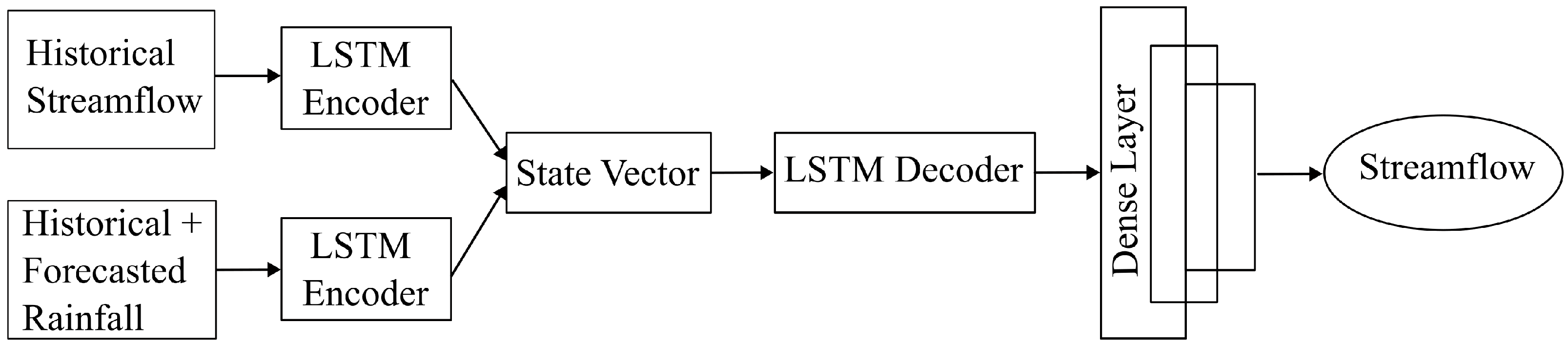
4.2. Model Design
4.3. Streamflow Prediction: Performance of Deterministic LSTMs
5. Streamflow Prediction with Emphasizing Peak Values
5.1. Proposed LSTMs to Capture Higher Streamflow Values
5.1.1. LSTM with a Pinball Loss Function
5.1.2. LSTM with an Asymmetric Peak Loss Function
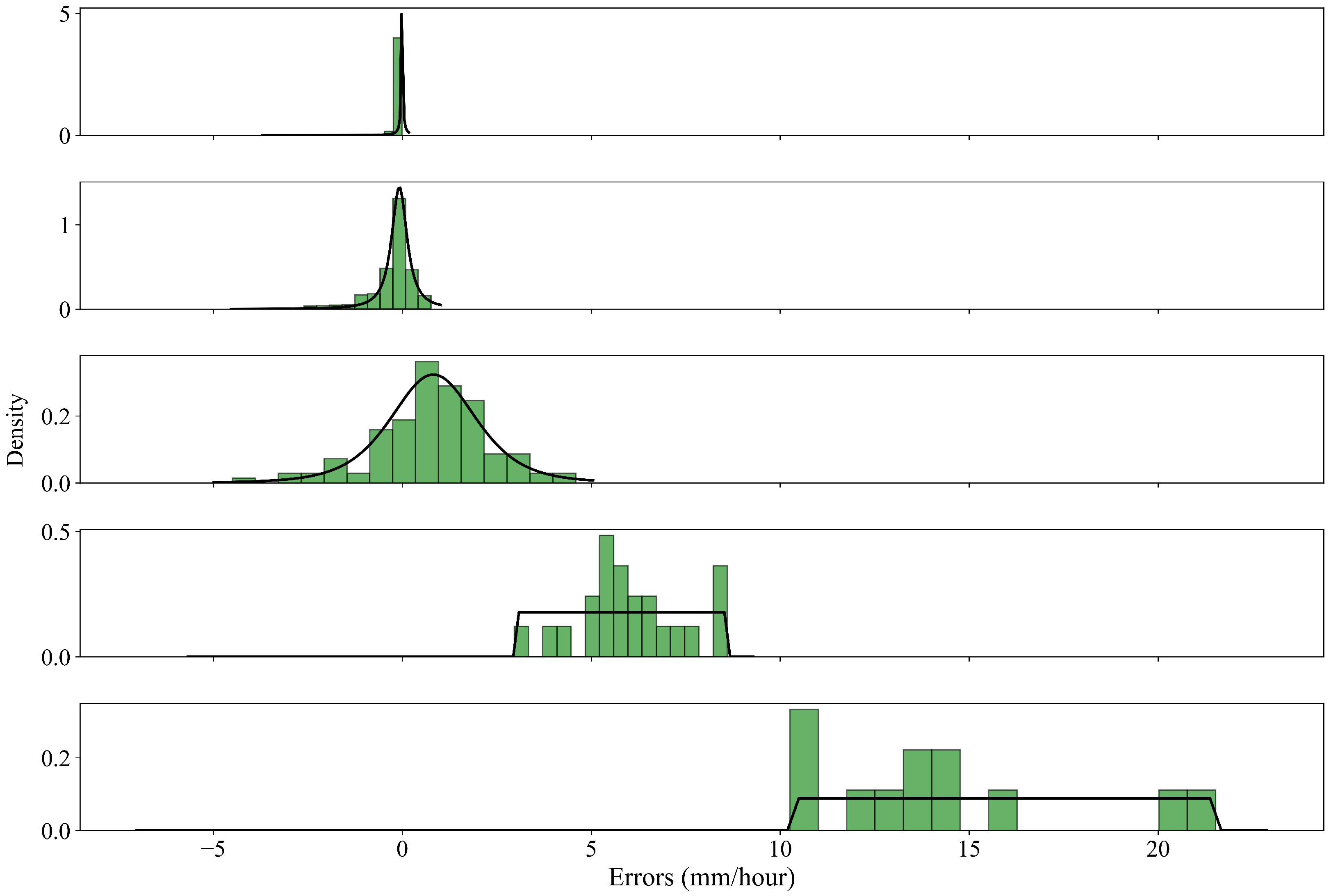
6. Streamflow Prediction with Rainfall Forecast Uncertainties
6.1. Rainfall Forecast Error Analysis
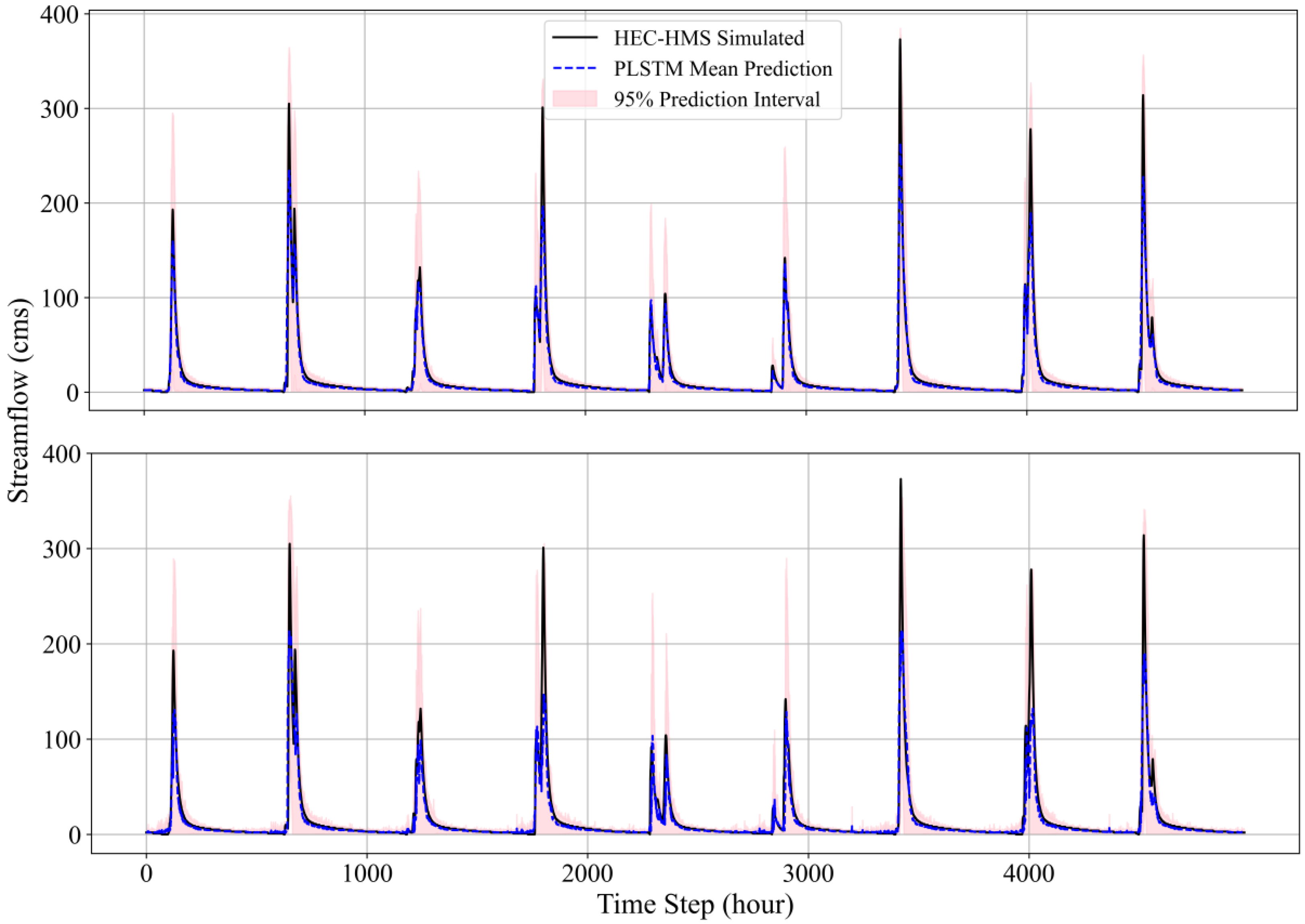
6.2. Probabilistic LSTM
6.3. Performance Evaluation Metrics
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine learning |
| SST | Stochastic storm transposition |
| LSTM | Long short-term memory |
| AI | Artificial intelligence |
| SVMs | Support vector machines |
| DL | Deep learning |
| RNNs | Recurrent neural networks |
| SWAT | Soil water assessment tool |
| AL | Active learning |
| PL | Pinball loss |
| PLSTM | Probabilistic long short-term memory |
| NLL | Negative log-likelihood |
| HMS | Hydrologic modeling system |
| DEM | Digital elevation model |
| SCS | Soil conservation service |
| CN | Curve number |
| NSE | Nash–Sutcliffe efficiency |
| RSR | Root mean squared error ratio |
| PBIAS | Percent bias |
| GS | Greedy sampling |
| AP | Asymmetric peak |
| CRPS | Continuous rank probability score |
| PICP | Prediction interval coverage probability |
| MPIW | Mean prediction interval width |
References
- Zhao, X.; Lv, H.; Wei, Y.; Lv, S.; Zhu, X. Streamflow forecasting via two types of predictive structure-based gated recurrent unit models. Water 2021, 13, 91. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Pham Van, C.; Nguyen, Q.-H.; Bui, Q.-T. Daily streamflow prediction based on the long short-term memory algorithm: A case study in the Vietnamese Mekong Delta. J. Water Clim. Change 2023, 14, 1247–1267. [Google Scholar] [CrossRef]
- Farfán-Durán, J.F.; Cea, L. Streamflow forecasting with deep learning models: A side-by-side comparison in Northwest Spain. Earth Sci. Inform. 2024, 17, 5289–5315. [Google Scholar] [CrossRef]
- Yifru, B.A.; Lim, K.J.; Lee, S. Enhancing streamflow prediction physically consistently using process-based modeling and domain knowledge: A review. Sustainability 2024, 16, 1376. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Khan, A.; Zhang, Y.; Kuang, X.; Liang, X.; Taccari, M.; Nuttall, J. Daily runoff forecasting by deep recursive neural network. J. Hydrol. 2021, 596, 126067. [Google Scholar] [CrossRef]
- Sarker, S.; Leta, O.T. Review of watershed hydrology and mathematical models. Eng 2025, 6, 129. [Google Scholar] [CrossRef]
- Paniconi, C.; Lauvernet, C.; Rivard, C. Exploration of coupled surface–subsurface hydrological model responses and challenges through catchment- and hillslope-scale examples. Front. Water 2025, 7, 1553578. [Google Scholar] [CrossRef]
- Xia, Q.; Fan, Y.; Zhang, H.; Jiang, C.; Wang, Y.; Hua, X.; Liu, D. A review on the development of two-way coupled atmospheric-hydrological models. Sustainability 2023, 15, 2803. [Google Scholar] [CrossRef]
- Jahanbani, H.; Ahmed, K.; Gu, B. Data-driven artificial intelligence-based streamflow forecasting: A review of methods, applications, and tools. JAWRA J. Am. Water Resour. Assoc. 2024, 60, 1095–1119. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; De Marinis, G. Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA’s storm water management model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Yan, J.; Jin, J.; Chen, F.; Yu, G.; Yin, H.; Wang, W. Urban flash flood forecast using support vector machine and numerical simulation. J. Hydroinform. 2018, 20, 221–231. [Google Scholar] [CrossRef]
- Shi, T.; Shide, K. A comparative analysis of LSTM, GRU, and Transformer models for construction cost prediction with multidimensional feature integration. J. Asian Archit. Build. Eng. 2025, 1–16. [Google Scholar] [CrossRef]
- Xiao, J.; Deng, T.; Bi, S. Comparative analysis of LSTM, GRU, and Transformer models for stock price prediction. In Proceedings of the International Conference on Digital Economy, Blockchain and Artificial Intelligence, Guangzhou, China, 23–25 August 2024; pp. 103–108. [Google Scholar]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, X.; Xu, Y.; Chen, H.; Gu, H.; Xie, J. AI-based techniques for multi-step streamflow forecasts: Application for multi-objective reservoir operation optimization and performance assessment. Hydrol. Earth Syst. Sci. 2021, 25, 5951–5979. [Google Scholar] [CrossRef]
- Yin, H.; Wang, F.; Zhang, X.; Zhang, Y.; Chen, J.; Xia, R.; Jin, J. Rainfall-runoff modeling using long short-term memory based step-sequence framework. J. Hydrol. 2022, 610, 127901. [Google Scholar] [CrossRef]
- Luppichini, M.; Barsanti, M.; Giannecchini, R.; Bini, M. Deep learning models to predict flood events in fast-flowing watersheds. Sci. Total Environ. 2022, 813, 151885. [Google Scholar] [CrossRef]
- Hunt, K.M.R.; Matthews, G.R.; Pappenberger, F.; Prudhomme, C. Using a long short-term memory (LSTM) neural network to boost river streamflow forecasts over the western United States. Hydrol. Earth Syst. Sci. 2022, 26, 5449–5472. [Google Scholar] [CrossRef]
- Arsenault, R.; Martel, J.; Brunet, F.; Brissette, F.; Mai, J. Continuous streamflow prediction in ungauged basins: Long short-term memory neural networks clearly outperform traditional hydrological models. Hydrol. Earth Syst. Sci. 2023, 27, 139–157. [Google Scholar] [CrossRef]
- Chen, S.; Huang, J.; Huang, J. Improving daily streamflow simulations for data-scarce watersheds using the coupled SWAT-LSTM approach. J. Hydrol. 2023, 622, 129734. [Google Scholar] [CrossRef]
- Tursun, A.; Xie, X.; Wang, Y.; Liu, Y.; Peng, D.; Rusuli, Y.; Zheng, B. Reconstruction of missing streamflow series in human-regulated catchments using a data integration LSTM model. J. Hydrol. Reg. Stud. 2024, 52, 101744. [Google Scholar] [CrossRef]
- Klotz, D.; Kratzert, F.; Gauch, M.; Sampson, A.K.; Brandstetter, J.; Klambauer, G.; Hochreiter, S.; Nearing, G. Uncertainty estimation with deep learning for rainfall–runoff modeling. Hydrol. Earth Syst. Sci. 2022, 26, 1673–1693. [Google Scholar] [CrossRef]
- Jahangir, M.S.; Quilty, J. Generative deep learning for probabilistic streamflow forecasting: Conditional variational auto-encoder. J. Hydrol. 2024, 629, 130498. [Google Scholar] [CrossRef]
- Tran, V.N.; Dwelle, M.C.; Sargsyan, K.; Ivanov, V.Y.; Kim, J. A novel modeling framework for computationally efficient and accurate real-time ensemble flood forecasting with uncertainty quantification. Water Resour. Res. 2020, 56, e2019WR025727. [Google Scholar] [CrossRef]
- Delottier, H.; Doherty, J.; Brunner, P. Data space inversion for efficient uncertainty quantification using an integrated surface and sub-surface hydrologic model. Geosci. Model Dev. 2023, 16, 4213–4231. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Wood, A.W.; Brissette, F.; Martel, J. Generating ensemble streamflow forecasts: A review of methods and approaches over the past 40 years. Water Resour. Res. 2021, 57, e2020WR028392. [Google Scholar] [CrossRef]
- Hauswirth, S.M.; Bierkens, M.F.P.; Beijk, V.; Wanders, N. The suitability of a seasonal ensemble hybrid framework including data-driven approaches for hydrological forecasting. Hydrol. Earth Syst. Sci. 2023, 27, 501–517. [Google Scholar] [CrossRef]
- Hao, Y.; Baik, J.; Tran, H.; Choi, M. Quantification of the effect of hydrological drivers on actual evapotranspiration using the Bayesian model averaging approach for various landscapes over Northeast Asia. J. Hydrol. 2022, 607, 127543. [Google Scholar] [CrossRef]
- Jahangir, M.S.; You, J.; Quilty, J. A quantile-based encoder-decoder framework for multi-step ahead runoff forecasting. J. Hydrol. 2022, 619, 129269. [Google Scholar] [CrossRef]
- Haddad, K. A comprehensive review and application of Bayesian methods in hydrological modelling: Past, present, and future directions. Water 2025, 17, 1095. [Google Scholar] [CrossRef]
- Gurbuz, F.; Mudireddy, A.; Mantilla, R.; Xiao, S. Using a physics-based hydrological model and storm transposition to investigate machine-learning algorithms for streamflow prediction. J. Hydrol. 2024, 628, 130504. [Google Scholar] [CrossRef]
- Alabbad, Y.; Demir, I. Comprehensive flood vulnerability analysis in urban communities: Iowa case study. Int. J. Disaster Risk Reduct. 2022, 74, 102955. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers, Rock Island District. Coralville Lake Water Control Plan Update Report with Integrated Environmental Assessment; U.S. Army Corps of Engineers: Rock Island, IL, USA, 2022. [Google Scholar]
- U.S. Army Corps of Engineers, Hydrologic Engineering Center. HEC-HMS User’s Manual, Version 4.13. Hydrol Eng Center: Davis, CA, USA. Available online: https://www.hec.usace.army.mil/confluence/hmsdocs/hmsum/latest (accessed on 11 October 2025).
- Moriasi, D.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wright, D.B. RainyDay: Rainfall Hazard Analysis System. Available online: https://github.com/HydroclimateExtremesGroup/RainyDay (accessed on 20 September 2025).
- Wu, D.; Lin, C.; Huang, J. Active learning for regression using greedy sampling. Inf. Sci. 2019, 474, 90–105. [Google Scholar] [CrossRef]
- Bi, J.; Xu, Y.; Conrad, F.; Wiemer, H.; Ihlenfeldt, S. A comprehensive benchmark of active learning strategies with AutoML for small-sample regression in materials science. Sci. Rep. 2025, 15, 37167. [Google Scholar] [CrossRef]
- Chen, Y.; Deierling, P.; Xiao, S. Exploring active learning strategies for predictive models in mechanics of materials. Appl. Phys. A 2024, 130, 588. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W. A critical review of RNN and LSTM variants in hydrological time series predictions. MethodsX 2024, 13, 102946. [Google Scholar] [CrossRef] [PubMed]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Dessain, J. Improving the Prediction of Asset Returns with Machine Learning by Using a Custom Loss Function. Adv. Artif. Intell. Mach. Learn. 2023, 3, 1640–1653. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic individual load forecasting using pinball loss guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.; Tian, Y.; Burrage, K.; Cao, T. Support vector regression with asymmetric loss for optimal electric load forecasting. Energy 2021, 223, 119969. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Hug, G. Cost-oriented load forecasting. Electr. Power Syst. Res. 2022, 205, 117723. [Google Scholar] [CrossRef]
- Tagasovska, N.; Lopez-Paz, D. Single-model uncertainties for deep learning. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 6417–6428. [Google Scholar]
- Tyralis, H.; Papacharalampous, G. Quantile-based hydrological modelling. Water 2022, 13, 3420. [Google Scholar] [CrossRef]
- Cao, C.; He, Y.; Cai, S. Probabilistic runoff forecasting considering stepwise decomposition framework and external factor integration structure. Expert Syst. Appl. 2024, 236, 121350. [Google Scholar] [CrossRef]
- NOAA. HRRR: High-Resolution Rapid Refresh. Available online: https://rapidrefresh.noaa.gov/hrrr/ (accessed on 11 October 2025).
- Iowa Environmental Mesonet. ASOS/AWOS Hourly Precipitation Data. Available online: https://mesonet.agron.iastate.edu/request/asos/hourlyprecip.phtml (accessed on 11 October 2025).
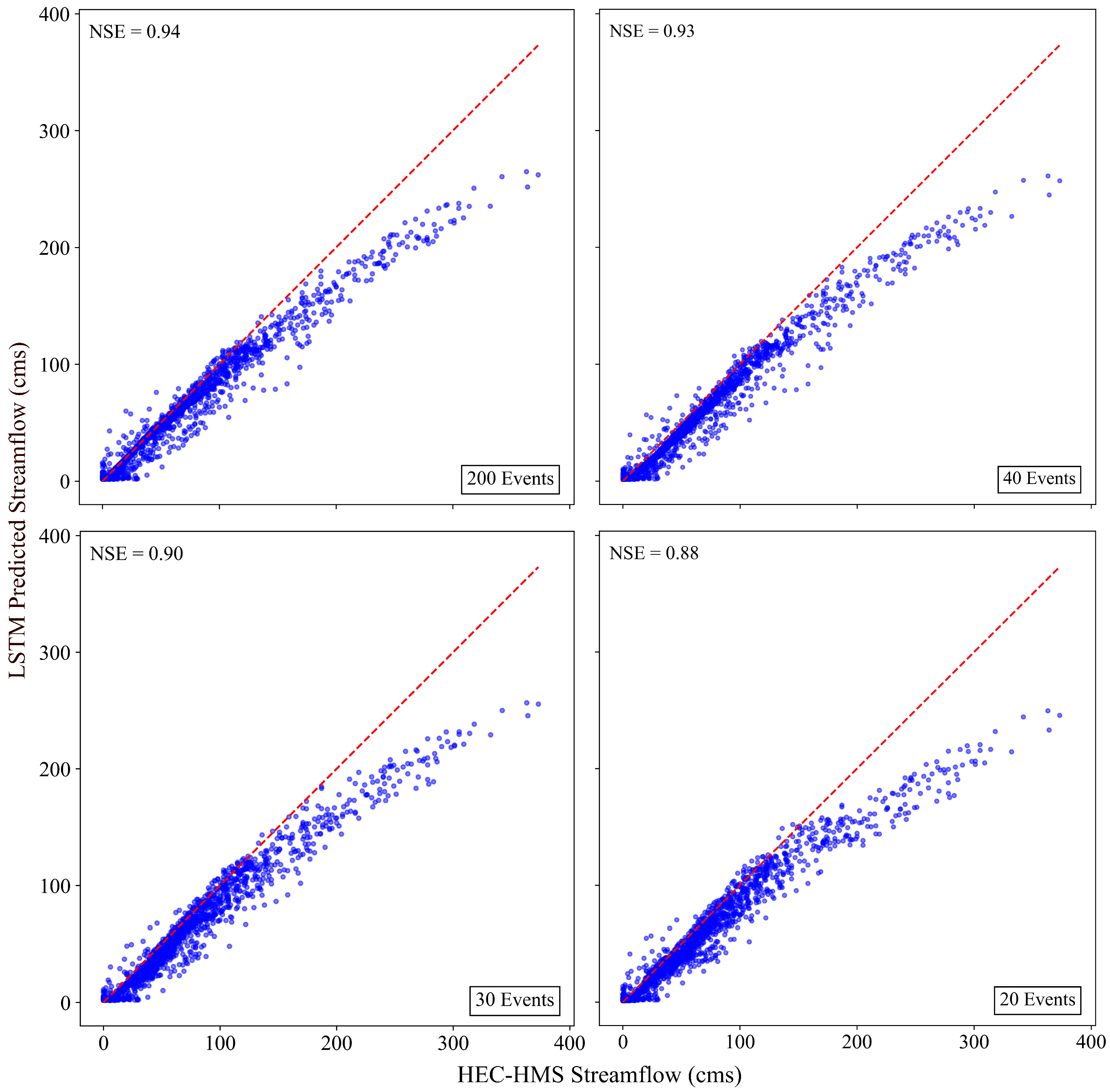
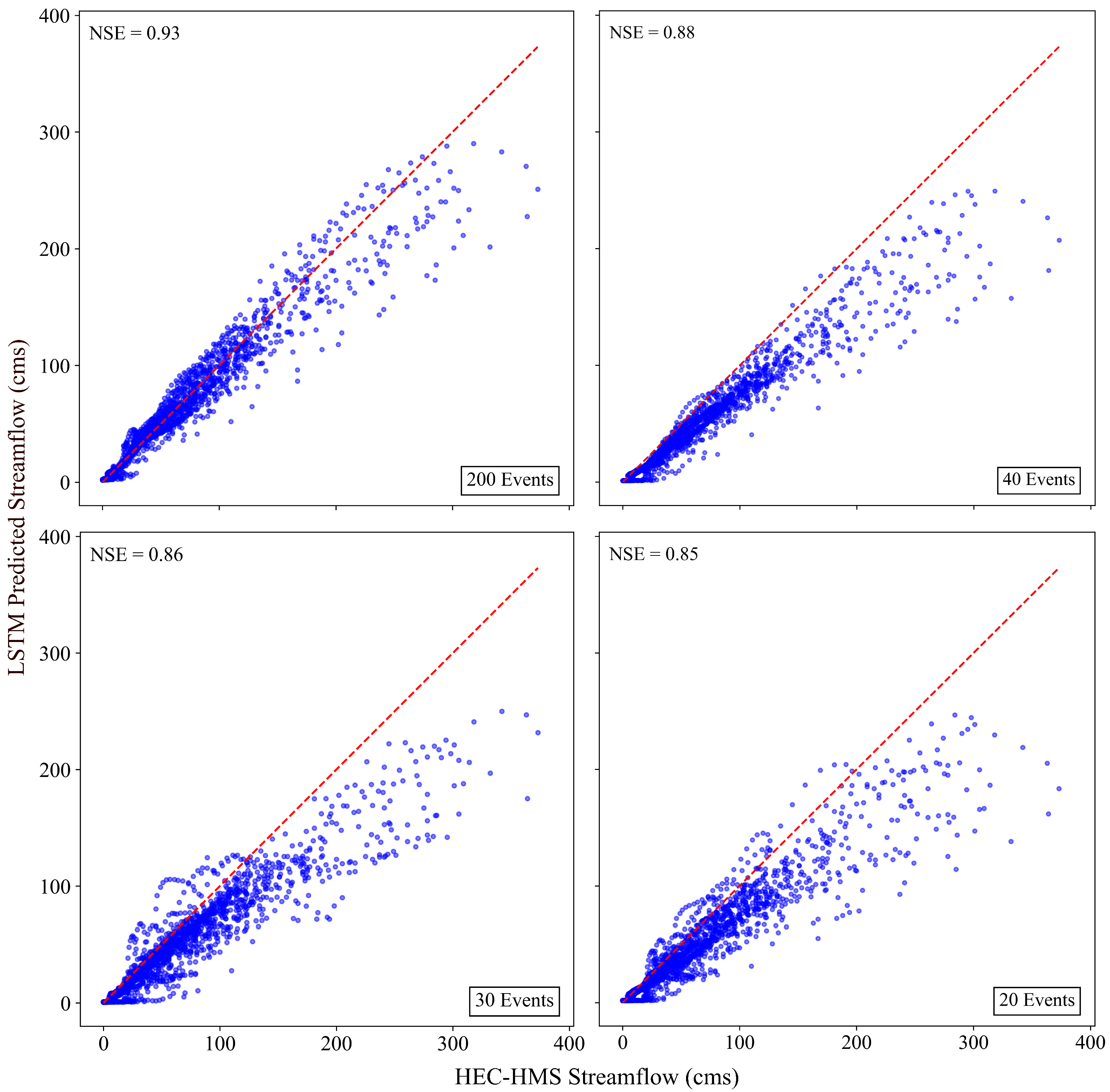
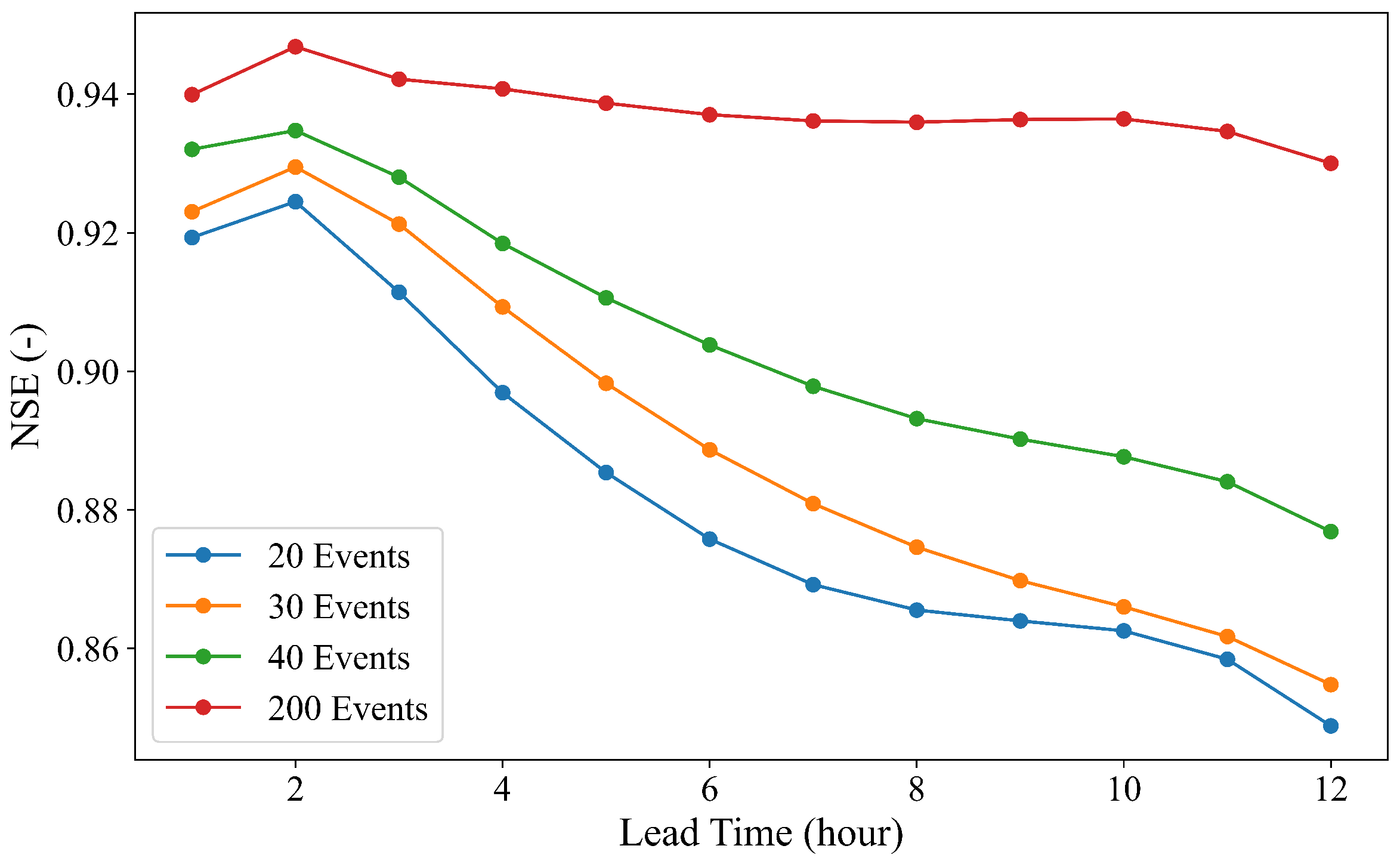

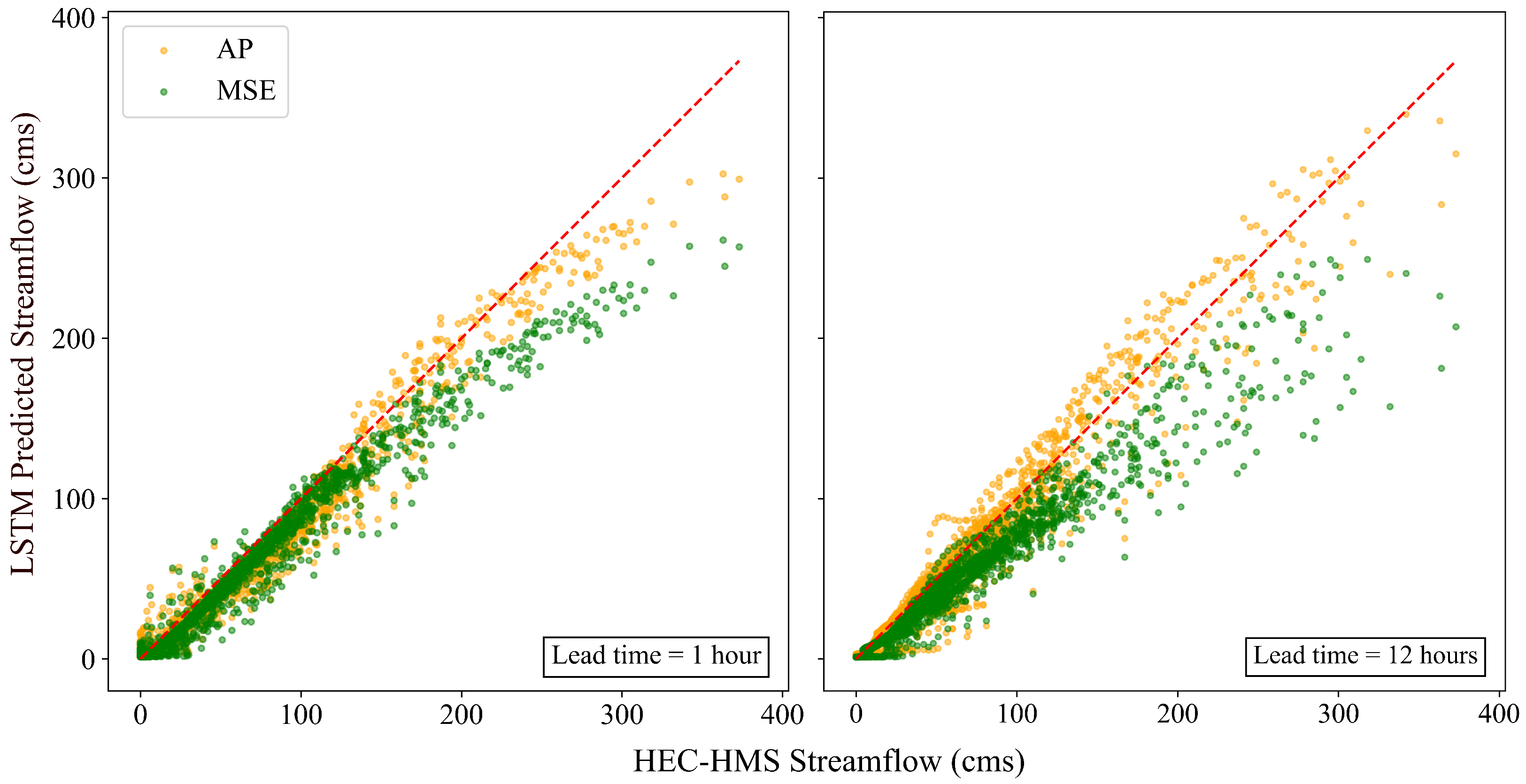


| Gauge Station | NSE | RSR | PBIAS (%) | NSE (Peak) | RSR (Peak) | PBIAS (Peak) (%) |
|---|---|---|---|---|---|---|
| Rowan | 0.90 | 0.30 | −1.72 | 0.57 | 0.60 | −1.40 |
| Marshalltown | 0.73 | 0.50 | 5.51 | 0.63 | 0.64 | 5.51 |
| Marengo | 0.87 | 0.40 | 4.23 | 0.75 | 0.53 | 3.50 |
| Iowa City | 0.96 | 0.20 | −3.49 | 0.96 | 0.20 | −3.22 |
| Lone Tree | 0.89 | 0.30 | 0.20 | 0.84 | 0.39 | 0.17 |
| Gauge Station | NSE | RSR | PBIAS (%) | NSE (Peak) | RSR (Peak) | PBIAS (Peak) (%) |
|---|---|---|---|---|---|---|
| Rowan | 0.68 | 0.6 | −8.72 | 0.54 | 0.72 | −8.2 |
| Marshalltown | 0.64 | 0.6 | −10.48 | 0.48 | 0.68 | −9.82 |
| Marengo | 0.71 | 0.5 | 9.23 | 0.68 | 0.6 | 8.72 |
| Iowa City | 0.91 | 0.4 | −5.36 | 0.90 | 0.4 | −4.95 |
| Lone Tree | 0.62 | 0.6 | 6.30 | 0.47 | 0.78 | 5.64 |
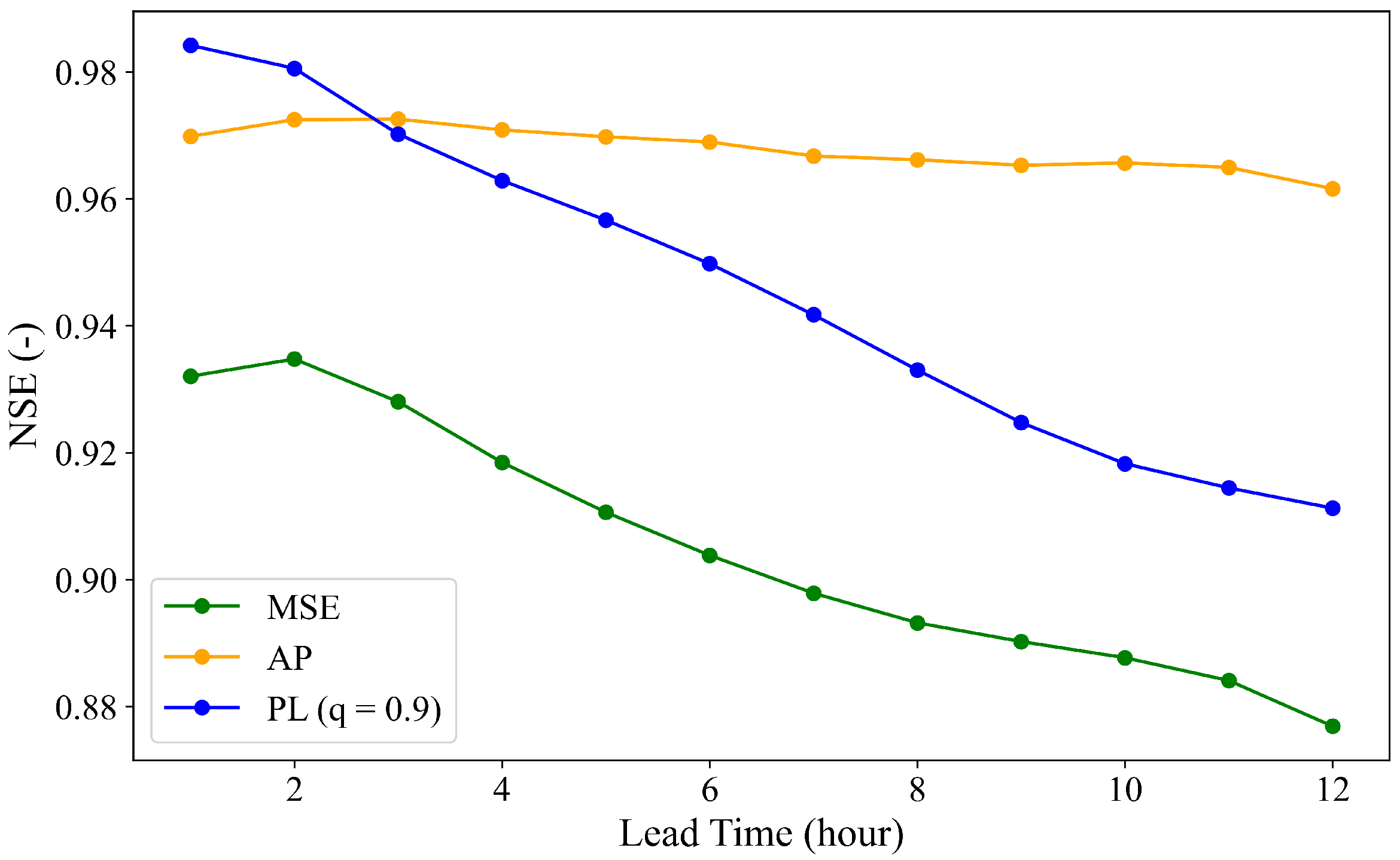
| Loss Function | Lead Time (Hour) | NSE | NSE ( 155 (cms)) |
|---|---|---|---|
| PL (q = 0.8) | 1 | 0.96 | 0.14 |
| PL (q = 0.9) | 1 | 0.98 | 0.82 |
| MSE | 1 | 0.93 | 0.12 |
| PL (q = 0.8) | 12 | 0.89 | −1.33 |
| PL (q = 0.9) | 12 | 0.91 | −0.91 |
| MSE | 12 | 0.88 | −0.90 |
| Loss Function | Lead Time (Hour) | NSE | NSE () |
|---|---|---|---|
| AP | 1 | 0.97 | 0.76 |
| PL (q = 0.9) | 1 | 0.98 | 0.82 |
| MSE | 1 | 0.93 | 0.12 |
| AP | 12 | 0.96 | 0.62 |
| PL (q = 0.9) | 12 | 0.91 | −0.91 |
| MSE | 12 | 0.88 | −0.90 |
| Lead Time (Hours) | NSE | PICP | MPIW | CRPS |
|---|---|---|---|---|
| 1 | 0.9451 | 0.9956 | 24.8358 | 2.2604 |
| 2 | 0.9289 | 0.9958 | 25.574 | 2.3803 |
| 3 | 0.9182 | 0.9953 | 25.1313 | 2.5248 |
| 4 | 0.9003 | 0.9937 | 25.0292 | 2.7112 |
| 5 | 0.8790 | 0.9922 | 25.057 | 2.9270 |
| 6 | 0.8557 | 0.9906 | 25.1636 | 3.1485 |
| 7 | 0.8325 | 0.9884 | 25.3285 | 3.3621 |
| 8 | 0.8102 | 0.9864 | 25.5347 | 3.5644 |
| 9 | 0.7893 | 0.9847 | 25.7526 | 3.7521 |
| 10 | 0.7704 | 0.9832 | 25.9451 | 3.9245 |
| 11 | 0.7532 | 0.9809 | 26.0816 | 4.0781 |
| 12 | 0.7352 | 0.9789 | 26.1311 | 4.2355 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tofighi, S.; Gurbuz, F.; Mantilla, R.; Xiao, S. Advancing Machine Learning-Based Streamflow Prediction Through Event Greedy Selection, Asymmetric Loss Function, and Rainfall Forecasting Uncertainty. Appl. Sci. 2025, 15, 11656. https://doi.org/10.3390/app152111656
Tofighi S, Gurbuz F, Mantilla R, Xiao S. Advancing Machine Learning-Based Streamflow Prediction Through Event Greedy Selection, Asymmetric Loss Function, and Rainfall Forecasting Uncertainty. Applied Sciences. 2025; 15(21):11656. https://doi.org/10.3390/app152111656
Chicago/Turabian StyleTofighi, Soheyla, Faruk Gurbuz, Ricardo Mantilla, and Shaoping Xiao. 2025. "Advancing Machine Learning-Based Streamflow Prediction Through Event Greedy Selection, Asymmetric Loss Function, and Rainfall Forecasting Uncertainty" Applied Sciences 15, no. 21: 11656. https://doi.org/10.3390/app152111656
APA StyleTofighi, S., Gurbuz, F., Mantilla, R., & Xiao, S. (2025). Advancing Machine Learning-Based Streamflow Prediction Through Event Greedy Selection, Asymmetric Loss Function, and Rainfall Forecasting Uncertainty. Applied Sciences, 15(21), 11656. https://doi.org/10.3390/app152111656






