Validating Express Rail Optimization with AFC and Backcasting: A Bi-Level Operations–Assignment Model to Improve Speed and Accessibility Along the Gyeongin Corridor
Abstract
1. Introduction
2. Materials and Methods
2.1. Review of Previous Studies
2.2. Key Assumptions and Mathematical Formulation for Model Development
2.2.1. UE Optimisation Assumptions
- (1)
- Objective Function (minimisation of total generalised cost):
- (ii)
- Equilibrium Condition (Wardrop’s first principle):
- (iii)
- Constraints:
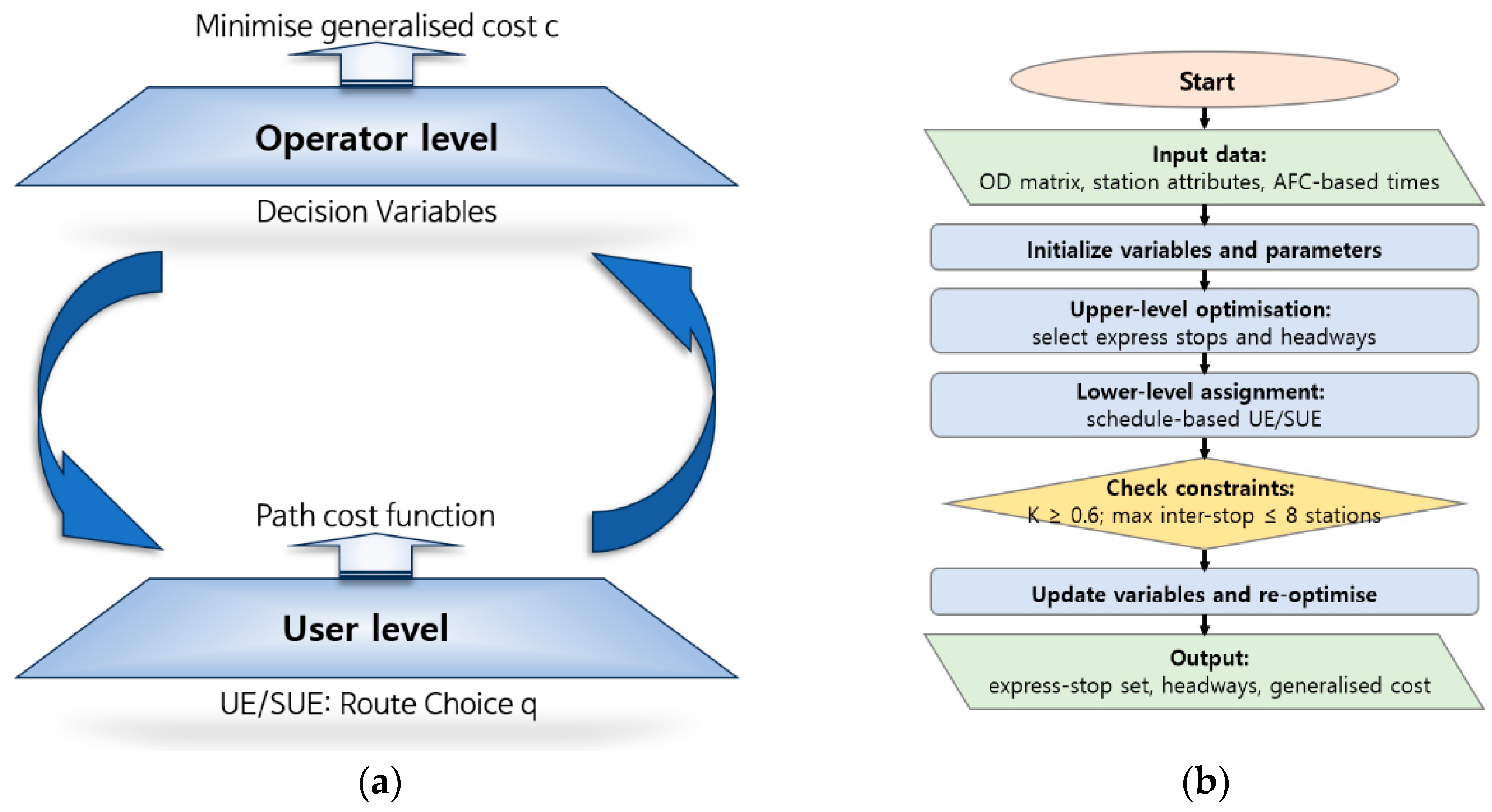
- Upper-Level Problem (operator’s decision):
- The operator selects the stopping pattern x and headway H to minimise the total generalised cost Z(x, H), which is computed endogenously from the lower-level solution. The optimisation is subject to constraints on the minimum coverage ratio, maximum inter-stop spacing, and allowable headway bounds. Candidate solutions are evaluated using metaheuristic techniques, such as genetic algorithms or simulated annealing, with the lower-level problem solved iteratively for each case.
- Lower-Level Problem (user equilibrium assignment):
- For a given (x, H) configuration, passengers choose routes based on UE principles until a stable demand distribution is attained. Convergence is deemed achieved when the cost difference between any utilised path and the minimum-cost path for the same OD pair falls below a defined threshold.
2.2.2. Key Variables Related to Urban Railway Operations
2.2.3. Characteristics of the Demand Assignment Theory for Express Operations
- Based on these premises, the station importance score (Si) detailed in Table 6 is calculated as the weighted sum of three factors: the peak two-hour boarding–alighting total (Di), temporal balance index (Bi, 0–1), and annual scaling factor (Ri).
- To integrate indicators with differing scales and units, linear normalisation is applied, as expressed in Equation (5):
- At the station importance score evaluation stage, the weighted sum is calculated as follows:
- Based on this scoring, stations are then sorted in descending order of Si, and the coverage ratio is calculated using actual demand Di rather than Si:
2.3. Solution Algorithm and Simulation Design
2.3.1. Data Structure and Parameterization Workflow
2.3.2. Scenario Design Rationale
2.4. Reproducible Solution Algorithm
3. Results
3.1. Analytical Variables
3.2. Main Analysis
3.2.1. Findings and Interpretation
3.2.2. Model Validation and Benchmarking
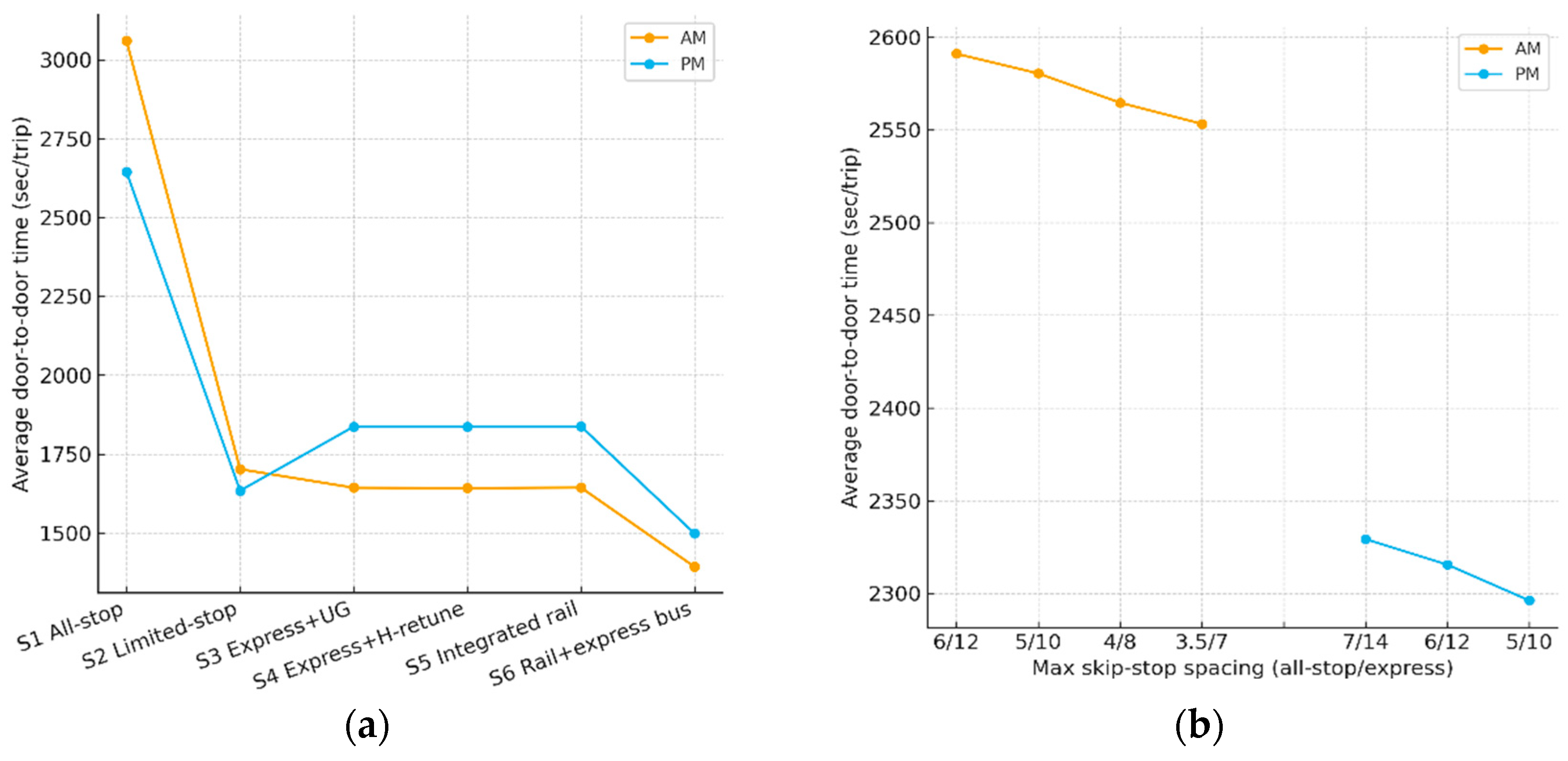
3.2.3. Scenario Analysis (S1–S6 Comparative Results)
3.2.4. Extended Sensitivity Analysis
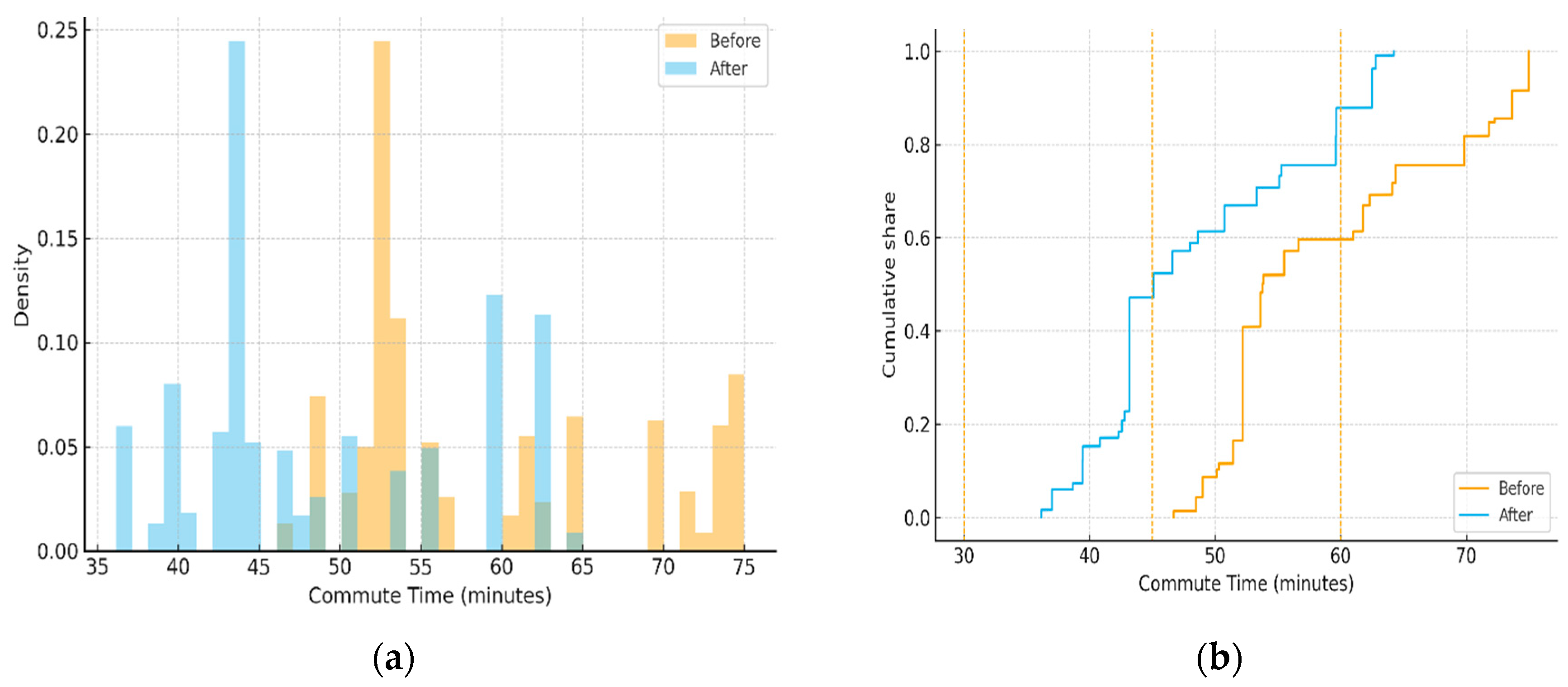
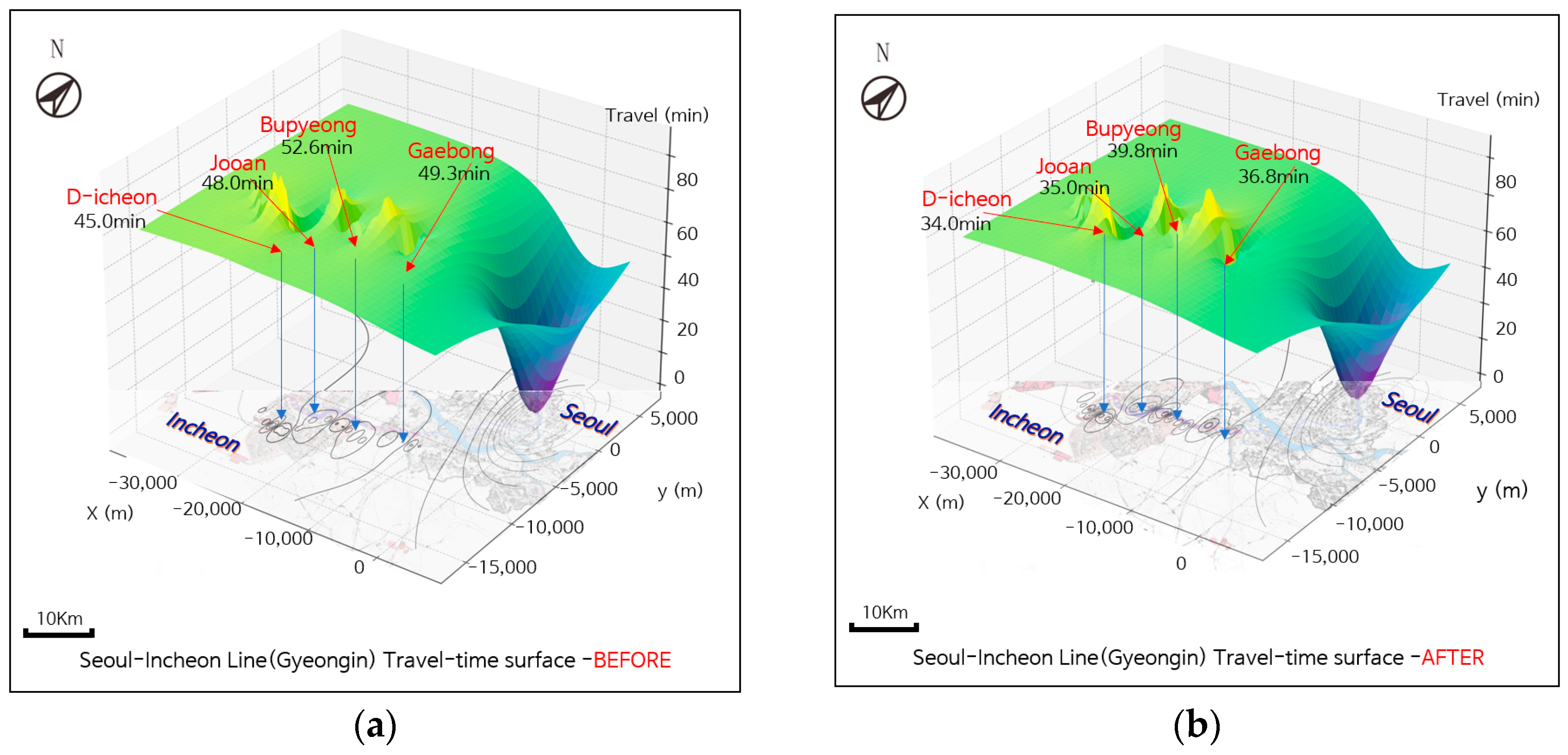
3.3. Accessibility and Spatial Rebalancing Analysis
3.3.1. Discussion and Policy Implications
3.3.2. Isochrone Expansion Effects
4. Discussion
4.1. Policy-Relevant Insights
4.2. External Validity and Scope
4.3. Limitations
4.4. Computational Considerations and Reproducibility
4.5. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFC | Automatic fare collection |
| B/C | Benefit–cost ratio |
| BPR | Bureau of Public Roads (volume–delay function) |
| CDF | Cumulative distribution function |
| CI | Confidence interval |
| GIS | Geographic information system |
| GTFS | General Transit Feed Specification |
| IQR | Interquartile range |
| KDE | Kernel density estimate |
| KPI | Key performance indicator |
| KS | Kolmogorov–Smirnov (test) |
| MAE | Mean absolute error |
| MSA | Method of successive averages |
| OD | Origin–destination |
| OPS | Operational performance statistics (screenline/throughput logs) |
| PM/AM | Evening/morning peak |
| RMSE | Root mean square error |
| SDG | Sustainable Development Goals |
| SUE | Stochastic user equilibrium |
| UE | User equilibrium |
| UG | Undergrounding |
References
- Cervero, R.; Kockelman, K. Travel demand and the 3Ds: Density, diversity, and design. Transp. Res. Part D 1997, 2, 199–219. [Google Scholar] [CrossRef]
- Jenelius, E. Personalized Predictive Public Transport Crowding Information: A Framework and Field Experiment. Transp. Res. Part C 2020, 117, 102635. [Google Scholar] [CrossRef]
- Incheon Institute (II). Operational Plan for Extending Express Train Service on the Gyeongin Line to Incheon Station (원제: 경인선 급행열차의 인천역 연장 운행방안); Policy Research Project 2019; Incheon Institute: Incheon, Republic of Korea, 2019; Available online: https://www.ii.re.kr/base/board/read?boardManagementNo=14&boardNo=15415&menuLevel=2&menuNo=76 (accessed on 26 September 2025). (In Korean)
- Mohring, H. Optimization and Scale Economies in Urban Bus Transportation. Am. Econ. Rev. 1972, 62, 591–604. Available online: https://www.jstor.org/stable/1806101 (accessed on 30 August 2025).
- Wardrop, J.G. Some Theoretical Aspects of Road Traffic Research. Proc. Inst. Civ. Eng. 1952, 1, 325–362. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985; ISBN 0-13-939729-9. [Google Scholar]
- Spiess, H.; Florian, M. Optimal Strategies: A New Assignment Model for Transit Networks. Transp. Res. Part B 1989, 23, 83–102. [Google Scholar] [CrossRef]
- Cepeda, M.; Cominetti, R.; Florian, M. A Frequency-Based Assignment Model for Congested Transit Networks with Strict Capacity Constraints: Characterization and Computation of Equilibria. Transp. Res. Part B 2006, 40, 437–459. [Google Scholar] [CrossRef]
- Wang, P.; Bešinović, N. Improving the Utilization of Regenerative Energy and Shaving Power Peaks by Railway Timetable Adjustment. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15742–15754. [Google Scholar] [CrossRef]
- Cats, O.; Jenelius, E. Planning for the Unexpected: The Value of Reserve Capacity for Public Transport Network Robustness. Transp. Res. Part A 2015, 81, 47–61. [Google Scholar] [CrossRef]
- Jenelius, E.; Cats, O. The Value of New Public Transport Links for Network Robustness and Redundancy. Transp. A Transp. Sci. 2015, 11, 819–835. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Russo, F.; Crisalli, U. A Doubly Dynamic Schedule-Based Assignment Model for Transit Networks. Transp. Sci. 2001, 35, 268–285. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Bierlaire, M. Discrete Choice Methods and Their Applications to Short-Term Travel Decisions. In Handbook of Transportation Science, 2nd ed.; Hall, R., Ed.; Kluwer: Boston, MA, USA, 1999; pp. 5–34. Available online: https://link.springer.com/chapter/10.1007/978-1-4615-5203-1_2 (accessed on 30 August 2025).
- Prato, C.G. Route Choice Modeling: Past, Present and Future Research Directions. J. Choice Model. 2009, 2, 65–100. [Google Scholar] [CrossRef]
- Frejinger, E.; Bierlaire, M.; Ben-Akiva, M. Sampling of Alternatives for Route Choice Modeling. Transp. Res. Part B 2009, 43, 984–994. [Google Scholar] [CrossRef]
- Train, K.E. Discrete Choice Methods with Simulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Xu, J.; Liang, Q.; Huang, X.; Wang, L. Optimization of Stop Plan for Skip-Stop Operation on Suburban Railway Line. Appl. Sci. 2021, 11, 9519. [Google Scholar] [CrossRef]
- Parbo, J.; Nielsen, O.A.; Prato, C.G. User Perspectives in Public Transport Timetable Optimisation. Transp. Res. Part C 2014, 48, 269–284. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Y.; Cats, O.; Zhao, Y. A Review of Public Transport Transfer Coordination at the Network Level. Transp. Res. Part C 2021, 132, 103450. [Google Scholar] [CrossRef]
- Seo, T.; Wada, K.; Fukuda, D. Fundamental Diagram of Urban Rail Transit Considering Train–Passenger Interaction. Transportation 2022, 50, 1399–1424. [Google Scholar] [CrossRef]
- Goverde, R.M.P. A Three-Level Framework for Performance-Based Railway Timetabling. Transp. Res. Part C 2016, 67, 62–83. [Google Scholar] [CrossRef]
- Lusby, R.M.; Larsen, J.; Ehrgott, M.; Ryan, D. A Survey on Robustness in Railway Planning. Eur. J. Oper. Res. 2018, 266, 1–15. [Google Scholar] [CrossRef]
- Hansen, W.G. How accessibility shapes land use. J. Am. Inst. Plan. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Geurs, K.T.; van Wee, B. Accessibility evaluation of land-use and transport strategies: Review and research directions. Transp. Rev. 2004, 24, 127–154. [Google Scholar] [CrossRef]
- Cacchiani, V.; Huisman, D.; Kidd, M.; Kroon, L.G.; Toth, P.; Veelenturf, L.P.; Wagenaar, J.C. An Overview of Recovery Models and Algorithms for Real-Time Railway Rescheduling. Transp. Res. Part B 2014, 63, 15–37. [Google Scholar] [CrossRef]
- Ingvardson, J.B.; Nielsen, O.A. Passenger Arrival and Waiting Time Distributions Dependent on Headway and Capacity in High-Frequency Metro. Transp. Res. Part B 2018, 117, 208–227. [Google Scholar] [CrossRef]
- Durán-Hormazábal, E.; Tirachini, A. Estimation of Travel Time Variability for Door-to-Door Public Transport Trips. Res. Transp. Econ. 2016, 59, 236–244. [Google Scholar] [CrossRef]
- Cats, O. Regularity-driven bus operation: Principles, implementation and business models. Transp. Policy 2014, 36, 223–230. [Google Scholar] [CrossRef]
- van Oort, N. Incorporating Service Reliability in Public Transport Design and Performance Requirements. Transp. Res. Rec. 2014, 48, 92–100. [Google Scholar] [CrossRef]
- Lee, Y.J.; Shariat, S.; Choi, K. Mathematical Modeling for Optimizing Skip-Stop Rail Transit Operation Strategy Using Genetic Algorithm. In Proceedings of the Transportation Research Board 92nd Annual Meeting; Washington, DC, USA, 13 January 2013. Available online: https://rosap.ntl.bts.gov/view/dot/23988/dot_23988_DS1.pdf (accessed on 30 August 2025).
- Lee, Y.-J.; Shariat, S.; Choi, K. Stop-Skipping Cheat-Sheet: Optimizing Skip-Stop Patterns for Urban Rail with Genetic Algorithms. J. Public Transp. 2014, 17, 74–93. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, R.; Wang, W.; Ye, Z. Passenger-Adapted Skip-Stop Plan for Urban Rail Transit Based on Passenger Flow. IET Intell. Transp. Syst. 2022, 16, 1101–1112. [Google Scholar] [CrossRef]
- Di Nardo, M.; Clericuzio, M.; Murino, T.; Madonna, M. An Adaptive Resilience Approach for a High Capacity Railway. Int. Rev. Civ. Eng. 2020, 11, 98–105. [Google Scholar] [CrossRef]
- Cats, O.; Yap, M.; van Oort, N. Exposing the Role of Service Reliability in Public Transport Mode Choice. Transp. Res. Part A 2016, 86, 236–252. [Google Scholar] [CrossRef]
- Wardman, M.; Whelan, G. Twenty Years of Rail Crowding Valuation Studies: Evidence and Lessons from British Experience. Transp. Rev. 2011, 31, 379–398. [Google Scholar] [CrossRef]
- de Palma, A.; Lindsey, R.; Monchambert, G. The Economics of Crowding in Rail Transit. J. Urban Econ. 2017, 101, 28–52. [Google Scholar] [CrossRef]
- Kim, K.M.; Hong, S.-P.; Ko, S.-J.; Kim, D. Does Crowding Affect the Path Choice of Metro Passengers? Transp. Res. Part A 2015, 77, 292–304. [Google Scholar] [CrossRef]
- Kroes, E.; Kouwenhoven, M.; Debrincat, L.; Pauget, N. On the Value of Crowding in Public Transport for Île-de-France. Transp. Res. Rec. 2014, 2417, 37–45. [Google Scholar] [CrossRef]
- Kato, H.; Kaneko, Y.; Inoue, S. Comparative Analysis of Transit Assignment: Evidence from Urban Railway System in the Tokyo Metropolitan Area. Transportation 2010, 37, 775–799. [Google Scholar] [CrossRef]
- Venables, A.J. Incorporating Wider Economic Impacts within Cost-Benefit Appraisal. International Transport Forum Discussion Paper 2016/05, OECD/ITF. 2016. Available online: https://ideas.repec.org/p/oec/itfaab/2016-05-en.html (accessed on 30 August 2025).
- Fosgerau, M.; Small, K.A. Hypercongestion in downtown metropolis. J. Urban Econ. 2013, 76, 122–134. [Google Scholar] [CrossRef]
- Jong, J.; Suen, C.; Chang, S. Decision support system to optimize railway stopping patterns: Application to Taiwan high-speed rail. Transp. Res. Rec. 2012, 2289, 24–33. [Google Scholar] [CrossRef]
- Duranton, G.; Turner, M.A. The Fundamental Law of Road Congestion. Am. Econ. Rev. 2011, 101, 2616–2652. [Google Scholar] [CrossRef]
- Vickrey, W.S. Congestion Theory and Transport Investment. Am. Econ. Rev. 1969, 59, 251–260. [Google Scholar]

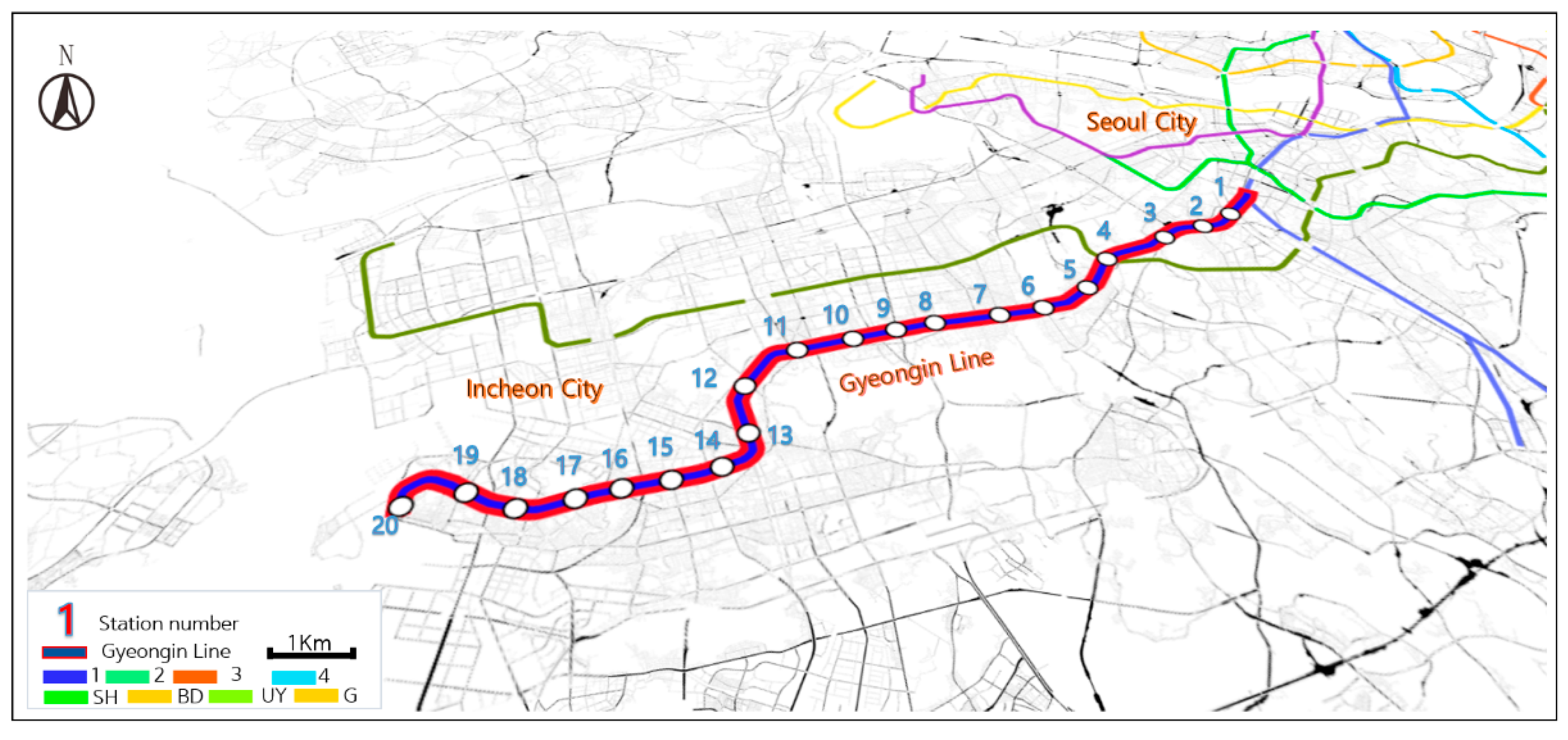
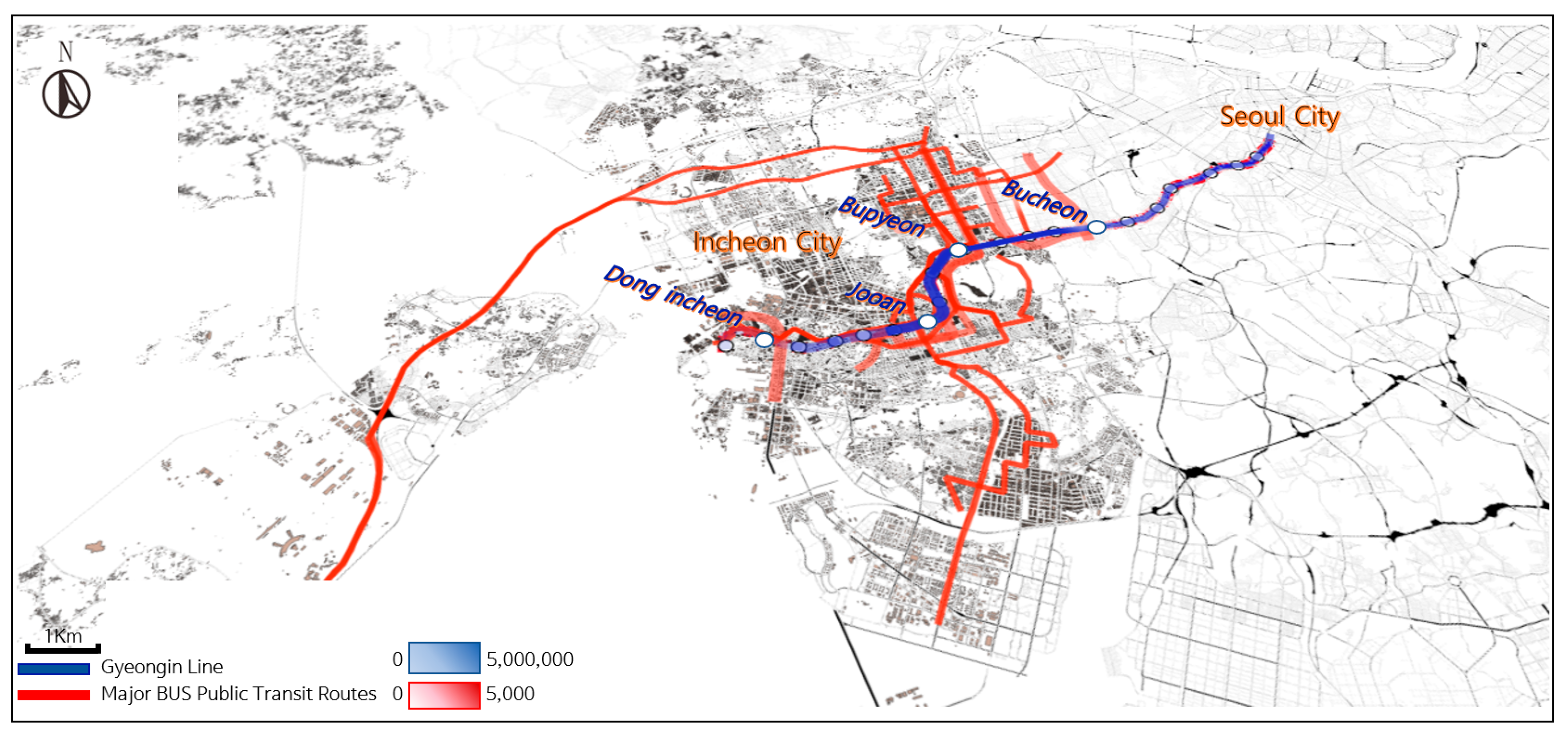
| Stream | Key Fields | Time Window and Binning | Use in Model |
|---|---|---|---|
| AFC (Smart card) | Card ID, tap time, tap station, direction, product type | Weekday peaks 07:00–09:00/17:30–19:30; 5- and 15-min bins | OD inference; platform accumulation; demand scaling |
| OPS (Operational logs) | Train ID, actual departure/arrival times, dwell, headway, seat occupancy | Synchronized to AFC bins; missingness flagged | Dwell calibration; validation |
| GTFS (Network) | Stop sequence, scheduled run times, transfer links, segment length and geometry | Service calendar; corridor topology | Lower-level costs; network build |
| Stream | Meaning | Default/Prior Range | Gyeongin Value (Estimated or Policy) | Source/Method |
|---|---|---|---|---|
| Free-run time of segment s | GTFS schedule ± tolerance | None | GTFS/OPS alignment | |
| Capacity of segment s | trains/h | None | OPS/platform rules | |
| BPR parameters (segment-wise) | ] | Nonlinear least squares | ||
| Dwell coefficients (load, variance) | OLS/GLS on OPS × AFC | |||
| Minimum coverage threshold | [0.6–0.9] of key stations | K ≥ 0.6 | Policy rule/sensitivity | |
| Maximum inter-stop spacing | By stations or distance cap | ≤8 stations | Best practice + sensitivity |
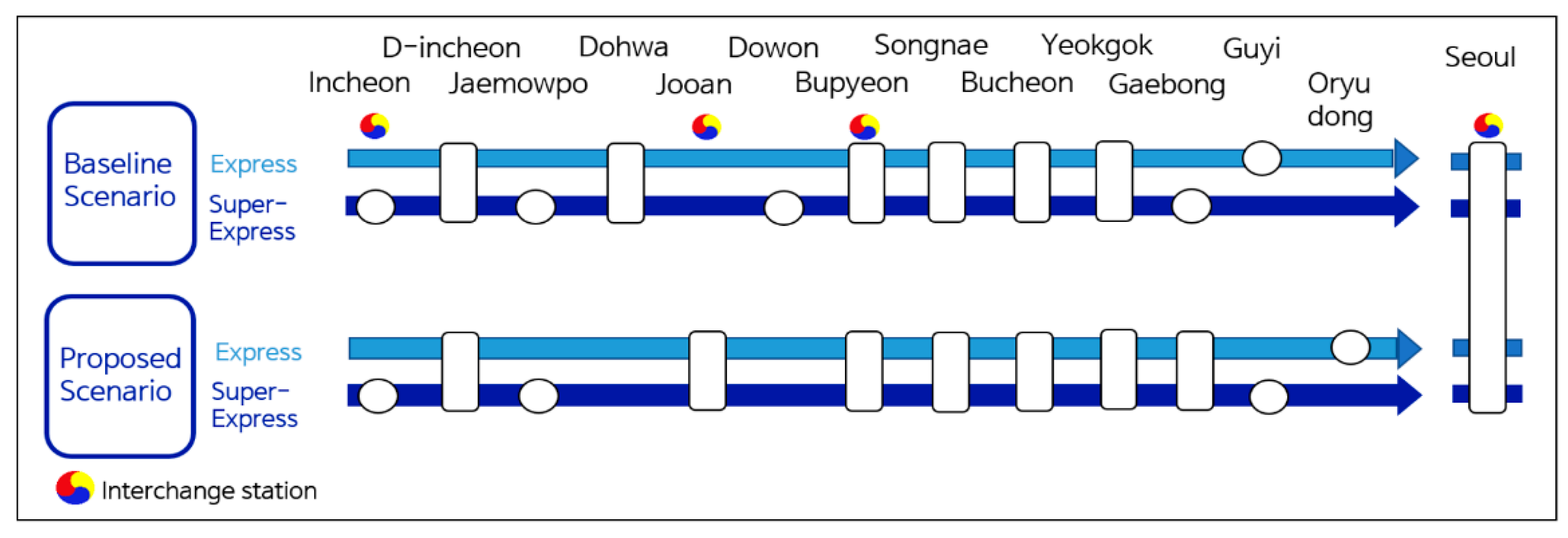
| Scenario | Stopping | Headway | Alignment | Dwell/Cong | Rationale |
|---|---|---|---|---|---|
| S1 Baseline | All-stop | Baseline timetable | Surface (observed) | Calibrated dwell; calibrated BPR (segment-wise) | Benchmark for door-to-door costs and express/local shares under current practice. |
| S2 Limited-stop | Express stops only | Baseline timetable | Surface (observed) | Same as S1 | Isolates pure stopping-pattern effects without changing frequency or geometry |
| S3 Express-alone | Express stops (as S2) | Fixed headways (as S2) | Underground/straightened run-time functions | Same calibration; geometry only affects run times | Identifies incremental gains enabled by civil works while holding headways constant. |
| S4 Express-parallel | Express stops (surface) | Time-of-day Retuning | Surface (observed) | Same as S1 | Operator-controllable lever; measures frequency gains without civil works |
| S5 Express-UG | Mixed layer (local + express) with transfers | Time-of-day Retuning | Surface (observed) | Same as S1 | Tests dispersion of flows, hub relief, and transfer penalties under a layered design |
| S6 Mixed | Mixed rail; add express bus layer | Time-of-day Retuning | Surface (observed; bus priority assumed) | Same as S1; road congestion abstracted | Prospective upper bound under institutional changes (priority, fare integration); excluded from ratio backcasting. |
| Variables | Data Sources | Analysis |
|---|---|---|
| Distance by railway section, average dwell time, boarding–alighting time per station, weekday operating timetable | Korail Open Data Portal; Seoul Metro annual distance and travel-time statistics (Open Data Plaza); Incheon Transit Corporation resources | Station-area importance; average travel-time distribution |
| Land use and spatial characteristics of Line 1 stations | National Spatial Data Infrastructure Portal | |
| Seoul Metro operating regulations; boarding–alighting volumes by station | Seoul Metropolitan Government Open Data Plaza; Korail Open Data Portal | |
| Metropolitan railway operating characteristics | National Transport Big Data Integrated Platform | |
| District-level population and employment | Local administrative statistics (Statistics Korea) | |
| Gyeongin Line underground construction plans | Gyeonggi Research Institute; Incheon Research Institute reports | Empirical analysis of Gyeongin Line |
| Station | Station–Platform Alignment (Incheon-Bound) 1 | Interstation Alignment (Incheon-Bound) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Depth (m) | Radius, R (m) | Straight Length, Ls (m) | Section Length, (m) | min. Curve Radius, (m) | Express Pass-Through Time (s) | All-Stop Run Time (s) | Bus Travel Time | ||
| 1 | Guyi | Ground | None | None | None | 400 | 100 | 240 | 780 |
| 2 | Gaebong | Ground | Ramp | None | 966 | 400 | 100 | 180 | 540 |
| 3 | Oryudong | −20 | 2500 | 1365 | 1365 | 2500 | 130 | 360 | 420 |
| 4 | Onsu | −30 | 1200 | 1356 | 1575 | 600 | 130 | 480 | 1080 |
| 5 | Yeokgok | −30 | 800 | 1059 | 1745 | 600 | 130 | 310 | 620 |
| 6 | Sosa | −30 | 1500 | 1040 | 1150 | 800 | 130 | 180 | 360 |
| 7 | Bucheon | −30 | Tangent | 820 | 1315 | 1500 | 130 | 240 | 500 |
| 8 | Jungdong | −35 | 2500 | 1530 | 1530 | 2500 | 100 | 130 | 380 |
| 9 | Songnae | −35 | Tangent | 940 | 1240 | Tangent | 130 | 180 | 320 |
| 10 | Bukae | −35 | Tangent | 997 | 1004 | Tangent | 110 | 190 | 220 |
| 11 | Bupyeong | −35 | Tangent | 1380 | 1426 | 400 | 130 | 390 | 1200 |
| 12 | Baewon | −35 | Tangent | 1025 | 1630 | 600 | 130 | 390 | 660 |
| 13 | Dongam | −35 | Tangent | 878 | 1680 | 400 | 130 | 400 | 590 |
| 14 | Ganseok | −20 | 600 | 368 | 1180 | Tangent | 130 | 390 | 600 |
| 15 | Jooan | −20 | 600 | 1000 | 1340 | 1200 | 130 | 450 | 590 |
| 16 | Dohwa | −20 | 600 | 659 | 1060 | 600 | 110 | 380 | 600 |
| 17 | Jaemowpo | −20 | 600 | 680 | 1089 | 900 | 110 | 300 | 430 |
| 18 | Dowon | Ground | Ramp | 828 | 1421 | Ramp | 120 | 240 | 460 |
| 19 | Dongincheon | Ground | None | 1020 | 1128 | None | 130 | 360 | 720 |
| 20 | Incheon | Ground | None | None | 1981 | None | 160 | 320 | 450 |
| Station * | Boarding/Alighting Records | Passenger Volume Proportion | Land Use and Development Variables Within the Station Area | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Daily Total Boarding/Alighting | AM Peak Boarding/Alighting | PM Peak Boarding/Alighting | Total Boarding/Alighting | Commuter/General Boarding/Alighting | Commercial Area | Commercial Share (%) | Residential Population | Residential Area (m2) | Residential Share (%) | ||
| 1 | Guyi | 7939/ 7789 | 25,491/ 11,991 | 12,036/ 22,468 | 1.15%/ 1.16% | 151.61%/ 288.45% | 11.3757 | 14.48% | 54,843 | 22.4265 | 28.54% |
| 2 | Gaebong | 24,017/ 23,497 | 95,391/ 19,472 | 24,350/ 80,404 | 3.49%/ 3.51% | 101.38%/ 342.27% | 2.9635 | 3.77% | 69,085 | 43.3809 | 55.24% |
| 3 | Oryudong | 12,859/ 12,090 | 5069/ 8443 | 10,968/ 41,471 | 1.87%/ 1.79% | 85.29%/ 343.02% | 14.3508 | 18.27% | 66,429 | 29.9364 | 38.12% |
| 4 | Onsu | 7147/ 6840 | 22,229/ 11,165 | 7732/ 19,523 | 1.04%/ 1.02% | 108.19%/ 285.42% | 1.8924 | 2.41% | 45,585 | 65.3421 | 83.21% |
| 5 | Yeokgok | 30,758/ 30,435 | 119,545/ 25,720 | 31,047/ 106,033 | 4.47%/ 4.53% | 100.94%/ 348.39% | 11.6065 | 14.78% | 65,762 | 57.1121 | 72.73% |
| 6 | Sosa | 9097/ 8681 | 28,297/ 10,624 | 9588/ 23,361 | 1.32%/ 1.29% | 105.41%/ 269.11% | 18.1609 | 23.12% | 67,354 | 47.2082 | 60.11% |
| 7 | Bucheon | 34,419/ 34,389 | 105,081/ 32,738 | 45,601/ 105,946 | 5.01%/ 4.53% | 132.49%/ 308.08% | 44.4975 | 56.66% | 46,394 | 29.0031 | 36.93% |
| 8 | Jungdong | 10,378/ 9777 | 40,736/ 8902 | 8891/ 31,463 | 1.51%/ 1.46% | 85.67%/ 321.81% | 2.9798 | 3.79% | 22,420 | 62.0158 | 78.97% |
| 9 | Songnae | 29,908/ 29,526 | 103,591/ 55,849 | 52,706/ 89,849 | 4.35%/ 4.41% | 176.23%/ 304.31% | 24.8431 | 31.63% | 33,974 | 32.4819 | 41.36% |
| 10 | Bukae | 9820/ 9150 | 39,637/ 8465 | 8685/ 29,356 | 1.43%/ 1.36% | 88.44%/ 320.83% | 2.5871 | 3.29% | 46,469 | 63.8894 | 81.35% |
| 11 | Bupyeong | 29,416/ 30,966 | 84,242/ 26,424 | 45,240/ 107,528 | 4.27%/ 4.61% | 153.81%/ 347.25% | 30.8231 | 39.25% | 50,283 | 35.9451 | 45.77% |
| 12 | Baewon | 8414/ 8274 | 31,349/ 7186 | 6876/ 26,601 | 1.22%/ 1.23% | 81.73%/ 321.51% | 1.1231 | 1.43% | 36,439 | 44.3514 | 56.48% |
| 13 | Dongam | 16,898/ 16,890 | 64,998/ 14,922 | 17,708/ 56,479 | 2.46%/ 2.51% | 104.79%/ 334.39% | 7.2089 | 9.18% | 45,592 | 55.2694 | 70.37% |
| 14 | Ganseok | 6506/ 6149 | 22,372/ 7081 | 7069/ 18,698 | 0.95%/ 0.92% | 108.66%/ 304.08% | 8.2179 | 10.46% | 49,066 | 56.2155 | 71.58% |
| 15 | Jooan | 21,047/ 19,407 | 62,305/ 25,120 | 30,184/ 59,605 | 3.06%/ 2.89% | 143.41%/ 307.13% | 34.0821 | 43.39% | 39,949 | 35.4859 | 45.18% |
| 16 | Dohwa | 4695/ 4371 | 16,100/ 5743 | 5038/ 11,212 | 0.68%/ 0.65% | 107.31%/ 256.51% | 10.6202 | 13.52% | 20,254 | 48.3842 | 59.06% |
| 17 | Jaemowpo | 12,359/ 11,733 | 36,760/ 2581 | 17,278/ 30,563 | 1.82%/ 1.75% | 139.82%/ 260.49% | 2.7962 | 3.56% | 42,296 | 32.4757 | 41.35% |
| 18 | Dowon | 3434/ 3533 | 7309/ 13,108 | 5548/ 7921 | 0.51%/ 0.53% | 161.58%/ 224.21% | 1.2432 | 1.58% | 64,654 | 57.1581 | 72.82% |
| 19 | Dongincheon | 15,717/ 14,927 | 41,322/ 27,921 | 28,899/ 35,046 | 2.28%/ 2.22% | 183.87%/ 234.78% | 41.3551 | 52.65% | 66,278 | 29.8248 | 37.97% |
| 20 | Incheon | 3848/ 2928 | 5594/ 7670 | 8372/ 3438 | 0.56%/ 0.44% | 217.55%/ 117.42% | 16.8659 | 21.47% | 63,374 | 17.5826 | 22.38% |
| Station | AM 1 Boardings | AM Alightings | PM 1 Boardings | PM Alightings | Peak Total | Yearly Total | Scaling Factor | |
|---|---|---|---|---|---|---|---|---|
| 1 | Guyi | 4,580,226 | 1,475,469 | 2,704,515 | 4,479,963 | 13,240,173 | 20,635,576 | 1.558558 |
| 2 | Gaebong | 4,443,042 | 2,468,402 | 2,743,041 | 3,141,931 | 12,796,416 | 16,143,073 | 1.261531 |
| 3 | Oryudong | 3,619,922 | 1,159,960 | 2,672,647 | 4,645,136 | 12,097,665 | 15,972,817 | 1.320322 |
| 4 | Onsu | 5,082,743 | 930,173 | 1,697,688 | 3,626,816 | 11,337,420 | 16,523,268 | 1.457410 |
| 5 | Yeokgok | 3,737,141 | 843,703 | 1,345,129 | 3,001,733 | 8,927,706 | 13,190,330 | 1.477460 |
| 6 | Sosa | 2,590,723 | 1,120,094 | 1,773,611 | 2,104,396 | 7,588,824 | 11,844,327 | 1.560759 |
| 7 | Bucheon | 2,416,841 | 687,418 | 1,083,742 | 2,028,176 | 6,216,177 | 9,428,845 | 1.516824 |
| 8 | Jungdong | 1,606,093 | 1,188,577 | 1,708,109 | 1,320,295 | 5,823,074 | 8,471,168 | 1.454759 |
| 9 | Songnae | 2,045,578 | 391,656 | 720,105 | 1,376,646 | 4,533,985 | 7,168,508 | 1.581061 |
| 10 | Bukae | 1,437,546 | 847,500 | 958,925 | 974,593 | 4,218,564 | 6,247,492 | 1.480952 |
| 11 | Bupyeong | 1,450,680 | 504,338 | 686,819 | 1,059,718 | 3,701,555 | 6,968,009 | 1.882455 |
| 12 | Baewon | 1,597,012 | 405,025 | 559,892 | 1,028,934 | 3,590,863 | 5,445,604 | 1.516517 |
| 13 | Dongam | 1,529,967 | 357,465 | 515,808 | 1,006,280 | 3,409,520 | 5,052,937 | 1.482008 |
| 14 | Ganseok | 1,072,110 | 459,367 | 531,401 | 970,871 | 3,033,749 | 3,961,889 | 1.305938 |
| 15 | Jooan | 1,227,093 | 373,527 | 484,818 | 895,534 | 2,980,972 | 4,324,477 | 1.450694 |
| 16 | Dohwa | 926,521 | 492,619 | 542,034 | 739,247 | 2,700,421 | 4,357,195 | 1.613524 |
| 17 | Jaemowpo | 971,614 | 253,072 | 386,026 | 684,628 | 2,295,340 | 3,521,821 | 1.534335 |
| 18 | Dowon | 284,747 | 554,993 | 353,659 | 277,945 | 1,471,344 | 1,884,027 | 1.280480 |
| 19 | Dongincheon | 589,679 | 226,718 | 297,498 | 357,013 | 1,470,908 | 2,480,027 | 1.686052 |
| 20 | Incheon | 218,130 | 277,099 | 538,922 | 171,928 | 1,206,079 | 1,971,232 | 1.634414 |
| 1 | 2 | 3 | 4 | 5 | |
| Station | Bucheon | Songnae | Bupyeong | Yeokgok | Gaebong |
| Peak total | 6,216,177 | 4,533,985 | 6,216,177 | 8,927,706 | 12,796,416 |
| 6 | 7 | 8 | 9 | 10 | |
| Station | Jooan | Dongam | Dongincheon | Oryudong | Jaemowpo |
| Peak total | 2,980,972 | 3,409,520 | 1,470,908 | 2,097,665 | 1,471,344 |
| Station 1 | Importance Score | Cumulative Score | Cumulative Ratio | |
|---|---|---|---|---|
| 1 | Gaebong | 13,374,479 | 13,374,479 | 0.13209 |
| 2 | Bupyeong | 13,240,173 | 26,614,652 | 0.26286 |
| 3 | Songnae | 12,796,146 | 39,410,798 | 0.38925 |
| 4 | Yeokgok | 11,337,420 | 50,748,218 | 0.50123 |
| 5 | Dongincheon | 8,354,731 | 59,102,949 | 0.58374 |
| 6 | Jooan | 7,588,842 | 66,694,791 | 0.65869 |
| 7 | Oryudong | 6,297,195 | 72,988,986 | 0.72089 |
| 8 | Bucheon | 5,610,283 | 78,599,269 | 0.77631 |
| Time | Scenario 1 | Total Trips 1 | Total Travel Time (Person-Min) 2 | Average Travel Time (Sec/Trip) | |
|---|---|---|---|---|---|
| AM | S1 | All-stop service (baseline) | 17,546,111 | 8.949 × 108 | 3060.2 |
| S2 | Limited-stop express (standalone) | 4.978 × 108 | 1702.1 | ||
| S3 | Express with undergrounding and alignment improvement | 4.806 × 108 | 1643.4 | ||
| S4 | Express with headway adjustment | 4.802 × 108 | 1642.1 | ||
| S5 | Integrated operation (local + express + transfers) | 4.808 × 108 | 1644.1 | ||
| S6 | Integrated + express bus (free transfer) | 4.073 × 108 | 1392.9 | ||
| PM | S1 | All-stop service (baseline) | 61,662,049 | 2.717 × 109 | 2644.3 |
| S2 | Limited-stop express (standalone) | 1.679 × 109 | 1634.1 | ||
| S3 | Express with undergrounding and alignment improvement | 1.887 × 109 | 1837.1 | ||
| S4 | Express with headway adjustment | 1.887 × 109 | 1836.6 | ||
| S5 | Integrated operation (local + express + transfers) | 1.889 × 109 | 1837.9 | ||
| S6 | Integrated + express bus (free transfer) | 1.539 × 109 | 1498.3 | ||
| Category 1 | 1 | 2 | 3 |
| Observed Ratio (Express/All-Stop) | Model Ratio (S2/All-Stop) | Deviation (Model—Observed) | |
| AM | 0.741 | 0.556 | −0.185 |
| PM | 0.741 | 0.618 | −0.123 |
| Category | 4 | 5 | 6 |
| Observed ratio (Special express/All-stop) | Model ratio (S3/All-stop) | Deviation (Model—Observed) | |
| AM | 0.655 | 0.537 | −0.119 |
| PM | 0.655 | 0.659 | 0.039 |
| Case | Penalty Multiplier | Effect on Δ (Qualitative) |
|---|---|---|
| Base | 1.00× | Reference |
| Low | 0.90×/0.80× | Δ more negative (farther from zero) |
| High | 1.10×/1.20× | Δ less negative (closer to zero) |
| Category | Max. Skip-Stop Spacing (All-Stop/Express) | Average Travel Time (Sec) 1 | Total Travel Time (Min) | |
|---|---|---|---|---|
| AM | 1 | 6/12 | 2591.1 | 259,112 |
| 2 | 5/10 | 2580.5 | 258,054 | |
| 3 | 4/8 | 2564.7 | 256,467 | |
| 4 | 3.5/7 | 2553.3 | 255,334 | |
| PM | 5 | 7/14 | 2329.3 | 232,930 |
| 6 | 6/12 | 2315.5 | 231,552 | |
| 7 | 5/10 | 2296.2 | 229,622 |
| Block | Varied Field | Baseline | Range/Cases | Affected Component 1 |
|---|---|---|---|---|
| Coverage | K | 0.60 | {0.50, 0.60, 0.70} | Feasible set (upper level), equity constraint |
| Spacing | Max. inter-stop Spacing | ≤8 stations | {6, 8, 10} stations | Feasible set (upper level) |
| Headway | Peak headway grid | As in §2.3 | {2.5, 3.0, 3.5, 4.0, 5.0} min | Waiting cost, meets/overtakes |
| Dwell | α (load slope) | Equation (8) | ±10%, ±20% | Dwell endogeneity, platform queues |
| Dwell | β (base term) | Equation (8) | ±10%, ±20% | Minimum door/turnover time |
| Demand (Scale) | OD multiplier | 1.00 | 0.8, 0.9, 1.1, 1.2 | Loads on links/stations |
| Demand (Elasticity) | ε = d ln Q/d ln C | 0 | −0.1, −0.2 | Endogenous OD response |
| Parameter (Δ) | TT Change (%) | A30 Change (%) | A60 Change (%) | ETT | Notes |
|---|---|---|---|---|---|
| Headway H (−1 min at AM peak) | −1.0 [−1.3, −0.8] | +~1.0 | +(smaller) | +0.05 | = −20% 1 |
| Coverage K (+0.10) | ~0 | +0.95 (conservative) | ~0 | ~0 | Station-count × near-threshold(10%); ≈20 stations ⇒ +2 key stations |
| Non-stop limit L (−2 stations) | ~0 | ~0 | ~0 | ~0 | To be provided after stop-pattern re-optimisation |
| Dwell α (+20%) | +0.8–1.3 (AM); +0.5–0.9 (PM) | ~0 | ~0 | ~+0.04–+0.07 | From dwell regression; corridor-scale second-order |
| Dwell β (+20%) | +0.4–0.7 | ~0 | ~0 | ~+0.02–+0.04 | |
| Demand (OD × 1.20) | +(near-linear) | ± | ± | ~+1.0 | Proportional scaling; qualitative only |
| Time elasticity ε = −0.2 | ±(dampening) | ±(small) | ±(small) | small | Ordering unchanged |
| City | Corridor/Service | Comparator (Definition) | Reported Magnitude | Source Note |
|---|---|---|---|---|
| Tokyo | JR rapid/local on Yamanote–Keihin hubs | Express vs. all-stop, peak door-to-door to central business district | ΔP50, ΔP90 (mins); ≤45/60% | Scope: rail-only; includes in-vehicle + transfer; excludes road legs |
| Taipei | Taipei Metro mixed stopping to central business district | Limited-stop vs. all-stop, AM peak | Avg −xx%; ≤45/60 +x p.p | Door-to-door where available; otherwise user-equilibrium-adjusted in-vehicle |
| London | Thameslink/Elizabeth fast–semi-fast pairs | Fast vs. stopping, AM/PM | Avg −xx%; tail −xx min | Includes interchange penalties where published |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.-X.; Yoon, C.-J. Validating Express Rail Optimization with AFC and Backcasting: A Bi-Level Operations–Assignment Model to Improve Speed and Accessibility Along the Gyeongin Corridor. Appl. Sci. 2025, 15, 11652. https://doi.org/10.3390/app152111652
Li C-X, Yoon C-J. Validating Express Rail Optimization with AFC and Backcasting: A Bi-Level Operations–Assignment Model to Improve Speed and Accessibility Along the Gyeongin Corridor. Applied Sciences. 2025; 15(21):11652. https://doi.org/10.3390/app152111652
Chicago/Turabian StyleLi, Cheng-Xi, and Cheol-Jae Yoon. 2025. "Validating Express Rail Optimization with AFC and Backcasting: A Bi-Level Operations–Assignment Model to Improve Speed and Accessibility Along the Gyeongin Corridor" Applied Sciences 15, no. 21: 11652. https://doi.org/10.3390/app152111652
APA StyleLi, C.-X., & Yoon, C.-J. (2025). Validating Express Rail Optimization with AFC and Backcasting: A Bi-Level Operations–Assignment Model to Improve Speed and Accessibility Along the Gyeongin Corridor. Applied Sciences, 15(21), 11652. https://doi.org/10.3390/app152111652






