A Comprehensive Review of Rubber Contact Mechanics and Friction Theories
Abstract
1. Introduction
2. Overview of Contact Mechanics
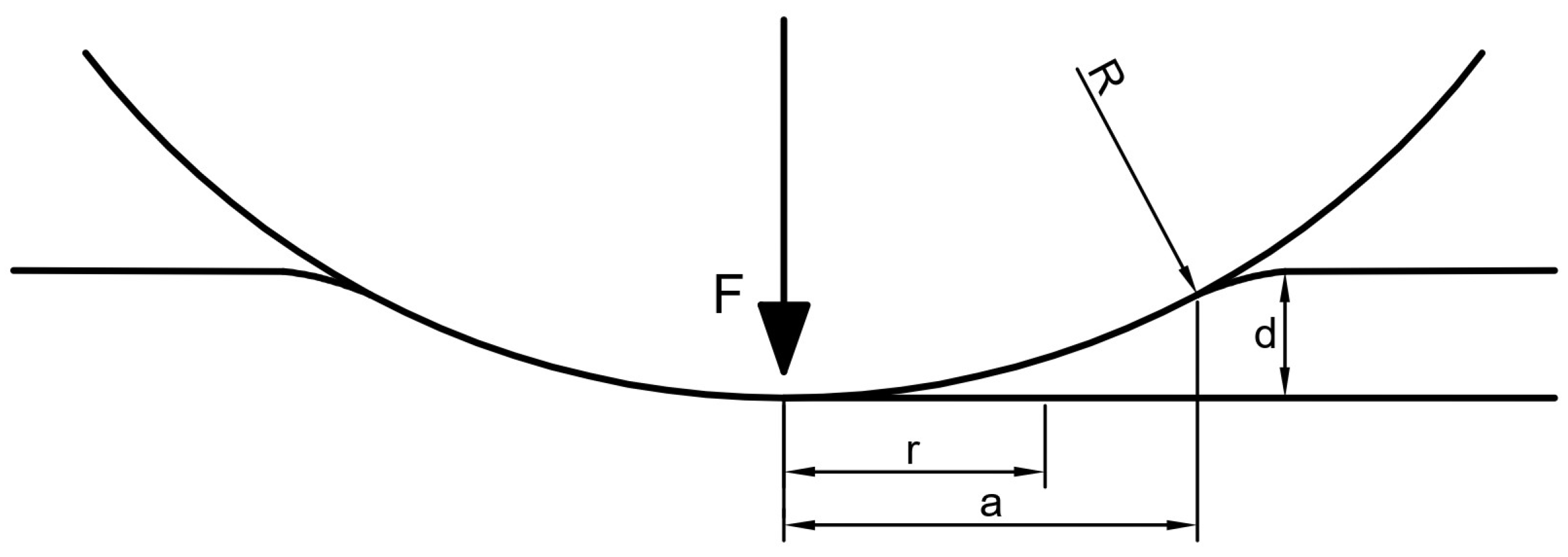
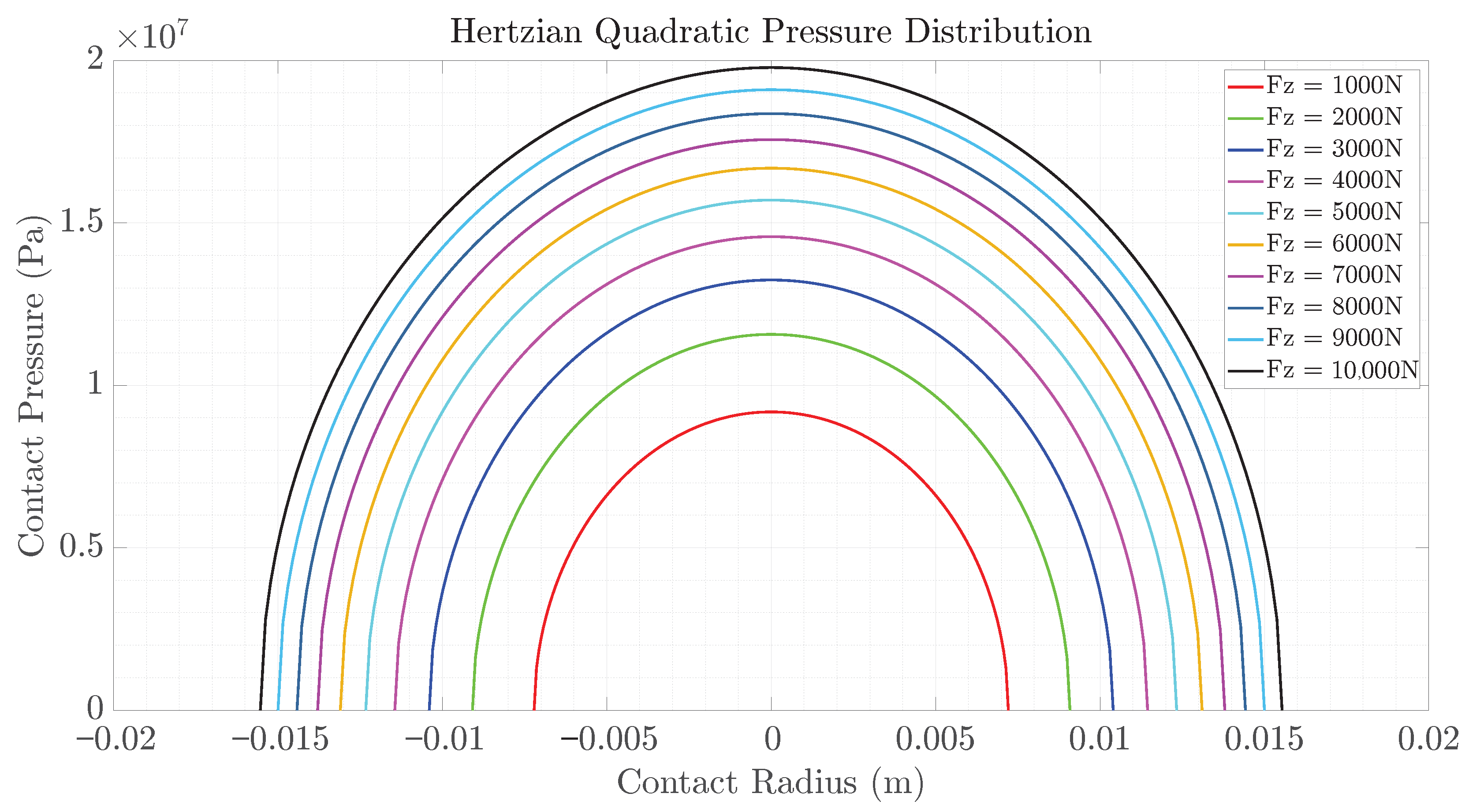
2.1. Hertzian Contact Theory
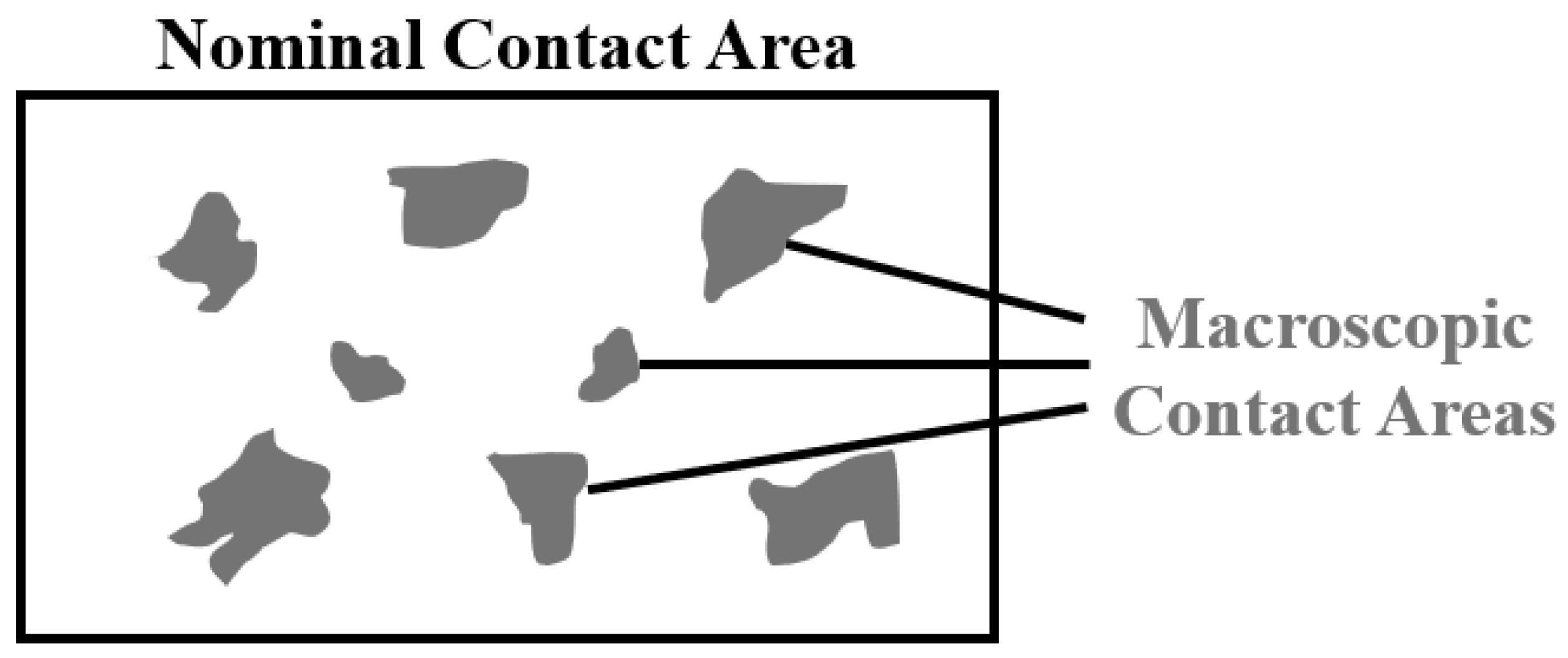
2.2. Surface Roughness in Contact Mechanics
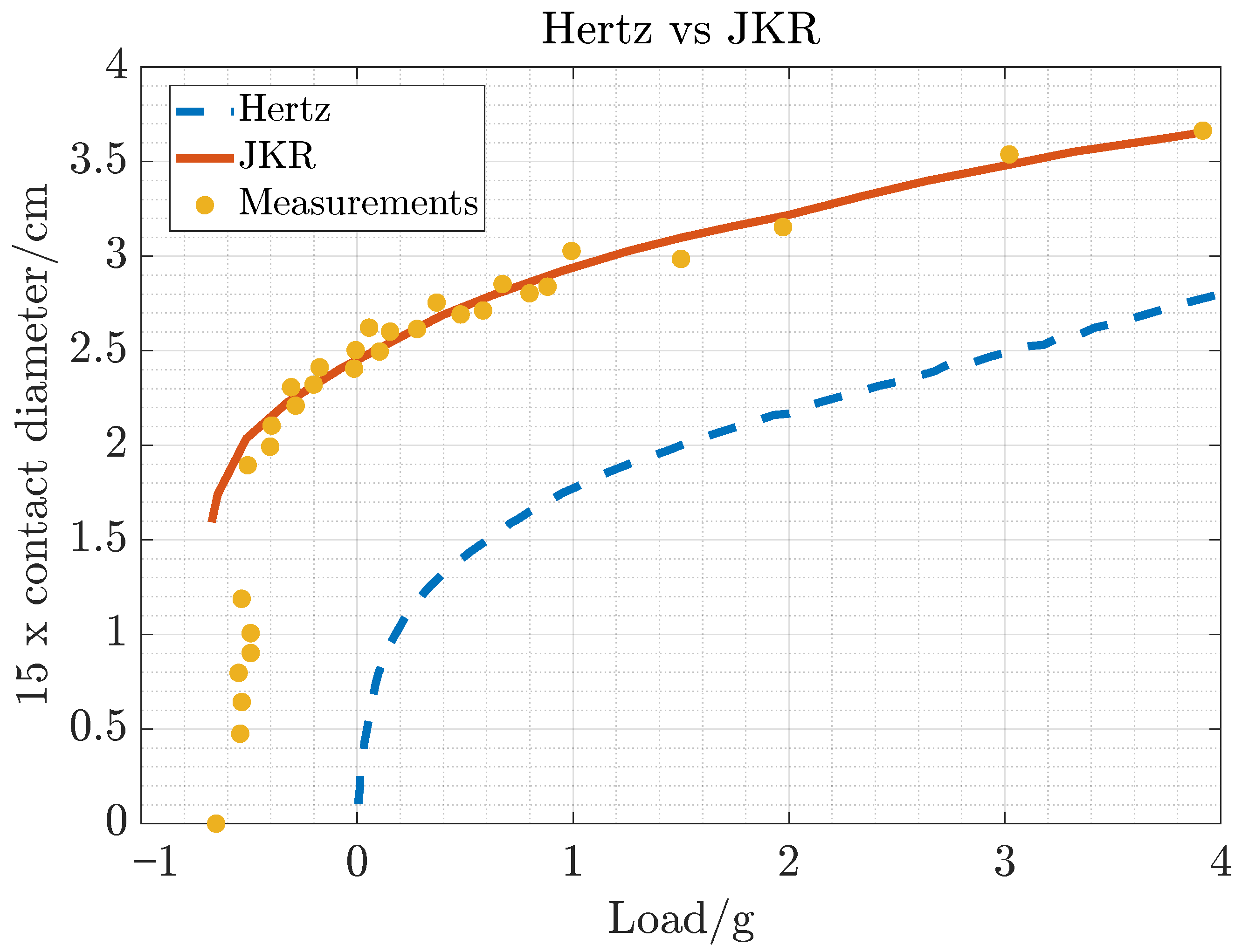
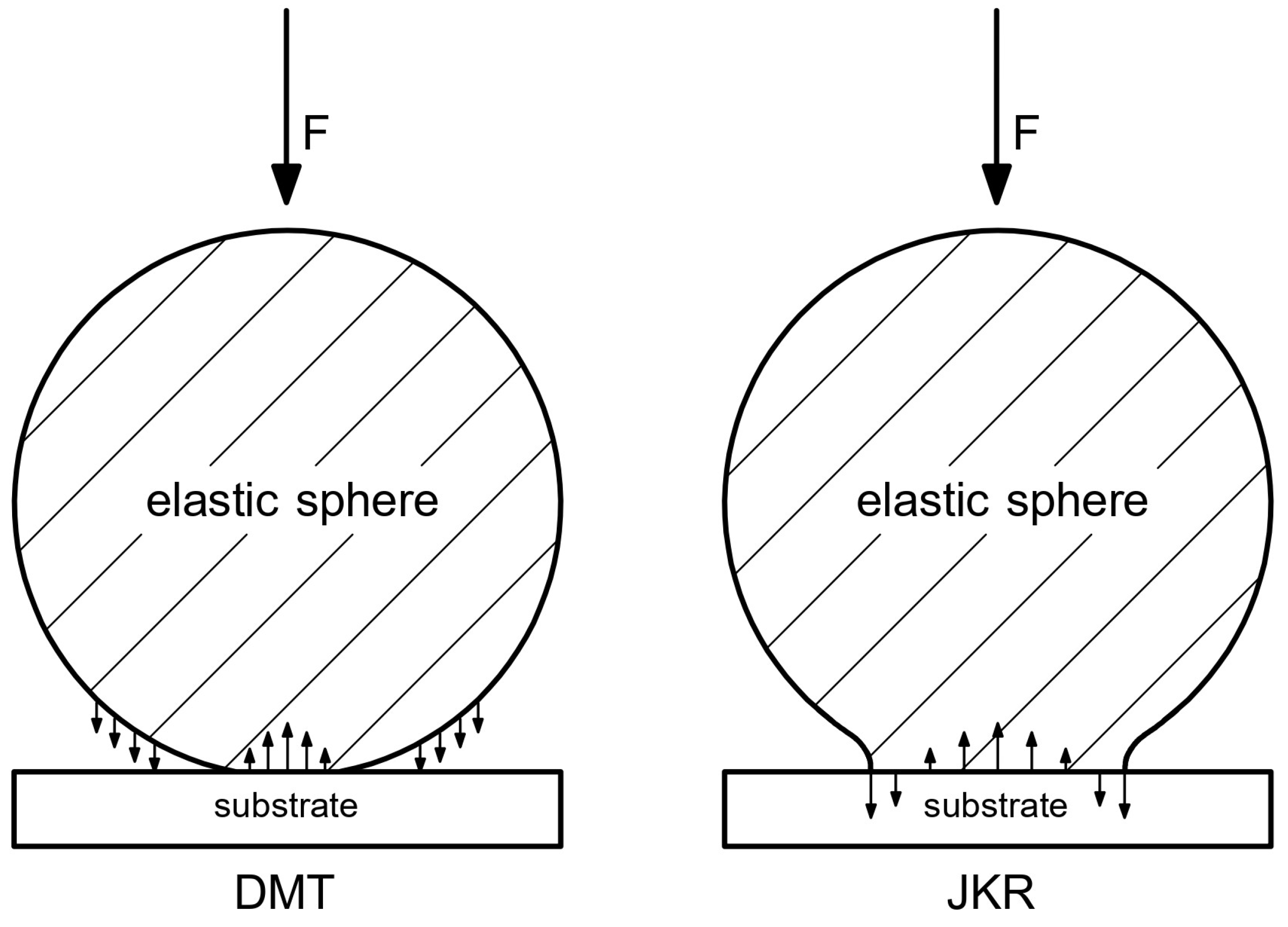
2.3. The Role of Adhesion in Contact Mechanics
- : DMT regime;
- : JKR regime.
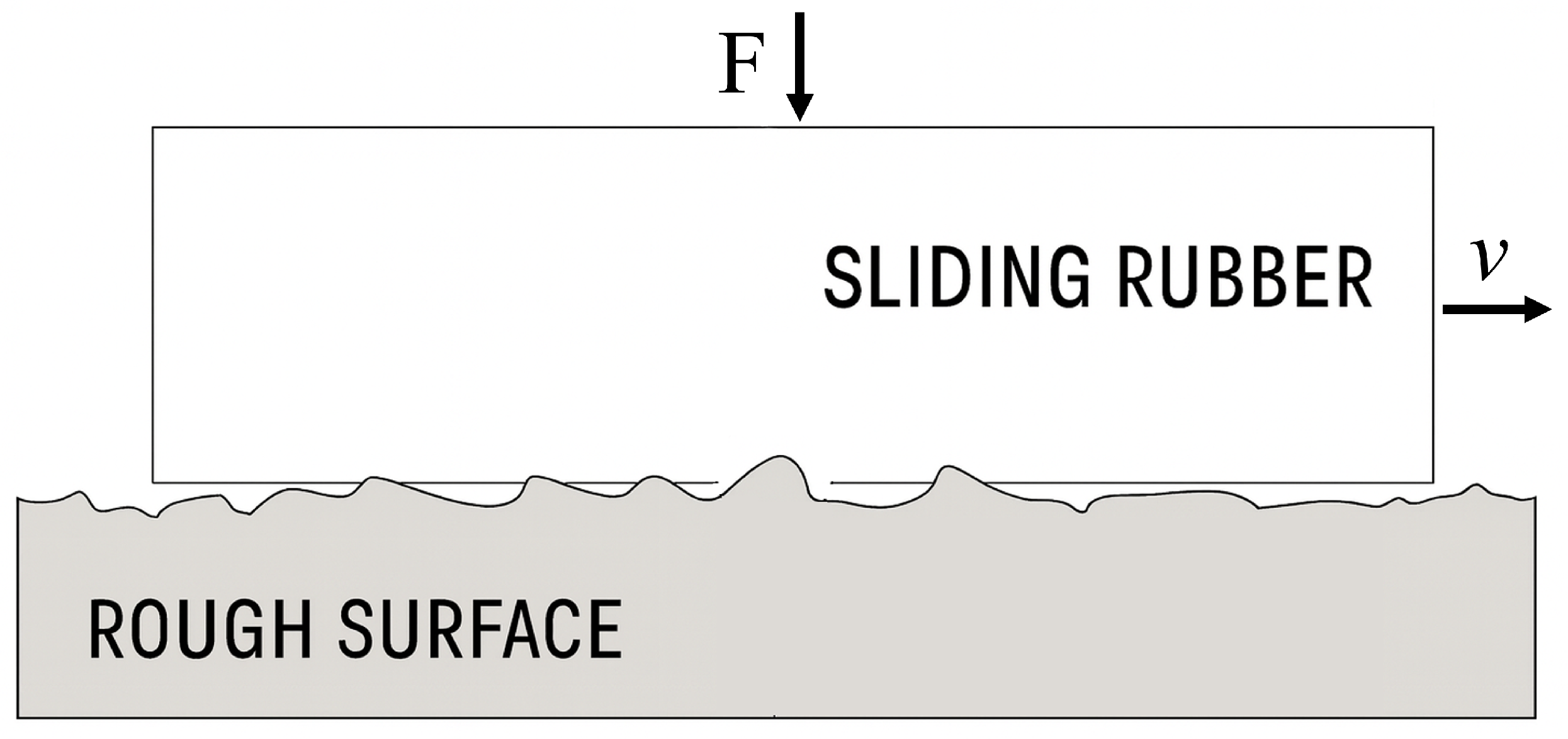
2.4. Modern Theories of Contact Mechanics: Rubber Block Sliding on Rough Surfaces
3. Fundamentals of Friction Theories
3.1. Grosch’s Experimental Tests
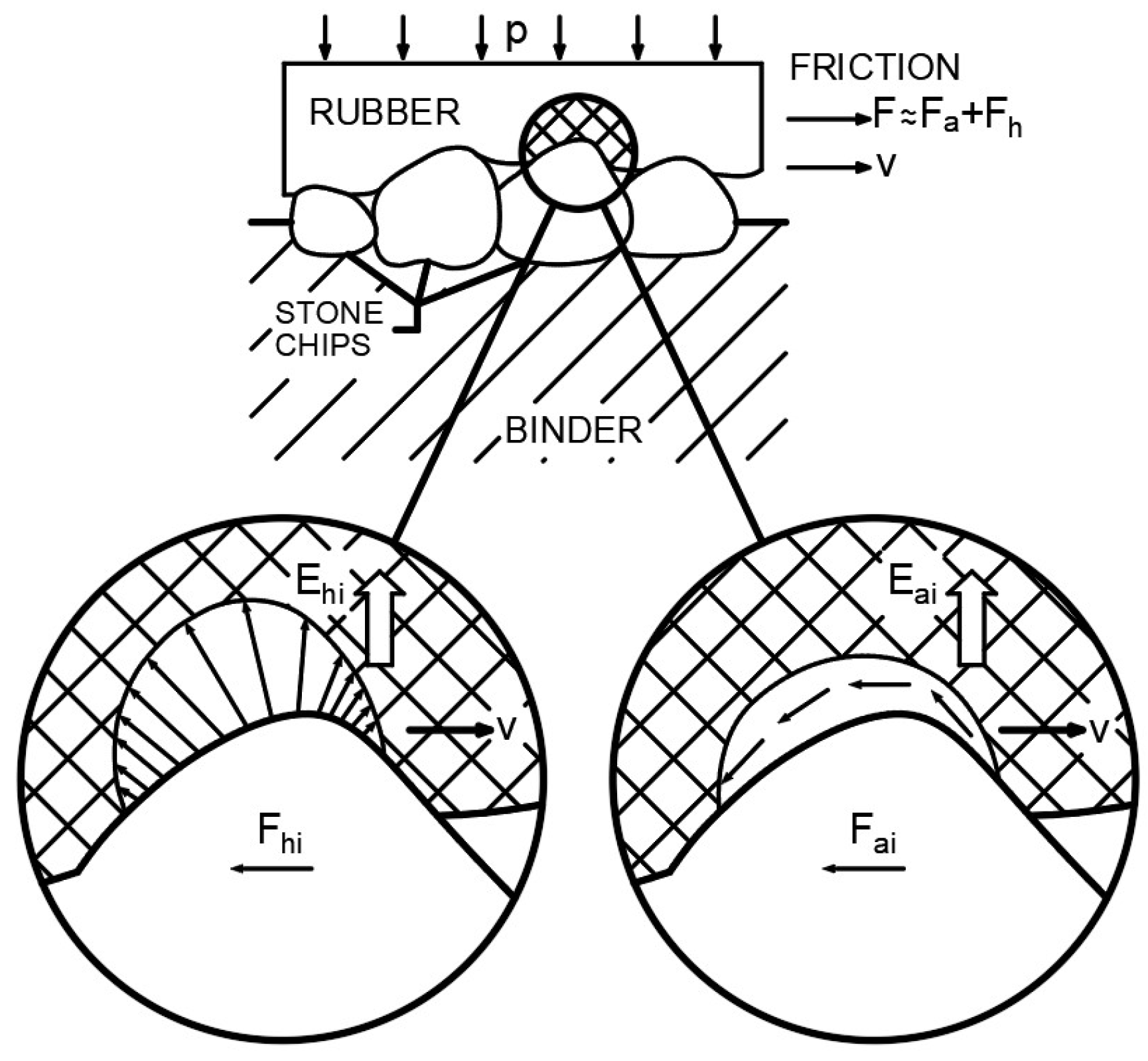
3.2. Klüppel and Heinrich’s Friction Model
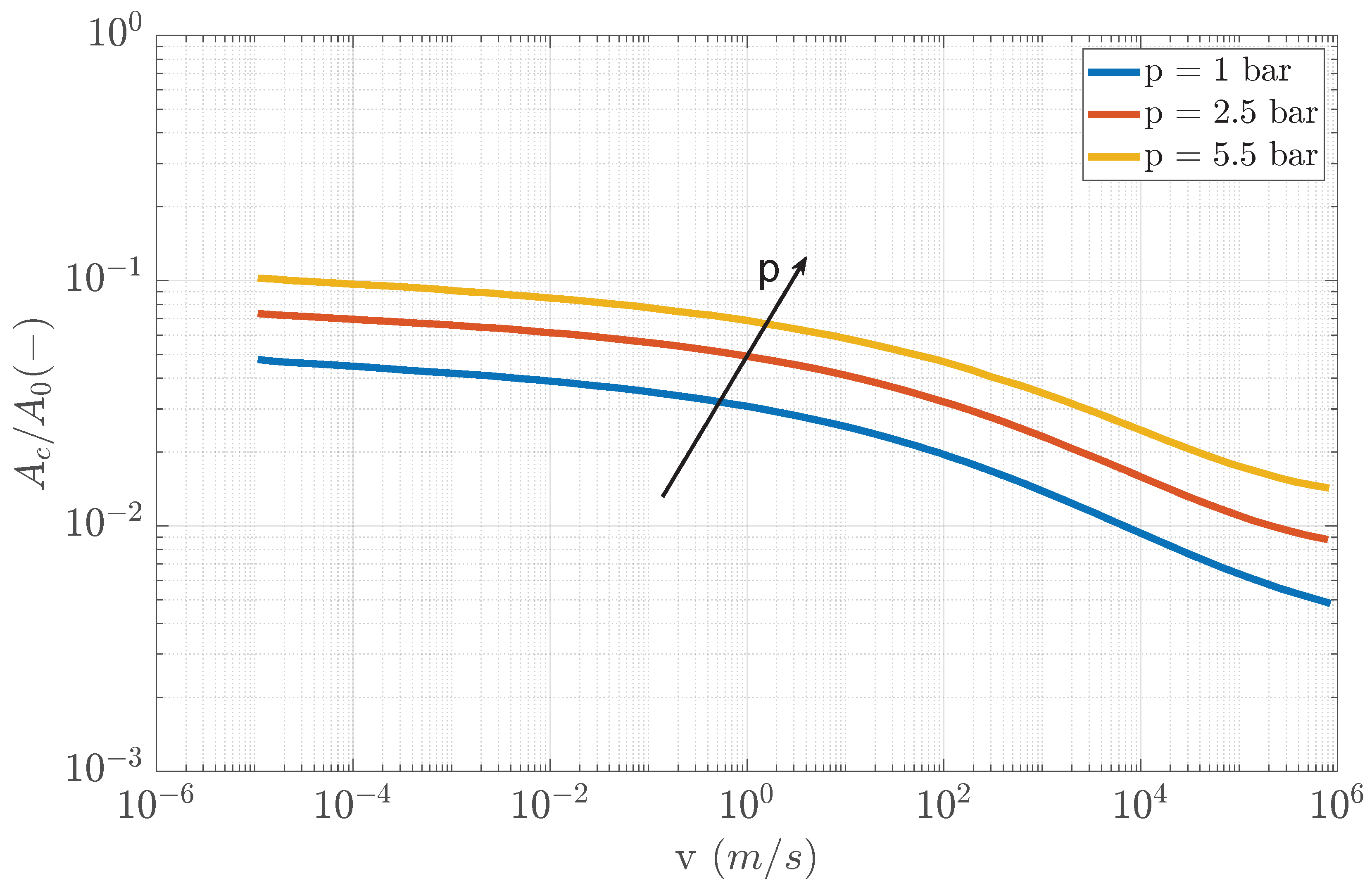
3.3. Persson’s Friction Model
4. Discussion and Research Gaps
4.1. Critical Analysis of Contact Mechanics Models
4.2. Comparative Discussion of Friction Models
4.3. Research Gaps and Future Challenges
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnson, K.L.; Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Alvarez, L.; Yi, J.; Horowitz, R.; Olmos, L. Dynamic friction model-based tire-road friction estimation and emergency braking control. J. Dyn. Sys. Meas. Control 2005, 127, 22–32. [Google Scholar] [CrossRef]
- Barber, J.R.; Ciavarella, M. Contact mechanics. Int. J. Solids Struct. 2000, 37, 29–43. [Google Scholar] [CrossRef]
- van Kuilenburg, J.; Masen, M.A.; van der Heide, E. A review of fingerpad contact mechanics and friction and how this affects tactile perception. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 243–258. [Google Scholar] [CrossRef]
- Barbaro, M.; Genovese, A.; Timpone, F.; Sakhnevych, A. Extension of the multiphysical magic formula tire model for ride comfort applications. Nonlinear Dyn. 2024, 112, 4183–4208. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Velychkovych, A.; Shatskyi, I.; Shopa, V. Efficient model of the interaction of elastomeric filler with an open shell and a chrome-plated shaft in a dry friction damper. Materials 2022, 15, 4671. [Google Scholar] [CrossRef]
- Shatskyi, I.; Velychkovych, A. Analytical model of structural damping in friction module of shell shock absorber connected to spring. Shock Vib. 2023, 2023, 4140583. [Google Scholar] [CrossRef]
- Velychkovych, A.; Mykhailiuk, V.; Andrusyak, A. Numerical model for studying the properties of a new friction damper developed based on the shell with a helical cut. Appl. Mech. 2025, 6, 1. [Google Scholar] [CrossRef]
- Velychkovych, A.; Mykhailiuk, V.; Andrusyak, A. Evaluation of the Adaptive Behavior of a Shell-Type Elastic Element of a Drilling Shock Absorber with Increasing External Load Amplitude. Vibration 2025, 8, 60. [Google Scholar] [CrossRef]
- Shull, K.R. Contact mechanics and the adhesion of soft solids. Mater. Sci. Eng. R Rep. 2002, 36, 1–45. [Google Scholar] [CrossRef]
- Bhushan, B. Contact mechanics of rough surfaces in tribology: Single asperity contact. Appl. Mech. Rev. 1996, 49, 275–298. [Google Scholar] [CrossRef]
- Jean, M. The non-smooth contact dynamics method. Comput. Methods Appl. Mech. Eng. 1999, 177, 235–257. [Google Scholar] [CrossRef]
- Tichy, J.A.; Meyer, D.M. Review of solid mechanics in tribology. Int. J. Solids Struct. 2000, 37, 391–400. [Google Scholar] [CrossRef]
- Persson, B. Rubber friction and tire dynamics. J. Phys. Condens. Matter 2010, 23, 015003. [Google Scholar] [CrossRef]
- Gravante, G.; Dell’Annunziata, G.N.; Barbaro, M.; Farroni, F. Experimental Methodology for Tire Ride Analysis Based on Outdoor Cleat Testing. SAE Int. J. Veh. Dyn. Stab. NVH 2025, 9, 357–376. [Google Scholar] [CrossRef]
- Ghaednia, H.; Wang, X.; Saha, S.; Xu, Y.; Sharma, A.; Jackson, R.L. A review of elastic–plastic contact mechanics. Appl. Mech. Rev. 2017, 69, 060804. [Google Scholar] [CrossRef]
- Jackson, R.L.; Ghaednia, H.; Lee, H.; Rostami, A.; Wang, X. Contact mechanics. In Tribology for Scientists and Engineers: From Basics to Advanced Concepts; Springer: New York, NY, USA, 2013; pp. 93–140. [Google Scholar]
- Goryacheva, I.G. Contact Mechanics in Tribology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 61. [Google Scholar]
- Zhang, S.; Li, D.; Liu, Y. Friction behavior of rough surfaces on the basis of contact mechanics: A review and prospects. Micromachines 2022, 13, 1907. [Google Scholar] [CrossRef] [PubMed]
- Popov, V.L. Contact Mechanics and Friction; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Popov, V.L.; Heß, M.; Willert, E. Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Raous, M.; Jean, M.; Moreau, J.J. Contact Mechanics; Plenum Press: New York, NY, USA, 1995. [Google Scholar]
- Gilardi, G.; Sharf, I. Literature survey of contact dynamics modelling. Mech. Mach. Theory 2002, 37, 1213–1239. [Google Scholar] [CrossRef]
- Eid, H.; Pamp, A. An Introductory Overview of Contact Mechanics and Adhesion; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ciavarella, M.; Joe, J.; Papangelo, A.; Barber, J. The role of adhesion in contact mechanics. J. R. Soc. Interface 2019, 16, 20180738. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Introduction to Contact Mechanics; Springer: New York, NY, USA, 2000. [Google Scholar]
- Johnson, K. Mechanics of adhesion. Tribol. Int. 1998, 31, 413–418. [Google Scholar] [CrossRef]
- Roberts, A.D. Rubber contact phenomena. Rubber Chem. Technol. 2014, 87, 383–416. [Google Scholar] [CrossRef]
- Dubois, G.; Cesbron, J.; Yin, H.P.; Anfosso-Lédée, F. Numerical evaluation of tyre/road contact pressures using a multi-asperity approach. Int. J. Mech. Sci. 2012, 54, 84–94. [Google Scholar] [CrossRef]
- Schallamach, A. Friction and abrasion of rubber. Wear 1958, 1, 384–417. [Google Scholar] [CrossRef]
- Müser, M.H.; Dapp, W.B.; Bugnicourt, R.; Sainsot, P.; Lesaffre, N.; Lubrecht, T.A.; Persson, B.N.; Harris, K.; Bennett, A.; Schulze, K.; et al. Meeting the contact-mechanics challenge. Tribol. Lett. 2017, 65, 118. [Google Scholar] [CrossRef]
- Mao, K.; Sun, Y.; Bell, T. Contact mechanics of engineering surfaces: State of the art. Surf. Eng. 1994, 10, 297–306. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angew. Math. 1881, 92, 156. [Google Scholar]
- Fischer-Cripps, A. The Hertzian contact surface. J. Mater. Sci. 1999, 34, 129–137. [Google Scholar] [CrossRef]
- Johnson, K.L. One hundred years of Hertz contact. Proc. Inst. Mech. Eng. 1982, 196, 363–378. [Google Scholar] [CrossRef]
- Wang, Q.J.; Zhu, D. Hertz theory: Contact of spherical surfaces. In Encyclopedia of Tribology; Springer: Boston, MA, USA, 2013; pp. 1654–1662. [Google Scholar]
- Tripp, J.H. Hertzian Contact in Two and Three Dimensions; National Aeronautics and Space Administration, Scientific and Technical Information Branch: Washington, DC, USA, 1985. [Google Scholar]
- Etter, J. Tutorial Report on Hertzian Contact Stress Theory; University of Arizona: Tucson, AZ, USA, 2000. [Google Scholar]
- Purushothaman, P.; Thankachan, P.; John, S.; Purushothaman, M. Hertz contact stress analysis and validation using finite element analysis. Int. J. Res. Appl. Sci. Eng. Technol. 2014, 2, 531–538. [Google Scholar]
- Dintwa, E.; Tijskens, E.; Ramon, H. On the accuracy of the Hertz model to describe the normal contact of soft elastic spheres. Granul. Matter 2008, 10, 209–221. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Galin, L. Kontakn’e Zadachi Teorii Uprugosti; Gosudarstvennoe Izdatel’stvo Tekhniko-Teoreticheskoi Literatury: Moscow, Russia, 1953. [Google Scholar]
- Bhushan, B. Contact mechanics of rough surfaces in tribology: Multiple asperity contact. Tribol. Lett. 1998, 4, 1–35. [Google Scholar] [CrossRef]
- Taylor, R.I. Rough surface contact modelling—A review. Lubricants 2022, 10, 98. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Characterization and modeling of surface roughness and contact mechanics. In Handbook of Micro/Nano Tribology; CRC Press: Boca Raton, FL, USA, 1995; pp. 109–165. [Google Scholar]
- Sofonea, M.; Matei, A. Mathematical Models in Contact Mechanics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bowden, F.P.; Tabor, D. The area of contact between stationary and moving surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 169, 391–413. [Google Scholar]
- Bowden, F.; Tabor, D. Friction, lubrication and wear: A survey of work during the last decade. Br. J. Appl. Phys. 1966, 17, 1521. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Oxford University Press: Oxford, UK, 2001; Volume 1. [Google Scholar]
- Tabor, D. Friction, surface science and tribology—A personal view. Proc. Inst. Mech. Eng. Part C Mech. Eng. Sci. 1991, 205, 365–378. [Google Scholar] [CrossRef]
- Carbone, G.; Bottiglione, F. Contact mechanics of rough surfaces: A comparison between theories. Meccanica 2011, 46, 557–565. [Google Scholar] [CrossRef]
- Archard, J. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Archard, J. Elastic deformation and the laws of friction. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 243, 190–205. [Google Scholar]
- Archard, J. Single contacts and multiple encounters. J. Appl. Phys. 1961, 32, 1420–1425. [Google Scholar] [CrossRef]
- Emami, A.; Khaleghian, S.; Taheri, S. Asperity-based modification on theory of contact mechanics and rubber friction for self-affine fractal surfaces. Friction 2021, 9, 1707–1725. [Google Scholar] [CrossRef]
- Adams, G.G.; Mu ftu, S.; Azhar, N.M. A scale-dependent model for multi-asperity contact and friction. J. Tribol. 2003, 125, 700–708. [Google Scholar] [CrossRef]
- Popov, V.L.; Dimaki, A.; Psakhie, S.; Popov, M. On the role of scales in contact mechanics and friction between elastomers and randomly rough self-affine surfaces. Sci. Rep. 2015, 5, 11139. [Google Scholar] [CrossRef]
- Hanaor, D.A.; Gan, Y.; Einav, I. Contact mechanics of fractal surfaces by spline assisted discretisation. Int. J. Solids Struct. 2015, 59, 121–131. [Google Scholar] [CrossRef]
- Buzio, R.; Boragno, C.; Biscarini, F.; Buatier De Mongeot, F.; Valbusa, U. The contact mechanics of fractal surfaces. Nat. Mater. 2003, 2, 233–236. [Google Scholar] [CrossRef]
- Borodich, F.M. Fractal contact mechanics. In Encyclopedia of Tribology; Springer: Boston, MA, USA, 2013; pp. 1249–1258. [Google Scholar]
- Majumdar, A.; Bhushan, B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Bush, A.; Gibson, R.; Thomas, T. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Ciavarella, M.; Greenwood, J.; Paggi, M. Inclusion of “interaction” in the Greenwood and Williamson contact theory. Wear 2008, 265, 729–734. [Google Scholar] [CrossRef]
- Ciavarella, M.; Delfine, V.; Demelio, G. A “re-vitalized” Greenwood and Williamson model of elastic contact between fractal surfaces. J. Mech. Phys. Solids 2006, 54, 2569–2591. [Google Scholar] [CrossRef]
- Adams, G.; Nosonovsky, M. Contact modeling—Forces. Tribol. Int. 2000, 33, 431–442. [Google Scholar] [CrossRef]
- Yakovenko, A.A.; Goryacheva, I.G. Analysis of the discrete contact characteristics based on the Greenwood-Williamson model and the localization principle. Friction 2024, 12, 1042–1056. [Google Scholar] [CrossRef]
- Ciavarella, M.; Leoci, F. An assessment of the Greenwood-Williamson and other asperities models, with special reference to electrical conductance. J. Tribol. 2006, 128, 10–17. [Google Scholar] [CrossRef]
- Farroni, F.; Stefanelli, R.; Dell’Annunziata, G.N.; Timpone, F. Impact of the tire/road local contact area on tire friction, with a novel approach based on Greenwood-Williamson theory and validation in both laboratory and outdoor racing environments. Tribol. Int. 2025, 210, 110772. [Google Scholar] [CrossRef]
- Zhao, T.; Feng, Y. Extended Greenwood–Williamson models for rough spheres. J. Appl. Mech. 2018, 85, 101007. [Google Scholar] [CrossRef]
- Li, C.Y.; Ding, Y.; Liang, X.M.; Wang, G.F. An improved elastic–plastic contact model with asperity interactions based on Greenwood–Williamson theory. Acta Mech. 2023, 234, 5187–5201. [Google Scholar] [CrossRef]
- McWaid, T.; Marschall, E. Application of the modified Greenwood and Williamson contact model for the prediction of thermal contact resistance. Wear 1992, 152, 263–277. [Google Scholar] [CrossRef]
- Jones, R.E. A Greenwood-Williamson model of small-scale friction. J. Appl. Mech. 2007, 74, 31–40. [Google Scholar] [CrossRef]
- Bush, A.; Gibson, R.; Keogh, G. The limit of elastic deformation in the contact of rough surfaces. Mech. Res. Commun. 1976, 3, 169–174. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Wang, L.; Yu, T. Mechanics of adhesion in MEMS—A review. J. Adhes. Sci. Technol. 2003, 17, 519–546. [Google Scholar] [CrossRef]
- Persson, B.N.; Albohr, O.; Tartaglino, U.; Volokitin, A.I.; Tosatti, E. On the nature of surface roughness with application to contact mechanics, sealing, rubberfriction and adhesion. J. Phys. Condens. Matter 2004, 17, R1. [Google Scholar] [CrossRef]
- Popov, V.L.; Li, Q.; Lyashenko, I.A. Contact mechanics and friction: Role of adhesion. Friction 2025, 13, 9440964. [Google Scholar] [CrossRef]
- Marshall, S.J.; Bayne, S.C.; Baier, R.; Tomsia, A.P.; Marshall, G.W. A review of adhesion science. Dent. Mater. 2010, 26, e11–e16. [Google Scholar] [CrossRef]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces; Interscience Publishers: New York, NY, USA, 1967; Volume 150. [Google Scholar]
- Lee, L.H. Fundamentals of Adhesion; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bhushan, B. Adhesion and stiction: Mechanisms, measurement techniques, and methods for reduction. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Processing, Meas. Phenom. 2003, 21, 2262–2296. [Google Scholar] [CrossRef]
- Kendall, K.; Roberts, A. van der Waals forces influencing adhesion of cells. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140078. [Google Scholar] [CrossRef]
- Roberts, A. A guide to estimating the friction of rubber. Rubber Chem. Technol. 1992, 65, 673–686. [Google Scholar] [CrossRef]
- Kendall, K. Adhesion: Molecules and mechanics. Science 1994, 263, 1720–1725. [Google Scholar] [CrossRef]
- Bradley, R.S. LXXIX. The cohesive force between solid surfaces and the surface energy of solids. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1932, 13, 853–862. [Google Scholar] [CrossRef]
- Nakajima, Y. Advanced Tire Mechanics; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Schultz, J.; Nardin, M. Theories and mechanisms of adhesion. Mater. Eng. N. Y. 1999, 14, 1–26. [Google Scholar]
- Packham, D. The mechanical theory of adhesion. In Handbook of Adhesive Technology; CRC Press: Boca Raton, FL, USA, 2003; pp. 69–93. [Google Scholar]
- Johnson, K.L.; Kendall, K.; Roberts, A. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar]
- Derjaguin, B.V.; Muller, V.M.; Toporov, Y.P. Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Barthel, E. Adhesive elastic contacts: JKR and more. J. Phys. D Appl. Phys. 2008, 41, 163001. [Google Scholar] [CrossRef]
- Hui, C.Y.; Baney, J.; Kramer, E. Contact mechanics and adhesion of viscoelastic spheres. Langmuir 1998, 14, 6570–6578. [Google Scholar] [CrossRef]
- Coetzee, C. Simplified johnson-kendall-roberts (sjkr) contact model. In University of Stellenbosch Report; University of Stellenbosch: Stellenbosch, South Africa, 2020. [Google Scholar]
- Charrault, E.; Gauthier, C.; Marie, P.; Schirrer, R. Experimental and theoretical analysis of a dynamic JKR contact. Langmuir 2009, 25, 5847–5854. [Google Scholar] [CrossRef]
- Johnson, K. The adhesion of two elastic bodies with slightly wavy surfaces. Int. J. Solids Struct. 1995, 32, 423–430. [Google Scholar] [CrossRef]
- Pashley, M. Further consideration of the DMT model for elastic contact. Colloids Surf. 1984, 12, 69–77. [Google Scholar] [CrossRef]
- Violano, G.; Demelio, G.P.; Afferrante, L. On the DMT adhesion theory: From the first studies to the modern applications in rough contacts. Procedia Struct. Integr. 2018, 12, 58–70. [Google Scholar] [CrossRef]
- Violano, G.; Afferrante, L. On DMT methods to calculate adhesion in rough contacts. Tribol. Int. 2019, 130, 36–42. [Google Scholar] [CrossRef]
- Greenwood, J. On the DMT theory. Tribol. Lett. 2007, 26, 203–211. [Google Scholar] [CrossRef]
- Prokopovich, P.; Perni, S. Comparison of JKR-and DMT-based multi-asperity adhesion model: Theory and experiment. Colloids Surf. A Physicochem. Eng. Asp. 2011, 383, 95–101. [Google Scholar] [CrossRef]
- Tabor, D. Surface forces and surface interactions. In Plenary and Invited Lectures; Elsevier: Amsterdam, The Netherlands, 1977; pp. 3–14. [Google Scholar]
- Muller, V.; Yushchenko, V.; Derjaguin, B. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane. J. Colloid Interface Sci. 1980, 77, 91–101. [Google Scholar] [CrossRef]
- Maugis, D. Adhesion of spheres: The JKR-DMT transition using a Dugdale model. J. Colloid Interface Sci. 1992, 150, 243–269. [Google Scholar] [CrossRef]
- Zhang, Y. Transitions between different contact models. J. Adhes. Sci. Technol. 2008, 22, 699–715. [Google Scholar]
- Maugis, D.; Gauthier-Manuel, B. JKR-DMT transition in the presence of a liquid meniscus. J. Adhes. Sci. Technol. 1994, 8, 1311–1322. [Google Scholar] [CrossRef]
- Maugis, D. The JKR-DMT transition in the presence of a liquid meniscus and the extension of the JKR theory to large contact radii. In Contact Mechanics; Springer: Boston, MA, USA, 1995; pp. 335–342. [Google Scholar]
- Maugis, D. On the contact and adhesion of rough surfaces. J. Adhes. Sci. Technol. 1996, 10, 161–175. [Google Scholar] [CrossRef]
- Maugis, D. Contact, Adhesion and Rupture of Elastic Solids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; Volume 130. [Google Scholar]
- Shi, X.; Zhao, Y.P. Comparison of various adhesion contact theories and the influence of dimensionless load parameter. J. Adhes. Sci. Technol. 2004, 18, 55–68. [Google Scholar] [CrossRef]
- Ramakrishna, S.N.; Nalam, P.C.; Clasohm, L.Y.; Spencer, N.D. Study of adhesion and friction properties on a nanoparticle gradient surface: Transition from JKR to DMT contact mechanics. Langmuir 2013, 29, 175–182. [Google Scholar] [CrossRef]
- Carbone, G.; Lorenz, B.; Persson, B.N.; Wohlers, A. Contact mechanics and rubber friction for randomly rough surfaces with anisotropic statistical properties. Eur. Phys. J. E 2009, 29, 275–284. [Google Scholar] [CrossRef]
- Scaraggi, M.; Persson, B.N. General contact mechanics theory for randomly rough surfaces with application to rubber friction. J. Chem. Phys. 2015, 143, 224111. [Google Scholar] [CrossRef]
- Flores, P. Contact mechanics for dynamical systems: A comprehensive review. Multibody Syst. Dyn. 2022, 54, 127–177. [Google Scholar] [CrossRef]
- Le Gal, A.; Yang, X.; Klüppel, M. Evaluation of sliding friction and contact mechanics of elastomers based on dynamic-mechanical analysis. J. Chem. Phys. 2005, 123, 014704. [Google Scholar] [CrossRef]
- Kluppel, M.; Heinrich, G. Rubber friction on self-affine road tracks. Rubber Chem. Technol. 2000, 73, 578–606. [Google Scholar] [CrossRef]
- Lang, A.; Klüppel, M. Influences of temperature and load on the dry friction behaviour of tire tread compounds in contact with rough granite. Wear 2017, 380, 15–25. [Google Scholar] [CrossRef]
- Heinrich, G.; Klüppel, M. Rubber friction, tread deformation and tire traction. Wear 2008, 265, 1052–1060. [Google Scholar] [CrossRef]
- Le Gal, A.; Klüppel, M. Modeling of rubber friction: A quantitative description of the hysteresis and adhesion contribution. In Constitutive Models for Rubber IV; Routledge: Oxfordshire, UK, 2017; pp. 509–514. [Google Scholar]
- Lang, A.; Klüppel, M. Modelling predictions and experimental investigations of rubber friction and tire traction. In Proceedings of the 4th International Tyre Colloquium: Tyre Models for Vehicle Dynamics Analysis, Guildford, UK, 20–21 April 2015; University of Surrey: Guildford, UK, 2015; pp. 228–233. [Google Scholar]
- Li, L.; Wang, K.C.; Luo, W. Pavement friction estimation based on the Heinrich/Klüppel model. Period. Polytech. Transp. Eng. 2016, 44, 89–96. [Google Scholar] [CrossRef]
- Lang, A.; Klüppel, M. Temperature and Pressure dependence of the friction properties of tire tread compounds on rough granite. In Proceedings of the KHK 11th Fall Rubber Colloquium, Hannover, Germany, 26–28 November 2014. [Google Scholar]
- Klüppel, M.; Müller, A.; Le Gal, A.; Heinrich, G.; Continental, A. Dynamic Contact of Tires Dynamic Contact of Tires with Road Tracks with Road Tracks; Rubber Division, American Chemical Society: San Francisco, CA, USA, 2003. [Google Scholar]
- Le Gal, A.; Yang, X.; Klüppel, M. Sliding friction and contact mechanics of elastomers on rough surfaces. In Analysis and Simulation of Contact Problems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 253–260. [Google Scholar]
- Le Gal, A.; Guy, L.; Orange, G.; Bomal, Y.; Klüppel, M. Modelling of sliding friction for carbon black and silica filled elastomers on road tracks. Wear 2008, 264, 606–615. [Google Scholar] [CrossRef]
- Le Gal, A.; Klüppel, M. Investigation and modelling of rubber stationary friction on rough surfaces. J. Phys. Condens. Matter 2007, 20, 015007. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelasticity; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Lakes, R.S. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Papazian, H.S. The Response of Linear Viscoelastic Materials in the Frequency Domain; The Ohio State University: Columbus, OH, USA, 1961. [Google Scholar]
- Schapery, R.A. On the characterization of nonlinear viscoelastic materials. Polym. Eng. Sci. 1969, 9, 295–310. [Google Scholar] [CrossRef]
- Tomanik, E.; Chacon, H.; Teixeira, G. A simple numerical procedure to calculate the input data of Greenwood-Williamson model of asperity contact for actual engineering surfaces. In Tribology Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 41, pp. 205–215. [Google Scholar]
- Nayak, P.R. Random process model of rough surfaces. J. Lubr. Technol. 1971, 93, 398–407. [Google Scholar] [CrossRef]
- Heinrich, G.; Klüppel, M.; Vilgis, T.A. Evaluation of self-affine surfaces and their implication for frictional dynamics as illustrated with a Rouse material. Comput. Theor. Polym. Sci. 2000, 10, 53–61. [Google Scholar] [CrossRef]
- Vanormelingen, K.; Degroote, B.; Vantomme, A. Quantitative characterization of the surface morphology using a height difference correlation function. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2006, 24, 725–729. [Google Scholar] [CrossRef]
- Torbruegge, S.; Wies, B. Characterization of pavement texture by means of height difference correlation and relation to wet skid resistance. J. Traffic Transp. Eng. (Engl. Ed.) 2015, 2, 59–67. [Google Scholar] [CrossRef]
- Landini, G.; Rigaut, J.P. A method for estimating the dimension of asymptotic fractal sets. Bioimaging 1997, 5, 65–70. [Google Scholar] [CrossRef]
- Persson, B.N. On the theory of rubber friction. Surf. Sci. 1998, 401, 445–454. [Google Scholar] [CrossRef]
- Persson, B.; Volokitin, A. Rubber friction on smooth surfaces. Eur. Phys. J. E 2006, 21, 69–80. [Google Scholar] [CrossRef]
- Yang, C.; Persson, B.N. Contact mechanics: Contact area and interfacial separation from small contact to fullcontact. J. Phys. Condens. Matter 2008, 20, 215214. [Google Scholar] [CrossRef]
- Persson, B.N. Sliding Friction: Physical Principles and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Persson, B.N. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Persson, B.N.; Tosatti, E. Physics of Sliding Friction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 311. [Google Scholar]
- Persson, B.N. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef]
- Persson, B. Adhesion between an elastic body and a randomly rough hard surface. Eur. Phys. J. E 2002, 8, 385–401. [Google Scholar] [CrossRef]
- Jacobs, T.D.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B.; Fortunato, G.; Giustiniano, M.; Baldoni, F. Rubber friction for tire tread compound on road surfaces. J. Phys. Condens. Matter 2013, 25, 095007. [Google Scholar] [CrossRef]
- Genovese, A.; Farroni, F.; Papangelo, A.; Ciavarella, M. A discussion on present theories of rubber friction, with particular reference to different possible choices of arbitrary roughness cutoff parameters. Lubricants 2019, 7, 85. [Google Scholar] [CrossRef]
- Sanyal, A. On the Short Wavelength Cutoff Limit in Persson’s Hysteresis Friction Theory. J. Tribol. 2026, 148, 014501. [Google Scholar] [CrossRef]
- Müser, M.H.; Dapp, W.B. The contact mechanics challenge: Problem definition. arXiv 2015, arXiv:1512.02403. [Google Scholar] [CrossRef]
- Müser, M.H.; Nicola, L. Modeling the surface topography dependence of friction, adhesion, and contact compliance. MRS Bull. 2022, 47, 1221–1228. [Google Scholar] [CrossRef]
- Farroni, F. Development of a Grip and Thermodynamics Sensitive Tyre/Road Interaction Forces Characterization Procedure Employed in High-Performance Vehicles Simulation; University of Naples Federico” II: Naples, Italy, 2014. [Google Scholar]
- Pennestrì, E.; Rossi, V.; Salvini, P.; Valentini, P.P. Review and comparison of dry friction force models. Nonlinear Dyn. 2016, 83, 1785–1801. [Google Scholar] [CrossRef]
- Van Der Steen, R. Tyre/Road Friction Modeling: Literature Survey; Eindhoven University of Technology: Eindhoven, The Netherlands, 2007. [Google Scholar]
- Persson, B.; Xu, R. Rubber Friction: Theory, Mechanisms, and Challenges. arXiv 2025, arXiv:2507.18782. [Google Scholar] [CrossRef]
- KUMMER, H.W. Rubber and Tire Friction; The Pennsylvania State University: University Park, PA, USA, 1965. [Google Scholar]
- Smith, R.H. Analyzing Friction in the Design of Rubber Products and Their Paired Surfaces; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Greenwood, J.; Minshall, H.; Tabor, D. Hysteresis losses in rolling and sliding friction. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1961, 259, 480–507. [Google Scholar]
- Moore, D.; Geyer, W. A review of hysteresis theories for elastomers. Wear 1974, 30, 1–34. [Google Scholar] [CrossRef]
- Heinrich, G. Hysteresis friction of sliding rubbers on rough and fractal surfaces. Rubber Chem. Technol. 1997, 70, 1–14. [Google Scholar] [CrossRef]
- Wojewoda, J.; Stefański, A.; Wiercigroch, M.; Kapitaniak, T. Hysteretic effects of dry friction: Modelling and experimental studies. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 747–765. [Google Scholar] [CrossRef]
- McFarlane, J.; Tabor, D. Relation between friction and adhesion. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 202, 244–253. [Google Scholar]
- Chernyak, Y.B.; Leonov, A. On the theory of the adhesive friction of elastomers. Wear 1986, 108, 105–138. [Google Scholar] [CrossRef]
- Zeng, H. Polymer Adhesion, Friction, and Lubrication; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Landheer, D.; De Gee, A. Adhesion, friction, and wear. MRS Bull. 1991, 16, 36–40. [Google Scholar] [CrossRef]
- Chaudhury, M.K.; Owen, M.J. Adhesion hysteresis and friction. Langmuir 1993, 9, 29–31. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Chen, Y.L.; Yoshizawa, H. Relationship between adhesion and friction forces. J. Adhes. Sci. Technol. 1994, 8, 1231–1249. [Google Scholar] [CrossRef]
- Popov, V.L. Adhesive contribution to friction. In Proceedings of the International Conference on Advanced Materials with Hierarchical Structure for New Technologies and Reliable Structures 2019, Tomsk, Russia, 1–5 October 2019; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2167, p. 020286. [Google Scholar]
- Savkoor, A. On the friction of rubber. Wear 1965, 8, 222–237. [Google Scholar] [CrossRef]
- Persson, B.N.; Tosatti, E. Qualitative theory of rubber friction and wear. J. Chem. Phys. 2000, 112, 2021–2029. [Google Scholar] [CrossRef]
- Moore, D.F. Friction and wear in rubbers and tyres. Wear 1980, 61, 273–282. [Google Scholar] [CrossRef]
- Grosch, K. The relation between the friction and visco-elastic properties of rubber. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1963, 274, 21–39. [Google Scholar]
- Grosch, K. The rolling resistance, wear and traction properties of tread compounds. Rubber Chem. Technol. 1996, 69, 495–568. [Google Scholar] [CrossRef]
- Grosch, K. Rubber friction and tire traction. In The Pneumatic Tire; 2006; p. 421. Available online: https://andrzejdebowski.wat.edu.pl/include/wiedza/kolo-ogumione/The%20Pneumatic%20Tire%20NHTSA.pdf (accessed on 27 October 2025).
- Grosch, K. Visco-elastic properties and the friction of solids: Relation between the friction and visco-elastic properties of rubber. Nature 1963, 197, 858–859. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Dagdug, L.; García-Colín, L. Generalization of the Williams–Landel–Ferry equation. Phys. A Stat. Mech. Its Appl. 1998, 250, 133–141. [Google Scholar] [CrossRef]
- Williams, M.L.; Ferry, J.D. Second approximation calculations of mechanical and electrical relaxation and retardation distributions. J. Polym. Sci. 1953, 11, 169–175. [Google Scholar] [CrossRef]
- Hertz, H. Miscellaneous Papers; Macmillan: New York, NY, USA, 1896. [Google Scholar]
- Le Gal, A. Investigation and modelling of adhesion friction on rough surfaces. Kautshcuk Gummi Kunststoffe 2006, 59, 308. [Google Scholar]
- Persson, B.; Brener, E. Crack propagation in viscoelastic solids. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 71, 036123. [Google Scholar] [CrossRef]
- Ciavarella, M. A simplified version of Persson’s multiscale theory for rubber friction due to viscoelastic losses. J. Tribol. 2018, 140, 011403. [Google Scholar] [CrossRef]
- Persson, B.N. Rubber friction: Role of the flash temperature. J. Phys. Condens. Matter 2006, 18, 7789. [Google Scholar] [CrossRef]
- Carbone, G.; Persson, B. Crack motion in viscoelastic solids: The role of the flash temperature. Eur. Phys. J. E 2005, 17, 261–281. [Google Scholar] [CrossRef]
- Persson, B. Role of frictional heating in rubber friction. Tribol. Lett. 2014, 56, 77–92. [Google Scholar] [CrossRef]
- Palade, L.; Verney, V.; Attane, P. Time-temperature superposition and linear viscoelasticity of polybutadienes. Macromolecules 1995, 28, 7051–7057. [Google Scholar] [CrossRef]
- Schallamach, A. How does rubber slide? Wear 1971, 17, 301–312. [Google Scholar] [CrossRef]
- Tolpekina, T.; Pyckhout-Hintzen, W.; Persson, B. Linear and nonlinear viscoelastic modulus of rubber. Lubricants 2019, 7, 22. [Google Scholar] [CrossRef]
- Genovese, A.; Carputo, F.; Ciavarella, M.; Farroni, F.; Papangelo, A.; Sakhnevych, A. Analysis of multiscale theories for viscoelastic rubber friction. In Proceedings of the Conference of the Italian Association of Theoretical and Applied Mechanics, Rome, Italy, 15–19 September 2019; Springer: Cham, Switzerland, 2019; pp. 1125–1135. [Google Scholar]
- Fina, E.; Gruber, P.; Sharp, R. Hysteretic rubber friction: Application of Persson’s theories to Grosch’s experimental results. J. Appl. Mech. 2014, 81, 121001. [Google Scholar] [CrossRef]
- Furlan, M.; Mavros, G. A neural network approach for roughness-dependent update of tyre friction. Simul. Model. Pract. Theory 2022, 116, 102484. [Google Scholar] [CrossRef]


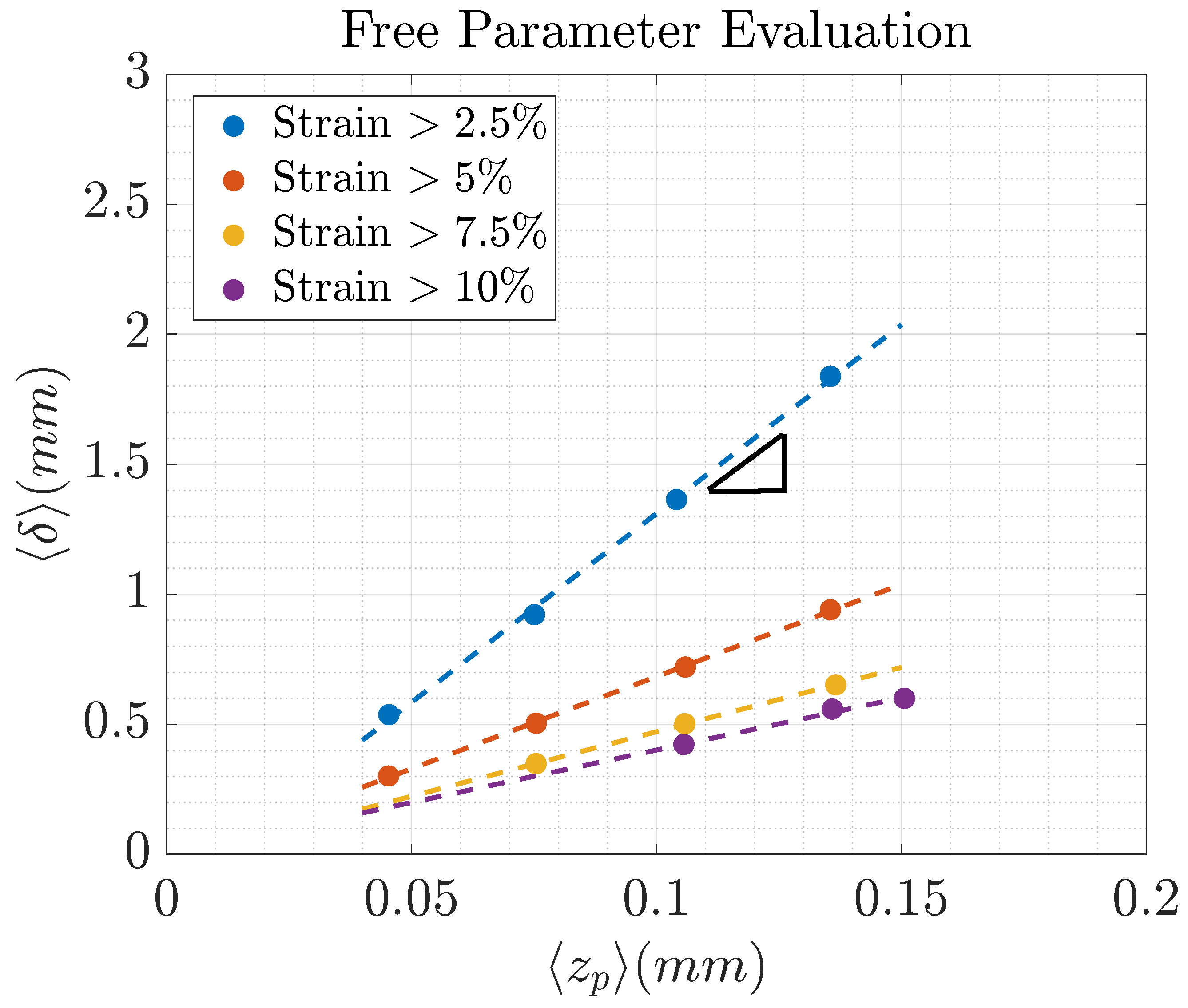
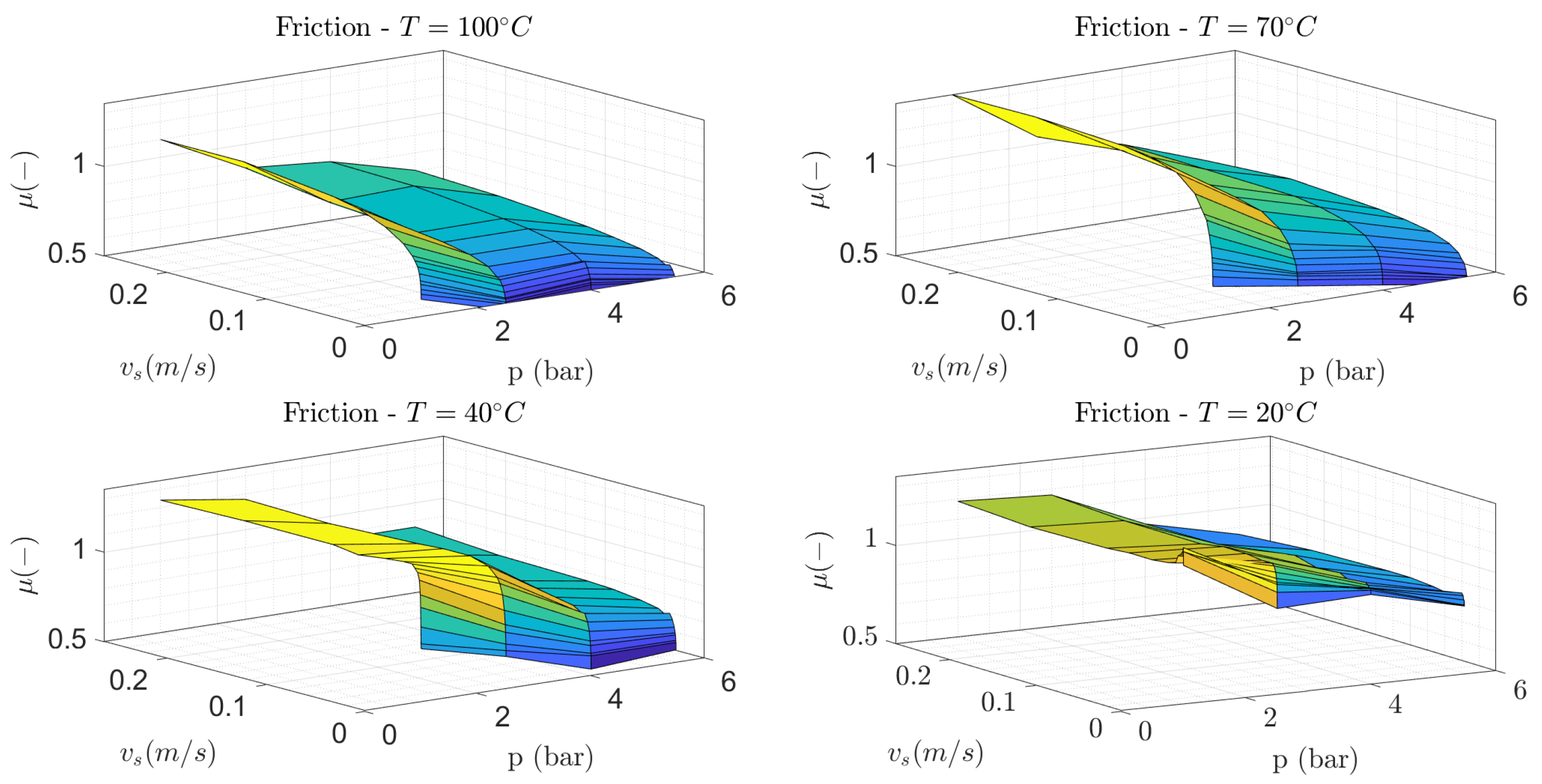
| Models | Strengths | Limitations |
|---|---|---|
| Hertz | Simple and analytically solvable Applicable for smooth, elastic bodies Closed-form solutions for stress, deformation and contact radius | Assumes idealized smooth surfaces Ignores roughness and adhesion Limited to small elastic deformations |
| JKR | Incorporates adhesion into contact analysis Relevant for soft materials and micro/nanoscale contacts Extends Hertz to include surface energy effects | Assumes perfectly smooth surfaces Limited for rough or multiscale contacts Strong dependence on surface energy estimates |
| Greenwood–Williamson | Introduces statistical roughness description Estimates contact area and pressure via asperity height distributions | Assumes identical, spherical, non-interacting asperities Neglects elastic coupling and scale dependence |
| Klüppel and Heinrich | Includes viscoelastic effects and scaling Defines minimum contact length and real contact evolution | Requires empirical cutoff parameters Relies on simplified statistical descriptors |
| Persson | Fully multiscale, PSD-based formulation Accounts for roughness and viscoelasticity across scales | Mathematically complex Sensitive to cutoff wavevectors and magnification |
| Models | Strengths | Limitations |
|---|---|---|
| Grosch Tests (1963) | First to demonstrate –frequency dependence Linked friction to viscoelastic modulus peaks Provided basis for later theoretical models | Purely empirical: no predictive capability Cannot compute from compound or surface parameters |
| Klüppel and Heinrich | Semi-analytical, multiscale approach Evaluates hysteresis and adhesion contributions Incorporates cutoff length and viscoelastic losses | Adhesion modeled empirically Requires parameter fitting No flash temperature treatment |
| Persson | Fully multiscale framework using PSD Directly links friction to viscoelastic moduli Includes flash temperature effects | Computationally expensive Sensitive to cutoff wavevector Adhesion term remains empirical |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanelli, R.; Fichera, G.; Genovese, A.; Napolitano Dell’Annunziata, G.; Sakhnevych, A.; Timpone, F.; Farroni, F. A Comprehensive Review of Rubber Contact Mechanics and Friction Theories. Appl. Sci. 2025, 15, 11558. https://doi.org/10.3390/app152111558
Stefanelli R, Fichera G, Genovese A, Napolitano Dell’Annunziata G, Sakhnevych A, Timpone F, Farroni F. A Comprehensive Review of Rubber Contact Mechanics and Friction Theories. Applied Sciences. 2025; 15(21):11558. https://doi.org/10.3390/app152111558
Chicago/Turabian StyleStefanelli, Raffaele, Gabriele Fichera, Andrea Genovese, Guido Napolitano Dell’Annunziata, Aleksandr Sakhnevych, Francesco Timpone, and Flavio Farroni. 2025. "A Comprehensive Review of Rubber Contact Mechanics and Friction Theories" Applied Sciences 15, no. 21: 11558. https://doi.org/10.3390/app152111558
APA StyleStefanelli, R., Fichera, G., Genovese, A., Napolitano Dell’Annunziata, G., Sakhnevych, A., Timpone, F., & Farroni, F. (2025). A Comprehensive Review of Rubber Contact Mechanics and Friction Theories. Applied Sciences, 15(21), 11558. https://doi.org/10.3390/app152111558










