A Novel Framework for Roof Accident Causation Analysis Based on Causation Matrix and Bayesian Network Modeling Methods
Abstract
1. Introduction
2. Related Works
2.1. Accident Causation Analysis Method
2.2. The Development and Application of Bayesian Network Models
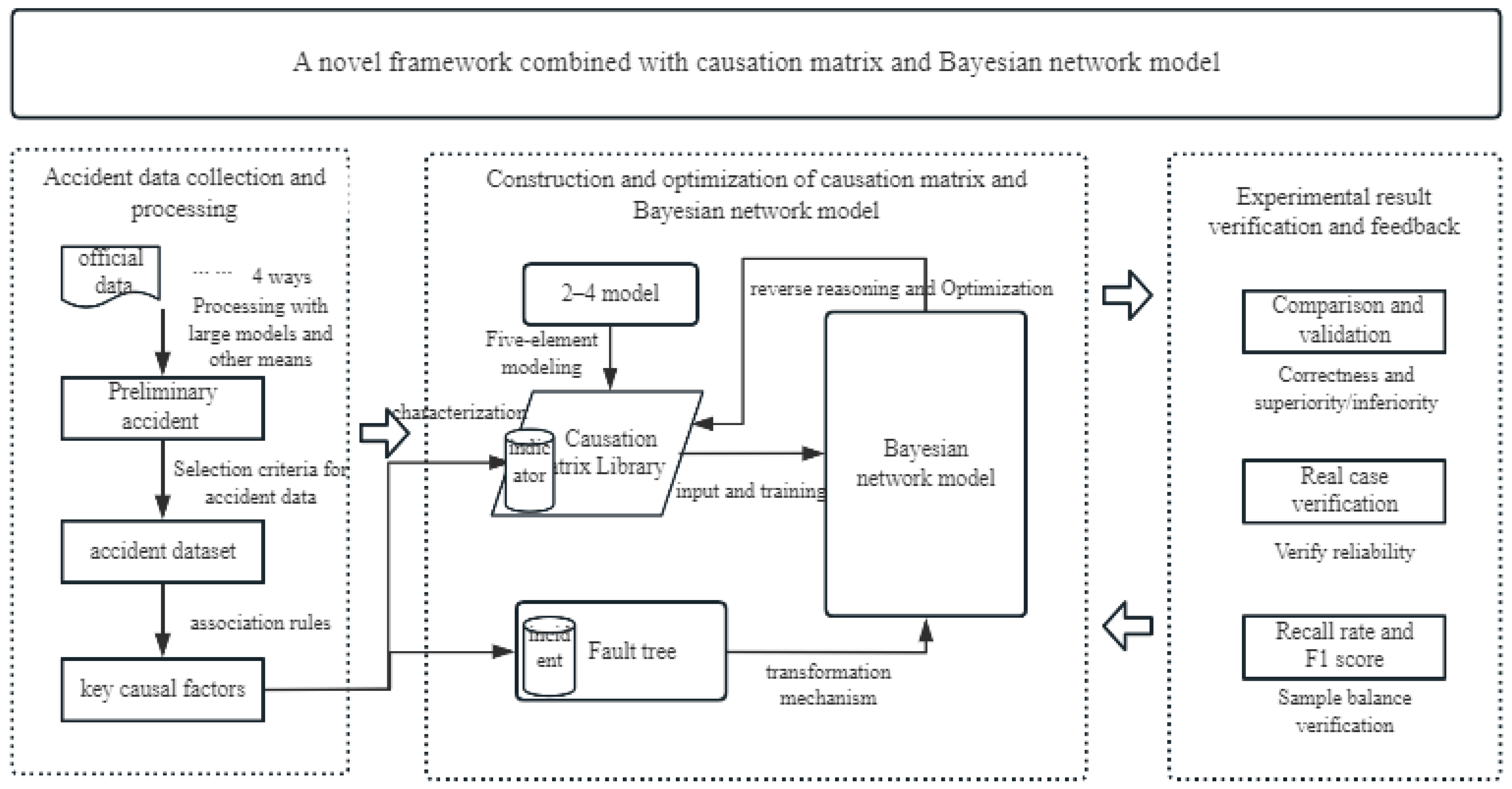
3. Materials and Methods
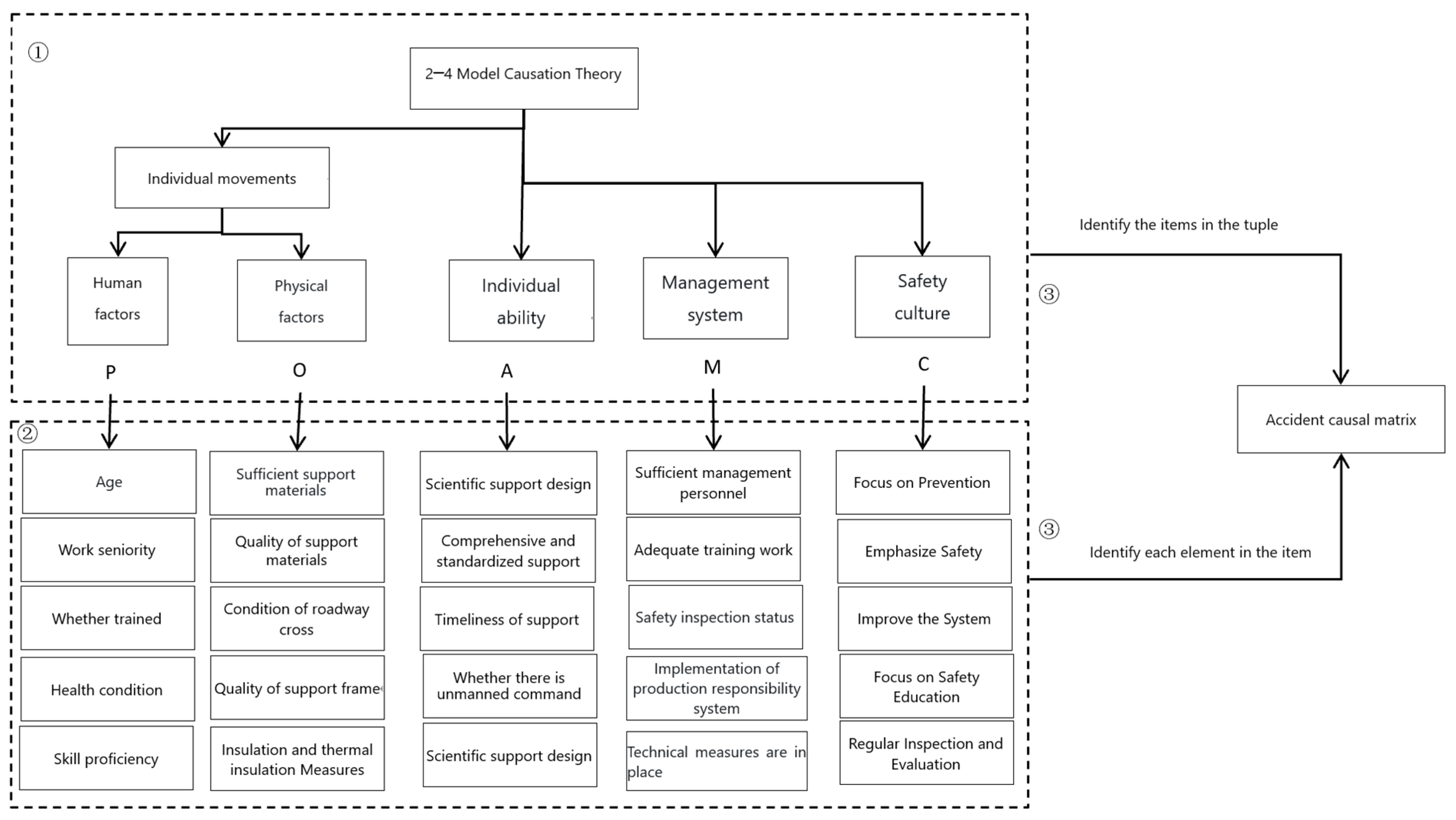
3.1. Construction of the Accident Causation Matrix
3.1.1. Definition of the Accident Causation Matrix
3.1.2. Modeling Process of the Accident Causation Matrix
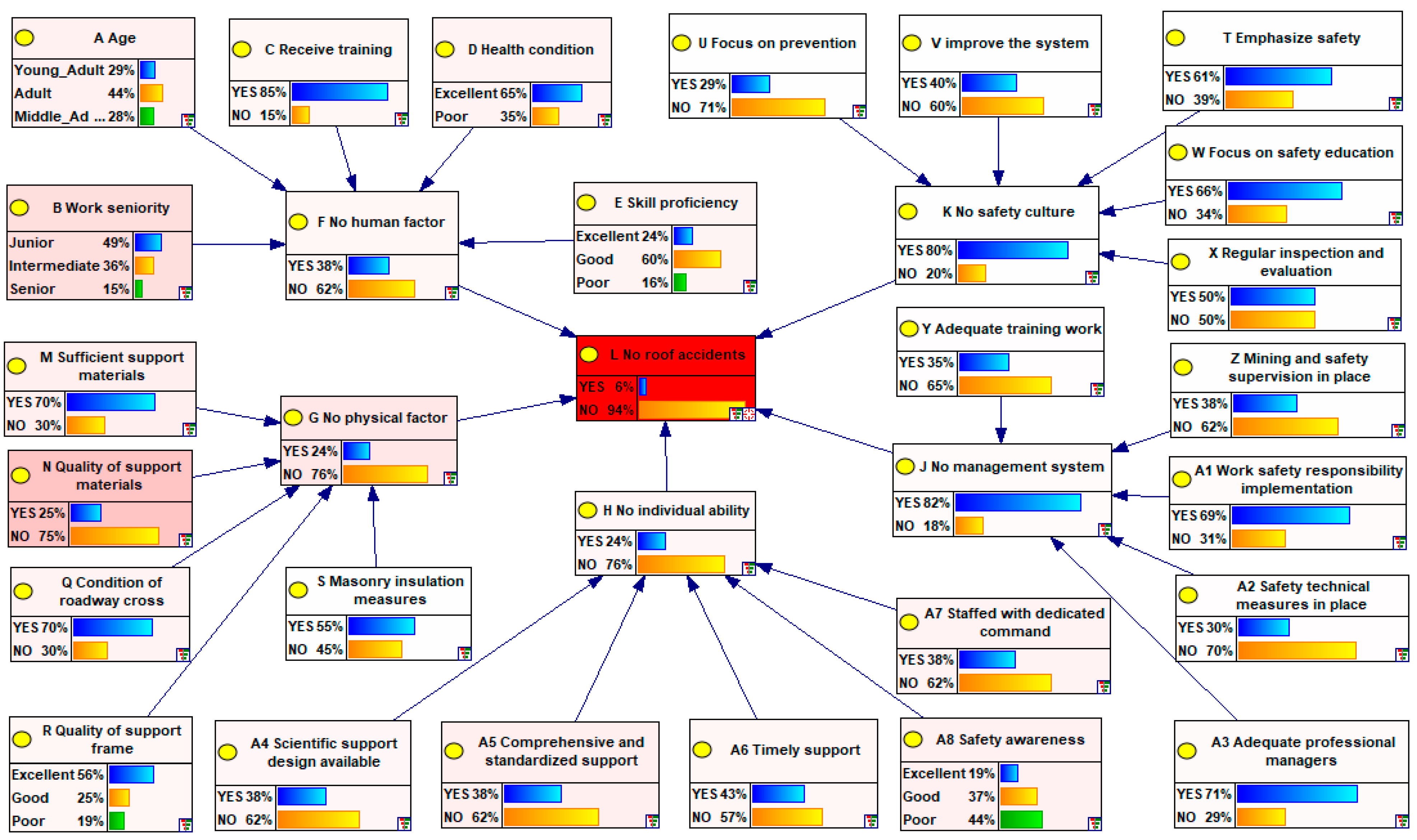
3.2. Construction and Optimization of Bayesian Network Model
3.2.1. Structural Learning of Bayesian Network Model
3.2.2. Parameter Learning of Bayesian Network Model
- E-step: Based on the current parameters and observed data, calculate the posterior probability distribution of the latent variable . Wherein, represents the sample index, which is used to distinguish different accident case samples; denotes the latent variable of the -th sample; stands for the observed variable of the -th sample; represents the model parameter at the -th iteration. The formula is as follows:
- M-step: Maximize and update parameter through iteration to maximize the expectation of the log-likelihood. In the formula, represents the parameter after the -th iterative update.
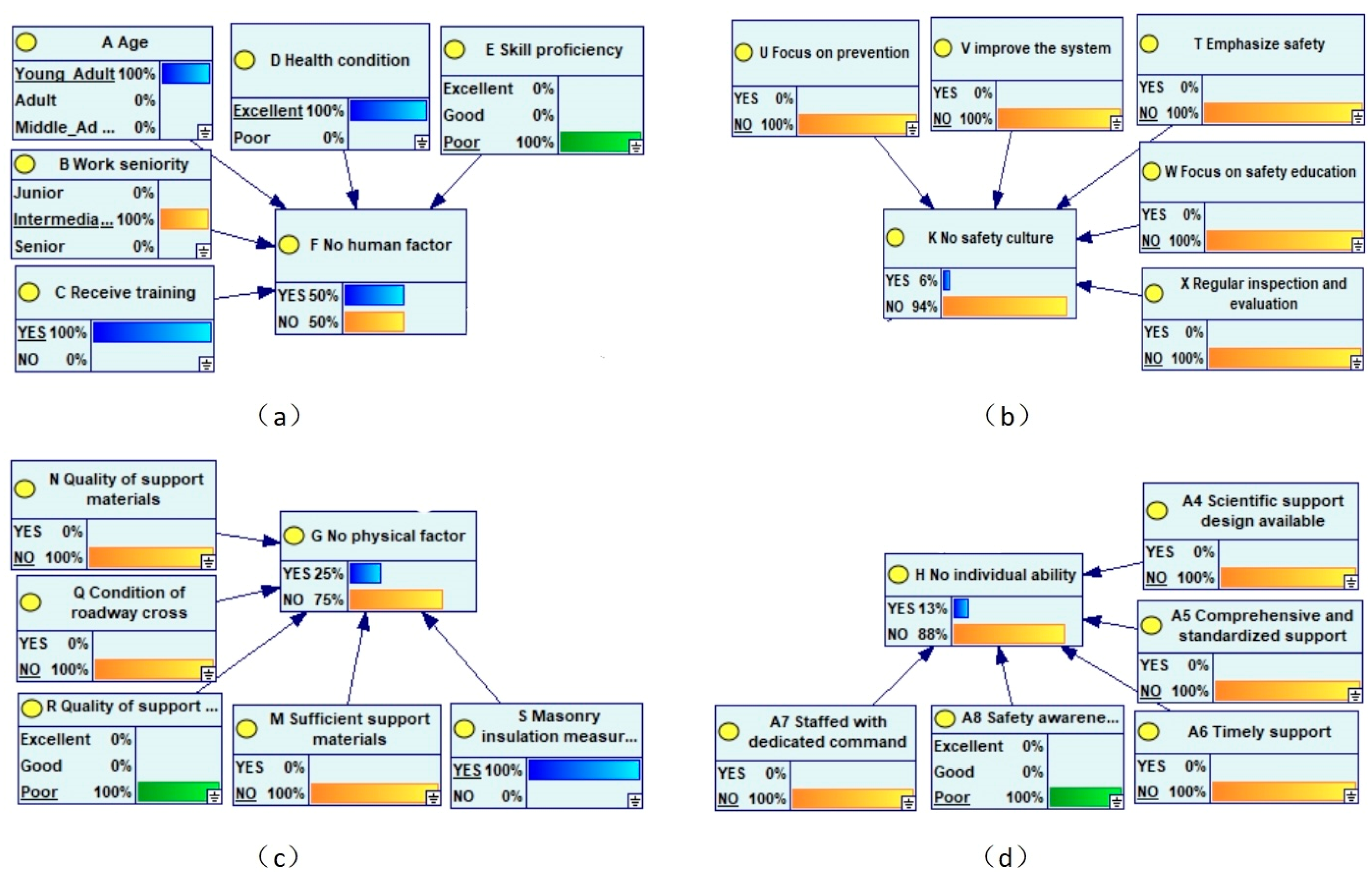
4. Results
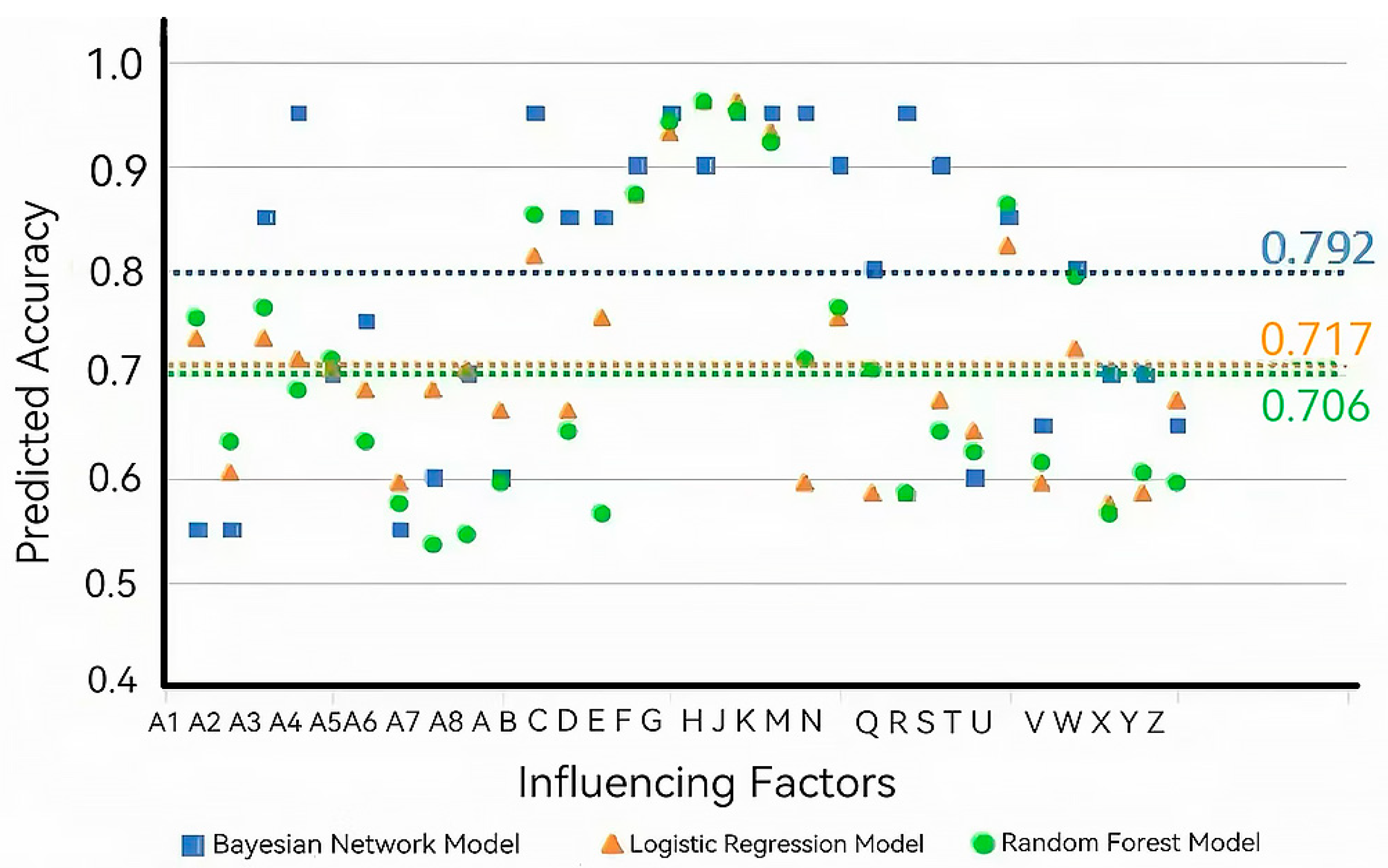
4.1. Experimental Analysis and Evaluation
4.1.1. Comparative Analysis of Model
4.1.2. Validation with Real Cases
5. Discussion
6. Conclusions
- (1)
- The accident causation matrix effectively characterizes complex accident causes and enables their visualization. This matrix format not only clarifies the relationships among various factors but also provides precise input data for the construction of the Bayesian network model, thereby achieving seamless integration from accident feature description to model construction. Furthermore, by quantifying and standardizing key information from accident reports, the accident causation matrix offers a scientific basis for coal mine enterprises to identify potential risk factors in advance and formulate preventive measures. This significantly enhances the efficiency and accuracy of accident analysis.
- (2)
- Leveraging the reverse reasoning capability of the Bayesian network, dynamic diagnosis of accident causation has been achieved. By inputting observed evidence to update the model, key factors contributing to accidents can be systematically identified. This method can be further enhanced by integrating additional scenario data and expert knowledge, optimizing the model’s accuracy and adaptability. This enables dynamic and refined analysis of accident causation, providing enterprises with more efficient and precise accident prevention and decision-making support.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BN | Bayesian Network |
| DAG | Directed Acyclic Graph |
| CPT | Conditional Probability Table |
| FT-BN | Fault Tree—Bayesian Network Conversion |
| FMEA | Failure Mode and Effect Analysis |
| FTA | Fault Tree Analysis |
| PHA | Preliminary Hazard Analysis |
| HHM | Hierarchical Holographic Mode |
| FHAP | Fuzzy Analytic Hierarchy Process |
Appendix A
| P (Human factors) | p1 (Age) | Young Adult (18–35) | O (Physical factors) | o1 (Whether support materials are sufficient) | YES |
| Adult (36–45) | NO | ||||
| Middle Adult (46–55) | o2 (Quality of support materials) | YES | |||
| p2 (Work seniority/year) | Junior (0–5) | NO | |||
| Intermediate (6–15) | o3 (Condition of roadway cross-section) | YES | |||
| Senior (16 and above) | NO | ||||
| p3 (Training) | YES | o4 (Quality of canopy frame) | Excellent | ||
| NO | Good | ||||
| p4 (Health condition) | Excellent | Poor | |||
| Poor | o5 (Insulation measures for masonry arch) | YES | |||
| P5 (Skill proficiency) | Excellent | NO | |||
| Good | |||||
| Poor | |||||
| A (Individual ability) | a1 Whether there is a scientific support design | YES | M (Management system) | m1 Whether management personnel are sufficient | Yes |
| NO | No | ||||
| a2 Whether the support is comprehensive &standardized | YES | m2 Whether training is in place | Yes | ||
| NO | No | ||||
| a3 Whether the support is timely | YES | m3 Whether safety inspections are in good condition | Yes | ||
| NO | No | ||||
| a4 Whether there is a designated person in command | YES | m4 Whether the production responsibility system is implemented | Yes | ||
| NO | No | ||||
| a5 Safety awareness status | Excellent | m5 Whether safety technical measures are in place | Yes | ||
| Good | No | ||||
| Poor | |||||
| C (Safety culture) | c1 Whether prevention is emphasized | Yes | C (Safety culture) | c4 Whether safety education is emphasized | Yes |
| No | No | ||||
| c2 Whether safety is emphasized | Yes | c5 Whether regular inspections &evaluations are conducted | Yes | ||
| No | No | ||||
| c3 Whether the safety system is sound | Yes | ||||
| No | |||||
Appendix B. Selection Criteria for 100 Roof Accident Reports
- Precise Positoning of Accident Type
- 2.
- Full Coverage of Accident Levels
- 3.
- Authoritative and Compliant Data Sources
- (1)
- Official sources: Accident Investigation Reports released by official platforms such as the National Mine Safety Administration and its local branches (e.g., Guizhou, Shaanxi, and Hebei Bureaus) and the Coal Mine Safety Network.
- (2)
- Literature sources: Accident data extracted from published dissertations and journal papers.
- (3)
- New reports: Relevant news coverage is available for some relatively serious accidents, which usually detail the specific causes and circumstances of the accidents.
- (4)
- Interviews: Insights from accident investigation specialists at local branches of the National Mine Safety Administration and safety management leaders of coal mining enterprises.
- 4.
- Full Coverage of Causal Factors Dimensions
Appendix C. Methods for Processing Accident Datasets
- Extraction Framework
- 2.
- Extraction Method
- 3.
- Variable Discretization
- 4.
- Matrix Construction
- 5.
- Model Training
References
- Li, F.; Duan, B.; Sun, Y.; He, X.; Li, Z.; Wang, B. Quantitative risk assessment model of working positions for roof accidents in coal mine. Saf. Sci. 2024, 178, 106628. [Google Scholar] [CrossRef]
- International Labour Organisation. Available online: https://www.ilo.org/ (accessed on 19 October 2025).
- Rahimi, E.; Shekarian, Y.; Shekarian, N.; Roghanchi, P. Accident Analysis of Mining Industry in the United States—A retrospective study for 36 years. J. Sustain. Min. 2022, 21, 27–44. [Google Scholar] [CrossRef]
- Baraza, X.; Cugueró-Escofet, N.; Rodríguez-Elizalde, R. Statistical analysis of the severity of occupational accidents in the mining sector. J. Saf. Res. 2023, 86, 364–375. [Google Scholar] [CrossRef]
- Sahu, A.; Mishra, D.P. Coal mine explosions in India: Management failure, safety lapses and mitigative measures. Extr. Ind. Soc. 2023, 14, 101233. [Google Scholar] [CrossRef]
- Shahani, N.M.; Sajid, M.J.; Zheng, X.; Brohi, M.A.; Jiskani, I.M.; Ul Hassan, F.; Qureshi, A.R. Statistical analysis of fatalities in underground coal mines in Pakistan. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 2189–2204. [Google Scholar] [CrossRef]
- Zhang, P.S.; Zhang, X.L.; Dong, Y.H.; Xu, D.Q. Analysis and prediction of coal mine accident laws in China from 2008 to 2021. Min. Saf. Environ. Prot. 2023, 50, 6. [Google Scholar]
- Baidu Wenku. Available online: https://wenku.baidu.com/view/f5eb90d8b90d6c85ed3ac6e1.html?wkts=1755610435938 (accessed on 11 June 2025).
- Qiu, Z.; Liu, Q.; Li, X.; Zhang, J.; Zhang, Y. Construction and analysis of a coal mine accident causation network based on text mining. Process Saf. Environ. Prot. 2021, 153, 320–328. [Google Scholar] [CrossRef]
- Gordon, J.E. The epidemiology of accidents. Am. J. Public Health 1949, 9, 504–515. [Google Scholar] [CrossRef]
- Lehto, M.; Salvendy, G. Models of accident causation and their application: Review and reappraisal. J. Eng. Technol. Manag. 1991, 8, 173–205. [Google Scholar] [CrossRef]
- Rasmussen, J. Risk management in a dynamic society: A modelling problem. Saf. Sci. 1997, 27, 183–213. [Google Scholar] [CrossRef]
- Nancy, L. A new accident model for engineering safer systems. Saf. Sci. 2004, 42, 237–270. [Google Scholar] [CrossRef]
- Hollnagel, E. FRAM: The Functional Resonance Analysis Method: Modelling Complex Socio-Technical Systems; Routledge: London, UK, 2012. [Google Scholar]
- Vivo, C.D.; Ellena, M.; Barbato, G.; Pugliese, A.; Marinucci, F.; Barilli, T.; Mercogliano, P. A co-design matrix-based approach to evaluate the climate risks for airports: A case study of bologna airport. Clim. Serv. 2025, 37, 100536. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Banihashemi, S.A.; Heidari, A.; Božanić, D.; Milić, A. Risk Analysis and Assessment of Water Supply Projects Using the Fuzzy DEMATEL-ANP and Artificial Neural Network Methods. Water 2025, 17, 1995. [Google Scholar] [CrossRef]
- Chen, T.T.; Wang, C.H. Fall risk assessment of bridge construction using bayesian network transferring from fault tree analysis. J. Civ. Eng. Manag. 2015, 23, 273–282. [Google Scholar] [CrossRef]
- Gheisari, S.; Meybodi, M.R. Bnc-pso: Structure learning of bayesian networks by particle swarm optimization. Inf. Sci. 2016, 348, 272–289. [Google Scholar] [CrossRef]
- Fang, W.; Zhang, W.; Ma, L.; Wu, Y.; Yan, K.; Lu, H.; Sun, J.; Wu, X.; Yuan, B. An efficient Bayesian network structure learning algorithm based on structural information. Swarm Evol. Comput. 2023, 76, 101224. [Google Scholar] [CrossRef]
- He, Y.C.; Chen, Z.G.; Wang, H.F.; Yang, D.S. Research on Bayesian network model for missile fault diagnosis based on Netica. Aero Weapon. 2020, 27, 89–95. [Google Scholar]
- Ibrahim, H.A.; Rao, P.J. Fire risk analysis in flng processing facility using Bayesian network. J. Eng. Sci. Technol. 2019, 14, 1497–1519. [Google Scholar]
- Zong, S.; Wang, Z.; Liu, K.; Wang, G.; Lu, Y.; Huang, T. Risk assessment of general FPSO supply system based on hybrid fuzzy fault tree and Bayesian network. Ocean Eng. 2024, 311, 118767. [Google Scholar] [CrossRef]
- Fan, Z.; Zhou, L.; Komolafe, T.E.; Ren, Z.; Tong, Y.; Feng, X. Learning Bayesian network parameters from limited data by integrating entropy and monotonicity. Knowl.-Based Syst. 2024, 291, 12. [Google Scholar] [CrossRef]
- Li, H.T.; Jin, G.; Zhou, J.L.; Zhou, Z.B.; Li, D.Q. A review of Bayesian network inference algorithms. Syst. Eng. Electron. 2008, 5, 935–939. [Google Scholar]
- Mishra, R.; Uotinen, L.; Rinne, M. A Bayesian network approach for geotechnical risk assessment in underground mines. J. South. Afr. Inst. Min. Metall. 2021, 121, 287–294. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H. Risk assessment of coal mine safety production management activities based on FMEA-BN. J. Comput. Methods Sci. Eng. 2022, 22, 123–136. [Google Scholar] [CrossRef]
- Li, L.; Fang, Z. Cause analysis of coal mine gas explosion based on bayesian network. Shock. Vib. 2022, 1, 1923734. [Google Scholar] [CrossRef]
- Sahu, A.R.; Kashi, V.K. Potential hazard analysis of accidents in indian underground mines using bayesian network model. Int. J. Syst. Assur. Eng. Manag. 2025, 16, 1501–1516. [Google Scholar] [CrossRef]
- Lin, Z.; Li, M.; He, S.; Shi, S.; Tian, X.; Wang, D. Risk assessment of gas explosion in coal mines based on game theory and Bayesian network. J. China Coal Soc. 2024, 49, 3484–3497. [Google Scholar]
- He, S.; Lu, Y.; Li, M. Probabilistic risk analysis for coal mine gas overrun based on FAHP and BN: A case study. Environ. Sci. Pollut. Res. 2022, 29, 28458–28468. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Xue, Y.G. A new fusion method to predict coal mine roof accidents. Qual. Reliab. Eng. Int. 2023, 39, 3041–3058. [Google Scholar] [CrossRef]
- Zheng, X.; Li, Y.; Tong, X.; Liu, Q. Precise quantitative evaluation of the risk level of coal mine water inrush accidents based on the cw-bn model. Earth Sci. Inform. 2025, 18, 315. [Google Scholar] [CrossRef]
- Hong, W.; Sheng, W. A dematel-ism-bn model of mine water inrush accidents. Mine Water Environ. 2023, 42, 178–186. [Google Scholar] [CrossRef]
- He, L.; Pan, R.; Wang, Y.; Gao, J.; Xu, T.; Zhang, N.; Wu, X.; Zhang, X. A case study of accident analysis and prevention for coal mining transportation system based on FTA-BN-PHA in the context of smart mining process. Mathematics 2024, 12, 1109. [Google Scholar] [CrossRef]
- Xu, T. Analysis of factors affecting emergency response linkage in coal mine gas explosion accidents. Sustainability 2024, 16, 6325. [Google Scholar] [CrossRef]
- Ministry of Emergency Management of the People’s Republic of China. Available online: https://www.mem.gov.cn/gk/zfxxgkpt/fdzdgknr/202508/t20250804_553277.shtml (accessed on 19 October 2025).
- Coal Mine Safety Network. Available online: https://www.mkaq.org/html/2024/12/27/696971.shtml (accessed on 11 June 2025).
- Hunan Bureau of the National Mine Safety Administration. Available online: https://hun.chinamine-safety.gov.cn/zwgk/jczfxxgk/sgdcbb/202410/t20241015_504003.html (accessed on 11 June 2025).
- Hunan Bureau of the National Mine Safety Administration. Available online: https://hun.chinamine-safety.gov.cn/zwgk/jczfxxgk/sgdcbb/202410/t20241015_504004.html (accessed on 11 June 2025).
- Guizhou Bureau of the National Mine Safety Administration. Available online: https://gz.chinamine-safety.gov.cn/detail.html?id=1687455662059192321 (accessed on 11 June 2025).
- Guizhou Bureau of the National Mine Safety Administration. Available online: https://gz.chinamine-safety.gov.cn/detail.html?type=headlines&id=1646107722376183810 (accessed on 11 June 2025).
- Shaanxi Bureau of the National Mine Safety Administration. Available online: https://shaanxi.chinamine-safety.gov.cn/main/397789491780862656.html (accessed on 11 June 2025).
- Coal Mine Safety Network. Available online: https://www.mkaq.org/html/2023/06/27/663535.shtml (accessed on 11 June 2025).
- National Mine Safety Administration. Available online: https://www.chinamine-safety.gov.cn/zfxxgk/fdzdgknr/sgcc/sgalks/202309/t20230928_464574.shtml (accessed on 11 June 2025).
- Hebei Bureau of the National Mine Safety Administration. Available online: https://hb.chinamine-safety.gov.cn/system/2024/12/26/030323620.shtml (accessed on 11 June 2025).
- Baidu Baike. Available online: https://www.un.org/zh/documents/treaty/A-RES-70-1 (accessed on 19 October 2025).


| Number | Basic Event | Number | Basic Event |
|---|---|---|---|
| X1 | Age | X16 | Sufficient management personnel |
| X2 | Physical factors | X17 | Adequate training work |
| X3 | Whether trained | X18 | Safety inspection status |
| X4 | Health condition | X19 | Implementation of production responsibility system |
| X5 | Skill proficiency | X20 | Technical measures are in place |
| X6 | Sufficient support materials | X21 | Focus on prevention |
| X7 | Quality of support materials | X22 | Emphasize safety |
| X8 | Condition of roadway cross | X23 | Improve the system |
| X9 | Quality of support frame | X24 | Focus on safety education |
| X10 | Masonry insulation measures | X25 | Regular inspection and evaluation |
| X11 | Scientific support design | M1 | Human factors |
| X12 | Comprehensive and standardized support | M2 | Physical factors |
| X13 | Timeless of support | M3 | Individual ability |
| X14 | Whether there is unmanned command | M4 | Management system |
| X15 | Scientific support design | M5 | Safety culture |
| Node | Sensitivity Coefficient | Node | Sensitivity Coefficient |
|---|---|---|---|
| N Quality of support materials | 0.02886 | A4 Scientific support design available | 0.00331 |
| B Work seniority | 0.01599 | A3 Adequate professional managers | 0.00213 |
| M Sufficient support materials | 0.00764 | A1 Work safety responsibility implementation | 0.00165 |
| A5 Comprehensive & standardized support | 0.00735 | Y Adequate training work | 0.00074 |
| A8 Safety awareness | 0.00637 | A2 Safety technical measures in place | 0.00073 |
| A Age | 0.00626 | W Focus on safety education | 0.00042 |
| D Health condition | 0.00538 | S Masonry insulation measures | 0.00042 |
| A7 Staffed with a dedicated command | 0.00537 | U Focus on prevention | 0.00033 |
| Q Condition of roadway cross | 0.00520 | T Emphasize safety | 0.00026 |
| E Skill proficiency | 0.00471 | Z Mining & safety supervision in place | 0.00023 |
| R Quality of support frame | 0.00397 | X Regular inspection and evaluation | 0.00017 |
| C Receive training | 0.00385 | V improve the system | 0.00000 |
| A6 Timely support | 0.00378 |
| Case Name | Occurrence Probability of Accident Node |
|---|---|
| “1 November” Roof Accident at Hanjiashan Coal Mine | 90.8% |
| “8 August” Roof Accident at Suitan’yan Coal Mine | 92.5% |
| “24 August” Roof Accident at Shichating Well | 95.2% |
| “7 April” Roof Accident at Baiping Coal Mine | 96.4% |
| “16 September” Roof Accident at Cizhulin Coal Mine | 94.6% |
| “27 April” General Roof Accident at Fugu Guoneng Coal Mine | 96.8% |
| “26 March” Roof Accident at Guojiawan Coal Mine | 87.9% |
| “15 October” Major Roof Accident at Fusheng Coal Mine | 96.1% |
| “4 July” General Roof Accident at Xingcheng Mine | 88.4% |
| Number of Positive Samples | Confusion Matrix | Number of Negative Samples | Recall Rate | Precision | F1 | |
|---|---|---|---|---|---|---|
| Probability of Predicting Positive Class | Probability of Predicting Negative Class | |||||
| 1 | 94.3% | 72.3% | 11 | 93.3% | 87.5% | 0.903 |
| 2 | 90.8% | 68.5% | 12 | |||
| 3 | 92.5% | 76.2% | 13 | |||
| 4 | 95.2% | 70.1% | 14 | |||
| 5 | 96.4% | 65.8% | 15 | |||
| 6 | 94.6% | 78.4% | 16 | |||
| 7 | 96.8% | 73.6% | 17 | |||
| 8 | 87.9% | 69.7% | 18 | |||
| 9 | 96.1% | 75.9% | 19 | |||
| 10 | 88.4% | 67.4% | 20 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Q.; Yu, M.; Tan, Y.; Cheng, G.; Zhang, Y.; Wang, H.; Tian, L. A Novel Framework for Roof Accident Causation Analysis Based on Causation Matrix and Bayesian Network Modeling Methods. Appl. Sci. 2025, 15, 11521. https://doi.org/10.3390/app152111521
Xia Q, Yu M, Tan Y, Cheng G, Zhang Y, Wang H, Tian L. A Novel Framework for Roof Accident Causation Analysis Based on Causation Matrix and Bayesian Network Modeling Methods. Applied Sciences. 2025; 15(21):11521. https://doi.org/10.3390/app152111521
Chicago/Turabian StyleXia, Qingxin, Minghang Yu, Yiyang Tan, Gang Cheng, Yunlei Zhang, Hui Wang, and Liqin Tian. 2025. "A Novel Framework for Roof Accident Causation Analysis Based on Causation Matrix and Bayesian Network Modeling Methods" Applied Sciences 15, no. 21: 11521. https://doi.org/10.3390/app152111521
APA StyleXia, Q., Yu, M., Tan, Y., Cheng, G., Zhang, Y., Wang, H., & Tian, L. (2025). A Novel Framework for Roof Accident Causation Analysis Based on Causation Matrix and Bayesian Network Modeling Methods. Applied Sciences, 15(21), 11521. https://doi.org/10.3390/app152111521







