Joint Optimization Model for Earthwork Allocation Considering Soil and Water Conservation Fees, Landscape Restoration Fees, and Road Transportation Intensity
Abstract
1. Introduction
- Constructed a joint optimization model for earthwork allocation that simultaneously integrates soil and water conservation fees, landscape restoration fees, and road transportation intensity, filling the gap in existing research for a multi-factor collaborative optimization framework.
- Proposed an improved ant colony algorithm that effectively enhances solution efficiency and robustness by dynamically adjusting volatility, introducing penalty factors, and incorporating NumPy vectorized computation.
- Verified the effectiveness of the model and algorithm through a case study, showing that considering transportation intensity can significantly reduce the peak road load and increase the proportion of direct filling with only a small increase in total cost, making the allocation plan more aligned with actual construction needs.
2. Composition of Earthwork Allocation System
3. Optimization Model for Earthwork Allocation Considering Road Transportation Intensity
3.1. Soil and Water Conservation Fee
- Soil erosion equation:
- 2.
- Soil and water conservation fee for waste disposal site:
- 3.
- Water and soil conservation fee for the transition site:
3.2. Landscape Restoration Fee for the Work Area
- 1.
- Cost of landscape restoration in the waste disposal area:
- 2.
- Cost of landscape restoration in the transit area:
3.3. Road Transportation Intensity
3.4. Optimization Model for Earthwork Allocation Cost
3.5. Optimization Model for Road Transport Intensity
3.6. Cost Optimization Model Considering Road Transportation Intensity
- 1.
- Objective function
- 2.
- Constraints
- 1.
- Equal excavation volume refers to the sum of the excavation volume of a certain excavation project during a certain period being equal to the sum of the transportation volume to all other possible locations during that period. Among them, represents the engineering quantity of the excavation project.
- 2.
- Equal filling amount refers to the sum of the filling amount of a certain filling project during a certain period of time being equal to the sum of all possible transportation volumes to that filling project during that period. Among them, represents the engineering quantity of the filling project.
- 3.
- Mining output limit of the quarry: The allocation volume from the quarry to the filling project cannot exceed the maximum capacity of the quarry. Among them, represents the material storage capacity of the material yard.
- 4.
- Capacity limit of waste disposal site: The amount of waste materials from all excavation projects, materials that cannot be directly used for filling, and other special earth and stone materials cannot exceed the maximum capacity of the waste disposal site. Among them, represents the capacity of the waste disposal site.
- 5.
- Capacity limitation of transfer site: Within the same time period, the difference between the allocation amount from the excavation project to the transfer site and the allocation amount from the transfer site to the filling project is greater than or equal to zero, and less than or equal to the maximum capacity of transfer site. Among them, represents the capacity of the transition field.
- 6.
- Non-negative constraint: Excavation projects, transfer sites, filling projects, waste disposal sites, and material yards all have a corresponding allocation of earthwork.
- 7.
- Facing the intersection V of the road section, prioritize choosing the route with the shortest total mileage of the transportation route.
- 8.
- In the set of intersection points v between starting point i and ending point j, the intersection point of the first layer q1 and the last layer qp should be the starting point i and the ending point j.
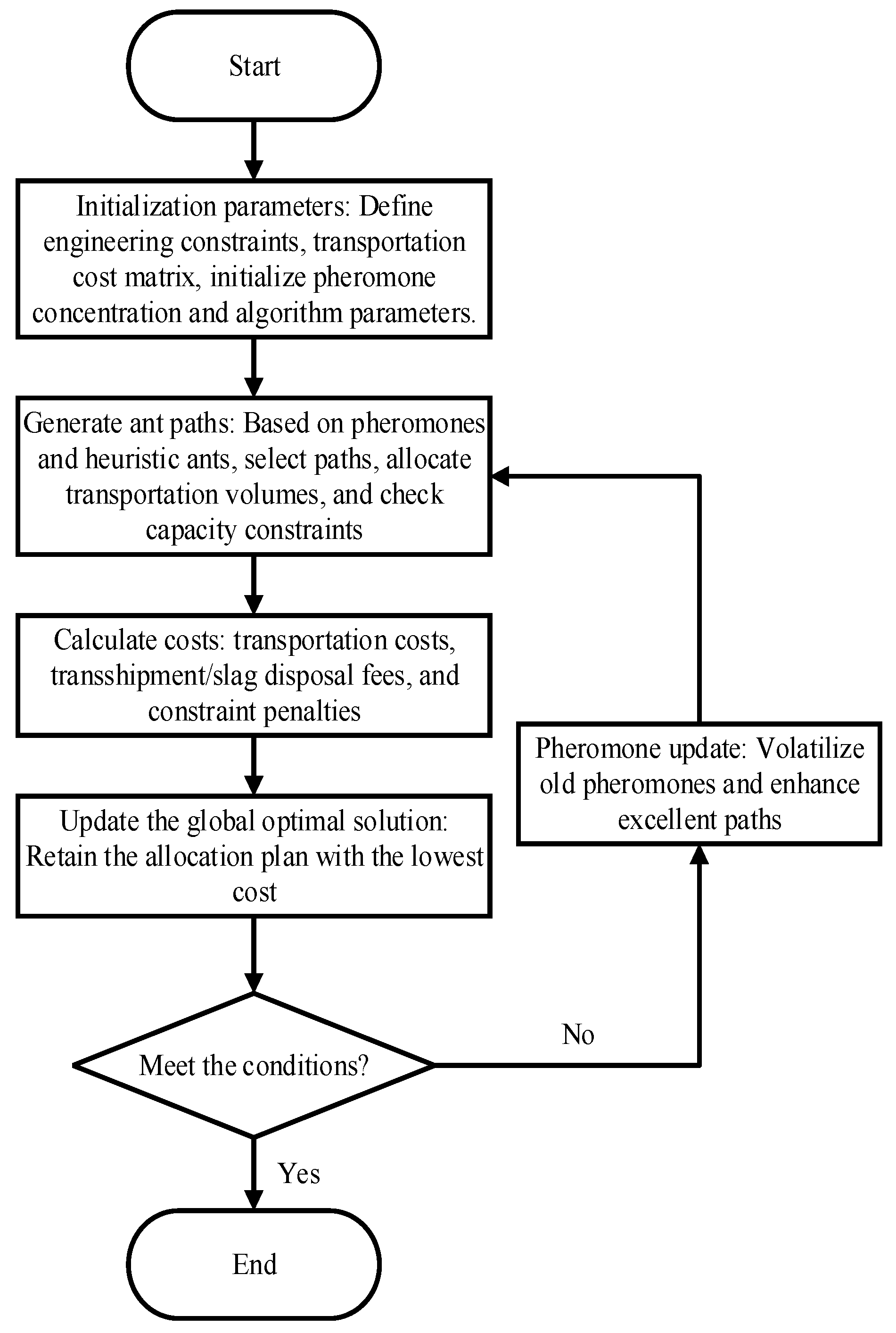
4. Model Solving Based on Improved Ant Colony Algorithm
- 1.
- Informational modeling: The concentration of pheromones on path (i, j) represents the advantages and disadvantages of historical blending schemes, and the higher the concentration, the greater the probability of the path being selected.
- 2.
- Heuristic information: Introduce the reciprocal of transportation cost as a local guide, prioritizing the path with lower cost.
- 3.
- State transition rule: The probability of ant k selecting the next node j at node i is
- 4.
- Dynamic update mechanism: After each iteration, pheromones decay according to their volatility , and excellent paths are enhanced based on the quality of ant paths.
- 1.
- Initialization parameters: Set the parameters of the ant colony algorithm, including the maximum number of iterations MaxDT, heuristic factor , pheromone evaporation coefficient , and penalty factor. Simultaneously input relevant information of earthwork nodes, such as node type (excavation, filling, transfer, waste disposal), location, initial earthwork volume, and maximum capacity. Initialize the pheromone matrix and heuristic information matrix , representing the pheromone concentration and heuristic information (such as the reciprocal of transportation costs) on the paths between nodes, respectively. Initialize the number of ants m and randomly place them at the excavation node.
- 2.
- Iterative search: In each iteration, each ant starts from the current node and selects the next node according to the state transition rule. The ant calculates the transition probability from the current node to the unvisited node, which is determined by the pheromone concentration and the heuristic information .
- 3.
- Pheromone update: After each iteration, update the pheromone matrix according to the pheromone update rule. The pheromone increment is inversely proportional to the ant path cost . The formula for calculating the increment of pheromones is
- 4.
- Termination condition: Determine whether the maximum iteration count MaxDT has been reached or whether a satisfactory optimization solution has been found.
- 5.
- Result output: Output the optimal path and cost, including the transportation volume and construction sequence between each node. At the same time, use data charts to visually display the allocation plan, clearly expressing information such as transportation routes, transportation volume, and construction sequence.
5. Example Analysis
5.1. Project Overview
5.2. Optimization of Earthwork Allocation Considering Road Transportation Intensity
- Optimization results of deployment
- 2.
- Optimization result analysis
- In the optimization calculation results of earthwork allocation without considering road usage, the maximum transportation intensity during the peak transportation period is 268,000 m3/month from excavation project W1 to filling project T1 in the fourth month, and 104,000 m3/month from excavation project W2 to filling project T2 in the fifth month. When considering road usage, according to Formula (7), the maximum transportation intensity limit Q0 during the peak transportation period from excavation project W1 to filling project T1 in the fourth month is 262,000 m3/month, and the route is W1→1→3→6→T1. The maximum transportation intensity limit Q0 during the peak transportation period from excavation project W2 to filling project T2 in the fifth month is 99,000 m3/month, and the route is W2→4→8→T2.
- 2.
- The proportion of earthwork directly used for filling in excavation projects W1 and W2 reached 92.1% and 88.4%, respectively. For example, the unit price of earthwork allocation from excavation project W2 to filling project T2 is 12 CNY/m3, and the unit prices of earthwork allocation from intermediate transfer site to filling project T1 and filling project T2 are 20 CNY/m3 and 18 CNY/m3, respectively. This reduces the transportation costs from the intermediate transfer site and material yard to the filling project, as well as the earthwork management costs of the intermediate transfer site and material yard.
- 3.
- (i) Pre-deployment stage. At the initial stage of construction, when the filling demand is zero from January to February, the accumulated excavation volume of 582,000 m3 for excavation project W1 will be temporarily stored in the transfer site Z1 to avoid waste disposal costs and reserve resources for subsequent filling. (ii) Peak period for filling. The storage capacity of the transition site during the construction period from July to December meets the peak demand for filling, such as the allocation of 1.564 million m3 from transition site Z1 to filling project T1 from July to December, prioritizing the high-priority demand (filling project T1 accounts for 67% of the entire filling demand). (iii) End of deployment. In December, 106,000 cubic meters were directly filled from excavation project W2 to filling project T2, combined with flexible supplementation from the borrow site, to balance the dynamic differences between excavation and filling, and to improve construction continuity by 15%.
- 4.
- (i) Nonlinear constraint processing, directly incorporating soil erosion rate (0.05) and landscape restoration rate (0.1), improves optimization accuracy by 14% compared to traditional linear programming. Multi-objective collaborative optimization: (ii) Generate multiple sets of approximate optimal solutions (such as prioritizing the use of transition Z1 or transition Z2), support dynamic decision-making (such as excavating project W2 to transition Z2 or borrowing site to filling project T2 in May), and increase scheme diversity by 22%. (iii) Real-time status synchronization, through a dynamic pheromone update mechanism, provides real-time feedback on transition capacity (such as 674,000 cubic meters of inventory in transition 1 in September), avoiding the risk of capacity conflicts in static planning and significantly enhancing engineering adaptability. After 4000 iterations of the ant colony optimization algorithm, the minimum cost of earthwork allocation optimization considering road transportation intensity (Table 6) was CNY 15.679 million. Compared with the minimum cost of earthwork allocation optimization without considering road transportation intensity (Table 5), which was CNY 15.658 million, the allocation cost increased by CNY 21,000, an increase of 0.91%. From the perspective of earthwork allocation in actual engineering, considering road transportation intensity, the allocation cost increased, and the proportion of earthwork directly entering the dam increased. The maximum capacity limit of the waste disposal site and intermediate transfer site was not exceeded, and the transportation route was more reasonable. The results of allocation optimization were more in line with the actual construction situation.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Symbol Explanation
| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| Wi | Excavation projects | R | Rainfall erosivity factor |
| Tj | Filling projects | K | Erodibility factor of soil and water |
| Zk | Transfer yards | L | Slope length factor |
| Ql | Waste disposal yards | S | Slope gradient factor |
| Cm | Material yards | C | Plant measure factor |
| Gt | Construction period | P | Soil and water conservation measure factor |
| Material allocation amount from the excavation project to the waste disposal site within the t-th month | Material allocation amount from the excavation project to the intermediate transfer site within the t-th month | ||
| Cost of losing 1 m3 of water and soil in the abandoned waste disposal site | Cost of 1 m3 of water and soil loss in the transition field | ||
| Average annual soil erosion of the waste disposal site | Average annual soil erosion of the transition zone | ||
| Current soil erosion intensity per unit area of the waste disposal site | Current soil erosion intensity per unit area of the transition zone | ||
| Cost of restoring the landscape of one square meter of the waste dump work area | Cost of restoring the landscape of one square meter of the transfer yard work area | ||
| Earthwork transportation volume of the m-th section eijm in the Eijk route within the t-th month | Material loss rate from starting point i to endpoint j in the t-th month | ||
| Transportation unit prices from excavation project to filling project | Material allocation quantities on route E from excavation project to filling project | ||
| Transportation unit prices from excavation project to the intermediate transfer site | Material allocation quantities on route E from excavation project to the intermediate transfer site | ||
| Transportation unit prices from excavation project to waste disposal site | Material allocation quantities on route E from excavation project to waste disposal site | ||
| Transportation unit prices from intermediate transfer site to filling project | Material allocation quantities on route E from intermediate transfer site to filling project | ||
| Transportation unit prices from material yard to filling project | Material allocation quantities on route E from material yard to filling project |
References
- Mayer, R.H.; Robert, M.S. Earth moving logistics. J. Constr. Div. 1981, 107, 297–312. [Google Scholar] [CrossRef]
- Moreb, A.A. Linear programming model for finding optimal roadway grades that minimize earthwork cost. Eur. J. Oper. Res. 1996, 93, 148–154. [Google Scholar] [CrossRef]
- Zheng, X.Z.; Lu, F.; Jin, L.H. Dynamic earthwork allocation model based on simple method and its application. Water Resour. Power 2014, 32, 123–125+113. [Google Scholar]
- Hu, C.S.; Zhong, D.H.; Zhang, J.; Hong, W.; Li, M.C. Study on the model and its visualization for dynamic allocation of earth. Chin. J. Eng. 2003, 12, 73–79. [Google Scholar]
- Henderson, D.; Vaughan, D.E.; Jacobson, S.H.; Wakefield, R.R.; Sewell, E.C. Solving the shortest route cut and fill problem using simulated annealing. Eur. J. Oper. Res. 2003, 145, 72–84. [Google Scholar] [CrossRef]
- Lim, A.; Rodrigues, B.; Zhang, J. Tabu search embedded simulated annealing for the shortest route cut and fill problem. J. Oper. Res. Soc. 2005, 56, 816–824. [Google Scholar] [CrossRef]
- Wang, R.C.; Zhang, P.C.; Xu, Y.M. Earthwork dynamic allocation based on the Monte Carlo tree search algorithm and its verification. J. Hydraul. Eng. 2020, 51, 391–401. [Google Scholar]
- Jiao, Y.B.; Zhai, Z.H.; Zhang, W.Y.; Gao, Z. Research on the earth-rock allocation model of rockfill dams based on green construction. China Rural. Water Hydropower 2015, 7, 137–139. [Google Scholar]
- Carmichael, D.G.; Williams, E.H.; Kaboli, A.S. Minimum operational emissions in earthmoving. Constr. Res. Congr. 2012, 1869–1878. [Google Scholar]
- Burdett, R.; Kozan, E.; Kenley, R. Block models for improved earthwork allocation planning in linear infrastructure construction. Eng. Optim. 2015, 47, 347–369. [Google Scholar] [CrossRef]
- Shen, M.L.; Liu, X.G.; Chen, G.; Cao, S.; Zhu, Y. Model for joint optimization of path transportation intensity and earth-rock work allocation of rockfill dam. Eng. J. Wuhan Univ. 2006, 5, 14–18. [Google Scholar]
- Marzouk, M.; Moselhi, O. Multiobjective optimization of earthmoving operations. J. Constr. Eng. Manag. 2004, 130, 105–113. [Google Scholar] [CrossRef]
- Huang, B.H.; Zhao, Y.; Lu, R.; Zheng, Q.; Xu, B. Earthwork allocation method based on ant colony algorithm. J. Civ. Eng. Manag. 2019, 36, 72–77+84. [Google Scholar]
- Zhao, Y. Study and Application of Earthwork Allocation Method Based on Intelligent Optimization Algorithm. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2019. [Google Scholar]
- Miao, K. Swarm Intelligence Algorithms for the 3D Route Location in Highway (Railway) Engineering Structures. Ph.D. Thesis, Central South University, Changsha, China, 2011. [Google Scholar]
- Sun, X. The Study and Realize of Highway Earthwork Allocation Based on GIS. Master’s Thesis, Central South University, Changsha, China, 2012. [Google Scholar]
- Li, A.; Li, Y.; Yao, B.W.; Li, Y.; Jiang, L. Optimal allocation model of earthwork and its application based on dynamic path planning. J. Henan Agric. Sci. 2025, 1–7. [Google Scholar]
- Zhang, J.C.; Zhang, Y.X.; Yang, Y.H. Quantitative analysis of highway engineering construction safety risk based on combinatorial weighted two-dimensional cloud model. Henan Sci. 2024, 42, 1458–1466. [Google Scholar]
- Zhang, Y.X.; Zhang, J.C.; Yang, Y.H.; Li, D.; Wang, B. Dynamic evaluation of highway engineering construction safety risk based on fuzzy dynamic Bayesian network. Henan Sci. 2024, 42, 653–659. [Google Scholar]
- Tan, Q.L. Investigation on hydropower projects soil erosion prediction program. Water Power 2006, 5, 9–11. [Google Scholar]
- Mavrovouniotis, M.; Yang, S. Ant colony optimization with self-adaptive evaporation rate in dynamic environments. In Proceedings of the IEEE Symposium on Computational Intelligence in Dynamic & Uncertain Environments, IEEE, Orlando, FL, USA, 9–12 December 2014. [Google Scholar]
- Meng, R.; Cheng, X.; Wu, Z.; Du, X. Improved ant colony optimization for safe path planning of AUV. Heliyon 2024, 10, e27753. [Google Scholar] [CrossRef] [PubMed]

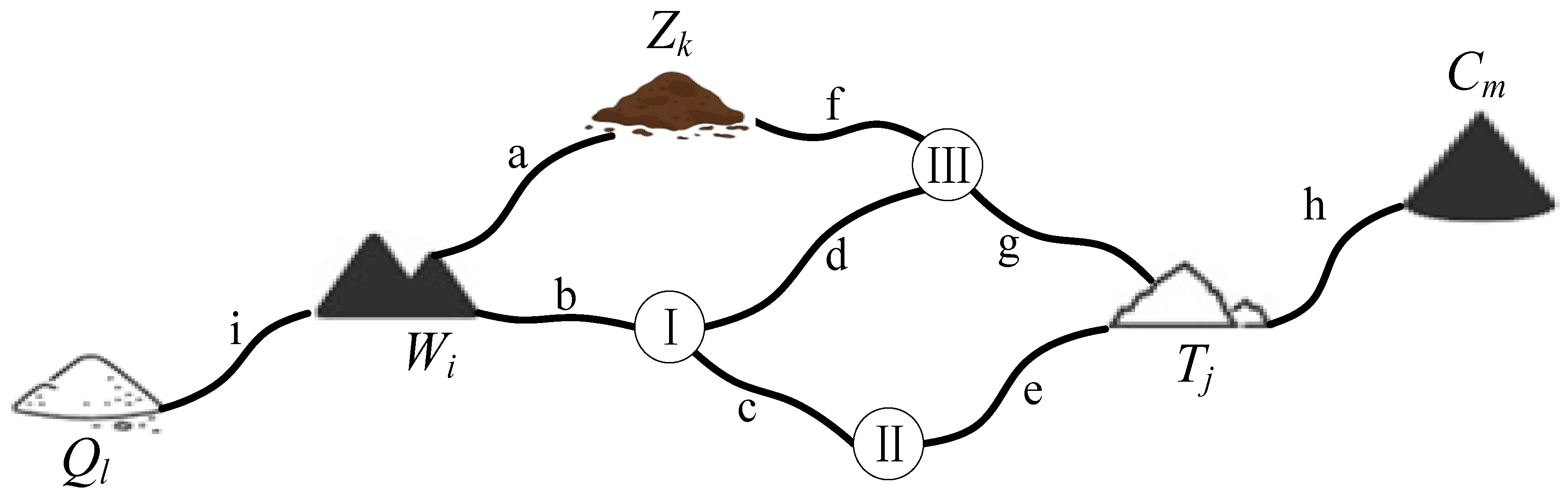

| Entry Name | First Month | Second Month | Third Month | Fourth Month | Fifth Month | Sixth Month | Seventh Month | Eighth Month | Ninth Month | Tenth Month | The 11th Month | The 12th Month |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| W1 | 30.2 | 28.0 | 30.2 | 28.0 | 26.6 | 25.8 | 24.8 | 26.0 | 28.2 | 27.4 | 28.7 | 28.0 |
| W2 | 0 | 0 | 0 | 0 | 28.2 | 24.0 | 25.8 | 24.8 | 24.6 | 24.8 | 25.6 | 25.0 |
| T1 | 0 | 0 | 25.4 | 26.8 | 25.0 | 25.0 | 25.2 | 26.4 | 26.6 | 26.8 | 26.8 | 24.6 |
| T2 | 0 | 0 | 0 | 0 | 10.4 | 10.2 | 10.6 | 11.0 | 12.6 | 11.2 | 10.6 | 10.6 |
| Venue Name | C1 | Z1 | Z2 | Q1 |
|---|---|---|---|---|
| Capacity/Storage | 63 | 186 | 286 | 80 |
| Material Source | T1 | T2 | Z1 | Z2 | Q1 |
|---|---|---|---|---|---|
| W1 | 15 | — | 10 | 9 | 20 |
| W2 | — | 12 | 9 | 10 | 25 |
| Z1 | 20 | 18 | — | — | — |
| Z2 | 18 | 20 | — | — | — |
| C1 | 16 | 15 | — | — | — |
| Parameter | Range | Parameter Values | Parameter Function Description |
|---|---|---|---|
| Pheromone weight | [1, 5] | 1.2 | The influence of pheromone concentration on ant selection on the control path, the larger the value, the more likely ants are to choose the path with higher historical pheromone concentration. |
| Heuristic information weight | [1, 5] | 2.5 | Control the influence of heuristic information (such as the reciprocal of transportation costs) on path selection, with larger values indicating that ants are more inclined to choose paths with lower costs. |
| Volatile rate of pheromones | [0.1, 0.5] | 0.15 | Control the evaporation rate of pheromones after each iteration, the larger the value, the faster the pheromone evaporation, and the stronger the algorithm’s ability to explore new paths. |
| Number of ants | [1, ∞] | 100 | The more ants are searched in parallel in each iteration, the higher the solution space coverage, but the computational cost increases. |
| Punishment factor | — | 1000 | Punish paths that violate capacity constraints (such as transition field exceeding limits) to avoid generating infeasible solutions. |
| Dynamic attenuation coefficient | [0.95, 0.99] | 0.98 | Used to adaptively adjust the heuristic information weight beta, gradually decreasing with increasing iteration times, balancing global exploration and local development. |
| Time/Month | Source | Destination | Quantity | Time/Month | Source | Destination | Quantity |
|---|---|---|---|---|---|---|---|
| 1 | W1 | Q1 | 5.2 | 8 | W1 | T1 | 26.0 |
| 1 | W1 | Z1 | 25.0 | 8 | Z1 | T1 | 0.4 |
| 2 | W1 | Z1 | 28.0 | 8 | W2 | T2 | 11.0 |
| 3 | W1 | T1 | 25.4 | 8 | W2 | Z2 | 13.8 |
| 3 | W1 | Z1 | 4.8 | 8 | C1 | T2 | 1.2 |
| 4 | W1 | T1 | 26.2 | 9 | W1 | T1 | 26.6 |
| 4 | W1 | Z1 | 1.8 | 9 | Z1 | T1 | 28.2 |
| 4 | Z1 | T1 | 0.6 | 9 | W2 | T2 | 12.6 |
| 5 | W1 | T1 | 25.0 | 9 | W2 | Z2 | 12.0 |
| 5 | W1 | Z1 | 1.6 | 10 | Z1 | T1 | 26.8 |
| 5 | W2 | T2 | 9.9 | 10 | W1 | Z1 | 27.4 |
| 5 | Z2 | T2 | 0.5 | 10 | W2 | T2 | 11.2 |
| 5 | W2 | Z2 | 18.3 | 10 | C1 | W2 | 4.0 |
| 5 | W2 | Q1 | 3.0 | 11 | W1 | T1 | 28.7 |
| 6 | W1 | T1 | 25.0 | 11 | C1 | T1 | 2.8 |
| 6 | W1 | Z1 | 0.8 | 11 | W2 | T2 | 10.6 |
| 6 | W2 | T2 | 10.2 | 11 | W2 | Z2 | 15.0 |
| 6 | W2 | Z2 | 13.8 | 12 | Z1 | T1 | 6.4 |
| 7 | Z1 | T1 | 25.2 | 12 | W1 | T1 | 20.2 |
| 7 | W1 | T1 | 24.8 | 12 | W1 | Z1 | 4.0 |
| 7 | W2 | T2 | 10.6 | 12 | W2 | T2 | 22.6 |
| 7 | W2 | Z2 | 15.2 | 12 | Z2 | T2 | 3.6 |
| 7 | Z2 | T2 | 4.8 | 12 | C1 | T2 | 2.4 |
| Time/Month | Source | Destination | Quantity | Time/Month | Source | Destination | Quantity |
|---|---|---|---|---|---|---|---|
| 1 | W1 | Q1 | 5.2 | 8 | W1 | T1 | 26.0 |
| 1 | W1 | Z1 | 25.0 | 8 | Z1 | T1 | 0.4 |
| 2 | W1 | Z1 | 28.0 | 8 | W2 | T2 | 11.0 |
| 3 | W1 | T1 | 25.4 | 8 | W2 | Z2 | 13.8 |
| 3 | W1 | Z1 | 4.8 | 8 | C1 | T2 | 1.2 |
| 4 | W1 | T1 | 26.2 | 9 | W1 | T1 | 26.6 |
| 4 | W1 | Z1 | 1.8 | 9 | Z1 | T1 | 28.2 |
| 4 | Z1 | T1 | 0.6 | 9 | W2 | T2 | 12.6 |
| 5 | W1 | T1 | 25.0 | 9 | W2 | Z2 | 12.0 |
| 5 | W1 | Z1 | 1.6 | 10 | Z1 | T1 | 26.8 |
| 5 | W2 | T2 | 9.9 | 10 | W1 | Z1 | 27.4 |
| 5 | Z2 | T2 | 0.5 | 10 | W2 | T2 | 11.2 |
| 5 | W2 | Z2 | 18.3 | 10 | C1 | W2 | 4.0 |
| 5 | W2 | Q1 | 3.0 | 11 | W1 | T1 | 28.7 |
| 6 | W1 | T1 | 25.0 | 11 | C1 | T1 | 2.8 |
| 6 | W1 | Z1 | 0.8 | 11 | W2 | T2 | 10.6 |
| 6 | W2 | T2 | 10.2 | 11 | W2 | Z2 | 15.0 |
| 6 | W2 | Z2 | 13.8 | 12 | Z1 | T1 | 6.4 |
| 7 | Z1 | T1 | 25.2 | 12 | W1 | T1 | 20.2 |
| 7 | W1 | T1 | 24.8 | 12 | W1 | Z1 | 4.0 |
| 7 | W2 | T2 | 10.6 | 12 | W2 | T2 | 22.6 |
| 7 | W2 | Z2 | 15.2 | 12 | Z2 | T2 | 3.6 |
| 7 | Z2 | T2 | 4.8 | 12 | C1 | T2 | 2.4 |
| Algorithm | Average Minimum Cost (CNY Ten Thousand) | Cost standard Deviation | Average Running Time (Seconds) | Average Number of Iterations |
|---|---|---|---|---|
| IACO | 1567.9 | 5.2 | 128 | 2850 |
| Standard GA | 1589.5 | 18.7 | 145 | 3200 |
| Standard PSO | 1575.3 | 12.1 | 95 | 2650 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Niu, S.; Yu, H.; Nie, X.; Fan, T. Joint Optimization Model for Earthwork Allocation Considering Soil and Water Conservation Fees, Landscape Restoration Fees, and Road Transportation Intensity. Appl. Sci. 2025, 15, 11516. https://doi.org/10.3390/app152111516
Wang B, Niu S, Yu H, Nie X, Fan T. Joint Optimization Model for Earthwork Allocation Considering Soil and Water Conservation Fees, Landscape Restoration Fees, and Road Transportation Intensity. Applied Sciences. 2025; 15(21):11516. https://doi.org/10.3390/app152111516
Chicago/Turabian StyleWang, Bo, Shibin Niu, Hui Yu, Xiangtian Nie, and Tianyu Fan. 2025. "Joint Optimization Model for Earthwork Allocation Considering Soil and Water Conservation Fees, Landscape Restoration Fees, and Road Transportation Intensity" Applied Sciences 15, no. 21: 11516. https://doi.org/10.3390/app152111516
APA StyleWang, B., Niu, S., Yu, H., Nie, X., & Fan, T. (2025). Joint Optimization Model for Earthwork Allocation Considering Soil and Water Conservation Fees, Landscape Restoration Fees, and Road Transportation Intensity. Applied Sciences, 15(21), 11516. https://doi.org/10.3390/app152111516





