Benchmarking ML Approaches for Earthquake-Induced Soil Liquefaction Classification
Abstract
1. Introduction
2. Material and Methods
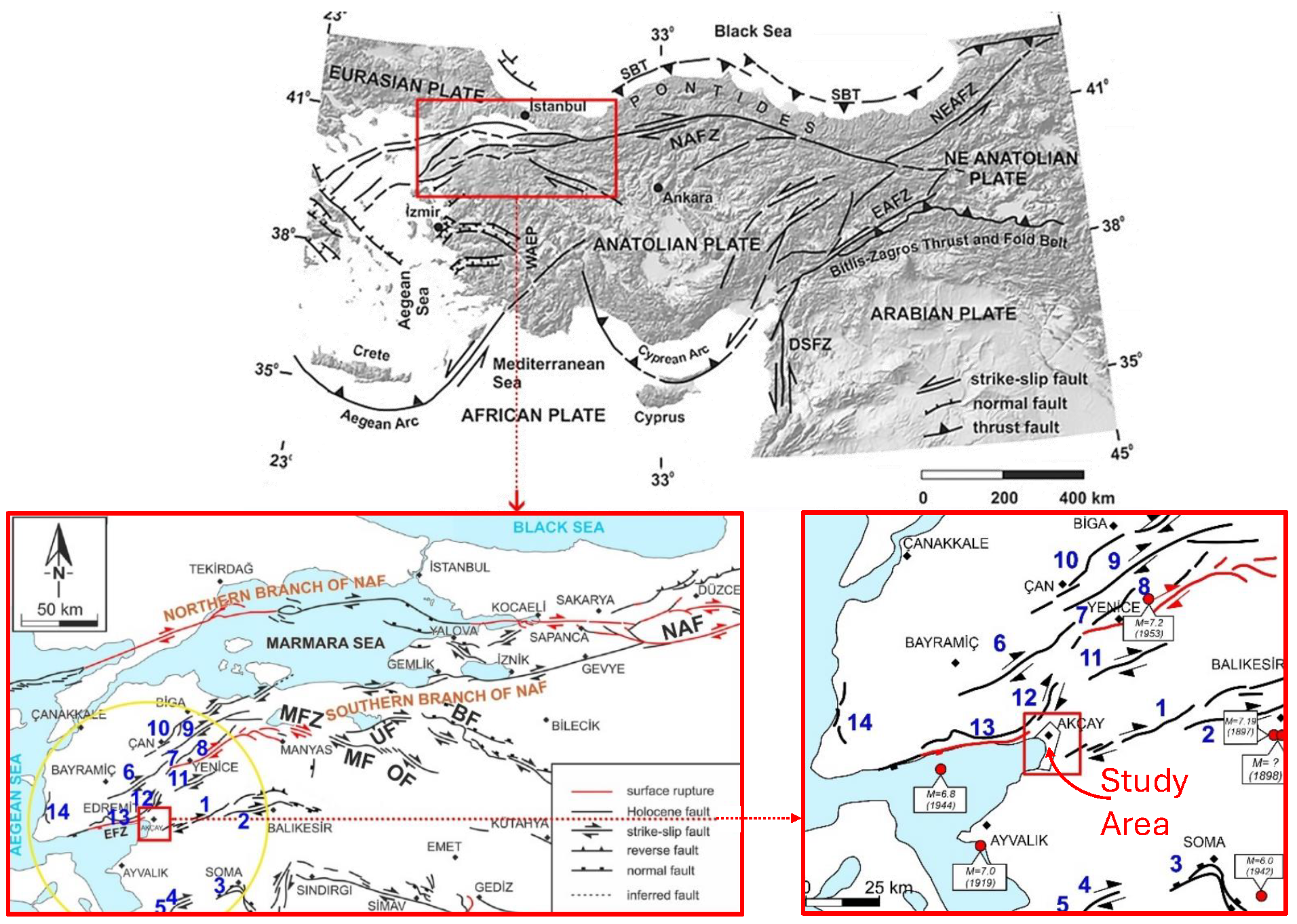
2.1. Description of the Study Area
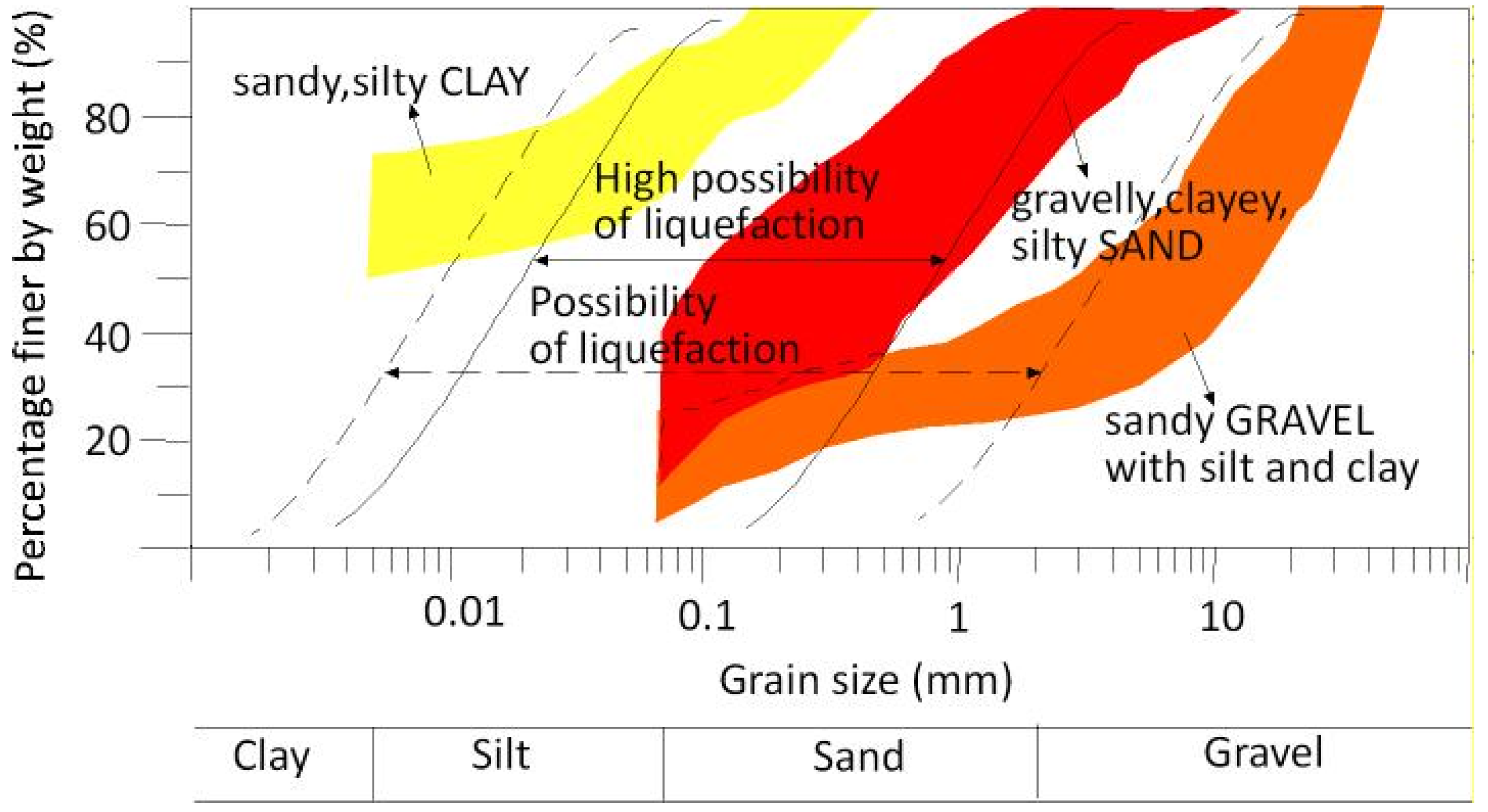
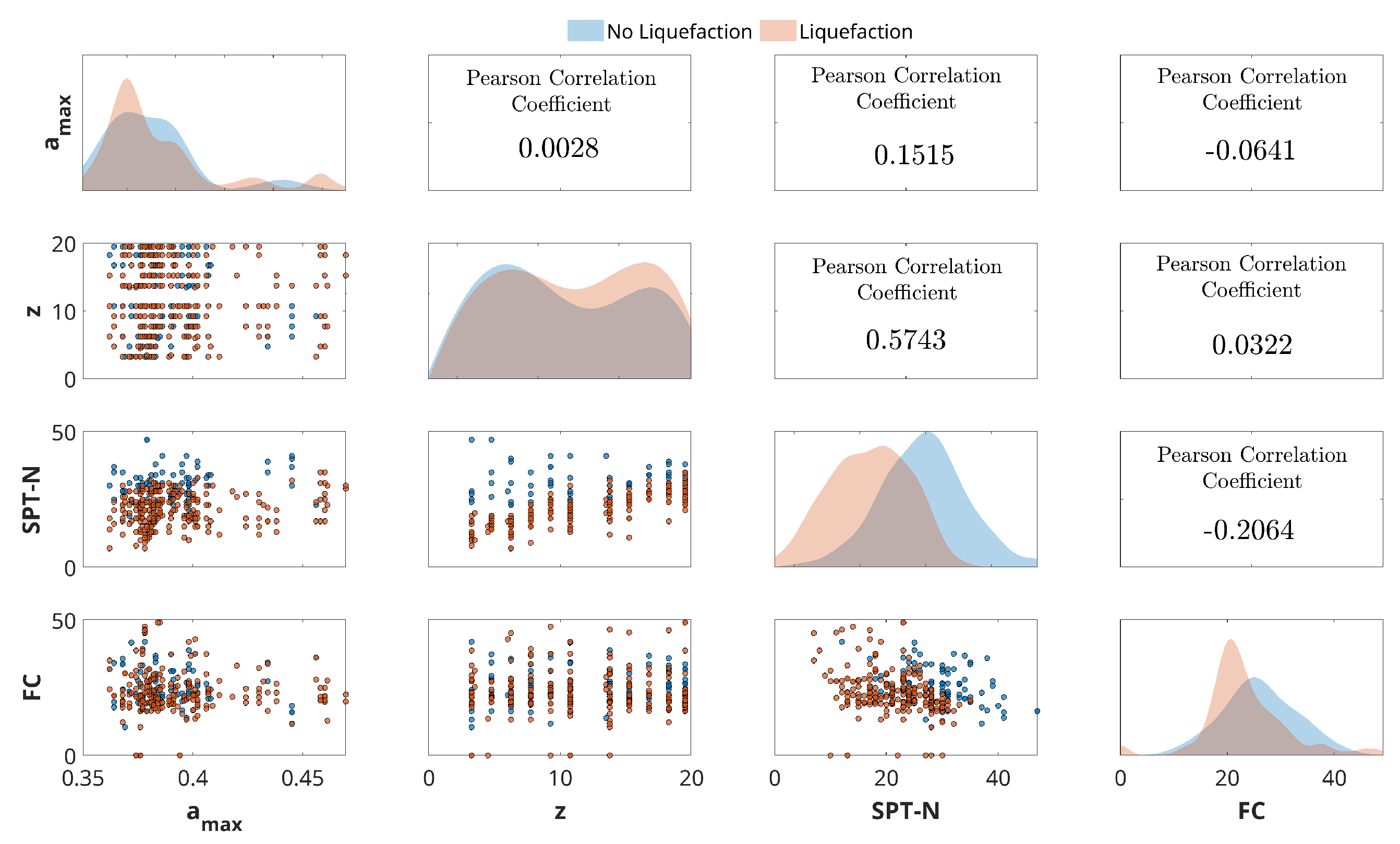
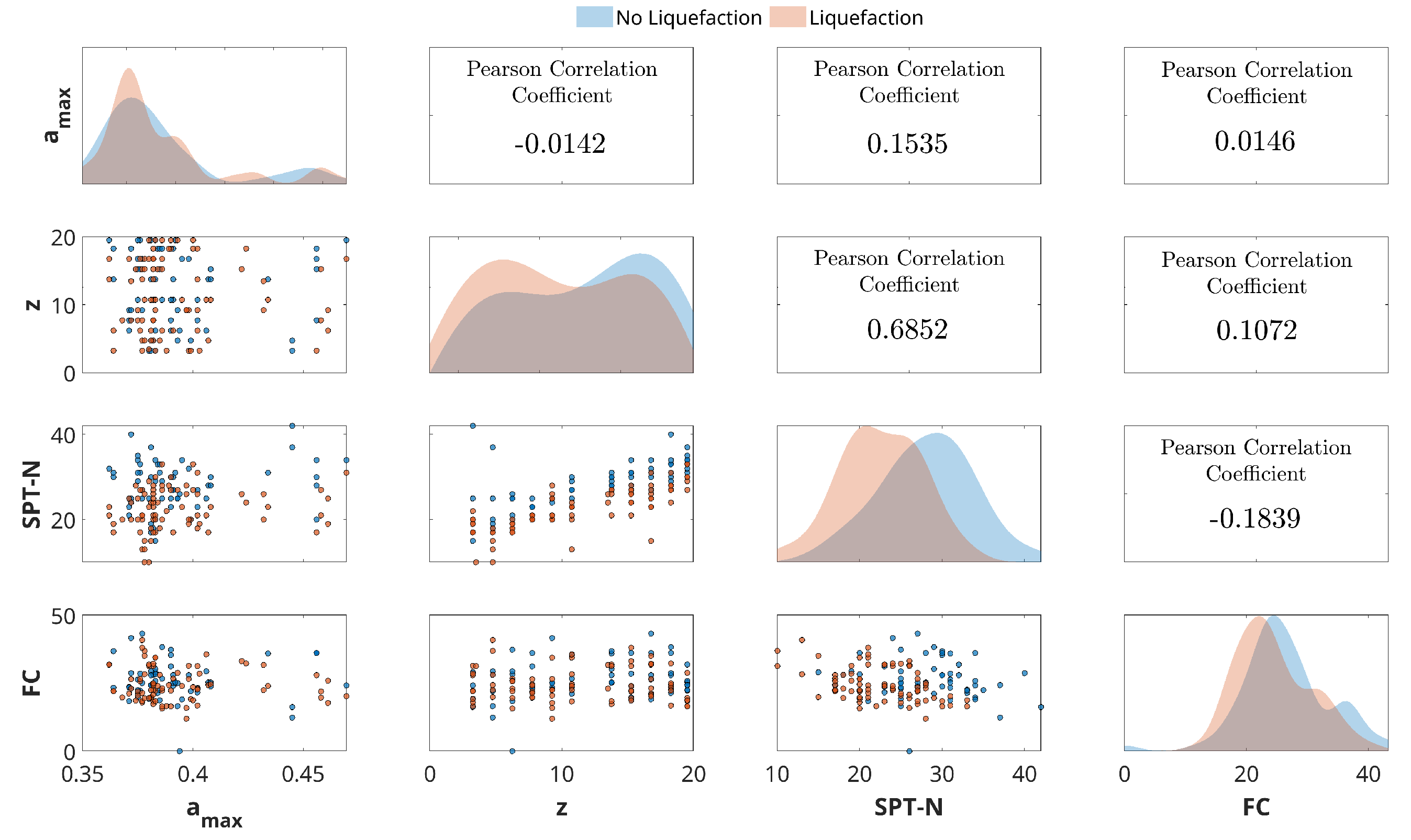
2.2. Dataset
2.3. Model Development
2.3.1. k-Nearest Neighbor (kNN)
2.3.2. Artificial Neural Network (ANN)
2.3.3. Decision Tree (DT)
2.3.4. Random Forest (RF)
2.3.5. Support Vector Machine (SVM)
2.3.6. Naive Bayes (NB)
2.4. Model Evaluation
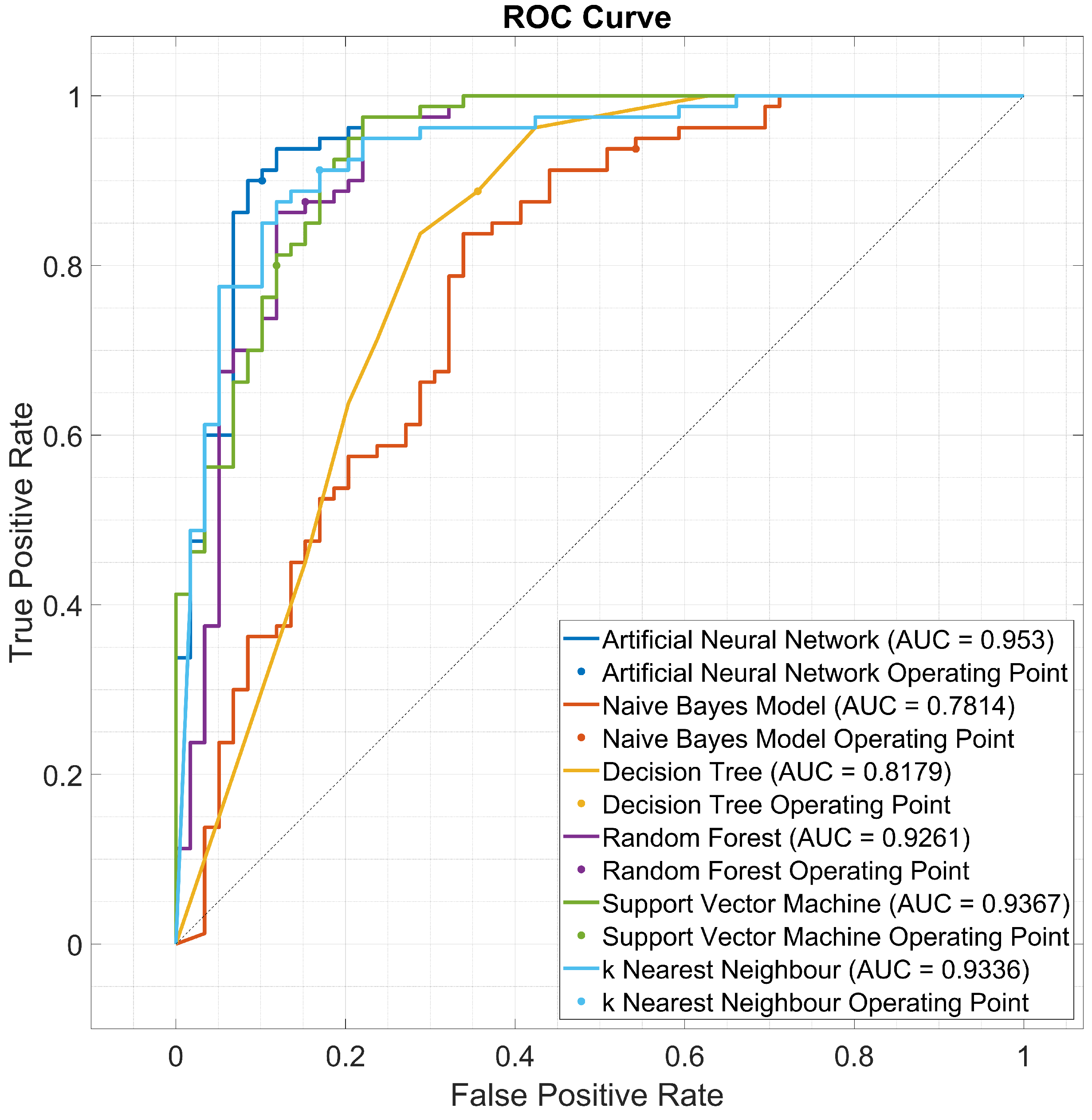
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Castro, G. On the behavior of soils during earthquakes–liquefaction. Dev. Geotech. Eng. 1987, 42, 169–204. [Google Scholar]
- Kumar, A.; Srinivas, B.V. Easy to use empirical correlations for liquefaction and no liquefaction conditions. Geotech. Geol. Eng. 2017, 35, 1383–1407. [Google Scholar] [CrossRef]
- Dengiz, O. Soil quality index for paddy fields based on standard scoring functions and weight allocation method. Arch. Agron. Soil Sci. 2020, 66, 301–315. [Google Scholar] [CrossRef]
- Youd, T. Ground failure investigations following the 1964 Alaska Earthquake. In Proceedings of the 10th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Ishihara, K.; Koga, Y. Case studies of liquefaction in the 1964 Niigata earthquake. Soils Found. 1981, 21, 35–52. [Google Scholar] [CrossRef] [PubMed]
- Seed, R.B.; Dickenson, S.; Idriss, I. Principal geotechnical aspects of the 1989 Loma Prieta earthquake. Soils Found. 1991, 31, 1–26. [Google Scholar] [CrossRef]
- Tanaka, Y. The 1995 great Hanshin Earthquake and liquefaction damages at reclaimed lands in Kobe Port. Int. J. Offshore Polar Eng. 2000, 10, ISOPE-00-10-1-064. [Google Scholar]
- Chu, D.B.; Stewart, J.P.; Lee, S.; Tsai, J.S.; Lin, P.; Chu, B.; Seed, R.B.; Hsu, S.; Yu, M.; Wang, M.C. Documentation of soil conditions at liquefaction and non-liquefaction sites from 1999 Chi–Chi (Taiwan) earthquake. Soil Dyn. Earthq. Eng. 2004, 24, 647–657. [Google Scholar] [CrossRef]
- Erken, A.; Kaya, Z.; Erdem, A. Ground deformations in Adapazari during 1999 Kocaeli Earthquake. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; pp. 29–32. [Google Scholar]
- Quigley, M.C.; Bastin, S.; Bradley, B.A. Recurrent liquefaction in Christchurch, New Zealand, during the Canterbury earthquake sequence. Geology 2013, 41, 419–422. [Google Scholar] [CrossRef]
- Nanda, G.; Mulyani, A. Analysis of landscape changes using high-resolution satellite images at former rice fields after earthquake and liquefaction in Central Sulawesi Province. IOP Conf. Ser. Earth Environ. Sci. 2021, 648, 012203. [Google Scholar] [CrossRef]
- Tobita, T.; Kiyota, T.; Torisu, S.; Cinicioglu, O.; Tonuk, G.; Milev, N.; Contreras, J.; Contreras, O.; Shiga, M. Geotechnical damage survey report on February 6, 2023 Turkey-Syria Earthquake, Turkey. Soils Found. 2024, 64, 101463. [Google Scholar] [CrossRef]
- Ceryan, S.; Ceryan, N. A new index for microzonation of earthquake prone settlement area by considering liquefaction potential and fault avoidance zone: An example case from Edremit (Balikesir, Turkey). Arab. J. Geosci. 2021, 14, 2216. [Google Scholar] [CrossRef]
- Zhao, H.B.; Ru, Z.L.; Yin, S. Updated support vector machine for seismic liquefaction evaluation based on the penetration tests. Mar. Georesources Geotechnol. 2007, 25, 209–220. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of liquefaction potential using field performance data. J. Geotech. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Idriss, I.; Boulanger, R. Semi-empirical procedures for evaluating liquefaction potential during earthquakes. Soil Dyn. Earthq. Eng. 2006, 26, 115–130. [Google Scholar] [CrossRef]
- Johari, A.; Khodaparast, A. Modelling of probability liquefaction based on standard penetration tests using the jointly distributed random variables method. Eng. Geol. 2013, 158, 1–14. [Google Scholar] [CrossRef]
- Rahman, M.Z.; Siddiqua, S. Evaluation of liquefaction-resistance of soils using standard penetration test, cone penetration test, and shear-wave velocity data for Dhaka, Chittagong, and Sylhet cities in Bangladesh. Environ. Earth Sci. 2017, 76, 207. [Google Scholar] [CrossRef]
- Andrus, R.D.; Stokoe, K.H.; Chung, R.M.; Juang, C.H. Draft Guidelines for Evaluating Liquefaction Resistance Using Shear Wave Velocity Measurements and Simplified Procedures; NIST Interagency/Internal Report (NISTIR); National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999.
- Kayen, R.; Moss, R.; Thompson, E.; Seed, R.; Cetin, K.; Kiureghian, A.D.; Tanaka, Y.; Tokimatsu, K. Shear-wave velocity–based probabilistic and deterministic assessment of seismic soil liquefaction potential. J. Geotech. Geoenviron. Eng. 2013, 139, 407–419. [Google Scholar] [CrossRef]
- Robertson, P. Comparing CPT and V s liquefaction triggering methods. J. Geotech. Geoenviron. Eng. 2015, 141, 04015037. [Google Scholar] [CrossRef]
- Johari, A.; Khodaparast, A.; Javadi, A. An analytical approach to probabilistic modeling of liquefaction based on shear wave velocity. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 263–275. [Google Scholar] [CrossRef]
- Chen, G.; Wu, Q.; Zhao, K.; Shen, Z.; Yang, J. A binary packing material–based procedure for evaluating soil liquefaction triggering during earthquakes. J. Geotech. Geoenviron. Eng. 2020, 146, 04020040. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M. Liquefaction resistance of soils: Summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef]
- Juang, C.H.; Yuan, H.; Lee, D.H.; Lin, P.S. Simplified cone penetration test-based method for evaluating liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2003, 129, 66–80. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Idriss, I. CPT-based liquefaction triggering procedure. J. Geotech. Geoenviron. Eng. 2016, 142, 04015065. [Google Scholar] [CrossRef]
- Pal, M. Support vector machines-based modelling of seismic liquefaction potential. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 983–996. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y. An ensemble method to improve prediction of earthquake-induced soil liquefaction: A multi-dataset study. Neural Comput. Appl. 2021, 33, 1533–1546. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Zhou, T.; Armaghani, D.J.; Qiu, Y. Employing a genetic algorithm and grey wolf optimizer for optimizing RF models to evaluate soil liquefaction potential. Artif. Intell. Rev. 2022, 55, 5673–5705. [Google Scholar] [CrossRef]
- Hanna, A.M.; Ural, D.; Saygili, G. Evaluation of liquefaction potential of soil deposits using artificial neural networks. Eng. Comput. 2007, 24, 5–16. [Google Scholar] [CrossRef]
- Zhang, X.; He, B.; Sabri, M.M.S.; Al-Bahrani, M.; Ulrikh, D.V. Soil liquefaction prediction based on bayesian optimization and support vector machines. Sustainability 2022, 14, 11944. [Google Scholar] [CrossRef]
- Huang, F.K.; Wang, G.S. A Method for Developing Seismic Hazard-Consistent Fragility Curves for Soil Liquefaction Using Monte Carlo Simulation. Appl. Sci. 2024, 14, 9482. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Zhou, H.; Tong, L.; Widanage, W.D.; Marco, J. Feature analyses and modeling of lithium-ion battery manufacturing based on random forest classification. IEEE/ASME Trans. Mechatronics 2021, 26, 2944–2955. [Google Scholar] [CrossRef]
- Ozkat, E.C.; Abdioglu, M.; Ozturk, U.K. Machine learning driven optimization and parameter selection of multi-surface HTS Maglev. Phys. C Supercond. Its Appl. 2024, 616, 1354430. [Google Scholar] [CrossRef]
- Goh, A.T.; Goh, S. Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data. Comput. Geotech. 2007, 34, 410–421. [Google Scholar] [CrossRef]
- Samui, P.; Kim, D.; Sitharam, T. Support vector machine for evaluating seismic-liquefaction potential using shear wave velocity. J. Appl. Geophys. 2011, 73, 8–15. [Google Scholar] [CrossRef]
- Karthikeyan, J.; Samui, P. Application of statistical learning algorithms for prediction of liquefaction susceptibility of soil based on shear wave velocity. Geomat. Nat. Hazards Risk 2014, 5, 7–25. [Google Scholar] [CrossRef]
- Shahri, A.A. Assessment and prediction of liquefaction potential using different artificial neural network models: A case study. Geotech. Geol. Eng. 2016, 34, 807–815. [Google Scholar] [CrossRef]
- Xue, X.; Xiao, M. Application of genetic algorithm-based support vector machines for prediction of soil liquefaction. Environ. Earth Sci. 2016, 75, 874. [Google Scholar] [CrossRef]
- Ahmad, M.; Tang, X.W.; Qiu, J.N.; Ahmad, F. Evaluating seismic soil liquefaction potential using bayesian belief network and C4. 5 decision tree approaches. Appl. Sci. 2019, 9, 4226. [Google Scholar] [CrossRef]
- Rahbarzare, A.; Azadi, M. Improving prediction of soil liquefaction using hybrid optimization algorithms and a fuzzy support vector machine. Bull. Eng. Geol. Environ. 2019, 78, 4977–4987. [Google Scholar] [CrossRef]
- Hu, J.; Liu, H. Bayesian network models for probabilistic evaluation of earthquake-induced liquefaction based on CPT and Vs databases. Eng. Geol. 2019, 254, 76–88. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, J.; Zhang, Y.; Xie, Y. The adoption of a support vector machine optimized by GWO to the prediction of soil liquefaction. Environ. Earth Sci. 2021, 80, 360. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S.; Yao, X.; Gao, H.; Wang, Z.; Shen, Z. Liquefaction evaluation based on shear wave velocity using random forest. Adv. Civ. Eng. 2021, 2021, 3230343. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G. A novel PSO-KELM based soil liquefaction potential evaluation system using CPT and Vs measurements. Soil Dyn. Earthq. Eng. 2021, 150, 106930. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, Y.; Zhang, Y.; Qiu, J.; Wu, S. The adoption of deep neural network (DNN) to the prediction of soil liquefaction based on shear wave velocity. Bull. Eng. Geol. Environ. 2021, 80, 5053–5060. [Google Scholar] [CrossRef]
- Kumar, D.; Samui, P.; Kim, D.; Singh, A. A novel methodology to classify soil liquefaction using deep learning. Geotech. Geol. Eng. 2021, 39, 1049–1058. [Google Scholar] [CrossRef]
- Demir, S.; Şahin, E.K. Liquefaction prediction with robust machine learning algorithms (SVM, RF, and XGBoost) supported by genetic algorithm-based feature selection and parameter optimization from the perspective of data processing. Environ. Earth Sci. 2022, 81, 459. [Google Scholar] [CrossRef]
- Ozsagir, M.; Erden, C.; Bol, E.; Sert, S.; Özocak, A. Machine learning approaches for prediction of fine-grained soils liquefaction. Comput. Geotech. 2022, 152, 105014. [Google Scholar] [CrossRef]
- Hanandeh, S.M.; Al-Bodour, W.A.; Hajij, M.M. A comparative study of soil liquefaction assessment using machine learning models. Geotech. Geol. Eng. 2022, 40, 4721–4734. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Wang, M.; Qiu, Y. Performance evaluation of hybrid GA–SVM and GWO–SVM models to predict earthquake-induced liquefaction potential of soil: A multi-dataset investigation. Eng. Comput. 2022, 38, 4197–4215. [Google Scholar] [CrossRef]
- Duan, W.; Zhao, Z.; Cai, G.; Wang, A.; Wu, M.; Dong, X.; Liu, S. V s-based assessment of soil liquefaction potential using ensembling of GWO–KLEM and Bayesian theorem: A full probabilistic design perspective. Acta Geotech. 2023, 18, 1863–1881. [Google Scholar] [CrossRef]
- Sui, Q.R.; Chen, Q.H.; Wang, D.D.; Tao, Z.G. Application of machine learning to the V s-based soil liquefaction potential assessment. J. Mt. Sci. 2023, 20, 2197–2213. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, Y. Study on Classification Method of Soil Liquefaction Potential Based on Decision Tree. Appl. Sci. 2023, 13, 4459. [Google Scholar] [CrossRef]
- Abbasimaedeh, P. Soil liquefaction in seismic events: Pioneering predictive models using machine learning and advanced regression techniques. Environ. Earth Sci. 2024, 83, 189. [Google Scholar] [CrossRef]
- Ghani, S.; Thapa, I.; Kumari, S.; Correia, A.G.; Asteris, P.G. Revealing the nature of soil liquefaction using machine learning. Earth Sci. Inform. 2025, 18, 198. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient kNN classification with different numbers of nearest neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1774–1785. [Google Scholar] [CrossRef] [PubMed]
- Ozkat, E.C. A method to classify steel plate faults based on ensemble learning. J. Mater. Mechatronics A 2022, 3, 240–256. [Google Scholar] [CrossRef]
- Guo, H.; Zhuang, X.; Chen, J.; Zhu, H. Predicting earthquake-induced soil liquefaction based on machine learning classifiers: A comparative multi-dataset study. Int. J. Comput. Methods 2022, 19, 2142004. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Fridline, M.M.; Roke, D.A. Decision tree approach for soil liquefaction assessment. Sci. World J. 2013, 2013, 346285. [Google Scholar] [CrossRef]
- Ahmad, M.; Tang, X.W.; Qiu, J.N.; Ahmad, F.; Gu, W.J. Application of machine learning algorithms for the evaluation of seismic soil liquefaction potential. Front. Struct. Civ. Eng. 2021, 15, 490–505. [Google Scholar] [CrossRef]
- Ekinci, Y.L.; Yiğitbaş, E. A geophysical approach to the igneous rocks in the Biga Peninsula (NW Turkey) based on airborne magnetic anomalies: Geological implications. Geodin. Acta 2012, 25, 267–285. [Google Scholar] [CrossRef]
- Sozbilir, H.; Ozkaymak, C.; Uzel, B.; Sumer, O. Criteria for Surface Rupture Microzonation of Active Faults for Earthquake Hazards in Urban Areas. In Handbook of Research on Trends and Digital Advances in Engineering Geology; IGI Global: Hershey, PA, USA, 2018; pp. 187–230. [Google Scholar]
- Ceryan, S.; Samui, P.; Ozkan, O.S.; Berber, S.; Tudes, S.; Elci, H.; Ceryan, N. Soil liquefaction susceptibility of Akcay residential area (Biga Peninsula, Turkey) close to North Anatolian fault zone. J. Min. Environ. 2023, 14, 1141–1153. [Google Scholar]
- Sozbilir, H.; Sumer, O.; Ozkaymak, C.; Uzel, B.; Guler, T.; Eski, S. Kinematic analysis and palaeoseismology of the Edremit Fault Zone: Evidence for past earthquakes in the southern branch of the North Anatolian Fault Zone, Biga Peninsula, NW Turkey. Geodin. Acta 2016, 28, 273–294. [Google Scholar] [CrossRef]
- Alsan, E.; Tezuçan, L.; Bath, M. An earthquake catalogue for Turkey for the interval 1913–1970. Tectonophysics 1976, 31, T13–T19. [Google Scholar] [CrossRef]
- Tsuchida, H. Prediction and countermeasure against the liquefaction in sand deposits. In Abstract of the Seminar in the Port and Harbor Research Institute; Scientific Research Publishing: Wuhan, China, 1970; pp. 31–333. [Google Scholar]
- Javanbakht, A.; Molnar, S.; Sadrekarimi, A.; Adhikari, S.R. Performance-based liquefaction analysis and probabilistic liquefaction hazard mapping using CPT data within the Fraser River delta, Canada. Soil Dyn. Earthq. Eng. 2025, 189, 109101. [Google Scholar] [CrossRef]
- Kamal, A.M.; Sahebi, M.T.; Hossain, M.S.; Rahman, M.Z.; Fahim, A.K.F. Liquefaction hazard mapping of the south-central coastal areas of Bangladesh. Nat. Hazards Res. 2024, 4, 520–529. [Google Scholar] [CrossRef]
- Demir, S.; Sahin, E.K. The effectiveness of data pre-processing methods on the performance of machine learning techniques using RF, SVR, Cubist and SGB: A study on undrained shear strength prediction. Stoch. Environ. Res. Risk Assess. 2024, 38, 3273–3290. [Google Scholar] [CrossRef]
- Dastjerdy, B.; Saeidi, A.; Heidarzadeh, S. Review of applicable outlier detection methods to treat geomechanical data. Geotechnics 2023, 3, 375–396. [Google Scholar] [CrossRef]
- Ozkat, E.C. Photodiode Signal Patterns: Unsupervised Learning for Laser Weld Defect Analysis. Processes 2025, 13, 121. [Google Scholar] [CrossRef]
- Ozkat, E.C.; Franciosa, P.; Ceglarek, D. A framework for physics-driven in-process monitoring of penetration and interface width in laser overlap welding. Procedia CIRP 2017, 60, 44–49. [Google Scholar] [CrossRef]
- Shao, W.; Yue, W.; Zhang, Y.; Zhou, T.; Zhang, Y.; Dang, Y.; Wang, H.; Feng, X.; Chao, Z. The application of machine learning techniques in geotechnical engineering: A review and comparison. Mathematics 2023, 11, 3976. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, B.; Wu, B.; Zhang, C.; Liu, W. Intelligent prediction of slope stability based on visual exploratory data analysis of 77 in situ cases. Int. J. Min. Sci. Technol. 2023, 33, 47–59. [Google Scholar] [CrossRef]
- Walters-Williams, J.; Li, Y. Comparative study of distance functions for nearest neighbors. In Advanced Techniques in Computing Sciences and Software Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 79–84. [Google Scholar]
- Kramer, O. Dimensionality Reduction with Unsupervised Nearest Neighbors; Springer: Berlin/Heidelberg, Germany, 2013; Volume 51. [Google Scholar]
- Rolnick, D.; Donti, P.L.; Kaack, L.H.; Kochanski, K.; Lacoste, A.; Sankaran, K.; Ross, A.S.; Milojevic-Dupont, N.; Jaques, N.; Waldman-Brown, A.; et al. Tackling climate change with machine learning. Acm Comput. Surv. (CSUR) 2022, 55, 1–96. [Google Scholar] [CrossRef]
- Güner, E.; Özkan, Ö.; Yalcin-Ozkat, G.; Ölgen, S. Determination of novel SARS-CoV-2 inhibitors by combination of machine learning and molecular modeling methods. Med. Chem. 2024, 20, 153–231. [Google Scholar] [CrossRef] [PubMed]
- Özkat, G.Y.; Aasim, M.; Bakhsh, A.; Ali, S.A.; Özcan, S. Machine learning models for optimization, validation, and prediction of light emitting diodes with kinetin based basal medium for in vitro regeneration of upland cotton (Gossypium hirsutum L.). J. Cotton Res. 2025, 8, 19. [Google Scholar] [CrossRef]
- Chala, A.T.; Ray, R. Assessing the performance of machine learning algorithms for soil classification using cone penetration test data. Appl. Sci. 2023, 13, 5758. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- He, Q.; Xu, Z.; Li, S.; Li, R.; Zhang, S.; Wang, N.; Pham, B.T.; Chen, W. Novel entropy and rotation forest-based credal decision tree classifier for landslide susceptibility modeling. Entropy 2019, 21, 106. [Google Scholar] [CrossRef]
- Kumar, D.R.; Samui, P.; Burman, A. Prediction of probability of liquefaction using soft computing techniques. J. Inst. Eng. (India) Ser. A 2022, 103, 1195–1208. [Google Scholar] [CrossRef]
- Ceryan, N.; Ozkat, E.C.; Korkmaz Can, N.; Ceryan, S. Machine learning models to estimate the elastic modulus of weathered magmatic rocks. Environ. Earth Sci. 2021, 80, 448. [Google Scholar] [CrossRef]
- Ikram, N.; Basharat, M.; Ali, A.; Usmani, N.A.; Gardezi, S.A.H.; Hussain, M.L.; Riaz, M.T. Comparison of landslide susceptibility models and their robustness analysis: A case study from the NW Himalayas, Pakistan. Geocarto Int. 2022, 37, 9204–9241. [Google Scholar] [CrossRef]
- Şehmusoğlu, E.H.; Kurnaz, T.F.; Erden, C. Estimation of soil liquefaction using artificial intelligence techniques: An extended comparison between machine and deep learning approaches. Environ. Earth Sci. 2025, 84, 130. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Kamchoom, V.; Gnananandarao, T.; Arunachalam, K.P. Developing data driven framework to model earthquake induced liquefaction potential of granular terrain by machine learning classification models. Sci. Rep. 2025, 15, 21509. [Google Scholar] [CrossRef]


| Reference | ML Model(s) | Dataset of Soil Liquefaction Evaluation | Inputs |
|---|---|---|---|
| [35] | SVM | CPT | , , , , , |
| [36] | SVM | , , , , soil type | |
| [37] | LSSVM and RVM | , | |
| [38] | ANN | SPT, | , , , , , FC, z, N, CSR, CRR, U, soil type |
| [39] | GA-SVM | CPT | , , , , , , CSR |
| [40] | BBN and DT | CPT | , , , , , , , , FC, , Ds |
| [41] | PSO/GA/Fuzzy-SVM | CPT | , , , , , , CSR |
| [42] | BNM | SPT, CPT, | , , z, GWT |
| [43] | DNN | SPT, | , , , , , , FC, z |
| [44] | RM | , , , k | |
| [45] | PSO-KELM | CPT, | , , , , , , , FC, ST, CSR |
| [46] | GWO-SVM | SPT, | , , , , , , FC, z |
| [47] | DL and EmBP | CPT | , |
| [48] | SVM, RF, andXGBoost | , , , , , , , CSR | |
| [49] | DT, LR, SVM, kNN, SGD, RF, and ANN | CPT | C%, , , IP, , FC, z |
| [50] | SVM, DT, and QDA | CPT | , , , , CSR |
| [51] | GA-SVM and GWO-SVM | SPT, , CPT | , , , , , , , , , , , , CSR, FC |
| [52] | GA | , , , , | |
| [53] | LDA, QDA, NB, ANN, and CT SVM, RM, LightGBM, and XGBoost | , , , , , , CSR | |
| [54] | LR and DT | , , , , , FC, z, Compactness, gradation, age | |
| [55] | LR, RF, and SVM | SPT, | , , , , FC |
| [56] | GBR, XGB, RF, and DT | SPT | , CSR, PGA, FC, |
| ML Model | Parameters | Value |
|---|---|---|
| DT | Number of splits | 18 |
| NB | Distribution names | Gaussian |
| SVM | Kernel function | Quadratic |
| Box constraint level | 0.3192 | |
| kNN | Number of neighbors | 10 |
| Distance metric | Cosine | |
| Distance weight | Squared inverse | |
| RF | Ensemble method | GentleBoost |
| Number of learners | 31 | |
| Learning rate | 0.1189 | |
| ANN | Activation function | ReLU |
| Lambda | ||
| Number of hidden layers | 1 | |
| Number of neurons | 206 |
| ML Model | Accuracy | Precision | Recall | F1 Score | ||||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |
| DT | 89.4% | 84.4% | 90.5% | 91.4% | 92.7% | 89.5% | 95.0% | 87.7% |
| NB | 85.4% | 88.5% | 85.5% | 88.8% | 90.3% | 92.8% | 95.6% | 97.3% |
| SVM | 97.8% | 94.8% | 97.0% | 93.6% | 98.5% | 96.7% | 100.0% | 100.0% |
| kNN | 95.1% | 93.8% | 94.6% | 93.5% | 96.6% | 96.0% | 98.8% | 98.6% |
| RF | 96.0% | 87.5% | 95.8% | 91.8% | 97.2% | 91.8% | 98.8% | 91.8% |
| ANN | 96.5% | 93.8% | 96.9% | 93.5% | 97.5% | 96.0% | 98.1% | 98.6% |
| ML Model | Training Time (s) | Min. Classification Error | Iterations to Min. Error |
|---|---|---|---|
| DT | 470.4 | 0.102 | 67 |
| NB | 1177.6 | 0.147 | 7 |
| SVM | 1139.3 | 0.044 | 97 |
| kNN | 255.2 | 0.053 | 66 |
| RF | 3249.8 | 0.050 | 7 |
| ANN | 3407.8 | 0.040 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korkmaz Can, N.; Ozkat, E.C.; Ceryan, N.; Ceryan, S. Benchmarking ML Approaches for Earthquake-Induced Soil Liquefaction Classification. Appl. Sci. 2025, 15, 11512. https://doi.org/10.3390/app152111512
Korkmaz Can N, Ozkat EC, Ceryan N, Ceryan S. Benchmarking ML Approaches for Earthquake-Induced Soil Liquefaction Classification. Applied Sciences. 2025; 15(21):11512. https://doi.org/10.3390/app152111512
Chicago/Turabian StyleKorkmaz Can, Nuray, Erkan Caner Ozkat, Nurcihan Ceryan, and Sener Ceryan. 2025. "Benchmarking ML Approaches for Earthquake-Induced Soil Liquefaction Classification" Applied Sciences 15, no. 21: 11512. https://doi.org/10.3390/app152111512
APA StyleKorkmaz Can, N., Ozkat, E. C., Ceryan, N., & Ceryan, S. (2025). Benchmarking ML Approaches for Earthquake-Induced Soil Liquefaction Classification. Applied Sciences, 15(21), 11512. https://doi.org/10.3390/app152111512







