Automated Modeling Method and Strength Analysis of Irregular Deformation of Floating Roof Caused by Welding—Taking Double-Layer Floating Roof Storage Tanks as an Example
Abstract
1. Introduction
2. Materials and Methods
2.1. Bottom Plate Deformation Data Measurement
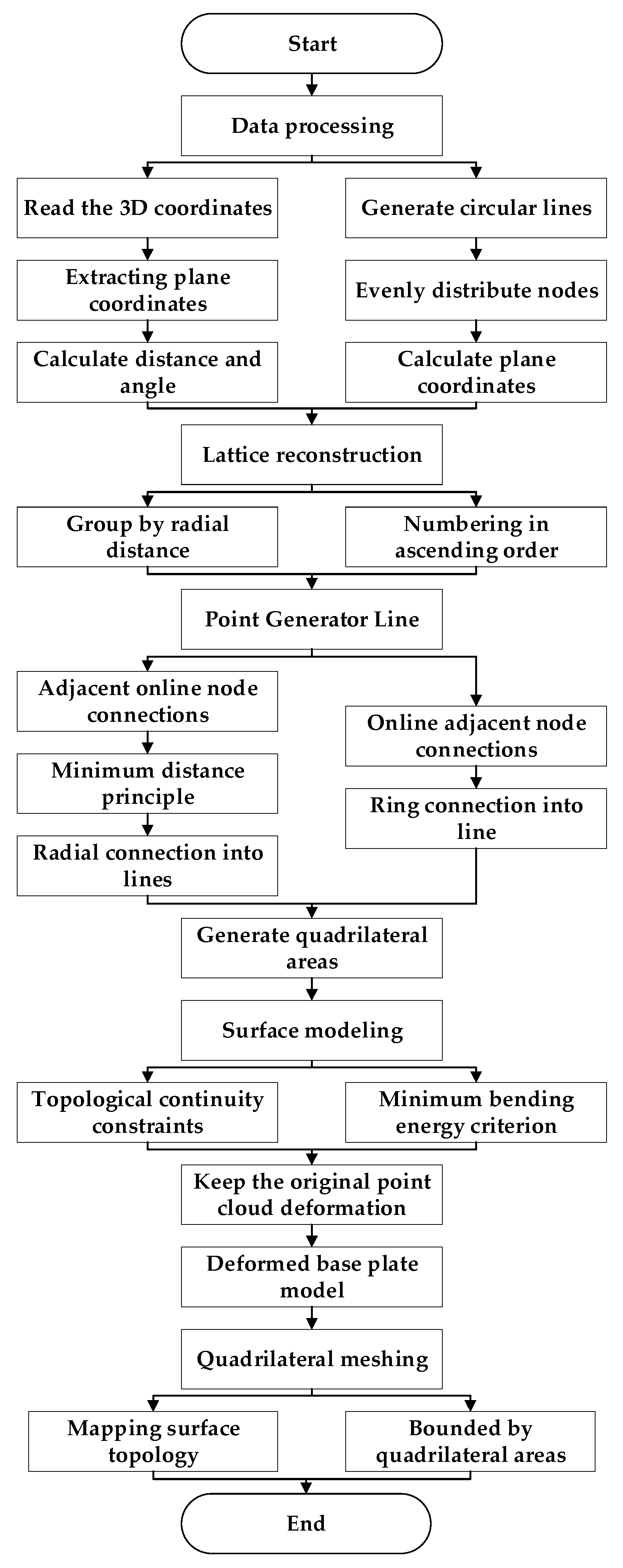
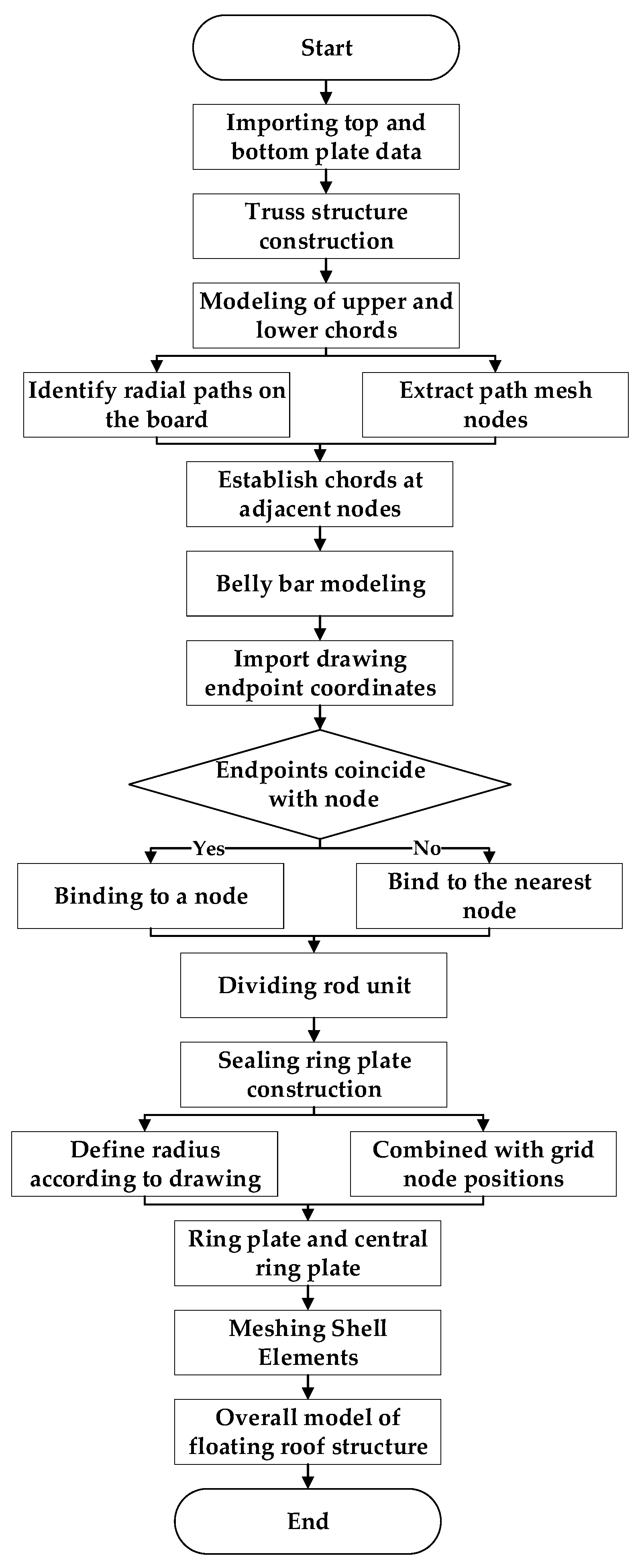
2.2. Floating Roof Automation Modeling
2.3. Mathematical Model
2.4. Boundary Conditions
3. Results
3.1. Normal Floating Condition
3.2. Extreme Rainfall Condition
3.3. Outrigger Bottoming Condition
3.4. Summary and Comparison
4. Conclusions
- The automated modeling approach developed in this study successfully reconstructs the three-dimensional geometry of the floating roof bottom plate based on measured deformation data, accurately capturing initial irregularities caused by welding. This method provides an efficient workflow for integrating irregular initial deformations into finite element analysis, enabling realistic simulation of structural responses under various operating conditions. The approach offers a practical tool for engineering design, assessment, and maintenance of large-scale floating roof storage tanks.
- Under the normal floating condition, the measured initial geometric deformation has a limited effect on the overall stress distribution pattern of the floating roof bottom plate. However, it significantly exacerbates local stress concentrations and deformation amplitudes, reduces structural stiffness and safety margins, and disrupts the symmetry and continuity of the stress and displacement fields. These results demonstrate that initial irregularities play a critical role in local mechanical responses and should be explicitly considered during the early design stage to ensure sufficient structural stiffness under atmospheric conditions.
- Under the extreme uniform rainfall condition, the initial irregular deformation of the floating roof bottom plate significantly amplifies local stress and displacement responses and reduces overall stiffness. It further induces non-uniform high-stress regions and warping deformation. Notably, stress fluctuations are pronounced in the central and edge areas, indicating heightened sensitivity to in-plane stress redistribution. The combination of high stress and deformation near plate edges highlights the importance of weld quality, plate thickness, and material toughness in resisting localized deformation. Design strategies should consider these factors to enhance service reliability under extreme environmental loads.
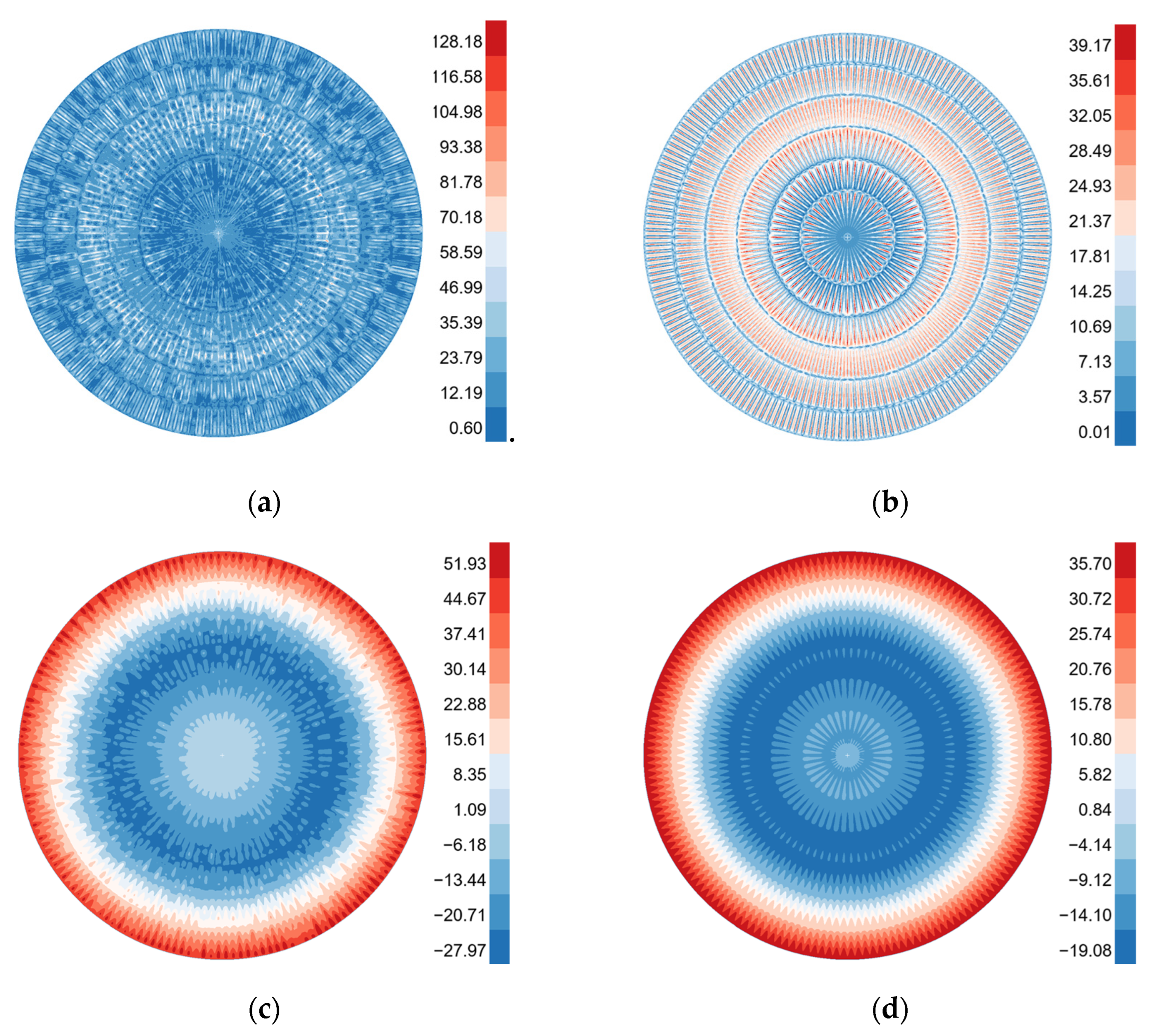
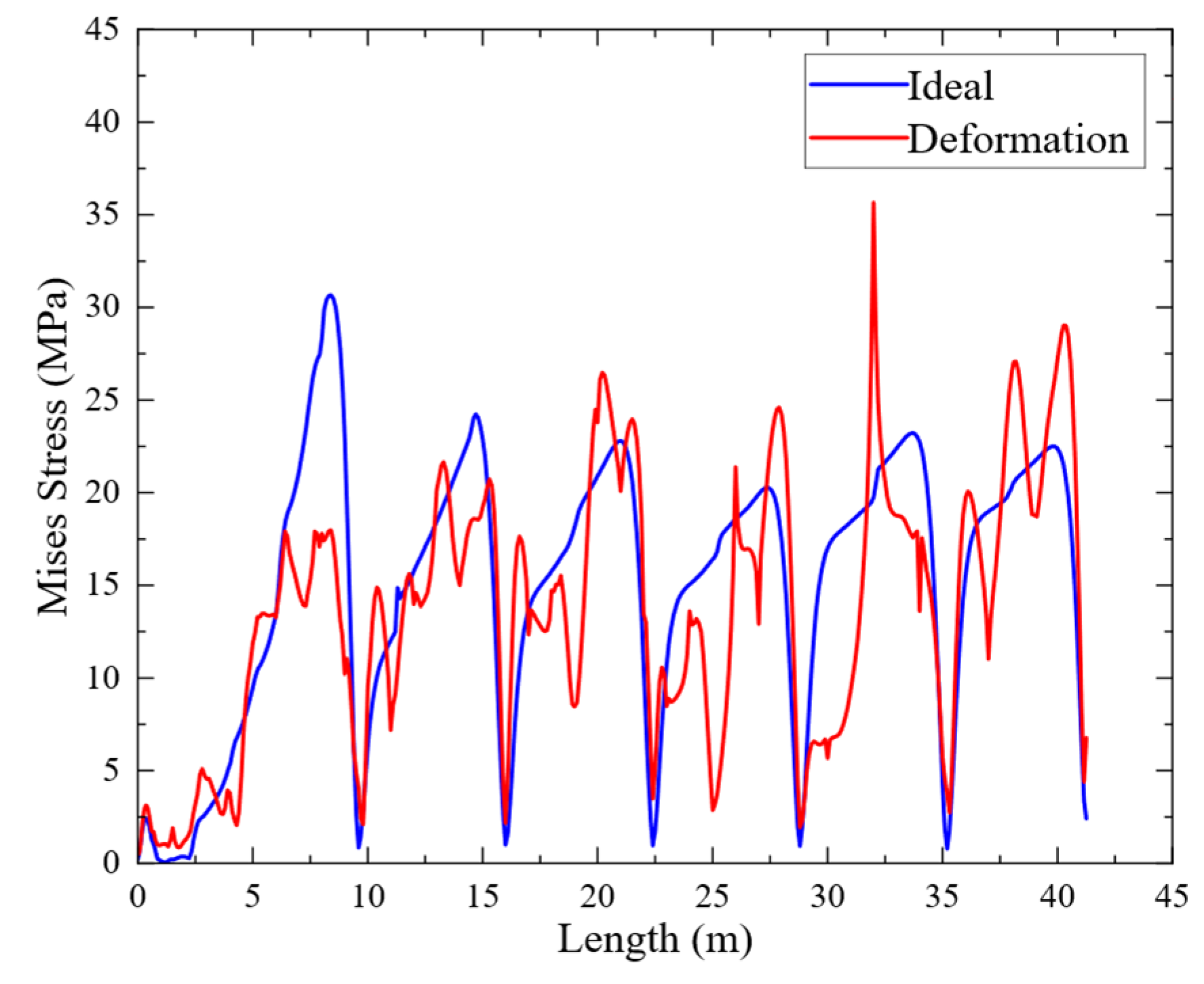
- Under the extreme non-uniform rainfall condition, the measured initial geometric deformation of the floating roof bottom plate significantly amplified the structural response, leading to a substantial increase in stress in the central region and the emergence of multiple localized high-stress areas. Compared with the ideal model, the deformed model exhibits more pronounced radial equivalent stress fluctuations, making it more susceptible to large deformations and localized warping under uneven loading.
- Under the outrigger bottoming condition, the initial geometric deformation markedly modifies the stress and displacement distribution of the base plate, resulting in increased local stress concentration and asymmetric deformation patterns. It induces a pronounced stress gradient near the support constraints, thereby amplifying their effect on structural stiffness and overall mechanical response. Therefore, the impact of initial deformation on the safety of the support area should be thoroughly considered during design, and local structural reinforcements should be implemented to mitigate stress concentration and maintain sufficient stiffness.
- Comparing the responses of the deformation model and the ideal model under three typical operating conditions reveals that initial irregular deformation significantly amplifies the stress and displacement responses of the floating roof’s bottom and top plates. This amplification effect is especially pronounced under extreme loads. This amplification effect reduces the effective coupling between stiffness and deformation, thereby lowering the safety margin of the roof. Consequently, accurate measurement, early correction of initial irregularities, and stiffness control should be integrated into the design process to improve the structural robustness of floating roofs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pouyakian, M.; Jafari, M.J.; Laal, F.; Nourai, F.; Zarei, E. A comprehensive approach to analyze the risk of floating roof storage tanks. Process Saf. Environ. Prot. 2021, 146, 811–836. [Google Scholar] [CrossRef]
- Lang, X.Q.; Liu, Q.Z.; Gong, H. Study of fire fighting system to extinguish full surface fire of large scale floating roof tanks. Procedia Eng. 2011, 11, 189–195. [Google Scholar] [CrossRef]
- Huang, W.; Huang, F.; Fang, J.; Fu, L. A calculation method for the numerical simulation of oil products evaporation and vapor diffusion in an internal floating-roof tank under the unsteady operating state. J. Pet. Sci. Eng. 2020, 188, 106867. [Google Scholar] [CrossRef]
- Shaluf, I.M.; Abdullah, S.A. Floating roof storage tank boilover. J. Loss Prev. Process Ind. 2011, 24, 1–7. [Google Scholar] [CrossRef]
- Yang, H.; Ren, B.; Huang, Y.; Zhang, Z.; Hu, W.; Liu, M.; Zhao, H.; Jiang, G.; Hao, Z. Volatile organic compounds (VOCs) emissions from internal floating-roof tank in oil depots in Beijing: Influencing factors and emission reduction strategies analysis. Sci. Total Environ. 2024, 916, 170222. [Google Scholar] [CrossRef] [PubMed]
- Hameed, A.S.; Salmi, H.; Hajri, Z. Successful Implementation of Innovative Technologies and Solutions for the Design and Construction of Heavy Wall Oversized Double Deck Floating Roof Tanks at MAF Tank Farm. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 12–14 May 2025; SPE: Richardson, TX, USA, 2025; p. D021S021R002. [Google Scholar]
- Mangushev, R.; Sotnikov, S. Comparison of deformations of the large floating-roof tanks with the results of long-term monitoring. E3S Web Conf. 2020, 164, 01022. [Google Scholar] [CrossRef]
- API Standard. Welded Tanks for Oil Storage; American Petroleum Institute: Washington, DC, USA, 2013; p. 1220. [Google Scholar]
- Jia, P.; Lv, J.; Sun, W.; Jin, H.; Meng, G.; Li, J. Modified analytic hierarchy process for risk assessment of fire and explosion accidents of external floating roof tanks. Process Saf. Prog. 2024, 43, 9–26. [Google Scholar] [CrossRef]
- Moshashaei, P.; Alizadeh, S.S.; Khazini, L.; Asghari-Jafarabadi, M. Investigate the causes of fires and explosions at external floating roof tanks: A comprehensive literature review. J. Fail. Anal. Prev. 2017, 17, 1044–1052. [Google Scholar] [CrossRef]
- Salimbeni, M.; De Angelis, M.; Ciucci, M. Modeling of floating roof tanks under seismic excitation, accounting for the influence of sealing system and the roof pounding. Structures 2024, 70, 107590. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, J. Buckling Mode Analysis of Floating Roof Storage Tank under Wind Load. J. Liaoning Univ. Pet. Chem. Technol. 2020, 40, 78. [Google Scholar]
- Sun, B.; Ma, D.; Gao, L.; He, M.; Peng, Z.; Li, X.; Wang, W. Wind buckling analysis of a large-scale open-topped steel tank with harmonic settlement-induced imperfection. Buildings 2022, 12, 1973. [Google Scholar] [CrossRef]
- Du, L.; Zhao, W.; Yan, H.; Liu, D. Stability and Strength Analysis of Internal Floating Roof Atmospheric Tank. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Wuhan, China, 14–16 June 2019; IOP Publishing: Bristol, UK, 2019; p. 012066. [Google Scholar]
- Żyliński, K.; Górski, J. Probabilistic estimation of diverse soil condition impact on vertical axis tank deformation. Bull. Pol. Acad. Sciences. Tech. Sci. 2023, 71, e144576. [Google Scholar] [CrossRef]
- Bernard, G.; Vera, D.; Lim, W.K. Seismic Response Analysis of Flexible Drain System Into External Floating Roof Storage Tanks. In Proceedings of the Pressure Vessels and Piping Conference, Waikoloa, HI, USA, 16–20 July 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; p. V008T08A019. [Google Scholar]
- Wang, M.; Sun, Z.; Sun, J.; Cui, L.; Wu, Y. Probabilistic seismic fragility assessment of vertical storage tank with a floating roof. Structures 2023, 48, 318–330. [Google Scholar] [CrossRef]
- Epstein, H.I. Stresses and displacements for floating pan roofs. Comput. Struct. 1982, 15, 433–438. [Google Scholar] [CrossRef]
- Chiappelloni, L.; Belardi, V.; Serraino, F.; Trupiano, S.; Gaetani, L.; Vivio, F. Structural behaviour of single-deck floating roof tanks subject to seismic loading. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Genova, Italy, 6–9 September 2023; IOP Publishing: Bristol, UK, 2024; p. 012002. [Google Scholar]
- Noaman, A.S.; El-Samanody, M.; Ghorab, A. Design and study of floating roofs for oil storage tanks. Int. J. Eng. Dev. Res. 2016, 4, 1–12. [Google Scholar]
- Goudarzi, M.A. Seismic behavior of a single deck floating roof due to second sloshing mode. J. Press. Vessel. Technol. 2013, 135, 11801. [Google Scholar] [CrossRef]
- Shi, L.; Shuai, J.; Wang, X.; Xu, K. Experimental and numerical investigation of stress in a large-scale steel tank with a floating roof. Thin-Walled Struct. 2017, 117, 25–34. [Google Scholar] [CrossRef]
- Nishi, H.; Yamada, M.; Zama, S.; Hatayama, K.; Sekine, K. Experimental study on the sloshing behavior of the floating roof using a real tank. J. High Press. Inst. Jpn. 2008, 46, 4–17. [Google Scholar]
- Rouzbahani, A.; Amirsradari, S.; Goudarzi, M. Experimental study of using an innovative porous floating roof for suppression of sloshing effects in cylindrical storage tanks. Ocean Eng. 2024, 310, 118735. [Google Scholar] [CrossRef]
- De Angelis, M.; Giannini, R.; Paolacci, F. Experimental investigation on the seismic response of a steel liquid storage tank equipped with floating roof by shaking table tests. Earthq. Eng. Struct. Dyn. 2010, 39, 377–396. [Google Scholar] [CrossRef]
- Kuś, J.; Wałach, S. Analysis of steel tank shell deformation and its impact on further utilisation. Int. J. Press. Vessel. Pip. 2021, 193, 104453. [Google Scholar] [CrossRef]
- Bernier, C.; Padgett, J.E. Fragility assessment of floating roof storage tanks during severe rainfall events. J. Perform. Constr. Facil. 2020, 34, 04020101. [Google Scholar] [CrossRef]
- Priyadarshan, S.S.; Iacono, S.; Vercelli, G. A UAV-Based Digital Twin Framework for Real-Time Monitoring and Risk Assessment of Floating Roof Storage Tanks. In Proceedings of the 2024 IEEE International Conference on Big Data (BigData), Washington, DC, USA, 15–18 December 2024; IEEE: New York, NY, USA, 2024; pp. 5526–5531. [Google Scholar]
- Al Omari, A.; Herzalla, O.; Toubar, A.; Almalood, N.; Al Hammadi, H. Floating roof storage tanks life extension: A novel risk revealed. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11–14 November 2019; SPE: Richardson, TX, USA, 2019; p. D021S036R003. [Google Scholar]
- Chen, Z.; Huang, S.; Fan, H. Strength and stability analysis of double-deck floating roof under wind load. In Proceedings of the Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; p. V01BT01A040. [Google Scholar]
- Qin, R.; Zhu, J.; Khakzad, N. Multi-hazard failure assessment of atmospheric storage tanks during hurricanes. J. Loss Prev. Process Ind. 2020, 68, 104325. [Google Scholar] [CrossRef]
- ASME SA-516/SA-516M-2021; Specification for Pressure Vessel Plates, Carbon Steel, for Moderate- and Lower-Temperature Service. American Society of Mechanical Engineers: New York, NY, USA, 2021.
- Tariverdilou, S.; Shabani, R.; Salarieh, H. Effect of flexural and membrane stiffness on the analysis of floating roofs. Arch. SID 2010, 23, 57–64. [Google Scholar]
- Hakim, G.; Abramovich, H. Large deflections of thin-walled plates under transverse loading—Investigation of the generated in-plane stresses. Materials 2022, 15, 1577. [Google Scholar] [CrossRef]
- Gharababaei, H.; Darvizeh, A. Experimental and analytical investigation of large deformation of thin circular plates subjected to localized and uniform impulsive loading#. Mech. Based Des. Struct. Mach. 2010, 38, 171–189. [Google Scholar] [CrossRef]
- Roylance, D. Transformation of Stresses And Strains. Lecture Notes in Mechanics of Materials; Department of Materials Science and Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 14 May 2001; Available online: https://resources.saylor.org/wwwresources/archived/site/wp-content/uploads/2012/09/ME1022.4.3.pdf (accessed on 1 September 2025).
- Velikanov, N.; Koryagin, S.; Sharkov, O. Stresses in circular plates with rigid elements. J. Phys. Conf. Ser. 2018, 1015, 052028. [Google Scholar] [CrossRef]
- Amstutz, S.; Novotny, A.A. Topological optimization of structures subject to von Mises stress constraints. Struct. Multidiscip. Optim. 2010, 41, 407–420. [Google Scholar] [CrossRef]
- Gujar, P.; Ladhane, K. Bending analysis of simply supported and clamped circular plate. Int. J. Civ. Eng. 2015, 2, 69–75. [Google Scholar] [CrossRef]

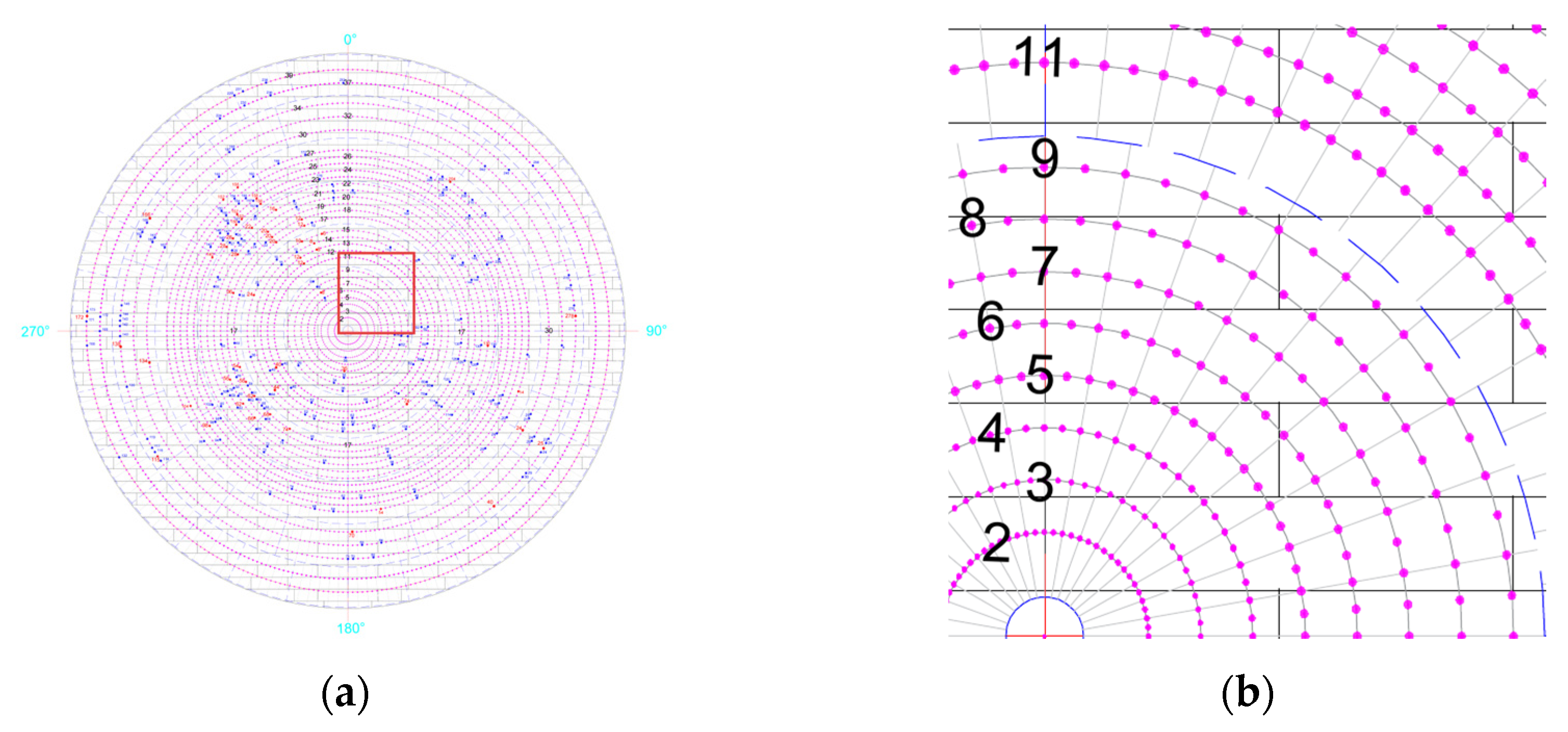
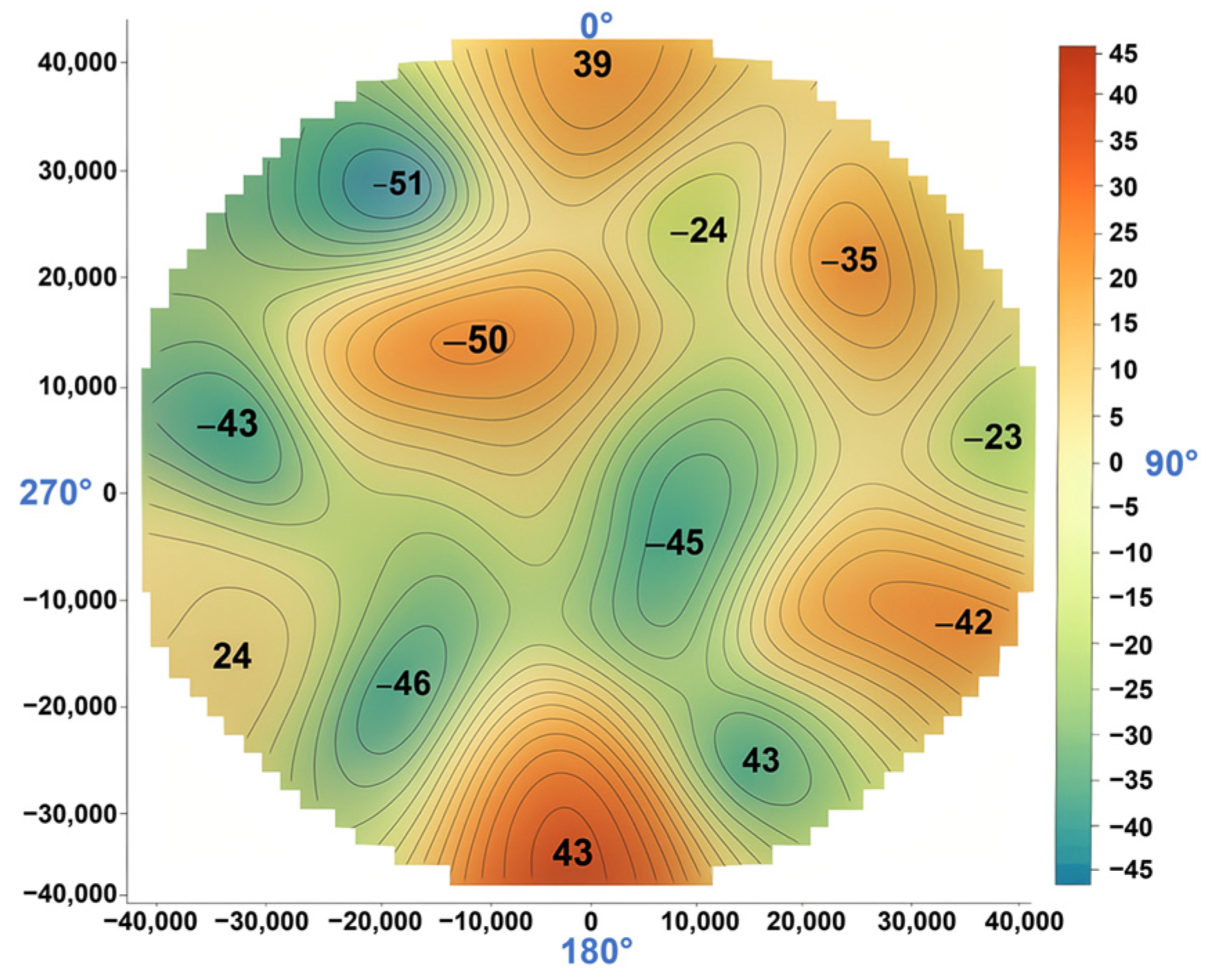




| Ring Area Number | Radius Range [m] | Number of Measuring Lines | Number of Measuring Points on the Measuring Line | Total Number of Regional Measuring Points |
|---|---|---|---|---|
| 1 | 2–9 | 8 | 72 | 576 |
| 2 | 11–15 | 5 | 120 | 600 |
| 3 | 17–22 | 6 | 176 | 1056 |
| 4 | 23–27 | 5 | 240 | 1200 |
| 5 | 30–34 | 3 | 280 | 840 |
| 6 | 37–39 | 2 | 336 | 672 |
| Conditions | Model | Bottom Plate | Top Plate | ||
|---|---|---|---|---|---|
| Maximum Stress [MPa] | Displacement Range [mm] | Maximum Stress [MPa] | Displacement Range [mm] | ||
| normal floating | deformation | 24.01 | −6.08–7.05 | 14.30 | −7.69–4.67 |
| ideal | 20.12 | −3.32–5.77 | 14.25 | −5.13–2.66 | |
| relative ratio | 19% | 22–83% | 0.35% | 49–75% | |
| extreme uniform rainfall | deformation | 67.29 | −4.53–17.51 | 66.09 | −15.26–9.22 |
| ideal | 53.97 | 3.74–13.68 | 65.34 | −14.53–5.76 | |
| relative ratio | 24% | 21–28% | 1.13% | 5–60% | |
| extreme non-uniform rainfall | deformation | 128.18 | −27.97–51.93 | 164 | −40.44–44.48 |
| ideal | 39.17 | −19.08–35.70 | 116.04 | −28.04–33.13 | |
| relative ratio | 227% | 45%–47% | 41% | 34–44% | |
| outrigger bottoming | deformation | 32.13 | −4.55–0.12 | 36.11 | −4.32–−0.01 |
| ideal | 25.66 | −4.55–0.01 | 29.15 | −4.47–0.24 | |
| relative ratio | 25% | –– | 24% | –– | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Jiang, Y.; Zhang, L.; Guan, W.; Zhou, Y. Automated Modeling Method and Strength Analysis of Irregular Deformation of Floating Roof Caused by Welding—Taking Double-Layer Floating Roof Storage Tanks as an Example. Appl. Sci. 2025, 15, 11473. https://doi.org/10.3390/app152111473
Li C, Jiang Y, Zhang L, Guan W, Zhou Y. Automated Modeling Method and Strength Analysis of Irregular Deformation of Floating Roof Caused by Welding—Taking Double-Layer Floating Roof Storage Tanks as an Example. Applied Sciences. 2025; 15(21):11473. https://doi.org/10.3390/app152111473
Chicago/Turabian StyleLi, Chunyang, Yuanyuan Jiang, Luyang Zhang, Wei Guan, and Yan Zhou. 2025. "Automated Modeling Method and Strength Analysis of Irregular Deformation of Floating Roof Caused by Welding—Taking Double-Layer Floating Roof Storage Tanks as an Example" Applied Sciences 15, no. 21: 11473. https://doi.org/10.3390/app152111473
APA StyleLi, C., Jiang, Y., Zhang, L., Guan, W., & Zhou, Y. (2025). Automated Modeling Method and Strength Analysis of Irregular Deformation of Floating Roof Caused by Welding—Taking Double-Layer Floating Roof Storage Tanks as an Example. Applied Sciences, 15(21), 11473. https://doi.org/10.3390/app152111473




