Dynamic Characteristics and Parametric Sensitivity Analysis of Underground Powerhouse in Pumped Storage Power Stations

Abstract

China has witnessed extensive construction of underground powerhouses for pumped storage power stations. With the continuous increase in unit capacity, vibration problems have become particularly pronounced. Intense vibrations may not only disrupt the normal operation of hydropower units but also compromise the overall structural safety of the powerhouse. Moreover, in dynamic analyses of powerhouse structures, different parameters exert varying degrees of influence on the results, making it essential to systematically examine their impacts. This study focuses on a large-scale underground powerhouse, establishing a three-dimensional finite element model of Unit #1 to investigate its dynamic characteristics and parametric sensitivity. Through modal and harmonic response analyses, the effects of key parameters—including the zone of surrounding rock, elastic modulus of surrounding rock, dynamic elastic modulus of concrete, and damping ratio—were systematically evaluated. Results indicate that an expanded surrounding rock zone reduces natural frequency and increases dynamic displacement, with a zone twice the span length offering an optimal balance between accuracy and computational efficiency. Increasing the elastic modulus of the surrounding rock raises the natural frequency and slightly reduces displacement, while having a limited impact on dynamic stress. The dynamic elastic modulus of concrete shows a square-root relationship with natural frequency and an inverse correlation with dynamic displacement. The damping ratio has negligible influence on natural frequency, dynamic displacement, and dynamic stress. These findings provide a theoretical basis and practical guidance for parameter selection in the dynamic analysis of underground powerhouse structures, enhancing the reliability of numerical simulations.

1. Introduction

Pumped storage power stations fulfill multiple critical functions, including balancing power generation and consumption, adjusting grid frequency and phase, enabling rapid black start-up, and providing standby reserves for electrical power systems. Therefore, they are regarded as an essential grid regulation tool, indispensable for building a “strong and smart” grid. The world’s first pumped storage power plant was built in Zurich, Switzerland, in 1882 [1]. However, the development of such plants progressed very slowly until the 1950s, with construction largely confined to several Western European nations. From the 1950s onward, the development of pumped storage power stations entered an initial growth phase. Annual new installations reached approximately 3 × 10⁴ kW, and by 1960, the total installed capacity had reached 350 × 10⁴ kW, accounting for 0.62% of the global total. With the rapid economic growth of China, both the energy demands of the power grid and the peak-to-valley load difference continue to widen. The expansion of pumped storage power stations is thus of considerable importance for optimizing the power supply structure and ensuring the secure and stable operation of China’s power grid in the 21st century [1,2]. Since the 1960s, China’s installed power generation capacity has experienced rapid growth, reaching 83,000 × 10⁴ kW by 1990, which accounted for 3.15% of the global total. In contrast, the installed capacity of pumped storage power stations increased 23-fold over the preceding three decades [3]. By the end of 2021, China’s installed capacity represented 22.2% of the world’s total, ranking first globally [4].

Pumped storage power stations are predominantly constructed in high-mountain gorge areas. To mitigate challenges posed by unfavorable surface topography, geological conditions, and climatic factors, the underground powerhouse option is frequently adopted. An underground powerhouse can be conceptualized as a composite system comprising the concrete structure of the plant and the surrounding rock mass, wherein the latter provides essential external constraints for the load-bearing concrete framework. Over the past two decades, China has established numerous large-scale underground structures for hydropower and pumped storage projects [5,6,7]. Notable examples include the Huanggou Pumped Storage Power Station in Heilongjiang Province [8], the Yulong Pumped Storage Power Station in Jiangsu Province [9], the Jinzhai Pumped Storage Power Station in Anhui Province [10], and the Okinawa Seawater Pumped Storage Power Plant in Japan [11]. With the continual increase in the installed capacity of hydropower units, vibration-related challenges have become increasingly prominent. Consequently, resonance phenomena have attracted significant attention from both design and operational management departments. Under the combined excitation of multiple vibration sources, the structural dynamic response of powerhouse buildings tends to be complex. Severe vibration not only risks compromising the stable operation of the units but may also endanger the safety and long-term durability of the powerhouse structure, posing potential threats to the occupational health of personnel [12,13]. Incidents involving powerhouse safety have been reported at China’s Xiaolangdi, Ertan, and Yantan hydropower stations to varying degrees. The most severe accident occurred at the Sayano-Shushenskaya hydropower station on Russia’s Yenisei River, where Unit #2 experienced intense vibration following operation beyond its rated capacity, leading to fatigue failure of the headcover bolts and resulting in substantial casualties and property loss [14].

The structural dynamic characteristics, particularly the natural frequencies and mode shapes, of underground powerhouse structures in hydropower stations serve as core parameters that directly determine their vibration resistance [15]. Li et al. [16], Nie et al. [17], and Yu et al. [18] investigated the dynamic response of underground powerhouses subjected to pulsating water pressure, demonstrating that the consideration of coupling effects between hydraulic pulses and unit dynamic loads leads to an amplified dynamic response and more severe outcomes. Consequently, it is recommended that the coupling effect between hydraulic pulses and unit dynamic loads be incorporated when analyzing structural vibrations in powerhouse buildings to identify the most critical operating conditions. Separately, Liu et al. [19], Yang et al. [20], and Zhang et al. [21] evaluated the dynamic response under various operational scenarios, confirming compliance with vibration control requirements in all cases. Notably, rotor blade vibration and hydraulic disturbance have been identified as the primary vibration sources in pumped storage power stations. The mitigation of structural vibrations in underground powerhouses can be achieved by increasing the vibration source frequency, reducing the amplitude of the vibration source, and enhancing the stiffness of the concrete structures surrounding the spiral casing.

When performing dynamic analysis of underground powerhouse structures, challenges are frequently encountered in defining boundary conditions, selecting material parameters, and determining the zone of surrounding rock. Given that these parameters differentially influence the outcomes of structural dynamic analysis, a systematic investigation of their effects is essential. Luo et al. [22] examined the effects of the dynamic elastic modulus of concrete, damping ratio, zone of surrounding rock, and boundary conditions on the natural vibration characteristics and dynamic response of a large underground powerhouse structure. Their findings indicate that the natural frequency of the overall structure is predominantly affected by the dynamic elastic modulus of concrete, the zone of surrounding rock, and the boundary conditions, while exhibiting negligible correlation with the damping ratio. Dynamic displacement is inversely related to the dynamic elastic modulus of concrete, shows low sensitivity to variations in the zone of surrounding rock and boundary conditions, and is only minimally influenced by the damping ratio. In contrast, dynamic stress demonstrates low sensitivity to changes in the dynamic elastic modulus of concrete, damping ratio, zone of surrounding rock, and boundary conditions. In a related study, Song et al. [23] analyzed the natural vibration characteristics of the underground powerhouse of a large pumped storage power station using different structural layouts. Through harmonic response analysis, dynamic performance variations, and the sensitivity of slab thickness were investigated under rated operating conditions. It was concluded that, under dynamic loads from generating units, modifications to floor slab configurations or the use of columns with differing cross-sectional dimensions have limited influence on the overall natural vibration characteristics within a certain range; moreover, structures with column-supported slabs exhibit higher vibration resistance compared to thick-slab systems. Furthermore, Zhang et al. [24] conducted a study on a large pumped storage power station, analyzing how different boundary conditions affect the dynamic response of the entire plant structure. The research elucidated the distribution pattern of maximum vibration displacement locations within the powerhouse, thereby providing a theoretical basis for the optimal placement of safety monitoring sensors.

To address the research gap concerning the ambiguous parameter sensitivity in the dynamic evaluation of underground powerhouse structures—particularly the lack of systematic quantification of how key parameters such as the zone of surrounding rock, elastic modulus of surrounding rock, dynamic elastic modulus of concrete, and damping ratio influence structural dynamic characteristics—this study aims to establish a three-dimensional finite element model of a structural unit in a large underground pumped storage power station. Through modal analysis and harmonic response analysis, the research systematically investigates the natural vibration characteristics and dynamic response of the powerhouse under operational loads. Furthermore, the sensitivity of the dynamic behavior to variations in the aforementioned parameters is quantitatively assessed. The findings are intended to provide a rational basis for parameter selection in numerical simulations, thereby enhancing the accuracy and reliability of dynamic analyses for underground powerhouse structures.

2. Basic Information and Computational Model of the Underground Powerhouse

BJSY pumped storage power station, with a total installed capacity of 1400 MW, is categorized as a Class I large-scale project. The underground powerhouse structure consists of the main powerhouse, auxiliary buildings, and an erection bay, arranged in a linear layout. This underground system accommodates four single-stage reversible mixed-flow pump-turbine units, each rated at 350 MW. The main powerhouse is structured across five distinct levels, arranged vertically as follows: the generator floor slab, the busbar floor slab, the turbine level, the spiral casing level, and the draft tube level.

The underground powerhouse section of Unit #1 at this hydropower station was selected for computational analysis, and a corresponding finite element model was established. The model encompasses the draft tube (including the elbow section) and its surrounding concrete, the stay ring, the spiral casing and the surrounding concrete, the machine pedestal, the air duct, all floor slabs, the sidewalls of the powerhouse, and the structural columns. Based on actual structural dimensions and pipe sizes, the finite element mesh was generated through manual segmentation. Following discretization, the final computational model consisted of 198,561 nodes and 166,869 elements. The finite element mesh of the computational model is presented in Figure 1. In the numerical simulation, structural joints were incorporated on both sides of the unit section. Floor slabs supported by beams and columns were modeled with free boundary conditions. The constraining effect of the rock mass on the upstream and downstream boundaries of the concrete structure was simulated using elastic supports, where elastic horizontal constraints were applied to the corresponding boundary nodes. The ground surface of the model was fully fixed. A Cartesian coordinate system was adopted for the computational model. The origin (Point O) is located at the leftmost point of the draft tube outlet. The X-axis represents the tangential direction, with positive values pointing toward the left bank. The Y-axis denotes the radial direction, with positive values pointing upstream. The Z-axis indicates the vertical direction, with positive values along the elevation axis pointing upward.

3. Theoretical Foundations of Finite Element Analysis

3.1. Theoretical Background of Modal Analysis

Modal analysis is employed to determine the vibration characteristics of structures, specifically their natural frequencies and corresponding mode shapes. This approach enables structural designs to avoid resonant conditions or to achieve vibration at targeted frequencies; it further facilitates the prediction of the structural response to different dynamic load types and supports the determination of control parameters for subsequent dynamic analyses, such as appropriate time steps. As the vibrational characteristics govern how a structure responds to various dynamic excitations, modal analysis consequently forms the foundational basis for other dynamic analysis types, including harmonic response analysis, transient dynamic analysis, and spectral analysis.

The underground powerhouse of a hydropower station represents a spatial structural system characterized by infinite degrees of freedom. Finite element theory provides an approximate numerical approach that discretizes this complex structure into a spatial system with finite degrees of freedom, thereby enabling practical dynamic analysis through numerical computation methods. According to the dynamic response equation:

$$M\left\{\ddot{x}\right\}+C\left\{\dot{x}\right\}+K\left\{x\right\}=F$$

(1)

where M is the mass matrix, C is the damping matrix, K is the stiffness matrix, F is the structural load matrix, {ẍ} is the acceleration matrix, {ẋ} is the velocity matrix, and {x} is the displacement matrix.

The natural frequency of a structure with a damping system is:

$${\omega }_D=\omega \sqrt{1-{\zeta }^2}$$

(2)

The difference between the damped natural frequency ω_D and the undamped natural frequency ω is negligible. Consequently, for modal analysis, the effect of damping can be disregarded, leading to the simplified equation:

$$M\left\{\ddot{x}\right\}+K\left\{x\right\}=0$$

(3)

Assuming the free vibration of a multi-degree-of-freedom system exhibits simple harmonic motion, the solution to the aforementioned equation can be expressed as:

$$\left\{\begin{array}{c}x\end{array}\right\}=\left\{\begin{array}{c}X\end{array}\right\}sin\left(\omega t+\alpha \right)$$

(4)

where {x} is the displacement amplitude vector, which remains constant in form but varies in amplitude over time, and α is the phase angle.

Taking the second derivative of the above equation yields the equation of free vibration acceleration:

$$\left\{\ddot{x}\right\}=-{\omega }^2\left\{X\right\}sin\left(\omega t+\alpha \right)=-{\omega }^2\left\{x\right\}$$

(5)

Substituting the expressions for {ẍ} and {x} into the free vibration equation with damping neglected yields:

$$-{\omega }^2\left[M\right]\left\{X\right\}sin\left(\omega t+\alpha \right)+\left[K\right]\left\{X\right\}sin\left(\omega t+\alpha \right)=\left\{0\right\}$$

(6)

which yields:

$$\left\{\begin{array}{c}x\end{array}\right\}=\left\{\begin{array}{c}X\end{array}\right\}sin\left(\omega t+\alpha \right)$$

(7)

The aforementioned expression constitutes a homogeneous equation in terms of the displacement amplitude {X}. For nonzero solutions of {X} to be obtained, the determinant of the coefficient matrix must vanish, thus yielding the characteristic equation:

$$\left|\left[\begin{array}{c}K\end{array}\right]\right.-{\omega }^2\left[M\right]|=\left\{\begin{array}{c}0\end{array}\right.\}$$

(8)

The above equation is the frequency equation of the system. Assuming the system has n degrees of freedom, expanding the determinant yields an nth-degree algebraic equation in the frequency parameter ω². Solving for the n roots of ω₁², ω₂², …, ω_n² yields the system’s n natural frequencies, ω₁, ω₂, …, ω_n, which are the structural system’s n natural frequencies. The vector formed by arranging all natural frequencies in ascending order is called the frequency vector {ω}, where the smallest frequency is termed the first frequency or fundamental frequency.

Let {Xⁱ} represent the modal vector corresponding to the natural frequency ω_i. Substitution of {Xⁱ} and ω_i into the homogeneous amplitude equation of the system yields:

$$\left(\left[K\right]-{\omega }^2\left[M\right]\right)\left\{X^i\right\}=\left\{0\right\}$$

(9)

Let {Xⁱ} represent the modal vector corresponding to each natural frequency ω_i. By assigning i = 1, 2, …, n, a system of n vector equations is obtained, from which the n mode shapes of the structure can be determined.

3.2. Theoretical Background of Dynamic Response Analysis

Dynamic response refers to the vibration behavior exhibited by a structure subjected to dynamic loading. Its analysis must account not only for the time-varying nature of both the external loads and the resulting structural response, but also for the inertial and damping forces induced by structural motion. By calculating the dynamic response based on known structural properties and dynamic load inputs, the vibration characteristics and resistance capacity of the structure can be elucidated. This approach thereby provides a scientific basis for optimizing the vibration-resistant design methodology of underground powerhouse structures in pumped storage power stations.

Structural dynamics problems can generally be described by the following second-order differential equations:

$$\left[\begin{array}{c}M\end{array}\right]\left\{\ddot{u}\right\}+\left[\begin{array}{c}C\end{array}\right]\left\{\dot{u}\right\}+\left[\begin{array}{c}K\end{array}\right]\left\{u\right\}=\left\{P\left(t\right)\right\}$$

(10)

where [M], [C], and [K] represent the structure’s mass matrix, damping matrix, and stiffness matrix, respectively, {ü}, {$\dot{u}$}, and {u} denote the acceleration, velocity, and displacement of the structure’s nodes at time t, respectively.

The incorporation of damping into vibration analysis presents considerable complexity. In practical engineering applications, Rayleigh damping is commonly adopted, defined as a linear combination of the mass and stiffness matrices:

$$\left[\begin{array}{c}C\end{array}\right]=\alpha \left[\begin{array}{c}M\end{array}\right]+\beta \left[\begin{array}{c}K\end{array}\right]$$

(11)

α and β are determined based on modal analysis, as follows:

$$\alpha +\beta {\omega }_i^2=2{\zeta }_i{\omega }_i$$

(12)

where ω_i is the natural circular frequency of the i-th mode, and ζ_j is the damping ratio corresponding to the natural circular frequency of the i-th mode.

Based on the damping ratios ζ corresponding to two natural frequencies, the coefficients α and β can be determined. Since measuring damping ratios for different vibration modes presents practical challenges, it is commonly assumed in engineering practice that the damping ratios across different modes are identical, i.e., ζ_i = ζ_j = ζ. This assumption leads to the following expression:

$$\alpha ={\displaystyle \frac{2{\omega }_i{\omega }_j}{{\omega }_i+{\omega }_j}}\zeta ; \beta ={\displaystyle \frac{2\zeta }{{\omega }_i+{\omega }_j}}$$

(13)

It is important to note that for most underground powerhouse structures in hydropower stations, the damping characteristics of the bedrock significantly exceed those of the powerhouse structure itself. Consequently, distinct values of the Rayleigh damping coefficients α and β must be assigned to the powerhouse structure and the bedrock, respectively. As a result, the different vibration modes are no longer orthogonal with respect to the resulting damping matrix [C], thus precluding modal decoupling in the conventional sense. This limitation necessitates the adoption of time-domain analysis methods to obtain an accurate dynamic response solution.

For second-order differential equations, a series of effective direct integration methods has been established for time-domain solutions. The distinguishing feature of these methods lies in their avoidance of coordinate transformations in the system’s dynamic equations; instead, numerical integration is performed directly within the discrete time domain. The fundamental principles underlying these approaches are based on the following physical principles: (1) The displacement {u(t)}, which satisfies the dynamic equilibrium equation at any continuous time, is replaced by a displacement {u(t)} that fulfills the equation solely at a finite set of discrete time points t₀, t₁, t₂, …, thereby yielding an approximate formulation of dynamic equilibrium valid at discrete time instances. (2) Within each time interval Δt = t_i+1 − t_i, the actual dynamic conditions are approximated by assumed variations in displacement, velocity, and acceleration. Consequently, a certain discrepancy inherently exists between the exact solution and the numerical approximation. The resulting error is governed by both the local truncation error and rounding error generated at each integration step, as well as the subsequent propagation of these errors through further computations. The former determines the convergence characteristics of the method, while the latter relates to the numerical stability of the algorithm itself. In practical implementations, uniform time steps are typically adopted. Starting from the initial condition at t₀ = 0 and proceeding to a specified terminal time t_n = T, the solution to the dynamic equilibrium equations is obtained through sequential time integration. The interval [0, T] is divided into n equal segments, yielding Δt = T/n. This discretization produces n + 1 discrete time points t_i = i·Δt (where i = 0, 1, …, n), from which the corresponding discrete time dynamic responses are derived.

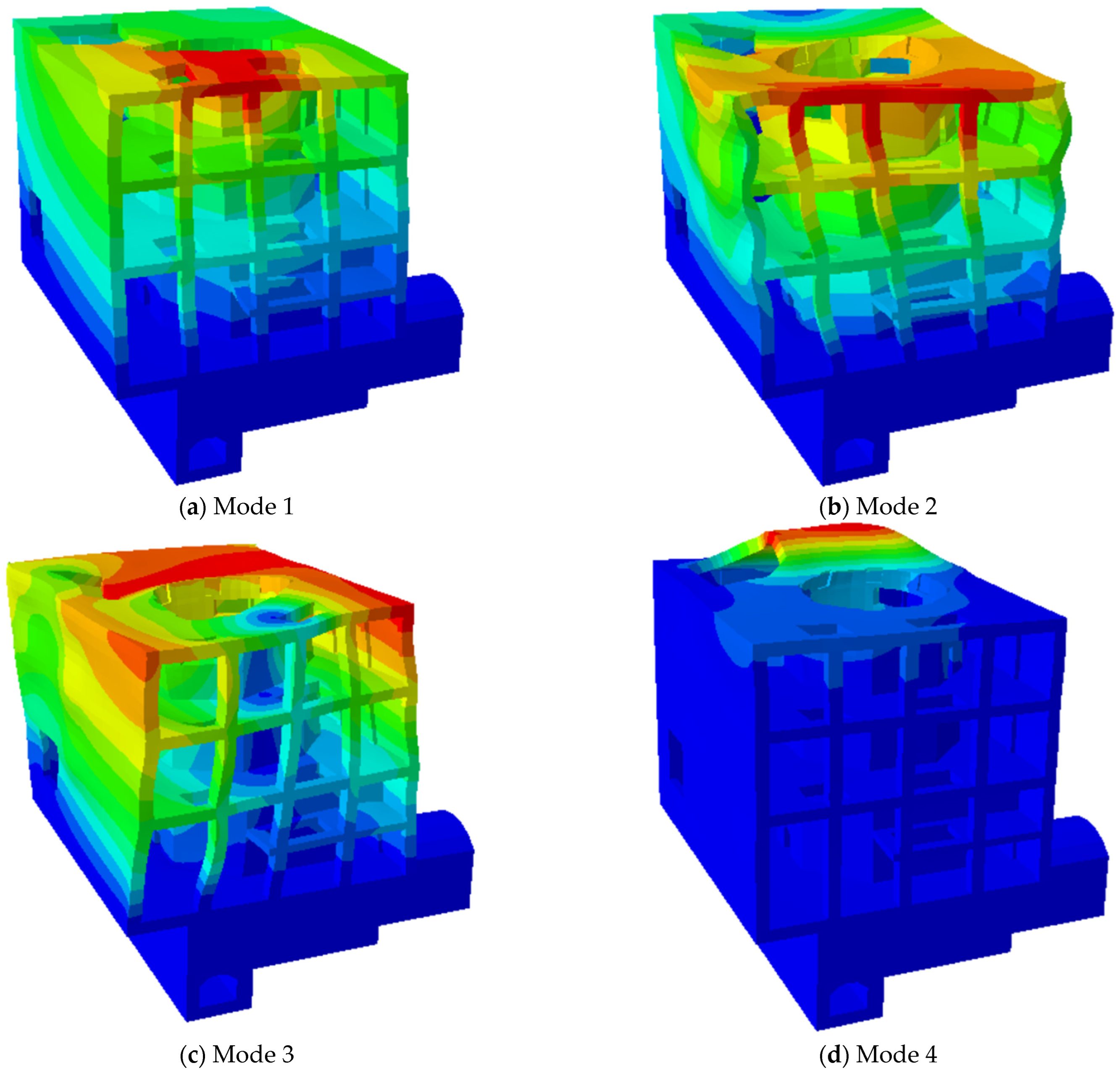
4. Dynamic Characteristics of the Underground Powerhouse

4.1. Natural Vibration Characteristics and Resonance Assessment of the Powerhouse Structure

Utilizing structural natural vibration analysis methods, with the surrounding rock classified as Class III and assigned an elastic modulus of 9 GPa, the first 20 natural frequencies and corresponding mode shapes of the overall structure were obtained. The fundamental natural frequency of the powerhouse structure was determined to be 31.128 Hz, with its mode shape characterized by vertical vibration of the generator floor slab coupled with longitudinal vibration of the overall structure. The second natural frequency was found to be 32.671 Hz, corresponding to a mode shape dominated by lateral vibration of the entire structure. The third natural frequency, 37.314 Hz, exhibited a torsional mode shape about the vertical axis. From the fourth natural frequency onward, the frequencies were densely distributed within the range of 40.741–62.652 Hz, with the associated mode shapes primarily reflecting local vibrations of individual floor slabs and vibrations of the columns connecting them. The first four mode shapes of the powerhouse structure are illustrated in Figure 2.

Numerous factors contribute to turbine unit vibration, which can be broadly categorized into mechanical, electromagnetic, and hydraulic sources. The rated rotational frequency of the unit and the pressure pulsation frequency of the turbine are typically identified as the primary excitation sources. In accordance with relevant design codes for structural resonance verification, the powerhouse structure must be assessed for potential resonance. The verification criterion requires that the frequency separation between the structure’s natural frequency and the forced vibration frequency exceeds 20% of the natural frequency [25]. Analysis of the first 20 natural frequencies of the overall underground structure, which range from 31 Hz to 63 Hz, confirmed sufficient frequency separation (exceeding 20%) for the following excitation sources: the rated rotational frequency, the unit runaway speed frequency, the primary frequencies of the low-frequency and mid-frequency vortex bands in the tailrace pipe, the pressure pulsation frequency behind the guide vanes, the pressure pulsation frequency in the pressurized zone of the penstock, the pressure pulsation frequency of the spiral casing and nozzle zone, and the pressure pulsation frequency at the guide vane outlet. Consequently, the risk of resonance for these sources is considered negligible. However, certain higher-order natural frequencies of the powerhouse structure exhibit insufficient frequency separation from specific electromagnetic vibration frequencies, with some differences falling below the 20% threshold, indicating potential resonance risks. Nevertheless, the high-frequency nature of electromagnetic vibrations is associated with relatively low energy levels and small modal participation factors, significantly mitigating the resonance risk. Furthermore, the transient duration of typical electromagnetic vibrations makes it difficult to sustain a significant structural dynamic response. Therefore, structural safety concerns due to resonance are deemed minimal, and the overall risk of resonance occurring in the powerhouse structure is considered very low.

4.2. Dynamic Response Analysis of the Underground Powerhouse Structure

Harmonic response analysis was conducted using finite element analysis software, with corresponding material properties assigned to the mesh. In the steady-state dynamic response calculations for various operating conditions, only the dynamic loads generated by the unit were considered, while the influence of other load effects was excluded. During unit operation, dynamic loads under different working conditions are transmitted through the stator foundation, lower frame foundation, and upper frame foundation. The specific dynamic loads acting on each foundation under various operating conditions are summarized in

Table 1. Design Load for Baseplate (KN).

Location	Condition	X	Y	Z
Upper Frame Foundation	Normal Operating		752
	Half of the Poles Short-Circuited		1050
	Two-Phase Short-Circuit
Stator Foundation	Normal Operating	374.3	94.4	472.1
	Half of the Poles Short-Circuited	904.4	94.4	472.1
	Two-Phase Short-Circuit	1837.4	94.4	472.1
Lower Frame Foundation	Normal Operating	69	137	1978
	Half of the Poles Short-Circuited	437	873	1978
	Two-Phase Short-Circuit

. For the dynamic response analysis of the powerhouse structure—the normal operating condition, specifically—full-load operation of the unit was selected, with the corresponding periodic excitation forces applied to the foundation surfaces. As shown in Table 1, the lower frame foundation is subjected to the highest dynamic loads. Notably, during normal operating conditions, the dynamic loads acting on both the stator foundation and lower frame foundation are primarily vertical in nature. Under normal operating conditions, the maximum principal stress in the entire building structure was identified at the lower frame foundation, with a peak value of 0.202 MPa. This stress level is relatively low, indicating minimal impact on structural safety. The maximum lateral dynamic displacement was 16.0 μm, the maximum longitudinal dynamic displacement was 18.09 μm, and the maximum vertical dynamic displacement was 69.52 μm. Among these, the vertical displacement was the largest; nevertheless, displacements in all directions satisfied the safety design specifications. The dynamic displacements and dynamic stresses at typical locations of the building structure are summarized in

Table 2. Maximum vibration responses at typical locations under normal operating conditions.

Location	Maximum Displacement/$\mathsf{\mu }\mathbf{m}$			Max Principal Stress/MPa
	X	Y	Z
Generator Floor Slab	4.35	4.30	11.65	0.057
Busbar Floor Slab	3.84	5.03	13.62	0.022
Lower Frame Foundation	16.00	17.13	112.40	0.424
Stator Foundation	10.35	10.87	87.38	0.273
Air Duct	10.59	11.48	19.50	0.359

. Vertical vibration was found to be dominant at all typical locations, with a maximum vertical dynamic displacement of 112.40 μm and a corresponding maximum principal stress of 0.424 MPa. Notably, the dynamic response in all directions at each typical location remained below the allowable limits for structural vibration and occupant comfort control stipulated in the relevant design codes.

5. Analysis of Factors Influencing the Dynamic Characteristics of the Underground Powerhouse Structure

To address parameter sensitivity in the dynamic analysis of underground powerhouse structures for pumped storage power stations, this study systematically investigated the influence of variations in key parameters—namely, the zone of surrounding rock, elastic modulus of surrounding rock, dynamic elastic modulus of concrete, and the damping ratio—on the structure’s natural frequencies, dynamic displacements, and dynamic stresses. The relative sensitivity of each parameter was clearly delineated.

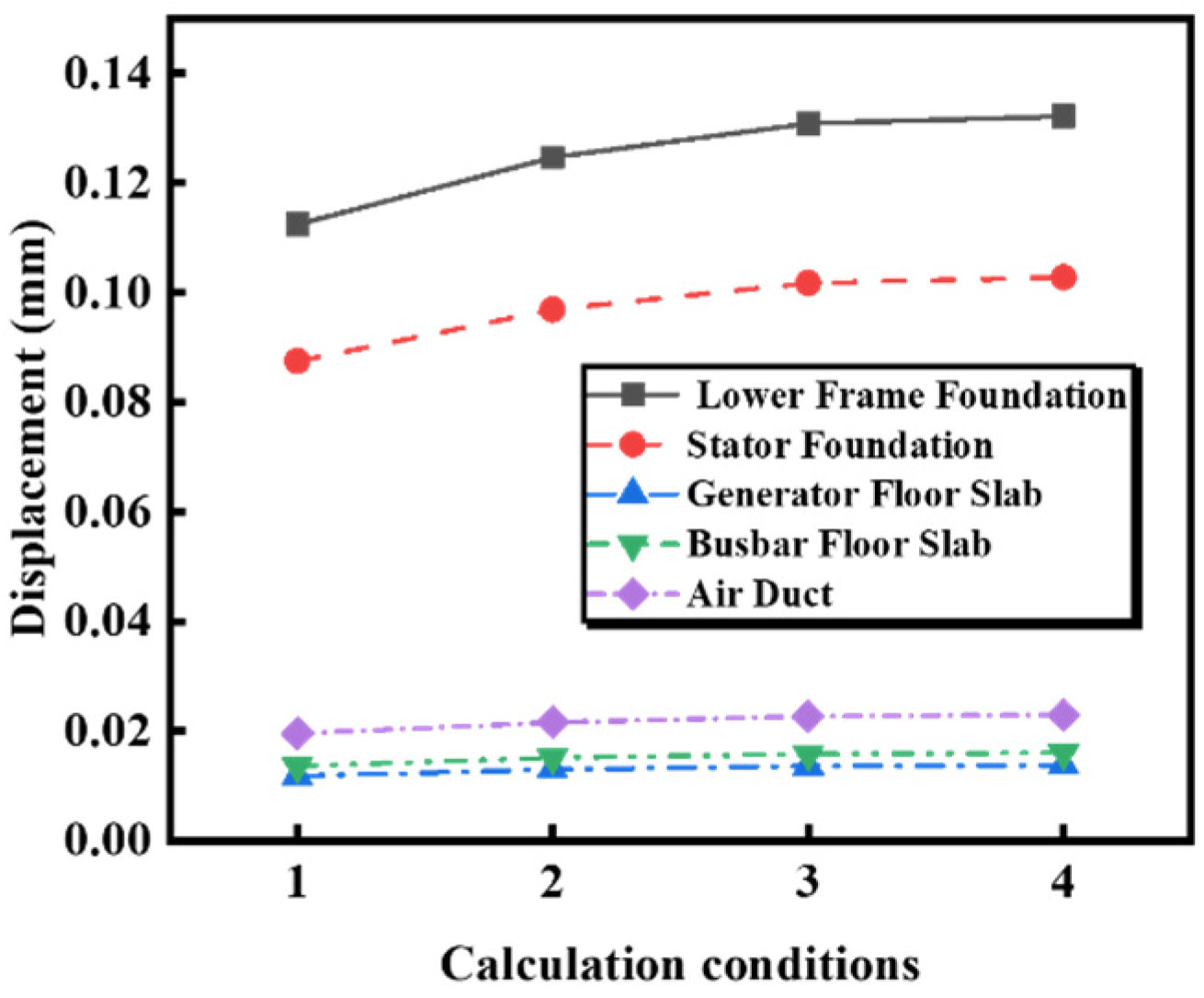
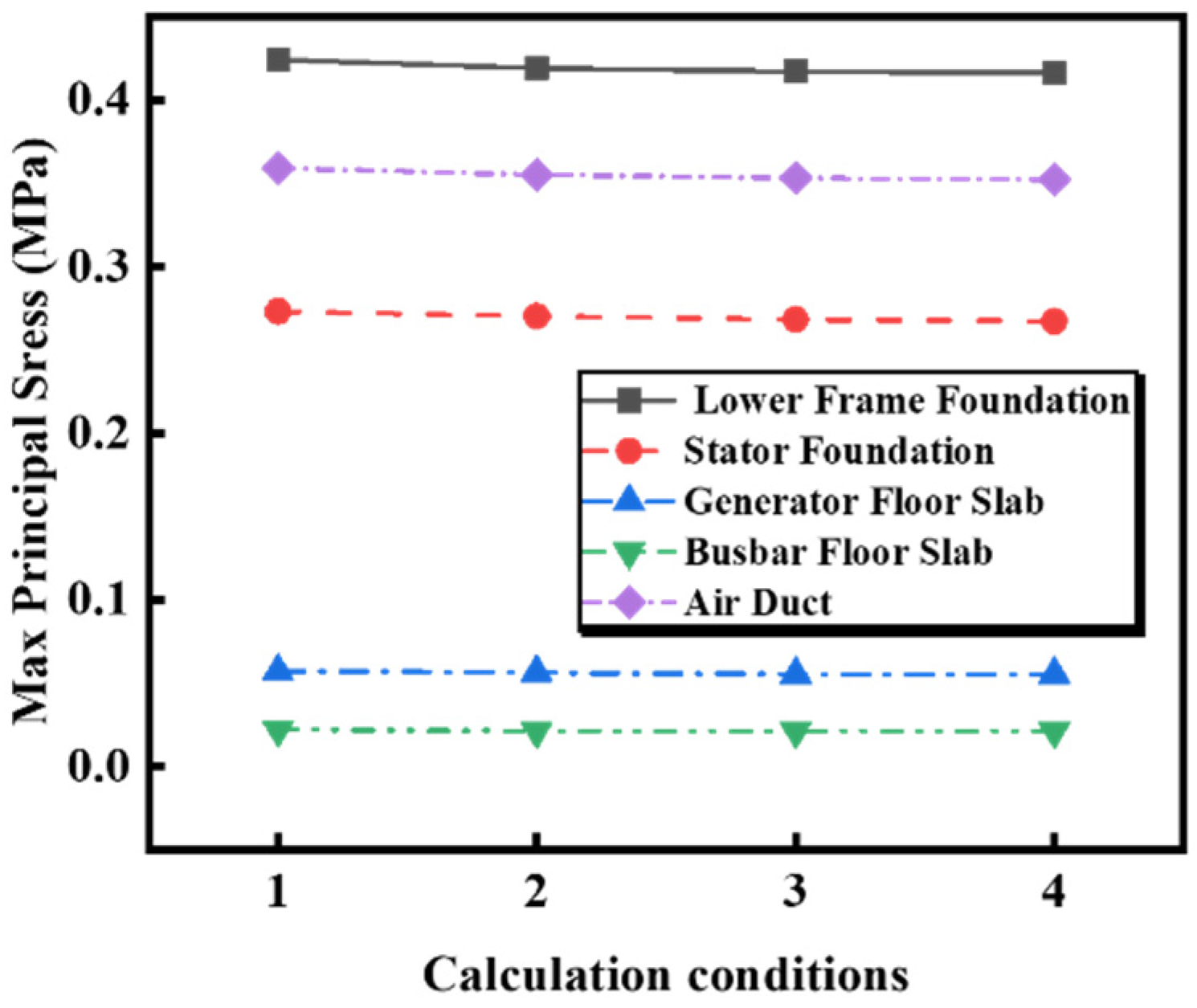
5.1. Sensitivity Analysis of the Model Boundary Extent

When studying the dynamic characteristics of underground powerhouse structures in hydropower stations, the zone of surrounding rock included in the model significantly affects computational accuracy. In finite element-based dynamic analysis of powerhouse structures, no unified standards exist regarding whether bedrock should be considered or how its extent should be defined. However, when viscoelastic artificial boundaries are applied, the numerical model should incorporate a zone of surrounding rock of at least 0.5 times the span length of the powerhouse [26]. As shown in

Table 3. Calculation conditions of the Zone of Surrounding Rock.

Conditions	1	2	3	4
Zone of Surrounding Rock	Without the surrounding rock	Surrounding rock within one unit-span distance	Surrounding rock within two unit-span distances	Surrounding rock within three unit-span distances

, to systematically evaluate the influence of the zone of surrounding rock on the dynamic characteristics of the underground powerhouse structure, the following four calculation conditions were established:

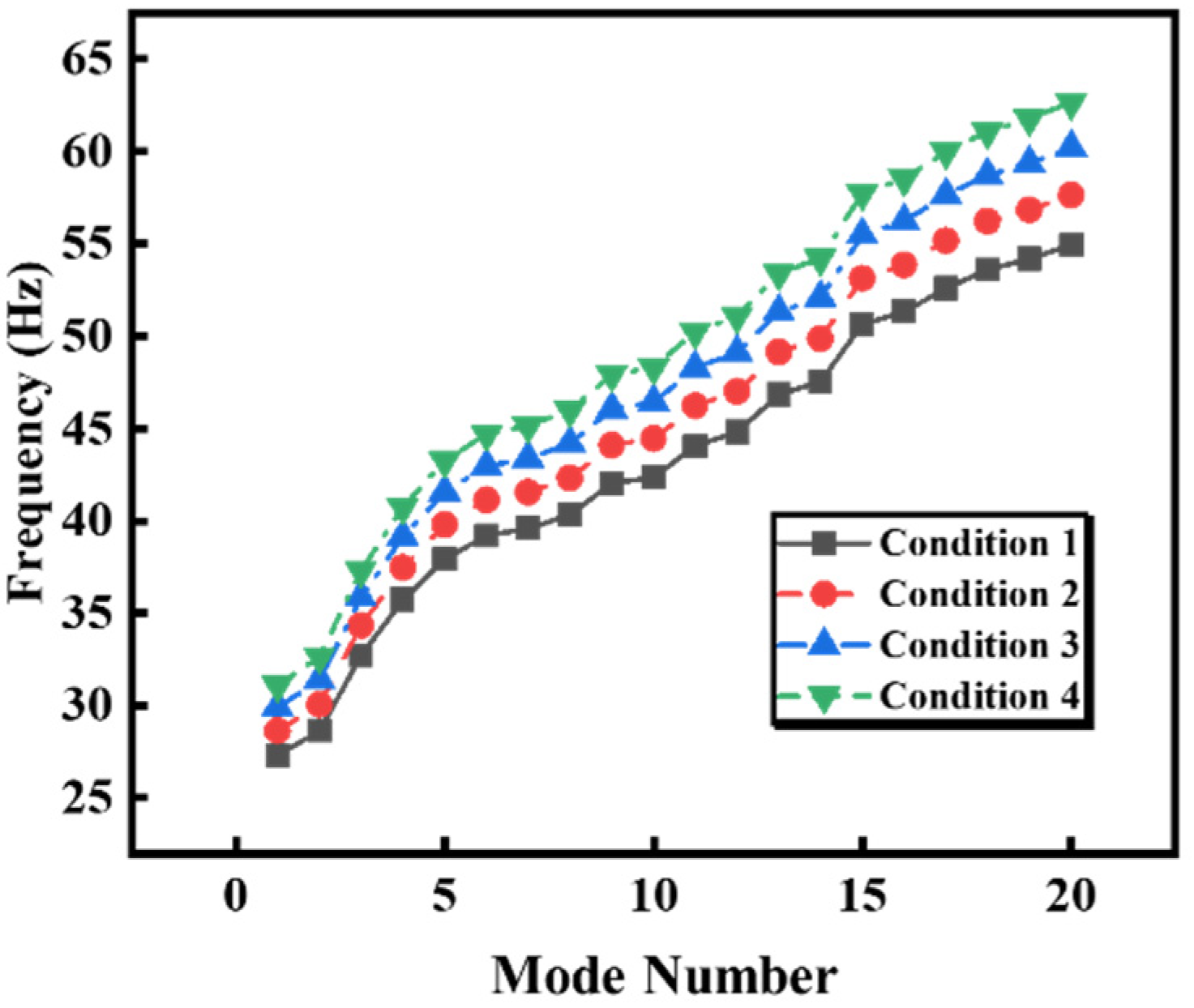
5.1.1. Effect of Zone of Surrounding Rock on Natural Vibration Characteristics of the Powerhouse Structure

For four different Zones of Surrounding Rock, the first 20 natural frequencies of the underground powerhouse’s overall structure were calculated under each scheme. A comparative analysis of their natural vibration characteristics was conducted. Figure 3 shows the comparison of the first 20 natural frequencies of the powerhouse’s overall structure under the four scenarios. As shown in Figure 3, the coupling effect of the surrounding rock significantly influences the natural frequencies of the powerhouse. The natural frequency at the same mode of the underground powerhouse structure decreases as the surrounding rock range increases. The average frequency reduction under a surrounding rock range of one unit span is approximately 14%. Under a surrounding rock range of two unit spans, the frequency decreases by an additional 7% compared to one unit span, while the frequency under rock coverage of three unit spans decreases by approximately 4% compared to the double span. This indicates that the effect of increased rock coverage on frequency gradually approaches saturation. As the rock coverage area expands, the increase in frequency also diminishes progressively. This demonstrates that as the flexible support effect of the rock increases, vibrational energy propagates toward infinite domains, thereby attenuating the vibrations.

5.1.2. Effect of Zone of Surrounding Rock on Dynamic Displacement

As indicated by the dynamic response analysis of the powerhouse structure presented in Section 4.2, the vertical dynamic displacement represents the largest displacement component across all structural elements. Based on the computational results obtained under the various calculation conditions, the maximum vertical dynamic displacements for the generator floor slab, busbar floor slab, stator foundation, lower frame foundation, and air duct were compiled, as shown in Figure 4. The vertical dynamic displacement of typical structural components in the underground powerhouse is observed to gradually increase as the zone of surrounding rock expands; however, the rate of increase diminishes with larger rock zones. A significant displacement increase occurs when the zone of surrounding rock is equivalent to one unit span. Beyond two unit spans, the displacement values tend to stabilize. Under a zone of three unit spans, the increase in dynamic displacement is less than 1% compared to the two-span condition, indicating that the dynamic response has effectively stabilized. Therefore, selecting a rock mass zone equivalent to twice the unit span in dynamic analysis can effectively simulate actual boundary conditions while achieving an optimal balance between computational efficiency and accuracy.

5.1.3. Effect of Zone of Surrounding Rock on Dynamic Stress

Figure 5 summarizes the maximum principal stresses for the generator floor slab, busbar floor slab, stator foundation, lower frame foundation, and air duct under the four different zones of surrounding rock conditions. As the zone of surrounding rock increases, the maximum principal stresses at each typical structural location exhibit a decreasing trend, with the rate of reduction gradually diminishing. The most pronounced stress reduction occurs when the rock zone spans one unit width. This reduction slows under a rock zone spanning two unit widths and stabilizes when the zone reaches three unit widths. This behavior indicates that the flexible support provided by the surrounding rock enhances the overall structural stiffness, effectively dissipating vibration energy and mitigating local stress concentrations. For practical engineering applications, it is recommended to adopt a rock mass zone spanning twice the unit span in dynamic analysis, as this approach ensures computational accuracy while maintaining satisfactory efficiency.

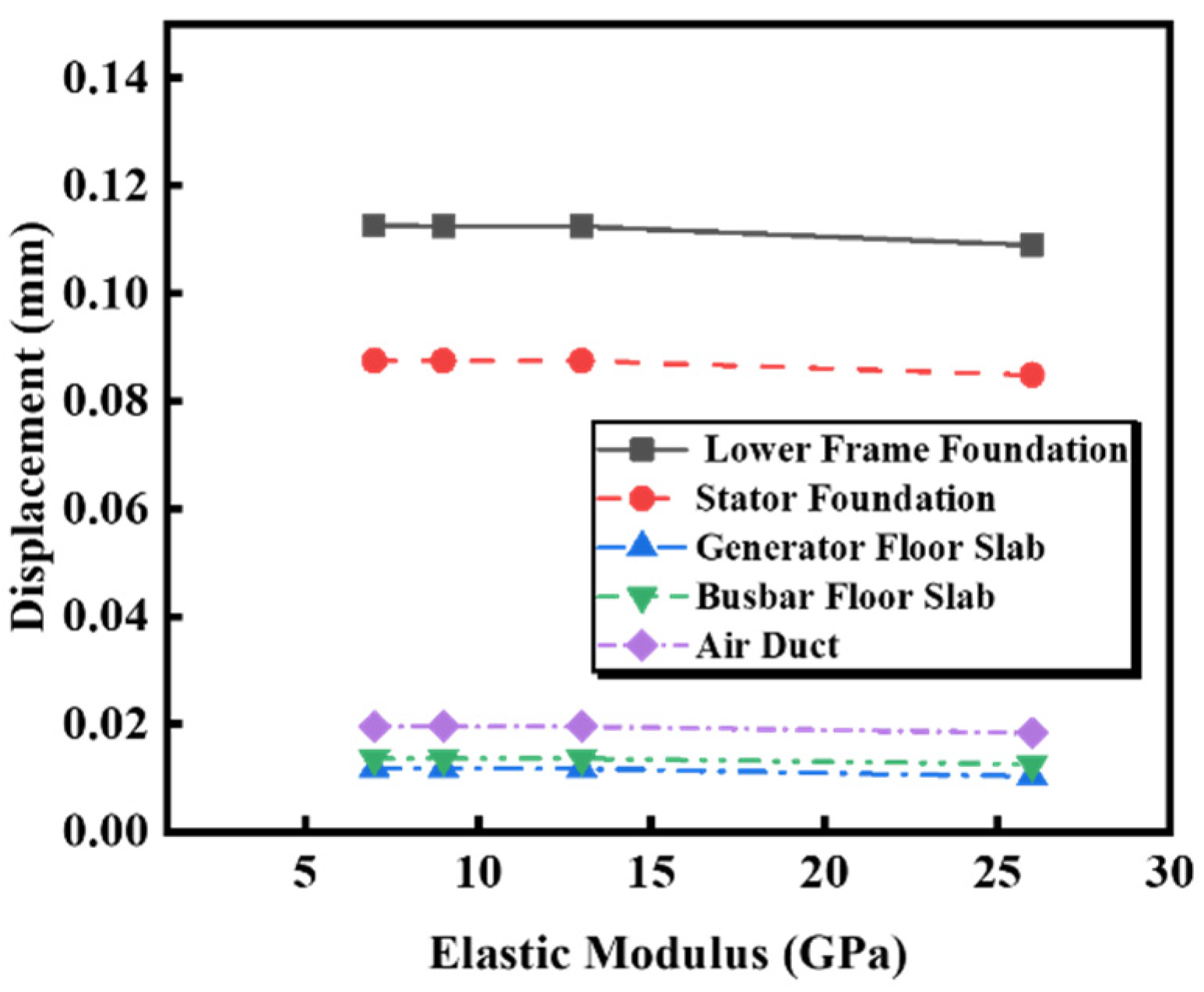
5.2. Sensitivity Analysis of the Surrounding Rock Elastic Modulus

To ensure the safety of underground structures, it is essential to investigate influencing factors based on actual construction conditions [27]. Engineering rock mass structures often exhibit complex and uncertain mechanical behavior during geological surveys. Although unavoidable measurement errors exist in determining rock mechanical parameters, the properties of both the rock mass and faults significantly influence the displacement and stress distributions in underground powerhouse structures. Sensitivity analysis assists engineers in evaluating how uncertainties in site investigation data affect the stability of underground chambers, thereby enhancing project reliability. For instance, Su Chao et al. performed numerical simulations by adjusting the elastic modulus values of rock and faults to 80%, 90%, 110%, and 120% of their baseline values to investigate the sensitivity of mechanical properties [28]. The surrounding rock of the present powerhouse is classified as Class III (RMR: 41–60), with an elastic modulus of 9 GPa. As shown in

Table 4. Calculation Conditions of Surrounding Rock Elastic Modulus.

Conditions	1	2	3	4
Surrounding Rock Elastic Modulus/GPa	7	9	13	26

, to examine the influence of the elastic modulus of the surrounding rock on the dynamic characteristics of the underground powerhouse, the following four calculation conditions were established:

5.2.1. Effect of Surrounding Rock Elastic Modulus on Natural Vibration Characteristics of the Powerhouse Structure

A modal analysis was performed to evaluate the first 20 natural frequencies of the underground powerhouse under the four calculation conditions. Figure 6 presents a comparison of the first 20 natural frequencies for the overall powerhouse structure under these four conditions. As shown in Figure 6, an increase in the surrounding rock elastic modulus enhances the constraining effect on the powerhouse structure, resulting in a gradual elevation of its natural frequencies. For the initial mode orders, the frequency increase per mode is pronounced. However, as the mode order increases, the incremental frequency rise diminishes progressively. In general, the frequency increase is more substantial for lower-order modes than for higher-order modes.

5.2.2. Effect of Surrounding Rock Elastic Modulus on Dynamic Displacement

Figure 7 compiles the maximum vertical dynamic displacements across all typical structural locations for the various calculation conditions. The vertical dynamic displacements at the lower frame foundation under the four conditions are 0.1126 mm, 0.1124 mm, 0.1124 mm, and 0.1089 mm, respectively. As the constraint provided by the surrounding rock increases, the overall displacement at each typical location gradually decreases. When the surrounding rock elastic modulus is set to 7, 9, and 13 GPa, respectively, the displacement values at typical locations exhibit minimal variation and remain largely stable. However, when the surrounding rock elastic modulus is increased to 26 GPa, the displacements decrease significantly. This indicates that, under the condition of direct elastic constraints applied at the outer boundary nodes of the powerhouse concrete structure, variations in the surrounding rock elastic modulus have a relatively limited influence on the dynamic displacement within the powerhouse.

5.2.3. Effect of Surrounding Rock Elastic Modulus on Dynamic Stress

The sensitivity of the maximum principal stress to the surrounding rock elastic modulus is quantified in Figure 8 for all typical structural locations. As shown in the figure, the maximum principal stresses in the upper powerhouse structure, such as the generator floor slab and air duct, decrease as the surrounding rock elastic modulus increases, with the rate of reduction becoming more gradual at higher modulus values. In contrast, for the lower powerhouse structure, including the lower frame foundation and stator foundation, the maximum principal stresses exhibit a slight increase or remain stable with increasing surrounding rock elastic modulus. This behavior can be attributed to the enhanced rock confinement, which redistributes stresses by absorbing vibration energy from the upper structure and transferring additional forced vibration stresses to the lower components. Overall, the stress values at typical locations within the underground powerhouse remain relatively stable across the range of surrounding rock elastic modulus values considered.

5.3. Sensitivity Analysis of the Dynamic Elastic Modulus of Concrete

The dynamic elastic modulus of concrete represents one of the most critical mechanical properties in the design and construction of structural concrete subjected to dynamic loads. A generally accepted linear relationship exists between the static and dynamic elastic moduli. For normal-strength concrete, the static-to-dynamic elastic modulus ratio ranges from 36% to 55%. When concrete is utilized in structures exposed to dynamic loads such as those induced by impact or seismic events, the use of the dynamic elastic modulus is more appropriate. For high-strength, medium-strength, and low-strength concrete, the dynamic elastic modulus typically exceeds the static modulus by approximately 20%, 30%, and 40%, respectively [29,30]. In the dynamic analysis of industrial building structures, the dynamic elastic modulus of concrete is often empirically taken as 1.2 times the static modulus. As shown in

Table 5. Calculation conditions of Dynamic Elastic Modulus.

Conditions	1	2	3	4
Dynamic Elastic Modulus	E	1.1 E	1.2 E	1.3 E

, to evaluate the influence of the dynamic elastic modulus of concrete on the dynamic characteristics of underground powerhouse structures, the following four calculation conditions were established:

5.3.1. Effect of Dynamic Elastic Modulus on Natural Vibration Characteristics of the Powerhouse Structure

To evaluate the effect of the dynamic elastic modulus, a modal analysis was performed to obtain the first 20 natural frequencies for all four conditions. Figure 9 presents a comparison of the first 20 natural frequencies for the overall powerhouse structure across these four conditions. The comparison reveals that as the dynamic elastic modulus of concrete increases, the natural frequency for each mode order also increases, exhibiting an approximately linear relationship with the modulus increment. The fundamental natural frequencies of the overall structure under the four conditions are 27.306 Hz, 28.637 Hz, 29.914 Hz, and 31.128 Hz, respectively. Their ratios correspond to the square root of the dynamic elastic modulus ratio (1:1.1:1.2:1.3). Furthermore, the ratios of the second to the twentieth natural frequencies are essentially consistent with the ratio observed for the fundamental frequency. These results demonstrate that the natural frequencies of the overall powerhouse structure are significantly influenced by the value of the dynamic elastic modulus of concrete, following a square-root relationship with the modulus value.

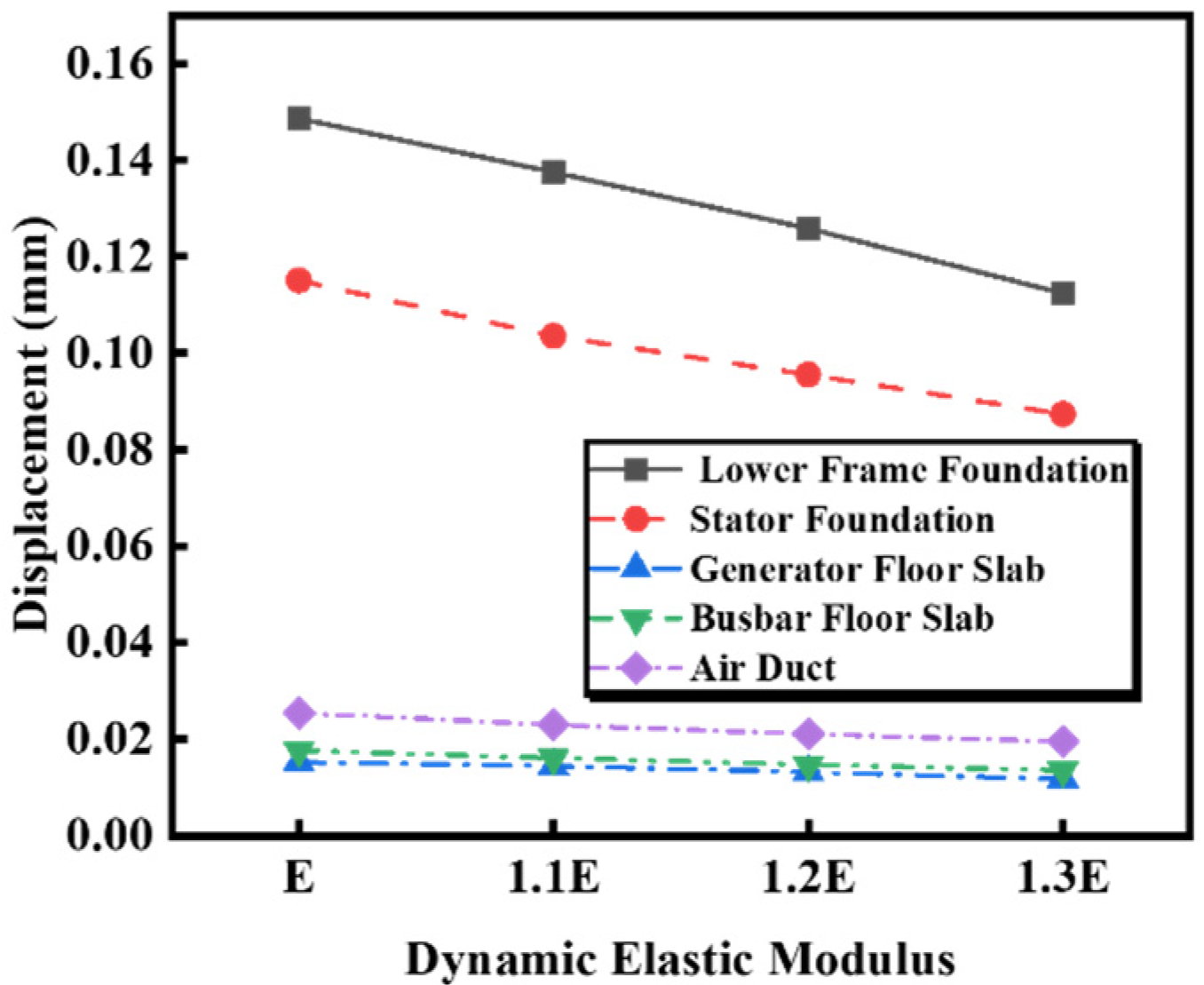
5.3.2. Effect of Dynamic Elastic Modulus on Dynamic Displacement

Figure 10 presents the maximum vertical dynamic displacements at the generator floor slab, busbar floor slab, stator foundation, lower frame foundation, and air duct for each calculation condition. Among the typical structural components under the four conditions, the lower frame foundation exhibits the largest vertical dynamic displacement, with values of 0.1486 mm, 0.1375 mm, 0.1258 mm, and 0.1124 mm, respectively. The ratio of these displacements is approximately 1:0.93:0.85:0.76, which is inversely proportional to the dynamic elastic modulus of concrete ratio of 1:1.1:1.2:1.3. Similarly, the vertical dynamic displacement ratios for other typical structural components fluctuate within the range of 1:0.93:0.85:0.76. These results indicate that the dynamic displacement of the powerhouse structure is correlated with the dynamic elastic modulus of concrete: a lower elastic modulus corresponds to a larger dynamic displacement, and vice versa. Specifically, the magnitude of the dynamic elastic modulus is inversely proportional to the computed dynamic displacement values.

5.3.3. Effect of Dynamic Elastic Modulus on Dynamic Stress

The maximum principal stresses across the generator floor slab, busbar floor slab, stator foundation, lower frame foundation, and air duct are summarized in Figure 11 for the four concrete dynamic modulus cases. Among these, the lower frame foundation exhibited the highest principal stress values across all conditions: 0.408 MPa, 0.416 MPa, 0.42 MPa, and 0.424 MPa, respectively. The principal stresses at typical structural locations showed a slight increase with rising dynamic elastic modulus of concrete, though the increment was modest, with growth rates remaining below 4%. These results indicate that the dynamic elastic modulus of concrete has a negligible influence on the dynamic stresses within the underground powerhouse structure.

5.4. Sensitivity Analysis of the Damping Ratio

The damping ratio represents a critical parameter governing the dynamic characteristics of underground powerhouse structures. While a value of 5% is commonly specified in seismic design codes for hydraulic structures, a damping ratio of approximately 1.5% is recommended for underground powerhouses in pumped storage power stations, irrespective of considerations such as low-frequency operation or high-frequency hydraulic pulsations [31]. As shown in

Table 6. Calculation conditions of Damping Ratio.

Conditions	1	2	3	4
Damping Ratio	0.01	0.02	0.035	0.05

, to evaluate the influence of the damping ratio on the dynamic characteristics of the underground powerhouse structure, the following four calculation conditions were established:

5.4.1. Effect of Damping Ratio on Natural Vibration Characteristics of the Powerhouse Structure

The first 20 natural frequencies of the overall underground powerhouse structure were compared across the four calculation conditions. Figure 12 presents the first 20 natural frequencies obtained under these four calculation conditions. As shown in Figure 3, the natural frequency of the underground powerhouse structure remains constant at 31.128 Hz across all four calculation conditions. Furthermore, the natural frequency at each corresponding mode order exhibits no variation with changes in the damping ratio. In a classically damped system, the mode shapes coincide with those of the undamped system, indicating that the damping ratio, within a certain range, has no influence on the natural vibration characteristics of the powerhouse structure.

5.4.2. Effect of Damping Ratio on Dynamic Displacement

The computational results for the maximum vertical dynamic displacements at typical structural locations are summarized in Figure 13. Figure 13 demonstrates that the vertical dynamic displacement of the lower frame foundation is the largest among all components under each calculation condition, with values of 0.1126 mm, 0.1125 mm, 0.1124 mm, and 0.1124 mm, respectively. The ratio of these displacements is approximately 1:1:1:1, whereas the ratio of the corresponding damping ratios is 1:2:3.5:5, indicating a pronounced discrepancy. This result suggests that, during dynamic response analysis of the powerhouse structure, the dynamic displacement is only minimally influenced by the damping ratio, and its effect can be considered negligible.

5.4.3. Effect of Damping Ratio on Dynamic Stress

Figure 14 presents the maximum principal stress at the five typical locations for the four damping ratio conditions. As illustrated in Figure 14, similar to the dynamic displacement patterns observed in the dynamic response analysis, the maximum principal stress ratios across typical structural components of the underground powerhouse remain approximately 1:1:1:1 under different damping ratios. This ratio differs substantially from the corresponding damping ratio values of 1:2:3.5:5, indicating that dynamic stresses in the powerhouse structure are only minimally influenced by the damping ratio during dynamic response analysis.

6. Conclusions

This study investigates the dynamic behavior of the underground powerhouse in a large pumped storage power station. A three-dimensional finite element model of the structural unit section was established to examine the natural vibration characteristics and dynamic response of the overall underground powerhouse structure under unit operating loads. The influence of key parameters, including the zone of surrounding rock, the surrounding rock elastic modulus, the dynamic elastic modulus of concrete, and the damping ratio, on the dynamic characteristics of the underground powerhouse structure was systematically evaluated. The following conclusions are drawn:

(1)

Expanding the model boundary reduces the natural frequency but increases the dynamic displacement of the structure. The effects saturate beyond a boundary extent of twice the unit span, which is recommended as the optimal zone for balancing computational accuracy and efficiency.

(2)

An increase in the elastic modulus of the surrounding rock raises the structure’s natural frequency and slightly reduces dynamic displacement. Its influence on dynamic stress is limited, causing a slight decrease in the upper structure and a minor increase or stability in the lower structure.

(3)

The natural frequency of the structure exhibits a square-root relationship with the dynamic elastic modulus of concrete, while the dynamic displacement is inversely proportional to it. The parameter has a negligible influence on dynamic stress, with the increment below 4%.

(4)

The damping ratio has no effect on the natural vibration characteristics of the structure. Its influence on both dynamic displacement and dynamic stress is negligible within the typical range considered for this type of structure.

In summary, this study elucidates the sensitivity of key parameters involved in the dynamic analysis of underground powerhouse structures. The findings provide a theoretical basis and practical reference for establishing rational numerical models and selecting appropriate parameters, offering significant implications for improving the seismic design and ensuring the safe operation of underground powerhouses in pumped storage power stations.