Single-Pass CNN–Transformer for Multi-Label 1H NMR Flavor Mixture Identification
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Flavor Library and Formulated Flavor Mixtures
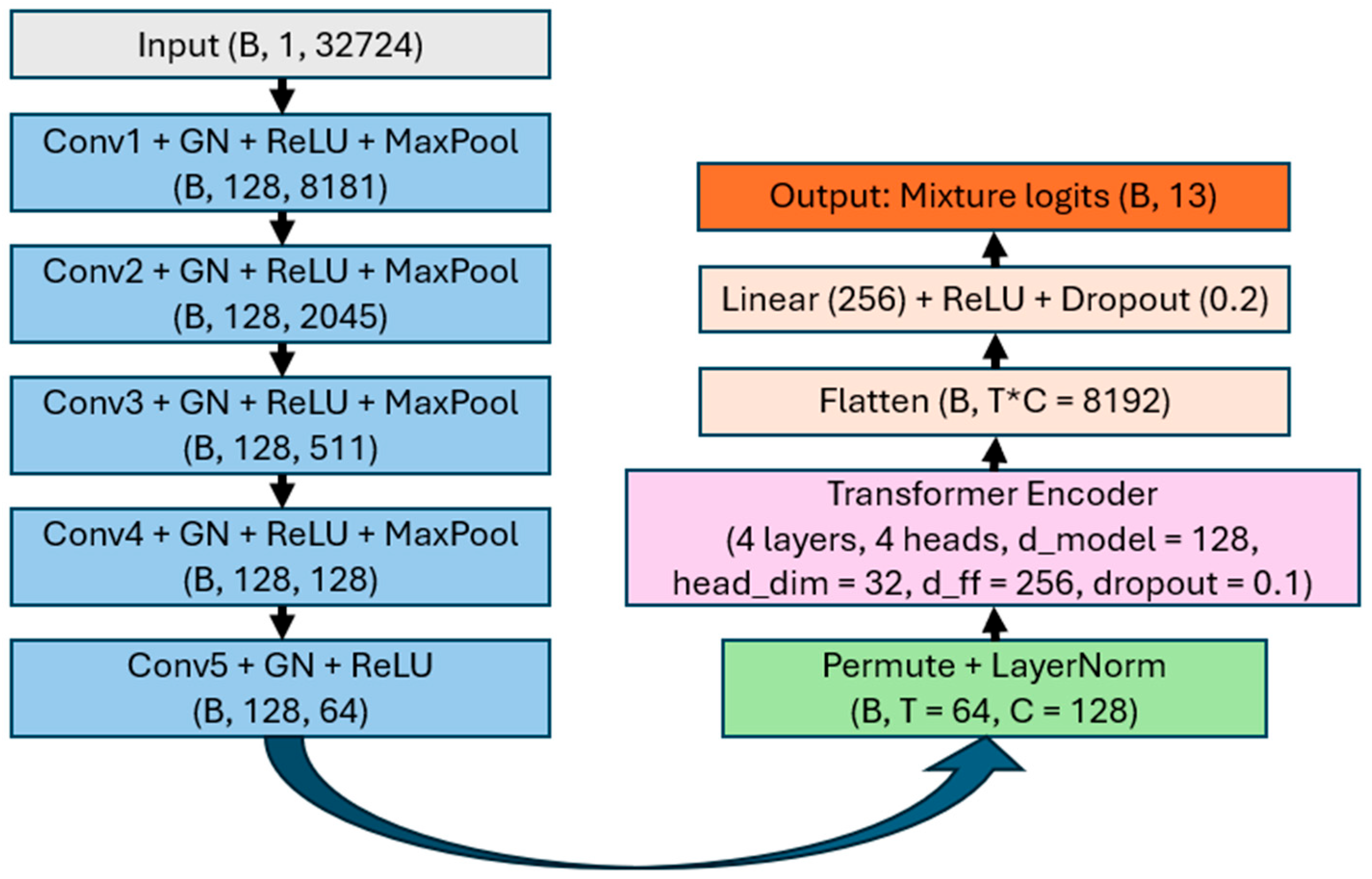
2.2. Model Architecture
2.3. Synthetic Mixture Generation and Augmentations
2.4. Evaluation Metrics (Multilabel) and Threshold Policy
2.5. Chemometric Baselines (Simulation-Trained)
2.6. Training Objective and Optimization
2.7. Ablation Study on Architectural Contributions
2.8. Open-Set Robustness Evaluation
2.9. Implementation
2.10. Statistical Testing
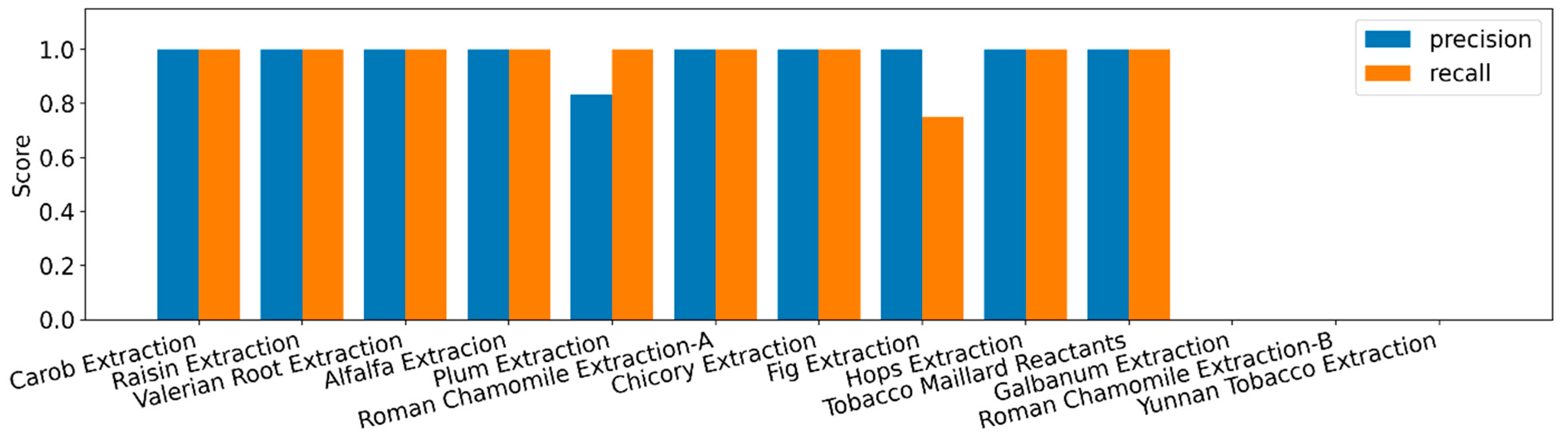
2.11. Visualization and Case Selection
2.12. Code Availability
3. Results
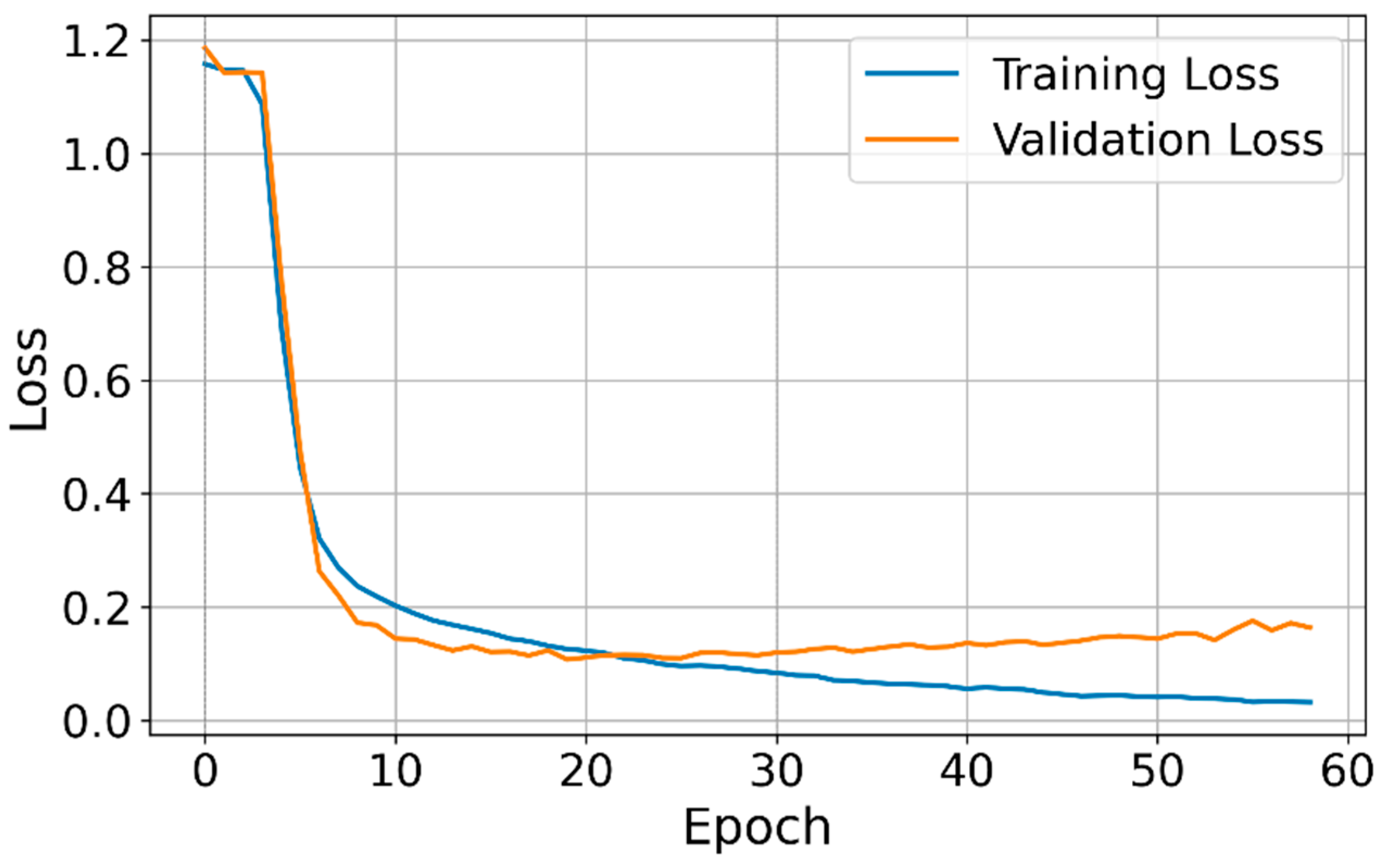
3.1. Model Training and Validation Losses
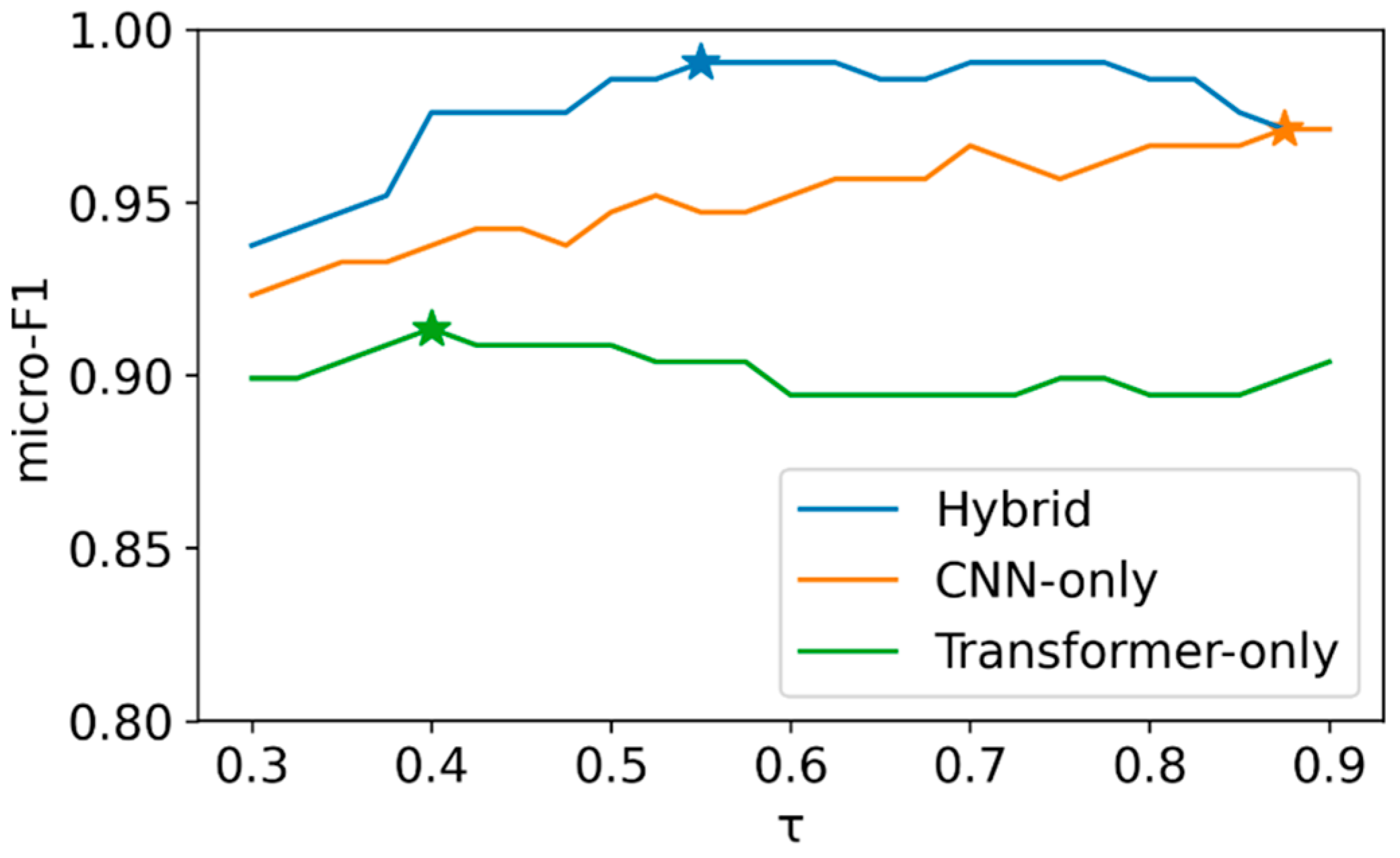
3.2. Model Performance (Fixed Threshold, τ = 0.70)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1H | Proton (hydrogen-1) |
| AUROC | Area Under the Receiver Operating Characteristic Curve |
| BCE | Binary Cross Entropy (loss) |
| Brier | Brier Score (mean squared error of probabilistic predictions) |
| CNN | Convolutional Neural Network |
| CPU | Central Processing Unit |
| ECE | Expected Calibration Error |
| FPR | False Positive Rate |
| F1 (micro-F1) | Micro-averaged F1 Score (precision–recall harmonic mean aggregated over all labels) |
| GPU | Graphics Processing Unit |
| ID | In-Distribution |
| LR | Learning Rate |
| NMR | Nuclear Magnetic Resonance |
| OOD | Out-of-Distribution |
| O(1), O(C) | Big-O Complexity: constant time; linear in number of classes (C) |
| ppm | Parts Per Million (chemical shift axis) |
| pSCNN/pSNN | Pseudo-Siamese Convolutional Neural Network/Pseudo-Siamese Neural Network |
| ROC | Receiver Operating Characteristic |
| SPP | Spatial Pyramid Pooling |
| τ | Decision threshold applied to class probabilities |
| TPR | True Positive Rate (recall) |
| Transformer | Self-attention–based neural network architecture |
| SIM | Simulated Spectra |
| “REAL” set | The 16 real 1H NMR mixtures from the DeepMID study (13 candidate components) |
References
- Li, W.; Sun, K.; Li, D.; Bai, T. Algorithm for Automatic Image Dodging of Unmanned Aerial Vehicle Images Using Two-Dimensional Radiometric Spatial Attributes. J. Appl. Remote Sens. 2016, 10, 36023. [Google Scholar] [CrossRef]
- Nagana Gowda, G.A.; Raftery, D. NMR Metabolomics Methods for Investigating Disease. Anal. Chem. 2023, 95, 83–99. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S. Quantitative Metabolomics Using NMR. TrAC Trends Anal. Chem. 2008, 27, 228–237. [Google Scholar] [CrossRef]
- Li, M.; Xu, W.; Su, Y. Solid-State NMR Spectroscopy in Pharmaceutical Sciences. TrAC Trends Anal. Chem. 2021, 135, 116152. [Google Scholar] [CrossRef]
- Holzgrabe, U. Quantitative NMR Spectroscopy in Pharmaceutical Applications. Prog. Nucl. Magn. Reson. Spectrosc. 2010, 57, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Fraga-Corral, M.; Carpena, M.; Garcia-Oliveira, P.; Pereira, A.G.; Prieto, M.A.; Simal-Gandara, J. Analytical Metabolomics and Applications in Health, Environmental and Food Science. Crit. Rev. Anal. Chem. 2022, 52, 712–734. [Google Scholar] [CrossRef] [PubMed]
- Monakhova, Y.B.; Godelmann, R.; Kuballa, T.; Mushtakova, S.P.; Rutledge, D.N. Independent Components Analysis to Increase Efficiency of Discriminant Analysis Methods (FDA and LDA): Application to NMR Fingerprinting of Wine. Talanta 2015, 141, 60–65. [Google Scholar] [CrossRef] [PubMed]
- Kruger, N.J.; Troncoso-Ponce, M.A.; Ratcliffe, R.G. 1H NMR Metabolite Fingerprinting and Metabolomic Analysis of Perchloric Acid Extracts from Plant Tissues. Nat. Protoc. 2008, 3, 1001–1012. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wei, W.; Du, W.; Cai, J.; Liao, Y.; Lu, H.; Kong, B.; Zhang, Z. Deep-Learning-Based Mixture Identification for Nuclear Magnetic Resonance Spectroscopy Applied to Plant Flavors. Molecules 2023, 28, 7380. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Wang, Y.; Liao, Y.; Lu, H.; Cai, J.; Cui, Y.; Ding, S.; Li, Y.; Zhao, Y.; Wang, Z. FlavorFormer: Hybrid Deep Learning for Identifying Compounds in Flavor Mixtures Based on NMR Spectroscopy. Microchem. J. 2025, 218, 115372. [Google Scholar] [CrossRef]
- Fidalgo, T.K.S.; Freitas-Fernandes, L.B.; Angeli, R.; Muniz, A.M.S.; Gonsalves, E.; Santos, R.; Nadal, J.; Almeida, F.C.L.; Valente, A.P.; Souza, I.P.R. Salivary Metabolite Signatures of Children with and without Dental Caries Lesions. Metabolomics 2013, 9, 657–666. [Google Scholar] [CrossRef]
- Head, T.; Giebelhaus, R.T.; Nam, S.L.; de la Mata, A.P.; Harynuk, J.J.; Shipley, P.R. Discriminating Extra Virgin Olive Oils from Common Edible Oils: Comparable Performance of PLS-DA Models Trained on Low-field and High-field 1H NMR Data. Phytochem. Anal. 2024, 35, 1134–1141. [Google Scholar] [CrossRef]
- Pembury Smith, M.Q.R.; Ruxton, G.D. Effective Use of the McNemar Test. Behav. Ecol. Sociobiol. 2020, 74, 133. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Y.; Yu, C.; Lv, Y.; Zhang, H.; Yang, Q.; Wen, M.; Lu, H.; Zhang, Z. A Universal and Accurate Method for Easily Identifying Components in Raman Spectroscopy Based on Deep Learning. Anal. Chem. 2023, 95, 4863–4870. [Google Scholar] [CrossRef]
- Zhang, P.; Yu, H.; Li, P.; Wang, R. TransHSI: A Hybrid CNN-Transformer Method for Disjoint Sample-Based Hyperspectral Image Classification. Remote Sens. 2023, 15, 5331. [Google Scholar] [CrossRef]
- Arkin, E.; Yadikar, N.; Xu, X.; Aysa, A.; Ubul, K. A Survey: Object Detection Methods from CNN to Transformer. Multimed. Tools Appl. 2023, 82, 21353–21383. [Google Scholar] [CrossRef]
- Li, Z.; Chen, G.; Zhang, T. A CNN-Transformer Hybrid Approach for Crop Classification Using Multitemporal Multisensor Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 847–858. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the International Conference on machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Zhao, J.; Kusnierek, K. A Fully Connected Network (FCN) Trained on a Custom Library of Raman Spectra for Simultaneous Identification and Quantification of Components in Multi-Component Mixtures. Coatings 2024, 14, 1225. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. A Baseline for Detecting Misclassified and Out-of-Distribution Examples in Neural Networks. arXiv 2016, arXiv:1610.02136. [Google Scholar]
| Name | Vendor |
|---|---|
| Alfalfa Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Carob Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Chicory Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Fig Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Galbanum Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Hops Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Plum Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Raisin Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Roman Chamomile Extraction-A | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Roman Chamomile Extraction-B | Zhuhai Guanglong Flavor Co., Ltd., Zhuhai, China |
| Tobacco Maillard Reactants | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Valerian Root Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Yunnan Tobacco Extraction | Guangzhou Huafang Tobacco Flavor Co., Ltd., Guangzhou, China |
| Block | Parameter | Symbol | Setting (Range) | Rationale |
|---|---|---|---|---|
| Library | Classes; length | C, L | C = 13; L = 32,724 | 13 pure references; full spectrum length |
| Mixture design | Components per mixture | K | {2, 3, 4, 5, p(K) ∝ (13 choose K)0.8} | Stratified over combinatorics |
| Class prior | Component indices | — | Uniform, no replacement | Balanced sampling |
| Ratios | Equal vs. Dirichlet | p_equal, α | p_equal = 0.80; Dirichlet α = {0.5, 1.0, 2.0} | Match real equal-ratio setting; add variability |
| Axes | Shift/warp/stretch | Δ, s | Δ ∈ [−12, 12]; warp 5–8 knots; s ∈ [0.985, 1.015] (p = 0.5) | Referencing + drift |
| Dilution | Level | d | D ∈ [0.01, 1.00]; scale by (1 − d) | Low-SNR realism |
| Lineshape | Smoothing/phase | σ, φ | Σ ∈ [0.06, 0.20]; φ ~ N(0, 4°) | Linewidth + jitter |
| Baseline and noise | Baseline/ripple/noise | a0, a1, a2; A, f | Quad baseline; ripple A ∈ [0, 0.006], f ∈ [1, 3]; white [2 × 10−4, 6 × 10−4]; LF λ ∈ [0, 2 × 10−4] | Instrumental artifacts |
| Polarity | Global flip | p_flip | 0.50 | Polarity invariance |
| Normalization | Robust scaling | — | 80%:/P90|x|; 20%:/max|x| | Avoid overfitting to one rule |
| Labels | Presence/targets | τ_pres, y | τ_pres = 0.01; y normalized over present | Polarity and dilution invariant |
| Dataset | Size/split | N | N = 30,000; train/val = 0.8/0.2 | Deterministic seeds/loaders |
| Model | Elem. Acc | Micro-F1 | Subset Acc | ECE | Brier | Best τ* | Elem. Acc (τ*) | Subset Acc (τ*) | Per-Class τ− | Elem. Acc (τ_c) | Subset Acc (τ_c) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hybrid | 0.990 | 0.990 | 0.875 | 0.698 | 0.018 | 0.55 | 0.990 | 0.875 | 0.723 | 0.990 | 0.875 |
| CNN-only | 0.966 | 0.966 | 0.688 | 0.683 | 0.038 | 0.875 | 0.971 | 0.688 | 0.744 | 0.971 | 0.688 |
| Transformer-only | 0.894 | 0.894 | 0.375 | 0.708 | 0.079 | 0.40 | 0.914 | 0.313 | 0.758 | 0.899 | 0.375 |
| Scenario | Thresholding Scheme | AUROC (Max-Prob) | Any-Pos FPR | Elem. FPR | Micro-F1 (Known) | Micro-P | Micro-R | Elem. FPR (Negatives) | Any-FP (per Spectrum) |
|---|---|---|---|---|---|---|---|---|---|
| Pure outsiders | fixed | 0.984 | 0.320 | 0.048 | – | – | – | – | – |
| per-class | 0.984 | 0.215 | 0.032 | – | – | – | – | – | |
| Mixed outsiders | fixed | – | – | – | 0.843 | 0.843 | 0.843 | 0.048 | 0.309 |
| per-class | – | – | – | 0.848 | 0.848 | 0.848 | 0.036 | 0.219 |
| Variant | Params (M) | Tokens × Dims | Best τ* | Micro-F1 (Real) | Subset acc | ms/Sample (GPU) |
|---|---|---|---|---|---|---|
| Hybrid | ~0.47 | 64 × 128 | 0.55 | 0.990 | 0.875 | 0.68 |
| CNN-only | ~0.37 | 64 × 128 (pre-flatten) | 0.875 | 0.971 | 0.688 | 0.28 |
| Transformer-only | ~0.44 | 64 × 128 | 0.40 | 0.913 | 0.313 | 0.37 |
| Level | Comparison | b (A Wrong/B Right) | c (A Right/B Wrong) | Discordant | p-Value |
|---|---|---|---|---|---|
| Elementwise | Hybrid vs. CNN-only | 1 | 6 | 7 | 0.125 |
| Elementwise | Hybrid vs. Transformer-only | 2 | 22 | 24 | 3.59 × 10−5 |
| Subset (exact-match) | Hybrid vs. CNN-only | 1 | 4 | 5 | 0.375 |
| Subset (exact-match) | Hybrid vs. Transformer-only | 0 | 8 | 8 | 0.00781 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Kusnierek, K. Single-Pass CNN–Transformer for Multi-Label 1H NMR Flavor Mixture Identification. Appl. Sci. 2025, 15, 11458. https://doi.org/10.3390/app152111458
Zhao J, Kusnierek K. Single-Pass CNN–Transformer for Multi-Label 1H NMR Flavor Mixture Identification. Applied Sciences. 2025; 15(21):11458. https://doi.org/10.3390/app152111458
Chicago/Turabian StyleZhao, Jiangsan, and Krzysztof Kusnierek. 2025. "Single-Pass CNN–Transformer for Multi-Label 1H NMR Flavor Mixture Identification" Applied Sciences 15, no. 21: 11458. https://doi.org/10.3390/app152111458
APA StyleZhao, J., & Kusnierek, K. (2025). Single-Pass CNN–Transformer for Multi-Label 1H NMR Flavor Mixture Identification. Applied Sciences, 15(21), 11458. https://doi.org/10.3390/app152111458






