Featured Application
This research presents a fuzzy DEMATEL-based evaluation methodology for gamified recommender systems, providing significant insights for adaptive system design in education, e-commerce, and healthcare. The framework emphasizes critical factors for adoption, such as usefulness, ease of use, and trust. It also provides advice on how to design: using rewards and competition in Points, Badges, and Leaderboards (PBL) design makes people more motivated in the short term. Acknowledgments, Objectives, and Progression (AOP) design makes things more open and helps things move along. Acknowledgments, Competition, and Time Pressure (ACT) design promotes productivity under competitive circumstances. Acknowledgments, Objectives, and Social Pressure (AOS) gets things done by using social responsibility and peer pressure. These results help developers to implement gamification elements with respect to domain-based objectives, enabling the active involvement of users.
Abstract
Gamified recommender systems, which mix game design with recommendation frameworks, are a new way to increase user involvement and satisfaction. Even though they have a lot of potential, there has not been any systematic research on how their design affects how people use them. This study introduces a fuzzy DEMATEL-based framework for the assessment and enhancement of gamified recommender systems. Four theoretically grounded gamified recommender system prototypes were developed as a novel contribution, as no readily available systems exist for these designs. The assessment utilized nine user-centric criteria—Effectiveness, Transparency, Persuasiveness, Satisfaction, Trust, Usefulness, Ease of Use, Efficiency, and Education—systematically derived from a PRISMA-guided literature review. This study integrates gamification theory, systematic review, and fuzzy decision-making to formulate a comprehensive framework for identifying the key factors influencing adoption. The fuzzy DEMATEL was applied to evaluate feedback from 25 end-users, and it was found that usefulness and ease of use were the most essential factors for satisfaction and system effectiveness. Analysis of design showed that competition in Points, Badges, and Leaderboards (PBL) design boosts short-term motivation, Acknowledgments, Objectives, and Progression (AOP) boosts progress and openness, Acknowledgments, Competition, and Time Pressure (ACT) boosts efficiency in competitive situations but might lower satisfaction, and Acknowledgments, Objectives, and Social Pressure (AOS) depends on social influence and accountability.
1. Introduction
Recommender systems (RS) are commonly used in today’s era. They recommend user-specific purchasing, learning, traveling, and entertainment [1,2,3,4,5,6]. By analyzing large amounts of data, RS improves decision-making. This boosts user satisfaction and engagement. Even though they are successful, keeping long-term use going is still a big problem, especially in situations where user motivation and tenacity are very important [7,8]. Digital platforms need recommender systems (RS) to guide users to shop, study, travel, and have fun [1,2,3,4,5,6]. Eliminating unnecessary information helps RS users make better decisions. It makes users satisfied and more engaged. Gamification elements also improve motivation, engagement, and behavior outside of games [9,10,11,12,13,14]. Trust, satisfaction, and system use were improved through the use of game elements in e-commerce, workplace technology, and healthcare and in education, learning performances, and engagement in gamification studies [13,15,16,17,18,19,20,21]. Gamified recommender systems (GRS) improve user adoption and user experience by combining personalization with incentive design [22,23,24,25,26,27,28]. GRS has been proposed for career promotion [29], tourism [22], adaptive learning [20,25], and consumer engagement [24]. Prior systematic reviews emphasize that explanations in recommender systems should not only enhance decision effectiveness and transparency, but also build trust, increase satisfaction, ensure usefulness and ease of use, improve efficiency, support persuasion, and even enable educational benefits [29]. These dimensions provide a comprehensive basis for evaluating the quality and impact of gamified recommender designs [16]. Recent reviews confirm their growing relevance and potential [30]. When designed well, gamification boosts user motivation and engagement [31].
However, most existing studies on GRS remain limited to conceptual domain-specific prototypes or narrative reviews [6,7,30,32,33,34]. Few works have examined the causal interrelationships among gamification elements that influence engagement and adoption. Prior research often employs descriptive or comparative approaches [10,11,24,32] with limited application of multiple-criteria decision-making (MCDM) techniques [34,35,36]. Prior reviews addressed the absence of analytical methods to inspect causal interrelations among gamified design frameworks [37]. Several multi-criteria decision-making (MCDM) techniques—such as the Analytic Hierarchy Process (AHP) [38], Analytic Network Process (ANP) [39], Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) [40], and Decision-Making Trial and Evaluation Laboratory (DEMATEL) [41]—have been applied to gamification evaluation and system design. Recent studies have emphasized the growing role of intelligent and hybrid decision-making approaches in evaluating user-centric systems and complex learning environments. For instance, one study showed hybrid MCDM approaches as spherical fuzzy DEMATEL, ANP, and VIKOR (VIekriterijumsko KOmpromisno Rangiranje) can improve the modeling of evaluation criteria interdependencies under uncertainty, which is also helpful in analyzing complex relationships among gamification elements in recommender system design [42]. Researchers [43] examined decision-making frameworks in engineering that utilize artificial intelligence, with a focus on how multi-criteria evaluation can facilitate the creation of adaptive learning environments. These developments align with the current study’s objective to employ fuzzy-based causal modeling for the examination of gamified recommender systems. AHP, ANP, and TOPSIS are some of the methods that have been used to evaluate gamification. They generally help people decide what to do initially rather than making cause-and-effect connections. Gabus and Fontela developed DEMATEL to demonstrate and quantify complex cause-and-effect relationships between system variables [41]. This helps people comprehend how different factors affect each other while making technology–people decisions [44]. DEMATEL has advanced with the inclusion of fuzzy set theory, hybrid extensions like gray DEMATEL, rough DEMATEL, and amalgamations with other MCDM methods like AHP and TOPSIS [45,46,47,48,49].
These changes have made it much better at modeling uncertainty and taking into account both direct and indirect effects between evaluation criteria. This makes fuzzy DEMATEL a very useful tool for studying systems design and behavioral assessment. In addition, the fuzzy DEMATEL approach has proven effective in modeling interdependencies in fields such as education [50], retail [21], and gamification research [24], yet its application to GRS design evaluation remains scarce. Similarly in one study, a personalized gamified learning recommender system that dynamically adapts game elements to learner profiles was proposed [51], yet such systems rarely use DEMATEL to examine the causal relationships between gamification factors that drive engagement and adoption. This methodological gap restricts the ability to identify which gamification elements act as key drivers and how they interact to shape user outcomes.
To bridge this gap, this study introduces a fuzzy DEMATEL-based evaluation framework for gamified recommender systems. Three layers of novelty are offered. First, four JavaScript React-based prototypes were developed—Points, Badges, and Leaderboards (PBL); Acknowledgments, Objectives, and Progression (AOP); Acknowledgments, Competition, and Time Pressure (ACT); and Acknowledgments, Objectives, and Social Pressure (AOS)—since no readily available systems exist for these theoretically grounded designs [24,26,37,51]. Second, nine user-centric evaluation criteria—Effectiveness, Transparency, Persuasiveness, User Satisfaction, Trust, Usefulness, Ease of Use, Efficiency, and Education—were systematically derived through a PRISMA-guided review of 823 studies, refined to 19 relevant works published between 2013 and 2023. These criteria are widely supported in the prior literature as central to gamification and recommender system evaluation [13,15,17,18,19,20]. Third, fuzzy DEMATEL was applied to capture the causal structure among criteria, distinguishing between driving and dependent factors and thereby revealing the most influential determinants of adoption whereas other studies used DEMATEL to map causal links in a sustainability performance framework, showing its suitability for gamified recommender system evaluation [52].
The significance of this study lies in its integration of theoretical, methodological, and practical contributions. Theoretically, it advances gamification research by operationalizing four distinct GRS prototypes beyond discussions. This study uses a systematic literature review and fuzzy DEMATEL analysis to model complicated interdependencies and provide a reproducible evaluation methodology. The findings suggest design objectives for adaptive, user-centered gamified systems. These priorities include utility, usability, and trust. These ideas help education, e-commerce, and healthcare by encouraging people to use, like, and stay using the service.
2. Related Research
Gamification is the use of game-like elements in non-game contexts. It is often used to increase motivation, involvement, and behavioral adjustment [9,10,11,12,13,14,32]. Its positive effects on learning outcomes, involvement, and user satisfaction in education highlight its importance in boosting effectiveness and educational value [13,15,17,18,19,20]. Systematic evaluations show that gamification can boost motivation and performance, provided that game mechanisms are designed to provide clear feedback and progression routes [10,15,32]. Gamification in workplace technology, retail, and tourism has shown persuasive and trust-enhancing effects on system adoption and use [16,21,22].
Recommender systems (RS) have also become very important on digital platforms because they help users make content their own and deal with too much information [1,2,3,4,6,8]. Collaborative filtering, content-based filtering, and hybrid models have been widely employed in diverse fields such as e-commerce, education, entertainment, and healthcare [2,5,6,7]. Recent research has examined RS via ethical, explanatory, and cognitive perspectives, pinpointing transparency, trust, and efficiency as essential determinants for enduring adoption [1,2,4]. Even with these improvements, it is still hard to keep people interested and find a balance between personalization and user freedom.
Gamified recommender systems (GRS) are a new type of system that combines personalization with motivational design to encourage more people to use them. Proposed applications encompass career advancement systems [29], tourism [22], customized learning trajectories [17,25], and entertainment [26,27]. For example, researchers in [53] developed a gamified word-of-mouth RS to foster customer engagement [24], while researchers in [30] provided a systematic overview of GRS design trends and applications. To structure such designs, prior works have emphasized different gamification strategies: Points, Badges, and Leaderboards (PBL) as classic extrinsic motivators [24,37]; Acknowledgments, Objectives, and Progression (AOP) for transparent progression and competence-based feedback [26]; Acknowledgments, Competition, and Time Pressure (ACT) for efficiency and engagement under competitive conditions [24]; and Acknowledgments, Objectives, and Social Pressure (AOS) for leveraging social accountability and persuasiveness [51]. However, it is important to note that such comprehensive gamified recommender system designs are not readily available in practice, as most existing works remain limited to conceptual discussions or isolated case studies. Developing functional prototypes therefore represent a novel contribution of this study.
To provide more systematic evaluations, researchers have applied multiple-criteria decision-making (MCDM) techniques such as AHP, ANP, and TOPSIS [24,34,35,36,37]. Although these methods facilitate prioritization, they seldom account for the causal interdependencies among evaluation criteria, including trust, ease of use, and efficiency. While traditional multi-criteria methods such as AHP, ANP, TOPSIS, and DEMATEL have been extensively applied, more recent studies advocate integrating sustainability-oriented and knowledge-driven decision frameworks. A study improved DEMATEL by using a threshold-based approach to determine the most influential aspects, which helps recommender system evaluation prioritize key gamification criteria [54].
Building on this perspective, the current research adopts a fuzzy DEMATEL framework to uncover the interdependencies among gamification criteria, extending the methodological line of recent MCDM and AI-enhanced decision studies [1,2,3]. The Decision-Making Trial and Evaluation Laboratory (DEMATEL), particularly in its fuzzy extension, has proven effective in modeling such cause–and–effect structures [55,56,57,58,59]. It has been successfully applied in higher education [49], retail [21], and environmental management [44], but its use in GRS design remains limited. Most existing works either list gamification features or apply comparative frameworks without addressing how these nine critical dimensions interact with specific design strategies (PBL, AOP, ACT, AOS) to shape user experience and adoption [10,11,32].
This review reveals two evident gaps. There are not many complete frameworks on GRS, and most of the research is based on individual case studies. Second, although MCDM approaches have been employed, there has been insufficient emphasis on determining which criteria—such as usefulness, satisfaction, or trust—act as drivers and which function as dependent outcomes. This study introduces a fuzzy DEMATEL-based evaluation framework designed to rectify the deficiencies present in gamified recommender systems. The contributions include the development of four prototypes utilizing JavaScript React (PBL, AOP, ACT, AOS), informed by the existing literature [23,24,26,37], the systematic identification of nine user-centric criteria through a PRISMA-guided review, and the application of fuzzy DEMATEL to elucidate causal interrelationships. These contributions create a strong and repeatable framework for making user-centered gamified recommender systems that can be used in education, e-commerce, and healthcare.
This study aims to identify the principal user-centric factors that facilitate the adoption of gamified recommender systems.
- RQ1: What are the causal relationships among main user-centric criteria?
- RQ2: What elements act as principal catalysts for the implementation of gamified recommender systems?
- RQ3: In what ways do various gamified designs (PBL, AOP, ACT, AOS) affect these relationships?
3. Materials and Methods
This study followed a systematic multi-step methodology to evaluate gamified recommender system (GRS) designs using fuzzy DEMATEL. The approach combined a systematic literature review for criteria identification, prototype development for alternative designs, decision makers’ elicitation for evaluation, and fuzzy DEMATEL analysis for cause–effect modeling.
3.1. Research Design
A multi-criteria decision-making (MCDM) framework was adopted, as such an approach provides structured tools for evaluating complex socio-technical systems with multiple interacting factors. The fuzzy Decision-Making Trial and Evaluation Laboratory (fuzzy DEMATEL) was selected due to its ability to model interdependencies among criteria and distinguish between driving and dependent factors.
3.2. Identification of Criteria
To evaluate gamified recommender systems (GRS), this study adopted a systematic literature review approach guided by the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) framework [60]. A total of 823 records were initially identified from IEEE Xplore, ScienceDirect, Scopus, and Web of Science. After applying inclusion and exclusion criteria, duplicate removal, and language filtering, 19 primary studies published between 2013 and 2023 were retained for full-text analysis.
From these 19 investigations, recurrent characteristics of user experience and system quality were extracted using a systematic coding process. User engagement, system adoption, and gamification results were the targets of a thorough literature review. Effectiveness, Transparency, Persuasiveness, Trust, Usefulness, Ease of Use, Efficiency, and Education are the nine user-focused evaluation criteria that were identified during the investigation. All of the criteria were based on research that actually happened in the real world. To determine its efficacy, we consulted research that examined engagement with gamification features and personalization [26,35,53,61,62]. Clarity and interpretability in gamified recommendation system processes were the focus of studies that eventually gave rise to transparency [23,25,27,63,64].
Research on motivational and behavioral change mechanisms [16,29,65,66,67] acknowledges persuasiveness.
Feedback dashboard and educational system studies focused on user satisfaction [17,68].
Gamification frameworks identified ease of use and usefulness in large-scale, user-friendly system designs [68].
Research on motivational and behavioral change pathways identified persuasiveness [16,29,65,66,67].
Efficiency was supported by studies emphasizing algorithmic accuracy and learning optimization [17,22].
Education was confirmed by gamification in MOOCs and e-learning contexts [67].
The final selection of criteria thus represents a comprehensive synthesis of recurring evaluation dimensions across multiple contexts, including education, tourism, healthcare, and smart cities. These nine criteria were subsequently employed in the fuzzy DEMATEL framework to capture causal interrelationships and identify the most influential dimensions in the evaluation of gamified recommender systems.
3.3. Developing Four Gamified Recommender System Designs
From the prior literature on gamification design frameworks [23,24,26], four gamified recommender system designs were conceptualized, each combining different game mechanics that personalize gamification based on empirical data from learners’ real experiences. The designs use basic motivational ideas like competence, autonomy, relatedness, and social influence to create a theory-based framework for customizing gamified learning environments. These designs show that combinations of elements fit with established motivational constructs and improve personalization by connecting gamification design to learners’ intrinsic motivation and contextual characteristics [26]. The choice of English language learning as the focus area stems from its worldwide demand and the existence of explicit, quantifiable goals, such as vocabulary acquisition, grammatical proficiency, and reading comprehension. Students often have trouble staying motivated and practicing regularly, which makes this setting a good place to use gamification. Recommender systems tailor content to individual learner requirements, while gamification enhances motivation, feedback, and perseverance. This domain is useful in real life and fits well with the nine evaluation criteria used in this study. We used the JavaScript React environment to write code. The four designs of the gamified recommender system are as follows (see Appendix A for full design details):
Design 1: Points, Badges, and Leaderboards (PBL)—based on Game Design Theory, specifically traditional gamification mechanics—has demonstrated the ability to enhance extrinsic motivation (see Figure 1).
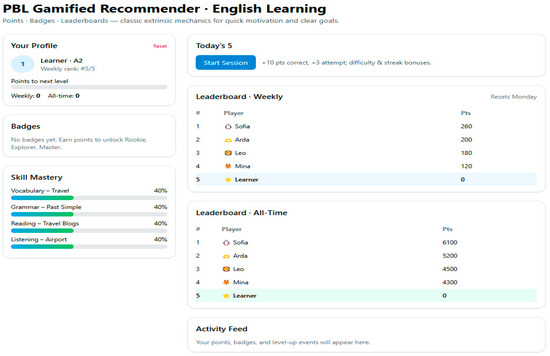
Figure 1.
Design 1 screenshot of PBL GRS.
Design 2: Acknowledgments, Objectives, and Progression (AOP) places a strong emphasis on Self-Determination Theory (SDT) by recognizing achievement and setting goals (Figure 2).
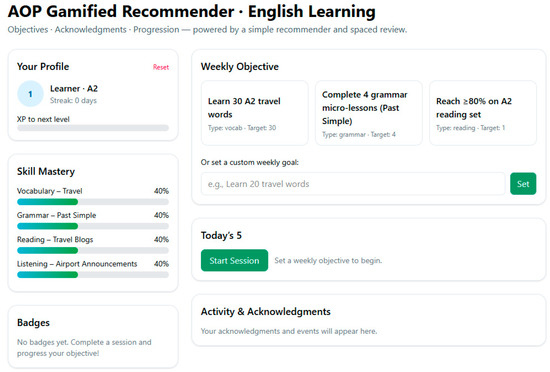
Figure 2.
Design 2 screenshot of AOP GRS.
Design 3: Acknowledgments, Objectives, and Social Pressure (AOS)—builds on Social Influence Theory, highlighting peer comparison and social accountability (see Figure 3).
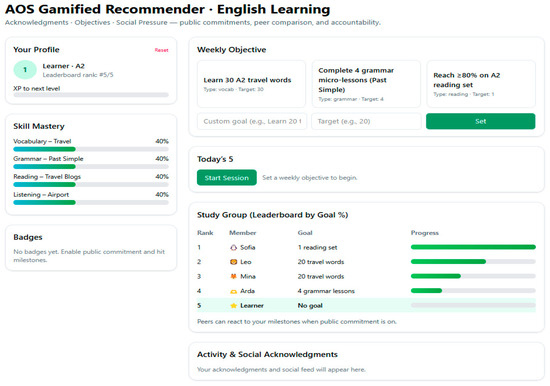
Figure 3.
Design 3 screenshot of AOS GRS.
Design 4: Acknowledgments, Competition, and Time Pressure (ACT) is based on Behaviorist Learning Theory, emphasizing that reinforcement and external stimuli, such as competition and urgency, influence behavior (Figure 4).
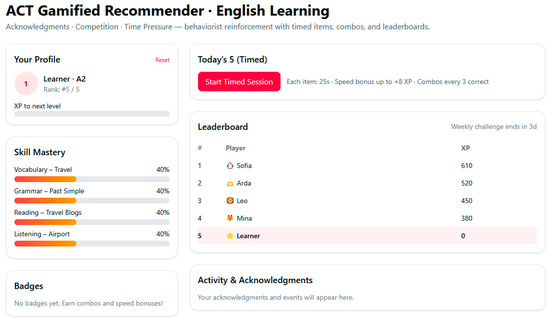
Figure 4.
Design 4 screenshot of ACT GRS.
The designs show different ways to motivate people in gamified settings and can be used as different ways to add gamification to recommendation systems.
Table 1 presents a comparison of four features of gamified recommender systems.

Table 1.
Gamification comparisons across four recommender system designs.
3.4. Data Collection
3.4.1. Participants
A group of 25 undergraduate students made the decisions. They had already used four gamified recommender systems in their classes and projects. Undergraduate participants were selected not as professional practitioners, but because they represent the end-users of educational recommender systems, aligning with the study’s context. The demographic characteristics of the 25 participants exhibit a combination of diversity and relevance to the study context. Of the 25 people who took part, 16 were males (64%) and 9 were females (36%). There were two groups of participants based on their academic backgrounds: Computer Information Systems, which had 14 participants (56%), and Management Information Systems, which had 11 participants (44%). Ten of the participants (40%) said they used recommender systems very often, and seven (28%) said they used them often. Five students (20%) used them less often, and three (12%) used them extremely rarely. Participants had different levels of platform experience, according to the data. Seven (28%) used Coursera and Khan Academy, six (24%) used Netflix and Amazon Prime Video, five (20%) used Spotify, four (16%) used Duolingo to learn a new language, and smaller groups used Strava (8%) and Fitbit (4%) to reach fitness goals.
This distribution highlights both the diversity of systems experienced by the participants and their practical awareness of recommender technologies, ensuring that their evaluations provide comprehensive and relevant insights for assessing gamified recommender systems.
3.4.2. Procedure
After ethical approval was granted by the researchers’ university ethical board on 25 April 2024 with the application number NEU/AS/2024/214, the decision makers tried four gamified recommender system designs throughout the coursework. They were presented with an evaluation survey for each gamified recommender system design. The decision makers provided pairwise comparisons of nine criteria using a linguistic questionnaire for each GRS design (e.g., “no influence,” “low influence,” “high influence”). Responses were aggregated into fuzzy direct-influence matrices using the geometric mean method to obtain the final cause–effect diagrams for each design.
3.5. Fuzzy DEMATEL Method
Let represent the evaluation criteria and the design alternatives.
Step 1—Define Criteria and Alternatives
Identify the nine evaluation criteria and the four designs (AOP, ACT, AOS, PBL).
Step 2—Collect Expert Evaluations
Experts provide pairwise influence judgments using linguistic terms mapped to triangular fuzzy numbers (TFNs):
For each decision maker :
Step 3—Aggregate Expert Opinions (Geometric Mean)
Step 4—Defuzzification (Centroid Method)
This produces the crisp direct-relation matrix .
Step 5—Normalize the Direct-Relation Matrix
Step 6—Compute the Total-Relation Matrix
Normalization guarantees , so the series converges ().
Step 7—Determine the Threshold Value
Step 8—Cause–Effect Analysis
Compute row and column sums:
Then calculate prominence and relation:
Criteria with belong to the cause group, and those with to the effect group. The pairs are plotted to generate the cause–effect diagram.
4. Results
Following the fuzzy DEMATEL procedure described in Section 3.5, the analysis for each gamified recommender design—Points, Badges, and Leaderboards (PBL); Acknowledgments, Objectives, and Progression (AOP); Acknowledgments, Competition, and Time Pressure (ACT); and Acknowledgments, Objectives, and Social Pressure (AOS)—was carried out in eight computational steps aligned with Equations (1)–(8).
Step 1–2. Expert Evaluations and Linguistic Judgments
The experts were presented with the following rating scale for each of the four different gamified recommender designs: For four gamified recommender system that experts earlier tested, they evaluated each system by comparing the impact of following criteria (Effectiveness, Transparency, Persuasiveness, User Satisfaction, Trust, Usefulness, Ease of Use, Efficiency, and Education) over each other using the rating scale (No influence (NO), Very Low influence (VL), Low influence (L), High influence (H), Very High influence (VH), given in Table 2). The sample evaluation rating scale is given below:

Table 2.
Rating scale for gamified recommender system design.
C1: Effectiveness: is the Gamified Recommendation System effective in achieving its intended aims?
C2: Transparency: are Gamified Recommendation Systems visible and open in the way they work?
C3: Persuasiveness: does the Gamified Recommendation System influence and motivate users?
C4: User Satisfaction: are you satisfied with the performance of the Gamified Recommendation System?
C5: Trust: is the Gamified Recommendation System stable and consistent?
C6: Usefulness: is the Gamified Recommendation System a helpful system?
C7: Ease of use: is the Gamified Recommendation System easy to use?
C8: Efficiency: does the Gamified Recommender System effectively use resources to achieve its purpose?
C9: Education: does the Gamified Recommendation System foster successful learning outcomes?
Twenty-five decision makers (DMs) assessed the pairwise causal influence of each criterion on using the five-term linguistic scale defined as No, Very Low, Low, High, and Very High, represented by triangular fuzzy numbers (TFNs) shown in Table 2 which defines the linguistic-to-TFN mapping applied to all subsequent analyses. Linguistic fuzzy scale for expert judgments were used to construct the individual matrices.
Each expert’s judgments generated a fuzzy direct-relation matrix as described in Equation (1), where diagonal elements were fixed to (0, 0, 0).
Because all designs share the same evaluation criteria, four parallel sets of matrices were created—one for each gamified design.
Step 3. Aggregation of Expert Opinions
The twenty-five individual matrices were aggregated through the geometric-mean operator (Equation (2)) to obtain the group fuzzy direct-relation matrix .
After defuzzification via the centroid method (Equation (3)), the crisp direct-relation matrices were generated for each design.
The mean causal influences of each criterion are computed in step 3.
Step 4. Normalization of the Direct-Relation Matrix
To guarantee comparability and convergence, each X was normalized according to Equation (4), resulting in the normalized fuzzy direct-relation matrices N.
The normalized matrices, essential for total-relation computation were performed in step 4.
Step 5. Computation of the Total-Relation Matrix
Utilizing Equation (5), , each normalized matrix was expanded to encompass both direct and indirect influences. The fuzzy total-relation matrices are computed.After the defuzzification process, the resulting crisp total-relation matrices were generated in step 5.
Step 6. Threshold Determination and Network Relation Map (NRM)
For each design, the average of all off-diagonal values was used as the threshold (Equation (6)).
Relations below were omitted to emphasize significant causal influences.
The thresholded total relation matrices for each design were calculated in step 6. The corresponding network relation maps (NRMs), which visually depict causal linkages among criteria, are illustrated in Figure 5 (PBL), Figure 6 (AOP), Figure 7 (AOS), and Figure 8 (ACT).
Step 7. Cause–Effect Computation
The sums of rows and columns of -provided and (Equation (7)). Prominence () and relation () were subsequently derived (Equation (8)).
The final output matrices were computed using step 7.
Step 8. Comparative and Interpretive Analysis
Positive values show cause criteria. Negative values denote effect criteria.
In all four designs, Perceived Usefulness (C6) and Ease of Use (C7) consistently emerge as primary causal factors influencing system behavior, while Engagement (C8) and Satisfaction (C9) serve as outcome criteria.
Among the designs, AOP exhibits the strongest overall interdependence, suggesting that acknowledgment and progression mechanisms amplify systemic influence propagation, while ACT shows moderate causal density governed by competition and time pressure components.
4.1. Results for Design 1: Points, Badges and Leaderboards (PBL)
Table 3, below, indicates the direct-relation matrix, which is the same as the pairwise comparison matrix of the decision makers in Design 1.

Table 3.
The direct-relation matrix—Design 1.
Table 4, below, shows the normalized fuzzy direct-relation matrix of Design 1.

Table 4.
The normalized fuzzy direct-relation matrix—Design 1.
Table 5, below, shows the fuzzy total-relation matrix of Design 1.

Table 5.
The fuzzy total-relation matrix—Design 1.
Table 6, below, shows the crisp total-relation matrix of Design 1.

Table 6.
The crisp total-relation matrix—Design 1.
In this design, the threshold value is equal to 0.533 (see Table 7).

Table 7.
The crisp total-relationships matrix by considering the threshold value—Design 1.
Table 8, below, shows the final output for Design 1.

Table 8.
The final output—Design 1.
The cause–effect diagram for Design 1 (PBL) is given below in Figure 5.
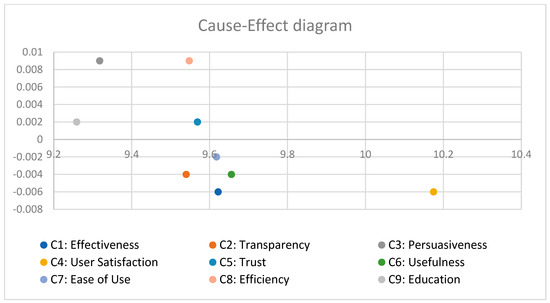
Figure 5.
Cause–effect diagram—Design 1.
4.2. Results for Design 2: Acknowledgments, Objectives, and Progression (AOP)
Table 9, below, indicates the direct-relation matrix, which is the same as the pairwise comparison matrix of the decision makers in Design 2.

Table 9.
The direct-relation matrix—Design 2.
Table 10, below, shows the normalized fuzzy direct-relation matrix of Design 2.

Table 10.
The normalized fuzzy direct-relation matrix—Design 2.
Table 11, below, shows the fuzzy total-relation matrix of Design 2.

Table 11.
The fuzzy total-relation matrix—Design 2.
Table 12, below, shows the crisp total-relation matrix of Design 2.

Table 12.
The crisp total-relation matrix—Design 2.
In this design, the threshold value is equal to 0.629 (see Table 13).

Table 13.
The crisp total-relationships matrix by considering the threshold value—Design 2.
The final output for Design 2 is shown in Table 14 below.

Table 14.
The final output—Design 2.
The cause–effect diagram for Design 2 (AOP) is shown in Figure 6.
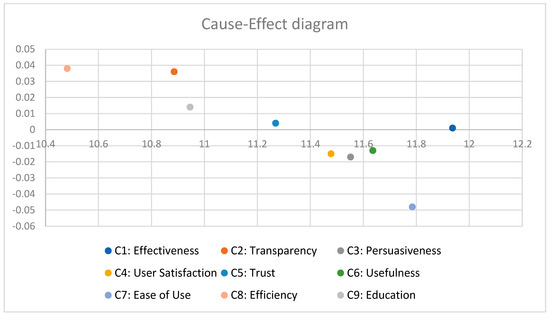
Figure 6.
Cause–effect diagram—Design 2.
4.3. Results for Design 3: Acknowledgments, Objectives, and Social Pressure (AOS)
Table 15 below indicates the direct-relation matrix, which is the same as the pairwise comparison matrix of the decision makers in Design 3.

Table 15.
The direct-relation matrix—Design 3.
Table 16, below, shows the normalized fuzzy direct-relation matrix of Design 3.

Table 16.
The normalized fuzzy direct-relation matrix—Design 3.
Table 17, below, shows the fuzzy total-relation matrix of Design 3.

Table 17.
The fuzzy total-relation matrix—Design 3.
Table 18, below, shows the crisp total-relation matrix of design 3.

Table 18.
The crisp total-relation matrix—Design 3.
In this design, the threshold value is equal to 0.472 (see Table 19).

Table 19.
The crisp total-relationships matrix by considering the threshold value—Design 3.
The final output was given in Table 20 below.

Table 20.
The final output—Design 3.
The cause–effect diagram for Design 3 is given in Figure 7 below.
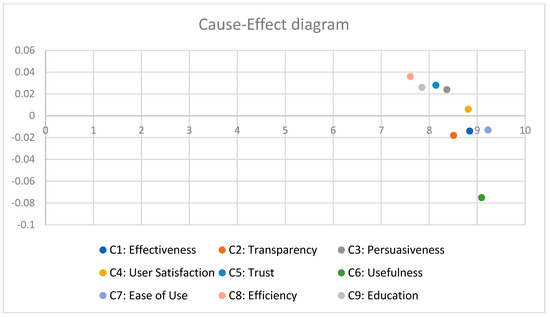
Figure 7.
Cause–effect diagram—Design 3.
4.4. Results for Design 4: Acknowledgments, Competition, and Time Pressure (ACT)
Table 21, below, indicates the direct-relation matrix, which is the same as the pairwise comparison matrix of the decision makers in Design 4.

Table 21.
The direct-relation matrix—Design 4.
Table 22, below, shows the normalized fuzzy direct-relation matrix of Design 4.

Table 22.
The normalized fuzzy direct-relation matrix—Design 4.
Table 23, below, shows the fuzzy total-relation matrix of Design 4.

Table 23.
The fuzzy total-relation matrix—Design 4.
Table 24, below, shows the crisp total-relation matrix of Design 4.

Table 24.
The crisp total-relation matrix—Design 4.
In this design, the threshold value is equal to 0.419 (see Table 25).

Table 25.
The crisp total-relationships matrix by considering the threshold value—Design 4.
The final output for design4 is given in Table 26 below:

Table 26.
The final output—Design 4.
The cause–effect diagram for Design 4 is shown in Figure 8 below.
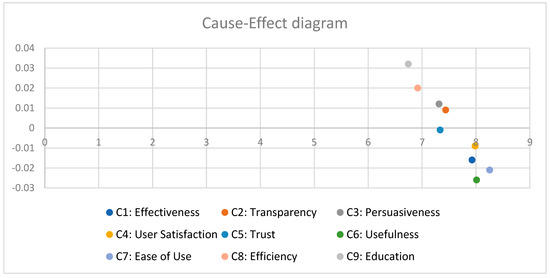
Figure 8.
Cause–effect diagram—Design 4.
4.5. Validation
Validations was ensured through the following:
- Aggregation of expert judgments to reduce individual bias.
- Threshold sensitivity analysis.
Threshold sensitivity analysis looks at how changes to a model’s input parameters, especially those that are close to a set threshold, change the model’s output. It helps to find the values of the parameters that cause the model’s behavior or decision-making to change a lot. In short, it is about figuring out how much a model’s results change when something changes around a critical point. In fuzzy DEMATEL, the threshold determines which relationships are sufficiently robust to be represented in the causal diagram. Higher thresholds make networks that are simpler and less connected, while lower thresholds make networks that are more connected.
The thresholds for the four designs were as follows: Design 1 = 0.533, Design 2 = 0.629, Design 3 = 0.472, and Design 4 = 0.419.
Design 2 (0.629): a simpler map that only shows the most important connections.
Design 1 (0.533): a balanced view that shows both major and minor effects.
Design 3 (0.472): a denser network with more indirect effects.
Design 4 (0.419): most connections are still there, but they are less clear.
Results showed that thresholds were stable, which confirmed that criteria and causal groupings were always important.
Thresholds used were D1 = 0.533, D2 = 0.629, D3 = 0.472, D4 = 0.419; sensitivity checks showed stable (D + R) orderings across plausible ranges.
- 3.
- Findings were validated through a comparison with previous applications of fuzzy DEMATEL in education, retail, and gamification. Researchers in [49] showed that it worked well to explain the main things that affect students’ choices of courses in school. In retail, [21] showed that it works well to find the most important things to consider when shopping in the metaverse. In gamification research, scholars in [23] emphasized its significance in examining intricate interrelations among gamification components. This study confirms the efficacy of fuzzy DEMATEL as a robust method for identifying cause–effect relationships in various domains, including the creation of gamified recommender systems.
5. Discussion
Fuzzy DEMATEL was used to evaluate four gamified recommender system architectures. The results helped demonstrate how things evolve and interact. Effectiveness, Transparency, Persuasiveness, User Satisfaction, Trust, Usefulness, Ease of Use, Efficiency, and Education were evaluated. The results show that various criteria have different effects and cause-and-effect correlations.
Two things made people satisfied, productive, and trustworthy: usefulness (C6) and ease of use (C7). This is consistent with previous research that demonstrated the significance of perceived usefulness and usability in technology adoption [21,24]. Trust (C5) functioned as a mediator, shaped by transparency and usability, thereby enhancing happiness and effectiveness, in alignment with prior research in education [51] and retail [21].
Satisfaction (C4), efficacy (C1), and education (C9) were the outcome criteria that were most affected by upstream causes. This pattern is in line with earlier research on gamification, which found that external factors boost short-term satisfaction but long-term effects depend on internal alignment [24]. C2 (transparency) and C8 (efficiency) had a moderate effect, especially on designs that are time-sensitive and deal with social issues. Persuasiveness (C3) affected designs that were based on competition and peers, which supports earlier research that showed that persuasive elements have a big impact on engagement [24].
Design-level comparisons showed that each group had a unique motivational pathway.
PBL (Design 1) was compelling but poor for learning and trust because it relied on external motivators. PBL increases short-term motivation, but this effect is not sustained, as shown in [23,24].
The most even construction was AOP Design 2. It was valuable and easy to use, improving teaching and learning. Its higher threshold (0.629) exhibited excellent causal clarity, supporting evidence indicating that explicit goals and controlled feedback improve long-term learning [51].
AOS (Design 3) employed social influence, so being honest and holding your friends accountable made people trust you and believe what you say. Education and retail research show that social approbation motivates people to try new things, reinforcing our understanding. It depended on teamwork, hence it did not work as well as prior methods.
ACT (Design 4) was more persuasive but less trustworthy and gratifying since it highlighted competitiveness and urgency. A previous study has shown that intense competition might lower intrinsic motivation [24]. The dense but unclear causal network with a threshold of 0.419 demonstrated this.
Overall, usefulness and user-friendliness are the most essential criteria for all designs, whereas satisfaction, efficacy, and education are the most important outcomes. Clarity and long-term attention make AOP the most pedagogically sustainable design. PBL and ACT may drive you temporarily, but they may damage trust and academic value. Working together helps individuals learn and stay interested, therefore AOS works best.
These results demonstrate that gamified recommender systems must go beyond points and competition. It needs goal setting, growth, and social transparency to keep people utilizing and making them work [24,51,53].
5.1. Limitations
The study has number of limitations. The study used undergraduate students as end-users to evaluate the gamified recommender systems, which may limit their applicability to younger learners, professional users, or varied cultural situations. Second, four gamification designs—PBL, AOP, AOS, and ACT—based on different theoretical frameworks were examined. These strategies are common, however, hybrid models and other designs may produce different results. The fuzzy DEMATEL approach involves subjective expert opinions. Even though group aggregation reduced individual bias, findings depend on participant perceptions. The study examined English language acquisition, however, applying the same paradigm to healthcare, e-commerce, or workplace training may provide different results. Despite their potential impact on real-world adoption, long-term engagement, cognitive load, and emotional responses were excluded from the analysis due to systematic review standards.
5.2. Implications of the Study
This work has various theoretical and practical implications. Game-based recommender system designs (AOP, ACT, AOS, PBL) are compared to show how different learning and behavioral theories affect user perception and system efficacy. This study shows that decision-making models can simplify complex design attribute interactions by integrating fuzzy DEMATEL with carefully stated criteria.
The findings can help educators, developers, and system designers integrate gamification into English language learning recommender systems. Finding causal and effect criteria can help you design better by ensuring that recognition, progress, competition, and social influence are leveraged to motivate learners and improve system usability. The methodology can be adjusted to numerous educational environments because the results are consistent across threshold levels.
5.3. Recommendations for Future Research
Based on the current results, several avenues for future research are proposed. The research could be augmented by assessing the suggested gamified recommender system designs with a broader and more heterogeneous learner demographic, inclusive of diverse educational levels and cultural contexts, to enhance generalizability. Subsequent research ought to include longitudinal studies to evaluate the enduring impacts of gamification elements on learner engagement, performance, and retention. Third, hybrid evaluation methods that combine fuzzy DEMATEL with other multi-criteria decision-making techniques, like ANP, TOPSIS, or fuzzy AHP, may give us better information about how important each criterion is compared to the others. Along with the fuzzy DEMATEL framework used in this study, future research could use other multi-criteria decision-making methods to confirm or build on these results. Distance-based methods, like the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), make it easier to rank gamification strategies based on how close they are to the best engagement results.
Utility-based methods like the Analytic Hierarchy Process (AHP) give you structured pairwise preferences that show what learners really care about. New hybrid and range-sensitive models, such as the Ranking based on the Distances and Range (RADAR) method, also make it possible to combine robustness with interpretability [69]. Using and comparing these methods on bigger datasets might make the analysis more reliable and give us a better picture of how causal–evaluative relationships work in the creation of gamified recommender systems. Generalizability may be improved by comprehensive empirical validation using learner datasets from varied educational contexts and longitudinal assessments. Using causal modeling and forecasting methodologies like machine learning-based recommender models helps us understand how gamification dynamics evolve over time and effect long-term learner engagement. The study’s methods show that making decisions based on more than one factor can help with complex rating problems. Fuzzy DEMATEL shows how different factors affect gamified system like how gray-correlation-based hybrid MCDM models help choose sustainable materials [70]. Future research should combine subjective user-centric elements with objective performance metrics like system usage statistics, response precision, and learning advancement indicators to improve fuzzy DEMATEL analysis of causal relationships’ reliability and external validity. To reduce subjectivity and improve causal inferences in gamified recommender system evaluations, future research should combine linguistic expert assessments with objective system interaction data like activity logs, completion rates, and engagement metrics. The paradigm could be effective in STEM education, job training, and workplace learning, not just in English. Future research should examine adaptive gamification, where system components dynamically adjust to learners’ profiles, preferences, and progress to improve personalized and effective instruction.
6. Conclusions
This research employed the fuzzy DEMATEL method to evaluate four sophisticated gamified recommender system designs for English language acquisition. A systematic review evaluated designs using nine criteria: Effectiveness, Transparency, Persuasiveness, Satisfaction, Trust, Usefulness, Ease of Use, Efficiency, and Education. Gamification strategies like Points, Badges, Leaderboards (PBL), Acknowledgments, Objectives, Progression (AOP), Acknowledgements, Objectives, Social Pressure (AOS), and Acknowledgements, Competition, Time Pressure (ACT) vary in clarity, motivation, and social influence.
This study used fuzzy DEMATEL to identify the main user-centric factors influencing GRS adoption. The proposed approach answered all three research questions.
The nine user-centric criteria in RQ1 showed unique causal linkages, demonstrating a hierarchy of causal and effective factors. Perceived Usefulness (C6) and Ease of Use (C7) consistently influenced Engagement (C8) and Satisfaction (C9) outcome variables. In all four gamified recommender system designs, Perceived Usefulness (C6) and Ease of Use (C7) were the main causal factors. These factors had minimal effects across configurations, but their relative importance and causal direction remained unchanged. This suggests that these parameters predict user engagement and adoption beyond design effects.
In response to RQ2, the analysis found factors C6 and C7 to be the main drivers of GRS adoption due to their predominance and positive correlation. This shows that usability and perceived value are essential for system engagement.
A comparison of four gamified designs—PBL, AOP, AOS, and ACT—showed that the Acknowledgments, Objectives, and Progression (AOP) design improved network connectivity and causal balance in response to RQ3. However, competition and time constraint in the ACT design had localized consequences.
Due to its high threshold, Design 2 had the greatest causal structure, but Design 1 was more egalitarian. The results are strong since causal network densities did not affect criteria importance across thresholds. Research shows that fuzzy DEMATEL efficiently analyzes gamification criteria’s interrelationships, making educational recommender systems easier to construct. Methodological comprehension is improved by providing fuzzy DEMATEL in gamified environments and providing practical guidance for adopting learner-centered gamification mechanics. As one of the first systematic attempts to combine gamification design with fuzzy DEMATEL in recommender systems, this study offers scholars and practitioners a new perspective. The study achieved its goals by (i) explaining causal interdependencies among user-centric criteria, (ii) identifying the most important adoption determinants, and (iii) showing how gamified design configurations alter these linkages. Fuzzy DEMATEL provides a structured approach for analyzing user-centric gamification strategies and improving system design. The study shows that fuzzy DEMATEL effectively investigates gamification criteria interdependencies, enabling educational recommender system creation. Methodological approaches are improved by testing fuzzy DEMATEL in gamified systems and offering practical guidance for choosing learner-centered gamification mechanics.
Importantly, this is among the first studies to systematically integrate gamification design with fuzzy DEMATEL for recommender systems, providing a novel perspective for both researchers and practitioners.
Author Contributions
Corresponding author, S.B., contributed to the manuscript’s theoretical development, analysis, interpretation, and writing. Conceptualization, S.B.; data curation, S.B.; formal analysis, A.M.T.; Investigation, S.B. and A.M.T.; Methodology, S.B.; Project administration, A.M.T.; resources, S.B. and A.M.T.; software use, S.B. and A.M.T.; supervision, S.B.; validation, S.B.; visualization, A.M.T.; writing—original draft, A.M.T.; writing—review and editing, S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Every ethical standard for research was followed in this article. The University’s Scientific Research Ethics Committee granted the study’s ethical approval 25/04/2024 (NEU/AS/2024/214). The participation was completely voluntary, and that consent might be revoked at any moment was also made clear to the participants.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| AHP | Analytic Hierarchy Process |
| ANP | Analytic Network Process |
| ACT | Acknowledgments, Competition, and Time Pressure |
| AOP | Acknowledgments, Objectives, and Progression |
| AOS | Acknowledgments, Objectives, and Social Pressure |
| DEMATEL | Decision-Making Trial and Evaluation Laboratory |
| DM | Decision Maker |
| GRS | Gamified Recommender System |
| MCDM | Multi-Criteria Decision-Making |
| PBL | Points, Badges, and Leaderboards |
| RS | Recommendation System |
| TFN | Triangular Fuzzy Number |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| XP | Experience Points |
Appendix A
Four different React-based prototypes of gamified recommender systems were made to back up the empirical analysis. Each system has a shared core that includes a lesson pool, an item recommendation function, mastery tracking, and local persistence. However, they all use different motivational mechanics that fit with gamification frameworks. There is a short description of each prototype below, followed by some common technical issues.
Appendix A.1. PBL (Points, Badges, Leaderboards)
The PBL prototype gives points for correct answers, unlocks tiered badges at certain levels, and keeps track of both weekly and all-time scores on leaderboards. Rival scores change over time, which makes the competition stronger. This design emphasizes success and comparison for motivation.
Appendix A.2. AOP (Acknowledgments, Objectives, Progression)
Toasts, feedback messages, set goals (such “complete five vocabulary lessons”), streak counters, XP accrual, and level advancement are part of the AOP prototype. This design motivates people by making them feel like they are progressing and in control.
Appendix A.3. AOS (Acknowledgments, Objectives, Social Pressure)
The AOS prototype uses personal objectives, public goal pledges, and a collective leaderboard to hold everyone accountable. Acknowledgements boost accomplishments, while the leaderboard shows how people compare to each other, which activates social motivation mechanisms.
Appendix A.4. ACT (Acknowledgments, Competition, Time Pressure)
The ACT prototype has a strict countdown timer (25 s per item), speed-based bonuses, and leaderboards that show who is winning. Acknowledgments prompt quick replies, and time pressure increases engagement by creating a sense of urgency and competition.
Appendix A.5. Shared Technical Features
Recommender Engine: All designs use a simple scoring function that takes mastery, recency, objective fit, and penalties for repeating tasks into account.
Updating Mastery: Mastery of an item goes up after correct answers and down over time, which makes sure that reinforcement is adaptive.
Persistence: To make sure that sessions continue, user progress, leaderboards, and goals are all saved in local storage.
A variety of items: Items include multiple-choice questions and short-answer tasks that test vocabulary, grammar, listening, and reading skills.
Appendix A.6. Implementation Notes and Improvements
Several improvements were found during testing of the prototype:
Reproducibility: The current use of random increments in rival/peer progress on leaderboards should be changed to seeded or fixed increments for reproducibility.
Mastery Functions Consistency: To keep methodological consistency, small differences in coefficients between designs should be smoothed out.
Unified Item Checking: A single function should make sure that all types of items have the same user input (for example, trimming and lowercasing).
Objective Progress Persistence: Updates to objectives and streaks should occur before acknowledgment messages to avoid race conditions.
Accessibility Enhancements: Adding ARIA labels for feedback messages and timers will improve usability for all learners.
Refactoring: Common functions (Gaussian, clamp, skill definitions) can be modularized to reduce redundancy across prototypes.
References
- Beheshti, A.; Yakhchi, S.; Mousaeirad, S.; Ghafari, S.M.; Goluguri, S.R.; Edrisi, M.A. Towards cognitive recommender systems. Algorithms 2020, 13, 176. [Google Scholar] [CrossRef]
- He, X.; Liu, Q.; Jung, S. The impact of recommendation system on user satisfaction: A moderated mediation approach. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 448–466. [Google Scholar] [CrossRef]
- Isinkaye, F.O.; Folajimi, Y.O.; Ojokoh, B.A. Recommendation systems: Principles, methods and evaluation. Egypt. Inform. J. 2015, 16, 261–273. [Google Scholar] [CrossRef]
- Jannach, D. Evaluating conversational recommender systems: A landscape of research. Artif. Intell. Rev. 2023, 56, 2365–2400. [Google Scholar] [CrossRef]
- Milano, S.; Taddeo, M.; Floridi, L. Recommender systems and their ethical challenges. AI Soc. 2020, 35, 957–967. [Google Scholar] [CrossRef]
- Roy, D.; Dutta, M. A systematic review and research perspective on recommender systems. J. Big Data 2022, 9, 45. [Google Scholar] [CrossRef]
- Nunes, I.; Jannach, D. A systematic review and taxonomy of explanations in decision support and recommender systems. User Model. User Adapt. Interact. 2017, 27, 393–444. [Google Scholar] [CrossRef]
- Pathak, B.; Garfinkel, R.; Gopal, R.; Venkatesan, R.; Yin, F. Empirical Analysis of the Impact of Recommender Systems on Sales. J. Manag. Inf. Syst. 2010, 27, 159–188. [Google Scholar] [CrossRef]
- Alsawaier, R.S. The effect of gamification on motivation and engagement. Int. J. Inf. Learn. Technol. 2018, 35, 56–79. [Google Scholar] [CrossRef]
- Dichev, C.; Dicheva, D. Gamifying education: What is known, what is believed and what remains uncertain: A critical review. Int. J. Educ. Technol. High. Educ. 2017, 14, 9. [Google Scholar] [CrossRef]
- Hamari, J.; Koivisto, J.; Sarsa, H. Does gamification work? A literature review of empirical studies on gamification. In Proceedings of the 47th Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 6–9 January 2014; pp. 3025–3034. [Google Scholar] [CrossRef]
- Huotari, K.; Hamari, J. A definition for gamification: Anchoring gamification in the service marketing literature. Electron. Mark. 2017, 27, 21–31. [Google Scholar] [CrossRef]
- Smiderle, R.; Rigo, S.J.; Marques, L.B.; Coelho, J.A.P.M.; Jaques, P.A. The impact of gamification on students’ learning, engagement and behavior based on their personality traits. Smart Learn. Environ. 2020, 7, 3. [Google Scholar] [CrossRef]
- Christopoulos, A.; Mystakidis, S. Gamification in education. Encyclopedia 2023, 3, 1223–1243. [Google Scholar] [CrossRef]
- Gachkova, M.; Somova, E.; Gaftandzhieva, S. Gamification of courses in the e-learning environment. IOP Conf. Ser. Mater. Sci. Eng. 2020, 878, 012035. [Google Scholar] [CrossRef]
- Nikolakis, N.; Siaterlis, G.; Alexopoulos, K. A machine learning approach for improved shop-floor operator support using a two-level collaborative filtering and gamification features. Procedia CIRP 2020, 93, 455–460. [Google Scholar] [CrossRef]
- Raftopoulou, N.-M.; Pallis, P.L. Gamified learning systems’ personalized feedback report dashboards via custom machine learning algorithms and recommendation systems. Sociol. Study 2023, 13, 127–139. [Google Scholar] [CrossRef]
- Park, S.; Kim, S. Leaderboard design principles to enhance learning and motivation in a gamified educational environment: Development study. JMIR Serious Games 2021, 9, e14746. [Google Scholar] [CrossRef]
- Barragán-Pulido, S.; Barragán-Pulido, M.L.; Alonso-Hernández, J.B.; Castro-Sánchez, J.J.; Rabazo-Méndez, M.J. Development of students’ skills through gamification and serious games: An exploratory study. Appl. Sci. 2023, 13, 5495. [Google Scholar] [CrossRef]
- Cubela, D.; Rossner, A.; Neis, P. Using problem-based learning and gamification as a catalyst for student engagement in data-driven engineering education: A report. Educ. Sci. 2023, 13, 1223. [Google Scholar] [CrossRef]
- Sharma, L.; Kaushik, N. Shaping virtual retail: Identifying key influences in metaverse shopping with fuzzy DEMATEL. J. Metaverse 2025, 5, 51–63. [Google Scholar] [CrossRef]
- Nuanmeesri, S. Development of community tourism enhancement in emerging cities using gamification and adaptive tourism recommendation. J. King Saud. Univ. Comput. Inf. Sci. 2022, 34, 8549–8563. [Google Scholar] [CrossRef]
- Rodrigues, L.; Toda, A.M.; Oliveira, W.; Palomino, P.T.; Vassileva, J.; Isotani, S. Automating gamification personalization to the user and beyond. IEEE Trans. Learn. Technol. 2022, 15, 199–212. [Google Scholar] [CrossRef]
- Schöbel, S.M.; Janson, A.; Söllner, M. Capturing the complexity of gamification elements: A holistic approach for analysing existing and deriving novel gamification designs. Eur. J. Inf. Syst. 2020, 29, 641–668. [Google Scholar] [CrossRef]
- Su, C.H. Designing and developing a novel hybrid adaptive learning path recommendation system for a gamification mathematics geometry course. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 2275–2298. [Google Scholar] [CrossRef]
- Tondello, G.F.; Orji, R.; Nacke, L.E. Recommender systems for personalized gamification. In Proceedings of the 25th Conference on User Modeling, Adaptation and Personalization (UMAP 2017), Bratislava, Slovakia, 9–12 July 2017; pp. 425–430. [Google Scholar] [CrossRef]
- Zhao, Z.; Arya, A.; Orji, R.; Chan, G. Effects of a personalized fitness recommender system using gamification and continuous player modeling: System design and long-term validation study. JMIR Serious Games 2020, 8, e19968. [Google Scholar] [CrossRef]
- Eliyas, S.; P, R. A Model of Gamification by Combining and Motivating E-Learners and Filtering Jobs for Candidates. Eng. Proc. 2023, 59, 7. [Google Scholar] [CrossRef]
- Akhriza, T.M.; Mumpuni, I.D. Gamification of the lecturer career promotion system with a recommender system. In Proceedings of the 2020 Fifth International Conference on Informatics and Computing (ICIC), Gorontalo, Indonesia, 4–5 November 2020; IEEE: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Fallahi, A.; Bastanfard, A.; Amini, A.; Saboohi, H. A study on enhancing user engagement by employing gamified recommender systems. arXiv 2025, arXiv:2508.01265. [Google Scholar] [CrossRef]
- Majuri, J.; Koivisto, J.; Hamari, J. Gamification of Education and Learning: A Review of Empirical Literature. In Proceedings of the 2nd International GamiFIN Conference (GamiFIN 2018), Pori, Finland, 21–23 May 2018; Koivisto, J., Hamari, J., Eds.; CEUR Workshop Proceedings, Vol. 2186; CEUR-WS: ISSN 1613-0073. pp. 11–19. Available online: https://trepo.tuni.fi/bitstream/handle/10024/104598/gamification_of_education_2018.pdf (accessed on 22 October 2025).
- Saleem, A.N.; Noori, N.M.; Ozdamli, F. Gamification applications in e-learning: A literature review. Technol. Knowl. Learn. 2022, 27, 139–159. [Google Scholar] [CrossRef]
- Taqi, A.M.; Qadous, M.; Salah, M.; Özdamlı, F. Gamification in recommendation systems: A systematic analysis. In Communications in Computer and Information Science; Springer: Cham, Switzerland, 2023; pp. 143–153. [Google Scholar] [CrossRef]
- Pelissari, R.; Alencar, P.S.; Amor, S.B.; Duarte, L.T. The use of multiple criteria decision aiding methods in recommender systems: A literature review. In Lecture Notes in Computer Science Intelligent Systems; Springer: Cham, Switzerland, 2022; pp. 535–549. [Google Scholar] [CrossRef]
- Kim, S. Decision support model for introduction of gamification solution using AHP. Sci. World J. 2014, 2014, 714239. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Nor, K.M.D.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications: A review of the literature from 2000 to 2014. Econ. Res. 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Mora, A.; Riera, D.; Gonzalez, C.; Arnedo-Moreno, J. A literature review of gamification design frameworks. In Proceedings of the 2015 7th International Conference on Games and Virtual Worlds for Serious Applications (VS-Games), Skövde, Sweden, 16–18 September 2015. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw–Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Fontela, E.; Gabus, A. The DEMATEL Observer; Battelle Geneva Institute: Geneva, Switzerland, 1976. [Google Scholar]
- Büyüközkan, G.; Karabulut, Y.; Göçer, F. Spherical fuzzy sets-based integrated DEMATEL, ANP, and VIKOR approach and its application for renewable energy selection in Turkey. Appl. Soft. Comput. 2024, 158, 111465. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, H.; Wang, D.; Yu, H.; Wang, L.; Yu, D.; Peng, Y. Preference-Based Multi-Attribute Decision-Making Method with Spherical-Z Fuzzy Sets for Green Product Design. Eng. Appl. Artif. Intell. 2023, 126, 106767. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. Perceptions of the World Problematique: Communication Procedure, Communicating with Those Bearing Collective Responsibility (DEMATEL Report No. 1); Battelle Geneva Research Centre: Geneva, Switzerland, 1973. [Google Scholar]
- Li, R.-J.; Tzeng, G.-H. Identification of a Threshold Value for the DEMATEL Method: Using the Maximum Mean De-Entropy Algorithm. In Cutting-Edge Research Topics on Multiple Criteria Decision Making; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 35, pp. 789–796. [Google Scholar] [CrossRef]
- Wu, W.-W. Choosing knowledge management strategies by using a combined ANP and DEMATEL approach. Expert. Syst. Appl. 2008, 35, 828–835. [Google Scholar] [CrossRef]
- Bai, C.; Sarkis, J. Green Supplier Development: Analytical Evaluation Using Rough Set Theory. Int. J. Clean. Prod. 2010, 18, 1200–1210. [Google Scholar] [CrossRef]
- Chen, I.-S. A Combined MCDM Model Based on DEMATEL and ANP for the Selection of Airline Service Quality Improvement Criteria: A Study Based on the Taiwanese Airline Industry. J. Air Transp. Manag. 2016, 57, 7–18. [Google Scholar] [CrossRef]
- Altınırmak, S.; Ergün, M.; Karamaşa, Ç. Implementation of the fuzzy DEMATEL method in higher education course selection: The case of Eskişehir Vocational School. J. Grad. Sch. Soc. Sci. 2017, 21, 1597–1614. [Google Scholar]
- Ou, Y.-C. Using a hybrid decision-making model to evaluate the sustainable development performance of high-tech listed companies. J. Bus. Econ. Manag. 2016, 17, 331–346. [Google Scholar] [CrossRef]
- Rodrigues, L.; Toda, A.; Pereira, F.; Palomino, P.T.; Klock, A.C.T.; Pessoa, M.; Oliveira, D.; Gasparini, I.; Teixeira, E.H.; Cristea, A.I.; et al. GARFIELD: A Recommender System to Personalize Gamified Learning. In Artificial Intelligence in Education; Rodrigo, M.M., Matsuda, N., Dimitrova, V., Eds.; Springer: Cham, Switzerland, 2022; pp. 666–672. [Google Scholar] [CrossRef]
- Al-Mawali, H. Proposing a Strategy Map Based on Sustainability Balanced Scorecard and DEMATEL for Manufacturing Companies. Sustain. Account. Manag. Policy J. 2023, 14, 565–590. [Google Scholar] [CrossRef]
- Hajarian, M.; Hemmati, S. A gamified word-of-mouth recommendation system for increasing customer purchase. In Proceedings of the 4th International Conference on Smart Cities, Internet of Things and Applications (SCIoT 2020), Mashhad, Iran, 16–17 September 2020; IEEE: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Li, C.; Tzeng, G. Identification of a threshold value for the DEMATEL method using the maximum mean de-entropy algorithm to find critical services provided by a semiconductor intellectual property mall. Expert. Syst. Appl. 2009, 36, 9891–9898. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G. Defuzzification within a multicriteria decision model. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2003, 11, 635–652. [Google Scholar] [CrossRef]
- Tsai, W.; Chou, W. Selecting management systems for sustainable development in SMEs: A novel hybrid model based on DEMATEL, ANP, and ZOGP. Expert. Syst. Appl. 2009, 36, 1444–1458. [Google Scholar] [CrossRef]
- Tseng, M.; Lin, Y.H. Application of fuzzy DEMATEL to develop a cause and effect model of municipal solid waste management in Metro Manila. Environ. Monit. Assess. 2009, 158, 519–533. [Google Scholar] [CrossRef] [PubMed]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Bennani, S.; Maalel, A.; Ghezala, H.B. AGE-Learn: Ontology-Based Representation of Personalized Gamification in E-Learning. Procedia Comput. Sci. 2020, 176, 1005–1014. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2020, 372, n71. [Google Scholar] [CrossRef]
- Cesário, V.; Nisi, V. Designing with Teenagers: A Teenage Perspective on Enhancing Mobile Museum Experiences. Int. J. Child-Comput. Interact. 2022, 33, 100454. [Google Scholar] [CrossRef]
- Khoshkangini, R.; Valetto, G.; Marconi, A.; Pistore, M. Automatic Generation and Recommendation of Personalized Challenges for Gamification. User Model. User Adapt. Interact. 2021, 31, 1–34. [Google Scholar] [CrossRef]
- Lex, E.; Kowald, D.; Seitlinger, P.; Tran, T.N.T.; Felfernig, A.; Schedl, M. Psychology-Informed Recommender Systems. Found. Trends Inf. Retr. 2021, 15, 134–242. [Google Scholar] [CrossRef]
- González-González, C.S.; Toledo-Delgado, P.A.; Muñoz-Cruz, V.; Torres-Carrion, P.V. Serious Games for Rehabilitation: Gestural Interaction in Personalized Gamified Exercises through a Recommender System. J. Biomed. Inform. 2019, 97, 103266. [Google Scholar] [CrossRef]
- Mostafa, L.; Elbarawy, A.M. Enhance Job Candidate Learning Path Using Gamification. In Proceedings of the 2018 28th International Conference on Computer Theory and Applications (ICCTA), Alexandria, Egypt, 30 October–1 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 88–93. [Google Scholar] [CrossRef]
- Kazhamiakin, R.; Marconi, A.; Martinelli, A.; Pistore, M.; Valetto, G. A Gamification Framework for the Long-Term Engagement of Smart Citizens. In Proceedings of the 2016 IEEE International Smart Cities Conference (ISC2), Trento, Italy, 12–15 September 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Khalil, M.; Wong, J.; De Koning, B.; Ebner, M.; Paas, F. Gamification in MOOCs: A review of the state of the art. In Proceedings of the 2018 IEEE Global Engineering Education Conference (EDUCON), Santa Cruz de Tenerife, Spain, 17–20 April 2018; pp. 1629–1638. [Google Scholar] [CrossRef]
- Talhaoui, M.A.; Daif, A.; Azzouazi, M.; Oubrahim, Y. A Gamified Recommendation Framework. Int. J. Eng. Technol. 2019, 8, 73–77. [Google Scholar] [CrossRef]
- Komatina, N.; Marinković, D.; Babič, M. Fundamental Characteristics and Applicability of the RADAR Method: Proof of Ranking Consistency. Spectr. Oper. Res. 2025, 3, 63–80. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, H.; Feng, Y.; Wang, D.; Peng, Y.; Jia, H. Green Decoration Materials Selection under Interior Environment Characteristics: A Grey-Correlation-Based Hybrid MCDM Method. Renew. Sustain. Energy Rev. 2018, 81, 682–692. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).