A 1DCNN-GRU Hybrid System on FPGA for Plant Electrical Signal Feature Classification

Abstract

Plant electrical signals are closely related to light conditions, and changes in light intensity lead to variations in the amplitude, frequency, and other characteristics of plant electrical signals. Therefore, real-time analysis of the relationship between plant electrical signals and light factors is crucial for monitoring plant growth status. In this study, Aloe Vera was chosen as the experimental subject, and electrical signal data were collected under different light intensities, followed by preprocessing including wavelet threshold denoising. Furthermore, a hybrid model architecture combining one-dimensional convolutional neural networks (1D-CNNs) and lightweight gated recurrent units (GRUs) was proposed to address the temporal signal characteristics of plant electrical signals and edge computing requirements. The 1D-CNN module extracts local spatial features, which are then modeled in time by the optimized GRU module with channel pruning. Model compression was achieved through parameter quantization. Finally, the computational and storage modules of the model were deployed on an FPGA development board using hardware description language for simulation verification. The results indicate that the system achieved a classification accuracy of 90.1%, a detection time of 43.2 ms, and a power consumption of 4.95 W, demonstrating the comprehensive advantages in terms of accuracy, response speed, and power consumption. This approach effectively improves data processing speed and reduces system power consumption while maintaining high classification accuracy, thereby providing technical support for the development of plant growth monitoring technologies.

1. Introduction

As global araable land continues to decrease and environmental resource issues become more pronounced, the pressure on crop production is intensifying [1]. Plant factories, as a highly intensive and intelligent agricultural production model, are internationally recognized as a key solution to overcoming land constraints and ensuring food security. They are considered an important direction for the future of agriculture [2]. In plant factories, light is a critical environmental factor, and precise control of light intensity can enhance both the yield and quality of plants [3]. Plant electrical signals, as the main physiological signals within plants, change in response to variations in light factors [4]. By extracting features from plant electrical signal data, subtle changes in plant growth can be detected in real-time, enabling the accurate establishment of the relationship between plant growth status and light conditions. This holds significant practical value for evaluating plant growth. Therefore, leveraging an appropriate deep learning computational framework and underlying computing system for feature extraction and real-time classification of plant electrical signals under different light intensities can provide a precise analysis of plant physiological responses in varying light environments [5]. This will, in turn, offer scientific support for the intelligent regulation of plant factories and help guide their development toward more optimal outcomes.

The technological advancements in the field of plant electrophysiological signal analysis have progressed through three key stages, transitioning from single-feature analysis to multi-modal intelligent integration. The first stage predominantly relied on traditional machine learning and signal processing techniques, where research teams constructed classification models through feature engineering. For instance, the team led by Zi-Lin Gao [6] proposed a signal denoising method based on autoregressive neural networks, significantly enhancing the signal-to-noise ratio; the team of Jin-Hai Li [7] improved the support vector machine algorithm, enhancing the classification accuracy of wheat leaf electrical signals; and the team of Gabriela Niemeyer Reissig [8] integrated Fourier transform and power spectral density analysis to establish a tomato fruit maturity classification system, which demonstrated improved classification efficiency compared to traditional methods. In the second stage, breakthroughs in deep learning addressed the challenges in time-series modeling. Chuang Liu team [9] developed a Long Short-Term Memory (LSTM) for dynamic prediction of greenhouse plant electrical signals, with a prediction error controlled within ±5%; Xiao Huang Qin team [10] proposed a fusion architecture combining one-dimensional convolutional neural networks (1D-CNN) and generative adversarial networks, improving the classification accuracy of salt-tolerant seedlings through data augmentation; and Xiang Ma team [11] performed a lightweight modification of the VGG16 architecture, creating the CornNet model, which improved maize seed purity detection efficiency, achieving an accuracy rate of 98.7%. The current stage reflects a trend towards interdisciplinary integration. The team of Chun-Hu Shang [12] developed a CNN-LSTM hybrid network to analyze plant electrical signal responses to light intensity with high temporal resolution; Lan Huang team [13] proposed a bidirectional LSTM and graph convolutional network fusion model, integrating electrical signals with proteomic features to enhance the prediction accuracy of plant protein–protein interaction relationships. These technological advances have facilitated the transition from static feature classification to dynamic prediction systems, providing real-time decision support for agricultural issues such as crop resistance mechanism analysis and precise phenotypic identification, driving plant physiology into a new phase of intelligence-driven research.

This study addresses common technical challenges in the field of plant electrophysiological signal analysis, specifically the limitations in dynamic feature extraction and real-time computational deployment. On one hand, traditional machine learning methods rely on manual feature design, which makes it difficult to effectively capture the non-stationary temporal characteristics of electrical signals [14]. On the other hand, existing deep learning models suffer from computational redundancy in spatiotemporal feature co-modeling and lack lightweight designs suitable for agricultural edge computing scenarios [15]. Furthermore, although complex network architectures can improve classification accuracy, their high computational complexity makes them unsuitable for real-time field monitoring applications.

To address these issues, this paper proposes a novel architecture based on the collaborative optimization of 1D-CNN and Gated Recurrent Unit (GRU), with innovation in three key areas: (1) The use of 1D-CNN spatial convolution kernels for automatic extraction of local features from electrical signals, overcoming the efficiency bottleneck of traditional manual feature selection. (2) The incorporation of GRUs to model temporal dependencies, enabling the dynamic learning of the nonlinear mapping relationship between light intensity changes and electrical signal responses. (3) The innovative introduction of FPGA(Field-Programmable Gate Array) hardware acceleration, utilizing parallel computation and pipeline optimization to significantly enhance system real-time processing capabilities. This method demonstrates unique advantages in plant electrical signal-environmental factor interaction analysis, providing an embedded solution for precision agriculture monitoring that combines both high accuracy and low latency.

2. Materials and Methods

2.1. Experimental Environment and Material Selection

The experimental samples selected were Aloe Vera plants in good growth condition with a growth period of three months. All three types of plants in the study were maintained under identical conditions to ensure consistent growth. They were planted in uniformly sized pots with soil of the same composition, including equivalent mineral content and fertility. Watering was scheduled from 9:00 AM to 9:30 AM daily. During the study, the laboratory environment was carefully controlled to avoid any interference, with temperature and humidity kept constant at 25 °C and 50%, respectively, using the RXG-350B plant growth incubator (Produced by Shanghai Chuanhong Experimental Instrument Co., Ltd., Shanghai, China). The electrical signals of Aloe Vera were transmitted through electrodes to the BL-420S signal acquisition and processing device(Produced by Chengdu Taimeng Co., Ltd., Chengdu, China), which was then connected to a computer via USB for real-time communication. In the data sampling configuration, a single acquisition channel index is employed to meet the single-point measurement requirements for plant electrical signals, thereby simplifying hardware complexity. Given that plant electrical signal amplitudes are only in the microvolt range—characterized as low-frequency bioelectric potential sampling—a 100 Hz sampling frequency is set to prevent high-frequency aliasing. Additionally, selecting a 1000 amplification factor effectively controls quantization error. To further filter out ultra-low-frequency noise caused by soil moisture variations, a high-pass cutoff frequency of 0.053 Hz is set to preserve the effective signal band. A low-pass filter of 5 Hz is configured to ensure the signal bandwidth is compatible with the wavelet denoising algorithm. Figure 1 shows the schematic diagram of the Aloe Vera electrical signal acquisition device.

2.2. Acquisition Methods and Procedures

The experiment involved selecting three Aloe Vera plants, which were placed in an artificial climate plant cultivation box on a shockproof platform. The light intensity was set at three levels: Level 0 (1000 Lux), Level 1 (5000 Lux), and Level 2 (10,000 Lux). As shown in Figure 2, three collection electrodes (A+, A−, and GND) were connected to the signal acquisition system. Electrodes A+ and A− were inserted into the phloem of the Aloe Vera leaves for signal collection, while the GND electrode was connected to the soil to serve as the reference electrode. The collected electrical signals from the Aloe Vera were transmitted to the BL-420S signal acquisition system, which was connected to a host computer for data storage.

2.3. Data Preprocessing of Plant Electrical Signals

Plant electrical signals are characterized by low frequency and weak amplitude, with the latter ranging from several microvolts to several hundred microvolts and the former typically below 5 Hz [16,17,18]. Owing to these inherent attributes, such signals are highly vulnerable to interference from the external environment.

To suppress mains frequency interference, a digital low-pass filter was integrated in-to the software of the sampling device. Specifically, the cutoff frequency of this filter was configured to 5 Hz in the software settings of device, which aligns with the upper frequency limit of the plant electrical signals and ensures effective attenuation of high-frequency mains frequency interference. This digital low-pass filter is designed based on the Butterworth filter topology, and its transfer function can be expressed as follows:

$$H\left(f\right)={\displaystyle \frac{1}{\sqrt{1+{{\displaystyle \left(\frac{f}{{{\displaystyle f}}_c}\right)}}^{2n}}}},$$

(1)

where $f_c$ denotes the cutoff frequency (configured as 5 Hz in this study), $f$ represents the frequency of the signal component, and $n$ stands for the filter order. The order $n$ is a key parameter that determines the roll-off rate of the filter beyond the cutoff fre-quency, which is how rapidly the filter attenuates signals with frequencies higher than $f_c$. In the present study, a second-order Butterworth filter was adopted. This filter type offers an optimal trade-off between roll-off rate and signal phase distortion characteris-tics: it achieves sufficient attenuation of high-frequency interference while minimizing phase shift-induced distortion, thereby preserving the integrity of the low-frequency components inherent to plant electrical signals.

To further validate the effectiveness of the second-order Butterworth filter and characterize the signal frequency distribution, Figure 3 presents the data spectrum derived from the filtered signals, which were obtained by subjecting the output of the acquisition device to a Fast Fourier Transform (FFT). Figure 3a depicts the spectrum plot with a linear frequency scale, where the amplitude is quantified in μV. To provide a more lucid illustration of the spectrum, Figure 3b showcases the spectrum plot with a logarithmic frequency scale, with the amplitude measured in dB. Spectral analysis indicates that the frequency components of the collected data are primarily concentrated below 20 Hz, with the vast majority falling within the 0–5 Hz range. This distribution aligns with the inherent frequency characteristics of plant electrical signals. However, low-frequency noise interference remains observable within the 5–20 Hz frequency band. Figure 4 illustrates the power spectral density of the Aloe Vera plant bioelectric signals. Through analysis, it is revealed that there is a high energy distribution in the low-frequency range, and the power spectral density decreases rapidly as the frequency increases. This further verifies that the acquired data conforms to the inherent frequency characteristics of plant bioelectric signals. Within the 0–10 Hz frequency range, the signal shows noise characteristics that are inversely proportional to the frequency. This residual noise is likely to stem from random white noise contamination during the data acquisition process and the intrusion of unexpected environmental noise, such as subtle electromagnetic fluctuations or mechanical vibrations existing in the measurement environment.

To address such noise and further enhance signal quality, the wavelet threshold denoising algorithm is introduced herein. This algorithm, featuring decorrelation, multi-scale, and multi-resolution properties, has been widely applied in the denoising of low-frequency weak signals [19,20,21]. Generally, it can be categorized into fixed-threshold wavelet denoising (including soft-threshold and hard-threshold wavelet denoising) and adaptive-threshold wavelet denoising algorithms.

The expressions of the soft and hard threshold wavelet denoising functions are given by Formulas (2) and (3), respectively:

$$\widehat{C}=\left\{\begin{array}{cc}\mathrm{sign}\left(C_i\right)\left(\left|C_i-\lambda \right|\right)& \left|C_i\right|>\lambda \\ 0& \left|C_i\right|\le \lambda \end{array}\right.,$$

(2)

$${\widehat{C}}_i=\left\{\begin{array}{cc}{C}_i& \left|C_i\right|>\lambda \\ 0& \left|C_i\right|\le \lambda \end{array}\right.,$$

(3)

where $C_i$ represents the original wavelet coefficients, $\lambda$ is the threshold, and ${\widehat{C}}_i$ is the coefficient after thresholding.

The expression of the adaptive threshold wavelet denoising function is given by Formula (4):

$$\lambda =\sigma \sqrt{2\log \left(N\right)},$$

(4)

where $\lambda$ is the computed threshold, $N$ is the signal length, and $\sigma$ is the noise standard deviation. As the high-frequency coefficients of the wavelet transform, the noise standard deviation is approximately $\sigma ={\displaystyle \frac{1}{\sqrt{2}}}$.

In this study, the collected Aloe Vera electrical signal data were processed using the three denoising methods described above. A comparative analysis revealed that, as shown in Figure 5, after noise separation using the adaptive threshold wavelet denoising method, the fluctuations in the details of the Aloe Vera electrical signal waveform became smoother, and the variations across different parts became more consistent.

This paper evaluates the performance of the three denoising methods mentioned above by calculating their Mean Squared Error and Signal-to-Noise Ratio.

The formula for calculating Mean Squared Error (MSE) is shown in Formula (5):

$$\mathrm{MSE}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{(x_i-{\widehat{x}}_i)}^2},$$

(5)

where $x_i$ represents the i-th sample of the original signal, ${\widehat{x}}_i$ represents the i-th sample of the denoised signal, and $N$ is the total number of samples in the signal.

The formula for calculating the Signal-to-Noise Ratio (SNR) is shown in Formula (6):

$$\mathrm{SNR}=10\lg ({\displaystyle \frac{\mathrm{Var}(x)}{\mathrm{MSE}}}),$$

(6)

where $\mathrm{Var}(x)$ represents the variance of the original signal.

Table 1. Signal-to-Noise Ratio and Mean Squared Error of Three Denoising Methods.

Denoising Algorithm	MSE (uV2)	SNR (dB)
Soft Threshold Wavelet Denoising	0.007955	11.62
Hard Threshold Wavelet Denoising	0.0029975	5.88
Adaptive Threshold Wavelet Denoising	0.0001556	18.73

presents the signal-to-noise ratio (SNR) and mean square error (MSE) results for the three denoising methods. The results show that the adaptive threshold wavelet denoising method achieves the highest SNR and the lowest MSE. Therefore, the adaptive threshold wavelet denoising method has a stronger noise suppression effect on plant electrical signals, and thus, this method was selected for denoising the collected raw signals in this study.

3. One-Dimensional CNN and GRU-Based Aloe Vera Electrical Signal Feature Fusion Classification Model

3.1. Construction of Aloe Vera Electrical Signal Dataset

To analyze in more detail the variations in the Aloe Vera electrical signal caused by different light intensities and the characteristic changes over different time periods, as shown in Figure 6, this study adopts a windowing technique to segment the data [22]. By dividing the data into multiple time windows, the complexity and redundancy of the data can be reduced, and the stage-specific characteristic variations in the Aloe Vera electrical signal under different light intensity stimuli at different time intervals can be effectively separated.

The Aloe Vera electrical signal data were collected under three different light intensity levels, with each dataset having a length of $L=320,000$ sampling points. To ensure that the window can capture as many features as possible from the data, the window length H and step size $S$ were set to 1500 sampling points (15 s) and 500 sampling points (5 s), respectively, based on the data length and waveform variation. Each window of data was treated as a separate sample. Specifically, the window length $H=1500$ sampling points (15 s) means that each window contains 1500 consecutive Aloe Vera electrical signal amplitude data points, while the step size $S=500$ sampling points (5 s) indicates that the adjacent windows move 500 data points (5 s) along the data sequence. The number of samples for each light intensity level, denoted as $N_{samples}$, can be calculated using the following formula:

$$N_{samples}=\left[{\displaystyle \frac{\left(L-H\right)}{S}}\right]+1,$$

(7)

where $N_{samples}$ denotes the number of samples for each light intensity level. Ultimately, each group of light intensity (i.e., Label 0: 1000 Lux, Label 1: 5000 Lux, Label 2: 10,000 Lux) yields 638 samples. With three groups of light intensity conditions included in the experiment, the entire dataset comprises a total of 1914 samples.

To accelerate the model convergence, normalization is applied to each data group after window segmentation. Each data point is normalized to the range of [−1, 1], as described in Formula (8):

$$\begin{array}{cc}{Y}_i=2\times {\displaystyle \frac{X_{i,j}-X_{j,\min }}{X_{j,\max }-X_{j,\min }}}-1& \left(i,j=1,2,\dots m\right)\end{array},$$

(8)

In the formula, $X_{i,j}$ represents the $j$-th feature of the $i$-th sample, $X_{i,\min }$ is the minimum value of the $i$-th feature, $n$ is the number of samples, and $m$ is the number of features. After processing, each data group is divided into training set (70%), test set (15%), and validation set (15%), and a data mean file is generated. The entire dataset creation process is shown in Figure 7.

3.2. One-Dimensional CNN-GRU Based Aloe Vera Electrical Signal Feature Fusion Classification Model

This paper presents a signal processing model that combines 1DCNN and GRU. The 1DCNN model is used for local feature extraction, while the GRUs are employed to dynamically learn temporal dependencies. The improvements are primarily reflected in the following aspects:

• Automatic Local Feature Extraction: the 1DCNN automatically extracts local features of the signal through multiple layers of convolution and pooling operations, simplifying the feature design process and enhancing the robustness and applicability of the model;
• Dynamic Temporal Dependency Learning: the GRUs are capable of dynamically learning the temporal variation patterns of the signal, capturing the nonlinear mapping relationship between light intensity changes and electrical signal responses, thereby improving the classification accuracy of the model.;
• Lightweight Design: by combining 1DCNN and GRU, the model reduces computational complexity while maintaining high classification performance, making it more suitable for edge computing scenarios.

The combined network structure is shown in Figure 8.

The implementation environment of this paper is based on Windows 11, using the NumPy library built on the PyTorch framework. The model training, validation, and testing were performed on a system equipped with an Intel(R) Core i5-13600KF Central Processing Unit (CPU) (3.50 GHz, 32 GB). The proposed model integrates 1D-CNN and GRU to extract local features from electrical signals through multiple convolutional and pooling operations, while capturing temporal dependencies dynamically with GRU. The 1D-CNN comprises five convolutional layers with kernel sizes of 9, 7, 5, 3, and 1, each followed by a max-pooling layer; the GRU component consists of a single layer with 32 hidden units. The feature fusion layer is composed of two fully connected layers (input layer → 128 neurons → 64 neurons) along with a ReLU activation layer; the classification layer also contains two fully connected layers (64 neurons → 32 neurons → 3 output categories) along with a ReLU activation layer. The model is trained using the Adam optimizer with a learning rate of 0.0001 and a batch size of 45. The other parameter details of the model are provided in

Table 2. 1D-CNN Network Architecture Parameters.

Layer Type	Kernel Size	Number of Kernels	Stride
Conv1	9 × 1	32	1
Conv2	7 × 1	32	1
Conv3	5 × 1	32	1
Conv4	3 × 1	32	1
Conv5	1 × 1	32	1
Pool1	2 × 1	2	2
Pool2	2 × 1	2	2
Pool3	2 × 1	2	2
Pool4	2 × 1	2	2
Pool5	2 × 1	2	2

,

Table 3. GRU Network Architecture Parameters.

Layer Type	Input Size	Hidden Units	Layers	Batch First
GRU Layer	32	32	1	True

and

Table 4. Parameters of Feature Fusion and Classification Layers.

Layer Type	Layers	Batch First
Fusion-1 Layer	32 × 45 × 2	128
ReLU Activation Layer	-	-
Fusion-2 Layer	128	64
Classifier-1 Layer	64	32
ReLU Activation Layer	-	-
Classifier-2 Layer	32	3

.

3.3. Model Classification Results

The one-dimensional convolutional neural network combined with gated recurrent unit (1D CNN-GRU) model, built on the above framework, was trained using standardized Aloe Vera electrical signal data. Figure 9 visualizes the training process of model. Analysis shows that during the 320-epoch training, the loss function curve has an overall downward trend. Minor fluctuations gradually decrease, which proves the model effective adaptation to the data. The training curve rises steadily. Eventually, the validation accuracy reaches 91.6%. Also, the training and validation accuracies consistently keep an effective gap. This confirms that the model has successfully learned features in the data. These results verify the model generalizability and robust performance.

Figure 10 illustrates the classification performance of the proposed model. Analysis of Figure 10b shows that all categories achieve relatively high classification accuracy. This indicates the model performs well in distinguishing Aloe Vera electrical signals under the three light intensity levels. However, Figure 10a reveals that misclassifications still exist. Detailed analysis demonstrates that errors mainly occur between adjacent light in-tensity levels. This may result from the training data fails to capture the complex features of Aloe Vera electrical signals under varying light conditions. The comprehensiveness of training data directly affects the completeness of the model feature learning and its generalization ability. Thus, Aloe Vera electrical signal data under 3000 Lux and 7000 Lux light intensities were added, with equal sample sizes. This setup simulates scenarios requiring finer-grained distinctions. It aims to investigate the performance of the model across more precisely defined categories.

Analysis of Figure 11b and Figure 12 shows that the model maintains strong performance when extended to a refined dataset with five light intensity levels. This finding confirms that the training data adequately captured the complex features of Aloe Vera electrical signals under varying light conditions. Consequently, it validates that the model has learned comprehensive and effective classification features for Aloe Vera electrical signals. It also demonstrates the robust generalization capabilities of the model.

In time series feature extraction, traditional recurrent neural network methods often use LSTM structures. However, this paper innovatively introduces GRU as the recurrent layer, aiming to simplify the model structure while improving training efficiency and classification performance. Through a comparative analysis of confusion matrices (see Figure 11), the classification performance of GRU and LSTM as recurrent layers on the data validation set is clearly demonstrated. The x-axis in the figure represents the predicted class labels, the y-axis represents the true class labels of the samples, and the integers in each matrix cell represent the total number of data corresponding to the class label on the x-axis. The experiment shows that GRU, while maintaining a lower computational complexity, exhibits classification capabilities comparable to, or even better than, LSTM, validating its effectiveness in the plant electrical signal classification task.

Figure 13 shows a comparison of the classification results for the two types of recurrent layers. The comparison shows that the model with GRU as the recurrent layer achieves a classification accuracy of 90.6%, while LSTM achieves 88.0%. The 1DCNN-GRU model outperforms the 1DCNN-LSTM in recognition rate. Additionally,

Table 5. Comparison of recurrent layer network parameter.

Network Model	Recurrent Network Layer Parameter Count	Recurrent Layer Parameters Proportion
1DCNN-GRU	6336	0.21%
1DCNN-LSTM	8448	0.29%

shows a difference in parameter counts between the two models. In the proposed hybrid deep learning model, LSTM and GRU are two variants of recurrent neural networks. Their main difference lies in the complexity of their gating mechanisms. Compared to the four-component gating system of LSTM, GRU adopts a simplified three-module design. This reduces computational complexity while maintaining time-series modeling capabilities. With the same input dimension (32) and hidden layer dimension (32), the LSTM layer contains 8448 parameters. This is 2112 more than the 6336 parameters in the GRU layer, an increase of 33.3%. The parameter efficiency advantage is reflected by the recurrent layer parameter proportion. This represents the ratio of recurrent layer parameters to total parameters, with specific calculations shown in Formula (9). Replacing LSTM with GRU can thus effectively reduce model parameters. This is highly beneficial for deploying plant electrical signal recognition algorithms on FPGA platforms, as it reduces memory resource usage. Considering classification accuracy, parameter count, and operating speed, this paper selects GRU as the recurrent neural network module for the classification model.

$$({\displaystyle \frac{P_{recurrent}}{P_{total}}})\times 100\%.$$

(9)

4. Hardware Design for Plant Electrical Signal Classification Algorithm

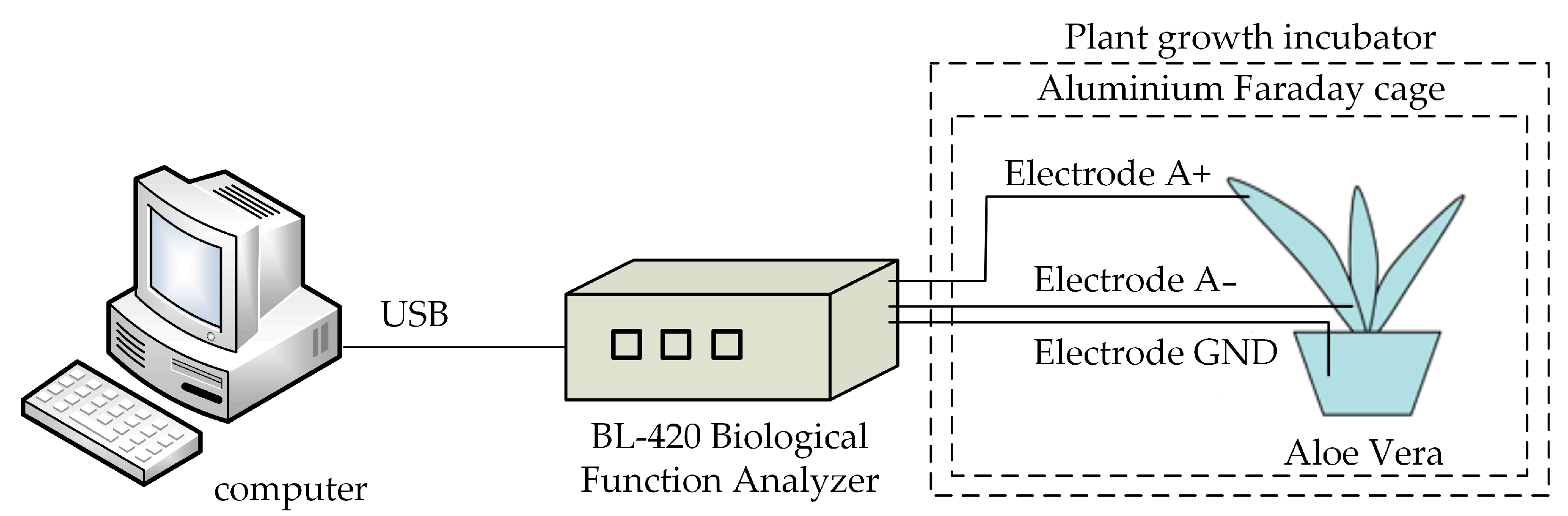
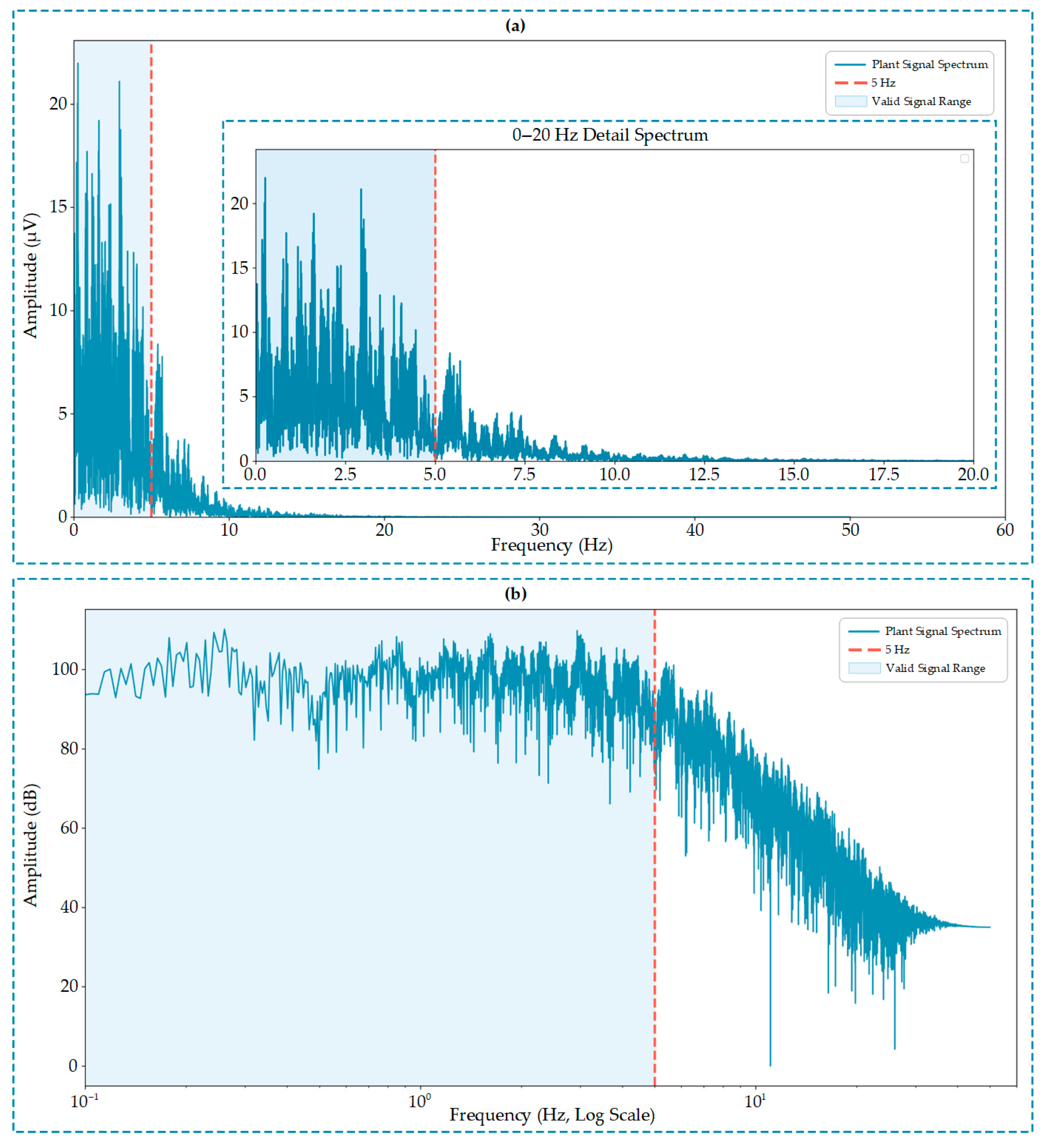
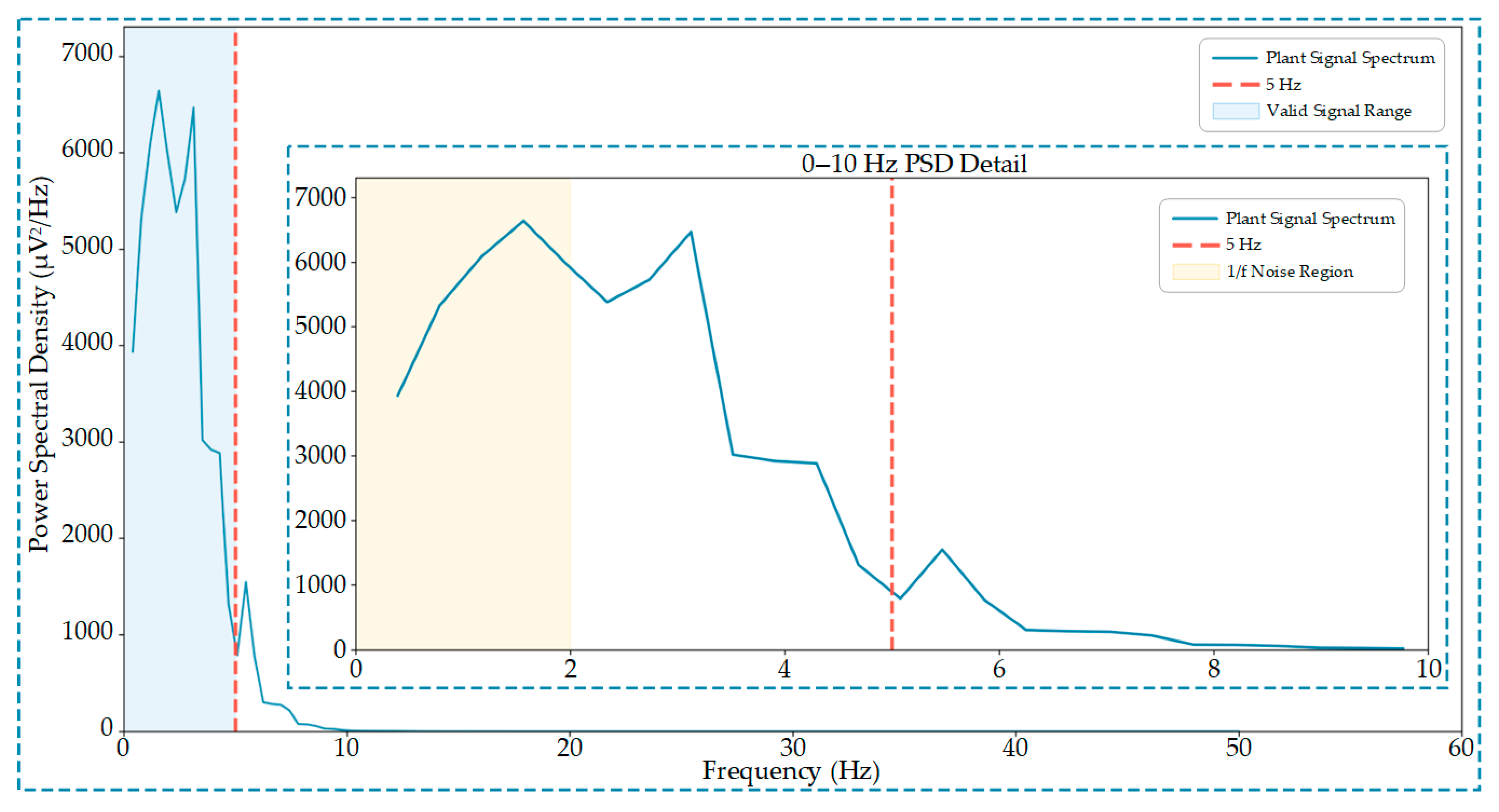
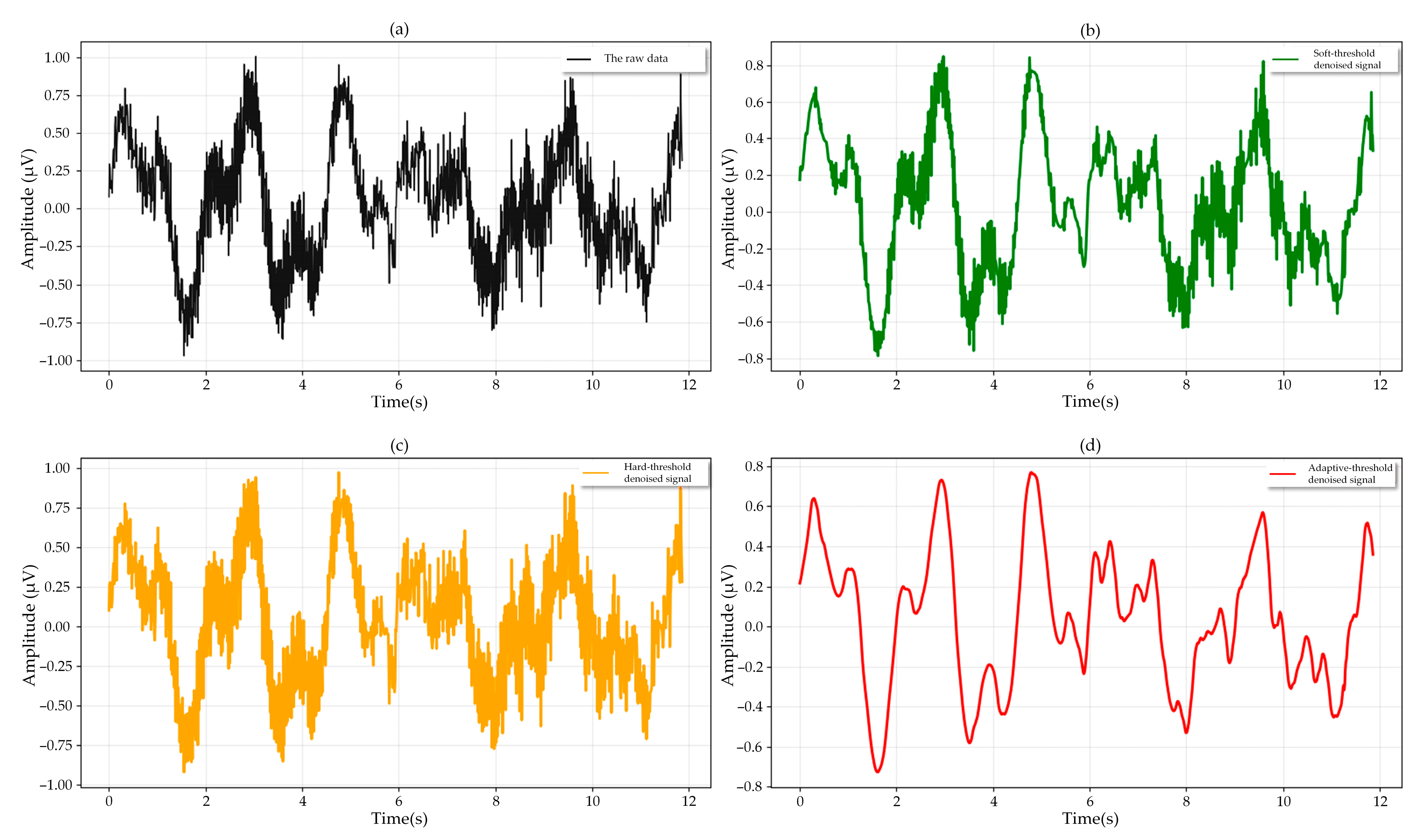
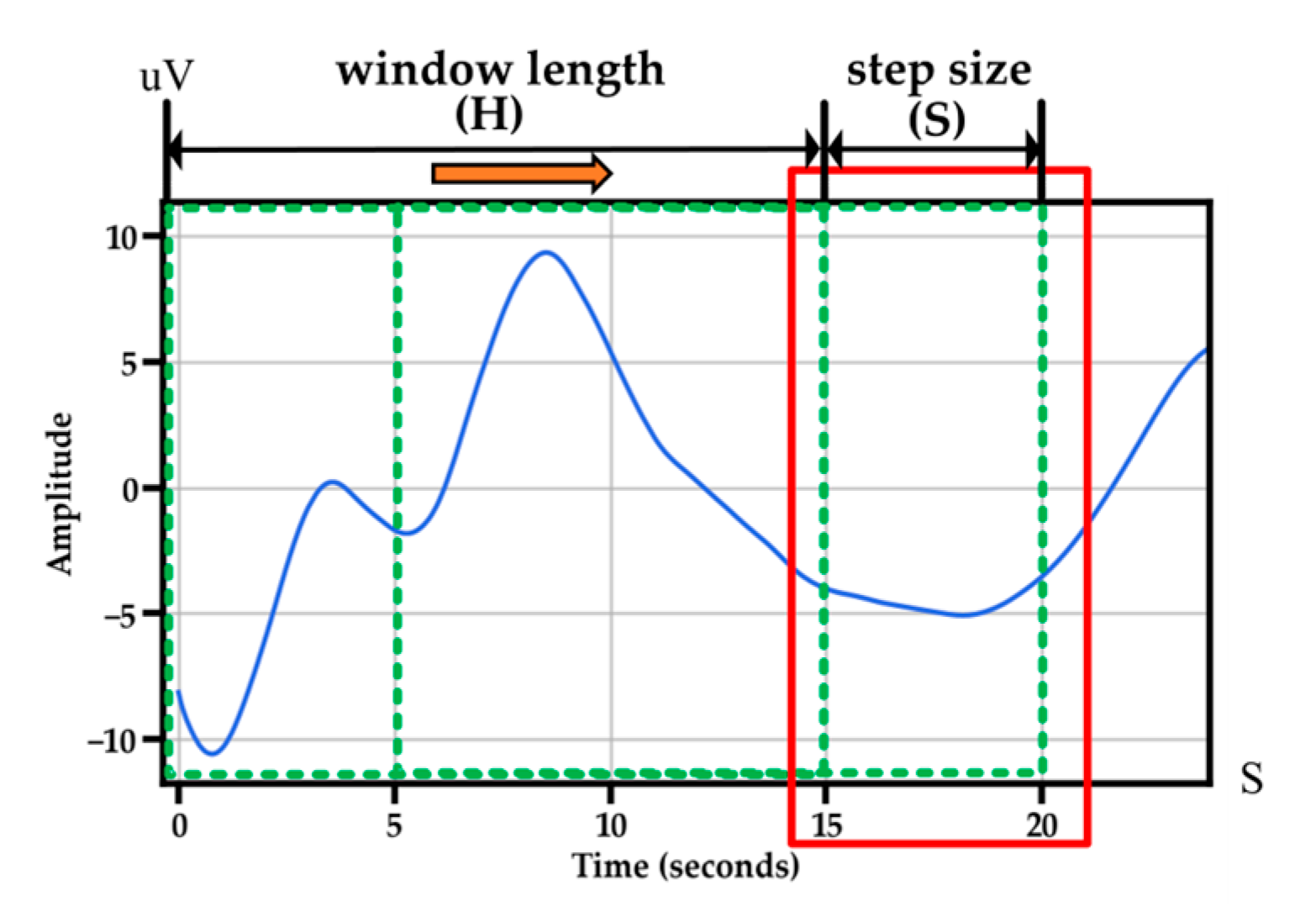
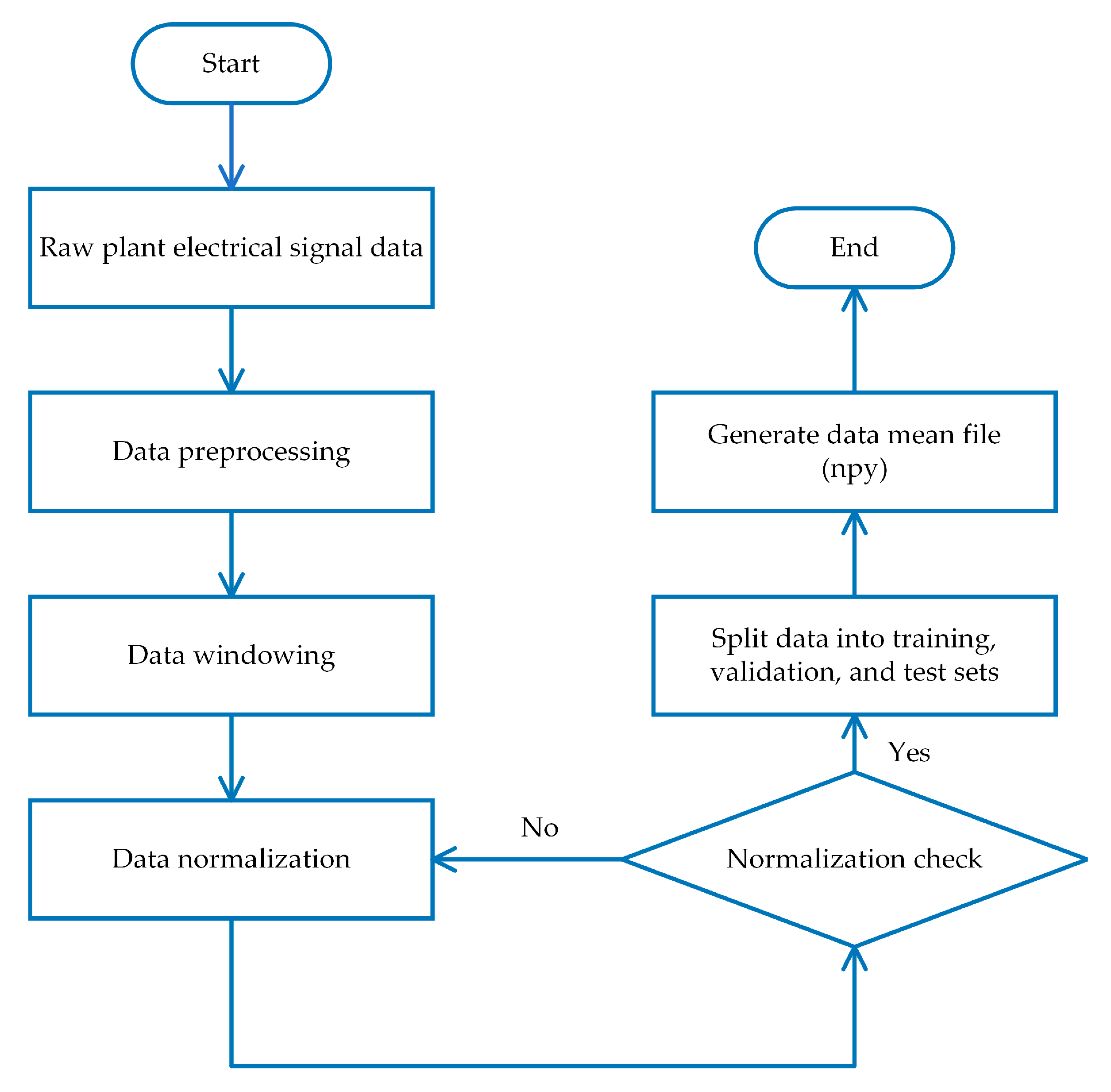
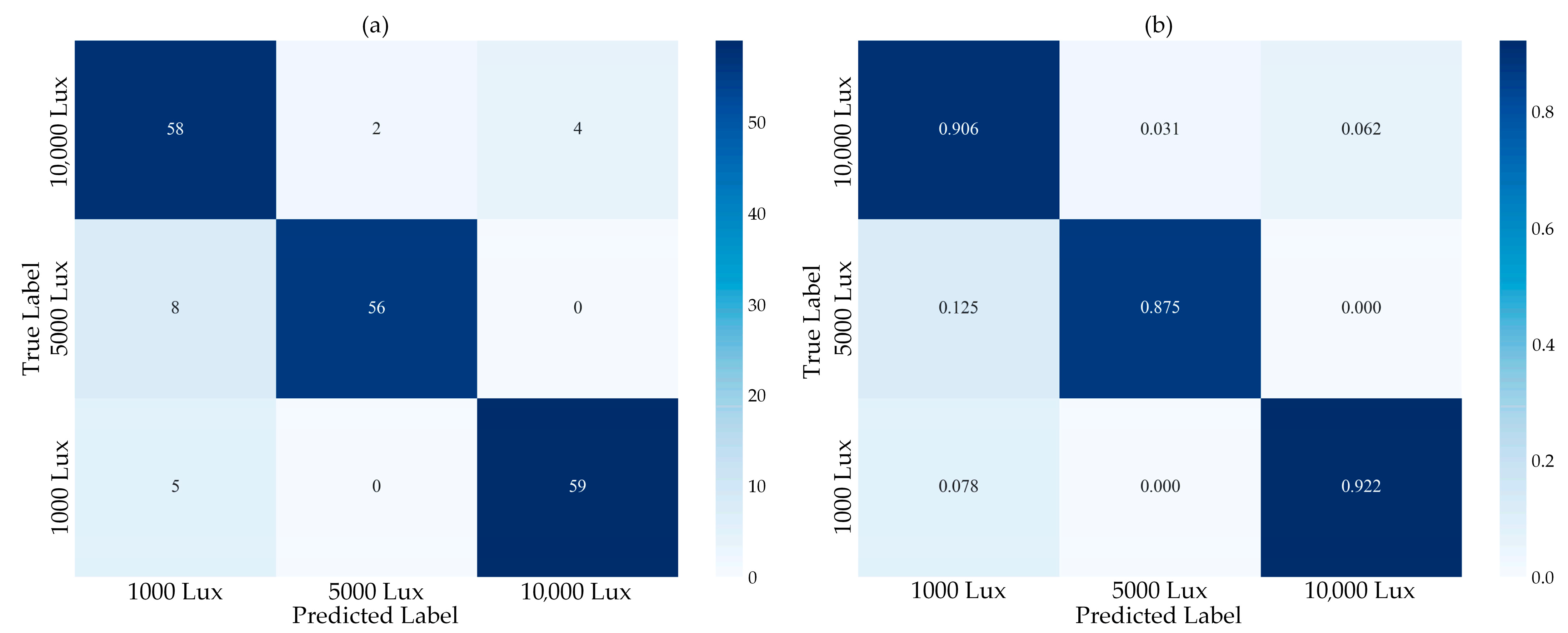
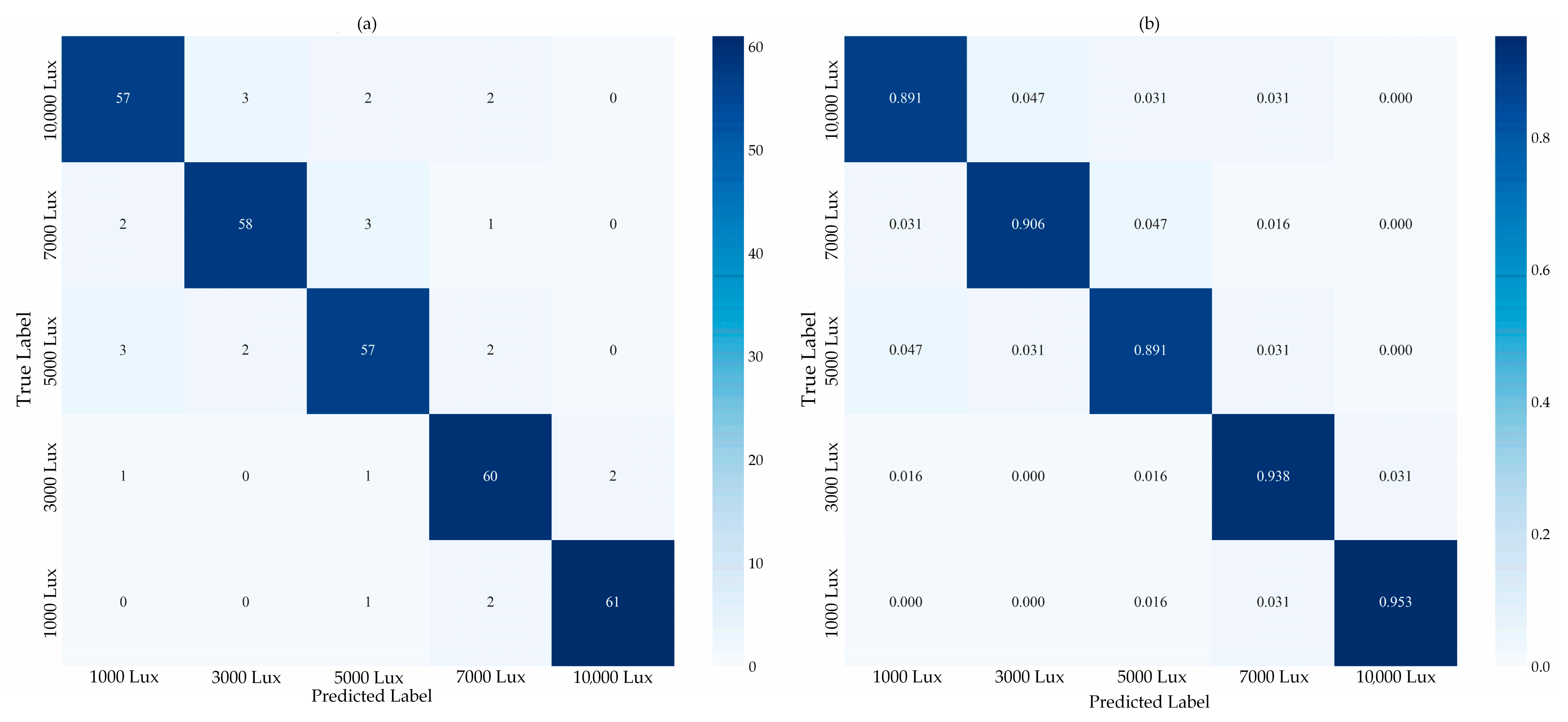
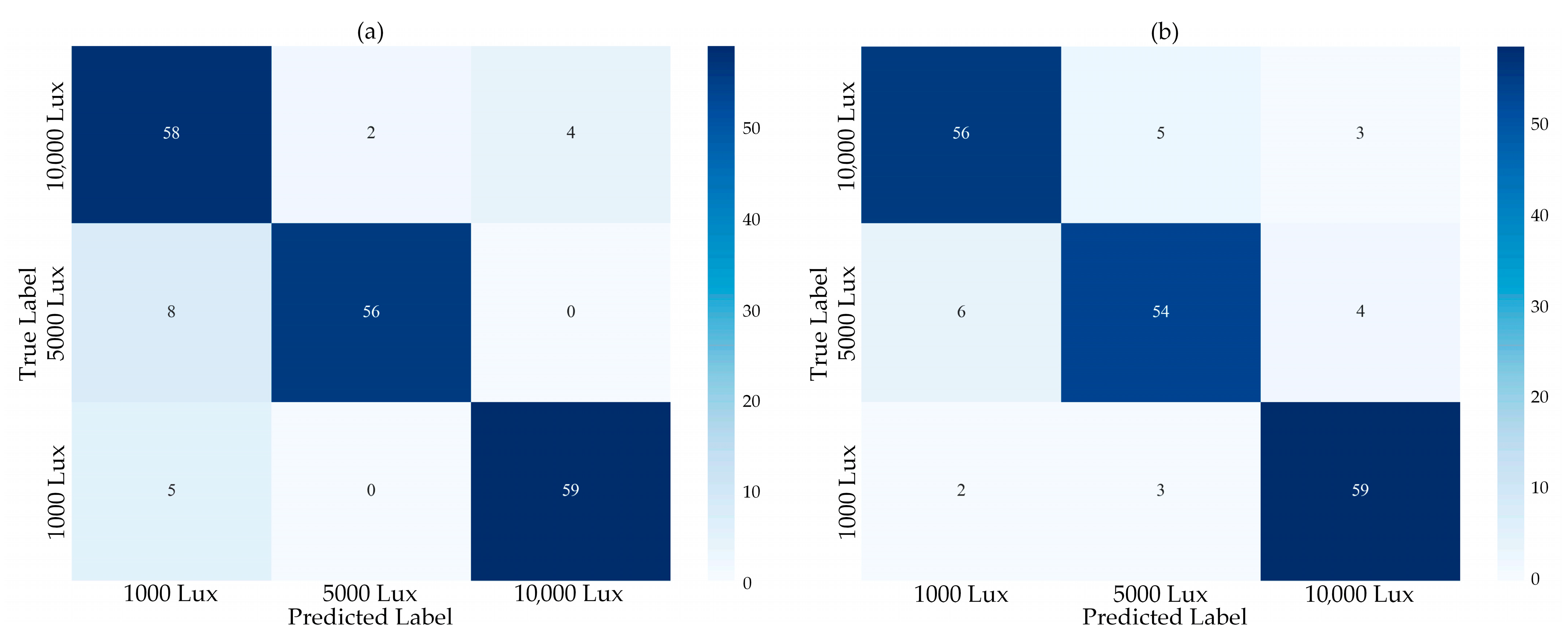
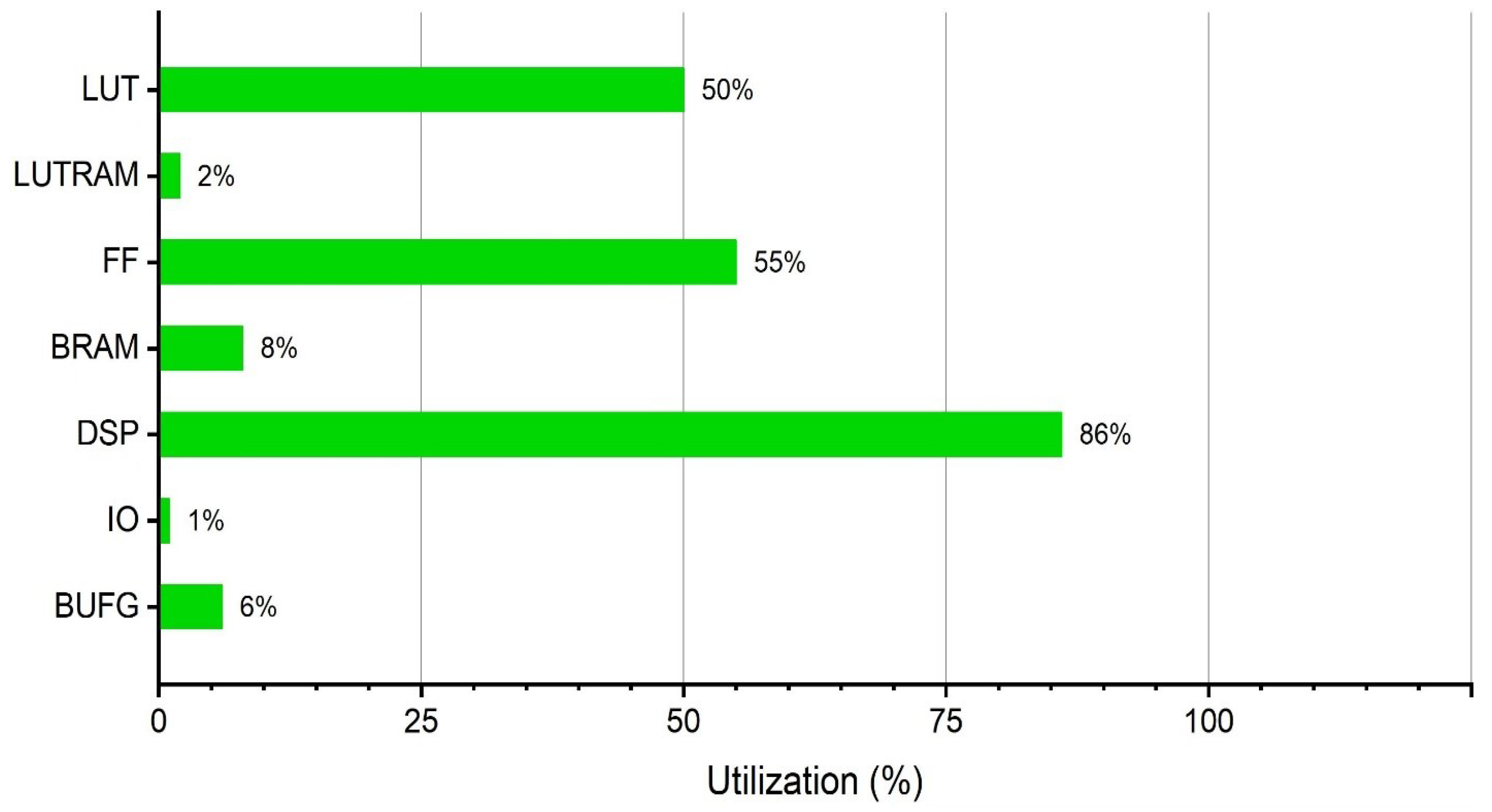
4.1. Deployment of the Classification Model on the FPGA Platform

The main structure of this model was built using PyTorch, with model quantization and ONNX format output achieved through the PyTorch Quantization Toolkit. The specific versions corresponding to the experimental tools are shown in

Table 6. Experimental Tools and Corresponding Versions.

Tool/System	Version
Windows	24H2
PyTorch	2.3.1
Vivado Design Suite	v2019.3
Vitis AI	v1.0

. The hardware implementation method was designed for the ZYNQ UltraScale+ XCZU7EV-2FFVC1156I (Produced by Xilinx, Inc. (now part of AMD), San Jose, CA, USA.) chip hardware platform, as shown in Figure 14. Convolution functionality was realized by designing a timing array using Verilog. The Xilinx Vitis AI tool converts ONNX to a DPU-executable format to obtain the HDL model, which is then simulated and validated in Vivado. Experimental tools and corresponding versions are listed in the table below.

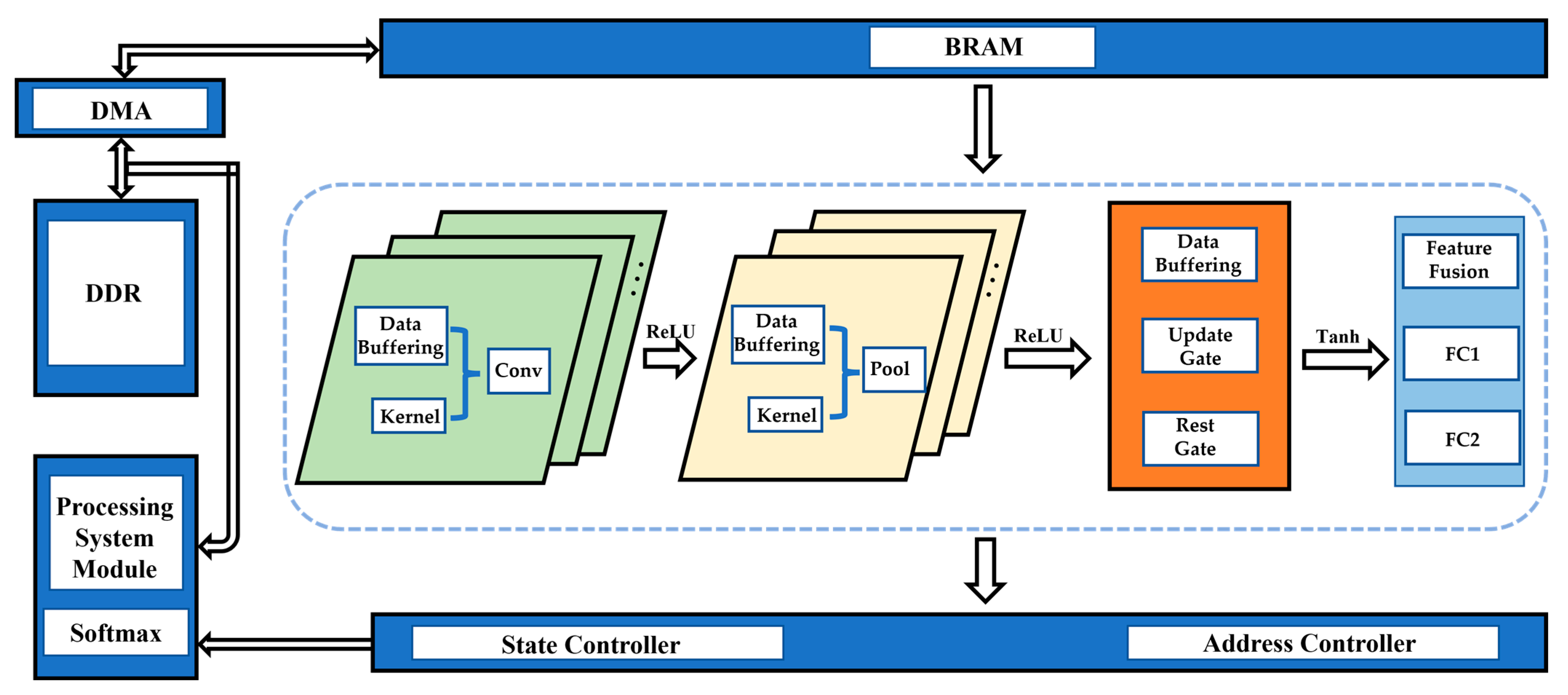
The FPGA acceleration architecture is shown in Figure 15. Based on the independence between the layers of the 1D-CNN, the design includes three components: model parameter quantization, storage module, and computation module.

In neural network hardware implementation, data type choice is critical for computational performance and hardware resource use. Software-based network training typically uses floating-point numbers (e.g., Pytorch represents neural network weights as floating-point numbers) due to their precision and wide numerical range. However, in hardware, floating-point advantages become drawbacks:

• Computational complexity: Floating-point operations involve complex hardware calculations and longer computation times;
• Hardware resource consumption: Floating-point calculations require more multipliers, adders, and other hardware resources, increasing hardware resource usage;
• Storage space requirements: Floating-point numbers occupy more storage space, requiring more storage units;
• Time delay: Floating-point calculations can cause greater time delays.

In contrast, fixed-point numbers, though with smaller range and lower precision than floating-point numbers, enhance computational efficiency and reduce hardware resource consumption. Thus, fixed-point numbers are more common in hardware design, especially on FPGA-based deep learning acceleration platforms. This paper uses 16-bit fixed-point numbers to represent neural network parameters. The specific settings are as follows:

• Bit width: 16-bit, with 1 bit for the sign, 6 bits for the integer part, and 9 bits for the fractional part.
• Numerical range: The decimal numerical range of this fixed-point number is from −64 to 63.998046875.
• Maximum precision: The maximum precision of the fixed-point number is approximately 0.00195.

Quantization process: The conversion of floating-point numbers to fixed-point numbers involves three steps: calculating the quantization step size, performing the quantization calculation, and executing the binary conversion. The specific method is as follows:

$$\Delta ={\displaystyle \frac{\max (x)}{2^q-1}},$$

(10)

$$Q(x)=\Delta \cdot \mathrm{round}({\displaystyle \frac{\Delta }{x}}),$$

(11)

$$I(x)=x\cdot 2^q,$$

(12)

where $q$ is the size of the fractional part, $x$ represents the original high-precision value in continuous space, $Q(x)$ denotes the quantized data in discrete space, $\Delta$ indicates the quantization step size, $\mathrm{round}()$ is the rounding function, and $I(x)$ is the binary conversion result.

In this paper, $q=9$ is selected to fix the decimal point position at 6. This ensures that the quantization process balances precision and range. As the quantization parameter $q$ increases, precision improves, but the representable numerical range decreases. Conversely, a smaller $q$ reduces precision but increases the representable numerical range. After converting the floating-point parameters to fixed-point numbers through quantization, efficient storage is achieved, and the calculation process on FPGA is significantly accelerated.

To efficiently implement 1DCNN-GRU for processing plant electrical signals on FPGA, a storage structure combining Double Data Rate SDRAM (DDR), Direct Memory Access (DMA), and Block Random Access Memory (BRAM) is used. The quantized convolutional kernel weights and biases are stored in DDR, while the input feature matrix is stored in BRAM to ensure fast parallel computation. BRAM is utilized to store input data due to its high data bandwidth, enabling more efficient data access and computation. At the same time, the quantized convolutional kernel weights and biases are stored in DDR, allowing a large set of parameters to be loaded into the FPGA and ensuring that these data can be quickly transferred to BRAM for computation when needed. Since Verilog does not support direct definition of two-dimensional arrays, a one-dimensional register array is used to replace the two-dimensional structure, with horizontal and vertical counters controlling the data access sequence to achieve efficient convolution operation execution. During the convolution operation, the kernel weights and input feature matrix of each layer are transferred from DDR to BRAM via DMA technology for parallel processing, significantly reducing the CPU load and improving data transfer efficiency. The output feature matrix is then stored back in BRAM to serve as the input data for the next layer.

The core of the entire computation module is the convolution module, which is designed using a sequential array approach in this paper. As shown in Figure 16, the convolution kernel weights are preloaded into the Processing Elements (PEs), and data flows through the PEs under the control of the clock, with the convolution multiply–accumulate results obtained at the end of the array. This design supports efficient parallel processing, where each PE can simultaneously process different parts of the data. Data only interacts with the external environment at the first and last PEs. The expression for a single processing element is given by Formula (13):

$$Y_i=X_i\times W_i+Y_i,$$

(13)

where $Y_i$ represents the output of the previous multiply–accumulate unit; $X_i$ is the input data; $W_i$ fand denotes the convolution kernel weights bound to the processing element.

The simulation results of the convolution module are presented in Figure 17. In this figure, $\mathrm{clk}$ denotes the clock signal, $\mathrm{rst}$ represents the reset signal, and $\mathrm{in}\_\mathrm{en}$ stands for the input enable signal. Input data is read from the memory module into the convolution module. When the $\mathrm{weight}\_\mathrm{en}$ signal is at a high level, the convolution module fetches weight parameters from the Block Random Access Memory (BRAM) and conducts convolution computation. Eventually, the result is divided into an integer part ($\mathrm{out}\_\mathrm{data}\_\mathrm{Int}$) and a decimal part ($\mathrm{out}\_\mathrm{data}\_\mathrm{Dec}$), and a floating-point format ($\mathrm{out}\_\mathrm{data}\_\mathrm{r}$) is also provided for validation. The signals $\mathrm{in}\_\mathrm{addr}$ and $\mathrm{weight}\_\mathrm{addr}$ indicate the addresses of the input and weight memories, respectively, while $\mathrm{in}\_\mathrm{data}$ and $\mathrm{weight}\_\mathrm{data}$ correspond to the input and weight values. The simulation demonstrates the dynamic variations in these signals during operation, which elucidates the data flow and processing within the convolution module.

4.2. Board-Level Resource Consumption Analysis

The model design was completed using the Vivado development platform. A comprehensive verification and analysis process was then conducted. This generated a bar chart illustrating the resource usage of the proposed algorithm, along with corresponding resource allocation data. Figure 18 presents the distribution of hardware resource usage.

Table 7. Hardware resource usage statistics.

Resource Usage	Resource Consumption	Total Resources
LUT	115,200	230,400
LUTRAM	2035	101,760
FF	253,440	460,800
BRAM	25	312
DSP	1486	1728
IO	7	700
BUFG	2	32

details the specific utilization data for each resource. The entire design relies on multiplication and addition operations. It also involves buffering weight parameters and intermediate values. This results in high consumption of DSP resources. Moreover, LUTs play a pivotal role in implementing complex logic functions. FFs are necessary for storing state information. Thus, each layer of the neural network typically requires a substantial number of logic circuits. These circuits ensure data synchronization and stability during the processing and storage of intermediate results. These factors explain why these three types of hardware resources are so prevalent in the system, while the usage rates of other resources remain reasonable.

This paper tests the accuracy, time consumption, and power consumption of an FPGA-based classification system. It also compares these metrics with those of two other computing devices: Graphics Processing Unit (GPU) and CPU. All model parameters are defined as 16-bit fixed-point numbers. Thus, the classification accuracy of the FPGA implementation is slightly lower than that of the other two devices. As shown in

Table 8. Comparison of Time and Power Consumption Across Different Hardware Platforms.

Device	Model	Accuracy	Time (ms)	Power (W)
GPU	RTX-4070	90.6%	28.5	142.5
CPU	i5-13600KF	90.6%	139.5	96.8
FPGA	ZYNQ MPSoc	90.1%	43.2	4.95

, the FPGA achieves a classification accuracy of 90.1%. However, FPGA shows significant advantages in time consumption and power consumption. Its power consumption is only 3.47% of the GPU. Its time consumption is nearly two-thirds less than that of the CPU. These results demonstrate the advantages of implementing the algorithm on FPGA.

5. Conclusions

This paper designs an FPGA-accelerated real-time classification system for Aloe Vera electrical signals based on 1DCNN-GRU. While ensuring classification accuracy, the convolutional neural network model has been optimized and simplified. The model is deployed on FPGA, an edge device. Tests were conducted on a dataset of 287 Aloe Vera electrophysiological signal samples. The FPGA-based system achieves an average classification accuracy of 90.1%. Beyond high accuracy, efficient hardware acceleration strategies were employed. These ensure real-time classification performance by reducing latency, increasing processing speed, and improving throughput. Furthermore, compared to GPU-based architectures, the power consumption of the FPGA is only 3.47% of the GPU, achieving significant energy reduction. Thus, the designed system not only effectively meets practical application requirements for plant electrical signal classification but also combines low power consumption with real-time performance. With fast processing speed and the ability to quickly provide classification results, the system demonstrates significant advantages in plant electrical signal classification. It offers more efficient and cost-effective solutions for applications such as plant factories.