Electrodynamics of Carbon Nanotubes with Non-Local Surface Conductivity
Abstract
1. Introduction
2. Self-Consistent Model of Dirac Fermion Motion in Electromagnetic Field
2.1. Dirac Pseudospin and Spatial Dispersion of Surface Conductivity in CNT
2.2. Derivation of Non-Locality Low
2.3. Optical Far-Infrared Properties of CNT
- (i)
- We consider a zigzag conductive CNT (m, 0) with m = 3q (q is integer value). Assuming m < 60 guarantees a small radius compared with the exciting wavelength;
- (ii)
- We consider the case of low temperature (, where are the Boltzmann constant and electrochemical potential, respectively);
- (iii)
- Collision-free electron motion ();
- (iv)
- The spatial dispersion is weak. This means that , although a simple analytical estimation of nonlocality is problematic. It was evaluated numerically via Equation (14), before numerical simulations of CNT scattering. As one can see, this condition is satisfied for practically reachable values of CNTs parameters;
3. Eigenmodes in CNT with Spatial Dispersion
4. Additional Boundary Conditions in CNT
4.1. Charges, Currents, Fields
4.2. Physical Analysis
5. Integral Equation for the Current Density in a CNT with Nonlocal Conductivity
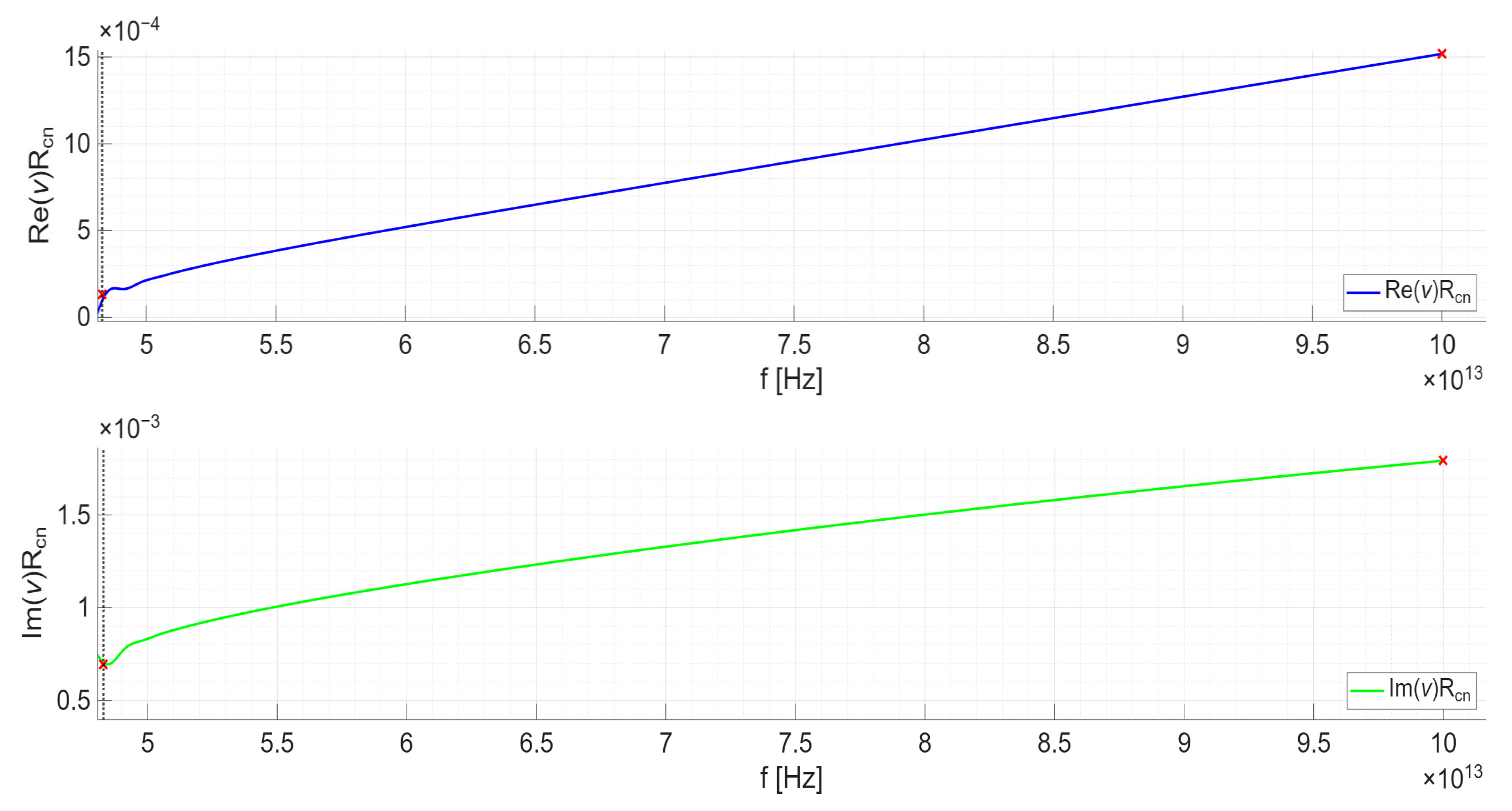
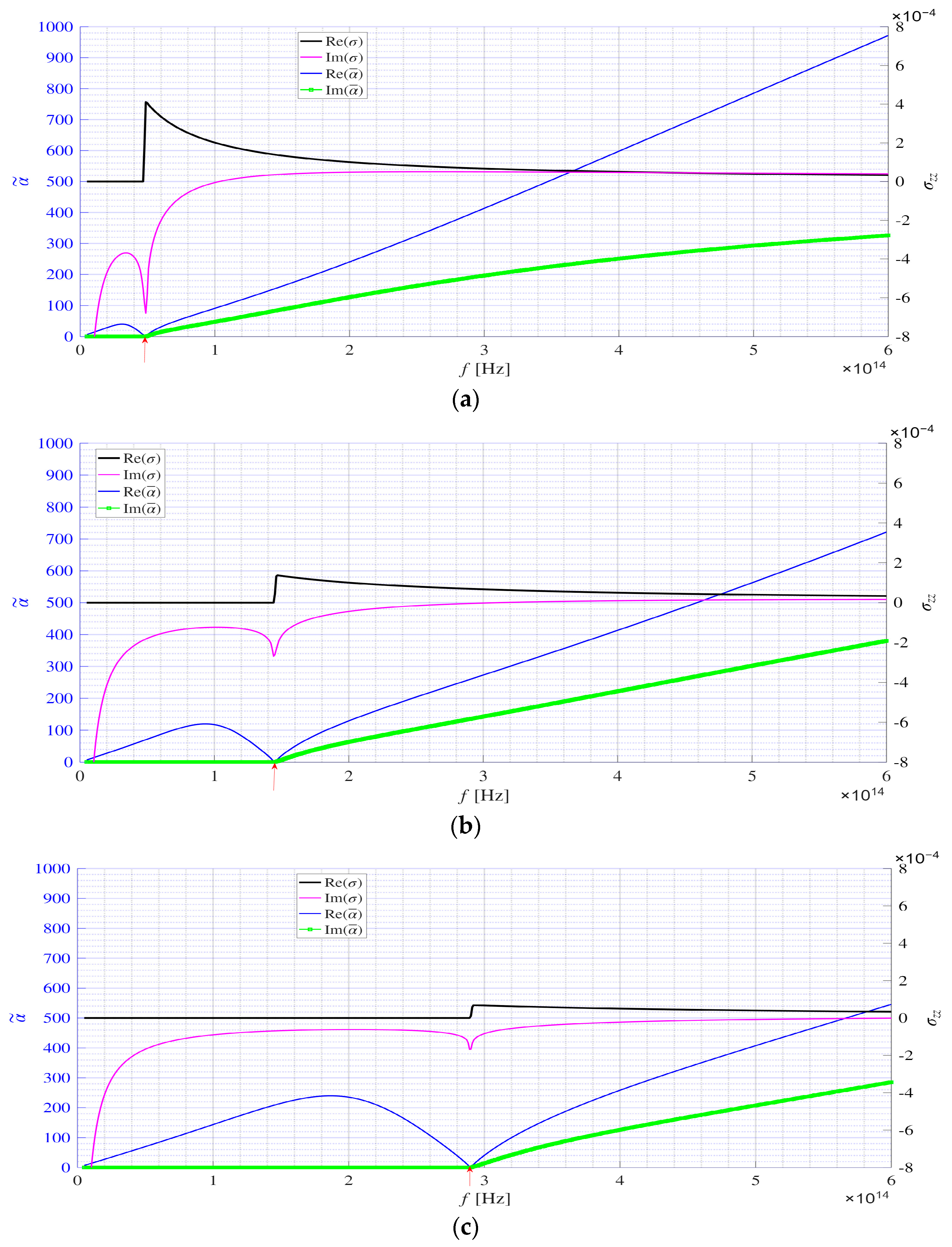
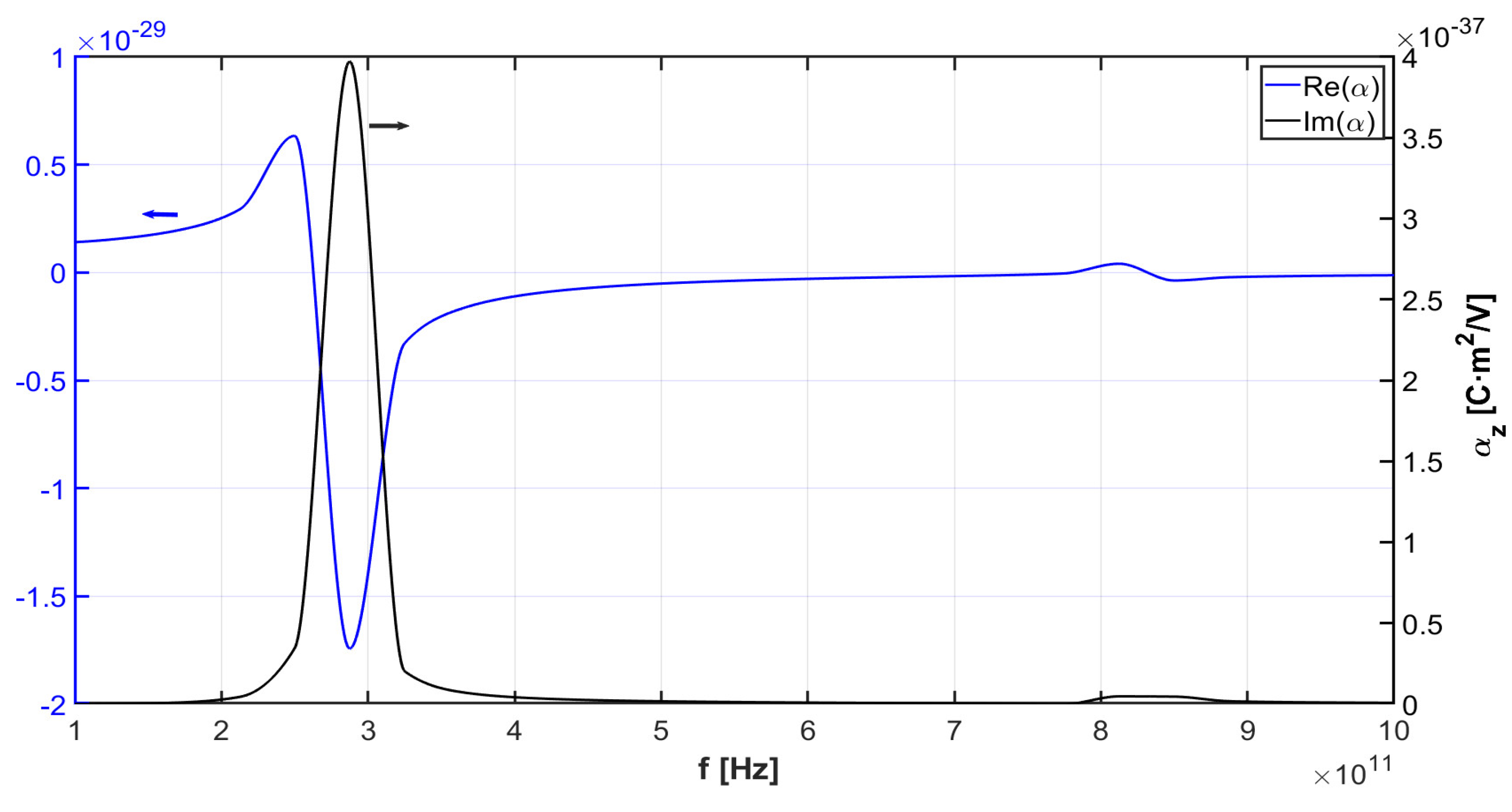
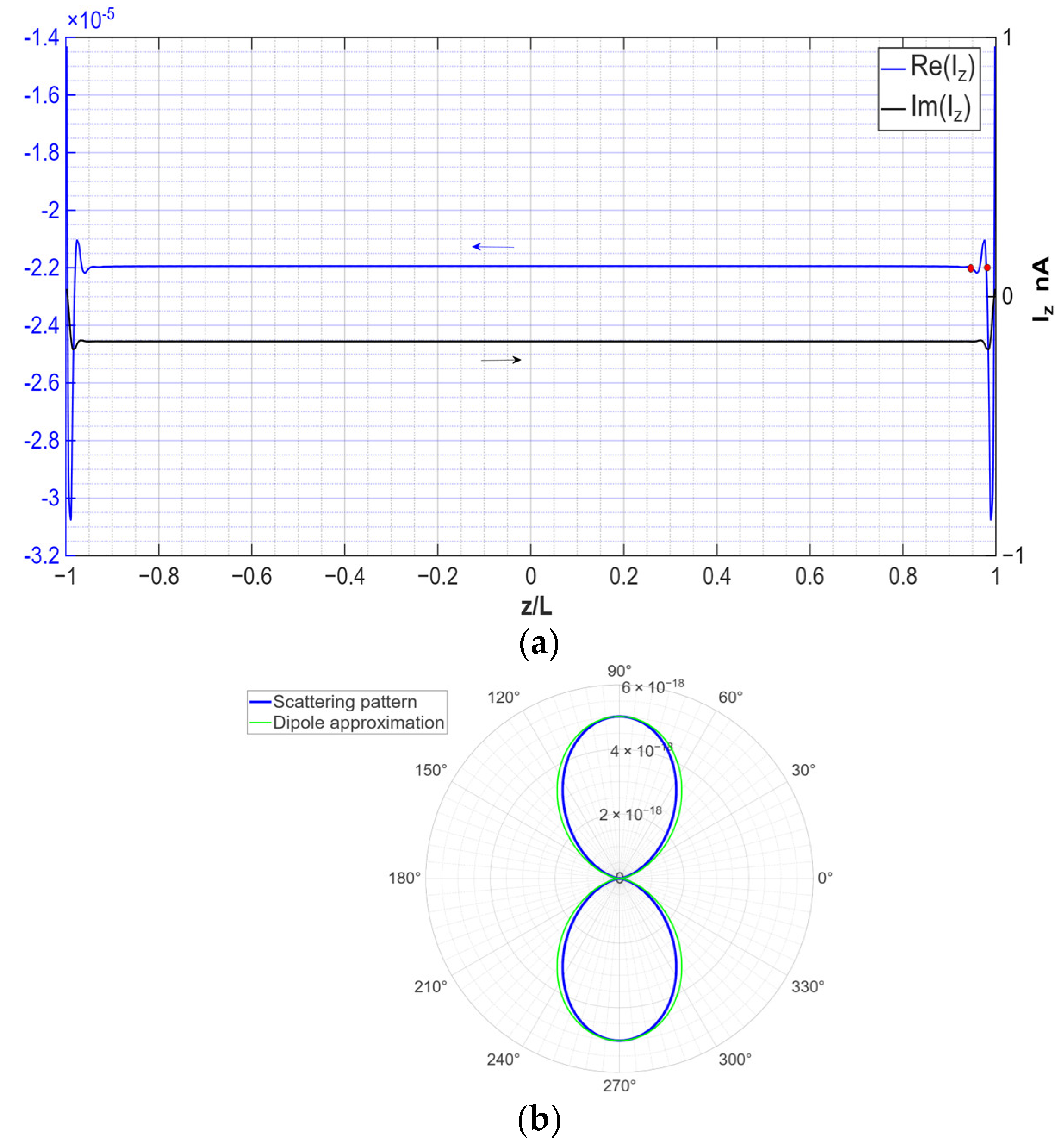
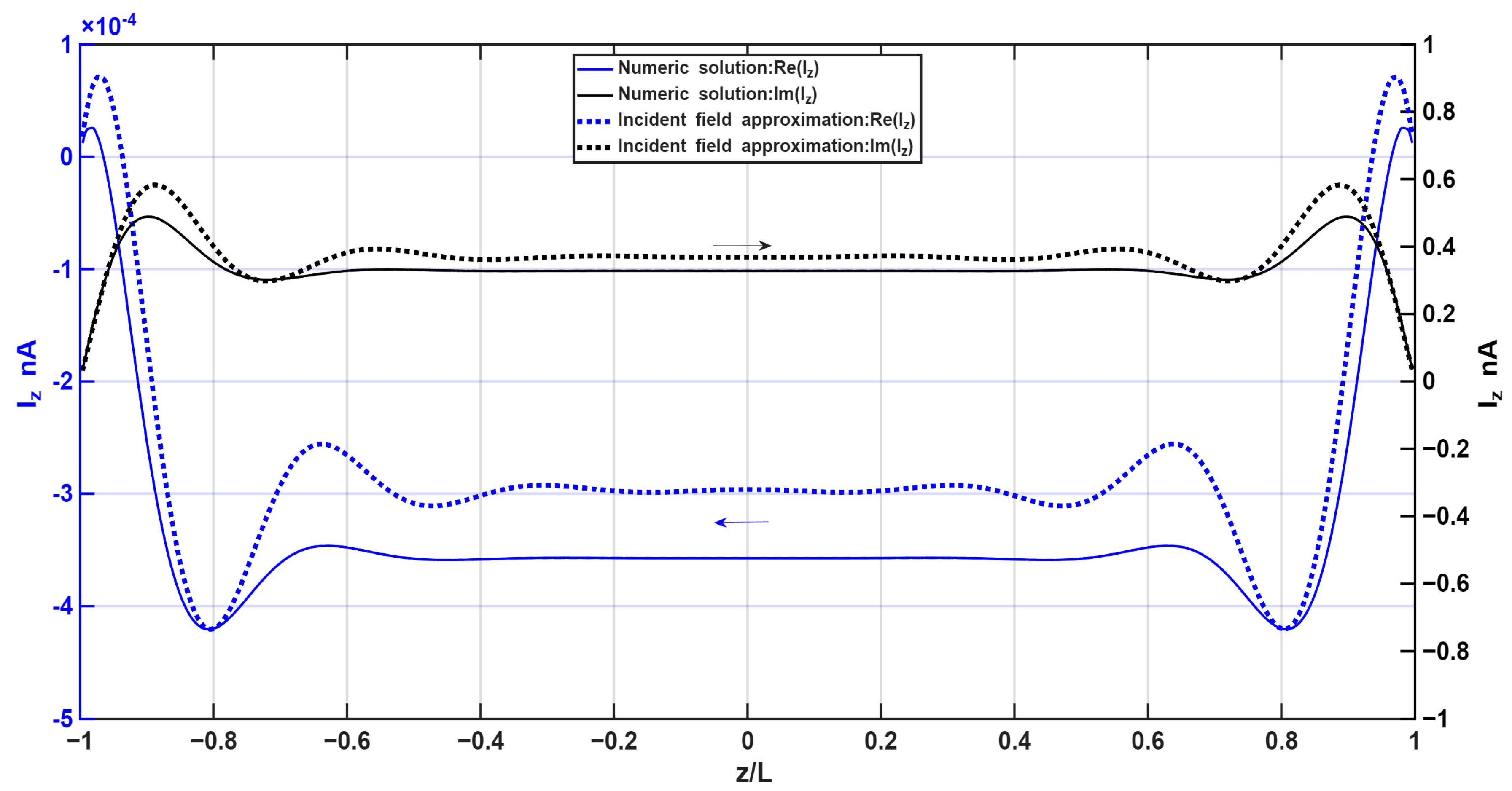
6. Numerical Simulations and Analysis
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
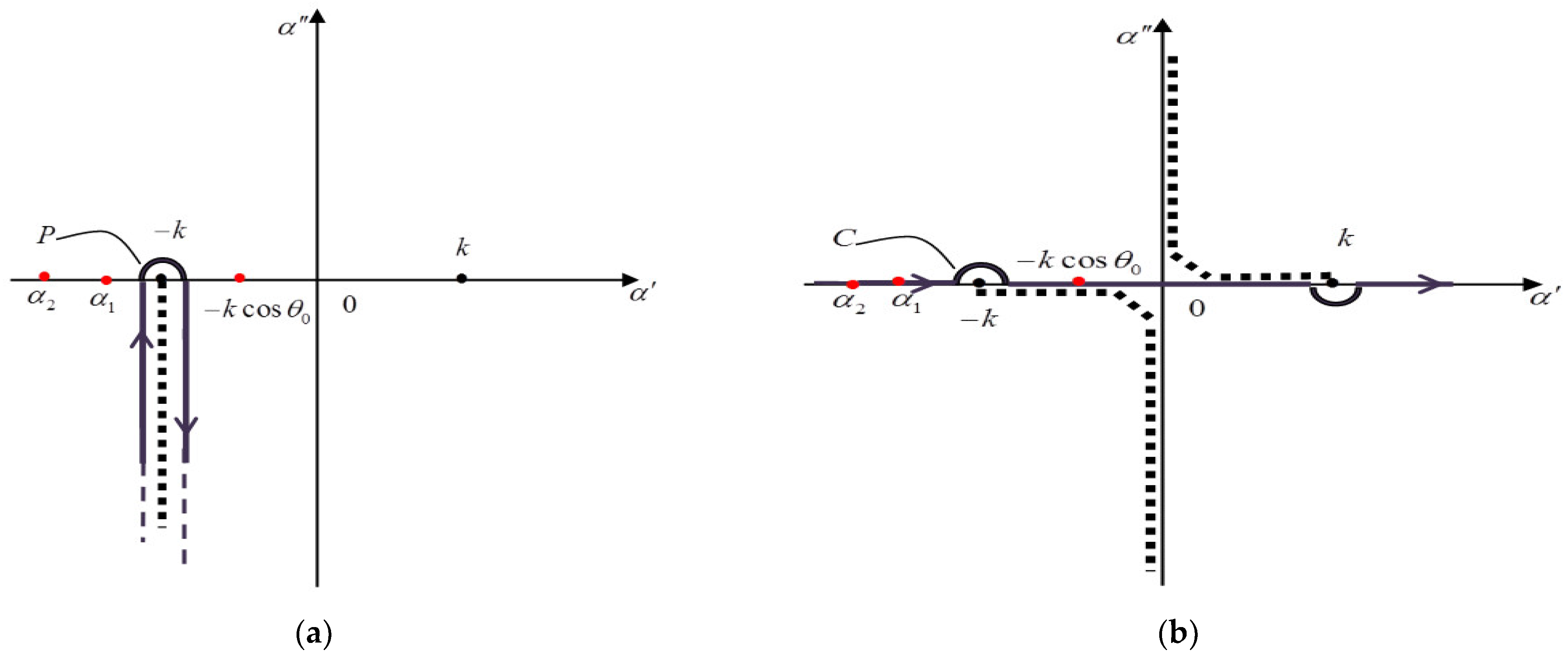
Appendix A. Wiener-Hopf Equation for Carbon Nanotube
Appendix A.1. Deduction of the Wiener-Hopf Equation
Appendix A.2. Solution of Wiener-Hopf Equation
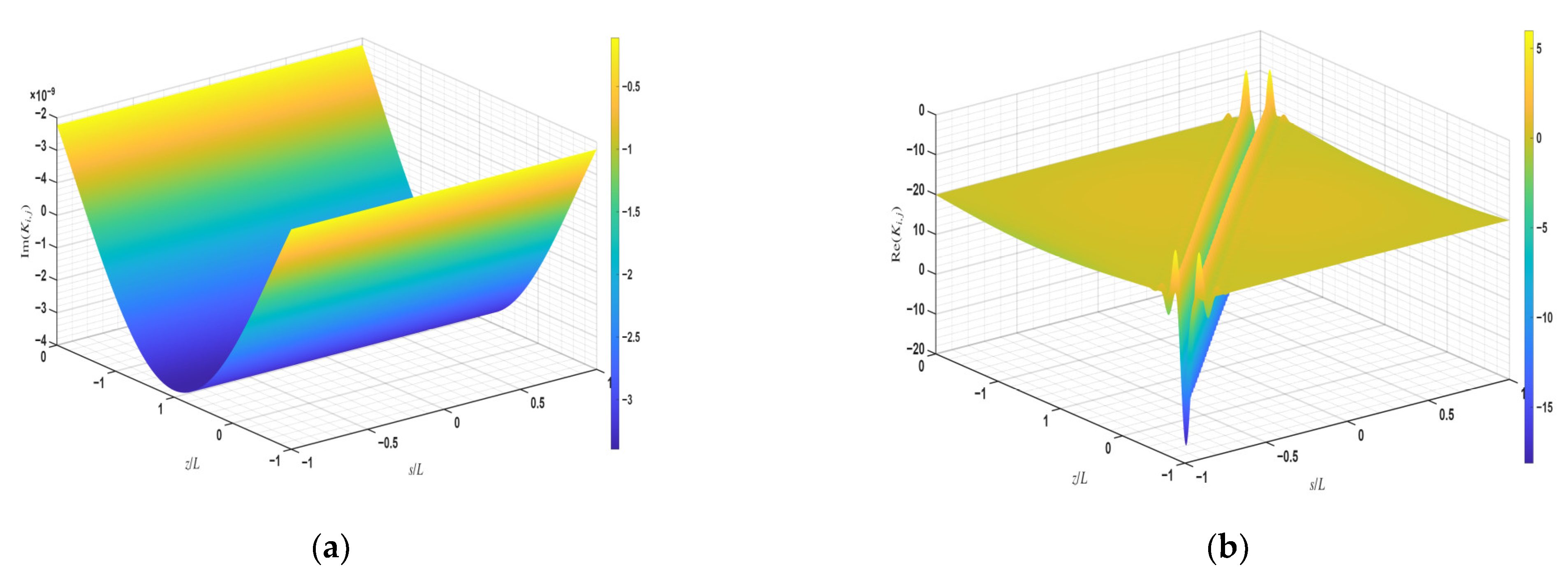
Appendix B. Derivation of the Renormalized Integral in Equation (57)
Appendix C. Alternate Form of the Kernel in Equation (55) Using a Cylindrical Wave Expansion
References
- Laird, E.A.; Kuemmeth, E.A.F.; Steele, G.A.; Grove-Rasmussen, G.A.K.; Nygård, J.; Flensberg, K.; Kouwenhoven, K.L.P. Quantum transport in carbon nanotubes. Rev. Mod. Phys. 2015, 87, 703. [Google Scholar] [CrossRef]
- Baydin, A.; Tay, F.; Fan, J.; Manjappa, M.; Gao, W.; Kono, J. Carbon Nanotube Devices for Quantum Technology. Materials 2022, 15, 1535. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Xie, L.; Hameed, S.; Wang, C.; Ying, Y. Mechanisms and applications of carbon nanotubes in terahertz devices: A review. Carbon 2018, 132, 42. [Google Scholar] [CrossRef]
- Hartmann, R.R.; Kono, J.; Portnoi, M.E. Terahertz science and technology of carbon nanomaterials. Nanotechnology 2014, 25, 322001. [Google Scholar] [CrossRef] [PubMed]
- Avouris, P.; Freitag, M.; Perebeinos, V. Carbon-nanotube photonics and optoelectronics. Nat. Photonics 2008, 2, 341. [Google Scholar] [CrossRef]
- Pistolesi, F.; Cleland, A.N.; Bachtold, A. Proposal for a Nanomechanical Qubit. Phys. Rev. X 2021, 11, 031027. [Google Scholar] [CrossRef]
- Zhang, L.; Bhattacharya, U.; Bachtold, A.; Forstner, S.; Lewenstein, M.; Pistolesi, F.; Grass, T. Steady-state Peierls transition in nanotube quantum simulator. Quantum Inf. 2023, 9, 7. [Google Scholar] [CrossRef]
- Basu, S.; Bisker, G. Near-Infrared Fluorescent Single-Walled Carbon Nanotubes for Biosensing. Small 2025, 21, 2502542. [Google Scholar] [CrossRef]
- Yadav, P.; Tyagi, S.; Negi, S. A Review on the Properties and Application of Carbon Nanotubes as Biological Nanomotors: Advantages and Challenges. Arab. J. Sci. Eng. 2025, 1, 29. [Google Scholar] [CrossRef]
- Slepyan, G.Y.; Shuba, M.V.; Maksimenko, S.A.; Thomsen, C.; Lakhtakia, A. Terahertz conductivity peak in composite materials containing carbon nanotubes: Theory and interpretation of experiment. Phys. Rev. B 2010, 81, 205423. [Google Scholar] [CrossRef]
- Shuba, M.V.; Paddubskaya, A.G.; Plyushch, A.O.; Kuzhir, P.P.; Slepyan, G.Y.; Maksimenko, S.A.; Ksenevich, V.K.; Buka, P.; Seliuta, D.; Kasalynas, I.; et al. Experimental evidence of localized plasmon resonance in composite materials containing single-wall carbon nanotubes. Phys. Rev. B 2012, 85, 165435. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, Q.; Pint, C.L.; Wójcik, A.K.; Bunney, M., Jr.; Arikawa, T.; Kawayama, I.; Tonouchi, M.; Hauge, R.H.; Belyanin, A.A.; et al. Collective antenna effects in the terahertz and infrared response of highly aligned carbon nanotube arrays. Phys. Rev. B 2013, 87, 161401. [Google Scholar] [CrossRef]
- Miano, G.; Forestiere, C.; Maffucci, A.; Maksimenko, S.A.; Slepyan, G.Y. Signal propagation in carbon nanotubes of arbitrary chirality. IEEE Trans. Nanotechnol. 2011, 10, 135. [Google Scholar] [CrossRef]
- Maffucci, A.; Miano, G.; Villone, F. A transmission line model for metallic carbon nanotube interconnects. Int. J. Circuit Theory Appl. 2008, 36, 31. [Google Scholar] [CrossRef]
- Seliuta, D.; Kašalynas, I.; Macutkevic, J.; Valušis, G.; Shuba, M.V.; Kuzhir, P.P.; Slepyan, G.Y.; Maksimenko, S.A.; Ksenevich, V.K.; Samuilov, V.; et al. Terahertz sensing with carbon nanotube layers coated on silica fibers: Carrier transport versus nanoantenna effects. Appl. Phys. Lett. 2010, 97, 073116. [Google Scholar] [CrossRef]
- Slepyan, G.Y.; Shuba, M.V.; Maksimenko, S.A.; Lakhtakia, A. Theory of optical scattering by achiral carbon nanotubes and their potential as optical nanoantennas. Phys. Rev. B 2006, 73, 195416. [Google Scholar] [CrossRef]
- Hanson, G.W. Fundamental Transmitting Properties of Carbon Nanotube Antennas. IEEE Trans. Antennas Propag. 2005, 53, 3426. [Google Scholar] [CrossRef]
- Hao, J.; Hanson, G.W. Infrared and Optical Properties of Carbon Nanotube Dipole Antennas. IEEE Trans. Nanotechnol. 2006, 5, 766. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, V.; Bougher, T.L.; Cola, B.A. A carbon nanotube optical rectenna. Nat. Nanotechnol. 2015, 10, 1027. [Google Scholar] [CrossRef]
- Kleinherbers, E.; Stegmann, T.; Szpak, N. Electronic transport in bent carbon nanotubes. Phys. Rev. B 2023, 107, 195424. [Google Scholar] [CrossRef]
- Li, P.B.; Xiang, Z.L.; Rabl, P.; Nori, F. Hybrid Quantum Device with Nitrogen-Vacancy Centers in Diamond Coupled to Carbon Nanotubes. Phys. Rev. Lett. 2016, 117, 015502. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, B.; Gao, X.; Xu, D. A review of the interfacial characteristics of polymer nanocomposites containing carbon nanotubes. RSC Adv. 2018, 8, 28048. [Google Scholar] [CrossRef] [PubMed]
- Fujimori, T.; Morelos-Gomez, A.; Zhu, Z.; Muramatsu, H.; Futamura, R.; Urita, K.; Terrones, M.; Hayashi, T.; Endo, M.; Hong, S.Y.; et al. Conducting linear chains of sulphur inside carbon nanotubes. Nat. Commun. 2013, 4, 2162. [Google Scholar] [CrossRef] [PubMed]
- Agranovich, V.M.; Ginzburg, V.L. Crystal Optics with Spatial Dispersion and Excitons; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Landau, L.D.; Pitaevskii, L.P.; Lifshitz, E.M. Electrodynamics of Continuous Media (Course of Theoretical Physics); Pergamon Press: Oxford, UK, 1984; Volume 8. [Google Scholar]
- Akhiezer, I.A.; Polovin, R.V.; Sitenko, A.G.; Stepanov, K.N. Plasma Electrodynamics: Linear Theory; Elsevier: Amsterdam, The Netherlands, 2017; Volume 1. [Google Scholar]
- Simovski, C. Composite Media with Weak Spatial Dispersion, 1st ed.; Jenny Stanford Publishing: New York, NY, USA, 2018. [Google Scholar]
- Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M. 3D metamaterials. Nat. Rev. Phys. 2019, 1, 198. [Google Scholar] [CrossRef]
- Shastri, K.; Monticone, F. Nonlocal flat optics. Nat. Photonics 2023, 17, 36. [Google Scholar] [CrossRef]
- Mortensen, N.A. Mesoscopic electrodynamics at metal surfaces, from quantum-corrected hydrodynamics to microscopic surface-response formalism. Nanophotonics 2021, 10, 2563. [Google Scholar] [CrossRef]
- Liberal, I.; Engheta, N. Near-zero refractive index photonics. Nat. Photonics 2017, 11, 149. [Google Scholar] [CrossRef]
- Căbuz, A.I.; Felbacq, D.; Cassagne, D. Spatial dispersion in negative-index composite metamaterials. Phys. Rev. A 2008, 77, 013807. [Google Scholar] [CrossRef]
- Forcella, D.; Prada, C.; Carminati, R. Causality, Nonlocality, and Negative Refraction. Phys. Rev. Lett. 2017, 118, 134301. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafez, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Mortensen, N.A.; Bozhevolnyi, S.I.; Alù, A. Topological nanophotonics. Nanophotonics 2019, 8, 1315. [Google Scholar] [CrossRef]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Phys. Rev. B 2008, 78, 085432. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Falkovsky, L.A.; Pershoguba, S.S. Optical far-infrared properties of a graphene monolayer and multilayer. Phys. Rev. B 2007, 76, 153410. [Google Scholar] [CrossRef]
- Zhu, T.; Antezza, M.; Wang, J.-S. Dynamical polarizability of graphene with spatial dispersion. Phys. Rev. B 2021, 103, 125421. [Google Scholar] [CrossRef]
- Lovat, G.; Hanson, G.W.; Araneo, R.; Burghignol, P. Semiclassical spatially dispersive intraband conductivity tensor and quantum capacitance of graphene. Phys. Rev. B 2013, 87, 115429. [Google Scholar] [CrossRef]
- Hanson, G.W. Drift-Diffusion: A Model for Teaching Spatial-Dispersion Concepts and the Importance of Screening in Nanoscale Structures. IEEE Antennas Propag. Mag. 2010, 52, 198. [Google Scholar] [CrossRef]
- Henneberger, K. Additional boundary conditions: An historical mistake. Phys. Rev. Lett. 1998, 80, 2889. [Google Scholar] [CrossRef]
- Nelson, D.F.; Chen, B. Comment on additional boundary conditions: An historical mistake. Phys. Rev. Lett. 1999, 83, 1263. [Google Scholar] [CrossRef]
- Zeyher, R. Comment on additional boundary conditions: An historical mistake. Phys. Rev. Lett. 1999, 83, 1264. [Google Scholar] [CrossRef]
- Halevi, P.; Hernndez-Cocoletzi, G. Additional boundary conditions—Critical comparison between theory and experiment. Phys. Rev. Lett. 1982, 48, 1500. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Novoselov, K.S. Graphene: New bridge between condensed matter physics and quantum electrodynamics. arXiv 2007, arXiv:0704.0438. [Google Scholar] [CrossRef]
- Bordag, M.; Khusnutdinov, N.; Klimchitskaya, G.L.; Mostepanenko, V.M. Comment on “Electric conductivity of graphene: Kubo model versus a nonlocal quantum field theory model”. arXiv 2025, arXiv:2506.10792. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Wang, J.S.; Antezza, M. Electric conductivity in graphene: Kubo model versus a nonlocal quantum field theory model. Phys. Rev. B 2025, 111, 115428. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics (Course of Theoretical Physics), 3rd ed.; Pergamon Press: Oxford, UK, 1980; Part 1, Volume 5. [Google Scholar]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. general theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570. [Google Scholar] [CrossRef]
- Noble, B. Methods Based on the Wiener—Hopf Technique for the Solution of Partial Differential Equations; Pergamon: New York, NY, USA, 1958. [Google Scholar]
- Weinstein, L.A. The Theory of Diffraction and the Factorization Method; Golem: New York, NY, USA, 1969. [Google Scholar]
- Ilyinsky, A.S.; Slepyan, G.Y.; Slepyan, A.Y. Propagation, Scattering and Dissipation of Electromagnetic Waves; IEE Electromagnetic Waves Series 36; Peter Peregrinus Ltd.: London, UK, 1993. [Google Scholar]
- Slepyan, G.Y.; Krapivin, N.A.; Maksimenko, S.A.; Lakhtakia, A.; Yevtushenko, O.M. Scattering of Electromagnetic Waves by a Semi-Infinite Carbon Nanotube. Int. J. Electron. Commun. 2001, 55, 273. [Google Scholar] [CrossRef]
- Margetis, D.; Stauber, T. Theory of plasmonic edge states in chiral bilayer systems. Phys. Rev. B 2021, 104, 115422. [Google Scholar] [CrossRef]
- Slepyan, G.Y.; Maksimenko, S.A.; Lakhtakia, A.; Yevtushenko, O.; Gusakov, A.V. Electrodynamics of carbon nanotubes: Dynamic conductivity, impedance boundary conditions, and surface wave propagation. Phys. Rev. B 1999, 60, 17136. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory-Analysis and Design, 3rd ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Hanson, G.W.; Yakovlev, A.B. Operator Theory for Electromagnetics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Ishimaru, A. Radiation and Electromagnetic Wave Propagation Scattering; Prentice-Hall, Englewood Cliffs: Hoboken, NJ, USA, 1991. [Google Scholar]
- Hallén, E. Theoretical investigation into the transmitting and receiving quality of antennae. Nova Acta Upsal. 1938, 11, 1–44. [Google Scholar]
- Levin, B. Antennas Rigorous Methods of Analysis and Synthesis, 1st ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Levin, M.L.; Rytov, S.M.; Shafranov, V.D.M.A. Leontovich’s researches in electrodynamics: For M. A. Leontovich’s 80th birthday. Sov. Phys. Usp. 1983, 26, 353. [Google Scholar] [CrossRef]
- Forati, E.; Mueller, A.D.; Yarandi, P.G.; Hanson, G.W. A new formulation of Pocklington’s equation for thin wires using the exact kernel. IEEE Trans. Antennas Propag. 2011, 59, 4355. [Google Scholar] [CrossRef]
- Papakanellos, P.J.; Fikioris, G.; Michalopoulou, A. On the oscillations appearing in numerical solutions of solvable and nonsolvable integral equations for thin-wire antennas. IEEE Trans. Antennas Propag. 2010, 58, 1635–1644. [Google Scholar] [CrossRef]
- Shuba, M.V.; Maksimenko, S.A.; Slepyan, G.Y. Absorption, cross-section and near-field enhancement in finite-length carbon nanotubes in the terahertz-to-optical range. J. Comput. Theor. Nanosci. 2009, 6, 2016–2023. [Google Scholar] [CrossRef]
- Shuba, M.V.; Melnikov, A.V.; Kuzhir, P.P.; Maksimenko, S.A.; Slepyan, G.Y.; Boag, A.; Conte, A.M.; Pulci, O.; Bellucci, S. Integral equation technique for scatterers with mesoscopic insertions: Application to a carbon nanotube. Phys. Rev. B 2017, 96, 205414. [Google Scholar] [CrossRef]
- Shuba, M.V.; Slepyan, G.Y.; Maksimenko, S.A.; Thomsen, C.; Lakhtakia, A. Theory of multiwall carbon nanotubes as waveguides and antennas in the infrared and the visible regimes. Phys. Rev. B 2009, 79, 155403. [Google Scholar] [CrossRef]
- Nemilentsau, A.M.; Slepyan, G.Y.; Maksimenko, S.A. Thermal radiation from carbon nanotubes in the terahertz range. Phys. Rev. Lett. 2007, 99, 147403. [Google Scholar] [CrossRef]
- Maksimenko, S.A.; Shuba, M.V.; Kuzhir, P.P.; Batrakov, K.G.; Slepyan, G.Y. Challenges and Perspectives of Nanoelectromag-netics in the THz range. In Proceedings of the IEEE Computer Society Annual Symposium, Montpellier, France, 8–10 July 2015. [Google Scholar]
- Melnikov, A.V.; Kuzhir, P.P.; Maksimenko, S.A.; Slepyan, G.Y.; Boag, A.; Pulci, O.; Shelykh, I.A.; Shuba, M.V. Scattering of electromagnetic waves by two crossing metallic single-walled carbon nanotubes of finite length. Phys. Rev. B 2021, 103, 075438. [Google Scholar] [CrossRef]
- Nemilentsau, A.M.; Slepyan, G.Y.; Maksimenko, S.A.; Lakhtakia, A.; Rotkin, S.V. Spontaneous decay of the excited state of an emitter near a finite-length metallic carbon nanotube. Phys. Rev. B 2010, 82, 235411. [Google Scholar] [CrossRef]
- Hao, J.; Hanson, G.W. Optical scattering from a planar array of finite-length metallic carbon nanotubes. Phys. Rev. B 2007, 75, 165416. [Google Scholar] [CrossRef]
- Katsnelson, M.I. Graphene: Carbon in Two Dimensions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Physical Kinetics (Course of Theoretical Physics), 3rd ed.; Pergamon Press: Oxford, UK, 1980; Volume 10. [Google Scholar]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review; Dover Civil and Mechanical Engineering Series; Courier Corporation: North Chelmsford, MA, USA, 2000. [Google Scholar]
- Meixner, J. The behavior of electromagnetic fields at edges. IEEE Trans. Antennas Propag. 1972, 20, 442. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Felsen, L.B.; Marcuvitz, N. Radiation and Scattering of Waves; IEEE Press Series on Electromagnetic Waves; Prentice-Hall: Englewood Cliffs, NJ, USA, 1972. [Google Scholar]
- Omoriyekomwan, J.E.; Tahmasebi, A.; Zhang, J.; Yu, J. Synthesis of super-long carbon nanotubes from cellulosic biomass under microwave radiation. Nanomaterials 2022, 12, 737. [Google Scholar] [CrossRef]
- Gao, Z.; Oudjedi, L.; Faes, R.; Moroté, F.; Jaillet, C.; Poulin, P.; Lounis, B.; Cognet, L. Optical detection of individual ultra-short carbon nanotubes enables their length characterization down to 10 nm. Sci. Rep. 2015, 5, 17093. [Google Scholar] [CrossRef]
- Fangohr, H.; Chernyshenko, D.S.; Franchin, M.; Fischbacher, T.; Meier, G. Joule heating in nanowires. Phys. Rev. B 2011, 84, 054437. [Google Scholar] [CrossRef]
- Lu, W.; Krasavin, A.V.; Lan, S.; Zayats, A.V.; Dai, Q. Gradient-induced long-range optical pulling force based on photonic band gap. Light Sci. Appl. 2024, 13, 93. [Google Scholar] [CrossRef]
- Tao, Y.; Gao, Y.; Liu, Z.; Chen, Y.; Liu, W.; Yu, G.; Ren, Y. Many-body electrohydrodynamic contactdynamics in alternating-current dielectrophoresis: Resolving hierarchical assembly of soft binarycolloids. Phys. Fluids 2025, 37, 082043. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berghaus, T.; Miloh, T.; Gottlieb, O.; Slepyan, G.Y. Electrodynamics of Carbon Nanotubes with Non-Local Surface Conductivity. Appl. Sci. 2025, 15, 11398. https://doi.org/10.3390/app152111398
Berghaus T, Miloh T, Gottlieb O, Slepyan GY. Electrodynamics of Carbon Nanotubes with Non-Local Surface Conductivity. Applied Sciences. 2025; 15(21):11398. https://doi.org/10.3390/app152111398
Chicago/Turabian StyleBerghaus, Tomer, Touvia Miloh, Oded Gottlieb, and Gregory Ya. Slepyan. 2025. "Electrodynamics of Carbon Nanotubes with Non-Local Surface Conductivity" Applied Sciences 15, no. 21: 11398. https://doi.org/10.3390/app152111398
APA StyleBerghaus, T., Miloh, T., Gottlieb, O., & Slepyan, G. Y. (2025). Electrodynamics of Carbon Nanotubes with Non-Local Surface Conductivity. Applied Sciences, 15(21), 11398. https://doi.org/10.3390/app152111398








