Abstract
Public CVE feeds add tens of thousands of entries each year, overwhelming patch-management capacity. We model the CWE–CVE–CPE triad and, for each CWE, build count-weighted product co-exposure graphs by projecting CVE–CPE links. Because native graphs are highly fragmented, we estimate graph-distance box-counting dimensions component-wise on the fragmented graphs using greedy box covering on unweighted shortest paths, then assess significance on the largest component of reconnected graphs. Significance is evaluated against degree-preserving nulls, reporting null percentiles, a z-score–based p-value, and complementary KS checks. We further characterise meso-scale organisation via normalized rich-club coefficients and k-core structure. Additionally, we quantify percolation sensitivity on the reconnected graphs by contrasting targeted removals with random failures for budgets of 1%, 5%, 10%, and 20%. This quantification involves tracking changes in largest-component size, average shortest-path length on the LCC, and global efficiency, and an amplification factor at 10%. Our corpus covers the MITRE CWE Top 25; we report high-level summaries for all 25 and perform the deepest null-model and sensitivity analyses on a subset of 12 CWEs selected on the basis of CVE volume. This links self-similar topology on native fragments with rich-club/core organisation and disruption sensitivity on reconnections, yielding actionable, vendor/software-type-aware mitigation cues. Structural indices are used descriptively to surface topological hotspots within CWE-conditioned product networks and are interpreted alongside, not in place of, EPSS/KEV/CVSS severity metrics.
1. Introduction
The National Vulnerability Database (NVD) publishes tens of thousands of CVEs (Common Vulnerabilities and Exposures) each year, and severity metrics such as CVSS and EPSS score each CVE largely in isolation. A mesoscale structure in the CWE–CVE–CPE triad adds actionable signals for prioritisation and mitigation, where CWE denotes Common Weakness Enumeration, CVE denotes Common Vulnerabilities and Exposures, and CPE denotes Common Platform Enumeration [1,2,3].
Positioning. This study integrates three strands that are often treated as separate: (i) complex-network analysis applied to vulnerability and asset management, (ii) explicit modeling of the CWE–CVE–CPE triad with bipartite projection to count-weighted product co-exposure graphs, and (iii) mesoscale structure detection under degree-preserving nulls (normalized rich-club, k-core), coupled with robustness/percolation sensitivity. The contribution links self-similar topology on native fragmented graphs to rich-club/core organization on a diagnostic -bridged view and interprets these signals as vendor/type-aware prioritization cues. This approach clarifies what is established in prior work and what is novel here.
All CVEs disclosed between 1 March 2022 and 20 June 2025 are ingested and mapped to their CWE class and affected CPE products. For each CWE, a weighted CPE co-occurrence graph is built (edge weight = number of CVEs linking the two products). These graphs are often fragmented into small cliques; therefore, to enable mesoscopic analysis, an algorithmic reconnection step is applied that adds low-weight edges between components sharing vendor or product affinities and merges very small fragments. Throughout, a notion of weighted exposure (aggregate CVE weight per product within a CWE) is used to rank structures of interest. The analysis pursues two intertwined objectives:
O1
Identify the CWE classes whose product co-occurrence graphs reveal disproportionate weighted exposure.
O2
Inform mitigation by revealing vendor/software-type structures (rich-clubs and high-core nodes) that shape cross-product exposure and can guide targeted patching and visual analytics.
These objectives yield three research questions:
RQ1:
On the fragmented graphs, do CWE-specific product graphs exhibit scale-invariant topology quantified by a non-trivial graph-distance box-counting dimension D?
RQ2:
Are the observed values of D (fragmented for estimation; reconnected LCC for significance) and rich-club coefficients statistically distinguishable from degree-preserving nulls (Chung–Lu, configuration, and edge-swap)?
RQ3:
On the reconnected graphs, does targeted removal of high-core or rich-club nodes reduce the largest connected component more than random or peripheral removals, indicating strong percolation sensitivity that could be useful for mitigation planning?
Prior research uses network methods to characterize technology ecosystems and spread/robustness patterns. Other work explicitly models CWE–CVE–CPE and discusses bipartite projection and statistical backbones. A separate line of work normalizes mesoscale effects via degree-preserving nulls and probes robustness through targeted vs. random removal. This work builds on these strands by measuring fractality on native fragments, applying normalized mesoscale probes on a diagnostic reconnection to avoid degree artefacts and using sensitivity contrasts to translate structure into actionable triage steps.
2. Background and Related Work
2.1. Theoretical Foundations
Fractality on Graphs. Let be a (possibly disconnected) graph endowed with the shortest-path distance . For , a box is a node set with . Denote by the minimum number of such boxes whose union covers V (or, equivalently, the sum of minima over connected components above a size threshold; see Methods). A power-law relation
with constant exponent indicates scale invariance; is the (graph) box-covering, or Minkowski–Bouligand, dimension [4]—this foundational method enables quantification of self-similarity in vulnerability networks. Because is discrete and networks are finite, estimation relies on finite-size scaling over a restricted range and on approximate box-covering algorithms (Methods). In vulnerability networks, is estimated on the fragmented CWE-specific product graphs (i.e., prior to the reconnection step) and goodness-of-fit is assessed against alternative scalings and degree-preserving null models. is estimated component-wise on fragmented graphs and, as a robustness check, significance is tested on the reconnected graph’s largest connected component against degree-preserving nulls (Section 3.6).
Structural Sensitivity Indicators. “Chaos-like” behaviour is viewed operationally as sensitivity of connectivity and efficiency to targeted perturbations rather than as deterministic chaos. Let H denote the reconnected product graph for a given CWE (vendor/product-aware low-weight bridging; see Methods). For a removal strategy s and budget (fraction of nodes removed), write for the residual graph after removing the top-p nodes by s (e.g., k-core index, betweenness centrality, or degree), and define
where restricts analysis to connected pairs. Sensitivity is tested by comparing under targeted removals (by degree, betweenness, or k-core index) against random failures on H.
2.2. Related Work
From Asset-Aware Scoring to Structural Context. Despite evidence that software weaknesses exhibit recurring patterns across decades, with certain vulnerability classes persistently affecting multiple software ecosystems [5], operational practice combines CPE-based asset filtering with exploit likelihood (EPSS) and the CISA KEV catalog to prioritise patches. However, these sources treat CVEs largely in isolation and provide limited mesoscale structure for reasoning across products [6,7,8]—motivating our structural approach to cross-product vulnerability analysis.
Triadic Knowledge Graphs: CWE–CVE–CPE. Threat knowledge graphs explicitly encode CWE–CVE–CPE relations for tasks such as link prediction and proactive defence [9,10]. This work differentiates itself by projecting the triad onto product co-exposure graphs for each CWE and analysing mesoscopic structure (fractality, cores, and rich-clubs) and percolation sensitivity relevant to mitigation. While knowledge graphs excel at entity–relation reasoning, the projection approach reveals structural patterns in product interdependencies that are obscured in the full tripartite representation.
Bipartite Projection and Edge Validation. Projecting a bipartite product–CVE graph onto products can inflate spurious ties if weights ignore multi-target CVEs. In this work, a count-weighted projection is used (each shared CVE contributes to the edge), following Newman’s collaborative network framework [11]. This approach is essential for constructing meaningful product co-exposure graphs from CVE–CPE bipartite data. Statistical edge validation [12] and backbone extraction [13]—powerful methods for filtering noise in projected networks—are not applied in the current pipeline but remain orthogonal enhancements that could further refine the signal-to-noise ratio in future iterations. Recent work shows that projected edges should be validated against bipartite null models with model-dependent thresholds and multiple-testing control [14]. Moreover, backbone extraction must respect edge constraints inherited from the bipartite graph; otherwise, spurious ties may persist or true ties be discarded [15].
Fractality and Box-Covering on Networks. Self-similarity in complex networks is commonly assessed via box-covering and the scaling of the minimum number of boxes versus scale [4]. This approach provides the theoretical foundation for our fractal dimension analysis. Studies on software-related graphs report non-trivial fractal dimensions and use such measurements for vulnerability/topology assessment [16,17], demonstrating the applicability of fractal analysis to security contexts. The box-counting dimension is estimated on fragmented CWE-specific product graphs, and significance is tested against degree-preserving nulls, extending these prior approaches to the specific domain of product co-exposure networks.
Null Models for Structure Detection. Degree-preserving surrogates underpin rigorous significance tests: configuration/Molloy–Reed models preserve the degree sequence [18]—used here for exact degree sequence preservation in our null ensembles—while Chung–Lu preserves expected degrees [19]—providing a complementary null family for validation. Edge-swapping (Maslov–Sneppen) provides an alternative rewiring approach for simple graphs [20]—and, as our third null family, ensures robustness of findings—and supports normalisation of rich-club effects.
Rich-Club, -Core, and Influence. Rich-club ordering captures elite, densely interlinked cores and should be normalised against nulls to avoid degree-driven artefacts [21]—normalized against configuration models in our analysis to isolate true preferential attachment. Weighted variants further reveal concentration of interaction strength [22]. Additionally, k-core decomposition identifies deeply embedded nodes [23,24]—used here to identify structurally critical products for targeted hardening—which often control connectivity and spreading dynamics. The network robustness literature shows that targeted removals (with targeting by degree/coreness/influence) can rapidly dismantle connectivity compared to random failures [25,26,27]—motivating our targeted-vs-random removal experiments and percolation sensitivity analysis. These tools are leveraged on reconnected product graphs to quantify percolation sensitivity and derive mitigation candidates (e.g., vendor/software-type aware hardening).
Positioning. Compared to prior work, this study (i) models CWE-specific product co-exposure with principled bipartite projection and potential for statistical validation; (ii) measures fractality on native fragmented graphs and validates against degree-preserving nulls; (iii) introduces a vendor/product-aware reconnection step to enable mesoscale analyses (rich-club, k-core, and sensitivity) while reporting robustness with/without artificial edges; and (iv) focuses the analysis on the MITRE CWE Top 25 [28], ensuring operational relevance to current vulnerability-management priorities.
Hypothesis 1
(H1 (Self-similar topology)). On fragmented graphs, the estimated differs significantly from degree-preserving surrogates, indicating self-similar wiring beyond degree effects.
Hypothesis 2
(H2 (Percolation sensitivity)). On reconnected graphs, targeted removal of a small fraction () of high-core/rich-club nodes yields larger drops in and than random removal or null surrogates.
Concurrent support for H1 and H2 characterises a CWE’s product network as self-similar and percolation-sensitive, properties that can be exploited for mitigation design (e.g., vendor/software-type-aware hardening).
3. Data and Methods
3.1. Corpus Collection
The complete NVD [3] JSON feeds were snapshotted on 2025-06-21, and CVEs published from 1 March 2022–20 June 2025 that specify at least one CWE and one CPE were retained. CPE 2.3 is canonicalised to part:vendor:product, and repeated CPEs per CVE are de-duplicated. Note: due to the 2025 NVD enrichment backlog, records without CWE/CPE may be under-represented in our sample.
3.2. CWE Selection and Weighted Exposure
Let denote the native (fragmented) product co-exposure graph for CWE w, as obtained via a count-weighted projection (each CVE that co-mentions two products contributes to the edge weight).
The product-level exposure of is defined as
and the CWE-level weighted exposure as . Unless stated otherwise, the main analysis focuses on the intersection of MITRE CWE Top 25 with our time window; for coverage statistics (e.g., share of exposure explained), is computed for sets of interest and 95% bootstrap CIs are reported.
3.3. Product Co-Exposure Graph Construction
For each CWE w, a weighted product co-exposure graph is built. The vertex set contains the unique CPE identifiers (part:vendor:product) that appear in CVEs associated with w. An undirected edge exists if there is at least one CVE that lists both products u and v under CWE w. The edge weight counts distinct CVEs that co-mention the two products:
where is the set of CVEs mapped to w and is the set of products (CPEs) affected by CVE e.
3.4. Graph Reconnection (Post-Processing): Parameters and Controls
Native CWE graphs are often fragmented into cliques. To enable mesoscale analyses (rich-club, k-core, and sensitivity) a reconnected graph is constructed by adding low-weight bridges under two heuristics:
Heuristic 1 (Same-vendor). If two components contain products from the same vendor, their highest-degree representatives are connected. Heuristic 2 (Related-product). If base product names (prefix before underscores) match across components, highest-degree representatives are connected.
Each artificial edge receives weight and metadata connection_type ∈ {same_vendor,related_product}. Candidates are iteratively added until either (i) the number of connected components reaches a target (default ) or (ii) no eligible pairs remain. Small components (size , default ) are then merged into the nearest large component under vendor match by adding a single edge with weight and tag merge_small. If the largest component already covers more than of nodes, reconnection is skipped for that CWE.
Safeguards. Parallel edges and self-loops are forbidden; results are reported both with and without artificial edges; metrics sensitive to reconnection (rich-club, k-core, and sensitivity) are computed on , while fractality is estimated on native components of .
Defaults. Unless otherwise stated, , , and are used. Results are reported both with and without these artificial edges.
3.5. Fractal Dimension
Native fragmented graphs. For each CWE w, the top five connected components by size (restricted to components with ) are considered. Box-counting is applied component-wise exclusively on connected native components meeting minimal acceptance criteria (size , ). On each such component, greedy box-covering is run using the unweighted shortest-path distance for integer radii , the corresponding minimum box counts are computed, and versus is fitted by ordinary least squares (OLS). An estimate is accepted if at least three scales are available and the coefficient of determination satisfies . At the CWE level, the mean across valid components, a dispersion measure, and the count of accepted components are reported; this summary does not assert a single global invariant over a disconnected union. All primary findings (fractality on native graphs, weighted exposure , fragmentation) are computed without artificial edges.
Significance on native graphs; Diagnostic (-bridges). Primary significance assessments are computed on native graphs (no -bridges). On the largest connected component of , greedy box-covering is repeated with logarithmically spaced radii up to . OLS fits are run over RANSAC-like subsamples and the best- fit is retained; at least five scales, , and are required.
Bridge weight selection. Low-weight -bridges (–) are introduced solely as a diagnostic device to enable mesoscale probes (rich-club, k-core) in otherwise hyper-fragmented graphs. The interval [0.05, 0.10] is chosen to be at least an order of magnitude smaller than typical native edge weights (≥1), ensuring that bridges serve as “epsilon links” that enable connectivity probes without materially affecting weighted metrics. Ablation tests at 0.05 vs. 0.10 show no material change in mesoscale findings. Such panels are presented side-by-side with native results, explicitly labelled as Diagnostic (-bridges), and are not interpreted as either exploit reachability or aggregated risk.
3.6. Null Models and Significance Tests
All null-model analyses and significance tests are performed on native (no -bridges). For each native , 1000 surrogates are generated for each of three degree-preserving nulls: (i) Chung–Lu (expected degrees; simple graphs), (ii) configuration (exact degree sequence; simple graphs), and (iii) degree-preserving edge-swaps (Numba-accelerated; successful swaps with up to attempts; loops and multi-edges rejected). For the fractal dimension, the following are reported: (i) the empirical percentile of the observed D within each null ensemble and the empirical p-value (fraction of null D greater than or equal to the observed); (ii) auxiliary z-score–based p-values and KS two-sample checks; and (iii) [2.5, 97.5] percentile bands for statistics of interest. Diagnostic (-bridges) panels, when shown, are excluded from null fitting and significance reporting. Beyond degree-preserving surrogates (configuration, Chung–Lu, edge-swaps), significance can also be incorporated at the projection stage via edge-wise tests derived from bipartite generative models [14]. This aligns with recent guidance on constructing backbones under explicit edge constraints for bipartite projections [15]. We therefore report degree-controlled null results and, where applicable, confirm robustness to optionally validated backbones.
Implementation Details
Chung–Lu sampling is restricted to simple graphs by rejection of self-loops and multi-edges; edge-swaps (Maslov–Sneppen) perform successful swaps (with attempts), while rejecting moves that create loops or multi-edges. For weighted tests, edge weights are reshuffled over a fixed topology to isolate topology from strength. Any use of -bridges is limited to clearly labelled Diagnostic visualizations and does not enter primary estimates, null comparisons, exposure , or fragmentation summaries.
3.7. Core and Rich-Club Structure
Primary core/rich-club results are computed on native graphs (no -bridges). Node coreness (Batagelj–Zaveršnik) and the normalized rich-club coefficient are computed, where the expectation is calculated over configuration-model surrogates. Rich-club significance is marked when and the empirical p-value (fraction of null exceeding ) is <0.05. When fragmentation precludes estimation, Diagnostic (-bridges) panels are shown side-by-side for qualitative context only; these do not support claims about exploit reachability or aggregate risk.
3.8. Sensitivity to Targeted Removal
Removal strategies degree, betweenness, k-core, and random are evaluated for on the native largest connected component (LCC). For each p, the following are measured: (i) the relative reduction in the largest connected component, (ii) the relative change in average shortest-path length on the LCC, and (iii) the relative change in global efficiency. Random removal is averaged over 50 trials.
Operational interpretation: The sensitivity analysis quantifies the potential topological impact of removing nodes/edges for triage and what-if planning. It does not imply immediate removal/patching and should be interpreted alongside operational constraints (maintenance windows, SBOM/dependency integrity, rollback readiness). For betweenness calculations, exact values are computed on the LCC where tractable; for larger graphs, a standard random-source approximation with multiple seeds is used and uncertainty is reported via bootstrap confidence intervals.
Impact is summarised at by the amplification factor (targeted vs. random reduction of the LCC), and full curves are included in the appendix. Diagnostic (-bridges) curves, when displayed, are side-by-side overlays for qualitative contrast and are excluded from aggregated metrics.
3.9. Vendor/Type Structure
For descriptive context, vendor composition within components is summarised and ecosystems are labelled (e.g., mono_vendor_X, dominated_X, diverse_ecosystem) based on vendor share, as determined by the analysis pipeline. Assortativity coefficients are not computed in the current implementation. Any Diagnostic (-bridges) visualizations serve purely illustrative purposes and are not part of the primary quantitative results.
4. Results and Discussion
4.1. Fractal Structure on Native Fragmented Graphs
As shown in Figure 1, CWE-78 product co-exposure graphs exhibit strong native fragmentation with isolated, vendor-specific clusters (panel a). Applying a lightweight diagnostic reconnection with -bridges (dashed edges, weight = 0.05) reveals mesoscale structure (panel b). This reconnection is used solely for structural analysis and does not imply exploit reachability.
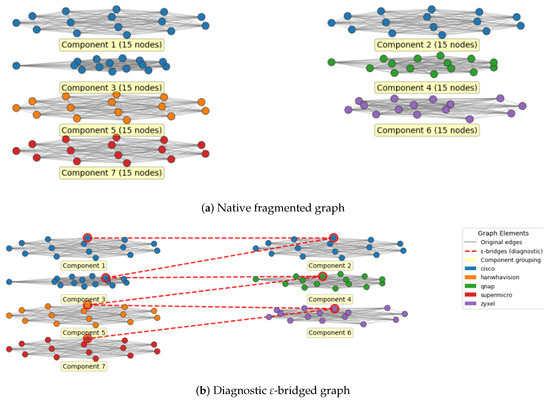
Figure 1.
Illustrative example of CWE-78 (OS Command Injection) product co-exposure graphs. (a) Native fragmented graph showing isolated vendor-specific clusters. (b) Diagnostic reconnected graph with -bridges (dashed lines, weight = 0.05) enabling mesoscale analysis. Note: reconnection is diagnostic and does not imply exploit reachability.
Table 1 shows the fractal dimension analysis performed on the native fragmented vulnerability networks before reconnection. The analysis examines the top five largest connected components for each CWE, with coverage ranging from a mere 22.2% (CWE-79) to 66.9% (CWE-416), highlighting the severe fragmentation in these native graphs. The number of nodes varies significantly across CWEs, ranging from 1507 (CWE-862) to 11971 (CWE-787), while the component counts range from 68 to 523, illustrating diverse fragmentation patterns. Notably, 10 out of 12 CWEs exhibit fractal properties in at least one of their top components, with accepted box-counting dimensions () spanning from 1.063 to 2.489. The variation in the number of components showing fractal behaviours (zero to four for each CWE) and the range of fractal dimensions suggest fundamentally different organizational principles across vulnerability classes. Two CWEs (CWE-352 and CWE-862) show no fractal structure in their top five components, possibly indicating either random organization or insufficient component size for reliable fractal analysis.

Table 1.
Fractal analysis of native fragmented product co-exposure graphs. We analyse the top five components for each CWE. Coverage is the share of nodes spanned by those components. Avg is the unweighted mean over components whose box-counting fits pass the acceptance rule (OLS on vs. , scales, ). “—” indicates that there is no accepted component.
Findings: A self-similar (fractal) signal appears in 10/12 CWEs, but it is localized within the largest native components. Average dimensions span a broad range, with higher values for CWE-476 (2.489), CWE-416 (2.339), and CWE-79 (2.297) and lower values for CWE-22 (1.063) and CWE-89 (1.404). CWE-787 shows strong intra-CWE heterogeneity (component-level from ≈1.06 to ≈3.05; mean 1.952). Two CWEs (CWE-352 and CWE-862) have no accepted component among the top five.
Implications: Coverage of the analysed components ranges from 22.2% to 66.9%, underscoring high fragmentation. Scale invariance concentrates in specific product clusters, which indicates the need for significance testing on the reconnected largest components and prioritizing CWEs with higher average for robustness/percolation experiments. The presence of fractal structure in the majority of CWEs, despite severe fragmentation, suggests that vulnerability co-exposure patterns exhibit self-similar organization at multiple scales. This finding implies that similar vulnerability-propagation mechanisms operate across different network scales, from local product clusters to larger vendor ecosystems. The absence of fractal properties in CWE-352 and CWE-862 warrants further investigation to clarify whether these represent fundamentally different vulnerability architectures or merely artefacts of extreme fragmentation.
4.2. Reconnection Effects and Implications for Mitigation
Figure 2 shows the distribution of bridge types introduced during the reconnection process. The analysis reveals that the majority of added links (64.8%) connect products from the same vendor (same_vendor), while connections between related products account for 17.4% and small component merges represent 17.8% of the total bridges. This distribution demonstrates that the reconnection process preserves vendor and product homophily rather than creating arbitrary cross-vendor shortcuts, suggesting that vendor-specific mitigation strategies could effectively address multiple vulnerability paths simultaneously.
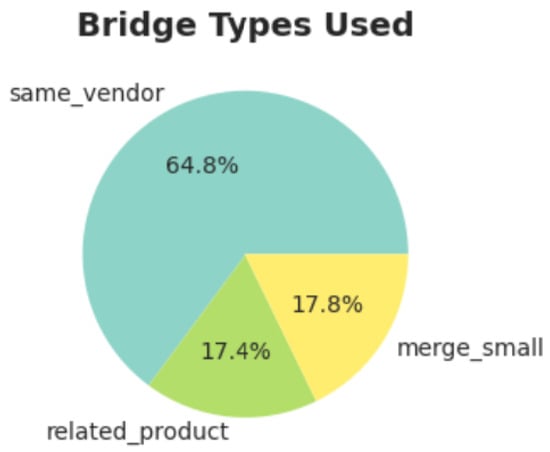
Figure 2.
Types of bridges added during reconnection. Most links are same_vendor (64.8%), followed by related_product (17.4%) and merge_small (17.8%). This mix indicates that bridging largely respects vendor/product homophily rather than adding arbitrary shortcuts.
Figure 3 shows the quantitative impact of reconnection on graph fragmentation across different CWEs. The percentage reduction in connected components ranges from approximately 30% to over 60%, with higher values indicating more successful defragmentation. These substantial reductions reveal previously hidden vendor and product relationships that were obscured by the initial fragmentation, enabling more comprehensive mesoscale network analysis and providing better insights into the true connectivity patterns within each vulnerability class.
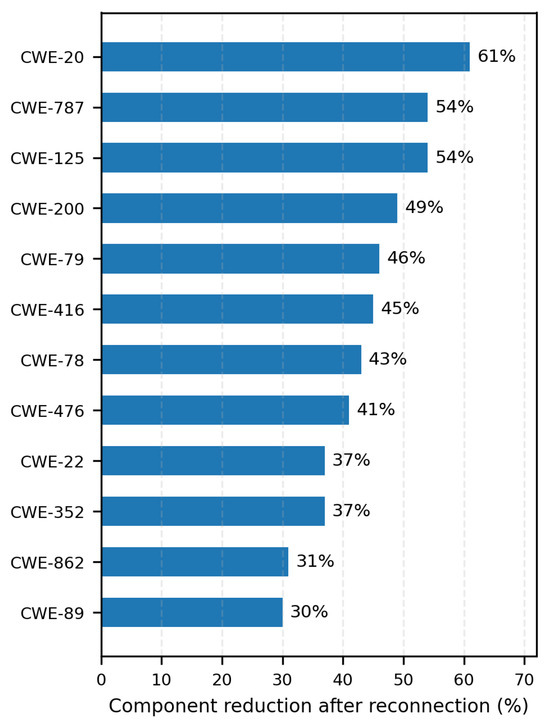
Figure 3.
Fragmentation reduction after reconnection. Bars show the percentage drop in the number of connected components for each CWE (higher is better). Large reductions expose latent vendor/product structure and enable mesoscale analysis on substantially more connected graphs.
In Figure 4, the growth factors for the largest connected component after reconnection compared to the native fragmented graphs are found. The LCC expansion ranges from 1.10× to 4.29×, with CWE-78 and CWE-79 showing particularly dramatic increases above 3×. These high growth factors indicate strong cross-product coupling within these vulnerability classes, suggesting that a relatively small set of vendors or products acts as central hubs governing vulnerability exposure propagation, making them critical targets for prioritized mitigation efforts.
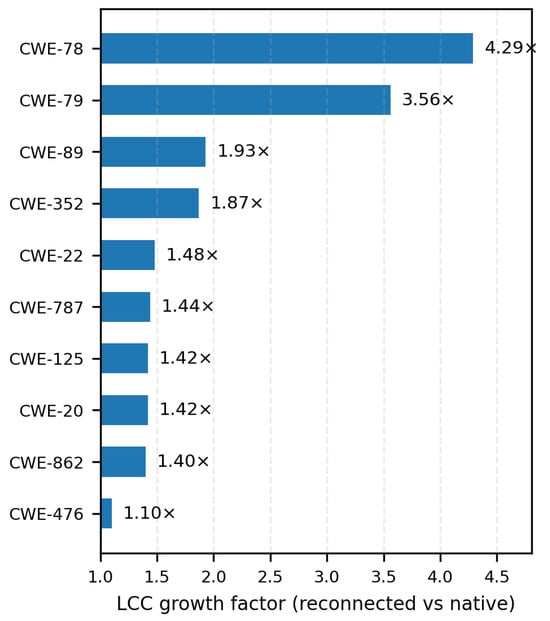
Figure 4.
Largest connected component (LCC) growth factor after reconnection (reconnected vs. native). Values above (e.g., CWE-78 and CWE-79) reveal strong cross-product coupling, suggesting that a small set of vendors/products governs exposure propagation within the class.
Reconnection impact. Reconnection reduces fragmentation by 30–61% across the top CWEs (Figure 3), with the largest drops for CWE-20 (61%), CWE-787/CWE-125 (54%), and CWE-200 (49%). The LCC expands by 1.10–4.29× (Figure 4); standout cases are CWE-78 (4.29×) and CWE-79 (3.56×), indicating concentrated, cross-product exposure.
CWE-78 (OS Command Injection). The strong LCC growth (4.29×) observed after diagnostic reconnection is consistent with cross-product reuse of command-execution modules within vendor ecosystems; this is a diagnostic signal for prioritizing controls and staged patches on that high-core/rich-club ring.
CWE-79 (Cross-Site Scripting). The 3.56× LCC growth suggests distributed but vendor-consistent pockets reflecting shared templating/rendering frameworks; the diagnostic structure highlights where CSP/sanitization controls yield outsized benefit.
CWE-22 (Path Traversal). The cohesive core aligns with shared path/file-handling components across services; this diagnostic pattern supports gating ingress and hardening shared handlers ahead of broad rollouts.
CWE-89 (SQL Injection). Concentration in a few vendor/type clusters likely reflects shared query-construction stacks; the diagnostic core guides early hardening of those stacks.
Takeaways for patching and risk. (1) The bridge mix (Figure 2) supports vendor-centric mitigation: batching patches across a vendor’s related products can neutralize many added paths at once. (2) Where LCC growth is high (Figure 4), exposure is systemic; these CWEs should be prioritized for targeted hardening of rich-club/k-core nodes in the reconnected graphs. (3) Combining Table 1 with Figure 4 highlights CWEs that are both fractal on native fragments (e.g., CWE-79 and CWE-416) and highly connected after reconnection; these are prime candidates for core-first patch strategies to curb cross-product spread. (4) Conversely, CWEs with modest LCC gains (e.g., CWE-476: ) may benefit more from per-product remediation than from centralized vendor-wide actions.
4.3. Rich-Club, Cores, and Percolation Sensitivity on Reconnected Graphs
Table 2 gives the rich-club analysis results for all examined CWEs on their reconnected largest connected components. The normalized rich-club coefficient ranges from 1.39 to 3.99, with CWE-78 exhibiting the strongest rich-club phenomenon at nearly 4 times the expected value from random networks. All CWEs demonstrate statistically significant rich-club organization (sustained bands with ), though the degree threshold at which maximum enrichment occurs varies dramatically, from 12 (CWE-416) to 732 (CWE-20). This universal presence of rich-club structure indicates that high-degree nodes preferentially interconnect across all vulnerability classes, forming tightly coupled cores that could serve as efficient targets for disrupting vulnerability propagation. The variation in both intensity () and degree threshold () suggests that there are different architectural patterns across CWEs, which should be considered when designing targeted mitigation strategies.

Table 2.
Rich-club summary on the reconnected LCC. and the degree at which it occurs are read from the annotated panels.
Table 3 gives the maximum k-core values across all CWEs, providing a complementary view of network cohesion beyond the rich-club analysis. The maximum coreness values span a wide range from 54 (CWE-862) to 772 (CWE-200), with the latter representing an exceptionally deep and resilient core structure. Several CWEs exhibit remarkably high maximum coreness values above 600 (CWE-125, CWE-200, CWE-352, and CWE-20), indicating the presence of densely interconnected subgraphs that would require coordinated removal of hundreds of nodes to dismantle. These deep cores suggest that certain vulnerability classes have evolved highly redundant exposure patterns where products are multiply connected through shared vulnerabilities. The correlation between high coreness and certain CWE types points to fundamental differences in how vulnerabilities manifest across software ecosystems, with implications for both the natural resilience of these networks and the difficulty of comprehensive remediation.

Table 3.
k-core distribution summary (maximum coreness as reported in panel titles). Larger values suggest deeper, more cohesive cores.
Table 4 gives the comparative effectiveness of different node-removal strategies for disrupting the reconnected vulnerability networks. Betweenness centrality emerges as the dominant strategy for network disruption, proving most effective in six out of eleven CWEs with high impact (greater than 1.8× improvement over random removal). This dominance of betweenness-based targeting underscores the importance of bridge nodes that connect different product clusters in vulnerability propagation. Interestingly, the networks exhibit a bimodal response pattern: while most CWEs show high sensitivity to targeted removal (marked as H), suggesting the existence of critical bottleneck nodes, others, like CWE-125, CWE-416, and CWE-200, demonstrate low sensitivity (L), indicating more homogeneous, globally fragile structures where targeted strategies offer little advantage over random removal. This dichotomy has profound implications for defence prioritization—CWEs with high targeted sensitivity can benefit from focused hardening of key nodes identified through betweenness analysis, while those with low sensitivity require broader, more distributed mitigation approaches across the entire product ecosystem.

Table 4.
Robustness summary from the LCC size-reduction curves. We report the best targeted strategy and a qualitative effect at – versus random removal (H = high ≳ 1.8×; M = moderate∼1.3–1.8×; L = low ≲ 1.3×).
Interpretation and mitigation value.
(1) Pronounced rich-clubs (CWE-78/79/89/125/20/200/352/862) indicate tightly interlinked, high-degree product elites. Prioritizing patches for nodes in the rich band (high k and ) should yield outsized reductions in cross-product exposure. (2) Bridging vulnerability. For CWE-78/79/20/22/862, the betweenness-targeted strategy consistently dominates (Table 4), implying a small set of products act as structural bridges; vendor-wide patch bundles and segmentation around those bridges are expected to maximize systemic risk reduction. (3) Degree is a practical proxy in CWE-89/352/476, where degree- and betweenness-guided removals have similar effects. In operational pipelines, prioritizing by degree can approximate the benefit at lower computational cost. (4) Core-centric risk. CWE-476 and, at higher budgets, CWE-22/352 show rising impact for k-core removals, pointing to cohesive deep cores; for these classes, a core-first hardening pass (patch or temporarily isolate top k-shells) is warranted. (5) Global fragility vs. targeted sensitivity. CWE-125 exhibits large random-failure impact at 20% (random line overtakes targeted), suggesting broadly dispersed exposure: mitigation should rely not solely on elite targeting but on wider patch rollout and blast-radius containment. Conversely, CWE-416/200 show low sensitivity, so per-product fixes are likely sufficient.
Actionable recommendations. Use Table 2 to identify CWEs with strong rich-clubs; within each of these, rank products by betweenness (or degree when indicated) and concentrate vendor-bundled patches on those nodes. Where Table 3 signals deep cores, include top k-shells in the first patch wave to break cohesive exposure clusters. Finally, validate progress by tracking LCC shrinkage under the corresponding targeted strategy (Table 4).
Figure 5 provides a detailed visualization of the rich-club phenomenon for CWE-78, which demonstrates the strongest rich-club coefficient among all analysed vulnerability classes. The normalized coefficient maintains statistical significance (, shown as red points) across a wide range of degrees, reaching a remarkable peak of at degree . This nearly four-fold enrichment compared to random expectation reveals that high-degree products in the CWE-78 network are almost four times more likely to be interconnected than would occur by chance. The broad significance band indicates that this preferential attachment is not limited to a narrow degree range but persists across multiple network scales. This structural feature identifies a tightly coupled elite of approximately 246 products that form the backbone of vulnerability propagation in this class, making them prime candidates for coordinated vendor-bundled patching initiatives.
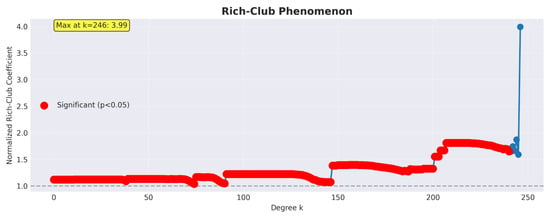
Figure 5.
CWE-78 rich-club on the reconnected LCC. The normalized coefficient (red points: ) shows a wide significance band and peaks at for , evidencing a tightly interlinked elite of products (blue line represents insignificance band). These nodes are prime mitigation targets for vendor-bundled patching.
Table 5 gives the comprehensive Structural Risk Index (SRI) that integrates multiple network metrics into a unified risk assessment framework. The SRI combines fractal dimension (weighted at 25%), LCC growth factor (30%), rich-club coefficient (25%), and betweenness-based removal effectiveness (20%) to produce normalized risk scores ranging from 0.30 to 0.83. CWE-78 and CWE-79 emerge as the highest-risk vulnerability classes with SRI values of 0.83 and 0.77, respectively, a result driven by their exceptional LCC growth (4.29× and 3.56×) and strong rich-club phenomena. All analysed CWEs exhibit fractal properties, confirming scale-invariant organization across the vulnerability landscape. The consistent dominance of betweenness-based targeting strategies across high-SRI CWEs reinforces the importance of identifying and hardening bridge nodes. The clear stratification of risk scores—with a top tier (CWE-78 and CWE-79), middle tier (CWE-476, CWE-20, and CWE-89), and lower tier (CWE-125)—provides a data-driven prioritization framework for allocating limited security resources.

Table 5.
Structural risk index (SRI) ranking for CWEs with both reconnection and rich-club analyses. (tilde = min–max normalization; higher ⇒ higher structural risk). Best s: Betw = betweenness; Deg = degree; Rand = random. SRI is a descriptive structural indicator, not a predictor of exploitation likelihood.
Figure 6 shows the robustness analysis for CWE-78, demonstrating how different node-removal strategies impact network connectivity at varying scales. The betweenness-guided removal strategy (likely shown as the steepest declining curve) consistently achieves the greatest LCC size reduction across all removal percentages, significantly outperforming degree-based, k-core-based, and random removal strategies. This superior performance of betweenness targeting indicates that the CWE-78 network contains critical bridging nodes whose removal can efficiently fragment the vulnerability-propagation paths. The divergence between targeted and random strategies becomes more pronounced as the removal percentage increases, suggesting that the network’s vulnerability to targeted attack intensifies at higher removal rates. The consistent hierarchy of strategy effectiveness (betweenness > degree > k-core > random) across different removal percentages confirms that a small set of high-betweenness products act as crucial connectors in the cross-product exposure network, making them optimal targets for prioritized patching efforts.
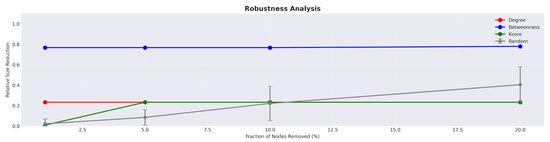
Figure 6.
CWE-78 robustness (relative LCC size reduction) under removals of 1%, 5%, 10%, and 20% of nodes. Betweenness-guided removal consistently outperforms degree, k-core, and random, indicating that a few bridging products concentrate cross-product exposure and should be prioritised. Legend: red line, Degree; blue line, Betweenness; green line, k-core; grey line, Random.
Figure 7 provides the k-core decomposition for CWE-89, revealing a maximum coreness of 225 and sustained node counts across high-order shells. The distribution pattern shows that significant numbers of nodes persist even at high k values, indicating a deeply nested core structure rather than a sharp drop-off typical of less cohesive networks. This sustained presence of nodes in high-k shells (likely visible as a gradual decline rather than abrupt termination) demonstrates that the CWE-89 vulnerability network contains a resilient, densely interconnected core that would require the coordinated removal of over 200 nodes to fully dismantle. The deep core structure suggests that simple targeted removal strategies may be insufficient; instead, a combined approach is needed that first addresses the innermost k-shells to break the cohesive centre and then employs betweenness-based targeting to disconnect the remaining fragments. This dual strategy—core-first hardening complemented by bridge removal—represents an optimal approach for mitigating CWE-89 vulnerabilities given its particular topological characteristics.
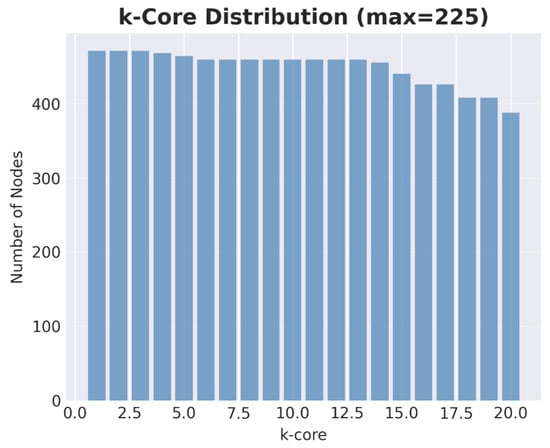
Figure 7.
CWE-89 k-core distribution (maximum coreness ). Sustained counts across high shells point to a relatively deep core; a core-first hardening pass, complemented by high-betweenness targeting, is appropriate for this class.
5. Conclusions and Operational Implications
Across the top 25 CWEs, the findings show the following: (i) there is a fractal signal in 10/12 classes on native fragments (Table 1); (ii) vendor/product–aware reconnection reduces fragmentation by 30–61% and expands the LCC by 1.10–4.29× (Figure 3 and Figure 4); (iii) there is pervasive rich-club ordering with peaks up to (CWE-78) and deep cores in some classes (e.g., in CWE-200) (see Table 2 and Table 3); (iv) there is strong percolation sensitivity: on several CWEs, removing only 5–10% high-betweenness nodes shrinks the LCC far more than random (Table 4), with CWE-78/79/20/22/862 most affected.
- Actionable mitigation playbook.
- Bridge-first patching. For CWEs where betweenness targeting dominates(CWE-78/79/20/22/862), prioritize patch bundles for top-betweenness products per vendor. The bridge mix (Figure 2, 64.8% same_vendor) implies vendor-centric campaigns neutralize many critical paths at once.
- Core-first hardening. Where k-core impact rises (CWE-476; at higher budgets also CWE-22/352), patch/isolate the highest shells () to break cohesive exposure clusters; combine with bridge-first for maximum effect.
- Rich-band suppression. In CWEs with strong rich-clubs(CWE-78/79/89/125/20/200/352/862), treat nodes in the significant band as an elite group to be remediated early (e.g., accelerated patch SLAs, config hardening, and temporary segmentation).
- When exposure is diffuse. For CWE-125, where random failures rival or exceed targeted effect at 20% (Table 4), favour broad rollouts based on weighted exposure rather than elite-targeting alone.
- Verification loop. Track post-patch LCC shrinkage and global efficiency drop on the reconnected graph as success metrics aligned to the sensitivity curves; reassess rich-club/k-core membership after each wave.
High SRI values (e.g., CWE-78/79) indicate classes where a small set of products controls systemic exposure and where targeted, vendor-bundled mitigation yields the largest payoff.
Operational use under patch latency and dependency constraints. The network-structural signals reported here are prioritization cues, not prescriptions for immediate patching. In device classes with long vendor windows (e.g., IoT fleets with 30–180 day cycles), the 1/5/10/20% sensitivity curves are used to identify a minimal effective set compatible with maintenance windows; where patching is deferred, operators apply compensating controls (virtual patching/WAF/IPS, protocol/TLS hardening), segmentation/micro-segmentation, and strict access controls to reduce the blast radius. For dependency-heavy hubs (e.g., OpenSSL), remediation follows staged roll-outs (canary/rings), SBOM-based impact assessment, ABI compatibility checks, and safe backports with automated rollback. Deferrals are time-bounded and linked to explicit control packages and monitoring. Thus, structure indicates where exposure is concentrated, while operational policy dictates how/when remediation proceeds.
SRI as descriptive complement. The Structural Risk Index (SRI) serves as a structure-aware descriptive index at the product-within-CWE level. By construction, SRI is orthogonal to per-CVE exploitation metrics (EPSS/KEV) and should be interpreted as complementary information highlighting topological concentration of exposure within CWE-specific product networks, not as a predictor of exploitation likelihood.
Limitations. Reconnection uses heuristics that, although vendor/type-aware, still introduce artificial links; significance checks and reporting with/without bridges mitigate this but do not fully eliminate bias. NVD enrichment gaps (2024–2025) may under-represent some CVEs/CWEs; the analysed corpus is restricted to CVEs containing both CWE and canonical CPE mappings within the time window (1 March 2022–20 June 2025). The temporal cutoff and data-completeness constraints mean that some MITRE Top-25 CWEs have insufficient data for full analysis; reported are 12 CWEs with sufficient volume for stable mesoscale estimates.
The current analysis uses part:vendor:product granularity for CPE canonicalization, which cannot reflect version-specific differences in vulnerability exposure. This choice was deliberately made to (i) avoid extreme sparsity from incomplete enrichment for 2024–2025 records and (ii) surface mesoscale regularities without confounding from version explosion. However, version-level granularity would better align with enterprise patch workflows where version-specific patching is common. Edge weights are count-based; statistical validation/backbone extraction was not applied in the present pipeline.
- Future work.
- Version granularity. Lift nodes to part:vendor:product:version and track time-sliced graphs to capture version-specific co-exposures and upgrade paths. This will involve (i) incorporating well-formed version fields, (ii) adding tech-stack granularity (e.g., major engine/runtime/library families) as attributes for roll-up views, (iii) normalizing cross-version connectivity via principled equivalence classes (e.g., semver-aware major/minor bucketing and LTS groupings), and (iv) evaluating version-aware backbones to control multi-target CVE inflation. Revisit sensitivity on rolling windows.
- Type/Language semantics. Add tags for software type and language (e.g., CMS/PHP) and extend reconnection to favour intra-type/-language bridging. This enables cross-vendor insights for ecosystems sharing code stacks.
- Edge validation. Incorporate bipartite statistical validation or weighted backbones to suppress spurious ties before reconnection; compare against vendor/type-preserving nulls.
- Operational coupling. Integrate exploit data and maintenance cadences to co-model structure and kinetics; evaluate risk reduction as a function of patch lead time on the reconnected backbone.
In summary, the observed self-similarity on native fragments, together with strong rich-club/bridge effects on reconnections, supports a structure-aware patching strategy consisting of vendor-bundled remediation of bridging elites, reinforced by core-first hardening where present, and broad exposure-based rollouts where fragility is diffuse.
Illustrative scenario (hypothetical). Consider CWE-78 (OS Command Injection). The native product co-exposure graph shows several vendor-consistent fragments; the diagnostic -bridged view reveals a cohesive high-core/rich-club ring around products exposing command-execution interfaces. A structure-aware rollout proceeds in two steps: (1) apply compensating controls on the identified ring (e.g., WAF/IPS rules on command endpoints, strict parameterization, mTLS on management channels, rate-limiting for administrative routes); (2) perform staged patching aligned to maintenance windows (canary → rings), beginning with the k-core/rich-club set. This scenario is illustrative, does not constitute a claim about any specific organization, and demonstrates how mesoscale cues inform a safe sequence under vendor patch latency and dependency stability constraints.
- Practitioner mapping (signal→action).
- Signal: High k-core/normalized rich-club on the diagnostic -view → Action: treat that ring as a priority set; deploy compensating controls on its ingress/management paths; stage patches there first with SBOM/rollback checks.
- Signal: Large LCC growth factor after diagnostic reconnection (e.g., CWE-78: 4.29×, CWE-79: 3.56×) → Action: expect cross-product coupling; harden shared execution/path modules before broad rollout.
- Signal: High targeted-vs-random amplification in sensitivity curves → Action: concentrate limited maintenance windows on the identified ring; defer periphery under monitored controls.
Author Contributions
Conceptualization, I.T.; methodology, I.T.; software, I.T.; validation, I.T.; formal analysis, I.T.; investigation, I.T.; resources, I.T.; data curation, I.T.; writing—original draft preparation, I.T. and M.C.C.; writing—review and editing, I.T. and M.C.C.; visualization, I.T. and M.C.C.; supervision, N.Ț.; project administration, N.Ț. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the Ministry of Research, Innovation and Digitization, CCCDI-UEFISCDI, project number PN-IV-P6-6.3-SOL-2024-2-0279, within PNCDI IV.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. Data are not publicly available due to privacy restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- About CVE–Common Vulnerabilities and Exposures. Available online: https://cve.mitre.org/about/ (accessed on 20 June 2025).
- Common Weakness Enumeration. Available online: https://cwe.mitre.org (accessed on 20 June 2025).
- NVD Vulnerability Details and Relations (CVE, CWE, CPE). Available online: https://nvd.nist.gov (accessed on 20 June 2025).
- Song, C.; Havlin, S.; Makse, H.A. Self-Similarity of Complex Networks. Nature 2005, 433, 392–395. [Google Scholar] [CrossRef]
- Gueye, A.; Galhardo, C.E.C.; Bojanova, I.; Mell, P. A Decade of Reoccurring Software Weaknesses. IEEE Secur. Priv. 2021, 19, 74–82. [Google Scholar] [CrossRef]
- Exploit Prediction Scoring System (EPSS): Model Documentation, Version 4.0. Available online: https://www.first.org/epss/ (accessed on 20 June 2025).
- Known Exploited Vulnerabilities Catalog. Available online: https://www.cisa.gov/known-exploited-vulnerabilities-catalog (accessed on 20 June 2025).
- Allodi, L. The Heavy Tails of Vulnerability Exploitation. In Proceedings of the Engineering Secure Software and Systems (ESSoS), Milan, Italy, 4–6 March 2015; LNCS. Volume 8978, pp. 133–148. [Google Scholar]
- Shi, Z.; Matyunin, N.; Graffi, K.; Starobinski, D. Uncovering CWE–CVE–CPE Relations with Threat Knowledge Graphs. arXiv 2023, arXiv:2305.00632. [Google Scholar] [CrossRef]
- Shi, Y.; Li, Z.; Wang, H. Threat Knowledge Graph Construction for Proactive Defence. ACM Trans. Priv. Secur. (TOPS) 2024, 27, 13. [Google Scholar]
- Newman, M.E.J. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys. Rev. E 2001, 64, 016132. [Google Scholar] [CrossRef]
- Tumminello, M.; Miccichè, S.; Lillo, F.; Piilo, J.; Mantegna, R.N. Statistically Validated Networks in Bipartite Complex Systems. PLoS ONE 2011, 6, e17994. [Google Scholar] [CrossRef]
- Serrano, M.Á.; Boguñá, M.; Vespignani, A. Extracting the multiscale backbone of complex weighted networks. Proc. Natl. Acad. Sci. USA 2009, 106, 6483–6488. [Google Scholar] [CrossRef]
- Cimini, G.; Carra, A.; Didomenicantonio, L.; Zaccaria, A. Meta-validation of bipartite network projections. Commun. Phys. 2022, 5, 76. [Google Scholar] [CrossRef]
- Neal, Z.P.; Neal, J.W. Illustrating the importance of edge constraints in backbones of bipartite projections. PLoS ONE 2024, 19, e0302973. [Google Scholar] [CrossRef] [PubMed]
- Gou, L.; Wei, B.; Sadiq, R.; Deng, Y. Topological Vulnerability Evaluation Model Based on Fractal Dimension of Complex Networks. PLoS ONE 2016, 11, e0146896. [Google Scholar] [CrossRef][Green Version]
- Wen, T.; Song, M.; Jiang, W. Evaluating Topological Vulnerability Based on Fuzzy Fractal Dimension. Int. J. Fuzzy Syst. 2019, 21, 823–835. [Google Scholar] [CrossRef]
- Molloy, M.; Reed, B. A critical point for random graphs with a given degree sequence. Random Struct. Algorithms 1995, 6, 161–180. [Google Scholar] [CrossRef]
- Chung, F.; Lu, L. The average distances in random graphs with given expected degrees. Proc. Natl. Acad. Sci. USA 2002, 99, 15879–15882. [Google Scholar] [CrossRef]
- Maslov, S.; Sneppen, K. Specificity and stability in topology of protein networks. Science 2002, 296, 910–913. [Google Scholar] [CrossRef]
- Colizza, V.; Flammini, A.; Serrano, M.A.; Vespignani, A. Detecting rich-club ordering in complex networks. Nat. Phys. 2006, 2, 110–115. [Google Scholar] [CrossRef]
- Opsahl, T.; Colizza, V.; Panzarasa, P.; Ramasco, J.J. Prominence and Control: The Weighted Rich-Club Effect. Phys. Rev. Lett. 2008, 101, 168702. [Google Scholar] [CrossRef]
- Seidman, S.B. Network structure and minimum degree. Soc. Netw. 1983, 5, 269–287. [Google Scholar] [CrossRef]
- Batagelj, V.; Zaveršnik, M. An O(m) Algorithm for Cores Decomposition of Networks. arXiv 2003, arXiv:cs/0310049. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabási, A.-L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Cohen, R.; Erez, K.; ben-Avraham, D.; Havlin, S. Breakdown of the Internet under intentional attack. Phys. Rev. Lett. 2001, 86, 3682–3685. [Google Scholar] [CrossRef]
- Morone, F.; Makse, H.A. Influence maximization in complex networks through optimal percolation. Nature 2015, 524, 65–68. [Google Scholar] [CrossRef] [PubMed]
- 2024 CWE Top 25 Most Dangerous Software Weaknesses. Available online: https://cwe.mitre.org/top25/archive/2024/2024_cwe_top25.html (accessed on 20 June 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).