Adaptive MEC–RBF Neural Network-Based Deflection Prediction for Prestressed Concrete Continuous Rigid Frame Bridges During Construction
Abstract
1. Introduction
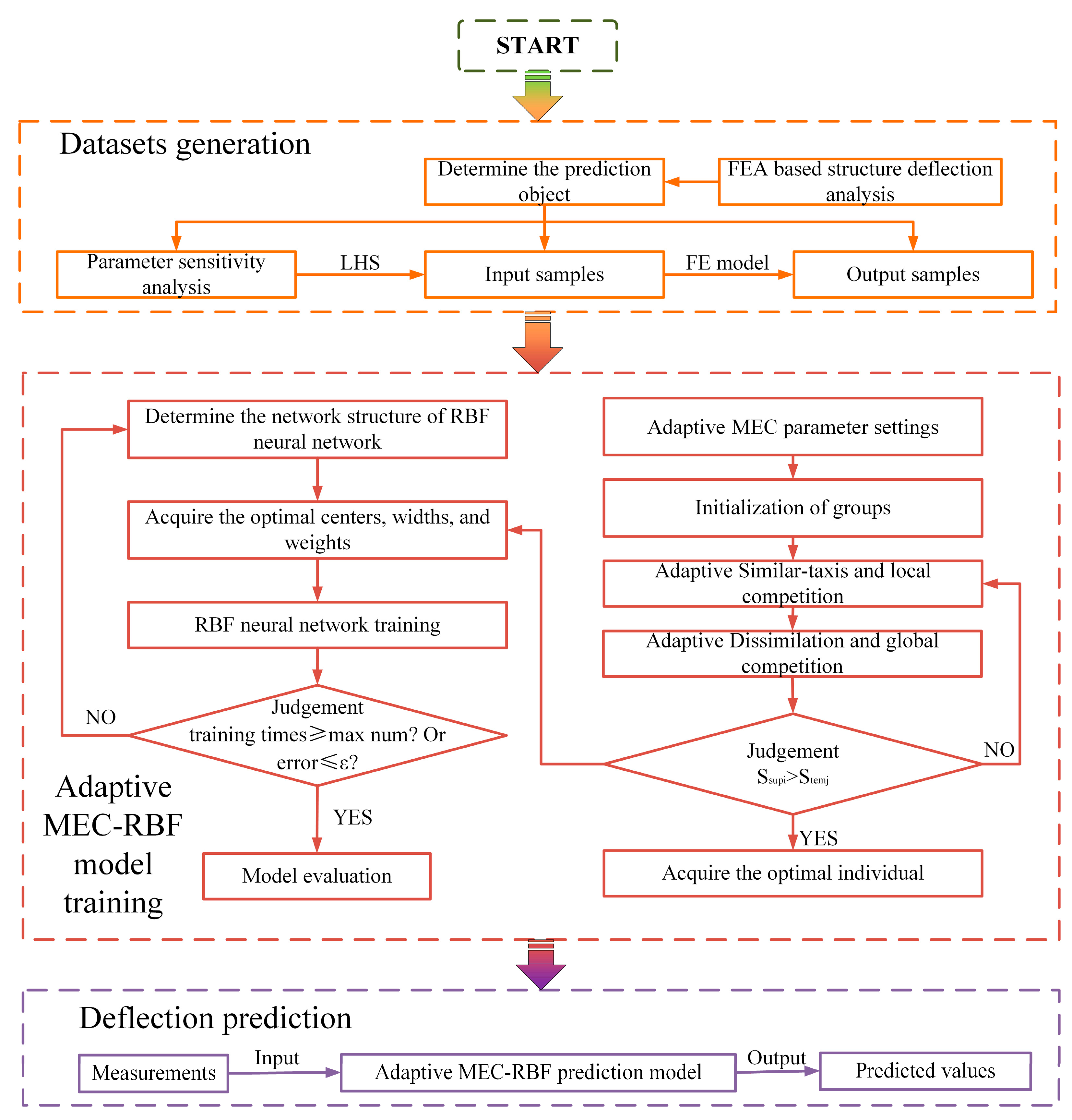
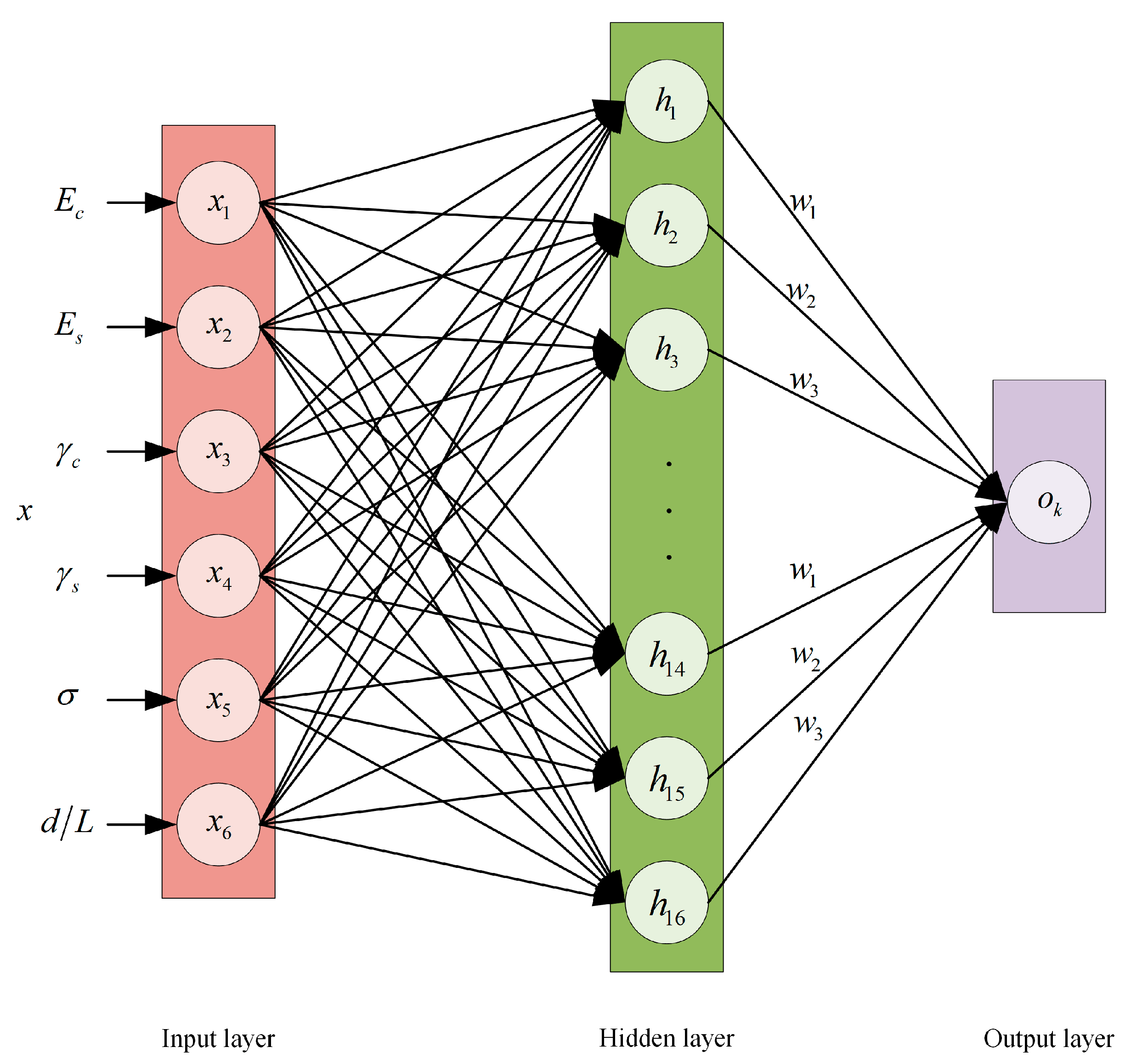
2. Deflection Prediction Method Based on an Adaptive MEC–RBF Neural Network
2.1. RBF Neural Network
2.2. Adaptive Mind Evolutionary Computation Algorithm
2.3. Framework for the Construction of a Deflection Prediction Method Based on an Adaptive MEC–RBF Neural Network
2.4. Evaluation Criteria
3. Case Study
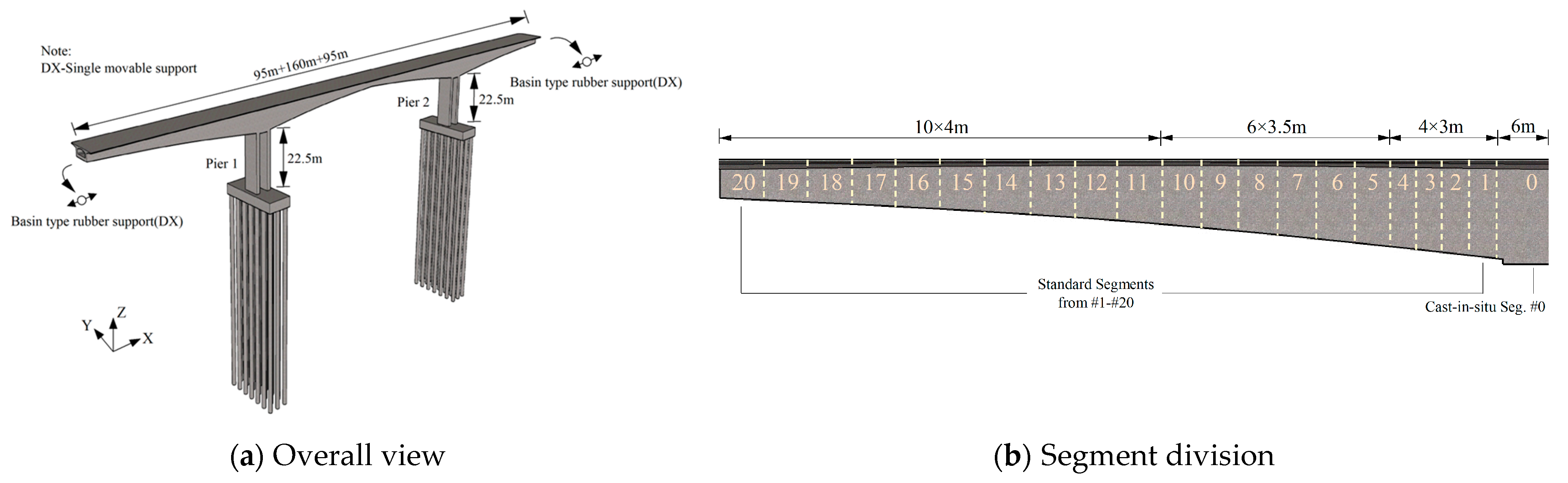
3.1. Bridge Overview
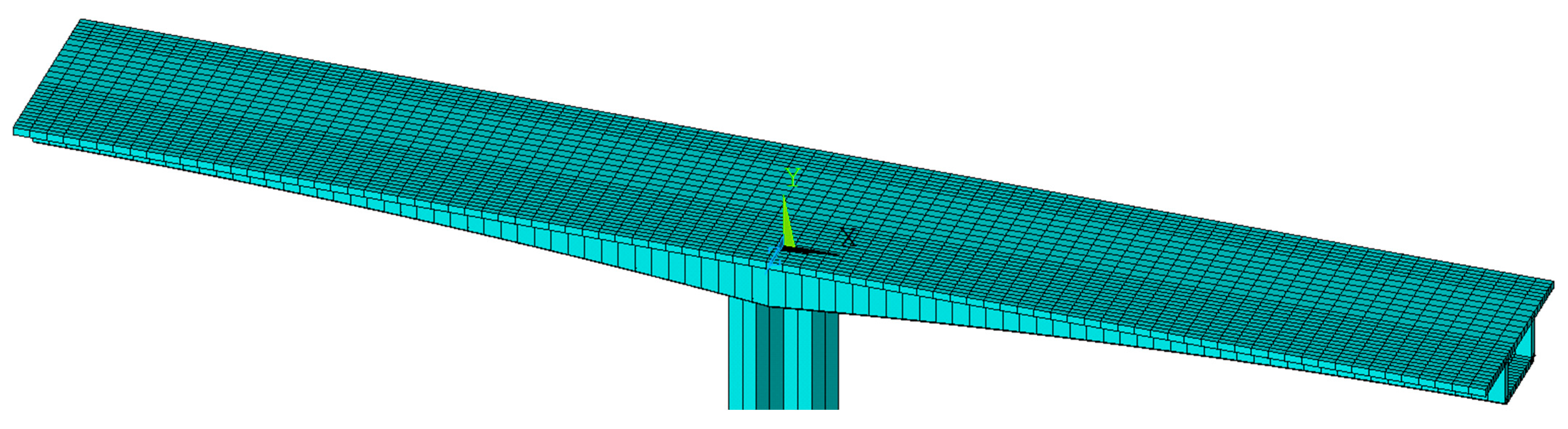
3.2. Finite Element Model
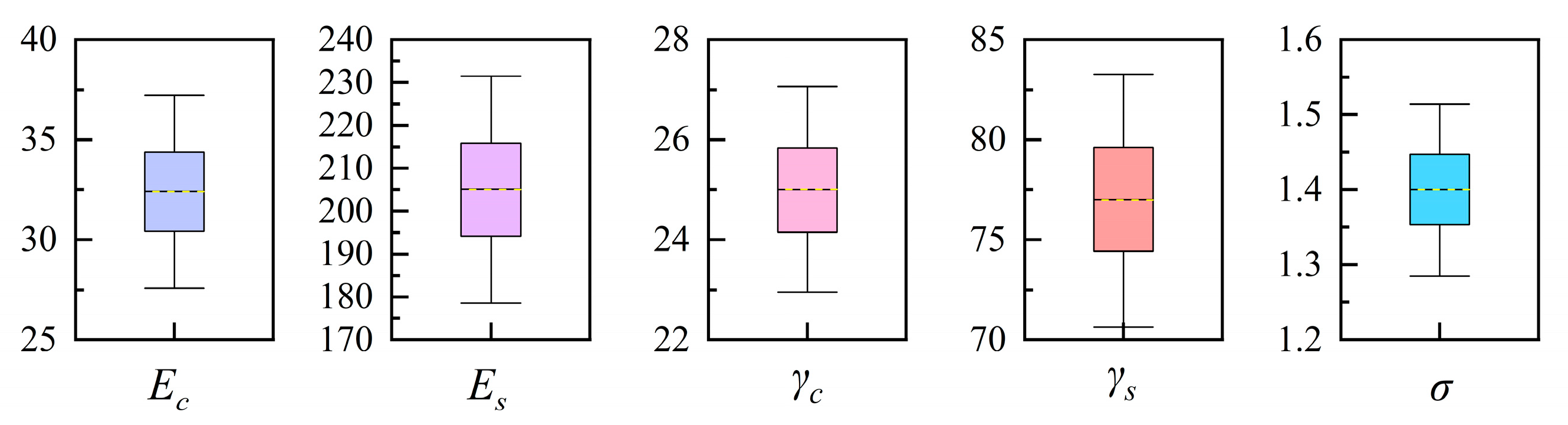
3.3. Parameter Selection and Sensitivity Analysis
3.4. Adaptive MEC–RBF Neural Network Prediction Model
3.4.1. Model Construction
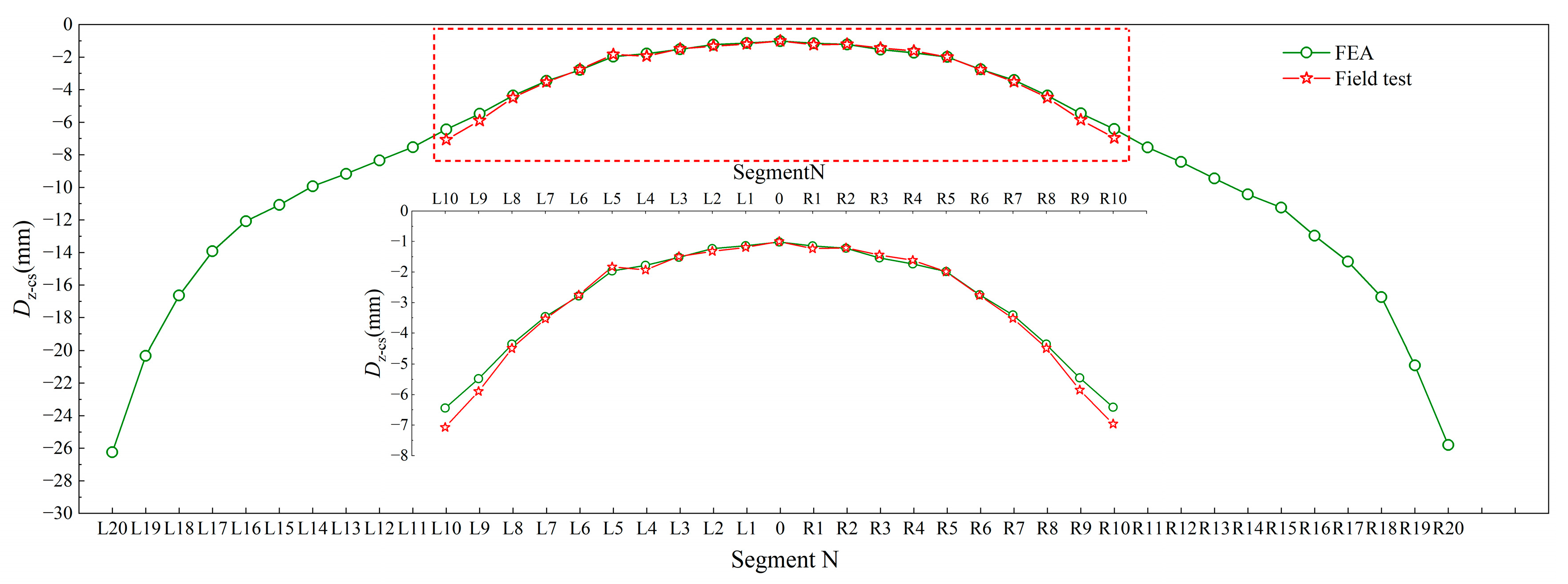
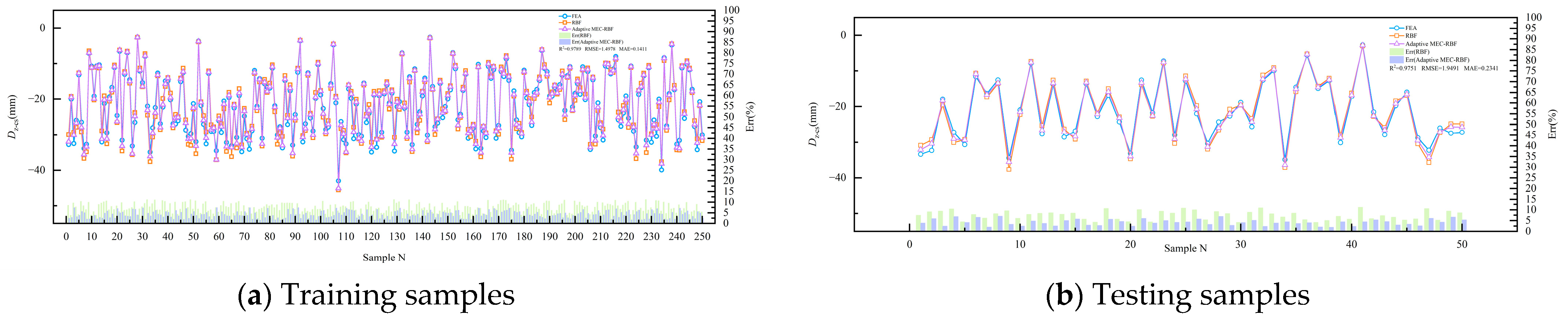
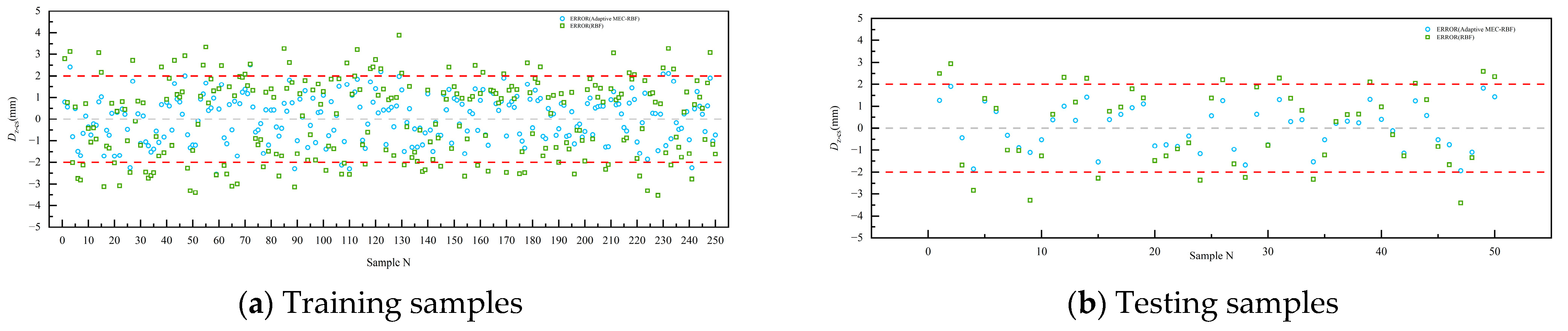
3.4.2. Model Validation
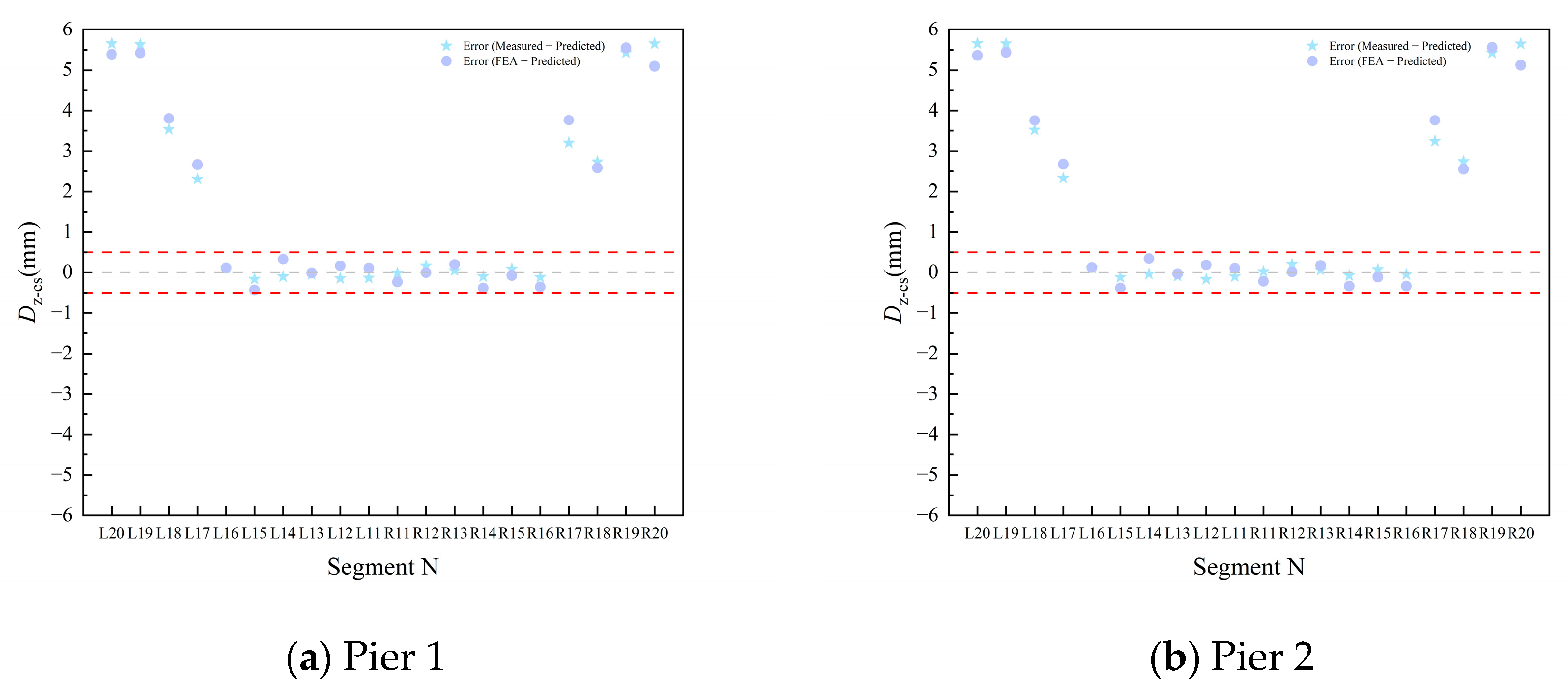
3.4.3. Analysis and Discussion of the Results
4. Conclusions
- The sensitivity analysis revealed that the parameter had the greatest influence on segment deflection, followed by the parameters , , , , and , whereas the other parameters exhibited relatively minor effects.
- A comparison with finite element analysis revealed that the adaptive MEC–RBF model achieved higher accuracy and computational efficiency than the conventional RBF model did, providing more precise deflection predictions during construction.
- Application of the adaptive MEC–RBF model to the Hannan Yangtze River Bridge demonstrated that its predictions were in good agreement with field measurements, confirming the accuracy and practical applicability of the proposed framework. These findings suggest that the approach can effectively support deflection control for prestressed concrete continuous rigid-frame bridges.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MEC | Mind evolutionary computation |
| RBF | Radial basis function |
| R2 | Coefficient of determination |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
References
- Petroski, H. Engineering: Infrastructure. Am. Sci. 2009, 97, 370–374. [Google Scholar] [CrossRef]
- Perez, A.I.; Ardaman, A.K. New infrastructure: Civil engineer’s role. J. Urban Plan. Dev. 1988, 114, 61–72. [Google Scholar] [CrossRef]
- Ge, Y.; Xiang, H. Concept and requirements of sustainable development in bridge engineering. Front. Archit. Civ. Eng. China 2011, 5, 432–450. [Google Scholar] [CrossRef]
- Paunova, D.; Tzonevska, D. Strategic development of the national road network. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1297, 012016. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, Z. Development of a novel type of open-web continuous reinforced-concrete rigid-frame bridge. J. Bridge Eng. 2020, 25, 05020005. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, B.; Li, R. Research on the intelligent construction and development of bridge engineering safety management. E3S Web Conf. 2024, 565, 03013. [Google Scholar] [CrossRef]
- Yang, J.; Xiang, F.; Li, R. Intelligent bridge management via big data knowledge engineering. Autom. Constr. 2022, 135, 104118. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Yang, H. An overview of intelligent construction and maintenance technology for highway subgrade engineering. Intell. Transp. Infrastruct. 2023, 2, liad019. [Google Scholar] [CrossRef]
- Carbonari, S.; Nicoletti, V.; Martini, R.; Gara, F. Dynamics of bridges during proof load tests and determination of mass-normalized mode shapes from OMA. Eng. Struct. 2024, 310, 118111. [Google Scholar] [CrossRef]
- Ferrara, M.; Bertagnoli, G.; Giordano, L. Model updating of different bridge types using ambient vibration and OMA identification. Procedia Struct. Integr. 2024, 62, 773–780. [Google Scholar] [CrossRef]
- Li, X.; Wang, M.; Liang, Y. Research into design and construction key technologies of prestressed concrete continuous rigid frame bridge. In Proceedings of the 2011 IEEE International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; pp. 617–621. [Google Scholar]
- Li, H.; Huang, Y.; Guo, E. Construction stage seismic vulnerability evaluation of a continuous girder bridge with the cast-in-place cantilever construction method. Adv. Civ. Eng. 2021, 2021, 9915947. [Google Scholar] [CrossRef]
- Zhou, Y. Pre-camber control of large-span prestressed concrete continuous rigid-frame bridges under cantilever construction. Arch. Civ. Eng. 2025, 71, 469–487. [Google Scholar] [CrossRef]
- Zhou, X.; Deng, T.; Chen, L. Application of Bayesian update method in the construction control of continuous rigid frame bridge girders with high piers and large spans. Buildings 2023, 13, 1556. [Google Scholar] [CrossRef]
- Wan, L.; Qiao, J.; Sun, Q.; Liu, J. Construction control of rigid frame-continuous girder bridge based on grey theory. J. Eng. Appl. Sci. 2024, 71, 171. [Google Scholar] [CrossRef]
- Dong, F.; Shi, Z.; Zhong, R. FE model updating of continuous beam bridge based on response surface method. Buildings 2024, 14, 960. [Google Scholar] [CrossRef]
- Wang, X.G.; Ma, M.; Zhao, B. Response surface model optimization algorithm for structural assessment based on vibration frequency. Shock Vib. 2025, 2025, 5446251. [Google Scholar] [CrossRef]
- Kovačević, M.; Ivanišević, N.; Stević, D. Decision-support system for estimating resource consumption in bridge construction based on machine learning. Axioms 2022, 12, 19. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Integrating BIM and AI for smart construction management: Current status and future directions. Arch. Comput. Methods Eng. 2023, 30, 1081–1110. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y. Intelligent prediction of prestressed steel structure construction safety based on BP neural network. Appl. Sci. 2022, 12, 1442. [Google Scholar] [CrossRef]
- Li, Q.; Xie, J. Bridge alignment prediction based on combination of grey model and BP neural network. Appl. Sci. 2024, 14, 7955. [Google Scholar] [CrossRef]
- Wang, X.; Miao, C.; Wang, X. Prediction analysis of deflection in the construction of composite box-girder bridge with corrugated steel webs based on MEC-BP neural networks. Structures 2021, 32, 691–700. [Google Scholar] [CrossRef]
- Yang, Y.; Xia, X.; Lo, D. Predictive models in software engineering: Challenges and opportunities. ACM Trans. Softw. Eng. Methodol. 2022, 31, 1–72. [Google Scholar] [CrossRef]
- Liao, S.; Li, S.; Liu, J. A zeroing neural dynamics-based acceleration optimization approach for optimizers in deep neural networks. Neural Netw. 2022, 150, 440–461. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Ma, Z.; Liu, X. A long-term prediction method of computer parameter degradation based on curriculum learning and transfer learning. Mathematics 2023, 11, 3098. [Google Scholar] [CrossRef]
- Zhang, Z. Pattern classification based on radial basis function neural network. In Proceedings of the 2020 IEEE 5th International Conference on Smart Grid and Electrical Automation (ICSGEA), Zhangjiajie, China, 13–14 June 2020; pp. 213–216. [Google Scholar]
- Dai, Y.; Wu, Q.; Zhang, Y. Generalized sparse radial basis function networks for multi-classification problems. Appl. Soft Comput. 2024, 154, 111361. [Google Scholar] [CrossRef]
- Chen, S.; Bai, W. Performance analysis of typical linear augmented observers for a class of MIMO systems with nonlinear uncertainty. ISA Trans. 2022, 128, 316–327. [Google Scholar] [CrossRef]
- He, X.J.; Zeng, J.C.; Jie, J. Artificial neural network weights optimization design based on MEC algorithm. In Proceedings of the 2004 IEEE International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004; Volume 6, pp. 3361–3364. [Google Scholar]
- Jie, J.; Zeng, J.; Zhang, S.L. Mind evolutionary computation for the constrained optimization. In Proceedings of the IEEE 2002 International Conference on Machine Learning and Cybernetics, Beijing, China, 4–5 November 2002; Volume 3, pp. 1582–1585. [Google Scholar]
- Sun, C.; Wang, J. Performance of MEC in high-dimensional space. In Proceedings of the 2002 IEEE International Conference on Control and Automation (ICCA), Xiamen, China, 19 June 2002; p. 231. [Google Scholar]
- Qin, J.; Huang, C.; Luo, Y. Adaptive multi-swarm in dynamic environments. Swarm Evol. Comput. 2021, 63, 100870. [Google Scholar] [CrossRef]
- Wang, H.; Yang, S. Memetic algorithms for dynamic optimization problems. In Evolutionary Computation for Dynamic Optimization Problems; Springer: New York, NY, USA, 2013; pp. 137–170. [Google Scholar]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Zheng, B. Parametric modeling and finite element analysis of the camshaft based on ANSYS APDL. In Proceedings of the 2018 IEEE 4th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 14–16 December 2018; pp. 1805–1808. [Google Scholar]
- Nie, J.G.; Zhu, L. Beam-truss model of steel–concrete composite box-girder bridges. J. Bridge Eng. 2014, 19, 04014023. [Google Scholar] [CrossRef]
- Zhang, W.; Chang, J.; Tian, G. FEM-based shape-finding and force-assessment of suspension bridges via completed loop adjustment. J. Bridge Eng. 2022, 27, 04021098. [Google Scholar] [CrossRef]
- Li, J.; Li, D.; Li, F. Finite element analysis of displacement and vibration characteristics of cantilevered plate. J. Phys. Conf. Ser. 2020, 1578, 012241. [Google Scholar] [CrossRef]
- Zhao, T.; Zheng, Y.; Wu, Z. Improving computational efficiency of machine-learning modeling of nonlinear processes using sensitivity analysis and active learning. Digit. Chem. Eng. 2022, 3, 100027. [Google Scholar] [CrossRef]
- Hisam, M.W.; Dar, A.A.; Elrasheed, M.O. The versatility of the Taguchi method: Optimizing experiments across diverse disciplines. J. Stat. Theory Appl. 2024, 23, 365–389. [Google Scholar] [CrossRef]
- Tong, Y.L. The Multivariate Normal Distribution; Springer: New York, NY, USA, 2012. [Google Scholar]



| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 (25.075) | 1 (167.25) | 1 (22.125) | 1 (67.625) | 1 (1.2255) | 1 (3.75) | 1 (0.063) | 1 (2.5) | −15.08 |
| 2 | 1 | 2 (189.9) | 2 (23.85) | 2 (73.25) | 2 (1.3302) | 2 (10.5) | 2 (0.060) | 2 (10) | −19.57 |
| 3 | 1 | 3 (205) | 3 (25) | 3 (77) | 3 (1.40) | 3 (15) | 3 (0.056) | 3 (15) | −23.45 |
| 4 | 1 | 4 (220.1) | 4 (26.15) | 4 (80.75) | 4 (1.4698) | 4 (19.5) | 4 (0.053) | 4 (20) | −29.57 |
| 5 | 1 | 5 (242.75) | 5 (27.875) | 5 (86.375) | 5 (1.5745) | 5 (26.25) | 5 (0.051) | 5 (27.5) | −31.55 |
| 6 | 2 (29.47) | 1 | 2 | 3 | 4 | 5 | 1 | 2 | −4.06 |
| 7 | 2 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | −6.28 |
| 8 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | −48.87 |
| 9 | 2 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | −56.85 |
| 10 | 2 | 5 | 1 | 2 | 3 | 4 | 5 | 1 | −38.60 |
| 11 | 3 (32.4) | 1 | 3 | 5 | 2 | 4 | 4 | 1 | −43.92 |
| 12 | 3 | 2 | 4 | 1 | 3 | 5 | 5 | 2 | −50.58 |
| 13 | 3 | 3 | 5 | 2 | 4 | 1 | 1 | 3 | −23.80 |
| 14 | 3 | 4 | 1 | 3 | 5 | 2 | 2 | 4 | −10.34 |
| 15 | 3 | 5 | 2 | 4 | 1 | 3 | 3 | 5 | −35.86 |
| 16 | 4 (35.33) | 1 | 4 | 2 | 5 | 3 | 5 | 3 | −35.12 |
| 17 | 4 | 2 | 5 | 3 | 1 | 4 | 1 | 4 | −28.00 |
| 18 | 4 | 3 | 1 | 4 | 2 | 5 | 2 | 5 | −19.88 |
| 19 | 4 | 4 | 2 | 5 | 3 | 1 | 3 | 1 | −23.78 |
| 20 | 4 | 5 | 3 | 1 | 4 | 2 | 4 | 2 | −28.50 |
| 21 | 5 (39.725) | 1 | 5 | 4 | 3 | 2 | 4 | 3 | −38.57 |
| 22 | 5 | 2 | 1 | 5 | 4 | 3 | 5 | 4 | −22.32 |
| 23 | 5 | 3 | 2 | 1 | 5 | 4 | 1 | 5 | −6.61 |
| 24 | 5 | 4 | 3 | 2 | 1 | 5 | 2 | 1 | −28.49 |
| 25 | 5 | 5 | 4 | 3 | 2 | 1 | 3 | 2 | −32.39 |
| 26 | 1 | 1 | 1 | 4 | 5 | 4 | 3 | 2 | −17.83 |
| 27 | 1 | 2 | 2 | 5 | 1 | 5 | 4 | 3 | −55.68 |
| 28 | 1 | 3 | 3 | 1 | 2 | 1 | 5 | 4 | −60.21 |
| 29 | 1 | 4 | 4 | 2 | 3 | 2 | 1 | 5 | −25.18 |
| 30 | 1 | 5 | 5 | 3 | 4 | 3 | 2 | 1 | −33.01 |
| 31 | 2 | 1 | 2 | 1 | 3 | 3 | 2 | 4 | −22.85 |
| 32 | 2 | 2 | 3 | 2 | 4 | 4 | 3 | 5 | −28.91 |
| 33 | 2 | 3 | 4 | 3 | 5 | 5 | 4 | 1 | −35.53 |
| 34 | 2 | 4 | 5 | 4 | 1 | 1 | 5 | 2 | −72.53 |
| 35 | 2 | 5 | 1 | 5 | 2 | 2 | 1 | 3 | −17.35 |
| 36 | 3 | 1 | 3 | 3 | 1 | 2 | 5 | 5 | −50.93 |
| 37 | 3 | 2 | 4 | 4 | 2 | 3 | 1 | 1 | −22.79 |
| 38 | 3 | 3 | 5 | 5 | 3 | 4 | 2 | 2 | −31.22 |
| 39 | 3 | 4 | 1 | 1 | 4 | 5 | 3 | 3 | −18.86 |
| 40 | 3 | 5 | 2 | 2 | 5 | 1 | 4 | 4 | −20.02 |
| 41 | 4 | 1 | 4 | 5 | 4 | 1 | 2 | 5 | −20.28 |
| 42 | 4 | 2 | 5 | 1 | 5 | 2 | 3 | 1 | −26.04 |
| 43 | 4 | 3 | 1 | 2 | 1 | 3 | 4 | 2 | −31.25 |
| 44 | 4 | 4 | 2 | 3 | 2 | 4 | 5 | 3 | −42.37 |
| 45 | 4 | 5 | 3 | 4 | 3 | 5 | 1 | 4 | −17.00 |
| 46 | 5 | 1 | 5 | 2 | 2 | 5 | 3 | 4 | −37.19 |
| 47 | 5 | 2 | 1 | 3 | 3 | 1 | 4 | 5 | −18.28 |
| 48 | 5 | 3 | 2 | 4 | 4 | 2 | 5 | 1 | −26.76 |
| 49 | 5 | 4 | 3 | 5 | 5 | 3 | 1 | 2 | −9.34 |
| 50 | 5 | 5 | 4 | 1 | 1 | 4 | 2 | 3 | −30.52 |
| −311.13 | −285.81 | −209.79 | −316.10 | −397.21 | −292.64 | −169.21 | −293.98 | ||
| −331.83 | −278.44 | −257.55 | −288.11 | −352.50 | −292.11 | −222.44 | −297.27 | ||
| −308.32 | −307.58 | −297.02 | −278.35 | −289.50 | −292.83 | −293.18 | −291.99 | ||
| −272.22 | −317.32 | −330.83 | −287.07 | −236.07 | −297.56 | −358.16 | −296.38 | ||
| −250.46 | −284.80 | −378.76 | −304.32 | −198.67 | −298.81 | −430.96 | −294.32 | ||
| 8.14 | 3.89 | 16.90 | 3.78 | 19.85 | 0.67 | 26.18 | 0.53 |
| Algorithm | Parameter | Definition | Levels |
|---|---|---|---|
| Adaptive MEC | M | The population size | 100, 200,…, 500 |
| Msup | The superior group size | 6 | |
| Mtem | The temporary group size | 6 | |
| Imax | The maximum number of iterations | 300 | |
| RBF | N1 | The number of neurons in the input layer | 6 |
| N2 | The number of neurons in the hidden layer | 4,…, 18 | |
| N3 | The number of neurons in the output layer | 1 | |
| ep | The number of iterations | 600 | |
| G | The training accuracy | 1 × 10−5 |
| Variable | Mean | Standard Deviation | Distribution Type | Remarks |
|---|---|---|---|---|
| 32.4 | 2.93 | Normal distribution | Young’s modulus (concrete) | |
| 205 | 15.1 | Normal distribution | Young’s modulus (steel) | |
| 25 | 1.15 | Normal distribution | Density (concrete) | |
| 77 | 3.75 | Normal distribution | Density (steel) | |
| 1.40 | 0.0698 | Normal distribution | Prestressing tendon tensile stress | |
| 15 | 4.5 | Normal distribution | Structural temperature | |
| 700 | 32.5 | Normal distribution | Uniformly distributed load |
| Model | Training Samples | Testing Samples | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| Adaptive MEC–RBF | 0.9789 | 1.4978 | 0.1411 | 0.9751 | 1.9491 | 0.2341 |
| RBF | 0.9711 | 2.7869 | 0.4211 | 0.9679 | 3.1807 | 0.5678 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Gao, Q.; He, Q.; Sun, L.; Tian, D. Adaptive MEC–RBF Neural Network-Based Deflection Prediction for Prestressed Concrete Continuous Rigid Frame Bridges During Construction. Appl. Sci. 2025, 15, 11326. https://doi.org/10.3390/app152111326
Zhou C, Gao Q, He Q, Sun L, Tian D. Adaptive MEC–RBF Neural Network-Based Deflection Prediction for Prestressed Concrete Continuous Rigid Frame Bridges During Construction. Applied Sciences. 2025; 15(21):11326. https://doi.org/10.3390/app152111326
Chicago/Turabian StyleZhou, Chunyu, Qingfei Gao, Qijun He, Liangbo Sun, and Dewei Tian. 2025. "Adaptive MEC–RBF Neural Network-Based Deflection Prediction for Prestressed Concrete Continuous Rigid Frame Bridges During Construction" Applied Sciences 15, no. 21: 11326. https://doi.org/10.3390/app152111326
APA StyleZhou, C., Gao, Q., He, Q., Sun, L., & Tian, D. (2025). Adaptive MEC–RBF Neural Network-Based Deflection Prediction for Prestressed Concrete Continuous Rigid Frame Bridges During Construction. Applied Sciences, 15(21), 11326. https://doi.org/10.3390/app152111326







