Pre-Processing Ensemble Modeling Based on Faster Covariate Selection Calibration for Near-Infrared Spectroscopy
Abstract
1. Introduction
2. Material and Methods
2.1. Datasets
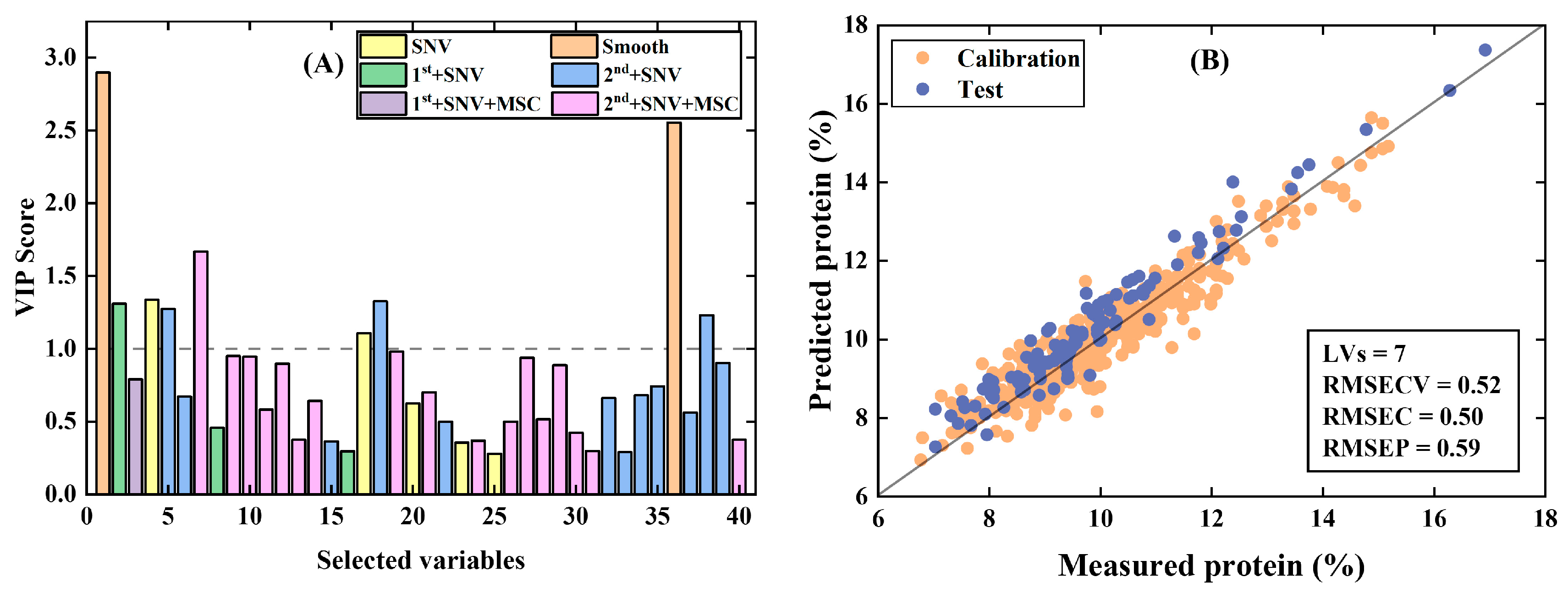
- Wheat data [27]: Near-infrared transmission spectra of wheat seeds were measured at 100 wavelengths and used to calibrate protein content. The dataset contains a calibration set of 415 samples and a test set of 108 samples.
- Meat data [28]: Near-infrared transmission spectroscopy at 100 wavelengths was measured on fine meat slices and used to calibrate fat content. The dataset contains a calibration set of 172 samples and a test set of 43 samples.
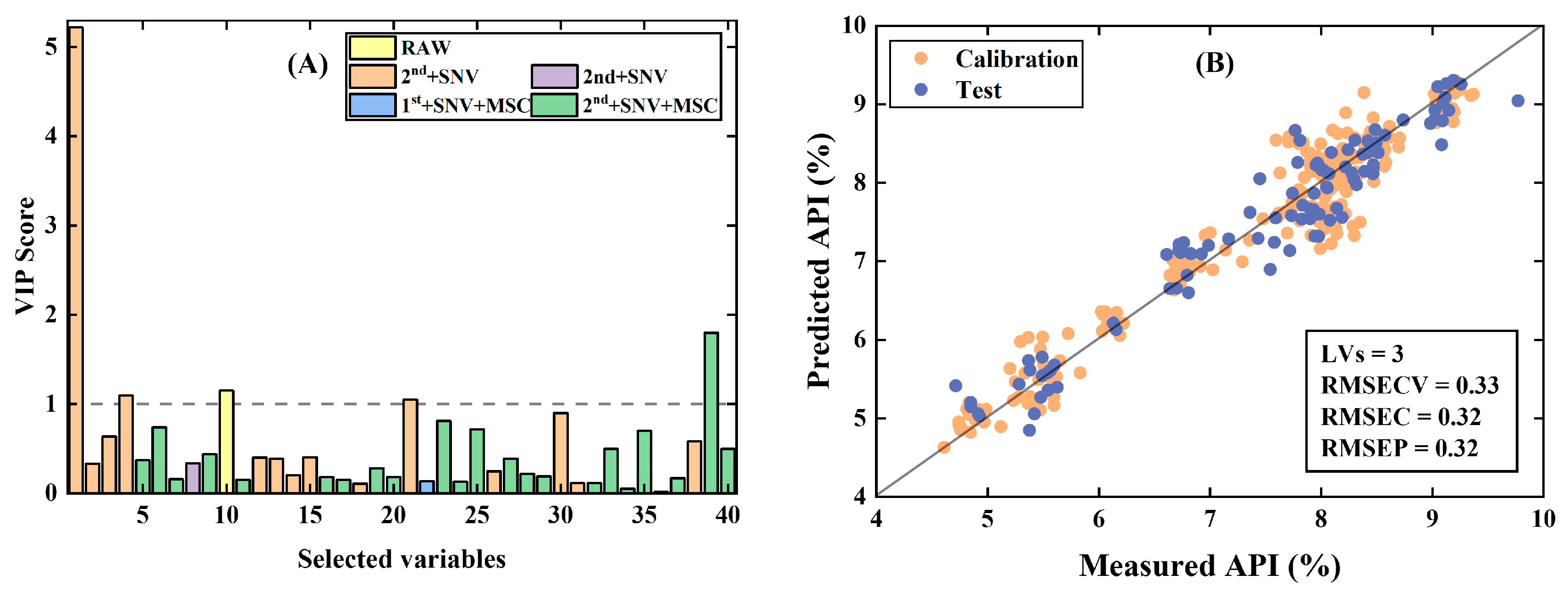
- Tablet data [29]: Tablet data were collected from the NIR spectra of 310 tablets with a spectral range of 7400~10,507 cm−1, and the relative active substance containing API (% w/w) of the tablet was determined. The data were divided into a training set of 210 samples and a test set of 100 samples by the Duplex algorithm.
2.2. Data Preparation
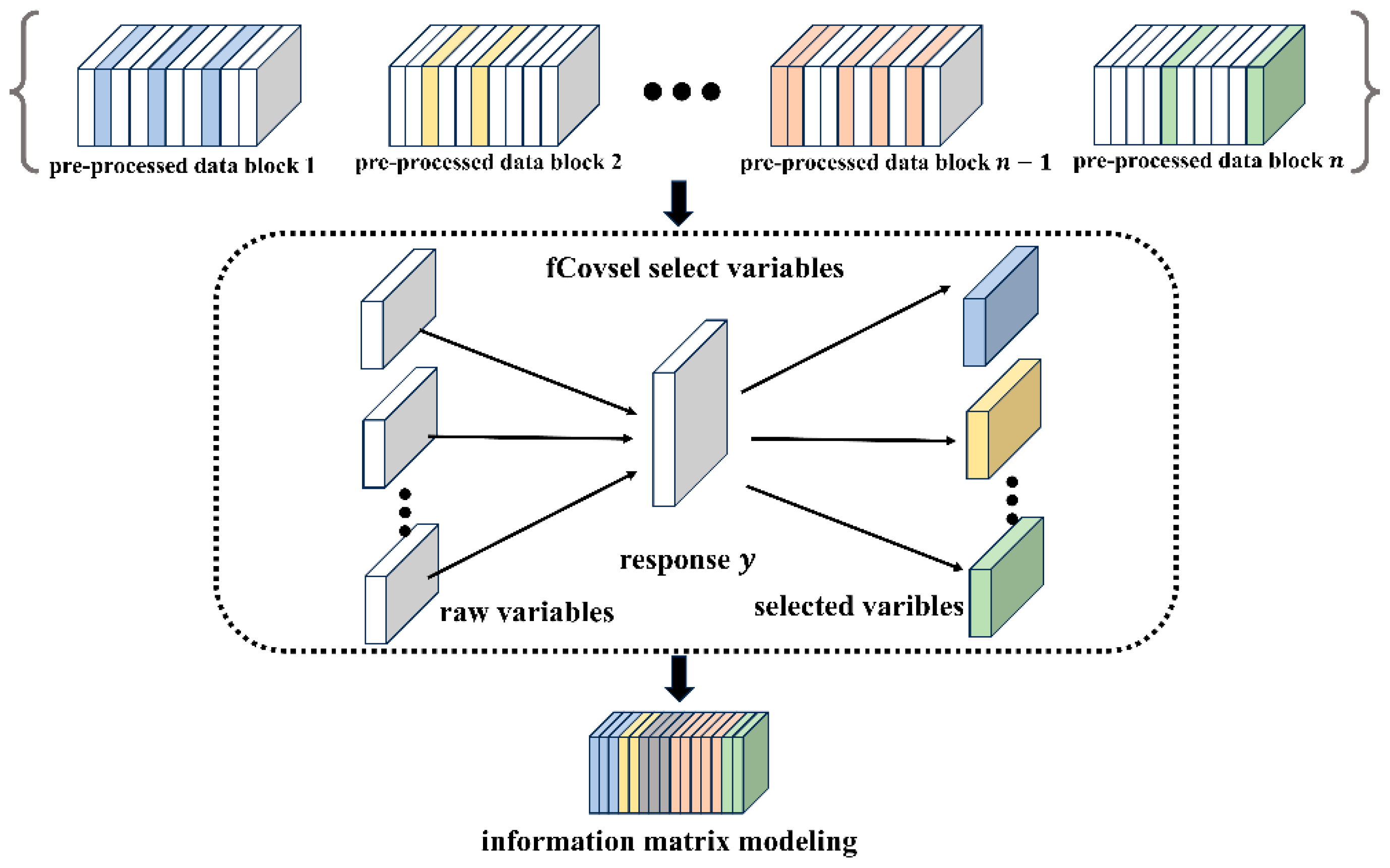
2.3. Our Method
| Algorithm 1: Pseudo-code for the PFCOVSC strategy |
| Input: k matrix blocks processed by different pre-processing methods, response variable y (), number of feature variables m. |
| Output: Feature matrix after fCovsel filtering: S (, rmsec, rmsep after model calibration.
1: Initialization: S = {Ø}, The i th selected feature variable: (i ≤ m), Parameter: j = 1 2: Construct the fusion matrix: 3: for i < m do 4: for j < q do 5: : the j th column of F) 6: end for 7: if i > 1: (G-S orthogonalization) 8: 9: 10: S ← 11: end for 12: 13: Cross-validation of to find the optimal number of latent variables and modeling. 14: end |
3. Results and Discussions
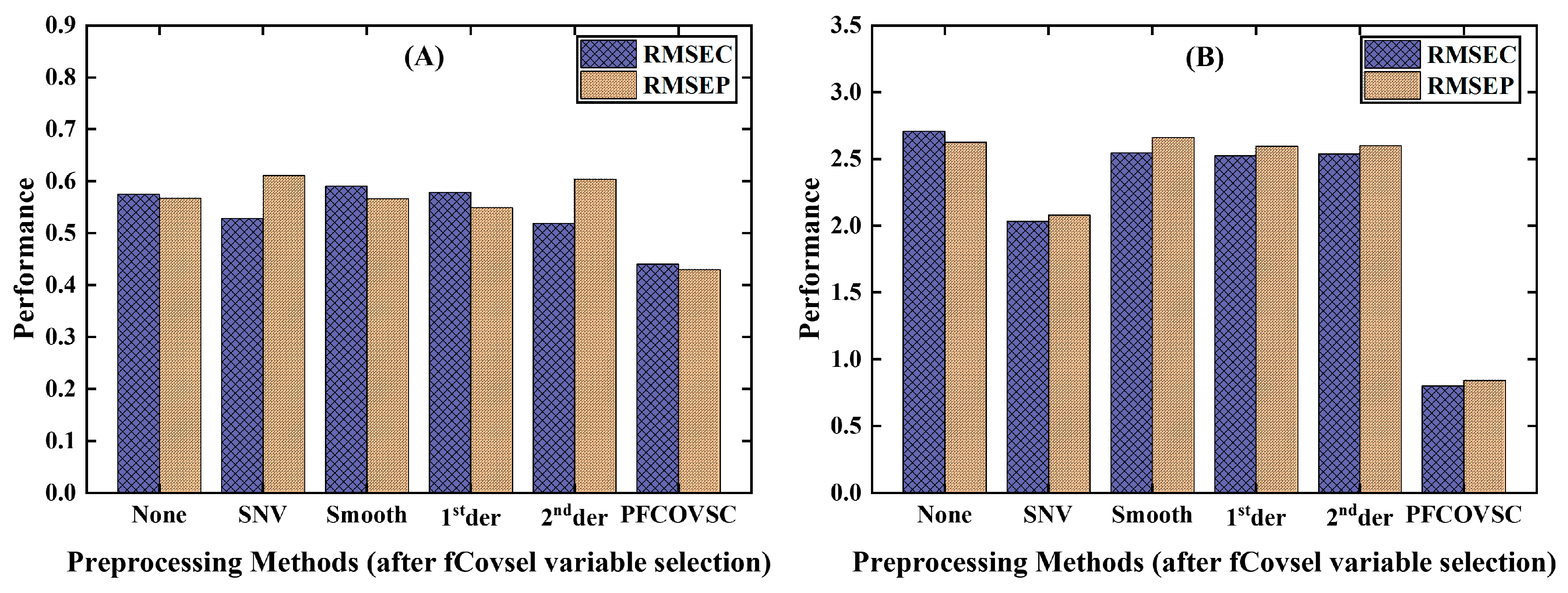
3.1. Comparison of PFCOVSC and Single Block Pre-Processing
3.1.1. PFCOVSC and Single Block Pre-Processing
3.1.2. PFCOVSC and Single Block Pre-Processing After fCovsel
3.2. Comparison of PFCOVSC with SPORT and PROSAC
3.2.1. Prediction Performance
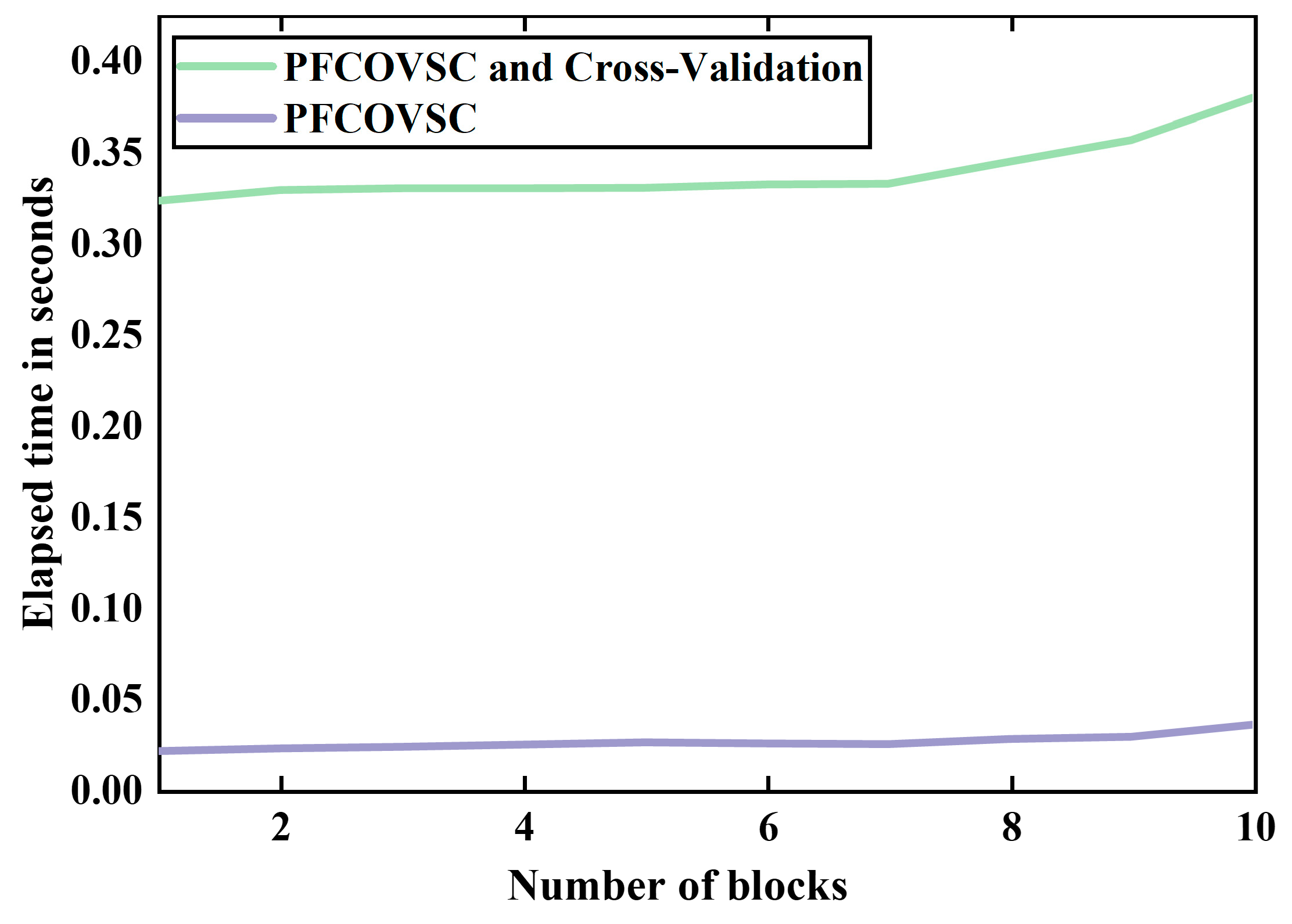
3.2.2. Computational Time
3.2.3. Model Interpretability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rinnan, Å.; Van Den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trac-Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Mishra, P.; Verkleij, T.; Klont, R. Improved prediction of minced pork meat chemical properties with near-infrared spectroscopy by a fusion of scatter-correction techniques. Infrared Phys. Technol. 2021, 113, 4. [Google Scholar] [CrossRef]
- Mishra, P.; Lohumi, S.; Khan, H.A.; Nordon, A. Close-range hyperspectral imaging of whole plants for digital phenotyping: Recent applications and illumination correction approaches. Comput. Electron. Agric. 2020, 178, 11. [Google Scholar] [CrossRef]
- Amigo, J.M.; Babamoradi, H.; Elcoroaristizabal, S. Hyperspectral image analysis. A tutorial. Anal. Chim. Acta 2015, 896, 34–51. [Google Scholar] [CrossRef]
- Bro, R. Multivariate calibration: What is in chemometrics for the analytical chemist? Anal. Chim. Acta 2003, 500, 185–194. [Google Scholar] [CrossRef]
- Saeys, W.; Do Trong, N.N.; Van Beers, R.; Nicolaï, B.M. Multivariate calibration of spectroscopic sensors for postharvest quality evaluation: A review. Postharvest Biol. Technol. 2019, 158, 110981. [Google Scholar] [CrossRef]
- van den Berg, R.A.; Hoefsloot, H.C.J.; Westerhuis, J.A.; Smilde, A.K.; Van Der Werf, M.J. Centering, scaling, and transformations: Improving the biological information content of metabolomics data. Bmc Genom. 2006, 7, 15. [Google Scholar] [CrossRef]
- Roger, J.M.; Biancolillo, A.; Marini, F. Sequential preprocessing through ORThogonalization (SPORT) and its application to near infrared spectroscopy. Chemom. Intell. Lab. Syst. 2020, 199, 4. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Isaksson, T.; Næs, T. The Effect of Multiplicative Scatter Correction (MSC) and Linearity Improvement in NIR Spectroscopy. Appl. Spectrosc. 1988, 42, 1273–1284. [Google Scholar] [CrossRef]
- Steinier, J.; Termonia, Y.; Deltour, J. Smoothing and differentiation of data by simplified least square procedure. Anal. Chem. 1972, 44, 1906–1909. [Google Scholar] [CrossRef]
- Xu, L.; Zhou, Y.-P.; Tang, L.-J.; Wu, H.-L.; Jiang, J.-H.; Shen, G.-L.; Yu, R.-Q. Ensemble preprocessing of near-infrared (NIR) spectra for multivariate calibration. Anal. Chim. Acta 2008, 616, 138–143. [Google Scholar] [CrossRef] [PubMed]
- Engel, J.; Gerretzen, J.; Szymańska, E.; Jansen, J.J.; Downey, G.; Blanchet, L.; Buydens, L.M.C. Breaking with trends in pre-processing? Trends Anal. Chem. 2013, 50, 96–106. [Google Scholar] [CrossRef]
- Gabrielsson, J.; Jonsson, H.; Airiau, C.; Schmidt, B.; Escott, R.; Trygg, J. OPLS methodology for analysis of pre-processing effects on spectroscopic data. Chemom. Intell. Lab. Syst. 2006, 84, 153–158. [Google Scholar] [CrossRef]
- Gerretzen, J.; Szymańska, E.; Jansen, J.J.; Bart, J.; van Manen, H.-J.; Heuvel, E.R.v.D.; Buydens, L.M.C. Simple and Effective Way for Data Preprocessing Selection Based on Design of Experiments. Anal. Chem. 2015, 87, 12096–12103. [Google Scholar] [CrossRef]
- Torniainen, J.; Afara, I.O.; Prakash, M.; Sarin, J.K.; Stenroth, L.; Töyräs, J. Open-source python module for automated preprocessing of near infrared spectroscopic data. Anal. Chim. Acta 2020, 1108, 1–9. [Google Scholar] [CrossRef]
- Martyna, A.; Menżyk, A.; Damin, A.; Michalska, A.; Martra, G.; Alladio, E.; Zadora, G. Improving discrimination of Raman spectra by optimising preprocessing strategies on the basis of the ability to refine the relationship between variance components. Chemom. Intell. Lab. Syst. 2020, 202, 16. [Google Scholar] [CrossRef]
- Mishra, P.; Roger, J.M.; Rutledge, D.N.; Woltering, E. SPORT pre-processing can improve near-infrared quality prediction models for fresh fruits and agro-materials. Postharvest Biol. Technol. 2020, 168, 10. [Google Scholar] [CrossRef]
- Mishra, P.; Nordon, A.; Roger, J.M. Improved prediction of tablet properties with near-infrared spectroscopy by a fusion of scatter correction techniques. J. Pharm. Biomed. Anal. 2021, 192, 4. [Google Scholar] [CrossRef]
- Mishra, P.; Roger, J.M.; Rutledge, D.N. A short note on achieving similar performance to deep learning with practical chemometrics. Chemom. Intell. Lab. Syst. 2021, 214, 6. [Google Scholar] [CrossRef]
- Mishra, P.; Biancolillo, A.; Roger, J.M.; Marini, F.; Rutledge, D.N. New data preprocessing trends based on ensemble of multiple preprocessing techniques. Trac-Trends Anal. Chem. 2020, 132, 12. [Google Scholar] [CrossRef]
- Mishra, P.; Roger, J.M.; Marini, F.; Biancolillo, A.; Rutledge, D.N. Pre-processing ensembles with response oriented sequential alternation calibration (PROSAC): A step towards ending the pre-processing search and optimization quest for near-infrared spectral modelling. Chemom. Intell. Lab. Syst. 2022, 222, 10. [Google Scholar] [CrossRef]
- Mishra, P.; Roger, J.-M.; Jouan-Rimbaud-Bouveresse, D.; Biancolillo, A.; Marini, F.; Nordon, A.; Rutledge, D.N. Recent trends in multi-block data analysis in chemometrics for multi- source data integration. Trac-Trends Anal. Chem. 2021, 137, 15. [Google Scholar] [CrossRef]
- Roger, J.M.; Palagos, B.; Bertrand, D.; Fernandez-Ahumada, E. CovSel: Variable selection for highly multivariate and multi-response calibration Application to IR spectroscopy. Chemom. Intell. Lab. Syst. 2011, 106, 216–223. [Google Scholar] [CrossRef]
- Mishra, P.; Metz, M.; Marini, F.; Biancolillo, A.; Rutledge, D.N. Response oriented covariates selection (ROCS) for fast block order- and scale-independent variable selection in multi-block scenarios. Chemom. Intell. Lab. Syst. 2022, 224, 9. [Google Scholar] [CrossRef]
- Mishra, P. A brief note on a new faster covariate’s selection (fCovSel) algorithm. J. Chemom. 2022, 36, e3397. [Google Scholar] [CrossRef]
- Nielsen, J.P.; Pedersen, D.K.; Munck, L. Development of nondestructive screening methods for single kernel characterization of wheat. Cereal Chem. 2003, 80, 274–280. [Google Scholar] [CrossRef]
- Borggaard, C.; Thodberg, H.H. Optimal minimal neural interpretation of spectra. Anal. Chem. 1992, 64, 545–551. [Google Scholar] [CrossRef]
- Dyrby, M.; Engelsen, S.B.; Nørgaard, L.; Bruhn, M.; Lundsberg-Nielsen, L. Chemometric Quantitation of the Active Substance (Containing C≡N) in a Pharmaceutical Tablet Using Near-Infrared (NIR) Transmittance and NIR FT-Raman Spectra. Appl. Spectrosc. 2002, 56, 579–585. [Google Scholar] [CrossRef]
- Tran, T.N.; Afanador, N.L.; Buydens, L.M.C.; Blanchet, L. Interpretation of variable importance in Partial Least Squares with Significance Multivariate Correlation (sMC). Chemom. Intell. Lab. Syst. 2014, 138, 153–160. [Google Scholar] [CrossRef]
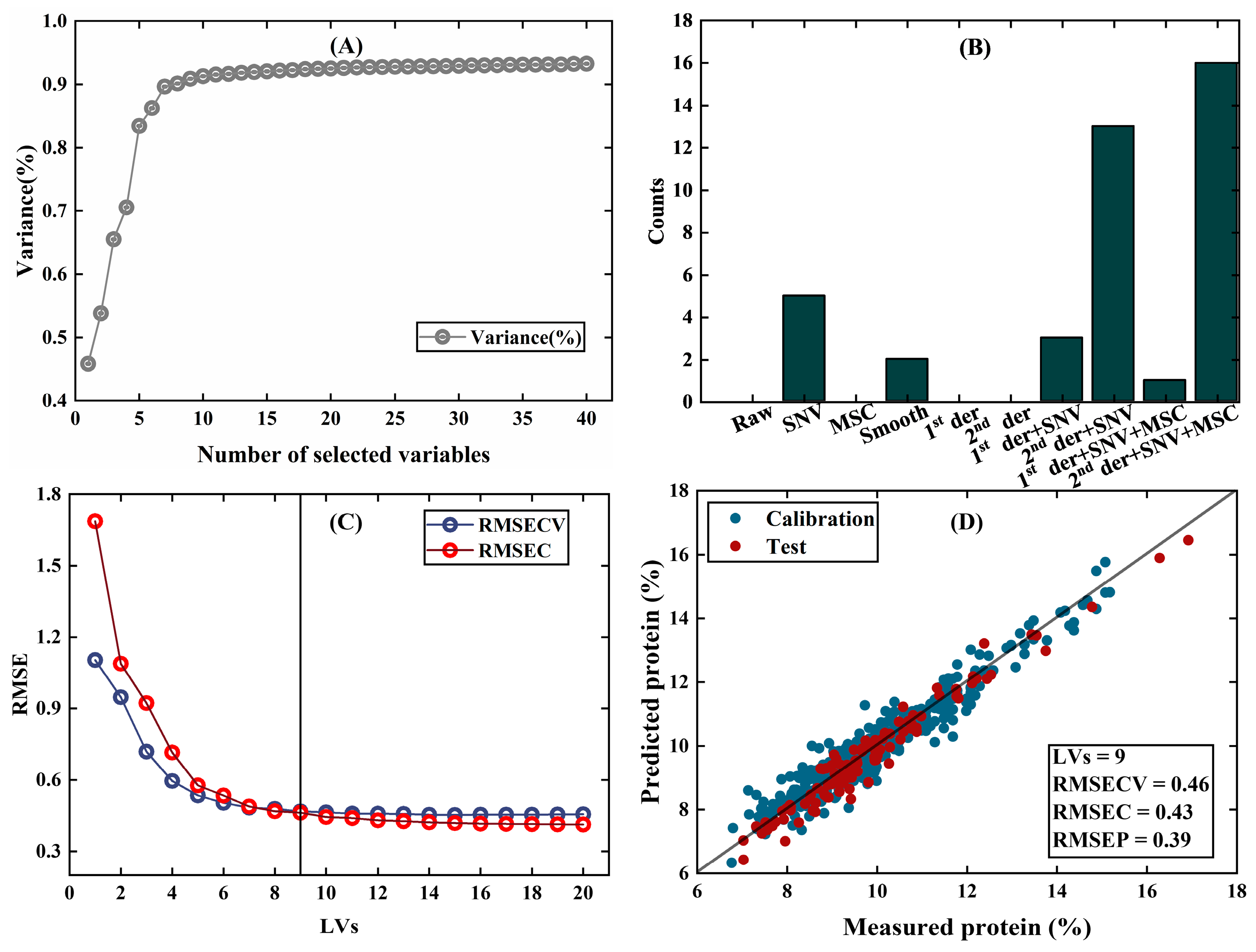
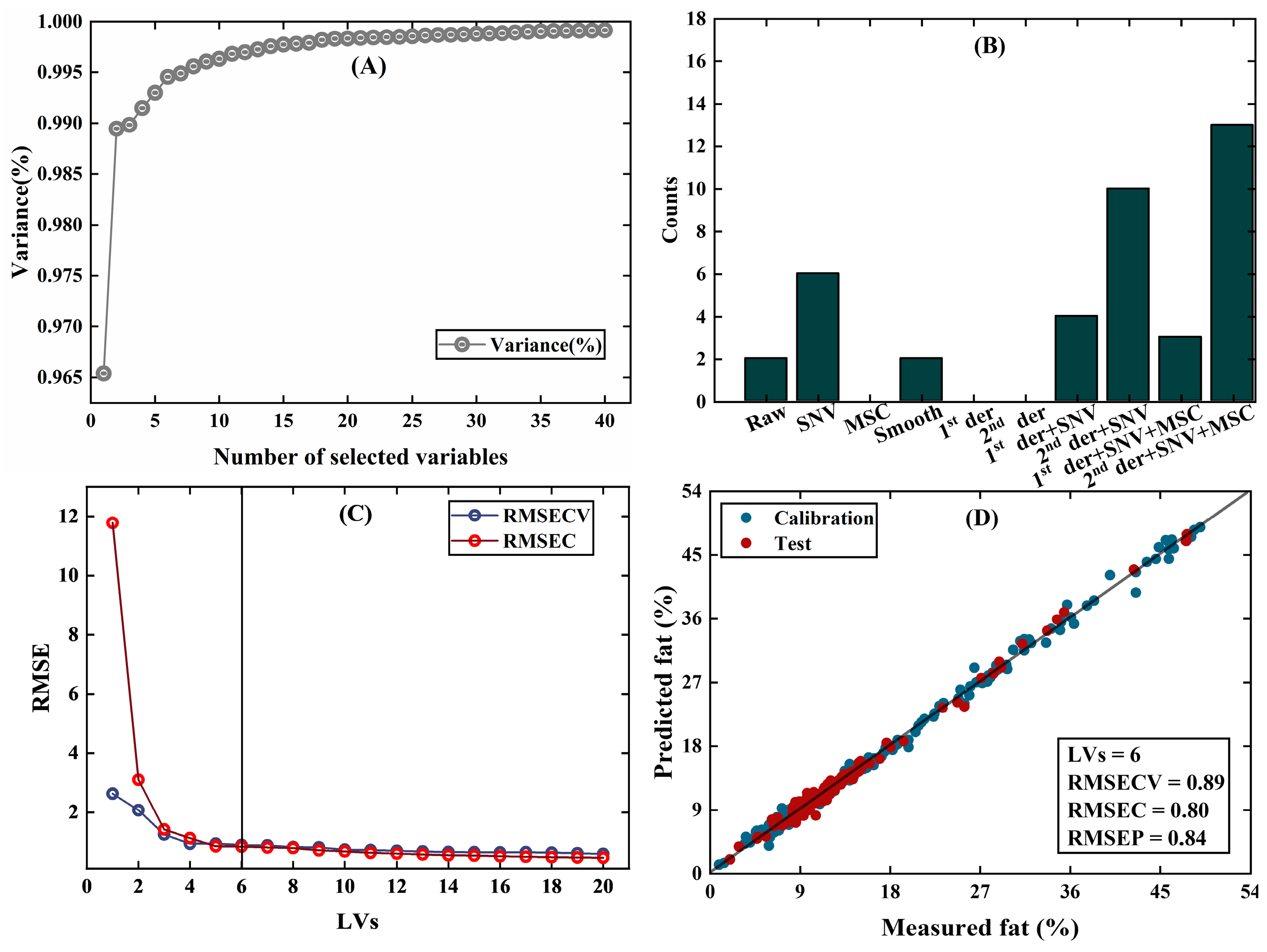


| Pre-Treatment | Wheat | Meat | Tablet | ||||||
|---|---|---|---|---|---|---|---|---|---|
| LVs | RMSEC | RMSEP | LVs | RMSEC | RMSEP | LVs | RMSEC | RMSEP | |
| - | 10 | 0.54 | 0.78 | 12 | 2.02 | 2.03 | 5 | 0.34 | 0.38 |
| SNV | 10 | 0.52 | 0.68 | 5 | 1.88 | 2.05 | 4 | 0.36 | 0.40 |
| MSC | 9 | 0.54 | 0.86 | 5 | 2.19 | 2.26 | 4 | 0.32 | 0.33 |
| SG-15-2-0 | 11 | 0.52 | 0.76 | 6 | 2.92 | 2.81 | 5 | 0.34 | 0.38 |
| SG-15-2-1 (1st der) | 7 | 0.62 | 0.74 | 9 | 2.55 | 2.64 | 4 | 0.33 | 0.36 |
| SG-15-2-2 (2nd der) | 8 | 0.51 | 0.74 | 14 | 2.07 | 2.24 | 3 | 0.34 | 0.37 |
| 1st der + SNV | 8 | 0.48 | 0.58 | 6 | 1.44 | 1.65 | 2 | 0.33 | 0.33 |
| 2nd der + SNV | 5 | 0.47 | 0.51 | 4 | 0.88 | 0.97 | 3 | 0.31 | 0.32 |
| 1st der + SNV + MSC | 7 | 0.48 | 0.61 | 7 | 2.84 | 3.28 | 3 | 0.31 | 0.32 |
| 2nd der + SNV + MSC | 5 | 0.46 | 0.51 | 9 | 0.80 | 0.93 | 2 | 0.31 | 0.32 |
| PFCOVSC | 9 | 0.43 | 0.39 | 6 | 0.80 | 0.84 | 3 | 0.31 | 0.33 |
| Strategy | Wheat | Meat | Tablets | ||||||
|---|---|---|---|---|---|---|---|---|---|
| LVs | RMSEC | RMSEP | LVs | RMSEC | RMSEP | LVs | RMSEC | RMSEP | |
| SPORT [a] | - | 0.47 | 0.47 | - | 1.50 | 1.65 | - | 0.27 | 0.33 |
| PROSAC | 5 | 0.46 | 0.45 | 3 | 0.99 | 1.03 | 4 | 0.32 | 0.34 |
| PFCOVSC | 9 | 0.43 | 0.39 | 6 | 0.80 | 0.84 | 3 | 0.31 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhou, Y.; Chen, X.; Xie, Z.; Ali, S.; Huang, G.; Yuan, L.; Shi, W.; Wang, X.; Zhang, L. Pre-Processing Ensemble Modeling Based on Faster Covariate Selection Calibration for Near-Infrared Spectroscopy. Appl. Sci. 2025, 15, 11325. https://doi.org/10.3390/app152111325
Wu Y, Zhou Y, Chen X, Xie Z, Ali S, Huang G, Yuan L, Shi W, Wang X, Zhang L. Pre-Processing Ensemble Modeling Based on Faster Covariate Selection Calibration for Near-Infrared Spectroscopy. Applied Sciences. 2025; 15(21):11325. https://doi.org/10.3390/app152111325
Chicago/Turabian StyleWu, Yonghong, Yukun Zhou, Xiaojing Chen, Zhonghao Xie, Shujat Ali, Guangzao Huang, Leiming Yuan, Wen Shi, Xin Wang, and Lechao Zhang. 2025. "Pre-Processing Ensemble Modeling Based on Faster Covariate Selection Calibration for Near-Infrared Spectroscopy" Applied Sciences 15, no. 21: 11325. https://doi.org/10.3390/app152111325
APA StyleWu, Y., Zhou, Y., Chen, X., Xie, Z., Ali, S., Huang, G., Yuan, L., Shi, W., Wang, X., & Zhang, L. (2025). Pre-Processing Ensemble Modeling Based on Faster Covariate Selection Calibration for Near-Infrared Spectroscopy. Applied Sciences, 15(21), 11325. https://doi.org/10.3390/app152111325






