Analysis of Dimensionless Numbers for Graphite Purification in the Electromagnetic Induction Furnaces
Abstract
1. Introduction
2. Mathematical Models
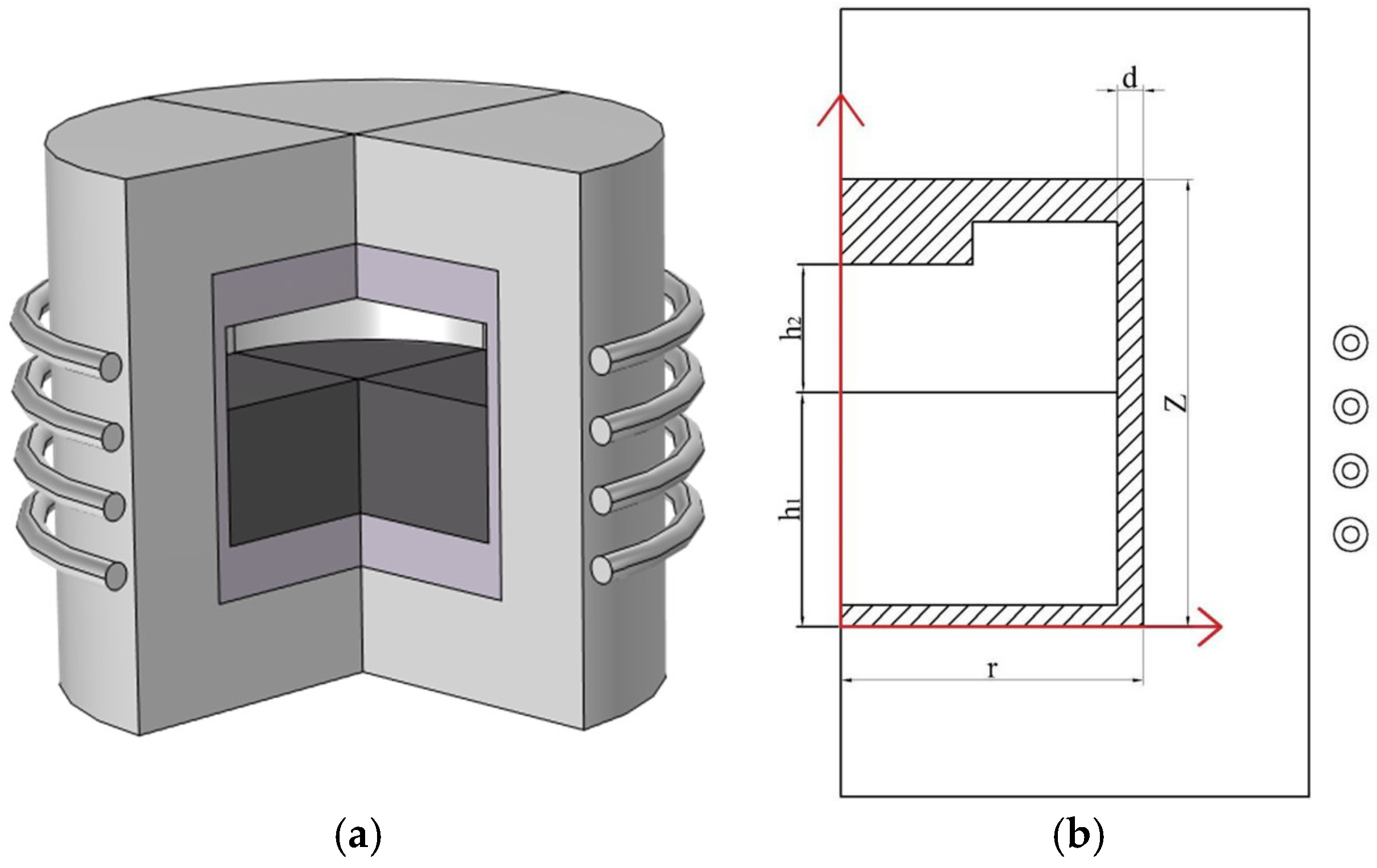
2.1. Physical Models
- (1)
- The graphite crucible is assumed to be in an ideal concentric position with the coil.
- (2)
- The graphite feedstock is assumed to be static under the action of air flow.
- (3)
- Heat transfer in the air domain outside the furnace is neglected.
2.2. Electromagnetic Field
2.3. Temperature Field
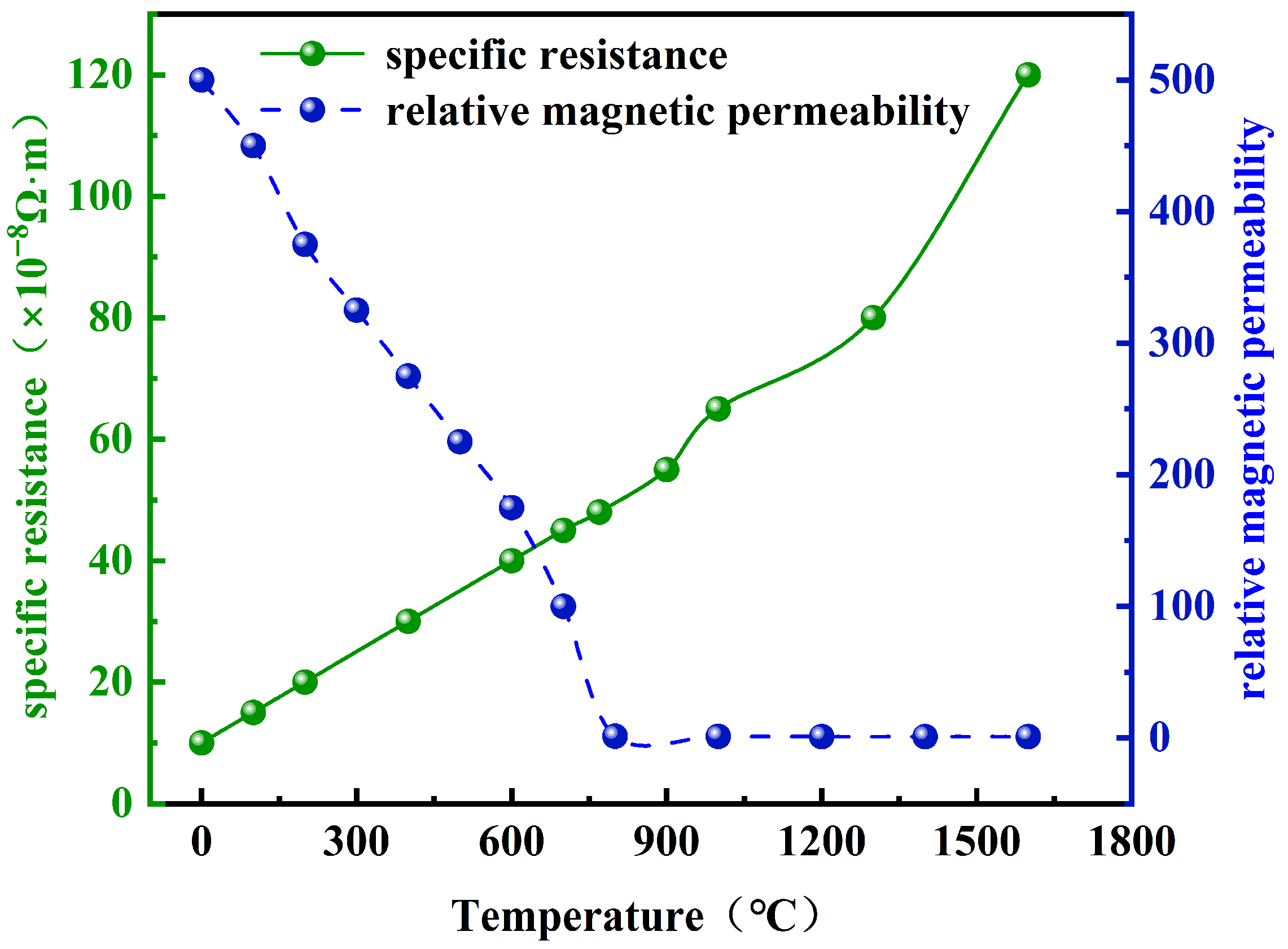
2.4. Dimensionless Analysis
3. Model Verification
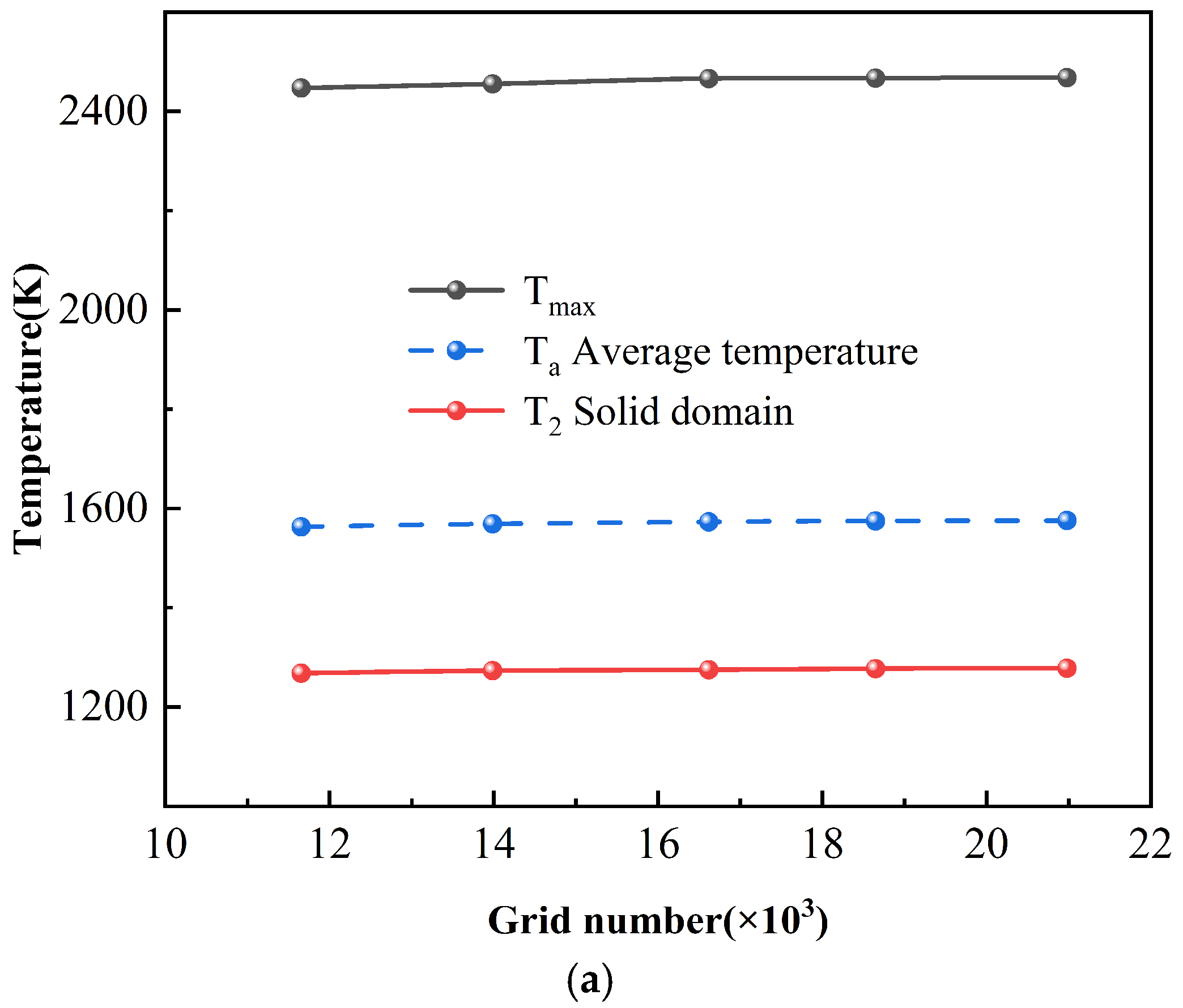
3.1. Mesh Independence Verification
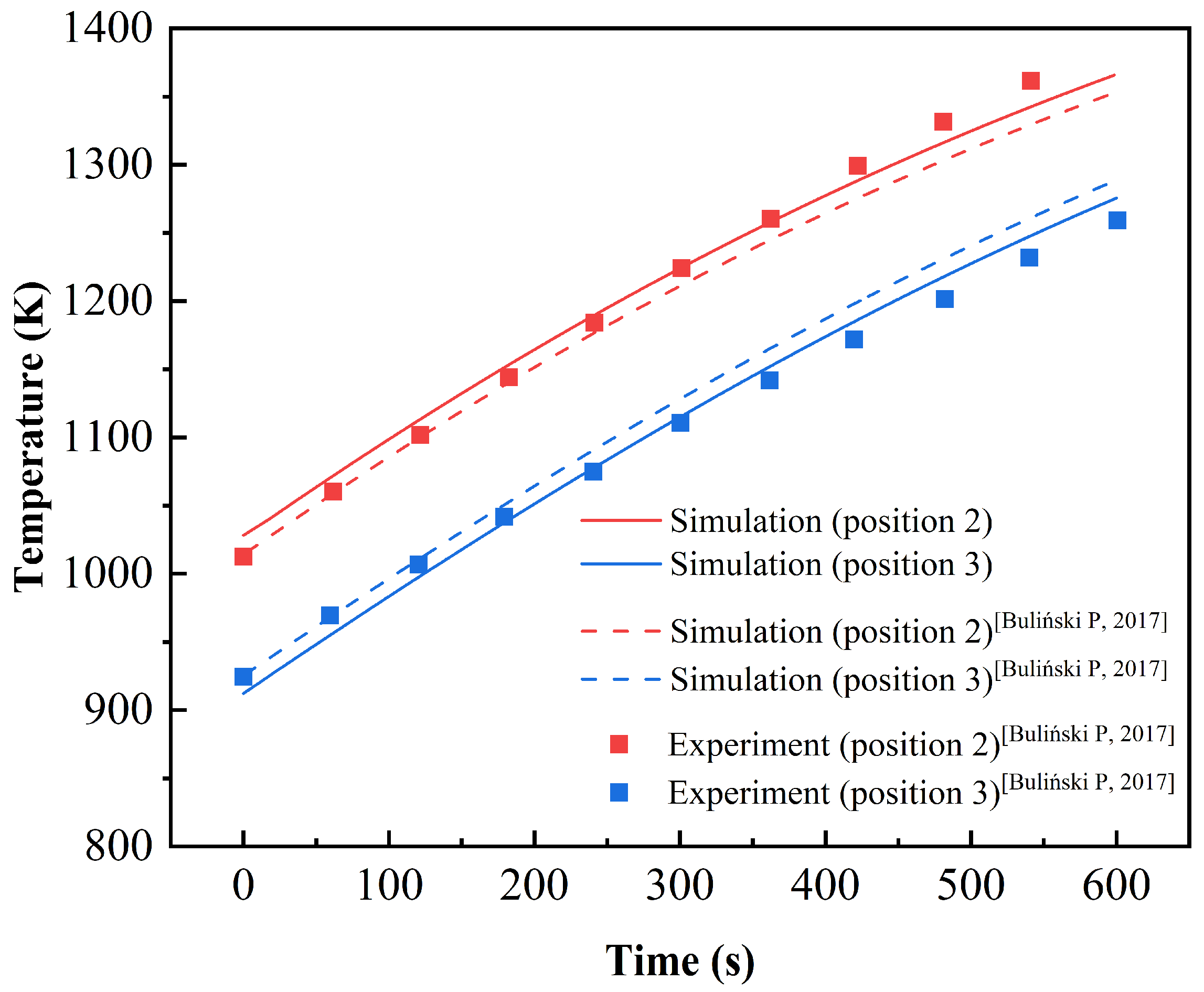
3.2. Verification of the Simulation
4. Results and Discussion
4.1. Furnace Temperature Analysis
4.2. Influence of Operating Parameters
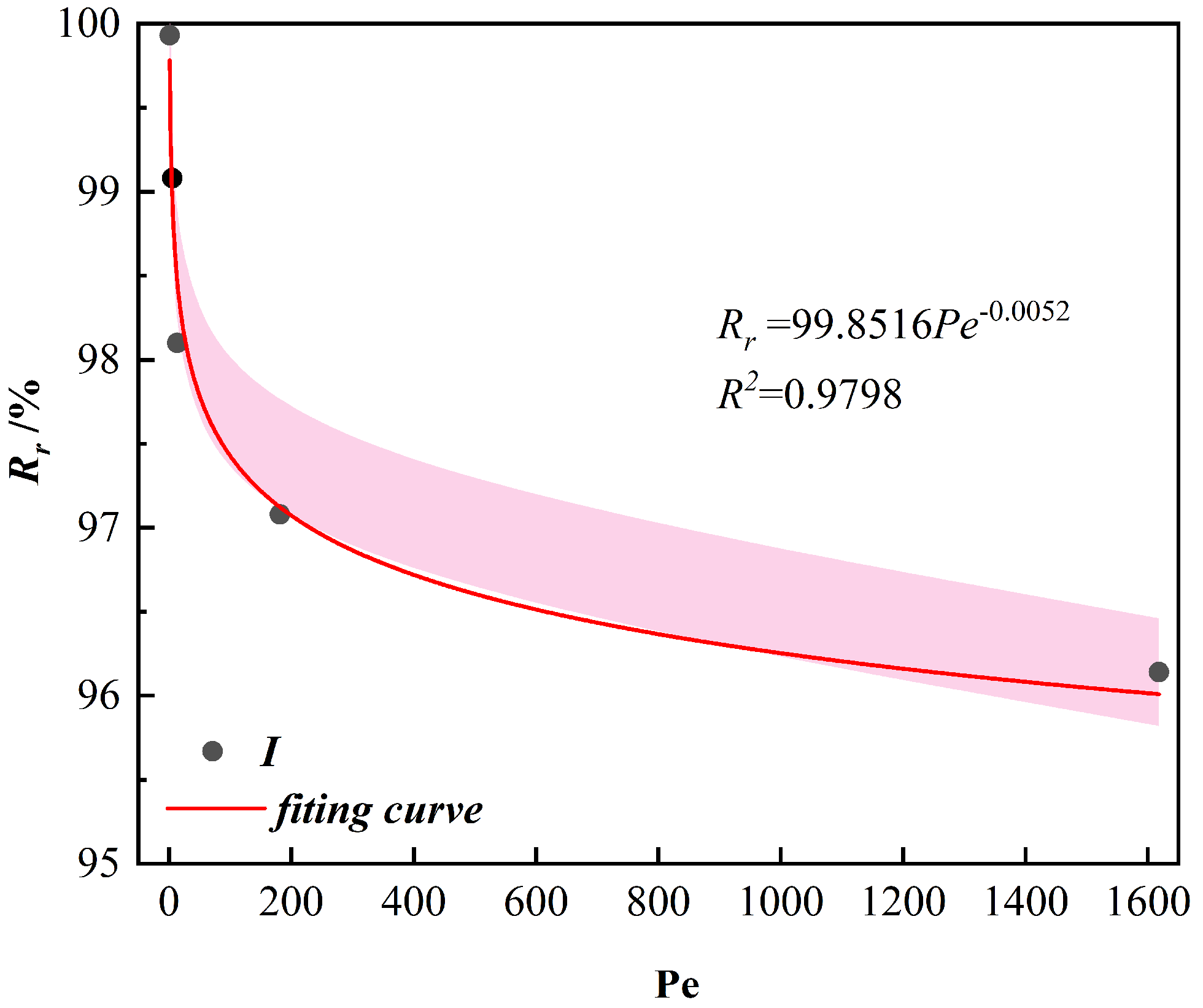
4.3. Influence of Dimensionless Numbers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jara, A.D.; Betemariam, A.; Woldetinsae, G.; Kim, J.Y. Purification, application and current market trend of natural graphite: A review. Int. J. Min. Sci. Technol. 2019, 29, 671–689. [Google Scholar] [CrossRef]
- Wang, J.-R.; Yang, D.-H.; Xu, Y.-J.; Hou, X.-L.; Ang, E.H.; Wang, D.-Z.; Zhang, L.; Zhu, Z.-D.; Feng, X.-Y.; Song, X.-H.; et al. Recent developments and the future of the recycling of spent graphite for energy storage applications. New Carbon Mater. 2023, 38, 787–803. [Google Scholar] [CrossRef]
- Wang, X.; Li, H.; Yao, H.; Chen, Z.; Guan, Q. Network feature and influence factors of global nature graphite trade competition. Resour. Policy 2019, 60, 153–161. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, J.; Jin, H.; Liang, G.; Ma, L.; Chen, Y.; Wang, C. Regenerating spent graphite from scrapped lithium-ion battery by high-temperature treatment. Carbon 2022, 189, 493–502. [Google Scholar] [CrossRef]
- Lan, Y.; Zhao, X.; Zhang, W.; Mu, L.; Wang, S. Investigation of the waste heat recovery and pollutant emission reduction potential in graphitization furnace. Energy 2022, 245, 123292. [Google Scholar] [CrossRef]
- Vedin, V.A.; Pirogov, V.I. Improving thermal insulation for graphitization furnaces. Refract. Ind. Ceram. 2008, 49, 416–417. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Heidari Gandoman, F.; Nowdeh, S.A.; Shiran, M.A.; Hadidian Moghaddam, M.J.; Davoodkhani, I.F. Optimal designing of static var compensator to improve voltage profile of power system using fuzzy logic control. Energy 2020, 192, 116665. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, J.; Zhang, W.; Zhu, X.; Yan, X. Multi-physical field coupling and modeling for induction heating of porous sodium chloride. J. Energy Storage 2024, 85, 111009. [Google Scholar] [CrossRef]
- Kang, D.G.; Sung, K.; Yong, H.; Jeong, K.; Choi, M.; Kim, H.-T.; Kwon, S.; Kim, S.M.; Myung, J.S.; Kim, D.W.; et al. Electrified inductive heating for sustainable utilization of liquid hydrogenated organics. Joule 2024, 8, 2374–2392. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, X.; Song, N.; He, J.; Cen, Z.; Li, C.; Wang, M.; Tang, H.; Liu, W.; Ren, X.; et al. Magnetic induction heating-driven rapid cold start of ammonia decomposition for hydrogen production. J. Am. Chem. Soc. 2024, 146, 28635–28641. [Google Scholar] [CrossRef]
- Adogwa, A.; Chukwu, E.; Malaj, A.; Punyapu, V.R.; Chamness, O.; Glisson, N.; Bruce, B.; Lee, S.; Zachman, M.J.; Bruce, D.A.; et al. Catalytic reaction triggered by magnetic induction heating mechanistically distinguishes itself from the standard thermal reaction. ACS Catal. 2024, 14, 4008–4017. [Google Scholar] [CrossRef]
- Asadi-Saghandi, H.; Karimi-Sabet, J.; Ghorbanian, S.; Moosavian, S.M.A. Dimensionless analysis on liquid–liquid two-phase flow patterns in a numbered-up microfluidic device. Chem. Eng. J. 2022, 429, 132428. [Google Scholar] [CrossRef]
- Amirsoleymani, A.; Ting, D.S.K.; Carriveau, R.; Brown, D.; McGillis, A. Two-phase flow pattern identification in CAES systems with dimensional analysis coupled with support vector machine. Int. J. Multiph. Flow 2023, 160, 104343. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, C.; Wang, X.; Yang, Z. Nondimensional prediction of thermal forming behaviour for the ship hull plate fabricated by induction heating. Ships Offshore Struct. 2019, 14, 510–522. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Aljabr, A.; Almehmadi, F.A.; Alqaed, S.; Sharaf, M.A. Numerical study of heat transfer, exergy efficiency, and friction factor with nanofluids in a plate heat exchanger. J. Therm. Anal. Calorim. 2023, 148, 11269–11281. [Google Scholar] [CrossRef]
- Lv, H.; Kang, L.; Wang, K.; Liu, Y. Parametric optimization of removing iron from solid waste melts based on analysis of real-time coupled two-phase interface in an induction heating furnace. Energy 2022, 261, 125195. [Google Scholar] [CrossRef]
- Lv, H.; Kang, L.; Liu, Y. Dimensional analysis and effects of dimensionless numbers on the iron removal process in electromagnetic induction heating furnaces. Int. J. Heat Mass Transf. 2024, 229, 125714. [Google Scholar] [CrossRef]
- Chen, R.; Yang, Y.; Wang, Q.; Ding, H.; Su, Y.; Guo, J. Dimensionless parameters controlling fluid flow in electromagnetic cold crucible. J. Mater. Process. Technol. 2018, 255, 242–251. [Google Scholar] [CrossRef]
- Li, B.; Wu, X.; Huang, D.; Ye, C.; Chen, X.; Cao, X.; Shen, K.; Liu, J. High-purity rayon-based carbon fiber felt prepared by halogen gas purification for superior thermal insulation and oxidation resistance. Carbon 2024, 224, 119056. [Google Scholar] [CrossRef]
- Magampa, P.P.; Manyala, N.; Focke, W.W. Properties of graphite composites based on natural and synthetic graphite powders and a phenolic novolac binder. J. Nucl. Mater. 2013, 436, 76–83. [Google Scholar] [CrossRef]
- Hu, X.-L.; Tang, X.; Zhou, Y.-B.; Dai, Y.; Huang, Q.-Z. A continuous high-temperature purification reactor for graphite using Freon-12. Carbon 2017, 114, 753–754. [Google Scholar] [CrossRef]
- Nikulin, I.L.; Perminov, A.V. Mathematical modelling of frequency and force impacts on averaged metal flows in alternating magnetic field. Int. J. Heat Mass Transf. 2019, 128, 1026–1032. [Google Scholar] [CrossRef]
- Liang, X.; Li, M.; Cheng, B.; Wu, F.; Luo, X. Effects of induction furnace conditions on lining refractory via multi-physics field simulation. Appl. Phys. A 2023, 129, 542. [Google Scholar] [CrossRef]
- Buliński, P.; Smolka, J.; Siwiec, G.; Blacha, L.; Golak, S.; Przyłucki, R.; Palacz, M.; Melka, B. Numerical examination of the evaporation process within a vacuum induction furnace with a comparison to experimental results. Appl. Therm. Eng. 2019, 150, 348–358. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, K.; Wang, F.; Zhang, Y.; Yang, F.; Cheng, F. Microwave heating of coal slime based on multi-physics field simulations: Regulating waveguide port size and sample radius to improve microwave utilization efficiency. Chem. Eng. J. 2023, 470, 143975. [Google Scholar] [CrossRef]
- Wenzel, P.M.; Radgen, P.; Westermeyer, J. Comparing exergy analysis and physical optimum method regarding an induction furnace. Energies 2021, 14, 1621. [Google Scholar] [CrossRef]
- Wang, W.; Tuci, G.; Duong-Viet, C.; Liu, Y.; Rossin, A.; Luconi, L.; Nhut, J.-M.; Nguyen-Dinh, L.; Pham-Huu, C.; Giambastiani, G. Induction Heating: An Enabling Technology for the Heat Management in Catalytic Processes. ACS Catal. 2019, 9, 7921–7935. [Google Scholar] [CrossRef]
- Li, J.; Yang, B. Multi-scale CFD simulations of bubbling fluidized bed methanation process. Chem. Eng. J. 2019, 377, 119818. [Google Scholar] [CrossRef]
- Carretero, C.; Lucia, O.; Acero, J.; Burdio, J.M. Computational modeling of twopartly coupled coils supplied by a double half-bridge besonant inverter for induction heating appliances. IEEE Trans. Ind. Electron. 2013, 60, 3092–3105. [Google Scholar] [CrossRef]
- Buliński, P.; Smolka, J.; Golak, S.; Przyłucki, R.; Palacz, M.; Siwiec, G.; Lipart, J.; Białecki, R.; Blacha, L. Numerical and experimental investigation of heat transfer process in electromagnetically driven flow within a vacuum induction furnace. Appl. Therm. Eng. 2017, 124, 1003–1013. [Google Scholar] [CrossRef]
- Wang, T.; Bai, F.; Yao, P.; Li, X.; Nie, F.; Yuan, G.; Lei, D. Experimental study of electromagnetic induction heating ceramic particles device (EIHCPD). Energy Convers. Manag. 2025, 345, 120398. [Google Scholar] [CrossRef]
- Nian, S.-C.; Huang, M.-S.; Tsai, T.-H. Enhancement of induction heating efficiency on injection mold surface using a novel magnetic shielding method. Int. Commun. Heat Mass Transf. 2014, 50, 52–60. [Google Scholar] [CrossRef]
- Chemloul, N.-E.S. Dimensional Analysis: Rayleigh Method and Vaschy-Buckingham Method; ISTE Ltd. and John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Guo, W.; Bai, S.; Ye, Y. Controllable fabrication and mechanical properties of C/C–SiC composites based on an electromagnetic induction heating reactive melt infiltration. J. Eur. Ceram. Soc. 2021, 41, 2347–2355. [Google Scholar] [CrossRef]
- Ridolfi, M.R.; Folgarait, P. Numerical modeling of secondary breakup in molten metals gas-atomization using dimensionless analysis. Int. J. Multiph. Flow 2020, 132, 103431. [Google Scholar] [CrossRef]

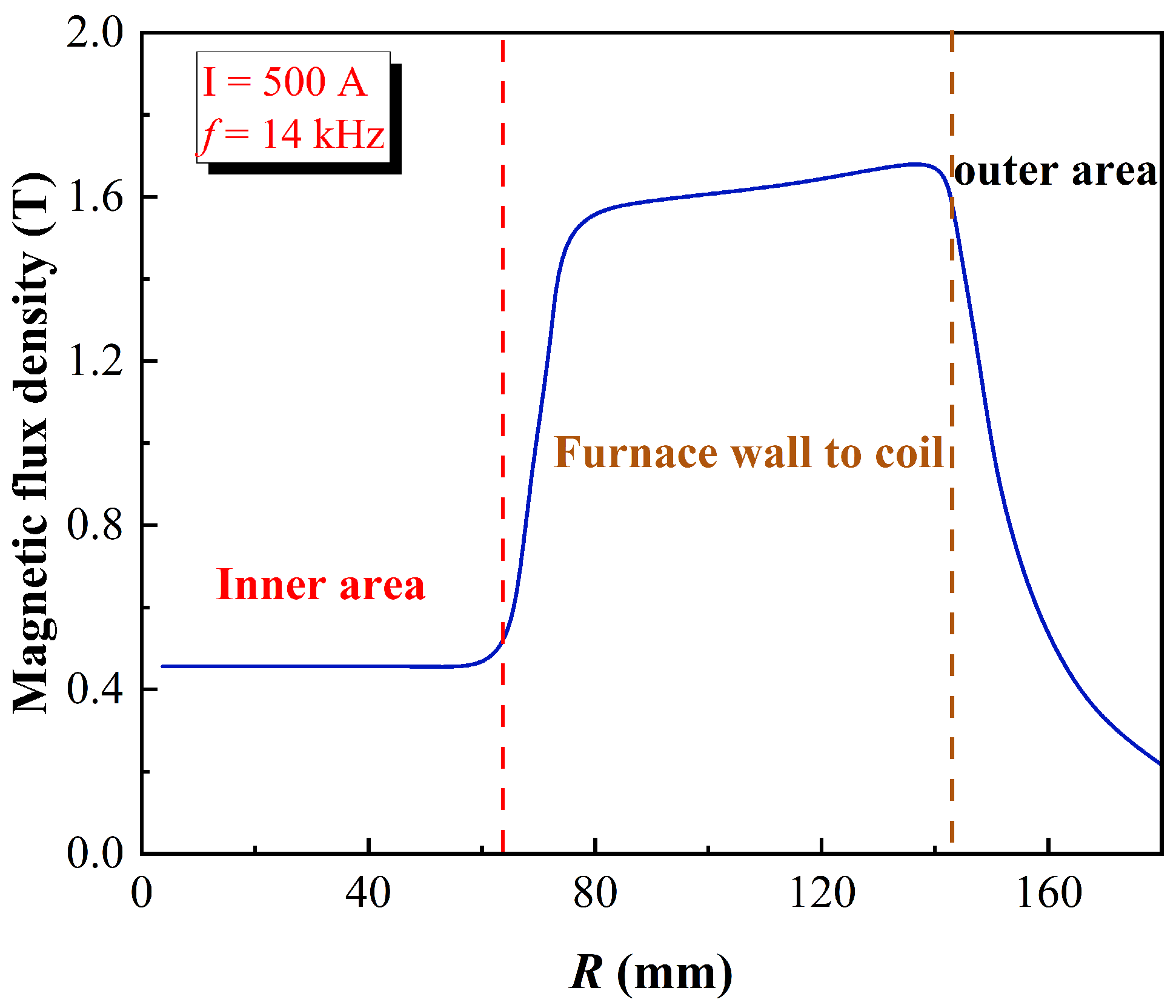
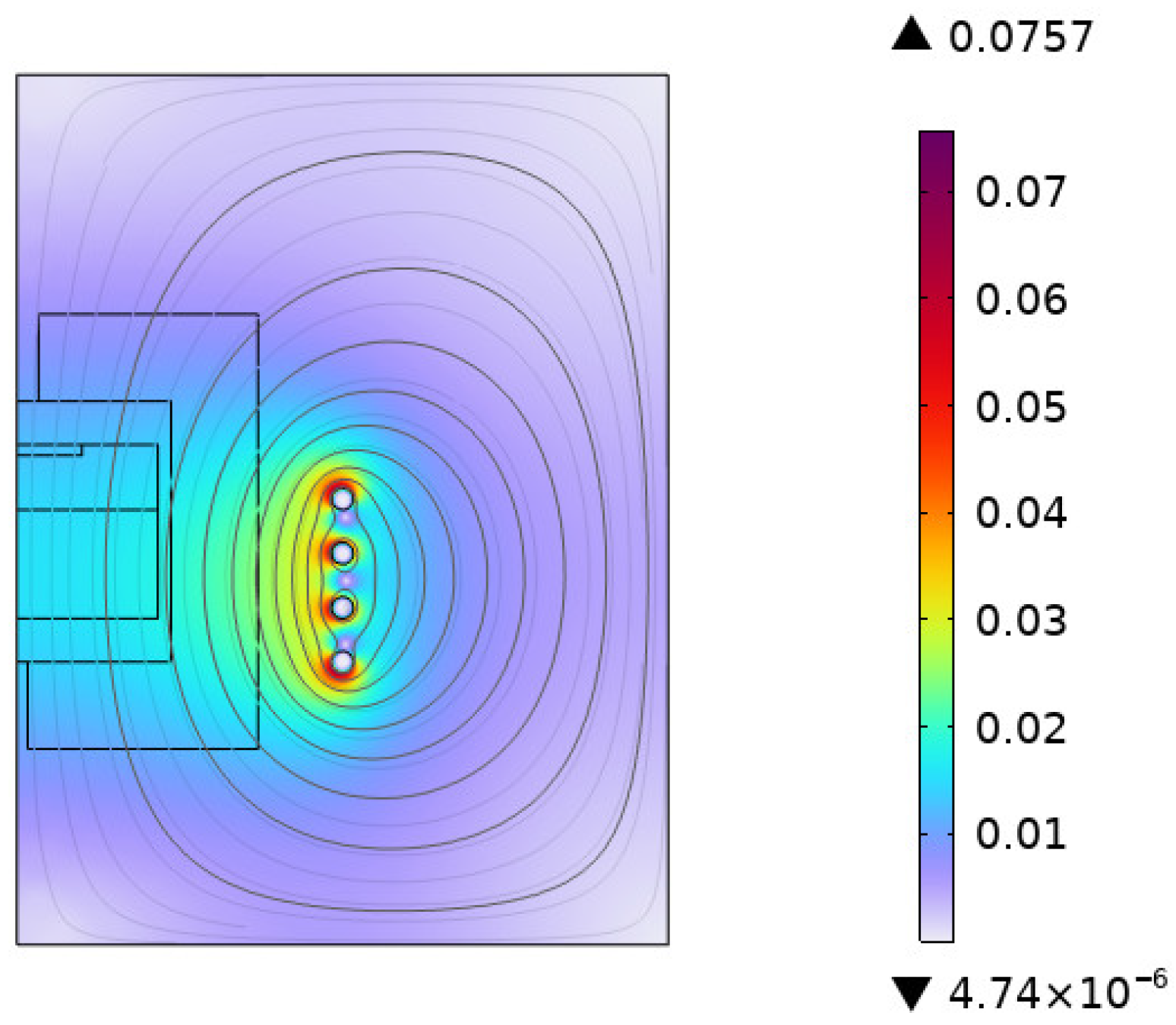

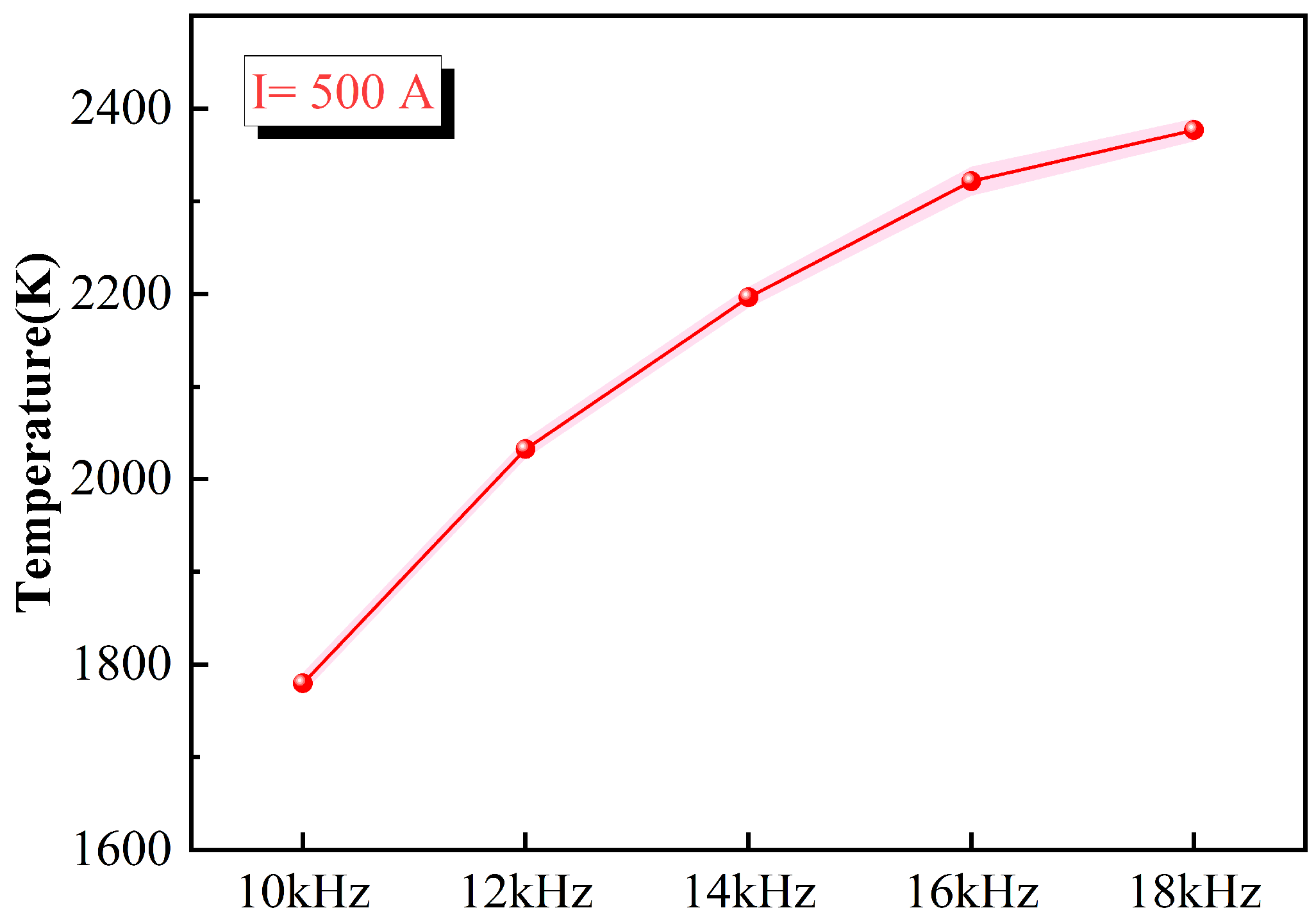
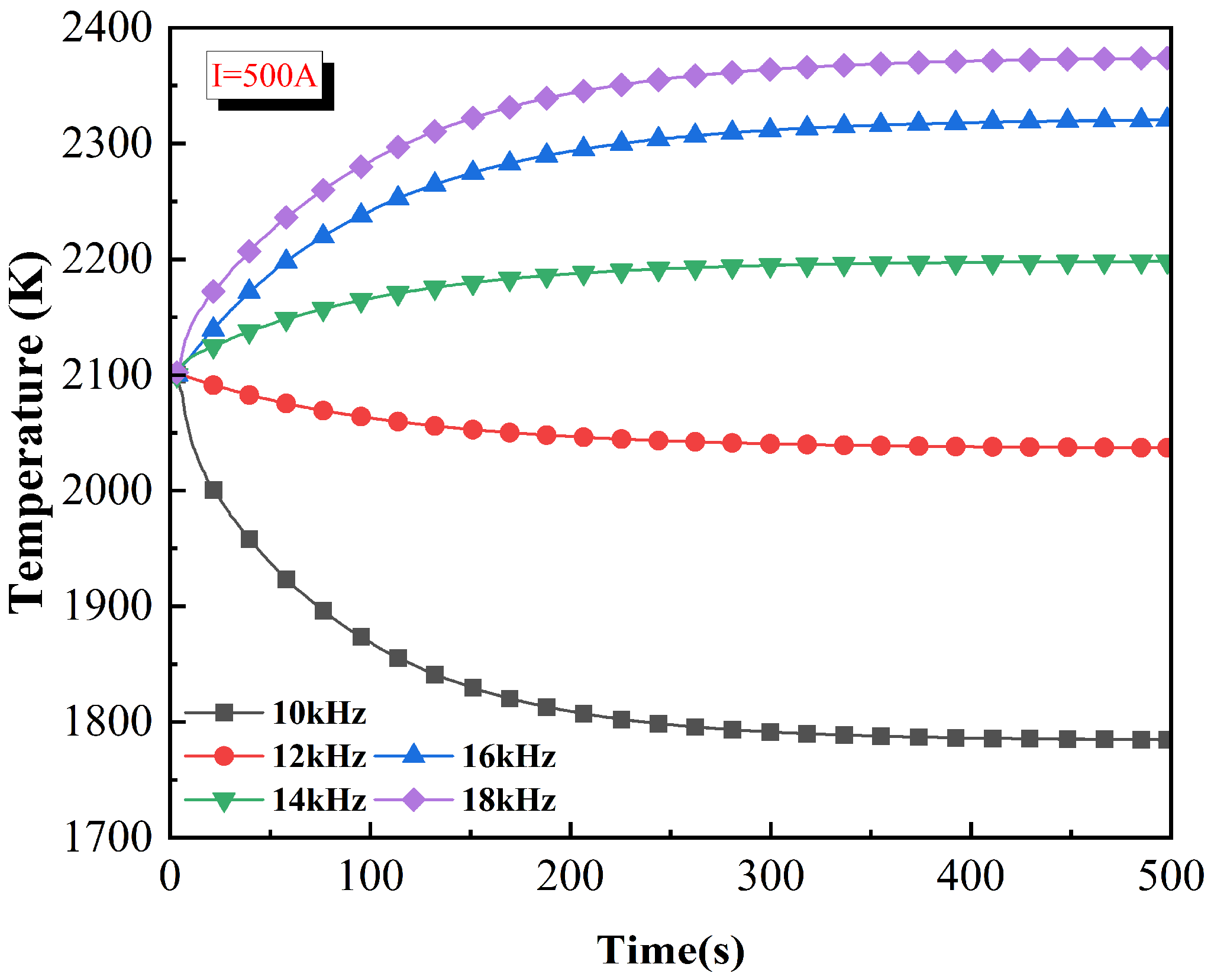


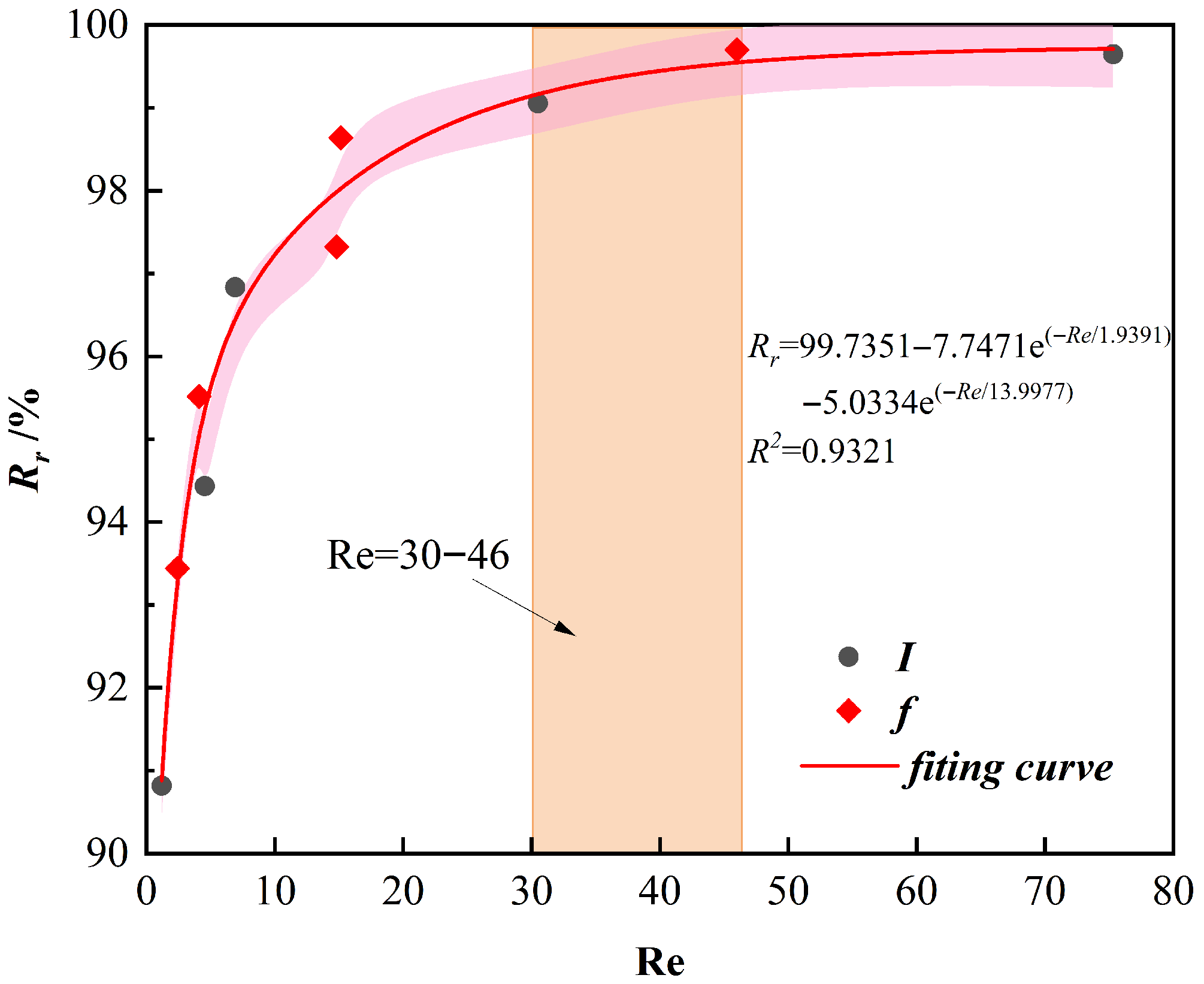
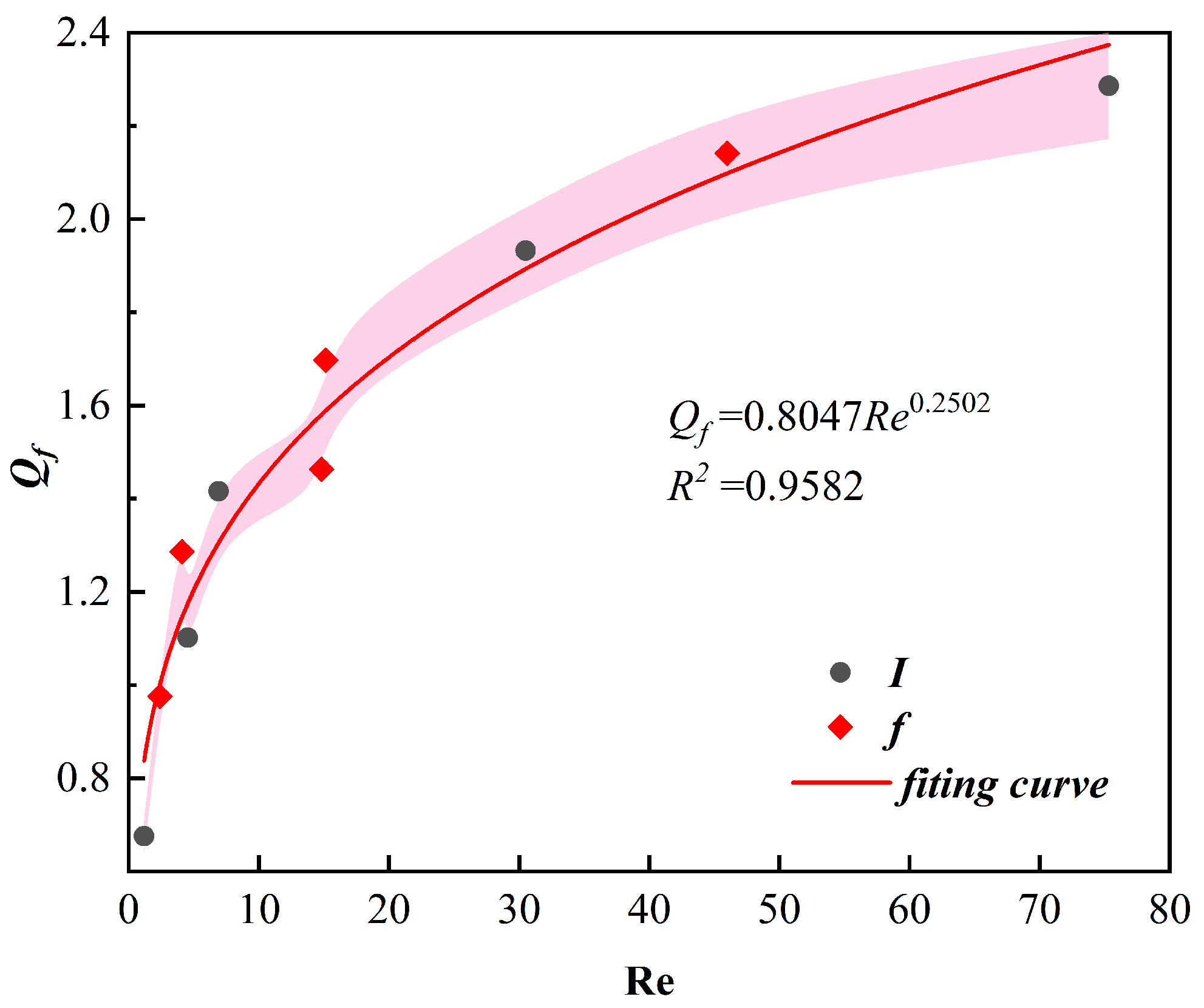
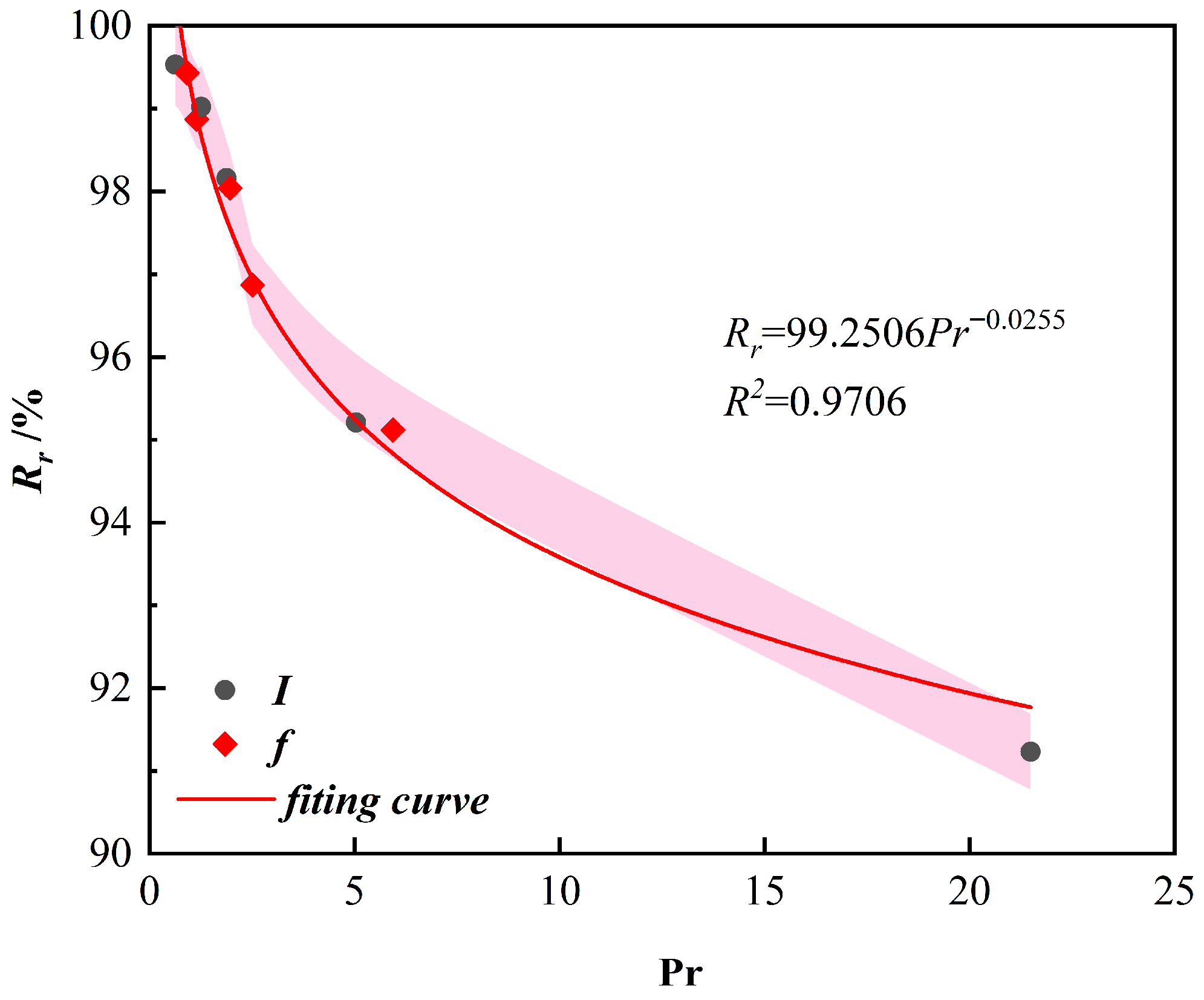
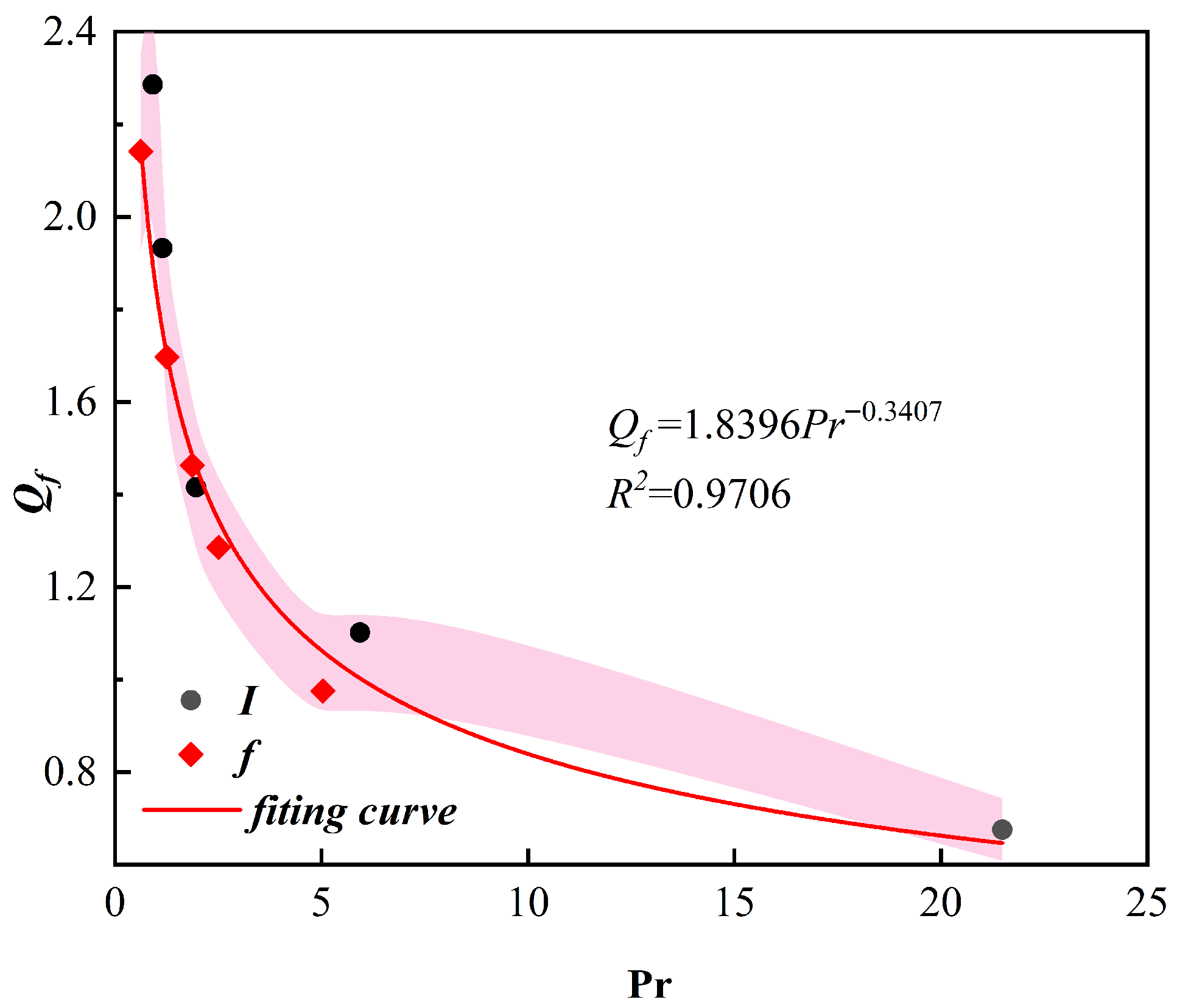
| Element | C | Fe2O3 | Al2O3 | MgO | B2O3 |
|---|---|---|---|---|---|
| Molar content/% | 97.1 | 2.3 | 0.32 | 0.24 | 0.04 |
| Physical Properties | Graphite Material | Furnace Wall | Coil |
|---|---|---|---|
| Relative magnetic permeability | 1 | 1 | 1 |
| Conductivity (S/m) | 3000 | 100 | 5998 |
| Specific heat (J/(kg·K)) | 710 | 200 | 385 |
| Relative permittivity | 1 | 1 | 1 |
| Density (kg/m3) | 1950 | 120 | 8960 |
| Heat conductivity (w/(m·k)) | 150 | 0.3 | 400 |
| Region | Coordinates | Electromagnetic | Flow | Thermal |
|---|---|---|---|---|
| Axis | r = 0 | ∇u = 0 | ∇T = 0 | |
| Infinite element domain | r → ∞ | B = 0 | / | / |
| Inner wall of the furnace | r = 65 | u = 0 | ||
| Outer wall of the furnace | z = 80 | / | ||
| Thickness of furnace wall | d = 6 | / | ||
| Gas domain | / | / | ε = 1 |
| Parameters | Symbolic | Value | ||||
|---|---|---|---|---|---|---|
| Electric current | I (A) | 450 | 500 | 550 | 600 | 650 |
| Magnetic frequency | F (kHz) | 10 | 12 | 14 | 16 | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Li, F.; Wang, S. Analysis of Dimensionless Numbers for Graphite Purification in the Electromagnetic Induction Furnaces. Appl. Sci. 2025, 15, 11294. https://doi.org/10.3390/app152011294
Zeng J, Li F, Wang S. Analysis of Dimensionless Numbers for Graphite Purification in the Electromagnetic Induction Furnaces. Applied Sciences. 2025; 15(20):11294. https://doi.org/10.3390/app152011294
Chicago/Turabian StyleZeng, Jun, Fashe Li, and Shuang Wang. 2025. "Analysis of Dimensionless Numbers for Graphite Purification in the Electromagnetic Induction Furnaces" Applied Sciences 15, no. 20: 11294. https://doi.org/10.3390/app152011294
APA StyleZeng, J., Li, F., & Wang, S. (2025). Analysis of Dimensionless Numbers for Graphite Purification in the Electromagnetic Induction Furnaces. Applied Sciences, 15(20), 11294. https://doi.org/10.3390/app152011294





