Assessment of Traffic-Induced Air Pollution and Its Effects on Intensity of Urban Heat Islands

Abstract

Due to intensive urbanization, global warming, and increasing energy demands, the impact of urban heat islands is becoming more significant. This study investigates the contribution of vehicular emissions to air pollution and its effects on urban heat island intensity in a selected area of Belgrade, Serbia, between March and September 2015, using a combination of experimental measurements and numerical simulations. Furthermore, this study presents the results of the research on the impact of assessment of traffic-induced air pollution on the appearance of thermal islands in the urban environment, as well as the characterization of thermal islands and their quantification. This study quantifies the effects of traffic-related emissions and urban meteorological parameters on the intensity of the urban heat island by combining field measurements with a validated three-dimensional numerical model and shows that higher traffic density increases pollutant concentrations and cooling energy demand in buildings. The study includes experimental measurements of traffic intensity and modeling of gas emissions from major roads. Using long-term and short-term field measurements, concentrations of carbon dioxide and other pollutants were analyzed with meteorological parameters and their cumulative impact to assess their impact on local air quality. A three-dimensional numerical model for simulating the dispersion of pollutants has been developed, confirmed and validated by experimental data. The results highlight a direct correlation between traffic density and pollutant concentrations, emphasizing the need for strategic urban planning and sustainable transport policies to mitigate the effects of air pollution. A validated numerical model was used to simulate dynamic changes in temperature fields and carbon dioxide concentrations caused by vehicular emissions. The findings reveal that the Urban Heat Island Intensity (UHII) for the selected area in Belgrade reached peaks of up to 12 °C during the summer measurement period, with typical values in July ranging from 5 °C to 9 °C. Furthermore, the validated numerical model demonstrated that the removal of urban trees would lead to a local air temperature increase of 1.5 °C to 3 °C, quantifying the significant cooling potential of green infrastructure. These results highlight a direct correlation between traffic density, pollutant concentrations, and the intensification of urban heat islands, emphasizing the need for strategic urban planning. Furthermore, the findings reveal that increased traffic not only elevates air pollutant levels but also enhances the intensity of urban heat islands, leading to higher cooling energy demands in buildings. These insights are vital for developing effective mitigation strategies to improve the sustainability of urban environments and living conditions. These findings provide a clear directive for urban planners: the integration and preservation of green infrastructure is a highly effective UHI mitigation strategy, capable of reducing local temperatures by 1.5–3 °C. Furthermore, the results strongly support the implementation of targeted traffic management policies in dense urban cores as a dual strategy to improve air quality and reduce local thermal loads.

1. Introduction

The urbanization of society in the physical sense causes major changes in local microclimatic conditions and affects air quality. One of the most commonly measured and best-documented parameters of microclimatic conditions is the increase in soil and air temperature. This well-known parameter is called the urban heat island. The main cause of this phenomenon is the concentration of a disproportionately large number of concrete objects (buildings), asphalt surfaces (streets, sidewalks, etc.) and other materials in one relatively large area, which, compared to natural materials and surfaces, green and water surfaces, and especially areas under forest, exhibit increased heat accumulation. The property of heat accumulation in these areas also occurs as a consequence of intensive traffic and industrial activity, which, at the same time, results in increased aerothermal pollution. The increased concentration of gases resulting from emissions due to heat transfer by radiation leads to greater heat retention, which significantly increases the air temperature in the urban environment. Urban heat islands are not spatially homogeneous. The structure of urban space is the main factor in this inhomogeneity. The state of urban heat islands is most often described using a quantity called heat island intensity. This quantity is defined as the difference in air temperature in an urban and corresponding rural environment [1,2,3,4]. Their intensity does not increase continuously from the periphery to the city center, which will be shown in this paper.

While changes in surface materials and urban geometry are primary drivers of the passive heating of a city, the UHI phenomenon is further amplified by direct anthropogenic heat emissions. Among these, vehicular traffic stands out as a major and dynamic contributor, releasing not only significant thermal energy but also air pollutants that alter the radiative properties of the urban atmosphere. This study, therefore, transitions from the general UHI context to a specific focus on traffic, as it represents a critical intersection of heat and pollution generation at the microscale, directly impacting both the thermal environment and local air quality. This link forms the central hypothesis of our investigation.

The aim of this paper is to quantify the impact and establish analytical dependence between urban (building layout, green space coverage, traffic intensity) and meteorological (air temperature, relative humidity, CO₂ concentration, solar radiation intensity, wind speed and direction) parameters on the value of urban heat island intensity, as well as determine the impact of urban heat islands on increased energy consumption (for cooling buildings, etc.) by applying modern experimental and numerical methods.

The study focusses on two key aspects:

The methodology: Traffic flows at seven busy Belgrade intersections were measured and COPERT was used to calculate emissions (CO₂, VOCs, NOx, CO, PM). CO₂ served as a critical input (S_CO2) for the model.

Modeling: A numerical 3D model links the dispersion of pollutants with heat transfer. The effective atmospheric emission coefficient (€’a) is directly linked to the local CO₂ concentration, so that the transport-derived CO₂ is the central variable in the simulation of urban temperature changes.

Focusing on traffic-related CO₂ emissions reveals hotspots at street level within urban heat islands. A validated numerical model shows that air temperatures near busy roads can be several degrees higher, quantifying the dynamic contribution of traffic. This approach provides usable insights for urban planning and enables targeted measures such as low-emission zones, traffic diversions or the promotion of public transport as well as strategies for green spaces.

Literature Review and Related Work

Urban climatologists have observed and documented the urban heat island effect in hundreds of cities around the world [5,6,7,8,9]. Based on the above documentation, a wide range of papers have been produced and published, defining complex scientific methodologies for measuring the intensity of the urban heat island. It is necessary to point out that in different publications there are often differences in the recommended methodology for measuring the intensity of the urban heat island, which also indicates the need for further research and the unification of the research methodology.

There are significant differences in the approach and criteria used for calculating the intensity of urban heat islands in published studies [10,11,12,13,14]. The aforementioned differences are primarily related to the method of measuring temperature in urban and rural environments, so it is first necessary to clearly define the way in which we want to define the intensity of heat islands. A review of the literature concluded that the following two methods of defining the intensity of urban heat islands can be distinguished: defining the intensity of urban heat islands based on air temperature and defining the intensity of heat islands based on the temperature of boundary surfaces. Air temperature values obtained through complex experimental measurements at real locations provide more precise and accessible data for energy simulations and urban heat island intensity calculations. Therefore, it was decided that in this study, an approach based on measured air temperature values will be used to calculate the intensity of urban heat islands.

Studies that looked at climatic characteristics were used to determine some common characteristics of heat islands in urban areas [15,16,17]. The impact of urban heat islands is manifested by an increase in the average daily, minimum and maximum air temperatures [18]. One of the basic characteristics of the urban heat island is that its intensity is greater at night than during the day [1]. In cities with larger populations, the impact of urban heat islands on the environment is more pronounced [18]. It is important to point out that the intensity of the urban heat island does not always have to be positive and directly related to the number of inhabitants [1,19]. The climatic zone of a city can influence the value of the intensity of urban heat islands, and in certain cases even eliminate it [20]. Several studies [21,22] have shown that the temperature difference increases with wind speed and that the turbulent transport of heated urban air increases. Due to high atmospheric pressure, which is recorded as a result of the increased intensity of thermal islands, there is a lower wind intensity and less cloudiness [23]. From the above, it can be concluded that the climatic conditions of the city and urban heat islands, as a separate phenomenon, are interconnected.

As urban heat islands are a non-stationary phenomenon, they are subject to both periodic and non-periodic changes. The maximum intensity of the urban heat island is usually reached a few hours after sunset [24]. As urban heat islands increase temperatures within urban environments, this often leads to negative health consequences for local urban populations. Meteorological events such as heat waves can lead to increased mortality [25]. The increase in air temperature in urban areas is a direct cause of the increase in the population’s energy needs for cooling [26,27]. It is important to realize that the local outdoor temperature, as an essential feature of the urban microclimate, directly determines the boundary conditions of the building envelope and thus influences heat transfer, cooling requirements and indoor comfort. The accurate consideration of this relationship improves the reliability of energy and comfort analyses in urban environments [28,29].

The urban heat island effect can be expressed as Surface UHI (SUHI), based on the land surface temperature, or as Canopy UHI (CUHI), defined as the air temperature difference between urban and rural areas. In this study, we analyze CUHI as it directly reflects the thermal environment relevant for the assessment of energy and comfort [30,31]. Few studies have linked traffic-related emissions and local microclimate to the intensity of UHI in the canopy layer and the energy demand of buildings. This work fills this gap by combining field measurements with a validated numerical model to quantify these relationships and their impact on urban energy consumption and comfort.

2. Experimental Methods

This section constitutes the first phase of the applied methodology, the experimental phase. It provides a detailed description of the field measurements carried out in both urban and rural environments, including temperature, humidity, solar radiation, wind characteristics, and traffic intensity. The aim of this phase is to obtain reliable data for quantifying the urban heat island intensity (UHII) and for generating input parameters for the subsequent numerical simulations. In this study, the urban heat island intensity (UHII) is rigorously defined as the difference between the air temperature measured at a representative urban location and that measured at a corresponding rural reference location under comparable meteorological conditions.

UHII is defined as the air temperature difference between the selected urban site (measured at 2 m above ground in the city center of Belgrade) and the rural reference site (Vinča settlement, also at 2 m height). The averaging period will be explicitly stated as hourly mean values, with both long-term (March–September 2015) and short-term (daily) sampling windows. The exact formula is: UHII = Turban (t) − Trural (t), where Turban (t) and Trural (t) denote the measured air temperatures at the urban and rural stations at time.

The most important characteristic of urban heat islands is the UHII. This quantity is defined as the difference in air temperature between urban and rural environments. Experimental measurements in this paper were used to determine the value of the UHII in a selected urban area of the city of Belgrade, as well as to analyze the impact of UHII on energy consumption. At a selected urban location in the city of Belgrade, in the immediate vicinity of the building of the Higher Textile School for Design, Technology and Management, as well as in a representative rural environment, the settlement of Vinča with Vinča Institute of Nuclear Sciences, detailed measurements of air temperature, radiant temperature, relative humidity, air velocity and solar radiation intensity were carried out. These parameters were used to calculate and estimate the impact of certain parameters on the value of UHII and as input data for the mathematical–numerical model. In addition, the number of vehicles, classified into seven typical categories, was measured in the urban location, which was used to calculate the emission of certain air pollutants due to traffic in the selected urban environment. The obtained emission values were used to form a base of pollutants from traffic in the urban environment, while the carbon dioxide value was also used as input data for a mathematical–numerical model.

Air temperature, carbon dioxide concentration, and air temperature values were measured at additional locations in the urban environment, more precisely in the immediate vicinity of the aforementioned school building, and the obtained results were used to validate the mathematical–numerical model. During the experimental measurement, modern measuring equipment was used, and the measurement procedures and processing of measured values with measurement uncertainty were carried out in accordance with applicable international regulations and standards. The experimental research was conducted in the period March–September 2015.

The urban site was located in the immediate vicinity of the Higher Textile School for Design, Technology and Management, in the Belgrade city center. This area is characterized by dense built-up structures, asphalt roads, and limited vegetation, with about only 8.5% of the total surface covered by greenery. The rural reference site was situated within the park of the Vinča Institute of Nuclear Sciences in the settlement of Vinča, surrounded predominantly by natural land cover and vegetation, with a negligible proportion of impervious surfaces.

The settlement of Vinča, located in the immediate vicinity of Belgrade, was chosen as a representative rural environment for this experimental research. The local meteorological station, installed within the Vinča Institute of Nuclear Sciences, measures physical parameters that are used to calculate the UHII. The physical parameters measured at the local meteorological station are: ambient air temperature, relative humidity, air velocity intensity and air flow direction, solar radiation, and diffuse radiation.

The location of the city center of Belgrade was chosen as a representative urban environment in this research. The measurement was carried out in the period from 2 March 2015 until 24 September 2015. Experimental measurements at this location can be divided into measurements taken over a longer period of time and daily or instantaneous measurements. All measuring instruments are calibrated in accredited laboratories of the Vinča Institute of Nuclear Sciences. Measurements of external temperature and relative humidity were carried out using a Testo 174H logger (Testo, Inc. 40 White Lake Rd. Sparta, NJ 07871, USA) throughout the entire research period. The intensity of direct solar radiation is measured with an instrument called a pyrheliometer, while the intensity of diffuse, global and reflected radiation is measured with a pyranometer. The instruments used for experimental measurements operate on the principle of thermocouples.

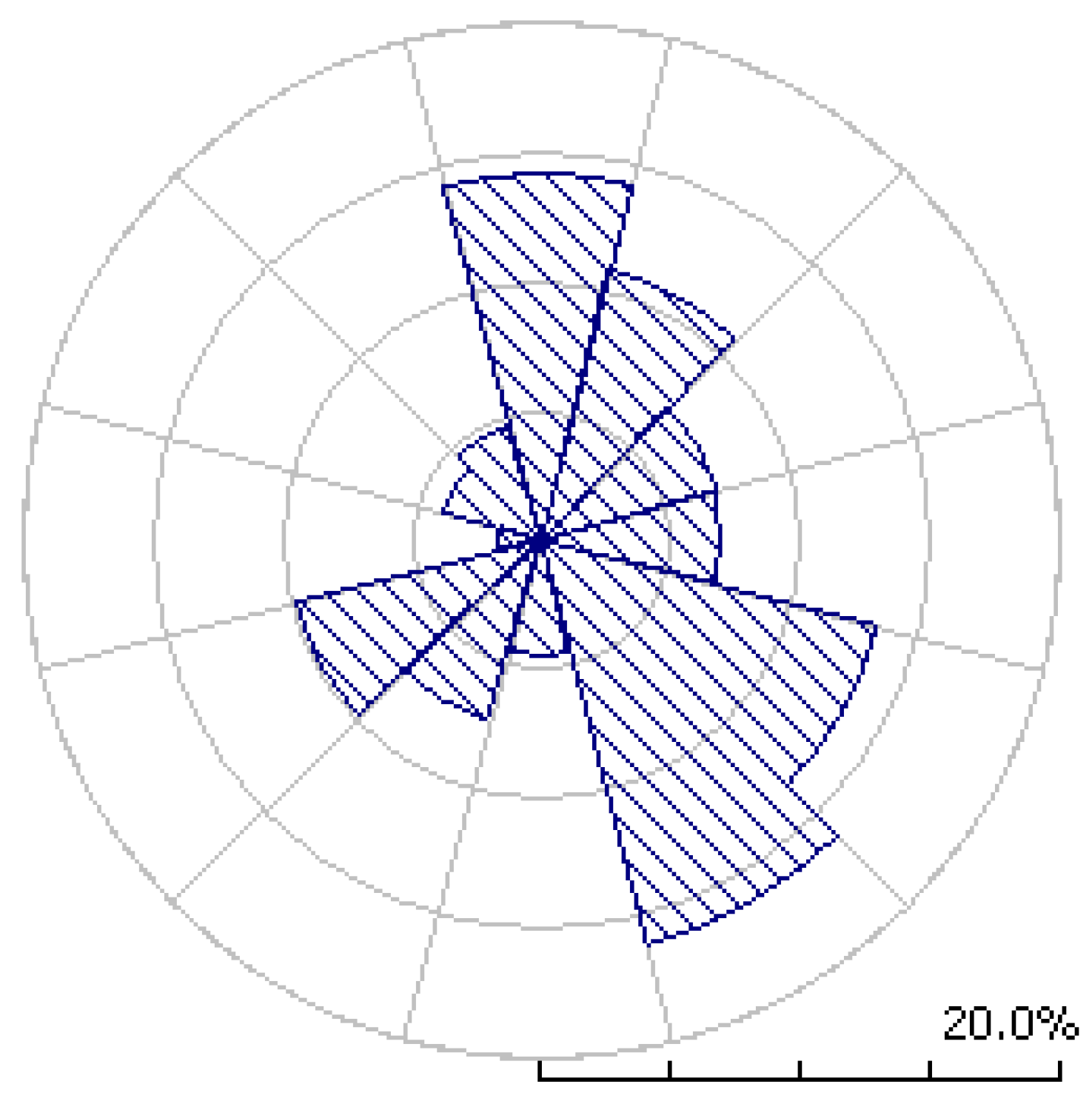
Based on the measured data, a wind rose was obtained for a given object (Figure 1), as well as a Weibull distribution of wind gust intensity for the meteorological station in urban location:

Traffic flow measurements were conducted at the seven busiest intersections located within a 500 m radius of the installed meteorological station in the city center. Vehicles were counted using manual monitoring in the period from 6:00 h to 19:00 h for three intersections and in the period from 6:00 h to 22:00 h for four intersections. Each registered vehicle is classified into one of seven categories: bicycle, motorcycle, passenger car, van, bus, light commercial vehicle, and heavy commercial vehicle.

The analysis of the measured data on vehicle flow was performed using the COPERT software tool (COPERT 4 version 11.2) (Computer Program to Calculate Emissions from Road Transport). The software was created with the aim of assessing the emissions of the most significant harmful substances and certain heavy metals emitted by different categories of vehicles (passenger cars, light and heavy goods vehicles, mopeds and motorcycles). For the calculation of exhaust emissions, in addition to the vehicle category obtained through manual monitoring, the input data used were the division of vehicles by type of fuel used, which was obtained based on statistical data and the database owned by the software itself for each country, the average speed of the vehicle and the distance traveled. The length of the path traveled by the vehicle is only observed for the physical model that was created. COPERT calculates emissions based on emission factors for each individual harmful substance. Based on the input data, CO2, VOC, NOx, CO and PM pollution are obtained at street level and intersection level. The results of the amount of street pollution from traffic intensity obtained by simulations using the COPERT Street Level software are shown in Appendix A,

Table A1. Results of numerical simulations of determination of CO₂, CO, NO_X, PM and VOC concentration values depending on traffic intensity.

Measurement Location	Pollutant [g]	06:00–07:00	07:00–08:00	08:00–09:00	09:00–10:00	10:00–11:00	11:00–12:00	12:00–13:00	13:00–14:00	14:00–15:00	15:00–16:00	16:00–17:00	17:00–18:00	18:00–19:00	19:00–20:00	20:00–21:00	21:00–22:00
Intersection 1-Cvijićeva-Zdravka Čelara-Starine Novaka	CO2	117,943	229,180	245,339	212,646	211,545	230,286	240,369	240,175	228,025	245,698	274,836	224,342	184,396	159,019	151,491	120,862
	CO	168.7	369.8	411.1	356.2	343.3	400.1	412.0	414.3	424.9	445.9	499.9	432.3	325.3	322.9	288.8	219.6
	NOX	265.6	406.4	452.7	372.5	383.7	428.8	452.0	453.5	390.6	406.2	447.3	381.5	327.7	292.9	274.3	220.5
	PM	4.8	7.3	8.3	7.0	7.1	8.2	8.6	8.6	7.4	7.5	8.2	7.2	5.9	5.6	5.1	4.0
	VOC	26.9	66.6	87.1	77.0	66.2	93.1	99.5	99.5	102.7	111.8	119.3	109.5	71.0	84.5	78.1	52.2
Street 1-Zdravka Čelara	CO2	43,298	94,691	119,007	110,435	106,533	116,204	122,476	126,806	116,064	114,700	158,119	118,277	91,670	70,250	68,790	48,804
	CO	61.9	152.8	199.4	185.0	172.9	201.9	209.9	218.7	216.3	208.2	287.6	227.9	161.7	142.7	131.2	88.7
	NOX	97.5	167.9	219.6	193.5	193.2	216.4	230.3	239.4	198.8	189.6	257.3	201.1	162.9	129.4	124.6	89.1
	PM	1.8	3.0	4.0	3.6	3.6	4.1	4.4	4.5	3.8	3.5	4.7	3.8	3.0	2.5	2.3	1.6
	VOC	9.9	27.5	42.3	40.0	33.4	47.0	50.7	52.6	52.3	52.2	68.6	57.7	35.3	37.3	35.5	21.1
Street 2-Cvijićeva (from Bul. Despota Stefana to intersection 1)	CO2	77,485	148,002	140,705	147,351	150,975	167,355	170,114	173,178	145,184	158,414	154,333	129,404	106,457	119,931	109,373	89,502
	CO	104.8	228.6	222.7	246.8	245.0	290.7	291.6	298.7	254.5	272.7	273.1	235.6	183.1	243.6	208.5	162.6
	NOX	185.2	275.2	267.8	258.1	273.8	311.6	319.9	327.0	269.2	279.4	267.5	230.5	190.9	220.9	198.0	163.3
	PM	3.3	4.9	4.8	4.9	5.0	6.0	6.1	6.2	5.0	5.1	4.9	4.2	3.4	4.2	3.7	3.0
	VOC	15.6	37.9	41.9	53.3	47.3	67.7	70.4	71.8	60.1	59.6	63.0	53.5	39.1	63.7	56.4	38.6
Street 3-Cvijićeva (from intersection 2 to Roosevelt)	CO2	56,499	115,047	117,740	78,871	83,854	84,709	93,777	86,506	122,731	132,894	135,614	124,390	101,448	72,172	69,851	58,210
	CO	78.4	183.1	193.7	132.1	136.1	147.2	160.7	149.2	219.3	232.6	229.2	224.4	174.9	146.6	133.2	105.8
	NOX	132.0	221.7	229.6	138.2	152.1	157.7	176.3	163.3	230.8	245.7	239.3	227.5	189.3	132.9	126.5	106.2
	PM	2.4	4.0	4.2	2.6	2.8	3.0	3.4	3.1	4.3	4.5	4.3	4.2	3.4	2.5	2.3	1.9
	VOC	12.3	33.6	41.4	28.6	26.3	34.2	38.8	35.9	51.4	54.7	49.7	54.2	39.4	38.4	36.0	25.1
Street 4- Starine Novaka	CO2	52,553	98,544	101,432	89,688	79,113	85,857	91,551	90,591	100,455	108,683	116,760	95,745	80,049	66,971	62,527	55,607
	CO	67.7	156.5	167.7	146.6	126.1	151.1	158.6	152.5	186.0	194.1	210.0	182.3	144.5	123.1	115.1	105.1
	NOX	134.0	186.9	190.3	162.6	146.4	160.0	172.2	168.2	181.0	191.7	201.4	170.9	145.2	122.8	116.7	102.3
	PM	2.4	3.3	3.4	3.0	2.6	3.0	3.2	3.1	3.4	3.5	3.7	3.2	2.6	2.2	2.1	1.9
	VOC	9.8	27.2	32.3	29.0	22.4	33.1	36.2	33.2	46.8	44.2	51.1	46.3	33.0	28.4	29.6	26.0
Intersection 2–27 March-Starine Novaka	CO2	98,936	184,355	176,695	164,050	154,413	154,527	176,841	173,478	219,759	219,190	203,433	188,740	171,030	161,180	141,348	125,444
	CO	120.9	289.2	287.9	261.6	241.5	275.8	310.0	284.5	405.0	386.5	360.8	355.6	314.7	274.3	253.0	243.2
	NOX	265.9	367.2	337.3	307.1	292.0	288.0	332.7	316.1	411.5	406.0	374.3	350.7	315.5	294.7	270.1	232.1
	PM	4.8	6.5	6.0	5.5	5.1	5.3	6.1	5.6	7.7	7.4	6.9	6.6	5.7	5.2	4.9	4.3
	VOC	16.6	49.0	49.4	46.9	38.6	56.2	66.3	54.5	105.1	80.7	89.8	90.4	74.7	56.2	62.1	61.9
Street 5-Kraljice Marije	CO2	32,468	77,183	83,443	76,198	81,135	81,072	93,025	90,865	98,119	95,538	95,777	92,580	86,187	86,346	74,543	63,826
	CO	47.3	122.8	138.6	121.5	126.9	144.7	163.1	149.0	188.9	181.2	182.0	177.8	170.9	146.9	133.4	123.7
	NOX	85.8	158.0	165.7	142.6	153.4	151.1	175.0	165.6	185.8	181.8	180.0	176.8	161.5	157.9	142.4	118.1
	PM	1.6	2.8	3.0	2.6	2.7	2.8	3.2	3.0	3.5	3.4	3.4	3.3	3.0	2.8	2.6	2.2
	VOC	8.2	23.3	26.5	21.8	20.3	29.5	34.9	28.6	51.2	42.6	49.8	45.9	46.0	30.1	32.8	31.5
Street 6-Belgrade	CO2	77,046	125,548	117,344	103,035	88,937	88,995	104,530	104,180	141,862	145,669	129,782	122,577	107,948	102,097	82,160	76,703
	CO	94.2	196.9	191.2	164.3	139.1	158.9	183.2	170.8	261.4	256.9	230.2	230.9	198.6	173.7	147.1	148.7
	NOX	207.1	250.0	224.0	192.9	168.2	165.9	196.7	189.8	265.6	269.8	238.8	227.8	199.2	186.7	157.0	141.9
	PM	3.7	4.4	4.0	3.5	2.9	3.1	3.6	3.4	5.0	4.9	4.4	4.3	3.6	3.3	2.8	2.6
	VOC	12.9	33.4	32.8	29.5	22.2	32.4	39.2	32.7	67.8	53.6	57.3	58.7	47.1	35.6	36.1	37.8
Street 7- 27. March	CO2	17,775	41,000	48,171	45,984	47,921	46,783	53,852	52,687	60,530	60,261	58,844	52,531	47,939	44,549	42,275	33,928
	CO	22.1	62.5	75.5	72.1	74.4	80.0	89.9	84.8	106.0	103.0	102.5	94.1	87.1	74.5	74.2	61.5
	NOX	46.0	81.8	92.0	86.4	90.5	85.5	100.2	96.6	112.1	110.0	106.7	96.2	87.4	81.2	79.3	63.6
	PM	0.8	1.4	1.6	1.5	1.6	1.6	1.8	1.7	2.1	2.0	1.9	1.8	1.6	1.4	1.4	1.1
	VOC	3.0	10.0	12.3	12.2	12.2	15.6	17.6	15.8	24.6	20.5	23.1	21.1	19.6	14.3	16.6	14.2
Intersection 3–27 March-Takovska	CO2	17,820	33,130	47,817	44,630	43,700	44,248	52,408	52,130	57,625	58,696	60,817	54,479	46,630	42,434	37,382	30,841
	CO	22.8	46.8	70.3	67.8	66.8	69.8	80.0	81.3	91.8	95.2	102.8	89.8	83.0	68.8	63.2	48.7
	NOX	42.9	66.4	91.4	84.4	82.4	78.2	95.6	96.4	104.8	104.6	107.7	97.6	83.4	77.0	67.5	59.1
	PM	0.8	1.2	1.6	1.5	1.5	1.4	1.7	1.7	1.9	1.9	1.9	1.7	1.5	1.3	1.2	1.0
	VOC	3.2	6.4	10.3	10.3	11.4	12.5	12.8	14.4	16.5	17.3	19.0	15.4	16.8	11.7	11.2	8.6
Street 8-Takovska (from intersection 3 to Jaše Prodanovića)	CO2	86,610	103,318	100,075	97,420	91,189	86,034	91,174	93,989	107,483	102,773	100,212	102,410	97,840	88,607	74,052	75,377
	CO	113.2	147.3	152.6	142.8	136.8	133.0	136.7	144.8	163.8	161.1	161.4	159.0	157.9	135.7	116.5	112.2
	NOX	197.0	200.5	192.3	187.3	174.9	157.9	170.9	178.4	201.6	190.5	179.6	192.2	180.7	166.3	139.4	147.2
	PM	3.5	3.5	3.5	3.4	3.2	2.8	3.1	3.2	3.6	3.4	3.1	3.3	3.1	2.8	2.4	2.5
	VOC	15.0	19.5	23.7	20.3	20.7	23.5	21.9	25.1	27.0	26.1	26.8	25.7	26.1	20.7	18.3	16.6
Street 9-Takovska (from intersection 3 to Svetogorska)	CO2	54,200	63,872	61,684	58,627	53,937	50,795	56,500	54,940	64,949	61,212	60,866	58,041	55,867	50,065	49,499	41,867
	CO	67.5	90.6	89.2	89.1	82.5	80.2	86.3	85.7	103.9	98.5	103.4	96.1	95.8	81.2	83.7	66.0
	NOX	137.0	128.1	120.7	110.8	101.7	89.7	103.1	101.6	125.4	113.1	110.7	107.3	100.8	90.8	89.4	80.3
	PM	2.5	2.2	2.1	2.0	1.9	1.6	1.8	1.8	2.3	2.0	2.0	1.9	1.8	1.6	1.6	1.4
	VOC	9.0	12.4	12.8	13.6	14.1	14.4	13.8	15.2	21.1	17.3	21.0	17.0	19.5	13.8	14.8	11.7
Street 10-George Washington	CO2	35,640	66,259	95,635	89,259	87,400	88,495	104,817	104,259	115,250	117,393	121,634	108,957	93,260	84,867	74,764	61,683
	CO	45.6	93.6	140.6	135.7	133.6	139.7	160.1	162.6	183.6	190.4	205.7	179.6	166.0	137.6	126.4	97.3
	NOX	85.8	132.7	182.7	168.8	164.9	156.3	191.2	192.8	209.6	209.2	215.4	195.2	166.8	153.9	135.0	118.3
	PM	1.5	2.3	3.3	3.0	3.0	2.8	3.4	3.5	3.7	3.7	3.8	3.4	3.0	2.7	2.3	2.1
	VOC	6.3	12.7	20.6	20.6	22.8	25.0	25.7	28.9	32.9	34.6	38.0	30.8	33.6	23.3	22.4	17.2
Intersection 4-Takovska-Svetogorska	CO2	135,304	193,979	19,7061	-	-	-	-	-	198,724	193,979	199,242	194,369	180,215	-	-	-
	CO	164.4	276.6	280.7	-	-	-	-	-	319.1	310.0	340.1	323.3	297.3	-	-	-
	NOX	356.4	389.2	394.4	-	-	-	-	-	405.9	370.6	371.8	369.6	328.0	-	-	-
	PM	6.4	6.7	6.9	-	-	-	-	-	7.4	6.5	6.7	6.5	5.8	-	-	-
	VOC	20.8	38.3	39.6	-	-	-	-	-	72.6	52.7	75.0	59.0	61.1	-	-	-
Street 11-Majora Ilića	CO2	11,120	24,151	25,632	-	-	-	-	-	30,173	25,694	26,726	30,276	27,050	-	-	-
	CO	13.5	34.4	36.5	-	-	-	-	-	48.4	41.1	45.6	50.4	44.6	-	-	-
	NOX	29.3	48.5	51.3	-	-	-	-	-	61.6	49.1	49.9	57.6	49.2	-	-	-
	PM	0.5	0.8	0.9	-	-	-	-	-	1.1	0.9	0.9	1.0	0.9	-	-	-
	VOC	1.7	4.8	5.1	-	-	-	-	-	11.0	7.0	10.1	9.2	9.2	-	-	-
Street 12-Takovska (from intersection 4 to King Alexander Boulevard)	CO2	169,307	212,855	211,752	-	-	-	-	-	212,250	209,250	211,794	200,442	187,840	-	-	-
	CO	205.8	303.5	301.7	-	-	-	-	-	340.8	334.4	361.5	333.5	309.9	-	-	-
	NOX	446.0	427.1	423.8	-	-	-	-	-	433.5	399.8	395.2	381.1	341.8	-	-	-
	PM	8.0	7.4	7.4	-	-	-	-	-	7.9	7.1	7.1	6.7	6.0	-	-	-
	VOC	26.1	42.0	42.5	-	-	-	-	-	77.5	56.8	79.7	60.8	63.7	-	-	-
Intersection 5-Ruzveltova-Cvijićeva	CO2	144,105	284,959	296,152	-	-	-	-	-	272,975	301,608	308,739	282,281	229,387	-	-	-
	CO	192.6	449.2	481.5	-	-	-	-	-	476.5	516.3	501.2	490.8	390.2	-	-	-
	NOX	350.7	577.9	596.9	-	-	-	-	-	537.5	592.9	566.8	535.6	439.3	-	-	-
	PM	6.3	10.4	11.0	-	-	-	-	-	10.0	10.8	10.1	9.8	7.9	-	-	-
	VOC	29.7	83.3	103.6	-	-	-	-	-	109.8	116.5	102.5	115.1	89.4	-	-	-
Street 13-Roosevelt	CO2	46,994	81,517	82,280	-	-	-	-	-	71,229	76,336	77,843	73,699	61,653	-	-	-
	CO	70.5	130.2	136.9	-	-	-	-	-	137.4	146.4	146.5	138.1	122.2	-	-	-
	NOX	119.4	168.6	167.7	-	-	-	-	-	138.0	149.6	147.0	142.6	117.6	-	-	-
	PM	2.2	3.1	3.1	-	-	-	-	-	2.6	2.8	2.8	2.6	2.2	-	-	-
	VOC	12.6	25.9	28.9	-	-	-	-	-	36.8	36.3	39.2	34.8	33.9	-	-	-

.

The determination of radiant temperature was performed by measuring the temperature of a black globe. This theory was explained in detail by L.A. Kuehn et al. in [32]. The temperature measured with a black globe is the result of heat gained and lost through radiation and convection [33]. The temperature of the black globe is a weighted average of the mean radiant temperature and the ambient (air) temperature. During the summer period, when the highest ambient temperature values are expected at a representative urban location, measurements of the parameters required for calculating the radiation temperature were performed.

Based on a detailed analysis of the intensity of total solar radiation measured in rural and urban areas using installed local meteorological stations, a high correlation was observed for the summer months of measurement. From the above, it can be concluded that the heat gains from solar radiation for rural and urban areas are of approximate intensity. This conclusion indicates that the UHII for the measurement period depends only on the structure of the city. 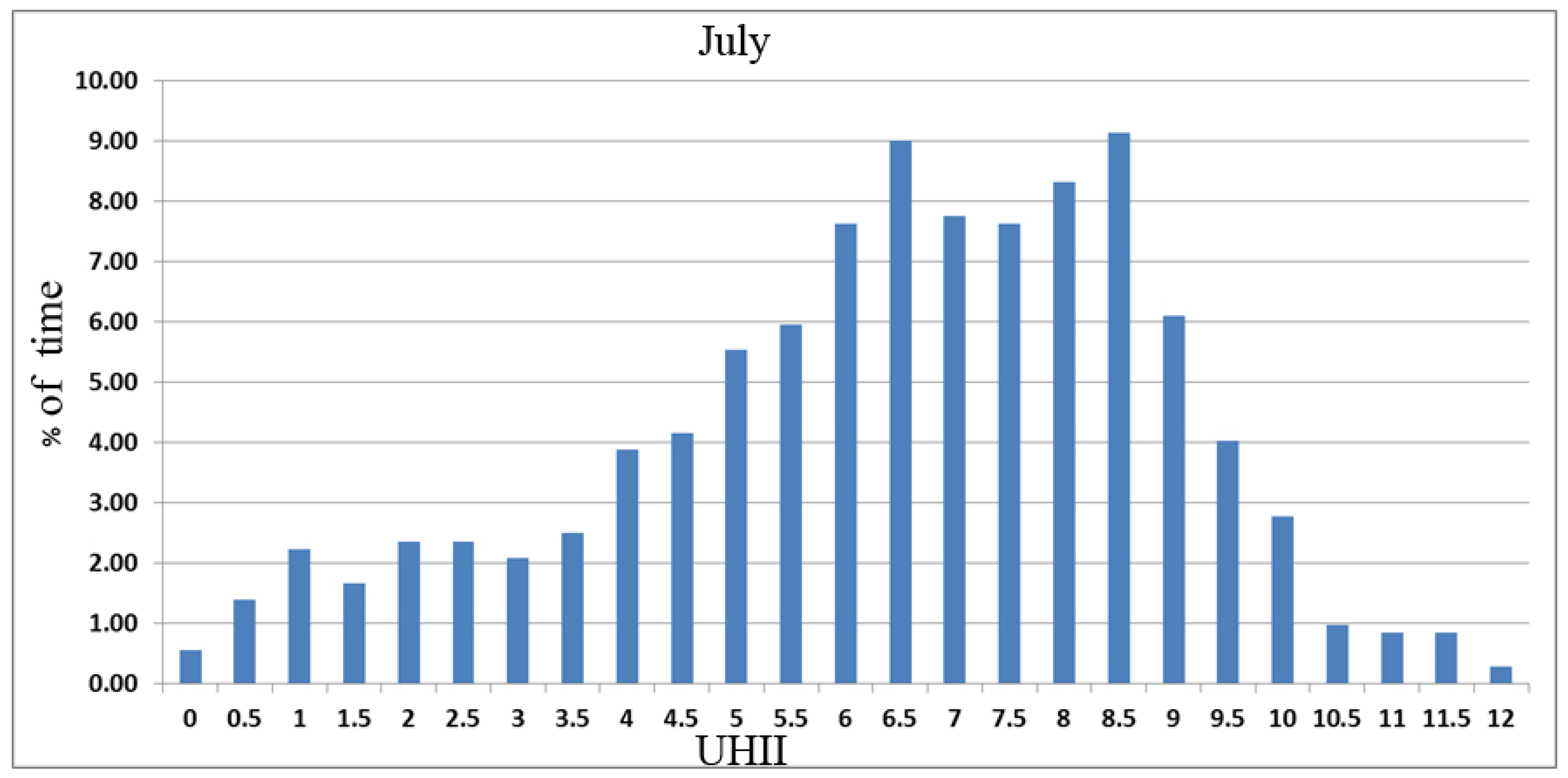Figure 2 shows the frequency of UHII values for the month of July, when the highest temperature value was measured of 46.1 °C at a representative urban location. The maximum value of the UHII in July ranged up to 12 °C, but the largest percentage, i.e., more than 65% of the time, the value of the UHII ranged in the interval 5–9 °C. Furthermore, higher values of UHII were observed during the night period.

At higher wind speeds, air mixing is more frequent and a decrease in ambient temperature is possible, and this also affects the lower value of the UHII. Measured wind speed data for urban and rural environments were used to analyze the impact of wind on the UHII. The obtained results show that the UHII decreases with increasing air flow, and that the measured wind speed is significantly higher in rural areas compared to urban areas. Regarding temperature, there is a greater correlation between the UHII and urban temperature, while this correlation with rural temperature is very small.

3. Mathematical–Numerical Model

This section represents the second phase of the methodology, the simulation phase. It introduces the mathematical–numerical model developed to simulate the dynamic behavior of temperature, velocity, and pollutant concentration fields in the urban environment. The experimental data obtained in the previous phase were used as input and boundary conditions, enabling validation of the model and ensuring consistency between measured and simulated results.

The paper presents a developed numerical–analytical model that predicts the dynamic behavior of the temperature, velocity and carbon dioxide concentration fields in urban environments. By analyzing the obtained experimental and numerical results, the dependence of the UHII on urban and meteorological parameters was established. The reliability of the numerical model for predicting the dynamic behavior of the temperature, velocity and carbon dioxide concentration fields in the urban environment was tested.

For the description of the current thermal processes for the observed case, assumptions are given on the basis of which the main transport equations used to describe the three-dimensional turbulent flow with heat transfer are defined. It is necessary to introduce basic assumptions for the class of flows modeled in this study:

- The flow is stationary, i.e., steady flow. This assumption is justified given that there are very small temporal changes in the physical parameters of the air state in the computational domain, during the time interval for which the calculation was performed. In mathematical terms, this assumption implies that all partial derivatives of physical parameters with respect to time are equal to zero.

- The flow is turbulent. As this class of flow is characterized by large local values of Reynolds number, a turbulent flow regime is present. In mathematical terms, this fact conditioned the modeling of turbulence; therefore, the standard two-equation k-ε (epsilon) turbulence model was adopted.

- In the observed problem, all three forms of heat transfer are present: conduction, convection, and radiation. When modeling the process of heat transfer by conduction and convection, both heat transfer mechanisms are calculated simultaneously, both through the base medium (air) and through the solid body. When modeling heat transfer by radiation, the basic medium (air) was treated as a non-transparent medium. Due to the introduction of the assumption of a non-transparent medium, it is necessary to define functional relations for determining the effective air emissivity coefficients and the radiation scattering coefficients in the air depending on the local concentration of carbon dioxide and water vapor in the air. In mathematical terms, when developing the radiation model, the concept of modeling heat transfer by radiation was adopted by applying the gradient approach model, which implies that the heat flux of heat transfer by radiation is defined in the form of a gradient (equivalent to the classical approach of the formulation of heat transfer by conduction).

- We consider air to be an ideal gas. This assumption ensures that the developed mathematical model has a unique solution (the number of relations equal to the number of independent variables).

The basic balance equations are used, i.e., when modeling turbulent fluid flow with heat transfer, the fluid flow is described with two scalar and one vector partial differential equation, which are formed on the basis of three basic conservation laws: conservation of mass or quantity (continuity equation), conservation of momentum (Navier–Stokes vector equation for viscous fluid), and the First Law of Thermodynamics (energy conservation). The CO₂ concentration maintenance equation was also used:

$$U_{\mathrm{j}}{\displaystyle \frac{{{\mathsf{\partial }C}_{CO}}_2}{\mathsf{\partial }{x}_j}}={\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}\left(D_{{CO}_2,air}+{\displaystyle \frac{{\nu }_t}{S_{Ct}}}\right){\displaystyle \frac{\mathsf{\partial }{C_{CO}}_2}{\mathsf{\partial }{x}_i}}+S_{{CO}_2}$$

(1)

where C_CO2 is the averaged CO₂ concentration in the air, U_j is the component of the averaged fluid velocity in direction j, D_CO2,air is the mass diffusion coefficient of CO₂ in the air, and S_CO2 is the source term for CO₂.

To model the kinematic turbulent viscosity ν_t a standard two-equation k-ε model was used. The two-equation k–ε model belongs to the group of Reynolds-averaged Navier–Stokes equations—RANS models [34]. RANS equations describe the behavior of averaged (mean) flow quantities, while the effects of turbulence (Reynolds stress tensor and turbulent heat flux vector) are modeled using turbulent kinematic viscosity (an eddy viscosity assumption). This significantly reduces the required calculation time and the required level of computing resources, making the two-equation k–ε model applicable to a wide range of engineering problems [35].

In the standard k–ε model, the unknown quantity ν_t is determined by applying the Boussinesq hypothesis on turbulent viscosity related to Reynolds stresses to the mean velocity gradients. This hypothesis assumes that the amount of motion caused by turbulent eddies can be modeled by introducing an additional quantity—turbulent viscosity. The above assumption was made based on an analogy with the way in which the amount of motion caused by the molecular motion of gas particles is described by molecular viscosity. Through the rate of dissipation of turbulent kinetic energy, the characteristic length scale l and the characteristic time scale τ of turbulence can be expressed, so that the turbulent kinematic viscosity ν_t is obtained using the following expression:

$${\nu }_t=C_{\mu }{\displaystyle \frac{k^2}{\epsilon }}$$

(2)

where Cμ is the empirical constant of the turbulent model, Cμ = 0.09.

Partial differential equations for the kinetic energy of turbulence k and the rate of dissipation of kinetic energy of turbulence ε are obtained by a semi-empirical modeling technique [36]. The values of the coefficients appearing in these differential equations were determined experimentally [37].

For the radiation heat transfer model in this study, a gradient model was adopted. The main drawback of the above model is the necessity of calculating the effective radiation coefficient, but in a mathematical and numerical sense it is the most suitable for treating the phenomenon of heat transfer by radiation in a space with solid bodies such as residential buildings, public buildings, etc. A new physical quantity was introduced—radiant temperature, which is a consequence only of radiation effects. The radiation conduction coefficient is determined as a function of: the radiant temperature, the emissivity coefficient ε’, the scattering coefficient s’ per unit length, and the distance between two adjacent surfaces (walls) of a solid body X_GAP, using the following expression:

$${\lambda }_{rad}={\displaystyle \frac{4\sigma T_{rad}^3}{0.75\left({\epsilon }^{\prime }+s^{\prime }+\frac{1}{X_{GAP}}\right)}}$$

(3)

By introducing the assumption that, based on dimensional uniqueness, the terms along 4σT_a³ can be summed, the final form of the expression for the reciprocal of the effective thermal conductivity for a gray medium is obtained.

$${\lambda }_{eff}^{-1}={\displaystyle \frac{3}{4}}{\displaystyle \frac{\left({\epsilon }^{\prime }+s^{\prime }+\frac{1}{X_{GAP}}\right)}{4\sigma T_a^3}}$$

(4)

In order to fully define the radiative heat transfer model, it is necessary to determine the values of the atmospheric emissivity coefficient and the scattering coefficient per unit length. The process of determining the effective atmospheric emissivity coefficient and scattering coefficient is very complex given the fact that their values are influenced by a number of different atmospheric parameters: ε(u(P⁄P₀)ⁿ), P₀, T. In the previous expression, u is the optical thickness which is a function of the pressure value P, the atmospheric pressure value P₀, and the average air temperature T. The value of the exponent n ranges from a minimum of approximately 0.7 m⁻¹ for the case of low atmospheric optical thickness to approximately 1.0 m⁻¹ for cases of high atmospheric optical thickness. For the purposes of determining the atmospheric emissivity coefficient, the following expression was adopted in this study [36]:

$${\epsilon }_a^{\prime }={\epsilon }_a^{\prime }\left(H_{2}O\right)+{\epsilon }_a^{\prime }\left(O_3\right)+{\epsilon }_a^{\prime }\left(overlap\right)+{\epsilon }_a^{\prime }\left({CO}_2\right)$$

(5)

Considering the atmospheric conditions during the measurement campaign (clear weather without clouds), constant values of relative air humidity and ozone concentration were adopted, while the concentration of carbon dioxide is directly related to the traffic intensity in the observed domain (part of the city). Based on the above, it is assumed that the first three terms in Equation (5) are constant and that the effective atmospheric emissivity coefficient and the scattering coefficient are defined by a function whose value depends only on the local carbon dioxide concentration [36].

To fully define the mathematical model, it is necessary to select the type and value of boundary conditions for each of the calculation quantities, i.e., for each transport equation of the model. The input data of atmospheric parameters, used to define the boundary conditions, were taken from the meteorological station. The size of the computational domain was 1536 m × 1425 m × 200 m. The flow quantities at the entrance to the computational domain are defined to represent the real flow in the atmospheric boundary layer. The boundary condition for the velocity at the entrance to the computational domain is defined by a velocity value with a vertical logarithmic distribution. The average wind speed values were determined based on the results of wind speed measurements on a meteorological station installed on the building of the Higher Textile School for Design, Technology and Management located within the calculation domain.

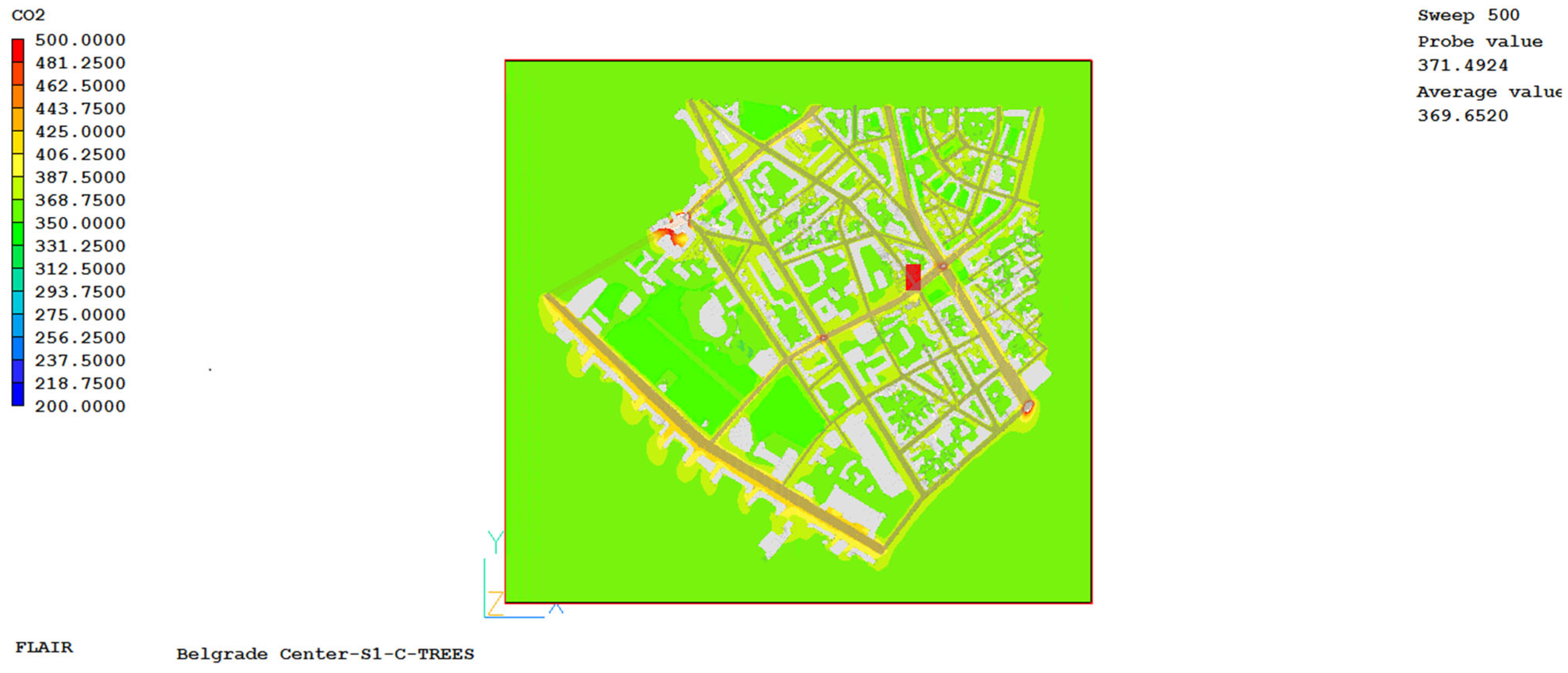
The velocity boundary condition for all outputs of the computational domain is that the velocity gradient value is equal to zero in the direction normal to the plane of the boundary surface. Analogously, as boundary conditions for turbulent kinetic energy and its dissipation at the output boundaries of the computational domain, the conditions that their gradients are equal to zero are set. The mean value of the experimentally measured air temperature was used as the boundary condition for the temperature at the entrance to the computational domain. As a boundary condition at all outputs from the computational domain, the condition that the temperature gradient value is equal to zero in the direction normal to the surface was used. The mean value of the measured CO₂ concentration was taken as the boundary condition for the CO₂ concentration at the entrance to the computational domain. As a boundary condition at all outputs from the computational domain, the value of the CO₂ concentration gradient was set to be zero in the direction normal to the surface. The values of the original S_CO2 members for CO₂ concentration were determined based on pollutant measurements (passenger and public vehicle transport) at various locations in the urban environment. The obtained current values at each measurement point are time-averaged and incorporated into the CO₂ concentration maintenance equation.

3.1. Numerical Model

The numerical simulations were carried out using the commercial CFD software CHAM PHOENICS (version PHOENICS 2015-19), which is based on the Finite Volume Method (FVM). The flow was considered steady, justified by the short, 1 h intervals simulated, during which temporal changes in atmospheric parameters are minimal. Turbulence model: The standard two-equation k-ϵ (epsilon) model was used to represent the turbulent flow regime, which is suitable for atmospheric boundary layer simulations [34,35]. Discretization and convergence: All transport equations were solved using the Hybrid Difference Scheme (HDS). A comprehensive grid independence study was conducted, resulting in the selection of a final mesh consisting of 2,167,500 finite volumes, ensuring an optimal balance between accuracy (deviation less than 1%) and computational cost. The convergence criterion was satisfied when the normalized residuals for all transport equations (velocity components, pressure, temperature, k, and ϵ) fell below 1 × 10⁻².

3.2. Computational Domain and Boundary Conditions

The numerical simulations were conducted within a three-dimensional computational domain measuring 1536 m × 1425 m × 200 m (x × y × z). The domain size was selected to minimize the potential influence of boundary effects on the flow field and scalar transport, ensuring that the simulated region of interest remained unaffected by artificial numerical constraints imposed by the domain boundaries [37].

Boundary Conditions

Inlet (Windward Boundary).

At the inlet, the incoming wind field was prescribed using a logarithmic vertical profile representative of the atmospheric boundary layer. Reference wind speed values were derived from measured hourly averages obtained during the field campaign. Scalar quantities such as temperature and CO₂ concentration were imposed as uniform inlet profiles, reflecting the mean values recorded at the school in city meteorological station for the corresponding simulation hour.

Outlet and Lateral Boundaries.

To allow for undisturbed outflow, a zero-gradient condition (∂Φ/∂x_i = 0) was applied for all transported variables (Φ). This approach permits the natural exit of momentum, heat, and mass fluxes from the domain while preventing non-physical backflow into the computational space.

Solid Boundaries (Building Surfaces and Ground).

All building façades and the ground surface were treated as no-slip walls (U_i = 0), ensuring realistic representation of shear stresses at solid–fluid interfaces. Surface thermal boundary conditions were defined by imposing measured surface temperatures corresponding to different times of day. Specifically, values were extracted from field observations, differentiating between morning, afternoon, and evening periods.

Heat Transfer and Radiative Processes.

The air was considered a non-transparent (gray) participating medium within the employed radiation model. A crucial aspect of the setup was the explicit coupling between the effective atmospheric emissivity coefficient (ϵ_a′) and the local CO₂ concentration. This formulation accounts for the role of traffic-induced CO₂ as an active agent in modifying radiative heat transfer, thereby directly influencing the urban surface energy balance and the near-surface thermal environment [36].

Operational Scenarios

The simulations were designed to capture the diurnal variability of the urban microclimate under extreme thermal stress conditions. Accordingly, three distinct cases were defined, each corresponding to a characteristic time window during the representative hot day of 5 July 2015:

• Case S1 (Morning): 08:00–09:00 h.
• Case S2 (Afternoon): 14:00–15:00 h.
• Case S3 (Evening): 18:00–19:00 h.

For each case, the boundary conditions were adapted based on field measurements, ensuring that the numerical results faithfully reproduced the prevailing meteorological and environmental conditions.

In this paper, the mathematical model is approximately solved using the finite volume method. Equations written in the form of the finite volume method are by definition conservation laws. The creation of the numerical network was achieved using the cut cell method (Cartesian grid method or embedded boundary method), which is available in the commercial software CHAM PHOENICS under the name Parabolic Hyperbolic Or Elliptic Numerical Integration Code Series [38]. This option allows for very easy and efficient mesh (grid) creation for complex geometries. This software uses a line-by-line iteration method. The line-by-line iteration method consists of solving finite volume differential equations along a single line using the Thomas algorithm (tridiagonal matrix algorithm).

The development of numerical methods has led to the definition of various differential schemes. The presented numerical model uses linear difference schemes, known in the literature as the central difference scheme—CDS, upwind (upstream) difference scheme—UDS, and hybrid difference scheme—HDS. The value of the dependent variable in a given cell can be determined based on the downstream and one or two upstream values. The first interpolation approach is that the value of the dependent variable on the surface (side) is equal to the arithmetic mean value at neighboring nodes, which is the approach of the central differential scheme. This scheme is suitable for Peclet numbers with low values, but in regions with a high-value Peclet number, it gives unrealistic (unbounded) values. For these reasons, the UDS was developed. There it is assumed that the value of the dependent variable in the cell face is the same as the value at the cell’s upstream node.

This scheme is unconditionally bounded and very stable, but has a large numerical diffusivity when the flow is at an angle to the grid. For these reasons, HDS is most often used, taking the good properties of CDS and UDS, with respect to the value of the Peclet number in a given cell. The HDS is adopted for all simulations in this study. A variant of the HDS was used, which, at low-value Peclet numbers, operates in the mode of the CDS, while at high-value Peclet numbers it operates with the contribution of the UDS up to 75%. The exact contribution of the UDS depends on the local value of the Peclet number in each cell of the computational domain, but due to the stability of the solution in the iterative process, it does not exceed the above-mentioned value of 75%.

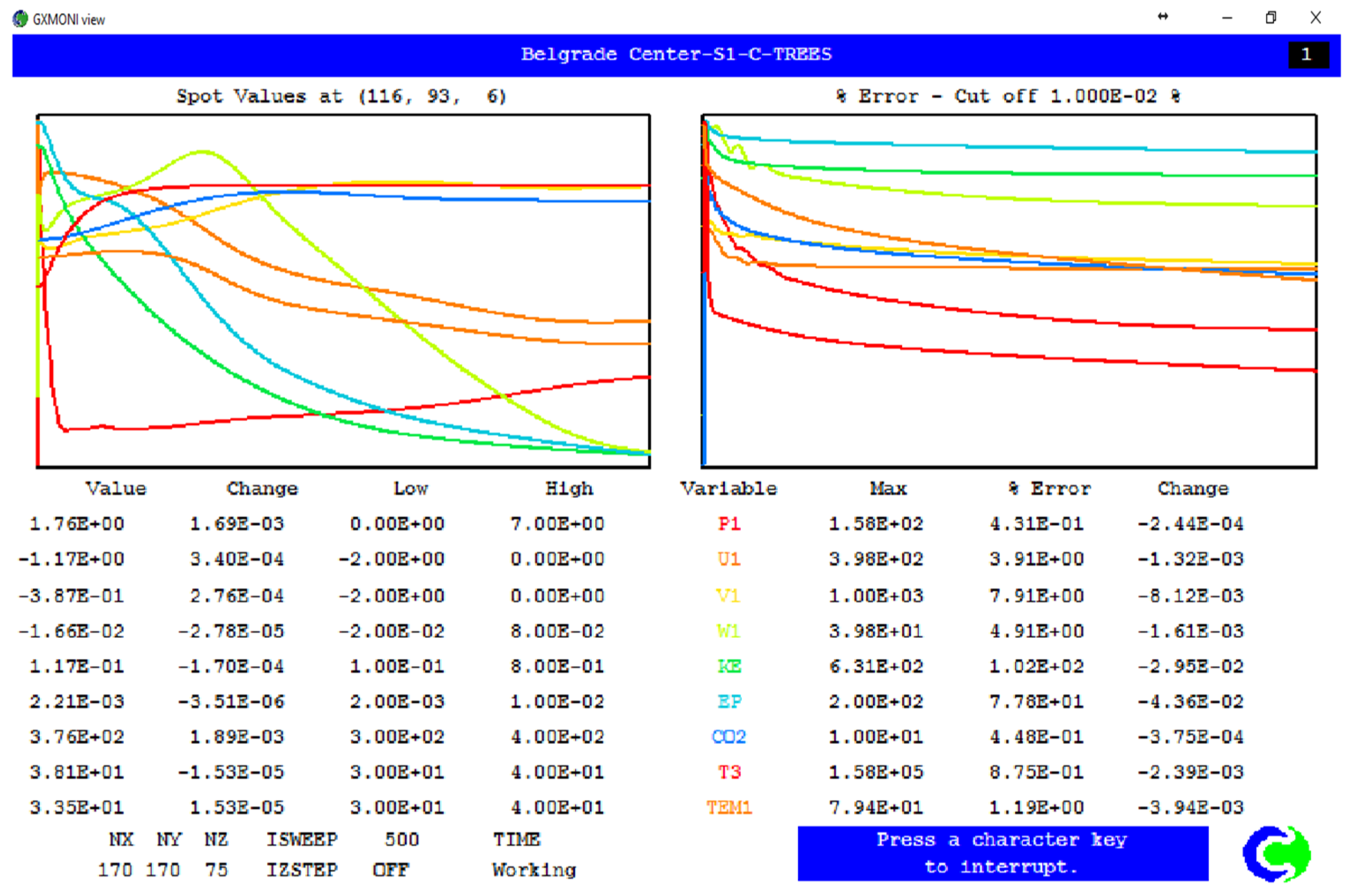
The convergence criterion was set so that the normalized residuals for all solved transport equations (velocity, pressure, temperature, k, ε, etc.) were below 1 × 10⁻². In addition to monitoring the residuals, the stabilization of key variable values at predefined control points was also tracked. All simulations were initially run for 500 iterations, which demonstrated a converged and stable solution, although computations were continued for several thousand iterations to ensure full convergence, as shown in the convergence plots. Spatial discretization was performed using HDS, and the system of equations was solved iteratively using a line-by-line procedure.

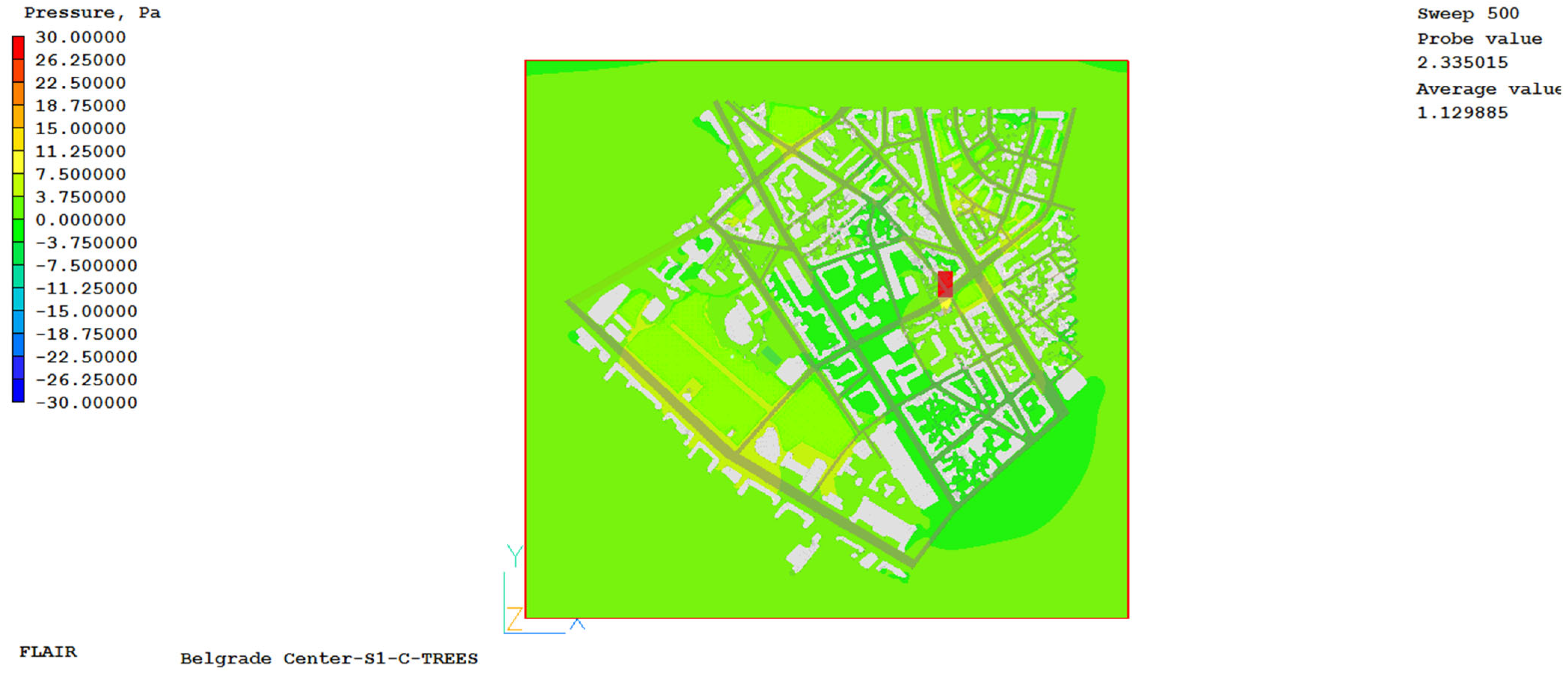
Five urban locations were selected where detailed measurements were made and marked on a three-dimensional numerical model. After creating the model geometry, the thermophysical properties of the material, boundary conditions, and numerical grid of the computational domain were defined. The number of cells in the computational grid was adjusted to help make the grid denser around the areas (buildings, streets, parks) that are the subject of this research, so that the flow in the immediate vicinity around the buildings could be determined with satisfactory accuracy. Graphical representations of the three-dimensional numerical model and the convergence flow processes for cases S1-C, S2-C and S3-C are given in Appendix B, Figure A1, Figure A2, Figure A3 and Figure A4.

The Influence of Vegetation and Wind on the UHII

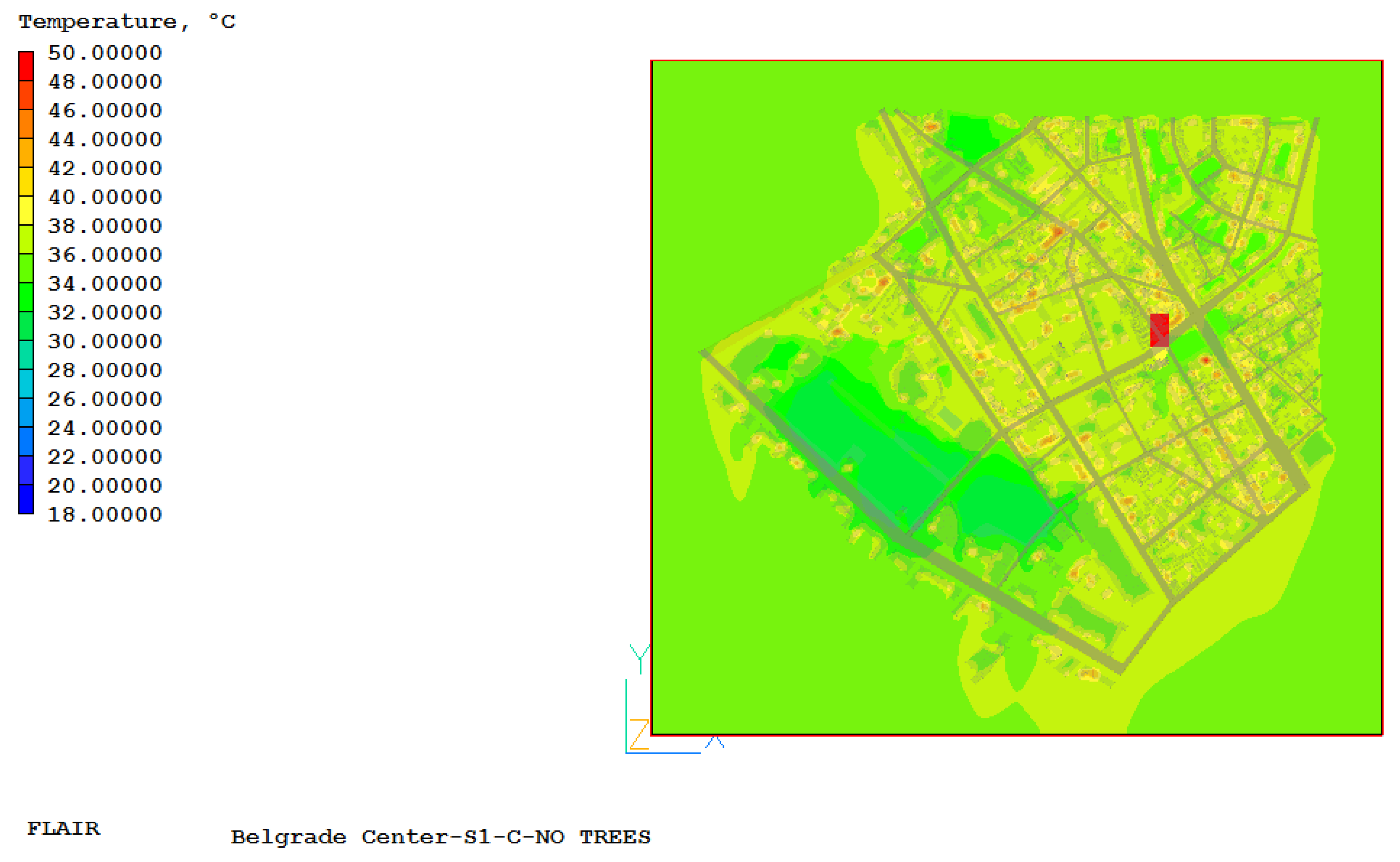
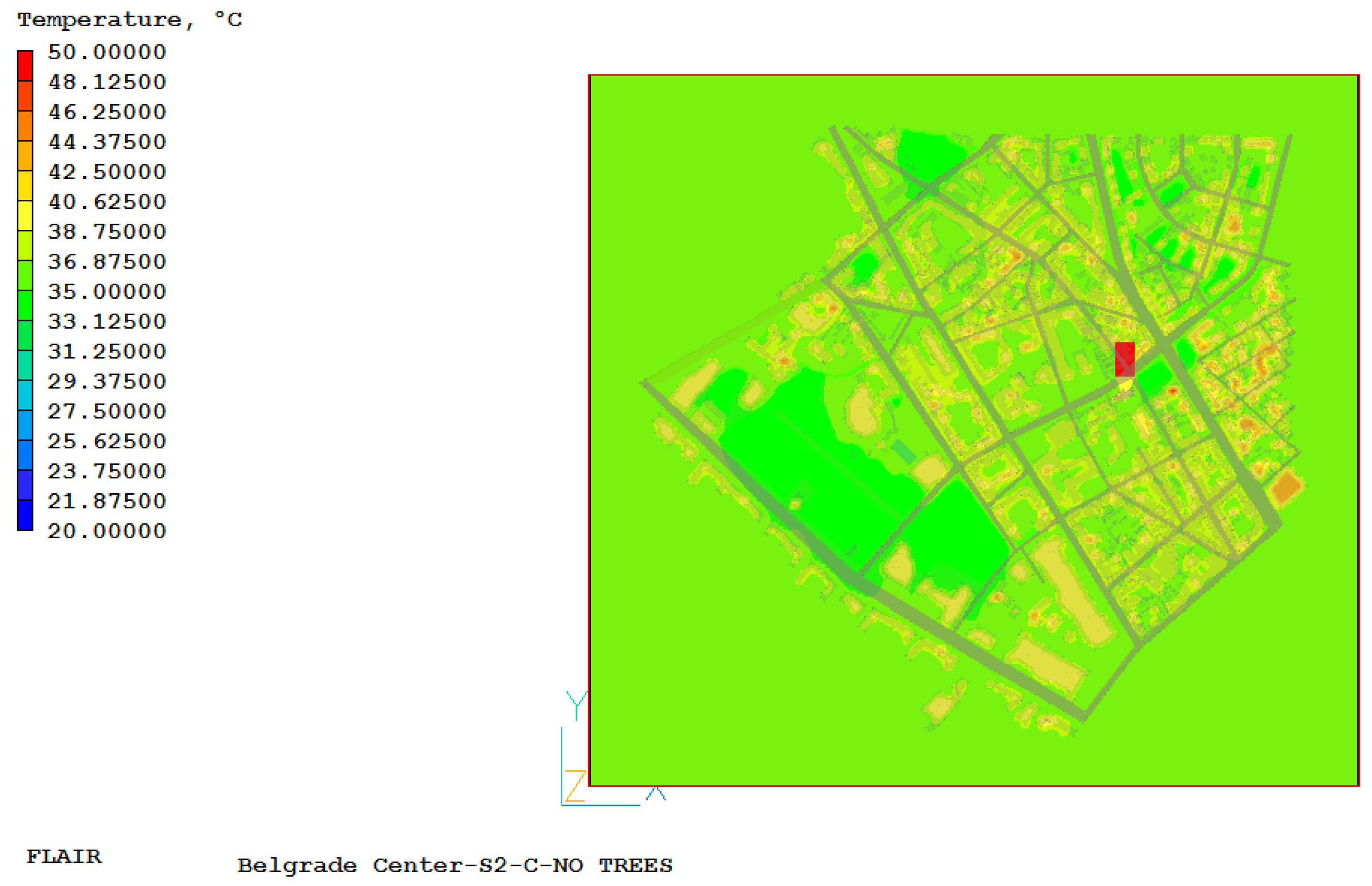
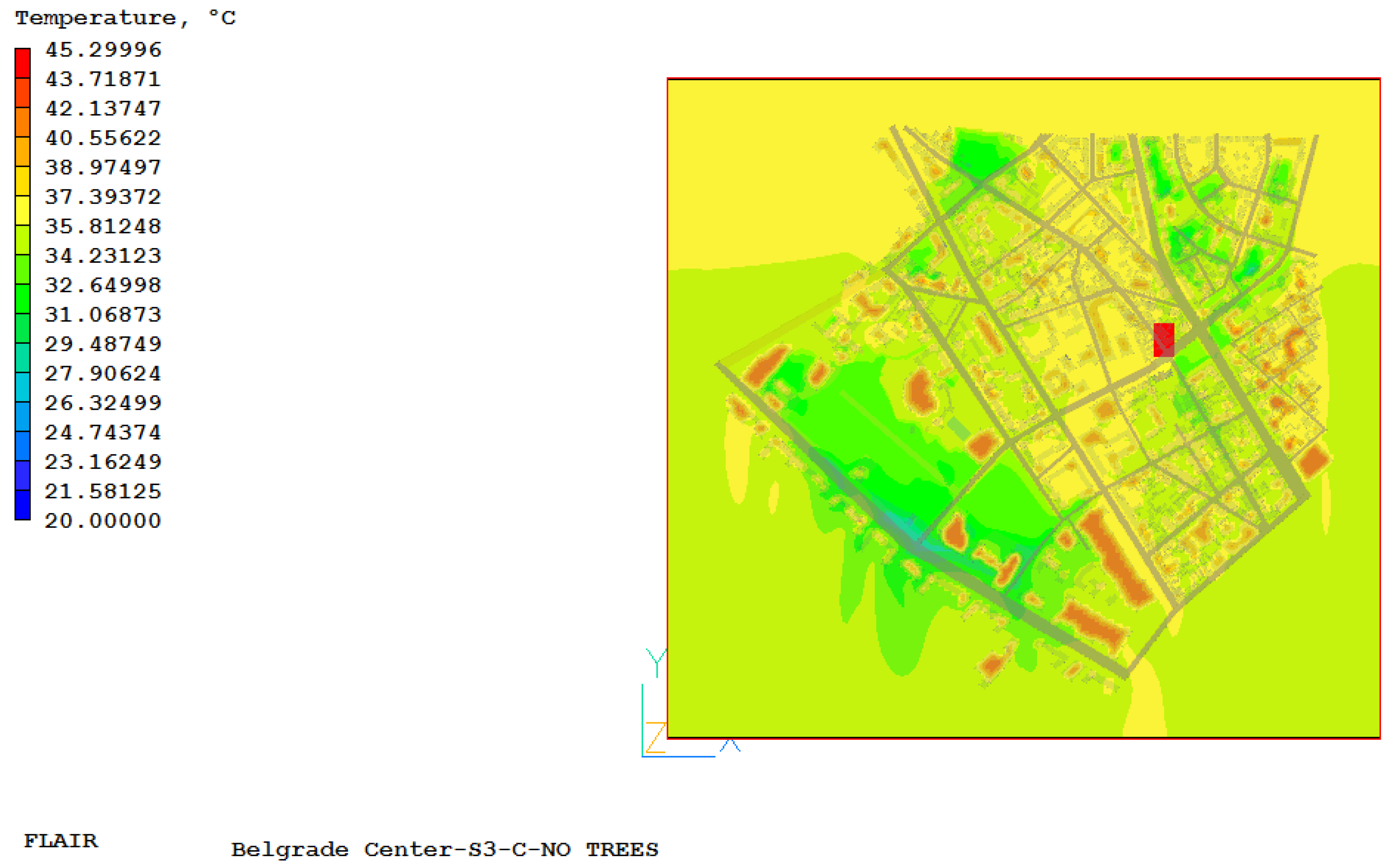
In order to show the impact of trees on the UHII, three additional numerical simulations were performed for the already defined cases with the same boundary conditions that we did in the previous analysis, except that in the parts where there were trees, there is now only a grassy surface (no trees). The objective of this ‘no-tree’ scenario was to assess the cumulative thermal impact of replacing forested areas with lawn. The simulation therefore quantifies the combined effects of the loss of shading, the cessation of evapotranspiration from tree canopies, and altered local wind patterns, without separating the individual contribution of each mechanism. In

Table A2. Values of observed parameters for case S1-C-NO TREES.

		Ta	Tmrt	va	pv	CO2	UTCI	Heat Load
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]	[°C]	[a/b]
1	Surroundings of the school building	35.78	39.15	0.74	−0.38	373	36.7	3/2
		32.00	38.07	1.4	2.33	371	32.9	3/3
2	Tašmajdan Park	32.14	32.75	0.34	1.81	365	31.6	4/3
		30.29	32.04	0.73	5.86	365	29.9	4/4
3	Palilula Market	36.25	35.00	0.92	0.64	368	36.1	3/2
		35.20	35.08	1.14	1.44	367	35.1	3/2
4	King Alexander Boulevard	36.54	39.05	0.65	0.17	404	37.3	3/2
		33.62	39.18	1.14	1.75	403	34.6	3/3
5	Intersection of March 27th and Starine Novaka	36.65	46.14	0.34	−0.97	497	39.1	2/2
		36.90	44.5	0.38	−1.53	505	39.0	2/2

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

,

Table A3. Values of observed parameters for case S2-C-NO TREES.

		Ta	Tmrt	va	pv	CO2	UTCI	Heat Load
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]	[°C]	[a/b]
1	Surroundings of the school building	35.86	38.58	1.35	−0.20	368	35.7	3/2
		34.93	37.97	0.50	1.24	372	34.5	3/3
2	Tašmajdan Park	33.95	34.29	1.19	2.17	365	32.9	3/3
		33.45	34.09	0.64	3.08	365	32.3	3/3
3	Palilula Market	36.29	34.90	2.36	1.24	372	35.0	3/3
		36.19	34.71	2.23	1.93	372	34.9	3/3
4	King Alexander Boulevard	36.30	38.98	1.91	0.79	383	36.1	3/2
		36.31	39.17	1.75	0.96	389	36.2	3/2
5	Intersection of March 27th and Starine Novaka	36.33	45.89	1.49	0.23	512	38.0	2/2
		36.83	44.91	0.99	−0.42	512	38.1	2/2

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

and

Table A4. Values of observed parameters for case S3-C-NO TREES.

		Ta	Tmrt	va	pv	CO2	UTCI	Heat Load
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]	[°C]	[a/b]
1	Surroundings of the school building	34.39	32.26	1.21	1.26	371	33.1	3/3
		29.17	32.03	1.79	4.67	368	28.0	4/4
2	Tašmajdan Park	33.05	30.40	1.29	2.30	365	31.3	4/3
		28.38	29.84	1.00	8.19	365	27.2	4/4
3	Palilula Market	35.30	32.20	1.09	1.53	372	33.9	3/3
		33.91	32.06	1.72	3.84	372	32.4	3/3
4	King Alexander Boulevard	35.76	32.46	2.27	1.15	390	34.2	3/3
		30.63	32.17	1.06	2.71	395	29.73	4/4
5	Intersection of March 27th and Starine Novaka	35.46	33.64	0.82	1.09	496	34.4	3/3
		35.04	33.40	1.36	2.16	489	33.9	3/3

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

, Appendix C, the simulation values in the case where there were trees are shown in green. Based on all of the above, it can be concluded that trees greatly affect the air temperature in the urban environment, and therefore the UHII and the energy needs of buildings located in that area. Based on numerical simulations, with and without trees in the urban environment, it can be concluded that the presence of trees in the urban environment significantly affects the temperature in the vicinity of parks and larger areas where trees are located. With a detailed analysis based on Figure A5, Figure A6 and Figure A7, Appendix C, it can be concluded that the average air temperature for the observed urban area is higher in the range of 1.5 °C to 3 °C depending on the observed time of day. In addition to the increased temperature, the thermal comfort coefficient for most of the observed locations increased by one, as shown in Table A2, Table A3 and Table A4, Appendix C.

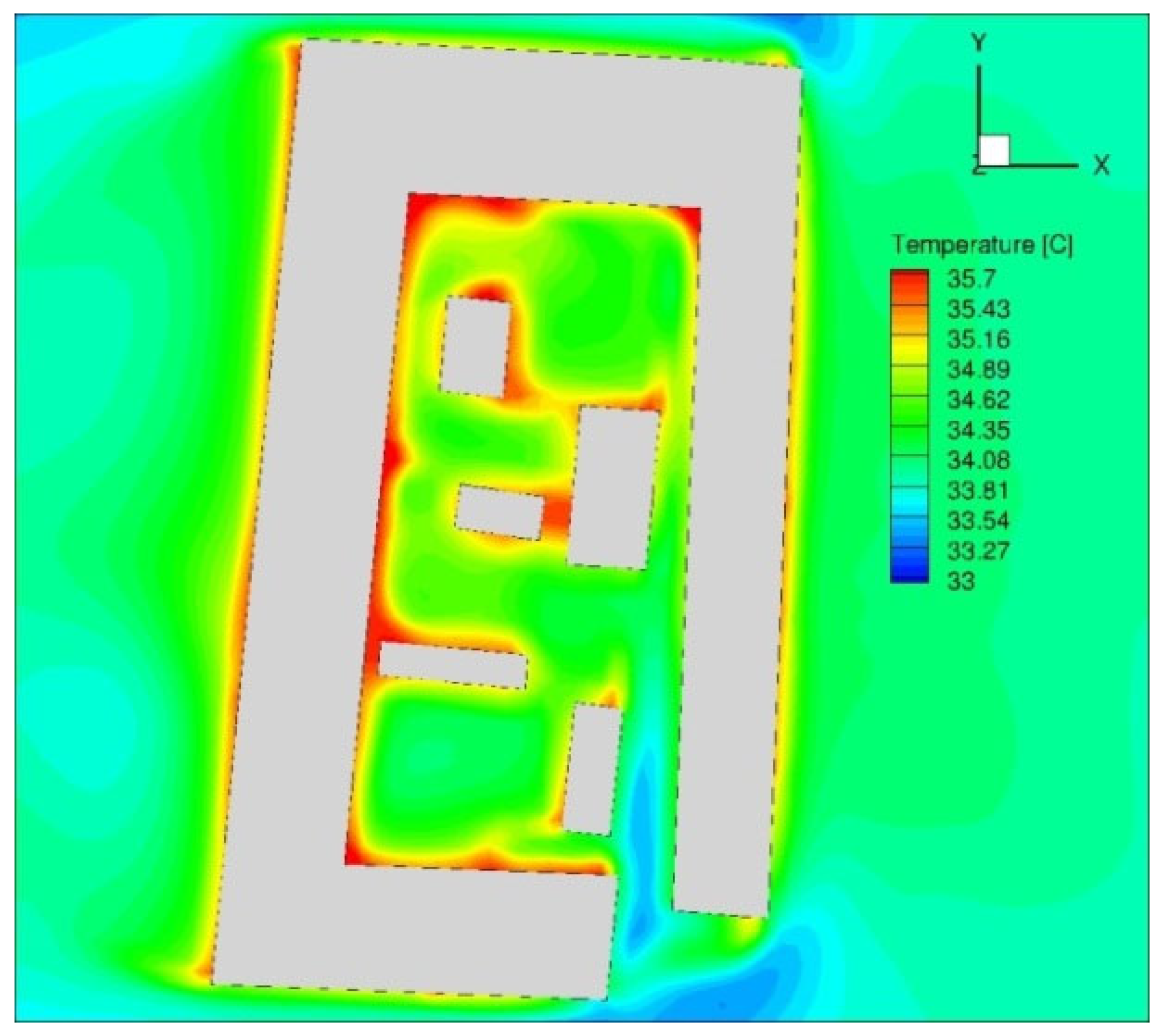
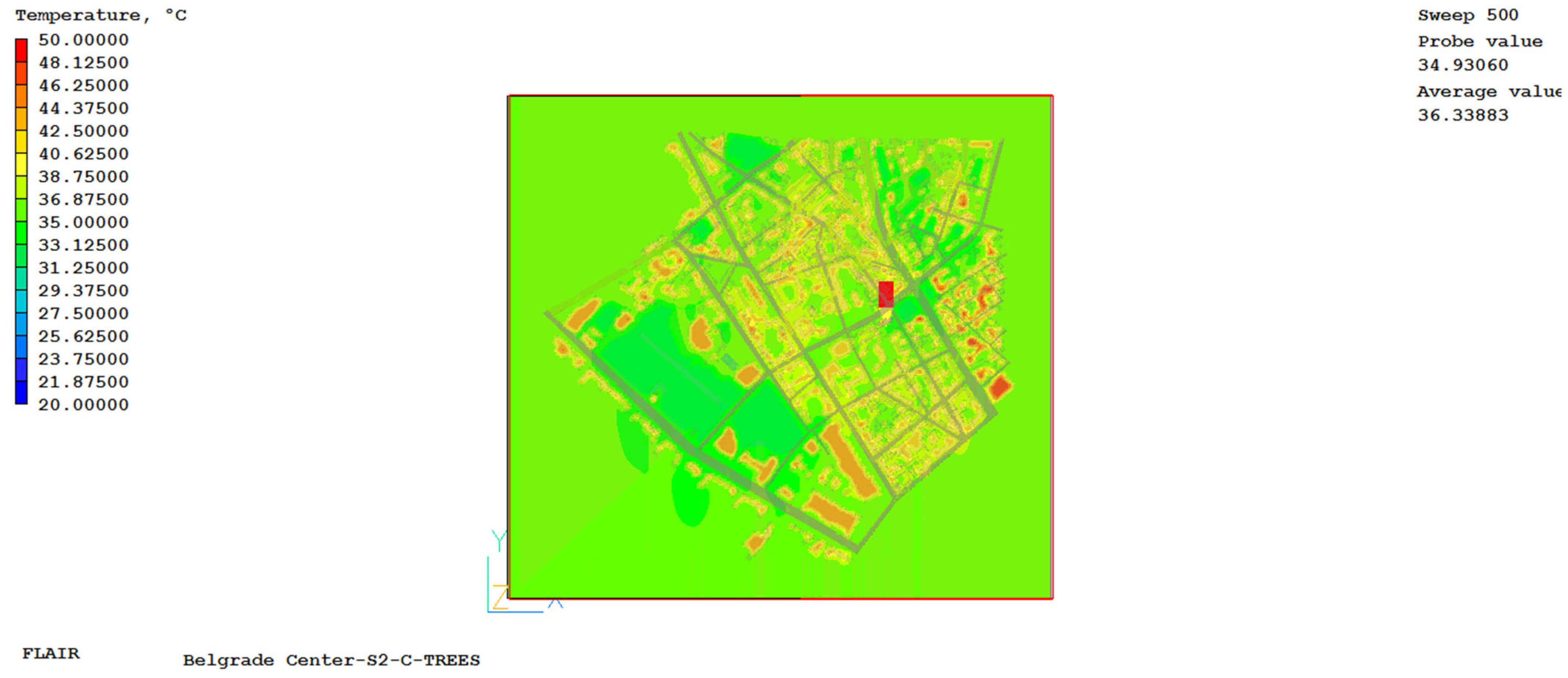
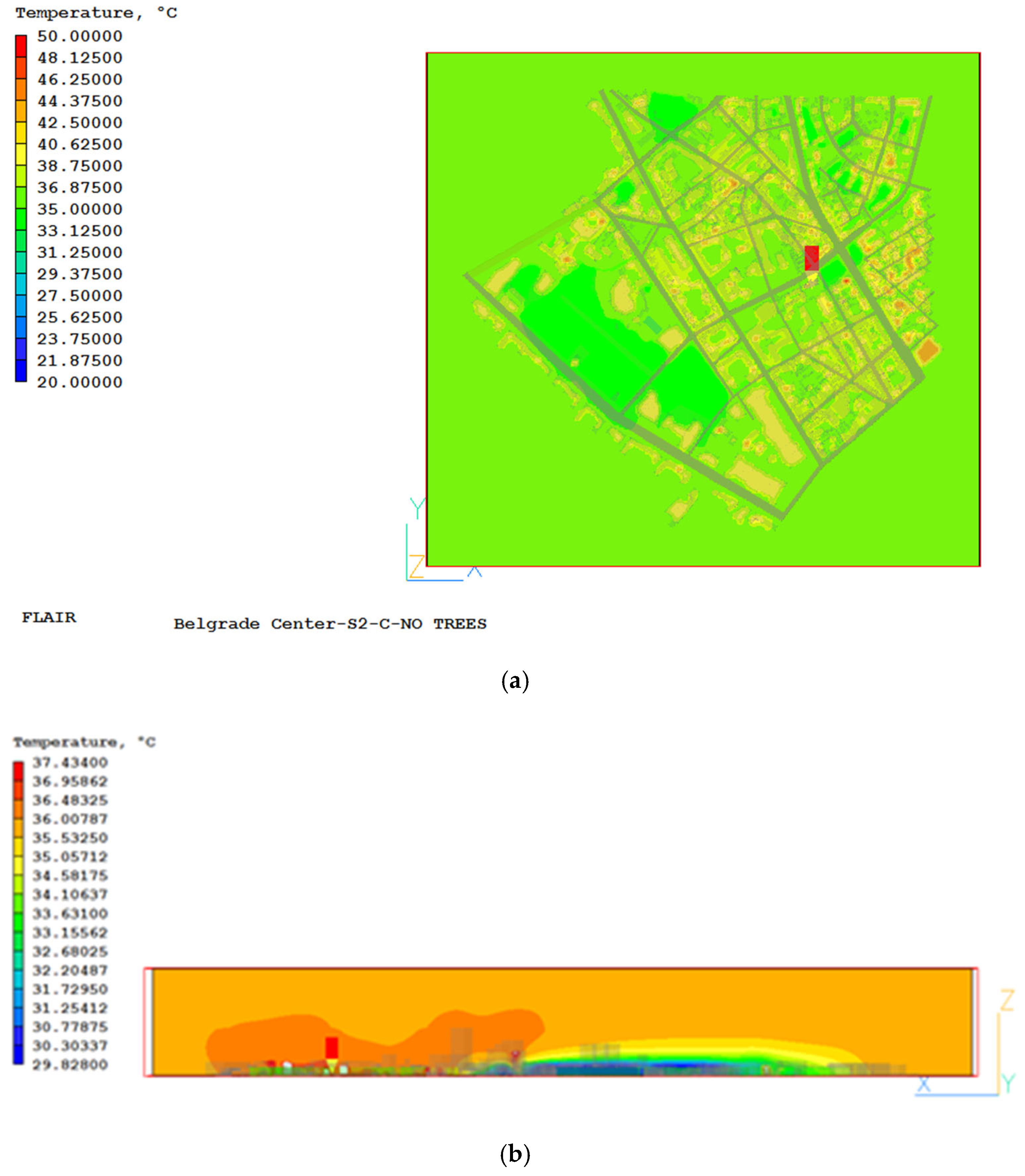
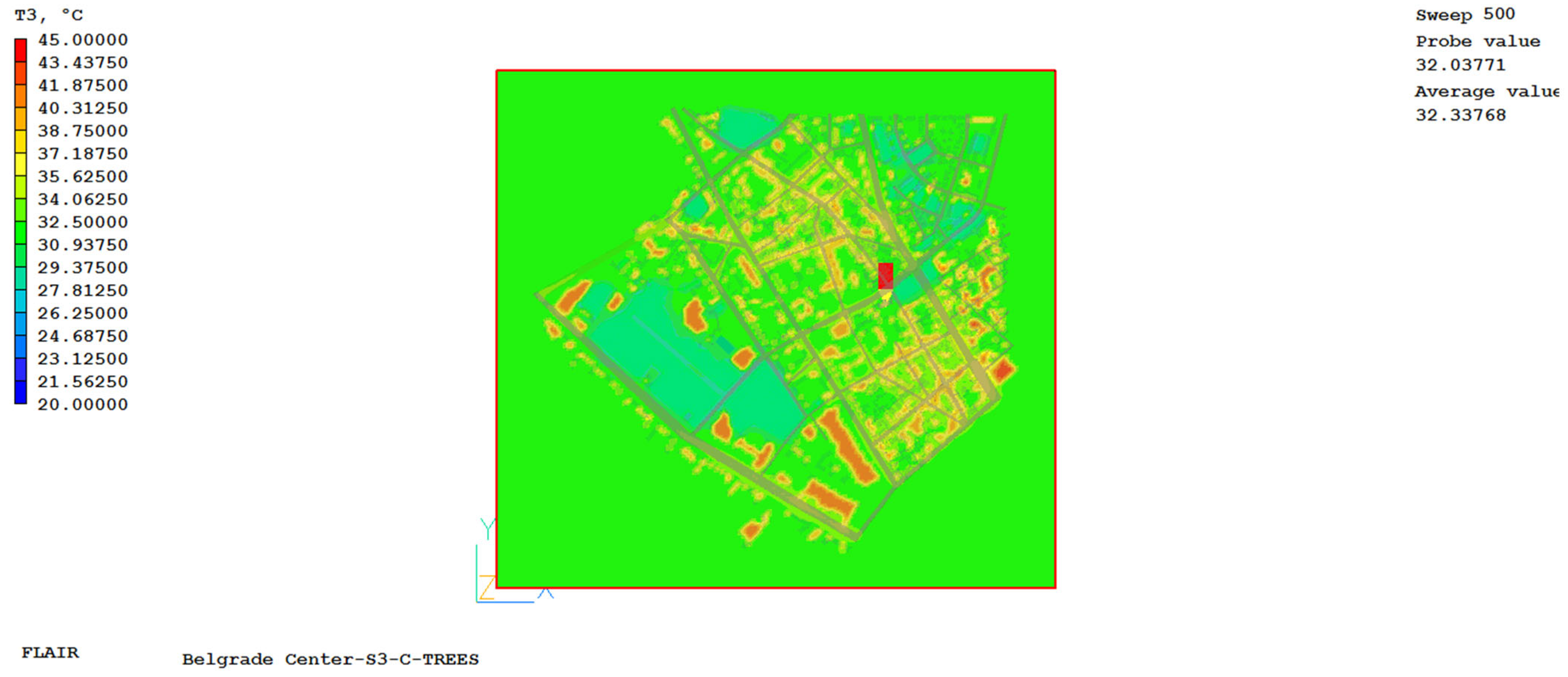
As an example of one result obtained, Figure 3 shows the air temperature field at a height of 1.85 m for the case S2-C-NO TREES.

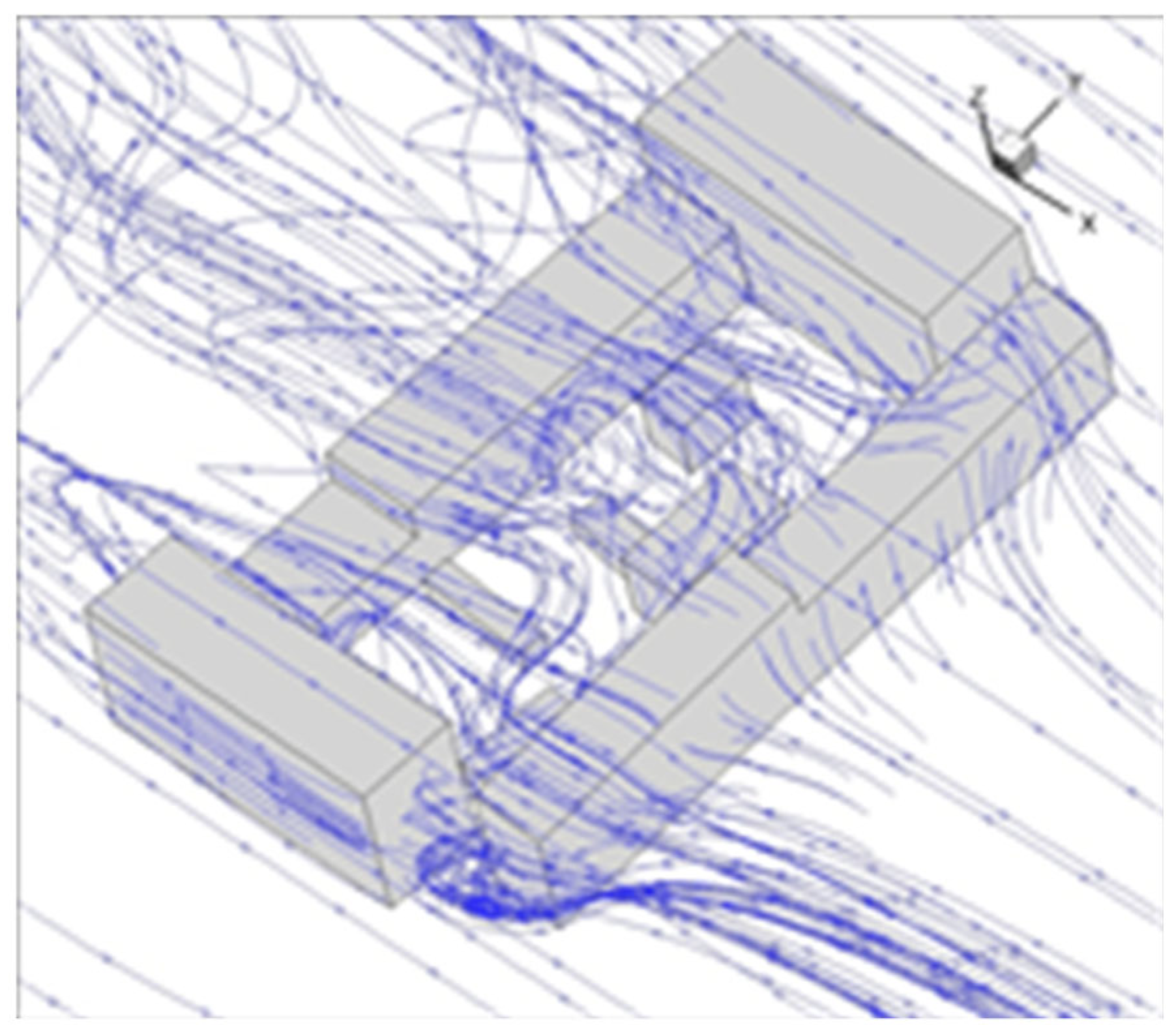
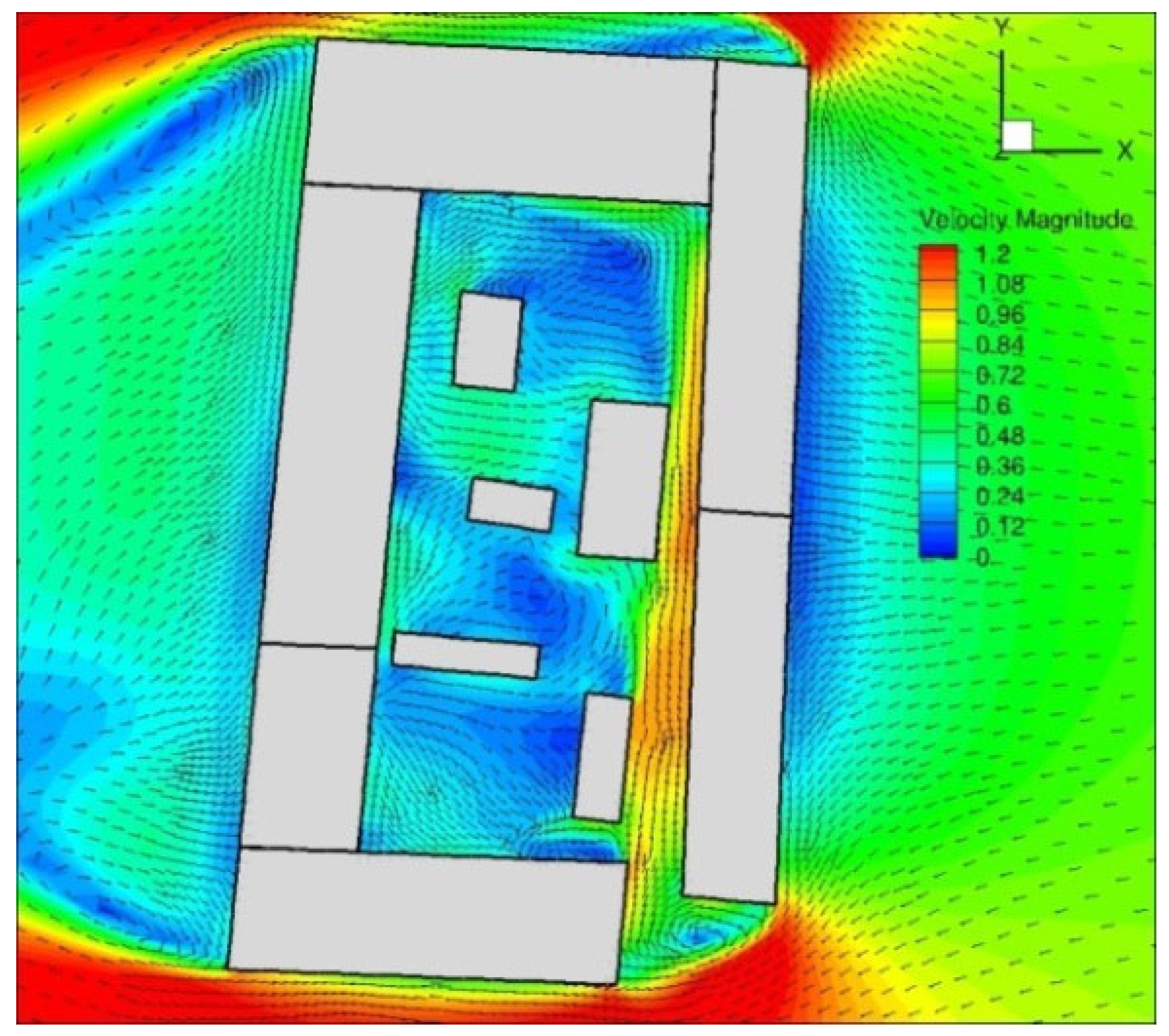
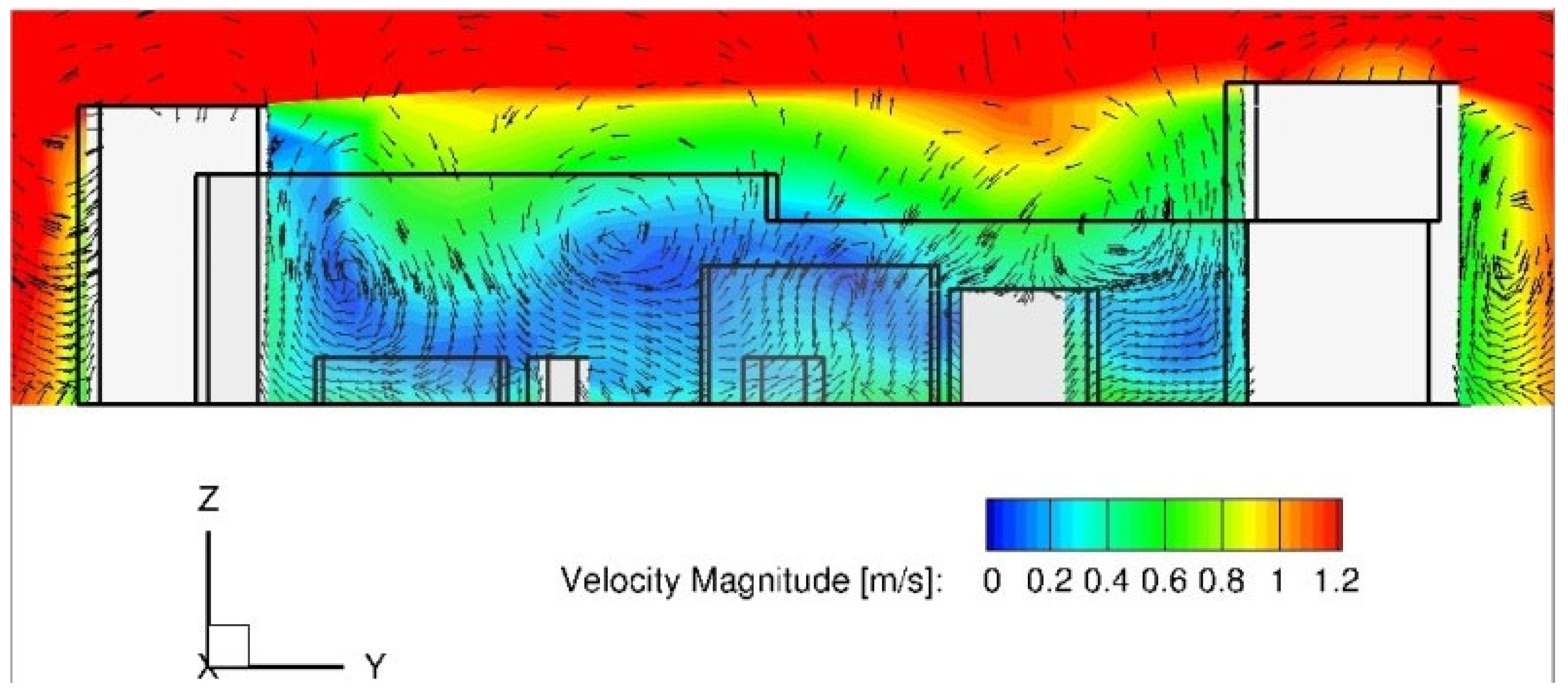
Given the good agreement between experimental and numerical results, the influence of wind on the local value of the external air temperature was analyzed using the example of a closed block of buildings from the observed urban environment, located in the immediate vicinity of a meteorological station placed on a school building. A detailed analysis of the flow field results inside a closed block of buildings showed that the negative effect leading to an increase in temperature in the blocks themselves is the appearance of quasi-stationary vortex structures. It has also been shown that the development of horizontal vortex zones is caused by the presence of lower buildings within a closed building block, as can be seen in Figure A7, Appendix C. Their presence intensifies heat transfer near ground level in such a way that when air comes into contact with the building envelope, convective heat transfer occurs from the wall to the air. Afterwards, the heat gained by transfer from the wall to the air is further transferred to the surface of the cavity opening where it mixes with the incoming cold air stream. Figure A8, Figure A9 and Figure A10, Appendix C show the occurrence of quasi-stationary vortex structures for the S2-C case.

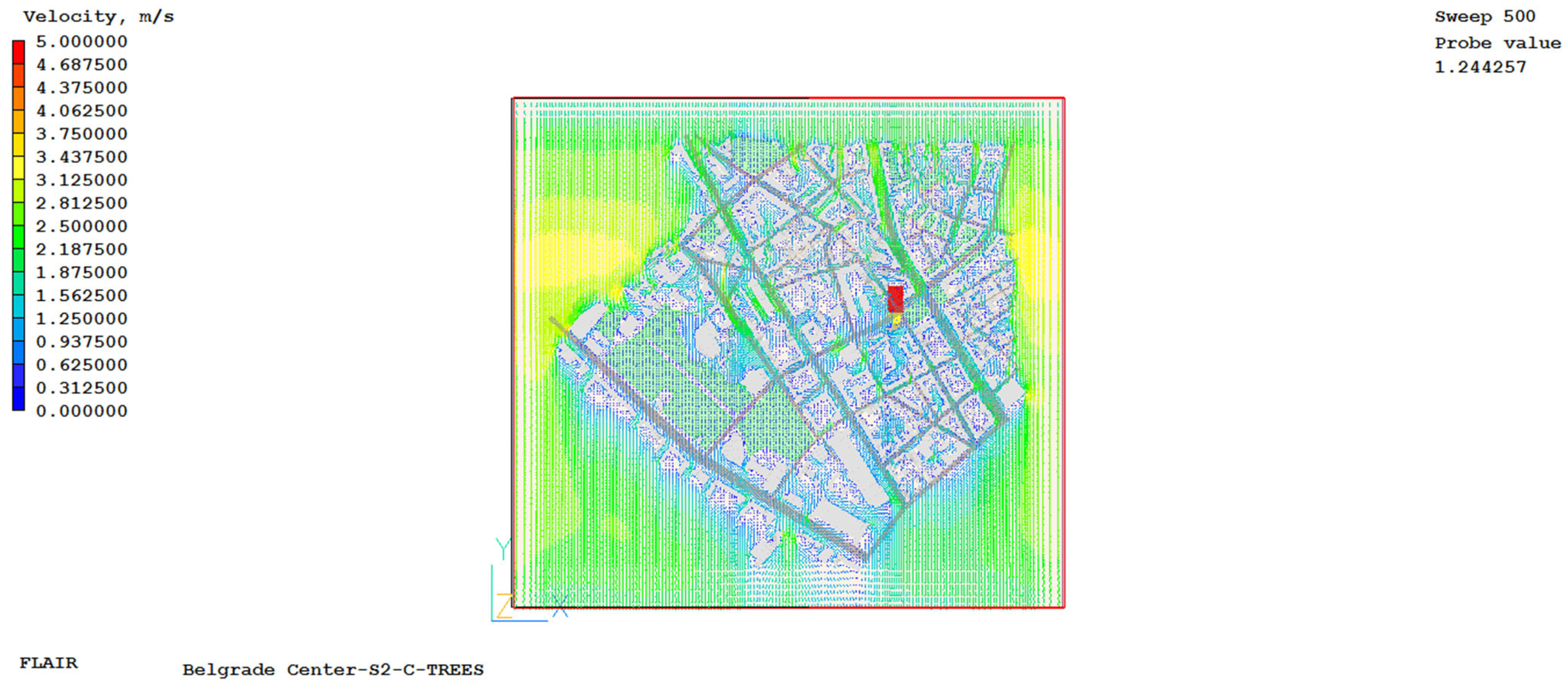
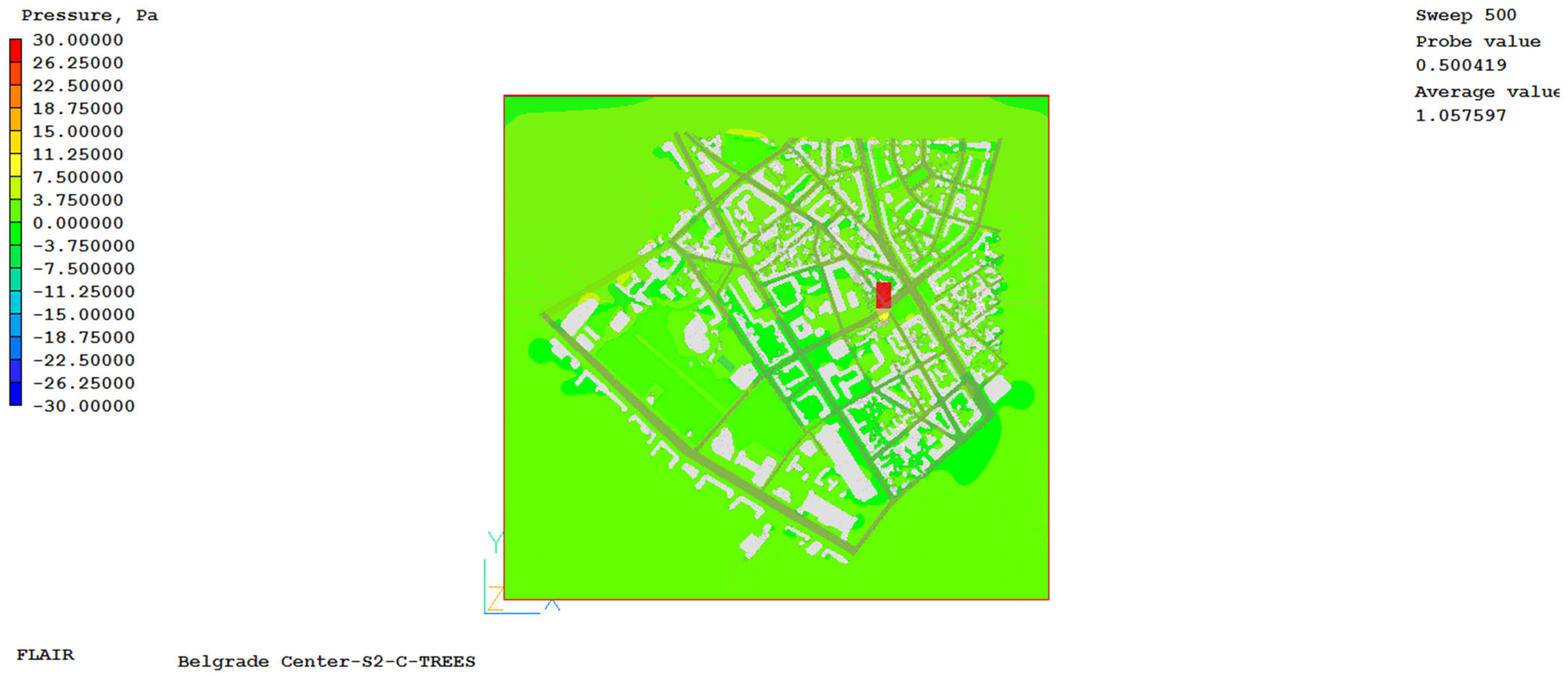
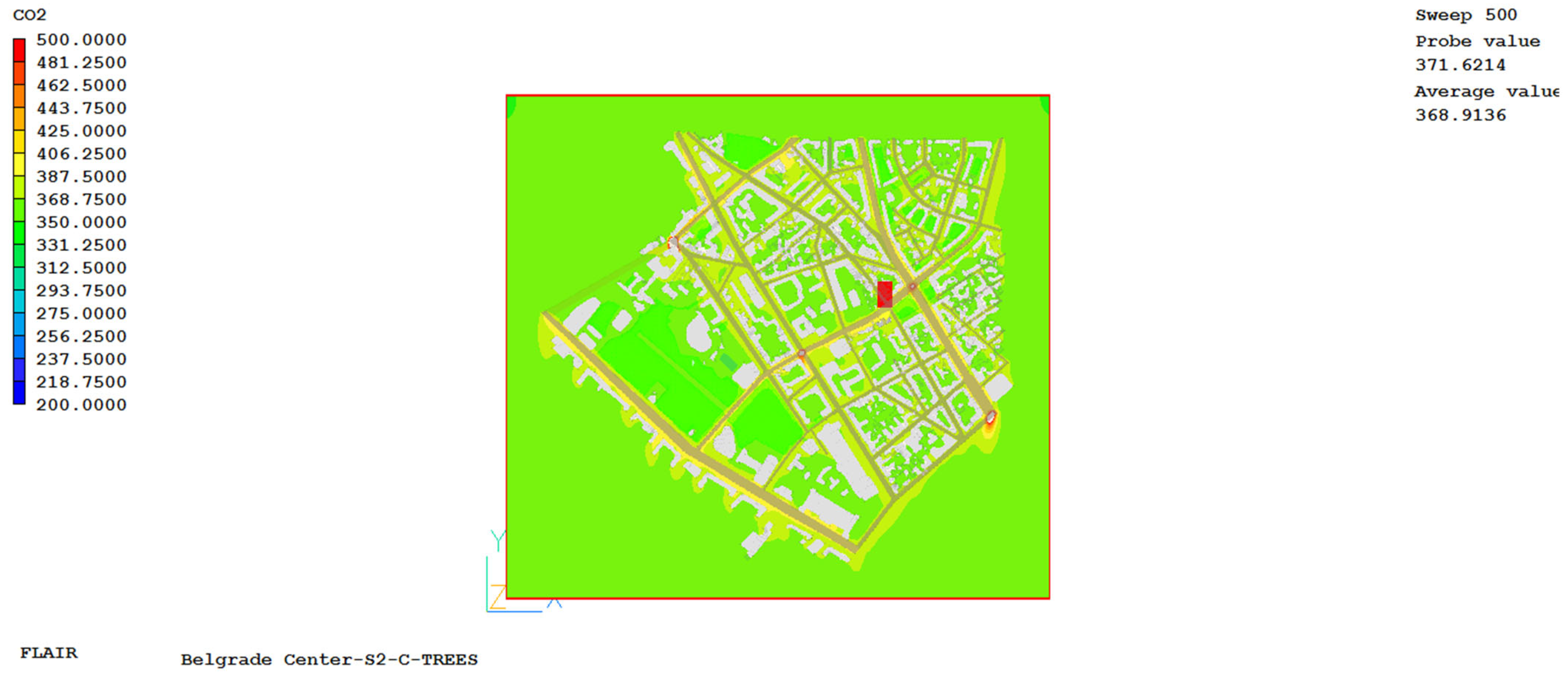
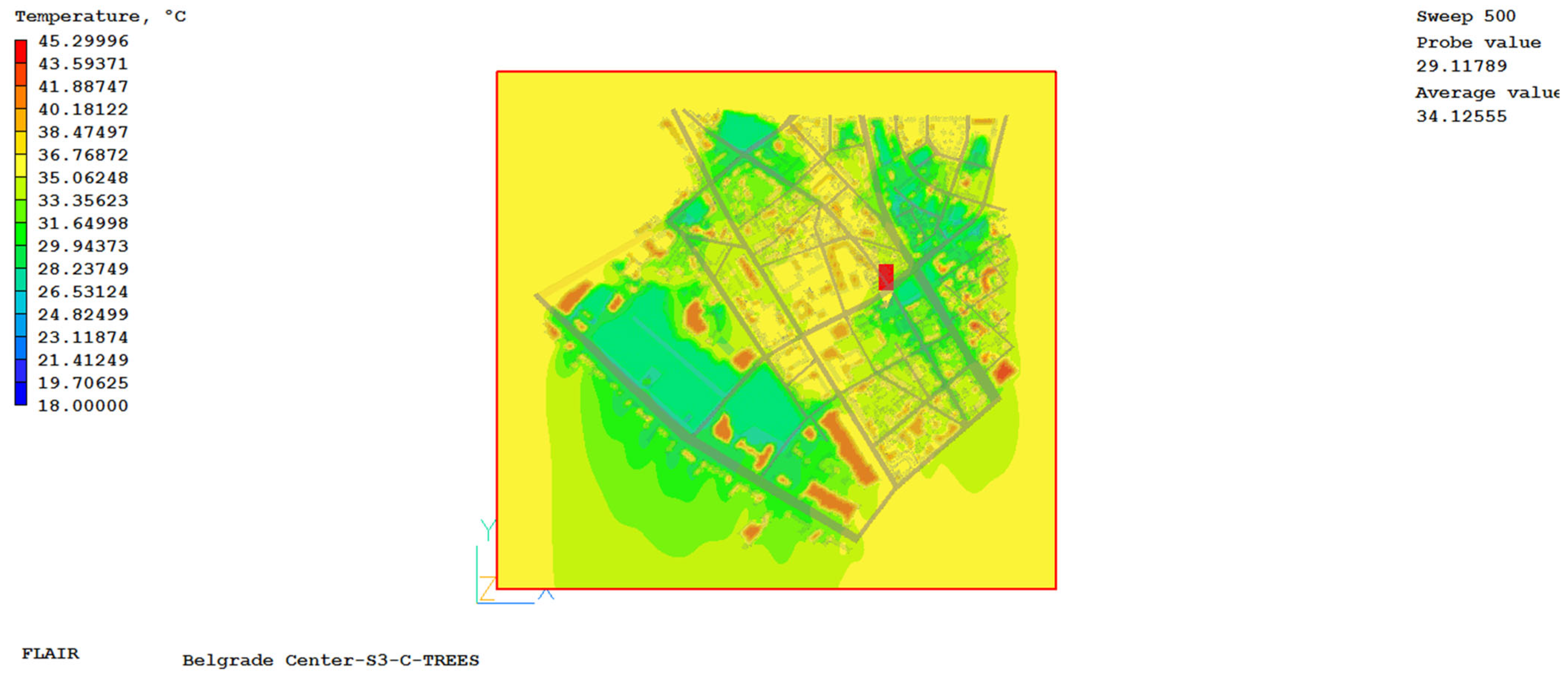
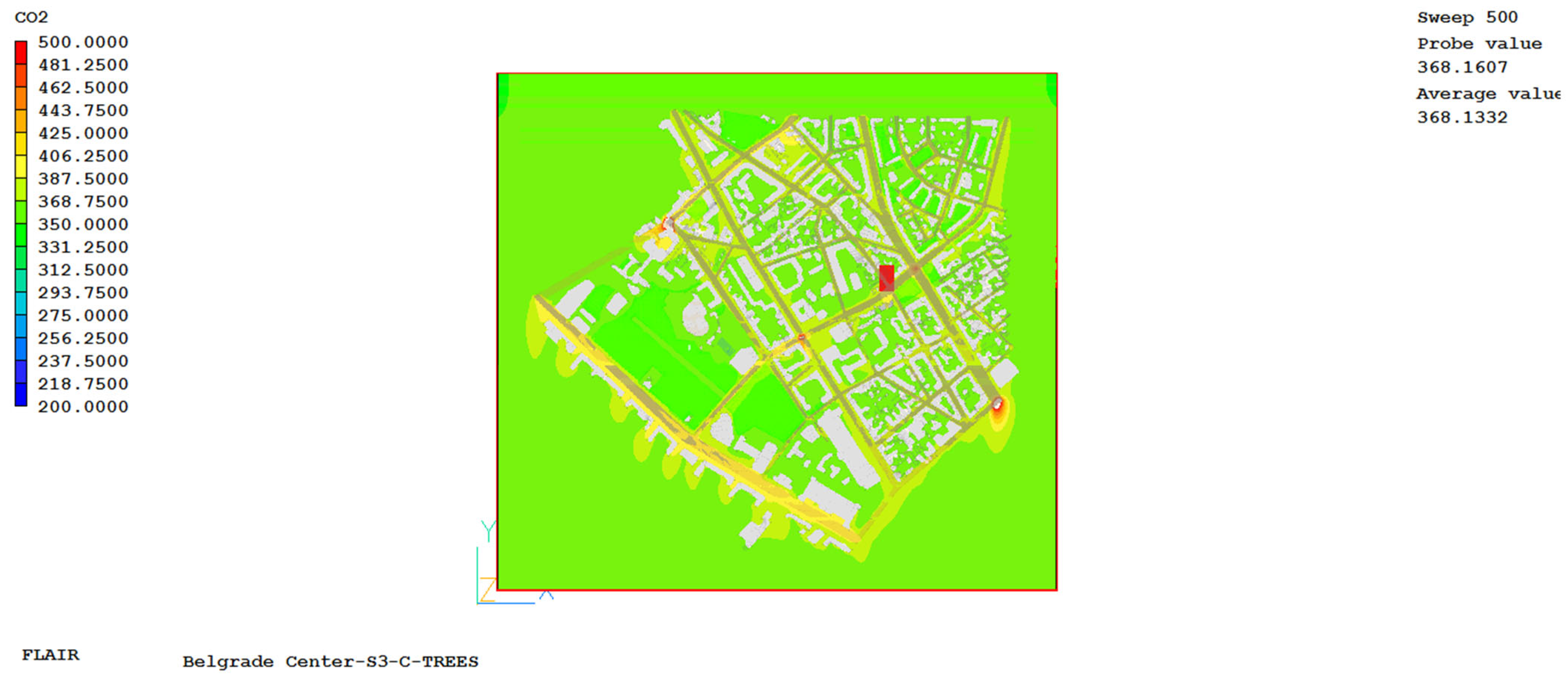
4. Numerical Simulation Results

Based on numerical simulations, we obtained data on the spatial distribution of ambient air temperature, radiant air temperature, air velocity, spatial distribution of partial water vapor pressure, and carbon dioxide concentration for the observed urban area. Based on these data, the values of the UHII and the universal thermal climate index were calculated for all locations, both those where experimental meteorological measurements were made and those where they were not. A representative example is a numerical simulation for 5 July 2015, which is one of the two hottest days for three different periods of the day, divided into 3 cases: case S1 covering the period from 8 to 9 a.m., case S2 covering the afternoon period from 2 to 3 p.m., and case S3 covering the pre-evening part of the day, i.e., the period from 6 to 7 p.m.

This temperature increase of 1.5 °C to 3 °C represents the net result of several interconnected physical processes that were not individually quantified in this study. The model inherently accounts for changes in radiative heat transfer (shading) and surface properties. However, the current analysis does not isolate the specific thermal contribution of evapotranspiration from that of shading or altered air mixing (natural ventilation). Therefore, the observed temperature rise should be interpreted as a consequence of their combined influence.

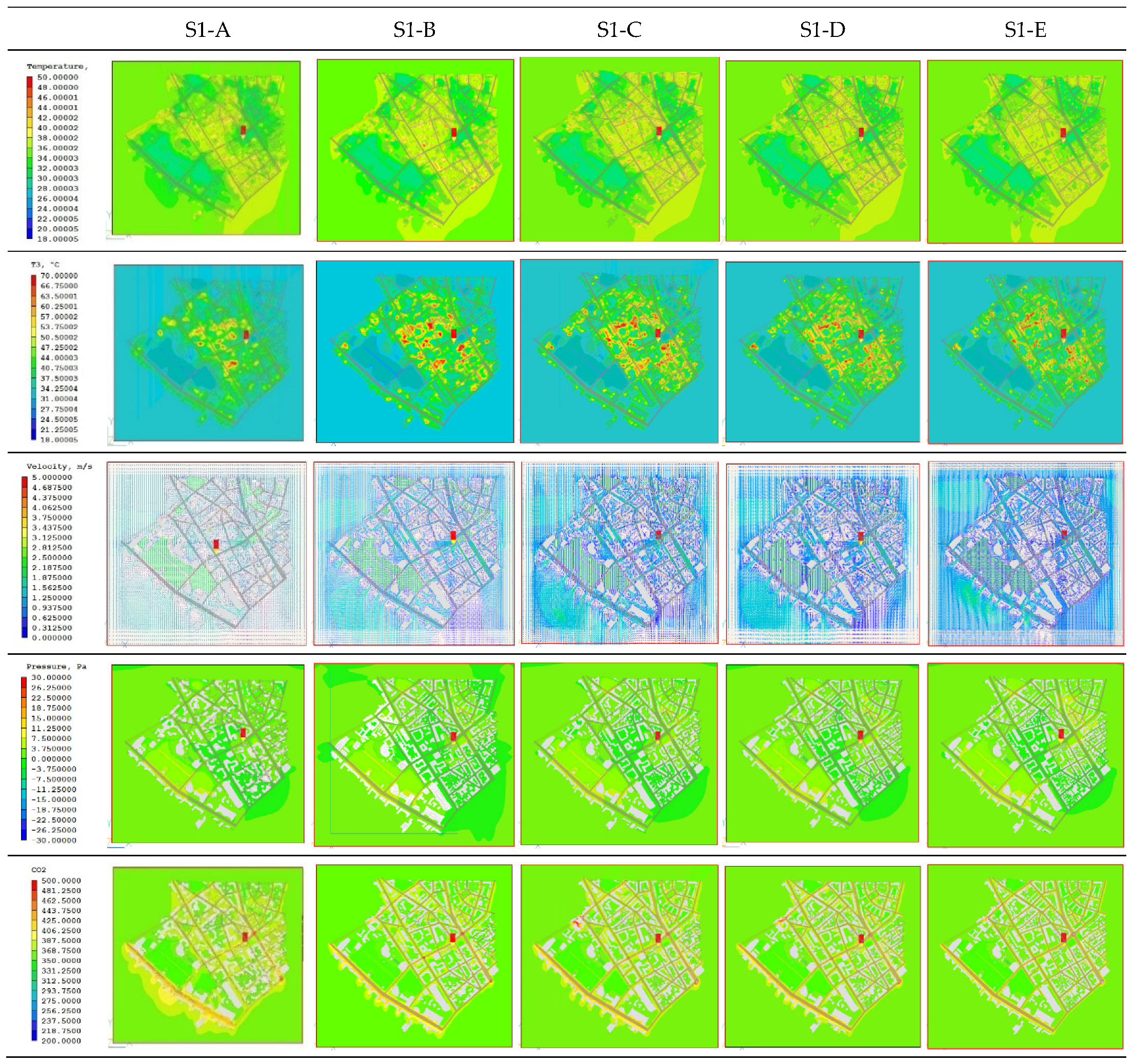
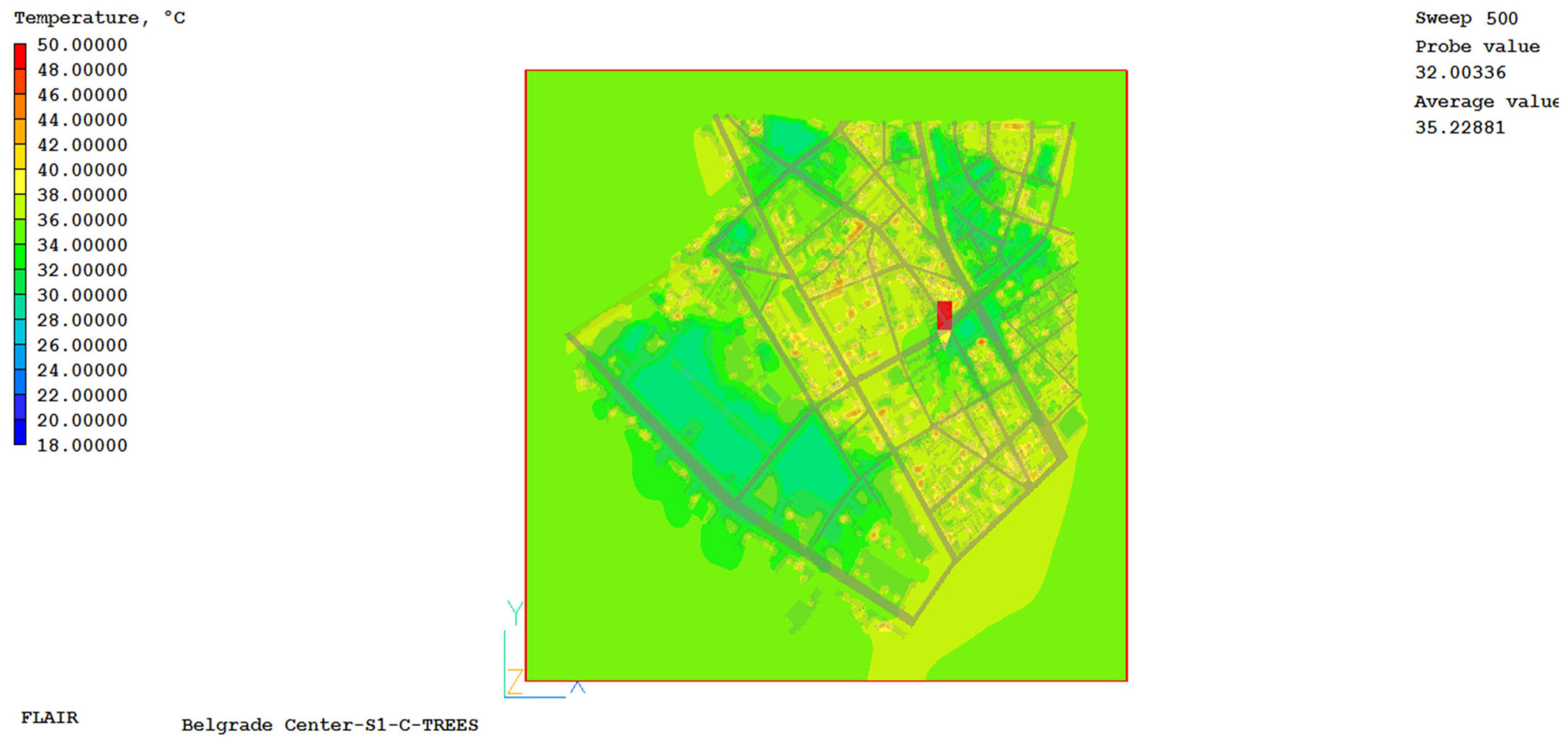
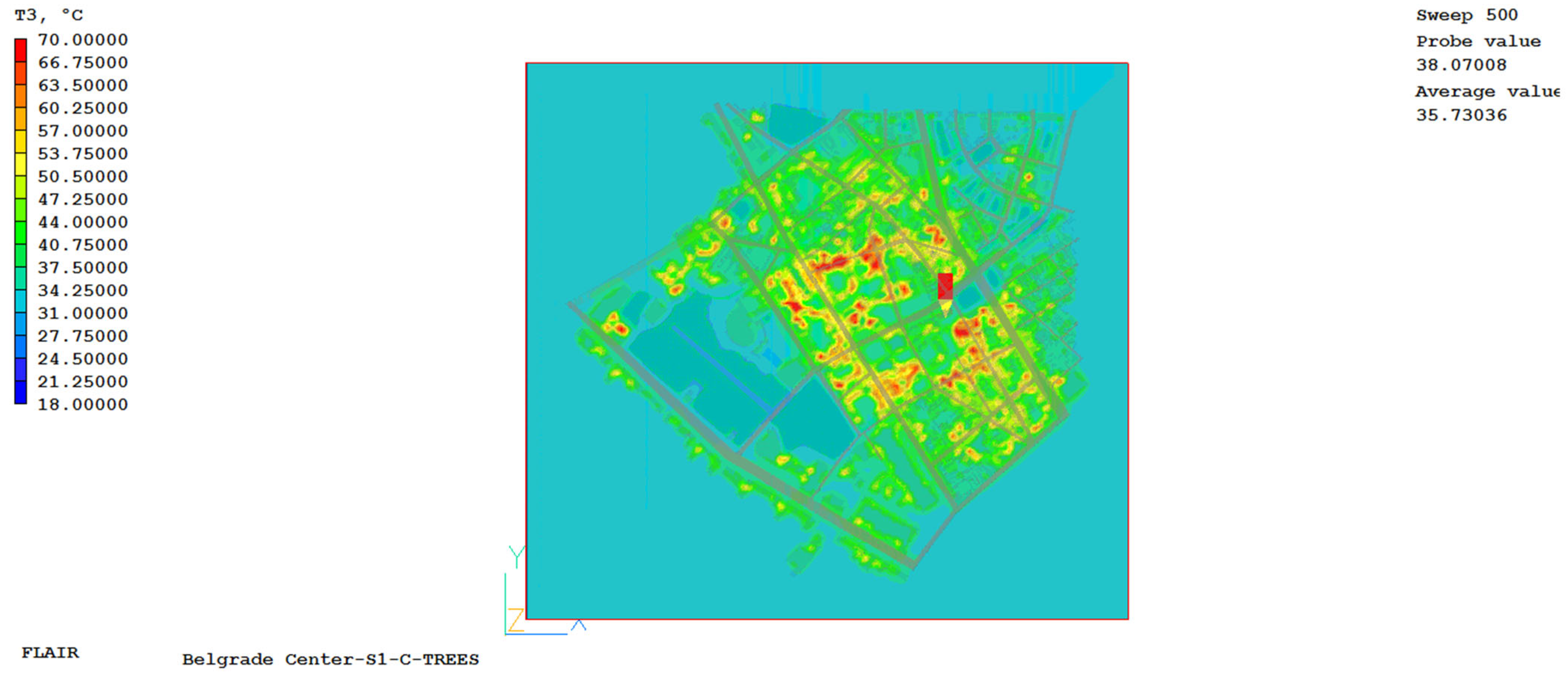
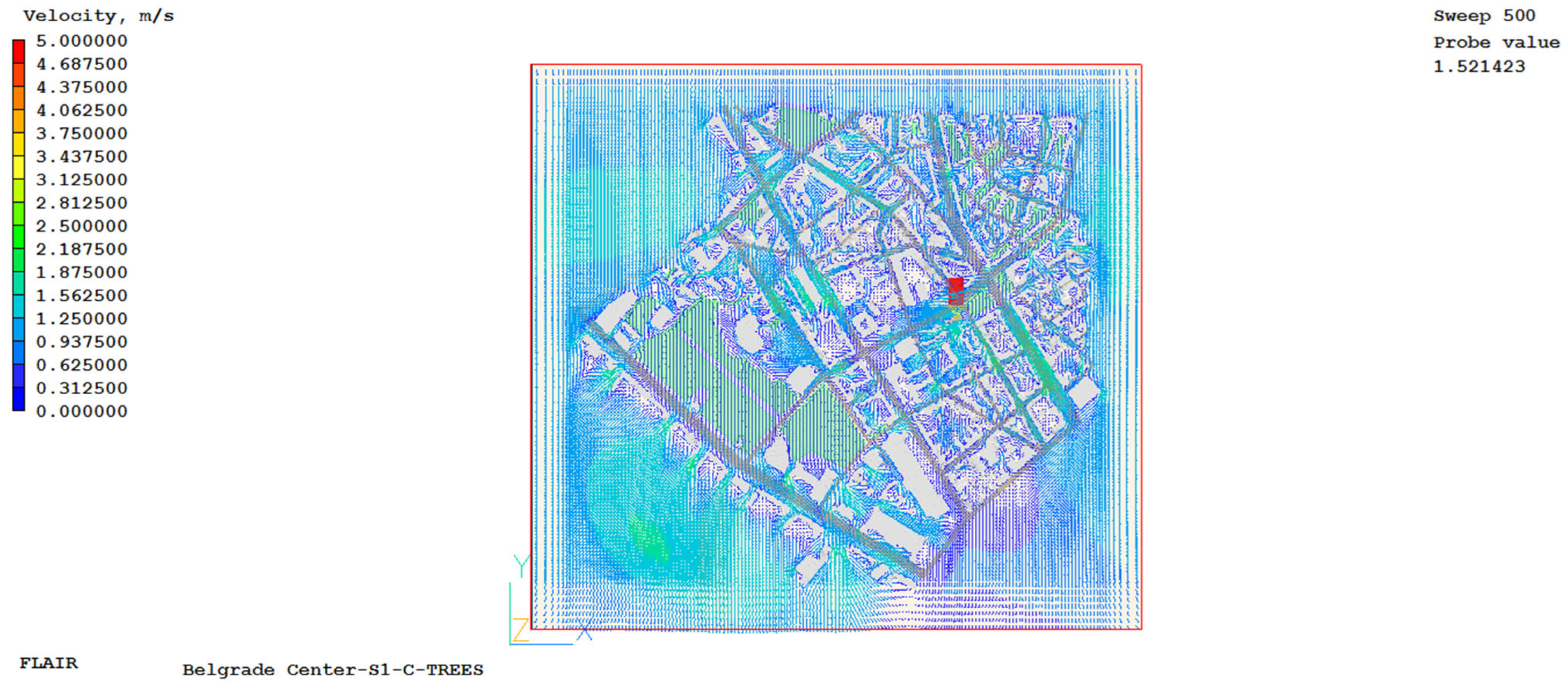
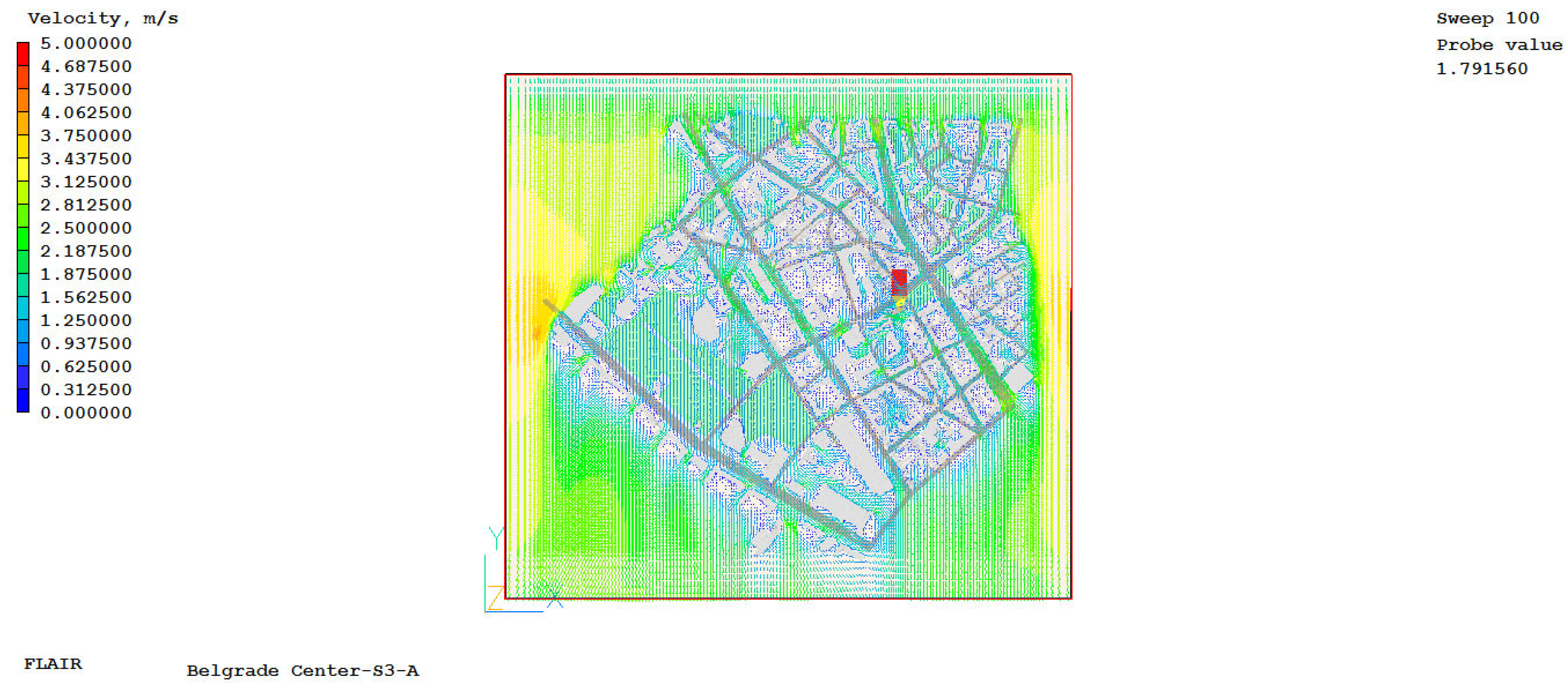
The grid independence study was performed for case S1, for 5 numerical grids that were classified by fineness (number of finite volumes) into the following cases: S1-A consisting of 430,000 finite volumes, S1-B consisting of 1,232,622 finite volumes, S1-C consisting of 2,167,500 finite volumes, S1-D consisting of 3,244,032 finite volumes, and S1-E consisting of 7,161,165 finite volumes. Based on the analysis of all the obtained results, the S1-C network was adopted for further calculation and research. The main reason for choosing this grid is that compared to the S1-D and S1-E grids, the results differ by less than 1%, and the time required for solution convergence is significantly shorter, while the differences in the results are negligibly small, as highlighted.

The values of ambient air temperature, radiant air temperature, air velocity, partial water vapor pressure, and carbon dioxide concentration at five control points, obtained by numerical simulations after 500 iterations, are shown in

Table A5. Values of the observed parameters for case S1-A.

		Ta	Tmrt	va	pv	CO2
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]
1	Surroundings of the school building	31.35	38.55	1.41	1.8	374
2	Tašmajdan Park	30.60	31.75	0.45	4.73	365
3	Palilula Market	35.68	35.54	0.80	0.86	366
4	King Alexander Boulevard	32.27	40.04	1.61	1.45	418
5	Intersection of March 27th and Starine Novaka	36.45	42.80	0.86	−1.22	478
	Mean value (of the entire area)	34.98	34.86	0.91	0.93	370

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

,

Table A6. Values of the observed parameters for case S1-B.

		Ta	Tmrt	va	pv	CO2
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]
1	Surroundings of the school building	32.25	38.12	1.42	1.42	372
2	Tašmajdan Park	30.42	32.13	0.76	0.76	365
3	Palilula Market	35.36	35.45	1.21	1.21	369
4	King Alexander Boulevard	33.78	39.47	1.25	1.81	407
5	Intersection of March 27th and Starine Novaka	36.99	44.64	0.40	−1.59	512
	Mean value (of the entire area)	35.35	35.79	0.98	1.18	369

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

,

Table A7. Values of the observed parameters for case S1-C.

		Ta	Tmrt	va	pv	CO2
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]
1	Surroundings of the school building	32.00	38.07	1.40	2.33	371
2	Tašmajdan Park	30.29	32.04	0.73	5.86	365
3	Palilula Market	35.20	35.08	1.14	1.44	367
4	King Alexander Boulevard	33.62	39.18	1.14	1.75	403
5	Intersection of March 27th and Starine Novaka	36.90	44.50	0.38	−1.53	505
	Mean value (of the entire area)	35.22	35.73	0.91	1.12	369

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

,

Table A8. Values of the observed parameters for case S1-D.

		Ta	Tmrt	va	pv	CO2
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]
1	Surroundings of the school building	31.90	37.60	1.38	3.00	371
2	Tašmajdan Park	30.22	31.97	0.70	6.15	365
3	Palilula Market	35.15	34.82	1.09	1.51	367
4	King Alexander Boulevard	33.59	38.74	1.08	1.46	402
5	Intersection of March 27th and Starine Novaka	36.85	44.30	0.32	−1.32	501
	Mean value (of the entire area)	35.16	35.69	0.90	1.08	369

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

and

Table A9. Values of the observed parameters for case S1-E.

		Ta	Tmrt	va	pv	CO2
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]
1	Surroundings of the school building	31.82	36.92	1.39	2.61	370
2	Tašmajdan Park	30.11	31.88	0.67	6.76	365
3	Palilula Market	35.08	34.41	1.04	1.41	366
4	King Alexander Boulevard	33.50	38.12	1.04	1.39	401
5	Intersection of March 27th and Starine Novaka	36.64	44.16	0.32	−1.31	499
	Mean value (of the entire area)	35.1	35.52	0.87	1.02	368

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

, Appendix D. The control points coincided with the places where experimental measurements of the mentioned meteorological quantities were made. A graphical representation of the results obtained from numerical simulations for case S1, differing in numerical grid density, is shown in Figure A13, Appendix D. Given that the average height at which experimental measurements of meteorological quantities were made was 1.85 m, the results of numerical simulations are shown for the horizontal plane at this height.

Table A10. Parameter values for case S1-C at a height of 1.85 m.

		Ta	Tmrt	va	pv	CO2	UTCI	Heat Load
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]	[°C]	[a/b]
1	Surroundings of the school building	32.00	38.07	1.4	2.33	371	32.9	3/3
2	Tašmajdan Park	30.29	32.04	0.73	5.86	365	29.9	4/4
3	Palilula Market	35.20	35.08	1.14	1.44	367	35.1	3/2
4	King Alexander Boulevard	33.62	39.18	1.14	1.75	403	34.6	3/3
5	Intersection of March 27th and Starine Novaka	36.90	44.5	0.38	−1.53	505	39.0	2/2

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

,

Table A11. Parameter values for case S2-C at a height of 1.85 m.

		Ta	Tmrt	va	pv	CO2	UTCI	Heat Load
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]	[°C]	[a/b]
1	Surroundings of the school building	34.93	37.97	0.50	1.24	372	34.5	3/3
2	Tašmajdan Park	33.45	34.09	0.64	3.08	365	32.3	3/3
3	Palilula Market	36.19	34.71	2.23	1.93	372	34.9	3/3
4	King Alexander Boulevard	36.31	39.17	1.75	0.96	389	36.2	3/2
5	Intersection of March 27th and Starine Novaka	36.83	44.91	0.99	−0.42	512	38.1	2/2

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

and

Table A12. Parameter values for case S3-C at a height of 1.85 m.

		Ta	Tmrt	va	pv	CO2	UTCI	Heat Load
No	Location	[°C]	[°C]	[m/s]	[hPa]	[ppm]	[°C]	[a/b]
1	Surroundings of the school building	29.17	32.03	1.79	4.67	368	28.0	4/4
2	Tašmajdan Park	28.38	29.84	1.00	8.19	365	27.2	4/4
3	Palilula Market	33.91	32.06	1.72	3.84	372	32.4	3/3
4	King Alexander Boulevard	30.63	32.17	1.06	2.71	395	29.73	4/4
5	Intersection of March 27th and Starine Novaka	35.04	33.40	1.36	2.16	489	33.9	3/3

Where T_a is air temperature, T_mrt is mean radiant temperature, ν_a is actual ambient air velocity, and p_v is atmospheric pressure.

, Appendix E, show the obtained results from numerical simulations for different time periods in the morning (S1), afternoon (S2) and evening (S3), using a grid with 2,167,500 final volumes. In addition to these values, the tables also show the universal thermal climate index values and the heat load value for different categories of people. Figure A14, Figure A15, Figure A16, Figure A17 and Figure A18, Appendix E, show the values obtained by numerical simulations for the created numerical model at a height of 1.85 m for the field of air temperature, air velocity, radiant air temperature, carbon dioxide concentration and partial water vapor pressure when experimental measurements were also performed at all locations in order to validate the values of the numerical simulations. The results are shown in the example of one day for three different cases. Figure A14, Figure A15, Figure A16, Figure A17 and Figure A18, Appendix E, show the result values related to the case S1, in the morning from 08 to 09 h, and whose values for 5 selected city locations are shown in Table A10, Appendix E. Figure A19, Figure A20, Figure A21, Figure A22 and Figure A23, Appendix E, show the result values related to the case S2, in the afternoon from 2 to 3 p.m. and whose values for 5 selected city locations are shown in Table A11, Appendix E. Figure A24, Figure A25, Figure A26, Figure A27 and Figure A28, Appendix E, show the result values related to the case S3, in the evening from 6 pm to 9 am, and whose values for 5 selected city locations are shown in Table A12, Appendix E.

A list of all instruments used in the study, their calibration sources, measurement accuracy and uncertainty, measurement intervals, installation heights, and protection details is provided in Appendix F,

Table A13. List of equipment used during the measurement.

Instrument Image	Name	Measurement Parameters	Range	Measurement Error
	Testo 435	Measuring parameters that depend on probe	-	-
	Testo 635	Measuring parameters that depend on probe	-	-
	Fluxmeter	heat flux	−2000 to +2000 W/m2	± 3%
	IAQ probe	temperature, relative humidity, carbon dioxide and atm. pressure	−20–70 °C, 0–100%, 0–10000 ppm, 600–1150 hPa	±0.3 °C ±2% RH ±3% CO2(0–5000 ppm) ±5% CO2 (5001–10,000 ppm)
	Type K thermocouple	temperature	−200 °C to +1350 °C
	Radio probe	temperature, humidity	−20–70 °C, 0–100%,	±0.3 °C ±2% RH
	Radio probe with thermocouple	temperature	−20–70 °C
	Contact probe	temperature	−60–300 °C	± 0.5%
	Testo 445	temperature, humidity, carbon dioxide	20–70 °C, 0–100% 0–9999 ppm	±0.2 °C (10–40 °C) ±0.4 °C (remaining range) ±2% RH ±3% CO2 (0–5000 ppm) ±5% CO2 (5001–10,000 ppm)
	Testo 174H	temperature and humidity	−20–70 °C, 0–100%	±0.5 °C ±3% RH
	FLIR Exx series	temperature	−20 °C do +650 °C	±2 °C or ±2%
	Black globe	Black globe temperature	−0–120 °C,	±0.5 °C
	Anemometer probe	flow rate	0–20 m/s	±0.4%
	Testo 830 T2	Non-contact temperature measurement of solid surfaces	−30–400 °C,	±0.5%

.

Validation of the accuracy of the results was performed based on the relative error between the value of the physical parameter at the measurement site obtained experimentally and the value of the physical parameter at the measurement site obtained by numerical simulation.

Table 1. Summary table of model relative errors for air temperature, carbon dioxide concentration, and radiant temperature.

Parameter	Measuring Point	Simulated			Measured			Error
		S1-C	S2-C	S3-C	S1-C	S2-C	S3-C	S1-C	S2-C	S3-C
Ta [°C]	1	32.00	34.93	29.17	32.8	36.5	30.5	2.4	4.3	4.4
	2	30.29	33.45	28.38	31.0	34.2	30.0	2.3	2.2	5.4
	3	35.20	36.19	33.91	36.5	38.0	35.5	3.6	4.8	4.5
	4	33.62	36.31	30.63	35.0	38.1	32.0	3.9	4.	4.3
	5	36.90	36.83	35.04	35.5	37.5	34.5	−3.9	1.8	−1.6
CO2 [ppm]	1	371	372	368	368	369	370	−0.8	−0.8	0.5
	2	365	365	365	368	369	368	0.8	1.1	0.8
	3	367	372	372	382	375	390	3.9	0.8	4.6
	4	403	389	395	412	400	400	2.2	2.7	1.3
	5	405	512	489	421	480	475	3.8	−6.7	−3.0
Tmrt [°C]	1	38.07	37.97	32.03	42.5	37.8	32.8	10.4	−0.5	2.4

summarizes the relative error values of numerical models compared to experimental data for air temperature, carbon dioxide, and calculated radiant temperature in the vicinity of the school building. The criteria for a valid model are adopted so that the relative error for physical parameters is less than 5%, while for radiant temperature, the relative error is assumed to be less than 10% because this value is obtained based on measurements of multiple parameters. In Table 1, fields with measurement points where parameter values do not meet the set relative error value are colored red. T_a is air temperature and T_mrt is the mean radiant temperature.

The few highlighted values that slightly exceed the predefined error thresholds can be attributed to the inherent complexities of modeling dynamic urban microclimates. The minor discrepancy in air temperature (T_a) is likely due to localized thermal fluctuations not fully captured by the model’s grid resolution. The deviation for CO₂ at a high-traffic intersection (point 5) can be explained by the stochastic nature of vehicle emissions (e.g., sudden accelerations), which create transient peaks that a model with time-averaged emission sources cannot perfectly replicate. Similarly, the larger error for mean radiant temperature (T_mrt) in the morning case (S1-C) is attributed to the complex effects of low sun angles and dynamic shadows, which are challenging for a steady-state radiation model to capture precisely. The model’s accuracy for T_mrt in other periods of the day was excellent.

Verification of numerical results was performed for each series of calculations and for all selected locations. It is concluded that the results of numerical simulations compared to the measured results have acceptable deviations, which is one of the conditions for this model to be used for further analysis and calculations.

While the detailed CFD analysis focuses on a representative hot day to investigate microscale mechanisms, long-term measurements provide essential seasonal context.

Table 2. Monthly Mean and Maximum Air Temperatures and Mean UHI Intensity (March–September 2015).

Month	Maximum Air Temperature [°C] School in Center	Average Air Temperature [°C] School in Center	Maximum Air Temperature [°C] Vinča	Average Air Temperature [°C] Vinča	Average Value UHI [°C]
March	25.6	10.2	22.2	7.5	2.60
April	32.9	15.1	26.7	11.6	3.5
May	38.6	20.6	31.0	16.7	3.8
June	42.0	24.2	33.0	19.7	4.5
July	46.1	29.9	37.1	23.6	6.2
August	43.1	28.2	37.1	23.1	5.0
September	42.0	23.3	34.7	19.2	4.0

summarizes the monthly statistics from the entire measurement campaign (March–September 2015). The data clearly shows a seasonal trend, with the mean monthly UHI intensity peaking in July at 6.2 °C, coinciding with the month of highest average and maximum temperatures. This seasonal data provides a robust framework for the detailed daily analysis and confirms that the conditions on 5 July, while extreme, are part of a broader seasonal pattern of urban heating.

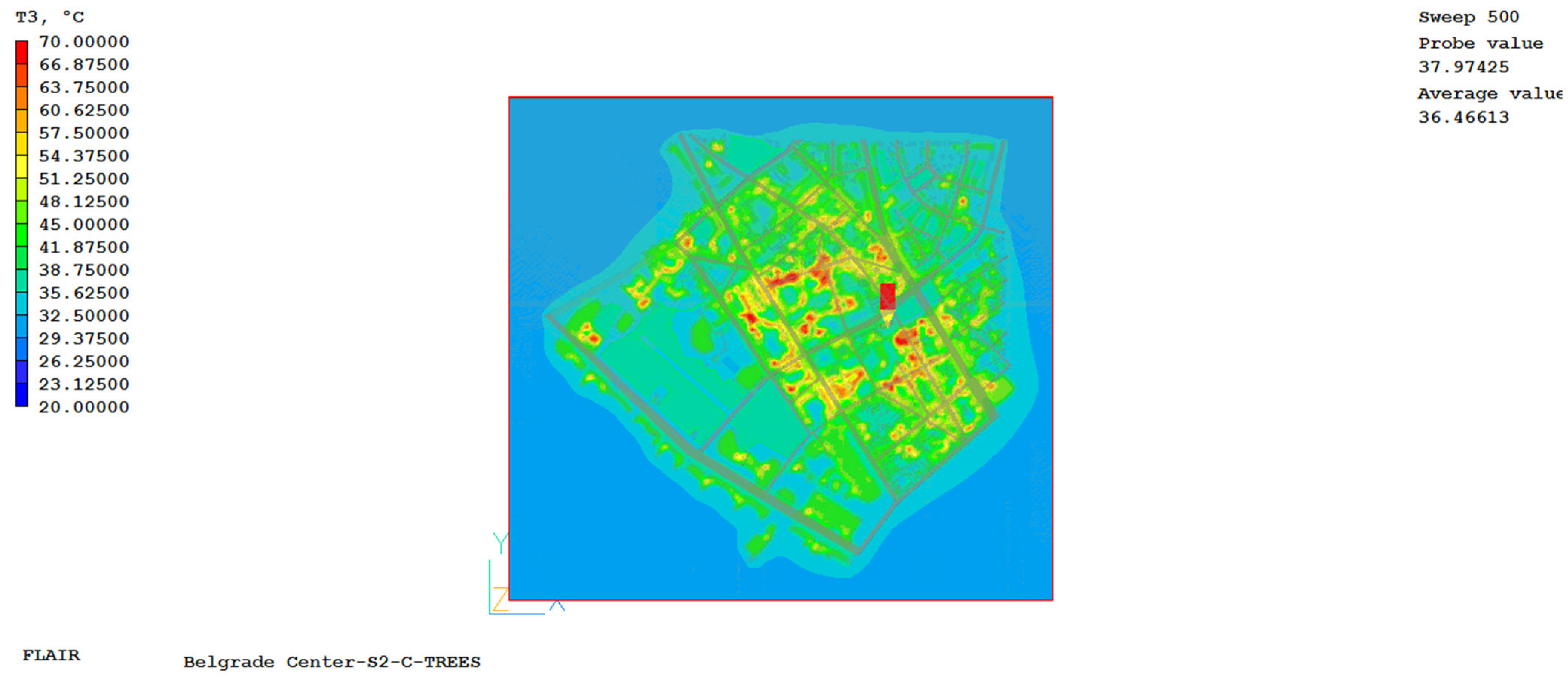
By analyzing the results obtained by simulation and the results measured in the rural area, the following conclusions emerge: the obtained values of UHII for the selected urban environment and for the selected time period are highest in the evening hours, after sunset, where its average value is 9.5 °C, in the morning hours this value is 8.1 °C, while it is lowest in the afternoon when it drops to 4.8 °C for the observed day. Also, it can be clearly observed that in areas where there are green areas, parks, the value of the UHII and air temperatures are lower compared to parts where there are only buildings. Based on the results obtained, it is evident that the ambient and radiant temperature near streets with more frequent traffic, but also in places with a higher density of buildings, is significantly higher than in other parts of the city, which means that in these areas the UHII has the highest value.

Figure A11 and Figure A12, Appendix C, clearly show the difference between the two urban environment structures consisting of buildings and other similar objects that have high heat absorption and a large area covered by vegetation. In the part of the city where there are only buildings, the air temperature is higher and a heat island is created at the city level. This directly results in an increase in temperature in those parts of the city, which further negatively affects external thermal comfort, but also leads to higher energy consumption for cooling the interior of those buildings. In the observed urban area, the area under vegetation occupies 8.5% of the total area. In the case of no vegetation, the average outdoor ambient temperature of the observed domain increases from 2% in the morning to 4% in the evening.

Analysis of the obtained results confirmed the need for and advantage of using a detailed methodology of computer simulations to determine the temperature field, radiant temperature, flow velocity and carbon dioxide concentration in a complex urban environment. Such simulations can significantly provide more accurate meteorological data that can be used to calculate the energy required for cooling in buildings.

5. Discussion

This study, as a continuation of our previous studies [39,40], successfully combined in situ measurements with a validated numerical model to investigate the relationship between traffic-induced pollution and Urban Heat Island (UHI) intensity in a complex urban core. The findings provide a quantitative basis for understanding the primary mechanisms shaping the local microclimate and its thermal characteristics.

The results strongly suggest that elevated UHI intensity is driven by several interacting factors. A primary mechanism is the dual role of vehicular traffic, which acts both as a direct source of thermal energy and as an indirect one through emissions. The clear correlation between traffic density, elevated CO₂ concentrations, and localized temperature hotspots indicates that pollutants accumulate in street canyons, where they impede the escape of longwave radiation and intensify local heating. Concurrently, the significant cooling effect of urban vegetation was quantified, with the “no-tree” scenario demonstrating that its removal results in an average air temperature increase of 1.5 °C to 3 °C. This highlights the cumulative importance of shading and evapotranspiration in mitigating urban heat. Furthermore, the simulations revealed how urban geometry can exacerbate these conditions through the formation of quasi-stationary vortex structures within building blocks, which trap warm air and reduce natural ventilation, creating persistent hotspots.

The UHI intensities observed in this Belgrade case study are consistent with and expand upon previous local and international research. Historically, the UHI in Belgrade showed a gradual increase over the 20th century, rising from approximately 0.1 °C to 0.9 °C. More recent studies focusing on high-traffic areas identified intensities between 1.5 and 6.1 °C. Our findings, with a typical summer intensity between 5 and 9 °C and a peak value of 12 °C in July, represent a significant intensification, placing Belgrade’s city center on par with other major European capitals. For instance, reported UHI intensities have reached up to 7 °C in London, 8 °C in Paris, 10 °C in Athens, and 12 °C in Łódź, Poland. This comparison underscores the generalizability of our findings to other large, dense urban environments in continental Europe. Furthermore, our confirmation that the UHI intensity is greatest at night aligns with well-established findings in urban climatology, which attribute this to the slow nocturnal release of heat from materials with high thermal capacity, such as concrete and asphalt.

It is important to acknowledge the limitations of this work. The numerical model employed steady-state assumptions for specific time windows, providing snapshots of thermal conditions rather than a fully transient daily cycle. Moreover, while the cooling benefit of vegetation was quantified as a whole, the model in its current form did not separate the individual contributions of shading, evapotranspiration, and their influence on air mixing. The study also focused on a single, albeit complex, urban area, meaning the direct transferability of results may be limited.

The data on vehicle fleet composition (percentage shares of passenger cars, buses, light and heavy-duty vehicles, etc.) and distribution by fuel type (petrol, diesel) were obtained from the built-in database of the COPERT software package, which contains specific statistical data for the vehicle fleet in the Republic of Serbia for the year under study. This approach follows the standard methodology recommended by the European Environment Agency (EEA) for official traffic emission calculations. We acknowledge that using aggregated national-level statistical data introduces some uncertainty, as the local vehicle fleet composition may differ from the national average.

Despite these constraints, the findings carry significant implications for urban planning and policy. The strong, quantified link between green spaces and lower temperatures provides compelling evidence for prioritizing the preservation and expansion of urban parks and canopy cover as a direct UHI mitigation strategy. Similarly, the connection between traffic, pollution, and thermal hotspots suggests that traffic management policies can be effective microclimate regulation tools. Looking forward, future research should aim to address this study’s limitations by employing transient simulations and developing models capable of local energy-balance diagnostics to disentangle the specific effects of shading and evapotranspiration. Applying this validated methodology to other urban typologies would further enhance our understanding and ability to design more resilient and comfortable cities.

6. Conclusions and Future Research

This study presents the results of research into the impact of UHII on the heating of the environment as well as on the energy consumption for cooling in buildings in larger urban areas. The research is based on the results of experimental determination of the required quantities and the results obtained by applying modern numerical methods and tools. Data on air temperature values recorded at 4 meteorological stations in different parts of the city of Belgrade (Mostar, Novi Beograd, Stari Grad and Vračar) during 2015 were collected and processed. At two previously selected locations in the city of Belgrade, ambient air temperatures, radiant temperatures, relative air humidity, solar and diffuse radiation intensity, wind speed and direction were measured. One of the selected locations is located in an urban area in the immediate vicinity of the building of the Higher Textile School for Design, Technology and Management. The second location was chosen in a rural area and is located in the park of the Vinča Institute of Nuclear Sciences in the settlement of Vinča. The measured values were used to estimate the UHII and as input data for the formed mathematical–numerical models.

Traffic flow measurements were carried out at seven selected intersections at the city location. For a determined number of vehicles, previously classified into seven categories according to the level of pollutant emissions, the amount of emissions generated by traffic was calculated. The results of measurements of air temperature, carbon dioxide concentration and radiant temperature in the immediate vicinity of the school building were used to validate the mathematical–numerical model. The measuring equipment is described in detail and measurement standards and procedures, as well as the method of data collection and processing, are given. Through field measurements, the spatial and temporal parameters of the complex operating mode of building use were determined. The collected and processed results of the presented measurements represent an extensive and complex database for continued research in this area, but also for some other scientific research. The advantage of the numerical simulations used in this research is that such simulations allow us to obtain different fields of temperature, wind speed and carbon dioxide concentration that correspond to different urban configurations by changing the input data and geometry. Thanks to these results, we can advance urban planning and improve outdoor thermal comfort, all in the interest of significantly greater use of urban spaces during summer periods of extreme temperatures.

Through a critical evaluation of the results, it was shown that UHII is not a homogeneous phenomenon but is highly dependent on specific operational conditions and urban micro-geometry, which represents the key finding of this study. Quantification of the influence of key urban factors confirmed that the removal of green infrastructure leads to an increase in the average air temperature in the observed domain in the range of 1.5 °C to 3 °C, directly worsening the UTCI thermal comfort index. These specific operational conditions contribute to the highest recorded UHII in the selected urban area reaching up to 12 °C in July, while average values during the summer period range between 5 °C and 9 °C. Such a thorough examination of specific operational conditions is essential for accurately understanding microclimatic changes and guiding future urban planning decisions.

This paper demonstrates the advantage of using numerical software for detailed characterization of current-thermal quantities and dispersion of a non-reactive pollutant (carbon dioxide). As the model for the selected complex urban environment of the city of Belgrade showed high accuracy, agreement of simulated and measured data, for the assessment of current fields and carbon dioxide concentration fields, it can be considered that this model is a useful tool for assessing the impact of other pollutants on the urban environment. Also, this numerical–mathematical model can be easily applied to other urban environments. Given that this is a very complex urban geometry, the size of the selected and calculated domain is large, and the difference between the obtained simulated and measured values is below 5%, it can be considered that the model met the goal and provided a realistic estimate of the observed parameters.

Building on the findings of this study, we present the following actionable recommendations. First, the quantified cooling effect of vegetation underscores the importance of mandating green spaces, such as parks and tree-lined streets in all new urban development and regeneration projects. Second, given the strong relationship between traffic emissions and localized heat islands, cities should priorities sustainable urban mobility plans that reduce vehicle density in central areas. Third, the demonstrated role of urban geometry in trapping heat and pollutants should be incorporated into building codes and zoning regulations, promoting designs that enhance natural ventilation. Together, these measures can foster more resilient, energy-efficient, and livable urban environments.

In further research, it is possible to apply the developed model to a large number of other locations and extend it to conditions of stable and unstable, not just neutral, atmospheres, which was considered in this work. Furthermore, future research should focus on refining the numerical model to enable a local energy-balance diagnostic. This would allow for the quantitative separation of the individual cooling effects of vegetation, such as shading, evapotranspiration, and their influence on natural ventilation (wind flow). Such a detailed analysis would provide a deeper understanding of the underlying mechanisms and offer more targeted strategies for urban planners to mitigate the urban heat island effect. In addition, in future work, it is planned to develop a numerical analysis that will take into account the results of numerical simulations of the air velocity field due to the influence of the shape of buildings and entire urban environments. This approach can improve urban microclimate conditions and outdoor thermal comfort in open spaces. Such analyses, in the early design phase, can contribute to the construction of more pleasant urban units, which will condition the use of those spaces to a greater extent.