Models for Predicting the Long-Term Strength of Rheonomic Materials
Abstract
1. Introduction
2. General Model of Long-Term Strength
2.1. Integral Equation
2.2. Damage Kernel
2.3. Definition of Parameters and
2.4. Instantaneous Strength
2.5. Time of Destruction
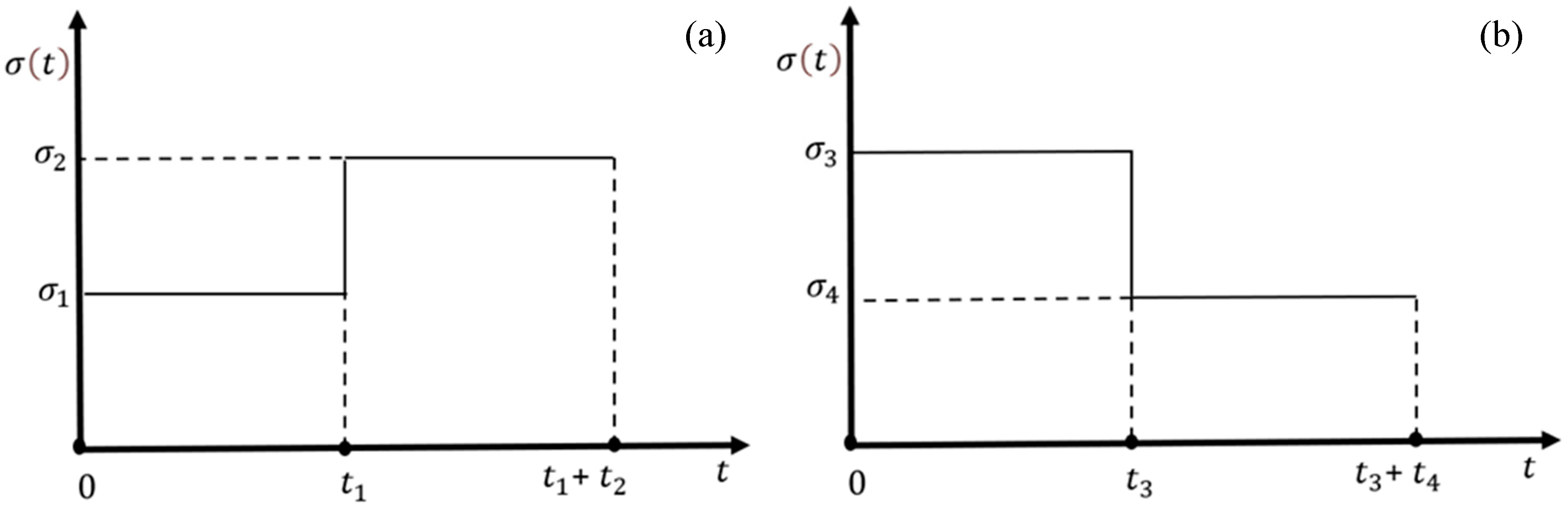
2.6. Long-Term Strength Under Step Loading
3. Materials and Methods
3.1. Materials
3.2. Sample Preparation
3.3. Testing
4. Results and Discussion
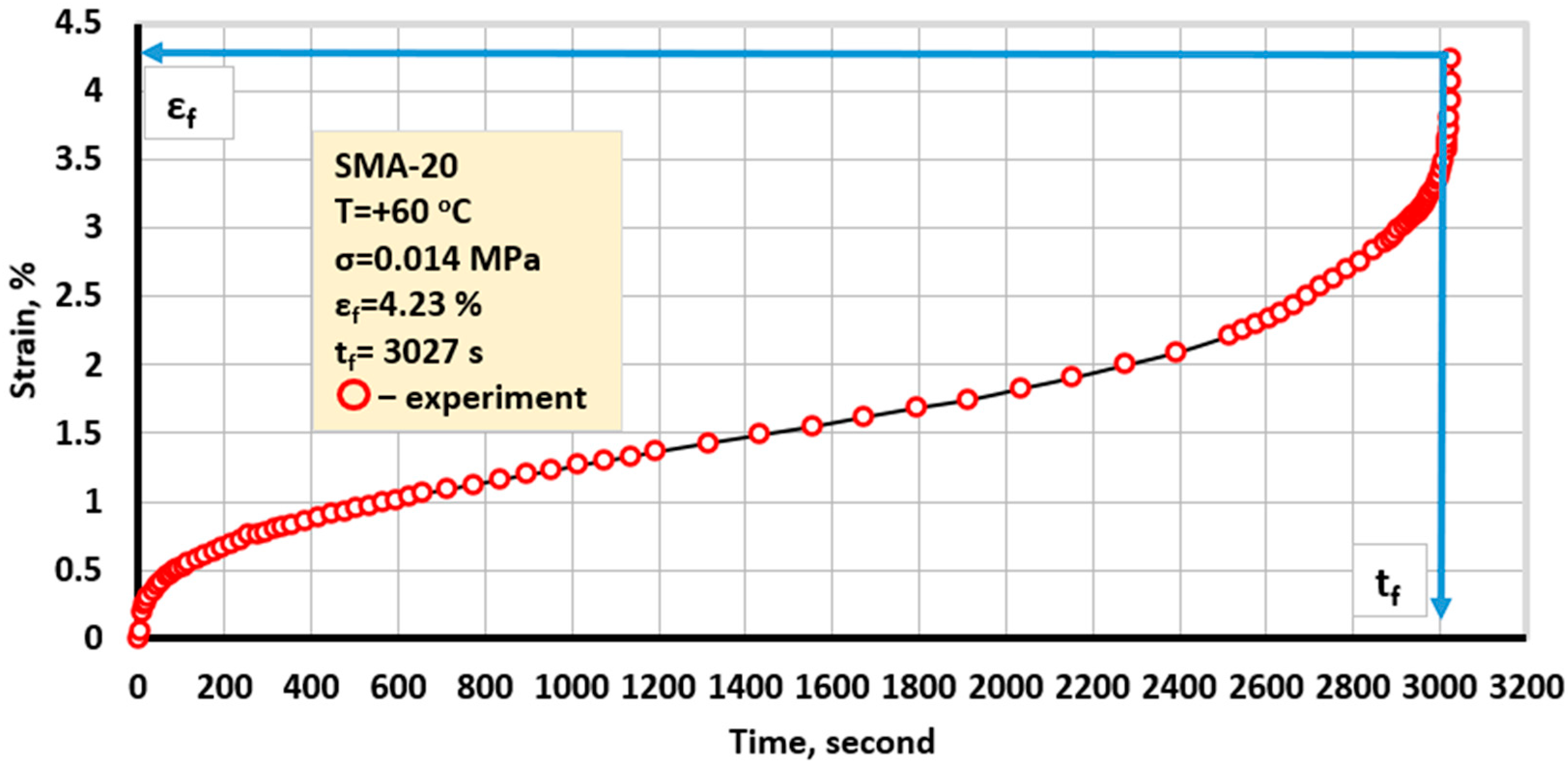
4.1. Long-Term Strength of Asphalt Concrete
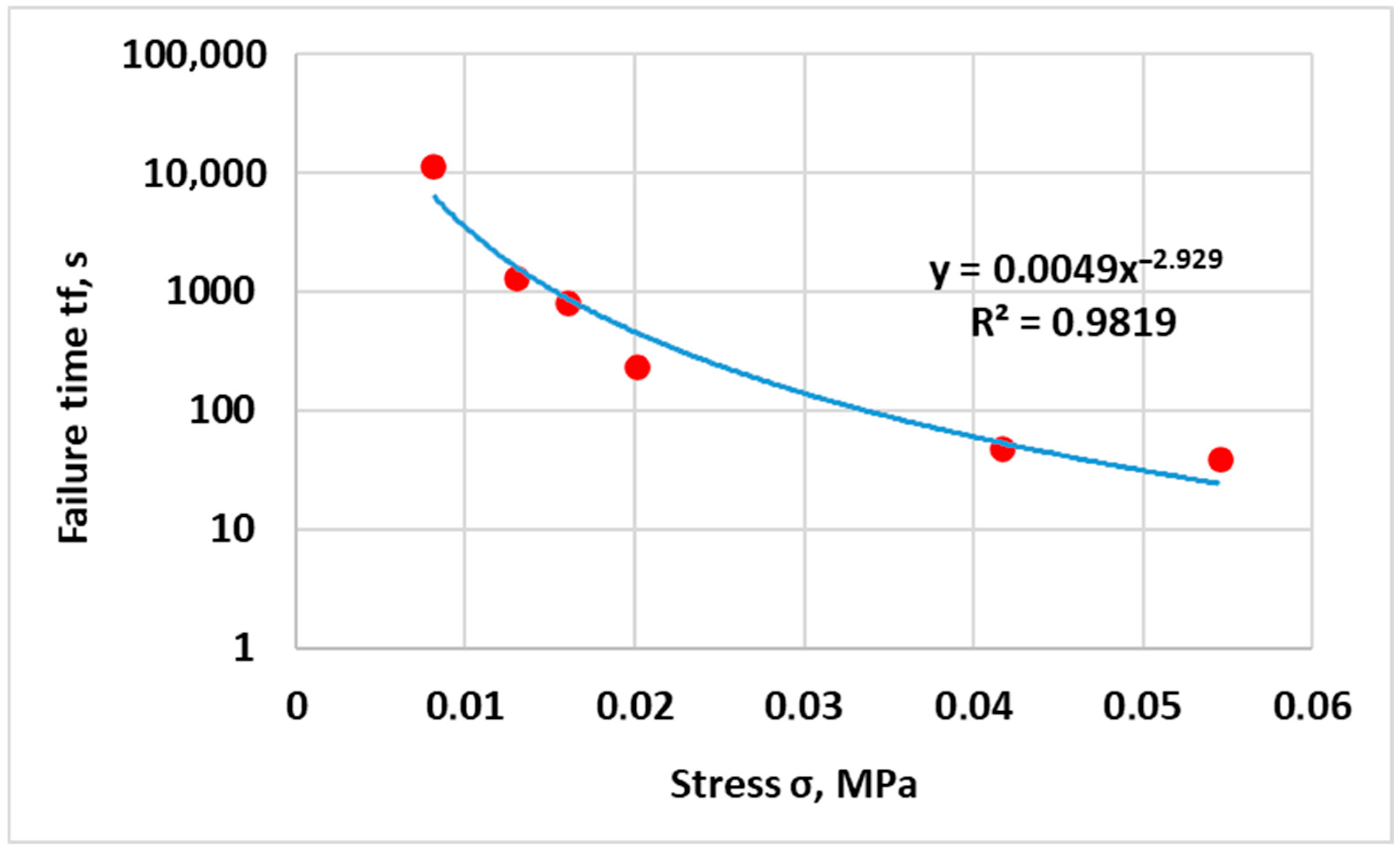
4.2. Long-Term Strength Under Constant Stress
4.3. Long-Term Strength Under Step Loading
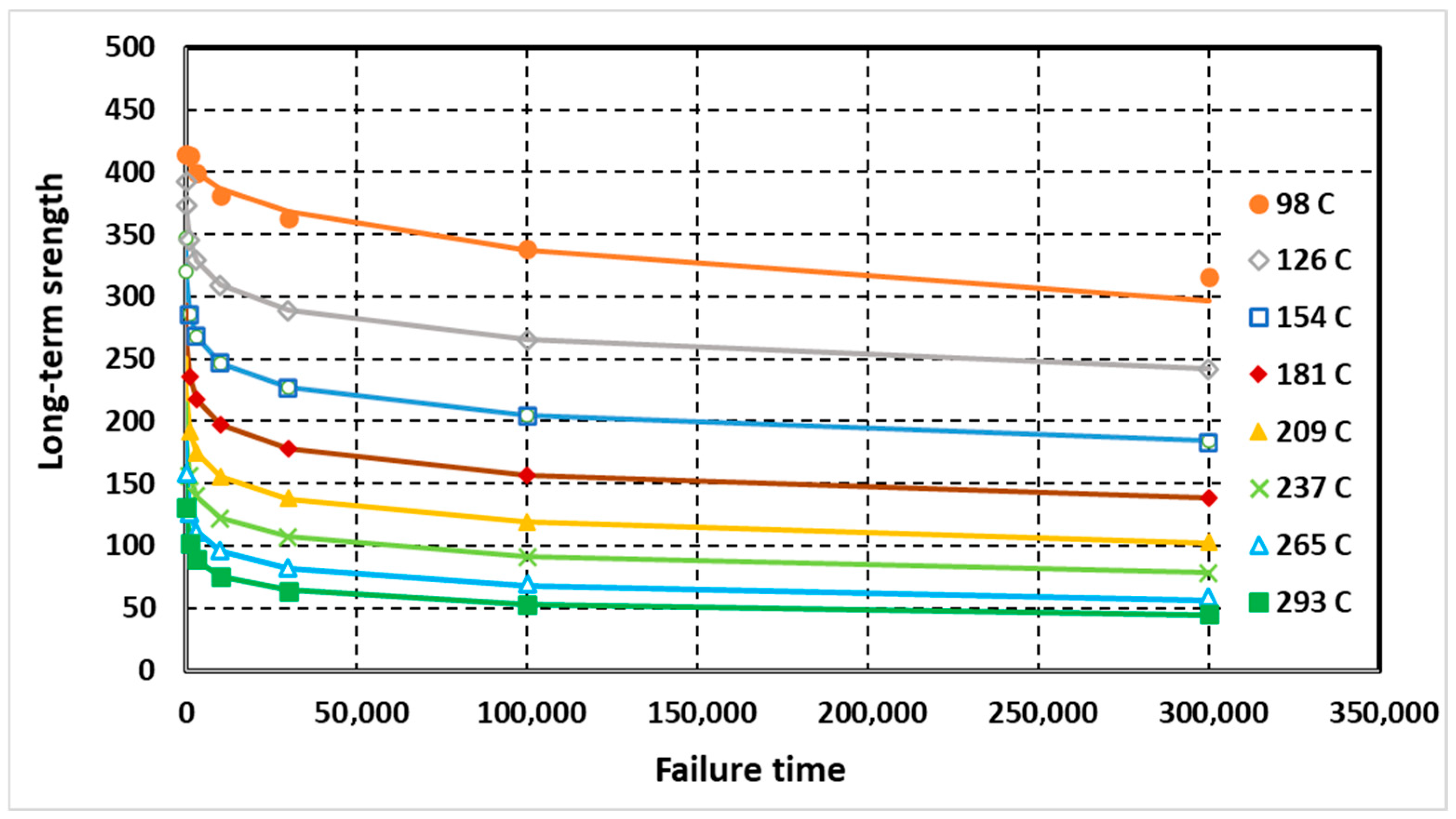
4.4. Prediction of Long-Term Strength from Short-Term Test Data
5. Conclusions
- A simple model was formulated in the form of a power function, achieving high accuracy (R2 = 0.9819) and easily describing the long-term strength of the asphalt concrete. In cases where the long-term strength of rheonomic materials and the corresponding stress values are known from experiments, the simplest functions and equations can be used as models.
- The developed models of long-term strength of rheonomic materials, particularly in the form of an integral equation with a kernel in the form of a power function that takes into account the accumulation of damage over time, adequately describe the long-term strengths of several types of materials. Using the developed models, the long-term strength of an optical fiber with moisture of 30% and 85% under constant stress from 1600 to 2100 MPa and an aluminum alloy under a step change in stress at a temperature of 180 °C were predicted with high accuracy; the long-term strength of a pearlitic steel was predicted based on short-term tests under constant stress at temperatures from 98 °C to 293 °C.
- 3.
- Using the developed models, it is possible to predict the long-term strength of rheonomic materials under variable environmental and operational conditions; in these cases, the mechanical characteristics included in the models should be represented as functions of environmental and operational parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhurkov, S.N. Kinetic Concept of Solid Body Strength. News Acad. Sci. USSR Ser. Inorg. Mater. 1967, 3, 1767–1777. [Google Scholar]
- Regel, V.R.; Slutsker, A.I.; Tomashevskiy, E.Y. Kinetic Nature of Solid Body Strength; Nauka: Moscow, Russia, 1974. [Google Scholar]
- ST RKSTRK1218-2003; Organic Binding Materials for Road and Airfield Construction. Test Methods; Kazakhstan Institute of Standardization and Metrology: Astana, Kazakhstan, 2003.
- Chai, Q.; Huang, S.; Wan, F.; Wu, F. A New Experimental Method to Measure and Calculate the Tensile Strength of Concrete. Front. Mater. 2023, 10, 1216747. [Google Scholar] [CrossRef]
- Stefanow, D.; Dudziński, P.A. Soil Shear Strength Determination Methods—State of the Art. Soil Tillage Res. 2021, 208, 104881. [Google Scholar] [CrossRef]
- Cosse, R.L.; van der Most, T.; Voet, V.S.D.; Folkersma, R.; Loos, K. Improving the Long-Term Mechanical Properties of Thermoplastic Short Natural Fiber Compounds by Using Alternative Matrices. Biomimetics 2025, 10, 46. [Google Scholar] [CrossRef]
- Sokołowska, J.J. Long-Term Compressive Strength of Polymer Concrete-like Composites with Various Fillers. Materials 2020, 13, 1207. [Google Scholar] [CrossRef]
- Ho, L.S.; Huynh, T.-P. Long-Term Mechanical Properties and Durability of High-Strength Concrete Containing High-Volume Local Fly Ash as a Partial Cement Substitution. Results Eng. 2023, 18, 101113. [Google Scholar] [CrossRef]
- Chudnovsky, A.; Sehanobish, K. Long-Term Strength of Materials: Reliability Assessment and Lifetime Prediction of Engineering Structures, 1st ed.; CRC Press: Boca Raton, FL, USA, 2023; pp. 1–224. [Google Scholar] [CrossRef]
- Novozhilov, V.V. On the prospects of a phenomenological approach to the problem of destruction. In Mechanics of Deformable Bodies and Structures; Nauka: Moscow, Russia, 1975; pp. 349–359. [Google Scholar]
- Palmgren, A. Die lebensdauer von Kugellagern. Z. Vereines Dtsch. Ingenieure 1924, 14, 339–341. [Google Scholar]
- Langer, B.F. Fatigue failure from stress cycles of varying amplitude. J. Appl. Mech. 1937, 59, A160–A162. [Google Scholar] [CrossRef]
- Bailey, J. Attempt to correlate some tensile strength measurement on glass. Glass Ind. 1939, 20, 21–30. [Google Scholar]
- Robinson, E.L. Effect of temperature variation on the long time rupture strength of steels. Trans. ASME 1952, 74, 777–780. [Google Scholar] [CrossRef]
- Kachanov, L.M. On the fracture time under creep conditions. News USSR Acad. Sci. Dept. Tech. Sci. 1958, 8, 26–31. [Google Scholar]
- Rabotnov, Y.N. Continuum Mechanics, 2nd ed.; Nauka: Moscow, Russia, 1988. [Google Scholar]
- Kachanov, L.M. Introduction to Continuum Damage Mechanics; Martinus Nijhoff Publishers: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Voyiadjis, G.Z. (Ed.) Handbook of Damage Mechanics: Nano to Macro Scale for Materials and Structures, 2nd ed.; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Iskakbayev, A.; Teltayev, B.B.; Rossi, C.O.; Yensebayeva, G.; Abu, B.; Kutimov, K. Impact of loading rate on asphalt concrete deformation and failure. Mag. Civ. Eng. 2020, 8, 10008. [Google Scholar]
- Teltayev, B.B.; Iskakbayev, A.I.; Abu, B.D. Steady-state deformation of asphalt concrete. Constr. Build. Mater. 2022, 349, 128754. [Google Scholar] [CrossRef]
- Lokoschenko, A.M.; Namestnikova, I.V.; Shesterikov, S.A. Description of epy long-term strength under stepwise stress changes. Strength Mater. 1981, 10, 47–51. [Google Scholar]
- Bykov, D.L. Modelling damage accumulation in filled polymers. Fatigue Fract. Eng. Mater. Struct. 1999, 11, 981–988. [Google Scholar] [CrossRef]
- Han, X.; Kloeden, P.E. Sigmoidal approximations of Heaviside functions in neural lattice models. J. Differ. Equ. 2020, 268, 5283–5300. [Google Scholar] [CrossRef]
- Hatano, N.; Ikeda, M.; Ishikawa, I.; Sawano, Y. Heaviside function as an activation function. J. Appl. Anal. 2022, 29, 1–22. [Google Scholar] [CrossRef]
- Marumo, N.; Okuno, T.; Takeda, A. Majorization-minimization-based Levenberg-Marquardt method for constrained nonlinear least squares. Comput. Optim. Appl. 2023, 84, 833–874. [Google Scholar] [CrossRef]
- Shao, W.Y.; Fan, J.Y. On the complexity of a stochastic Levenberg-Marquardt method. J. Inequal. Appl. 2024, 20, 1011–1027. [Google Scholar] [CrossRef]
- Iskakbayev, A.; Teltayev, B.; Aitbayev, Y.; Zhaisanbayev, A. Accelerated creep of asphalt concrete at medium temperatures. Appl. Sci. 2024, 14, 9393. [Google Scholar] [CrossRef]
- ST RK 1225-2019; Road, Airfield Asphalt Concrete Mixtures and Asphalt Concrete. Technical specifications; National Standard of Republic of Kazakhstan: Nur-Sultan, Kazakhstan, 2019.
- ST RK 2373-2019; Road, Airfield Stone-Mastic Asphalt Concrete Mixtures and Stone-Mastic Asphalt Concrete. Technical Specifications; National Standard of Republic of Kazakhstan: Nur-Sultan, Kazakhstan, 2019.
- ST RK 1373-2013; Bitumens and Bitumen Binders, Oil Road Viscous Bitumens. Technical Specifications; National Standard of Republic of Kazakhstan: Nur-Sultan, Kazakhstan, 2013.
- BS EN 12697-26; Bituminous Mixtures, Test Method for Hot Mix Asphalt. Part 26: Specimen Prepared by Roller Compactor; BSI: London, UK, 2003.
- Ermolov, S.B.; Potapov, Y.N. To assess the durability of polymers in a wide temperature-time range. Mech. Polym. 1976, 4, 746–749. [Google Scholar]
- Goldhoff, R.M. The effect of creep prestrain on creep rupture properties of variable notch sensitivity Cr-Mo-V steel. Mater. Res. 1962, 1, 26–32. [Google Scholar]
- Arshakuni, A.L. Prediction of the long-term strength of metals. Mech. Solids 1997, 32, 108–114. [Google Scholar]
- ASME. Gases of ASME Boiler and Pressure Vessel Code. ASME: New York, NY, USA, 1988; Volume 159. [Google Scholar]
- Larson, F.R.; Miller, I. A time-temperature relationship for rupture and creep stresses. Trans. ASME 1952, 74, 765–775. [Google Scholar] [CrossRef]



| Stress σ, MPa | Failure Time, s | Difference, % | |
|---|---|---|---|
| Experimental te | Calculated tcal | ||
| moisture W = 30% | |||
| 2100 | 3446.40 | 3448.60 | +0.06 |
| 2000 | 9957.14 | 9960.03 | +0.03 |
| 1950 | 15,965.54 | 15,959.08 | −0.04 |
| 1900 | 30,286.00 | 30,266.88 | −0.06 |
| moisture W = 85% | |||
| 2000 | 614.80 | 614.80 | 0 |
| 1900 | 2397.08 | 2397.08 | 0 |
| 1700 | 8541.45 | 8541.45 | 0 |
| 1600 | 15,550.51 | 15,550.53 | 0 |
| Loading Scheme | Stress, MPa | Duration of the First Step t1, h | Time of Destruction, h | Difference | ||||
|---|---|---|---|---|---|---|---|---|
| First Step σ1 | Second Step σ2 | te | TBR | tcal | ∆1 | ∆2 | ||
| Figure 1a | 126.3 | 140.6 | 115 | 237 | 309 | 240 | +30.9 | +1.3 |
| Figure 1b | 140.6 | 126.3 | 114 | 573 | 449 | 573 | −21.6 | 0 |
| Figure 1b | 140.6 | 98.3 | 69 | 2590 | 2127 | 2600 | −17.9 | +0.4 |
| Figure 1a | 98.3 | 140.6 | 211 | 200 | 346 | 200 | +73.0 | 0 |
| Temperature T, °C | Parameters | , MPa | |
|---|---|---|---|
| α | δo, hour(α−1) | ||
| 98 | 0.50125 | 0.000368 | 414.96 |
| 126 | 0.8 | 0.012449 | 430.49 |
| 154 | 0.825 | 0.024532 | 420.41 |
| 181 | 0.8 | 0.024883 | 352.28 |
| 209 | 0.7875 | 0.029114 | 306.74 |
| 237 | 0.796875 | 0.040985 | 282.95 |
| 265 | 0.78125 | 0.049509 | 257.40 |
| 293 | 0.796875 | 0.070326 | 244.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iskakbayev, A.; Teltayev, B.; Rossi, C.O.; Aitbayev, Y.; Zhaisanbayev, A. Models for Predicting the Long-Term Strength of Rheonomic Materials. Appl. Sci. 2025, 15, 11236. https://doi.org/10.3390/app152011236
Iskakbayev A, Teltayev B, Rossi CO, Aitbayev Y, Zhaisanbayev A. Models for Predicting the Long-Term Strength of Rheonomic Materials. Applied Sciences. 2025; 15(20):11236. https://doi.org/10.3390/app152011236
Chicago/Turabian StyleIskakbayev, Alibay, Bagdat Teltayev, Cesare Oliviero Rossi, Yerbol Aitbayev, and Azamat Zhaisanbayev. 2025. "Models for Predicting the Long-Term Strength of Rheonomic Materials" Applied Sciences 15, no. 20: 11236. https://doi.org/10.3390/app152011236
APA StyleIskakbayev, A., Teltayev, B., Rossi, C. O., Aitbayev, Y., & Zhaisanbayev, A. (2025). Models for Predicting the Long-Term Strength of Rheonomic Materials. Applied Sciences, 15(20), 11236. https://doi.org/10.3390/app152011236








