Featured Application
The proposed model, a generalization of Weibull-type distributions, finds wide application in analyzing data concerning the lifetime of technical and biological components. It may be particularly useful in reliability engineering, for example, for modeling the failure rate of mechanical devices, electronic systems, or critical infrastructure components, as well as in medicine for analyzing patient survival. Thanks to the flexibility of shaping the hazard function, the model enables a more accurate fit to data compared to classical approaches, which can support maintenance planning, risk forecasting, and resource optimization. Potential applications also include the analysis of large datasets from IoT sensors, which opens the possibility of its use in predictive maintenance systems.
Abstract
The paper is intended to put forward a modified Weibull-type lifetime model. Modification consists of replacing the shape parameter of the original Weibull model with the shape function. It is self-evidently a novelty among lifetime models. The model in question will further be named the Weibull-sf model. To present the Weibull-sf, we need appropriate background. The background comes from an extensive review performed on 165 Weibull-type lifetime models we found in the source literature. Performing this review, we focused on two properties of the models: modality of failure density functions, as well as shape of the hazard rate functions. It does not matter that these are strongly interrelated, incidentally. The Weibull-sf lifetime model has the valuable property of flexibility. It may have a bathtub-like hazard rate function and bimodal density function. This is exactly what reliability analysts want to have. Foreseeing the huge numerical problems one will face when trying the maximum-likelihood method, we promote the method of the least absolute values that is a “close relative” to the method of least squares. Examples of fitting the Weibull-sf to real data are given. The cumulative failure functions of bimodal models with a bathtub-like hazard rate function and R codes are given.
1. Introduction
Without any particular exaggeration, one may say that nearly everything in lifetime data analysis revolves around the hazard rate function (HRF). Lifetime models (LTMs) are categorized according to the shapes of their HRFs. Special attention is paid to the LTMs of “flat-bottomed” HRFs that are commonly named bathtub HRFs. Unfortunately, over time, this name has been used to describe any HRF having a minimum and evidently not being flat-bottomed. The true, i.e., flat-bottomed bathtub hazard rate [1], is specific to a non-homogeneous population. This population consists of subpopulations of “weak” and “strong” items.
Categorized roughly, LTMs may fall into monolithic or hybrid categories. The most representative monolithic LTMs to be recalled here seem to be the Weibull (W) [2], Gamma (G) and Gamma Weibull (GW). Their failure density functions (FDFs) are
where is the scale parameter, are the shape parameters, is the failure free time parameter and is the step function defined as
Please note that LTM (3) came into being by embedding (1) into (2). It makes (3) more flexible than both (1) and (2) owing to the second shape parameter, namely . However, none of the LTMs in question is sufficiently flexible to be applicable to non-homogeneous populations. It is because they cannot be bimodal. The reader may check it on their own.
The prime example of the hybrid LTM is the compound Weibull (CW) proposed by [3]. Its FDF is given by
where .
As mentioned above, monolithic LTMs are unimodal. In contrast, hybrid LTMs may be bimodal. Of course, they can also be unimodal for (1) or (2), to the great surprise of the analyst, which turns out to be inapplicable to a homogeneous population. Struck by the superiority of (5) over (1)–(3), one must not overlook the fact that (5) has twice as many parameters as (3). Therefore, employing (5), one should have at its disposal much more input data than when employing (3). It is essential to guarantee that the (5) and (3) sets of estimates are at the same level of accuracy. We face the problem of equilibrating flexibility and data consumption.
To familiarize ourselves with the problem, let us consider the results of the following simple, but very instructive, Monte Carlo experiment. A set of input data that comprises one hundred samples each of 30 items was drawn from the exponential population. The population scale parameter was set equal to one. Then the (1)–(3) LTMs were sequentially fitted to the dataset. Parameters were estimated with the maximum-likelihood (ML) method. Table 1 shows standard deviations of scale parameter estimates.

Table 1.
Standard deviation of scale parameter estimate for LTMs.
LTM (3) produced scale parameter estimates of standard deviation more than five times greater than LTM (1) did. The explanation is simple, saying freely, “underfeeding” of the scale parameter took place because the shape parameters have “eaten” most of the input data for their estimation purposes.
In general, no one disputes the need for LTMs to be flexible. On the other hand, does the LTM need to have as many as eight parameters? The LTM below, called the Kumaraswamy transmuted exponentiated additive Weibull (KTEAW) [4], satisfies the mentioned criterion. The cumulative failure function (CFF) of the KTEAW is defined as
where
In general, there are currently two techniques to increase flexibility of LTMs: In the formula of the failure density function, more parameters or the same parameter are embedded in more than one place. The reader is prompted to compare (1) with (2). The Weibull distribution turned out to be a little more flexible than the Gamma distribution in Monte Carlo experiments.
The shape parameter can be called static in the sense that it shapes the LTM identically at each time point. In this paper, we will be able to shape the LTM dynamically owing to the following modification: we replace the shape parameter with the shape function. This is an innovative idea. The subject of modification, of course, will be the Weibull LTM, further named the Weibull distribution with shape function (WDSF). The CFF and FDF take the following forms:
The above FDF is a sum of two components. This is a unique property of the LTM in question. Although born as a monolithic LTM, the WDSF turns out to be a hybrid-like LTM. Please note that WDSF is free of the fraction parameter , which is a data guzzler in (5). As it is easy to guess, we, further in this paper, consider the simplest version of WDSF that involves a linear shape function.
By the end of this section, let us return to the very origins of the reliability domain. Let us recall two books published by reliability pathfinders of that time. These are [5,6]. A device stops working properly, not because the Finger of Fate points it out and says “fail”. It does it because the physical failure process reached its critical level. In the mentioned books, commonly used LTMs have assigned a particular mathematical failure mechanism or process.
For instance, both books assign the Weibull LTM to the model of the weakest link of the chain of elements forming a very long series reliability structure. This point of view appears to be timeless. Therefore, in this paper we have the courage to extend the Weibull LTM assigning the following failure process: As time flows and the wear-out process advances, the series reliability structure steadily elongates, causing device reliability to decrease. Referential mathematical considerations will be presented in Section 3.
The main goal of our work is to complement the literature on the theory of reliability models by introducing a new distribution with a linear shape function, which is a modification of the Weibull LTM. The additional goal of our paper is to define an estimation method that measures the absolute values of the differences between the empirical and theoretical reliability functions (RFs) (see Section 4).
The rest of the paper is organized as follows. Section 2 is devoted to the review of modified Weibull distributions. The properties of the two-version WDSF such as the CFF, RF, FDF, HRF, hazard rate average function (HRAF), quantile (Q) and pseudo-random number generator (PRNG) are described in Section 3. The estimation methods used are described in Section 4. Illustrative examples of the applicability and flexibility of the WDSF are presented in Section 5. Concluding remarks are provided in Section 7. CFF formulas of bimodal LTMs defined with five to eight parameters and having a bathtub HRF are provided in Appendix A. As the popularity of the R environment has increased significantly recently, main properties of the new distribution have been implemented in R software, version 4.3.1 [7]. Their full codes are in Appendix B.
2. A Review of Modified Weibull Distributions
Generalized Weibull distributions can be constructed in many ways. The first, and in our opinion, the most important way is to define distributions with the Weibull distribution as their special case (including a mixture of two or more Weibull variables). Other ways are, i.e., adding a constant to the hazard rate of the Weibull model; transformations (linear, inverse or log) of the Weibull random variable; transformations of the CFF or survival function of the Weibull models in such a way that the new model remains a CFF or survival function. More details can be found in [8].
By reviewing the statistical literature, we found 165 generalized Weibull distributions with 2–8 parameters. Among them, four distributions have a domain different from . They are the reflected Weibull distribution [9] defined for as well as the Log-Weibull [10,11], modified odd Weibull normal [12] and extended odd Weibull normal [13] distributions defined for .
In the rest of this section, we will focus on such generalized Weibull distributions for which the Swedish research’s distribution is their special case. In this case, the large family of generalized Weibull distributions reduces to 71 distributions with three to eight parameters, named by the authors as modified Weibull distributions.
Modified Weibull distributions are divided into six groups, according to the number of their parameters. The list of these models is presented below. Information on hazard rate function shapes is provided in the superscript (1unimodal, 2increasing, 3decreasing, 4bathub). Pseudo-bimodal lifetime models with bathtub hazard rate function are in underline (22 models). Bimodal lifetime models with bathtub hazard rate function are in bold (seven models) and their CFFs are presented in Appendix A.
Group I includes 19 models with three parameters. These are the following: generalized Gamma or Gamma Weibull1–4 [14], generalization of Gamma Weibull1–4 [15], exponentiated Weibull1–4 [16], generalized Weibull1–4 [17], exponentiated Weibull1–4 [18], power generalized Weibull1–4 [19], modified Weibull extension2–4 [20], modified Weibull2–4 [21], Marshall–Olkin Extended Weibull1–4 [22], extended Weibull type1,4 [23], generalized power Weibull2–4 [24], Extended Weibull1–4 [25], Sarhan and Zaindin’s Modified Weibull2,3 [26], Weibull Geometric1–4 [27], transmuted Weibull1–4 [28], complementary Weibull geometric1–4 [29], Alpha power Weibull1–4 [30], MIT Weibull1–4 [31] and Semi-Modified Alpha Power Weibull Distribution [32].
Group II includes 18 models with four parameters. These are the following: four-parameter generalized Gamma1–4 [33], additive Weibull2–4 [34], Generalized Modified Weibull1,2,4 [35], Kumaraswamy Weibull1–4 [36], Exponentiated Generalized Gamma1,4 [37], exponentiated modified Weibull1–4 [38], Transmuted modified Weibull2 [39], Exponentiated transmuted Weibull2–4 [40], Generalized Weibull-Exponential1–3 [41], Weibull Lomax2,3 [42], generalized power generalized Weibull1–4 [43], Generalization of Generalized Gamma1–4 [44], Weibull Lomax2–4 [45], additive Chen-Weibull2,4 [46], Poisson modified Weibull1–4 [47], modified power generalized Weibull1–4 [48], Generalized New Extended Weibull [49] and new modified exponentiated Weibull (NMEW)2,4 [50].
Group III includes 27 models with five parameters. These are the following: Beta modified Weibull1–4 [51], Kumaraswamy generalized Gamma1–4 [52], beta generalized Weibull1–4 [53], Transmuted Exponentiated Modified Weibull2,3 [54], Beta Generalized Gamma1–4 [55], transmuted additive Weibull2,4 [56], Exponentiated Kumaraswamy Weibull1–4 [57], new modified Weibull2–4 [58], Kumaraswamy modified Weibull1–4 [59], beta transmuted Weibull1–3 [60], McDonald Weibull1–4 (McW) [61], Exponentiated Transmuted Modified Weibull1,2,4 [62], exponentiated generalized modified Weibull2,4 [63], Gamma generalized modified Weibull [64], generalized modified Weibull geometric4 [65], additive modified Weibull2–4 [66], transmuted exponentiated Weibull geometric1–4 [67], transmuted new generalized Weibull2–3 [68], Burr XII modified Weibull1–4 [69], log-logistic modified Weibull1,2,4 [70], Kumaraswamy alpha power Weibull1–4 [71], exponentiated additive Weibull1–4 (EAW) [72,73], generalized extended exponential Weibull1–4 [74], generalized Weibull generalized exponential1–2 [75], new generalized modified Weibull1–4 [76] and improved modified Weibull3,4 [77].
Group IV includes seven models with six parameters. These are the following: the mixture of two Weibull4 [3], McDonald modified Weibull1–4 (McMW) [78], McDonald extended Weibull1–4 (McEW) [79], Additive Weibull log logistic1–4 [80], underbarBeta exponentiated modified Weibull1–4 [81], exponentiated power generalized Weibull binomial1–4 [82], and McDonald Generalized Power Weibull1–4 (McGPW) [83].
Concluding the review of modified Weibull distributions, we would like to mention two distributions with seven and eight parameters. The Kumaraswamy transmuted exponentiated modified Weibull1–4 (KTEMW) with 54 special cases forms group V [84]. The Kumaraswamy transmuted exponentiated additive Weibull1–4 (KTEAW) [4] with 79 special cases (including KTEMW) forms group VI.
3. Properties of Weibull Distribution with Shape Function
The main goal of the paper is to present the two-version Weibull distribution with the shape function previously denoted as the WDSF. This section describes its properties such as the CFF, RF, FDF, HRF, hazard rate average function (HRAF), quantile (Q), and pseudo-random number generator (PRNG). Both versions of our model will be used in Section 5.
We assume that the device of our interest has a long series reliability structure. It makes the real lifetime distribution close to the Weibull distribution. The formula below is the Weibull LTM with the elongation coefficient of the device’s reliability structure.
We impose two weak conditions on with and . Owing to such weak conditions, a wide scope opens itself for defining functions not only of reasonable forms but also of monstrous ones. One reasonable form is because it introduces only one parameter into the Weibull LTM and therefore equilibrates flexibility and data consumption. Thus, we get
Definition 1.
Definition 2.
Let from (7) or (8) be a linear shape function with three parameters given by then the CFF of the Weibull distribution with linear shape function in the second version (WDSFII) is defined as
where , is the failure free time parameter, is the step function (4) and . If , then we get the first version of our proposal.
Proposition 1.
The RFs of the WDSFI and WDSFII are defined, respectively, as
Proof of Proposition 1.
The proof based on the RF definition is trivial. □
It is interesting to compare the and Weibull models on the Weibull probability paper. Taking the logarithm of both sides (11) twice, we get
Let then
Figure 1 presents the Weibull probability paper with transformed reliability functions plotted on it. The figure is intended to visualize similarity and dissimilarity between the WDSFI and Weibull models. One may easily notice the following:
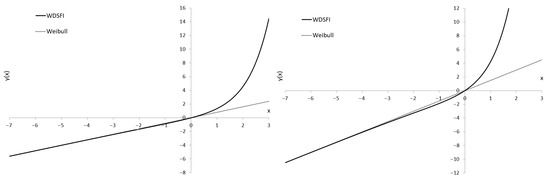
Figure 1.
Weibull probability paper when (left) and (right).
- There may exist even relatively long-time intervals inside in which the functions are indistinguishable. It lasts as long as b is much greater as .
- Both reliability functions cross a horizontal line in the same point.
- As time passes, functions slowly but steadily part. This is the region of the second mode of the WDSFI lifetime model.
Proposition 2.
The FDFs of the WDSFI and WDSFII are respectively given by
where .
Proof of Proposition 2.
By computing the derivatives based on (9) and (10) regarding the lifetime t, we easily obtain Formulas (13) and (14). Recall that and the Formulas (13) and (14) are non-negative.
Let . has a maximum value of 0.135335 for .
Let ; then we have from (13)
Let , then we have from (14)
□
Figure 2 shows the RF of the WDSFI and WDSFII. Pseudo-bimodality or bimodality is visible here. The R codes (R Core Team 2021) for calculating the RF values of the WDSFI and WDSFII are provided in Appendix B.
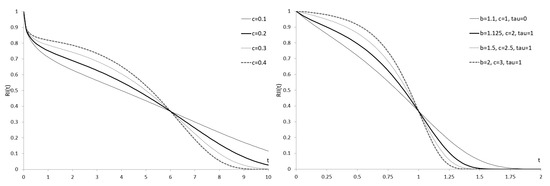
Figure 2.
RF of the WDSFI with the parameter vector (left) and the RF of WDSFII with the parameter vector (right).
Figure 3 shows the FDF of the WDSFI and WDSFII. We see the pseudo-bimodality (on the left) and bimodality (on the right). The R codes for calculating the FDF values of WDSFI and WDSFII are provided in Appendix B.
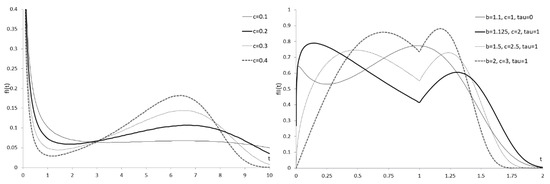
Figure 3.
FDF of the WDSFI with the parameter vector (left) and the FDF of WDSFII with the parameter vector (right).
The WDSFII with FDF given by (14) is identifiable in the parameter space . This identifiability is apparent at the first glance. Particular parameters of the WDSFII lifetime model have very strictly prescribed roles to impact failure density function. It causes that, for example, an impact of the scale parameter in no way can be compensated with shape and location parameters. In turn, it causes that it is impossible to obtain the same two values of the density function for two different sets of parameters. It is a meaningful fact that during over forty years of my activity in the reliability domain, I never encountered any validation of the Weibull lifetime model. Despite not being in any way validated, the model has for decades kept itself on the second place in the ranking of applicability.
Proposition 3.
The HRFs of the WDSFI and WDSFII have, respectively, forms
Proof of Proposition 3.
The proof based on the HRF definition is trivial. □
Figure 4 shows the bathtub HRF of the WDSFI and WDSFII. The curves flatten as c decreases. The R codes for calculating the HRF values of WDSFI and WDSFII are provided in Appendix B.
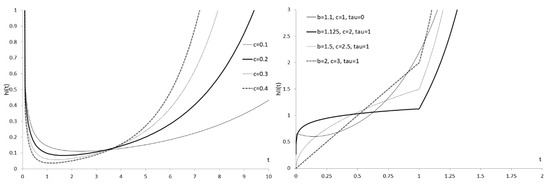
Figure 4.
HRF of the WDSFI with the parameter vector (left) and the HRF of WDSFII with the parameter vector (right).
Proposition 4.
The HRAFs of the WDSFI and WDSFII are, respectively, defined as [85]
Proof of Proposition 4.
Figure 5 shows the bathtub HRAF of the WDSFI and WDSFII. HRAF curves are flatter than HRF curves. The R codes for calculating the HARF values of WDSFI and WDSFII are provided in Appendix B.
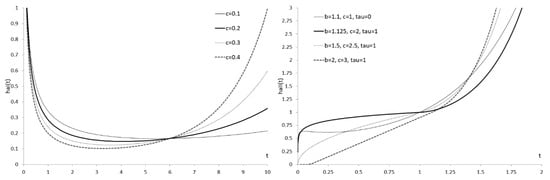
Figure 5.
HRAF of the WDSFI with the parameter vector (left) and the HRAF of WDSFII with the parameter vector (right).
Figure 6 shows the logarithm of theoretical and empirical HRAFs for the WDSFI and sample size .
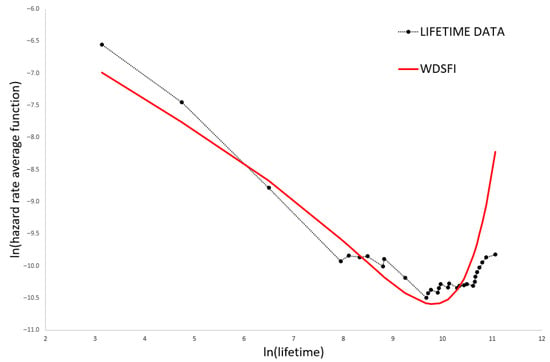
Figure 6.
Logarithm of theoretical and empirical HRAF for WDSFI and sample size .
Proposition 5.
Let . The Qs and of the WDSFI and WDSFII are, respectively, solutions of the equations
Proposition 6.
Let , and follow the WDSFI and WDSFII, respectively. We can obtain and in two ways.
- The first way. The and are respectively solutions of the equations
- The second way. The algorithm for obtaining the and is as follows:
- 1.
- Let , , .
- 2.
- Let
- 3.
- , .
- 4.
- If , then go to step 2.
- 5.
- Return , .
Proof of Proposition 6.
In this passage, we focus on Figure 7 and Figure 8 to answer such questions: what is a small sample used for and what is a large one used for? Conventionally, small samples are those of size . Analysts of lifetime data as a rule deal with small samples. Thus, Figure 7 presents the empirical and theoretical reliability functions for sample size n = 30. This figure impresses on readers how far empirical points may depart from the actual reliability function. Figure 8 presents the empirical and theoretical reliability functions for sample size n = 1000. Empirical points practically do not depart from the actual reliability function. This figure impresses on readers that the Weibull-sf random number generator works satisfactorily.
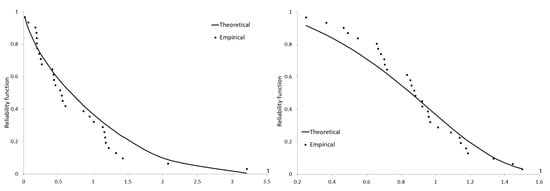
Figure 7.
Empirical and theoretical reliability functions when (left) and (right). Sample size .
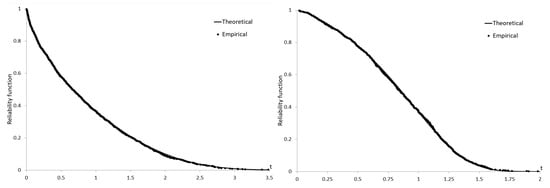
Figure 8.
Empirical and theoretical reliability functions when (left) and (right). Sample size .
4. Estimation Methods
An additional goal for this article is outlined in this section.
Looking through the literature searching for distributions that are modifications of the Weibull distribution, we find that the most dominant method of parameter estimation is the maximum-likelihood (ML) method. However, the question remains whether this choice is right. The younger the paper, the more often the parameters are estimated using other methods, e.g., the ordinary least-squares (LS) and weighted least-squares (WLS) ones; see, e.g., [48,86,87,88,89].
What relates to the WDSFII is that the main fraction of the probability mass is concentrated on the “contractual” end of the distribution. Thus, for small and medium values of t, the Weibull and WDSFII are practically indistinguishable in terms of the reliability or density functions. Censoring appears to be inapplicable to the Weibull-sf except in some special cases. This is the reason why in the reviewed paper a problem of censoring has been omitted. Please notice that this is the same inconvenient situation as with the compound Weibull lifetime model. Finally, one should not marvel at this because the WDSFII has been designed as a “lighter” version of the compound Weibull lifetime model.
Let be parameter vectors and be a random sample of size n from the WDSFI and WDSFII. To estimate unknown values of parameters, we use estimation methods such as the ML, LS, WLS and least absolute values (LAWs). The LAW, which is the first additional goal of the work, measures the absolute values of the differences between the empirical and theoretical RFs.
The likelihood functions (LFs) of the WDSFI and WDSFII, based on (13) and (14), are given by, respectively,
where .
The log-likelihood functions (LLFs) of the WDSFI and WDSFII, based on (25) and (26), are defined as, respectively,
Formulas have complex forms, so in practice we maximize the LF (27) and (28) or the LLFs (29) and (30) to obtain the ML estimates.
To obtain the OLS estimates of the WDSFI and WDSFII parameters, we minimize the following objective functions, respectively.
To obtain the WLS estimates of the WDSFI and WDSFII parameters, we minimize the following objective functions, respectively.
Let be the empirical RF. To obtain the LAW estimates of the WDSFI and WDSFII parameters, we minimize the following objective functions, respectively.
The following three books with many real-world data examples are particularly interesting. The first one is the Lai and Xie’s book [90]. The analysed examples are characterized by sample sizes with . The second one is the Lee and Wang’s book [91]. The analysed examples are characterized by sample sizes with . The third one is the Nelson’s book [92]. The analysed examples are characterized by sample sizes with .
Based on the above sample size data, a simulation study was performed with samples with a size of . The samples were drawn from the WDSFII with , where . To obtain highly accurate parameter estimates, the optimization procedure was run times with random initial values for and for c and for . Our estimates for a given sample are the values that minimize (29), (31) and (33) and maximize (25) or (27).
The biases (Bs) and the root mean squared errors (RMSEs) of the WDSFII estimates are shown in Table 2, Table 3 and Table 4. We observe that as the sample size increases, the estimates approach the true values, which means that the estimates are consistent. Bs and RMSE values are the lowest for . The Bs are the largest for ( and (. The RMSEs are the highest for . The Bs increase with the value of c for . The RMSEs increase with the value of c for and decrease for . The Bs and RMSEs are the lowest (highest) for the ML (LAW) method associated with and . The ML method is not suitable for estimating scale parameters. In this case, the lowest Bs and RMSE values are for the WLS method.

Table 2.
Biases and RMSEs of the estimates obtained using various methods (M). Samples of size n were drawn from WDSFII with .

Table 3.
Biases and RMSEs of the estimates obtained using various methods (M). Samples of size n were drawn from WDSFII with .

Table 4.
Biases and RMSEs of the estimates obtained using various methods (M). Samples of size n were drawn from WDSFII with .
To examine the accuracy of the coverage probability of the asymptotic confidence intervals (CIs), another simulation study was performed with samples using sample sizes of . The study focused on the parameters and samples drawn from the WDSFII with and . The coverage probabilities of the obtained CIs for reported in Table 5 are very close to the nominal level. The results suggested that the obtained standard errors and hence the asymptotic CIs are reliable.

Table 5.
Coverage probability for the standard asymptotic CIs. Samples of size n were drawn from WDSFII with and .
5. Applications
In this section, we illustrate the importance of the WDSFI and WDSFII distributions using three real-life datasets. The new models are compared with bimodal LTMs, characterized by unimodal, increasing, decreasing and bathub HRF, such as exponentiated additive Weibull, McDonald Weibull, McDonald modified Weibull, McDonald extended Weibull, McDonald generalized Power Weibull, Compound Weibull, Kumaraswamy transmuted exponentiated modified Weibull, and Kumaraswamy transmuted exponentiated additive Weibull. CFFs of the mentioned models are presented in “Appendix A”.
All calculations for comparison were performed in R software, version 4.3.1. To avoid local maxima, the optimization procedure was run times with random starting model parameter values that are widely scattered in the parameter space. The final parameter estimates are those parameter values that best maximize the log-likelihood function. AIC, BIC, HQIC criteria and the Kolmogorov–Smirnov (KS) statistic are calculated. Let us remind the reader that
where l is the log-likelihood function, n is the sample size and p is the number of model parameters. The KS statistic is given by
5.1. Failure Times of Devices
As the first real dataset, 50 failure times of the devices [1,90] presented in Appendix C are used. ML estimates (MLEs), AIC, BIC, HQIC and KS values are given in Table 6. Better values are marked in bold. Figure 9 shows the estimated FDFs for compared models. The WDSFII model is more appropriate based on information criteria and KS values. The adaptability of the WDSFII model can also be observed in Figure 9.

Table 6.
MLE, IC and KS values of models fitted to 50 failure times of devices.
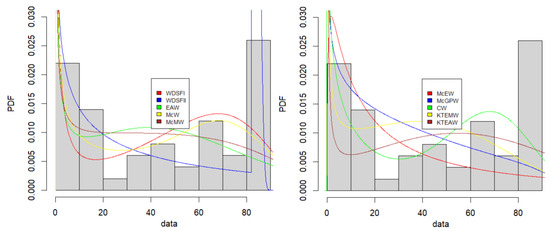
Figure 9.
Estimated FDFs for compared models for the failure times of devices.
5.2. 500 MW Generators
As the second real dataset, 36 times to the first failure of 500 MW generators collected over a 6-year period [90,93], presented in Appendix C, are used. ML estimates (MLE), AIC, BIC, HQIC and KS values are given in Table 7. The WDSFI model is more appropriate based on information criteria. The adaptability of the WDSFI model can also be observed in Figure 10.

Table 7.
MLE, IC and KS values of models fitted to 36 times to the first failure of 500 MW generators.
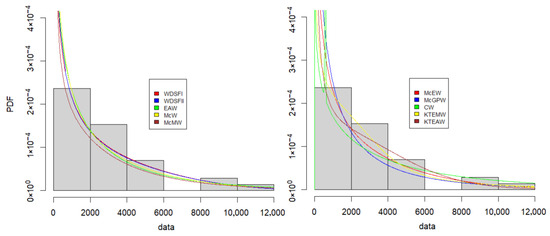
Figure 10.
Estimated PDFs for compared models for the times to the first failure of 500 MW generators.
6. Discussion
The results obtained in this study demonstrate that the proposed WDSFI and WDSFII models provide a flexible and accurate framework for modelling full-life-cycle data with a wide range of hazard ratio shapes, including monotonic, bathtub, and pseudobimodal patterns. Parameter estimation using OLS, WLS, and LAW methods yielded consistent results, with the LAW approach often demonstrating improved robustness in the presence of irregularities in the empirical reliability function.
From the perspective of previous research, our findings are consistent with, and even extend, previous work on generalizations of the Weibull distribution and its modified forms. Similar to these studies, we observed that introducing additional parameters can significantly improve model fit, allowing for more complex hazard ratio shapes. However, the WDSFI and WDSFII models differ in structure, offering better adaptation to datasets where existing models still exhibit systematic biases.
Regarding our working hypotheses, empirical analyses support the assumption that additional flexibility in scale structure and distribution shape leads to better data representation without sacrificing interpretability. The models’ performance on real-world datasets suggests they may be particularly well-suited for applications in engineering reliability, biomedical survival analysis, and materials degradation studies, where multiphase failure mechanisms are present.
In a broader context, these findings contribute to the growing literature on extended-life models and highlight the continuing need for statistical tools capable of capturing various hazardous behaviours. Such tools are crucial for risk assessment, preventive maintenance planning, and decision-making in safety-critical systems.
Future research directions include te following:
- Extending the proposed models to more precisely process censored, truncated, and interval data.
- Investigation of Bayesian inference methods to incorporate a priori information and quantify uncertainty.
- Development of multivariate or concatenated life-cycle models to capture inter-component dependencies.
- Incorporation of models into regression frameworks, such as proportional hazards or accelerated failure time models, to assess the impact of interdependent variables.
Overall, this study confirms the practical value of the WDSFI and WDSFII models and opens promising avenues for both theoretical development and applied research in reliability and survival analysis.
7. Conclusions
This article presents a three- and four-parameter flexible modified Weibull LTM called the Weibull distribution with a linear shape function. An innovative idea is to replace the Weibull shape parameter with a shape function. An estimation method based on theoretical and empirical reliability functions is proposed. An extensive literature review was performed, considering the modalities and shapes of the risk rate function. The simulation study is carried out using ML, LS, WLS and LAW methods. Furthermore, to check the suitability and flexibility, the new LTMs are validated with two real datasets and compared with other bimodal LTMs with a bathtub HRF.
The paper shows that even a three-parameter distribution can compete in data modelling with LTM distributions that have two or even almost three times more parameters.
Regarding further research, there is a lot to be accomplished. It appears that there is only one way to succeed—laborious numerical experiments. Research is to be carried out in two directions. The first is to strive to elongate and flatten the central segment of the hazard rate function. To do so, replace a linear shape function with a nonlinear one. Theoretically, any function that is strictly increasing and convex downward may be useful, but probably to different degrees. The second is to carry out Monte Carlo experiments to assess the accuracy of the parameter estimation.
Author Contributions
Conceptualization, P.S. and A.D.; methodology, P.S. and A.D.; software, P.S.; validation, P.S.; formal analysis, P.S. and A.D.; investigation, P.S.; resources, P.S. and A.D.; data curation, P.S.; writing—original draft preparation, P.S.; writing—review and editing, P.S. and A.D.; visualization, P.S.; supervision, A.D.; project administration, P.S. and A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
R codes for the RF, CFF, FDF, HRF, HRAF, quantile and pseudo-random number generator are available at www.github.com/PiotrSule/WDSF (accessed on 1 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFF | Cumulative Failure Function |
| CW | Compound Weibull |
| EAW | Exponentiated Additive Weibull |
| FDF | Failure Density Function |
| G | Gamma |
| GW | Gamma Weibull |
| HRAF | Hazard Rate Average Function |
| HRF | Hazard Rate Function |
| KTEAW | Kumaraswamy Transmuted Exponentiated Additive Weibull |
| KTEMW | Kumaraswamy Transmuted Exponentiated Modified Weibull |
| LAW | Least Absolute Weighted |
| LLF | Log-Likelihood Function |
| LTM | Lifetime Model |
| McGPW | McDonald Generalized Power Weibull |
| McMW | McDonald Modified Weibull |
| McW | McDonald Weibull |
| ML | Maximum Likelihood |
| NMEW | New Modified Exponentiated Weibull |
| OLS | Ordinary Least Squares |
| PRNG | Pseudo-Random Number Generator |
| Q | Quantile |
| RF | Reliabity Function |
| W | Weibull |
| WDSF | Weibull Distribution With Shape Function |
| WLS | Weighted Least Squares |
Appendix A
Let be the model parameters and
- Beta function: ,
- Lower incomplete beta function: ,
- Regularized incomplete beta function: .
Below are the CFFs of bimodal LTMs with unimodal, increasing, decreasing and bathub HRF. The number of model parameters is given in parentheses.
- Exponentiated additive Weibull (5)
- McDonald Weibull (5)
- McDonald modified Weibull (6)
- McDonald extended Weibull (6)
- McDonald generalized Power Weibull (6)
- Compound Weibull (6)
- Kumaraswamy transmuted exponentiated modified Weibull (8)
- Kumaraswamy transmuted exponentiated additive Weibull (8)
Appendix B
R codes for the RF, CFF, FDF, HRF, HRAF, quantile and pseudo-random number generator are as follows:
# step function
SF=function(x) return(ifelse(x>=0,1,0))
# RF of WDSF_I
sWDSF1=function(t,a,b,c){
u=b+c*t
t1=t/a
w=b/a/c-0.135335
if (t1>0&a>0&b>0&c>0&w>=0) res=exp(-t1^u)
else res=‘‘error’’
return(res)}
# RF of WDSF_II
sWDSF2=function(t,a,b,c,Ä){
t1=t/a
u1=b+c*(t-Ä)*SF(t-Ä)
u2=t1^u1
w=(b-c*Ä)/a/c-0.135335
if (t1>0&a>0&b>0&c>0&Ä>=0&w>=0) res=exp(-u2)
else res=‘‘error’’
return(res)}
# CFF of WDSF_I
pWDSF1=function(t,a,b,c){
t1=t/a
w=b/a/c-0.135335
if (t1>0&a>0&b>0&c>0&w>=0) res=1-exp(-t1^(b+c*t))
else res=‘‘error’’
return(res)}
# CFF of WDSF_II
pWDSF2=function(t,a,b,c,Ä){
t1=t/a
w=(b-c*Ä)/a/c-0.135335
if (t1>0&a>0&b>0&c>0&Ä>=0&w>=0) res=1-exp(-t1^(b+c*(t-Ä)*
SF(t-Ä)))
else res=‘‘error’’
return(res)}
# FDF of WDSF_I
dWDSF1=function(t,a,b,c){
u=b+c*t
t1=t/a
w=b/a/c-0.135335
if (t1>0&a>0&b>0&c>0&w>=0) res=exp(-t1^u)*t1^(u-1)*((b/a+c*t1)+
t1*c*log(t1))
else res=‘‘error’’
return(res)}
# FDF of WDSF_II
dWDSF2=function(t,a,b,c,Ä){
t1=t/a
u1=b+c*(t-Ä)*SF(t-Ä)-1
u2=t1^u1
w=(b-c*Ä)/a/c-0.135335
if (t1>0&a>0&b>0&c>0&Ä>=0&w>=0) res=exp(-u2*t1)*u2*((u1+1)/
a+c*t*SF(t-Ä)/a*log(t1))
else res=‘‘error’’
return(res)}
# HRF of WDSF_I
hWDSF1=function(t,a,b,c){
u=b+c*t
t1=t/a
w=b/a/c-0.135335
if (t1>0&a>0&b>0&c>0&w>=0) res=t1^u*(u/t+c*log(t1))
else res=‘‘error’’
return(res)}
# HRF of WDSF_II
hWDSF2=function(t,a,b,c,Ä){
t1=t/a
u1=b+c*(t-Ä)*SF(t-Ä)
u2=t1^u1
w=(b-c*Ä)/a/c-0.135335
if (t1>0&a>0&b>0&c>0&Ä>=0&w>=0) res=(u1/t+c*SF(t-Ä)*
log(t1))*u2
else res=‘‘error’’
return(res)}
# HRAF of WDSF_I
haWDSF1=function(t,a,b,c){
u=b+c*t
t1=t/a
w=b/a/c-0.135335
if (t1>0&a>0&b>0&c>0&w>=0) res=t1^u/t
else res=‘‘error’’
return(res)}
# HRAF of WDSF_II
haWDSF2=function(t,a,b,c,Ä){
t1=t/a
u1=b+c*(t-Ä)*SF(t-Ä)
u2=t1^u1
w=(b-c*Ä)/a/c-0.135335
if (t1>0&a>0&b>0&c>0&Ä>=0&w>=0) res=u2/t
else res=‘‘error’’
return(res)}
# quantile of WDSF_I
qWDSF1=function(p,a,b,c){
u1=function(t,a,b,c) 1-exp(-(t/a)^(b+c*t))-p
return(uniroot(u1, c(0,1e05), tol = 0.000001,
a=a, b=b, c=c)$root)}
# quantile of WDSF_II
qWDSF2=function(p,a,b,c,Ä){
u2=function(t,a,b,c,Ä) 1-exp(-(t/a)^(b+c*SF(t-Ä)*
(t-Ä)))-p
return(uniroot(u2, c(0,1e05), tol = 0.000001, a=a, b=b,
c=c,
Ä=Ä)$root)}
# pseudo-random number generator of WDSF_I
rWDSF1=function(n,a,b,c){
x=numeric(n)
for (i in 1:n){
t=0;te=1
R=runif(1,0,1)
while (abs(te)>1e-10){
temp=t
t=a*(-log(R))^(1/(b+c*t))
te=abs(t-temp)
}
x[i]=t
}
return(x)}
# pseudo-random number generator of WDSF_II
rWDSF2=function(n,a,b,c,Ä){
x=numeric(n)
for (i in 1:n){
t=0;te=1
R=runif(1,0,1)
while (abs(te)>1e-10){
temp=t
t=a*(-log(R))^(1/(b+c*SF(t-)*(t-)))
te=abs(t-temp)
}
x[i]=t
}
return(x)}
Appendix C
- Dataset of failure times of 50 devices: 0.1, 0.2, 1, 1, 1, 1, 1, 2, 3, 6, 7, 11, 12, 18, 18, 18, 18, 18, 21, 32, 36, 40, 45, 46, 47, 50, 55, 60, 63, 63, 67, 67, 67, 67,72, 75, 79, 82, 82, 83, 84, 84, 84, 85, 85, 85, 85, 85, 86, 86.
- Dataset of 36 times to the first failure of 500 MW generators collected over a 6-year period: 58, 70, 90, 105, 113, 121, 153, 159, 224, 421, 570, 596, 618, 834, 1019, 1104, 1497, 2027,2234, 2372, 2433, 2505, 2690, 2877, 2879, 3166, 3455, 3551, 4378, 4872, 5085, 5272, 5341,8952, 9188, 11399.
References
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Kao, J.H. A graphical estimation of mixed Weibull parameters in life-testing of electron tubes. Technometrics 1959, 1, 389–407. [Google Scholar] [CrossRef]
- Nofal, Z.M.; Afify, A.Z.; Yousof, H.M.; Granzotto, D.C.; Louzada, F. Kumaraswamy transmuted exponentiated additive Weibull distribution. Int. J. Stat. Probab. 2016, 5, 78–99. [Google Scholar] [CrossRef]
- Gertsbakh, I.; Kordonskiy, K.B. Models of Failure; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kao, J.H.K. Reliability Handbook. Part 2; Ireson, W.G., Ed.; McGraw-Hill: Toronto, ON, Canada; London, UK; Sydney, Australia, 1966. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 5 August 2025).
- Lai, C.D. Generalized Weibull Distributions; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Cohen, A.C. The reflected Weibull distribution. Technometrics 1973, 15, 867–873. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar] [CrossRef]
- Almalki, S.J.; Nadarajah, S. Modifications of the Weibull distribution: A review. Reliab. Eng. Syst. Saf. 2014, 124, 32–55. [Google Scholar] [CrossRef]
- Chesneau, C.; El Achi, T. Modified odd Weibull family of distributions: Properties and applications. J. Indian Soc. Probab. Stat. 2020, 21, 259–286. [Google Scholar] [CrossRef]
- Alizadeh, M.; Altun, E.; Afify, A.Z.; Ozel, G. The extended odd Weibull-G family: Properties and applications. Commun. Fac. Sci. Univ. Ankara Ser. A1 Math. Stat. 2018, 68, 161–186. [Google Scholar] [CrossRef]
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Stacy, E.W.; Mihram, G.A. Parameter estimation for a generalized gamma distribution. Technometrics 1965, 7, 349–358. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Kollia, G.D. Generalized Weibull family: A structural analysis. Commun. Stat. Theory Methods 1994, 23, 1149–1171. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K.; Freimer, M. The exponentiated Weibull family: A reanalysis of the bus-motor-failure data. Technometrics 1995, 37, 436–445. [Google Scholar] [CrossRef]
- Bagdonavicius, V.; Nikulin, M. Accelerated Life Models: Modeling and Statistical Analysis; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar] [CrossRef]
- Xie, M.; Tang, Y.; Goh, T.N. A modified Weibull extension with bathtub failure rate function. Reliab. Eng. Syst. Saf. 2002, 76, 279–285. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M.; Murthy, D.N.P. A modified Weibull distribution. IEEE Trans. Reliab. 2003, 52, 33–37. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Hussaini, E.K.; Al-Jarallah, R.A. Marshall–Olkin extended Weibull distribution and its application to censored data. J. Appl. Stat. 2005, 32, 1025–1034. [Google Scholar] [CrossRef]
- Al-Saleh, J.A.; Agarwal, S.K. Extended Weibull type distribution and finite mixture of distributions. Stat. Methodol. 2006, 3, 224–233. [Google Scholar] [CrossRef]
- Nikulin, M.; Haghighi, F. A chi-squared test for the generalized power Weibull family for the head-and-neck cancer censored data. J. Math. Sci. 2006, 133, 1333–1341. [Google Scholar] [CrossRef]
- Zhang, T.; Xie, M. Failure data analysis with extended Weibull distribution. Commun. Stat. Simul. Comput. 2007, 36, 579–592. [Google Scholar] [CrossRef]
- Sarhan, A.M.; Zaindin, M. Modified Weibull distribution. Appl. Sci. 2009, 11, 123–136. [Google Scholar]
- Barreto-Souza, W.; de Morais, A.L.; Cordeiro, G.M. The Weibull-geometric distribution. J. Stat. Comput. Simul. 2011, 81, 645–657. [Google Scholar] [CrossRef]
- Aryal, G.; Tsokos, C.P. Transmuted Weibull distribution: A generalization of the Weibull probability distribution. Eur. J. Pure Appl. Math. 2011, 4, 89–102. [Google Scholar]
- Tojeiro, C.; Louzada, F.; Roman, M.; Borges, P. The complementary Weibull geometric distribution. J. Stat. Comput. Simul. 2014, 84, 1345–1362. [Google Scholar] [CrossRef]
- Nassar, M.; Alzaatreh, A.; Mead, M.; Abo-Kasem, O. Alpha power Weibull distribution: Properties and applications. Commun. Stat. Theory Methods 2017, 46, 10236–10252. [Google Scholar] [CrossRef]
- Lone, M.A.; Dar, I.H.; Jan, T.R. A new family of generalized distributions with an application to Weibull distribution. Thail. Stat. 2024, 22, 1–16. [Google Scholar]
- Azam, S.; Iqbal, M.; Zaman, Q.; Ali, M. Semi Modified Alpha Power Weibull Distribution and Its Statistical Properties. Metall. Mater. Eng. 2025, 31, 104–113. [Google Scholar]
- Harter, H.L. Maximum-likelihood estimation of the parameters of a four-parameter generalized gamma population from complete and censored samples. Technometrics 1967, 9, 159–165. [Google Scholar] [CrossRef]
- Xie, M.; Lai, C.D. On the increase of the expected lifetime by parallel redundancy. Asia-Pac. J. Oper. Res. 1996, 13, 171. [Google Scholar]
- Carrasco, J.M.; Ortega, E.M.; Cordeiro, G.M. A generalized modified Weibull distribution for lifetime modeling. Comput. Statist. Data Anal. 2008, 53, 450–462. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Franklin Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Silva, G.O. The exponentiated generalized gamma distribution with application to lifetime data. J. Stat. Comput. Simul. 2011, 81, 827–842. [Google Scholar] [CrossRef]
- Elbatal, I. Exponentiated Modified Weibull distribution. Econ. Qual. Control 2011, 26, 189–200. [Google Scholar] [CrossRef]
- Khan, M.S.; King, R. Transmuted modified Weibull distribution: A generalization of the modified Weibull probability distribution. Eur. J. Pure Appl. Math. 2013, 6, 66–88. [Google Scholar]
- Ebraheim, A.N.E. Exponentiated transmuted Weibull distribution: A generalization of the Weibull distribution. Int. J. Math. Comput. Sci. 2014, 8, 903–911. [Google Scholar]
- Salem, H.M.; Selim, M.A. The generalized Weibull-exponential distribution: Properties and applications. Int. J. Stat. Appl. 2014, 4, 102–112. [Google Scholar]
- Tahir, M.H.; Cordeiro, G.M.; Mansoor, M.; Zubair, M. The Weibull-Lomax distribution: Properties and applications. Hacet. J. Math. Stat. 2015, 44, 455–474. [Google Scholar] [CrossRef]
- Selim, M.A. The generalized power generalized Weibull distribution: Properties and applications. arXiv 2018, arXiv:1807.10763. [Google Scholar]
- Shanker, S.; Shukla, K.K. A generalization of generalized gamma distribution. Int. J. Comput. Theor. Stat. 2019, 6, 33–42. [Google Scholar]
- Osagie, S.A.; Osemwenkhae, J.E. Lomax-Weibull distribution with properties and applications in lifetime analysis. Int. J. Math. Sci. Optim. Theory Appl. 2020, 2020, 718–732. [Google Scholar]
- Thanh Thach, T.; Briš, R. An additive Chen-Weibull distribution and its applications in reliability modeling. Qual. Reliab. Eng. Int. 2021, 37, 352–373. [Google Scholar] [CrossRef]
- Abd El-Monsef, M.M.E.; Marei, G.A.; Kilany, N.M. Poisson modified Weibull distribution with inferences on stress-strength reliability model. Qual. Reliab. Eng. Int. 2022, 38, 2649–2669. [Google Scholar] [CrossRef]
- Shama, M.S.; Alharthi, A.S.; Almulhim, F.A.; Gemeay, A.M.; Meraou, M.A.; Mustafa, M.S.; Aljohani, H.M. Modified generalized Weibull distribution: Theory and applications. Sci. Rep. 2023, 13, 12828. [Google Scholar] [CrossRef]
- Al-Moisheer, A.S.; Sultan, K.S.; Radwan, H.M. A novel adaptable Weibull distribution and its applications. Axioms 2025, 14, 490. [Google Scholar] [CrossRef]
- Rangoli, A.M.; Talawar, A.S.; Agadi, R.P.; Sorganvi, V. New modified exponentiated Weibull distribution: A survival analysis. Cureus 2025, 17, e77347. [Google Scholar] [CrossRef]
- Silva, G.O.; Ortega, E.M.; Cordeiro, G.M. The beta modified Weibull distribution. Lifetime Data Anal. 2010, 16, 409–430. [Google Scholar] [CrossRef] [PubMed]
- Pascoa, M.A.P.; Ortega, E.M.M.; Cordeiro, G.M.; Paranaíba, P.F. The Kumaraswamy-generalized gamma distribution with application in survival analysis. Stat. Methodol. 2011, 8, 411–433. [Google Scholar] [CrossRef]
- Singla, N.; Jain, K.; Sharma, S.K. The beta generalized Weibull distribution: Properties and applications. Reliab. Eng. Syst. Saf. 2012, 102, 5–15. [Google Scholar] [CrossRef]
- Eltehiwy, M.; Ashour, S. Transmuted exponentiated modified Weibull distribution. Int. J. Basic Appl. Sci. 2013, 2, 258–269. [Google Scholar] [CrossRef][Green Version]
- Cordeiro, G.M.; Castellares, F.; Montenegro, L.C.; de Castro, M. The beta generalized gamma distribution. Statistics 2013, 47, 888–900. [Google Scholar] [CrossRef]
- Elbatal, I.; Aryal, G. On the transmuted additive Weibull distribution. Austrian J. Stat. 2013, 42, 117–132. [Google Scholar] [CrossRef]
- Eissa, F.H.; Abdulaziz, R.K. The exponentiated Kumaraswamy–Weibull distribution with application to real data. Int. J. Stat. Probab. 2017, 6, 167–182. [Google Scholar] [CrossRef]
- Almalki, S.J.; Yuan, J. A new modified Weibull distribution. Reliab. Eng. Syst. Saf. 2013, 111, 164–170. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Silva, G.O. The Kumaraswamy modified Weibull distribution: Theory and applications. J. Stat. Comput. Simul. 2014, 84, 1387–1411. [Google Scholar] [CrossRef]
- Pal, M.; Tiensuwan, M. The beta transmuted Weibull distribution. Austrian J. Stat. 2014, 43, 133–149. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Hashimoto, E.M.; Ortega, E.M. The McDonald Weibull model. Statistics 2014, 48, 256–278. [Google Scholar] [CrossRef]
- Pal, M.; Tiensuwan, M. Exponentiated transmuted modified Weibull distribution. Eur. J. Pure Appl. Math. 2015, 8, 1–14. [Google Scholar]
- Aryal, G.; Elbatal, I. On the exponentiated generalized modified Weibull distribution. Commun. Stat. Appl. Methods 2015, 22, 333–348. [Google Scholar] [CrossRef]
- Oluyede, B.; Huang, S.; Yang, T. A new class of generalized modified Weibull distribution with applications. Austrian J. Stat. 2015, 44, 45–68. [Google Scholar] [CrossRef]
- Bagheri, S.F.; Samani, E.B.; Ganjali, M. The generalized modified Weibull power series distribution: Theory and applications. Comput. Statist. Data Anal. 2016, 94, 136–160. [Google Scholar] [CrossRef]
- He, B.; Cui, W.; Du, X. An additive modified Weibull distribution. Reliab. Eng. Syst. Saf. 2016, 145, 28–37. [Google Scholar] [CrossRef]
- Saboor, A.; Elbatal, I.; Cordeiro, G.M. The transmuted exponentiated Weibull geometric distribution: Theory and applications. Hacet. J. Math. Stat. 2016, 45, 973–987. [Google Scholar] [CrossRef]
- Khan, M.S.; King, R.; Hudson, I.L. Transmuted new generalized Weibull distribution for lifetime modeling. Commun. Stat. Appl. Methods 2016, 23, 363–383. [Google Scholar] [CrossRef][Green Version]
- Mdlongwa, P.; Oluyede, B.; Amey, A.; Huang, S. The Burr XII modified Weibull distribution: Model, properties and applications. Electron. J. Appl. Stat. Anal. 2017, 10, 118–145. [Google Scholar][Green Version]
- Oluyede, B.O.; Bindele, H.F.; Makubate, B.; Huang, S. A new generalized log-logistic and modified Weibull distribution with applications. Int. J. Stat. Probab. 2018, 7, 72–93. [Google Scholar] [CrossRef][Green Version]
- Mead, M.E.; Afify, A.; Butt, N.S. The modified Kumaraswamy Weibull distribution: Properties and applications in reliability and engineering sciences. Pak. J. Stat. Oper. Res. 2020, 16, 433–446. [Google Scholar] [CrossRef]
- Aljouiee, A.; Elbatal, I.; Al-Mofleh, H. A new five-parameter lifetime model: Theory and applications. Pak. J. Stat. Oper. Res. 2018, 14, 403–420. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Ghazal, M.G.M. Exponentiated additive Weibull distribution. Reliab. Eng. Syst. Saf. 2020, 193, 106663. [Google Scholar] [CrossRef]
- Shakhatreh, M.K.; Lemonte, A.J.; Cordeiro, G.M. On the generalized extended exponential-Weibull distribution: Properties and different methods of estimation. Int. J. Comput. Math. 2020, 97, 1029–1057. [Google Scholar] [CrossRef]
- Badmus, N.I.; Olanrewaju, F. Modeling lifetime data by generalized Weibull-generalized exponential distribution. Asian J. Probab. Stat. 2020, 9, 65–75. [Google Scholar] [CrossRef]
- Alizadeh, M.; Khan, M.N.; Rasekhi, M.; Hamedani, G.G. A new generalized modified Weibull distribution. Stat. Optim. Inf. Comput. 2021, 9, 17–34. [Google Scholar] [CrossRef]
- Jiang, D.; Han, Y.; Cui, W.; Wan, F.; Yu, T.; Song, B. An improved modified Weibull distribution applied to predict the reliability evolution of an aircraft lock mechanism. Probabilist. Eng. Mech. 2023, 72, 103449. [Google Scholar] [CrossRef]
- Merovci, F.; Elbatal, I. The McDonald modified Weibull distribution: Properties and applications. arXiv 2013, arXiv:1309.2961. [Google Scholar]
- Hashimoto, E.M.; Ortega, E.M.; Cordeiro, G.M.; Pascoa, M.A. The McDonald extended Weibull distribution. J. Stat. Theory Pract. 2015, 9, 608–632. [Google Scholar] [CrossRef]
- Hemeda, S. Additive Weibull log logistic distribution: Properties and application. J. Adv. Res. Appl. Math. Stat. 2018, 3, 8–15. [Google Scholar]
- Shahzad, M.N.; Ullah, E.; Hussanan, A. Beta exponentiated modified Weibull distribution: Properties and application. Symmetry 2019, 11, 781. [Google Scholar] [CrossRef]
- Aldahlan, M.A.; Jamal, F.; Chesneau, C.; Elbatal, I.; Elgarhy, M. Exponentiated power generalized Weibull power series family of distributions: Properties, estimation and applications. PLoS ONE 2020, 15, e0230004. [Google Scholar] [CrossRef]
- Sayibu, S.B.; Luguterah, A.; Nasiru, S. McDonald generalized power Weibull distribution: Properties and applications. J. Stat. Appl. Probab. 2024, 13, 297–322. [Google Scholar]
- Al-Babtain, A.; Fattah, A.A.; Ahmed, A.H.N.; Merovci, F. The Kumaraswamy-transmuted exponentiated modified Weibull distribution. Commun. Stat. Simul. Comput. 2017, 46, 3812–3832. [Google Scholar]
- Barlow, R.E.; Proschan, F. Mathematical Theory of Reliability; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar] [CrossRef]
- Afify, A.Z.; Mohamed, O.A. A new three-parameter exponential distribution with variable shapes for the hazard rate: Estimation and applications. Mathematics 2020, 8, 135. [Google Scholar] [CrossRef]
- Nassar, M.; Afify, A.Z.; Shakhatreh, M.K.; Dey, S. On a new extension of Weibull distribution: Properties, estimation, and applications to one and two causes of failures. Qual. Reliab. Eng. Int. 2020, 36, 2019–2043. [Google Scholar] [CrossRef]
- Almongy, H.M.; Almetwally, E.M.; Aljohani, H.M.; Alghamdi, A.S.; Hafez, E.H. A new extended Rayleigh distribution with applications of COVID-19 data. Results Phys. 2021, 23, 104012. [Google Scholar] [CrossRef]
- Almetwally, E.M. The odd Weibull inverse Topp–Leone distribution with applications to COVID-19 data. Ann. Data Sci. 2022, 9, 121–140. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M. Stochastic Ageing and Dependence for Reliability; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lee, E.T.; Wang, J. Statistical Methods for Survival Data Analysis; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Nelson, W.B. Applied Life Data Analysis; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Dhillon, B.S. Life distributions. IEEE Trans. Reliab. 1981, 30, 457–460. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).