Featured Application
This study provides practical guidelines for warehouse managers seeking to improve order-picking efficiency in manual distribution centers. By demonstrating how storage allocation strategies have a stronger impact than routing methods in a real multi-block warehouse, the research supports decision-makers in selecting effective policies without the need for complex optimization tools. The findings can be directly applied to similar warehouses to reduce picker travel time, enhance productivity, and lower operational costs.
Abstract
Order-picking is one of the most labor- and cost-intensive operations in warehouses, especially under the pressures of e-commerce growth and supply chain disruptions. Globally, order-picking accounts for 50–75% of total warehouse operating costs and nearly 55% of labor time, making it a dominant factor in logistics performance. Improving picking efficiency is therefore essential not only for reducing operational costs but also for enhancing resilience and sustainability in logistics. This study investigates the combined impact of storage space allocation and picker routing strategies on performance in a real-world edible oil factory warehouse with a three-block U-shaped layout. Three allocation policies (dedicated, turnover-based class storage, and family-based class storage) and three routing methods (S-shape, return, and midpoint) were tested in nine combinations over a five-week period. Results show that storage allocation has a stronger influence on picking efficiency than routing decisions. The family-based (Class 2) allocation with return routing achieved the lowest weekly picking time, reducing retrieval effort by concentrating items in low-level storage locations. Beyond efficiency gains, the findings highlight how simple, low-cost adjustments to storage policies can reduce picker travel, lower energy use, and support sustainable warehouse operations. This case study provides practical guidance for managers of small and medium-sized warehouses and offers baseline insights for the development of digital twin models and smart warehousing solutions in Industry 4.0.
1. Introduction
Warehouses storing raw materials, work-in-process materials, and finished products act as crucial links in a logistic chain. The main objective of a warehouse management system is to achieve the desired level of customer service at minimal cost. Warehouse operations include inventory tracking, picking and packing, and receiving and stowing. Inventory tracking is to obtain accurate records of stock levels with their exact locations. Picking and packing are the mechanisms of customer orders retrieval; it is the process of finding and extracting products from a warehouse to fulfill customer orders. Receiving and stowing is the process of unloading incoming items and storing them in their predetermined locations. Typical warehouse management decision problems are layout design, picking policies on a strategic level, storage space allocation, and routing decisions on an operational level. Layout design concerns the layout of both the facility containing the order-picking system and the order-picking system. A conventional warehouse layout is rectangular-shaped, single or multi-block, where picking is performed in picking aisles that are perpendicular to cross aisles. A non-conventional warehouse layout does not arrange all picking aisles or cross aisles in parallel to each other. The fishbone layout is an example. A picking policy is the organization of groups of customer orders or items in picking tours. A storage space allocation policy decides where items are to be stored in the warehouse. A routing strategy gives the sequence of picks for a picking tour. If order fulfillment time and accuracy come into interest, then efficient order-picking is required. Storage space allocation and picker routing are predetermined decisions that affect the order-picking time and accuracy.
Beyond cost savings, warehouse efficiency directly contributes to sustainable logistics by reducing labor intensity, travel distance, and energy use. Recent research emphasizes that operational decisions, such as item placement and routing, can indirectly support environmental performance by lowering carbon emissions and resource consumption. Therefore, efficient order-picking is not only an operational issue but also a sustainability concern. The rapid expansion of e-commerce and disruptions caused by the COVID-19 pandemic have increased the pressure on warehouses to fulfill orders quickly and cost-effectively. As order-picking accounts for a major share of operational costs, even small improvements in allocation and routing decisions can have significant impacts on throughput and resilience. This highlights the continued importance of studying picking efficiency in real-world warehouse settings. Although increasing attention is being paid to automated and digital solutions in warehousing, such as digital twins, AI-based optimization, and robotics, many industries—especially SMEs—still rely heavily on manual systems. Empirical studies in such environments remain essential, as they provide baseline knowledge that can inform the development and validation of future smart warehouse technologies. In this regard, this study aims to bridge the gap between theoretical models and practical industrial applications.
Recent literature has increasingly focused on intelligent and sustainable warehousing, integrating AI, digital twins, and adaptive decision-making [1,2,3]. However, most studies emphasize algorithmic or automated systems with limited validation in manual, multi-block layouts. This gap highlights the need for empirical evidence in small and medium-sized warehouses still reliant on picker-to-part operations. The presented work addresses this by experimentally evaluating allocation and routing strategies in a real warehouse.
Despite extensive research on storage assignment and routing optimization, empirical investigations in multi-block conventional warehouse layouts remain scarce. Most existing studies validate strategies through simulation or heuristic modeling, which limits their applicability to complex real-world configurations operating under industrial constraints. This study addresses this gap by providing field-based evidence on the integrated effects of storage allocation and routing decisions within a U-shaped, multi-block warehouse, thereby offering practical insights into how these strategies perform under actual operating conditions. Accordingly, the objectives of this study are as follows:
- Empirically evaluate the combined impact of storage allocation and routing policies in a real three-block warehouse layout;
- Identify which decision type—allocation or routing—has a stronger influence on picking performance; and
- Provide transferable insights to support low-cost, sustainable warehouse optimization.
The work presented in this paper focuses on storage space allocation and order-picker routing. A case study on an edible oil factory warehouse is investigated. This warehouse is for filling and packaging raw materials. It is a narrow-aisle conventional warehouse where the picker-to-part system is used. The warehouse consists of three blocks conforming to a U-shaped layout, where the depot position is located between blocks in the center of the layout. As order-picking time must decrease, more efficient storage allocation and picker routing are required. The warehouse under study makes one inventory replenishment order per week. Steady state demand is observed. Therefore, receiving and stowing is scheduled once a week. The week-long picking process of the filling department orders is observed. A real experiment is performed, tracing the behavior of applying combinations of both decisions. Three storage space allocation policies and three picker routing methods, resulting in nine combinations, are examined. Storage space allocation policies include a dedicated method and two class-based methods. Picker routing methods are adapted to match the existing warehouse layout; they are S-Shape, Returned, and Mid-point routing strategies. For each of the nine combinations, the total picking time for a week’s orders (time between two successive inventory replenishments) is traced and analyzed. Despite the extensive body of research on order-picking, most studies focus on algorithmic optimization in simplified layouts or simulate warehouse models. Empirical evidence from real, multi-block conventional warehouses with U-shaped layouts remains limited. This paper contributes to the literature in three ways:
- It presents a real-world case study in an edible oil warehouse, empirically testing nine allocation-routing combinations.
- It demonstrates that allocation policies exert a stronger influence on picking performance than routing rules, offering actionable insights for low-cost efficiency improvements.
- It provides practical, data-driven recommendations for warehouse managers seeking to enhance performance without automation.
- It situates these findings within the broader context of sustainable logistics and Industry 4.0, offering baseline knowledge for developing digital twin and smart warehouse systems.
The remainder of this paper is organized as follows: Section 2 reviews some of the related literature presented. Section 3 describes the methodology used. Problem determinants and rationale of the solution can be found in Section 4. Results and analysis of findings, followed by conclusions, are found in Section 5.
2. Literature Review
Order-picking remains one of the most critical and cost-intensive warehouse operations, often accounting for 50–75% of total operating expenses [4,5]. Accordingly, storage allocation policies and routing strategies have long been recognized as key determinants of operational efficiency [6,7]. Traditional research has largely approached these problems independently, storage allocation methods focusing on space utilization and travel minimization, and routing rules addressing picker path optimization [4,8]. However, recent developments emphasize the importance of integrated, adaptive, and sustainable approaches. Reviews of order-picking planning problems can be found in the literature. Du et al. (2021) [9] reviewed optimization approaches for manual picking systems, focusing on efficiency improvement methods and technological trends. Vanheusden et al. (2023) [5] classified practical factors influencing order-picking planning, emphasizing real-world implementation and performance trade-offs. Keshavarz et al. (2021) [10] surveyed order-picking systems by integrating various planning problems to present a comprehensive view of combined optimization models. Reyes, Solano-Charris, & Montoya-Torres (2019) [7]. Reviewed literature on the storage location assignment problem, analyzing models that enhance warehouse layout and retrieval efficiency. Masae, Glock, & Grosse (2019) [4] provided a systematic review of order-picker routing strategies in warehouses, highlighting optimization models and practical challenges.
The storage space allocation problem is NP-hard due to varying product sizes and warehouse configurations. Typical classifications of storage space allocation policies are random, dedicated, and class-based storage. Different algorithms were developed to solve the storage space allocation problem in the literature. Fontana et al. (2020) [11] introduced a hybrid approach based on a multi-objective genetic algorithm and multi-criteria decision-making to optimize storage utilization and minimize travel time in a picker-to-part system. This study intended to utilize the used storage space and to minimize travel distance and travel time for the retrieval operation. Zhang et al., 2020 [12] proposed an optimization model based on a genetic algorithm and inversion operation to minimize traveling time between input and output points, decreasing the distance between related items, and ensuring the stability of shelves. Improvement of the order-picking process and reduction in the total travel distance are achieved by the work done by Wang et al., 2020 [13], by using item orders directly to decide the allocation plan without applying statistical concepts to the entered data. They mentioned that an improved allocation plan can be extracted by iteratively using the good move pair concept. Xu & Ren, 2020 [14] transformed the traditional storage space allocation problem into a multi-stage storage space allocation process to cope with variable demand in a retail warehouse. Items’ locations in the warehouse are adjusted dynamically at run time. They mentioned that dynamic storage space allocation can effectively improve picking efficiency when the average order size is small and a large demand correlation exists. Zhou et al., 2020 [15] combined both genetic algorithm and simulated annealing methods to find the minimum travel time and distance between related items and the lowest orthocenter of the shelf. Tu et al., 2021 [16] improved the efficiency of order-picking by applying a cyber–physical system and a multi-objective genetic algorithm in an e-commerce-based warehouse.
Albert, Rönnqvist, and Lehoux, 2023 [1] highlighted that many allocation studies assume homogeneous inventory and standard layouts, overlooking heterogeneous products and non-conventional designs. More recent contributions, such as that from Winkelmann et al., 2022 [17], propose integrated storage assignment models that simultaneously consider station, shelf, and demand patterns (e.g., day-of-week fluctuations), achieving superior performance compared to sequential methods. These findings stress the importance of dynamic allocation and layout-aware strategies.
At the operational level, the picker routing problem plays an important role in improving order-picking process efficiency. Engels et al., 2022 [18] offered exact analytical insights into the expected picking times under different heuristics, allowing more rigorous comparison of routing policies. Both exact optimal solutions based on dynamic programming algorithms and near-optimal solutions based on heuristic approaches are used for different warehouse sizes and layouts [4]. Early foundational work by Ratliff and Rosenthal, 1983 [19] modeled order-picking in a two-block rectangular warehouse with a middle main aisle, where crossovers are constrained to be only at the ends of aisles as a solvable case of the Traveling Salesman Problem (TSP), deriving optimal solutions for specific layouts. Another exact solution method is developed to find the minimum picking distance in a warehouse of parallel aisles where order-pickers change aisles at the end and across aisles halfway [8]. Koster and Poort, 1998 [20] counted for both conventional and modern warehouses and extended the work of Ratliff & Rosenthal, 1983 [19], routing time improvement was obtained between 7 and 34%. Masae, Glock, & Vichitkunakorn, 2020 [4], presented an optimal algorithm for a conventional warehouse of two blocks and random picking starting and ending points by applying the concepts of Ratliff & Rosenthal, 1983 [19], and Roodbergen & De Koster, 2001 [8]. Koster and Poort, 1999 [20] presented a case study on a heavy workload distribution center warehouse. They mentioned that a reduction in route time can be obtained by clustering small orders in a single route. Zhou et al., 2022 [21] studied the impact of applying return and S-shape routing policies in a fishbone warehouse layout with class-based space allocation, underscoring how layout, allocation, and routing must be evaluated jointly. The experiment showed that the return routing strategy is superior to the S-shape strategy due to warehouse geometry. A comparison of the performance of three heuristics can be found at Sebo & Busa Jr, 2020 [22], namely the genetic algorithm, the experienced warehouse picker algorithm, and the brute-force algorithm in a mid-sized dual-zone warehouse. The results showed that the brute-force algorithm is superior, and adapting the genetic algorithm can generate better solutions.
For efficient order-picking, integrating a solution for warehouse management planning problems is important [23]. The expected travel time was calculated for traversal and return routing policies in a picker-to-part conventional narrow aisles warehouse, where storage space allocation decision is based on the cubic-per-order ratio (COI) [24]. They mentioned that the selection of an adequate routing policy depends on the number of picks per aisle. The results showed that for COI-based storage systems, the return policy is superior to the traversal policy in case of low demand. Bolanos Zuniga et al., 2020 [25] developed a mathematical model considering item weight. They aimed at improving the order-picking while simultaneously solving the storage space allocation and the picker-routing problem, considering precedence constraints based on the item weight, as the only location for each item in a warehouse with a general layout. Another integrated model is a simulation-analytical model of different combinations of three storage space allocations and four routing strategies. Allocation strategies are random, class-based, and order-oriented slotting storage allocations. Routing strategies are traversal, largest gap, optimal, and adaptive policies [26]. Kübler et al. (2020) [27] introduced an iterative heuristic for simultaneous optimization of storage, batching, and routing, demonstrating travel-distance reductions. Silva et al., 2020 [28] developed a General Variable Neighborhood Search metaheuristic that integrates storage allocation and the order-picking problem and four routing policies (return, S-shape, mid-point, and largest gap).
Scaling optimization for large warehouses has inspired new computational techniques. Bengtsson, Wittsten, and Waidringer, 2025 [29] propose GPU-accelerated routing combined with clustering and dynamic modeling, significantly reducing both travel distance and computation time. Casella et al., 2023 [30] similarly stress that hybrid approaches, which integrate allocation and routing simultaneously, outperform traditional sequential strategies. These studies reflect a broader trend toward computationally intensive but more efficient integrated models.
The rise in Industry 4.0 has brought attention to digital twins (DTs), AI, and IoT in warehousing. Galkin et al., 2025 [2] show that DTs are increasingly deployed at object, infrastructure, and system levels, providing real-time simulation, monitoring, and optimization. Roman et al., 2025 [31] further emphasize DTs’ role in resilience and disruption management, particularly through scenario testing and agile decision-making. Beyond efficiency, sustainability has become a priority: Bandara et al., 2024 [3] analyzed DT adoption in sustainable logistics, showing how such technologies can reduce energy use and environmental impact, though empirical implementations remain scarce.
Despite these technological advances, several research gaps persist. Many studies assume steady demand, with limited empirical validation under fluctuating or uncertain environments [17]. Non-traditional layouts have been explored, but mostly under narrow policy combinations [15]. Furthermore, empirical case studies—especially those incorporating digital twins and sustainability metrics—are limited, despite strong calls for practice-oriented research [1,2]. These gaps highlight the need for integrated, real-world evaluations of storage and routing policies. Unlike many recent hybrid and algorithmic optimization models (e.g., Silva et al., 2020 [28], Kübler et al., 2020 [27], and Casella et al., 2023 [30]), which focus on simulation-based or metaheuristic approaches, the present research adopts an empirical design executed under actual operational constraints. This distinction ensures that the findings reflect realistic human–system interactions, providing actionable insights for manual warehouses that lack automation infrastructure.
In this context, the present study contributes empirical evidence from a real-world edible oil warehouse with a three-block U-shaped layout, evaluating nine combinations of allocation and routing policies. By bridging theoretical models and industrial practice, it provides insights into low-cost yet impactful strategies, while also offering a baseline for the development of sustainable, digitalized, and smart warehousing solutions. Although based on a single site, the decision framework (selecting low-cost allocation-routing combinations) can be replicated in other warehouses by substituting layout parameters such as aisle length, rack height, and depot position. This makes the approach transferable without major structural changes.
3. Materials and Methods
3.1. Research Methodology Overview
The research methodology adopted in this study follows a structured empirical approach designed to systematically evaluate the combined effects of storage space allocation and picker routing strategies in a real warehouse environment. The process comprises four main stages: (1) Data Collection and System Mapping, where the physical characteristics of the edible oil warehouse—such as layout, rack configuration, item categories, and picker travel times—were documented through direct observation and time measurements; (2) Experimental Design, in which a full factorial design of three storage allocation policies and three routing strategies was established, resulting in nine test scenarios; (3) Implementation and Data Recording, where each scenario was applied sequentially over a five-week period under normal operating conditions, ensuring consistent demand and replenishment cycles; and (4) Performance Evaluation and Analysis, involving the computation and comparison of total weekly picking times, horizontal travel distances, and retrieval times. This methodological framework emphasizes empirical validation under real-world constraints, distinguishing it from purely simulation-based or algorithmic optimization studies. The novelty of the approach lies in demonstrating how practical combinations of simple allocation and routing rules can yield measurable improvements in picking efficiency and sustainability without the need for advanced automation or optimization software.
Unlike optimization-based models (e.g., Kübler et al., 2020 [27] and Silva et al., 2020 [28]) that rely on simulated demand, this study tests policies under real-world steady operations. While not algorithmically optimized, the empirical results validate that policy-level adjustments can achieve comparable gains with minimal computational effort. The study follows a full factorial experimental design, where three storage allocation policies (dedicated, turnover-based, and family-based) were combined with three routing strategies (S-shape, return, and midpoint), yielding nine experimental scenarios. Each scenario was tested under real operating conditions for one week, and performance was measured using average order-picking time as the primary response variable. For each combination total picking time is calculated based on the warehouse layout. In the following parts description of each used strategy of both storage space allocation and picker routing is introduced. The nine combinations of names and abbreviations are presented in Table 1.

Table 1.
Nine combinations and abbreviations.
In a dedicated storage space allocation strategy, a storage location or group of locations is allocated to specific items over the planning horizon. The first class-based strategy is based on the turnover of items, where the highest turnover is stored in the nearest locations to the depot. It is called a volume-based storage strategy. The second class-based strategy is family-based, where all related items form a group.
3.2. Routing Strategies
The study considered three routing strategies: S-shape, return, and midpoint strategies, because they are the most commonly applied and validated heuristics for narrow-aisle, multi-block warehouses (Masae et al., 2019 [4] and Roodbergen & De Koster, 2001 [8]). These methods were selected to ensure comparability with previous studies and because they can be feasibly implemented in the case warehouse without layout modification or additional technology.
3.2.1. S-Shape Routing
The S-shape routing method, also known as the traversal approach, directs the picker to move through each aisle that contains items from one end to the other before proceeding to the next aisle, as shown in Figure 1. The picker begins the route from the depot and enters the nearest aisle with required items, continuing in a systematic zigzag pattern until all aisles containing picks have been traversed. Aisles without requested items are skipped. Once the final item in the last aisle is collected, the picker exits toward the front cross-aisle and returns to the depot.
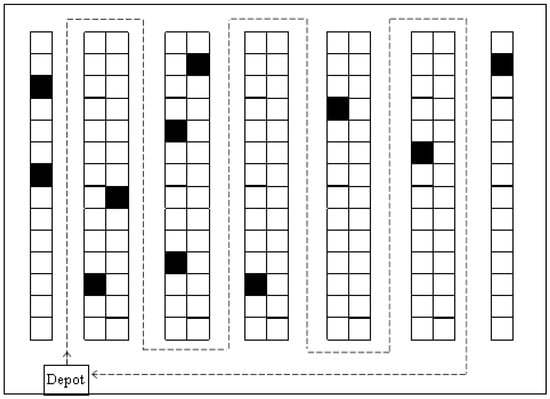
Figure 1.
The S-shape routing strategy.
In multi-block warehouse layouts, such as the studied three-block configuration, the picker first moves from the depot to the closest main aisle, as shown in Figure 2. Each active aisle is then traversed completely within its block, ensuring all pick locations are visited in sequence. After finishing one block, the picker crosses to the next block through the nearest cross-aisle and repeats the same pattern. The route ends when all blocks containing items have been served and the picker returns to the depot. This routing method is simple to apply, provides predictable movement patterns, and ensures that each aisle is visited only once when necessary. Although it may not always minimize travel distance, its straightforward structure makes it particularly suitable for narrow-aisle warehouses and manual picking operations.
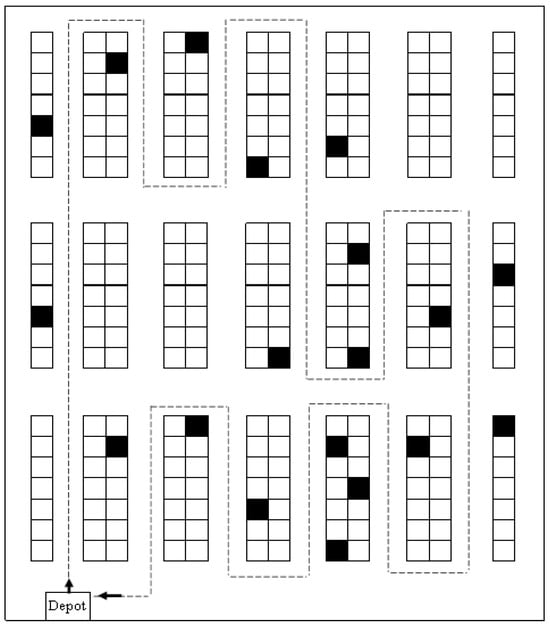
Figure 2.
S-shape routing strategy with multiple block warehouses.
3.2.2. Return Routing
With the return routing strategy, the aisles are entered and left from the same side after picking the items in this aisle, as shown in Figure 3. In case of multiple blocks with cross aisles warehouse the order-picker follows the same steps just as the S-shape strategy, except using the return method for each block instead of traversing each aisle containing items.
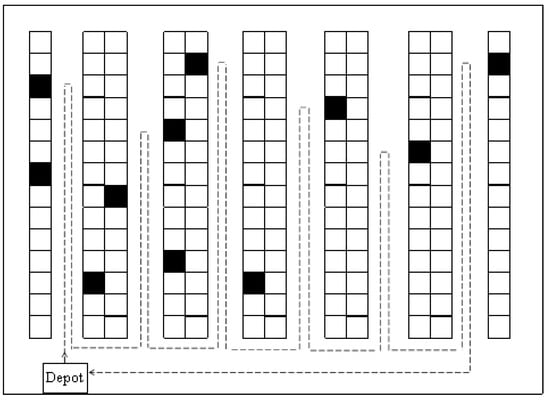
Figure 3.
Return routing strategy.
3.2.3. Mid-Point Routing
The mid-point routing strategy divides each warehouse block into two virtual zones—front and rear—based on the distance from the depot. For items stored in the front zone, the picker enters and exits through the front cross-aisle, while items located in the rear zone are accessed through the back cross-aisle. This approach allows the picker to avoid traversing full aisles unnecessarily, thereby reducing total travel time. An illustration is presented in Figure 4. In the multi-block layout used in this study, the picker begins at the depot and proceeds to the nearest main aisle containing required items. Within each block, only the first and last aisles are completely traversed; other aisles are entered halfway, depending on whether items are in the front or rear zone. When the picking in one block is completed, the picker crosses to the next block through the central cross-aisle and repeats the process until all items are retrieved. The picker then returns directly to the depot. This routing method strikes a balance between the return and S-shape strategies. It offers moderate route lengths while maintaining manageable complexity for manual operations. In practice, it can effectively shorten travel distance compared with complete aisle traversal, especially when most picks are concentrated near the center of the warehouse.
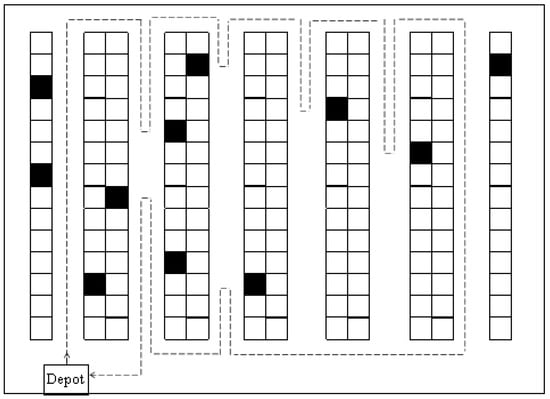
Figure 4.
Mid-Point routing strategy.
3.3. Case Description
The warehouse’s existing practice—dedicated storage with S-shape routing—served as the baseline scenario. Each of the nine tested combinations was evaluated relative to this configuration to quantify actual improvements achieved through alternative allocation and routing policies. The problem under study is a warehouse of raw materials of the filling and packaging department of an edible oil manufacturing company. Materials in the warehouse include containers of tubes of bottles, covers, sticker rolls, carton packs, and utility materials (glue and lubricants). These materials are used to obtain different sizes of oil containers. The filling department consists of three filling lines. The first line is used to obtain regular cylindrical oil bottles of sizes: 250, 500, and 1000 milliliters. The second line is used for filling two-liter oil bottles. The third line is a special line that is dedicated to large five-liter cans of oil. From this classification, it can be noticed that each type of oil container has its own set of materials. Raw material group sets are listed in Table 2. As this warehouse serves the company’s filling and packaging department, the ordering operation is performed according to the running plan of the department. By observing the steady state operation, the following was observed in the long run: the first line performs on average five orders daily, and each of the second and third lines performs on average two orders daily. The warehouse is replenished once every week with a quantity enough to satisfy the maximum expected ordering quantity.

Table 2.
Raw material group sets.
As illustrated in Figure 5, the considered warehouse is a conventional picker-to-part system warehouse with narrow main aisles where a picker can retrieve items from both sides of an aisle in the same direction. The warehouse consists of three storage blocks, each block consists of some racks of a total of thirty-two racks all over the storage. Block number one consists of four racks, eighteen for block number two, and the third consists of ten racks. The order preparation area is located between block number one and block number three. One cross aisle of two meters width separates block number two from the order preparation area. Narrow main aisles of one meter width located between racks enable pickers to pick items in one direction from both sides. Back aisles are also one meter wide. Each rack contains five bays and five levels with a total of twenty-five storage locations per one rack. Each storage location is enough to store one container unit of raw materials used in the warehouse.
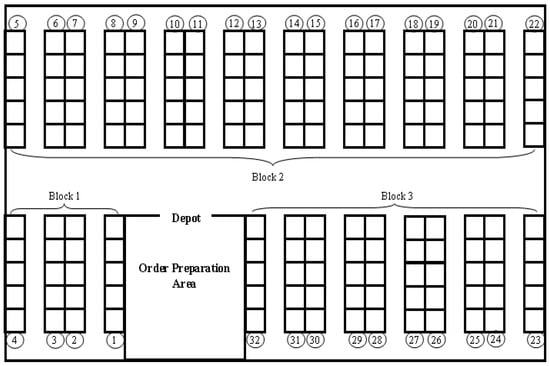
Figure 5.
Layout of the case warehouse.
The picker-to-part system, in which the order-picker moves to storage locations to perform scheduled picks of the required items, is used in the current situation. Picker routes between racks in horizontal motion (within aisles), vertical motion (multi-level racks), in addition to the picking movement of an item. Meaning that total picking time consists of horizontal travel time, vertical travel time, and item picking time. For horizontal travel time, the order-picker moves with a 50 m per minute velocity from the depot to the item locations, between racks and bays to collect all items within an order. A rack width equal 0.8 m and a bay width equal one meter. For vertical travel time, one bay height equals 0.8 m. The picker can handle items of the first three levels without making vertical motion; vertical motion is calculated for ups and downs of the fourth and fifth levels. For picking time, it takes 0.3 min for picking items in the first three levels, and items in the fourth and fifth levels take 2 min for picking, including the vertical motion.
To apply the dedicated storage space allocation in our situation, each item type has its own group of racks. For example, bottles of all sizes are stored in block number three, and two racks are assigned for each bottle size. Also, covers of all sizes are stored in three racks near the preparation area; one rack is assigned for each cover size, and so on. Dedicated locations allocation for the studied warehouse is illustrated in Figure 6.
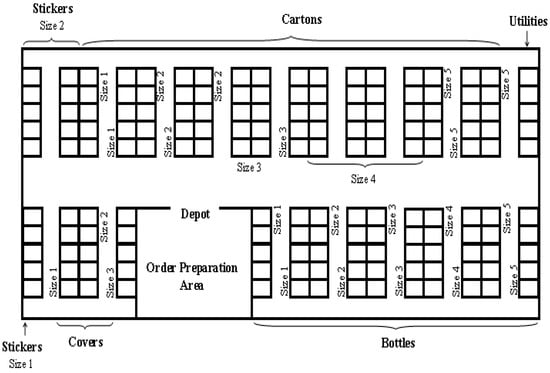
Figure 6.
Dedicated storage space allocation for the studied warehouse.
For the volume-based storage, Table 3 lists the first thirty near locations to the depot. The number of locations assigned to each item and its order in position to the depot are listed in Table 4. For family-based storage, items ordered by a specific line form a group, meaning that there are three groups, one for each line. Line number one is the largest size family, so it is located near the depot. The second group is for line number 2, and the third is for line number three. Inside each group, locations are assigned on a volume basis just as performed in the previous strategy. The number of locations assigned to each item and its order in position to the depot are listed in Table 5.

Table 3.
The nearest 30 locations to the depot.

Table 4.
Space allocation according to volume-based classification of items.

Table 5.
Space allocation according to the Family-based classification of items.
3.3.1. Steps of S-Shape Routing
For the warehouse layout under study steps of S-shape routing are interpreted to the following steps:
- Move to the nearest main aisle containing items either from block number one or block number three.
- Using the S-shape policy, pick all items in this block.
- After picking the last item in this block, move to block number two, keeping in mind that moving to the left-most main aisle (containing items) if moving from block number one, and moving to the right-most main aisle (containing items) if moving from block number three.
- Using the S-shape policy, pick all items in this block.
- After picking the last item in this block, move to the third block
- Using the S-shape policy, pick all items in this block.
- After picking the last item in this block, return to the depot
3.3.2. Steps of Return Routing
Steps of return routing are modified to the following steps:
- Move to the nearest main aisle containing items either from block number one or block number three.
- Using the return policy, pick all items in this block.
- After picking the last item in this block, move to block number two, keeping in mind that moving to the left-most main aisle (containing items) if moving from block number one and moving to the right-most main aisle (containing items) if moving from block number three.
- Using the return policy, pick all items in this block.
- After picking the last item in this block, move to the third block
- Using the return policy, pick all items in this block.
- After picking the last item in this block, return to the depot
3.3.3. Steps of Mid-Point Routing
Steps of return routing are modified to the following steps:
- Move to the nearest main aisle containing items either from block number one or block number three.
- Using the mid-point policy, pick all items in this block.
- After picking the last item in this block, move to block number two, keeping in mind that moving to the left-most main aisle (containing items) if moving from block number one and moving to the right-most main aisle (containing items) if moving from block number three.
- Using the mid-point policy, pick all items in this block.
- After picking the last item in this block, move to the third block
- Using the mid-point policy, pick all items in this block.
- After picking the last item in this block, return to the depot
Steps of S-shape, return, and Mid-point routing are illustrated in Figure 7:
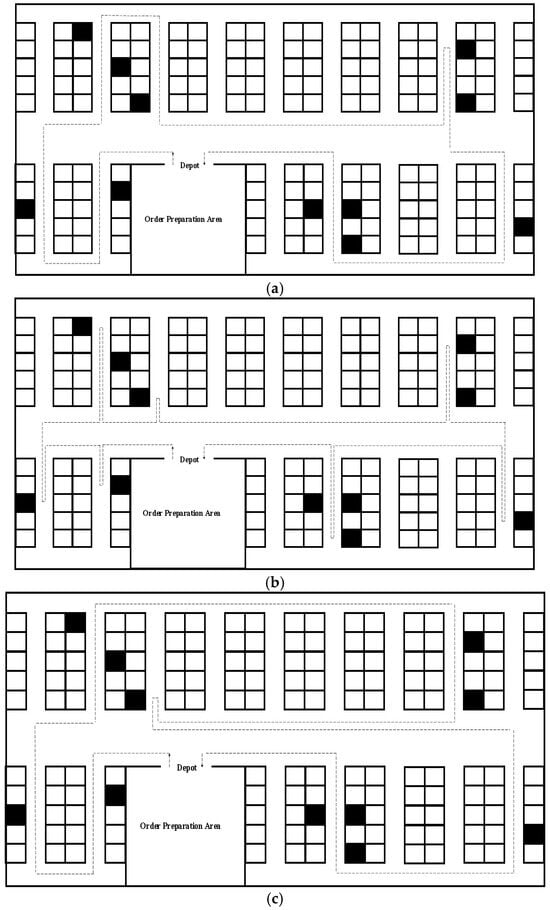
Figure 7.
Routing examples of the studied warehouse: (a) S-shape, (b) Return, (c) Mid-point routing.
4. Results and Discussion
Total picking time, which consists of both routing time and item retrieval time from shelves, is the focus of this study. For the nine combinations, the average weekly picking time is traced. The total number of orders per day is nine orders (five for line number one, two orders for each of line numbers two and three), meaning that it is required to make nine routes per day and forty-five orders per week. The order picking time for each combination can be found in Figure 8.
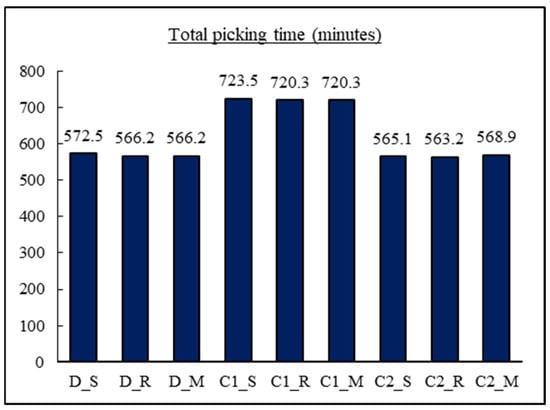
Figure 8.
Total picking time for all combinations.
The least obtained total picking time is that of combination number eight (class (2) allocation with return routing). It can be observed that approximately the same low results appear at both dedicated and class (2) storage space allocation for all routing strategies. The same picking time is obtained by the same routing policy can be explained as the depot is central between blocks, and the same crossing time for both back and cross aisles. By analyzing each line, orders same results for routing strategies are obtained. For line number 1, class (2) storage space allocation strategy gives a lower total picking time than other allocation policies, as shown in Figure 9. Class (1) is better for line number two; for line number three, dedicated storage gives a lower total picking time.
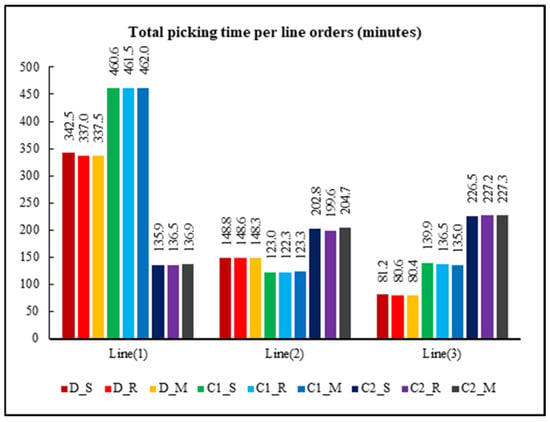
Figure 9.
Total picking time for orders of each line.
4.1. Statistical Validation of Performance Differences
To confirm whether the differences among the nine allocation–routing combinations were statistically significant, a one-way ANOVA was conducted using total weekly picking time as the dependent variable. The results revealed a highly significant effect of strategy combination on picking performance, F(8,18) = 1819.64, p < 0.001, indicating that storage–routing configurations produced meaningfully distinct outcomes.
Post hoc Tukey HSD comparisons (α = 0.05) showed that the Class 2–Return (C2R) combination achieved a significantly lower mean picking time than all other configurations. In contrast, Dedicated–S-shape (C1S) and Class 1-based setups exhibited the highest mean times. These results confirm that allocation policy exerts a stronger influence on overall performance than routing choice.
The large observed F-value and narrow within-group variance further indicate that the differences are operationally significant, not attributable to normal variation. Thus, the family-based (Class 2) allocation—especially when combined with return routing—provides the most efficient configuration, validating the observed empirical trend with statistical rigor.
As mentioned before, the total picking time consists of two main parts these parts are horizontal travel time and retrieval time. Horizontal travel time is calculated as the time consumed in horizontal moves from/to the depot, crossing aisles, and moving between racks to reach racks where items are stored. Retrieval time is the time required to pick an item and put it into the cart. Retrieval time is related to the level of storage in the rack. For low level storage (levels 1, 2, and 3), retrieval time per item is 0.3 min, for high level storage (levels 4 and 5), retrieval time per item is approximately two minutes. Allocation of items to each storage location and, therefore, to either low or high level is different from one allocation strategy to another. For both dedicated and class (2) storage space allocation strategies, nearly 70% of items are stored in low level storage locations, and about 30% are stored in high levels. For class (1), storage space allocation strategy slightly more than half of the items are stored in low level stage locations, and the other half is stored in the high levels; the exact numbers are given in Figure 10. Allocation of items into storage levels for each line is illustrated in Figure 11. This outcome reflects the allocation logic grouping items by production line, which naturally places frequently picked goods closer to ground level and near the main depot, thus reducing retrieval time and improving ergonomic efficiency. For dedicated storage, the ratio is approximately the same for the three lines, two-thirds in low level storage to one-third in high storage. For class (1), the storage ratio is half to half between line number one and line number three. For line number two, nearly 80% is stored in low level storage. For class (2) storage, all items of line number one are stored in low level storage, and all items of line number three are stored in high level storage, the ratio remains half to half in line number two.
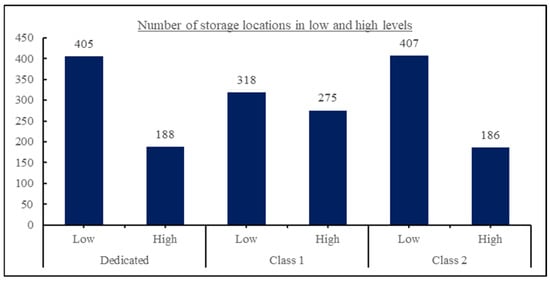
Figure 10.
Storage locations in low and high levels of storage for different storage allocations.
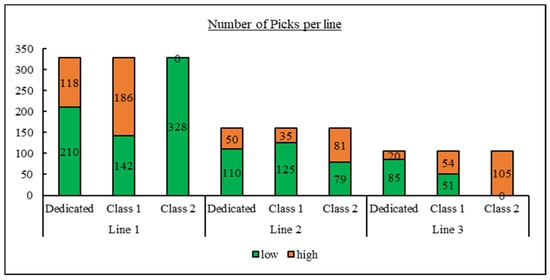
Figure 11.
Number of items in low and high levels of storage for each line for each storage allocation.
Total horizontal travel distance and total retrieval time for each combination are shown in Figure 12 and Figure 13. It can be noticed that the lowest horizontal travel time is achieved by the second combination (dedicated allocation and returned routing), and combination number three (dedicated allocation and midpoint routing) gives approximate results. For retrieval time, combination number eight (class (2) allocation and returned routing) gives the lowest retrieval time; approximate results can be obtained by combinations number one, two, seven, and nine. By observing combination number eight, it also has the minimum obtained total retrieval time and the fifth horizontal travel distance. It can be concluded that lowering retrieval time affects decreasing total picking time more than performed by lowering horizontal travel distance. Horizontal travel time and retrieval time for each line are given in Figure 14 and Figure 15.
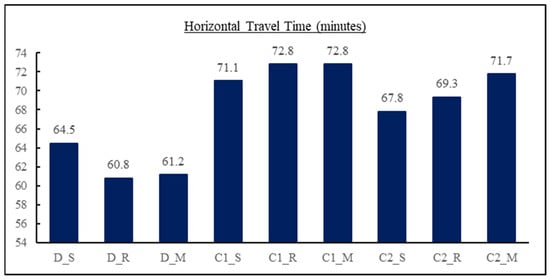
Figure 12.
Total horizontal travel time in minutes for each combination.
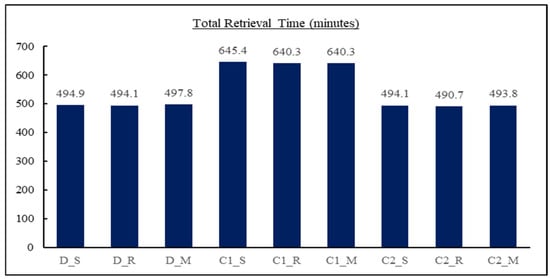
Figure 13.
Total retrieval time in minutes for each combination.
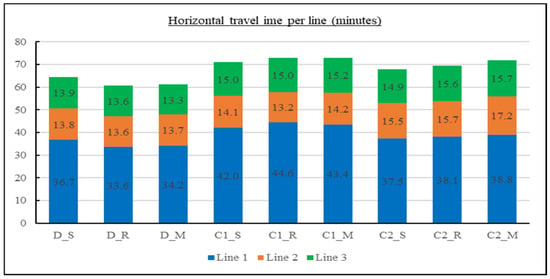
Figure 14.
Horizontal travel time in minutes per line for each combination.
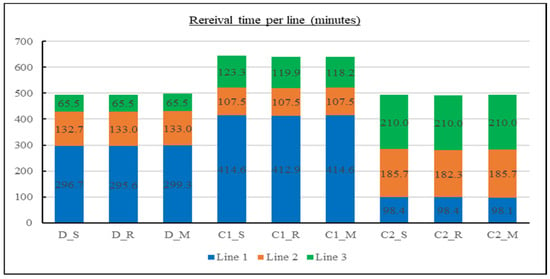
Figure 15.
Retrieval time in minutes per line for each combination.
For all combinations, horizontal travel time for line one is more than horizontal time for both line two and line three, as this line has five orders per day, and the other line has only two orders per line daily. Dedicated strategy seems to be the best for all lines to achieve less horizontal travel time; for line two, class one gives the same results. By noticing the retrieval time, the class two allocation strategy is better for line one, the class one allocation strategy is better for line two, and the dedicated strategy is better for line three.
The stronger impact of storage allocation policies arises primarily from retrieval-time optimization rather than horizontal travel reduction. Family-based (Class 2) allocation concentrates frequently retrieved items in low-level racks close to the depot, thereby minimizing lifting and reach time, which collectively account for a larger portion of total picking duration than horizontal movement. In contrast, routing strategies mainly influence travel paths and distances, producing smaller incremental gains. The ANOVA results confirm that these allocation-driven differences are statistically significant (p < 0.05).
4.2. Discussion
The experimental results of this study reinforce existing evidence that storage allocation policies exert a stronger impact on order-picking performance than routing strategies (Zhou et al., 2022 [15] and Silva et al., 2020 [28]). The observed 8–12% improvement in total picking time achieved through the family-based (Class 2) allocation approach is consistent with the simulation outcomes reported by Wang et al. (2020) [13], who demonstrated similar gains when grouping frequently co-ordered items. This alignment across empirical and simulated contexts suggests that well-structured allocation rules can significantly enhance efficiency, even without algorithmic optimization. In contrast to prior research that relies on complex metaheuristic or AI-driven models, the current study validates a simpler, rule-based framework implemented under real operational conditions. The comparable performance achieved through these low-cost methods highlights their practicality and scalability for SMEs, which often lack the resources or infrastructure to deploy advanced automation or optimization systems. Moreover, the findings emphasize that meaningful performance improvements can be realized through data-driven policy adjustments alone, offering a pragmatic pathway toward more sustainable and efficient warehouse operations. The statistical validation further supports the observed patterns, confirming that the differences among allocation–routing combinations are significant (p < 0.05). This reinforces the practical reliability of the empirical findings and strengthens confidence in their generalizability.
5. Conclusions, Limitations, and Future Work
The novelty of this study lies not in developing new algorithms but in empirically validating established warehouse strategies under real operational conditions. By demonstrating that simple rule-based allocation–routing combinations can achieve measurable efficiency gains, the research provides practical, transferable insights for manual warehouses—especially SMEs—that lack advanced automation infrastructure. This study provides empirical evidence on the combined effects of storage allocation and routing strategies in a real industrial warehouse, contributing to the scarce body of field-based research on integrated warehouse optimization. Scientifically, it demonstrates that allocation rules exert statistically stronger influence than routing heuristics, offering a validated baseline for future digital twin and AI-based optimization models.
This study examined the combined effects of three storage space allocation strategies and three picker routing policies on order-picking performance in a real edible oil warehouse with a three-block U-shaped layout. The main findings demonstrate that:
- Storage allocation exerts a greater impact on picking efficiency than routing decisions.
- The family-based allocation (Class 2) combined with return routing achieved the lowest weekly picking time, reducing retrieval effort by concentrating items in low-level storage.
- While routing policies produced broadly similar results, allocation strategies varied in effectiveness across production lines, reflecting differences in product demand and item grouping.
5.1. Managerial and Sustainability Implications
- Warehouse managers should prioritize revising storage policies before modifying routing rules.
- Implementing family- or turnover-based allocation can deliver substantial efficiency gains without costly automation or software investments.
- By reducing picker travel and retrieval effort, these strategies also contribute to sustainable logistics through reduced labor intensity, energy use, and operational costs.
- The results are particularly relevant for SMEs facing e-commerce growth and supply chain disruptions, where rapid yet low-cost improvements are vital for competitiveness and resilience.
5.2. Study Limitations
Although the study is grounded in a single U-shaped, three-block warehouse, the proposed decision framework—focused on selecting cost-effective combinations of allocation and routing policies—can be readily adapted to other facilities by adjusting key layout parameters such as aisle length, rack height, and depot location. This adaptability makes the approach transferable across diverse warehouse settings without requiring significant structural modifications. The experimental period covered five consecutive operational weeks, which, although sufficient for testing the nine combinations under stable demand, may not capture seasonal fluctuations or longer-term variability. Future studies should extend the observation period or include multiple seasonal cycles to account for potential demand variation and operational disruptions. Further limitations include:
- The study assumed steady demand and a fixed replenishment cycle, without accounting for real-world demand variability.
- The analysis focused solely on picking time, excluding factors such as labor cost, error rate, and environmental impact.
- The investigation was limited to manual picker-to-part operations; results may differ in automated or hybrid warehouse systems.
5.3. Future Research Directions
Building upon these findings, future research could:
- Extend the analysis to non-conventional layouts and high-density layouts, examining their effects on combined allocation–routing efficiency.
- Investigate dynamic allocation policies that adapt to fluctuating demand using AI or reinforcement learning.
- Integrate allocation, batching, and routing into joint optimization frameworks for holistic decision-making.
- Apply metaheuristics and digital twin models to simulate and optimize strategies in smart warehouse contexts.
- Broaden performance evaluation to include other relevant metrics such as picking accuracy, labor cost, and fatigue, and sustainability indicators, such as energy consumption, labor ergonomics, and carbon footprint.
- Validate results across industries, including food, e-commerce, and pharmaceuticals, to assess generalizability.
Author Contributions
G.R.E. led the study, contributing to the conceptualization, methodology design, investigation, formal analysis, visualization, and preparation of the original draft. J.A.B. contributed to data curation, validation of results, review and editing of the manuscript, and provided supervision and project administration support. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R914), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Ethical review and approval were waived for this study, as it did not involve human participants or animals.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting the findings of this study are contained within the manuscript.
Acknowledgments
The authors would like to express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R914), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Albert, P.W.; Rönnqvist, M.; Lehoux, N. Trends and new practical applications for warehouse allocation and layout design: A literature review. SN Appl. Sci. 2023, 5, 378. [Google Scholar] [CrossRef]
- Galkin, A.; Samchuk, G.; Kopytkov, D.; Thompson, R.G. Digital twins in logistics: A comprehensive bibliometric analysis for advancing smart cities and sustainable development. Discov. Sustain. 2025, 6, 853. [Google Scholar] [CrossRef]
- Bandara, L.V.; Buics, L. Digital Twins in Sustainable Supply Chains: A Comprehensive Review of Current Applications and Enablers for Successful Adoption. Eng. Proc. 2024, 79, 64. [Google Scholar] [CrossRef]
- Masae, M.; Glock, C.; Grosse, E. Order-picker routing in warehouses: A systematic literature review. Int. J. Prod. Econ. 2019, 224, 107564. [Google Scholar] [CrossRef]
- Vanheusden, S.; van Gils, T.; Ramaekers, K.; Cornelissens, T.; Caris, A. Practical factors in order-picking planning: State-of-the-art classification and review. Int. J. Prod. Res. 2022, 61, 2032–2056. [Google Scholar] [CrossRef]
- Quader, S.; Castillo-Villar, K.K. Design of an enhanced multi-aisle order-picking system considering storage assignments and routing heuristics. Robot Comput. Integr. Manuf. 2018, 50, 13–29. [Google Scholar] [CrossRef]
- Reyes, J.J.R.; Solano-Charris, E.L.; Montoya-Torres, J.R. The storage location assignment problem: A literature review. Int. J. Ind. Eng. Comput. 2019, 10, 199–224. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; De Koster, R. Routing order-pickers in a warehouse with a middle aisle. Eur. J. Oper. Res. 2001, 133, 32–43. [Google Scholar] [CrossRef]
- Du, M.; Wang, X.; Geng, J.; Ye, L. A Review of The Optimization of The Manual Picking System. In Proceedings of the ICEME 2021: The 2021 12th International Conference on E-business, Management and Economics, Beijing, China, 17–19 July 2021; pp. 661–666. [Google Scholar] [CrossRef]
- Keshavarz, A.R.A.; Jaafari, D.; Khalaj, M.; Dokouhaki, P. A survey of the literature on order-picking systems by combining planning problems. Appl. Sci. 2021, 11, 10641. [Google Scholar] [CrossRef]
- Fontana, M.E.; Nepomuceno, V.S.; Garcez, T.V. A hybrid approach development to solving the storage location assignment problem in a picker-to-parts system. Braz. J. Oper. Prod. Manag. 2020, 17, 1–14. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, J.; Yuan, R. Optimization of Automated Warehouse Storage Location Assignment Problem Based on Improved Genetic Algorithm. In LISS2019; Springer: Singapore, 2020; pp. 297–311. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, R.Q.; Fan, K. Improving order-picking operation through efficient storage location assignment: A new approach. Comput. Ind. Eng. 2020, 139, 106186. [Google Scholar] [CrossRef]
- Xu, X.; Ren, C. Research on Dynamic Storage Location Assignment of Picker-to-Parts Picking Systems under Traversing Routing Method. Complexity 2020, 2020, 1621828. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, J.; Liu, H.; Wang, F.; Yang, J.; Wang, S. Stochastic models of routing strategies under the class-based storage policy in fishbone layout warehouses. Sci. Rep. 2022, 12, 12876. [Google Scholar] [CrossRef] [PubMed]
- Tu, M.; Yang, M.F.; Kao, S.L.; Lin, F.C.; Wu, M.H.; Lin, C.K. Using a heuristic multi-objective genetic algorithm to solve the storage assignment problem for CPS-based pick-and-pass system. Enterp. Inf. Syst. 2021, 15, 1238–1259. [Google Scholar] [CrossRef]
- Winkelmann, D.; Tolkmitt, F.; Ulrich, M.; Römer, M. Integrated storage assignment for an e-grocery fulfilment centre: Accounting for day-of-week demand patterns. Flex. Serv. Manuf. J. 2024, 37, 558–598. Available online: https://arxiv.org/pdf/2209.03998 (accessed on 25 September 2025). [CrossRef]
- Engels, T.; Adan, I.; Boxma, O.; Resing, J. An exact analysis and comparison of manual picker routing heuristics. Queueing Syst. 2024, 108, 611–660. [Google Scholar] [CrossRef]
- Ratliff, H.D.; Rosenthal, A.S. Order-picking in a rectangular warehouse: A solvable case of the traveling salesman problem. Oper. Res. 1983, 31, 507–521. [Google Scholar] [CrossRef]
- De Koster, R.Â.; Poort, E.V.D. Routing orderpickers in a warehouse: A comparison between optimal and heuristic solutions. IIE Trans. 1998, 30, 469–480. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, X.; Chen, L.; You, S.; Li, F.; Cao, Y. Effective storage location assignment model based on a genetic simulation annealing algorithm. Int. J. Wirel. Mob. Comput. 2020, 19, 9–17. [Google Scholar] [CrossRef]
- Sebo, J.; Busa, J. Comparison of advanced methods for picking path optimization: Case study of dual-zone warehouse. Int. J. Simul. Model. 2020, 19, 410–421. [Google Scholar] [CrossRef]
- van Gils, T.; Ramaekers, K.; Caris, A.; de Koster, R.B.M. Designing efficient order-picking systems by combining planning problems: State-of-the-art classification and review. Eur. J. Oper. Res. 2018, 267, 1–15. [Google Scholar] [CrossRef]
- Caron, F.; Marchet, G.; Perego, A. Routing policies and COI-based storage policies in picker-to-part systems. Int. J. Prod. Res. 1998, 36, 713–732. [Google Scholar] [CrossRef]
- Zuñiga, J.B.; Martínez, J.A.S.; Fierro, T.E.S.; Saucedo, J.A.M. Optimization of the storage location assignment and the picker-routing problem by using mathematical programming. Appl. Sci. 2020, 10, 534. [Google Scholar] [CrossRef]
- Kovac, M.; Djurdjevic, D. Optimization of order-picking systems through tactical and operational decision making. Int. J. Simul. Model. 2020, 19, 89–99. [Google Scholar] [CrossRef]
- Kübler, P.; Glock, C.; Bauernhansl, T. A new iterative method for solving the joint dynamic storage location assignment, order batching and picker routing problem in manual picker-to-parts warehouses. Comput. Ind. Eng. 2020, 147, 106645. [Google Scholar] [CrossRef]
- Silva, A.; Coelho, L.C.; Darvish, M.; Renaud, J. Integrating storage location and order-picking problems in warehouse planning. Transp. Res. E Logist. Transp. Rev. 2020, 140, 102003. [Google Scholar] [CrossRef]
- Bengtsson, M.; Wittsten, J.; Waidringer, J. warehouse storage and retrieval optimization via clustering, dynamic systems modeling, and GPU-accelerated routing. arXiv 2025, arXiv:2504.20655. Available online: http://arxiv.org/abs/2504.20655 (accessed on 25 September 2025). [CrossRef]
- Casella, G.; Volpi, A.; Montanari, R.; Tebaldi, L.; Bottani, E. Trends in order-picking: A 2007–2022 review of the literature. Prod. Manuf. Res. 2023, 11, 2191115. [Google Scholar] [CrossRef]
- Roman, E.-A.; Stere, A.-S.; Roșca, E.; Radu, A.-V.; Codroiu, D.; Anamaria, I. State of the Art of Digital Twins in Improving Supply Chain Resilience. Logistics 2025, 9, 22. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).