Driving Mechanisms of Urban Form on Anthropogenic Carbon Emissions: An RSG-Net Ensemble Model for Targeted Carbon Reduction Strategies
Abstract
1. Introduction
2. Materials and Methods
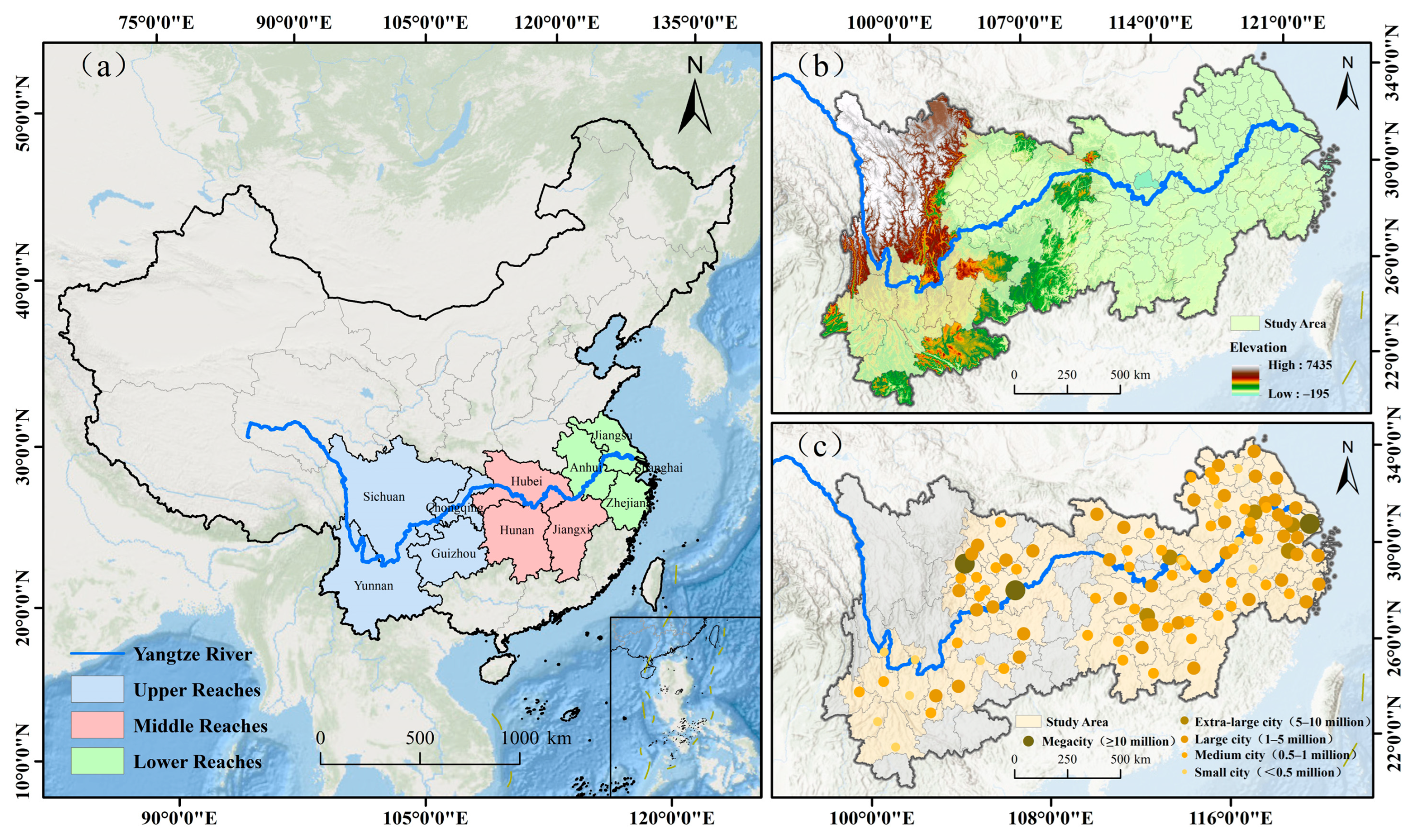
2.1. Study Area
2.2. Data Sources
2.3. Research Methods
2.3.1. ACE Accounting Method
2.3.2. UF Extraction Method
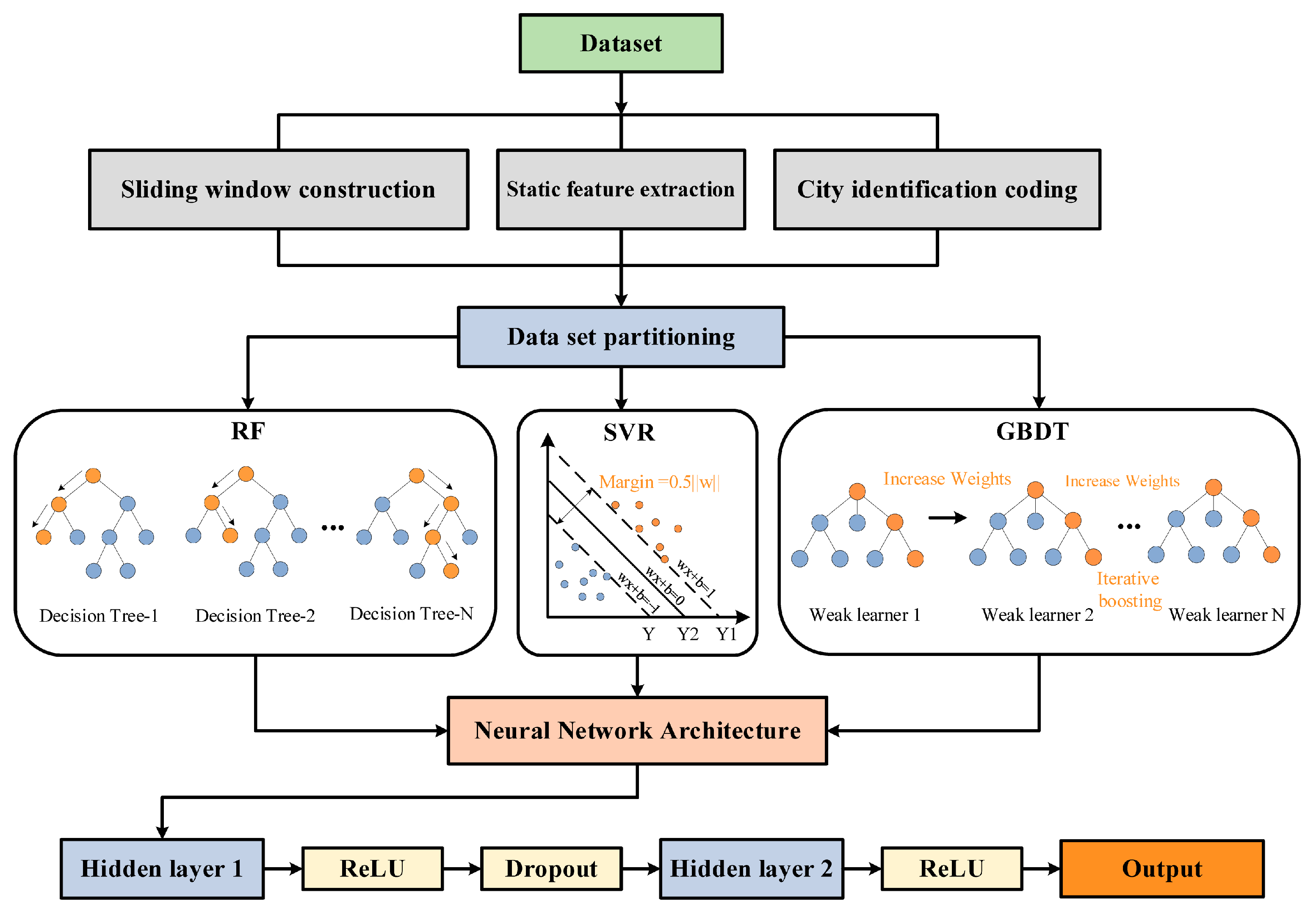
2.3.3. Modeling Methods
- 1.
- GBDT
- 2.
- RF
- 3.
- SVR
- 4.
- RSG-Net
2.3.4. Evaluation of Model Accuracy
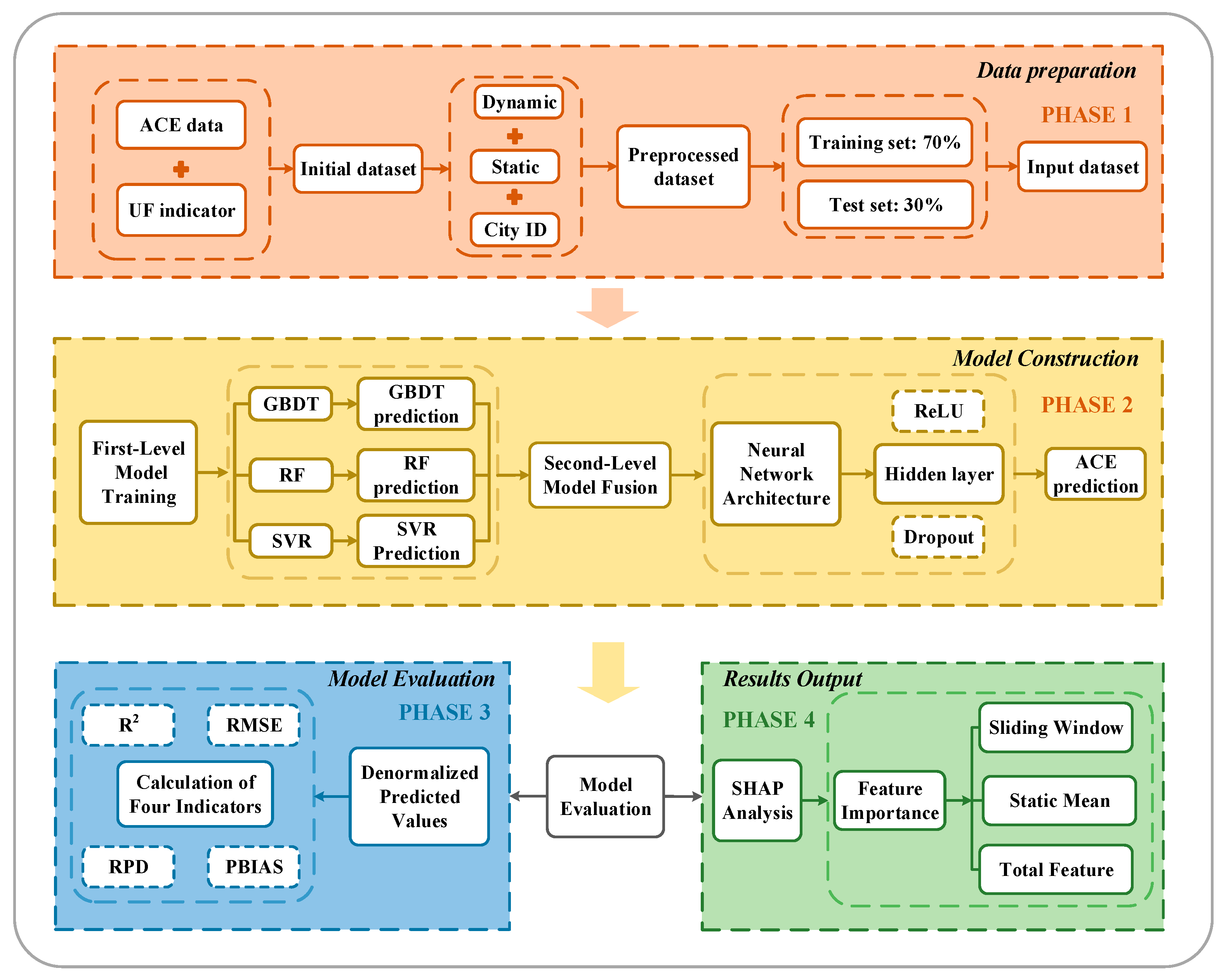
2.3.5. Model Building
3. Results
3.1. ACE Inversion Analysis
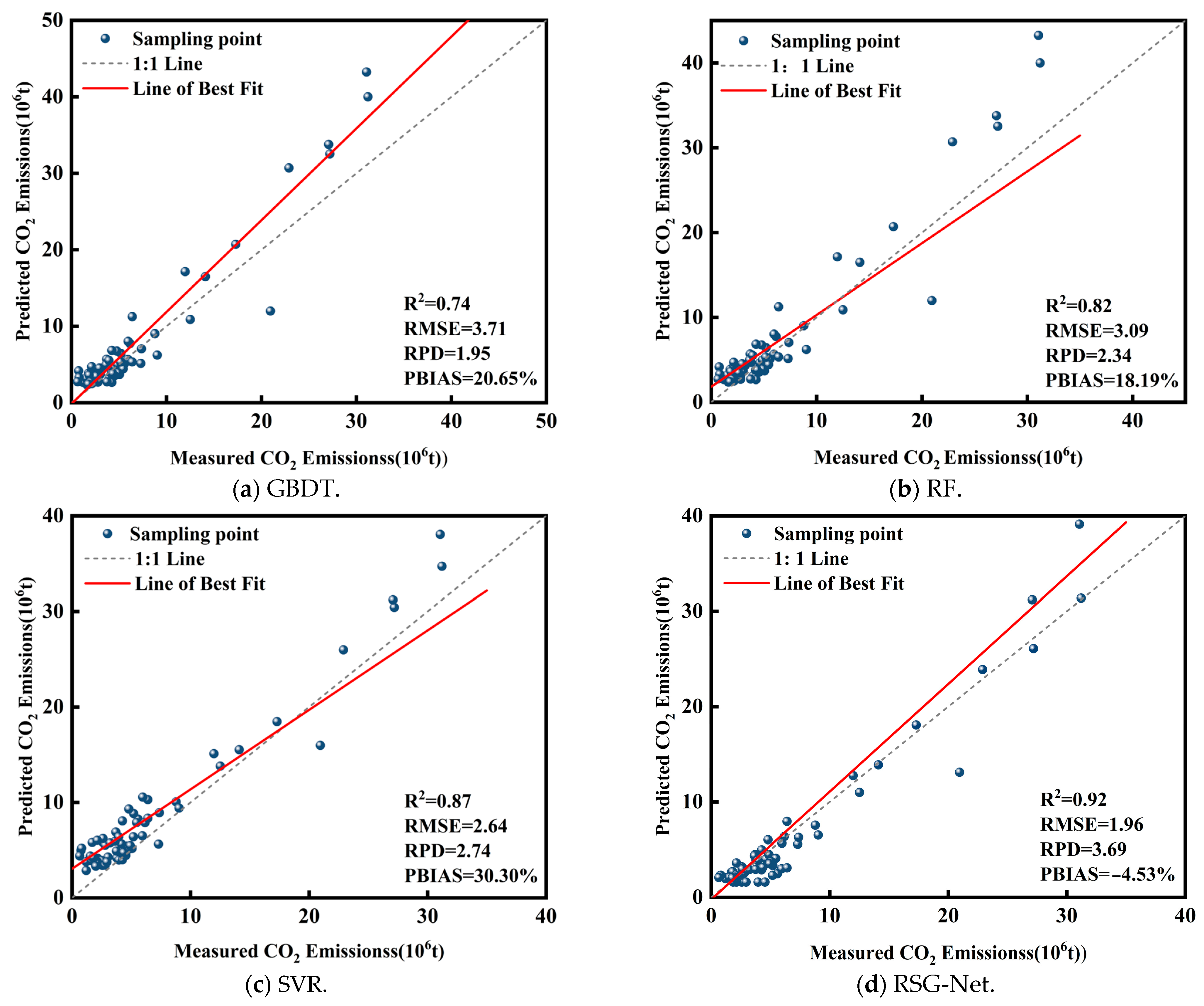
3.1.1. CO2 Prediction Model
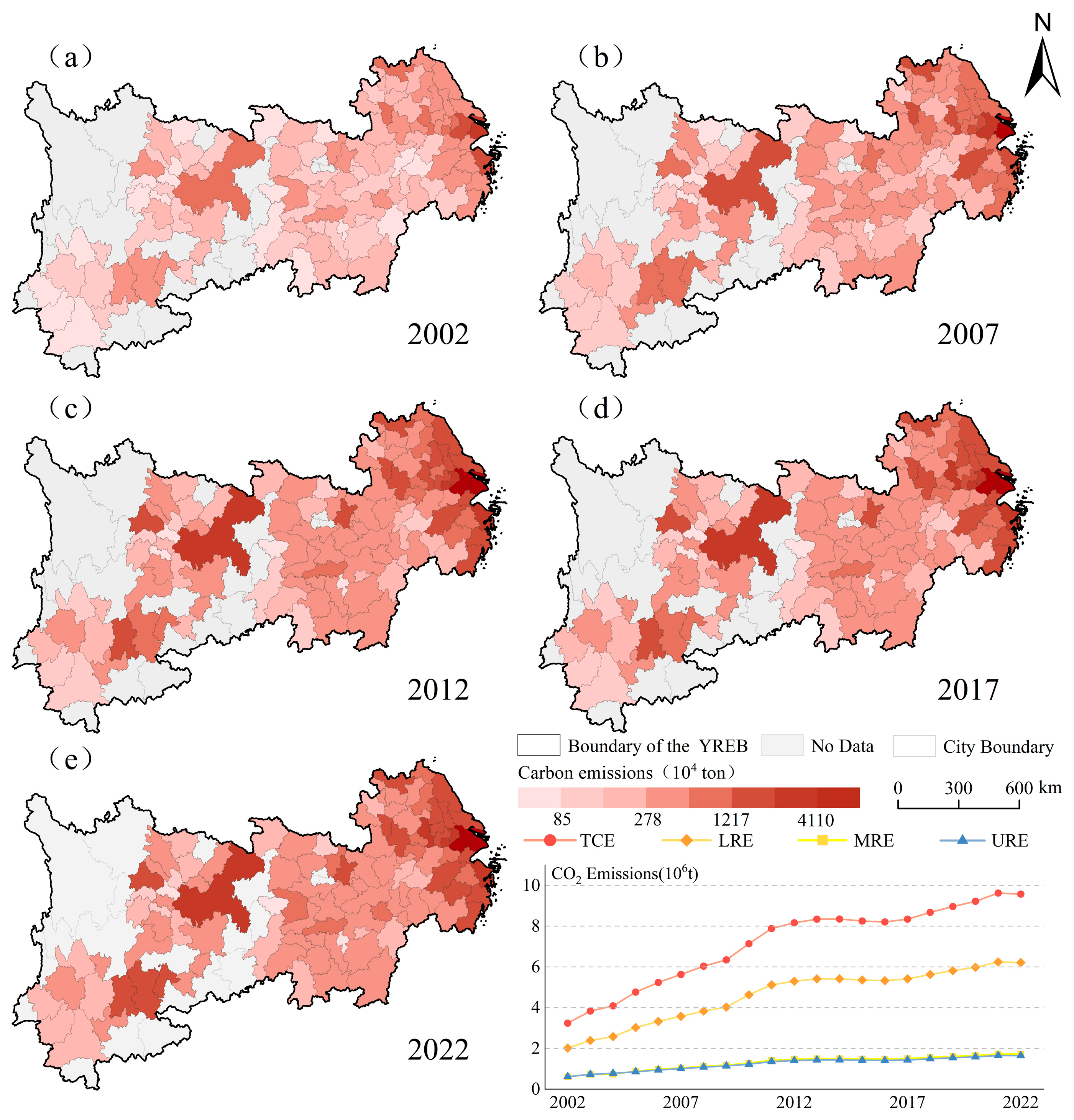
3.1.2. ACE Spatio-Temporal Evolution Analysis
3.2. UF Indicators Analysis
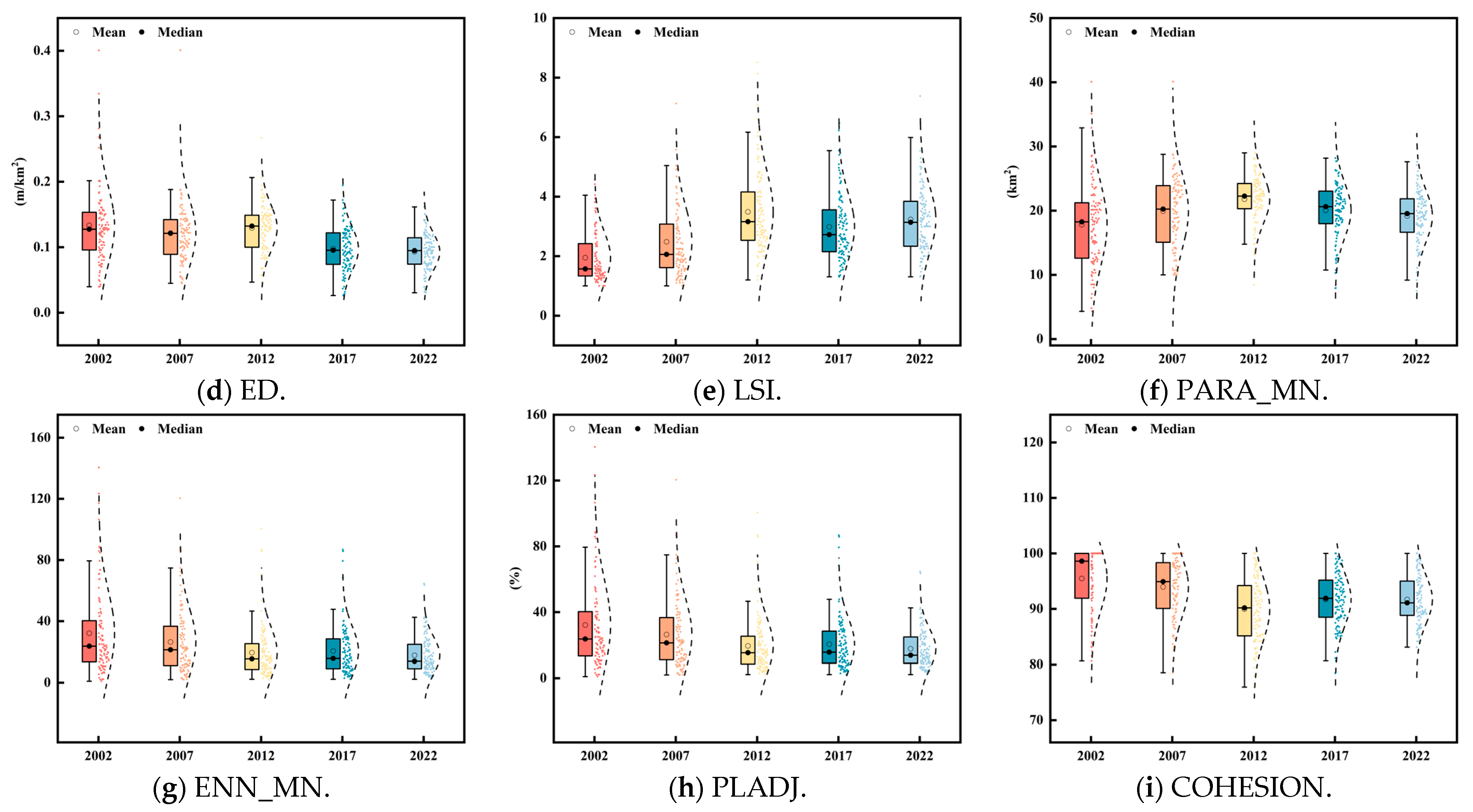
3.2.1. UF Landscape Pattern Index Analysis
3.2.2. UF Characteristic Element Analysis
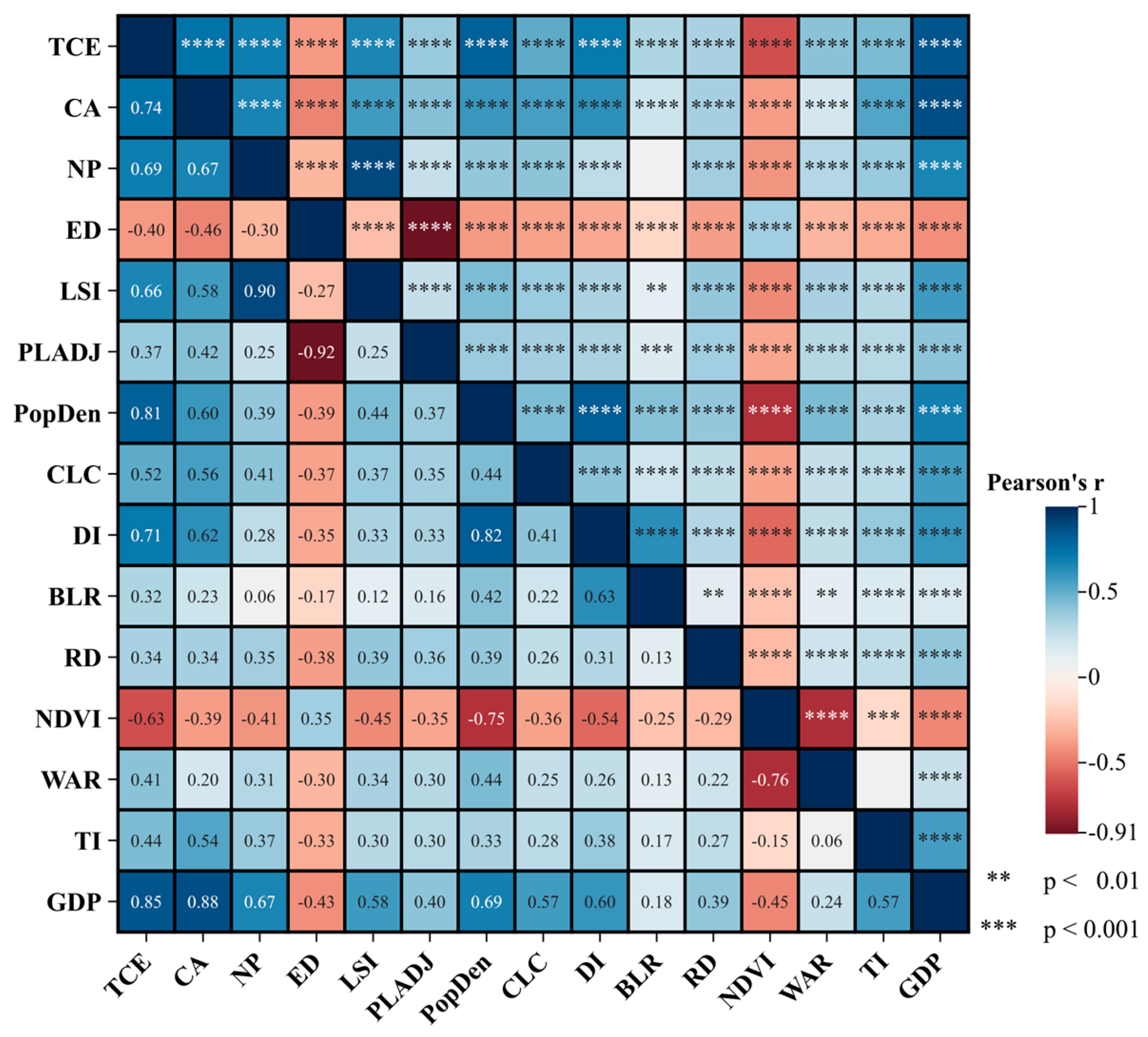
3.3. Correlation Analysis Between ACE and UF Indicators
3.4. Model Analysis
4. Discussion
4.1. Model Performance
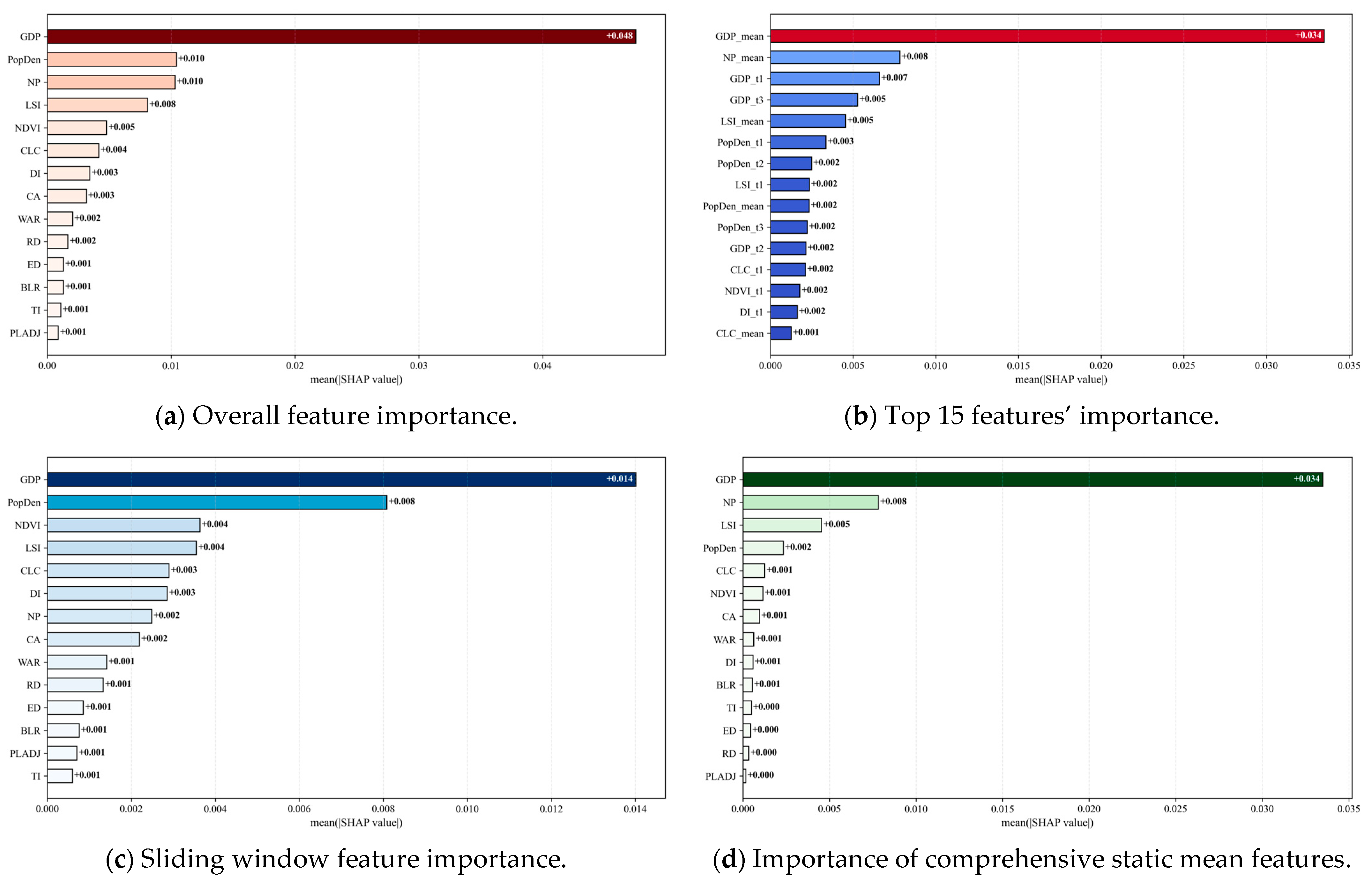
4.2. The Importance of Indicators
4.3. Carbon Reduction Pathways
5. Conclusions
- (1)
- From 2002 to 2022, the TCE of the YREB increased from 323.64 Mt to 957.42 Mt (Table 5), with its growth rate exhibiting a pattern of rapid growth, slowdown, and recovery (Figure 4). Spatially, the distribution pattern evolved from a unipolar agglomeration centered on the Yangtze River Delta in 2002, progressed through the diffusion of secondary growth poles in the Wuhan Metropolitan Area and Chengdu-Chongqing Urban Agglomeration during 2007–2017, and finally transformed into a new multipolar synergistic spatial model featuring watershed-wide coordination by 2022.
- (2)
- The RSG-Net ensemble model outperforms individual base models in ACE prediction, achieving an R2 of 0.93, an RPD of 3.69, an RMSE of 1.96 Mt, and a PBIAS of 4.53%. These results indicate that the two-stage hybrid architecture effectively mitigates the limitations of GBDT, RF, and SVR, such as sensitivity to outliers, weak temporal dependency capture, and limited accuracy without optimization. By integrating the complementary strengths of the base learners, RSG-Net significantly enhances prediction stability and accuracy, confirming the effectiveness of combining ensemble learning with meta-learning in carbon emission modeling.
- (3)
- By combining Pearson correlation and SHAP feature importance analysis, a significant correlation between UF and ACE is confirmed: ACE is positively correlated with CA, NP, LSI, PopDen, GDP, CLC, and WAR, and negatively correlated with PD, LPI, ED, ENN_MN, NDVI, and SI. The key UF factors, ranked by importance, are GDP, PopDen, NP, LSI, NDVI, and CLC. Based on their mechanism, implementing measures such as promoting low-carbon economic transformation, enhancing urban spatial agglomeration, and strengthening ecological carbon sequestration can effectively reduce ACE values and facilitate precise urban carbon reduction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Year | STA | DV | IV | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TCE (104 t) | CA (km2) | NP (n) | PD (%) | LPI (%) | ED (m/km2) | LSI (−) | PARA_MN (km2) | ENN_MN (−) | PLADJ (%) | COHESION (−) | ||
| 2002 | Max | 2988.04 | 549.58 | 16.00 | 0.67 | 100.00 | 0.40 | 4.57 | 40.07 | 140.47 | 90.11 | 100.00 |
| Min | 19.63 | 2.60 | 1.00 | 0.00 | 31.78 | 0.04 | 1.00 | 4.30 | 0.99 | 0.00 | 47.10 | |
| Mean | 302.47 | 67.57 | 3.14 | 0.09 | 85.12 | 0.13 | 1.95 | 17.80 | 32.10 | 66.87 | 94.54 | |
| Std | 378.90 | 83.72 | 3.15 | 0.10 | 18.69 | 0.06 | 0.87 | 6.34 | 27.71 | 14.69 | 8.07 | |
| 2007 | Max | 5423.49 | 885.67 | 27.00 | 1.01 | 100.00 | 0.40 | 7.13 | 40.13 | 120.47 | 88.82 | 100.00 |
| Min | 39.12 | 11.60 | 1.00 | 0.01 | 23.91 | 0.04 | 1.00 | 10.00 | 1.99 | 0.00 | 0.00 | |
| Mean | 526.19 | 91.51 | 5.02 | 0.07 | 79.36 | 0.12 | 2.48 | 19.91 | 26.39 | 69.79 | 93.09 | |
| Std | 701.54 | 125.98 | 4.91 | 0.11 | 19.07 | 0.05 | 1.19 | 5.86 | 21.70 | 12.70 | 10.49 | |
| 2012 | Max | 7456.85 | 1051.71 | 49.00 | 0.22 | 100.00 | 0.27 | 8.51 | 29.01 | 100.47 | 88.37 | 100.00 |
| Min | 55.64 | 15.18 | 1.00 | 0.01 | 23.46 | 0.05 | 1.20 | 8.44 | 2.23 | 33.33 | 75.96 | |
| Mean | 763.26 | 127.04 | 8.98 | 0.07 | 65.36 | 0.13 | 3.49 | 21.78 | 19.44 | 67.83 | 89.96 | |
| Std | 1034.27 | 167.79 | 7.85 | 0.04 | 17.30 | 0.04 | 1.35 | 3.73 | 16.94 | 8.80 | 5.56 | |
| 2017 | Max | 7614.04 | 1423.09 | 42.00 | 0.14 | 100.00 | 0.19 | 6.47 | 28.18 | 86.76 | 93.49 | 100.00 |
| Min | 56.74 | 22.50 | 1.00 | 0.00 | 33.68 | 0.03 | 1.31 | 7.92 | 2.23 | 51.72 | 78.45 | |
| Mean | 779.82 | 164.29 | 8.36 | 0.05 | 70.41 | 0.10 | 2.99 | 20.05 | 20.48 | 75.75 | 91.72 | |
| Std | 1056.53 | 209.58 | 7.00 | 0.03 | 16.45 | 0.03 | 1.11 | 4.19 | 16.05 | 8.22 | 4.70 | |
| 2022 | Max | 8735.16 | 1640.80 | 49.00 | 0.11 | 100.00 | 0.16 | 7.38 | 27.62 | 64.60 | 92.45 | 100.00 |
| Min | 65.05 | 23.24 | 1.00 | 0.00 | 32.42 | 0.03 | 1.31 | 7.48 | 2.23 | 59.81 | 83.11 | |
| Mean | 894.78 | 193.69 | 9.68 | 0.05 | 65.89 | 0.09 | 3.23 | 19.17 | 17.70 | 76.88 | 91.69 | |
| Std | 1212.21 | 252.11 | 7.59 | 0.02 | 17.01 | 0.03 | 1.11 | 3.93 | 12.14 | 6.96 | 4.27 | |
| Year | STA | DV | IV | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TCE (10−4 t) | PopDen (Person/km2) | RD (km/km2) | SI (%) | TI (%) | GDP (Billion Yuan) | NDVI (−) | WAR (%) | DI (−) | BLR (%) | CLC (−) | ||
| 2002 | Max | 2988.04 | 2585.49 | 1.26 | 68.70 | 56.15 | 5795.02 | 0.82 | 0.37 | 0.29 | 3.32 | 0.30 |
| Min | 19.63 | 56.64 | 0.23 | 19.70 | 24.10 | 36.95 | 0.49 | 0.00 | 0.00 | 0.10 | 0.00 | |
| Mean | 302.47 | 473.39 | 0.50 | 43.02 | 36.58 | 454.50 | 0.74 | 0.05 | 0.01 | 0.97 | 0.05 | |
| Std | 378.90 | 326.61 | 0.19 | 10.21 | 5.64 | 676.72 | 0.05 | 0.06 | 0.03 | 0.29 | 0.06 | |
| 2007 | Max | 5423.49 | 3119.80 | 1.81 | 71.32 | 59.44 | 12,878.68 | 0.84 | 0.36 | 0.38 | 2.74 | 0.38 |
| Min | 39.12 | 58.48 | 0.28 | 23.79 | 23.92 | 84.82 | 0.51 | 0.00 | 0.00 | 0.43 | 0.00 | |
| Mean | 526.19 | 485.62 | 1.02 | 47.04 | 36.38 | 998.73 | 0.76 | 0.04 | 0.01 | 1.03 | 0.08 | |
| Std | 701.54 | 375.85 | 0.34 | 9.84 | 6.30 | 1536.70 | 0.05 | 0.05 | 0.04 | 0.24 | 0.08 | |
| 2012 | Max | 7456.85 | 3781.76 | 2.24 | 75.86 | 62.33 | 21,305.59 | 0.84 | 0.35 | 0.46 | 2.91 | 0.46 |
| Min | 55.64 | 58.65 | 0.32 | 25.20 | 20.66 | 212.24 | 0.45 | 0.00 | 0.00 | 0.01 | 0.00 | |
| Mean | 763.26 | 501.48 | 1.21 | 51.74 | 35.23 | 2172.80 | 0.75 | 0.05 | 0.02 | 1.00 | 0.08 | |
| Std | 1034.27 | 443.03 | 0.39 | 8.25 | 8.14 | 2889.03 | 0.07 | 0.05 | 0.05 | 0.27 | 0.08 | |
| 2017 | Max | 7614.04 | 4034.45 | 2.33 | 66.40 | 69.84 | 30,429.26 | 0.87 | 0.34 | 0.30 | 1.91 | 0.34 |
| Min | 56.74 | 60.25 | 0.38 | 19.48 | 17.71 | 330.03 | 0.50 | 0.00 | 0.00 | 0.74 | 0.01 | |
| Mean | 779.82 | 519.65 | 1.34 | 45.24 | 43.31 | 3354.16 | 0.77 | 0.05 | 0.02 | 0.98 | 0.08 | |
| Std | 1056.53 | 466.46 | 0.41 | 7.17 | 7.96 | 4362.24 | 0.06 | 0.05 | 0.03 | 0.13 | 0.07 | |
| 2022 | Max | 8735.16 | 4729.46 | 2.63 | 4737.00 | 74.12 | 44,653.00 | 0.88 | 0.31 | 0.17 | 1.42 | 1.21 |
| Min | 65.05 | 58.10 | 0.00 | 12.81 | 35.27 | 592.00 | 0.49 | 0.00 | 0.00 | 0.62 | 0.01 | |
| Mean | 894.78 | 518.14 | 1.50 | 85.11 | 48.46 | 4997.47 | 0.76 | 0.04 | 0.02 | 0.96 | 0.11 | |
| Std | 1212.21 | 519.93 | 0.49 | 451.89 | 6.85 | 6408.03 | 0.07 | 0.05 | 0.02 | 0.11 | 0.18 | |
References
- Cai, B.; Zhang, L. Urban CO2 Emissions in China: Spatial Boundary and Performance Comparison. Energy Policy 2014, 66, 557–567. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Fang, C.; Li, S. Estimating the Impacts of Urban Form on CO2 Emission Efficiency in the Pearl River Delta, China. Cities 2019, 85, 117–129. [Google Scholar] [CrossRef]
- Xiang, W.; Lan, Y.; Gan, L.; Li, J. How Does New Urbanization Affect Urban Carbon Emissions? Evidence Based on Spatial Spillover Effects and Mechanism Tests. Urban Clim. 2024, 56, 102060. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, Z.; Davis, S.J.; Giron, C.; Ciais, P. Monitoring Global Carbon Emissions in 2021. Nat. Rev. Earth Environ. 2022, 3, 217–219. [Google Scholar] [CrossRef]
- Wei, L.; Liu, Z. Spatial Heterogeneity of Demographic Structure Effects on Urban Carbon Emissions. Environ. Impact Assess. Rev. 2022, 95, 106790. [Google Scholar] [CrossRef]
- Li, J.S.; Zhou, H.W.; Meng, J.; Yang, Q.; Chen, B.; Zhang, Y.Y. Carbon Emissions and Their Drivers for a Typical Urban Economy from Multiple Perspectives: A Case Analysis for Beijing City. Appl. Energy 2018, 226, 1076–1086. [Google Scholar] [CrossRef]
- Lei, H.; Zeng, S.; Namaiti, A.; Zeng, J. The Impacts of Road Traffic on Urban Carbon Emissions and the Corresponding Planning Strategies. Land 2023, 12, 800. [Google Scholar] [CrossRef]
- Du, L.; Li, X.; Zhao, H.; Ma, W.; Jiang, P. System Dynamic Modeling of Urban Carbon Emissions Based on the Regional National Economy and Social Development Plan: A Case Study of Shanghai City. J. Clean. Prod. 2018, 172, 1501–1513. [Google Scholar] [CrossRef]
- Xie, R.; Fang, J.; Liu, C. The Effects of Transportation Infrastructure on Urban Carbon Emissions. Appl. Energy 2017, 196, 199–207. [Google Scholar] [CrossRef]
- Beller, E.E.; Kelly, M.; Larsen, L.G. From Savanna to Suburb: Effects of 160 Years of Landscape Change on Carbon Storage in Silicon Valley, California. Landsc. Urban Plan. 2020, 195, 103712. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, S.; Tong, X.; Lei, Z.; Gao, C.; Wang, J. Modeling Changes in China’s 2000–2030 Carbon Stock Caused by Land Use Change. J. Clean. Prod. 2020, 252, 119659. [Google Scholar] [CrossRef]
- Bereitschaft, B.; Debbage, K. Urban Form, Air Pollution, and CO2 Emissions in Large U.S. Metropolitan Areas. Prof. Geogr. 2013, 65, 612–635. [Google Scholar] [CrossRef]
- Shi, F.; Liao, X.; Shen, L.; Meng, C.; Lai, Y. Exploring the Spatiotemporal Impacts of Urban Form on CO2 Emissions: Evidence and Implications from 256 Chinese Cities. Environ. Impact Assess. Rev. 2022, 96, 106850. [Google Scholar] [CrossRef]
- Ding, G.; Guo, J.; Pueppke, S.G.; Yi, J.; Ou, M.; Ou, W.; Tao, Y. The Influence of Urban Form Compactness on CO2 Emissions and Its Threshold Effect: Evidence from Cities in China. J. Environ. Manag. 2022, 322, 116032. [Google Scholar] [CrossRef]
- Wu, J.; Li, C. Illustrating the Nonlinear Effects of Urban Form Factors on Transportation Carbon Emissions Based on Gradient Boosting Decision Trees. Sci. Total Environ. 2024, 929, 172547. [Google Scholar] [CrossRef]
- Li, M.; Zhou, Q.; Yang, Y. Study on the Influence of Urban Factors on Land Surface Temperature in Xi’an Based on Support Vector Machine. Intell. Build. Smart City 2023, 11, 13–15. [Google Scholar] [CrossRef]
- Dodangeh, E.; Choubin, B.; Eigdir, A.N.; Nabipour, N.; Panahi, M.; Shamshirband, S.; Mosavi, A. Integrated Machine Learning Methods with Resampling Algorithms for Flood Susceptibility Prediction. Sci. Total Environ. 2020, 705, 135983. [Google Scholar] [CrossRef]
- Chaturvedi, V.; De Vries, W.T. Machine Learning Algorithms for Urban Land Use Planning: A Review. Urban Sci. 2021, 5, 68. [Google Scholar] [CrossRef]
- Xing, Y.; Song, X.; Li, F.; Li, M.; Guo, Q.; Zhang, L. Ensemble Learning Algorithm Combined with Empirical Models for the Prediction of Urban Air Pollutant Emissions. Environ. Monit. China 2025, 41, 14–23. [Google Scholar] [CrossRef]
- Jiang, S.; Tian, S. Stacked Ensemble Learning for Predicting Carbon Emissions Throughout the Life Cycle of Buildings. In Proceedings of the 2025 4th International Conference on Distributed Computing and Electrical Circuits and Electronics (ICDCECE), Ballari, India, 25–26 April 2025; pp. 1–8. [Google Scholar]
- Requia, W.J.; Di, Q.; Silvern, R.; Kelly, J.T.; Koutrakis, P.; Mickley, L.J.; Sulprizio, M.P.; Amini, H.; Shi, L.; Schwartz, J. An Ensemble Learning Approach for Estimating High Spatiotemporal Resolution of Ground-Level Ozone in the Contiguous United States. Environ. Sci. Technol. 2020, 54, 11037–11047. [Google Scholar] [CrossRef]
- Yan, L.; Wang, L.; Liu, S.; Ding, Y. EnsembleCI: Ensemble Learning for Carbon Intensity Forecasting. In Proceedings of the 16th ACM International Conference on Future and Sustainable Energy Systems, Rotterdam, The Netherlands, 17–20 June 2025; pp. 208–212. [Google Scholar]
- Yang, D.; Luan, W.; Qiao, L.; Pratama, M. Modeling and Spatio-Temporal Analysis of City-Level Carbon Emissions Based on Nighttime Light Satellite Imagery. Appl. Energy 2020, 268, 114696. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, N.; Deng, H.; Wang, P.; Yang, F.; Qu, J.J.; Zhou, X. Monitoring Urban Carbon Emissions from Energy Consumption over China with DMSP/OLS Nighttime Light Observations. Theor. Appl. Climatol. 2022, 149, 983–992. [Google Scholar] [CrossRef]
- Song, M.; Wang, Y.; Han, Y.; Ji, Y. Estimation Model and Spatio-Temporal Analysis of Carbon Emissions from Energy Consumption with NPP-VIIRS-like Nighttime Light Images: A Case Study in the Pearl River Delta Urban Agglomeration of China. Remote Sens. 2024, 16, 3407. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H. Monitoring Spatiotemporal Characteristics of Land-Use Carbon Emissions and Their Driving Mechanisms in the Yellow River Delta: A Grid-Scale Analysis. Environ. Res. 2022, 214, 114151. [Google Scholar] [CrossRef]
- Chang, P.; Pang, X.; He, X.; Zhu, Y.; Zhou, C. Exploring the Spatial Relationship Between Nighttime Light and Tourism Economy: Evidence from 31 Provinces in China. Sustainability 2022, 14, 7350. [Google Scholar] [CrossRef]
- Liu, X.; Yang, X. The Accuracy of Nighttime Light Data to Estimate China’s Provincial Carbon Emissions: A Comparison with Carbon Emissions Allocated by International Carbon Database. Remote Sens. Technol. Appl. 2022, 37, 319–332. [Google Scholar]
- Xu, L.; Du, H.; Zhang, X. Driving Forces of Carbon Dioxide Emissions in China’s Cities: An Empirical Analysis Based on the Geodetector Method. J. Clean. Prod. 2021, 287, 125169. [Google Scholar] [CrossRef]
- Yang, W.; Yang, P.; Sun, X.; Han, B. Changes of landscape pattern and its impacts on multiple ecosystem services in Beijing. Acta Ecol. Sin. 2022, 42, 6487–6498. [Google Scholar]
- Lan, T.; Shao, G.; Xu, Z.; Tang, L.; Dong, H. Considerable Role of Urban Functional Form in Low-Carbon City Development. J. Clean. Prod. 2023, 392, 136256. [Google Scholar] [CrossRef]
- He, X.; Guan, D.; Yang, X.; Zhou, L.; Gao, W. Quantifying the Trends and Affecting Factors of CO2 Emissions Under Different Urban Development Patterns: An Econometric Study on the Yangtze River Economic Belt in China. Sustain. Cities Soc. 2024, 107, 105443. [Google Scholar] [CrossRef]
- Guan, D.; Shi, Y.; Zhou, L.; Zhu, X.; Zhao, D.; Peng, G.; He, X. Construction and Application of Carbon Emissions Estimation Model for China Based on Gradient Boosting Algorithm. Remote Sens. 2025, 17, 2383. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, G.; Li, P.; Wang, H.; Zhang, M.; Liang, X. An Improved Random Forest Based on the Classification Accuracy and Correlation Measurement of Decision Trees. Expert. Syst. Appl. 2024, 237, 121549. [Google Scholar] [CrossRef]
- Tang, Z.; Mei, Z.; Liu, W.; Xia, Y. Identification of the Key Factors Affecting Chinese Carbon Intensity and Their Historical Trends Using Random Forest Algorithm. J. Geogr. Sci. 2020, 30, 743–756. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Hao, P.Y. Shrinking the Tube: A New Support Vector Regression Algorithm with Parametric Insensitive Model. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; pp. 1871–1874. [Google Scholar]
- Song, X.; Zhang, X.; Sun, H.; Lin, S. Modelling of the fore-and-aft in-line seat transmissibility using the support vector regression with hyperparameter optimization algorithms. J. Vib. Eng. 2025, 8. [Google Scholar] [CrossRef]
- Pan, B.; Liu, W.; Diao, Z.; Gao, Q.; Huang, L.; Feng, S.; Du, J.; Wang, Q.; Li, J.; Cheng, J. Assessment of a Hyperspectral Remote Sensing Model Performance for Particulate Phosphorus in Optically Shallow Lake Water. J. Spectrosc. 2025, 2025, 9683030. [Google Scholar] [CrossRef]
- Li, H.; Long, M.; Li, G. Spatial-temporal dynamics of carbon dioxide emissions in China based on DMSP/OLS nighttime stable light data. China Environ. Sci. 2018, 38, 2777–2784. [Google Scholar] [CrossRef]
- Meng, L.; Graus, W.; Worrell, E.; Huang, B. Estimating CO2 (Carbon Dioxide) Emissions at Urban Scales by DMSP/OLS (Defense Meteorological Satellite Program’s Operational Linescan System) Nighttime Light Imagery: Methodological Challenges and a Case Study for China. Energy 2014, 71, 468–478. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, H.; Wang, H.; Che, Y.; Wang, J.; Liao, Y.; Lv, S. High-Carbon Expansion or Low-Carbon Intensive and Mixed Land-Use? Recent Observations from Megacities in Developing Countries: A Case Study of Shanghai, China. J. Environ. Manag. 2023, 348, 119294. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, G.; Zhang, Y. How Did Polycentric Spatial Structure Affect Carbon Emissions of the Construction Industry? A Case Study of 10 Chinese Urban Clusters. Eng. Constr. Archit. Manag. 2025, 32, 1186–1210. [Google Scholar] [CrossRef]
- Irwin, E.G.; Bockstael, N.E. The Evolution of Urban Sprawl: Evidence of Spatial Heterogeneity and Increasing Land Fragmentation. Proc. Natl. Acad. Sci. USA 2007, 104, 20672–20677. [Google Scholar] [CrossRef]
- Manley, W.; Tran, T.; Prusinski, M.; Brisson, D. Modeling Tick Populations: An Ecological Test Case for Gradient Boosted Trees. Peer Community J. 2023, 3, e116. [Google Scholar] [CrossRef]
- Djaballah, S.; Saidi, L.; Meftah, K.; Hechifa, A.; Bajaj, M.; Zaitsev, I. A Hybrid LSTM Random Forest Model with Grey Wolf Optimization for Enhanced Detection of Multiple Bearing Faults. Sci. Rep. 2024, 14, 23997. [Google Scholar] [CrossRef] [PubMed]
- Ehtsham, M.; Rotilio, M.; Cucchiella, F.; Di Giovanni, G.; Schettini, D. Investigating the Effects of Hyperparameter Sensitivity on Machine Learning Algorithms for PV Forecasting. E3S Web Conf. 2025, 612, 01002. [Google Scholar] [CrossRef]
- Hu, S.; Li, S.; Gong, L.; Liu, D.; Wang, Z.; Xu, G. Carbon Emissions Prediction Based on Ensemble Models: An Empirical Analysis from China. Environ. Model. Softw. 2025, 188, 106437. [Google Scholar] [CrossRef]
- Tang, D.; Zhang, Y.; Bethel, B.J. An Analysis of Disparities and Driving Factors of Carbon Emissions in the Yangtze River Economic Belt. Sustainability 2019, 11, 2362. [Google Scholar] [CrossRef]
- Patle, S.; Ghuge, V.V. Examining How Land Cover Variability and Urban Fragmentation Influence Land Surface Temperature and Thermal Comfort for Semi-Arid Cities. Sustain. Cities Soc. 2025, 130, 106540. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, W. Revealing Urban Carbon Dioxide (CO2) Emission Characteristics and Influencing Mechanisms from the Perspective of Commuting. Sustainability 2019, 11, 385. [Google Scholar] [CrossRef]
- Feng, R.; Wang, F.; Liu, S.; Qi, W.; Zhengchen, R.; Wang, D. Synergistic Effects of Urban Forest on Urban Heat Island-Air Pollution-Carbon Stock in Mega-Urban Agglomeration. Urban For. Urban Green. 2025, 103, 128590. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, X.; Peng, S. Effects of Urban Land Intensive Use on Carbon Emissions in China: Spatial Interaction and Multi-Mediating Effect Perspective. Environ. Sci. Pollut. Res. 2023, 30, 7270–7287. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hayashi, Y.; Chen, J.; Li, Q. Changing Urban Form and Transport CO2 Emissions: An Empirical Analysis of Beijing, China. Sustainability 2014, 6, 4558–4579. [Google Scholar] [CrossRef]



| Data Name | Period | Data Description | Data Source | Format |
|---|---|---|---|---|
| NPP-VIIRS-like nightlight data | 2002–2022 | Based on DMSP-OLS and NPP-VIIRS data, with a resolution of 500 m. | Harvard Dataverse | GeoTIFF |
| ODIAC Fossil Fuel Emission Data | Integrating multi-source data with a resolution of 1 × 1 km. | NIES | ||
| China 30-m Annual Land Cover Dataset | China’s annual land cover product (CLCD) from 1985 to 2022, with a spatial resolution of 30 m. | NCDDC (https://zenodo.org/records/8176941, accessed on 16 September 2025) | ||
| NDVI Dataset | Combine these monthly data to generate annual data with a spatial resolution of 1 km. | Global Resources Data Cloud(http://www.gis5g.com, accessed on 16 September 2025) | ||
| Socioeconomic statistics data | Involving population, transportation, land, economy, and other aspects. | China Urban Statistical Yearbook | Microsoft Excel | |
| Administrative boundaries | 2022 | The provincial and municipal boundaries were derived from the 2022 national boundary dataset. | National Basic Geographic Information Centre (http://www.ngcc.cn, accessed on 16 September 2025) | ESRI Shapefile |
| Dimensions | Indicator | Equation | Description | |
|---|---|---|---|---|
| LSPI | Sprawl | Class areas () | is area (km2) of urban patch . | |
| Number of Patches () | is the number of urban patches. | |||
| Edge density () | is total edge length (km) of urban patch . | |||
| Extended Nearest Neighbor with Mutual Neighborhood () | is the Euclidean nearest-neighbor distance of patch to its closest patch of the same type. is count of patches possessing valid nearest-neighbor relationships. | |||
| Complexity | Patch density () | is the number of urban patches. is total landscape area (km2). | ||
| Landscape shape index () | is total edge length (km) between patch types and . | |||
| Mean perimeter-area ratio ) | is perimeter (m) of urban patch k is area (km2) of urban patch . | |||
| Aggregation | Largest patch index () | is total landscape area (km2). | ||
| Proportion of like adjacencies () | is number of like adjacencies (joins) between pixels of patch types and based on the double-count method. | |||
| Patch cohesion index () | is perimeter of urban patch i in terms of number of cells. is the area of urban patch i in terms of number of cells. is the total number of cells in the landscape. | |||
| UMC | Population | Population Density (PopDen) | All indicators of characteristic elements are quantified based on socioeconomic statistical data. | |
| Road | Road Density (RD) | |||
| Land | Construction Land Concentration (CLC) | |||
| Development Intensity (DI) | ||||
| Built-up Land Ratio (BLR) | ||||
| UMC | Economy | Gross Domestic Product (GDP) | Added value of primary industry | All indicators of characteristic elements are quantified based on socioeconomic statistical data. |
| Share of Secondary Industry (SI%) | ||||
| Share of Tertiary Industry (TI%) | ||||
| Natura | Water Area Ratio (WAR) | The areas of each land cover category are extracted from the CLCD dataset. | ||
| NDVI | - | Based on monthly data, the average fusion generates annual synthetic data. | ||
| Sample Set | Number | Min (106 t) | Max (106 t) | Standard Deviation (106 t) |
|---|---|---|---|---|
| Training Set | 149 | 0.57 | 87.35 | 12.70 |
| Test Set | 65 | 0.65 | 31.22 | 7.24 |
| State | Regression Results | |||
|---|---|---|---|---|
| Regression Equation | R2 | F Value | p Value | |
| Anhui | y = 88.977x + 4636 | 0.918 | 133.946 | 0.00 |
| Guizhou | y = 89.173x + 2116.7 | 0.917 | 120.914 | 0.00 |
| Hubei | y = 74.804x + 2875.6 | 0.879 | 79.614 | 0.00 |
| Hunan | y = 85.948x + 2604.6 | 0.911 | 133.327 | 0.00 |
| Jiangsu | y = 105.64x + 8760.8 | 0.894 | 134.833 | 0.00 |
| Jiangxi | y = 73.209x + 1848.7 | 0.906 | 77.238 | 0.00 |
| Shanghai | y = 162.96x + 396.14 | 0.942 | 225.608 | 0.00 |
| Sichuan | y = 55.685x + 2727.7 | 0.910 | 121.393 | 0.00 |
| Yunnan | y = 99.487x + 2654.9 | 0.888 | 119.347 | 0.00 |
| Zhejiang | y = 77.01x + 5837 | 0.871 | 94.368 | 0.00 |
| Chongqing | y = 77.01x + 5837 | 0.890 | 105.624 | 0.00 |
| Type | Annual Total | ||||
|---|---|---|---|---|---|
| 2002 | 2007 | 2012 | 2017 | 2022 | |
| URE | 60.88 | 104.56 | 146.59 | 149.80 | 171.88 |
| MRE | 61.19 | 100.91 | 140.17 | 143.25 | 164.38 |
| LRE | 201.57 | 357.56 | 529.93 | 541.37 | 621.16 |
| TCE | 323.64 | 563.03 | 816.69 | 834.41 | 957.42 |
| Type | Indicators | ||||
|---|---|---|---|---|---|
| LSPI | CA | NP | PD | LPI | ED |
| 0.740 | 0.697 | −0.244 | −0.133 | −0.389 | |
| LSI | PARA_MN | ENN_MN | PLADJ | COHESION | |
| 0.662 | 0.089 | −0.280 | 0.375 | 0.130 | |
| UMC | PopDen | CLC | DI | BLR | RD |
| 0.793 | 0.512 | 0.706 | 0.319 | 0.320 | |
| NDVI | WAR | SI | TI | GDP | |
| −0.609 | 0.396 | −0.011 | 0.450 | 0.855 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, B.; Li, J.; Diao, Z.; Wang, Q.; Gao, Q.; Liu, W.; Shu, Y.; Feng, S. Driving Mechanisms of Urban Form on Anthropogenic Carbon Emissions: An RSG-Net Ensemble Model for Targeted Carbon Reduction Strategies. Appl. Sci. 2025, 15, 11175. https://doi.org/10.3390/app152011175
Pan B, Li J, Diao Z, Wang Q, Gao Q, Liu W, Shu Y, Feng S. Driving Mechanisms of Urban Form on Anthropogenic Carbon Emissions: An RSG-Net Ensemble Model for Targeted Carbon Reduction Strategies. Applied Sciences. 2025; 15(20):11175. https://doi.org/10.3390/app152011175
Chicago/Turabian StylePan, Banglong, Jiayi Li, Zhuo Diao, Qi Wang, Qianfeng Gao, Wuyiming Liu, Ying Shu, and Shaoru Feng. 2025. "Driving Mechanisms of Urban Form on Anthropogenic Carbon Emissions: An RSG-Net Ensemble Model for Targeted Carbon Reduction Strategies" Applied Sciences 15, no. 20: 11175. https://doi.org/10.3390/app152011175
APA StylePan, B., Li, J., Diao, Z., Wang, Q., Gao, Q., Liu, W., Shu, Y., & Feng, S. (2025). Driving Mechanisms of Urban Form on Anthropogenic Carbon Emissions: An RSG-Net Ensemble Model for Targeted Carbon Reduction Strategies. Applied Sciences, 15(20), 11175. https://doi.org/10.3390/app152011175






