The Mechanical Properties, Microstructure Analysis and Damage Behavior of AlMg7 Matrix Composites Reinforced with α-Al2O3 Particles
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Method of Composite Manufacturing
2.3. Material Characterization Methods
3. Results
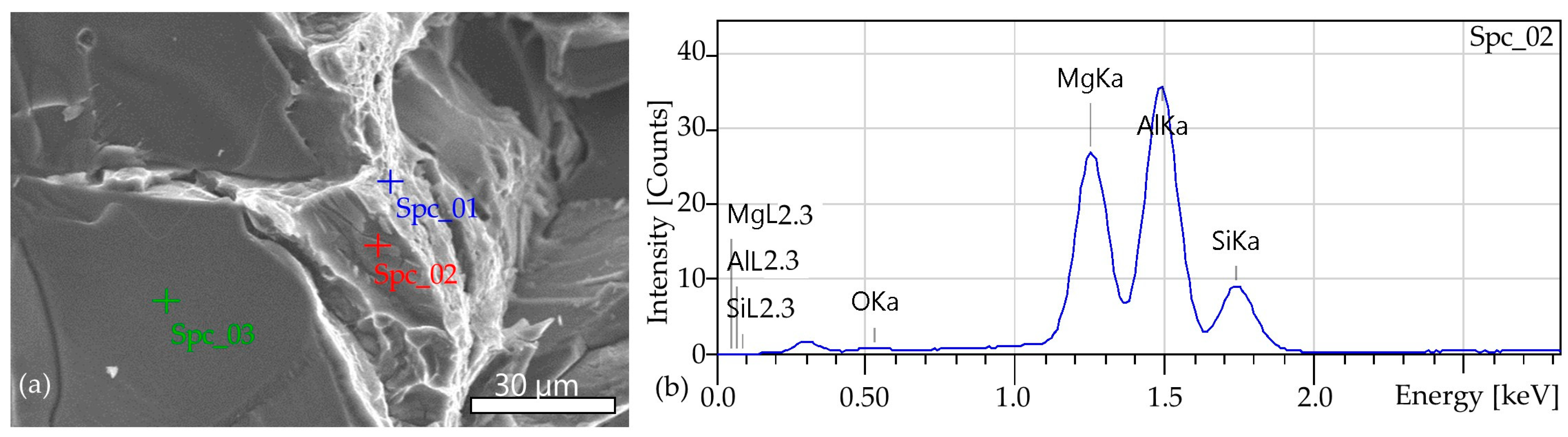
3.1. Identification and Microstructure
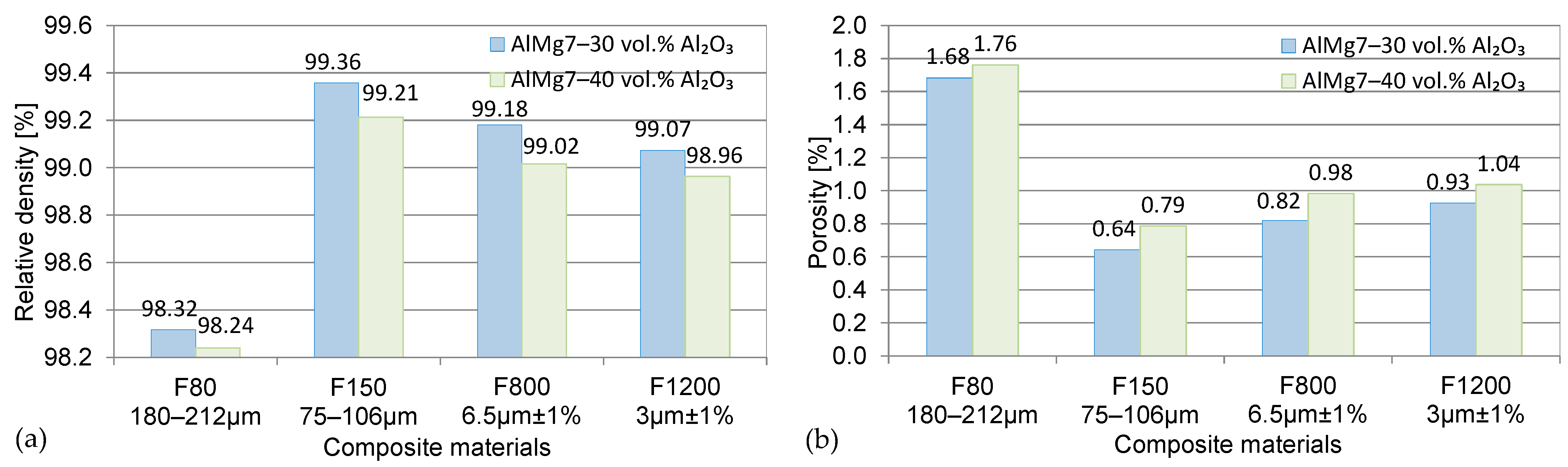
3.2. Density and Porosity
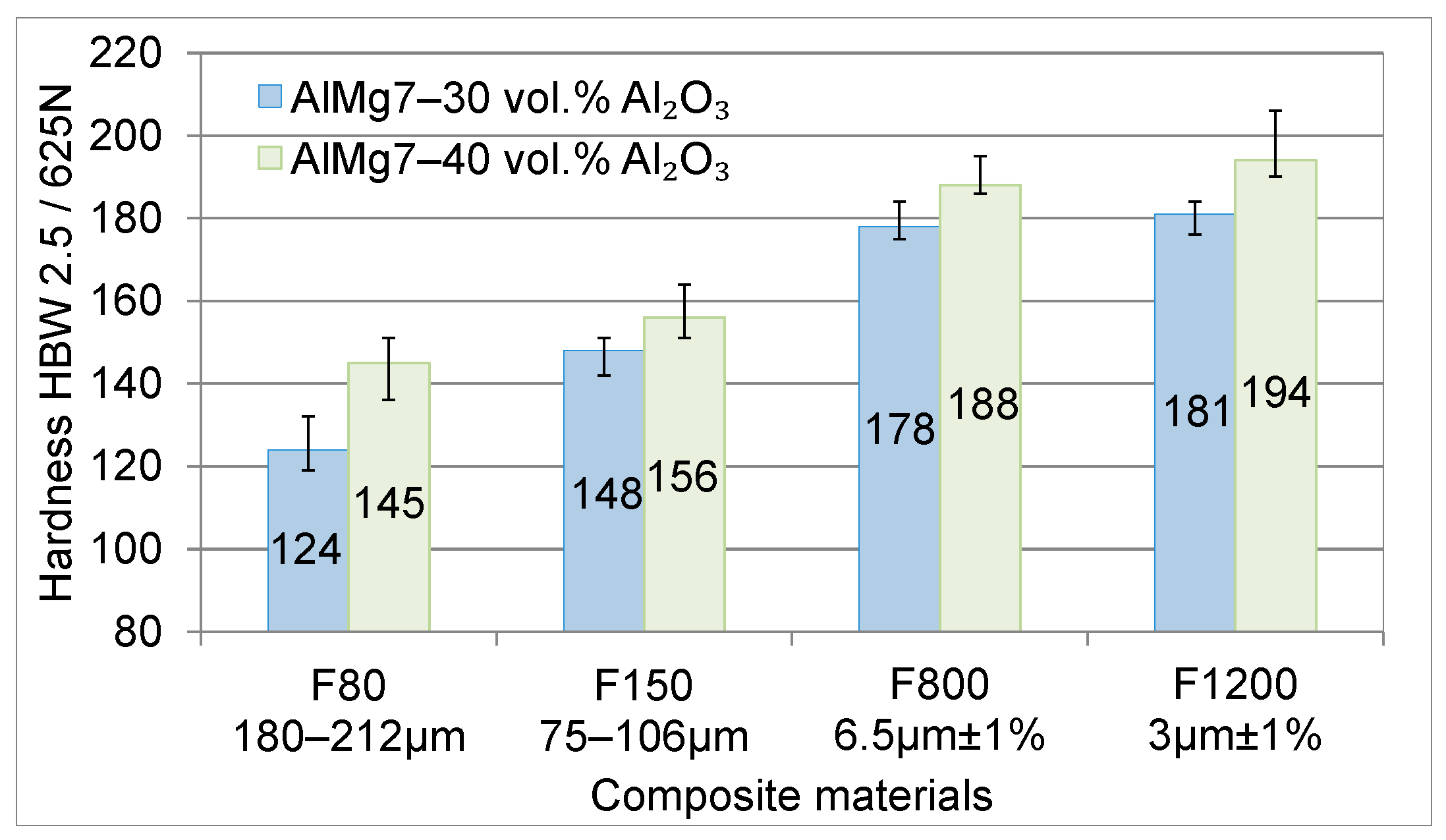
3.3. Hardness
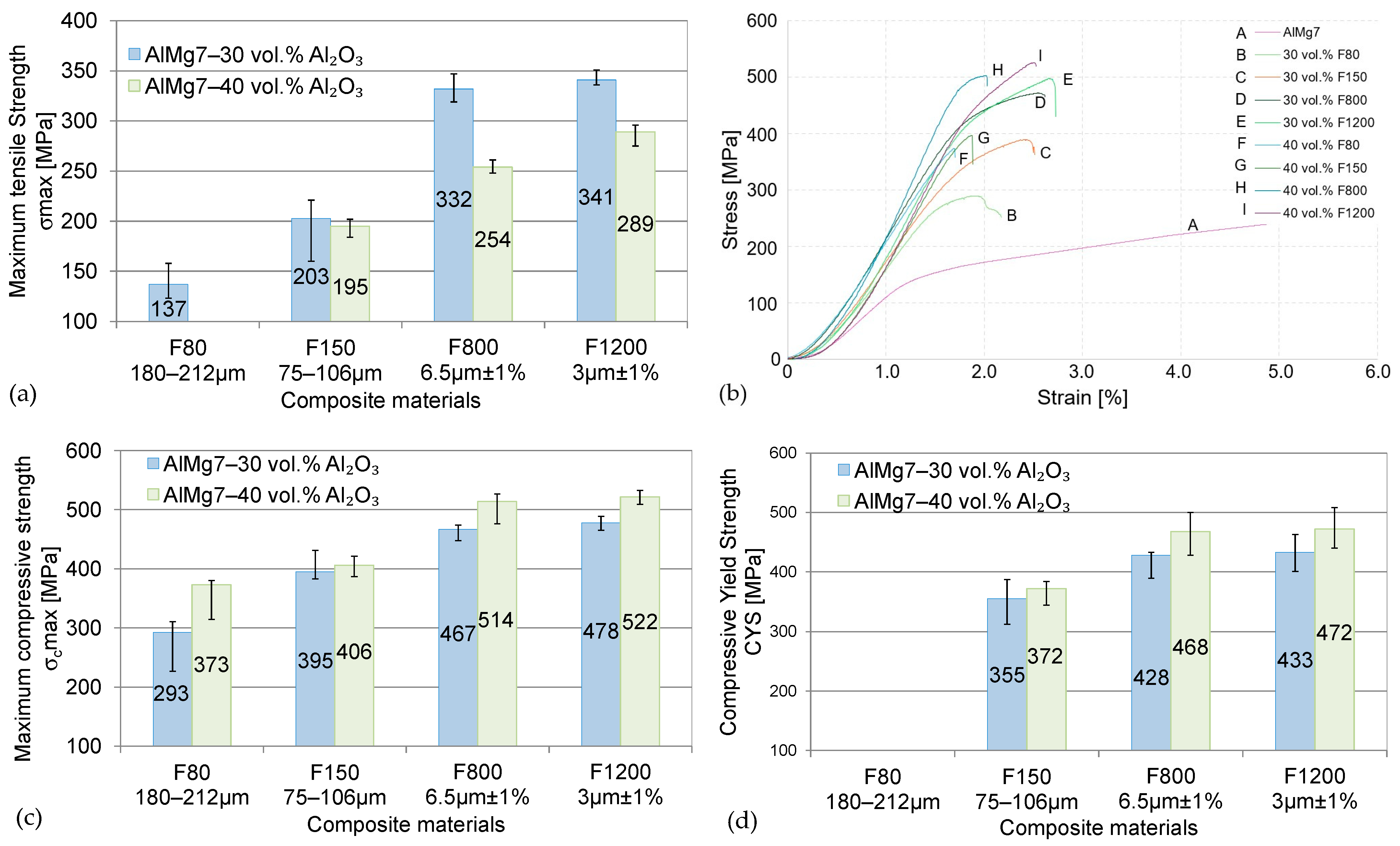
3.4. Tensile and Compressive Test
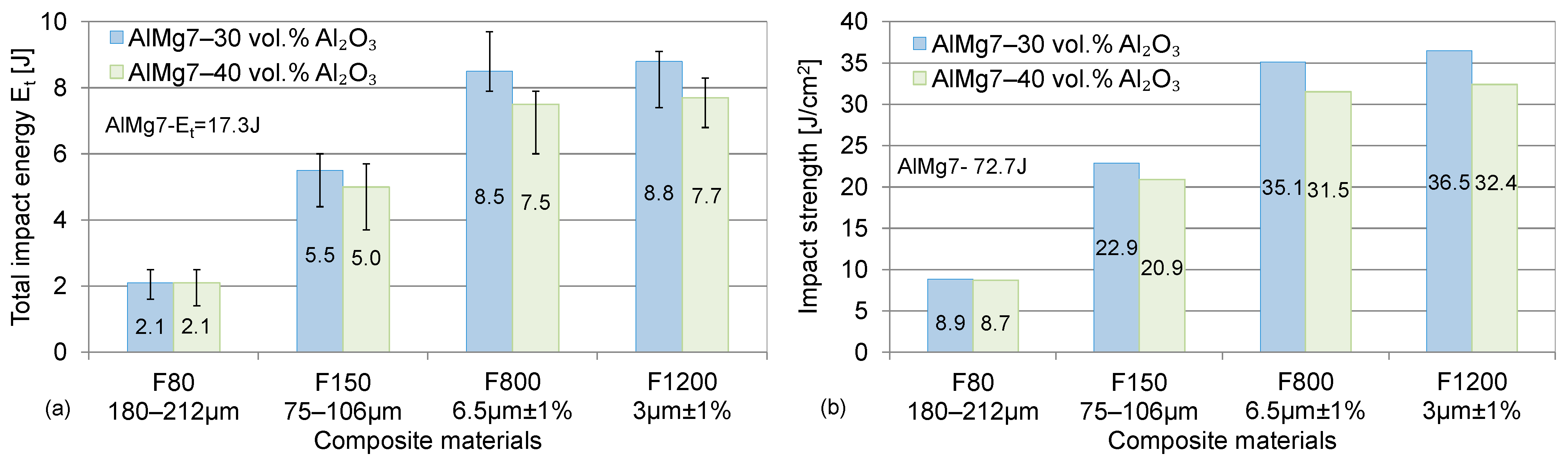
3.5. Impact Strength
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jurczak, W. Problemy i perspektywy stopów aluminiowych w zastosowaniu na konstrukcje morskie. Zesz. Nauk. Akad. Mar. Wojennej 2010, 51, 89–106. [Google Scholar]
- Mathew, G.; Kottur, V.K.N. Effect of ceramic reinforcements on the mechanical and tribological properties of aluminium metal matrix composites—A review. Mater. Today Proceedings 2023, in press. [CrossRef]
- Singh, L.; Sehgal, S.; Saxena, K.K. Behaviour of Al2O3 in aluminium matrix composites: An overview. E3S Web Conf. 2021, 309, 01028. [Google Scholar] [CrossRef]
- Dobrzański, L. Advanced Composites with Aluminum Alloys Matrix and Advanced Aluminium Composites and Alloys; IntechOpen: London, UK, 2021; pp. 3–15. [Google Scholar] [CrossRef]
- Song, C.-R.; Donga, B.-X.; Zhang, S.-Y.; Yang, H.-Y.; Liu, L.; Kang, J.; Meng, J.; Luo, C.-J.; Wang, C.-G.; Cao, K.; et al. Recent Progress–Mgalloys: Forming and preparation process, microstructure manipulation and application. J. Mater. Res. Technol. 2024, 31, 3255–3286. [Google Scholar] [CrossRef]
- Borowski, J.; Płaczek, G.; Andrzejewski, D.; Jurczak, H.; Leśniak, D. Mechanical properties of extruded profiles made of AlMg alloys. Met. Form. 2016, XXVII, 273–282. [Google Scholar]
- Zha, M.; Li, Y.; Mathiesen, R.H.; Bjørge, R.; Roven, H.J. High ductility bulk nanostructured Al–Mg binary alloy processed by equal channel angular pressing and inter-pass annealing. Scr. Mater. 2015, 105, 22–55. [Google Scholar] [CrossRef]
- Karandikar, P.; Watkins, M.; Aghajanian, M.; Kiler, E.M.; McWilliams, B. Al/Al2O3 Metal Matrix Composites (MMCs) and Macrocomposites for Armor Applications. In Proceedings of the 37th International Conference and Exposition on Advanced Ceramics and Composites (ICACC), Daytona Beach, FL, USA, 27 January–1 February 2013. [Google Scholar]
- Burziċ, Z.; Burzi, M. Influence of the reinforcement volume fraction on impact energy values of the cast Al-SiCp composites. In Proceedings of the 10th International Research/Expert Conference, Barcelona-Lloret de Mar, Spain, 11–15 September 2006. [Google Scholar]
- Endramawan, T.; Sifa, A.; Suwandi, D.; Riyanto, E. Manufacture of Aluminum-Magnesium Reinforced Metal Matrix Composite Silicon Carbide with Powder Metallurgy Method. In Proceedings of the 5th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES); SciTePress: Setúbal, Portugal, 2022; pp. 50–55. [Google Scholar] [CrossRef]
- Geng, L.; Zhang, H.; Li, H.; Guan, L.; Huang, L. Effects of Mg content on microstructure and mechanical properties of SiCp/Al-Mg composites fabricated by semi-solid stirring technique. Trans. Nonferrous Met. Soc. China 2010, 20, 1851–1855. [Google Scholar] [CrossRef]
- De Brito, C.C.; Magalhães, F.D.; Costa, A.L.M.; Siqueira, C.A. Microstructural analysis and tensile properties of squeeze cast Al-7%Mg Alloy. Mater. Sci. Forum 2010, 643, 119–123. [Google Scholar] [CrossRef]
- Pelevin, J.A.; Nalivaiko, A.Y.; Ozherelkov, D.Y.; Shinkaryov, A.S.; Chernyshikhin, S.V.; Arnautov, A.N.; Zmanovsky, S.V.; Gromov, A.A. Selective Laser Melting of Al-Based Matrix Composites with Al2O3 Reinforcement: Features and Advantages. Materials 2021, 14, 2648. [Google Scholar] [CrossRef] [PubMed]
- Taşkın, V.; Kılıç, C.; Yakut, R.; Taşkın, N.Ü. The Effects of Different Reinforcement Ratios on Wear Behaviors in EN AW 5754 (AlMg3)/SiCp Composite Materials Produced with the Squeeze Casting Method. BSEU J. Sci. 2022, 9, 42–51. [Google Scholar] [CrossRef]
- Giri, M.K.; Choubey, V.K.; Upadhyay, V. Evaluation of microstructure and mechanical behavior of a strengthened Al 5083 hybrid composite fabricated by squeezed assisted liquid metallurgy technique. Int. J. Interact. Des. Manuf. 2024, 18, 1611–1625. [Google Scholar] [CrossRef]
- Channi, A.S.; Cahnni, M.K. A Comparative Review on Mechanical and Tribological Properties of Al-TiB2 Composites Fabricated by Stir Casting and Squeeze Casting Techniques. IJISEM 2025, 4, 176–184. [Google Scholar] [CrossRef]
- Gül, K.A.; Sahin, H.; Dispinar, D. Assessment of Mechanical Behaviors of Sand Cast Al-Mg7-Cu2 Aluminum Alloy in Tilt and Vertical Gravity Casting Conditions. Arch. Foundry Eng. 2025, 25, 169–179. [Google Scholar] [CrossRef]
- Karthik, A.; Karunanithi, R.; Srinivasan, S.A.; Prashanth, M. The optimization of squeeze casting process parameter for AA2219 alloy by using the Taguchi method. Mater. Today Proc. 2020, 27, 2556–2561. [Google Scholar] [CrossRef]
- Szymański, P.; Popielarski, P.; Czarnecka-Komorowska, D.; Sika, R.; Gawdzińska, K. Determination of Saturation Conditions of the Aluminum Metal Matrix Composites Reinforced with Al2O3 Sinter. Materials 2023, 16, 6106. [Google Scholar] [CrossRef]
- Kumar, N.; Soren, S. Selection of reinforcement for Al/Mg alloy metal matrix composites. Mater. Today Proc. 2020, 21, 1605–1609. [Google Scholar] [CrossRef]
- Vinodh, D.; Lakshmaiya, N. Integration of ceramic reinforcements in AA5083 composites for enhanced mechanical and thermal properties in friction stir welding. Eng. Res. Express 2025, 7, 035519. [Google Scholar] [CrossRef]
- Siddaraju, N.; Satish, N.; Chandrashekar, A.; Reddappa, H.N.; Ajaykumar, B.S. Assessment of Tensile and Hardness Property of AA5083/Nano Al2O3 Metal Matrix Composites. Int. J. Compos. Mater. Matrices 2015, 1. Available online: https://www.academia.edu/33517366/International_Journals_of_Composite_Materials_And_Matrices_Assessment_of_Tensile_and_Hardness_Property_of_AA5083_Nano_Al_2_O_3_Metal_Matrix_Composites (accessed on 10 October 2025).
- Chandrashekar, A.; Chaluvaraju, B.A.; Afzal, A.; Vinnik, D.A.; Kaladgi, A.R.; Alamri, S.; C., A.S.; Tirth, V. Mechanical and Corrosion Studies of Friction Stir Welded Nano Al2O3 Reinforced Al-Mg Matrix Composites: RSM-ANN Modelling Approach. Symmetry 2021, 13, 537. [Google Scholar] [CrossRef]
- Tosun, G.; Kurt, M. The porosity, microstructure, and hardness of Al-Mg composites reinforced with micro particle SiC/Al2O3 produced using powder metallurgy. Compos. Part B 2019, 174, 106965. [Google Scholar] [CrossRef]
- Kurzawa, A.; Kaczmar, J.W. Bending Strength of Composite Materials with EN AC-44200 Matrix Reinforced with Al2O3 Particles. Arch. Foundry Eng. 2017, 17, 103–108. [Google Scholar] [CrossRef]
- Akcay, S.B.; Varol, T.; Aksa, H.C.; Güler, O. Al2024/SiC Kompozitlerin Yüksek SiC Takviyesi ile Üretimi ve Karakterizasyonu. AKU J. Sci. Eng. 2022, 22, 353–365. [Google Scholar] [CrossRef]
- Lee, T.; Lee, J.; Lee, D.; Jo, I.; Lee, S.K.; Ryu, H.J. Effects of particle size and surface modification of SiC on the wear behavior of high volume fraction Al/SiCp composites. J. Alloys Compd. 2020, 831, 154647. [Google Scholar] [CrossRef]
- Kurzawa, A.; Pyka, D.; Jamroziak, K. Analysis of Ballistic Resistance of Composites with EN AW-7075 Matrix Reinforced with Al2O3 Particles. Arch. Foundry Eng. 2020, 20, 73–78. [Google Scholar] [CrossRef]
- Prasath, V.M.; Kumar, S.D.; Kumar, S.S. Influence of cryogenic treatment on mechanical and ballistic properties of AA5754 alloy friction stir welded joints. Def. Technol. 2025, 46, 184–198. [Google Scholar] [CrossRef]
- Rusu, O.; Rusu, I. Comparative study on antiballistic behaviour of AlMg10-SiCp type cellular ultralight composite metal materials. IOP Conf. Ser. Mater. Sci. Eng. 2019, 591, 012039. [Google Scholar] [CrossRef]
- Kurzawa, A.; Pyka, D.; Jamroziak, K.; Bajkowski, M.; Bocian, M.; Magier, M.; Koch, J. Assessment of the Impact Resistance of a Composite Material with EN AW-7075 Matrix Reinforced with-Al2O3 Particles Using a 7.62 39 mm Projectile. Materials 2020, 13, 769. [Google Scholar] [CrossRef]
- Park, D.-H.; Choi, S.-W.; Kim, J.-H.; Lee, J.-M. Cryogenic mechanical behavior of 5000- and 6000-series aluminum alloys: Issues on application to offshore plants. Cryogenics 2015, 68, 44–58. [Google Scholar] [CrossRef]
- Ye, T.; Jia, Z.-Y.; Ma, J.-W.; Yu, W.-J.; Wang, J.-S.; Zhang, L.-W.; Tian, X.-B.; Wang, S. Mechanical and tribological properties of 5A06 aluminum alloy at low temperature. Surf. Topogr. Metrol. Prop. 2023, 11, 015011. [Google Scholar] [CrossRef]
- Jin, F.; Ji, X. Effects of Composite Processing on Microstructures and Properties of Al-Mg Alloy. In Proceedings of the 2021 4th World Conference on Mechanical Engineering and Intelligent Manufacturing, Shanghai, China, 12–14 November 2021. [Google Scholar] [CrossRef]
- Cheng, X.; Yu, H.; Lyu, F.; Jiang, X.; Zhong, Y. Mechanical properties and microstructure evolution of 5A06 aluminum alloy under two-step dynamic tension. Mater. Sci. Eng. A 2025, 926, 147958. [Google Scholar] [CrossRef]
- Heyduk, F.; Grabiec, D.; Lijewski, M. Manufacture by means of KOBO cold extrusion method of welding wire with increased magnesium content for welding profiles of aluminum alloys. Met. Form. 2018, XXIX, 87–96. [Google Scholar]
- Zayed, E.M.; El-Tayeb, N.S.M.; Ahmed, M.M.Z.; Rashad, R.M. Development and Characterization of AA5083 Reinforced with SiC and Al2O3 Particles by Friction Stir Processing. Eng. Des. Appl. Adv. Struct. Mater. 2019, 92, 11–26. [Google Scholar] [CrossRef]
- Kurzawa, A.; Pyka, D.; Jamroziak, K.; Bocian, M.; Kotowski, P.; Widomski, P. Analysis of ballistic resistance of composites based on EN AC-44200 aluminum alloy reinforced with Al2O3 particles. Compos. Struct. 2018, 201, 834–844. [Google Scholar] [CrossRef]
- Kosedag, E.; Ekici, R. Low-velocity and ballistic impact resistances of particle reinforced metal–matrixcomposites: An experimental study. J. Compos. Mater. 2022, 56, 991–1002. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Wagih, A.; Melaibari, A.; Fathy, A.; Lubineau, G. Effect of Al2O3 Particles on Mechanical and Tribological Properties of Al Mg dual-matrix Nanocomposites. Ceram. Int. 2020, 46, 5779–5787. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, C.; Liu, Y.; Yan, Y.; Xu, P.; Jiang, Y.; Cao, X. Comparing the Corrosion Resistance of 5083 Al and Al2O33D/5083 Al Composite in a Chloride Environment. Materials 2023, 16, 86. [Google Scholar] [CrossRef]
- Yogavardhan, S.G.N.; Kashinath, S.V.G.; Lavanya, K.V. Influence of Varying Particle Size on Mechanical &Tribological Properties of A356-Al2O3 Metal Matrix Composites. IJRASET 2024, 12, XII. [Google Scholar] [CrossRef]
- Renreng, I.; Arsyad, H.; Tarminsyah, T. Comparative Analysis of Microscale and Nanoscale Alumina Reinforcement in Al-Cu-MgAl2O3 Composites: Impacts on Density, Porosity, and Hardness. IIETA 2023, 33, 399–409. [Google Scholar] [CrossRef]
- Rahmalina, D.; Sofyan, B.T.; Suharno, B.; Siradj, E.S. Development of Steel Wire Rope—Reinforced Aluminium Composite for Armour Material Using the Squeeze Casting Process. Adv. Mater. Res. 2011, 277, 27–35. [Google Scholar] [CrossRef]
- Haider, K.; Alam, M.A.; Redhewal, A.R.; Saxena, V. Investigation of Mechanical Properties of Aluminium Based Metal Matrix Composites Reinforced With Sic & Al2O3. Int. J. Eng. Res. Appl. 2015, 5, 63–69. [Google Scholar]
- PN-EN ISO 6506-1:2023-09; Metale—Oznaczanie Twardości Metodą Brinella—Część 1: Metoda Badań (Metals—Brinell Hardness Test—Part 1: Test Method). Polski Komitet Normalizacyjny: Warsaw, Poland, 2023.
- PN-EN ISO 148-1:2017-02; Metale—Badanie Udarności—Część 1: Metoda Badań Char-Py’ego (Metals—Impact Testing—Part 1: Charpy Test Method). Polski Komitet Norma-lizacyjny: Warsaw, Poland, 2017.
- Kurzawa, A.; Kaczmar, J. Impact strength of composite materials based on EN AC-44200 matrix reinforced with Al2O3 particles. Arch. Foundry Eng. 2017, 17, 73–78. [Google Scholar] [CrossRef]
- PN-EN ISO 6892-1:2020-05; Metale—Próba Rozciągania—Część 1: Metoda Badania w Temperaturze Otoczenia. Polski Komitet Normalizacyjny: Warszawa, Poland, 2020.
- PN-EN ISO 6892-1:2020-5; Metale—Próba Rozciągania—Część 1: Metoda Badania w Temperaturze Otoczenia. Polski Komitet Normalizacyjny: Warszawa, Poland, 2020.
- Kurzawa, A.; Naplocha, K.; Kaczmar, J. Właściwości materiałów kompozytowych na osnowie stopu aluminium EN AW-2024 i miedzi. Zesz. Nauk. Politech. Rzesz. Mech. 2018, 35, 335–344. [Google Scholar] [CrossRef]
- ASTM E3-11(2017); Standard Guide for Preparation of Metallographic Specimens. ASTM International: West Conshohocken, PA, USA, 2017.
- Seth, P.P.; Parkash, O.; Kumar, D. Structure and mechanical behavior of in situ developed Mg2Si phase in magnesium and aluminum alloys—A review. RSC Adv. 2020, 10, 37327. [Google Scholar] [CrossRef]
- Kapłon, H.; Dmitruk, A.; Naplocha, K. Investment casting of AZ91 Magnesium Open-Cell Foams. Arch. Foundry Eng. 2023, 23, 11–16. [Google Scholar] [CrossRef]
- Son, Y.G.; Jung, S.S.; Park, Y.H.; Lee, Y.C. Effect of Semi-Solid Processing on the Microstructure and Mechanical Properties of Aluminum Alloy Chips with Eutectic Mg2Si Intermetallics. Metals 2021, 11, 1414. [Google Scholar] [CrossRef]
- Ji, S.; Yan, F.; Fan, Z. A high strength aluminium alloy for high pressure die casting. In Light Metals 2016; The Minerals, Metals & Materials Society; Springer: Cham, Switzerland, 2016; pp. 207–208. [Google Scholar]
- Liao, Y.; Xie, J.; Lv, B.; Wu, D.; Xiao, Q.; Xie, Q. The Degradation Mechanism of Mg2Si during Exploitation at High Temperature. Phys. Status Solidi B 2021, 258, 2100425. [Google Scholar] [CrossRef]
- Ko, S.; Park, H.; Lee, Y.-H.; Shin, S.; Jo, I.; Kim, J.; Lee, S.-B.; Kim, Y.; Lee, S.-K.; Cho, S. Fabrication of TiB2–Al1050 Composites with Improved Microstructural and Mechanical Properties by a Liquid Pressing Infiltration Process. Materials 2020, 13, 1588. [Google Scholar] [CrossRef] [PubMed]
- Askeland, D.R.; Phulé, P.P.; Wright, W.J. The Science and Engineering of Materials, 6th ed.; 17-2 Particulate Composites; Cengage Learning: Independence, KY, USA, 2010; pp. 656–657. [Google Scholar]
- Guo, X.; Guo, Q.; Nie, J.; Liu, Z.; Li, Z.; Fan, G.; Xiong, D.-B.; Su, Y.; Fan, J.; Zhang, D. Particle size effect on the interfacial properties of SiC particle—Reinforced Al-Cu-Mg composites. Mater. Sci. Eng. A 2018, 711, 643–649. [Google Scholar] [CrossRef]
- Maddaiah, K.C.; Kumar, G.B.V.; Pramod, R. Studies on the Mechanical, Strengthening Mechanisms and Tribological Characteristics of AA7150-Al2O3 Nano-Metal Matrix Composites. J. Compos. Sci. 2024, 8, 97. [Google Scholar] [CrossRef]
- Tian, T.; Zha, M.; Jia, H.-L.; Hua, Z.-M.; Ma, P.-K.; Wang, H.-Y. The effect of high solid solution Mg contents (7–13 wt%) on the dynamic strain aging behavior of Al–Mg alloys. Mater. Sci. Eng. A 2023, 880, 145376. [Google Scholar] [CrossRef]
- Mahmoud, E.R.I.; Shaharoun, A.; Elmahroogy, F.O.; Almohamadi, H. Microstructure and mechanical characterizations of LM6-Al/Al2O3 metal matrix composites produced by stir casting technique. J. Teknol. 2021, 83, 27–34. [Google Scholar] [CrossRef]
- Zhao, K.; Duan, Z.; Liu, J.; Kang, G.; An, L. Strengthening Mechanisms of 15 vol.% Al2O3 Nanoparticles Reinforced Aluminum Matrix Nanocomposite Fabricated by High Energy Ball Milling and Vacuum Hot Pressing. Acta Metall. Sin. 2021, 35, 915–921. [Google Scholar] [CrossRef]
- Snopiński, P.; Król, M. Microstructure, Mechanical Properties and Strengthening Mechanism Analysis in an AlMg5 Aluminium Alloy Processed by ECAP and Subsequent Ageing. Materials 2018, 8, 969. [Google Scholar] [CrossRef]
- Reddy, A.C. Evaluation of Mechanical Behavior of Al-Alloy/Al2O3 Metal Matrix Composites with respect to their constituents using Taguchi Technique. Int. J. Emerg. Technol. Appl. Eng. Technol. Sci. 2011, 4, 26–32. [Google Scholar]
- Hu, Z.; Li, P.; Fan, C.; Xiao, Y.; Huang, J.; Ma, W. Research progress on aluminum matrix composites reinforced by medium and high volume fraction hybrid particles. Mater. Express 2024, 14, 353–369. [Google Scholar] [CrossRef]
- Pragathi, P.; Elansezhian, R. Mechanical and microstructure behaviour of aluminum nanocomposite fabricated by squeeze casting and ultrasonic aided squeeze casting: A comparative study. J. Alloys Compd. 2023, 956, 170203. [Google Scholar] [CrossRef]
- Suo, Y.; Li, J.; Deng, Z.; Wang, B.; Wang, Q.; Ni, D.; Jia, P.; Suo, T. High-Temperature Compressive Response of SiCp/6092Al Composites under a Wide Range of Strain Rates. Materials 2021, 14, 6244. [Google Scholar] [CrossRef]
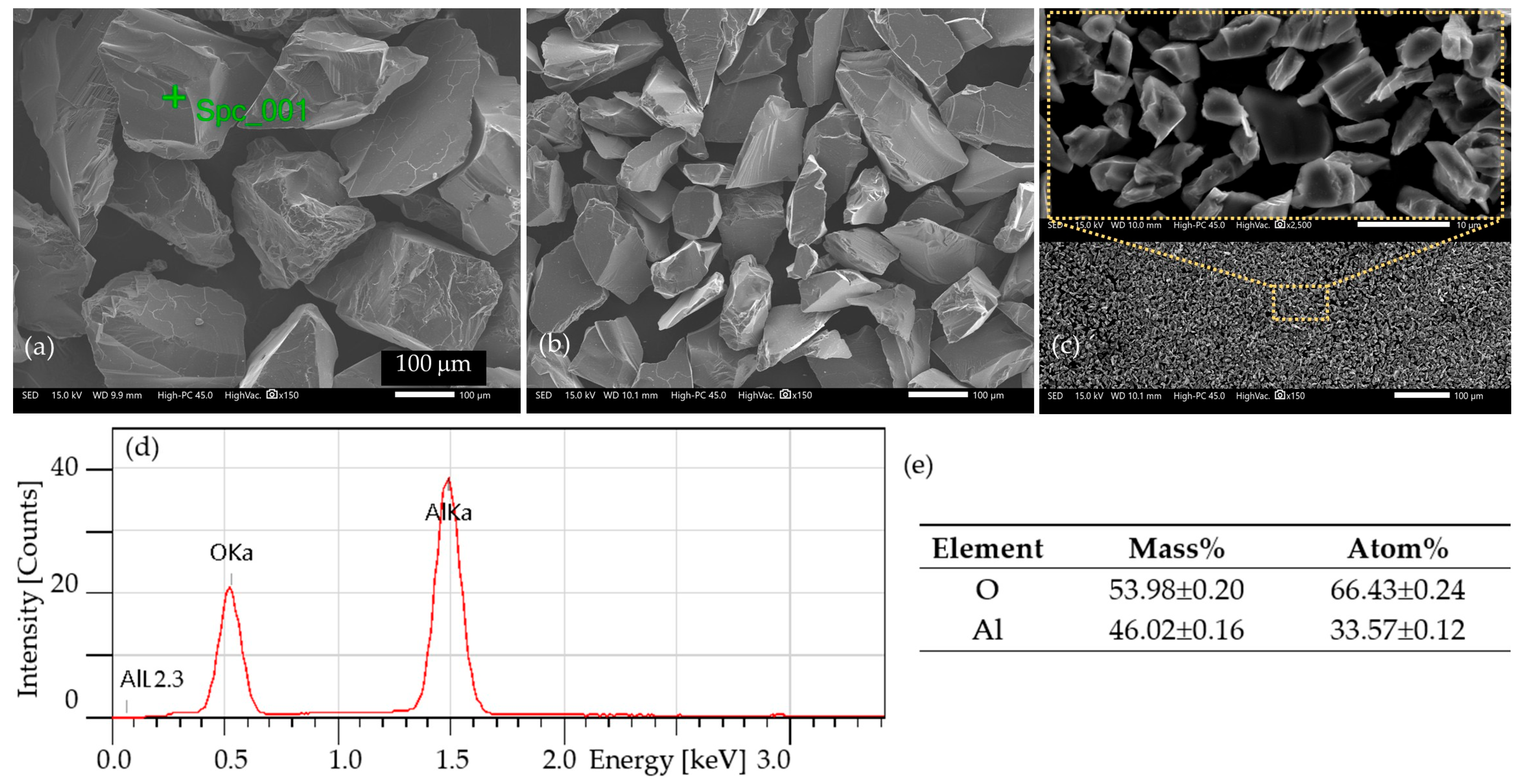
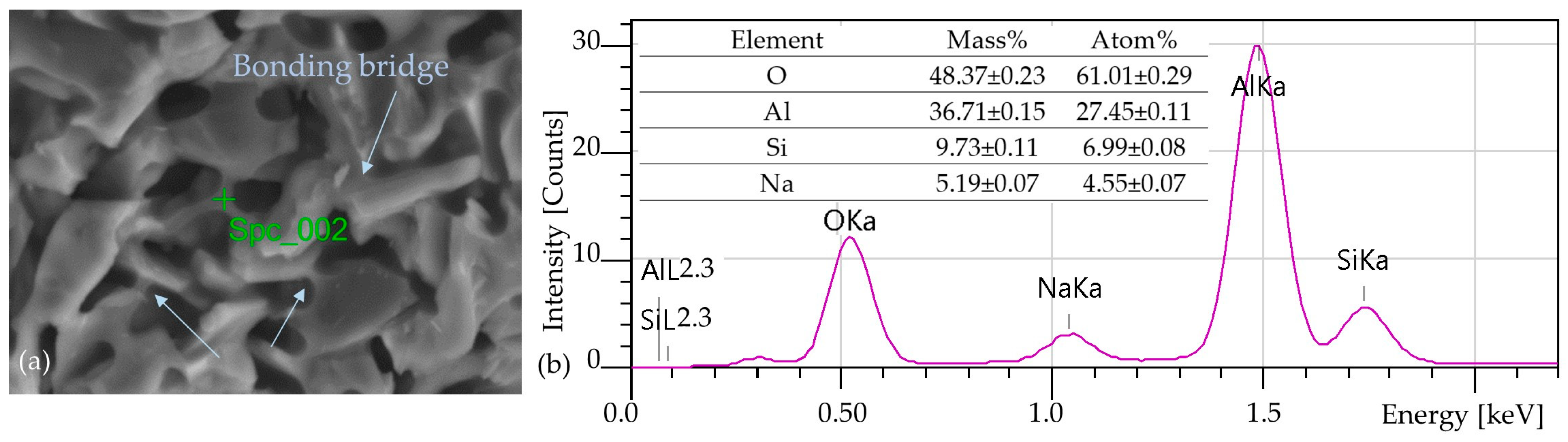



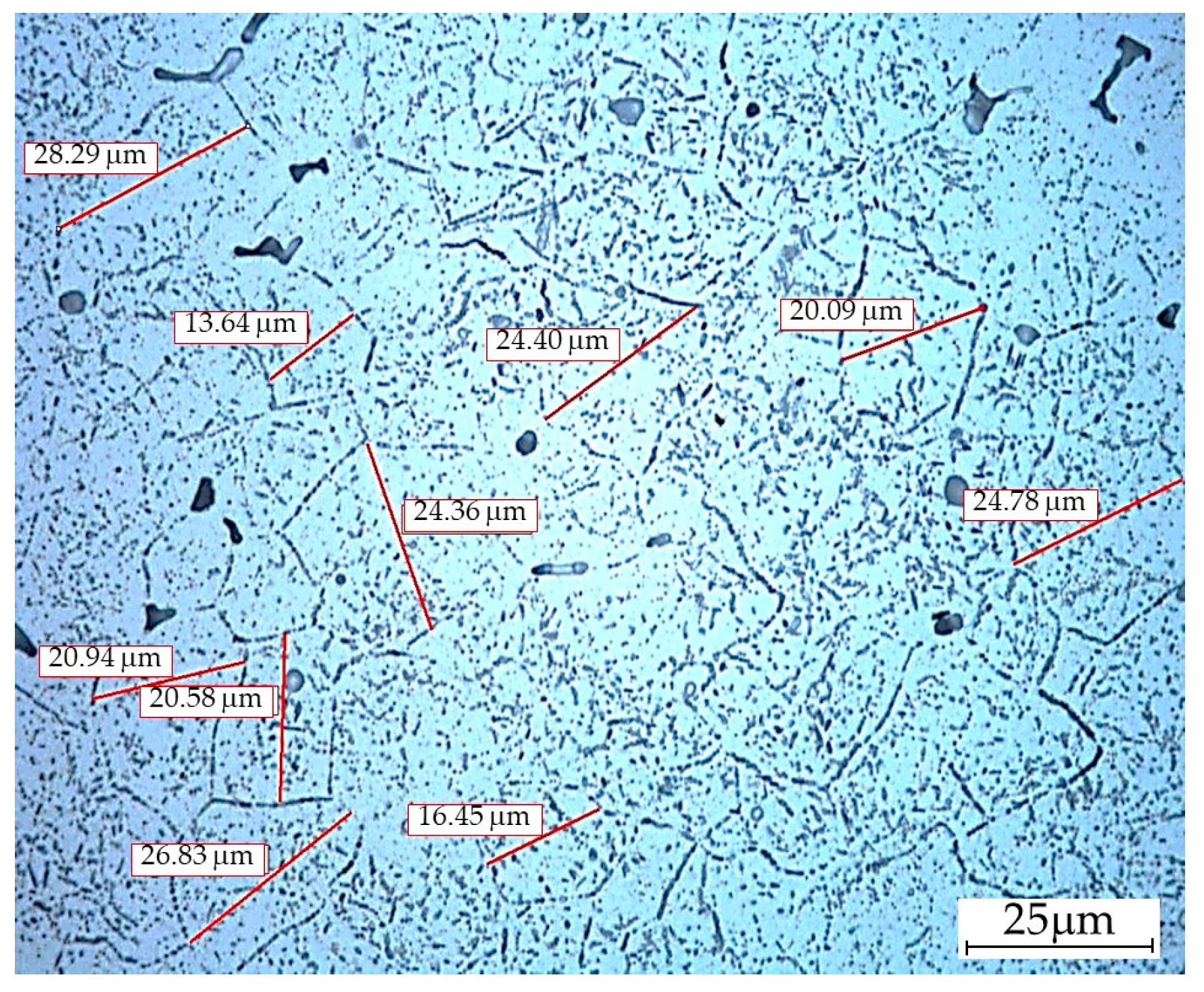

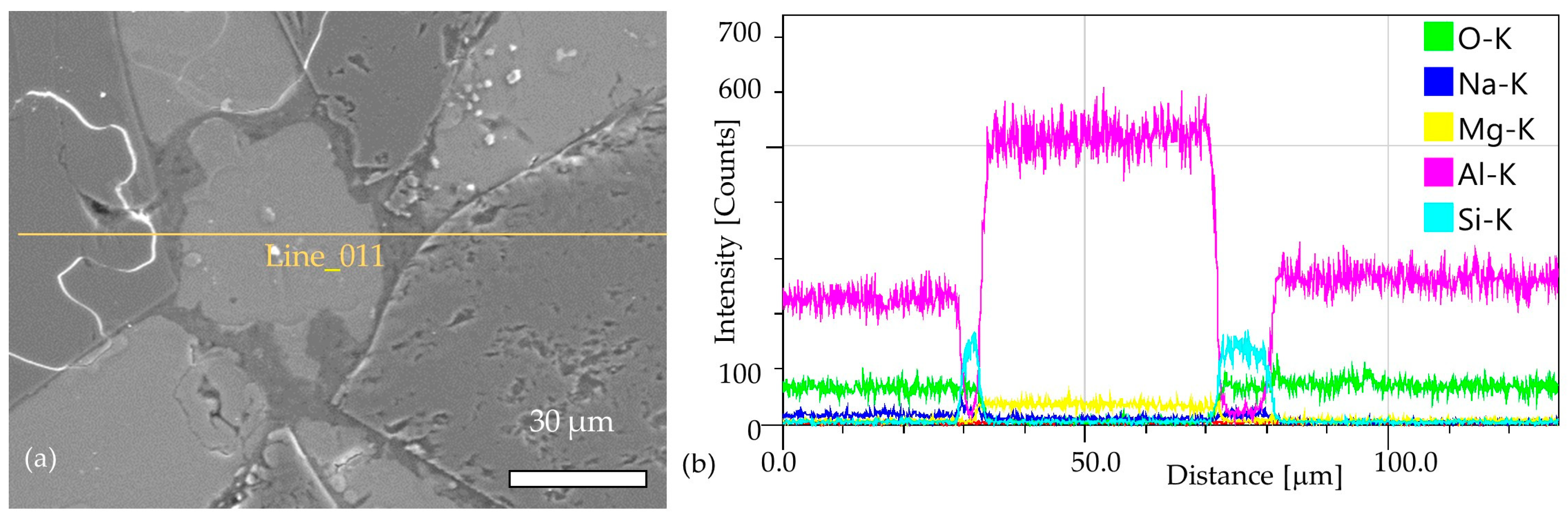







| Element [% wt] | Mg | Mn | Si | Fe | Ti | Zn | Cu | Al |
|---|---|---|---|---|---|---|---|---|
| Results of analysis | 7.15 | 0.92 | 0.06 | 0.10 | 0.02 | 0.32 | 0.02 | balance |
| Chemical Composition [% wt] | α-Al2O3 | SiO2 | Fe2O3 | Na2O | CaO | TiO2 | K2O |
|---|---|---|---|---|---|---|---|
| >99.0 | <0.03 | <0.04 | <0.19 | <0.01 | <0.01 | <0.01 | |
| Specific density: 3.95±0.5 [g/cm3] | |||||||
| Particle size: F80: 180 ÷ 212 [μm]; F150: 75 ÷ 106[μm]; F800: 6.5 ± 1% [μm]; F1200: 3 ± 1% [μm] | |||||||
| Materials | Theoretical Density [g/cm3] | Experimental Density [g/cm3] | Relative Density [%] | Porosity [%] |
|---|---|---|---|---|
| AlMg7 | 2.68 | 2.6680 | 99.55 | 0.45 |
| F80-30 vol.% Al2O3 | 3.06 | 3.0095 | 98.32 | 1.68 |
| F150-30 vol.% Al2O3 | 3.06 | 3.0413 | 99.36 | 0.64 |
| F800-30 vol.% Al2O3 | 3.06 | 3.0359 | 99.18 | 0.82 |
| F1200-30 vol.% Al2O3 | 3.06 | 3.0327 | 99.07 | 0.93 |
| F80-40 vol.% Al2O3 | 3.19 | 3.1318 | 98.24 | 1.76 |
| F150-40 vol.% Al2O3 | 3.19 | 3.1629 | 99.21 | 0.79 |
| F800-40 vol.% Al2O3 | 3.19 | 3.1566 | 99.02 | 0.98 |
| F1200-40 vol.% Al2O3 | 3.19 | 3.1550 | 98.96 | 1.04 |
| Materials | Maximum Tensile Strength σmax [MPa] | Maximum Compressive Strength σc max [MPa] | ||||
|---|---|---|---|---|---|---|
| min | max | Mean | min | max | Mean | |
| AlMg7 | 178 | 203 | 193 | 152 * | 165 * | 161 * |
| F80-30 vol.% Al2O3 | 133 | 168 | 147 | 359 | 310 | 293 |
| F150-30 vol.% Al2O3 | 160 | 221 | 203 | 383 | 431 | 395 |
| F800-30 vol.% Al2O3 | 319 | 347 | 332 | 448 | 474 | 467 |
| F1200-30 vol.% Al2O3 | 336 | 351 | 341 | 465 | 489 | 478 |
| F80-40 vol.% Al2O3 | - | - | - | 314 | 380 | 373 |
| F150-40 vol.% Al2O3 | 184 | 202 | 195 | 387 | 421 | 406 |
| F800-40 vol.% Al2O3 | 248 | 261 | 254 | 476 | 527 | 514 |
| F1200-40 vol.% Al2O3 | 275 | 296 | 289 | 509 | 533 | 522 |
| Name | O | Al | Mg | Si | Na | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| wt% | at.% | wt% | at.% | wt% | at.% | wt% | at.% | wt% | at.% | |
| Spc_01 | 18.25 | 27.17 | 75.28 | 66.45 | 5.70 | 5.59 | 0.77 | 0.79 | ||
| Spc_02 | 4.32 | 6.95 | 50.91 | 48.53 | 24.70 | 26.13 | 20.07 | 18.38 | ||
| Spc_03 | 53.13 | 65.65 | 46.87 | 34.35 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurzawa, A. The Mechanical Properties, Microstructure Analysis and Damage Behavior of AlMg7 Matrix Composites Reinforced with α-Al2O3 Particles. Appl. Sci. 2025, 15, 11173. https://doi.org/10.3390/app152011173
Kurzawa A. The Mechanical Properties, Microstructure Analysis and Damage Behavior of AlMg7 Matrix Composites Reinforced with α-Al2O3 Particles. Applied Sciences. 2025; 15(20):11173. https://doi.org/10.3390/app152011173
Chicago/Turabian StyleKurzawa, Adam. 2025. "The Mechanical Properties, Microstructure Analysis and Damage Behavior of AlMg7 Matrix Composites Reinforced with α-Al2O3 Particles" Applied Sciences 15, no. 20: 11173. https://doi.org/10.3390/app152011173
APA StyleKurzawa, A. (2025). The Mechanical Properties, Microstructure Analysis and Damage Behavior of AlMg7 Matrix Composites Reinforced with α-Al2O3 Particles. Applied Sciences, 15(20), 11173. https://doi.org/10.3390/app152011173






