Evaluation of Plasma Dynamic Parameters of a Multi-Layer MIF Target Under Exposure to External Broadband Radiation
Abstract
1. Introduction
2. Mathematical Model and Computational Algorithm
- We will assume that plasma formation (monatomic plasma composition) consists of dissociated neutral and ionized gas. The mathematical description of the dynamics of such a plasma formation is based on a multi-liquid (single-velocity), high-temperature, chemically non-reactive continuous plasma medium.
- The calculation of dynamic processes (absorption and scattering) related to the solution of the Vlasov (or Fokker–Planck) kinetic equation for relativistic “suprathermal” electrons in a magnetic field is not considered.
- At the initial time, the plasma formation and the surrounding medium can be differentiated by specifying distinct thermodynamic parameters, as well as the degree of ionization α = ne/n, where ne and n are the electron and heavy particle concentrations, respectively.
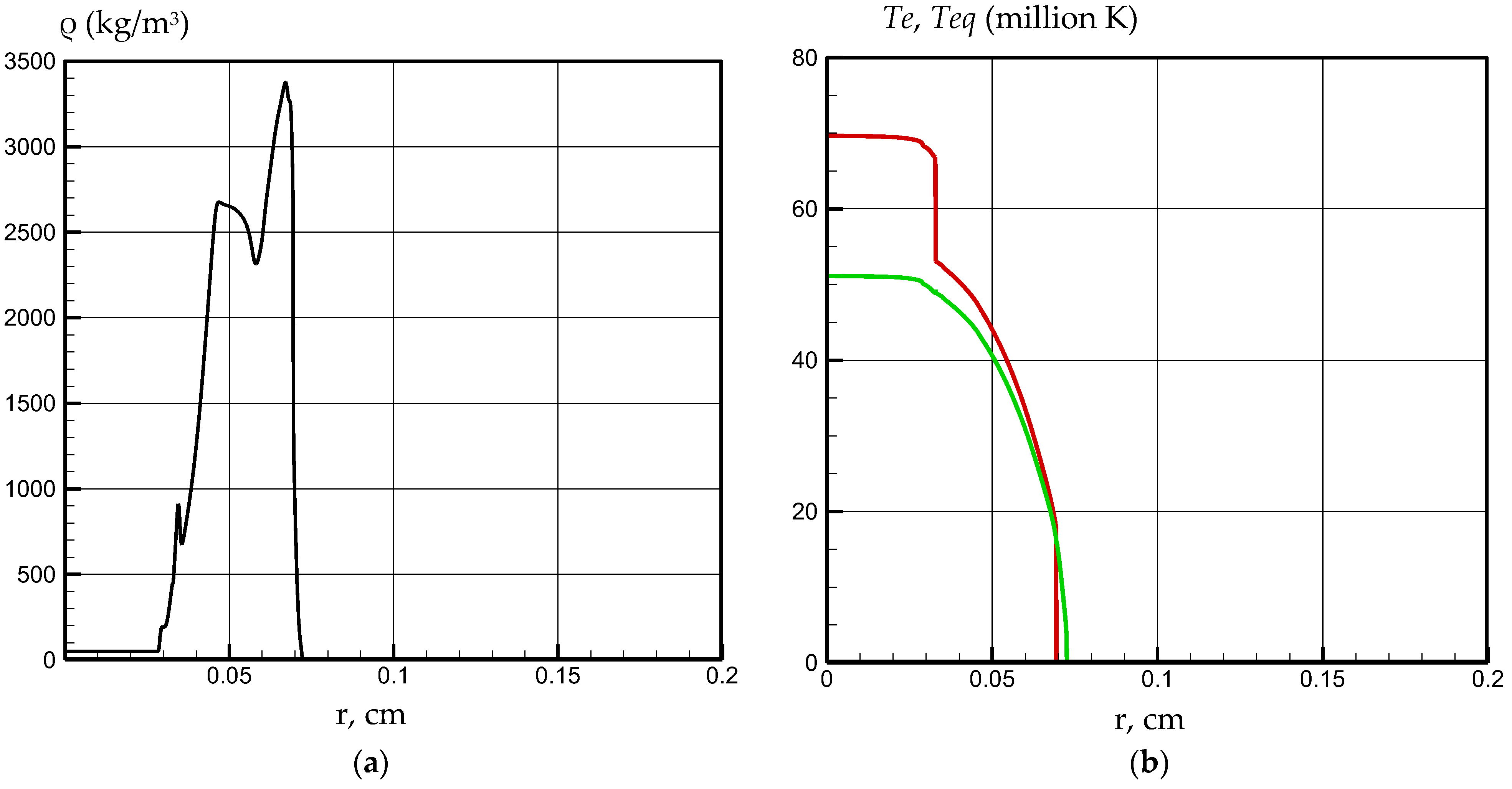
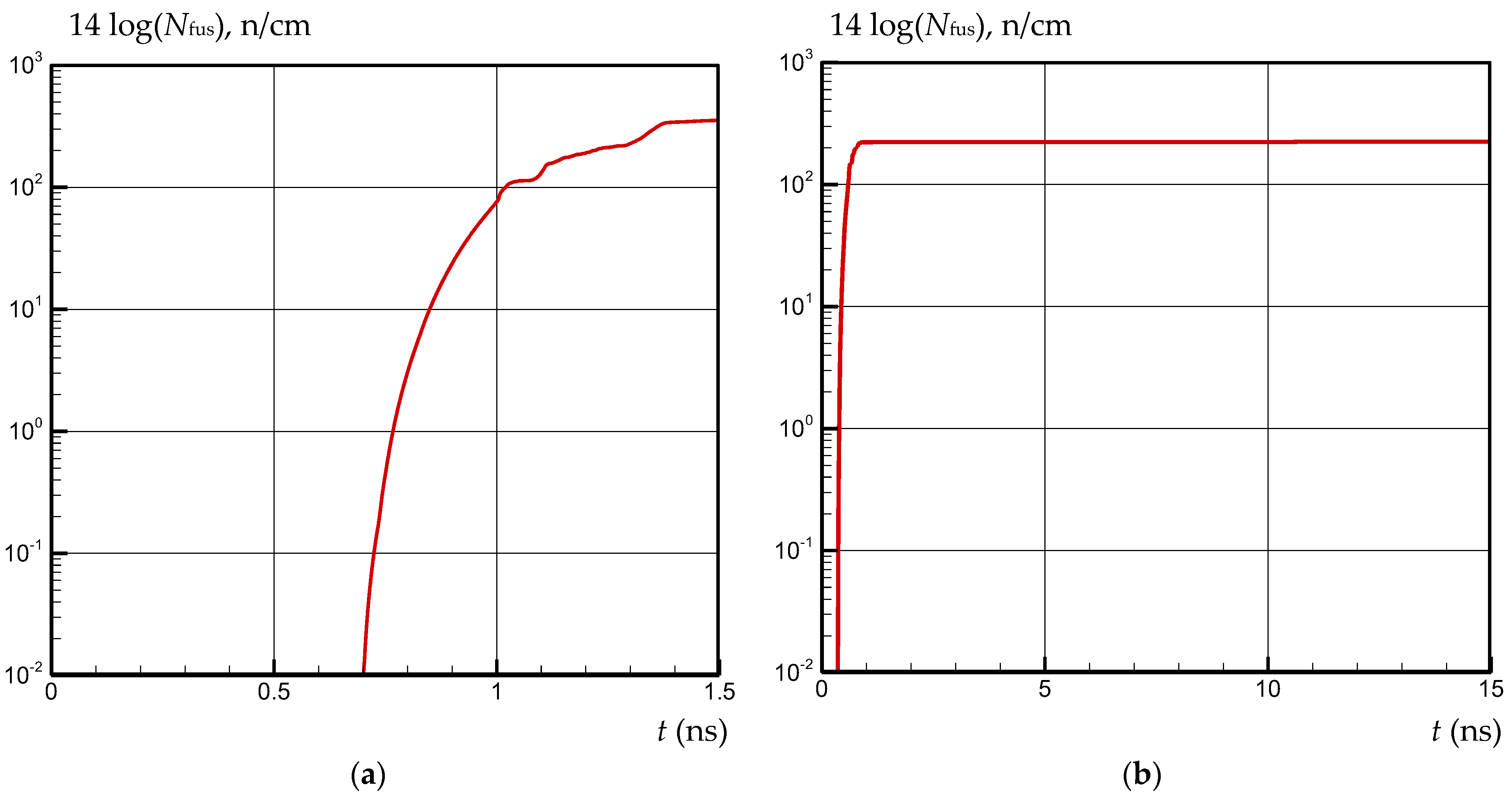
3. Calculation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | the speed of light |
| Bz | external magnetic field, T |
| EF | Fermi degenerate energy |
| Ef | energy of the thermonuclear reaction |
| E | energy, W/kg |
| H | magnetic induction, T |
| jr | current density, A/m2 |
| k | Boltzmann constant |
| K | plasma-specific scaling factor |
| Nfus | number of neutrons |
| n | heavy particle, cm−1 |
| ne | electron concentration, cm−1 |
| P | pressure, Pa |
| Pe | electron pressure, Pa |
| Pi | ion pressure, Pa |
| Pf | fusion power per unit volume, W/m3 |
| Qei | energy transferred per unit time per unit volume from electrons to ions |
| Qfus | local (thermonuclear) energy release to the electron component |
| q | broadband radiation intensity, W/cm2 |
| qL | Laser intensity, W/cm2 |
| qr | energy flux from the magnetic field, W/cm2 |
| qv | spectral broadband radiation flux, W/cm2 |
| qterm | density of the external broadband radiation flux perpendicular to the target |
| r | radial coordinate, m |
| t | time, s |
| Teq | average plasma temperature |
| Te | electron temperature, K |
| Ti | ion plasma temperature, K |
| u | velocity along the coordinate, m/s |
| Uν | spectral flux and volumetric density of broadband radiation |
| VD | velocity of the photodetonation wave, m/s |
| velocity of the thermonuclear reaction, m/s | |
| average frequency of electron–ion collisions, Hz | |
| ρ | density, kg/m3 |
| λe | electron thermal conductivity coefficient, W/(m K) |
| λi | ion thermal conductivity coefficient, W/(m K) |
| τ | the duration of the broadband radiation pulse, s |
| φ | the azimuthal angle |
| Z1 | proton number of the interacting nuclei 1 |
| Z2 | proton number of the interacting nuclei 2 |
| equilibrium average charge of heavy particles | |
| θ | plasma degeneracy parameter |
| χ | radiative thermal diffusivity coefficient |
| χν | spectral absorption coefficient |
| γ | adiabatic index of Hugoniot |
References
- Ananyev, S.; Kukushkin, A. Calculation of Consistent Plasma Parameters for DEMO-FNS Using Ionic Transport Equations and Simulation of the Tritium Fuel Cycle. Appl. Sci. 2023, 13, 8552. [Google Scholar] [CrossRef]
- Dlougach, E.; Panasenkov, A.; Kuteev, B.; Serikov, A. Neutral Beam Coupling with Plasma in a Compact Fusion Neutron Source. Appl. Sci. 2022, 12, 8404. [Google Scholar] [CrossRef]
- Garanin, S.G.; Ivanovskii, A.V.; Kulikov, S.M.; Mamyshev, V.I.; Pevny, S.N.; Rogachev, V.G. Inertial Thermonuclear Fusion Using Explosive Magnetic Generators. Plasma Phys. Rep. 2022, 48, 111–120. [Google Scholar] [CrossRef]
- Mitrofanov, K.N.; Aleksandrov, V.V.; Branitski, A.V.; Grabovskiy, E.V.; Gritsuk, A.N.; Oleinik, G.M.; Frolov, I.N.; Olkhovskaya, O.G.; Gasilov, V.A. Progress in researching the implosion of nested arrays of mixed composition and the generation of soft X-ray power pulse. Plasma Phys. Control Fusion 2022, 64, 045007. [Google Scholar] [CrossRef]
- Chetverushkin, B.N.; D’Ascenzo, N.; Saveliev, V.I. Kinetically consistent magnetogasdynamics equations and their use in supercomputer computations. Dokl. Math. 2014, 90, 495–498. [Google Scholar] [CrossRef]
- Zel’Dovich, Y.B.; Rajzer, Y.P. Physics of Shock Waves and High Temperature Phenomena of Hydrodynamic Phenomena; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Braginskij, S.I. Transport Processes in a Plasma; Reviews of Plasma Physics; Leontovich, M.A., Ed.; Consultants Bureau: New York, NY, USA, 1965; pp. 205–311. [Google Scholar]
- Samarskij, A.A.; Popov, I.P. Difference Methods for Solving Problems of Gas Dynamics; Nauka: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Development of a Method for Solving Elliptic Differential Equations Based on a Nonlinear Compact-Polynomial Scheme. J. Comput. Appl. Math. 2024, 451, 116098. [Google Scholar] [CrossRef]
- Surzhikov, S.T. Computing System for Solving Radiative Gasdynamic Problems of Entry and Re-Entry Space Vehicles. In Proceedings of the 1st International Workshop on Radiation of High Temperature Gases in Atmospheric Entry, ESA-533, Lisabon, Portugal, 8–10 October 2003; pp. 111–118. [Google Scholar]
- Kuzenov, V.V.; Ryzhkov, S.V.; Shumaev, V.V. Application of Thomas-Fermi model to evaluation of thermodynamic properties of magnetized plasma. Probl. At. Sci. Technol. 2015, 1, 97–99. [Google Scholar]
- Xu, Z.; Shu, C.-W. Anti-diffusive flux corrections for high order finite difference WENO schemes. J. Comput. Phys. 2005, 205, 458–485. [Google Scholar] [CrossRef]
- Xu, Z.; Shu, C.-W. Anti-diffusive finite difference WENO methods for shallow water with transport of pollutant, J. Comput. Math. 2006, 24, 239–251. [Google Scholar]
- Raizer, Y.P. Breakdown and heating of gases under the influence of a laser beam, Sov. Phys. Usp. 1966, 8, 650–673. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Small-sized plasma generators—Sources of high-energy particle and neutron fluxes (review). Fusion Sci. Technol. 2025, 81, 1–11. [Google Scholar] [CrossRef]
- Derzhiev, V.I.; Zhidkov, A.G.; Yakovlenko, S.I. Radiation of Ions in a Nonequilibrium Dense Plasma; Energoatomizdat: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Paradis, C.; Hammond, D.; Thoma, J.; Loescher, A.; Le Touzé, G.; Friedman, G.; Le Garrec, B.; Chériaux, G. Advances in laser technology for direct drive inertial fusion energy. Proc. SPIE—Int. Soc. Opt. Eng. 2025, 13343, 1334302. [Google Scholar] [CrossRef]
- Follett, R.K.; Colaïtis, A.; Seaton, A.G.; Wen, H.; Turnbull, D.; Froula, D.H.; Palastro, J.P. Ray-based cross-beam energy transfer modeling for broadband lasers. Phys. Plasmas 2023, 30, 042102. [Google Scholar] [CrossRef]
- Zhang, X.; Ji, L.L.; Liu, D.; Gao, Y.Q.; Sui, Z.; Zhao, X.H.; Xiang, X. Numerical simulation on third-harmonic generation of super-luminescent light by mixing broadband and narrowband lasers. Chin. J. Lasers 2021, 48, 2108001. [Google Scholar] [CrossRef]
- Zudin, I.; Gushchin, M.; Korobkov, S.; Strikovskiy, A.; Katkov, A.; Kochedykov, V.; Petrova, I. Transformation of the Shape and Spectrum of an Ultrawideband Electromagnetic Pulse in a “Gigantic” Coaxial Line Filled with Magnetized Plasma. Appl. Sci. 2024, 14, 705. [Google Scholar] [CrossRef]
- Nikolenko, A.S.; Gushchin, M.E.; Korobkov, S.V.; Strikovskiy, A.V.; Loskutov, K.N. Dynamics of a Plasma Cloud Generated by a Compact Coaxial Gun upon Expansion into Vacuum and Large-Volume Background Plasma in an External Magnetic Field. Plasma Phys. Rep. 2023, 49, 1284–1299. [Google Scholar] [CrossRef]
- Es’kin, V.A.; Korobkov, S.V.; Gushchin, M.E.; Kudrin, A.V. Propagation of an Ultrawideband Electromagnetic Pulse Along a Plasma-Filled Coaxial Line. IEEE Trans. Plasma Sci. 2023, 51, 374–380. [Google Scholar] [CrossRef]
- Sladkov, A.; Fegan, C.; Yao, W.; Bott, A.F.A.; Chen, S.N.; Ahmed, H.; Filippov, E.D.; Lelièvre, R.; Martin, P.; McIlvenny, A.; et al. Saturation of the compression of two interacting magnetized plasma toroids evidenced in the laboratory. Nat. Commun. 2024, 15, 10065. [Google Scholar] [CrossRef] [PubMed]
- Korobkov, S.V.; Nikolenko, A.S.; Gushchin, M.E.; Strikovsky, A.V.; Zudin, I.Y.; Aidakina, N.A.; Shaikhislamov, I.F.; Rumenskikh, M.S.; Zemskov, R.S.; Starodubtsev, M.V. Features of Dynamics and Instability of Plasma Jets Expanding into an External Magnetic Field in Laboratory Experiments with Compact Coaxial Plasma Generators on a Large-Scale “Krot” Stand. Astron. Rep. 2023, 67, 93–103. [Google Scholar] [CrossRef]
- Savenko, N.O.; Urvachev, E.M.; Losseva, T.V.; Grushin, A.S.; Poklad, Y.V.; Gasilov, V.A. Numerical Simulation of Plasma Jet Expansion in a Laboratory Experiment. Plasma Phys. Rep. 2025, 51, 697–707. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuzenov, V.V.; Ryzhkov, S.V.; Polyanskiy, A.G. Evaluation of Plasma Dynamic Parameters of a Multi-Layer MIF Target Under Exposure to External Broadband Radiation. Appl. Sci. 2025, 15, 11155. https://doi.org/10.3390/app152011155
Kuzenov VV, Ryzhkov SV, Polyanskiy AG. Evaluation of Plasma Dynamic Parameters of a Multi-Layer MIF Target Under Exposure to External Broadband Radiation. Applied Sciences. 2025; 15(20):11155. https://doi.org/10.3390/app152011155
Chicago/Turabian StyleKuzenov, Victor V., Sergei V. Ryzhkov, and Artem G. Polyanskiy. 2025. "Evaluation of Plasma Dynamic Parameters of a Multi-Layer MIF Target Under Exposure to External Broadband Radiation" Applied Sciences 15, no. 20: 11155. https://doi.org/10.3390/app152011155
APA StyleKuzenov, V. V., Ryzhkov, S. V., & Polyanskiy, A. G. (2025). Evaluation of Plasma Dynamic Parameters of a Multi-Layer MIF Target Under Exposure to External Broadband Radiation. Applied Sciences, 15(20), 11155. https://doi.org/10.3390/app152011155






