Safety Evaluation of Composite Wall Systems Subjected to Projectile Impact
Abstract
Featured Application
Abstract
1. Introduction
2. Composite Materials and Systems for Impact Protection
3. Formulation for Reliability Analysis of Composite Wall System
3.1. Mathematical Representation of the Limit State Function
3.2. Ballistic Limit of a Composite Wall System
- represents the projectile mass.
- denotes the equivalent thickness of the target (i.e., composite wall).
- is the perimeter of the projectile’s cross-section, given by .
- is the diameter of the projectile’s aft body.
- represents the spacing of steel rebars.
- indicates the percentage of steel rebars, calculated as, .
- is the area (i.e., cross-sectional area) of the steel bars.
- is the effective depth of the equivalent monolithic wall.
- represents the concrete compressive strength.
3.3. Reliability Assessment
- Select those variables that have significant uncertainty as the random variables. Estimate the nominal values of these variables and calculate their required statistics, such as mean, variance, standard deviation, coefficient of variation, etc.
- Select appropriate probability distributions for all the random variables and calculate the parameters of the probability distributions.
- Simulate using Monte Carlo Simulation N (~around 1.5 million) composite walls by considering randomness in the material, geometry, and impact-related parameters of the composite walls.
- Compare each simulated wall’s ballistic limit with the velocity of the impacting projectile.
- Count the failing number of (composite) walls, i.e., the number of walls having their ballistic limit less than the projectile impact velocity (i.e., having a negative value of the limit state function); say it is
- Calculate the probability of failure of the composite wall ( and its reliability index ( using the following formulas: and ; in this formulation, represents the quantile of the standard normal distribution, obtained via the inverse of its cumulative distribution function [51].
4. Test Program
Equivalent Thickness and Ballistic Limit
5. Input Data for Reliability Assessment
6. Discussion of Results
6.1. Composite Walls of Equal Thickness
6.2. Composite Walls with Non-Identical Thicknesses
7. Parametric Study
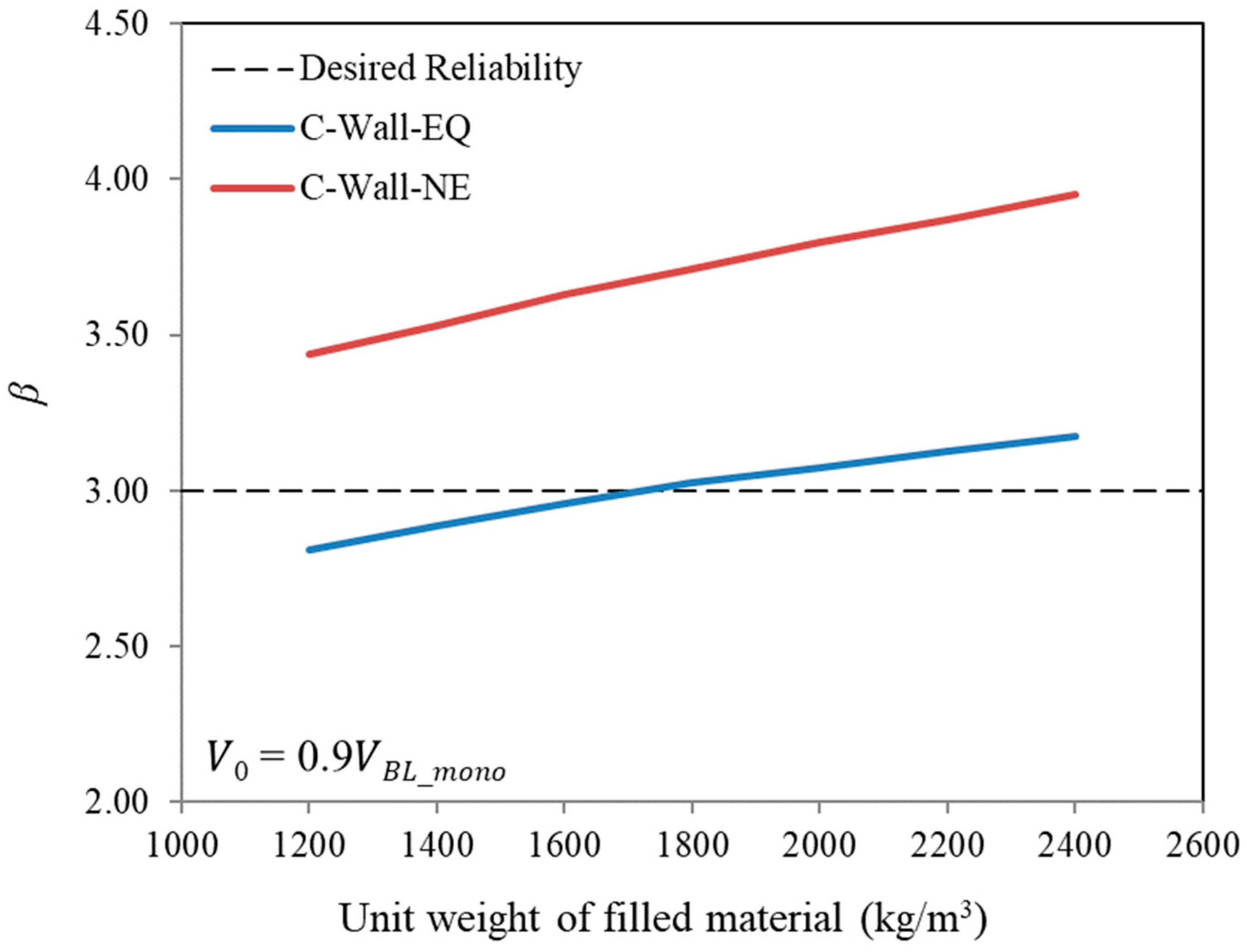
7.1. Effect of Unit Weight of the Filling Material
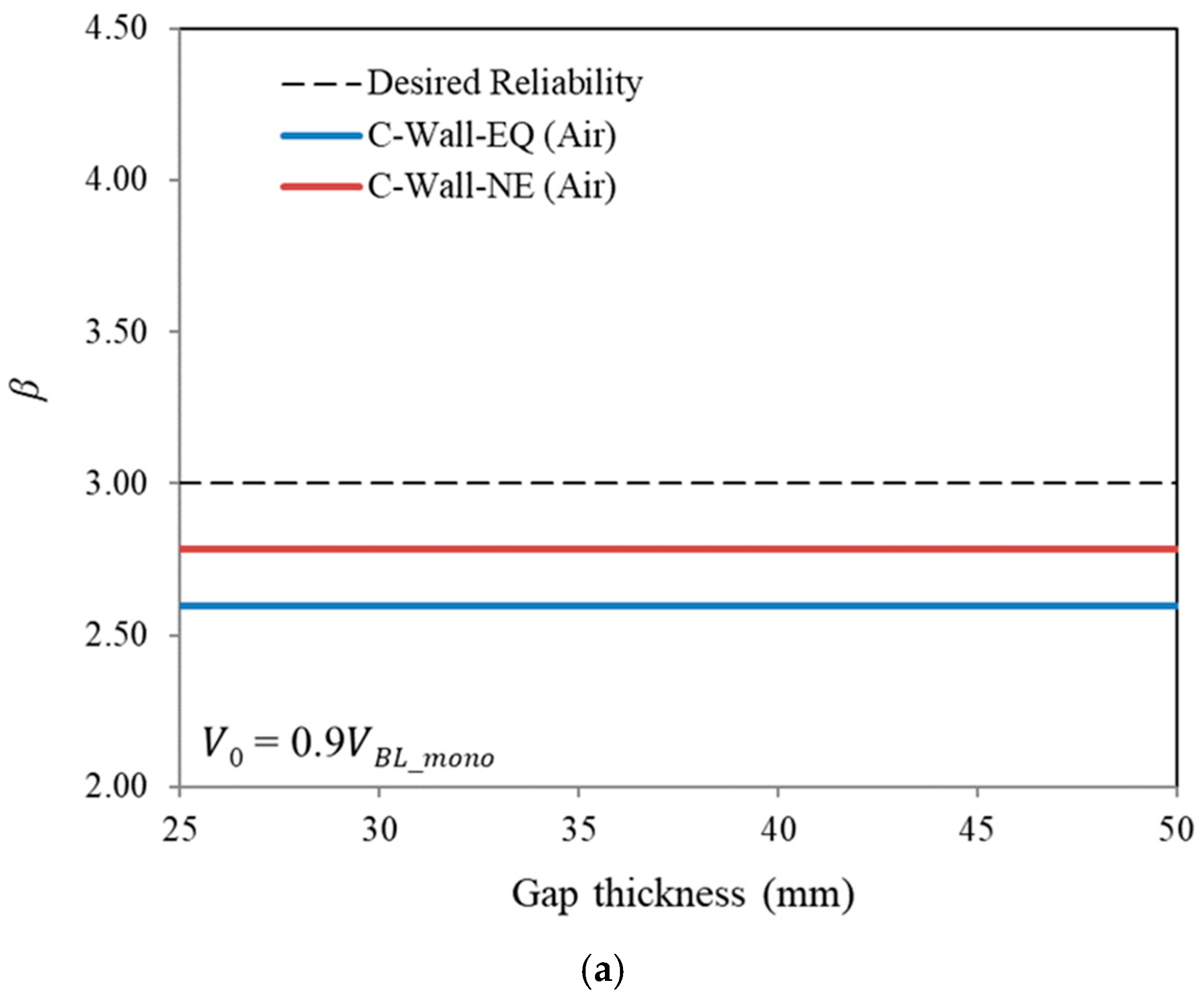
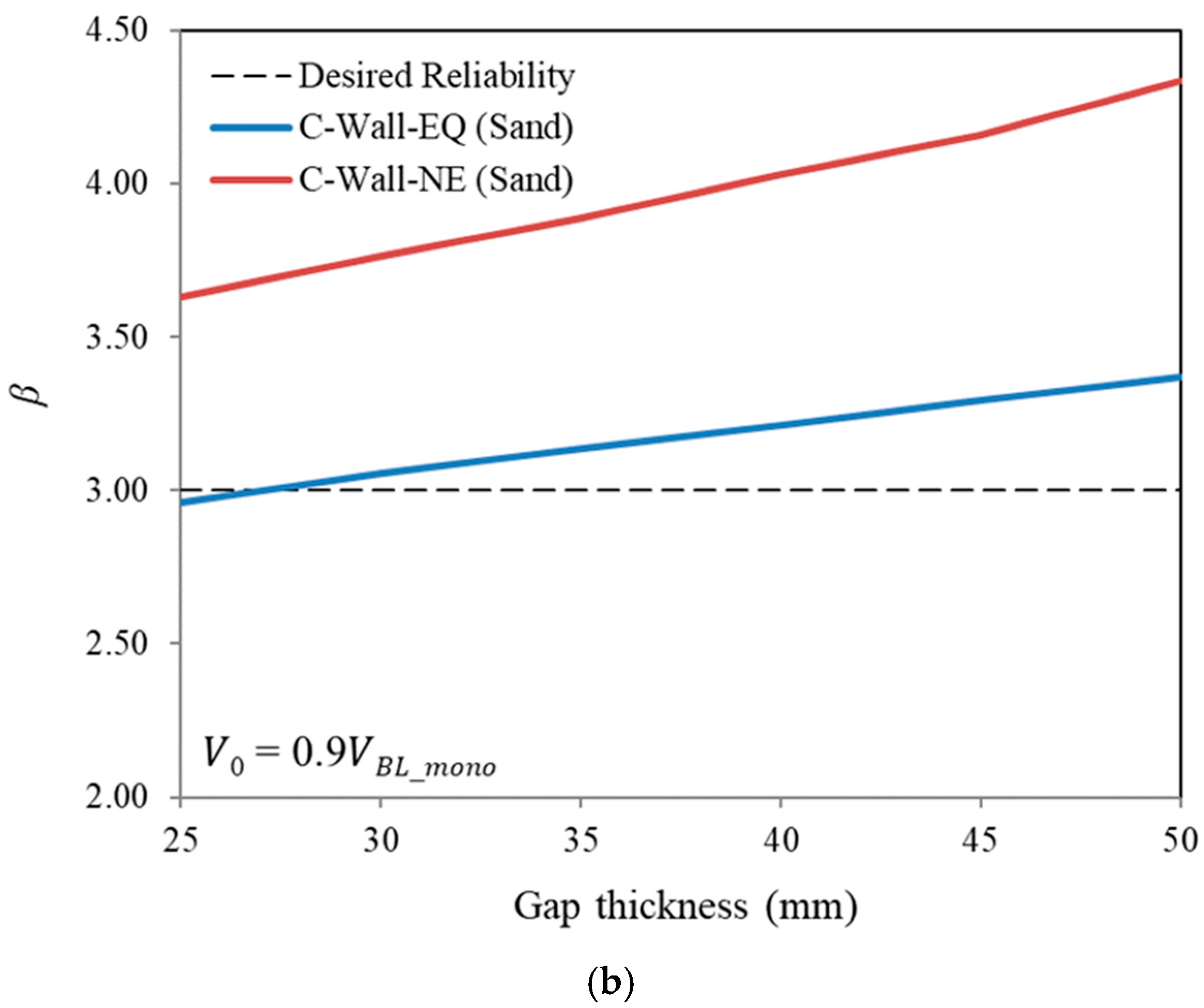
7.2. Effect of Gap Thickness
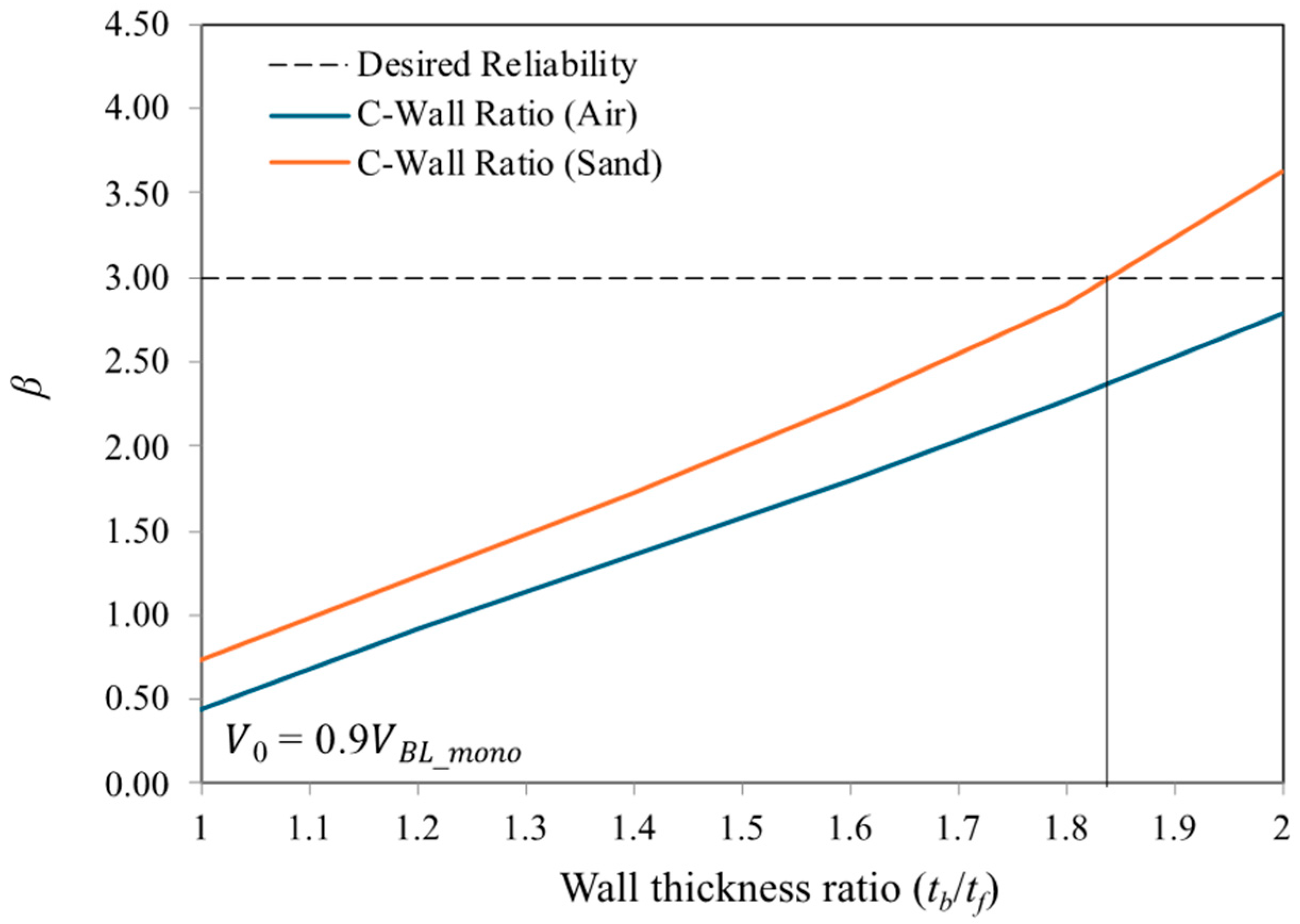
7.3. Influence of the Thickness Ratio of Front to Rear Walls
8. Conclusions
- The composite wall system provides a greater safety margin compared to a monolithic wall of the same total thickness and reinforcement. When no filling material was present between two walls of equal thickness, the target’s reliability was 49.2% higher than that of the one-piece concrete wall. Introducing infill materials such as compacted sand and recycled concrete aggregates (RCA) resulted in reliability improvements of 68.2% and 68.9% for the composite walls, respectively.
- Compared to a monolithic wall of equal total thickness, RC targets constructed with walls of varying thicknesses showed markedly enhanced reliability—62% for an unfilled gap, 95% for a sand-filled gap, and 96% for a gap filled with RCA. These findings emphasize the enhanced synergistic behavior of double-wall targets, especially when the walls differ in thickness yet maintain the same total reinforcement as a monolithic RC wall.
- When the filling material is lightweight (unit weight less than 1600 kg/m3), the present composite wall system with equally thick front and rear walls possesses a reliability value less than the minimum required level of safety. However, the reliability index is more than the minimum required value for unequal-thickness composite wall systems, even when the filling material is lightweight.
- A thicker filled gap causes the projectile to dissipate more energy before striking the rear wall. As a result of this energy dissipation, the projectile impacts the rear wall at a reduced velocity, thereby raising the ballistic limit and enhancing the overall reliability of the composite wall system.
- Even when the thickness ratio is double, the reliability of the composite wall system having no material between the gap has a reliability index less than the desired reliability of 3.0. However, if the gap is filled with sand, the desired reliability is achieved even when the ratio is much less than 2.0 (i.e., less than 1.85).
- RC targets with unequal thickness double walls exhibit higher reliability than those with equal thickness. Using unequal thickness offers greater advantages, as the thinner front wall serves as a sacrificial layer, absorbing the initial impact. Damage to the front wall can be addressed with less complexity and expense, which contributes to greater maintainability and efficiency of the composite wall system.
- This study is limited to the specific composite configurations, filler materials, projectile types, and single-impact scenarios tested. Future research should explore a wider variety of filler materials, different projectile shapes and velocities, and multiple-impact scenarios to assess the performance and reliability of these systems comprehensively. Such investigations would enhance the general applicability of the proposed methods and provide valuable guidance for designing cost-effective and resilient protective structures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbas, H.; Al-Dabaan, M.; Siddiqui, N.; Almusallam, T.; Al-Salloum, Y. Performance of reinforced concrete composite wall systems under projectile impact. J. Mater. Res. Technol. 2023, 23, 3062–3090. [Google Scholar] [CrossRef]
- Szydlowski, R.; Bednarz, K. Material and construction solutions of war shelters with the example of Hitler’s main headquarters in the Wolf’s Lair. Czas. Tech. 2018, 1, 87–101. [Google Scholar]
- Tao, Q.; Ren, P.; Shi, L.; Zhao, Z.; Tang, Y.; Ye, R.; Zhang, W.; Cui, J. Energy absorption and impact behavior of composite sandwich panels under high-velocity spherical projectile. Int. J. Impact Eng. 2022, 162, 104143. [Google Scholar] [CrossRef]
- Zhang, P.; Kong, X.; Wang, Z.; Zheng, C.; Liu, H.; Shi, G.; Dear, J.P.; Wu, W. High velocity projectile impact of a composite rubber/aluminium fluid-filled container. Int. J. Lightweight Mater. Manuf. 2021, 4, 1–8. [Google Scholar]
- Aktay, L.; Johnson, A.F.; Holzapfel, M. Prediction of impact damage on sandwich composite panels. Comput. Mater. Sci. 2005, 32, 252–260. [Google Scholar] [CrossRef]
- Gupta, N.K.; Iqbal, M.A.; Sekhon, G.S. Effect of projectile nose shape, impact velocity and target thickness on the deformation behavior of layered plates. Int. J. Impact Eng. 2008, 35, 37–60. [Google Scholar] [CrossRef]
- Siddiqui, N.A.; Khateeb, B.M.; Almusallam, T.H.; Abbas, H. Reliability of double-wall containment against the impact of hard projectiles. Nucl. Eng. Des. 2014, 270, 143–151. [Google Scholar] [CrossRef]
- Dancygier, A.N.; Katz, A.; Benamou, D.; Yankelevsky, D.Z. Resistance of double-layer reinforced HPC barriers to projectile impact. Int. J. Impact Eng. 2014, 67, 39–51. [Google Scholar] [CrossRef]
- Siddiqui, N.A.; Khateeb, B.M.; Almusallam, T.H.; Al-Salloum, Y.A.; Iqbal, R.A.; Abbas, H. Reliability of RC shielded steel plates against the impact of sharp nose projectiles. Int. J. Impact Eng. 2014, 69, 122–135. [Google Scholar] [CrossRef]
- Wu, H.; Fang, Q.; Gong, Z.M.; Peng, Y. Hard projectile impact on layered SFRHSC composite target. Int. J. Impact Eng. 2015, 84, 88–95. [Google Scholar] [CrossRef]
- Wu, H.; Fang, Q.; Peng, Y.; Gong, Z.M.; Kong, X.Z. Hard projectile perforation on the monolithic and segmented RC panels with a rear steel liner. Int. J. Impact Eng. 2015, 76, 232–250. [Google Scholar] [CrossRef]
- Feng, J.; Sun, W.; Liu, Z.; Cui, C.; Wang, X. An armour-piercing projectile penetration in a double-layered target of ultra-high-performance fiber reinforced concrete and armour steel: Experimental and numerical analyses. Mater. Des. 2016, 102, 131–141. [Google Scholar]
- Ebrahimi, H.; Ghosh, R.; Mahdi, E.; Nayeb-Hashemi, H.; Vaziri, A. Honeycomb sandwich panels subjected to combined shock and projectile impact. Int. J. Impact Eng. 2016, 95, 1–11. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.X.; Ye, L. High velocity impact responses of sandwich panels with metal fibre laminate skins and aluminium foam core. Int. J. Impact Eng. 2017, 100, 139–153. [Google Scholar] [CrossRef]
- Li, D.; Hou, H.; Chen, C.; Zhu, X.; Li, M.; Yi, Q. Experimental study on the combined damage of multi-layered composite structures subjected to close-range explosion of simulated warheads. Int. J. Impact Eng. 2018, 114, 133–146. [Google Scholar]
- Lai, J.; Yang, H.; Wang, H.; Zheng, X.; Wang, Q. Properties and Modeling of Ultra-High-Performance Concrete Subjected to Multiple Bullet Impacts. J. Mater. Civ. Eng. 2018, 30, 04018256. [Google Scholar]
- Wang, F.; Liu, J.B.; Bao, X.; Li, S.T.; An, Z.Y. Experimental study of the resistance of RC walls with different transverse reinforcements subjected to large-scale rigid projectile impacts. Eng. Struct. 2022, 251, 113558. [Google Scholar] [CrossRef]
- Choi, J.I.; Park, S.E.; Nguyễn, H.H.; Lee, Y.; Lee, B.Y. Resistance of hybrid layered composite panels composed of fiber-reinforced cementitious composites against high-velocity projectile impact. Compos. Struct. 2022, 281, 114993. [Google Scholar]
- Salhan, P.; Rashid, F.M. Effect of shape and obliquity of projectiles on the ballistic response of sandwich structures with carbon/epoxy face sheet subjected to low-velocity impact. Mater. Today Proc. 2022, 62, 6780–6787. [Google Scholar]
- Zhang, M.; Deng, G.; Du, Y.; Gao, W.; Sun, G.; Luo, D. Experimental investigation of the anti-penetration mechanism of UHPC reinforced with high-strength steel bars subjected to projectile impact. Constr. Build. Mater. 2023, 372, 130820. [Google Scholar]
- Remennikov, A.; Gan, E.C.; Ngo, T.; Netherton, M.D. The development and ballistic performance of protective steel-concrete composite barriers against hypervelocity impacts by explosively formed projectiles. Compos. Struct. 2019, 207, 625–644. [Google Scholar] [CrossRef]
- Shao, R.; Wu, C.; Su, Y.; Liu, Z.; Liu, J.; Xu, S. Numerical analysis on impact response of ultra-high strength concrete protected with composite materials against steel ogive-nosed projectile penetration. Compos. Struct. 2019, 220, 861–874. [Google Scholar] [CrossRef]
- Mahesh, V.; Joladarashi, S.; Kulkarni, S.M. A comprehensive review on material selection for polymer matrix composites subjected to impact load. Def. Technol. 2021, 17, 257–277. [Google Scholar] [CrossRef]
- Hazell, P.J. Armour: Materials, Theory, and Design; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Karhankova, M.; Adamek, M.; Krstulović-Opara, L.; Mach, V.; Bagavac, P.; Stoklasek, P.; Mizera, A. Composites in Ballistic Applications Focused on Ballistic Vests—A Review. J. Compos. Sci. 2024, 8, 415. [Google Scholar] [CrossRef]
- Tamjid, M.I.; Abtew, M.A.; Kopot, C. Lightweight Textile and Fiber-Reinforced Composites for Soft Body Armor (SBA): Advances in Panel Design, Materials, and Testing Standards. J. Compos. Sci. 2025, 9, 337. [Google Scholar] [CrossRef]
- Toader, G.; Diacon, A.; Axinte, S.M.; Mocanu, A.; Rusen, E. State-of-the-art polyurea coatings: Synthesis aspects, structure–properties relationship, and nanocomposites for ballistic protection applications. Polymers 2024, 16, 454. [Google Scholar] [CrossRef]
- Safri, S.N.A.; Sultan, M.T.H.; Jawaid, M.; Jayakrishna, K. Impact behaviour of hybrid composites for structural applications: A review. Compos. Part B Eng. 2018, 133, 112–121. [Google Scholar] [CrossRef]
- Kevlar® Technical Guide. DuPont. Available online: https://www.dupont.com/content/dam/dupont/amer/us/en/safety/public/documents/en/Kevlar_Technical_Guide_0319.pdf (accessed on 24 September 2025).
- Yang, H.H. Kevlar Aramid Fiber; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Cunniff, P.M. Dimensionless parameters for optimization of textile-based body armor systems. In Proceedings of the 18th International Symposium on Ballistics, San Antonio, TX, USA, 15–19 November 1999; Technomic Publishing Co., Inc.: Lancaster, PA, USA, 1999; Volume 2, pp. 1303–1310. [Google Scholar]
- Duan, Y.; Keefe, M.; Bogetti, T.A.; Cheeseman, B.A. Modeling the role of friction during ballistic impact of a high-strength plain-weave fabric. Compos. Struct. 2005, 68, 331–337. [Google Scholar] [CrossRef]
- Das, S.; Jagan, S.; Shaw, A.; Pal, A. Determination of inter-yarn friction and its effect on ballistic response of para-aramid woven fabric under low velocity impact. Compos. Struct. 2015, 120, 129–140. [Google Scholar]
- Hani, A.A.; Roslan, A.; Mariatti, J.; Maziah, M. Body armor technology: A review of materials, construction techniques and enhancement of ballistic energy absorption. Adv. Mater. Res. 2012, 488, 806–812. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Chen, J.; Hao, X.; Wang, S.; Feng, X.; Guo, Y. Effects of solar UV irradiation on the tensile properties and structure of PPTA fiber. Polym. Degrad. Stab. 2006, 91, 2761–2767. [Google Scholar] [CrossRef]
- Wakatsuki, K.; Matsubara, M.; Watanabe, N.; Bao, L.; Morikawa, H. Effects of m-Aramid/p-Aramid blend ratio on tensile strength due to UV degradation for firefighter clothing fabrics and development of predictive equation for tensile strength. Polymers 2022, 14, 3241. [Google Scholar] [CrossRef]
- Phoenix, S.L.; Porwal, P.K. A new membrane model for the ballistic impact response and V50 performance of multi-ply fibrous systems. Int. J. Solids Struct. 2003, 40, 6723–6765. [Google Scholar] [CrossRef]
- Biradar, A.; Arulvel, S.; Kandasamy, J. Significance of ballistic parameters and nanohybridization in the development of textile-based body armor: A review. Int. J. Impact Eng. 2023, 180, 104700. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, M.; Nie, J.; Liu, G.; Tan, J.; Yang, B.; Song, S.; Zhao, J.R. A deep insight into the structure and performance evolution of aramid nanofiber films induced by UV irradiation. Polym. Degrad. Stab. 2019, 167, 170–178. [Google Scholar] [CrossRef]
- Hussain, M.; Naqvi, R.A.; Abbas, N.; Khan, S.M.; Nawaz, S.; Hussain, A.; Zahra, N.; Khalid, M.W. Ultra-high-molecular-weight-polyethylene (UHMWPE) as a promising polymer material for biomedical applications: A concise review. Polymers 2020, 12, 323. [Google Scholar] [CrossRef]
- Luz, F.S.D.; Garcia Filho, F.D.C.; Oliveira, M.S.; Nascimento, L.F.C.; Monteiro, S.N. Composites with natural fibers and conventional materials applied in a hard armor: A comparison. Polymers 2020, 12, 1920. [Google Scholar] [CrossRef]
- Ding, L.; Gu, X.; Shen, P.; Kong, X. Ballistic limit of UHMWPE composite armor under impact of ogive-nose projectile. Polymers 2022, 14, 4866. [Google Scholar] [CrossRef]
- Zhu, Y.; Song, Y.; Wu, W.; Ma, J.; Fan, Z.; Wen, Y.; Xu, C.; Xia, M.; Da, W. Impact Response Features and Penetration Mechanism of UHMWPE Subjected to Handgun Bullet. Polymers 2024, 16, 1427. [Google Scholar] [CrossRef] [PubMed]
- Deitzel, J.M.; McDaniel, P.; Gillespie, J.W., Jr. High performance polyethylene fibers. In Structure and Properties of High-Performance Fibers; Woodhead Publishing: Cambridge, UK, 2017; pp. 167–185. [Google Scholar]
- Medvedovski, E. Alumina ceramics for ballistic protection. Part 1. Am. Ceram. Soc. Bull. 2002, 81, 27–31. [Google Scholar]
- Medvedovski, E. Alumina ceramics for ballistic protection. Part 2. Am. Ceram. Soc. Bull. 2002, 81, 45–50. [Google Scholar]
- Nael, M.A.; Dikin, D.A.; Admassu, N.; Elfishi, O.B.; Percec, S. Damage resistance of Kevlar® Fabric, UHMWPE, PVB multilayers subjected to concentrated drop-weight impact. Polymers 2024, 16, 1693. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.M.; Reid, S.R.; Wen, H.M.; Telford, A.R. Local impact effects of hard missiles on concrete targets. Int. J. Impact Eng. 2005, 32, 224–284. [Google Scholar] [CrossRef]
- Almusallam, T.H.; Abadel, A.A.; Al-Salloum, Y.A.; Siddiqui, N.A.; Abbas, H. Effectiveness of hybrid-fibers in improving the impact resistance of RC slabs. Int. J. Impact Eng. 2015, 81, 61–73. [Google Scholar] [CrossRef]
- Almusallam, T.H.; Siddiqui, N.A.; Iqbal, R.A.; Abbas, H. Response of hybrid-fiber reinforced concrete slabs to hard projectile impact. Int. J. Impact Eng. 2013, 58, 17–30. [Google Scholar] [CrossRef]
- Nowak, A.S.; Collins, K.R. Reliability of Structures; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Siddiqui, N.; Abbas, H.; Almusallam, T.; Li, Q.M.; Al-Salloum, Y. Reliability assessment of steel-lined and prestressed FRC slabs against projectile impact. Appl. Sci. 2023, 13, 90. [Google Scholar] [CrossRef]
- Almusallam, T.; Al-Salloum, Y.; Alsayed, S.; Iqbal, R.; Abbas, H. Effect of CFRP strengthening on the response of RC slabs to hard projectile impact. Nucl. Eng. Des. 2015, 286, 211–226. [Google Scholar] [CrossRef]
- Siddiqui, N.A.; Al-Salloum, Y.A.; Almusallam, T.H.; Abadel, A.A.; Abbas, H. Reliability assessment of HFRC slabs against projectile impact. Int. J. Concr. Struct. Mater. 2018, 12, 58. [Google Scholar] [CrossRef]
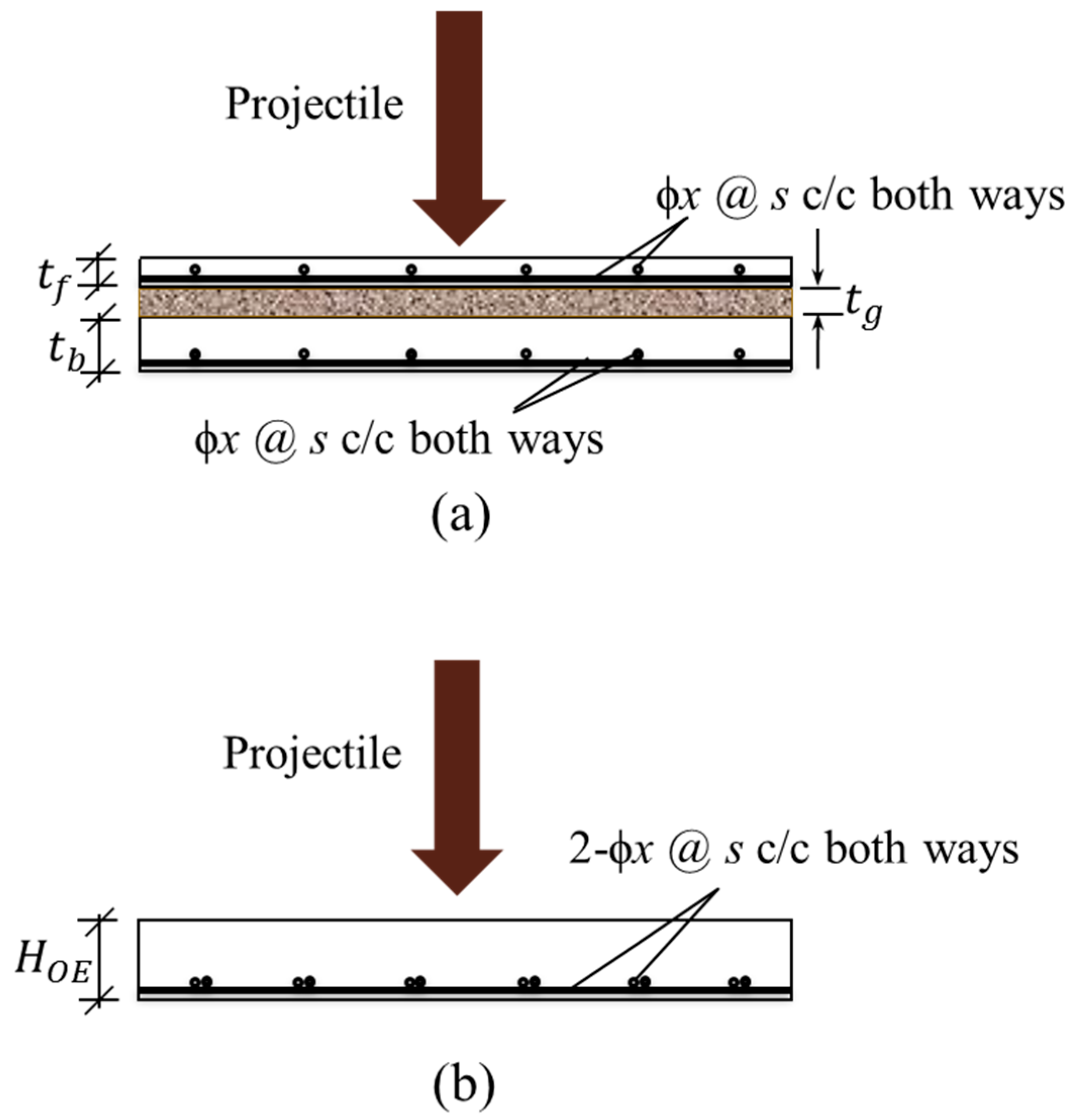

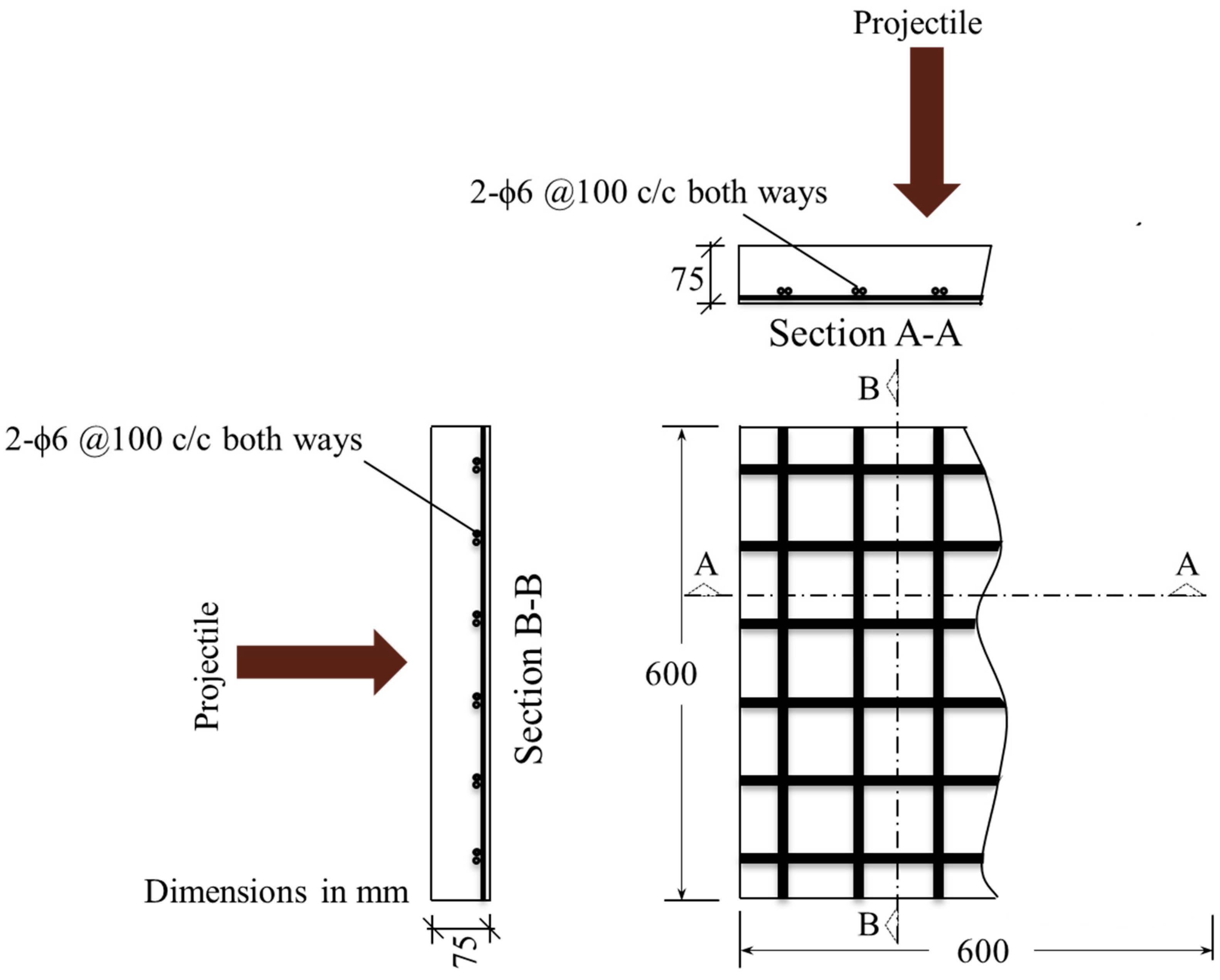
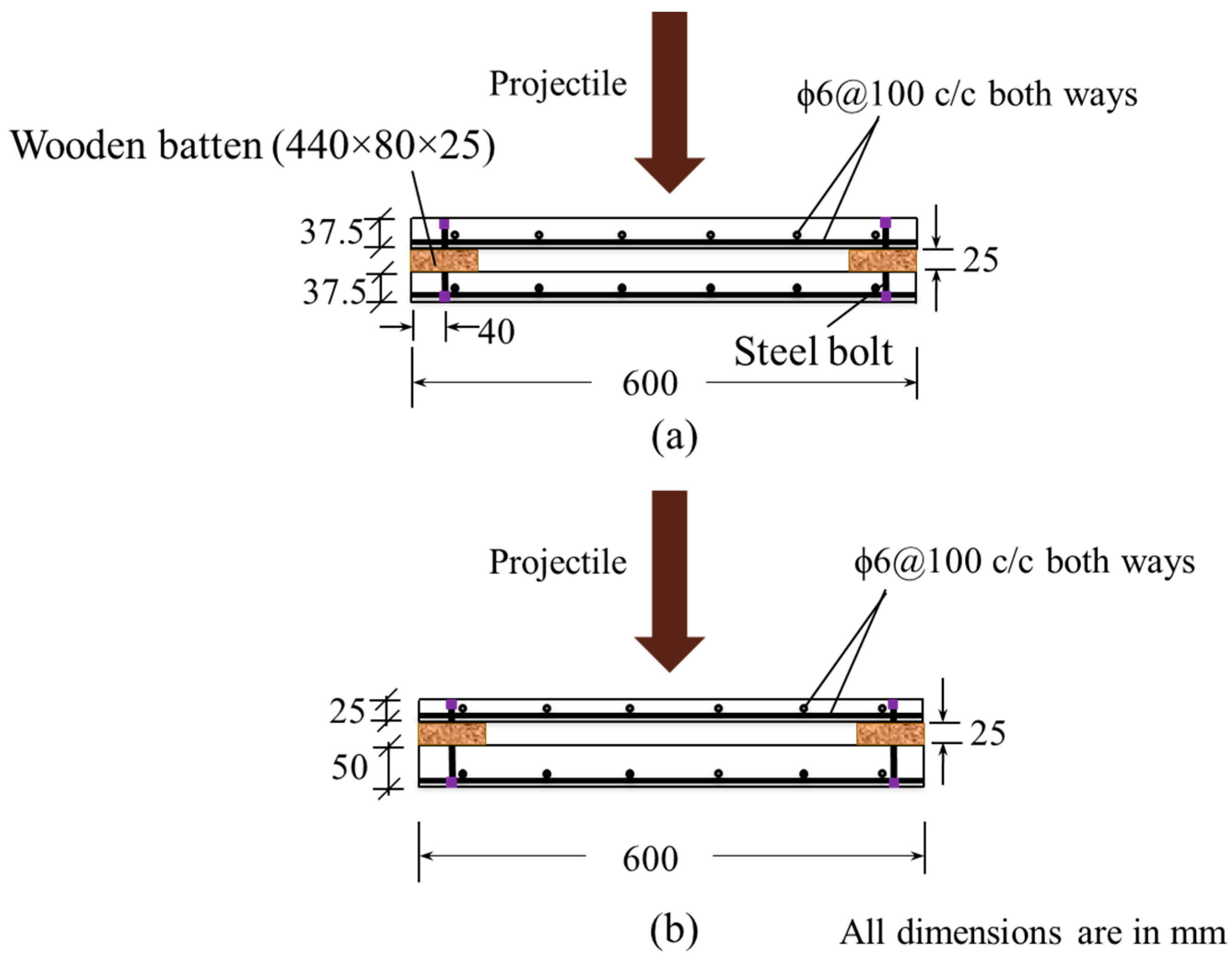
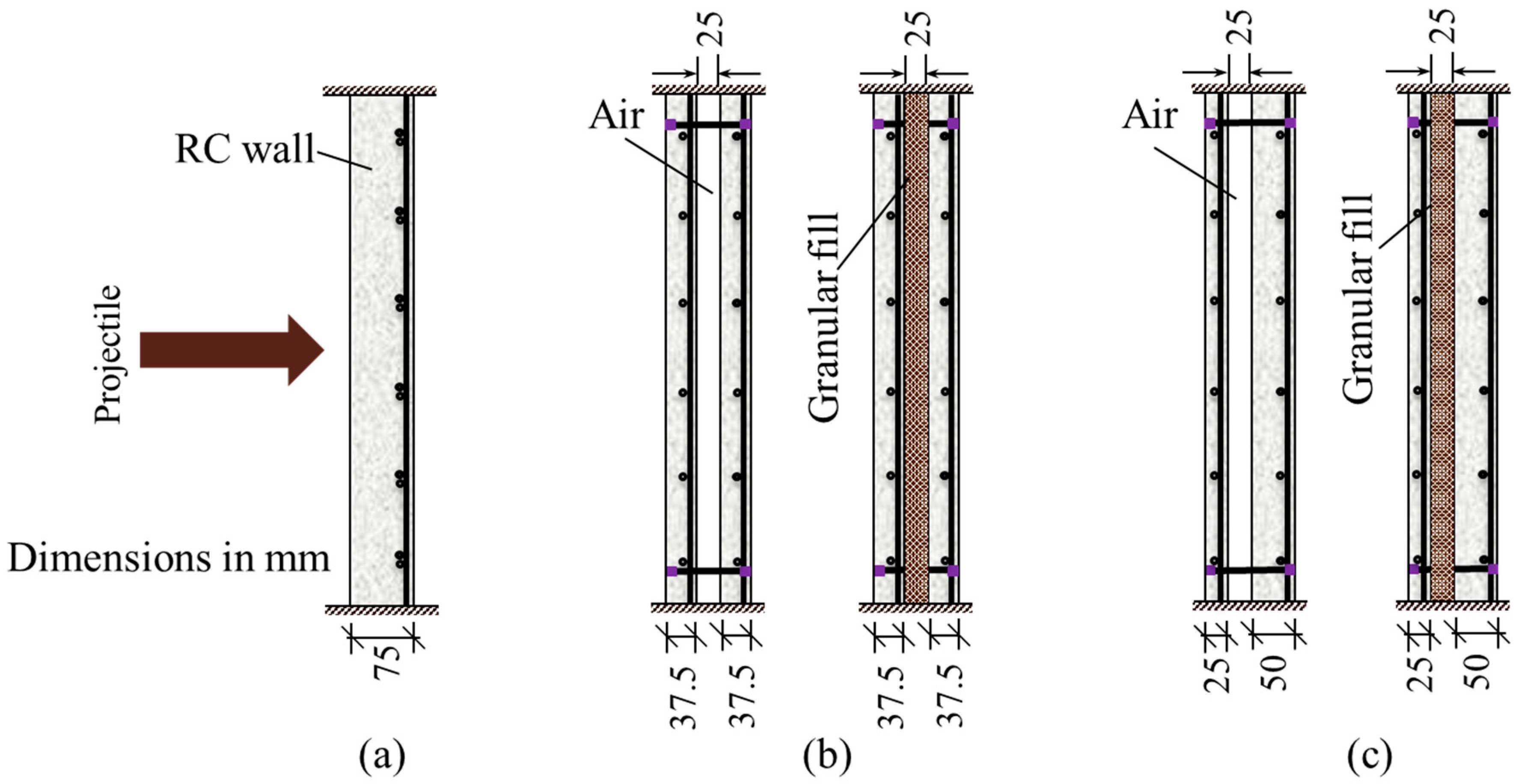



| Test Specimen | (mm) | (mm) | (mm) | Equivalent Steel Ratio, r (%) | Experimental Perforation Energy [1] | Experimental Ballistic Limit (m/s) [1] | Estimated Ballistic Limit (m/s) | Error |
|---|---|---|---|---|---|---|---|---|
| Group-1: Solid Monolithic RC Wall | ||||||||
| Wall-Monolithic | 75 | - | - | - | 1919 | 69 | 61.8 | 10.4% |
| Group 2: Equal-thickness Composite Wall Systems | ||||||||
| C-Wall-EQ-A | 37.5 | 37.5 | 88.9 | 0.74% | 2599 | 81 | 77.3 | 4.6% |
| C-Wall-EQ-S | 37.5 | 37.5 | 92.7 | 0.70% | 2713 | 82 | 85.1 | −3.8% |
| C-Wall-EQ-R | 37.5 | 37.5 | 93.0 | 0.70% | 2738 | 83 | 85.6 | −3.1% |
| Group 3: Non-identical Thickness Composite Wall Systems | ||||||||
| C-Wall-NE-A | 25 | 50 | 91.5 | 0.72% | 2624 | 81 | 82.6 | −2.0% |
| C-Wall-NE-S | 25 | 50 | 99.2 | 0.65% | 3961 | 100 | 98.3 | 1.7% |
| C-Wall-NE-R | 25 | 50 | 99.7 | 0.65% | 3961 | 100 | 99.3 | 0.7% |
| Variables Considered Random | Nominal Value | Bias Factor | Coefficient of Variation (%) | Distribution |
|---|---|---|---|---|
| Monolithic and Composite Walls | ||||
| Concrete density, (kg/m3) | 2500 | 1.05 | 10 | Log-normal distribution |
| Concrete strength, (MPa) | 30 | 1.1 | 10 | Log-normal distribution |
| Thickness of the concrete slab, (mm), | Variable | 1.0 | 5 | Gaussian distribution |
| Ratio of reinforcement, (%) | Variable | 1.1 | 10 | Gaussian distribution |
| Spacing of steel rebars, (mm) | 100 | 0.9 | 5 | Log-normal distribution |
| Impacting Projectile | ||||
| Projectile mass, (kg) | 0.8 | 1.1 | 5 | Log-normal distribution |
| Diameter of projectile, (mm) | 40 | 1.05 | 5 | Gaussian distribution |
| Velocity of impact, (m/s) | Varied | 0.9 | 10 | Type I Extreme Value (EV-I) distribution |
| Specimen ID * | (mm) | (mm) | (mm) | (kg/m3) | β | ||
|---|---|---|---|---|---|---|---|
| Wall-Monolithic | 75 | - | - | - | 0.8 | 1.69 × 10−2 | 2.124 |
| 0.9 | 6.15 × 10−2 | 1.543 | |||||
| Composite walls made up of equal-thickness walls at 25 mm apart | |||||||
| C-Wall-EQ-A | 37.5 | 37.5 | 25 (Air) | ~ 0 | 0.8 | 7.44 × 10−4 | 3.177 |
| 0.9 | 4.70 × 10−3 | 2.597 | |||||
| C-Wall-EQ-S | 37.5 | 37.5 | 25 (Sand) | 1600 | 0.8 | 1.78 × 10−4 | 3.571 |
| 0.9 | 1.53 × 10−3 | 2.961 | |||||
| C-Wall-EQ-R | 37.5 | 37.5 | 25 (Recycled aggregate) | 1700 | 0.8 | 1.67 × 10−3 | 3.588 |
| 0.9 | 1.38 × 10−3 | 2.994 | |||||
| Composite walls made up of unequal-thickness walls at 25 mm apart | |||||||
| C-Wall-NE-A | 25 | 50 | 25 (Air) | ~0 | 0.8 | 2.87 × 10−4 | 3.444 |
| 0.9 | 2.68 × 10−3 | 2.784 | |||||
| C-Wall-NE-S | 25 | 50 | 25 (Sand) | 1600 | 0.8 | 1.60 × 10−4 | 4.159 |
| 0.9 | 1.40 × 10−4 | 3.633 | |||||
| C-Wall-NE-R | 25 | 50 | 25 (Recycled aggregate) | 1700 | 0.8 | 1.47 × 10−5 | 4.179 |
| 0.9 | 1.19× 10−4 | 3.674 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqui, N.A.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Safety Evaluation of Composite Wall Systems Subjected to Projectile Impact. Appl. Sci. 2025, 15, 11128. https://doi.org/10.3390/app152011128
Siddiqui NA, Abbas H, Almusallam T, Al-Salloum Y. Safety Evaluation of Composite Wall Systems Subjected to Projectile Impact. Applied Sciences. 2025; 15(20):11128. https://doi.org/10.3390/app152011128
Chicago/Turabian StyleSiddiqui, Nadeem A., Husain Abbas, Tarek Almusallam, and Yousef Al-Salloum. 2025. "Safety Evaluation of Composite Wall Systems Subjected to Projectile Impact" Applied Sciences 15, no. 20: 11128. https://doi.org/10.3390/app152011128
APA StyleSiddiqui, N. A., Abbas, H., Almusallam, T., & Al-Salloum, Y. (2025). Safety Evaluation of Composite Wall Systems Subjected to Projectile Impact. Applied Sciences, 15(20), 11128. https://doi.org/10.3390/app152011128






