The Influence of Temperature-Induced Deformation on Dynamic Characteristics of Novel Fabricated Track Beam-End Expansion Area at Long-Span Bridge: A Case Study in China
Abstract
1. Introduction
2. The Refined Model for the Prefabricated Track and Beam-End System
2.1. Finite Element Model of the Long-Span Cable-Stayed Bridge
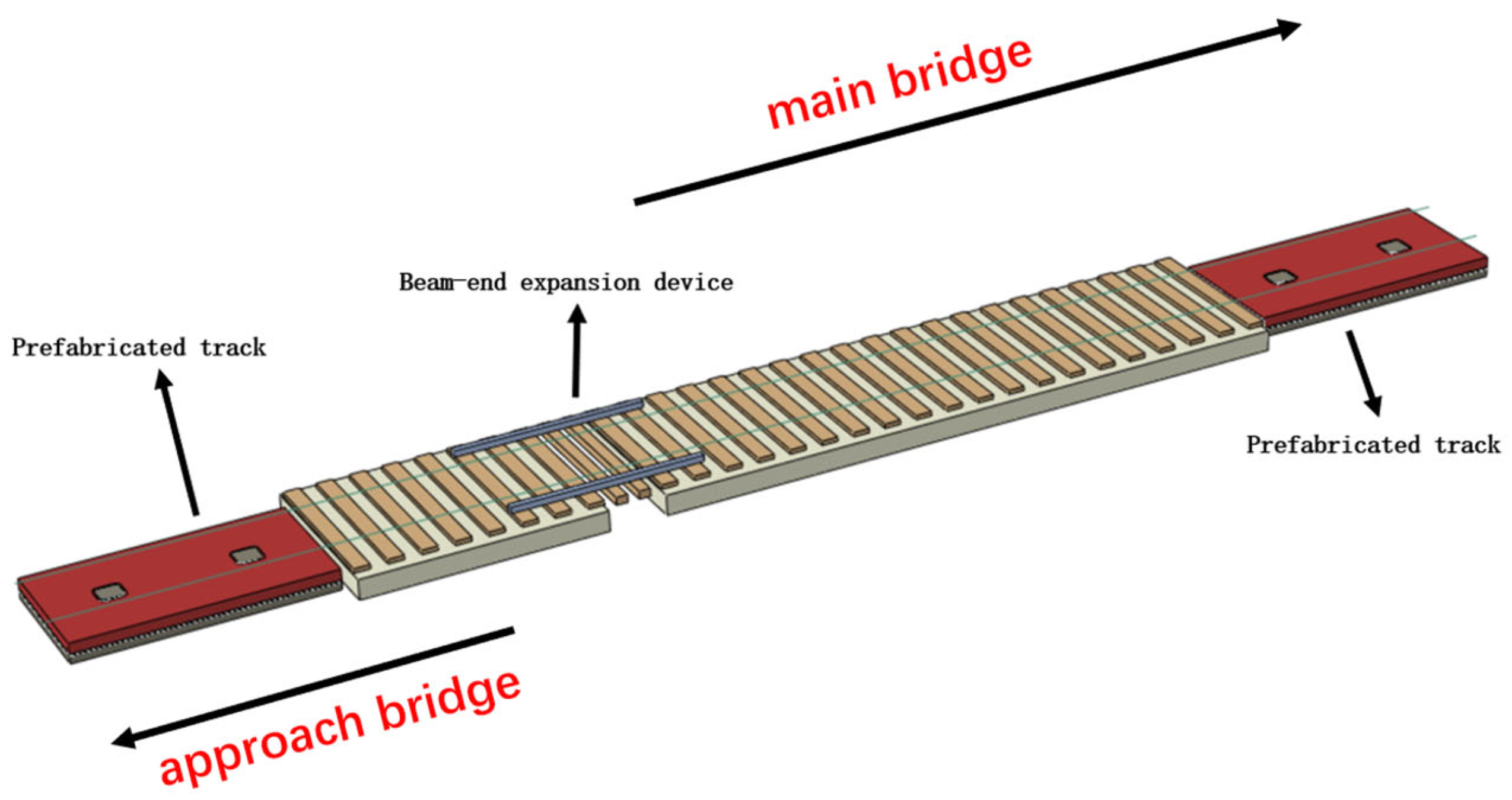
2.2. Beam-End Expansion Area Model
2.3. Vehicle–Rail–Bridge Coupling Dynamic Model
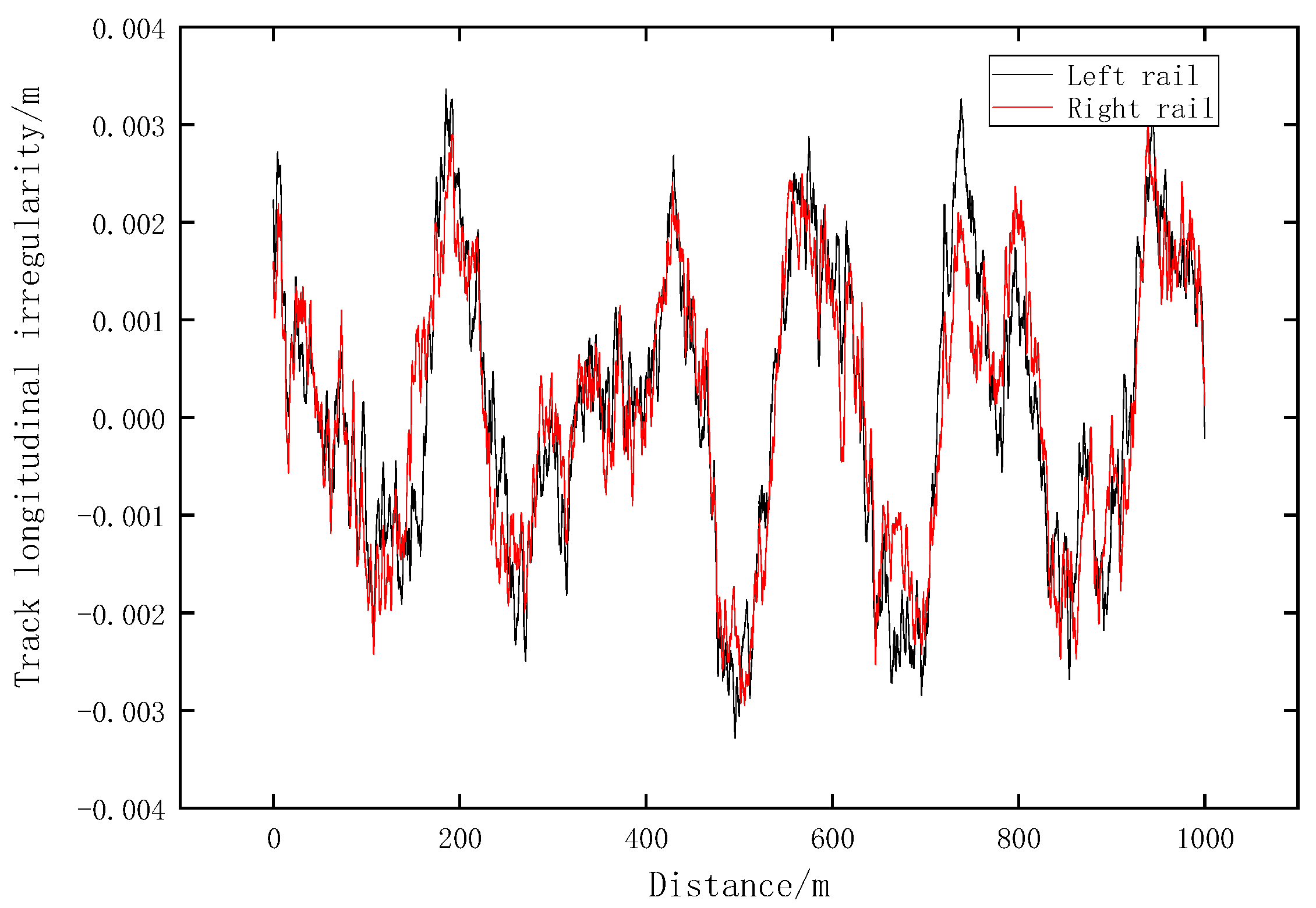
2.4. Model Validation
3. Analysis of the Train-Rail-Bridge Dynamic Performance at Beam Ends Under Complex Temperature Load Conditions
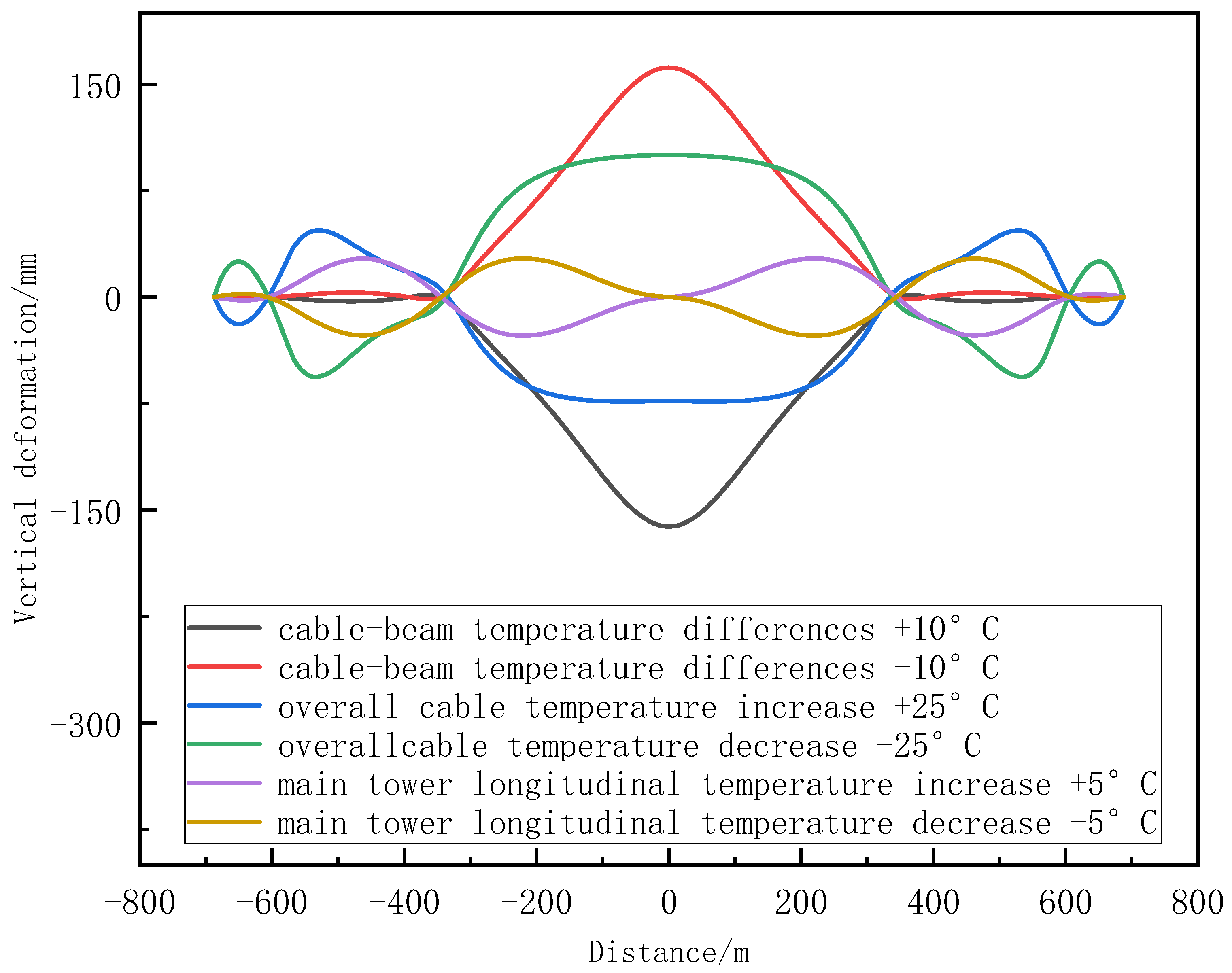
3.1. Load Conditions
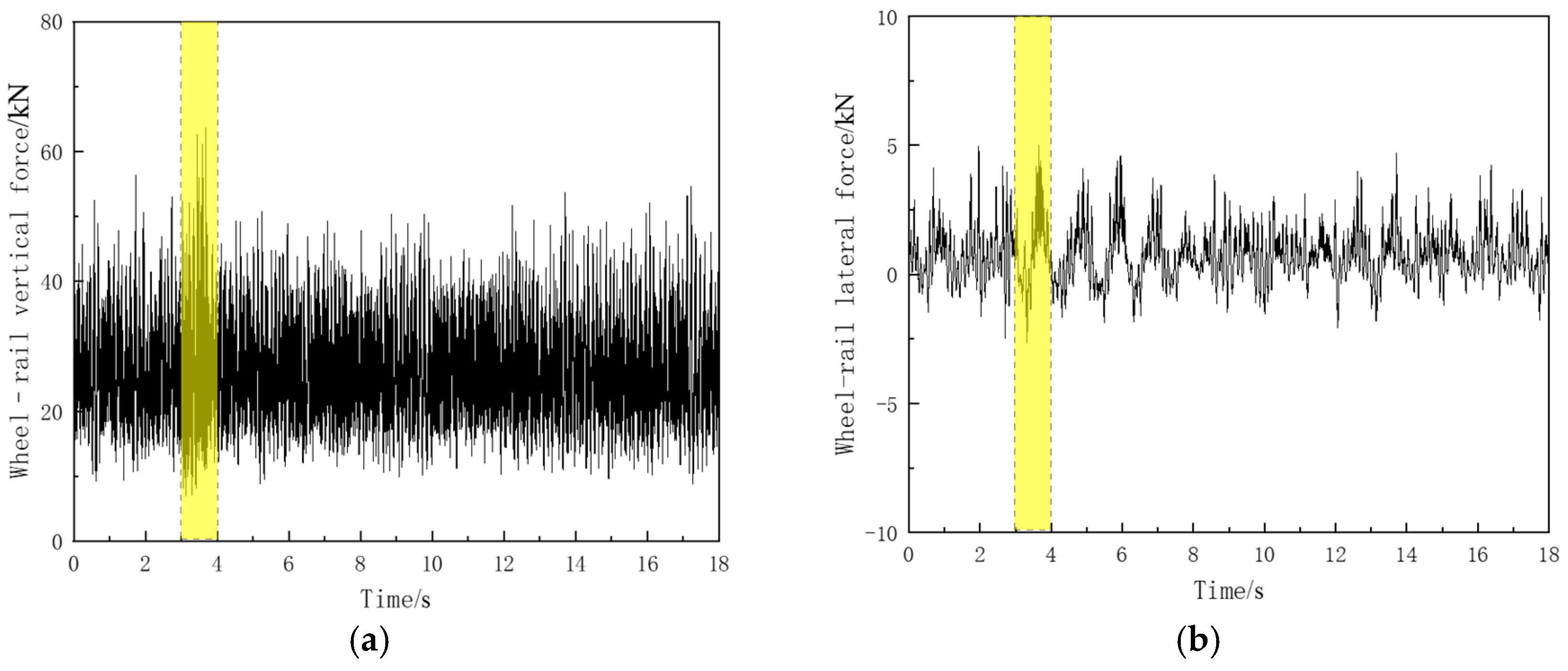
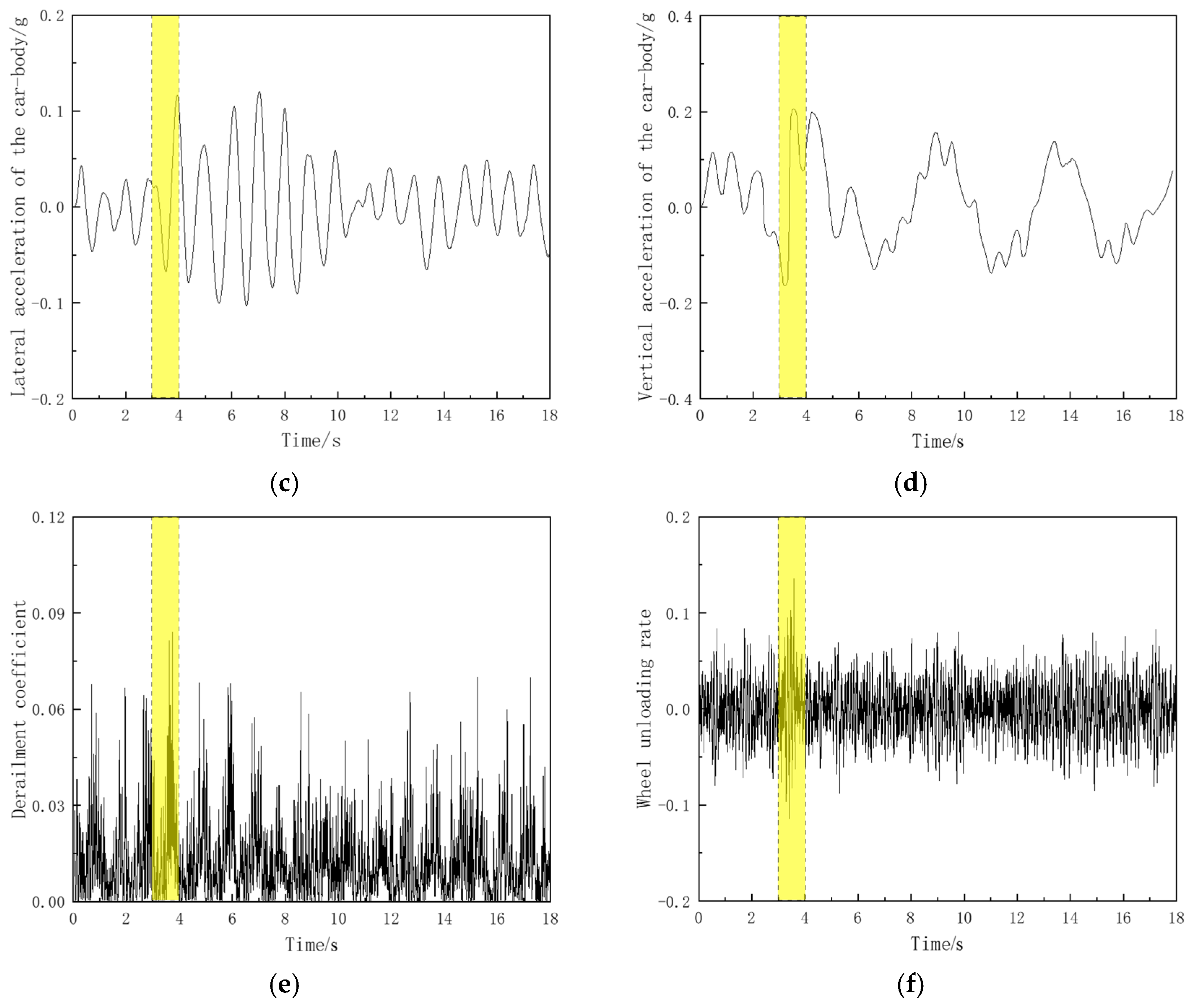
3.2. Dynamic Response Analysis of Train in the Beam-End Expansion Area
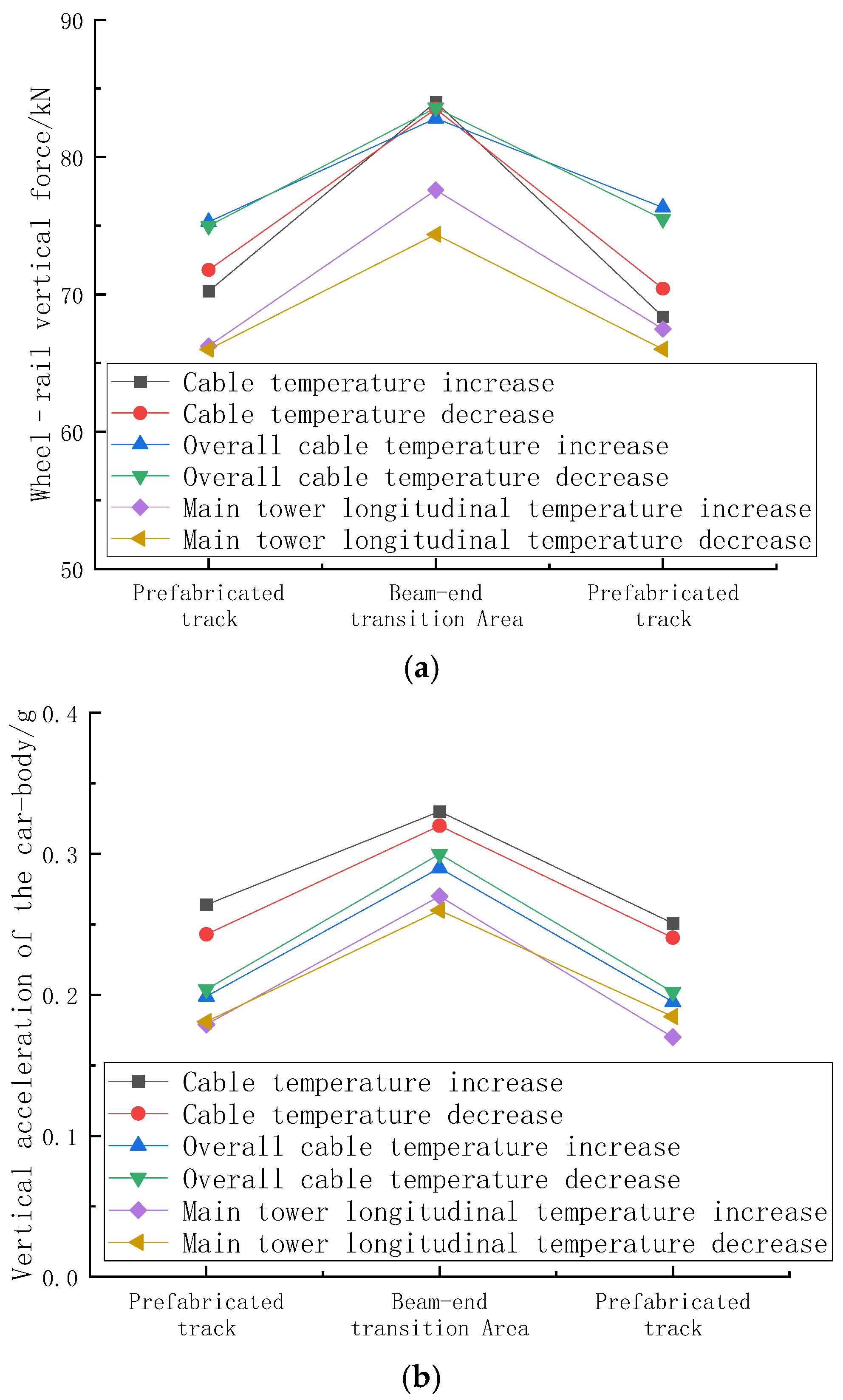
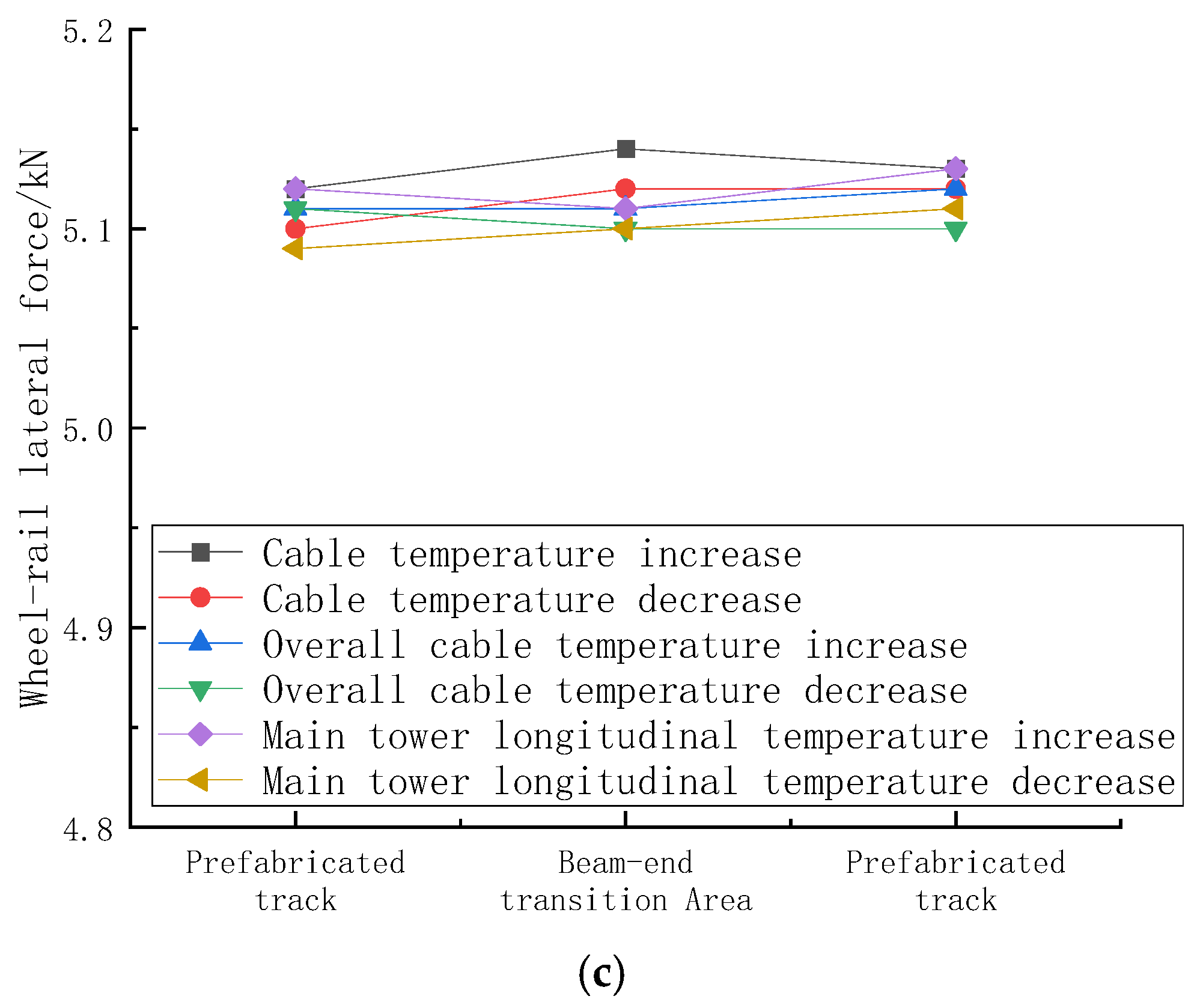
3.3. The Impact of Temperature-Induced Deformation in the Beam-End Expansion Area on the Train’s Dynamic Response
3.4. Beam-End Expansion Area Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H. Research on the static characteristics of ballastless track on urban railway bridge. J. Railw. Eng. Soc. 2023, 40, 31–37. [Google Scholar]
- Peng, S. Exploring passenger volume forecast method for suburban railway: A case study of ningbo-xiangshan line. Railw. Constr. Technol. 2022, 6, 117–120. [Google Scholar]
- Zhu, B.; Ren, X. Design and mechanical characteristics study of prefabricated track structure for urban railways. China Railw. 2022, 8, 48–54. [Google Scholar]
- Chang, L.; Lee, Y. Evaluation of performance of bridge deck expansion joints. J. Perform. Constr. Facil. 2002, 16, 3–9. [Google Scholar] [CrossRef]
- Zuada, C.B.; Vervuurt, A.H.J.M.; Peelen, W.H.A.; Leendertz, J.S. Dynamics of modular expansion joints: The Martinus Nijhoff Bridge. Eng. Struct. 2013, 48, 144–154. [Google Scholar] [CrossRef]
- McCarthy, E.; Wright, T.; Padgett, J.E.; DesRoches, R.; Bradford, P. Development of an experimentally validated analytical model for modular bridge expansion joint behavior. J. Bridge Eng. 2014, 19, 235–244. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, W.; Au, F.T.K. Effect of dynamic impact at modular bridge expansion joints on bridge design. Eng. Struct. 2016, 127, 645–662. [Google Scholar] [CrossRef]
- Li, G.; Han, W.; Zhang, L.; Zhang, Y. Service state evaluation for expansion joints of suspension bridge under extreme vehicle braking load. J. Vib. Shock. 2022, 41, 186–195. [Google Scholar]
- Sun, Z.; Zhang, Y. Failure Mechanism of expansion joints in a suspension bridge. J. Bridge Eng. 2016, 21, 05016005. [Google Scholar] [CrossRef]
- Deng, L.; Yan, W.; Zhu, Q. Vehicle impact on the deck slab of concrete box-girder bridges due to damaged expansion joints. J. Bridge Eng. 2016, 21, 06015006. [Google Scholar] [CrossRef]
- Li, G.; Han, W.; Zhang, L.; Xu, X. Method of wear evaluation on sliding supports in expansion joints based on theories of mechanism motion and wear. China J. Highw. Transp. 2023, 36, 166–178. [Google Scholar]
- Guo, H.; Jiang, J.; Gao, M.; Liu, X.; Zhao, H.; Su, P.; Zhu, Y.; He, D. Design and research on the expansion and contraction device at the end of large-span steel bridges on high-speed railways. Railw. Eng. 2020, 60, 1–7. [Google Scholar]
- Zhang, X. Research on steel rail expansion adjuster and beam end expansion device of wuhu yangtze river public railway bridge on shanghehang high speed railway. China Railw. 2020, 6, 38–43. [Google Scholar]
- Zheng, W.; Zhu, Z.; Sheng, X.; Li, D.; Guo, S. Theoretical and experimental research on deformation adaptability of ballastless tracks on long-span cable-stayed bridge in high-speed railway. J. Railw. Sci. Eng. 2024, 21, 1286–1297. [Google Scholar]
- Hou, J.; Wang, J.; Xu, W.; Chen, Y.; Wang, B.; Liu, J.; Shen, B.; Li, Y.; Sun, H. An analysis method of vehicle-bridge coupling vibration considering effects of expansion joint parameters and its application. Struct. Control. Health Monit. 2022, 29, e3065. [Google Scholar] [CrossRef]
- Xiao, T.; Hong, Y.; Xu, J.; Pu, Q.; Wen, X. Performance evaluation of cable-stayed bridge expansion joints based on Lasso dimensionality reduction and temperature-displacement-model. Adv. Struct. Eng. 2024, 27, 981–994. [Google Scholar] [CrossRef]
- Wang, S.; Tao, T.; Wang, H. Comparison of extraction methods for temperature-induced displacement of expansion joint of long-span cable-stayed bridge. J. Southeast Univ. (Nat. Sci. Ed.) 2023, 53, 664–671. [Google Scholar]
- Zhang, Q.; Cai, X.; Xie, K.; Zhang, Y.; Wang, Q.; Wang, T. Multi-objective optimization for switch rail declining values of rail expansion joint on cable-stayed bridge. Struct. Multidiscip. Optim. 2024, 67, 29. [Google Scholar] [CrossRef]
- Wang, H.; Shen, R.; Wen, W.; Dai, Q.; Bai, L. Investigation of longitudinal movements of girder ends considering various longitudinal non-linear resistances in railway suspension bridges. J. Constr. Steel Res. 2024, 214, 108446. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, M.; Yang, F. Study on the vertical stiffness of bridge expansion joints based on the vehicle-track-bridge coupled model. Shock. Vib. 2022, 2022, 2814807. [Google Scholar] [CrossRef]
- Meng, X.; Yao, J.; Liu, P.; Wang, W.; Yang, Y.; Ke, Z. On site testing and analysis of dynamic characteristics of dashengguan yangtze river bridge. China Railw. Sci. 2015, 36, 30–36. [Google Scholar]
- Lin, W.; Yoda, T.; Taniguchi, N. Effects of bridge accessories in steel-concrete composite railway bridges in service condition. J. Bridge Eng. 2016, 21, 0401050. [Google Scholar] [CrossRef]
- Zhang, S. Analysis of Mechanical Characteristics of CRTS III Slab Ballastless Ttrack Sstructure on Bridge Under Complex Loads. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2020. [Google Scholar]
- Tan, X. Study on Mechanical and Deformation Characteristics of CRTSIS III Ballastless Track Under Complicated Temperature. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Wang, Y.L. Study on the -Track-Bridge Dynamic Response and Track Irregularity at Long Span Bridge Beam End. Ph.D. Thesis, China Academy of Railway Sciences, Beijing, China, 2023. [Google Scholar]
- Wang, S. Research on the Influence Analysis and Prediction Method of Rail Corrugation on Subway-Induced Environmental Vibrations. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2024. [Google Scholar]
- Yang, Y.; Xin, T.; Li, Q.; Wang, S.; Dai, C.; Kong, C. Application of novel fabricated ballastless track on new designed long-span urban bridges. Adv. Bridge Eng. 2024, 5, 29. [Google Scholar] [CrossRef]
- Luo, Y. Research on Static and Dynamic Interaction Between Long-Span Cable-Stayed Bridge and Ballastless Track. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2023. [Google Scholar]




| Track Structure | Elements Type | Material | Connection Method |
|---|---|---|---|
| Base slab | solid | C60 concrete | tie |
| Restrict boss | solid | C60 concrete | tie |
| Rubber pads | solid | Rubber | frictional |
| Track slab | solid | C50 concrete | tie |
| Fastening | spring | WJ-7 | elastic |
| Rail | beam | rail steel | elastic |
| Modal Order | Self-Developed Software | MIDAS Modal | Error |
|---|---|---|---|
| 1 | 0.387 | 0.402 | 3.73% |
| 2 | 0.425 | 0.418 | 1.67% |
| 3 | 0.440 | 0.421 | 4.51% |
| 4 | 0.476 | 0.450 | 5.78% |
| 5 | 0.587 | 0.570 | 2.98% |
| 6 | 0.788 | 0.807 | 2.35% |
| 7 | 0.823 | 0.807 | 1.98% |
| 8 | 0.991 | 0.967 | 2.48% |
| 9 | 1.102 | 1.099 | 0.27% |
| 10 | 1.619 | 1.507 | 7.43% |
| Evaluating Indicator | Without Temperature Load | Cable Temperature Increase | Cable Temperature Decrease | Overall Cable Temperature Increase | Overall Cable Temperature Decrease | Main Tower longitudinal Temperature Increase | Main Tower Longitudinal Temperature Decrease |
|---|---|---|---|---|---|---|---|
| Wheel–rail vertical force/kN | 66.90 | 83.06 | 83.51 | 84.66 | 85.32 | 77.59 | 74.37 |
| Wheel-rail lateral force/kN | 5.10 | 5.14 | 5.12 | 5.11 | 5.10 | 5.11 | 5.10 |
| Wheel-axle lateral force/kN | 8.05 | 8.09 | 8.10 | 8.06 | 8.05 | 8.03 | 8.03 |
| Derailment coefficient | 0.12 | 0.10 | 0.10 | 0.10 | 0.09 | 0.10 | 0.07 |
| Wheel unloading rate | 0.03 | 0.28 | 0.28 | 0.30 | 0.31 | 0.19 | 0.14 |
| Lateral acceleration of the train body/(m·s−1) | 0.23 | 0.24 | 0.23 | 0.24 | 0.23 | 0.22 | 0.22 |
| Vertical acceleration of the train body/(m·s−1) | 0.21 | 0.29 | 0.31 | 0.32 | 0.33 | 0.27 | 0.26 |
| Vertical stability index | 2.28 | 2.31 | 2.28 | 2.31 | 2.28 | 2.25 | 2.25 |
| Lateral stability index | 2.22 | 2.45 | 2.50 | 2.52 | 2.54 | 2.40 | 2.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Xin, T.; Dai, C.; Tong, S.; Kong, C. The Influence of Temperature-Induced Deformation on Dynamic Characteristics of Novel Fabricated Track Beam-End Expansion Area at Long-Span Bridge: A Case Study in China. Appl. Sci. 2025, 15, 11117. https://doi.org/10.3390/app152011117
Yang Y, Xin T, Dai C, Tong S, Kong C. The Influence of Temperature-Induced Deformation on Dynamic Characteristics of Novel Fabricated Track Beam-End Expansion Area at Long-Span Bridge: A Case Study in China. Applied Sciences. 2025; 15(20):11117. https://doi.org/10.3390/app152011117
Chicago/Turabian StyleYang, Yi, Tao Xin, Chuanqing Dai, Shuang Tong, and Chao Kong. 2025. "The Influence of Temperature-Induced Deformation on Dynamic Characteristics of Novel Fabricated Track Beam-End Expansion Area at Long-Span Bridge: A Case Study in China" Applied Sciences 15, no. 20: 11117. https://doi.org/10.3390/app152011117
APA StyleYang, Y., Xin, T., Dai, C., Tong, S., & Kong, C. (2025). The Influence of Temperature-Induced Deformation on Dynamic Characteristics of Novel Fabricated Track Beam-End Expansion Area at Long-Span Bridge: A Case Study in China. Applied Sciences, 15(20), 11117. https://doi.org/10.3390/app152011117






