Power Smoothing in a Wave Energy Conversion Using Energy Storage Systems: Benefits of Forecasting-Enhanced Filtering for Reduction in Energy Storage Requirements
Abstract
Featured Application
Abstract
1. Introduction
2. Methodology
- A WEC model (prime mover + PTO), which allows for the evaluation of the electrical power output profile of a single WEC under a given sea state. This model accounts for the relative position of the WEC with respect to other devices and for the directional characteristics of the incident waves. This enables the aggregation of individual power profiles to determine the total output of a wave energy farm (see Section 2.1).
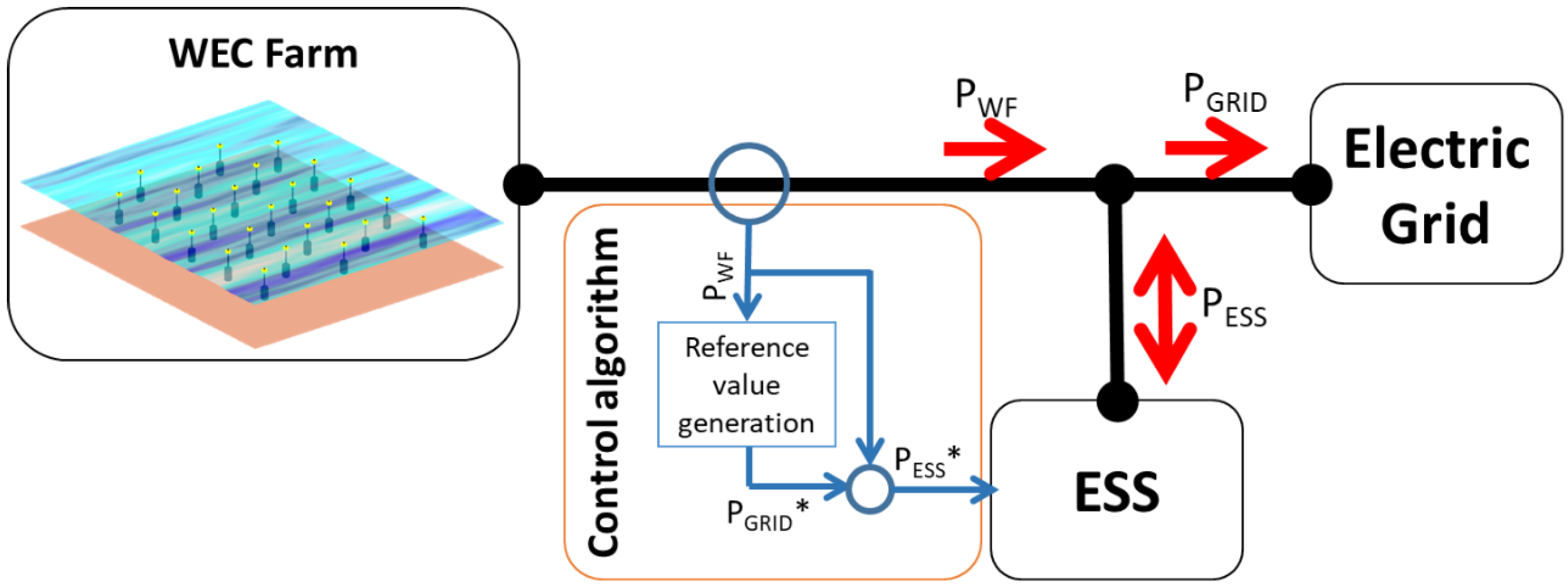
- An energy storage system model, coupled with a power smoothing control algorithm. In this case study, the storage system is modeled as an “agnostic” energy storage unit, and a moving average filter is used as the smoothing algorithm (see Section 2.2).
- A forecasting algorithm, which complements the power smoothing control algorithm of the storage system by enabling the estimation of the real-time moving average filter (MAF) using past power output samples and predicted values as future samples (see Section 2.3).
2.1. Description of the WEC and Wave Farm Model
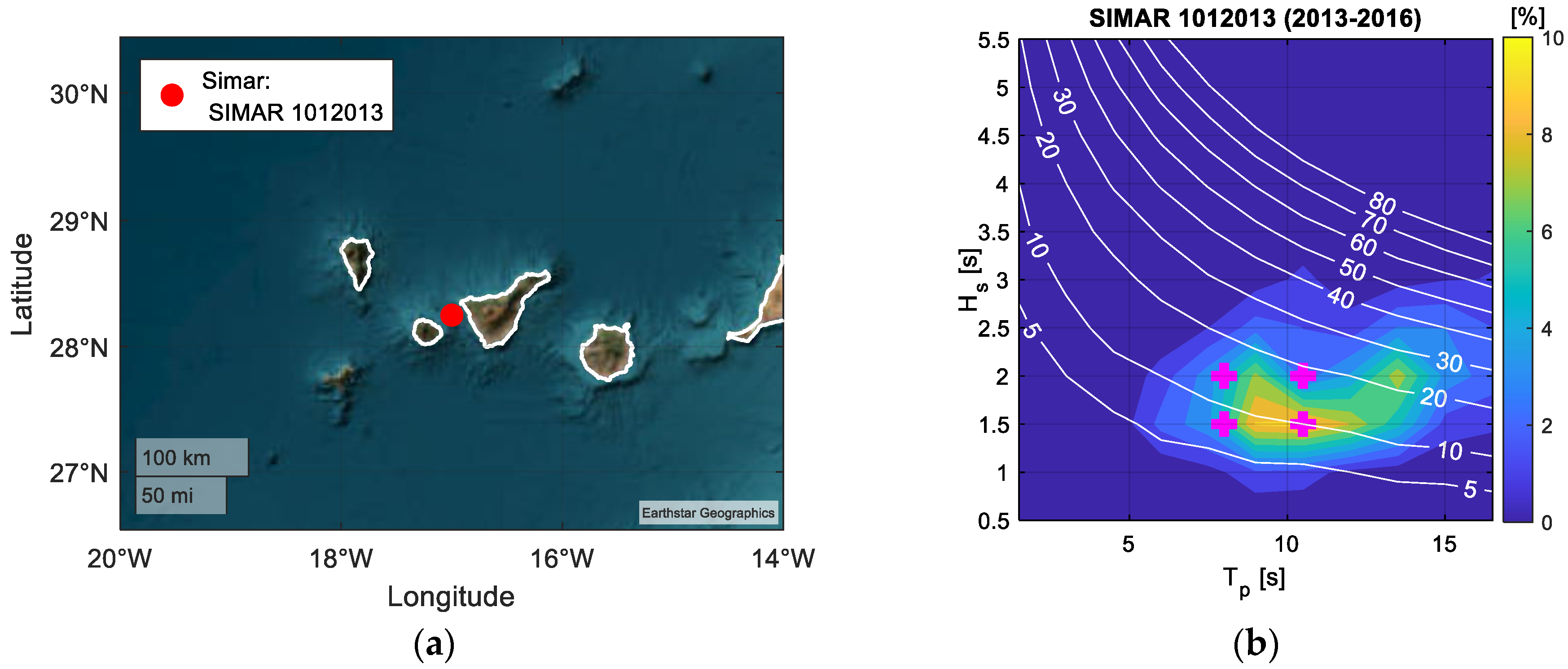
- Ocean wave data are obtained as described in Section 2.1.1, considering the WF location at latitude 28.4° N and longitude 17° W.
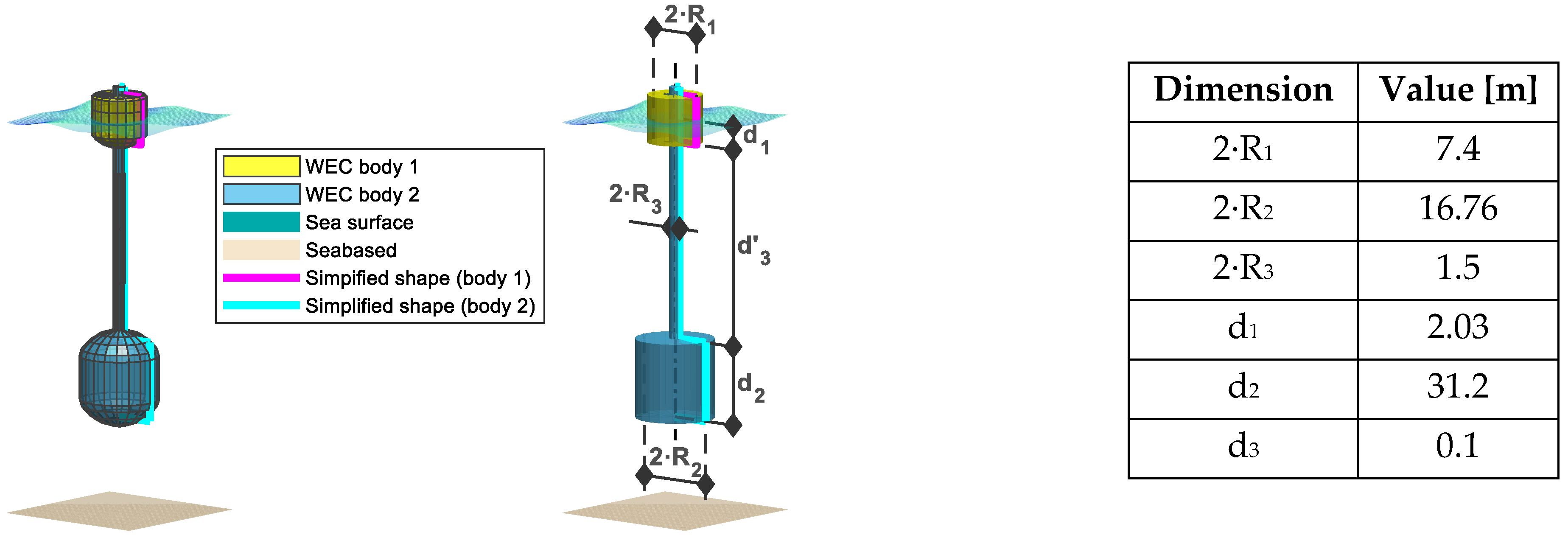
- The primary WEC device is a point absorber with a peak power output of 160 kW. The Power Take-Off (PTO) system consists of a direct-drive linear electric generator rated at 160 kW.
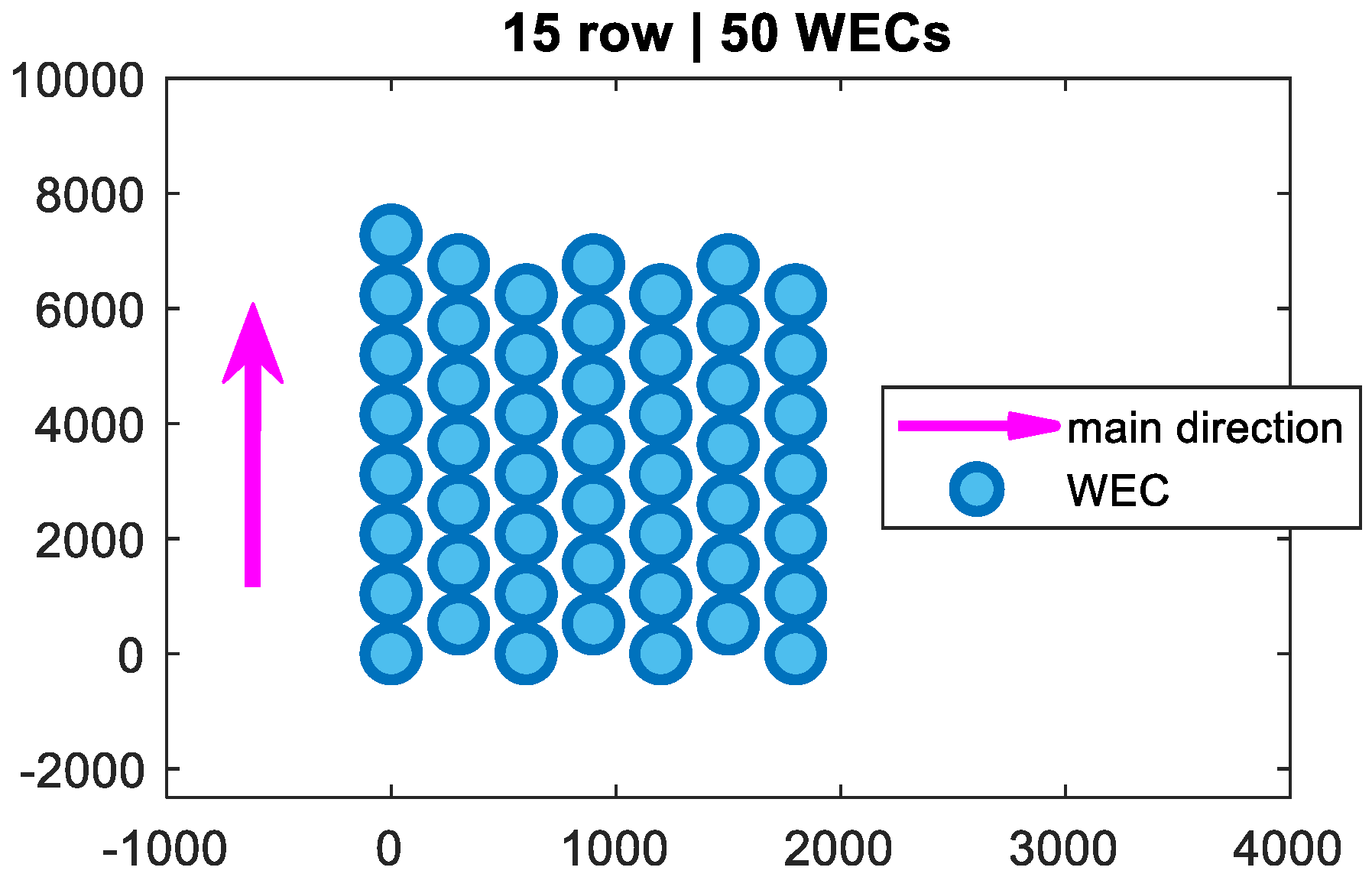
- The WF is composed of 15 groups of WEC units arranged in 9 rows following a triangular layout.
2.1.1. Wave Resource Conditions
2.1.2. WEC Model
2.1.3. Wave Farm Model
2.2. Description of the Energy Storage System Model
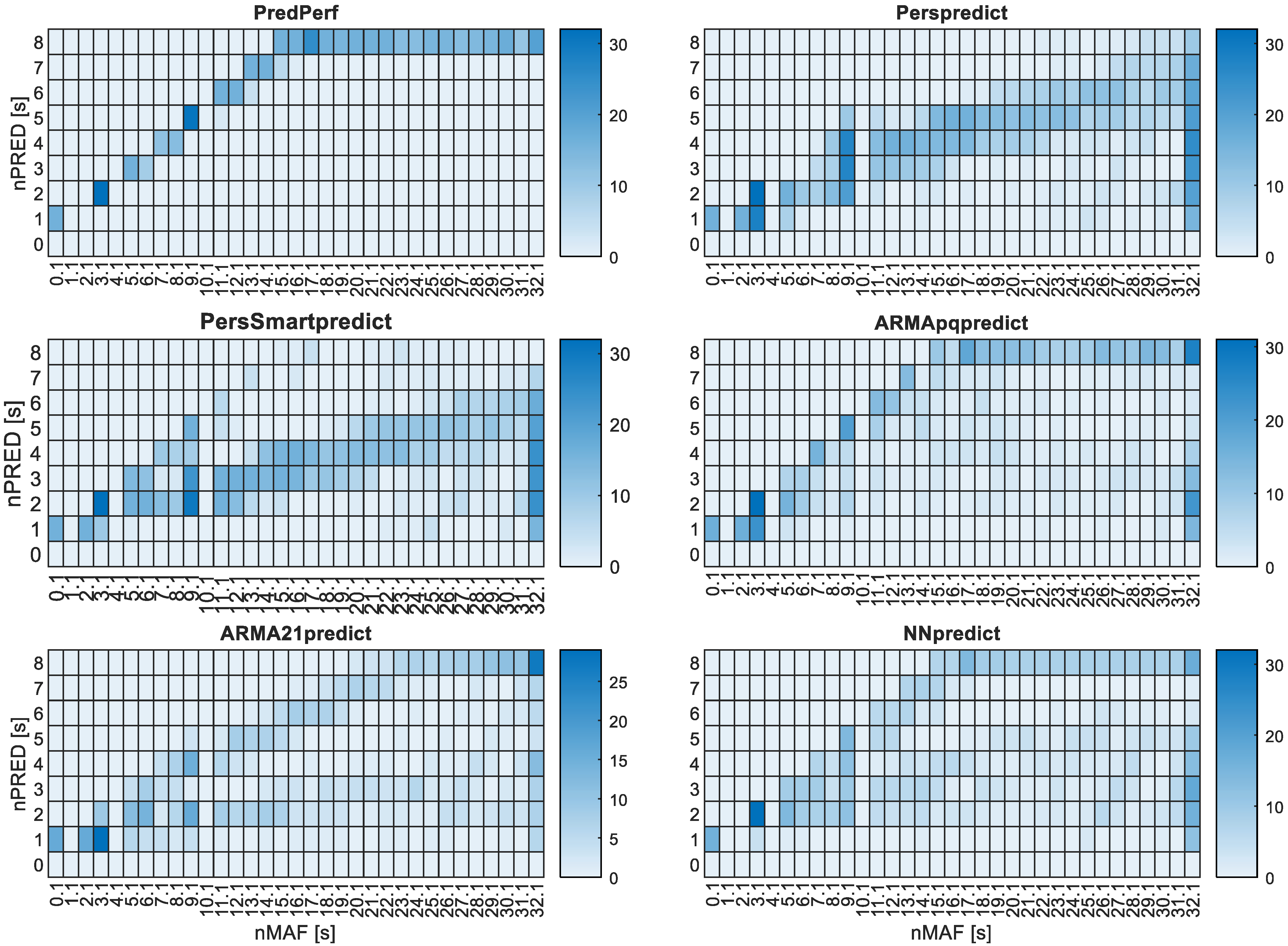
2.3. Forecasting Algorithms
2.3.1. Naïve Models
2.3.2. Linear Models
2.3.3. Artificial Neural Networks
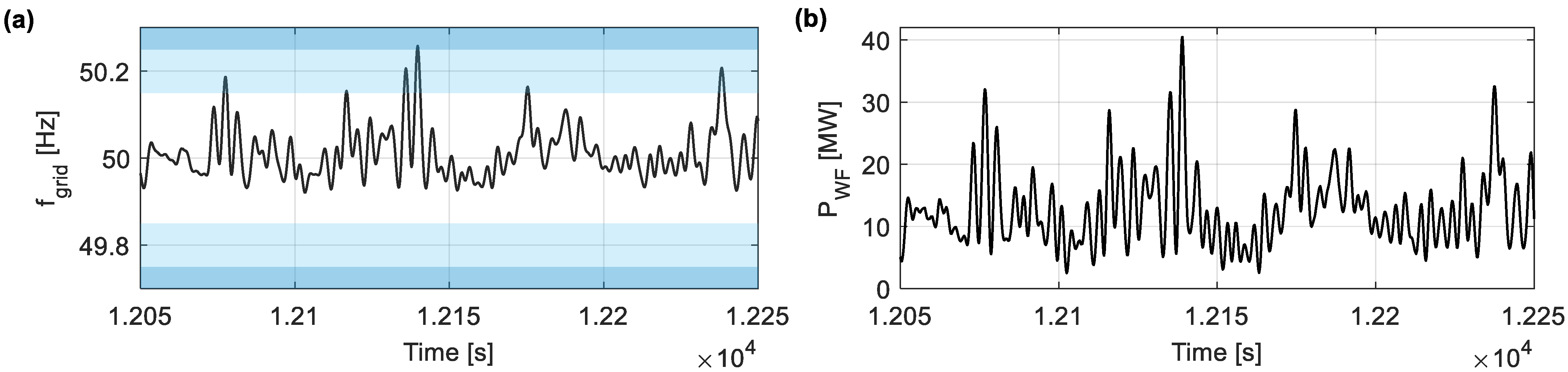
3. Case Study
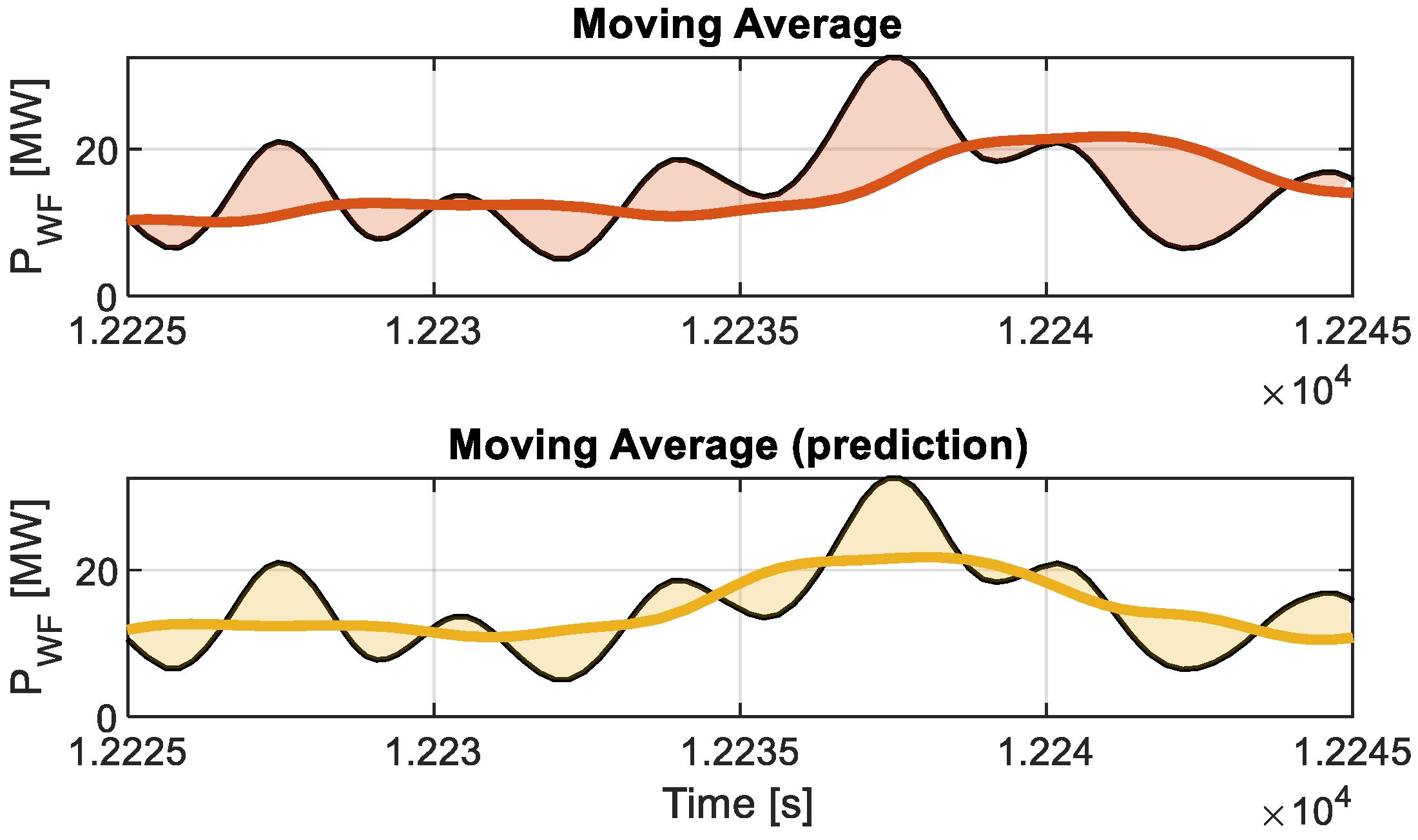
3.1. Application Example: Forecasting in Moving Average Filtering
- Moving average filter.
- Moving average filter considering future (predicted/forecasted) values. In this example (Section 3.1), it is considered perfect prediction.
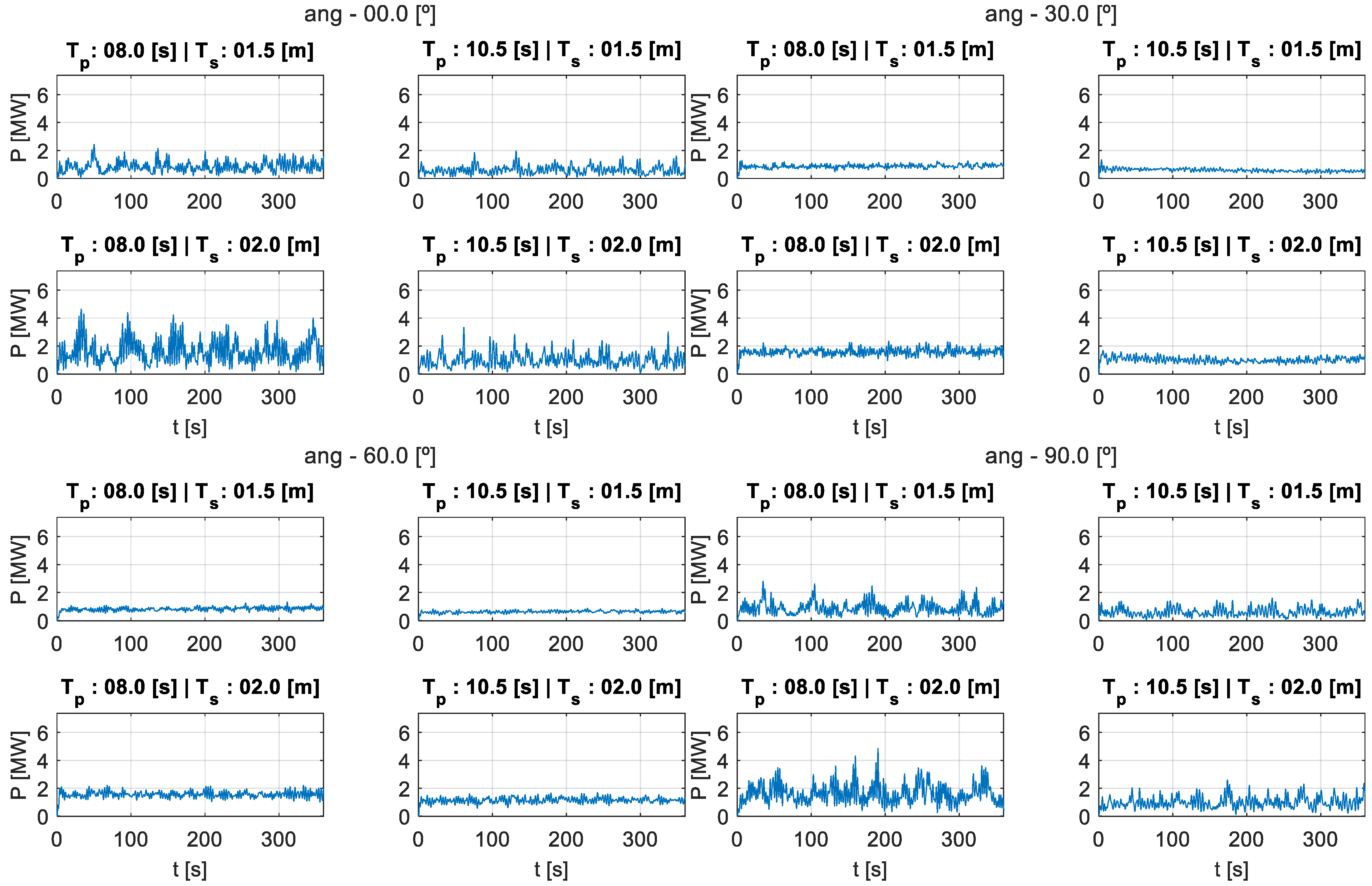
3.2. Description of the Case Study
- Total window size: Ns_MAF: [0, 10, 20, …, 320] samples; nMAF: [0, 1, 2, …, 32] seconds;
- Forecast window size: Ns_Pred: [0, 10, …, 80] samples; nPred: [0, 1, …, 8] seconds.
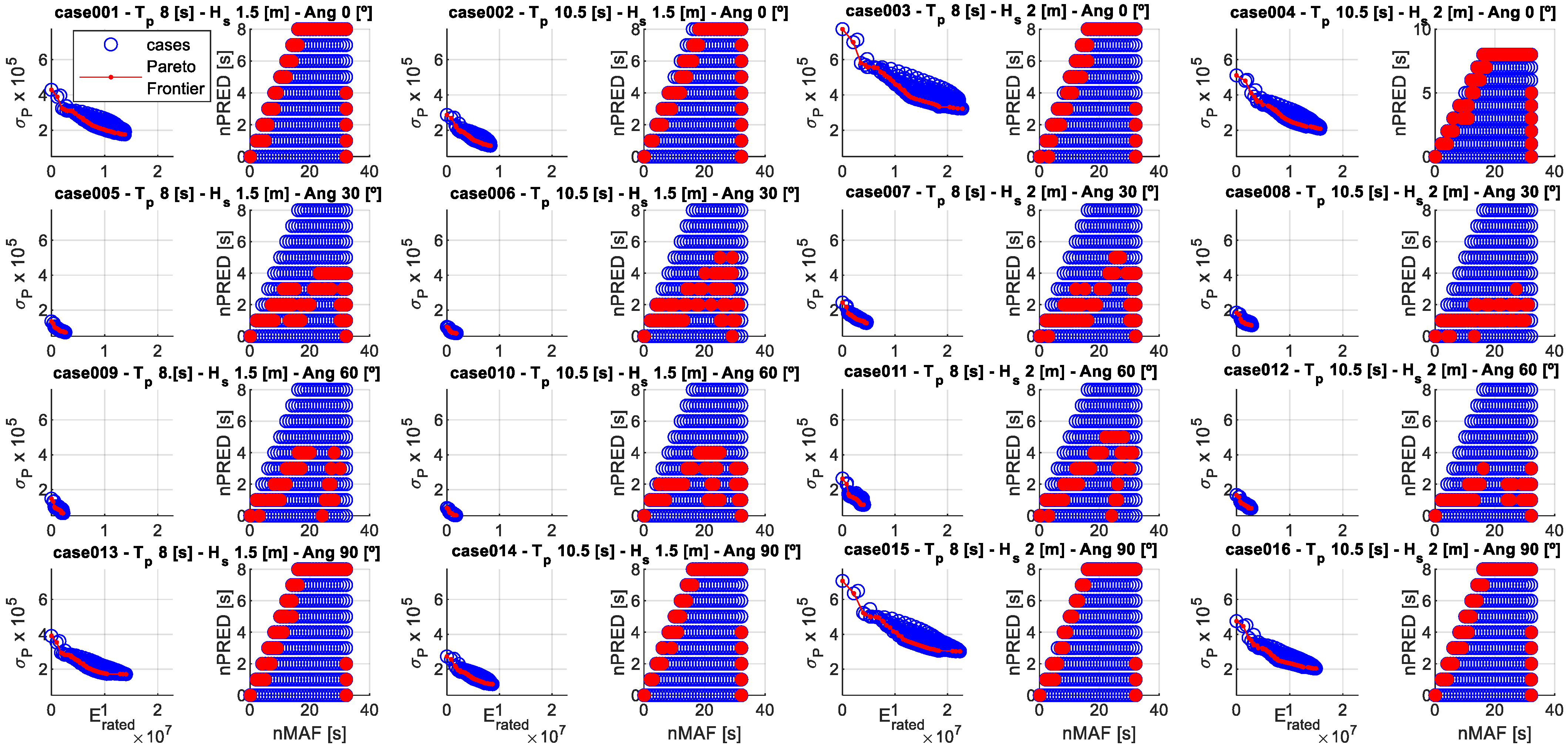
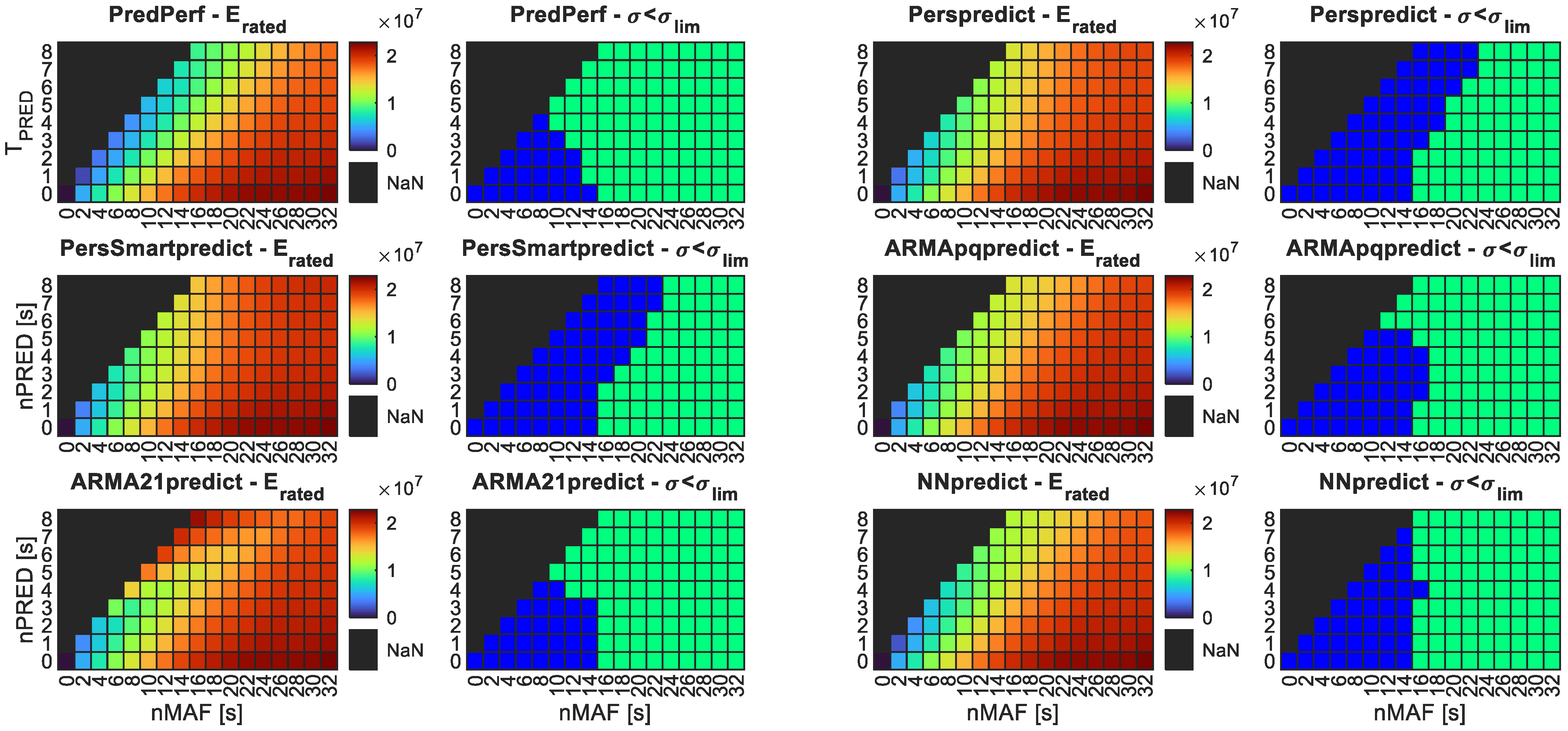
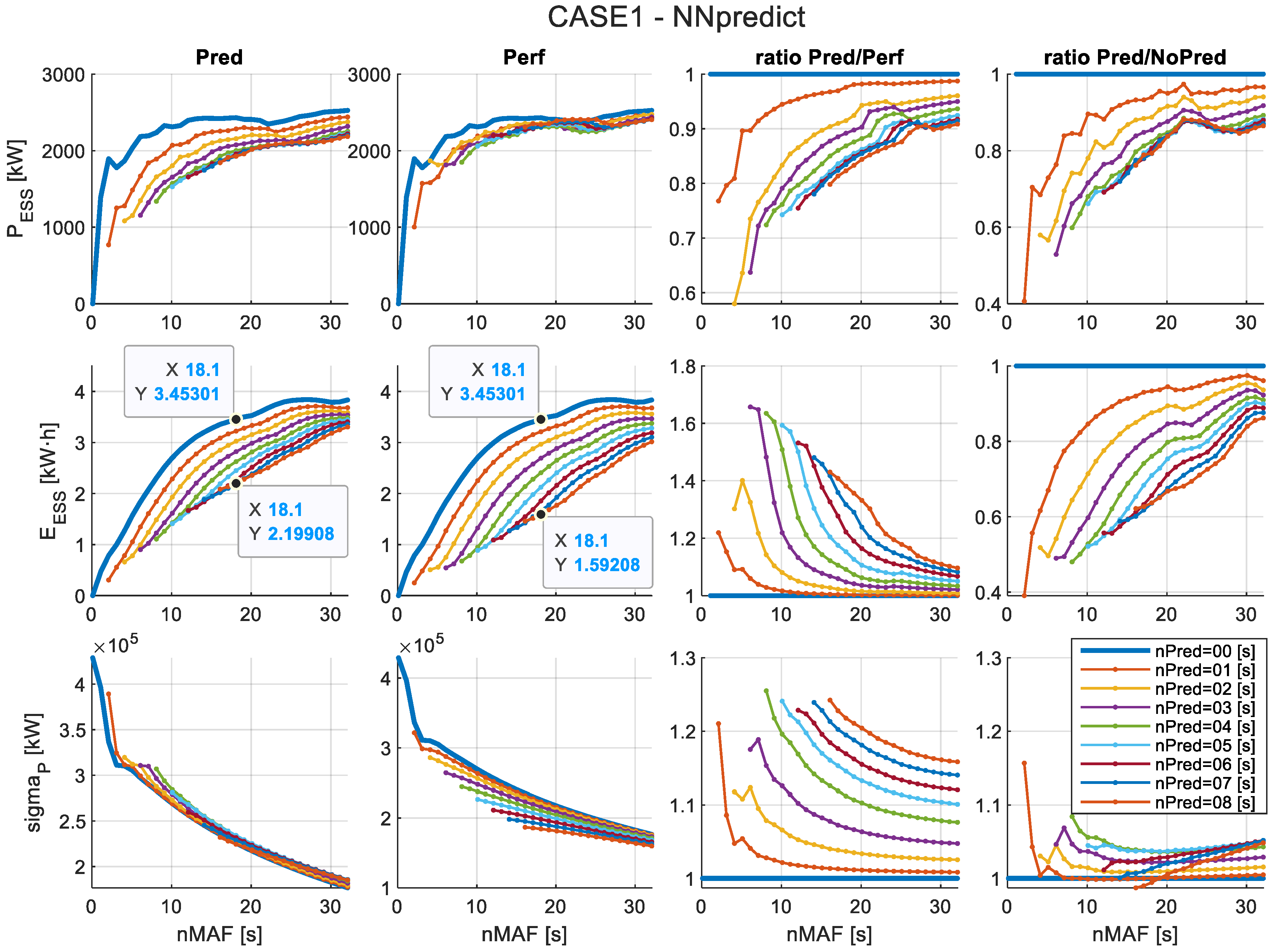
- The reduction in power variance is primarily driven by the total filtering window size nMAF, with limited influence from the forecasting window.
- The decrease in ESS capacity requirements, particularly energy, is strongly influenced by the forecast window size nPred.
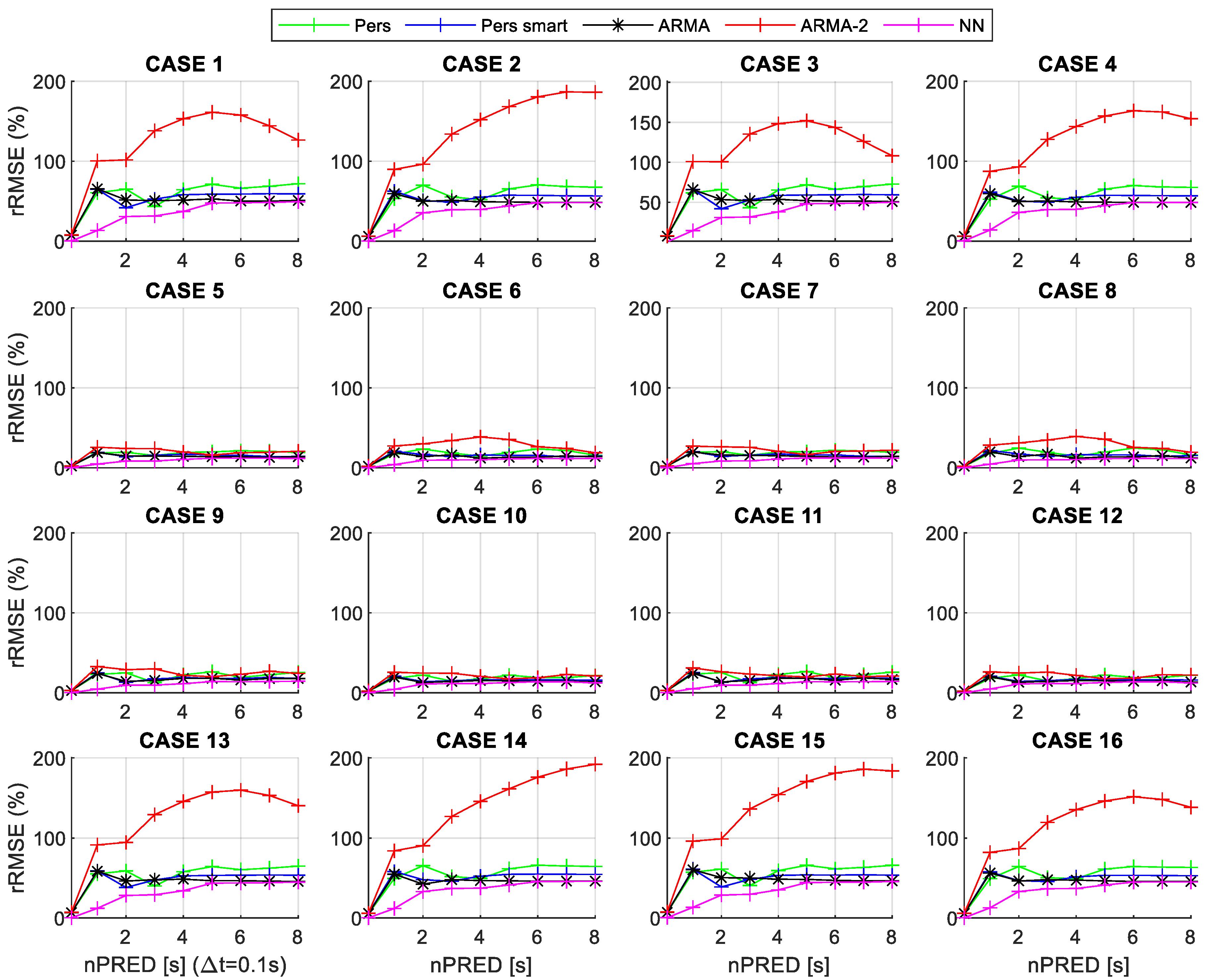
4. Results
4.1. Training of Neural Networks and Tuning of Forecasting Models
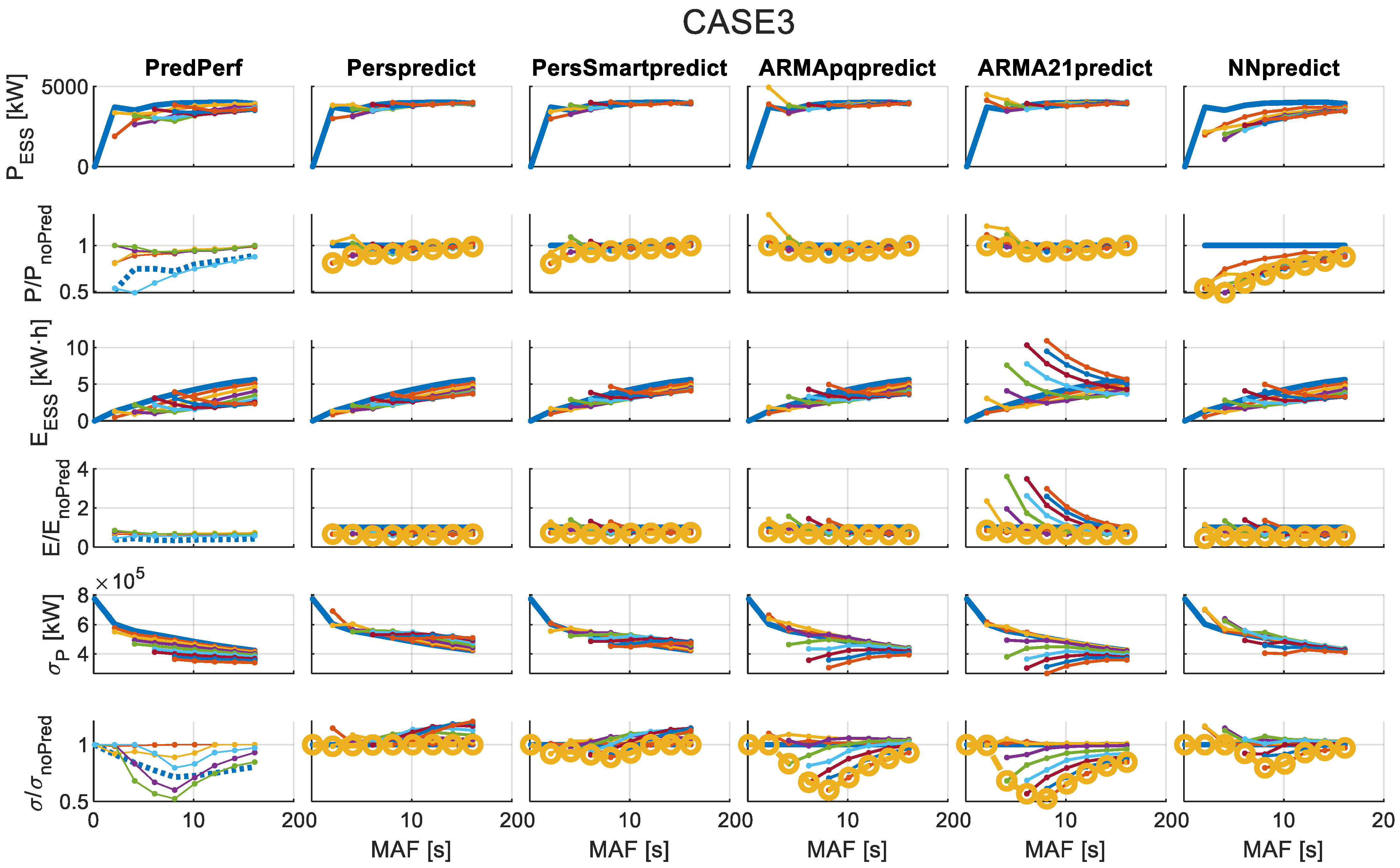
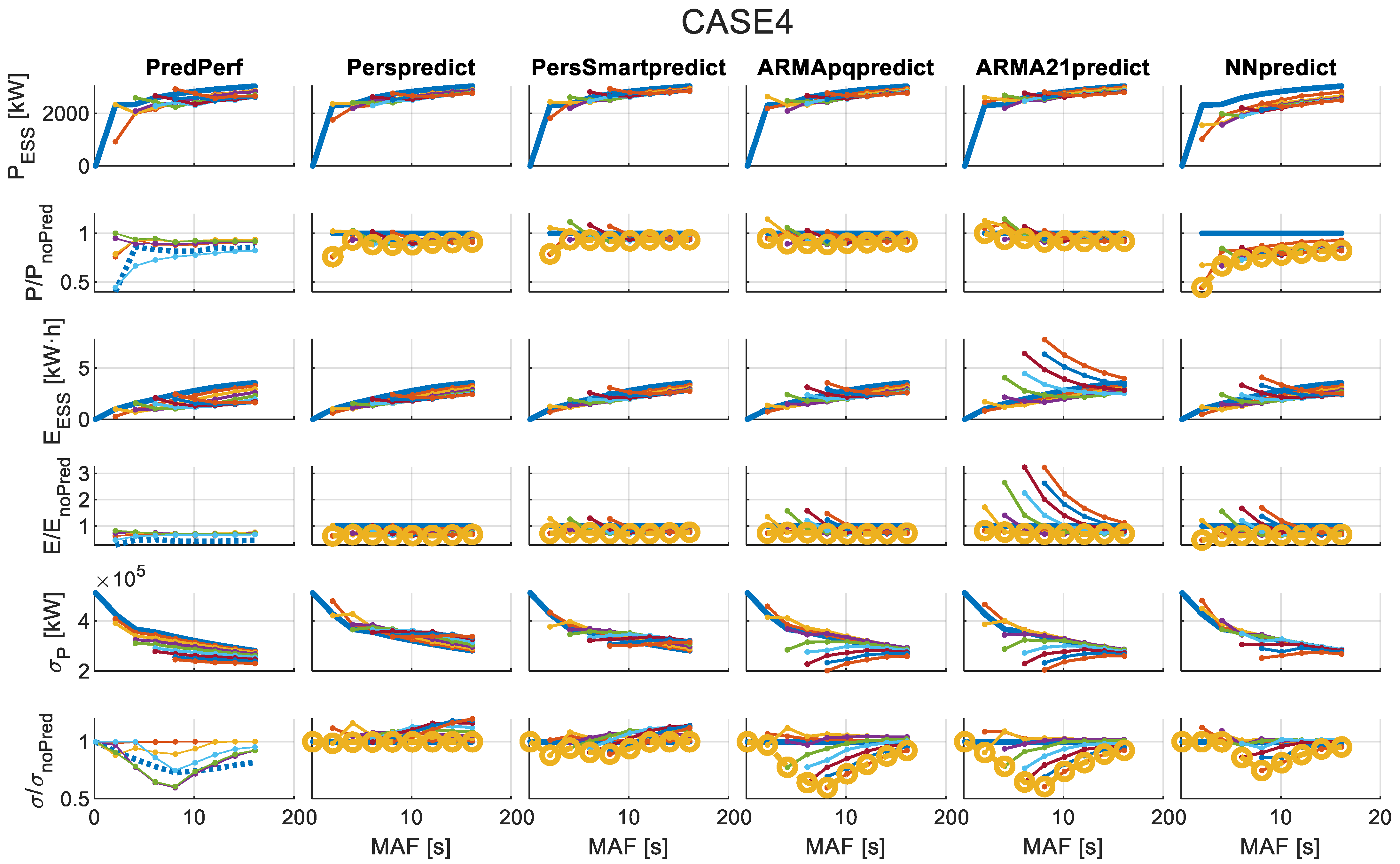
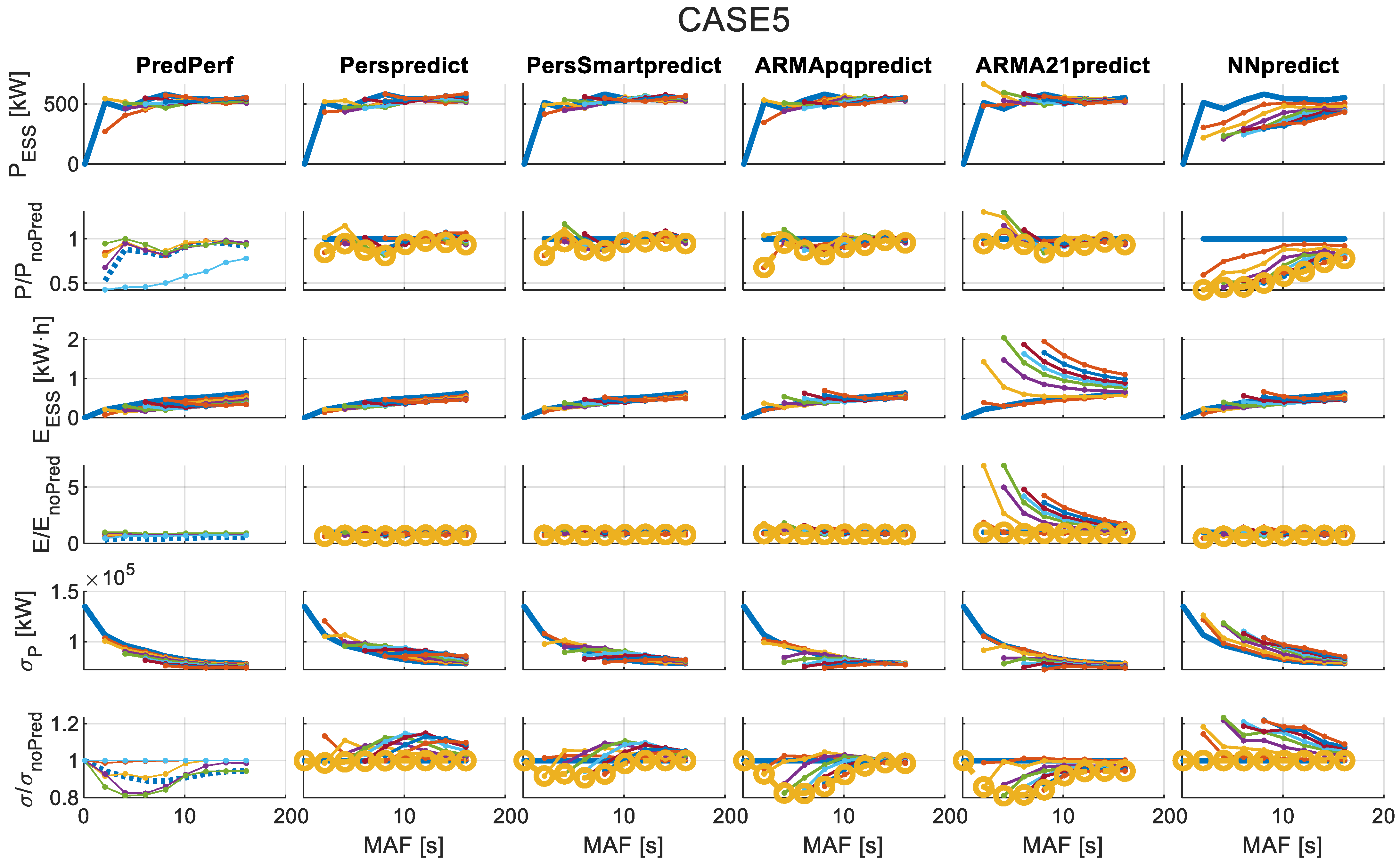
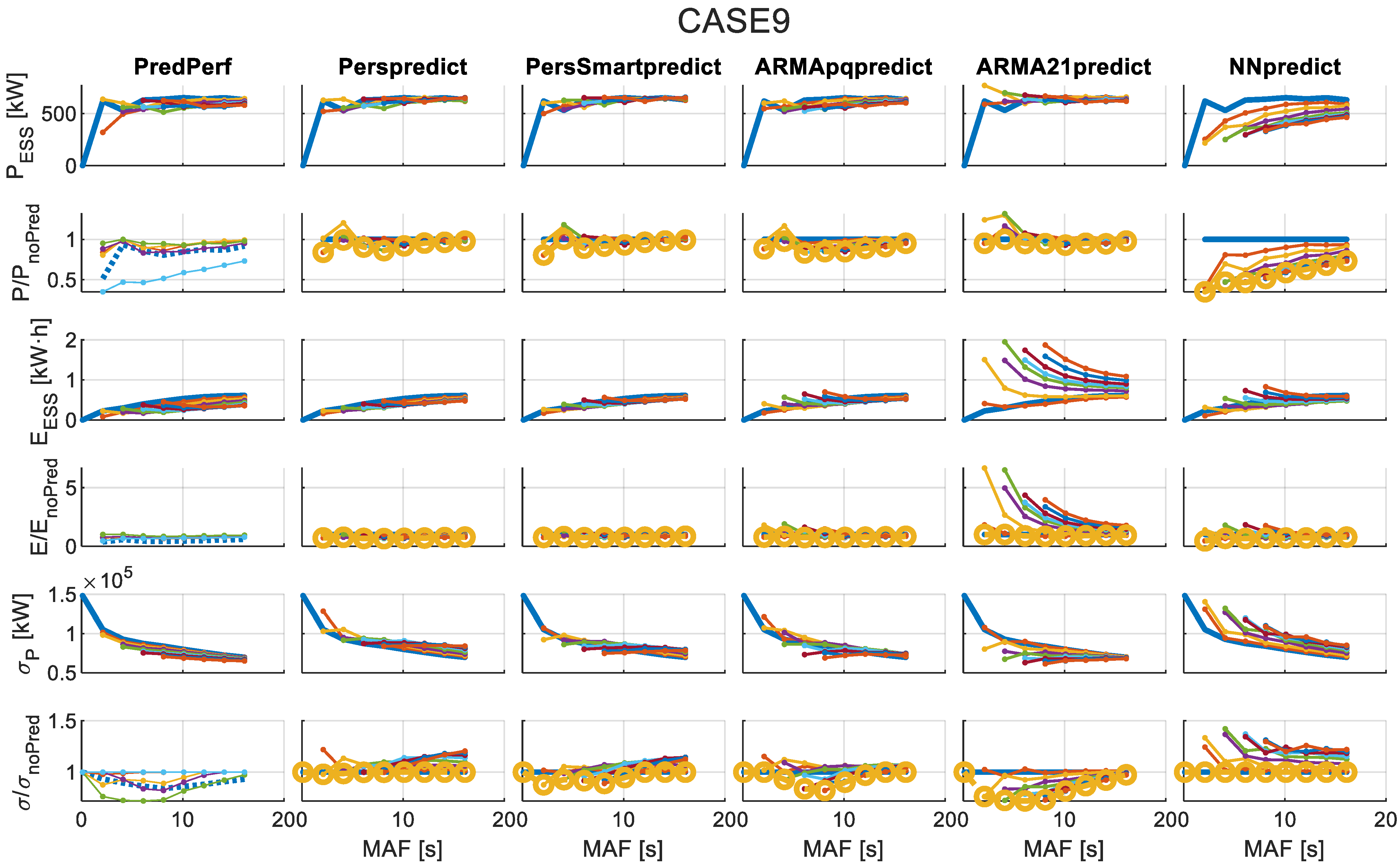
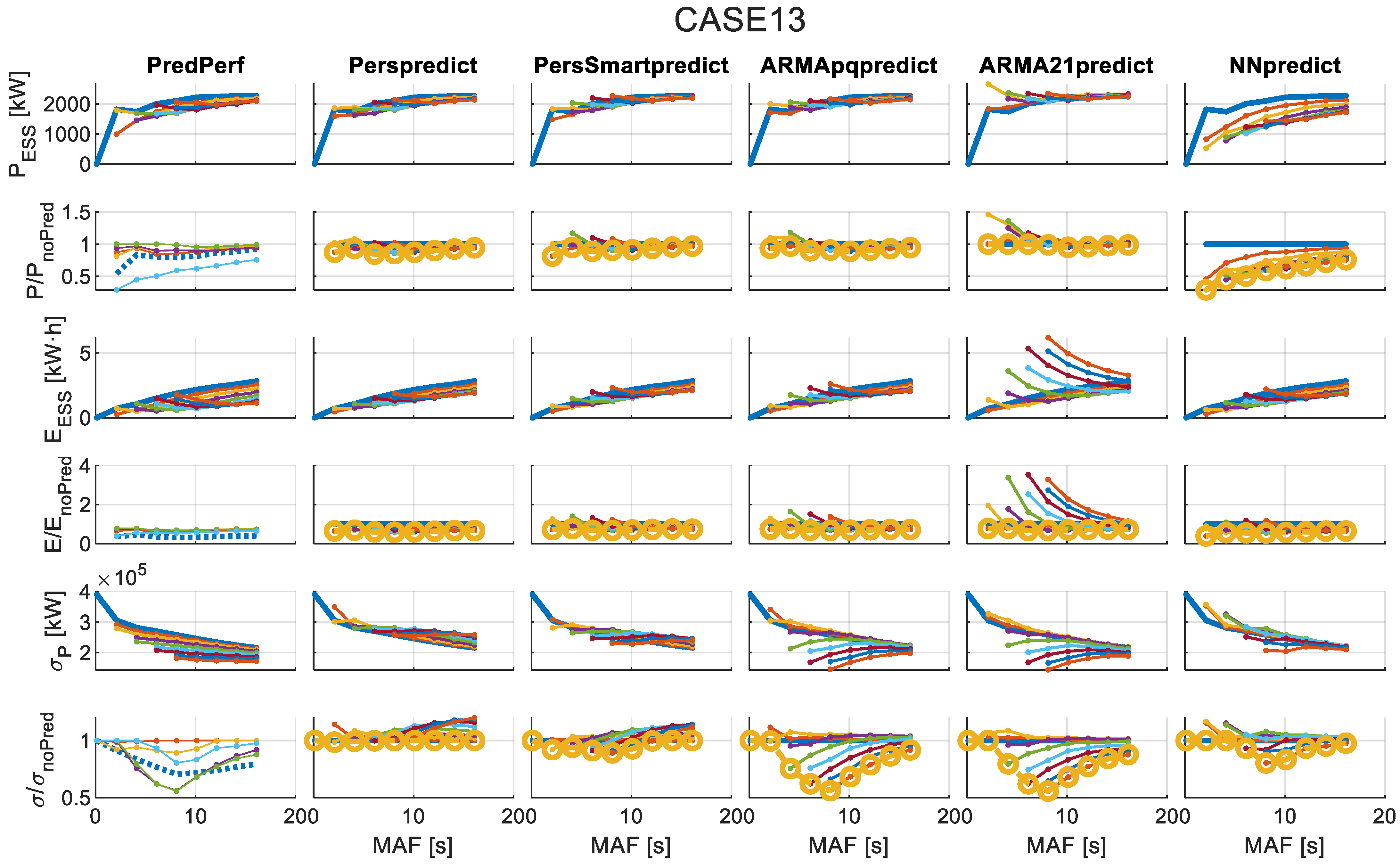
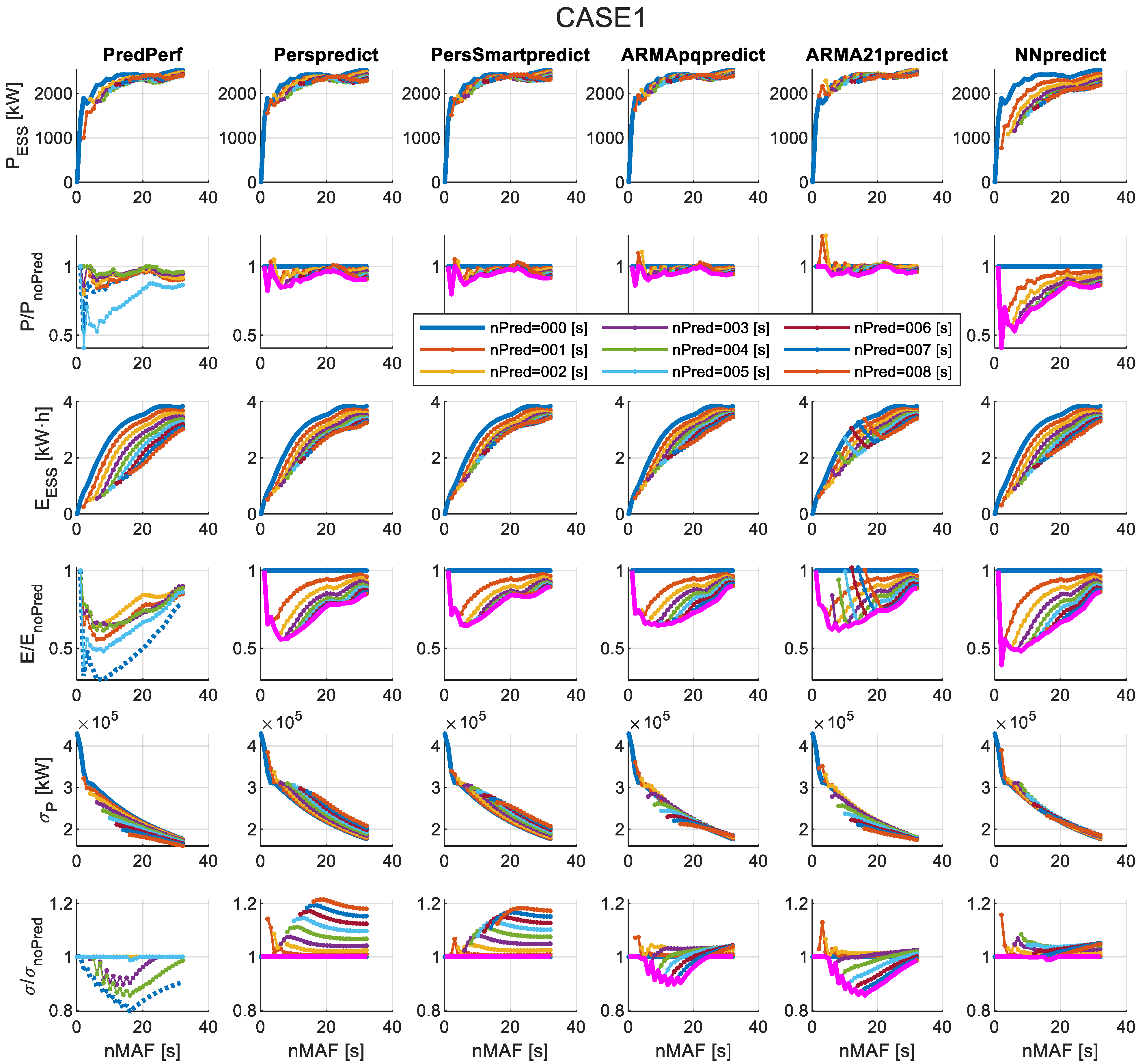
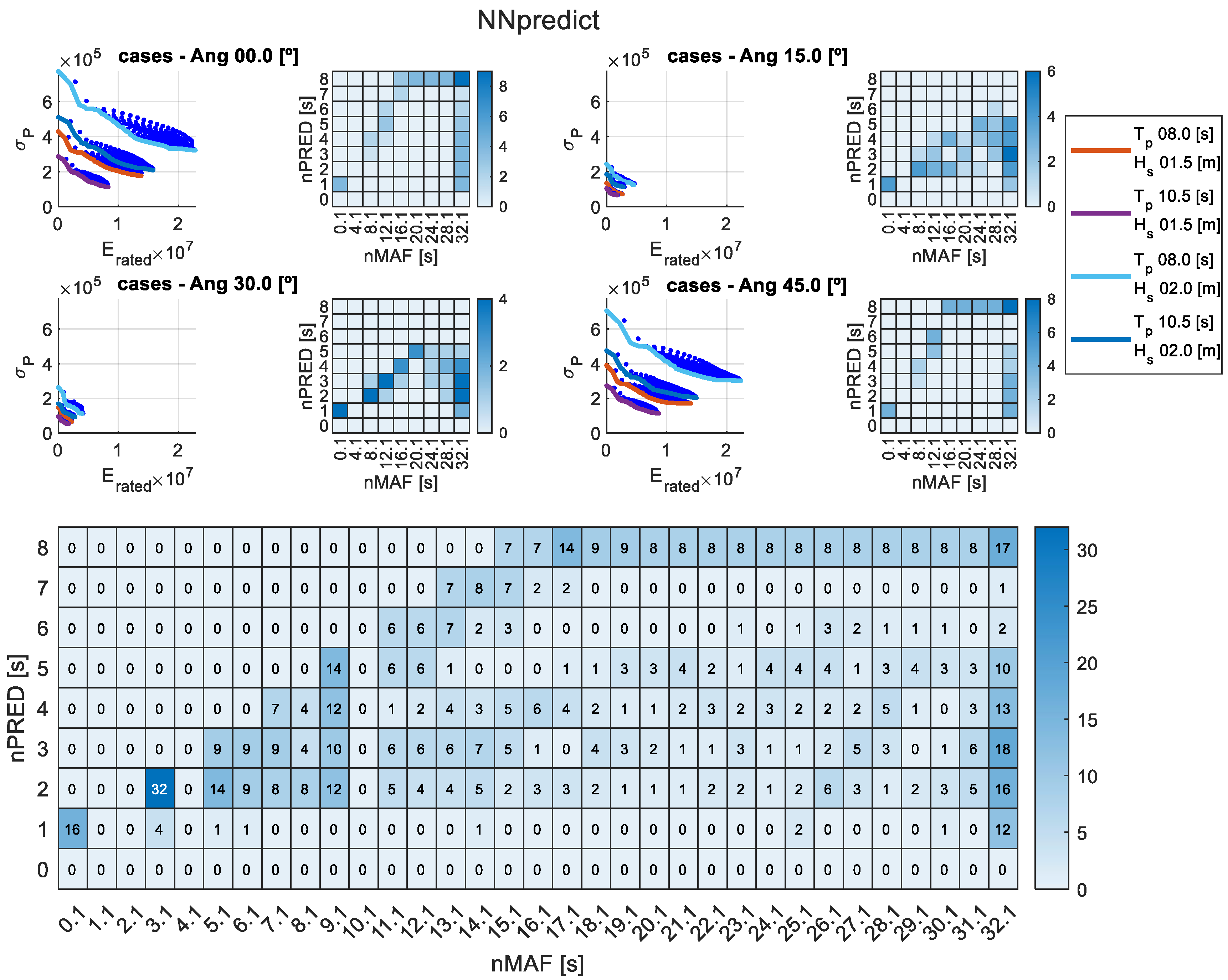
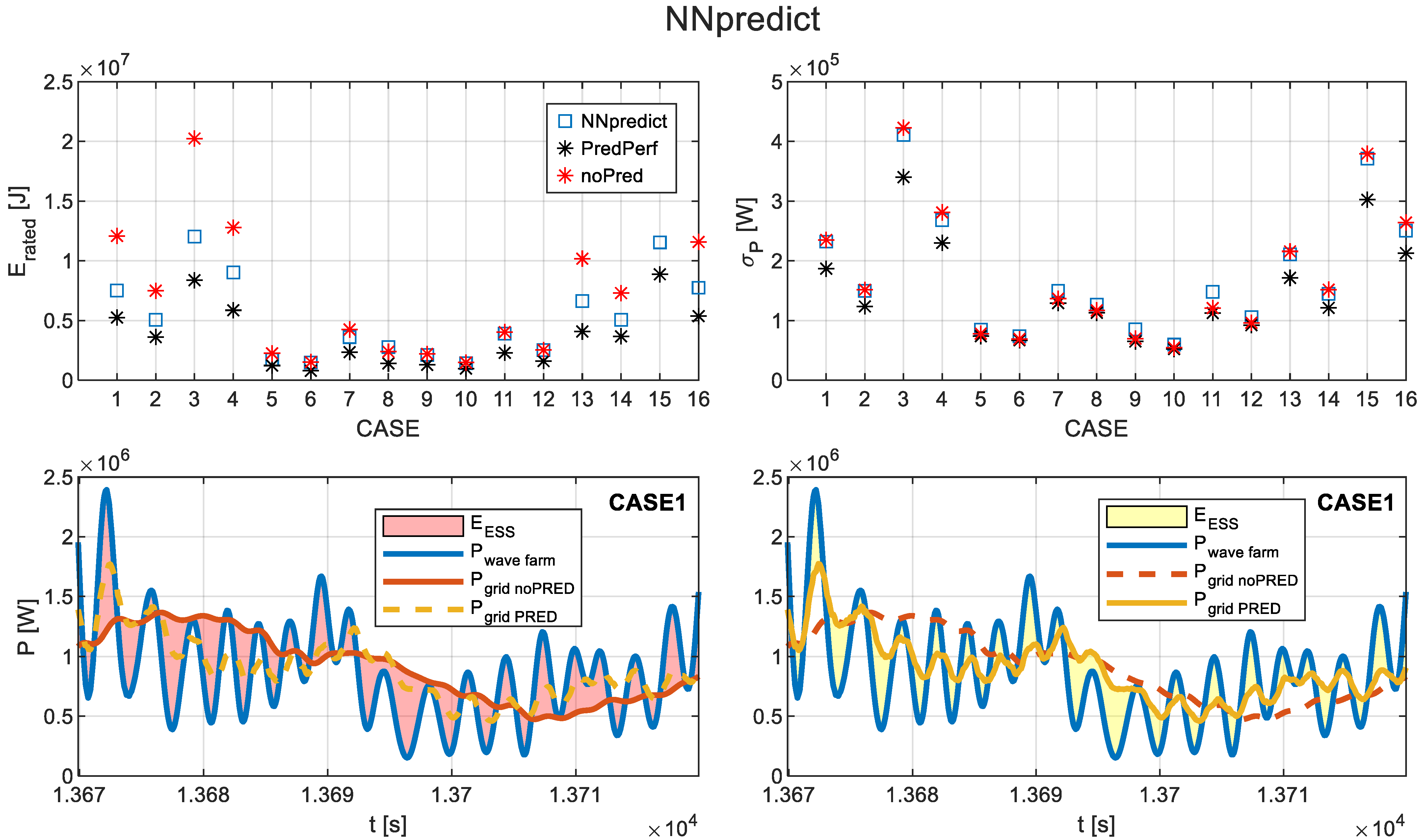
4.2. Results of Applying the Forecast-Enhanced Filtering Strategy to the Case Study
- Required rated power for the ESS ()—Equation (3).
- Required rated energy for the ESS ()—Equation (4).
- Standard deviation of grid-injected power after filtering via MAF and ESS ()—Equation (14).
- Ratio of compared to the no-forecasting case.
- Ratio of compared to the no-forecasting case.
- Ratio of compared to the no-forecasting case.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Required power in the ESS ()—Equation (3).
- Required energy in the ESS ()—Equation (4).
- Standard deviation of the power injected into the electrical grid after filtering through MAF and ESS (σp)—Equation (14).
- Ratio of required power in the ESS relative to the case without forecasting.
- Ratio of required energy in the ESS is relative to the case without forecasting.
- Ratio of the standard deviation of injected power relative to the case without forecasting.











References
- Gunn, K.; Stock-Williams, C. Quantifying the Global Wave Power Resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- Europea, C.; de Asuntos Marítimos y Pesca, D.G.; Borriello, A.; Calvo Santos, A.; Feyen, L.; Ghiani, M.; Guillén, J.; McGovern, L.; Petrucco, G.; Pistocchi, A.; et al. The EU Blue Economy Report 2025; Oficina de Publicaciones de la Unión Europea: Luxembourg, 2025. [Google Scholar]
- Apolonia, M.; Fofack-Garcia, R.; Noble, D.R.; Hodges, J.; da Fonseca, F.X. Legal and Political Barriers and Enablers to the Deployment of Marine Renewable Energy. Energies 2021, 14, 4896. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. The Economics of Wave Energy: A Review. Renew. Sustain. Energy Rev. 2015, 45, 397–408. [Google Scholar] [CrossRef]
- Magagna, D. Ocean Energy Technology Development Report; European Commission JRC: Brussels, Belgium, 2019. [Google Scholar]
- Magagna, D. Ocean Energy Technology Market Report; European Commission JRC: Brussels, Belgium, 2019. [Google Scholar]
- Mi, J.; Wu, X.; Capper, J.; Li, X.; Shalaby, A.; Wang, R.; Lin, S.; Hajj, M.; Zuo, L. Experimental Investigation of a Reverse Osmosis Desalination System Directly Powered by Wave Energy. Appl. Energy 2023, 343, 121194. [Google Scholar] [CrossRef]
- Chakravarthi, T.V.S.K.; Chaudhuri, A.; Samad, A. Wave Powered Desalination Systems—Recent Developments. In Proceedings of the IEEE 2024 International Conference on Sustainable Energy: Energy Transition and Net-Zero Climate Future (ICUE), Pattaya City, Thailand, 21–23 October 2024; pp. 1–7. [Google Scholar]
- Hasan, I.; Karayaka, H.B.; Kandil, T.; Yu, Y.-H. Analysis of Ocean Wave Energy-Driven Desalination Methods for Sustainable Water Production. In Proceedings of the 2025 IEEE Green Technologies Conference (GreenTech), Wichita, KS, USA, 26–28 March 2025; pp. 26–30. [Google Scholar]
- Ocean Energy TWG. SET-Plan Ocean Energy Implementation Plan; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Ruiz-Minguela, P.; Berque, J.; Villate, J.L.; Pirttimaa, L.; Gruet, R.; Noble, D.; Jeffrey, H. Strategic Research and Innovation Agenda for Ocean Energy; ETIP Ocean: Brussels, Belgium, 2024. [Google Scholar]
- Tedeschi, E.; Molinas, M. Wave-to-Wave Buoys Control for Improved Power Extraction under Electro-Mechanical Constraints. In Proceedings of the 2010 IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010; pp. 1–6. [Google Scholar]
- Salter, S.H.; Taylor, J.R.M.; Caldwell, N.J. Power Conversion Mechanisms for Wave Energy. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2002, 216, 1–27. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems, Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002; ISBN 9780511754630. [Google Scholar]
- Blanco, M.; Navarro, G.; Najera, J.; Lafoz, M.; Sarasua, J.I.; García, H.; Martínez-Lucas, G.; Pérez-Díaz, J.I.; Villalba, I. Wave Farms Integration in a 100% Renewable Isolated Small Power System—Frequency Stability and Grid Compliance Analysis. In Proceedings of the 15th European Wave and Tidal Energy Conference, Bilbao, Spain, 3–7 September 2023; Volume 15. [Google Scholar] [CrossRef]
- Göteman, M.; Engström, J.; Eriksson, M.; Isberg, J. Optimizing Wave Energy Parks with over 1000 Interacting Point-Absorbers Using an Approximate Analytical Method. Int. J. Mar. Energy 2015, 10, 113–126. [Google Scholar] [CrossRef]
- Blavette, A.; O’Sullivan, D.L.; Lewis, A.W.; Egan, M.G. Impact of a Wave Farm on Its Local Grid: Voltage Limits, Flicker Level and Power Fluctuations. In Proceedings of the 2012 OCEANS—Yeosu, Yeosu, Republic of Korea, 21–24 May 2012; pp. 1–9. [Google Scholar]
- ENTSO-E. Continental Europe Operation Handbook; ENTSO-E: Brussels, Belgium, 2009. [Google Scholar]
- ENTSO-E. Network Code on Load-Frequency Control and Reserves; ENTSO-E: Brussels, Belgium, 2013; Volume 6. [Google Scholar]
- Robles, E.; Haro-Larrode, M.; Santos-Mugica, M.; Etxegarai, A.; Tedeschi, E. Comparative Analysis of European Grid Codes Relevant to Offshore Renewable Energy Installations. Renew. Sustain. Energy Rev. 2019, 102, 171–185. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D. Power System Analysis; McGraw-Hill: New York, NY, USA, 1994; ISBN 0070612935. [Google Scholar]
- LiVecchi, A.; Copping, A.; Jenne, D.; Gorton, A.; Preus, R.; Gill, G.; Robichaud, R.; Green, R.; Geerlofs, S.; Gore, S.; et al. Exploring Opportunities for Marine Renewable Energy in Maritime Markets; U.S. Department of Energy (DOE): Washington, DC, USA, 2019. [Google Scholar]
- Villalba, I.; Blanco, M.; Pérez-Díaz, J.I.; Fernández, D.; Díaz, F.; Lafoz, M. Wave Farms Grid Code Compliance in Isolated Small Power Systems. IET Renew. Power Gener. 2019, 13, 171–179. [Google Scholar] [CrossRef]
- Sarasua, J.I.; Martínez-Lucas, G.; García-Pereira, H.; Navarro-Soriano, G.; Molina-García, Á.; Fernández-Guillamón, A. Hybrid Frequency Control Strategies Based on Hydro-power, Wind, and Energy Storage Systems: Application to 100% Renewable Scenarios. IET Renew. Power Gener. 2022, 16, 1107–1120. [Google Scholar] [CrossRef]
- Pelosi, D.; Gallorini, F.; Alessandri, G.; Barelli, L. A Hybrid Energy Storage System Integrated with a Wave Energy Converter: Data-Driven Stochastic Power Management for Output Power Smoothing. Energies 2024, 17, 1167. [Google Scholar] [CrossRef]
- Bielewski, M.; Pfrang, A.; Bobba, S.; Kronberga, A.; Georgakaki, A.; Letout, S.; Kuokkanen, A.; Mountraki, A.; Ela, I.; Shtjefni, D.; et al. Clean Energy Technology Observatory: Batteries for Energy Storage in the European Union—2022 Status Report on Technology Development, Trends, Value Chains and Markets; Publications Office of the European Union: Brussels, Belgium, 2022. [Google Scholar]
- European Commision Com(2020) 798/3 Final—Regulation of the European Parliament and of the Council Concerning Batteries and Waste Batteries, Repealing Directive 2006/66/EC and Amending Regulation (EU) No 2019/1020. 2020. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A52020PC0798 (accessed on 1 September 2025).
- Lafoz, M.; Blanco, M.; Beloqui, L.; Navarro, G.; Moreno-Torres, P. Dimensioning Methodology for Energy Storage Devices and Wave Energy Converters Supplying Isolated Loads. IET Renew. Power Gener. 2016, 10, 1468–1476. [Google Scholar] [CrossRef]
- Moreno-Torres Concha, P.; Lafoz Pastor, M.; Navarro Soriano, G.; Blanco Aguado, M.; García-Tabarés Rodríguez, L. System for the Conditioning of the Electrical Power Generated in a Wave Generation System. Spanish Patent ES2547029A1, 8 July 2015. [Google Scholar]
- Murray, D.B.; Hayes, J.G.; O’Sullivan, D.L.; Egan, M.G. Supercapacitor Testing for Power Smoothing in a Variable Speed Offshore Wave Energy Converter. IEEE J. Ocean. Eng. 2012, 37, 301–308. [Google Scholar] [CrossRef]
- Elamin, A.Y.; Wahyudie, A. Optimal Control of a Supercapacitor Energy Storage System for Smoothing Wave Output Power. In Proceedings of the IEEE 2022 International Conference on Electrical and Computing Technologies and Applications (ICECTA), Ras al-Khaimah, United Arab Emirates, 23–25 November 2022; pp. 186–189. [Google Scholar]
- Torres, J.; Blanco, M.; Lafoz, M.; Navarro, G.; Nájera, J.; Santos-Herran, M. Dimensioning Methodology of Energy Storage Systems for Power Smoothing in a Wave Energy Conversion Plant Considering Efficiency Maps and Filtering Control Techniques. Energies 2020, 13, 3380. [Google Scholar] [CrossRef]
- Basheer, Y.; Pérez-Díaz, J.I.; Blanco, M.; Fraile-Ardanuy, J.; Nájera, J.; Navarro, G.; Sarasúa, J.I. Active Power Control of a Hybrid Power Plant Comprising Hydropower, Battery and Supercapacitor to Provide Frequency Control. In Proceedings of the 9th Hybrid Power Plants & Systems Workshop, Åland Islands, Finland, 3–4 June 2025. [Google Scholar]
- Szostek, K.; Mazur, D.; Drałus, G.; Kusznier, J. Analysis of the Effectiveness of ARIMA, SARIMA, and SVR Models in Time Series Forecasting: A Case Study of Wind Farm Energy Production. Energies 2024, 17, 4803. [Google Scholar] [CrossRef]
- Bahri, M.; Vahidnia, S.; Ghignone, L.; Mohtashamkhani, M. Wind Speed Prediction Using a SEEMD-LSTM Model. In Proceedings of the IEEE 2023 International Conference on Engineering and Emerging Technologies (ICEET), Istanbul, Turkiye, 27–28 October 2023; pp. 1–6. [Google Scholar]
- Fusco, F.; Ringwood, J.V. A Study of the Prediction Requirements in Real-Time Control of Wave Energy Converters. Sustain. Energy IEEE Trans. 2012, 3, 176–184. [Google Scholar] [CrossRef]
- Kaiser, M.S.; Iida, T.; Taniguchi, T.; Katayama, T.; Yoshimura, R.; Irifune, K. Optimal Prediction Horizon Length in Model Predictive Control to Maximise Energy Absorption by a Point Absorber Wave Energy Converter. Ocean Eng. 2025, 329, 121130. [Google Scholar] [CrossRef]
- Li, D.; Wang, T.; Tao, J.; Sharma, S.; Borthwick, A.G.L.; Dong, X.; Shi, H. Model Predictive Control of a Single-Buoy Wave Energy Converter with Coupled Constraints and Model Adaptation. Ocean Eng. 2025, 315, 119887. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, D.; Huang, Q.; Cui, Z. Multiple-Step Accurate Prediction of Wave Energy: A Hybrid Model Based on Quadratic Decomposition, SSA and LSTM. Int. J. Green Energy 2025, 22, 100–123. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Shen, Q.; Zhang, L.; Li, Y.; Hou, Z.; Chen, R. Short-Term Prediction Model of Wave Energy Converter Generation Power Based on CNN-BiLSTM-DELA Integration. Electronics 2024, 13, 4163. [Google Scholar] [CrossRef]
- Elkhrachy, I.; Alhamami, A.; Alyami, S.H.; Alviz-Meza, A. Novel Ocean Wave Height and Energy Spectrum Forecasting Approaches: An Application of Semi-Analytical and Machine Learning Models. Water 2023, 15, 3254. [Google Scholar] [CrossRef]
- Teixeira, R.; Cerveira, A.; Pires, E.J.S.; Baptista, J. Advancing Renewable Energy Forecasting: A Comprehensive Review of Renewable Energy Forecasting Methods. Energies 2024, 17, 3480. [Google Scholar] [CrossRef]
- Sengupta, M.; Habte, A.; Wilbert, S.; Gueymard, C.; Remund, J.; Lorenz, E.; van Sark, W.; Jensen, A.R. Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications, 4th ed.; NREL: Golden, CO, USA, 2024. [Google Scholar]
- Raj, N.; Prakash, R. Assessment and Prediction of Significant Wave Height Using Hybrid CNN-BiLSTM Deep Learning Model for Sustainable Wave Energy in Australia. Sustain. Horiz. 2024, 11, 100098. [Google Scholar] [CrossRef]
- Demonte Gonzalez, T.; Anderlini, E.; Yassin, H.; Parker, G. Nonlinear Model Predictive Control of Heaving Wave Energy Converter with Nonlinear Froude–Krylov Forces. Energies 2024, 17, 5112. [Google Scholar] [CrossRef]
- Elamin, A.Y.; Wahyudie, A.; Hashfi, T.B.; Shareef, H.; Errouissi, R.; Laghari, M.S.; Mubin, M.B.; Mekhilef, S. Real-Time Model Predictive Control Framework for a Point Absorber Wave Energy Converter with Excitation Force Estimation and Prediction. IEEE Access 2024, 12, 4078–4098. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, S.-R.; Zhao, G.-W.; Dai, S.-S.; He, F.; Yuan, Z.-M. Model Predictive Control of Wave Energy Converters. Ocean Eng. 2024, 301, 117430. [Google Scholar] [CrossRef]
- Guo, R.; Wu, Y.; Ma, X.; Aggidis, G.; Zhao, N. Grid Integration of a Novel Linear-Generator-Based Wave Power Conversion System. In Proceedings of the 2024 International Conference on Smart Energy Systems and Technologies (SEST), Torino, Italy, 10–12 September 2024; pp. 1–6. [Google Scholar]
- Pelosi, D.; Trombetti, L.; Piccio, A.; Ottaviano, P.A.; Gallorini, F.; Barelli, L. Seawater Batteries as Sustainable Energy Storage Systems for the Future Renewables-Based Grids. In Proceedings of the 2024 IEEE International Humanitarian Technologies Conference (IHTC), Bari, Italy, 25–27 November 2024; pp. 1–6. [Google Scholar]
- Zhu, X.; Huang, X.; Xiao, X. A Model Predictive Control Strategy for Smoothing Power Fluctuations of Wave Energy Converter Arrays Using Supercapacitors. In Proceedings of the IEEE 2024 UKACC 14th International Conference on Control (CONTROL), Southampton, UK, 10–12 April 2024; pp. 19–24. [Google Scholar]
- Blanco, M.; Santos-Herran, M.; Navarro, G.; Torres, J.; Najera, J.; Villaba, I.; Lafoz, M.; Ramírez, D. Meta-heuristic Optimisation Approach for Wave Energy Converter Design by Means of a Stochastic Hydrodynamic Model. IET Renew. Power Gener. 2021, 15, 548–561. [Google Scholar] [CrossRef]
- Blanco, M.; Navarro, G.; Lafoz, M.; Pérez, J.I. Study of the Impact of Wave Energy Generation in the Frequency of an Island Electric Grid. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–2 September 2017; Volume 12, pp. 1–8. [Google Scholar]
- Harris, M. Officials Sign Agreement for Canary Islands Wave Power Development. Available online: http://www.hydroworld.com/articles/2014/02/officials-sign-agreement-for-canary-islands-wave-power-development.html (accessed on 1 September 2025).
- Veigas, M.; Iglesias, G. A Hybrid Wave-Wind Offshore Farm for an Island. Int. J. Green Energy 2015, 12, 570–576. [Google Scholar] [CrossRef]
- Veigas, M.; Iglesias, G. Potentials of a Hybrid Offshore Farm for the Island of Fuerteventura. Energy Convers. Manag. 2014, 86, 300–308. [Google Scholar] [CrossRef]
- Veigas, M.; Iglesias, G. Wave and Offshore Wind Potential for the Island of Tenerife. Energy Convers. Manag. 2013, 76, 738–745. [Google Scholar] [CrossRef]
- Prediccion de Oleaje, Nivel Del Mar; Boyas y Mareografos—Puertos Del Estado. Available online: http://www.puertos.es/es-es/oceanografia/Paginas/portus.aspx (accessed on 26 December 2017).
- École Centrale de Nantes; Kurnia, R.; Guillaume, D. NEMOH—Homepage. Available online: https://lheea.ec-nantes.fr/valorisation/logiciels-et-brevets/nemoh-presentation (accessed on 30 August 2024).
- WEC-Sim (Wave Energy Converter SIMulator) [Computer Software]. Available online: https://github.com/WEC-Sim/WEC-Sim (accessed on 1 August 2025).
- Eidsmoen, H. Hydrodynamic Parameters for a Two-Body Axisymmetric System. Appl. Ocean Res. 1995, 17, 103–115. [Google Scholar] [CrossRef]
- Yu, Z.; Falnes, J. State-Space Modelling of a Vertical Cylinder in Heave. Appl. Ocean Res. 1995, 17, 265–275. [Google Scholar] [CrossRef]
- Yu, Z.; Falnes, J. State-Space Modelling of Dynamic Systems in Ocean Engineering. J. Hydrodyn. 1998, 10, 1–17. [Google Scholar]
- Blanco, M.; Santos-Herran, M.; Navarro, G.; Torres, J.J.; Najera, J.; García-Tabarés, L. Simplified Model of a Novel Direct-Drive PTO Based on an Azimuthal Linear Switched Reluctance Generator. In Proceedings of the 14th European Wave and Tidal Energy Conference (EWTEC), Plymouth, UK, 5–9 September 2021. [Google Scholar]
- Hals, J.; Falnes, J.; Moan, T. A Comparison of Selected Strategies for Adaptive Control of Wave Energy Converters. J. Offshore Mech. Arct. Eng. 2011, 133, 31101. [Google Scholar] [CrossRef]
- Lorenz, E.; Heinemann, D. Prediction of Solar Irradiance and Photovoltaic Power. In Comprehensive Renewable Energy; Elsevier: Amsterdam, The Netherlands, 2012; pp. 239–292. [Google Scholar]
- Hoff, T.E.; Perez, R. Modeling PV Fleet Output Variability. Sol. Energy 2012, 86, 2177–2189. [Google Scholar] [CrossRef]
- Boland, J. Time Series Modelling of Solar Radiation. In Modeling Solar Radiation at the Earth’s Surface; Springer: Berlin/Heidelberg, Germany, 2008; pp. 283–312. [Google Scholar]
- Boland, J. Time-Series Analysis of Climatic Variables. Sol. Energy 1995, 55, 377–388. [Google Scholar] [CrossRef]
- Box, G. Box and Jenkins: Time Series Analysis, Forecasting and Control. In A Very British Affair; Palgrave Macmillan: London, UK, 2013; pp. 161–215. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995; ISBN 9780198538493. [Google Scholar]
- MacKay, D.J.C. A Practical Bayesian Framework for Backpropagation Networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Lauret, P.; Fock, E.; Randrianarivony, R.N.; Manicom-Ramsamy, J.-F. Bayesian Neural Network Approach to Short Time Load Forecasting. Energy Convers. Manag. 2008, 49, 1156–1166. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521642989. [Google Scholar]
- Penny, W.D.; Roberts, S.J. Bayesian Neural Networks for Classification: How Useful Is the Evidence Framework? Neural Netw. 1999, 12, 877–892. [Google Scholar] [CrossRef] [PubMed]
- Lafoz, M.; Blanco, M.; Ramirez, D. Grid Connection for Wave Power Farms. In Proceedings of the IEEE 2011-14th European Conference on Power Electronics and Applications (EPE 2011), Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Red Eléctrica de España, P.O. SENP 1: Funcionamiento de Los Sistemas Eléctricos Insulares y Extrapeninsulares 2019. Available online: https://www.ree.es/sites/default/files/2023-11/BOE-A-2019-18275_ministerio_para_la_transicion_ecologica.pdf (accessed on 1 September 2025).
- Mazorra-Aguiar, L.; Díaz, F. Solar Radiation Forecasting with Statistical Models. In Wind Field and Solar Radiation Characterization and Forecasting; Springer: Cham, Switzerland, 2018; pp. 171–200. [Google Scholar]
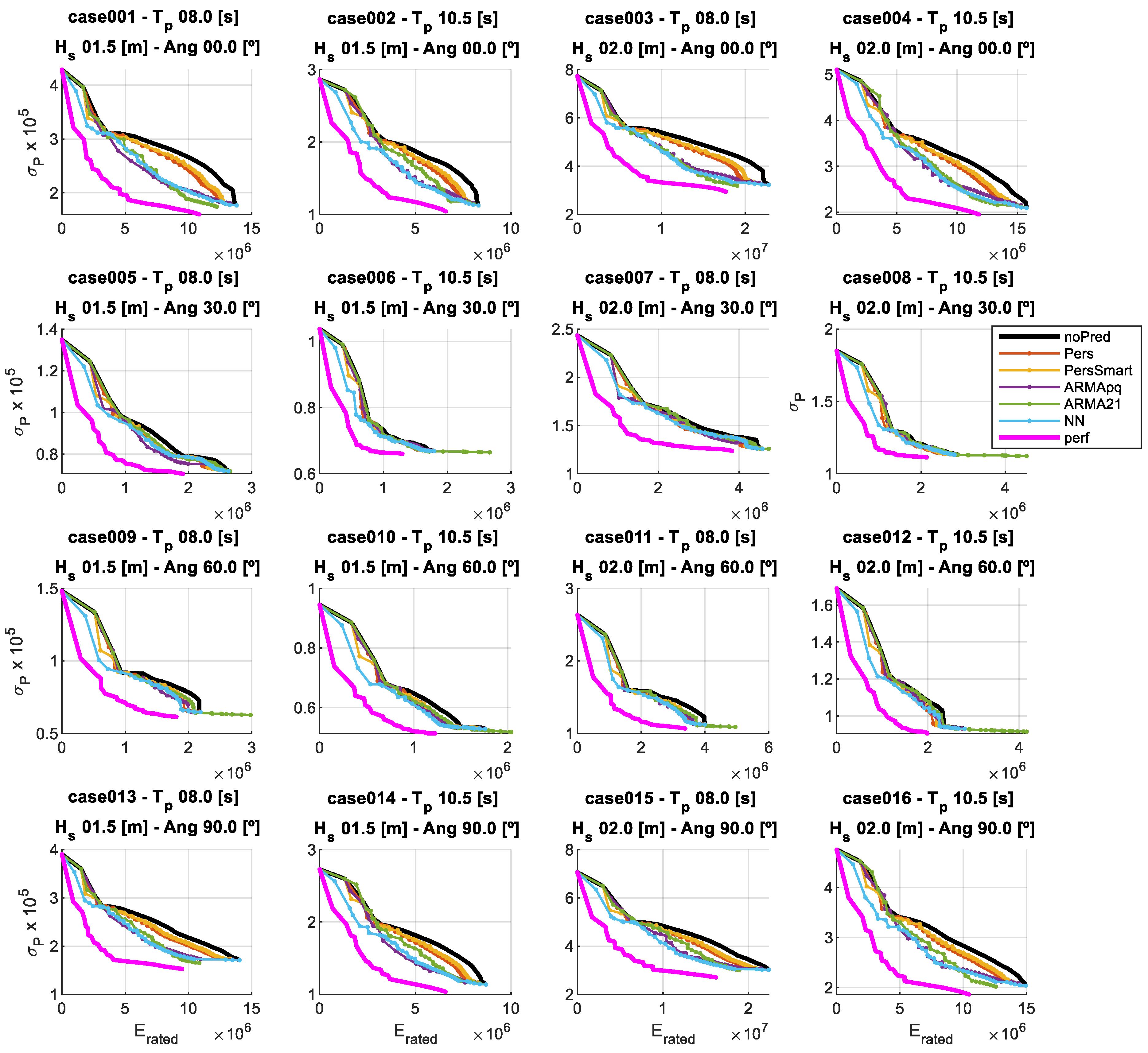
| No. Case | Hs [m] | Tp [s] | αW [°] | Pj [kW/m] |
|---|---|---|---|---|
| CASE 1 | 1.5000 | 8.0000 | 0 | 7.63 |
| CASE 2 | 1.5000 | 10.5000 | 0 | 10.02 |
| CASE 3 | 2.0000 | 8.0000 | 0 | 13.57 |
| CASE 4 | 2.0000 | 10.5000 | 0 | 17.81 |
| CASE 5 | 1.5000 | 8.0000 | 15 | 7.63 |
| CASE 6 | 1.5000 | 10.5000 | 15 | 10.02 |
| CASE 7 | 2.0000 | 8.0000 | 15 | 13.57 |
| CASE 8 | 2.0000 | 10.5000 | 15 | 17.81 |
| CASE 9 | 1.5000 | 8.0000 | 30 | 7.63 |
| CASE 10 | 1.5000 | 10.5000 | 30 | 10.02 |
| CASE 11 | 2.0000 | 8.0000 | 30 | 13.57 |
| CASE 12 | 2.0000 | 10.5000 | 30 | 17.81 |
| CASE 13 | 1.5000 | 8.0000 | 45 | 7.63 |
| CASE 14 | 1.5000 | 10.5000 | 45 | 10.02 |
| CASE 15 | 2.0000 | 8.0000 | 45 | 13.57 |
| CASE 16 | 2.0000 | 10.5000 | 45 | 17.81 |
| Control Algorithm | σ (PWEC) | σ (fgrid) | No. Alert Events [Δ(fgrid) > 150 mHz] | No. Emerg. Events [Δ(fgrid) > 250 mHz] | ESS Rated Power [KW] (PESS) | ESS Rated Energy [kW·h] (EESS) |
|---|---|---|---|---|---|---|
| base case (no ESS) | 4854.688 | 0.05011 | 340 | 14 | 0 | 0 |
| MAF | 3117.836 | 0.03170 | 7 | 0 | 2647 | 2.257 |
| MAF with Pred. | 3116.857 | 0.03169 | 7 | 0 | 2239.80 | 0.900 |
| Type | Acronym | Prediction Values Acronym | Description/Complete Name |
|---|---|---|---|
| Base Case | noPred | noPred | No forecasting algorithm in MAF (extra case) |
| Naïve models (Section 2.3.1) | Pers | PresPredict | Simple persistence |
| PersSmart | PersSmartPredict | Smart persistence | |
| Linear models (Section 2.3.2) | ARMApq | ARMAPQpredict | ARMA with optimal p and q values |
| ARMA12 | ARMA12predict | Simple ARMA modelo (p = 1; q = 2) | |
| Artificial Neural Networks (Section 2.3.3) | NN | NNpredict | Artifical Neural Network (Bayesian Framework) |
| Limit Case | PredPerf | PredPerf | Prefect prediction values in MAF (extra case) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco, M.; Mazorra, L.; Villalba, I.; Navarro, G.; Nájera, J.; Lafoz, M. Power Smoothing in a Wave Energy Conversion Using Energy Storage Systems: Benefits of Forecasting-Enhanced Filtering for Reduction in Energy Storage Requirements. Appl. Sci. 2025, 15, 11106. https://doi.org/10.3390/app152011106
Blanco M, Mazorra L, Villalba I, Navarro G, Nájera J, Lafoz M. Power Smoothing in a Wave Energy Conversion Using Energy Storage Systems: Benefits of Forecasting-Enhanced Filtering for Reduction in Energy Storage Requirements. Applied Sciences. 2025; 15(20):11106. https://doi.org/10.3390/app152011106
Chicago/Turabian StyleBlanco, Marcos, Luis Mazorra, Isabel Villalba, Gustavo Navarro, Jorge Nájera, and Marcos Lafoz. 2025. "Power Smoothing in a Wave Energy Conversion Using Energy Storage Systems: Benefits of Forecasting-Enhanced Filtering for Reduction in Energy Storage Requirements" Applied Sciences 15, no. 20: 11106. https://doi.org/10.3390/app152011106
APA StyleBlanco, M., Mazorra, L., Villalba, I., Navarro, G., Nájera, J., & Lafoz, M. (2025). Power Smoothing in a Wave Energy Conversion Using Energy Storage Systems: Benefits of Forecasting-Enhanced Filtering for Reduction in Energy Storage Requirements. Applied Sciences, 15(20), 11106. https://doi.org/10.3390/app152011106










