Prediction of High-Risk Failures in Urban District Heating Pipelines Using KNN-Based Relabeling and AI Models
Abstract
1. Introduction
2. Research Method and Basic Unit Definition
2.1. Research Method
2.2. Definition of Basic Units of Heating Pipelines
2.2.1. Data
2.2.2. Basic Unit Definition
Integration via Attribute Information
Maximum and Minimum Length Criteria
Basic Unit Homogeneity Rule
2.2.3. Failure History Data
2.2.4. Reproducibility and Implementation Details
- 1.
- Data preprocessing:
- -
- Remove missing/abnormal values
- -
- Standardize continuous attributes (diameter, insulation level, installation year)
- -
- Encode categorical attributes (purpose, burial environment)
- -
- Generate derived features (diameter × environment, environment×insulation, environment_purpose)
- 2.
- KNN-based relabeling:
- -
- Calculate Euclidean distance between normal and failure samples
- -
- Select top 10% of normal records most similar to failure cases and relabel as high risk
- 3.
- Data balancing:
- -
- Apply stratified train/validation/test split with fixed seed
- 4.
- Model development:
- -
- Hyperparameter optimization via Optuna for XGBoost and LightGBM
- -
- Determine optimal classification threshold using F2-score on validation data
- 5.
- Evaluation:
- -
- Report ACC, Precision, Recall, F1, F2, AUC metrics
- -
- Compare performance across K values to select the most balanced condition
- -
- Output: Final high-risk prediction model (XGB with K = 2)
3. Data Characteristics and Correlation Analysis
3.1. Data Characteristics
3.2. Correlation Analysis
4. High-Risk Data Selection for Heating Pipelines
5. Development of the High-Risk Prediction Model for Heating Pipelines
5.1. XGBoost (eXtreme Gradient Boosting, XGB)
5.2. LightGBM (Light Gradient Boosting Machine, LGBM)
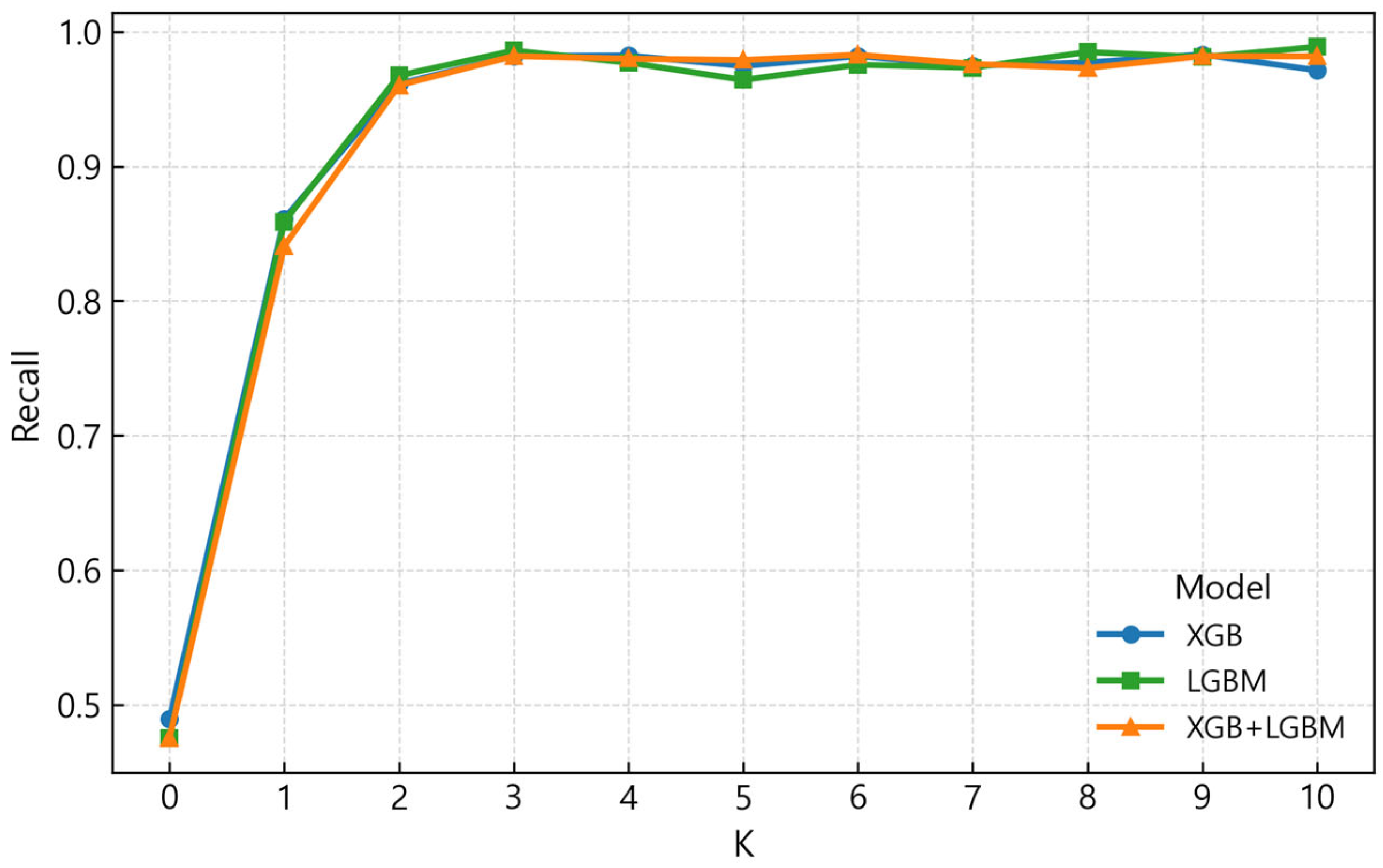
5.3. Model Evaluation Metrics
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, S.; O’Neill, Z.; O’Neill, C. A review of leakage detection methods for district heating networks. Appl. Therm. Eng. 2018, 137, 567–574. [Google Scholar] [CrossRef]
- Rafati, A.; Shaker, H.R. Predictive maintenance of district heating networks: A comprehensive review of methods and challenges. Therm. Sci. Eng. Prog. 2024, 53, 102722. [Google Scholar] [CrossRef]
- van Dreven, J.; Boeva, V.; Abghari, S.; Grahn, H. Intelligent Approaches to Fault Detection and Diagnosis in District Heating: Current Trends, Challenges, and Opportunities. Electronics 2023, 12, 1448. [Google Scholar] [CrossRef]
- Ihwnagu, U.T.I.; Debnath, R.; Ahmed, A.A.; Alam, M.J.B. An Integrated Approach for Earth Infrastructure Monitoring Using UAV and ERI: A Systematic Review. Drones 2025, 9, 225. [Google Scholar] [CrossRef]
- Ravindran, G. Evaluation of New Technologies to Support Asset Management of Metro Systems; UCL: London, UK, 2020. [Google Scholar]
- Guan, H.; Xiao, T.; Luo, W.; Gu, J.; He, R.; Xu, P. Automatic fault diagnosis algorithm for hot water pipes based on infrared thermal images. Build. Environ. 2022, 218, 109111. [Google Scholar] [CrossRef]
- Adegboye, M.A.; Fung, W.-K.; Karnik, A. Recent advances in pipeline monitoring and oil leakage detection technologies: Principles and approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, J.; Fu, Q.; Wu, H.; Wang, Y.; Lu, Y. Detection of district heating pipe network leakage fault using UCB arm selection method. Buildings 2021, 11, 275. [Google Scholar] [CrossRef]
- Valinčius, M.; Žutautaitė, I.; Dundulis, G.; Rimkevičius, S.; Janulionis, R.; Bakas, R. Integrated assessment of failure probability of the district heating network. Reliab. Eng. Syst. Saf. 2015, 133, 314–322. [Google Scholar] [CrossRef]
- Kong, M.; Kang, J. Methodology for Estimating the Probability of Damage to a Heat Transmission Pipe. J. Korean GEO-Environ. Soc. 2023, 22, 15–21. (In Korean) [Google Scholar]
- Langroudi, P.P.; Weidlich, I. Applicable Predictive Maintenance Diagnosis Methods in Service-Life Prediction of District Heating Pipes. Environ. Clim. Technol. 2020, 24, 294–304. [Google Scholar] [CrossRef]
- Pishvaie, M.R.; Hadipoor, M.; Jafari, S.; Baghery, S. Intelligent Approaches to Fault Detection and Diagnosis in District Heating Systems: A Review. Processes 2023, 11, 2512. [Google Scholar]
- Zhu, Q.; Zhu, L.; Wang, Z.; Zhang, X.; Li, Q.; Han, Q.; Yang, Z.; Qin, Z. Hybrid Triboelectric–Piezoelectric Nanogenerator Assisted Intelligent Condition Monitoring for Aero-Engine Pipeline System. Chem. Eng. J. 2025, 519, 165121. [Google Scholar] [CrossRef]
- Shirzad, M.; Vahdani, B.; Yazdi, M. A Machine Learning Approach for Failure Prediction of Water Distribution Networks. Reliab. Eng. Syst. Saf. 2021, 210, 107558. [Google Scholar]
- Christodoulou, S.E.; Gagatsis, A.; Xanthos, S.; Aslani, P. Risk-Based Prioritization of Water Pipe Replacement Using Statistical Failure Models. Urban Water J. 2010, 7, 121–134. [Google Scholar]
- Le Gauffre, P.; Joannis, C.; Le Gat, Y.; Breysse, D. A GIS-Based Method for Pipe Network Diagnosis and Rehabilitation. Autom. Constr. 2007, 16, 525–536. [Google Scholar]
- Hutton, C.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savić, D.A. Failure Predictions in Water Distribution Pipes Using Condition Assessment and Hydraulic Models. J. Infrastruct. Syst. 2016, 22, 04016017. [Google Scholar]
- Kleiner, Y.; Rajani, B. Comprehensive Review of Structural Deterioration of Water Mains: Statistical Models. Urban Water 2001, 3, 131–150. [Google Scholar] [CrossRef]
- Rajani, B.; Kleiner, Y. Protecting Critical Infrastructure: Structural Reliability of Buried Pipes. J. Infrastruct. Syst. 2001, 7, 120–128. [Google Scholar]
- Park, J.; Jung, D.; Kim, H.; Lee, S. Spatial Analysis of District Heating Pipe Failures Using GIS Data in Korea. Appl. Sci. 2022, 12, 10345. [Google Scholar]
- Xu, Y.; Zhang, L.; Yang, H. Application of Deep Learning in Leakage Detection of Urban Pipelines. Sensors 2020, 20, 6760. [Google Scholar]
- Sun, L.; Wang, P.; He, X. Data-Driven Prediction of Pipeline Failures under Imbalanced Datasets. Reliab. Eng. Syst. Saf. 2022, 223, 108500. [Google Scholar]
- Zhang, W.; Liu, G.; Zhou, J. Remaining Life Estimation of Buried Pipelines Considering Soil–Pipe Interaction. Tunn. Undergr. Space Technol. 2019, 83, 237–248. [Google Scholar]
- Mesri, G.; Stark, T.D. Long-Term Performance of Buried Infrastructure: Lessons from Case Histories. Can. Geotech. J. 2018, 55, 1089–1102. [Google Scholar]
- Euroheat & Power. Guidelines for District Heating Pipe System Reliability Assessment; Euroheat & Power: Brussels, Belgium, 2018. [Google Scholar]
- CEN/TC 107. EN 253; District Heating Pipes—Preinsulated Bonded Pipe Systems for Directly Buried Hot Water Networks. European Committee for Standardization: Brussels, Belgium, 2019.
- Lee, S.Y.; Kang, J.M.; Kim, J.Y. Prediction modeling of ground subsidence risk based on machine learning using the attribute information of underground utilities in urban areas in Korea. Appl. Sci. 2023, 13, 5566. [Google Scholar] [CrossRef]
- Lee, S.; Kang, J.; Kim, J.; Kong, M. AI-Based Damage Risk Prediction Model Development Using Urban Heat Transport Pipeline Attribute Information. Appl. Sci. 2025, 15, 8003. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, S.H.; Kang, U.S.; Kim, W.C.; Kim, J.G. Evaluation of electrochemical properties and life prediction of sensor wire in leak detection systems of underground heating pipelines. J. Electrochem. Soc. 2024, 171, 103508. [Google Scholar] [CrossRef]
- Lidén, P.; Adl-Zarrabi, B.; Hagentoft, C.E. Diagnostic Protocol for Thermal Performance of District Heating Pipes in Operation. Part 2: Estimation of Present Thermal Conductivity in Aged Pipe Insulation. Energies 2021, 14, 5302. [Google Scholar] [CrossRef]
- Song, S.; Kim, J. Advanced monitoring technology for district heating pipelines using fiber optic cable. In Proceedings of the 15th International Symposium on District Heating and Cooling, Seoul, Republic of Korea, 4–7 September 2016; pp. 1–8. [Google Scholar]
- Ebenuwa, A.U.; Tee, K.F. Fuzzy reliability and risk-based maintenance of buried pipelines using multiobjective optimization. J. Infrastruct. Syst. 2020, 26, 04020008. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Xu, H.; Deng, Y. Dependent evidence combination based on shearman coefficient and Pearson coefficient. IEEE Access 2018, 6, 11634–11640. [Google Scholar] [CrossRef]
- Aslam, M.; Smarandache, F. Chi-square test for imprecise data in consistency table. Front. Appl. Math. Stat. 2023, 9, 1279638. [Google Scholar] [CrossRef]
- Zhou, Q. Using chi-square categorical testing to analyse the survey data and find people’s attitude towards inequalities. J. Educ. Humanit. Soc. Sci. 2023, 24, 330–339. [Google Scholar] [CrossRef]
- Xi, D.; Lu, H.; Zou, X.; Fu, Y.; Ni, H.; Li, B. Development of trenchless rehabilitation for underground pipelines from an academic perspective. Tunn. Undergr. Space Technol. 2024, 144, 105515. [Google Scholar] [CrossRef]
- Ruys, W.L.; Ghafouri, A.; Chen, C.; Biros, G. Scalable k-NN graph construction for heterogeneous architectures. ACM Trans. Parallel Comput. 2025, 12, 1–35. [Google Scholar] [CrossRef]
- Yang, S.; Xie, J.; Liu, Y.; Yu, J.X.; Gao, X.; Wang, Q.; Peng, Y.; Cui, J. Revisiting the index construction of proximity graph-based approximate nearest neighbor search. Proc. VLDB Endow. 2025, 18, 1825–1838. [Google Scholar] [CrossRef]
- Halder, R.K.; Uddin, M.N.; Uddin, M.A.; Aryal, S.; Khraisat, A. Enhancing K-nearest neighbor algorithm: A comprehensive review and performance analysis of modifications. J. Big Data 2024, 11, 113. [Google Scholar] [CrossRef]
- Bekker, J.; Davis, J. Learning from positive and unlabeled data: A survey. Mach. Learn. 2020, 109, 719–760. [Google Scholar] [CrossRef]
- Mensink, T.E.J.; Verbeek, J.; Perronnin, F.; Csurka, G. Distance-Based Image Classification: Generalizing to New Classes at Near-Zero Cost. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2624–2637. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Zhang, Y.; Haghani, A. A gradient boosting method to improve travel time prediction. Transp. Res. Part C Emerg. Technol. 2015, 58, 308–324. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, H.D.; Zulfiqar, H.; Yuan, S.S.; Huang, Q.L.; Zhang, Z.Y.; Deng, K.J. iBLP: An XGBoost-Based Predictor for Identifying Bioluminescent Proteins. Comput. Math. Methods Med. 2021, 2021, 6664362. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Lv, J.; Wang, C.; Gao, W.; Zhao, Q. An Economic Forecasting Method Based on the LightGBM-Optimized LSTM and Time-Series Model. Comput. Intell. Neurosci. 2021, 2021, 8128879. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Zhu, L.; Cai, Z. Evaluation measures of the classification performance of imbalanced data sets. In Proceedings of the ISICA 2009—The 4th International Symposium on Computational Intelligence and Intelligent Systems, Huangshi, China, 23–25 October 2009; pp. 461–471. [Google Scholar]
- Bekkar, M.; Djemaa, H.K.; Alitouche, T.A. Evaluation measures for models assessment over imbalanced data sets. J. Inf. Eng. Appl. 2013, 3, 27–38. [Google Scholar]
- Gietz, H.; Sharma, J.; Tyagi, M. Machine learning for automated sand transport monitoring in a pipeline using distributed acoustic sensor data. IEEE Sens. J. 2024, 24, 22444–22457. [Google Scholar] [CrossRef]
- Chen, X.; Karin, T.; Jain, A. Automated defect identification in electroluminescence images of solar modules. Sol. Energy 2022, 242, 20–29. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Vega, A.; Yarahmadi, N.; Jakubowicz, I. Determination of the long-term performance of district heating pipes through accelerated ageing. Polym. Degrad. Stab. 2018, 153, 15–22. [Google Scholar] [CrossRef]
- Khan, L.R.; Tee, K.F. Risk-cost optimization of buried pipelines using subset simulation. J. Infrastruct. Syst. 2016, 22, 04016001. [Google Scholar] [CrossRef]











| Attribute | Data Characteristics |
|---|---|
| Spatial information | Shp |
| Facility ID | Numeric |
| Purpose | String |
| Diameter | Numeric |
| Year of burial | Numeric |
| Insulation level | Numeric |
| Burial environment | String |
| Statistic | Diameter (Normal) | Diameter (Failure) | Insulation Level (Normal) | Insulation Level (Failure) | Year of Burial (Normal) | Year of Burial (Failure) |
|---|---|---|---|---|---|---|
| Mean | −270.43 | −306.61 | −10.30 | −3.27 | −2008.39 | −1997.52 |
| Standard deviation | −206.87 | −239.18 | −3.32 | −3.46 | −9.58 | −8.57 |
| Min | −20 | −20 | −0 | −0 | −1987 | −1987 |
| Max | −1100 | −850 | −13 | −13 | −2024 | −2023 |
| Factor | Corr | p-Value |
|---|---|---|
| Diameter | 0.013 | 0.000 |
| Insulation level | −0.159 | 0.000 |
| Year of burial | −0.086 | 0.000 |
| Factor | p-Value | |
|---|---|---|
| Burial environment | 1165.017 | 0.000 |
| Purpose | 295.585 | 0.000 |
| K | Incorporated Data | Pseudo Mean Metric | All Mean Metric |
|---|---|---|---|
| 1 | 32,751 | 0.1011 | 0.6748 |
| 2 | 32,266 | 0.2218 | 0.9420 |
| 3 | 32,275 | 0.2972 | 1.0754 |
| 4 | 32,281 | 0.3511 | 1.1738 |
| 5 | 32,333 | 0.3928 | 1.2400 |
| 6 | 32,267 | 0.4311 | 1.2961 |
| 7 | 32,264 | 0.4640 | 1.3468 |
| 8 | 32,393 | 0.4932 | 1.3891 |
| 9 | 32,314 | 0.5201 | 1.4254 |
| 10 | 32,303 | 0.5446 | 1.4584 |
| Confusion Matrix | Prediction | ||
|---|---|---|---|
| Negative | Positive | ||
| Reference | Negative | True Negative (TN) | False Positive (FP) |
| Positive | False Negative (FN) | True Positive (TP) | |
| AUC | Evaluation |
|---|---|
| AUC ≥ 0.9 | Excellent |
| 0.8 ≤ AUC < 0.9 | Good |
| 0.7 ≤ AUC < 0.8 | Fair |
| AUC < 0.7 | Poor |
| Input | Output | |||||||
|---|---|---|---|---|---|---|---|---|
| Diameter | Insulation level | Year of burial | Purpose | Burial environment | Diameter × burial environment | Insulation level × burial environment | Purpose × burial environment | High-risk of failure |
| Model | F2-Score | Accuracy | Recall | AUC |
|---|---|---|---|---|
| XGB (K = 2) | 0.921 | 0.964 | 0.975 | 0.993 |
| LGBM (K = 2) | 0.912 | 0.961 | 0.968 | 0.991 |
| XGB + LGBM (K = 2) | 0.910 | 0.962 | 0.960 | 0.992 |
| Model | n_Estimators | Learning_Rate | Max_Depth |
|---|---|---|---|
| XGB (K = 2) | 120 | 0.0854 | 5 |
| LGBM (K = 2) | 117 | 0.0891 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kang, J.; Kim, J.; Kong, M. Prediction of High-Risk Failures in Urban District Heating Pipelines Using KNN-Based Relabeling and AI Models. Appl. Sci. 2025, 15, 11104. https://doi.org/10.3390/app152011104
Lee S, Kang J, Kim J, Kong M. Prediction of High-Risk Failures in Urban District Heating Pipelines Using KNN-Based Relabeling and AI Models. Applied Sciences. 2025; 15(20):11104. https://doi.org/10.3390/app152011104
Chicago/Turabian StyleLee, Sungyeol, Jaemo Kang, Jinyoung Kim, and Myeongsik Kong. 2025. "Prediction of High-Risk Failures in Urban District Heating Pipelines Using KNN-Based Relabeling and AI Models" Applied Sciences 15, no. 20: 11104. https://doi.org/10.3390/app152011104
APA StyleLee, S., Kang, J., Kim, J., & Kong, M. (2025). Prediction of High-Risk Failures in Urban District Heating Pipelines Using KNN-Based Relabeling and AI Models. Applied Sciences, 15(20), 11104. https://doi.org/10.3390/app152011104






