1. Introduction
High-volume operational decisions are of great value for organizations and their customers [
1]. This is, in one way, due to the large volume of data resulting from these decisions, which could be used for creating and making smarter decisions [
2,
3]. Furthermore, operational decisions could have a positive or negative impact on a person’s day-to-day life. For example, a government’s operational decision might involve the issuance of a residence permit, a decision that can have a substantial impact on an individual’s overall welfare. Another example of the impact of operational decision-making would be in hospitals where a wrongly executed decision could directly affect a person’s quality of life. In this paper, we adhere to the following definition of an operational decision:
“The act of determining an output value from a number of input values, using decision logic defining how the output is determined from the inputs” [
4]. An important component of how the decision is made is referred to as ‘decision logic’ in the above definition. In this paper, we adhere to the following definition of decision logic: “
a collection of business rules, business decision tables, or executable analytic models to make individual business decisions” [
4]. These definitions identify business rules and decision tables as specific components, providing potential benefits when separating and managing them from the rest of the software and processes.
This evolution has led to the separation of various concerns (SoCs) over time. Separating concerns started with the separation of the ‘data concern’ from software in the 1970s, followed by the separation of the ‘user interface concern’ in the 1980s and the ‘workflow/process concern’ in the 1990s, as noted by [
5]. Studies conducted by Boyer and Mili [
6] and Smit [
7] indicate that a logical progression in the field of IT involves isolating business rules as an independent ‘concern.’ This line of thinking has become particularly relevant for the development of intelligent systems, where decisions and their logic are increasingly separated from processes and data to support adaptability and transparency. Several researchers go even further with the SoC and separate decisions from data and processes [
8,
9,
10,
11,
12]. Provided the impact of decisions, its separate and explicit management becomes even more important. However, it could be for several reasons that an organization has no explicit decision management. One of the reasons could be that the organization is familiar with the fact that a certain decision exists, but the choice is made not to model the actual decision. Another reason could be that the organization is not familiar with the existence of certain decisions and is therefore unmanaged. Explicit decision modeling, however, can contribute to the design of decision support systems by enhancing consistency, explainability, and automation of decision logic. For either reason, having an explicit decision model certainly has benefits for the decision management of an organization. For example, one of the industry standards in the realm of decision modeling is the Decision Model and Notation (DMN) from the Object Management Group (OMG) [
4]. DMN supports the use of comprehensible diagrams that are designed to be understood by organizational stakeholders. These diagrams serve as a foundation for constructive discussions, leading to consensus regarding the scope and nature of decision-making processes, but also support validation by stakeholders. Furthermore, by breaking down requirements into graphical components, these objectives reduce the complexity and associated risks of automating decision processes. Decision tables, as a part of this standard, enable the structured definition of business rules. In addition, they simplify the development of information systems, offering specifications that can be automatically verified and executed, i.e., using Friendly Enough Expression Language (FEEL) modeling. It is also designed to align, both from a modeling and technical perspective, with the Business Process Management and Notation (BPMN) standard [
13]. Ultimately, it facilitates the creation of a library of reusable decision-making components, fostering efficiency and consistency in the decision-making process. DMN therefore contributes to the separation of concerns of decisions from data and processes. This makes it particularly suitable for embedding in decision support systems that depend on rule-based transparency and decision traceability [
14,
15].
Combining (business) data analytics with decision management solutions is something that is conducted often [
1]. Recorded data resulting from previously made decisions can be used for creating and making smarter future decisions [
2,
3]. The added value of collecting the relevant data related to these decisions and, in turn, analyzing the data resulting from these decisions could be of added value for designing, implementing, and executing said decisions [
16]. Therefore, discovering and analyzing decisions and its related decision logic is relevant for increasing the quality of operational decision-making [
17]. A method that could be utilized in order to discover decisions and its related decision logic is decision mining [
10,
11,
12]. Decision mining is “
the method of extracting and analyzing decision logs with the aim to extract information from such decision logs for the creation of business rules, to check compliance to business rules and regulations, and to present performance information” [
12]. Decision mining has the potential to positively ground public values such as (1) transparency (by making the decision-making explicit) [
16,
17], (2) accountability (decision-making by whom and based on which data) [
18,
19,
20,
21], and (3) fairness (revealing biases or inconsistencies in the decision-making could lead to more equitable outcomes) [
20,
22]. As such, decision mining forms a promising basis for data-driven decision support systems that aim to operationalize responsible decision-making.
Due to this reason, the algorithms used in decision mining should be evaluated themselves in order to have a positive effect on public values. Similar to how the FAIR principles [
23] have established findability, accessibility, interoperability, and reusability as guiding criteria for the responsible management of data, evaluation frameworks for decision discovery algorithms should ensure comparable qualities such as transparency, traceability, and reusability of decision logic.
The evaluation of decision discovery algorithms could be conducted through the utilization of quality dimensions. Quality dimensions ensure that discovery algorithms can be characterized, evaluated, and selected for a certain purpose. Subsequently, the discovered process or decision model (the outcome of the discovery algorithms) could be held in some regard with the characterization of the discovery algorithms. However, on the one hand, to the knowledge of the authors, the current body of knowledge on decision mining does not contain detailed contributions on quality dimensions. On the other hand, we know that process mining is a neighboring field of study to decision mining that shows a high similarity [
12]. Process mining is defined as “
the discovery, monitoring and improvement of real processes by extracting knowledge from event logs readily available in today’s information systems” [
24]. Three types of process mining exist, which are as follows [
24]: (1) process discovery, (2) conformance checking, and (3) process improvement. The high similarity between decision mining and process mining can guide us towards exploring the quality dimensions of Precision, Fitness, Simplicity, and Generalization in the process mining domain for the utilization in the decision mining domain [
25,
26,
27]. However, while these quality dimensions are well developed for processes, adapting them to decisions involves new challenges due to differences in structure, granularity, and logic representation. Additionally, while optimization approaches in generalized multi-scale decision systems highlight the impact of representational choices on model quality [
28,
29], decision discovery operates under stricter constraints: decision logic-based models are often a translation from policy or legislation and changing this is highly undesirable as it risks immediate regulatory non-compliance. This further underlines the need for quality dimensions such as precision, fitness, generalization, and simplicity to evaluate the fidelity of discovery algorithms.
Encouraged by the exaptation strategy from Hevner and Gregor [
30], we leverage quality dimensions of process mining for the field of decision mining. Therefore, we aim to answer the following research question in this study:
How can the precision, fitness, generalization, and simplicity quality dimensions from process mining be adapted to effectively evaluate decision discovery algorithms in the decision mining domain?This contribution fills an identified gap by tailoring evaluation metrics for decision mining and showing their practical application. While existing studies in process mining provide well-defined quality dimensions such as precision and fitness, their adaptation to the decision mining domain remains underexplored. This lack of a concrete methodology for evaluating decision discovery algorithms impedes the effective implementation of decision management solutions in practice [
31,
32]. This research aims to bridge this gap by proposing precision, fitness, generalization, and simplicity metrics tailored to decision mining and demonstrating their application through a practical example.
The remainder of the paper is structured as follows: Firstly, the background and related work are discussed containing concepts relating to conformance checking in process mining and decision mining, and the process and decision discovery algorithm quality dimensions. Secondly, the implementation of the decision quality dimensions of precision, fitness, generalization, and simplicity is discussed using a running example. Finally, the study and its outcomes are discussed, and conclusions are drawn to answer the research question, which is followed by possible future research directions.
2. Background and Related Work
Several application domains of intelligent systems, such as healthcare diagnostics, environmental regulation, loan approval, and supply chain optimization, rely heavily on structured decision logic. Yet, the accuracy and interpretability of this logic remain under-evaluated in most operational contexts. Recent work has highlighted the growing need for explainable and auditable decision support systems (e.g., [
33]). While many decision support systems embed decision rules, few employ a systematic quality evaluation of the decision models they contain. This study addresses this gap by proposing precision, fitness, generalization, and simplicity metrics tailored to decision mining, enabling decision support systems to improve the quality of their internal decision logic. This is particularly relevant for applications where decisions have legal, financial, or medical consequences and require both correctness and transparency.
Several methods exist that focus on discovering, checking, and improving patterns from data. The field of data mining focuses on knowledge discovery, or more specifically, aggregation patterns [
34], where the specific fields of process mining [
24] and decision mining [
12] focus on process and decision patterns. Process mining and decision mining are two fields that have a similar approach. This approach could be summarized into three phases: discovery of processes or decisions, checking processes or decisions on conformance, and/or enhancing or improving processes or decisions. Previous studies exist that focus on discovering decisions from data [
8,
9,
11,
35]. Mannhardt et al. [
36] introduced methods to discover overlapping rules in decision mining, while Scheibel and Rinderle-Ma [
37] proposed time series-based decision mining techniques with automatic feature generation. Furthermore, Banham et al. [
31] and Wais and Rinderle-Ma [
32] emphasized the need for a comprehensive evaluation framework for decision rules, moving beyond simple accuracy metrics to consider conformance and performance dimensions. Nonetheless, research exists on multi-scale decision systems, which states that that the selection of attributes scales has a direct effect on classification performance and rule extraction [
28,
29]. However, such optimization presupposes that the underlying decision logic can be freely adjusted, which is highly undesirable as it risks immediate regulatory non-compliance. Therefore, a major gap in the literature is the lack of a concrete methodology for evaluating decision discovery algorithms using quality dimensions such as precision, fitness, generalization, and simplicity.
Precision, fitness, generalization, and simplicity are well-established metrics in data mining and process mining. In data mining, precision is defined as the proportion of true positive predictions among all positive predictions, while fitness, often referred to as recall, measures the proportion of actual positives that are correctly identified [
34]. These metrics provide a robust framework for evaluating the accuracy and reliability of classification algorithms. In process mining, the focus lies on diagnosing the event logs and the process models. This is (partly) conducted by analyzing the used discovery algorithm which discovers process models from event logs. This diagnosis includes the characterization of the discovery algorithm using the process quality dimensions [
25,
26]. Four quality dimensions exist to characterize a discovery algorithm for process mining [
24,
25,
26,
27,
38].
In contrast to prior work, our method specifically focuses on evaluating the structure and behavior of decision logic models using quality dimensions derived from process mining. Where existing approaches typically assess individual rules or trees using predictive performance (e.g., accuracy or F1-score), our approach evaluates decision models holistically with respect to their conformance to actual decision behavior. In particular, we adapt process-oriented concepts such as ‘trace fitness’ and ‘model overgeneralization’ to decision artifacts, including fact types, fact values, and layered decision structures such as those in DMN. This allows for more informative assessments in decision support system contexts, where rule transparency, reuse, and auditability are crucial.
However, while precision, fitness, generalization, and simplicity are widely applied in data mining and process mining, their adaptation to decision mining requires careful consideration. Decision mining focuses on discovering decision logic from decision logs rather than classifying discrete outcomes. Therefore, the definitions of precision, fitness, generalization, and simplicity must be recontextualized to evaluate whether a discovered decision model accurately reflects the decision patterns captured in the decision log. The adoption of these quality metrics in decision mining remains limited, and existing studies often overlook how the distinct characteristics of decision models, such as their layered structure (for example in DMN’s Decision Requirements Diagram and Decision Logic Layer), influence the evaluation process [
4]. Additionally, while precision, fitness, generalization, and simplicity are widely used in classification contexts, their specific adaptation to decision mining requires a more tailored approach that considers decision-specific artifacts like fact types and fact values [
12].
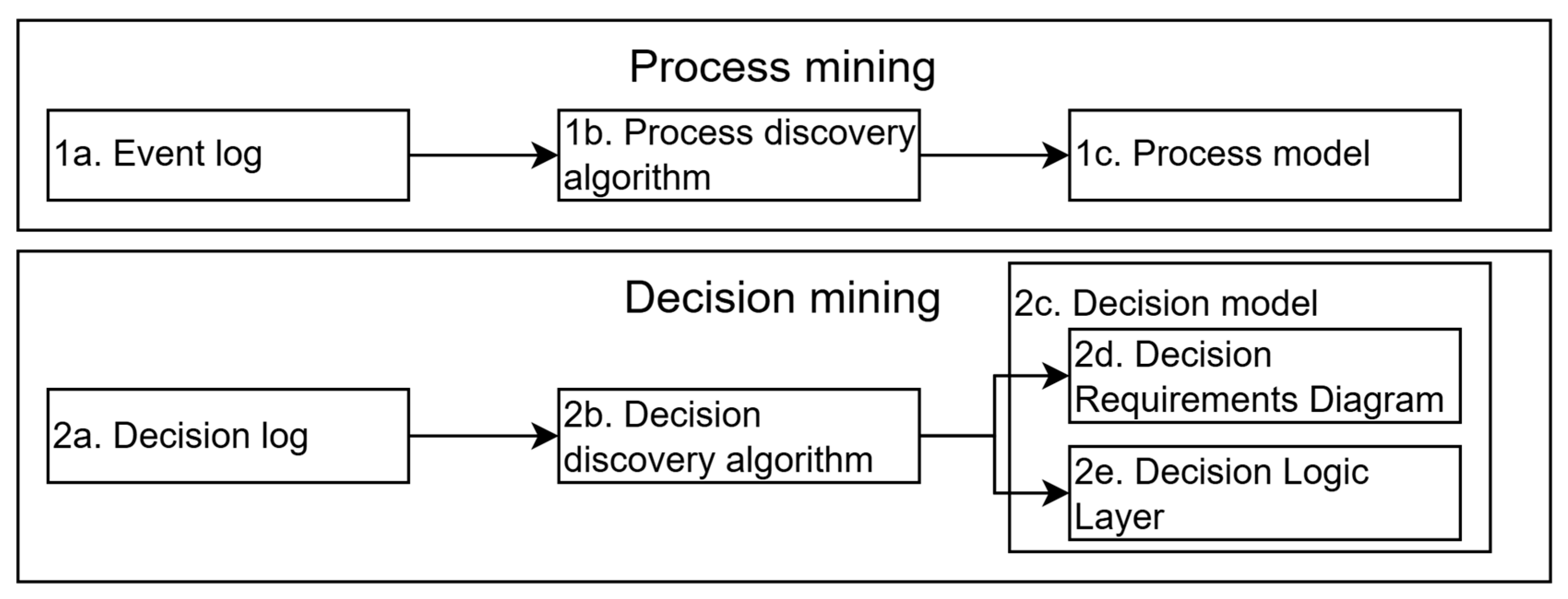
Several key concepts are defined to better understand the quality dimensions in relation to process mining and decision mining, starting with the key concepts of quality dimensions in the process mining domain. The first concept is the event log: a log file containing detailed information about the activities that have been executed, as shown on the left in
Figure 1. The event log consists of a case ID, events, and related attributes such as activity, time, costs, and resources [
24]. The second concept is the process model (such as BPMN [
13] or Petri nets [
39]): a (graphical) representation of the flow of work of activities, shown on the right in
Figure 1. The third concept is behavior: a combination of activities which could be combined into a process, as shown in
Figure 1. The fourth and last concept is a trace: a single case under a unique case ID of a specific combination of activities which could be combined into a process. An example of a trace of events would be: A → B → C (trace for case ID 1) or A → D (trace for case ID 2), as shown in
Figure 1 on the left and right.
To better address the decision concern, it is important to define fundamental decision-related concepts for the adaptation of the quality dimensions from the process mining domain to the decision mining domain. The first fundamental concept is a fact, which is defined as a piece of information that represents an objective reality or state of affairs [
6,
17,
40]. For example: “
The individual has accumulated five full years of service at their present employer”. The fact in this case is Person Employment Years. The second fundamental concept is fact value, which is an element of information (i.e., a data point within a specific context) and an expression of a fact [
17]. In this case, the fact value corresponds to the numerical value “five,” representing the number of years in the context of the individual’s years of service at their current employer. The third fundamental concept is fact type, which refers to the identifier or label assigned to a specific fact [
17]. Building forth on the previous example: a fact type for this is EmploymentYears.
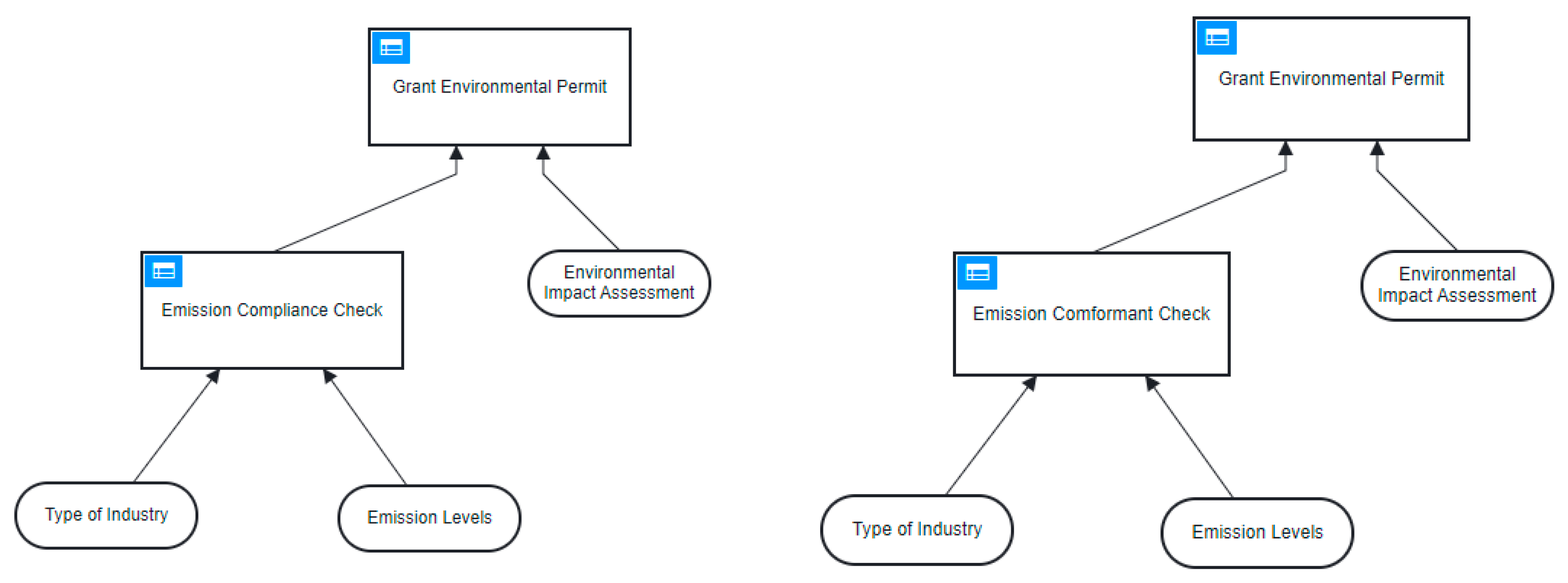
The input data between process mining and decision mining are different due to the fact that process mining focuses on sequencing patterns and decision mining on dependency patterns [
41]. Therefore, process mining utilizes an event log (1a), as shown in
Figure 2. Decision mining utilizes a decision log (2a), which is a log file containing detailed information about the decisions that have been executed. The decision log consists of an ID, a timestamp, a combination of fact types and fact values, as shown in
Figure 2 [
10,
12].
Due to the different input data (and resulting output data), the discovery algorithm is different in nature. The process discovery algorithm (1b) must handle event data from the event log and should provide a process model (1c) as its resulting model. The same argument could be used for the decision discovery algorithm (2b). Different input- and output data result in a different discovery algorithm compared to a process discovery algorithm. This decision discovery algorithm should handle a decision log as input data and should provide a decision model as output data. A decision model is a (graphical) representation of a combination of decisions and its underlying decision logic. Examples are the Decision Model and Notation (DMN) [
4], The Decision Model (TDM) [
17], and Semantics Of Business Vocabulary And Business Rules (SBVRs) [
42].
The separation in the decision model between a decision requirements diagram and a decision logic layer is not unique to just the decision modeling language of DMN, for this is also the case in other decision modeling languages, such as TDM [
17] and SBVR [
42].
The mapping of the decision discovery algorithms on decision quality dimensions in the conformance checking phase involves the utilization of both a decision log (2a) and a decision model (2c) in order to evaluate adherence to a set of constraints specific to each quality dimension, as shown in
Figure 2.
5. Precision, Fitness, Generalization, and Simplicity Demonstration
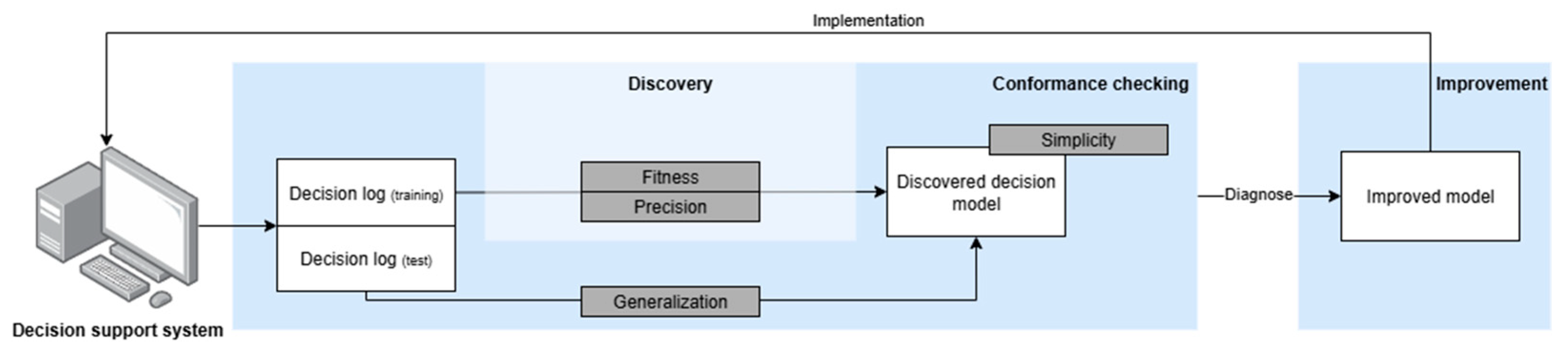
In this section, we elaborate in more detail on how the quality dimensions of precision, fitness, generalization, and simplicity are implemented in order to be used for decision mining. The flowchart as presented in
Figure 5 illustrates a high-level overview of the integration of precision, fitness, generalization, and simplicity metrics into the decision mining process. It provides a step-by-step overview of how decision discovery algorithms and decision models are evaluated and used for the improvement of decision models.
The process begins with the collection of decision logs, which serve as the primary input for generating decision models through decision discovery algorithms. Once a decision model is discovered, precision, fitness, generalization, and simplicity quality dimensions are applied to assess its quality.
Precision measures how accurately the decision model aligns with the observed behavior in the decision log (as depicted in
Figure 5), highlighting any unnecessary complexity or over-specification.
Fitness evaluates how well the decision model replicates all valid cases from the decision log (as depicted in
Figure 5), identifying gaps or under-specification in the model.
Generalization assesses the model’s ability to reproduce unseen or future decision cases (as depicted in
Figure 5), ensuring that the discovered model performs beyond the training data and is not overfitted to only the training data.
Simplicity captures the level of simplicity of the decision model by quantifying the absence of unnecessary complexity (as depicted in
Figure 5), indicating how easily the model can be understood by human actors.
In the context of decision mining, the optimal solution is defined not merely by achieving perfect fitness, precision, generalization, or simplicity in isolation, but by finding the balance between them. The optimal decision model is one that exhibits high fitness without compromising the other quality dimensions.
Based on these quality dimensions, a diagnosis is provided and used as input for an improved decision model. Finally, the decision model could be implemented in a decision support system.
The following sections focus on a more in-depth description of the technical implementation of the fitness, precision, generalization, and simplicity functions. First, the formal definitions are provided, following with the explanation of the fitness, precision, generalization, and simplicity functions. Finally, each function is provided with an evaluation in order to show the actual output for each function.
5.1. Definitions
Let M denote a decision model.
Facttype(x) is a predicate where x is a fact type.
A = {a: a ∈ M ^ Facttype(a)}. Stands for the set of fact types in the decision model (M).
Let L denote a decision log.
B = {b: b ∈ L ^ Facttype(x)}. Stands for the set of fact types in the decision log (L).
Factvalue(y) is a predicate where y is a fact value.
C = {e: e ∈ M ^ Factvalue(e)}. Stands for the set of fact values in the decision model (M).
D = {f: f ∈ L ^ Factvalue(f)}. Stands for the set of fact values in the decision log (L).
Length(G): Represents the length function, which returns the number of items in a set G. It is crucial for calculating percentages that assess the fitness of the decision model.
U = Unused Fact Types: Represents the set of fact types found in the decision log but not in the decision model, indicating a lack of coverage or anticipation by the decision model.
V = Used Fact Types: Denotes the set of fact types that are found in both the decision log and the decision model, showing alignment and expected use.
W = Unused Fact Values: This set contains fact values that appear in the decision log but are not recognized by the decision model, suggesting potential gaps in the decision model.
X = Used Fact Values: The set of fact values present in both the decision log and the decision model, affirming that the decision model accurately reflects the decision log.
Y = Extra Fact Types: The set of fact types present in the decision model and not in the decision log.
Z = Extra Fact Values: The set of fact values present in the decision model and not in the decision log.
CM = The observed structural complexity of decision model
M, defined in the work of Hasić and Vanthienen [
44]. Other methods could be used for determining complexity and, therefore, we do not determine a specific method and only refer to the work of Hasić and Vanthienen [
44] as an example.
Cmax = The maximum acceptable complexity threshold, set by human actors, used for normalizing the simplicity score.
NCS(M) = expresses the relative complexity of a decision model by comparing its observed complexity CM to a reference threshold Cmax. It ranges from 0 (minimal complexity) to 1 (above-threshold complexity).
Ltrain = A partition of the decision log L into a training set (Ltrain).
Ltest = A partition of the decision log a test set (Ltest).
Fitnesstrain(M) = The fitness of decision model M on the training log Ltrain.
Fitnesstest(M) = The fitness of decision model M on the test log Ltest.
5.2. Fitness
The precision, fitness, generalization, and simplicity implementations both compare the decision model and the decision log. Fitness assesses the degree to which the discovered decision model can accurately replicate the cases in the decision log. The concepts of overfitting and underfitting arise when dealing with the case of assessing a decision model on fitness. In an underfitting model, we might include too few input variables or overly simplistic decision logic. The consequences of an underfitting decision model can be substantial. An underfitted model exhibits low generalizability because it fails to capture essential conditions, causing it to produce incorrect outputs for significant portions of the input space when deployed. Moreover, such a model cannot adequately explain the causal mechanisms present in the original decision log, resulting in a representation that does not reliably reflect the organization’s actual decision-making behavior. In an overfitting model, we might include too much decision logic, leading to a model that performs very well on the training data but poorly on new, unseen data. The fitness implementation checks for two constraints are as follows: to assess whether there are fact types and fact values in the decision log that are missing in the decision model (underfitting) and whether there are extra fact types and fact values used in the decision model, which are not there in the decision log. The fitness function evaluates the congruence between a decision model and a decision log, if a decision model and decision log are in perfect balance, and if all fact types and fact values in the decision log are represented in the decision model.
The function generates a dictionary containing the fitness percentage and information regarding unused and new facts (fact types and fact values). We propose the following procedure to calculate the fitness of the decision model as follows:
- 1.
Classify Fact Types as Used or Unused: Iterates over each fact type used in the decision model or not. Fact types not in the decision model are added to the unused set U, and those in both the log and model are added to the used set V.
- 2.
Classify Fact Values as Used or Unused: Similar to fact types, this step classifies each fact value from the log as either unused (W) or used (X) based on its presence in the model.
- 3.
Calculate Fitness Percentages: Calculates the percentage of used fact types and fact values relative to the total fact types and fact values observed in the decision log, providing a measure of how well the decision model fits the real-world data represented in the decision log.
Fitness testcase
As described in the Fitness function, the output of the function is as follows: a fitness percentage, a list of unused fact types, a list of used fact types, a list of unused fact values, and used fact values. The following fitness-related information is a result of the comparison of the running example through the fitness function:
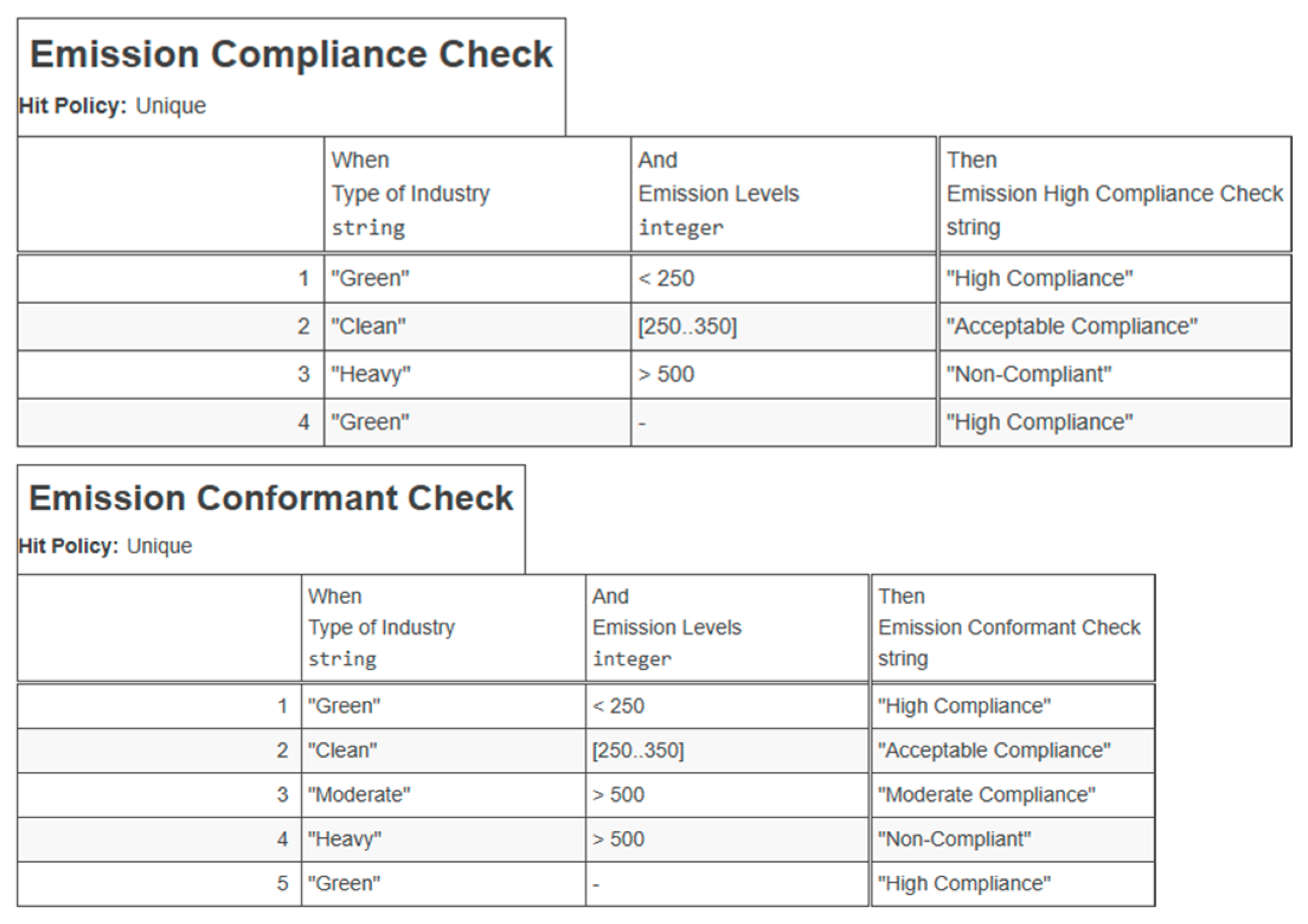
Fitness Percentage: 86.7%
Unused Fact Types: Emission Conformant Check
Used Fact Types: Type of Industry, Emission Levels, Environmental Impact Assessment, and Grant Environmental Permit
Unused Fact Values: Moderate
Used Fact Values: Green, <250, High Compliance, Positive, TRUE, Clean, [250..350], Acceptable Compliance, >500, Moderate Compliance, Neutral, FALSE, Heavy, and Non-Compliant
The fitness outcome indicates that the discovered model has an 86.7% fitness percentage due to the ‘emission conformant check’ fact type and ‘moderate’ fact value being unused.
5.3. Precision
In contrast to fitness, precision quantifies the portion of the discovered decision model’s behavior that remains unobserved in the decision log. The precision implementation checks for one constraint. Whether the decision model shows extra fact types and fact values is not directly visible in the decision log. In addition, both quality dimensions check how often a constraint occurs. The precision function estimates the precision of a decision model by comparing it to the decision log. The function generates a dictionary containing the extra fact types and fact values observed in the decision model. We propose the following procedure to calculate the precision of a decision model as follows:
- 1.
Identify Extra Fact Types: Evaluates each fact type in the decision model to see if it is not included in the decision log. Fact types not found are considered “extra” as they represent over-specification in the decision model. The logic is as follows:
- 2.
Identify Extra Fact Values: Similar to identifying extra fact types, it checks the each extra fact values in the decision model against those in the decision log. The fact values not present in the decision log are tagged as “extra”, indicating potential over-specification in the decision model. The logic is as follows:
- 3.
Calculate Precision Percentage: Calculates the percentage of fact types and fact values in the decision model that are actually used according to the decision log. Higher percentages indicate a decision model more (or to) finely tuned to the decision log’s content. The logic is as follows:
Precision testcase
As described in the Precision function, the output of the function is as follows: a precision percentage, a list of unused fact types, a list of used fact types, a list of unused fact values, and used fact values. The following precision-related information is a result of the comparison of the running example through the precision function:
Precision percentage: 79.5%
Extra Fact Types: Emission Compliance Check and Emission High Compliance Check
Extra Fact Values: Low Compliance and Negative
The precision outcome indicates that the discovered model has a 79.5% precision due to that the ‘Emission Compliance Check’ and ‘Emission High Compliance Check’ fact types are unused, and ‘Low compliance’ and ‘Negative’ fact values are used.
5.4. Generalization
Generalization measures the capacity of a discovered model to represent cases that were not used during the model’s training. This concept ensures the model has learned the essential, underlying structure and logic from the training data, rather than merely memorizing its specifics. In practice, this means new, unseen data (or out-of-sample data) should fit within the bounds and structure defined by the model without breaking its logic or requiring unacceptable adjustments. Several steps are necessary to ensure the proper calculation of the generalization metric:
- 1.
Log Partitioning: The historical decision log L is partitioned into two disjoint subsets: a training set, Ltrain, which is used to discover the decision model, and a test set, Ltest, which serves as out-of-sample data to evaluate the model. The formal definition is as follows:
- 2.
Metric Calculation: The existing fitness metric would then be calculated using the test set. A high fitness score on the test set indicates high generalization. Applying the fitness calculation to the test set (ensuring an out-of-sample dataset) with the discovered model provides a basis for assessing the generalizability of the model.
- 3.
Generalization calculation: whether the discovered model can correctly reproduce future or unseen cases. It prevents overfitting by validating the model on a separate test set. Generalization is reported as the fitness on the test set (as seen in
Figure 5):
Generalization Test case
Using the running example (environmental permit decision), the log was split 80/20 (training/test). Applying the previously defined Fitness function yields the following:
Fitnesstrain = 86.7%
Fitnesstest = 84.2%
Generalization: 84.2%. The test fitness is slightly lower than the training fitness. The model generalizes reasonably well to unseen cases.
5.5. Simplicity
Simplicity assesses the structural complexity and understandability of the discovered decision model. A simpler model is easier for human actors to validate, maintain, and trust. This quality dimension differs from the other dimensions of fitness, precision, and generalization. While these three dimensions can typically be expressed as percentages and through the presentation of (un)used DMN elements, simplicity is, to some extent, subjective. For this study, we use the work of Hasić and Vanthienen [
44] as an example to calculate complexity. These types of metrics assess structural aspects of the DRD and the decision tables, such as the number of decisions, the number of input variables, the depth of dependencies, and the number of rules. Existing approaches lack a normalized measure for which it is necessary to calculate the level of simplicity over 26 different complexity measures. Therefore, this function proposes the following missing measures to calculate simplicity:
- 1.
Calculating observed structural complexity: For demonstration purposes, we define and apply a selected set of complexity metrics. These metrics serve to illustrate the proposed approach and can be replaced or extended by other measures as needed. The metrics presented here are conceptually derived from the complexity metrics introduced by Hasić and Vanthienen [
45], who provide a broader set of structural and logical indicators for DMN decision models, as follows:
I(M) = The number of input data elements in the DRD of decision model M.
D(M) = The number of decision nodes in the DRD of decision model M.
DEP(M) = The maximum dependency depth in M, i.e., the length of the longest path from an input node to the top decision.
R(M) = The total number of rules across all decision tables in M.
C(M) = The total number of conditions across all decision table in M.
The total structural complexity could be calculated as follows:
- 2.
Setting domain-expert threshold: In the simplicity function, a threshold should be specified (when is a model simple?) by a domain-expert. This threshold is necessary to indicate simplicity and not just complexity.
Therefore, the following definition of the domain-expert threshold is introduced, as follows:
Cmax = The maximum acceptable complexity threshold, set by human actors, used for normalizing the simplicity score.
- 3.
Calculating Normalized Complexity Score: Several complexity metrics for decision models have been proposed in the literature, ranging from structural measures (e.g., number of decisions, dependency depth) to logical measures (e.g., number of rules, number of input conditions). These metrics, however, operate on different scales, which makes direct comparison and aggregation problematic. To address this imbalance, we introduce a Normalized Complexity Score (NCS). The NCS expresses the relative complexity of a decision model by comparing its observed complexity CM to a reference threshold Cmax. It ranges from 0 (minimal complexity) to 1 (maximum or above-threshold complexity). The Normalized Complexity Score (NCS) of M is defined as follows:
- 4.
Calculate Simplicity percentage: the NCS of M is translated to a Simplicity percentage through the following calculation:
A low percentage indicates that the model is complex, while a high percentage indicates that the model is simple. When the observed complexity CM exceeds the expert-defined threshold Cmax, the simplicity score is 0% (as the model is considered maximally complex). Conversely, the greater the gap between CM and Cmax (with CM < Cmax), the higher the resulting simplicity percentage.
The challenge in applying simplicity as a quality dimension lies in defining appropriate thresholds. In other words, at what point, for example, does a rule count of 25 represent a simple or a complex model. Especially in the decision domain, this should be conducted by a domain- or subject-matter expert.
Simplicity testcase
As described in the simplicity function, the output is a simplicity percentage (high percentage = a simple model, low percentage = Complex model). In the simplicity function, a threshold should be specified (when is a model simple?) by a human actor (for the testcase this is threshold is 25). Using the running example (
Figure 3 and
Figure 4), the following complexity metrics could be calculated:
Complexity metrics:
I(M) = 3
D(M) = 2
DEP(M) = 2
R(M) = 5
C(M) = 2
Human actor set threshold (Cmax): 25
Simplicity percentage: 44%
6. Discussion
The goal of this study is to identify the differences between precision, fitness, generalization, and simplicity in the context of process mining and decision mining and how to bridge this gap so that precision, fitness, generalization, and simplicity can be defined in relation to decision models.
Previous studies, such as Mannhardt et al. [
36] and Scheibel and Rinderle-Ma [
37], have addressed decision mining methodologies but often lacked a concrete evaluation framework for discovery algorithms. This study contributes to the field by providing a structured approach to evaluate decision models, filling a gap in the literature identified by Banham et al. [
31] and Wais and Rinderle-Ma [
32], who called for metrics beyond simple accuracy. Unlike prior research, this study specifically adapts precision, fitness, generalization, and simplicity metrics from process mining to decision mining, accounting for unique characteristics such as fact types and fact values. Baseline algorithms in decision mining, such as ID3- or C4.5-based decision tree learning [
45], are typically optimized for prediction rather than model quality in terms of representativeness or conformance. Our precision, fitness, generalization, and simplicity metrics instead offer model-level insights, supporting decision support system developers in selecting or refining decision logic that balances complexity and behavioral accuracy.
The fitness, precision, generalization, and simplicity functions are proposed, which demonstrate the unique aspects that should be taken into consideration when utilizing the quality dimensions of process mining in the decision mining domain. The current study has certain limitations that need to be addressed. Firstly, the implementation of precision, fitness, generalization, and simplicity is based on the implementation of these quality dimensions in the field of process mining. However, it is important to note that the concepts and characteristics of decisions differ from those of processes, and therefore, the assumptions that are suitable for process mining may not be applicable to decision mining. For example, decision models consist of two different layers, one focused on the visual representation of dependencies and one focused on decision logic. Process models solely have a process diagram layer. Despite this, it should be emphasized that the implementation of precision, fitness, generalization, and simplicity in this paper considers the unique elements of a decision, such as the decision model (including a decision requirement diagram and decision logic layer) and the presence of fact types and fact values.
Additionally, it is important to mention that the body of knowledge on decision discovery algorithms, especially from a decision viewpoint, is rather scarce [
41]. Therefore, validating the decision quality dimensions of decision discovery algorithms is limited by the amount of currently available decision discovery algorithms with a focus on the decision viewpoint. The ability for fully validating the decision quality dimensions is hindered. When decision discovery algorithms are more widely available, future research should focus on validating the quality dimensions through test scenarios and comparing the results more thoroughly.
A key limitation of the study is its reliance on a single running example for demonstration and application purposes. While this example demonstrates the implementation of the precision, fitness, generalization, and simplicity metrics, it inherently limits the generalizability of this study and the proposed metrics. For future research, we refer to the utilization of synthetic test scenarios compared to real-life test scenarios, because it provides the researchers with the ability to control the variables in synthetic scenarios. However, real-life test scenarios should be employed as well to improve generalization towards practice.
Lastly, in the conformance phase, process mining focuses purely on checking the event log and process model in conformance with the process mining quality dimensions. This leaves out diagnosing the discovered process model or the already existing process model on any syntax or semantical violations. Utilizing a process model (discovered or already existing) containing syntax or semantical violations could affect the quality of business operations. The potential ramifications of suboptimal business operations are significant. Moreover, when process or decision models fail to meet the stipulated quality standards, it merely marks the initial phase of a broader issue. Inadequate quality in business processes and decision-making can yield adverse consequences extending beyond the mere failure to satisfy quality requirements. These repercussions may manifest as legal disputes, financial penalties, and the erosion of the organization’s overall reputation [
46]. Encouragingly, industry professionals are already demonstrating a heightened awareness of this impending hazard, as indicated by recent research findings [
12].
For future decision mining research, the possibility to check syntax and semantic violations in existing or discovered decision models should be further studied. This is especially important due to the direct effect of a decision model on decision-making. The contributions of [
39,
40] are a first step in automatically checking any syntax violations in the DRD and decision logic layer for the DMN modeling language. Beyond ensuring syntactic and semantic correctness, future research should also consider how quality dimensions can be operationalized for non-technical users. Embedding these metrics into decision modeling environments (e.g., DMN modeling environments) would transform abstract numerical measures into actionable visual indicators, thereby improving usability and supporting informed decision-making by non-technical practitioners.
7. Conclusions
This study aimed to answer the following research question: How can the precision, fitness, generalization, and simplicity quality dimensions from process mining be adapted to effectively evaluate decision discovery algorithms in the decision mining domain? To do so, the quality dimensions of process mining were taken as a starting point for the description of the quality dimensions of precision, fitness, generalization, and simplicity. The process mining body of knowledge was used for the operationalization of precision, fitness, generalization, and simplicity in the decision mining domain. The fitness function quantifies the congruence between the decision model and decision log and returns a dictionary containing the fitness percentage and information on unused and new facts. The precision function quantifies the precision of the decision model by comparing it to the decision log and returns a dictionary containing information on the extra behavior observed in the decision model. The generalization function evaluates how well the discovered decision model performs on unseen cases by testing it on an out-of-sample dataset of the decision log. The simplicity function assesses the complexity of the decision model relative to a human actor-defined threshold, returning a percentage that indicates the model’s overall simplicity.
From a theoretical viewpoint, this study adds to the body of knowledge on how precision, fitness, generalization, and simplicity can be implemented to be used as decision mining quality dimensions for decision discovery algorithms as part of conformance checking in decision mining. This contribution focuses on developing the conformance checking phase of decision mining and thereby providing the body of knowledge with the first step of evaluating decision discovery algorithms. Additionally, the following differences are identified between the precision, fitness, generalization, and simplicity implementation in the process mining problem space compared to the precision, fitness, generalization, and simplicity in the decision mining problem space:
The difference between a process model and a decision model is taken into consideration when developing decision quality dimensions. A process model consists of one layer and a decision model consists of multiple layers (decision requirement diagram and decision logic layers).
The difference between an event log and decision log is taken into consideration when developing decision quality dimensions. An event log consists of sequencing patterns and a decision log consists of dependency patterns [
12].
From a practical viewpoint, this study enables researchers and practitioners to implement decision discovery algorithms with the ability to characterize them on the decision quality dimensions, thereby providing some context to the uncertainty of statistical analyses. Furthermore, this study will help practitioners to explicitly consider relevant public values when designing and implementing a decision mining solution. Additionally, the following difference is identified between the precision, fitness, generalization, and simplicity implementation in the process mining problem space compared to the precision, fitness, generalization, and simplicity in the decision mining problem space:
The importance of the implementation of precision, fitness, generalization, and simplicity in the decision mining problem space could be higher due to its impact. A decision discovery algorithm, which is evaluated with low precision, has a higher effect on decision-making, and in turn, an organization than a process model with low precision.
Decision mining has the potential to support public values such as transparency, accountability, and fairness [
20]. By providing a method to assess the quality of decision models, this study indirectly contributes to these values. A decision model with high precision, fitness, generalization, and simplicity not only aligns with regulatory requirements but also helps organizations build trust with stakeholders by ensuring that decision-making processes are both transparent and consistent. Lastly, for these quality dimensions to be utilized by non-technical users, future work must focus on their integration into a decision support system or an environment that utilizes graphical decision models (such as DMN). This integration is crucial for usability, as it enables the translation of abstract numerical scores into meaningful visual cues (e.g., color-coding, simplified dashboards) that non-technical practitioners can instantly recognize and act upon.