Higher-Order Sliding-Mode Velocity Observer-Based Exponential Stabilization of the Second-Order Chained-Form System

Abstract

This work addresses the problem of globally stabilizing underactuated systems with two inputs and three degrees of freedom. Through appropriate transformations, such dynamics can be expressed as second-order nonholonomic systems in chained form. A time-varying control framework is developed to overcome the absence of smooth static feedback laws and to drive the system trajectories to the origin. Explicit criteria for selecting feedback gains are derived, and velocity signals are reconstructed using a higher-order sliding-mode observer. A complete stability analysis is provided, ensuring exponential convergence of the closed-loop system under the proposed design. To illustrate its effectiveness, the method is applied to two benchmark problems: an underactuated hovercraft and a vertical takeoff and landing (VTOL) aircraft. Simulation results confirm the practicality and robustness of the proposed observer-based stabilization scheme for second-order chained systems.

1. Introduction

The control of mechanical systems has long been a central topic in both industrial applications and academic research. From the early speed regulation of Watt’s steam engine during the industrial revolution, through classical control in the mid-20th century, to the development of optimal, adaptive, and robust control in later decades, advances in theory have continually shaped engineering practice. Modern robotic systems and advanced aircraft represent prime examples of how control theory has been applied to increasingly complex mechanical systems.

Among these, underactuated systems—those with fewer control inputs than degrees of freedom due to inherent constraints or actuator limitations—have attracted sustained attention. Their control is challenging because the design must exploit the coupling between actuated and unactuated states to achieve desired objectives.

Early investigations focused on specific benchmark systems such as the Acrobot, Pendubot [1], inverted pendulums, and overhead cranes [2,3,4,5]. These studies provided valuable insights but were often limited in scope, as the derived controllers could not always be generalized. To broaden applicability, Reyhangoglu et al. [6] proposed a uni0fied framework for analyzing controllability and stability of underactuated dynamics. Xu and Özgüner [7] applied sliding-mode control to stabilize an underactuated quadrotor, while Olfati-Saber [8,9] explored cascade normal forms and smooth state-feedback strategies for Acrobots, rotating pendulums, and VTOL aircraft with strong input couplings. Teel [10] developed nested saturation methods for nonlinear cascade systems, and subsequent work [11,12,13,14] extended asymptotic and exponential stabilization methods to surface vessels. Liu and Yu [15] provided a comprehensive survey of underactuated system modeling, classification, and control approaches.

Underactuated systems are typically divided into two categories: those with first-order nonholonomic constraints (non-integrable velocity constraints) [16,17,18], and those with second-order nonholonomic constraints (non-integrable acceleration constraints) [19,20]. Since the 1990s, first-order nonholonomic systems have been extensively studied for motion planning and stabilization. For example, Murray and Sastry [21] showed that chained systems can be maneuvered using sinusoidal inputs. Yuan and Qu [22] later proposed smooth time-varying feedback laws, Li et al. [23] employed receding horizon control, and Zuyev [24] introduced oscillatory inputs for exponential stabilization of the Brockett integrator.

Second-order nonholonomic systems are equally rich in applications. Examples include robotic manipulators with passive joints (Acrobot, Pendubot), flexible and wheeled robots [25], legged locomotion systems, overhead cranes, VTOL aircraft, helicopters, quadrotors, spacecraft attitude control, marine vessels, hovercraft, and classical benchmarks such as beam-and-ball systems and inertia-wheel pendulums. Research has produced a wide range of strategies: Lizarraga et al. [26] considered robust stabilization under disturbances; Ma and Yu [19] and Tian and Li [27] proposed smooth time-varying controllers; He et al. [20] developed finite-time non-smooth feedback laws; and Yoshikawa et al. [28] employed coordinate and input transformations for planar manipulators.

Hybrid approaches such as robust [26], adaptive [15], intelligent optimal [15], and backstepping controls [4] have also been applied. While effective under certain conditions, they often require restrictive assumptions, complex structures, or high computational load. In contrast, the present study develops a time-varying control law combined with a higher-order sliding-mode observer. The proposed method provides a systematic and relatively simple framework for achieving global exponential stabilization of second-order chained systems, without state or input transformations or heavy parameter tuning.

The main contributions of this paper are as follows: (i) a direct time-varying control scheme for second-order chained systems; (ii) rigorous stability analysis establishing exponential convergence; and (iii) a finite-time higher-order sliding-mode observer enabling output-feedback implementation. Unlike many existing methods, the proposed design does not impose restrictive conditions on initial states, making it broadly applicable.

The remainder of the paper is organized as follows: Section 2 introduces the motivating hovercraft example and outlines the control design. Section 3 presents the proposed time-varying stabilization scheme with the velocity observer. Section 4 extends the approach to VTOL aircraft. Section 5 provides simulation results, and Section 6 concludes the paper.

2. The Motivating Example and Control Example

This section first presents the motivating example of an underactuated hovercraft and then illustrates the design concept behind the time-varying control for stabilizing the second-order nonholonomic chained system.

2.1. The Motivating Example

Considering the underactuated hovercraft as shown in Figure 1, we can formulate the following dynamic model:

$$m\ddot{x}=-\eta \dot{x}+\left(F_1+F_2\right)cos\theta$$

(1)

$$m\ddot{y}=-\eta \dot{y}+\left(F_1+F_2\right)sin\theta$$

(2)

$$J\ddot{\theta }=-\psi \dot{\theta }+\left(F_1-F_2\right)r$$

(3)

where $m$ denotes the mass of the hovercraft, $J$ is the rotational inertia, $F_1$ and $F_2$ are the control forces, $x$ and $y$ are the positions of the hovercraft, $\theta$ is the angular position, $r$ is the minimum length from the center of mass to the lines along the control forces, $\eta$ is the coefficient of viscous friction, and $\psi$ is the coefficient of rotational friction.

Define

$$z_1=x$$

$$z_2=tan\theta$$

$$z_3=y$$

and

$$u_1={\displaystyle \frac{1}{m}}\left(F_1+F_2\right)cos\theta$$

$$u_2=2tan\theta {sec}^2\theta {\dot{\theta }}^2-{\displaystyle \frac{\psi }{J}}{sec}^2\theta \dot{\theta }+{\displaystyle \frac{r}{J}}\left(F_1-F_2\right){sec}^2\theta$$

From the above definitions and the dynamic model (1)–(3), we have

$${\ddot{z}}_1=u_1-{\displaystyle \frac{\eta }{m}}{\dot{z}}_1$$

(4)

$${\ddot{z}}_2=u_2$$

(5)

$${\ddot{z}}_3=z_2{u}_1-{\displaystyle \frac{\eta }{m}}{\dot{z}}_3$$

(6)

Notice that (4)–(6) form a second-order nonholonomic chained system if $\eta$ is zero in (4) and (6).

2.2. Control Design

Consider the second-order nonholonomic chained system

$${\ddot{x}}_1=u_1$$

(7)

$${\ddot{x}}_2=u_2$$

(8)

$${\ddot{x}}_3=x_2{u}_1$$

(9)

The system (7)–(9) is underactuated because it has only two control inputs, and the system has six state variables ($x_i, {\dot{x}}_i, i=1, 2, 3)$.

Assuming $k_i\left(i=1,2,\dots ,6\right)$ are positive constants, the control $u_1$ is designed such that

$${\ddot{x}}_1=u_1=-k_1{x}_1-k_2{\dot{x}}_1+\beta e^{-\alpha t}$$

(10)

where $\alpha >0$ and $\beta$ is a constant.

In (10), the terms $-k_1{x}_1-k_2{\dot{x}}_1$ are used to compensate ${\ddot{x}}_1$ and $\beta e^{-\alpha t}$ is added such that the control can drive the state $x_1$ from the initial condition $x_1\left(0\right)=0$ and ${\dot{x}}_1\left(0\right)=0$.

Define $x_{2d}$ as the desired trajectory for $x_2$ and rearrange (9) as

$${\ddot{x}}_3=x_{2d}{u}_1+\left(x_2-x_{2d}\right)u_1$$

(11)

Now, we can ignore $\left(x_2-x_{2d}\right)u_1$ for design and treat this term as uncertainties. The control law for the nominal system becomes

$${\ddot{x}}_3=x_{2d}{u}_1$$

(12)

Here, the desired trajectory $x_{2d}$ can be regarded as a virtual control for the under-actuated system.

The state ${\ddot{x}}_3$ is compensated as

$${\ddot{x}}_3=x_{2d}{u}_1=-k_5{x}_3-k_6{\dot{x}}_3$$

(13)

We can assign $x_{2d}$ from (10) and (13)

$$x_{2d}={\displaystyle \frac{-k_5{x}_3-k_6{\dot{x}}_3}{-k_1{x}_1-k_2{\dot{x}}_1+\beta e^{-\alpha t}}}\approx {\displaystyle \frac{-k_5{x}_3-k_6{\dot{x}}_3}{\beta e^{-\alpha t}}}$$

(14)

where $k_1$ and $k_2$ are selected such that $\beta e^{-\alpha t}$ converges slower than $x_1$ and ${\dot{x}}_1$.

In other words, the control gain is selected to satisfy

$$k_2>2\alpha$$

(15)

Now we can track the desired state $x_{2d}$ by the control $u_2$

$${\ddot{x}}_2=u_2=-k_3\left(x_2-x_{2d}\right)-k_4\left({\dot{x}}_2-{\dot{x}}_{2d}\right)+{\ddot{x}}_{2d}$$

(16)

$$\approx -k_3\left(x_2-x_{2d}\right)-k_4{\dot{x}}_2$$

where ${\dot{x}}_{2d}$ and ${\ddot{x}}_{2d}$ can be ignored to simplify the control design.

3. Time-Varying Stabilization Control and Higher-Order Sliding-Mode Velocity Observer

After introducing the design concept, we will present the stability analysis in this section and address the output stabilization via the higher-order sliding-mode velocity observer.

3.1. Time-Varying Control

From the control design in (10), (14), and (16), we propose the following time-varying control

$$u_1=-k_1{x}_1-k_2{\dot{x}}_1+\beta e^{-\alpha t}$$

(17)

$$u_2=-k_3\left(x_2-x_{2d}\right)-k_4{\dot{x}}_2$$

(18)

and

$$x_{2d}={\displaystyle \frac{-k_5{x}_3-k_6{\dot{x}}_3}{\beta e^{-\alpha t}}}$$

(19)

Theorem 1.

For the dynamic systems (7)–(9), with the stabilization controls (17) and (18), the states  $x_i and {\dot{x}}_i\left(i=1, 2, 3 \right)$ are globally exponentially convergent to zero if feedback gains  $k_i\left(i=1, 2, \dots , 6\right)$  are chosen such that the conditions in (15), (21)–(22), and (29)–(33) are satisfied.

Proof. 

Substituting (17) into (7), we can solve for $x_1$ as

$$x_1=e^{-{\alpha }_{1}t}\left(Acos{\beta }_{1}t+Bsin{\beta }_{1}t\right)+C{e}^{-\alpha t}$$

(20)

and

$${\alpha }_1=-{\displaystyle \frac{k_2}{2}},$$

$${\beta }_1=\sqrt{k_1-{\displaystyle \frac{k_2^2}{4}}},$$

where $k_1$ and $k_2$ satisfy the following:

$$k_1>k_2\alpha$$

(21)

$$k_1>k_2^2/4$$

(22)

and

$$C={\displaystyle \frac{\beta }{{\alpha }^2+k_1-k_2\alpha }}$$

$$A=x_1\left(0\right)-C$$

$$B={\displaystyle \frac{1}{{\beta }_1}}\left. [x_1^{\prime }\left(0\right)+\alpha C+{\alpha }_1(x_1\left(0\right)-C)\right]$$

Define the following state variables:

$$z_1=x_2, z_2={\dot{x}}_2, z_3=e^{\alpha t}{x}_3, z_4=e^{\alpha t}{\dot{x}}_3$$

It follows that

$${\dot{z}}_1=z_2$$

(23)

$${\dot{z}}_2=-k_3{z}_1-k_4{z}_2-{\displaystyle \frac{k_3{k}_5}{\beta }}{z}_3-{\displaystyle \frac{k_3{k}_6}{\beta }}{z}_4$$

(24)

and

$${\dot{z}}_3={\alpha z}_3+z_4$$

(25)

Taking derivative of $z_4$ yields

$${\dot{z}}_4={\gamma }_1{z}_2+{\alpha z}_4+{\gamma }_2\left(t\right)z_2$$

(26)

where

$${\gamma }_1={\displaystyle \frac{\beta {\alpha }^2}{{\alpha }^2-k_2\alpha +k_1}}$$

$$\begin{gathered} {\gamma }_2\left(t\right)=-k_1{e}^{-({\alpha }_1-\alpha )t}\left(Acos{\beta }_{1}t+Bsin{\beta }_{1}t\right) \\ +k_2{e}^{-{\alpha }_{1}t}\left. [\left({\alpha }_{1}A+B{\beta }_1\right)cos{\beta }_{1}t+({\alpha }_{1}B+A{\beta }_1)sin{\beta }_{1}t\right] \end{gathered}$$

Define the vector

$$z={\left. [\begin{array}{ccc}{z}_1& z_2{z}_3& z_4\end{array}\right]}^T$$

We can express (23)–(26) as

$$\dot{z}\left(t\right)=\left(A_1+A_2\left(t\right)\right)z$$

(27)

where

$$A_1=\left[\begin{array}{cccc}0& 1& 0& 0\\ -k_3& -k_4& {-k}_3{k}_5/\beta & {-k}_3{k}_6/\beta \\ 0& 0& \alpha & 1\\ {\gamma }_1& 0& 0& \alpha \end{array}\right]$$

and

$$A_2=\left. [\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ {\gamma }_2\left(t\right)& 0& 0& 0\end{array}\right]$$

The eigenvalue $\lambda$ of matrix $A_1$ can be calculated from the following characteristic equation:

$${\lambda }^4+\left(k_4-2\alpha \right){\lambda }^3+\left(k_3+{\alpha }^2-2k_4\alpha \right){\lambda }^2+a_1\lambda +a_0=0$$

(28)

where

$$a_0=k_3\left. [{\alpha }^2+{\gamma }_1\left(k_5-\alpha k_6\right)/\beta \right]$$

$$a_1=k_4{\alpha }^2-{2\alpha k}_3+k_3{k}_6{\gamma }_1/\beta$$

It is straightforward to show that $A_1$ is Hurwitz if the following conditions are satisfied:

$$k_1>\alpha k_2$$

(29)

$${ k}_4>2\alpha$$

(30)

$$k_5>\alpha k_6$$

(31)

$${∆}_1=k_3{k}_4+{4{\alpha }^{2}k}_4-2{\alpha }^3-2\alpha k_4^2-k_3{k}_6{\gamma }_1/\beta >0$$

(32)

$${∆}_2=\left. [{∆}_1{a}_1-{\left(k_4-2\alpha \right)}^2{a}_0\right]/\left(k_4-2\alpha \right)>0$$

(33)

The matrix $A_2$ is bounded and $A_2\to 0 as t\to \infty$. From the Lyapunov analysis of linear time-varying systems (4.20) in [29], we can conclude that $the state z_i\left(i=1,2,3,4\right)$ exponentially converge to zero. Therefore, it follows from the definitions that the state $x_i and {\dot{x}}_i\left(i=2,3\right)$ exponentially converge to zero. In addition, $x_1$ and ${\dot{x}}_1$ also converge to zero from (20). This completes the proof of Theorem 1. □

By exploiting the control design in (17)–(19), one can make the following assumptions to simplify the gain selections:

$$\begin{gathered} k_1=5{\alpha }^2,k_2=4\alpha , k_3=100{\alpha }^2,k_4=10\alpha , \\ {k}_5=9{\alpha }^2,k_6=6\alpha . \end{gathered}$$

We can show that ${∆}_1=538{\alpha }^3>0$ and ${∆}_2=5397.5{\alpha }^5>0$ from (32) and (33), respectively.

3.2. Higher-Order Sliding-Mode Velocity Observer

Next, we will design a higher-order sliding-mode observer [30] to replace the velocity measurement for the proposed control scheme to stabilize the second-order chained system to the origin.

Define the variable

$$y_1=x_1,y_2={\dot{x}}_1,y_3=x_2,y_4={\dot{x}}_2,y_5=x_3,y_6={\dot{x}}_3$$

and the error

$$e_i=y_i-{\widehat{y}}_i,i=1,2,\dots ,6$$

where ${\widehat{y}}_i$ is the estimate of $y_i$.

The dynamic model in (7)–(9) can be expressed as

$$\begin{array}{l}{\dot{y}}_1=y_2\\ {\dot{y}}_2=u_1\\ {\dot{y}}_3=y_4\\ {\dot{y}}_4=u_2\\ {\dot{y}}_5=y_6\\ {\dot{y}}_6={y_{3}u}_1\end{array}$$

(34)

Denoting the function ${\lceil ·\rfloor }^{\gamma }={\left|·\right|}^{\gamma }sign\left(·\right)$, we propose the following sliding-mode observer

$$\begin{array}{l}{\dot{\widehat{y}}}_1={\widehat{y}}_2+k_{o1}{\lceil e_1\rfloor }^{{\displaystyle \frac{1}{1+\mu }}}\\ {\dot{\widehat{y}}}_2=k_{o2}{\lceil e_1\rfloor }^{{\displaystyle \frac{1-\mu }{1+\mu }}}+u_1+z_1\\ {\dot{z}}_1=k_{o3}sign\left(e_1\right)\\ {\dot{\widehat{y}}}_3={\widehat{y}}_4+k_{o4}{\lceil e_2\rfloor }^{{\displaystyle \frac{1}{1+\mu }}}\\ {\dot{\widehat{y}}}_4=k_{o5}{\lceil e_2\rfloor }^{{\displaystyle \frac{1-\mu }{1+\mu }}}+u_2+z_2\\ {\dot{z}}_2=k_{o6}sign\left(e_2\right)\\ {\dot{\widehat{y}}}_5={\widehat{y}}_6+k_{o7}{\lceil e_3\rfloor }^{{\displaystyle \frac{1}{1+\mu }}}\\ {\dot{\widehat{y}}}_6=k_{o8}{\lceil e_3\rfloor }^{{\displaystyle \frac{1-\mu }{1+\mu }}}+y_3{u}_1+z_3\\ {\dot{z}}_3=k_{o9}sign\left(e_3\right)\end{array}$$

(35)

where the parameter can be selected as $\mu ={\displaystyle \frac{1}{2}}$ for higher-order sliding-mode observer.

Subtracting (35) from (34), we obtain the error dynamics

$$\begin{array}{l}{\dot{e}}_1=e_2-k_{o1}{\lceil e_1\rfloor }^{{\displaystyle \frac{1}{1+\mu }}}\\ {\dot{e}}_2={-k}_{o2}{\lceil e_1\rfloor }^{{\displaystyle \frac{1-\mu }{1+\mu }}}-z_1\\ {\dot{z}}_1=k_{o3}sign\left(e_1\right)\\ {\dot{e}}_3=e_4-k_{o4}{\lceil e_2\rfloor }^{{\displaystyle \frac{1}{1+\mu }}}\\ {\dot{e}}_4=-k_{o5}{\lceil e_2\rfloor }^{{\displaystyle \frac{1-\mu }{1+\mu }}}-z_2\\ {\dot{z}}_2=k_{o6}sign\left(e_2\right)\\ {\dot{e}}_5=e_6-k_{o7}{\lceil e_3\rfloor }^{{\displaystyle \frac{1}{1+\mu }}}\\ {\dot{e}}_6={-k}_{o8}{\lceil e_3\rfloor }^{{\displaystyle \frac{1-\mu }{1+\mu }}}-z_3\\ {\dot{z}}_3=k_{o9}sign\left(e_3\right)\end{array}$$

(36)

It follows from [31] that $e_i$ will converge to zero in finite time for the higher-order sliding-mode observer ($\mu ={\displaystyle \frac{1}{2}}).$

In summary, the proposed methodology consists of three main stages: (i) modeling the underactuated system in second-order chained form, (ii) designing a time-varying exponential stabilization controller based on the proposed stability conditions, and (iii) integrating a higher-order sliding-mode velocity observer to estimate unmeasured states for output feedback. These stages are demonstrated using two representative applications—a hovercraft and a VTOL aircraft—to illustrate the method’s practicality and effectiveness.

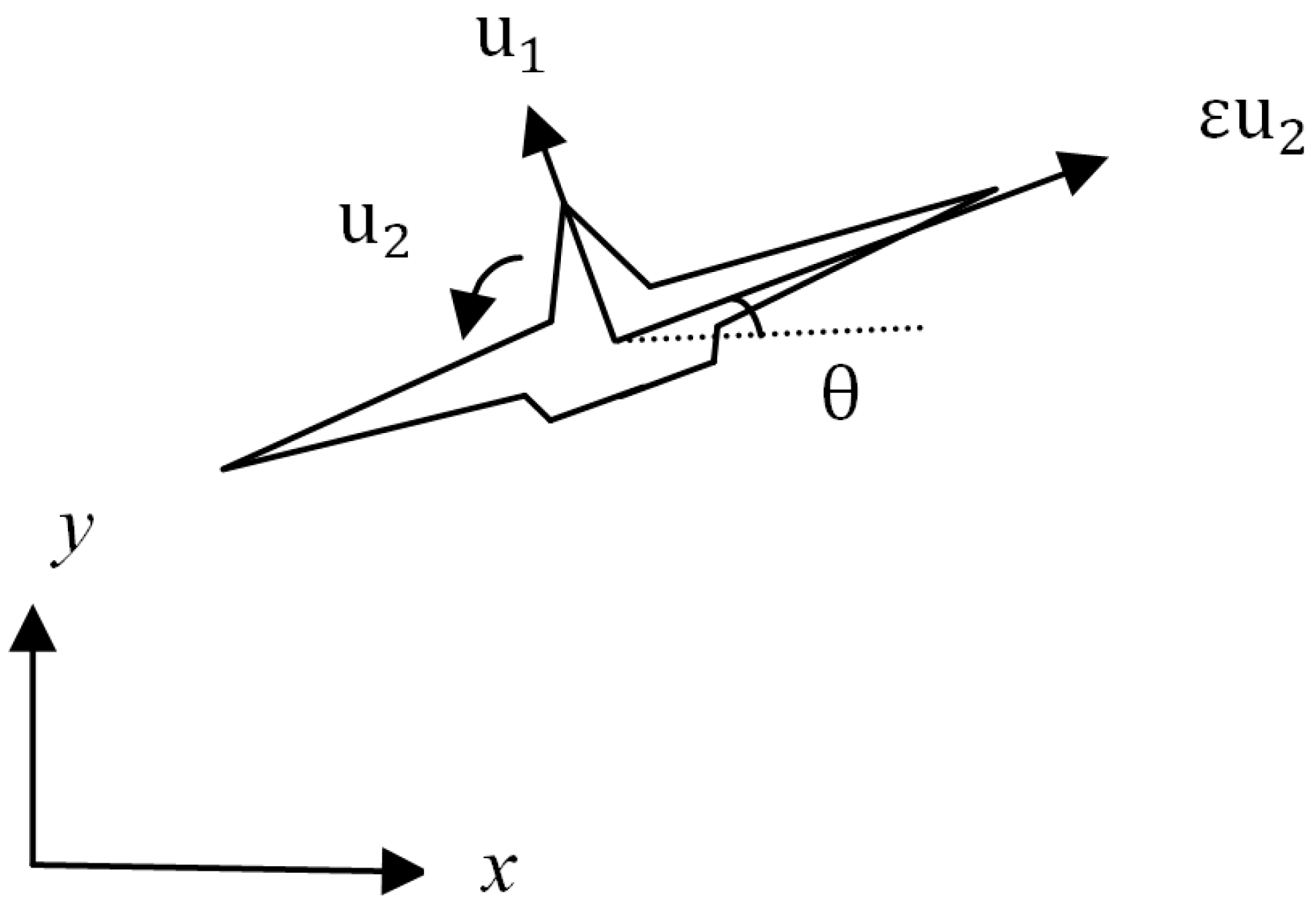
4. Extension to Stabilization of VTOL Aircraft

In this section, we derive a dynamic model for VTOL aircraft and show that this model can be transformed into a second-order chained-form-like model. The time-varying stabilization control scheme proposed in the previous sections is general enough to be extended to the case of VTOL aircraft.

4.1. Dynamic Model of VTOL and Control Design

Considering the VTOL aircraft shown in Figure 2, the dynamics can be described by the following equations of motion [9]:

$$\begin{array}{l}\ddot{x}={-v}_{1}sin\theta +ϵv_{2}cos\theta \\ \ddot{y}=v_{1}cos\theta +ϵv_{2}sin\theta -g \\ \ddot{\theta }=v_2\end{array}$$

(37)

Define the state variables

$$\begin{array}{l}{x}_1=y+ϵ(cos\theta -1)\\ x_2=-tan\theta \\ x_3=x-ϵsin\theta \end{array}$$

and the control

$$u_1=v_{1}cos\theta -ϵcos\theta {\dot{\theta }}^2$$

(38)

$$u_2=-v_2{sec}^2\theta +2tan\theta {sec}^2\theta {\dot{\theta }}^2$$

(39)

We have

$${\ddot{x}}_1=u_1-g$$

(40)

$${\ddot{x}}_2=u_2$$

(41)

$${\ddot{x}}_3=x_2{u}_1$$

(42)

The systems (40)–(42) are underactuated because they only have two control inputs over six state variables.

Assuming $k_i\left(i=1,2,\dots ,6\right)$ are positive constants, the control $u_1$ is designed such that

$${\ddot{x}}_1=u_1-g=-k_1{x}_1-k_2{\dot{x}}_1$$

(43)

Notice that the terms $-k_1{x}_1-k_2{\dot{x}}_1$ are used to compensate ${\ddot{x}}_1$ and the control $u_1$ will not vanish for the initial condition $x_1\left(0\right)=0$ and ${\dot{x}}_1\left(0\right)=0$.

We can define $x_{2d}$ as the desired trajectory for $x_2$ and rearrange (42) as

$${\ddot{x}}_3=x_{2d}{u}_1+\left(x_2-x_{2d}\right)u_1$$

(44)

The term $\left(x_2-x_{2d}\right)u_1$ can be treated as uncertainties, we propose the control law for the nominal system

$${\ddot{x}}_3=x_{2d}{u}_1$$

(45)

Here, we consider the desired trajectory $x_{2d}$ as a virtual control for the under-actuated system.

The state ${\ddot{x}}_3$ can be compensated as

$${\ddot{x}}_3=x_{2d}{u}_1=-k_5{x}_3-k_6{\dot{x}}_3$$

(46)

Then, we can assign $x_{2d}$ from (43) and (46)

$$x_{2d}={\displaystyle \frac{-k_5{x}_3-k_6{\dot{x}}_3}{g-k_1{x}_1-k_2{\dot{x}}_1}}$$

(47)

Now we can design the tracking control $u_2$ to follow the desired state $x_{2d}$

$${\ddot{x}}_2=u_2=-k_3\left(x_2-x_{2d}\right)-k_4\left({\dot{x}}_2-{\dot{x}}_{2d}\right)+{\ddot{x}}_{2d}$$

(48)

4.2. Time-Varying Control

From the control design in (43), (47), and (48), we can propose the following time-varying control:

$$u_1=g-k_1{x}_1-k_2{\dot{x}}_1$$

(49)

$$u_2=-k_3\left(x_2-x_{2d}\right)-k_4\left({\dot{x}}_2-{\dot{x}}_{2d}\right)+{\ddot{x}}_{2d}$$

(50)

and

$$x_{2d}={\displaystyle \frac{-k_5{x}_3-k_6{\dot{x}}_3}{g-k_1{x}_1-k_2{\dot{x}}_1}}$$

(51)

Notice that $x_1$ and ${\dot{x}}_1$ can be solved by substituting (49) into (40). It follows from (46) that the state $x_3$ and ${\dot{x}}_3$ converge exponentially to zero. Given the typical constraint on the acceleration, for example $\left|k_1{x}_1+k_2{\dot{x}}_1\right|<0.5 g$, it is easy to verify from (48) and (51) that the state $x_2$ and ${\dot{x}}_2$ also tend to zero exponentially.

4.3. Differentiator Design for ${\dot{x}}_{2d}$ and ${\ddot{x}}_{2d}$

Now, we show how to use the exact differentiator to obtain ${\dot{x}}_{2d}$ and ${\ddot{x}}_{2d}$ in (50).

We propose the following second-order differentiator

$${\dot{\xi }}_0=v_0$$

(52)

$${\dot{\xi }}_1=-{\lambda }_1{\lceil {\xi }_1-v_0\rfloor }^{{\displaystyle \frac{1}{2}}}+{\xi }_2$$

(53)

$${\dot{\xi }}_2={-\alpha }_{1}sign\left({\xi }_1-v_0\right)$$

(54)

$${\dot{w}}_0={-\alpha }_0{\lceil {\xi }_0-x_{2d}\rfloor }^{{\displaystyle \frac{1}{3}}}$$

(55)

$$v_0=-{\lambda }_0{\lceil {\xi }_0-x_{2d}\rfloor }^{{\displaystyle \frac{2}{3}}}+w_0+{\xi }_1$$

(56)

where ${\alpha }_0={\alpha }_{c0}{L}^{{\displaystyle \frac{2}{3}}},{\alpha }_1={\alpha }_{c1}L,{\lambda }_0={\lambda }_{c0}{L}^{{\displaystyle \frac{1}{3}}},{\lambda }_1={\lambda }_{c1}{L}^{{\displaystyle \frac{1}{2}}}.$ After a finite time, the differentiator can generate the following:

$${\xi }_0=x_{2d}, {\xi }_1={\dot{x}}_{2d}, {\xi }_2={\ddot{x}}_{2d}.$$

The convergence property of the differentiators (52)–(56) can be guaranteed by Theorem 5 in Levant [30].

5. Numerical Simulation

To show the effectiveness of the proposed control scheme, we conduct numerical simulations for the hovercraft and the VTOL aircraft.

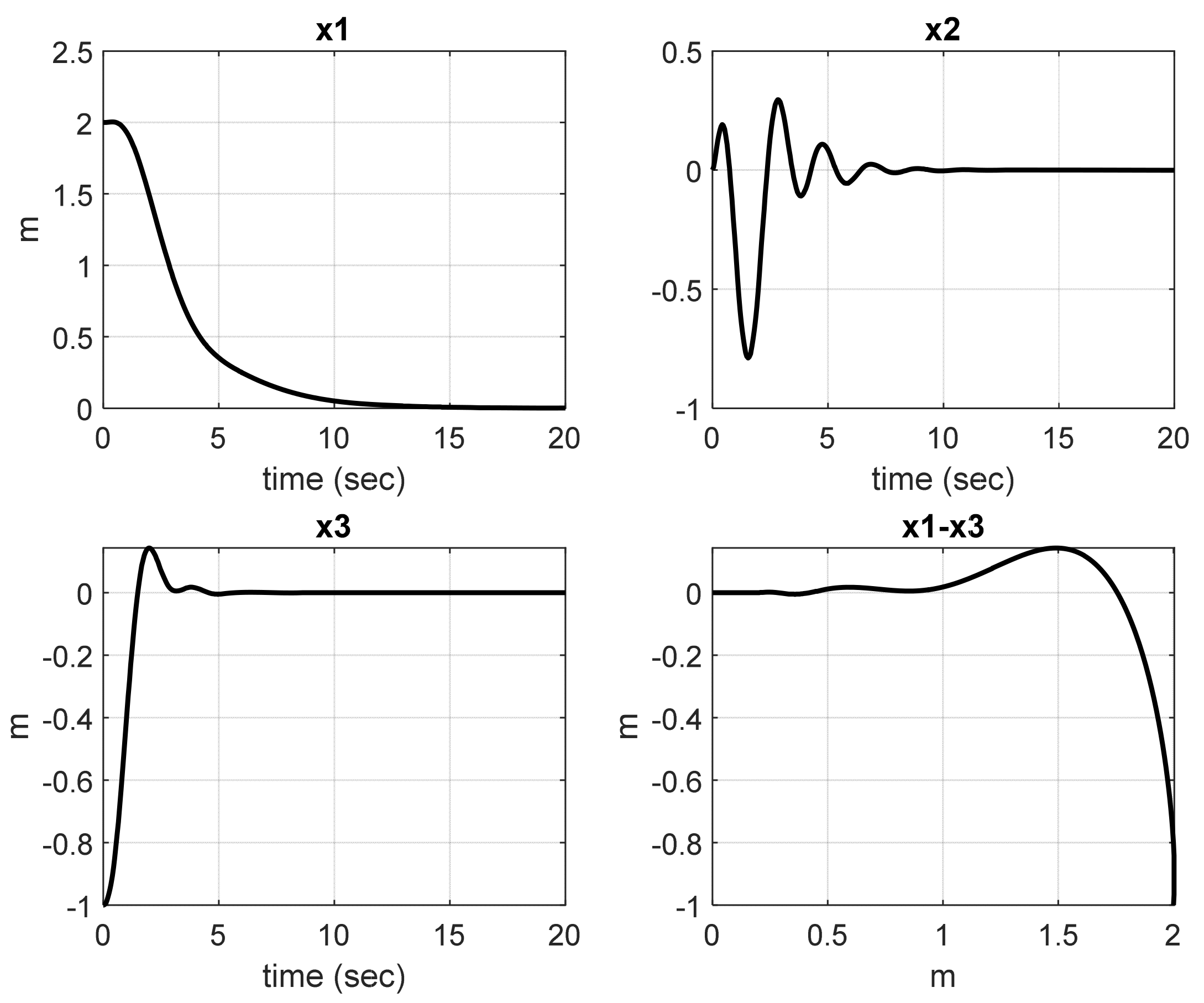
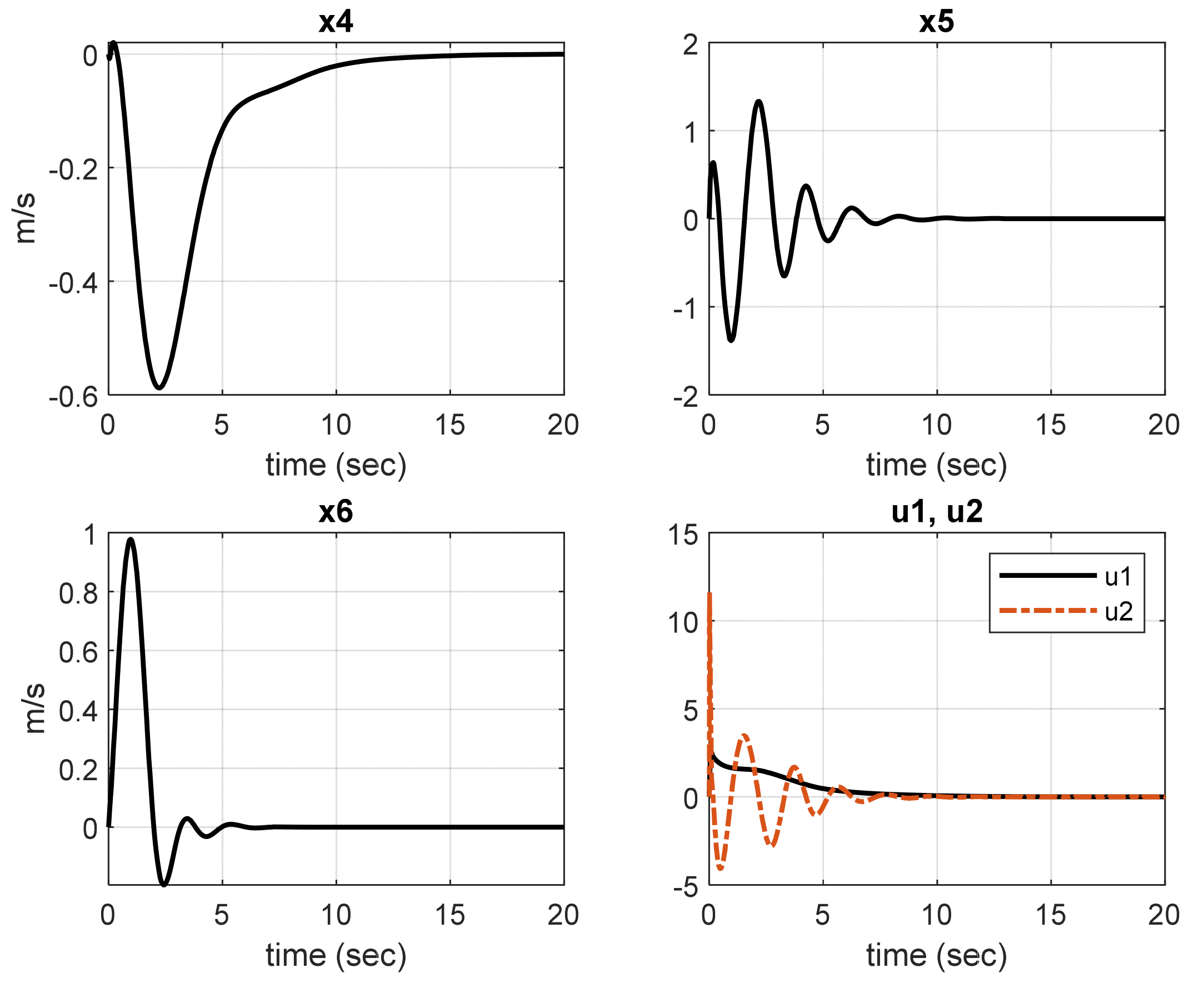
5.1. Hovercraft

The following parameters are used in the simulation [32]:

$$m=5 \mathrm{kg},J=0.05 \mathrm{kg}{\mathrm{m}}^2, r=0.124 \mathrm{m}, \eta =5.5 \mathrm{kg}/\mathrm{s},\psi =0.084 \mathrm{kg}{\mathrm{m}}^2/\mathrm{s}$$

We select the following control gains:

$$\begin{gathered} k_1=4.5{\alpha }^2,k_2=3.5\alpha , k_3=120{\alpha }^2,k_4=12\alpha , \\ {k}_5=9{\alpha }^2,k_6=6\alpha ,\alpha =0.4, \beta =4. \end{gathered}$$

It follows that

$${∆}_1=53.63>0 \mathrm{and} {∆}_2=82.55>0$$

The eigenvalues of matrix $A_1$ are

$$-1.7580\pm 3.1855i,-0.2420\pm 0.7222i$$

For the sliding-mode velocity observer, the following gains are chosen:

$$k_{o1}=12,k_{o2}=36, k_{o3}=50,k_{o4}=40,k_{o5}=400,k_{o6}=100, k_{o7}=12,k_{o8}=36,k_{o9}=50.$$

Figure 3 shows the position trajectories $x_1$ to $x_3$ of the hovercraft from (−2, 1) to (0, 0). The velocity trajectories with the initial condition $\left. [\begin{array}{ccc}2& 0& -1 \begin{array}{ccc}0& 0& 0\end{array}\end{array}\right]$ are present in Figure 4. From the simulation results, the proposed stabilization control successfully drives the system from the initial position to the origin. Figure 5 presents the estimation error trajectories of the higher-order sliding-mode velocity observer, respectively. The results clearly indicate that the higher-order sliding-mode observer is superior to the linear observer in terms of convergence time and accuracy.

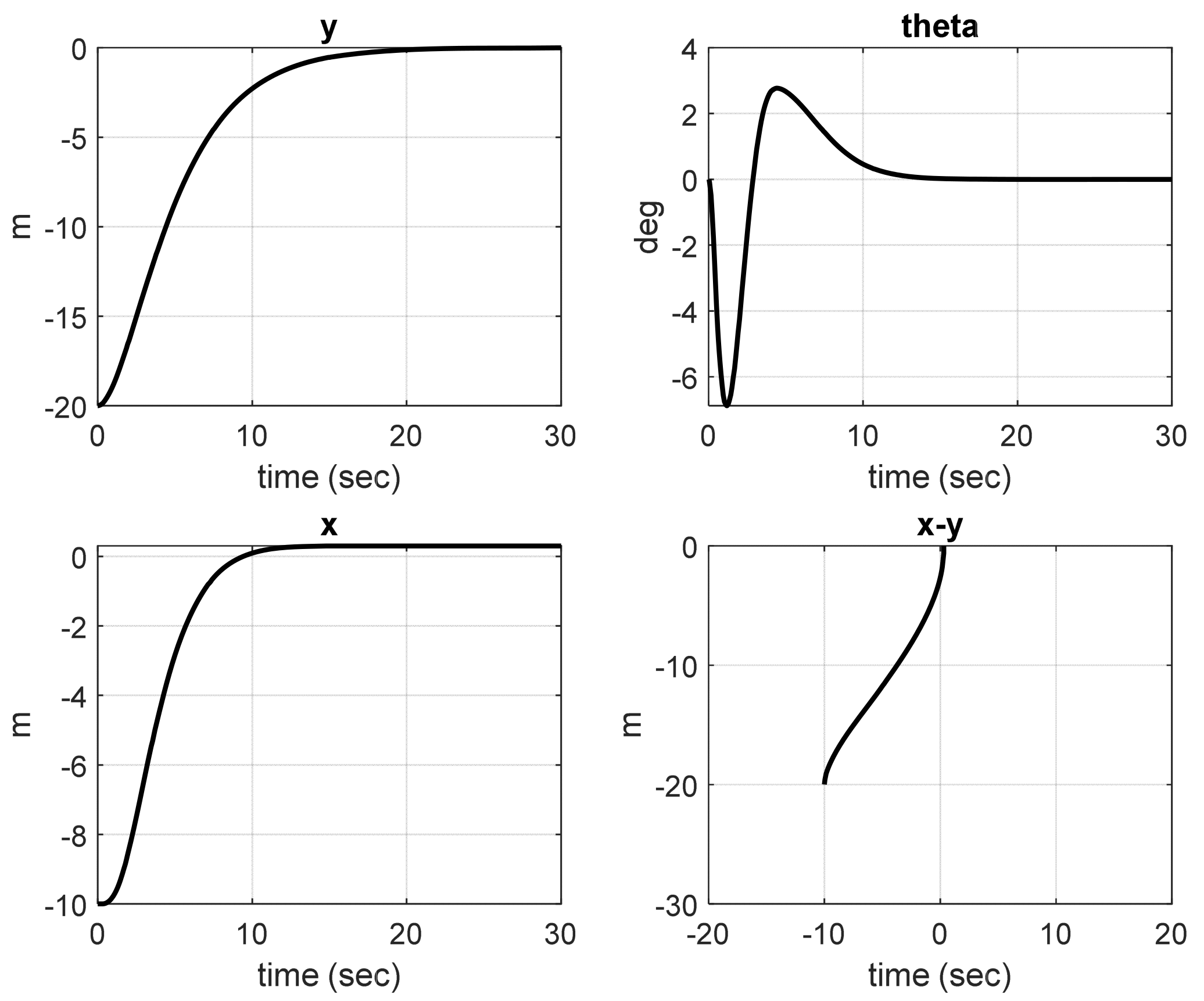
5.2. VTOL Aircraft

We use the following gains for controls (49)–(51):

$$k_1=0.15,k_2=0.8, k_3=1,k_4=2,k_5=0.8,k_6=1.8.$$

and the following for the differentiators (52)–(56)

$${\alpha }_{c0}=4, {\alpha }_{c1}=8, {\lambda }_{c0}=20, {\lambda }_{c1}=10,L=1.$$

Figure 6 shows the state trajectories and controls with the initial condition $\left. [\begin{array}{ccc}x& y& \theta \end{array}\right]=\left. [\begin{array}{ccc}-10& -20& 0\end{array}\right]$. As shown in Figure 7, the proposed differentiator can soon provide the exact first and second differentiation of the desired trajectory $x_{2d}$ due to the finite-time convergence.The control gains were selected to keep the control inputs within a feasible range, implicitly addressing actuator constraints and preventing unrealistic saturation effects.

It is worth noting that conventional methods such as backstepping [4] and adaptive control [15] are well-established for nonlinear systems. However, these techniques cannot be directly applied to second-order chained-form underactuated systems without substantial modification, since they do not inherently handle nonholonomic constraints. In contrast, the proposed time-varying control with a higher-order sliding-mode observer provides a straightforward stabilization strategy without requiring additional transformations or complex adaptive structures.

The proposed control scheme was implemented with modest computational requirements and showed consistent convergence under small perturbations in the simulations. A more comprehensive quantitative analysis of performance metrics such as mean squared error, computational cost, and robustness will be addressed in future work to maintain focus on the main theoretical contributions of this paper.

6. Conclusions

This paper has presented a time-varying control strategy for stabilizing second-order chained-form nonholonomic systems at the origin. A higher-order sliding-mode observer was incorporated to estimate unmeasured velocity signals, enabling an output-feedback implementation. Rigorous stability analysis was carried out, along with explicit guidelines for selecting feedback gains to guarantee exponential convergence. Numerical studies with two representative benchmarks—a hovercraft and a VTOL aircraft—demonstrated that the proposed method achieves stabilization effectively without the need for state or input transformations. The results highlight the practicality of the design and its ability to handle underactuated dynamics in a systematic manner. Beyond these contributions, the proposed framework establishes a foundation for future research. Potential extensions include addressing actuator saturation, enhancing robustness under stronger disturbances, and applying the method to more complex multi-agent or cooperative underactuated systems.