Estimation of Tunnel Pressure Arch Zone Based on Energy Density Difference of Surrounding Rock
Abstract
1. Introduction
2. Boundary Delineation Criterion and Numerical Modeling of Pressure Arch Based on Energy Density Theory
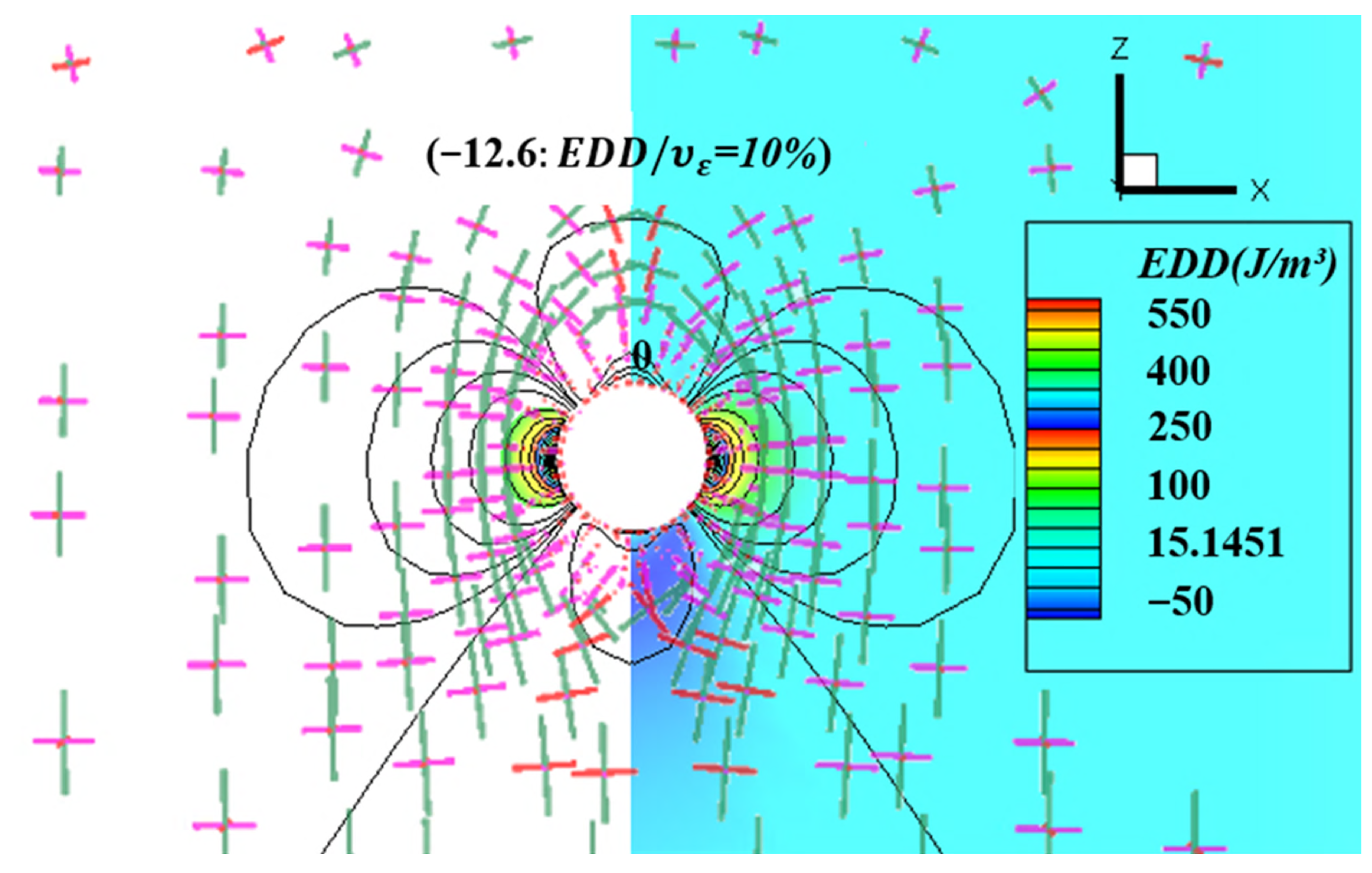
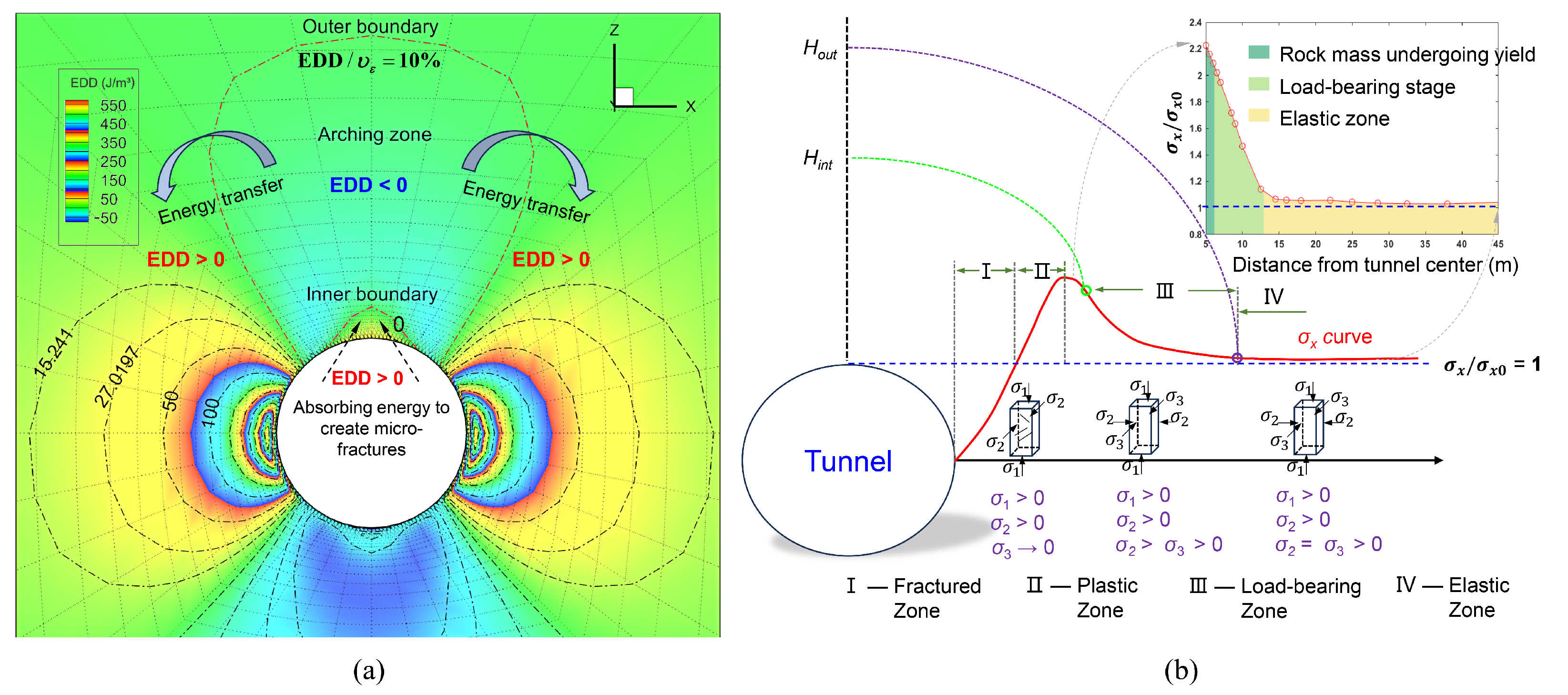
2.1. Relationship Between Surrounding Rock Energy Density and Pressure Arch
2.2. Numerical Implementation of the EDD Method for Tunnel-Surrounding Rock Mass
| Algorithm 1 Pseudocode for the EDD approach to determine pressure arch zone |
|
| Note: Tolerable unbalanced force and T are set to N and 6000, respectively, as a demonstration. |
2.3. Numerical Simulation Scheme
3. Assessment of Energy Density Field and Pressure Arch Zone in the Surrounding Rock of Circular Tunnels
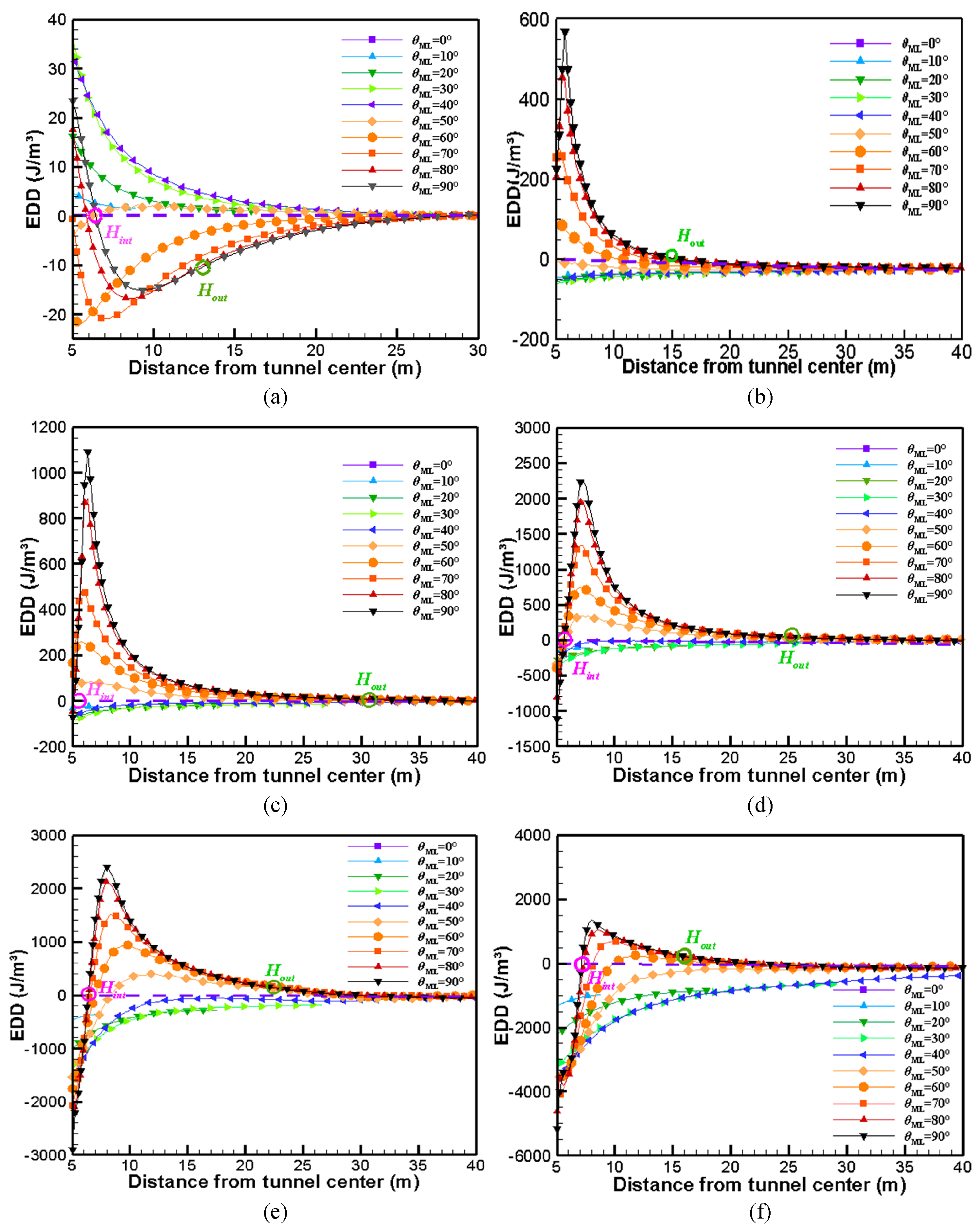
3.1. Effect of Tunnel Span
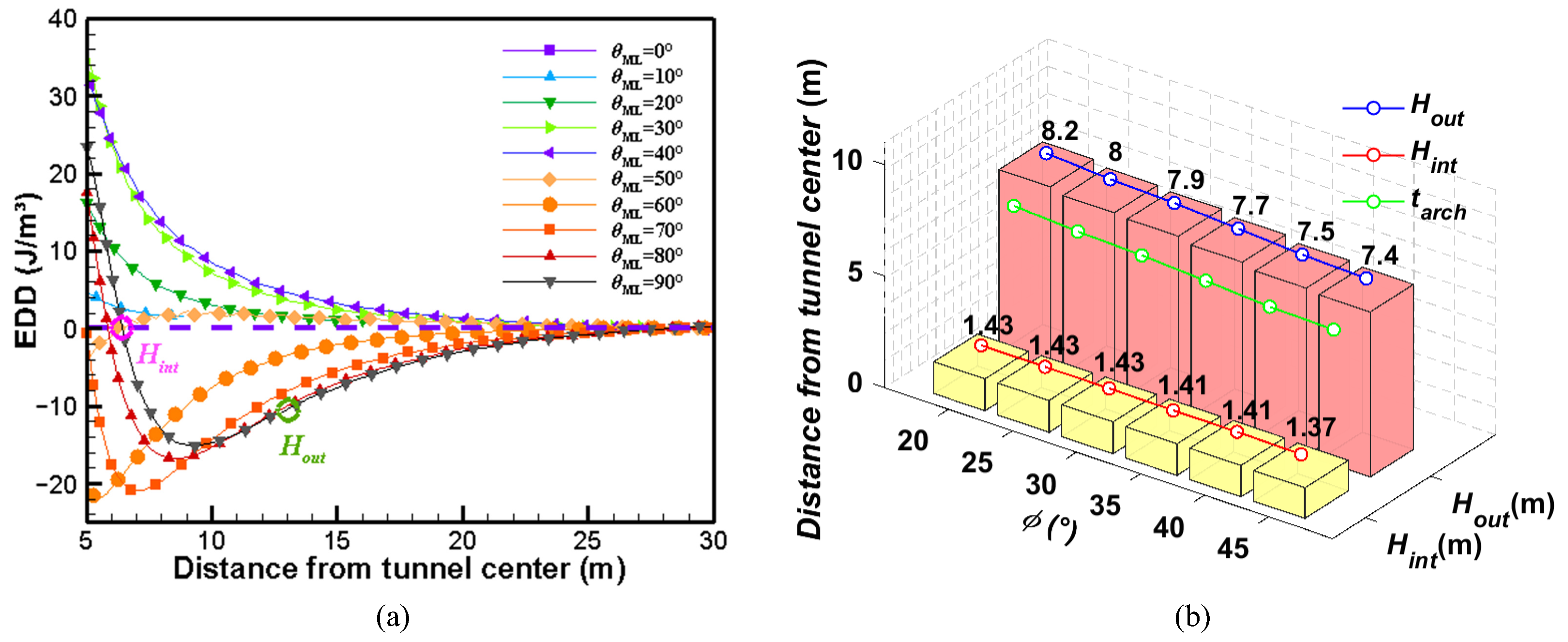
3.2. Effect of Internal Friction Angle of the Surrounding Rock
3.3. Effect of Lateral Pressure Coefficient
4. Discussion
4.1. Comparison with Pressure Arch Discrimination Method Based on Tangential Stress of Surrounding Rock
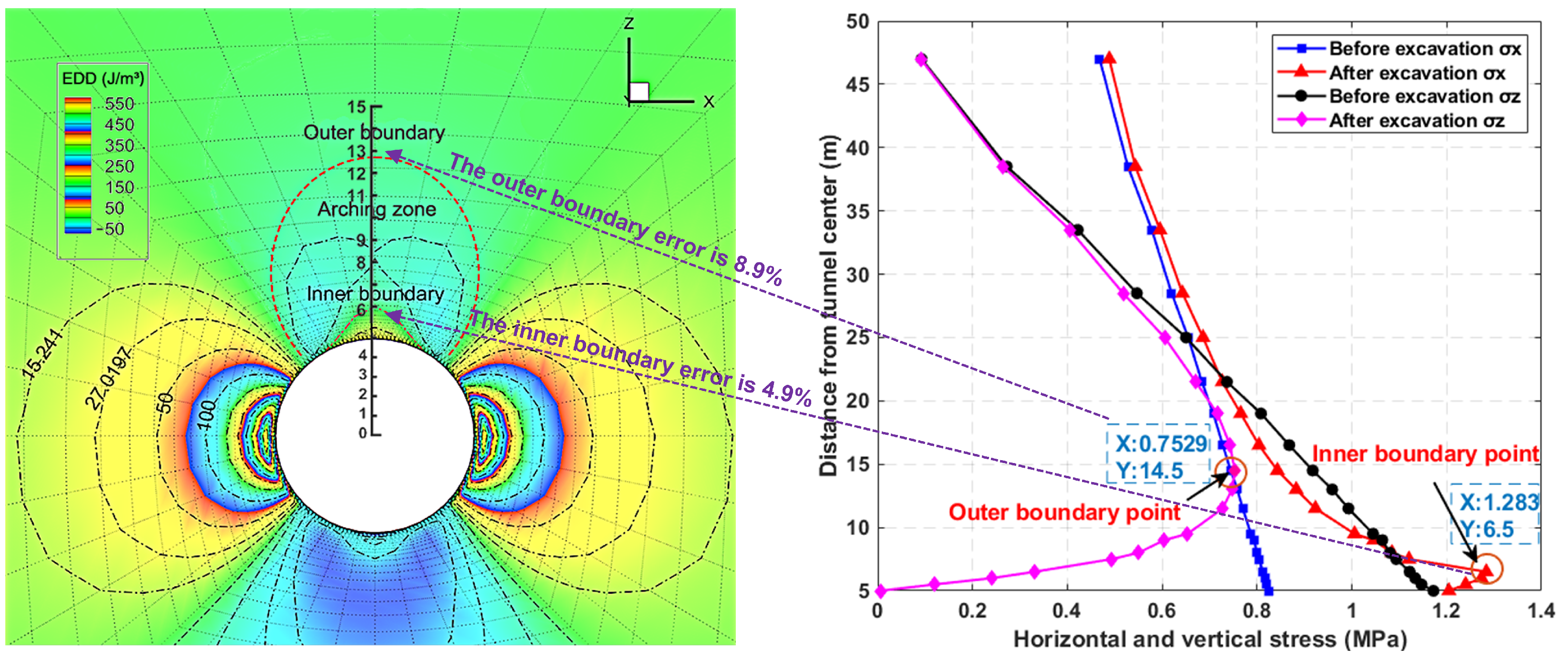
4.2. Comparison with Pressure Arch Discrimination Methods Based on Inflection Points of Principal Stress–Depth Curves
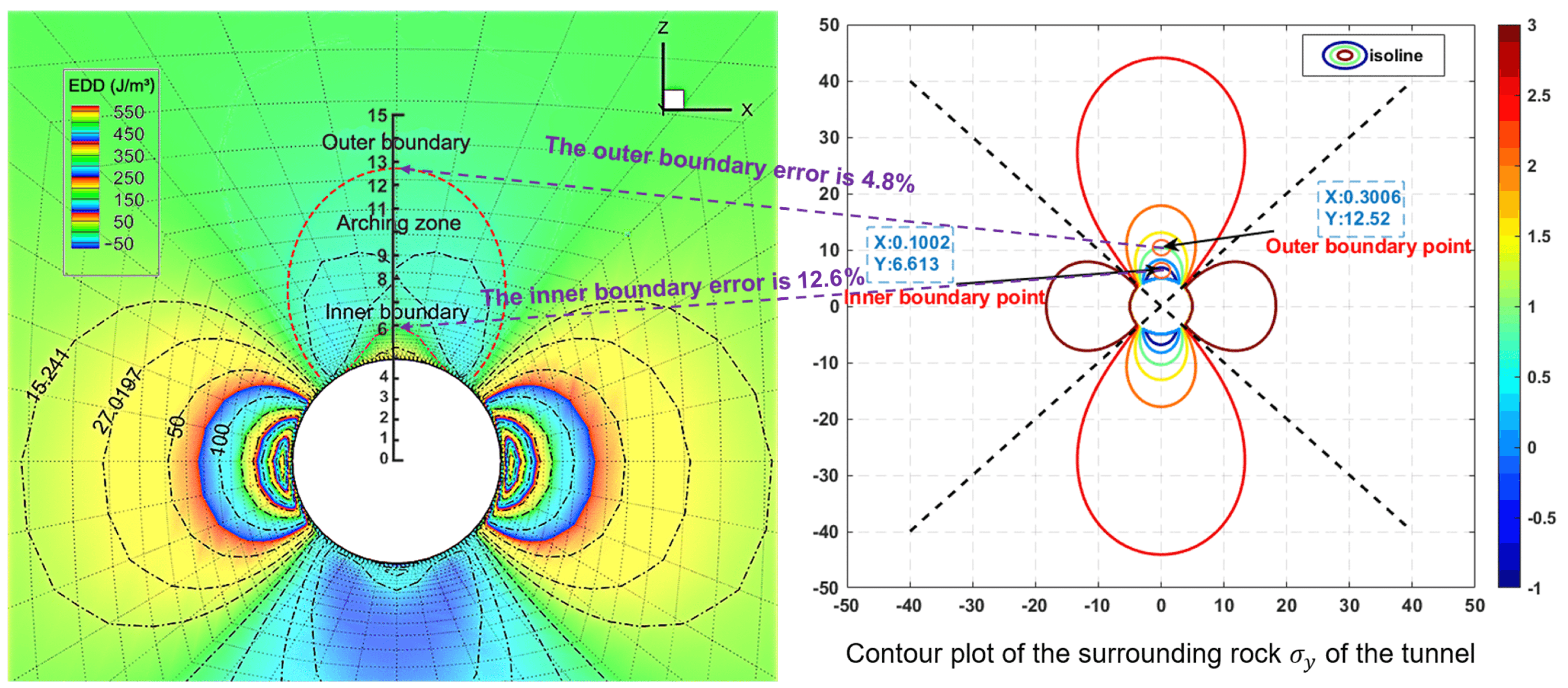
4.3. Comparison with the Pressure Arch Determination Method Based on the Contour Lines of Vertical Stress in Surrounding Rock
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akl, S.A.; Metwally, K.G. Optimizing arching creation for Abou Muharik Tunnel in Egypt using numerical analysis. KSCE J. Civ. Eng. 2017, 21, 160–167. [Google Scholar] [CrossRef]
- Bi, Z.; Gong, Q.; Guo, P.; Cheng, Q. Experimental study of the evolution of soil arching effect under cyclic loading based on trapdoor test and particle image velocimetry. Can. Geotech. J. 2019, 57, 903–920. [Google Scholar] [CrossRef]
- George, T.I.; Dasaka, S.M. Mechanics of arch action in soil arching. Acta Geotech. 2022, 18, 1991–2009. [Google Scholar] [CrossRef]
- Khosravi, M.H.; Sarfaraz, H.; Pipatpongsa, T.; Sharifdeljuyi, A. Active Earth Pressure Distribution inside Narrow Backfill Considering Soil-Arching Effect. Int. J. Geomech. 2022, 22, 06022013. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley and Sons: New York, NY, USA, 1943. [Google Scholar]
- Khatami, H.; Deng, A.; Jaksa, M. The arching effect in rubber–sand mixtures. Geosynth. Int. 2020, 27, 432–450. [Google Scholar] [CrossRef]
- Tangjarusritaratorn, T.; Miyazaki, Y.; Sawamura, Y.; Kishida, K.; Kimura, M. Numerical investigation on arching effect surrounding deep cylindrical shaft during excavation process. Undergr. Space 2022, 7, 944–965. [Google Scholar] [CrossRef]
- Khandouzi, G.; Khosravi, M.H. An analytical investigation of soil arching induced by tunneling in sandy ground. Tunn. Undergr. Space Technol. 2023, 140, 105242. [Google Scholar] [CrossRef]
- Sadrekarimi, J.; Abbasnejad, A. Arching effect in fine sand due to base yielding. Can. Geotech. J. 2010, 47, 366–374. [Google Scholar] [CrossRef]
- Iglesia, G.R.; Einstein, H.H.; Whitman, R.V. Investigation of Soil Arching with Centrifuge Tests. J. Geotech. Geoenviron. Eng. 2014, 140, 04013005. [Google Scholar] [CrossRef]
- Franza, A. Tunneling and Its Effects on Piles and Piled Structures. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2016. [Google Scholar]
- Park, J.J.; Cho, I.S.; Lee, I.M.; Lee, S.W. Tunnel reinforcement by using pressure-induced inflatable pipes method. J. Geotech. Geoenviron. Eng. 2012, 138, 1483–1491. [Google Scholar] [CrossRef]
- Lee, J.S.; Sagong, M.; Park, J.; Choi, I.Y. Experimental analysis of penetration grouting in umbrella arch method for tunnel reinforcement. Int. J. Rock Mech. Min. Sci. 2020, 130, 104346. [Google Scholar] [CrossRef]
- Morovatdar, A.; Palassi, M.; Ashtiani, R.S. Effect of pipe characteristics in umbrella arch method on controlling tunneling-induced settlements in soft grounds. J. Rock Mech. Geotech. Eng. 2020, 12, 984–1000. [Google Scholar] [CrossRef]
- He, L.; Zhang, Q. Numerical investigation of arching mechanism to underground excavation in jointed rock mass. Tunn. Undergr. Space Technol. 2015, 50, 54–67. [Google Scholar] [CrossRef]
- Li, T.; Zhang, Z.; Luo, M.; Liu, B.; Wang, Y.; Li, L. Analytical Solution of Loosening Pressure Model for Shallow Tunnel Based on Pile-Beam-Arch Method. KSCE J. Civ. Eng. 2022, 26, 3648–3662. [Google Scholar] [CrossRef]
- Cui, X.; Li, P.; Wu, J.; Wei, Y. Stability analysis of a shield tunnel in unsaturated soil considering the soil arch effect. Int. J. Geomech. 2024, 24, 04024041. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Z. Stress arch bunch and its formation mechanism in blocky stratified rock masses. J. Rock Mech. Geotech. Eng. 2012, 4, 19–27. [Google Scholar] [CrossRef]
- Xia, B.; Zhang, X.; Yu, B.; Jia, J. Weakening effects of hydraulic fracture in hard roof under the influence of stress arch. Int. J. Min. Sci. Technol. 2018, 28, 951–958. [Google Scholar] [CrossRef]
- Huang, X.; Ruan, H.; Shi, C.; Kong, Y. Numerical simulation of stress arching effect in horizontally layered jointed rock mass. Symmetry 2021, 13, 1138. [Google Scholar] [CrossRef]
- He, J.; Liao, S.; Liu, M.; Sun, J.; Xi, X. The soil arching effect induced by shield tunnelling under asymmetric surface loading. Comput. Geotech. 2023, 154, 105145. [Google Scholar] [CrossRef]
- Li, R.; Zhang, D.; Song, Y.; Li, A.; Luo, J. Pressure Arch Effect of Deeply Buried Symmetrically Distributed Triple Tunnels. Symmetry 2023, 15, 673. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Y.; Liang, C.; Zhu, Z. Experimental and theoretical study on the stratum cavity collapse induced by water and sand leakage in subway tunnels. Int. J. Geomech. 2024, 24, 04024079. [Google Scholar] [CrossRef]
- Fu, H.L.; Zhang, J.B.; Chen, W.; Huang, Z.; Yuan, W. Study on the range of pressure arch of surrounding rock in deeply buried circular karst tunnels. J. Hunan Univ. Nat. Sci. 2008, 45, 117–124. [Google Scholar]
- Kong, X.; Liu, Q.; Zhang, Q.; Wu, Y.; Zhao, J. A method to estimate the pressure arch formation above underground excavation in rock mass. Tunn. Undergr. Space Technol. 2018, 71, 382–390. [Google Scholar] [CrossRef]
- Zheng, K.; Ding, W.; Jin, W. Formation law of pressure arch in circular tunnel by TBM based on model test and FEM. J. China Coal Soc. 2015, 40, 1270–1275. [Google Scholar]
- Yang, J.; Wang, S.; Li, C. Analysis of arching mechanism and evolution characteristics of tunnel pressure arch. Jordan J. Civ. Eng. 2015, 9, 125–132. [Google Scholar]
- Huang, Z.; Broch, E.; Lu, M. Cavern roof stability—Mechanism of arching and stabilization by rockbolting. Tunn. Undergr. Space Technol. 2002, 17, 249–261. [Google Scholar] [CrossRef]
- Chen, C.N.; Huang, W.Y.; Tseng, C.T. Stress redistribution and ground arch development during tunneling. Tunn. Undergr. Space Technol. 2011, 26, 228–235. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, D.; Xu, T.; Chen, X. Formation estimation and evolution mechanism of the pressure arch for non-circular tunnels under asymmetrical stress field. Sci. China Technol. Sci. 2024, 67, 2919–2938. [Google Scholar] [CrossRef]
- Li, W.T.; Su, L.Y.; Yin, X.F.; Wang, K.; Li, Z.; Wang, L.Y.; Mei, Y.C.; Zeng, Z.N. A new evaluating approach for pressure arch stability of the surrounding rock in a shallow-buried rock tunnel. Phys. Fluids 2025, 37, 087202. [Google Scholar] [CrossRef]
- Zhang, C.; Ren, Z.; He, J.; Ma, J. Model of overburden pressure arch in mining areas considering thick-hard rock layer and application. China Min. Mag. 2025, 34, 113–124. [Google Scholar] [CrossRef]
- Lee, C.; Wu, B.; Chen, H.; Chiang, K. Tunnel stability and arching effects during tunneling in soft clayey soil. Tunn. Undergr. Space Technol. 2006, 21, 119–132. [Google Scholar] [CrossRef]
- Kong, X.X.; Liu, Q.S.; Pan, Y.C.; Liu, J.P. Stress redistribution and formation of the pressure arch above underground excavation in rock mass. Eur. J. Environ. Civ. Eng. 2021, 25, 722–736. [Google Scholar] [CrossRef]
- Wang, S.; Wu, X.; Zhao, Y.; Hagan, P. Mechanical performances of pressure arch in thick bedrock during shallow coal mining. Geofluids 2018, 2018, 2419659. [Google Scholar] [CrossRef]
- Qiu, S.; Han, Y.; Wang, B.; Nie, X.; Zhang, Z.; He, J.; Lyu, L.; Wang, X.; Tang, K. Calculation method of shield tunnel displacement in the case of pit excavation and in-tunnel loading. China Min. Mag. 2024, 33, 179–185. [Google Scholar]
- An, F.H.; Cheng, Y.P.; Wang, L.; Li, W. A numerical model for outburst including the effect of adsorbed gas on coal deformation and mechanical properties. Comput. Geotech. 2013, 54, 222–231. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Hagan, P.C.; Guo, W. Evolution characteristics of pressure-arch and elastic energy during shallow horizontal coal mining. Teh. Vjesn.-Tech. Gaz. 2018, 25, 867–875. [Google Scholar] [CrossRef]
- Lin, X.T.; Chen, R.P.; Wu, H.N.; Meng, F.Y.; Su, D.; Han, K. Calculation of earth pressure distribution on the deep circular tunnel considering stress-transfer mechanisms in different zones. Tunn. Undergr. Space Technol. 2022, 119, 104211. [Google Scholar] [CrossRef]
- Wu, J.H.; Ohnishi, Y.; Nishiyama, S. Simulation of the mechanical behavior of inclined jointed rock masses during tunnel construction using Discontinuous Deformation Analysis (DDA). Int. J. Rock Mech. Min. Sci. 2004, 41, 731–743. [Google Scholar] [CrossRef]
- Shariatmadari, N.; Mahdi, M. Back analysis of Tehran Metro Tunnel construction using FLAC-3D. In Proceedings of the International Geotechnical Conference, Moscow, Russia, 7–10 June 2010; pp. 97–106. [Google Scholar]
- Tang, Z.; Wu, Z.; Jia, D.; Lv, J. The distribution law of ground stress field in Yingcheng Coal Mine based on Rhino surface modeling. Processes 2024, 12, 668. [Google Scholar] [CrossRef]
- Huang, X.; Jin, J.; Tong, Y.; Mei, G. Evolution of 3D stress arch in surrounding rock during segmented excavation of a circular tunnel. Geotech. Geol. Eng. 2025, 43. [Google Scholar] [CrossRef]
- Li, K. Pressure Arch Theory Study of Horizontal Bedded Tunnel Surrounding Rock. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2010. [Google Scholar]
- Lv, Y.; Liang, G.; Lu, L.; Lin, S.; Wu, X.C.; Li, D. Analytical study on the pressure arch range of surrounding rock in circular tunnel. West China Explor. Eng. 2022, 28, 165–169. [Google Scholar]
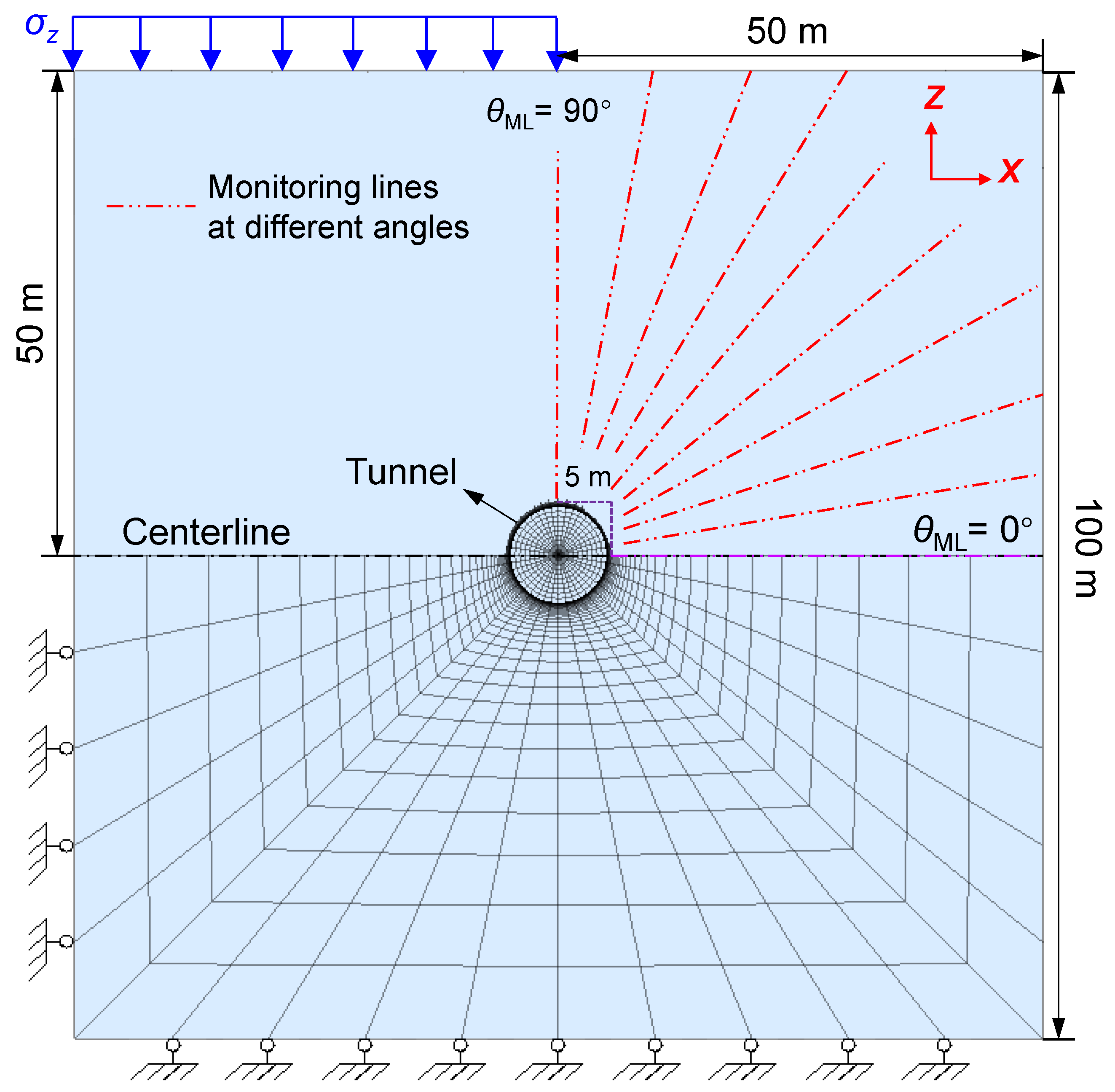

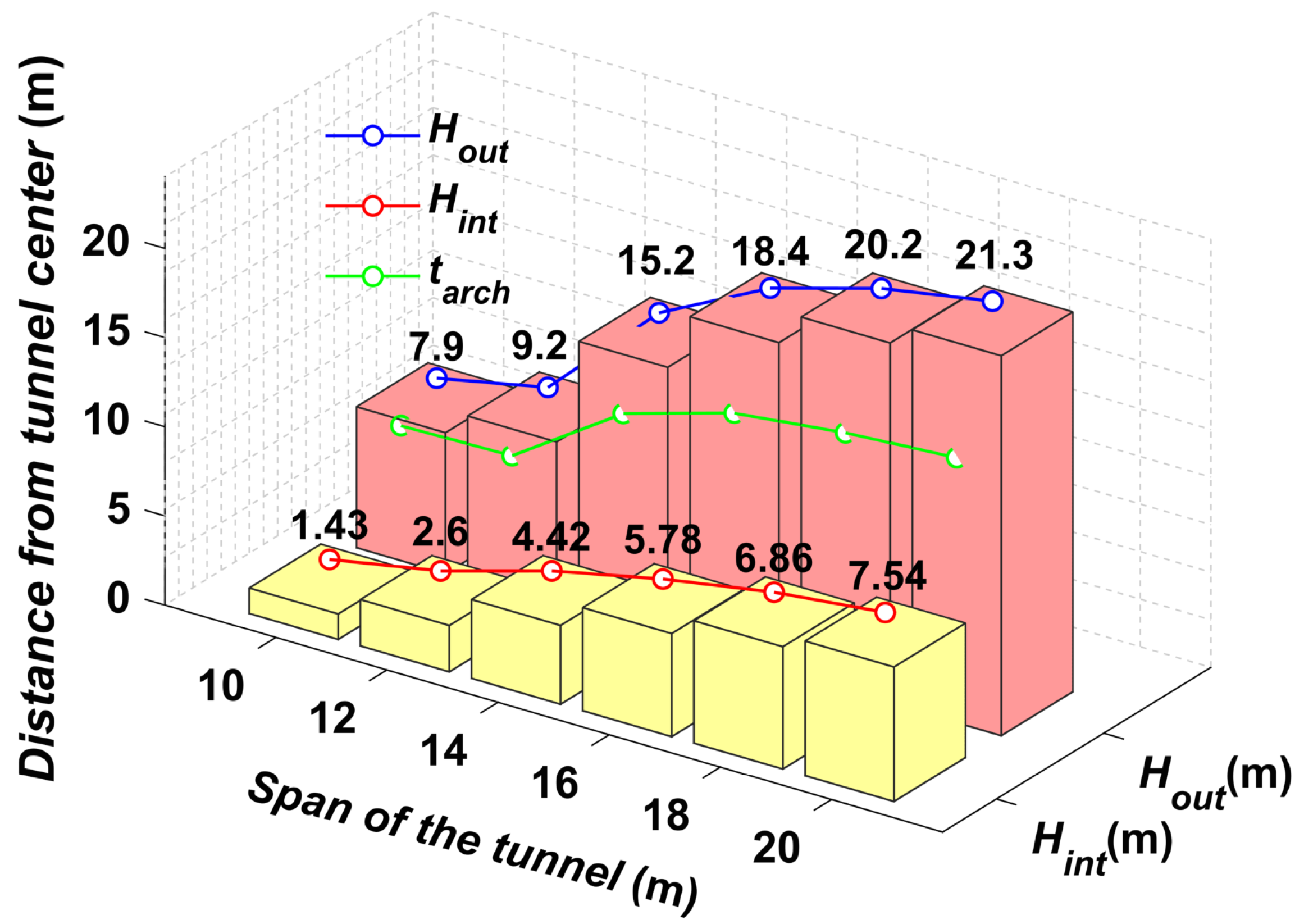



| Series | Case | D (m) | (°) | |
|---|---|---|---|---|
| A | A1 | 10 | 30 | 0.5 |
| A2 | 12 | |||
| A3 | 14 | |||
| A4 | 16 | |||
| A5 | 18 | |||
| A6 | 20 | |||
| B | B1 | 10 | 20 | 0.5 |
| B2 | 25 | |||
| B3 | 30 | |||
| B4 | 35 | |||
| B5 | 40 | |||
| B6 | 45 | |||
| C | C1 | 10 | 30 | 0.5 |
| C2 | 0.8 | |||
| C3 | 1.0 | |||
| C4 | 1.5 | |||
| C5 | 2.0 | |||
| C6 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Li, S.; Yu, Y.; Yu, Z. Estimation of Tunnel Pressure Arch Zone Based on Energy Density Difference of Surrounding Rock. Appl. Sci. 2025, 15, 10990. https://doi.org/10.3390/app152010990
Huang X, Li S, Yu Y, Yu Z. Estimation of Tunnel Pressure Arch Zone Based on Energy Density Difference of Surrounding Rock. Applied Sciences. 2025; 15(20):10990. https://doi.org/10.3390/app152010990
Chicago/Turabian StyleHuang, Xiao, Siyuan Li, Yicong Yu, and Zetao Yu. 2025. "Estimation of Tunnel Pressure Arch Zone Based on Energy Density Difference of Surrounding Rock" Applied Sciences 15, no. 20: 10990. https://doi.org/10.3390/app152010990
APA StyleHuang, X., Li, S., Yu, Y., & Yu, Z. (2025). Estimation of Tunnel Pressure Arch Zone Based on Energy Density Difference of Surrounding Rock. Applied Sciences, 15(20), 10990. https://doi.org/10.3390/app152010990







