Deep Learning for Predicting Surface Elevation Change in Tailings Storage Facilities from UAV-Derived DEMs
Abstract
1. Introduction
2. State of the Art
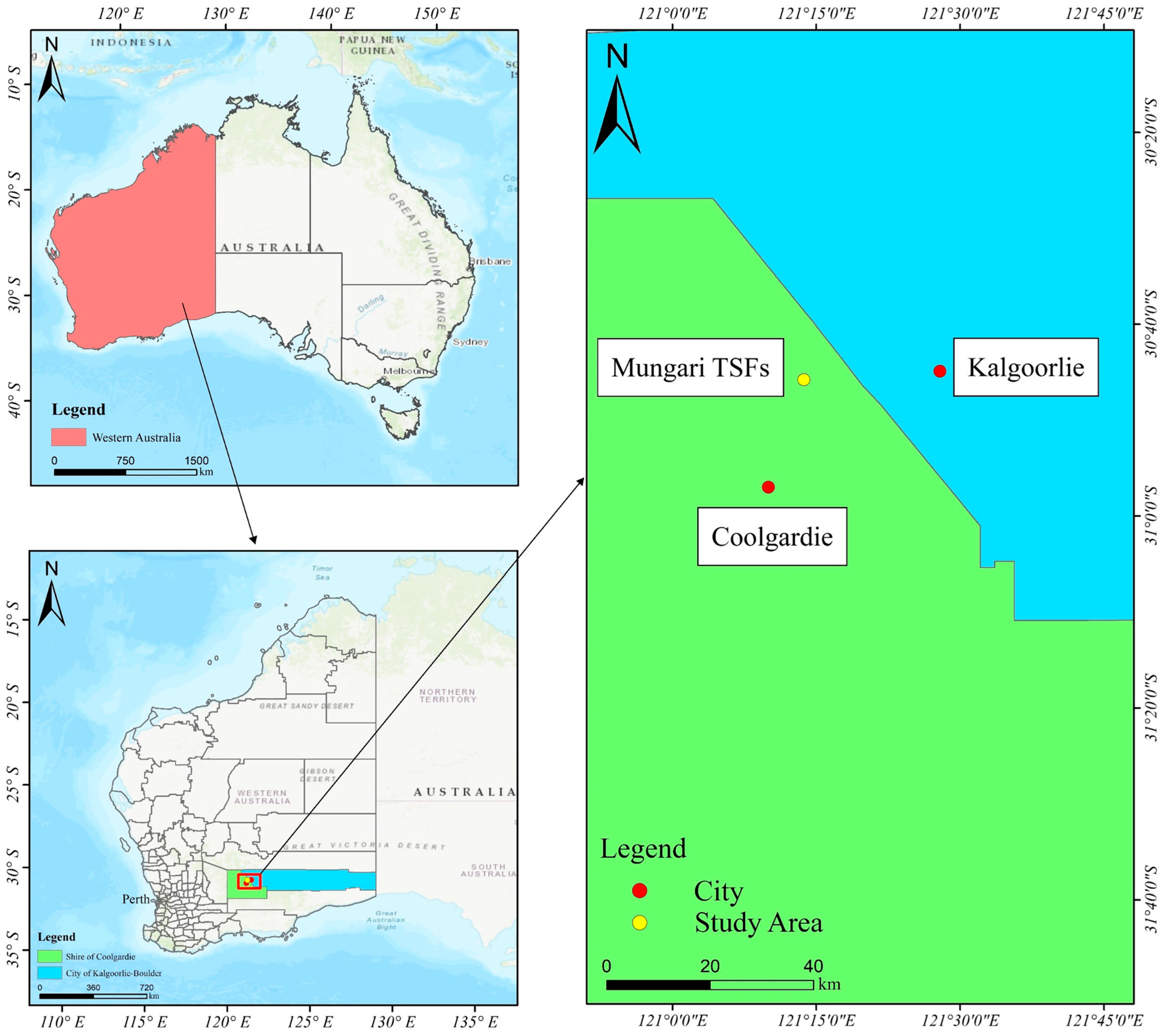
3. Study Area
4. Materials and Methods
4.1. Data Acquisition and Preprocessing
4.2. DEM of Difference
4.3. Terrian Factors
4.4. Dataset Partitioning and Spatial Configuration
4.5. Deep Learning (DL) Algorithms
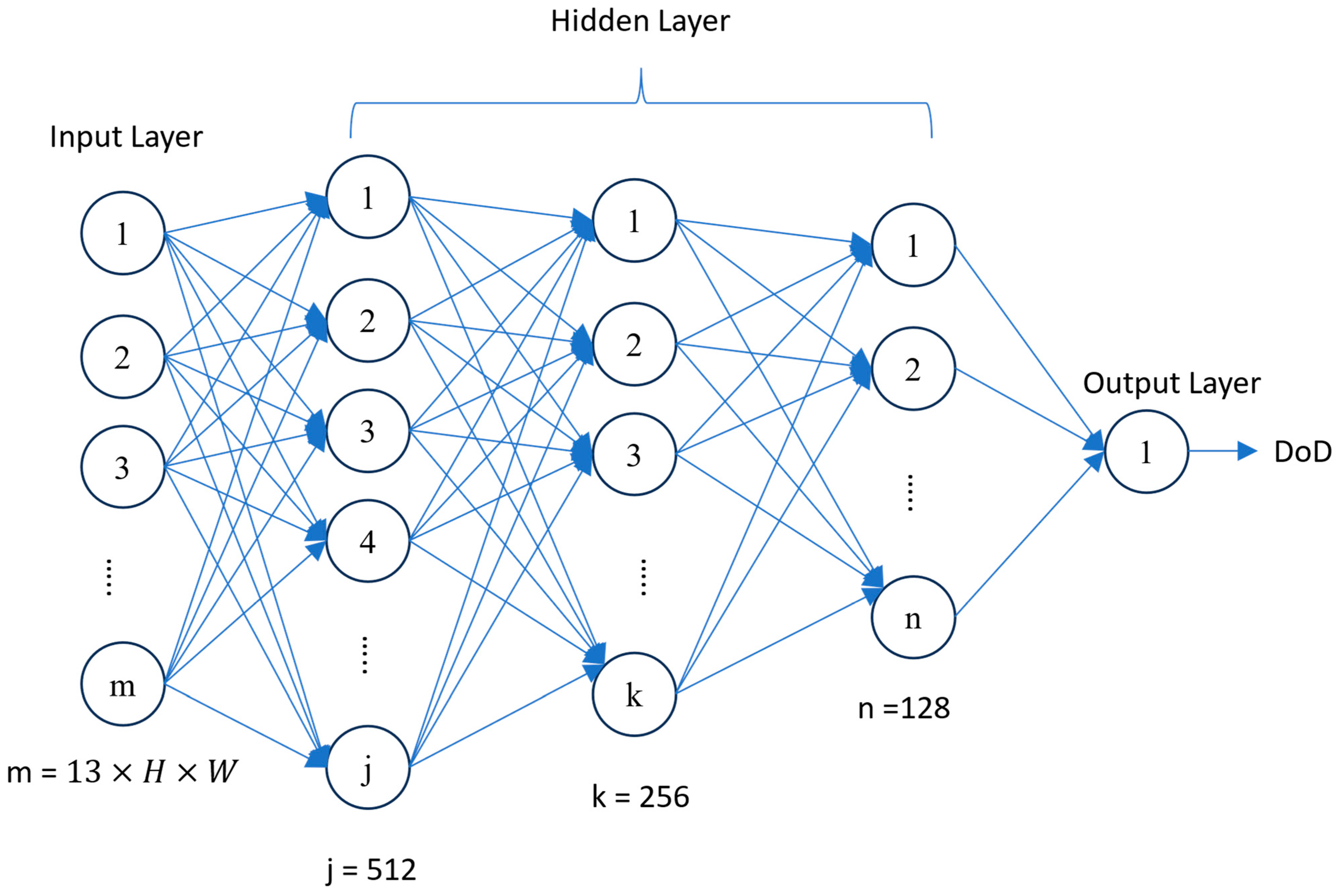
4.5.1. Multilayer Perceptron (MLP)
4.5.2. Fully Convolutional Network (FCN)
4.5.3. Residual Network (ResNet)
4.6. Evaluation Metrics
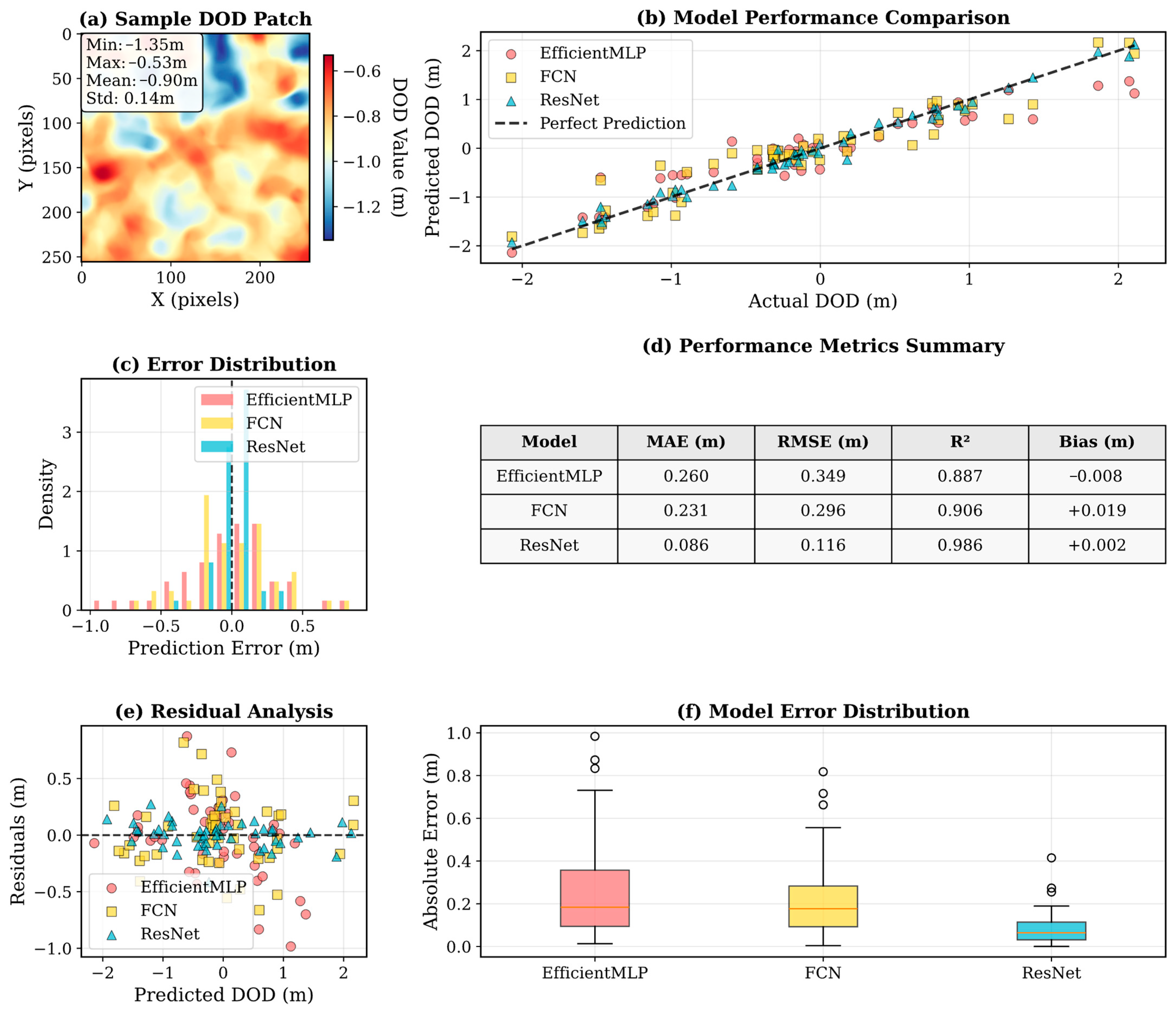
5. Results
5.1. Prediction Model
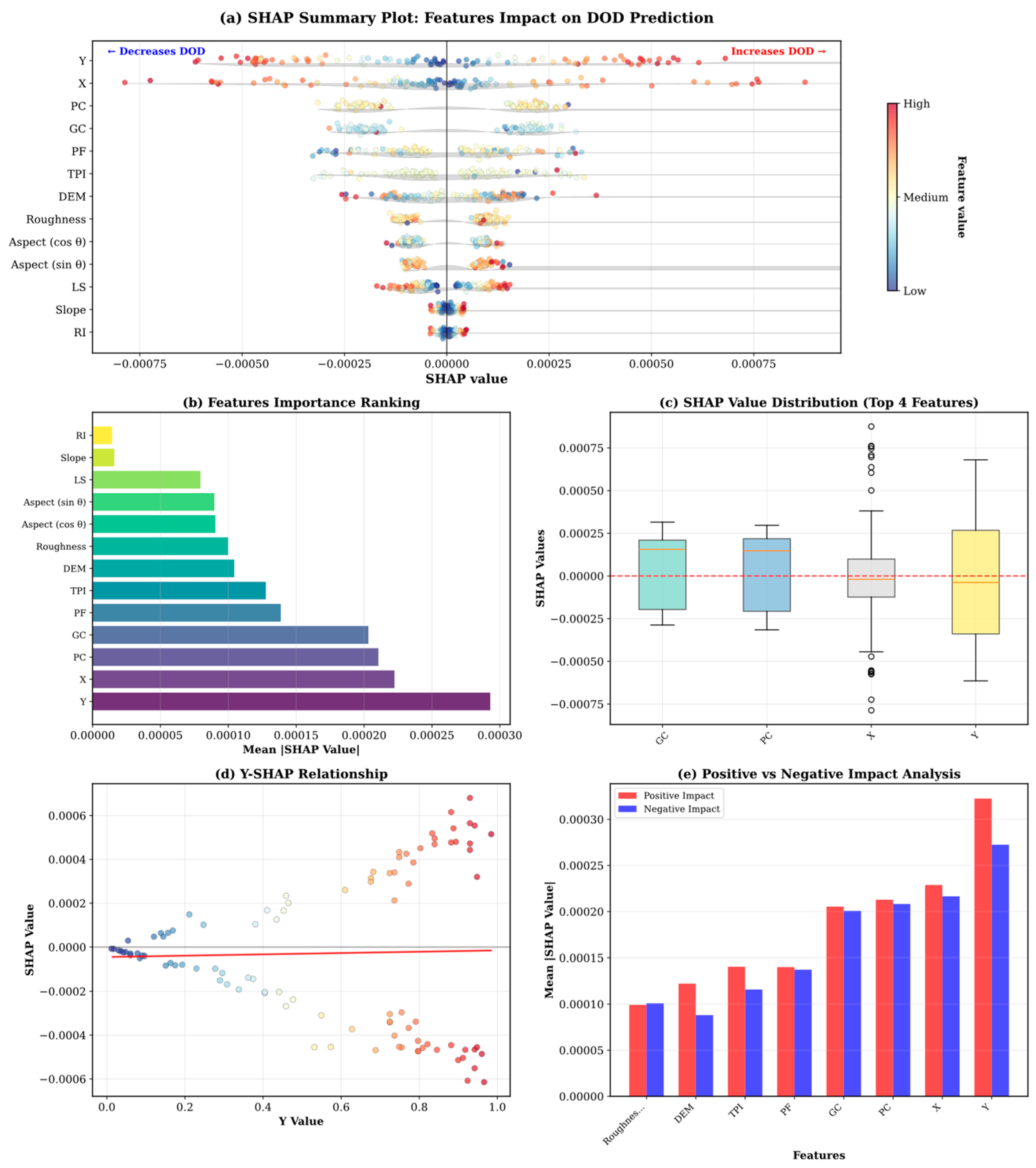
5.2. Model Interpretability Based on SHAP
6. Discussion
6.1. Interpretation of Dominant Factors on Tailings Deposition
6.2. Significance of DL for Predictive Geomorphic Modeling
6.3. Practical Implications for TSF Management
6.4. Limitations and Future Direction
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- CSP2. TSF Failures from 1915. Available online: http://www.csp2.org/tsf-failures-from-1915 (accessed on 5 June 2025).
- ICOLD. World Register of Dams. Available online: https://www.icold-cigb.org/ (accessed on 5 June 2025).
- Chambers, D.M.; Higman, B. Long Term Risks of Tailings Dam Failure; Center for Science in Public Participation: Bozeman, MT, USA, 2011; pp. 1–21. [Google Scholar]
- Chambers, D.M. The Increasing Number of Tailings Facility Failures: Navigating the Decade 2020–2029; Canadian Dam Association Annual Congress: Ottawa, ON, USA, 2019. [Google Scholar]
- Rotta, L.H.S.; Alcântara, E.; Park, E.; Negri, R.G.; Lin, Y.N.; Bernardo, N.; Mendes, T.S.G.; Souza Filho, C.R. The 2019 Brumadinho tailings dam collapse: Possible cause and impacts of the worst human and environmental disaster in Brazil. Int. J. Appl. Earth Obs. Geoinf. 2020, 90, 102119. [Google Scholar] [CrossRef]
- Bussular, C.Z.; Burtet, C.G.; Antonello, C.S. The actor-network theory as a method in the analysis of Samarco disaster in Brazil. Qual. Res. Organ. Manag. Int. J. 2020, 15, 176–191. [Google Scholar] [CrossRef]
- Department of Industry, Science and Resources, Australia. Tailings Management Handbooks. Available online: https://www.industry.gov.au/publications/leading-practice-handbooks-sustainable-mining/tailings-management (accessed on 5 June 2025).
- International Council on Mining and Metals (ICMM); United Nations Environment Programme (UNEP); Principles for Responsible Investment (PRI). Global Industry Standard on Tailings Management. Available online: https://globaltailingsreview.org/ (accessed on 5 June 2025).
- Mining Association of Canada. A Guide to the Management of Tailings Facilities, Third Edition. Available online: https://mining.ca/resources/guides-manuals/a-guide-to-the-management-of-tailings-facilities-third-edition/ (accessed on 5 June 2025).
- Obermeyer, J.; Alexieva, T. Design, Construction and Operation of a Large Centerline Tailing Storage Facility with High Rate of Rise. 2011. Available online: https://open.library.ubc.ca/soa/cIRcle/collections/59368/items/1.0107726 (accessed on 29 August 2025).
- Simms, P.; Williams, M.P.A.; Fitton, T.G.; McPhail, G. Beaching angles and evolution of stack geomoetry for thickened tailings—A review. In Paste 2011: 14th International Seminar on Paste and Thickened Tailings; Australian Centre for Geomechanics: Perth, Australia, 2011; pp. 323–338. [Google Scholar]
- Fitton, T.G.; Chryss, A.G.; Bhattacharya, S.N. Tailings beach slope prediction: A new rheological method. Int. J. Min. Reclam. Environ. 2006, 20, 181–202. [Google Scholar] [CrossRef]
- Li, A.L. Prediction of tailings beach slopes and tailings flow profiles. In Paste 2011: Proceedings of the 14th International Seminar on Paste and Thickened Tailings; Jewell, R., Fourie, A.B., Eds.; Australian Centre for Geomechanics: Perth, Australia, 2011; pp. 307–322. [Google Scholar] [CrossRef]
- Adamo, N.; Al-Ansari, N.; Sissakian, V.; Laue, J.; Knutsson, S. Dam Safety: Monitoring of Tailings Dams and Safety Reviews. J. Earth Sci. Geotech. Eng. 2021, 11, 249–289. [Google Scholar] [CrossRef]
- Adiansyah, J.S.; Rosano, M.; Vink, S.; Keir, G. A framework for a sustainable approach to mine tailings management: Disposal strategies. J. Clean. Prod. 2015, 108, 1050–1062. [Google Scholar] [CrossRef]
- Le Borgne, V.; Siamaki, A.; Dulmage, A. Review of Modern Recommendations for Monitoring of Tailings Storage Facilities. In Proceedings of the Tailings and Mine Waste Conference, Denver, CO, USA, 6–9 November 2022; pp. 578–587. [Google Scholar]
- Nan, X.; Liu, X.; Wu, B.; Zhang, H.; Song, K.; Wang, X. Coupled CFD-DEM simulation and experimental study of particle distribution and accumulation during tailings seepage process. J. Clean. Prod. 2023, 427, 139229. [Google Scholar] [CrossRef]
- Gao, J.; Fourie, A. Studies on thickened tailings deposition in flume tests using the computational fluid dynamics (CFD) method. Can. Geotech. J. 2018, 56, 249–262. [Google Scholar] [CrossRef]
- Islam, S.; Williams, D.J.; Llano-Serna, M.; Zhang, C.M. Settling, consolidation and shear strength behaviour of coal tailings slurry. Int. J. Min. Sci. Technol. 2020, 30, 849–857. [Google Scholar] [CrossRef]
- Tian, S.; He, Y.; Bai, R.; Chen, J.; Wang, G. Experimental study on consolidation and strength properties of tailings with different particle size distribution characteristics. Nat. Hazards 2022, 114, 3683–3699. [Google Scholar] [CrossRef]
- Jewell, R.J. Putting beach slope prediction into perspective. In Paste 2012: Proceedings of the 15th International Seminar on Paste and Thickened Tailings; Jewell, A.B.F.R., Paterson, A., Eds.; Australian Centre for Geomechanics: Perth, Australia, 2012; pp. 85–92. [Google Scholar] [CrossRef]
- Pirouz, B.; Williams, M. Prediction of non-segregating thickened tailings beach slopes–a new method. In Proceedings Tenth International Seminar on Paste and Thickened Tailings (Paste07); Fourie, A.B., Jewell, R.J., Eds.; Australian Centre for Geomechanics: Perth, Australia, 2007; pp. 13–15. [Google Scholar]
- Fortuna, J.; Waterhouse, J.; Chapman, P.; Gowan, M. Applying Practical Hydrogeology to Tailings Storage Facility Design and Management. Mine Water Environ. 2021, 40, 50–62. [Google Scholar] [CrossRef]
- Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Neal, A.L.; Mendoza, G.F.; Todd Walter, M. Incorporating variable source area hydrology into a curve-number-based watershed model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
- Balaniuk, R.; Isupova, O.; Reece, S. Mining and Tailings Dam Detection in Satellite Imagery Using Deep Learning. Sensors 2020, 20, 6936. [Google Scholar] [CrossRef]
- Bayaraa, M.; Sheil, B.; Rossi, C. Comparison of Insar and Numerical Modelling for Tailings Dam Monitoring the Cadia Failure, Australia. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 4–7. [Google Scholar]
- Cacciuttolo, C.; Cano, D. Spatial and Temporal Study of Supernatant Process Water Pond in Tailings Storage Facilities: Use of Remote Sensing Techniques for Preventing Mine Tailings Dam Failures. Sustainability 2023, 15, 4984. [Google Scholar] [CrossRef]
- Du, Z.; Ge, L.; Ng, A.H.-M.; Zhu, Q.; Horgan, F.G.; Zhang, Q. Risk assessment for tailings dams in Brumadinho of Brazil using InSAR time series approach. Sci. Total Environ. 2020, 717, 137125. [Google Scholar] [CrossRef]
- Thomas, A.; Edwards, S.J.; Engels, J.; McCormack, H.; Hopkins, V.; Holley, R. Earth observation data and satellite InSAR for the remote monitoring of tailings storage facilities: A case study of Cadia Mine, Australia. In Paste 2019: Proceedings of the 22nd International Conference on Paste, Thickened and Filtered Tailings; Paterson, A.J.C., Fourie, A.B., Reid, D., Eds.; Australian Centre for Geomechanics: Cape Town, South Africa, 2019; pp. 183–195. [Google Scholar] [CrossRef]
- NASA. Landsat Science and Data Access. Available online: https://landsat.gsfc.nasa.gov/ (accessed on 5 June 2025).
- Rana, N.M.; Delaney, K.B.; Evans, S.G.; Deane, E.; Small, A.; Adria, D.A.M.; McDougall, S.; Ghahramani, N.; Take, W.A. Application of Sentinel-1 InSAR to monitor tailings dams and predict geotechnical instability: Practical considerations based on case study insights. Bull. Eng. Geol. Environ. 2024, 83, 204. [Google Scholar] [CrossRef]
- Santosa, P.B. Evaluation of Satellite Image Correction Methods Caused by Differential Terrain Illumination. Forum Geogr. 2016, 30, 1. [Google Scholar] [CrossRef]
- Thangaswamy, S.S.; Kadarkarai, R.; Thangaswamy, S.R.R. Developing an efficient technique for satellite image denoising and resolution enhancement for improving classification accuracy. J. Electron. Imaging 2013, 22, 013013. [Google Scholar] [CrossRef]
- Rauhala, A.; Tuomela, A.; Davids, C.; Rossi, P.M. UAV Remote Sensing Surveillance of a Mine Tailings Impoundment in Sub-Arctic Conditions. Remote Sens. 2017, 9, 1318. [Google Scholar] [CrossRef]
- Wang, K.; Yang, P.; Hudson-Edwards, K.A.; Lyu, W.S.; Yang, C.; Jing, X.F. Integration of DSM and SPH to Model Tailings Dam Failure Run-Out Slurry Routing Across 3D Real Terrain. Water 2018, 10, 1087. [Google Scholar] [CrossRef]
- Gomez, J.A.; Kamran-Pishhesari, A.; Sattarvand, J. Automated Rill Erosion Detection in Tailing Dams Using UAV Imagery and Machine Learning. Arab. J. Sci. Eng. 2025, 50, 6711–6726. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Z.; Yang, X.; Wang, D.; Zhu, L.; Yuan, S. Enhanced Tailings Dam Beach Line Indicator Observation and Stability Numerical Analysis: An Approach Integrating UAV Photogrammetry and CNNs. Remote Sens. 2024, 16, 3264. [Google Scholar] [CrossRef]
- Niculiță, M.; Mărgărint, M.C.; Tarolli, P. Chapter 10—Using UAV and LiDAR data for gully geomorphic changes monitoring. Dev. Earth Surf. Process. 2020, 23, 271–315. [Google Scholar] [CrossRef]
- Xiang, J.; Chen, J.; Sofia, G.; Tian, Y.; Tarolli, P. Open-pit mine geomorphic changes analysis using multi-temporal UAV survey. Environ. Earth Sci. 2018, 77, 220. [Google Scholar] [CrossRef]
- Department of Mines Industry Regulation and Safety. Mining Proposal: Mungari TSF expansion: Cells 3 and 4 [Report Prepared by Talis Consultants]. Available online: https://minedex.dmirs.wa.gov.au/Web/sites/details/6f6f5c6b-099a-4801-a985-615940373990 (accessed on 5 June 2025).
- Boix-Fayos, C.; Martínez-Mena, M.; Arnau-Rosalén, E.; Calvo-Cases, A.; Castillo, V.; Albaladejo, J. Measuring soil erosion by field plots: Understanding the sources of variation. Earth-Sci. Rev. 2006, 78, 267–285. [Google Scholar] [CrossRef]
- Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for uncertainty in DEMs from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
- Li, Y.; Lu, X.; Washington-Allen, R.A.; Li, Y. Microtopographic Controls on Erosion and Deposition of a Rilled Hillslope in Eastern Tennessee, USA. Remote Sens. 2022, 14, 1315. [Google Scholar] [CrossRef]
- Abrahams, A.D.; Parsons, A.J. Resistance to Overland Flow on Desert Pavement and Its Implications for Sediment Transport Modeling. Water Resour. Res. 1991, 27, 1827–1836. [Google Scholar] [CrossRef]
- Darboux, F.; Huang, C.-H. Does Soil Surface Roughness Increase or Decrease Water and Particle Transfers? Soil Sci. Soc. Am. J. 2005, 69, 748–756. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. On the extraction of channel networks from digital elevation data. Hydrol. Process. 1991, 5, 81–100. [Google Scholar] [CrossRef]
- Shen, H.; Zheng, F.; Wen, L.; Lu, J.; Jiang, Y. An experimental study of rill erosion and morphology. Geomorphology 2015, 231, 193–201. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K. A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences 2015, 5, 117–126. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1200–1213. [Google Scholar] [CrossRef]
- Rosenblatt, F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms; Spartan Books: Washington, DC, USA, 1962; Volume 55. [Google Scholar]
- Zahnle, K.J. Photochemistry of methane and the formation of hydrocyanic acid (HCN) in the Earth’s early atmosphere. J. Geophys. Res. 1986, 91, 2819–2834. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Li, Y.; van Zyl, D. Analysing the segregation of coarse tailings particles with a zone-formation differential settling model. In Paste 2024: Proceedings of the 26th International Conference on Paste, Thickened and Filtered Tailings; Fourie, A.B., Reid, D., Eds.; Australian Centre for Geomechanics: Perth, Australia, 2024; pp. 271–282. [Google Scholar] [CrossRef]
- Sabzevari, T.; Talebi, A. Effect of hillslope topography on soil erosion and sediment yield using USLE model. Acta Geophys. 2019, 67, 1587–1597. [Google Scholar] [CrossRef]
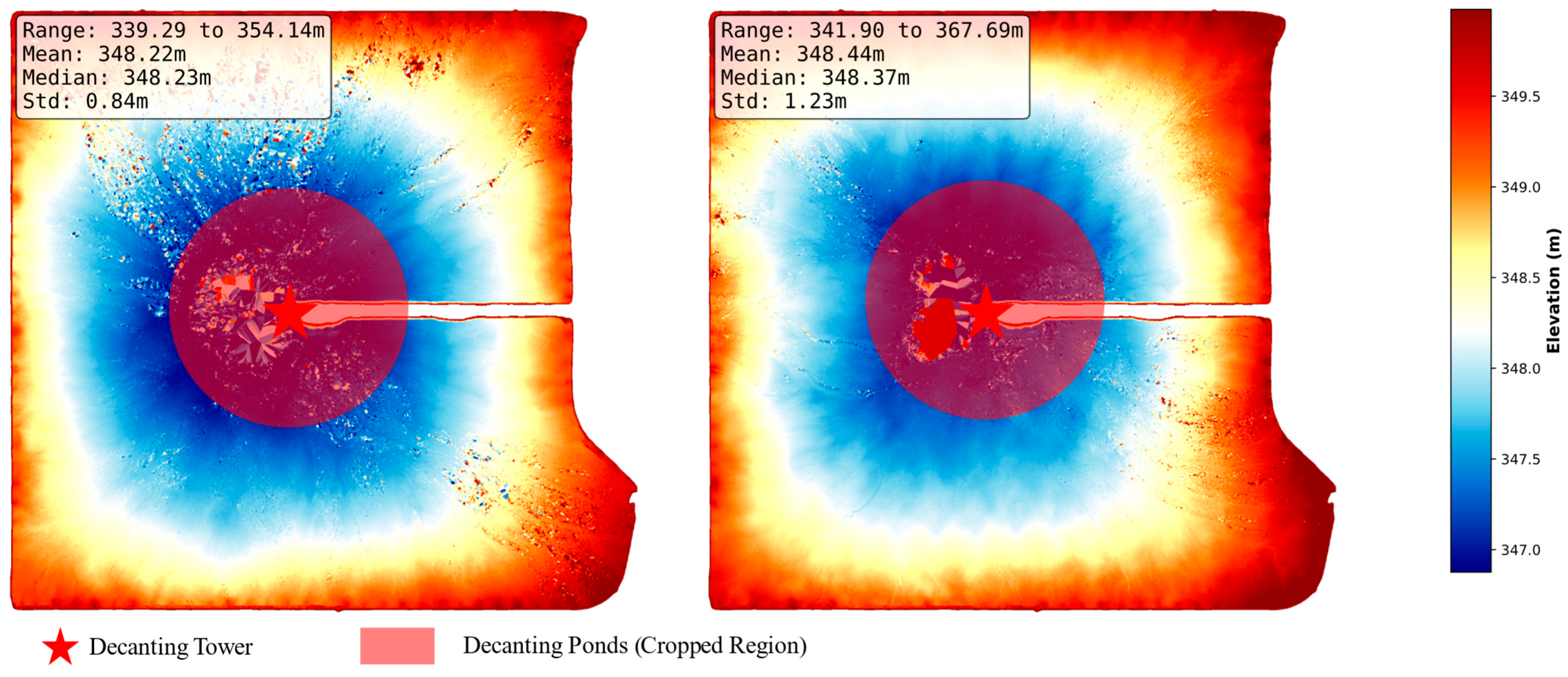
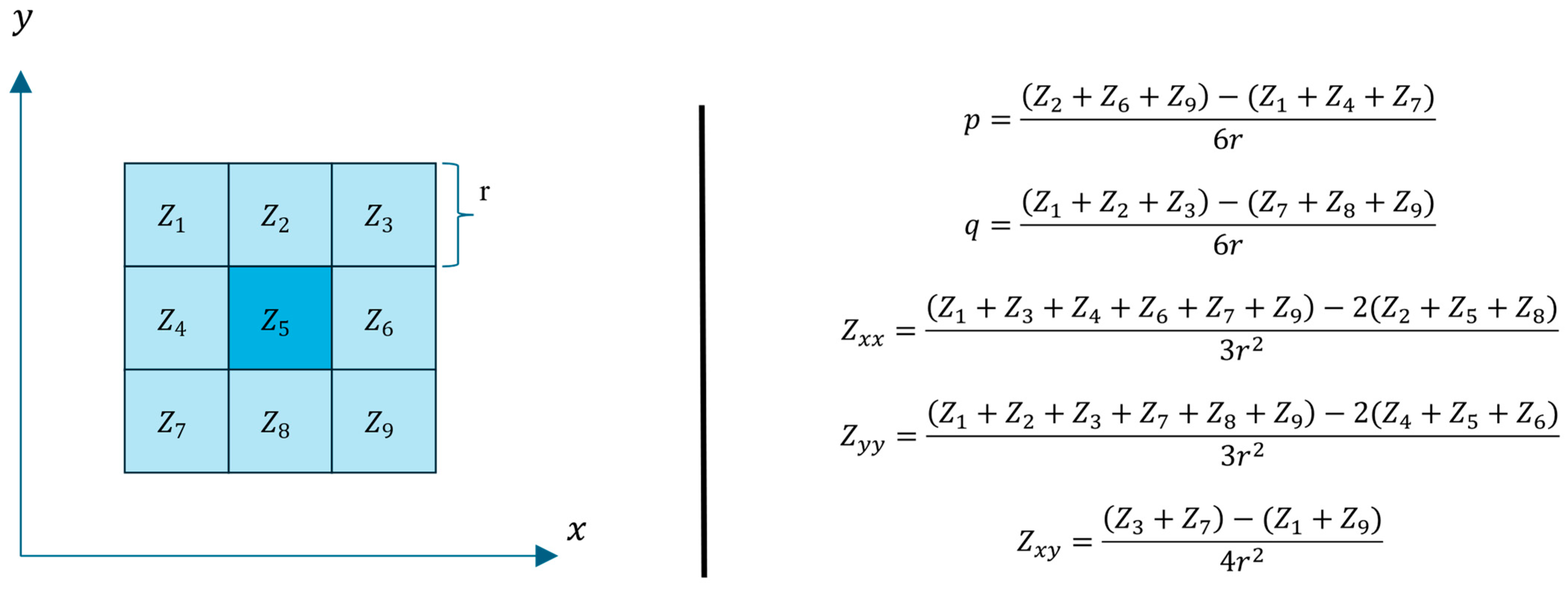
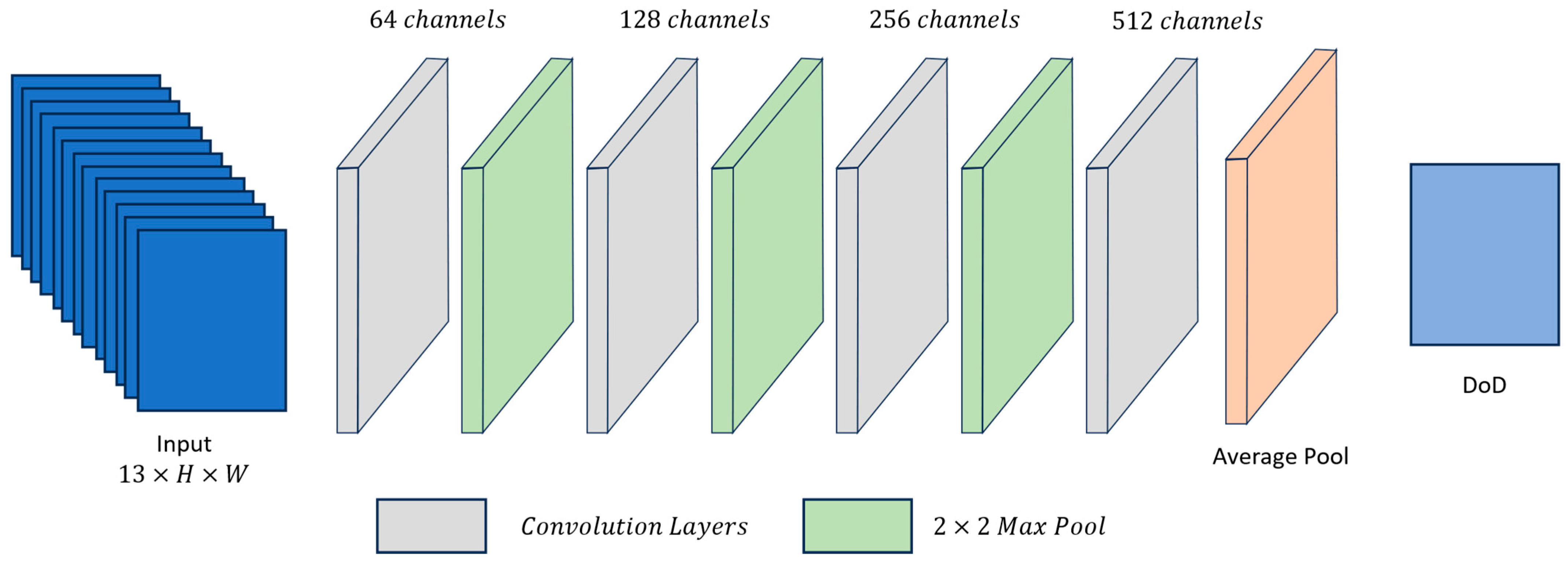
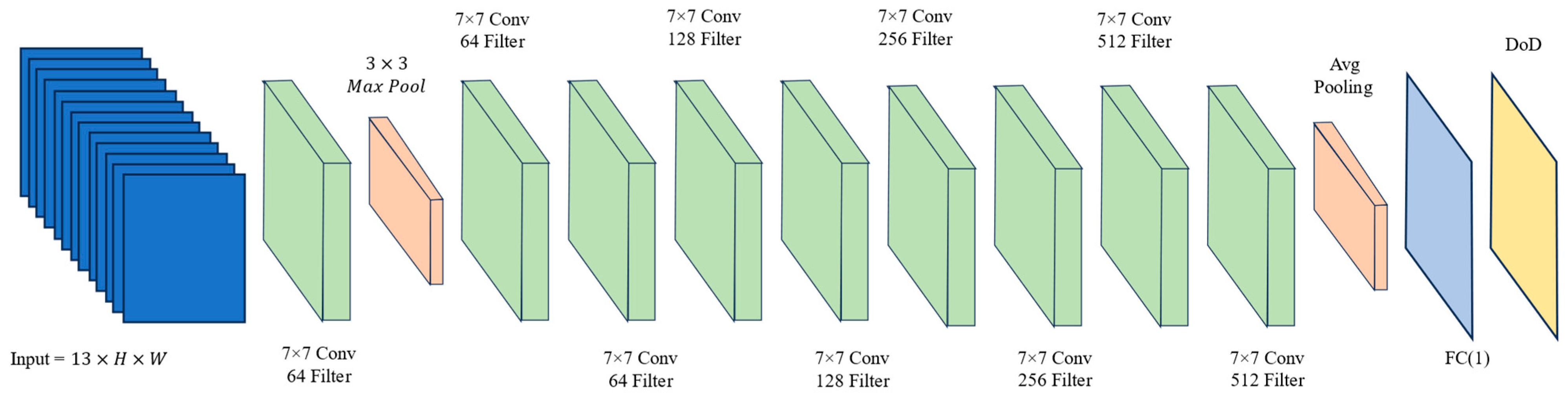
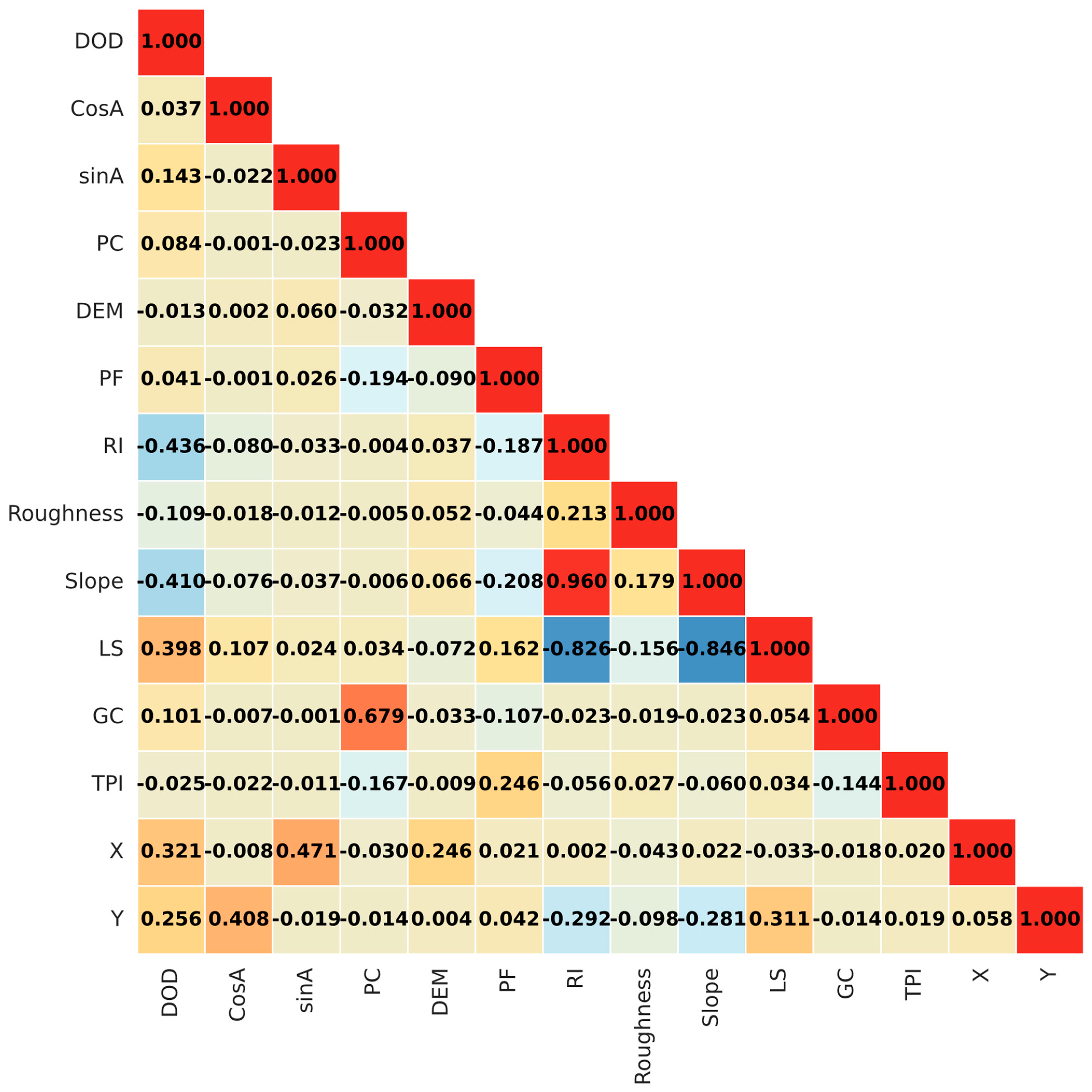
| Feature | DEM 1 (29 January 2025) | DEM 2 (26 February 2025) |
|---|---|---|
| Coordinate Reference System (CRS) | EPSG: 28351 | EPSG: 28351 |
| Effective Pixels | 90.41% | 90.41% |
| Pixel Resolution (m) | 0.03750 | 0.02634 |
| Maximum Elevation (m) | 354.1 | 367.7 |
| Minimum Elevation (m) | 339.3 | 341.9 |
| Average Elevation (m) | 348.2 | 348.4 |
| Median Elevation (m) | 348.2 | 348.4 |
| Standard Deviation (Std) | 0.838 | 1.231 |
| Model | Patch Size | Training Performance | Testing Performance | Residual Analysis | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | RMSE | MSE | MAE | RMSE | Mean | Std | ||||
| MLP | 64 × 64 | 0.1812 | 0.3307 | 0.4257 | 0.8335 | 0.5379 | 0.5523 | 0.7334 | 0.5056 | 0.0169 | 0.7332 |
| 128 × 128 | 0.5144 | 0.5572 | 0.7172 | 0.4402 | 0.5066 | 0.5451 | 0.7117 | 0.4487 | 0.1040 | 0.7040 | |
| 256 × 256 | 0.1572 | 0.3046 | 0.3965 | 0.7989 | 0.3132 | 0.4339 | 0.5596 | 0.5994 | −0.0120 | 0.5594 | |
| FCN | 64 × 64 | 0.2087 | 0.3537 | 0.4569 | 0.8082 | 0.1769 | 0.3224 | 0.4206 | 0.8374 | −0.0140 | 0.4203 |
| 128 × 128 | 0.4021 | 0.4927 | 0.6341 | 0.5623 | 0.2905 | 0.4252 | 0.5390 | 0.6838 | −0.0841 | 0.5324 | |
| 256 × 256 | 0.1306 | 0.2848 | 0.3614 | 0.8329 | 0.0988 | 0.2491 | 0.3143 | 0.8736 | 0.0004 | 0.3142 | |
| ResNet | 64 × 64 | 0.0749 | 0.2097 | 0.2737 | 0.9312 | 0.3424 | 0.4343 | 0.5852 | 0.6853 | −0.0121 | 0.5850 |
| 128 × 128 | 0.2473 | 0.3870 | 0.4973 | 0.7309 | 0.3209 | 0.4326 | 0.5664 | 0.6508 | −0.0383 | 0.5651 | |
| 256 × 256 | 0.0161 | 0.0987 | 0.1268 | 0.9794 | 0.0893 * | 0.2304 * | 0.2988 * | 0.8857 * | 4.56e-3 | 0.2988 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Shirani Faradonbeh, R.; Xie, H.; Stothard, P. Deep Learning for Predicting Surface Elevation Change in Tailings Storage Facilities from UAV-Derived DEMs. Appl. Sci. 2025, 15, 10982. https://doi.org/10.3390/app152010982
Lu W, Shirani Faradonbeh R, Xie H, Stothard P. Deep Learning for Predicting Surface Elevation Change in Tailings Storage Facilities from UAV-Derived DEMs. Applied Sciences. 2025; 15(20):10982. https://doi.org/10.3390/app152010982
Chicago/Turabian StyleLu, Wang, Roohollah Shirani Faradonbeh, Hui Xie, and Phillip Stothard. 2025. "Deep Learning for Predicting Surface Elevation Change in Tailings Storage Facilities from UAV-Derived DEMs" Applied Sciences 15, no. 20: 10982. https://doi.org/10.3390/app152010982
APA StyleLu, W., Shirani Faradonbeh, R., Xie, H., & Stothard, P. (2025). Deep Learning for Predicting Surface Elevation Change in Tailings Storage Facilities from UAV-Derived DEMs. Applied Sciences, 15(20), 10982. https://doi.org/10.3390/app152010982








