Self-Calibration Method for the Four Buckets Phase Demodulation Algorithm in Triangular Wave Hybrid Modulation
Abstract
1. Introduction
2. Principles
2.1. Two-Beam Interference
2.2. Four Buckets Phase Demodulation Algorithm
3. Method
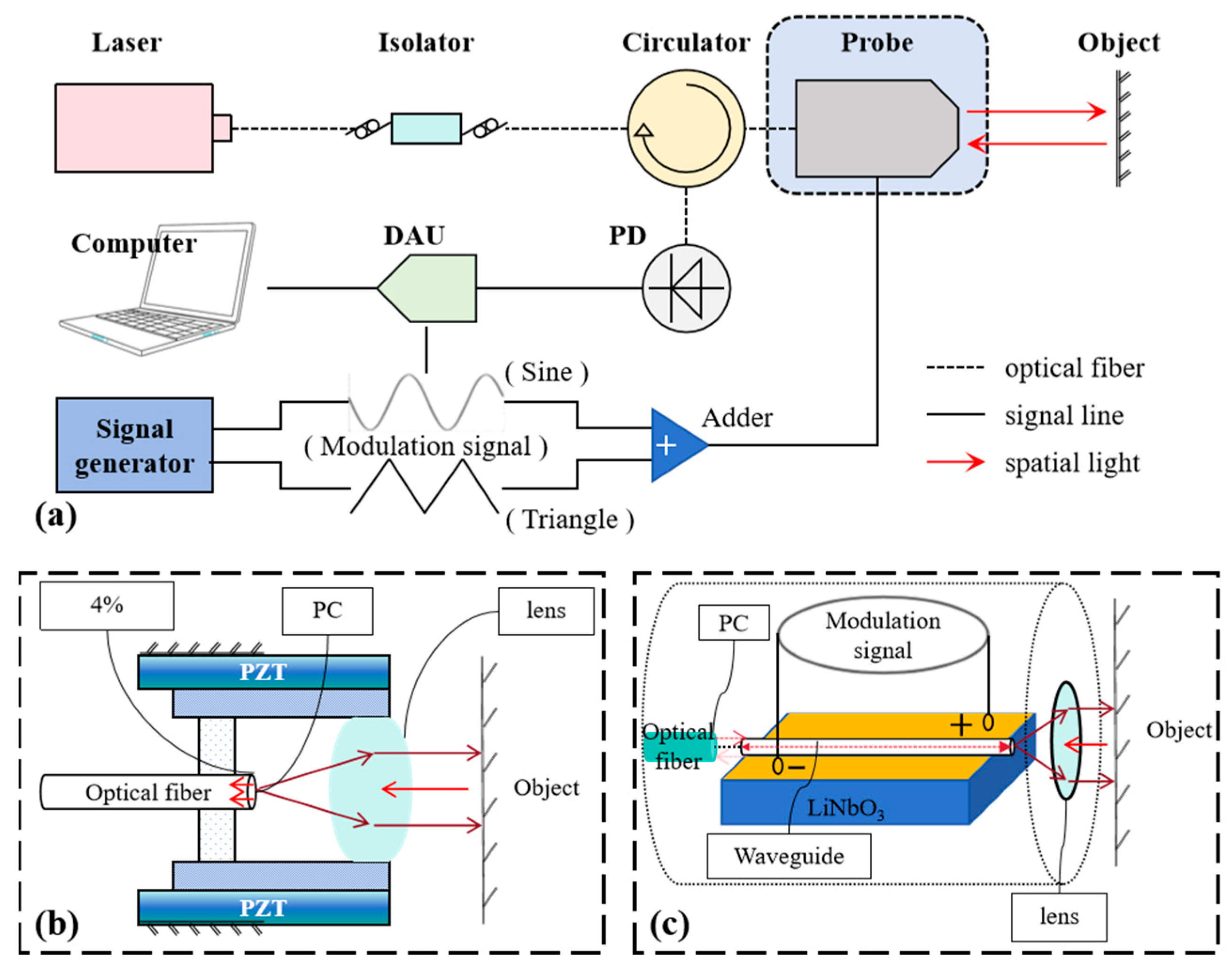
3.1. Measurement System Structure
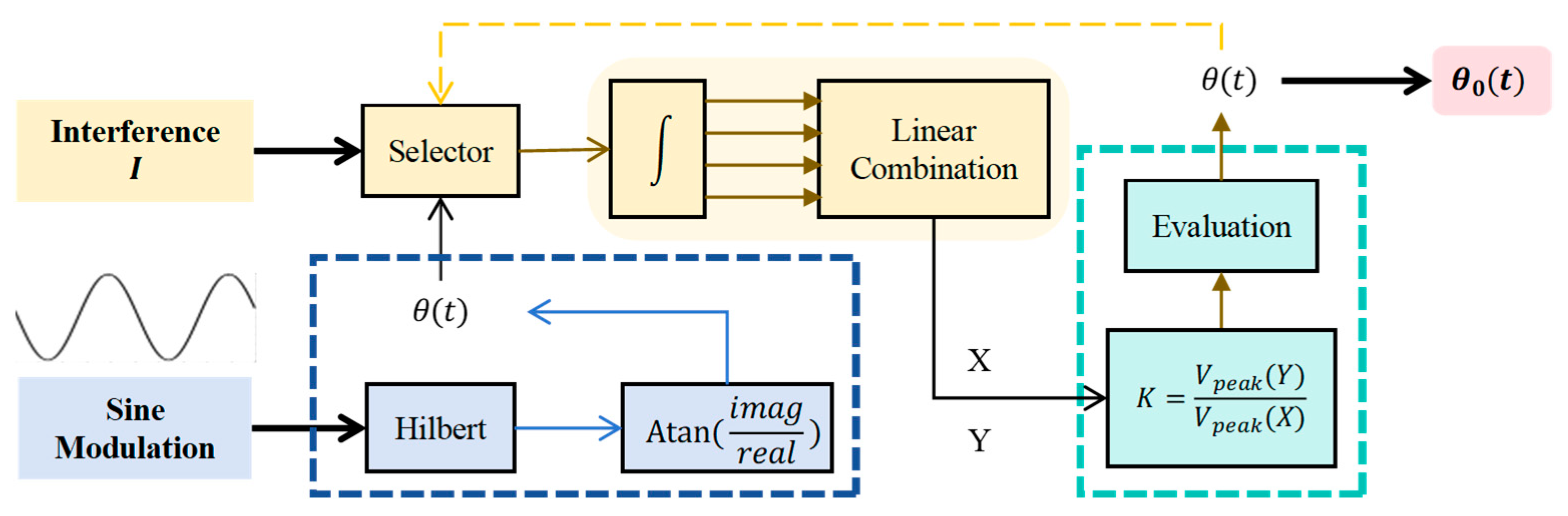
3.2. Signal Processing Method
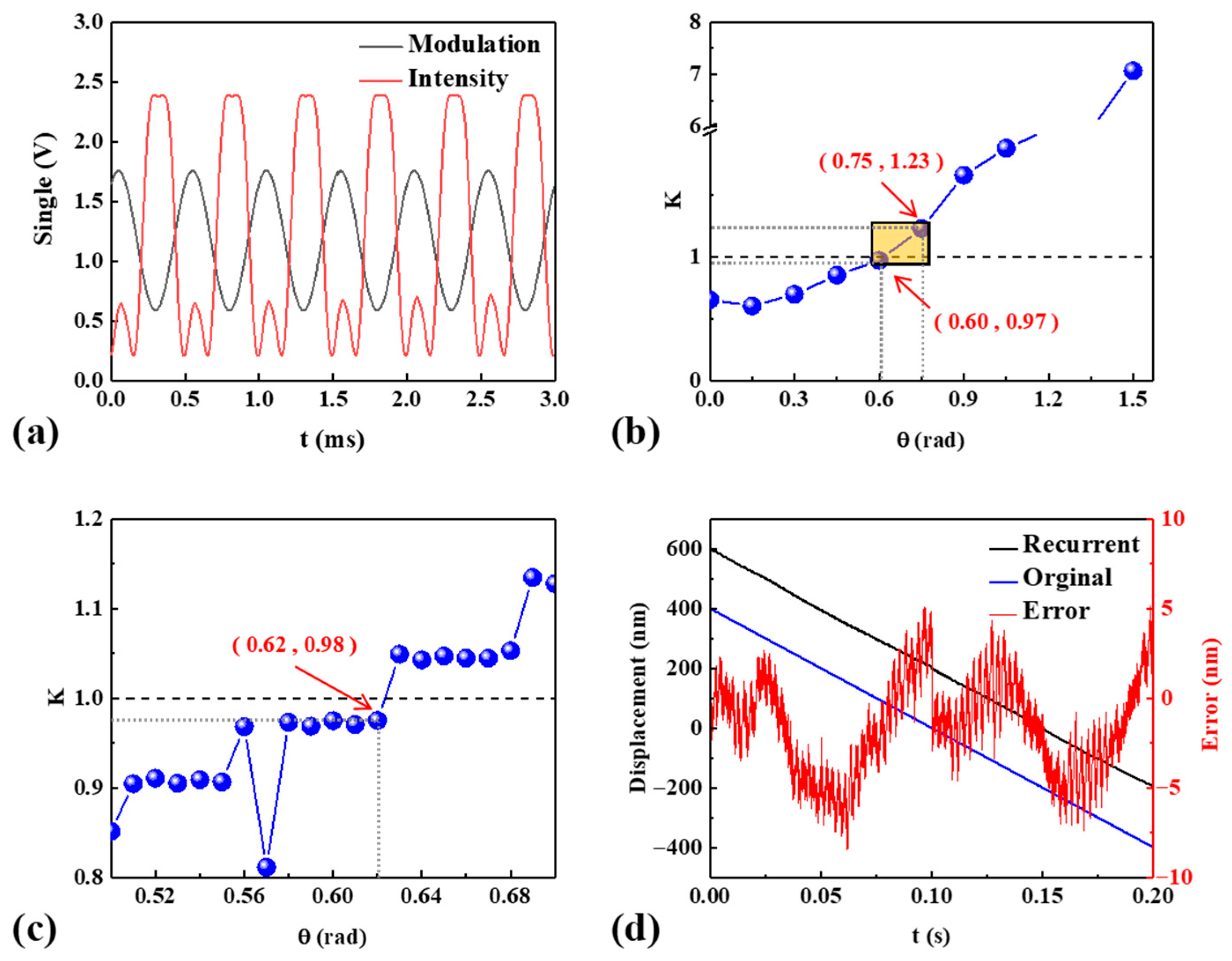
4. Simulation
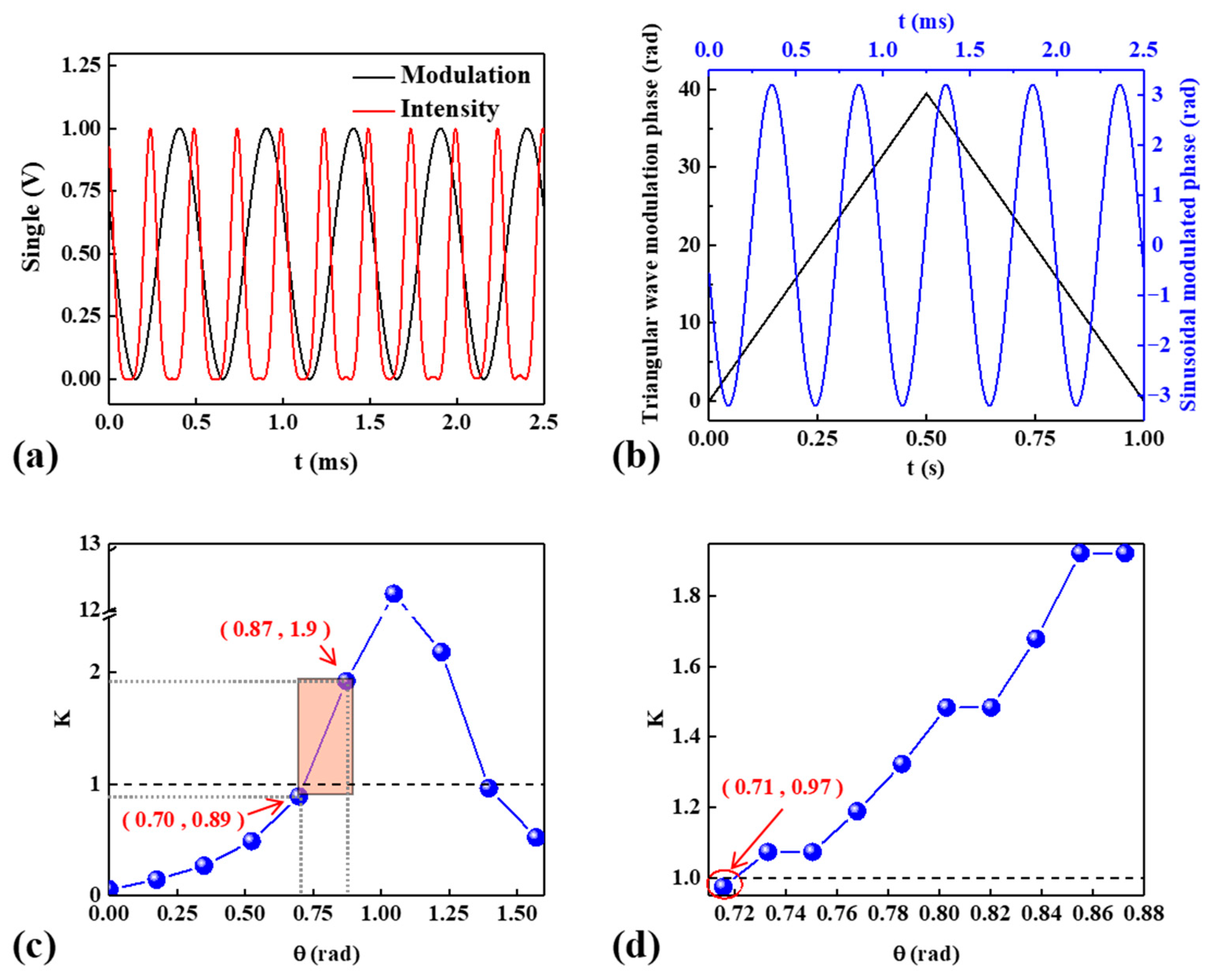
4.1. Modulation Depth Matching Verification
4.2. Phase Delay Calibration
5. Experiment
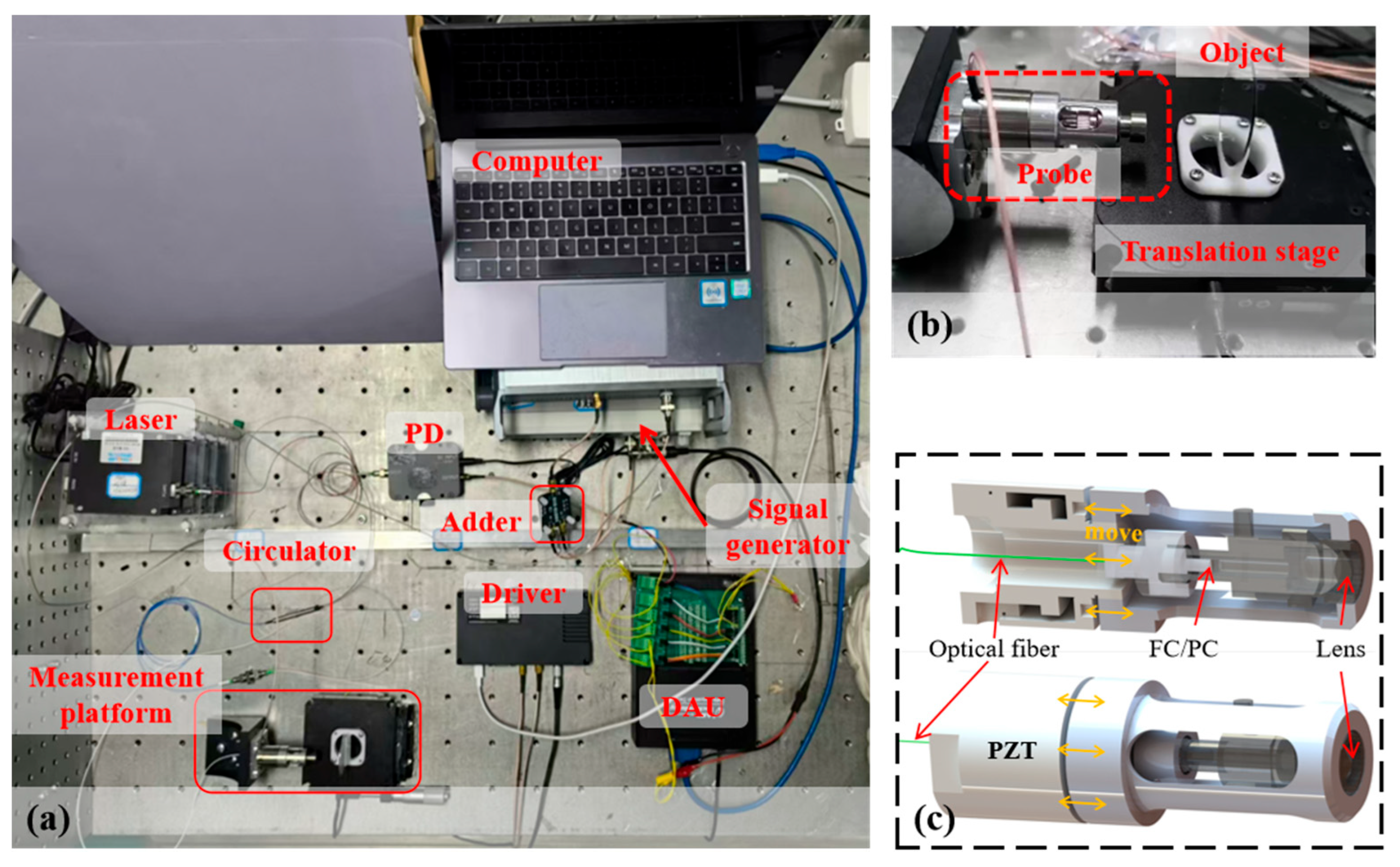
5.1. Experimental Platform
5.2. Calibration Experiment in Static State
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, J.; Jiang, S.; Wang, Z.; Cheng, X.; Li, B.; Shi, Y.; Tsai, D.P.; Liu, A.Q.; Huang, W.; Zhu, W. Metasurface micro/nano-optical sensors: Principles and applications. ACS Nano 2022, 16, 11598–11618. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.Y.; Zhao, Y.; Hou, C.Y.; Zhu, X.; Cai, Y.D.; Jin, Z.J.; Kang, R.K. On-machine measurement of tool nose radius and wear during precision/ultra-precision machining. Adv. Manuf. 2022, 10, 368–381. [Google Scholar] [CrossRef]
- Fu, Y.; Shang, Y.; Hu, W.; Li, B.; Yu, Q. Non-contact optical dynamic measurements at different ranges: A review. Acta Mech. Sin. 2021, 37, 537–553. [Google Scholar] [CrossRef]
- Kim, S.; Jeon, J.; Kim, Y.; Sugita, N.; Mitsuishi, M. Design and assessment of phase-shifting algorithms in optical interferometer. Int. J. Precis. Eng. Manuf.-Green Technol. 2023, 10, 611–634. [Google Scholar] [CrossRef]
- Eisenhauer, F.; Monnier, J.D.; Pfuhl, O. Advances in optical/infrared interferometry. Annu. Rev. Astron. Astrophys. 2023, 61, 237–285. [Google Scholar] [CrossRef]
- Berger, G.; Petter, J. Non-contact metrology of aspheric surfaces based on MWLI technology. In Proceedings of the SPIE Optifab 2013, Rochester, NY, USA, 14–17 October 2013. [Google Scholar]
- Sharma, S.; Eiswirt, P.; Petter, J. Study on Interferometric Stability Based on Modulating Frequency, Operating Wavelengths and Temperature using an Electro Optic Multi-Wavelength Distance Sensor. Sens. Transducers 2018, 225, 1–7. [Google Scholar]
- Guo, D.; Wang, M.; Tan, S. Self-mixing interferometer based on sinusoidal phase modulating technique. Opt. Express 2005, 13, 1537–1543. [Google Scholar] [CrossRef] [PubMed]
- Dubois, A. Phase-map measurements by interferometry with sinusoidal phase modulation and four integrating buckets. J. Opt. Soc. Am. A (Opt. Image Sci. Vis.) 2001, 18, 1972–1979. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Li, D.; Sun, H.; Qu, T.; Liu, X.; Wang, J. Phase Modulation Depth Deviation Effect Correction for Extended Displacement Sensing Range in Fiber-Optic Sinusoidal Frequency Modulation Interferometer. J. Light. Technol. 2025, 43, 3808–3821. [Google Scholar] [CrossRef]
- Duan, F.; Bao, R.; Huang, T.; Fu, X.; Zhang, C. Scale factor calibration method for integrating-bucket sinusoidal phase shifting interferometry(Article). Opt. Laser Technol. 2020, 127, 106149. [Google Scholar] [CrossRef]
- Liu, Q.; Lin, J.; Liu, J.; Lai, T.; Luo, G.; Li, Z.; Chen, S. Self-alignment method for four integral bucket phase demodulation in displacement interferometry. Opt. Laser Technol. 2025, 191, 113288. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, D. Enhanced PGC displacement sensors: Center frequency stabilization and sub-nanometer precision measurement utilizing laser intensity modulation. Meas. J. Int. Meas. Confed. 2025, 246, 116686. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, X.; Duan, H.; Xu, Z.; Yan, S.; Sun, Q.; Liang, Y.; Zhou, Z. Low-Frequency High-Resolution Fiber Fabry–Perot Interferometric Accelerometer Based on Double-Spring-Supported Oscillator. IEEE Sens. J. 2024, 24, 17500–17506. [Google Scholar] [CrossRef]
- Zhao, X.; Suzuki, T.; Sasaki, O. Sinusoidal phase modulating laser diode interferometer using an additive operating type of integrating bucket method. Proc. SPIE—Int. Soc. Opt. Eng. 2002, 4919, 275–282. [Google Scholar]
- Sharma, S.; Eiswirt, P.; Petter, J. Electro optic sensor for high precision absolute distance measurement using multiwavelength interferometry. Opt. Express 2018, 26, 3443–3451. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhang, M.; Zhang, C.; Yang, W.; Chen, T.; Perchoux, J.; Ramírez-Miquet, E.E.; Moreira, R.d.C. Micro Particle Sizing Using Hilbert Transform Time Domain Signal Analysis Method in Self-Mixing Interferometry. Appl. Sci. 2019, 9, 5563. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, L.; Chen, B.; Xu, Z.; Xie, J. Real-time phase delay compensation of PGC demodulation in sinusoidal phase-modulation interferometer for nanometer displacement measurement. Opt. Express 2017, 25, 472–485. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Li, X.; Fu, X.; Zhang, C.; Duan, F. Exposure time shortened integrating-bucket method for sinusoidal phase shifting interferometry. Opt. Commun. 2019, 451, 333–337. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, G.; Lei, W.; Dong, X.; Wang, J. X-Ray Mirror Surface Profile Measurement with Nanometer Accuracy Based on Three-Displacement Sensors. Guangxue Xuebao/Acta Opt. Sin. 2025, 45, 0512003. [Google Scholar]
- Zhou, Y.; Mo, J.; Peng, L.; Shen, B.; Yu, Y. Measurement of surface profile for transparent flats under dense cavity lengths using wavelength tuning interferometry based on subspace orthogonality. Meas. J. Int. Meas. Confed. 2025, 251, 117291. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Sampling rate (kHz) | 500 |
| Wavelength (nm) | 1530 |
| Displacement (nm) | 0 |
| DC/AC light intensity (V) | 0.5 |
| Modulation frequency (kHz) | 2 |
| Amplitude of triangle (rad) | 20 |
| Triangle frequency (Hz) | 1 |
| (rad) | 1.8 | 2 | 2.2 | 2.4 | 2.45 | 2.6 | 2.8 | 3 | 3.2 | 3.4 |
| (rad) | 0.55 | 0.73 | 0.86 | 0.96 | 0.98 | 1.04 | 1.11 | 1.17 | 1.23 | 1.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Chen, S.; Lai, T.; Li, G.; Lin, J.; Liu, J. Self-Calibration Method for the Four Buckets Phase Demodulation Algorithm in Triangular Wave Hybrid Modulation. Appl. Sci. 2025, 15, 10956. https://doi.org/10.3390/app152010956
Liu Q, Chen S, Lai T, Li G, Lin J, Liu J. Self-Calibration Method for the Four Buckets Phase Demodulation Algorithm in Triangular Wave Hybrid Modulation. Applied Sciences. 2025; 15(20):10956. https://doi.org/10.3390/app152010956
Chicago/Turabian StyleLiu, Qi, Shanyong Chen, Tao Lai, Guiqing Li, Jiajun Lin, and Junfeng Liu. 2025. "Self-Calibration Method for the Four Buckets Phase Demodulation Algorithm in Triangular Wave Hybrid Modulation" Applied Sciences 15, no. 20: 10956. https://doi.org/10.3390/app152010956
APA StyleLiu, Q., Chen, S., Lai, T., Li, G., Lin, J., & Liu, J. (2025). Self-Calibration Method for the Four Buckets Phase Demodulation Algorithm in Triangular Wave Hybrid Modulation. Applied Sciences, 15(20), 10956. https://doi.org/10.3390/app152010956









