Harnessing Quantum Entanglement and Fidelity in Hydrogen Atoms: Unveiling Dynamics Under Dephasing Noise

Abstract

We investigate the quantum dynamics of entanglement and fidelity in the hyperfine structure of hydrogen atoms under dephasing noise, modeled via the Lindblad master equation. The effective Hamiltonian captures the spin–spin interaction between the electron and proton, with dephasing incorporated through local Lindblad operators. Analytical solutions for the time-dependent density matrix are derived for various initial states, including separable, partially entangled, and maximally entangled configurations. Entanglement is quantified using the concurrence, while fidelity measures the similarity between the evolving state and the initial state. Numerical results demonstrate that entanglement exhibits oscillatory decay modulated by the dephasing rate, with anti-parallel spin states displaying greater robustness compared to parallel configurations, often leading to entanglement sudden death. Fidelity dynamics reveal similar damped oscillations, underscoring the interplay between coherent hyperfine evolution and environmental dephasing. These insights elucidate strategies for preserving quantum correlations in atomic systems, with implications for quantum information processing and metrology.

1. Introduction

In quantum mechanics, a comprehensive characterization of a composite system is achievable, with the state of each subsystem defined by its quantum correlations with others, leading to the formation of entangled states [1,2]. Quantum entanglement, distinguished by nonlocal correlations between separate physical systems [3,4,5], serves as a foundational pillar of quantum technologies. The exploration of entanglement, the primary manifestation of quantum correlation, combined with the outcomes of quantum measurement, has profoundly deepened our understanding and addressed numerous physical problems [6,7]. Recent advances in quantum information processing (QIP) have generated a wide array of insights, significantly expanding the literature on entanglement and improving the performance of QIP and quantum metrology applications [8,9,10,11,12,13]. The pivotal role of entanglement in a wide range of applications has driven research into higher-dimensional Hilbert spaces, revealing new facets of these correlations in multiparticle quantum systems [14]. Furthermore, recent studies have demonstrated scalable entanglement generation in trapped ion systems, enhancing the prospects for quantum computing [15], while investigations into entanglement swapping in photonic networks have opened new avenues for quantum communication protocols [16]. In the study of non-classical phenomena, the creation of such quantum correlations remains a central goal in experimental quantum research.

Due to its remarkably straightforward configuration, the hydrogen atom has long functioned as a fundamental basis for understanding quantum mechanics, yielding significant revelations regarding electron–nucleus interactions in a broad range of physical, chemical, and biological environments [17,18,19,20].

The hydrogen atom, while a cornerstone of quantum theory, also serves as a exemplary model system within quantum information science due to its intrinsic bipartite quantum structure. The coupled spin states of the electron and proton constitute a natural two-qubit register, providing a well-defined Hilbert space for probing the dynamics of quantum correlations [21]. The magnitude and character of these correlations, often measured via entanglement monotones like concurrence and quantum coherence, are fixed by fundamental physical constants—including the Planck constant, Boltzmann constant, and the electron and proton gyromagnetic ratios—as well as atomic parameters such as the Bohr radius.

Within the hyperfine manifold, the ground-state sublevels manifest authentic quantum entanglement at cryogenic temperatures. This non-classicality, however, is thermally fragile; it decays with increasing temperature and is entirely extinguished above a critical energy scale corresponding to $E_c\approx 5.35\times {10}^{-6}\mathrm{eV}$. This phase transition is governed by the thermal population redistribution among the hyperfine levels, where the interplay between the hyperfine splitting energy and thermal fluctuations dictates the survival of entanglement [22,23,24].

Recent investigations have identified nuclear-polarized states of hydrogen atoms embedded in solid H₂ matrices [22,25], revealing significant deviations from the Boltzmann distribution for the case of low temperature regimes [22,23,24], prompting intriguing questions about quantum effects in these systems. Recent advancements in quantum research have unveiled novel mechanisms governing entanglement and coherence within hydrogen atomic systems. Notably, the cosmological expansion of the universe has been demonstrated to trigger the onset of quantum entanglement in the hyperfine structure of hydrogen atoms, leading to a phenomenon termed “entanglement sudden birth” over extended cosmological timescales [26]. More recently, employing the Lindblad master equation has elucidated the time-dependent decay of quantum coherence and purity in hyperfine states, highlighting the impact of environmental dissipation on maintaining quantum properties in these atomic systems [27].

This work undertakes a dynamical analysis of two key quantum information metrics—entanglement and state fidelity—within the hydrogen atom’s hyperfine-interacting spin system. We focus specifically on its open-system evolution when coupled to a pure-dephasing environment, a process formally described by a Lindblad-type master equation. Our methodological approach centers on obtaining closed-form, time-dependent expressions for the system’s density operator. These solutions, which span a spectrum of initial conditions from product states to maximal entanglement, enable the systematic tracking of quantum correlations via the concurrence and entanglement of formation measures. Simultaneously, we employ fidelity as a metric to assess the proximity of the decohering state to designated target states throughout its temporal trajectory. Our contributions include elucidating the interplay between coherent spin–spin interactions and dissipative dephasing effects, demonstrating phenomena such as oscillatory entanglement decay, sudden death in specific subspaces, and differential robustness between anti-parallel and parallel spin states. These findings offer valuable insights into mitigating decoherence in atomic quantum systems, with potential implications for enhancing the performance of quantum information processing and metrology protocols.

The manuscript is organized as follows. Section 2 outlines the system Hamiltonian and introduces the Lindblad formalism for modeling dephasing dynamics in the hyperfine structure, including exact analytical solutions for key initial states. Section 3 presents the measures of entanglement and fidelity, together with their formal expressions for the model under consideration. Section 4 explores the time-resolved dynamics of entanglement and fidelity in open quantum systems, supported by numerical results and illustrative figures. Finally, in Section 5 we provide a summary of the key findings of the manuscript.

2. Hyperfine Coupling in Hydrogen and Lindblad Dynamics

The origin of the hyperfine structure in atomic hydrogen is the magnetic dipole–dipole coupling between the electron and proton spins. For the ground state ($1s$), the orbital angular momentum is zero ($\ell =0$), which precludes any orbital contribution to the magnetic field at the nucleus. The resulting energy level splitting is, therefore, a direct manifestation of the spin–spin interaction. Consequently, the hyperfine splitting originates entirely from the spin–spin magnetic dipole coupling [20]. This interaction is responsible for the celebrated $21\mathrm{cm}$ (1420 MHz) line, which has profound implications in radio astronomy and precision spectroscopy [28].

A rigorous description can be formulated using first-order perturbation theory, where the interaction Hamiltonian is proportional to the scalar product of the nuclear and electron spin operators. When an external magnetic field is applied, the Hamiltonian generalizes to include Zeeman-type contributions, producing tunable level splittings that are of immense importance for quantum sensing and metrology applications [28,29,30].

2.1. Hyperfine Hamiltonian and Spin Basis

For the ground state, the effective hyperfine Hamiltonian can be expressed as

$$H_{\mathrm{hf}}=B{\mathit{\sigma }}_e·{\mathit{\sigma }}_p=B\left({\sigma }_x^{\left(e\right)}{\sigma }_x^{\left(p\right)}+{\sigma }_y^{\left(e\right)}{\sigma }_y^{\left(p\right)}+{\sigma }_z^{\left(e\right)}{\sigma }_z^{\left(p\right)}\right),$$

(1)

where B denotes the hyperfine coupling constant, and ${\mathit{\sigma }}_e$, ${\mathit{\sigma }}_p$ are the Pauli vectors that act on the spins of electrons and protons, respectively. The coupling constant is determined by the magnetic moment densities at the nucleus and can be explicitly written as [28]:

$$B={\displaystyle \frac{{\mu }_0{g}_e{g}_p{e}^2{\hslash }^2}{12\pi m_e{m}_p{a}_0^3}},$$

(2)

where ${\mu }_0$ is the vacuum permeability, $a_0$ is the Bohr radius, $g_e$ and $g_p$ are the g-factors, and $m_e$, $m_p$ are the masses of the electron and proton. This formula encapsulates the strength of the magnetic dipole–dipole interaction mediated by the electron probability density at the nucleus.

The composite spin system is naturally described in a four-dimensional Hilbert space with a computational basis:

$$\mathcal{B}={\left\{\right|\uparrow }_e{\uparrow }_p{\rangle ,|\uparrow }_e{\downarrow }_p{\rangle ,|\downarrow }_e{\uparrow }_p{\rangle ,|\downarrow }_e{\downarrow }_p\rangle \}.$$

Diagonalizing $H_{\mathrm{hf}}$ yields a non-degenerate singlet state:

$$|S\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left({|\uparrow }_e{\downarrow }_p{\rangle -|\downarrow }_e{\uparrow }_p\rangle \right),$$

with eigenenergy $E_S=-3B$, and a triplet manifold:

$$|T_{+}{\rangle =|\uparrow }_e{\uparrow }_p\rangle ,|T_0\rangle ={\displaystyle \frac{1}{\sqrt{2}}}{\left(\right|\uparrow }_e{\downarrow }_p{\rangle + |\downarrow }_e{\uparrow }_p\rangle ),|T_{-}{\rangle =|\downarrow }_e{\downarrow }_p\rangle ,$$

with degenerate energy $E_T=B$. The energy gap $\Delta E=4B\approx 5.88\mu \mathrm{eV}$ corresponds to the well-known 21 cm transition. Without an external field, the system’s ground state is the entangled singlet; under an applied magnetic field, the triplet degeneracy is lifted, yielding Zeeman splitting and controllable transitions [30]. This tunability underpins key applications in quantum control and atomic clocks.

2.2. Decoherence Dynamics: Pure Dephasing Model

Decoherence is unavoidable in realistic quantum systems. In hydrogen’s hyperfine manifold, one dominant noise channel is pure dephasing, whereby random phase fluctuations degrade coherence while leaving populations unaltered. Such noise typically arises from magnetic field fluctuations that couple differently to the electron and proton spins.

The time evolution of the density matrix $\rho \left(t\right)$ is modeled using the Lindblad formalism:

$${\displaystyle \frac{d\rho }{dt}}=-i[H_{\mathrm{hf}},\rho ]+\mathcal{L}\left[\rho \right],$$

(3)

where $\mathcal{L}\left[\rho \right]$ encodes the dissipative dynamics. For independent local dephasing, the Lindblad operators are

$$L_e={\sigma }_z^{\left(e\right)}\otimes I_p,L_p=I_e\otimes {\sigma }_z^{\left(p\right)},$$

(4)

with respective rates ${\gamma }_e$, ${\gamma }_p$. The dissipator takes the form:

$$\mathcal{L}\left[\rho \right]={\gamma }_e(L_e\rho L_e-\rho )+{\gamma }_p(L_p\rho L_p-\rho ),$$

(5)

where we exploited the property $L_e^2=L_p^2=I$. This framework is well-suited for analyzing coherence decay in entangled spin systems. We note that the conventional Lindblad form involves a prefactor of $1/2$ in the dissipative terms. Here, since the dephasing operators $L_e$ and $L_p$ are Hermitian, this factor has been absorbed into the definition of the decay rates ${\gamma }_e$ and ${\gamma }_p$. This choice is purely conventional and does not affect the physical results, as the effective decay strengths are given in terms of the coupling constants.

• Dynamics of Density Matrix Components

Let $A=B/\hslash$. In the computational basis, the evolution equations under pure dephasing are

• Populations:

$$\begin{array}{cc}\hfill {\dot{\rho }}_{11}& =0,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{22}& =-2iA({\rho }_{23}-{\rho }_{32}),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{33}& =2iA({\rho }_{23}-{\rho }_{32}),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{44}& =0.\hfill \end{array}$$

(9)

• Coherences:

$$\begin{array}{cc}\hfill {\dot{\rho }}_{12}& =-2iA({\rho }_{12}-{\rho }_{13})-2{\gamma }_p{\rho }_{12},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{13}& =-2iA({\rho }_{13}-{\rho }_{12})-2{\gamma }_e{\rho }_{13},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{14}& =-2({\gamma }_e+{\gamma }_p){\rho }_{14},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{23}& =-2iA({\rho }_{22}-{\rho }_{33}+{\rho }_{23})-2({\gamma }_e+{\gamma }_p){\rho }_{23},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{24}& =-2iA({\rho }_{24}-{\rho }_{34})-2{\gamma }_e{\rho }_{24},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{34}& =-2iA({\rho }_{24}-{\rho }_{34})-2{\gamma }_p{\rho }_{34},.\hfill \end{array}$$

(15)

with ${\rho }_{ij}^{*}={\rho }_{ji}$. These equations make explicit that while populations remain invariant, off-diagonal coherences decay exponentially due to dephasing. The coupling between ${\rho }_{22},{\rho }_{33},$ and ${\rho }_{23}$ shows that phase noise indirectly modulates population transfer within the entangled manifold. We note here that the appearance of ${\rho }_{23}$ inside the parentheses of Equation (13) is a direct consequence of the coherent part of the dynamics generated by the hyperfine Hamiltonian. In particular, when evaluating the commutator $[H_{\mathrm{hf}},\rho ]$, cross terms proportional to ${\rho }_{23}$ emerge and combine with the population difference $({\rho }_{22}-{\rho }_{33})$.

2.3. Exact Solutions for Key Initial States

We now provide closed-form solutions for physically relevant initial conditions. These solutions allow for direct analysis of the interaction between coherent hyperfine coupling and environmental dephasing.

• Case I: Coherent Superposition in the Singlet-Triplet Subspace.

Consider:

$$|\psi \left(0\right)\rangle ={cos\alpha |\uparrow }_e{\downarrow }_p{\rangle +sin\alpha |\downarrow }_e{\uparrow }_p\rangle ,$$

(16)

a superposition of opposite spin states. This is not an eigenstate of $H_{\mathrm{hf}}$ and thus exhibits nontrivial dynamics. Define the following:

$$\Gamma ={\gamma }_e+{\gamma }_p,\Omega =\sqrt{16A^2-{\Gamma }^2}.$$

(17)

The elements of the non-zero density matrix are

$$\begin{array}{cc}\hfill {\rho }_{22}\left(t\right)& =\frac{1}{2}+\frac{1}{2}cos\left(2\alpha \right)e^{-\Gamma t}\left(\frac{\Gamma }{\Omega }sin(\Omega t)+cos(\Omega t)\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\rho }_{33}\left(t\right)& =\frac{1}{2}-\frac{1}{2}cos\left(2\alpha \right)e^{-\Gamma t}\left(\frac{\Gamma }{\Omega }sin(\Omega t)+cos(\Omega t)\right),\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\rho }_{23}\left(t\right)& =\frac{1}{2}sin\left(2\alpha \right)e^{-2\Gamma t}+2i\frac{A}{\Omega }cos\left(2\alpha \right)e^{-\Gamma t}sin(\Omega t).\hfill \end{array}$$

(20)

We note here that the two decay factors in ${\rho }_{23}\left(t\right)$ originate from different physical processes. The term $\frac{1}{2}sin\left(2\alpha \right)e^{-2\Gamma t}$ represents the decay of the initial coherence between opposite-spin states, which is affected by both electron and proton dephasing channels, giving a rate $2\Gamma$. In contrast, the oscillatory term $2i{\displaystyle \frac{A}{\Omega }}cos\left(2\alpha \right)e^{-\Gamma t}sin(\Omega t)$ arises from coherent hyperfine-induced oscillations, which are modulated by the combined but single-effective dephasing rate $\Gamma$. A detailed derivation is provided in Appendix A.

All other elements vanish. The dynamics reveal coherent oscillations at frequency $\Omega$ superimposed with exponential decoherence at rate $\Gamma$. In particular, the dynamics remains confined to the two-dimensional ${|\uparrow }_e{\downarrow }_p{\rangle ,|\downarrow }_e{\uparrow }_p\rangle$ subspace.

• Case II: Entangled Aligned Spins.

For the initial Bell-like state:

$$|\varphi \left(0\right)\rangle ={cos\alpha |\uparrow }_e{\uparrow }_p{\rangle +sin\alpha |\downarrow }_e{\downarrow }_p\rangle ,$$

(21)

The only nonzero components are

$$\begin{array}{cc}\hfill {\rho }_{11}\left(t\right)& ={cos}^2\alpha ,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\rho }_{14}\left(t\right)& ={\rho }_{41}\left(t\right)=sin\left(\alpha \right)cos\left(\alpha \right)e^{-2\Gamma t},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\rho }_{44}\left(t\right)& ={sin}^2\alpha .\hfill \end{array}$$

(24)

Here populations are stationary, while coherence decays exponentially with rate $2\Gamma$. Interestingly, the Hamiltonian coupling A does not influence the evolution because this state lies within an eigenspace of $H_{\mathrm{hf}}$. The decoherence is, therefore, purely environmental. The coherence ${\rho }_{14}\left(t\right)$ decays purely as $e^{-2\Gamma t}$ because it connects the states ${|\uparrow }_e{\uparrow }_p\rangle$ and ${|\downarrow }_e{\downarrow }_p\rangle$, which differ in both electron and proton spins. Consequently, dephasing acts on both spins simultaneously, leading to a total decay rate of $2\Gamma =2({\gamma }_e+{\gamma }_p)$, in contrast to the single-spin-modulated decay observed in oscillatory terms such as those in ${\rho }_{23}\left(t\right)$.

These results highlight the intricate interplay between coherent hyperfine dynamics and dephasing. They illustrate how entanglement robustness depends sensitively on both the initial state and the structure of environmental noise. In later sections, we analyze the behavior of quantum correlations and entanglement measures under these dynamics.

3. Quantum Correlation Quantifiers: Entanglement and Fidelity

We undertake a systematic investigation of entanglement and fidelity within a rigorous resource-theoretic framework. Two distinct quantitative measures are introduced and thoroughly analyzed, each defined through explicit formal expressions and critically evaluated against well-established criteria to ensure their physical validity and operational significance.

3.1. Entanglement Quantification via Entanglement of Formation

In this section, we provide a rigorous quantification of quantum entanglement using entanglement of formation (EoF), a well-established measure directly linked to the concurrence [31]. The EoF is particularly suitable for bipartite two-qubit systems, as it effectively discriminates between separable, partially entangled, and maximally entangled states.

For a given two-qubit density matrix $\rho$, the entanglement of formation is defined as

$$E\left(\rho \right)=H\left[{\displaystyle \frac{1}{2}}\left(1+\sqrt{1-C^2\left(\rho \right)}\right)\right],$$

(25)

where $H\left(f\right)$ denotes the binary entropy function [10,31,32,33,34]:

$$H\left(f\right)=-f{log}_{2}f-(1-f){log}_2(1-f),$$

(26)

and $C\left(\rho \right)$ is the concurrence, given by [31,35,36,37]:

$$C\left(\rho \right)=max\left\{0,\sqrt{{\epsilon }_1}-\sqrt{{\epsilon }_2}-\sqrt{{\epsilon }_3}-\sqrt{{\epsilon }_4}\right\},$$

(27)

where ${\epsilon }_i$ are the eigenvalues, arranged in decreasing order, of the matrix:

$$R=\sqrt{\rho }\tilde{\rho }\sqrt{\rho },$$

(28)

with the spin-flipped density matrix defined as

$$\tilde{\rho }=({\widehat{\sigma }}_y\otimes {\widehat{\sigma }}_y){\rho }^{*}({\widehat{\sigma }}_y\otimes {\widehat{\sigma }}_y),$$

(29)

and ${\rho }^{*}$ denoting the complex conjugate of $\rho$. The Pauli matrix ${\widehat{\sigma }}_y$ acts as the spin-flip operator, playing a central role in quantifying entanglement symmetries.

The concurrence $C\left(t\right)$ varies from 0 (completely separable states) to 1 (maximally entangled states), with intermediate values describing partially entangled or mixed states. Its direct relation to the EoF makes it a robust and operationally meaningful tool for tracking the dynamics of entanglement, particularly in the presence of decoherence or nonunitary evolution. This framework allows for a precise assessment of how entanglement resources degrade or persist under different physical conditions.

3.2. Fidelity as a Quantifier of Quantum State Similarity

Fidelity is a fundamental quantity in quantum information theory, widely employed to characterize the similarity or closeness between two quantum states [38,39,40,41]. For two arbitrary mixed states $\rho$ and $\sigma$, the fidelity is defined using the Uhlmann expression:

$$F(\rho ,\sigma )={\left(\mathrm{Tr}\sqrt{\sqrt{\rho }\sigma \sqrt{\rho }}\right)}^2.$$

(30)

This measure satisfies $0\le F(\rho ,\sigma )\le 1$, attaining $F=1$ if and only if $\rho =\sigma$, and $F=0$ when the states are perfectly distinguishable (orthogonal).

In the special case where both states are pure, $\rho =|\xi \rangle \langle \xi |$ and $\sigma =|\eta \rangle \langle \eta |$, the fidelity reduces to the squared modulus of their inner product:

$$F(\rho ,\sigma )={\left|\langle \xi |\eta \rangle \right|}^2,$$

(31)

providing a direct geometric interpretation of state overlap.

Fidelity serves as a key diagnostic tool for assessing the performance of quantum operations, including the precision of quantum gate implementations, the reliability of quantum channels, and the effectiveness of quantum error correction protocols. It is also widely used in quantum state tomography, where an experimentally reconstructed state is compared with an ideal or target state [5,42]. High-fidelity values signify strong similarity between states, whereas lower values indicate deviations due to noise or decoherence.

In the context of the present work, fidelity is employed to analyze the temporal evolution of the density matrix of the system $\rho \left(t\right)$ under Lindblad dynamics by comparing it with a reference state $\sigma$. This approach offers a complementary perspective to entanglement measures, revealing not only the amount of quantum correlations but also how faithfully the evolving state approximates an idealized or maximally entangled target as decoherence and dissipative effects take place.

For all cases considered in this study, the fidelity $F\left(t\right)$ is calculated relative to the corresponding initial state of the system, rather than with respect to an external target state, such as a Bell state with a maximal entanglement. This ensures that $F\left(t\right)$ directly quantifies the similarity between the evolving state and its initial preparation.

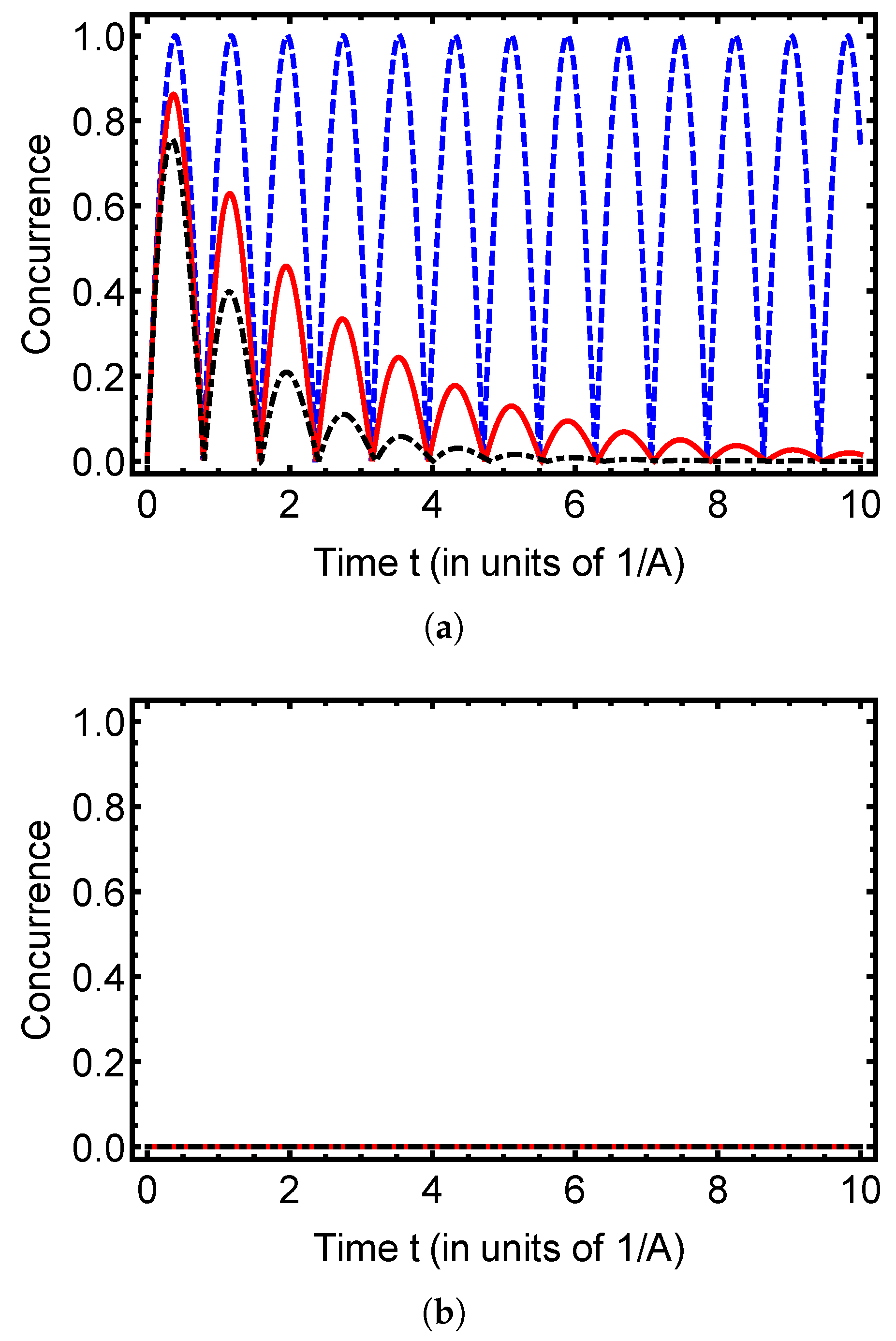
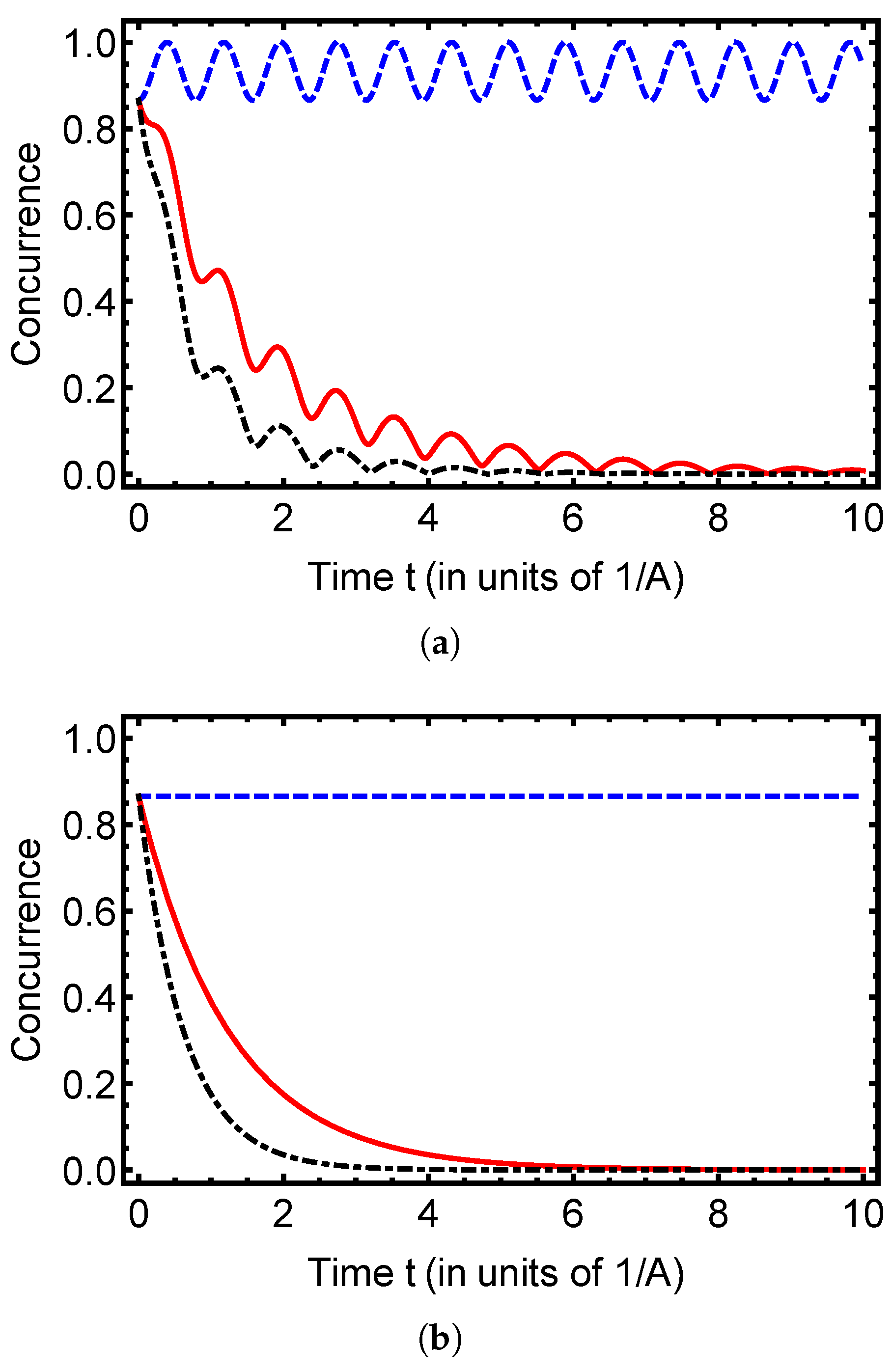
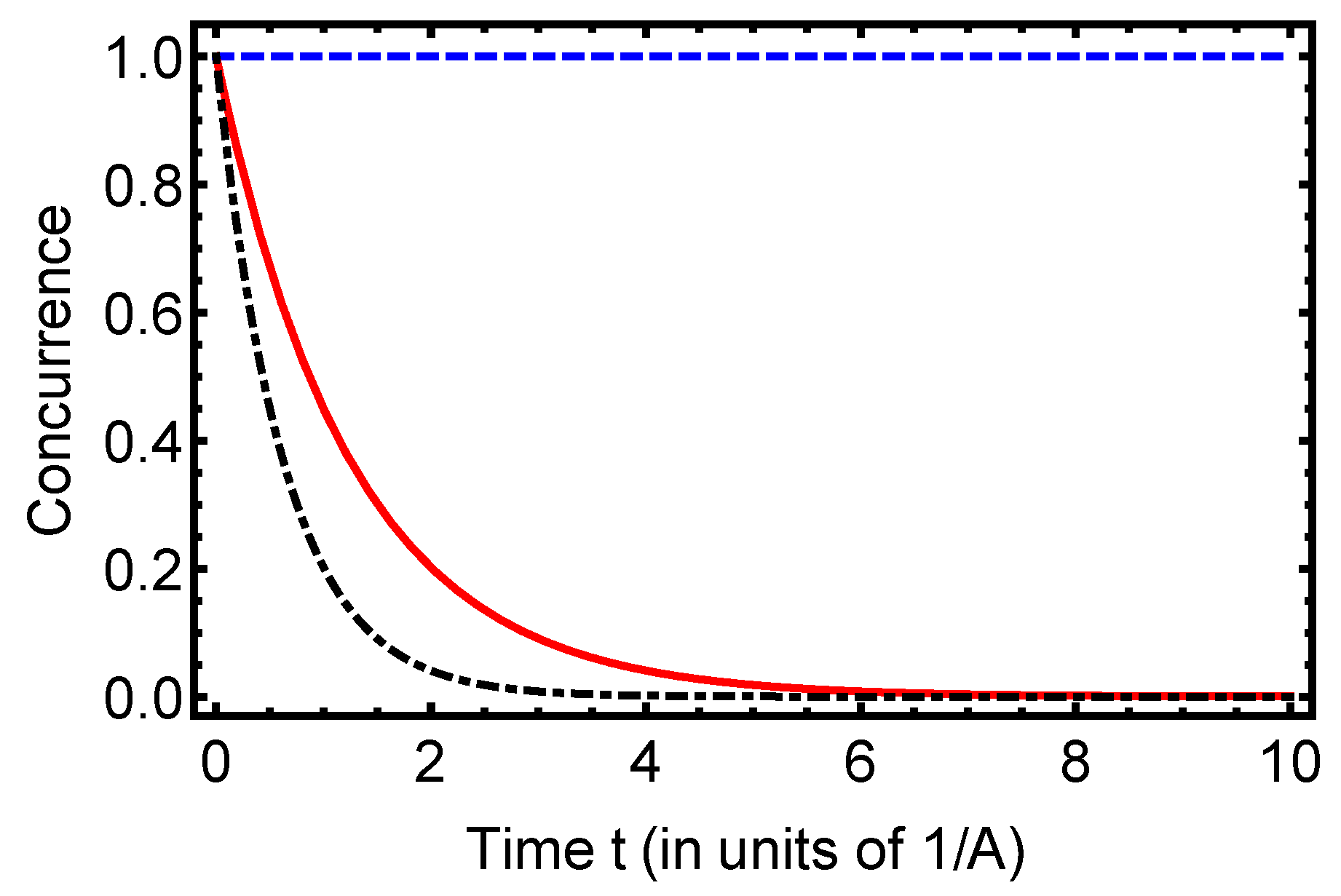
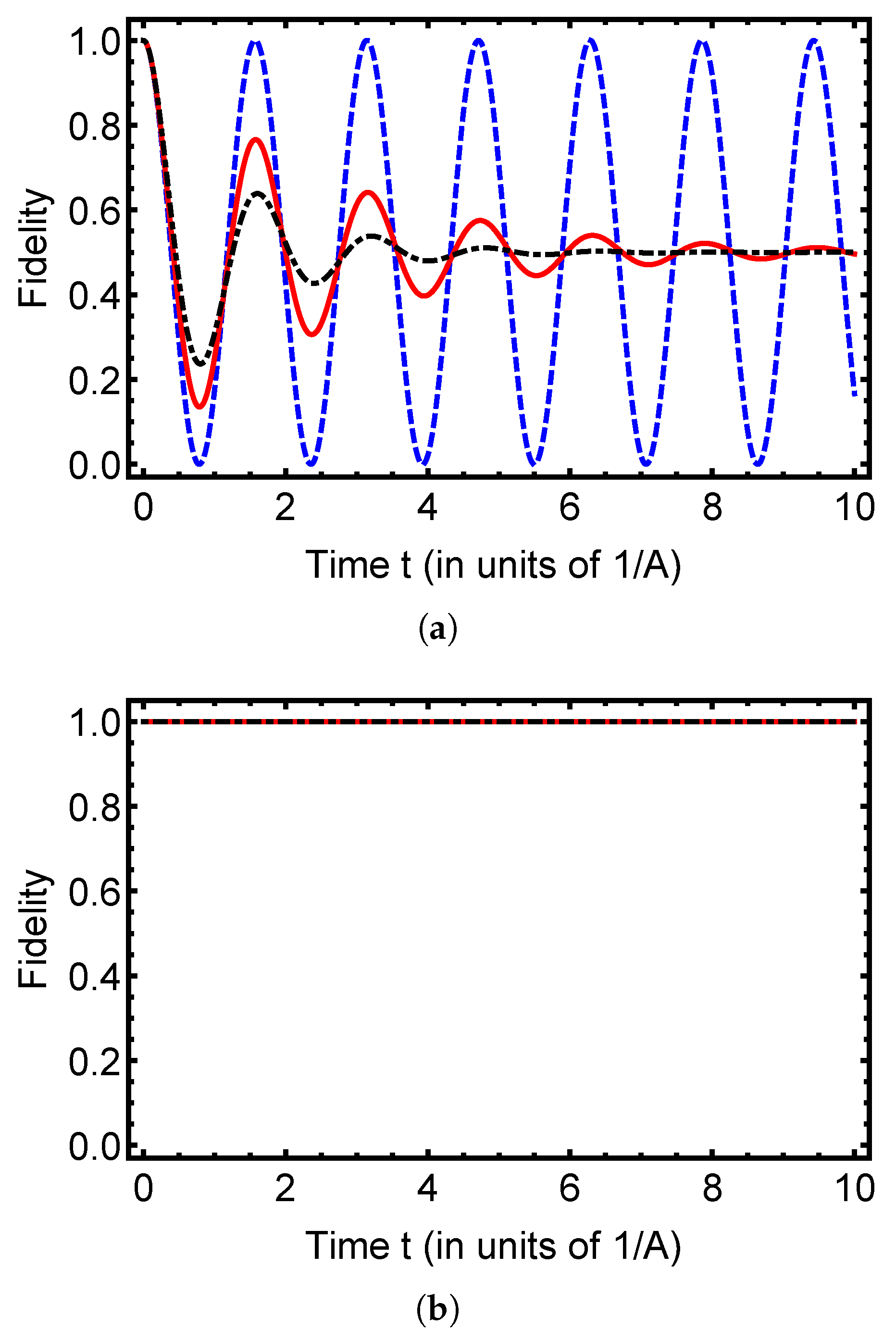
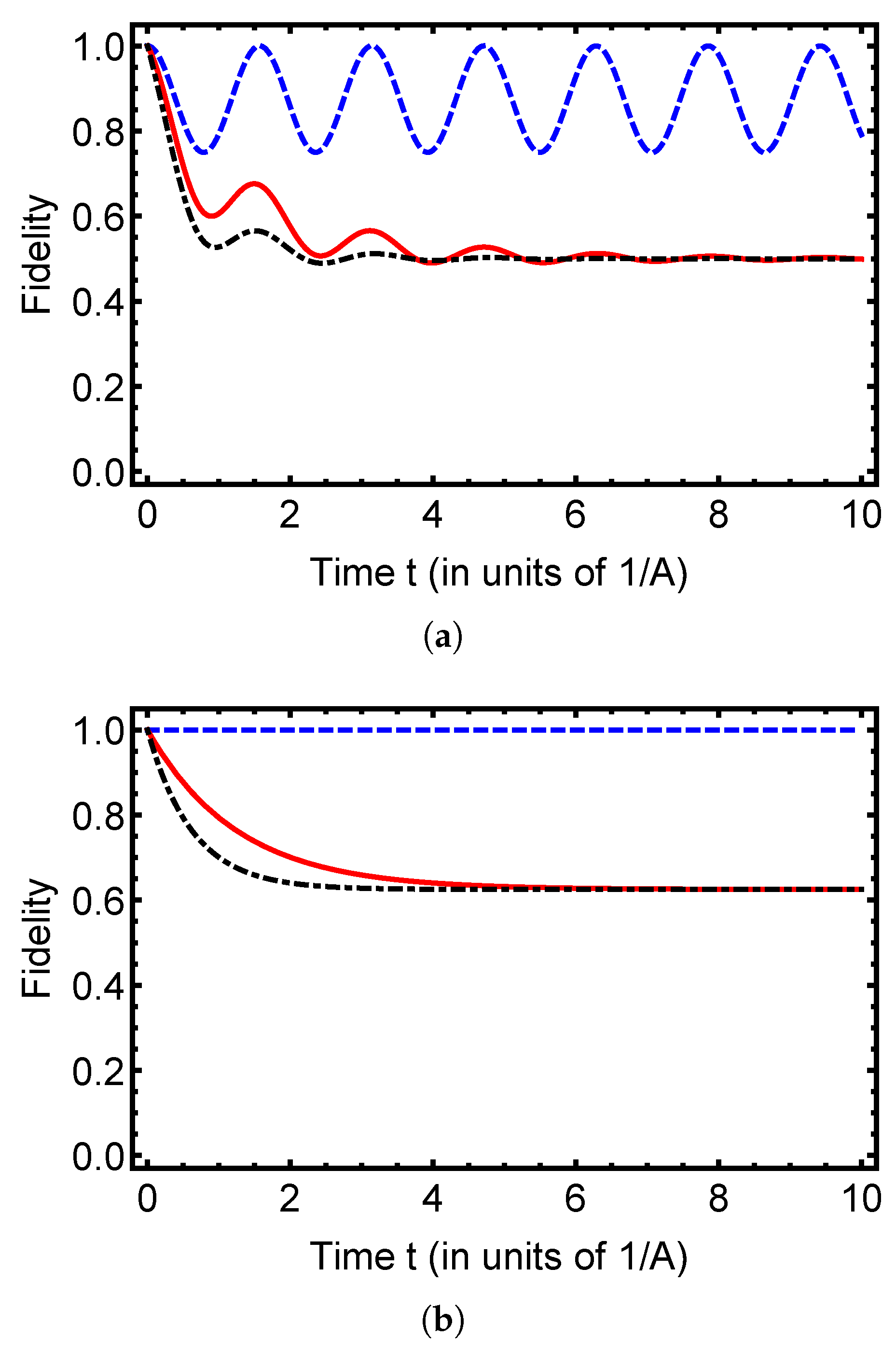
4. Probing Entanglement and Fidelity Dynamics in Open Quantum Systems

In this section, we investigate the time-dependent behavior of key quantum properties, namely entanglement and fidelity, in the hyperfine states of the hydrogen atom. By employing the Lindblad formalism to model pure dephasing and other decoherence channels, we analyze how the system’s quantum correlations evolve under environmental influences. Entanglement provides a measure of nonclassical correlations between the electron and nuclear spins, while fidelity quantifies the closeness of the evolving state to a desired reference state. Together, these metrics offer complementary perspectives: Entanglement captures the internal coherence of the system, whereas fidelity monitors the preservation of specific target states. The following results highlight the interplay between coherent dynamics driven by the hyperfine interaction and dissipative effects arising from external noise, revealing the conditions under which quantum correlations are robust or fragile.

Figure 1 shows the concurrence dynamics for the initial separable states under the hyperfine interaction in hydrogen with Lindblad dephasing. In panel (a), corresponding to the anti-parallel state $|\Psi \rangle$, the unitary hyperfine dynamics coherently mix $|{\uparrow }_e{\downarrow }_p\rangle$ and $|{\downarrow }_e{\uparrow }_p\rangle$, producing oscillations of the concurrence between 0 and nearly 1 when $\Gamma =0$, with frequency $2A$. The presence of dephasing ($\Gamma >0$) suppresses these oscillations, as the off-diagonal terms decay as $e^{-2\Gamma t}$, yielding an entanglement envelope of the form $C\left(t\right)\sim e^{-2\Gamma t}|sin\left(2At\right)|$. Increasing $\Gamma$ from 0 to $0.4A$ and $0.8A$ strongly damps both the amplitude and duration of entanglement, with only a few weak peaks remaining when $\Gamma \gtrsim A/2$. By contrast, panel (b), corresponding to the parallel state $|\varphi \rangle$, shows that concurrence remains zero at all times regardless of $\Gamma$, since the states $|{\uparrow }_e{\uparrow }_p\rangle$ and $|{\downarrow }_e{\downarrow }_p\rangle$ are eigenstates of the hyperfine Hamiltonian and are not coupled by its flip–flop term. Thus, while entanglement generation is possible in the anti-parallel sector, it is entirely absent in the parallel sector, and the robustness of the generated correlations is limited by the strength of the dephasing process.

Figure 2 shows the dynamics of the concurrence for the initially entangled state $|\Psi \rangle \mathrm{and}|\varphi \rangle$ with ($\alpha =\pi /6$) under a Lindblad dephasing model reveals a strong dependence on the states’ symmetry relative to the noise. For the $|\Psi \rangle$ state (panel a), in the ideal case without dephasing ($\Gamma =0$, dashed curve), the concurrence displays periodic oscillations between its initial value and unit, indicating that entanglement is preserved by the coherent evolution of the system. When moderate dephasing is present ($\Gamma =0.4A$, solid curve), the oscillations are strongly damped and the concurrence decays monotonically, reflecting a progressive loss of entanglement. For stronger dephasing ($\Gamma =0.8A$, dash-dotted curve), this decay is further accelerated and leads to entanglement sudden death, where the concurrence vanishes within a finite time. This behavior highlights that entanglement persistence is governed not only by the decoherence rate but also by the initial state’s inherent symmetry and its encoding within protected subspaces. In contrast, the $|\varphi \rangle$ state (panel b), which occupies the single-excitation subspace, in the ideal case without dephasing ($\Gamma =0$, dashed curve), remains constant over all the time. For the initial parallel-spin state $|\varphi \rangle$, the concurrence decays exponentially under dephasing and approaches zero asymptotically, without vanishing at a finite time. Therefore, strict entanglement sudden death (ESD) does not occur for this initial configuration, in contrast to certain anti-parallel states where ESD is observed.

The evolution of concurrence in Figure 3 shows that, for both initial states $|\Psi \rangle$ (panel a) and $|\varphi \rangle$ (panel b), the behavior under dephasing noise is qualitatively identical. In both cases, the concurrence decays monotonically without oscillations, with the rate of decay strongly dependent on the dephasing strength. For $\Gamma =0$, the entanglement remains maximal, while for $\Gamma =0.4A$ and $\Gamma =0.8A$ the entanglement rapidly diminishes, vanishing completely at finite times in the stronger dephasing scenario. These results indicate that, unlike in situations where state symmetry provides partial protection, here both classes of entangled states are equally fragile under phase noise, leading to inevitable disentanglement.

It is worth noting that the relative fragility of the two initial states depends on both the degree of initial entanglement and the spin configuration. For separable or partially entangled states (Figure 1 and Figure 2), the parallel-spin state $|\varphi \rangle$ is more sensitive to dephasing, since both electron and proton contributions act simultaneously on the coherence, leading to faster decay of concurrence. In contrast, for the maximally entangled Bell state ($\alpha =\pi /4$) shown in Figure 3, the population and coherence terms evolve symmetrically, resulting in similar decay rates for both $|\Psi \rangle$ and $|\varphi \rangle$. Consequently, the concurrence dynamics of the two states become qualitatively similar, and the enhanced fragility of the parallel-spin state is no longer observed.

The Figure 4 illustrate the time evolution of the fidelity $F\left(t\right)$ for two distinct initial separable states of an electron–proton spin system under the influence of dephasing. The fidelity measures how well the quantum state at time t matches the initial state, with $F\left(t\right)=1$ indicating perfect preservation and $F\left(t\right)=0$ signifying complete loss of the initial information. The dynamics are governed by the hyperfine coupling A and the total dephasing rate $\Gamma ={\gamma }_e+{\gamma }_p$. The fidelity dynamics presented in Figure 4 reveal distinct behaviors for the initial separable state ($\alpha =0$) depending on whether the system is prepared in $|\Psi \rangle$ (panel a) or $|\varphi \rangle$ (panel b).

In Panel (a), the initial state is given by $|\Psi \left(0\right)\rangle =|{\uparrow }_e{\downarrow }_p\rangle$, which is not an eigenstate of the hyperfine interaction Hamiltonian, ${\mathbf{S}}_e·{\mathbf{I}}_p$. Consequently, without dephasing ($\Gamma =0$, dashed curve), the system experiences coherent Rabi-like oscillations. The fidelity varies between 1 and a minimum value, indicating periodic spin polarization exchange between the electron and proton. The oscillation frequency is controlled by the hyperfine coupling constant $2A$. When dephasing is introduced $(\Gamma >0)$, two key effects are observed: the coherent oscillations are damped, and the fidelity convergence. The solid $(\Gamma =0.4A)$ and dash-dotted $(\gamma =0.8A)$ curves show a rapid decay in the amplitude of the fidelity oscillations due to dephasing destroying the quantum coherence necessary for the oscillatory dynamics. For times $t\gg 1/\Gamma$, the fidelity decays to an asymptotic value of $F(\infty )=0.5$. This occurs as the system evolves into a statistical mixture with equal overlap with the initial state and its orthogonal counterpart, leading to a steady state fidelity of 1/2, and a higher dephasing rate Γ causes this asymptotic value to be reached more quickly as is shown in Appendix B.

In Panel (b), the initial state is given by $|{\uparrow }_e{\uparrow }_p\rangle$, which is a triplet state and is an eigenstate. This fundamental difference leads to dramatically different dynamics compared to panel (a). In the coherent case ($\Gamma =0$), since the initial state is an eigenstate, it remains stationary under coherent evolution. There is no energy exchange, and the fidelity remains constant at $F\left(t\right)=1$ for all times (dashed curve). More importantly, when decay is introduced ($\Gamma >0$), this state is also immune to the specific dephasing mechanism considered. The dephasing likely occurs on the basis ${\sigma }_z^{\left(e\right)}\otimes {\sigma }_z^{\left(p\right)}$, and since $|{\uparrow }_e{\uparrow }_p\rangle$ is already a maximal eigenstate of both ${\sigma }_z^{\left(e\right)}$ and ${\sigma }_z^{\left(p\right)}$, the dephasing noise commutes with the state, leaving it unaffected. The state does not acquire a random phase relative to itself and thus maintains perfect fidelity. Thus, the comparison reveals a crucial principle for protecting the quantum state. States that are not eigenstates (Panel a) suffer from both coherent evolution and dephasing, leading to fidelity loss. Certain eigenstates (Panel b) can be completely protected against specific types of environmental noise when the noise operators commute with the state. This makes $|{\uparrow }_e{\uparrow }_p\rangle$ a potentially valuable state for quantum memory applications in this system. The complete immunity of $|{\uparrow }_e{\uparrow }_p\rangle$ to dephasing highlights the importance of carefully selecting initial states and understanding the symmetry properties of both the system Hamiltonian and the environmental coupling.

Figure 5 shows the dynamics of the fidelity for the initially entangled states $|\Psi \rangle$ and $|\varphi \rangle$ with ($\alpha =\pi /6$) under a Lindblad dephasing model, revealing a strong dependence on the states’ symmetry relative to the noise.

The fidelity evolution for entangled initial states reveals distinct decoherence pathways depending on the state’s symmetry properties. For the initial Bell-like state $|\Psi \left(0\right)\rangle ={cos(\pi /6)|\uparrow }_e{\downarrow }_p{\rangle +sin(\pi /6)|\downarrow }_e{\uparrow }_p\rangle$ in panel (a), which represents a superposition within the singlet-triplet manifold, the fidelity shows damped oscillations under dephasing. The coherent oscillations present at $\Gamma =0$ are progressively suppressed with increasing dephasing rates ($\Gamma =0.4A$ and $0.8A$), eventually decaying to a steady-state value that reflects the competing effects of hyperfine-driven evolution and environmental noise. In contrast, panel (b) demonstrates significantly enhanced robustness for the initial state $|\varphi \left(0\right)\rangle ={cos(\pi /6)|\uparrow }_e{\uparrow }_p{\rangle +sin(\pi /6)|\downarrow }_e{\downarrow }_p\rangle$, which maintains higher fidelity across all dephasing rates. This improved protection stems from the alignment of the state with the ${\sigma }_z^{\left(e\right)}\otimes {\sigma }_z^{\left(p\right)}$ symmetry of the dephasing noise, since both the basis states ${|\uparrow }_e{\uparrow }_p\rangle$ and ${|\downarrow }_e{\downarrow }_p\rangle$ are eigenstates of the dominant dephasing operators, thereby reducing the state’s susceptibility to phase decoherence. The comparison highlights how entanglement structure combined with symmetry considerations can provide substantial protection against specific decoherence channels in quantum systems. The long-time behavior of the fidelity reveals that dephasing does not completely erase the memory of the initial state but instead drives the system into mixed states with partial overlap with the starting configuration. For the $|\Psi \rangle$ state, the fidelity saturates at $0.5$, indicating that in the presence of strong dephasing the system retains only half of its initial-state information, consistent with a statistical mixture of orthogonal components generated by phase noise. In contrast, the $|\varphi \rangle$ state saturates at a higher value, reflecting a greater robustness of this configuration under dephasing, as part of its structure remains aligned with a subspace less affected by phase fluctuations. This difference highlights how the asymptotic fidelity strongly depends on the symmetry of the initial state relative to the noise environment. This is consistent with the analytic calculation presented in Appendix B.

Figure 6 illustrates the dynamics of fidelity for the initial entangled states $|\Psi \rangle$ and $|\varphi \rangle$ with $\alpha =\pi /4$ under a Lindblad dephasing model. The results reveal no qualitative distinction between the two states, as both exhibit identical behavior under dephasing noise. In each case, the fidelity decays monotonically and eventually saturates at $0.5$ when the dephasing is present, indicating that strong dephasing drives the system into a maximally mixed state with equal probability of overlap with the initial configuration and its orthogonal counterpart.

It is interesting to note that, in certain thermal noise environments, entanglement and fidelity can exhibit non-monotonic behavior: thermal backgrounds may enhance quantum entanglement [43] or improve the fidelity of quantum teleportation [44]. In contrast, our study considers pure dephasing noise modeled via local Lindblad operators acting on the hyperfine spin states of hydrogen. We find that entanglement and fidelity exhibit damped oscillatory decay, with anti-parallel spin states showing greater robustness than parallel configurations. This comparison underscores that the type and nature of the environmental noise critically influence quantum correlations, highlighting the relevance of our analytical treatment for understanding and preserving entanglement and fidelity in atomic systems.

5. Conclusions

In this work, we have provided a comprehensive analysis of the quantum dynamics of entanglement and fidelity in the hyperfine structure of hydrogen atoms subjected to pure dephasing noise, modeled using the Lindblad master equation. By deriving exact analytical solutions for the time-dependent density matrix across a spectrum of initial states, ranging from separable to partially and maximally entangled configurations, we have elucidated the intricate interplay between coherent hyperfine interactions and environmental decoherence. Our results demonstrate that entanglement, quantified through concurrence and entanglement of formation, exhibits oscillatory decay modulated by the dephasing rate, with anti-parallel spin states ($|\Psi \rangle$) showing greater robustness compared to parallel configurations ($|\varphi \rangle$), which often experience entanglement sudden death. The fidelity analysis further reveals oscillatory decay patterns, underscoring the sensitivity of quantum state preservation to dephasing noise. Beyond their fundamental significance, these insights contribute to the broader effort to identify strategies for protecting quantum resources against environmental disturbances. In particular, the identification of state-dependent robustness under dephasing noise highlights potential pathways for encoding information in symmetry-protected subspaces. Our findings thus offer valuable guidance for quantum information processing protocols that exploit atomic systems, where the control and preservation of entanglement and fidelity are essential for future quantum technologies.