Low-Carbon Economic Collaborative Scheduling Strategy for Aluminum Electrolysis Loads with a High Proportion of Renewable Energy Integration
Abstract
1. Introduction
- (1)
- Focusing on the power regulation capability of aluminum electrolysis, a refined coupling model of aluminum electrolysis load considering operational stability constraints was constructed, a dynamic constraint system for the aluminum electrolysis production process was established, and the stability boundaries under different regulation depths, rates, and durations were quantified.
- (2)
- This research proposes the dynamic response relationship between electrolytic cell power regulation and multi-functional overhead crane operating characteristics, establishes a dynamic coupling model between electrolytic cells and multi-functional crane operating characteristics, and achieves coordinated scheduling optimization of primary and auxiliary equipment.
- (3)
- Based on three key perspectives—the adjustable load characteristics of aluminum electrolysis, abundant renewable energy resources, and national energy transition strategy—this research develops a three-objective optimization strategy for source–storage–load coordinated scheduling in aluminum electrolysis parks under different renewable energy penetration rates.
2. Adjustable Characteristics of Aluminum Electrolysis Loads
- (1)
- Power Constraints
- (2)
- Temperature and Power Coupling Constraints
- (3)
- Adjustable Time Constraints
- (4)
- Operational State Constraints
- (5)
- Temperature and Efficiency Constraints
- (6)
- Coupling Between Current Efficiency of Aluminum Electrolytic Cells and Alumi-num Production
- (7)
- Coupling Constraints between Multi-functional Gantry Crane Load and Aluminum Production
3. Coordinated Optimization Model for the Source–Load of Aluminum Electrolysis Load
3.1. System Architecture
3.2. Objective Function
3.2.1. Objective Function 1
- (1)
- Operating Cost of Renewable Energy Units
- (2)
- Operating Costs of Thermal Power Units
- (3)
- Adjustment Cost of Aluminum Electrolysis Load
- (4)
- Adjustment Cost of Multifunctional Overhead Crane Load
- (5)
- Operating Cost of Energy Storage
- (6)
- Cost of Power Exchange with the Grid
3.2.2. Objective Function 2
- (1)
- Carbon Emissions from Carbon Anodes
- (2)
- Carbon Emissions from Anode Effects
- (3)
- Carbon Emissions from Renewable Energy Units
- (4)
- Carbon Emissions from Thermal Power Units
- (5)
- Carbon Emissions from Grid Power Exchange
3.2.3. Objective Function 3
3.3. Variable Constraints
- (1)
- Renewable Energy Constraints
- (2)
- Thermal Power Unit Output Constraints
- (3)
- Thermal Power Unit Ramp Rate Constraints
- (4)
- Aluminum Electrolysis Load Regulation Constraints, refer to Equations (1)–(19).
- (5)
- Grid Power Exchange Constraints
4. Model Solution
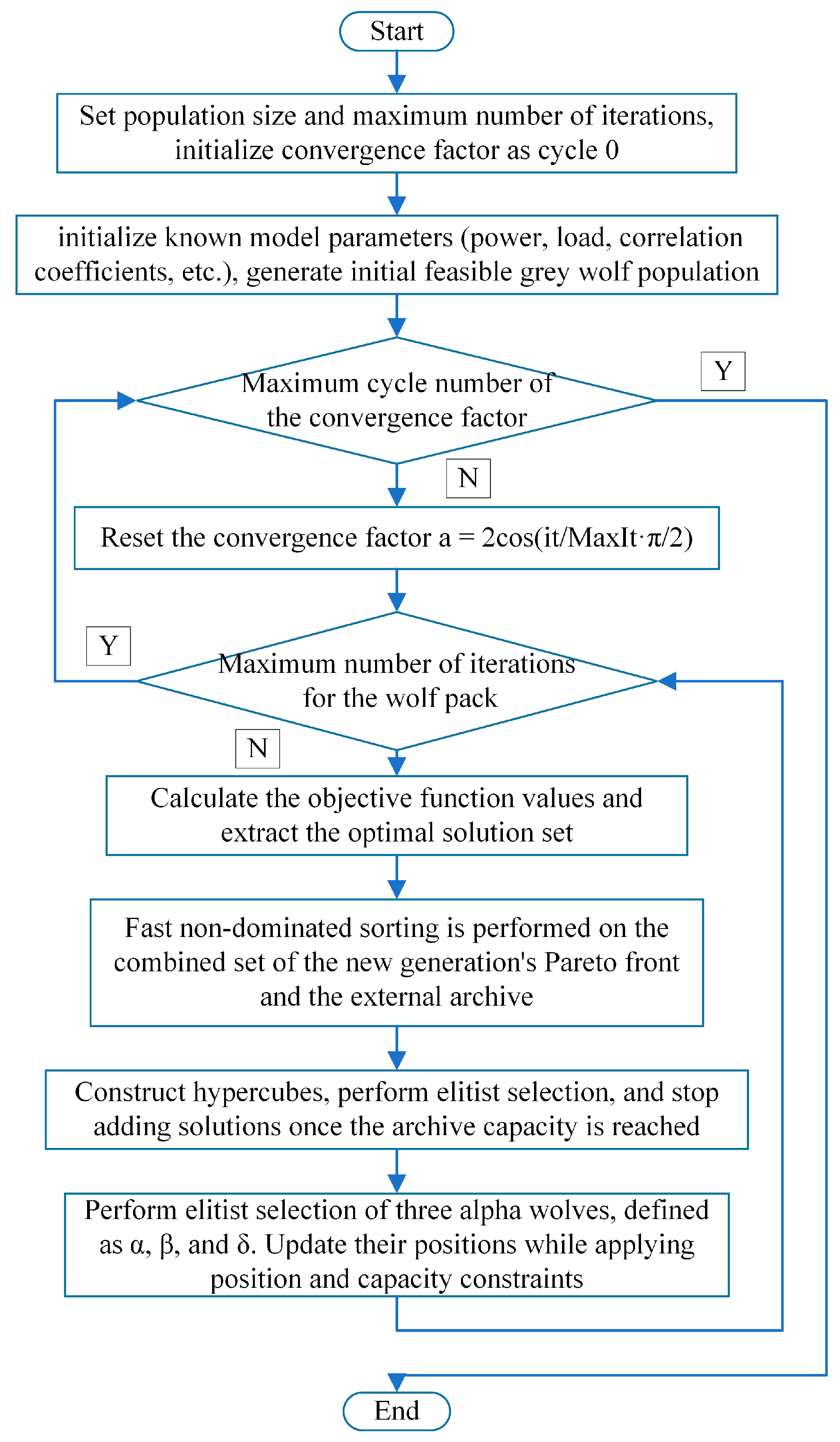
- (1)
- Step 1: Initialize grey wolf algorithm, set population size and maximum iterations, import known model parameters (power, load, correlation coefficients, etc.), initialize population matrix arrangement as position, fitness function value, Pareto rank, crowding distance, and initialize convergence factor as cycle 0.
- (2)
- Step 2: Reset current iteration count for single convergence factor cycle wolf pack, and reset convergence factor as a = 2cos(it/MaxItpi/2), control search range, prepare for next iteration round.
- (3)
- Step 3: Calculate objective function values: operating cost, carbon emissions, renewable energy consumption rate; perform non-dominated sorting on population, determine each wolf’s superiority, establish Archive population, perform crowding distance sorting on Archive population, retain optimal and uniformly distributed solutions before entering the iteration process.
- (4)
- Step 4: Construct a hypercube, place particles into the hypercube, then perform elite selection based on particle crowding degree, and stop adding when the accumulated storage capacity is reached.
- (5)
- Step 5: Select three representative alpha wolves (Alpha, Beta, and Delta) from the repository, representing the current best, second-best, and third-best solutions. Update all grey wolves’ positions based on alpha wolves’ positions, process boundary violations of new positions to ensure variables remain within a reasonable range, proceed to the next round of objective function calculation and sorting.
- (6)
- Step 6: Check if the current single cycle maximum iterations reached (inner loop), check if the maximum number of cycles reached (outer loop).
- (7)
- Step 7: If the maximum number of cycles is reached, the algorithm terminates, output optimal solution set (Pareto front) for subsequent decision analysis.
5. Case Study
5.1. Case Introduction
- (1)
- Setting a basic scenario with economic benefits as the core objective, allowing daily production to fluctuate within 90–110% of rated production, which is significant for verifying the daily adjustability of aluminum electrolysis loads.
- (2)
- In fixed-production scenario analysis, the study is divided into two directions: conventional economic optimization without considering adjustable characteristics, focusing on traditional cost-effectiveness; and three-objective collaborative optimization considering economics, carbon emissions, and renewable energy consumption rate.
- (3)
- In fixed-production multi-objective scenario analysis, the three-objective optimization study focusing on economics, carbon emissions, and renewable energy consumption rate is further deepened by expanding the renewable energy integration scale.
- (4)
- Based on the different emphasis of three-objective optimization analysis, pairwise analysis of economics, carbon emissions, and renewable energy consumption rate reveals the inherent correlations and trade-off characteristics between objectives.
- (5)
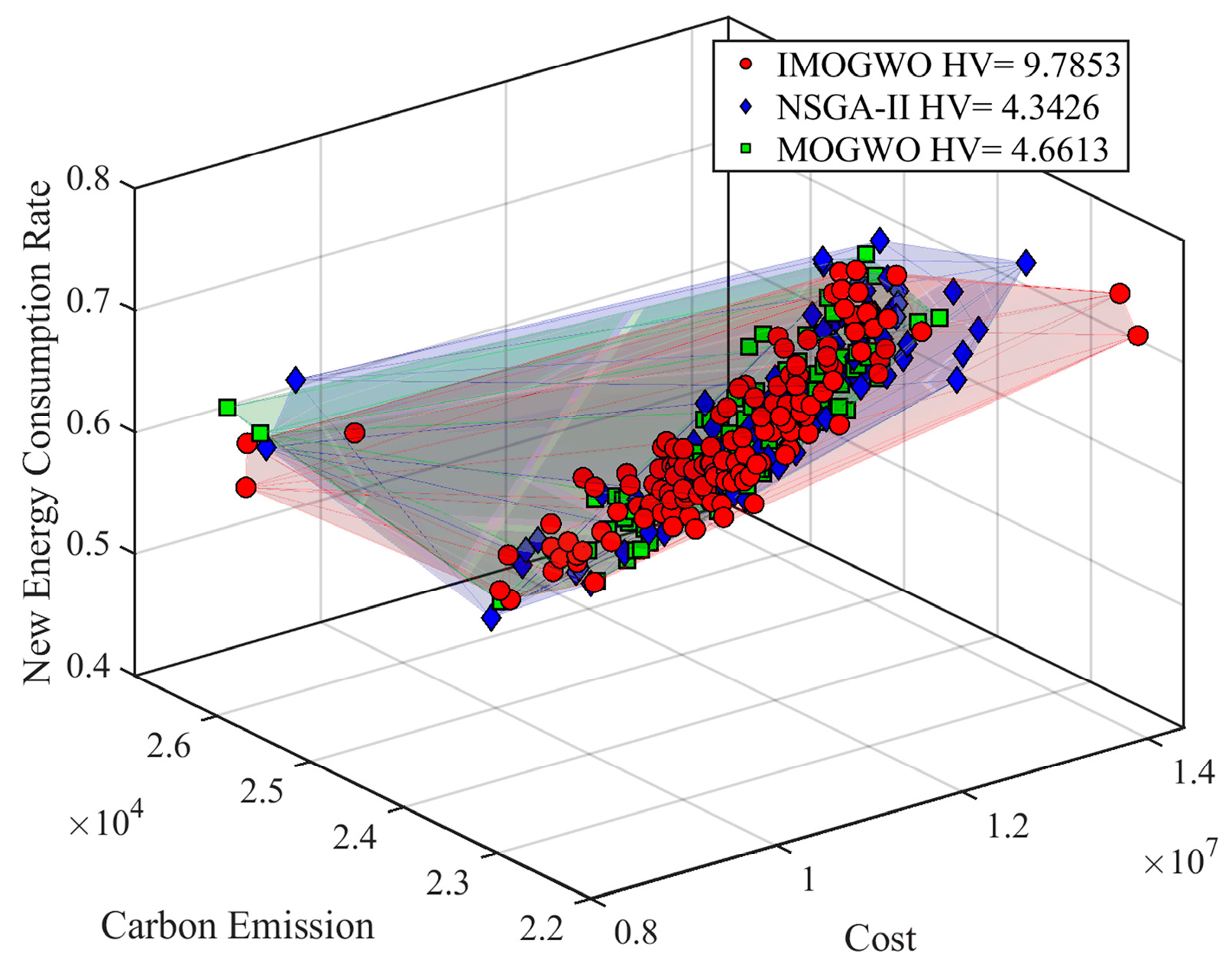
- To verify the effectiveness and advancement of the proposed model and algorithm, comparisons with benchmark models highlight the superiority of the proposed model in application. Subsequently, IMOGWO is compared with mainstream algorithms such as NSGA-II and MOGWO.
5.2. Results Analysis
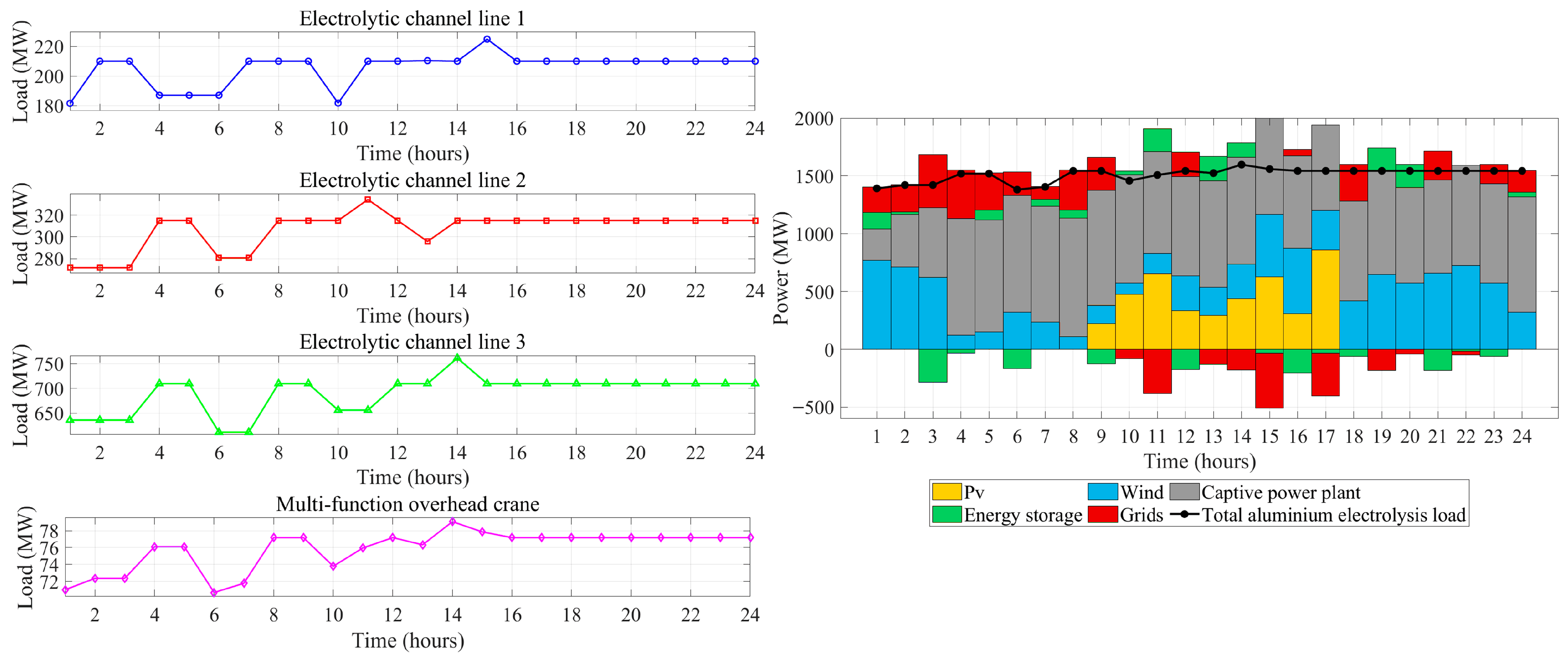
5.2.1. Analysis of Aluminum Electrolysis Load Regulation
5.2.2. Multi-Objective Optimization Dispatch Study of Aluminum Electrolysis Load
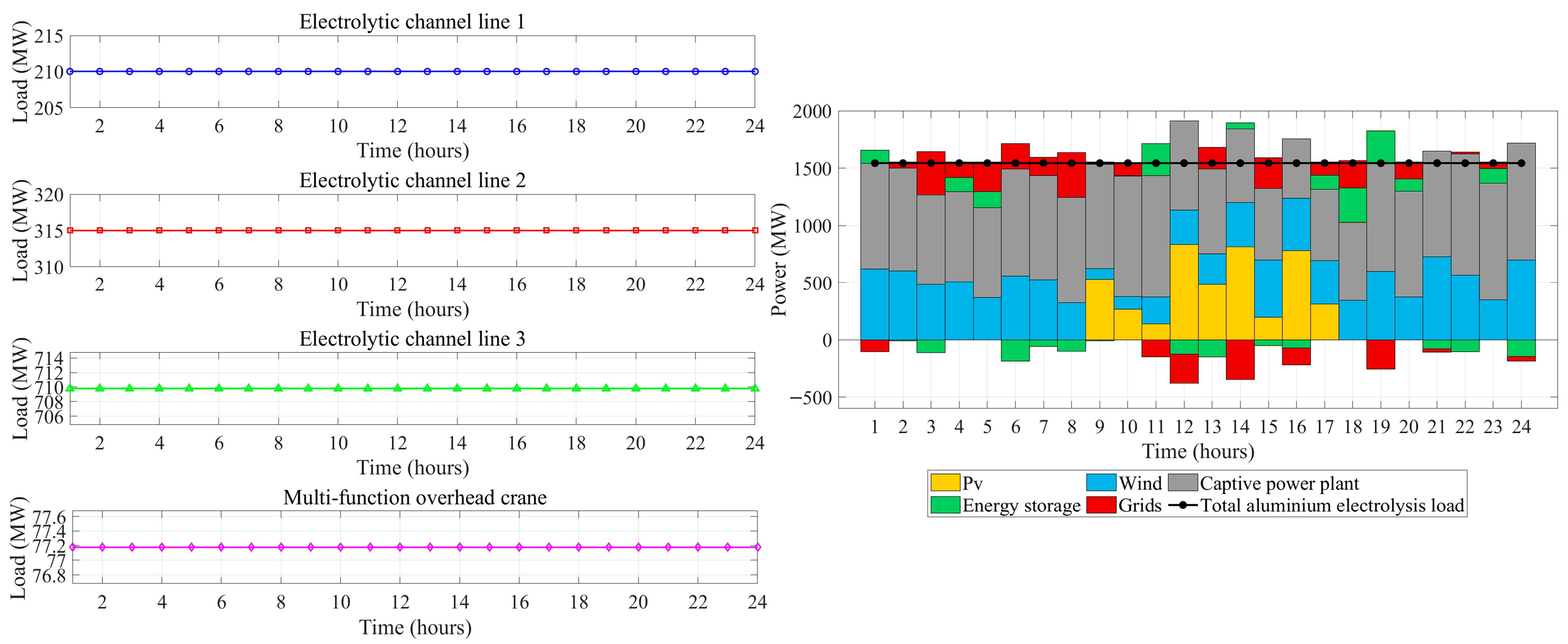
5.2.3. Multi-Objective Optimization Dispatch Analysis with a Higher Proportion of Renewable Energy Integration
5.2.4. Correlation Analysis Between Multiple Objectives
5.2.5. Validation of Model and Algorithm Effectiveness
6. Conclusions
- Including operational characteristics of auxiliary equipment (multi-functional cranes) in aluminum electrolysis load modeling has significant practical implications. Considering the impact of multi-functional crane loads on overall system energy consumption reflects the dynamic load characteristics of the entire production system, enabling a more comprehensive evaluation of aluminum electrolysis enterprises’ regulation capability.
- The multi-objective optimization strategy in the proposed source–storage–load coordinated optimization mode can systematically coordinate operating costs, overall carbon emissions, and renewable energy consumption of the aluminum electrolysis park, yielding decision solutions that balance overall economic and low-carbon objectives.
- The significant advantages of multi-objective optimization under large-scale renewable energy integration conditions are explored. This not only provides an effective pathway for the current green transformation of the aluminum electrolysis industry but also offers valuable reference for the sustainable development of other energy-intensive industries.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Unit Model Number | Number of Units | Maximum Output (MW) | Minimum Output (MW) | Start–Stop Cost (CNY) | Cost Parameters a/b/c (CNY/MW2) (CNY/MW)(CNY) | Minimum Up/Down Time (h) | Maximum Ramp Rate (MW/h) | CO2 Emission Intensity (N.m3CO2/kWh) |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 85 | 40 | 1820 | 0.00553/193.9/3360 | 3/3 | 80/80 | 0.46 |
| 2 | 3 | 130 | 65 | 3920 | 0.01477/115.5/4790 | 5/5 | 100/100 | 0.46 |
| 3 | 1 | 455 | 230 | 35000 | 0.00217/121.1/6790 | 5/5 | 200/200 | 0.46 |
| Values | |
|---|---|
| Charging efficiency | 0.92 |
| Discharging efficiency | 0.92 |
| Maximum charge/discharge power (MW) | 300 |
| Maximum capacity (MWh) | 1200 |
| Initial capacity (MWh) | 360 |
| Minimum state of charge | 0.1 × 1200 |
| Maximum state of charge | 0.9 × 1200 |
| Operation and maintenance cost (CNY/kWh) | 0.025 |
| Energy Type | Carbon Emission Coefficient g/(kW·h) |
|---|---|
| Self-owned power plant | Calculated based on thermal power unit carbon emission intensity |
| Power grid | 0.5703 |
| Wind power generation | 0.02362 |
| Solar power generation | 0.04191 |
| Energy storage | 0 |

References
- Tregnago, G. Fifty years of change in the energy sector. Nat. Energy 2025, 10, 3–5. [Google Scholar] [CrossRef]
- National Security Emergency Preparedness (NSEP) Network. Electricity Consumption Growth Ranking by Industry in China 2023. Available online: https://news.bjx.com.cn/html/20240223/1362664.shtml (accessed on 24 September 2025).
- Hepburn, C.; Qi, Y.; Stern, N.; Ward, B.; Xie, C.; Zenghelis, D. Towards carbon neutrality and China’s 14th Five-Year Plan: Clean energy transition, sustainable urban development, and investment priorities. Environ. Sci. Ecotechnol. 2021, 8, 100130. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.; Wu, Z. Reinforcement Learning-Based Time of Use Pricing Design Toward Distributed Energy Integration in Low Carbon Power System. IEEE Trans. Netw. Sci. Eng. 2025, 12, 997–1010. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, Z.; Wei, L.; Yang, L.; Yuan, B.; Zhou, M. Understanding the synergy of energy storage and renewables in decarbonization via random forest-based explainable AI. Appl. Energy 2025, 390, 125891. [Google Scholar] [CrossRef]
- Harrison-Atlas, D.; Murphy, C.; Schleifer, A.; Grue, N. Temporal complementarity and value of wind-PV hybrid systems across the United States. Renew. Energy 2022, 201, 111–123. [Google Scholar] [CrossRef]
- Lindberg, O.; Arnqvist, J.; Munkhammar, J.; Lingfors, D. Review on power-production modeling of hybrid wind and PV power parks. J. Renew. Sustain. Energy 2021, 13, 042702. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, C.; Chen, T.; Lei, M.; Wattana, S.; Wattana, B. Strategies of a Wind–Solar–Storage System in Jiangxi Province Using the LEAP–NEMO Framework for Achieving Carbon Peaking Goals. Energies 2025, 18, 1135. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, Y.; Zhang, Y.; Xiang, M. Optimized Configuration Method of Park-level Hydrogen Energy System for Coordinated Operation of Hybrid Electrolyzers. Dianwang Jishu/Power Syst. Technol. 2025, 49, 3256–3265. [Google Scholar] [CrossRef]
- Li, C.; Li, R.; Wang, W.; Tang, Q.; Zhu, Y. Configuration optimization of distributed PV-storage system in industrial park considering load management. J. Renew. Sustain. Energy 2025, 17, 034102. [Google Scholar] [CrossRef]
- Sun, H.; Chen, F. The impact of green finance on China’s regional energy consumption structure based on system GMM. Resour. Policy 2022, 76, 102588. [Google Scholar] [CrossRef]
- Li, S.W.; Hui, H.Y.; Bao, M.L. Quantified Adjustability of Aluminum Smelter Loads and Their Participation in Coordinated Scheduling of Power System. Proc. CSU-EPSA 2024, 36, 70–80. [Google Scholar] [CrossRef]
- Yue, X.; Liao, S.; Fu, L.; Xu, J.; Ke, D.; Wang, H.; Li, L.; He, X. Hierarchical Optimization Strategy of High-penetration Wind Power System Considering Electrolytic Aluminum Energy-intensive Load Regulation and Deep Peak Shaving of Thermal Power. Dianwang Jishu/Power Syst. Technol. 2024, 48, 3186–3196. [Google Scholar] [CrossRef]
- Zheng, W.; Yu, P.; Xu, Z.; Fan, T.; Liu, H.; Yu, M.; Zhang, J.; Li, J. Day-ahead Intra-day Economic Dispatch Methodology Accounting for the Participation of Electrolytic Aluminum Loads and Energy Storage in Power System Peaking. In Proceedings of the 2nd IEEE International Conference on Power Science and Technology, ICPST 2024, Dali, China, 9–11 May 2024; pp. 2201–2206. [Google Scholar] [CrossRef]
- Ding, X.; Xu, J.; Sun, Y.; Liao, S. Source-load coordinated control strategy for smoothing wind power fluctuation in grid-connected high energy consuming electrolytic aluminum industrial power grid. Dianli Zidonghua Shebei/Electr. Power Autom. Equip. 2022, 42, 47–55. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, H.; Zhu, H. Source-load coordinated optimal planning method of electrolytic aluminum industrial park. Dianli Zidonghua Shebei/Electr. Power Autom. Equip. 2024, 44, 132–140. [Google Scholar] [CrossRef]
- Yue, X.; Fu, L.; Liao, S.; Xu, J.; Ke, D.; Wang, H.; Feng, S.; Yang, J.; He, X. A source-load collaborative stochastic optimization method considering the electricity price uncertainty and industrial load peak regulation compensation benefit. Int. J. Electr. Power Energy Syst. 2025, 167, 110630. [Google Scholar] [CrossRef]
- Dai, L.; Kang, Z.; Chen, R.; Wang, L. Study on multi-objective maintenance decision optimization for bridge networks based on NSGA-III. Tumu Gongcheng Xuebao/China Civ. Eng. J. 2024, 57, 41–52. [Google Scholar] [CrossRef]
- El Qouarti, O.; Nasser, T.; Essadki, A.; Akarne, Y. AC/DC hybrid microgrid energy management optimization as a decisive factor towards De-Carbonization and rational integration of electrical self-generating units using three-objective grey wolf optimization algorithm-power to X and renewable energies solutions. Int. J. Hydrogen Energy 2025, 138, 1116–1130. [Google Scholar] [CrossRef]
- Ullah, K.; Hafeez, G.; Khan, I.; Ullah, S.; Alghamdi, B.; Alsafran, A.S.; Kraiem, H. Energy optimization using hybrid demand response, renewable energy, and storage battery: A tri-objective optimization approach. Sustain. Cities Soc. 2025, 122, 106145. [Google Scholar] [CrossRef]
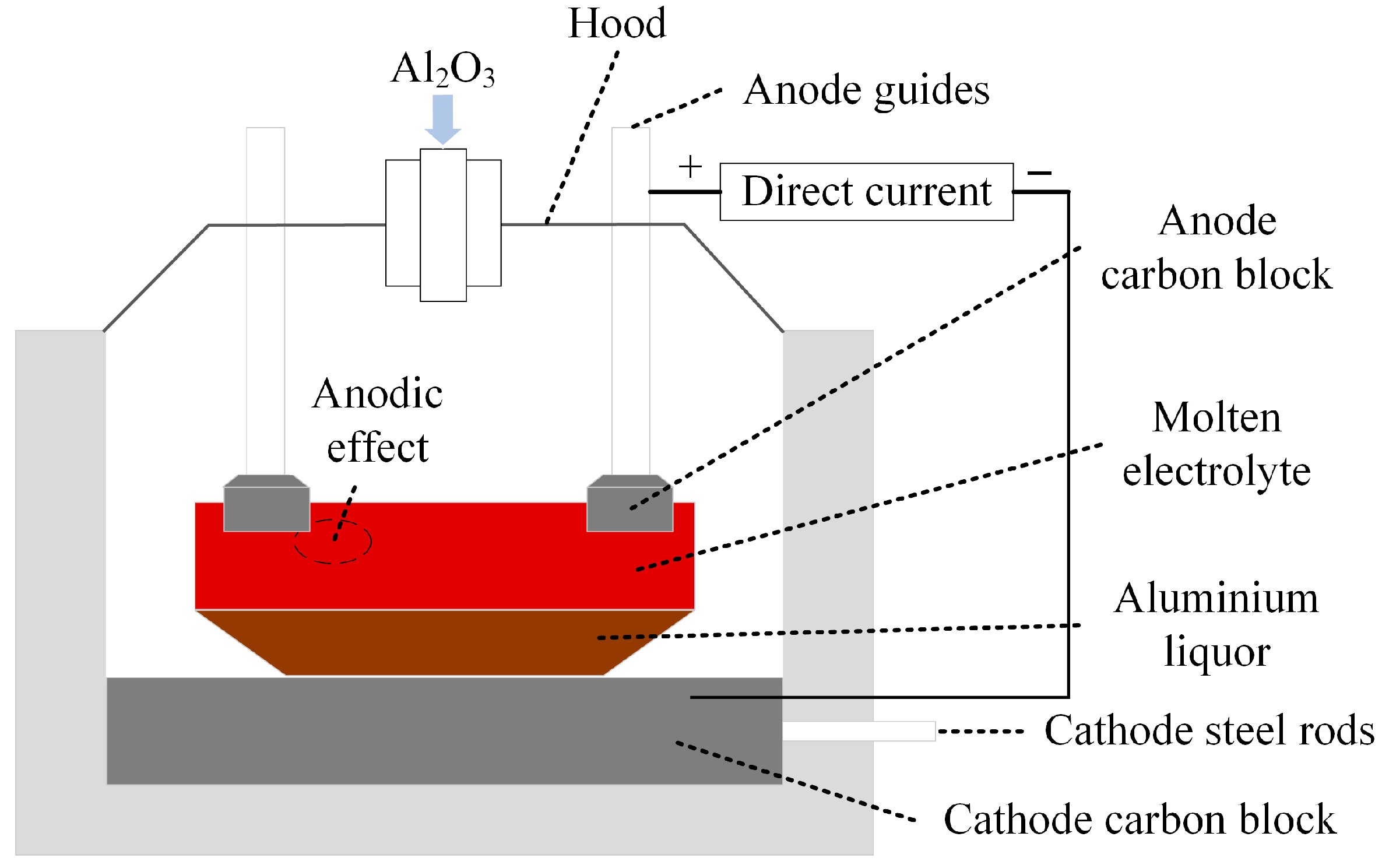
- Haarberg, G.M. Electrowinning of Aluminum—Challenges and Possibilities for Reducing the Carbon Footprint. Electrochemistry 2024, 92, 043002. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, X.; Zhao, J.; Chen, C.; He, G.; Zhang, L. The study of thermal-electrical coupling numerical simulation of aluminum electrolytic cell anode assembly and parameter optimization of steel claws. Results Eng. 2025, 26, 104738. [Google Scholar] [CrossRef]
- Xu, J.; Liao, S.; Sun, Y.; Ma, X.Y.; Gao, W.; Li, X.; Gu, J.; Dong, J.; Zhou, M. An Isolated Industrial Power System Driven by Wind-Coal Power for Aluminum Productions: A Case Study of Frequency Control. IEEE Trans. Power Syst. 2015, 30, 471–483. [Google Scholar] [CrossRef]
- Gao, B.; Niu, H.; Guan, Y.; Wang, Z.; Liu, J.; Taylor, M.P.; Chen, J.J.J. Visualization of Anode Effect in Aluminum Electrolysis. J. Electrochem. Soc. 2022, 169, 013505. [Google Scholar] [CrossRef]
- Morishige, T.; Haarberg, G.M.; Gudbrandsen, H.; Skybakmoen, E.; Solheim, A.; Takenaka, T. Effects of Composition and Temperature on Current Efficiency for Aluminium Electrolysis from Cryolite-Based Molten Alumina Electrolytes. ECS Trans. 2017, 77, 997. [Google Scholar] [CrossRef]
- Tang, F.; Liu, B. The crane development of furnace tending assembly based on virtual design. Light Met. 2010, 5, 39–41. [Google Scholar] [CrossRef]
- Lian, X.; Gao, H.; Shen, L.; Yu, Y.; Wang, Y.; Peng, Z. Life Cycle Assessment of Primary Aluminum Production. Processes 2025, 13, 419. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, J.; Liu, Y.; Gong, F. Demand-Side Flexibility Series: Overview of Flexibility Potential in Aluminum Electrolysis Industry. Available online: https://rmi.org.cn/insights/industrial-dsf/ (accessed on 15 September 2023).
- Sun, K.; Li, J.; Zhang, H.; Li, T.; Li, J. First-Principles Study on the Mechanism of Greenhouse Gas Generation in Aluminum Electrolysis. Metals 2021, 11, 1118. [Google Scholar] [CrossRef]
- Liu, T.; Wu, Y.; Xu, H. Multi-task assisted multi-objective optimization algorithm for autonomous underwater vehicle path planning. Memetic Comput. 2025, 17, 8. [Google Scholar] [CrossRef]
- Chen, L.; Cao, L.; Wen, Y.; Chen, H.; Jiang, S.-L. A knowledge-based NSGA-II algorithm for multi-objective hot rolling production scheduling under flexible time-of-use electricity pricing. J. Manuf. Syst. 2023, 69, 255–270. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Wu, Y.; Li, K. MBB-MOGWO: Modified Boltzmann-Based Multi-Objective Grey Wolf Optimizer. Sensors 2024, 24, 1502. [Google Scholar] [CrossRef]
- Shao, X.; Fan, Y. An Improved Beetle Antennae Search Algorithm Based on the Elite Selection Mechanism and the Neighbor Mobility Strategy for Global Optimization Problems. IEEE Access 2021, 9, 137524–137542. [Google Scholar] [CrossRef]
- Maduka, A.C.; Ogwu, S.O.; Ekesiobi, C.S. Assessing the moderating effect of institutional quality on economic growth—Carbon emission nexus in Nigeria. Environ. Sci. Pollut. Res. 2022, 29, 64924–64938. [Google Scholar] [CrossRef] [PubMed]


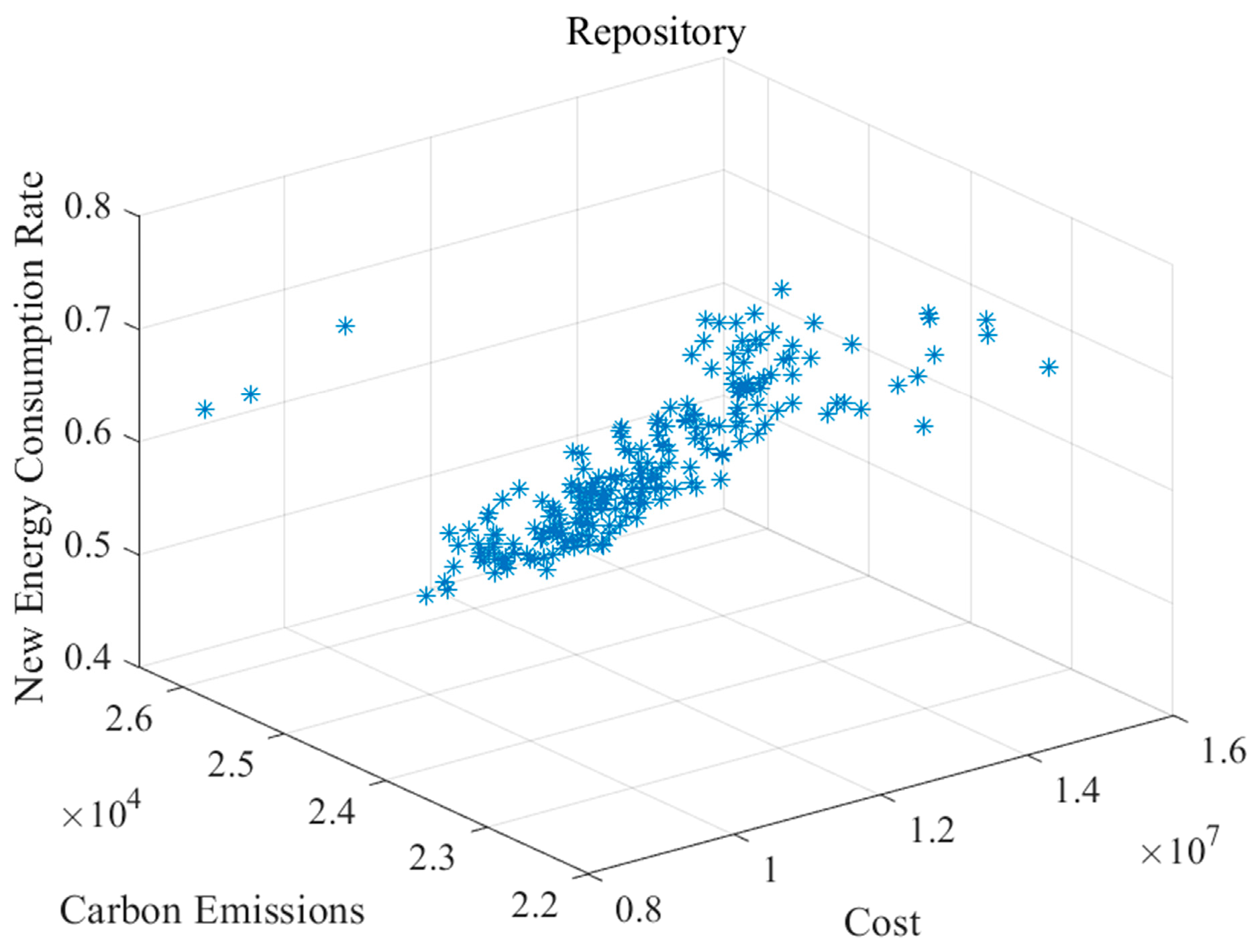
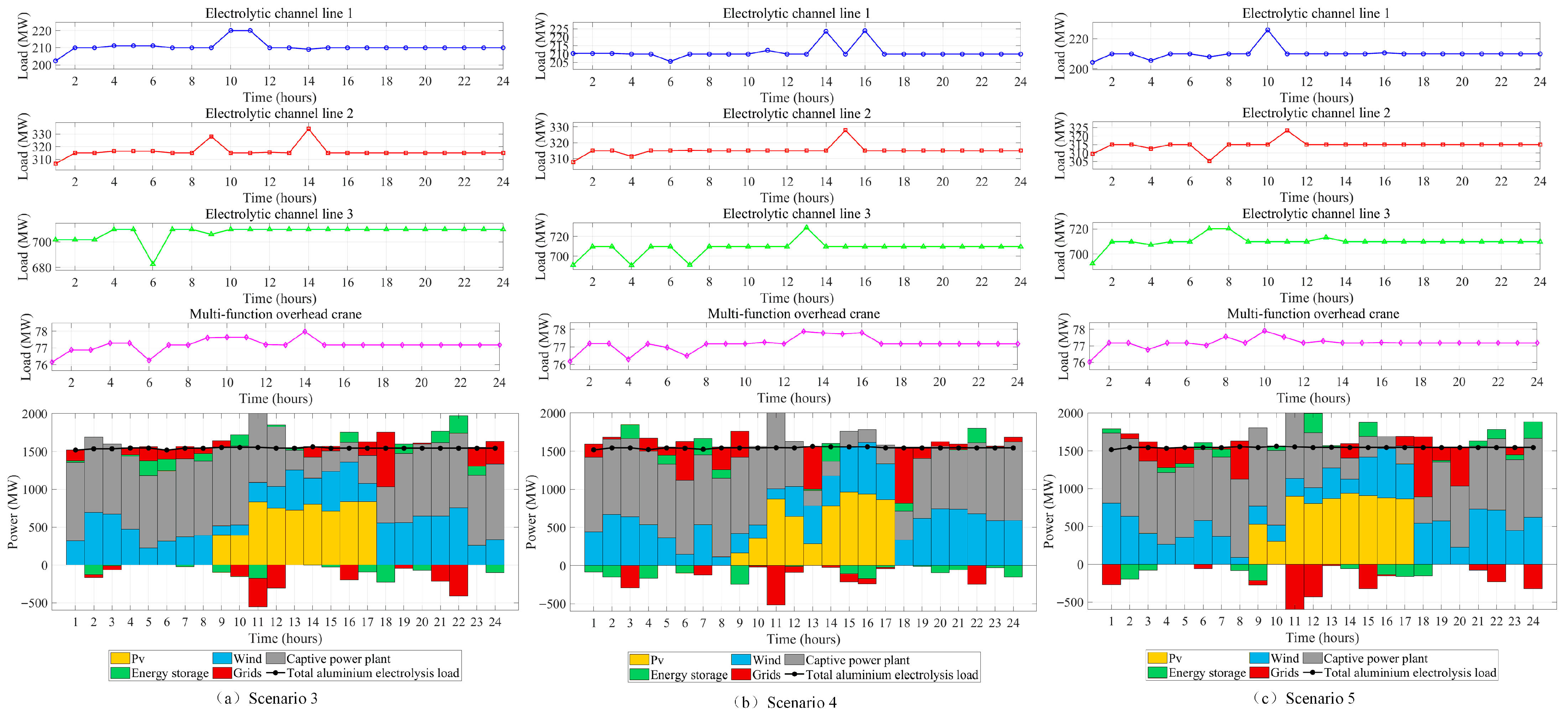

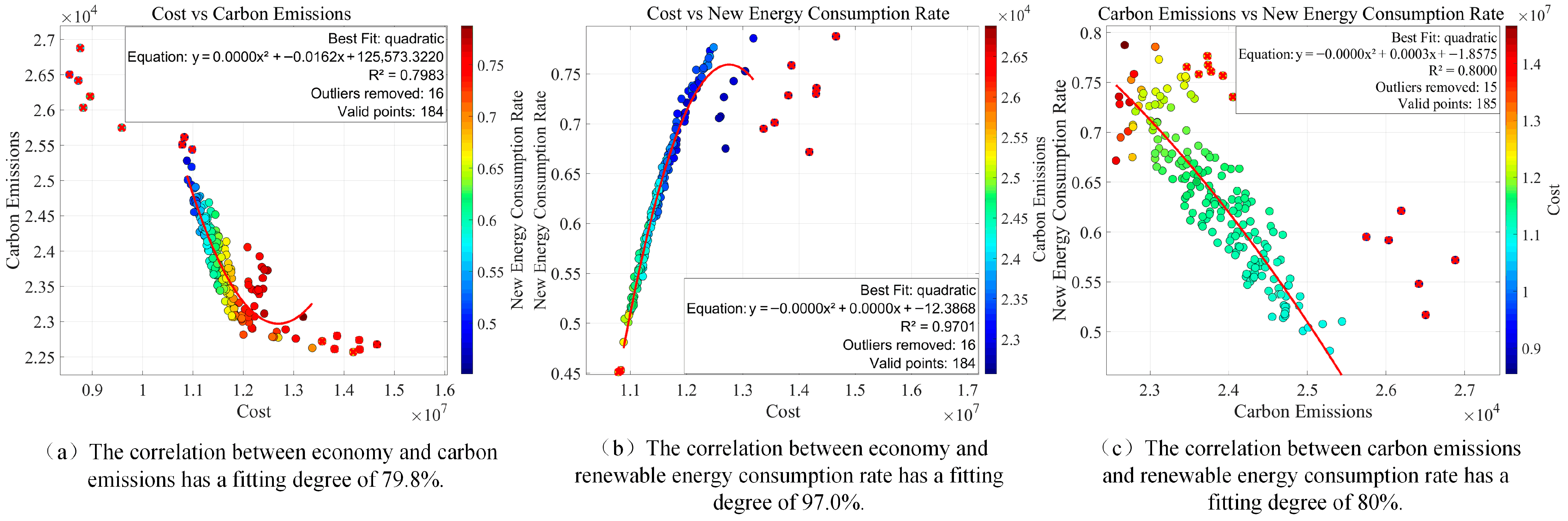
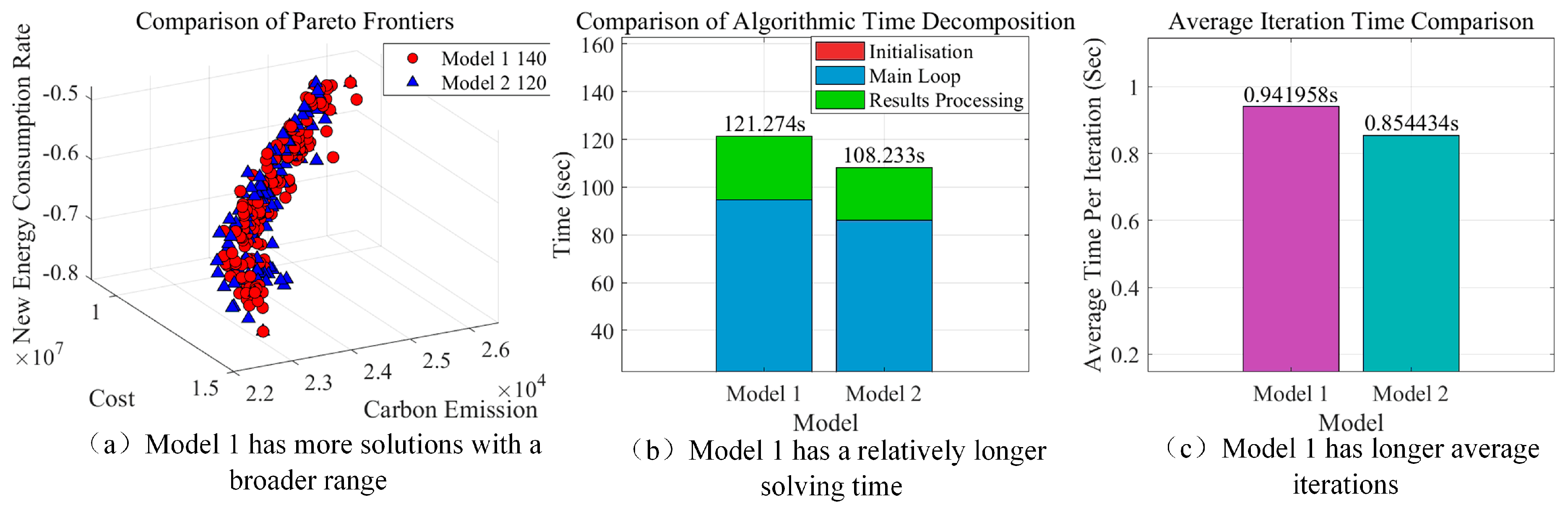
| Algorithm | |||
|---|---|---|---|
| Scenario 3 vs. 6 | 0.4 | 0.3 | 0.3 |
| Scenario 4 vs. 7 | 0.3 | 0.4 | 0.3 |
| Scenario 5 vs. 8 | 0.3 | 0.3 | 0.4 |
| Renewable Energy Penetration Rate | Cost (10,000 CNY) | Carbon Emissions (t) | RE Consumption Rate | |
|---|---|---|---|---|
| 67.8% (1200 MW Wind + 1120 MW Solar) | Scenario 3 | 1199.63 | 23,283.58 | 73.36% |
| Scenario 4 | 1292.60 | 22,636.69 | 76.74% | |
| Scenario 5 | 1260.26 | 22,873.14 | 77.82% |
| Renewable Energy Penetration Rate | Cost (10,000 CNY) | Carbon Emissions (t) | RE Consumption Rate | |
|---|---|---|---|---|
| 76.2% (2400 MW Wind + 1120 MW Solar) | Scenario 6 | 991.56 | 18,126.18 | 83.63% |
| Scenario 7 | 1270.72 | 16,053.07 | 83.47% | |
| Scenario 8 | 1146.54 | 17,385.37 | 84.57% |
| Algorithm | Population | Iterations | Specific Parameters |
|---|---|---|---|
| NSGA-II | 500 | 100 | pMutation = 0.4; pCrossover = 0.7 |
| MOGWO | 500 | 100 | alpha = 0.1; nGrid = 10; beta = 4; gamma = 2; |
| IMOGWO | 500 | 100 | alpha = 0.1; nGrid = 10; beta = 4; gamma = 2; |
| Algorithm | Number of Solution Sets | HV (Mean ± Std) | Runtime (s) |
|---|---|---|---|
| NSGA-II | 97 | 4.3426 | 1653.38 |
| MOGWO | 98 | 4.6613 | 239.25 |
| IMOGWO | 135 | 9.783 | 96.7543 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Chen, Y.; Liu, G.; Han, R. Low-Carbon Economic Collaborative Scheduling Strategy for Aluminum Electrolysis Loads with a High Proportion of Renewable Energy Integration. Appl. Sci. 2025, 15, 10919. https://doi.org/10.3390/app152010919
Li J, Chen Y, Liu G, Han R. Low-Carbon Economic Collaborative Scheduling Strategy for Aluminum Electrolysis Loads with a High Proportion of Renewable Energy Integration. Applied Sciences. 2025; 15(20):10919. https://doi.org/10.3390/app152010919
Chicago/Turabian StyleLi, Jingyu, Yuanyu Chen, Guangchen Liu, and Ruyue Han. 2025. "Low-Carbon Economic Collaborative Scheduling Strategy for Aluminum Electrolysis Loads with a High Proportion of Renewable Energy Integration" Applied Sciences 15, no. 20: 10919. https://doi.org/10.3390/app152010919
APA StyleLi, J., Chen, Y., Liu, G., & Han, R. (2025). Low-Carbon Economic Collaborative Scheduling Strategy for Aluminum Electrolysis Loads with a High Proportion of Renewable Energy Integration. Applied Sciences, 15(20), 10919. https://doi.org/10.3390/app152010919





