From Predictive Coding to EBPM: A Novel DIME Integrative Model for Recognition and Cognition
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. The Theoretical Framework of the EBPM Model
- Sensory components (e.g., visual edges and colors, auditory timbres, tactile cues);
- Motor components (articular configurations, force vectors);
- Interoceptive and emotional components (visceral state, affective value);
- Cognitive components (associations, abstract rules).
- These engrams are constructed through experience and consolidated by Hebbian plasticity and spike-timing-dependent plasticity (STDP) mechanisms [4,8]. They are composed of elementary sub-engrams (feature primitives), such as edge orientations or elementary movements, which can be reused in multiple combinations.
- 1.
- Stimulus activation—sensory input activates elementary engram units (sub-engrams) such as edges, textures, tones, and motor or interoceptive signals.
- 2.
- Engram co-activation—shared sub-engrams may partially activate multiple parent engrams in parallel.
- 3.
- Scoring and aggregation—each parent engram accumulates an activation score based on the convergence of its sub-engrams.
- 4.
- Winner selection—if a single engram surpasses the recognition threshold, it is fully activated and determines the output; if several engrams are partially active, the strongest one prevails through lateral inhibition.
- 5.
- Novelty detection—if all activation scores remain below the threshold, the system enters a novelty state: no complete engram is recognized.
- 6.
- Attention engagement—attention is mobilized to increase neuronal gain and plasticity, strengthening the binding of co-active sub-engrams into a proto-engram.
- 7.
- Consolidation vs. fading—if the stimulus/event is repeated or behaviorally relevant, the proto-engram is consolidated into a stable engram; if not, the weak connections gradually fade.
2.2. The Theoretical Framework of Predictive Coding (PC)
- Internal generative models (hierarchical representations of the environment);
- Prediction errors (differences between input and predictions);
- Adaptive updating (learning through error minimization).
2.3. Comparison of EBPM and PC
2.3.1. Theoretical Foundation
2.3.2. Processing Dynamics in the Two Models
- Predictive Coding (PC)
- The brain generates hierarchical top-down predictions.
- Sensory input is compared with predictions.
- Prediction errors are transmitted upward and correct the internal model.
- Perception arises as the result of minimizing the difference between prediction and input.
- EBPM
- The input activates elementary engram units.
- The elementary engram units simultaneously activate multiple engrams.
- Through lateral inhibition, the most active engram prevails.
- If no winner exceeds the threshold, attention is triggered, and a new engram is formed.
- Perception is the complete reactivation of a pre-existing network, not a reconstruction process.
2.3.3. Comparative Advantages and Limitations
2.3.4. Divergent Experimental Predictions
2.3.5. Interpretive Analysis
- EBPM better explains rapid recognition, complex reflexes, and sudden cue-based recall.
- PC is superior in situations with incomplete or ambiguous data due to its generative reconstruction capability.
- The two models are therefore complementary, each having its own set of advantages and limitations.
2.3.6. EBPM vs. Related Theories—Method-by-Method Comparison
| Algorithm 1. EBPM (step-by-step) with prior-art mapping. |
|
2.3.7. Distinctive Contributions of EBPM (Beyond Attractors/CLS/HTM/PC)
- Multimodal Engram as the Computational Unit: EBPM defines an engram as a compositional binding of sensory, motor, interoceptive/affective, and cognitive facets. This goes beyond classic attractor networks (binary pattern vectors) and metric-learning embeddings by specifying the unit of recall and action as a multimodal assembly.
- Novelty-First Decision with Explicit Abstention: By design, EBPM yields near-zero classification on truly novel inputs. Partial activation of sub-engrams is treated as a reliable novelty flag—not as a misclassification. This sharp separation of recognition versus novelty is absent from PC’s iterative reconstruction loop and from generic prototype schemes.
- Attention-Gated Proto-Engram Formation: EBPM assigns a concrete role to attention and neuromodulatory gain (e.g., LC-NE) in binding co-active sub-engrams into a proto-engram during novelty, followed by consolidation. This specifies “when and how new representations form” more explicitly than attractors/CLS/HTM.
- Real-Time Reuse without Iterative Inference: For familiar inputs, EBPM supports one-step reactivation of stored engrams (winner selection via lateral inhibition), avoiding costly predictive iterations. This explains ultra-fast recognition and procedural triggering in overlearned contexts.
- Integration Readiness via DIME: EBPM is not an isolated alternative: the DIME controller provides a formal arbitration (α) that privileges EBPM under high familiarity and shifts toward PC under uncertainty, yielding a principled hybrid.
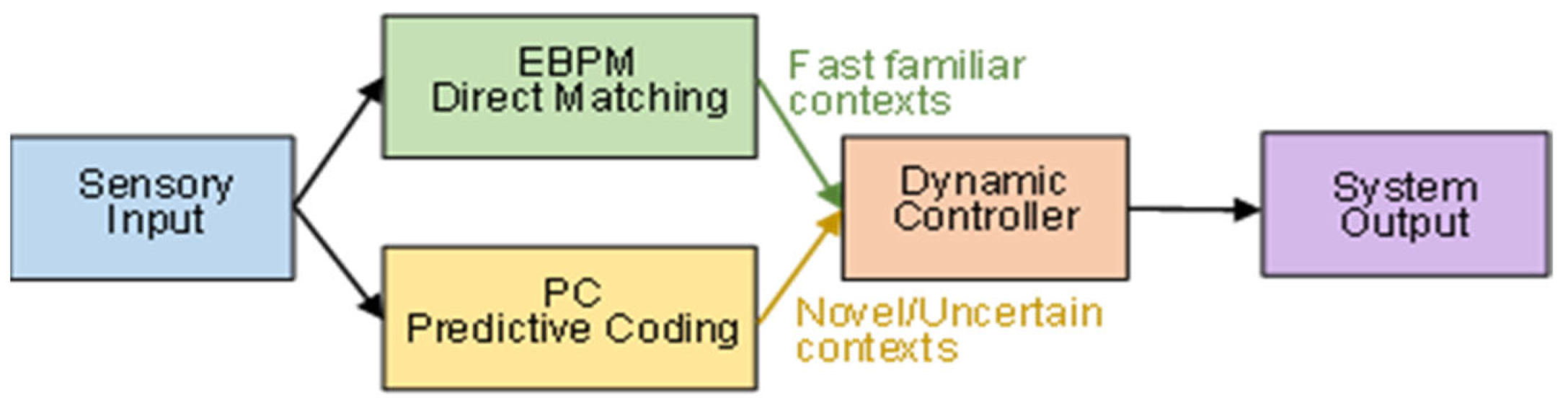
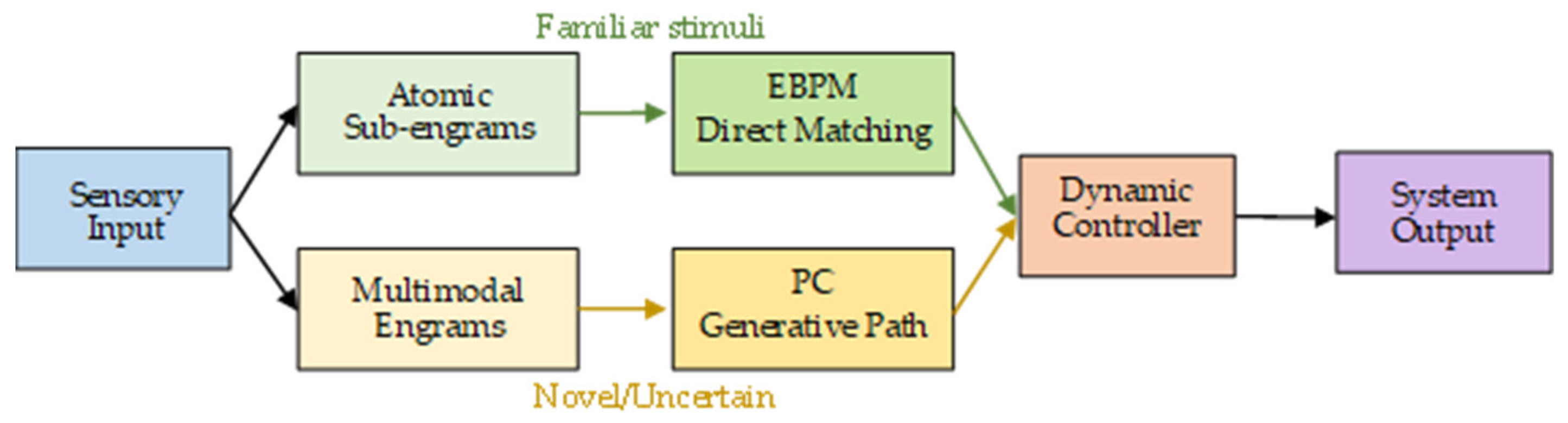
2.4. The DIME Integrative Model
- Dual-path processing: sensory input is processed simultaneously through direct engram matching (EBPM) and top-down prediction (PC).
- Dynamic controller: a central mechanism evaluates the context (level of familiarity, uncertainty, noise) and selects the dominant pathway.
- Adaptive flexibility: in familiar environments → EBPM becomes dominant; in ambiguous environments → PC is engaged.
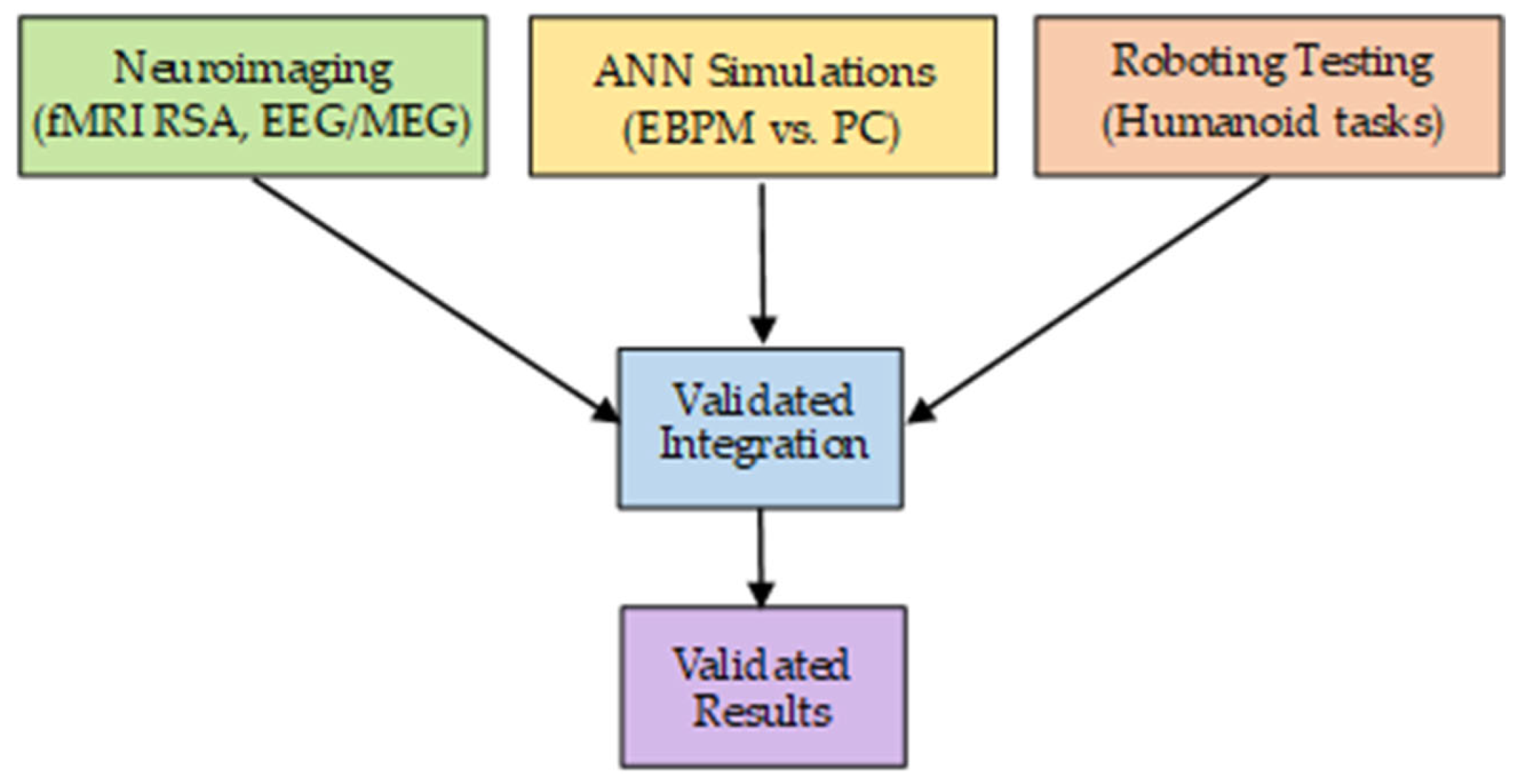
2.5. Methodology of Experimental Validation
Testable Predictions and Analysis Plan
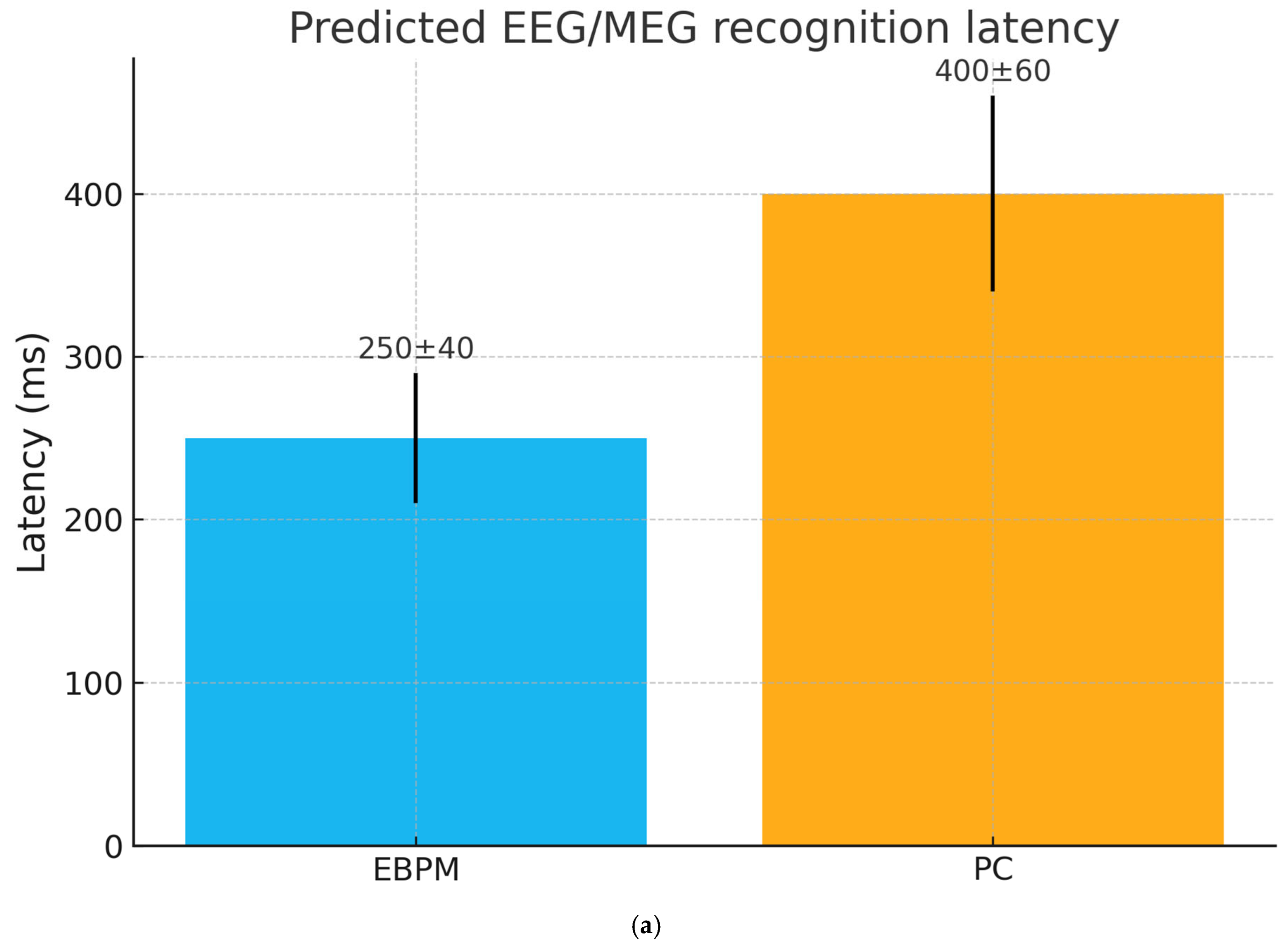
- H1 (EEG/MEG latency): EBPM-dominant trials (familiar stimuli) yield shorter recognition latencies (≈200–300 ms) compared to PC-dominant trials (≈350–450 ms). We base the ≈200–300 ms range on recent EEG evidence indicating that recognition memory signals emerge from around 200 ms post-stimulus across diverse stimulus types [29].
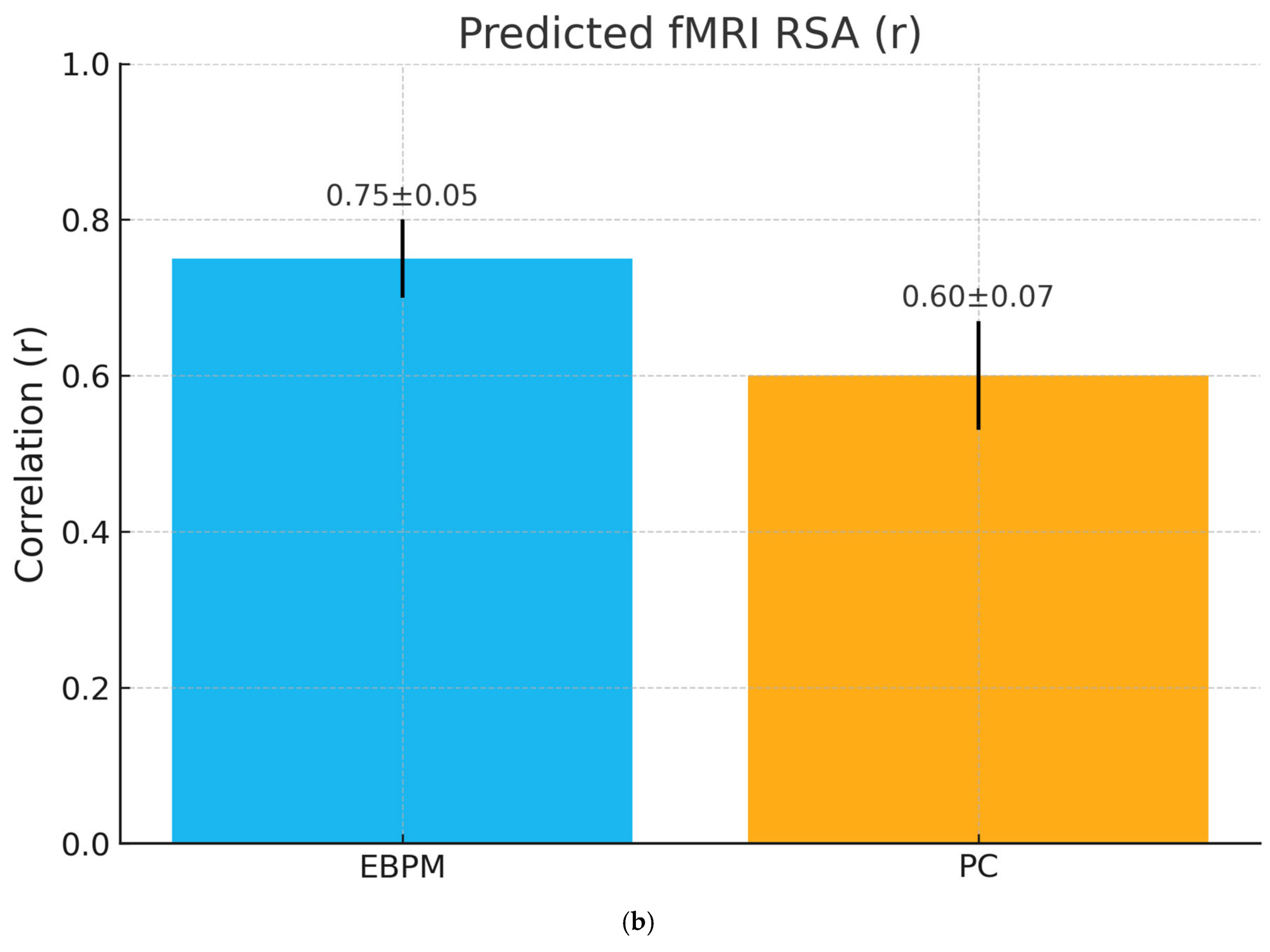
- H2 (fMRI representational similarity): EBPM produces higher RSA between learning and recognition patterns in hippocampal/cortical regions; PC shows anticipatory activation in higher areas under uncertainty.
- H3 (Cue-based recall completeness): Partial cues reinstantiate full engram patterns under EBPM, while PC engages reconstructive dynamics without full reinstatement.
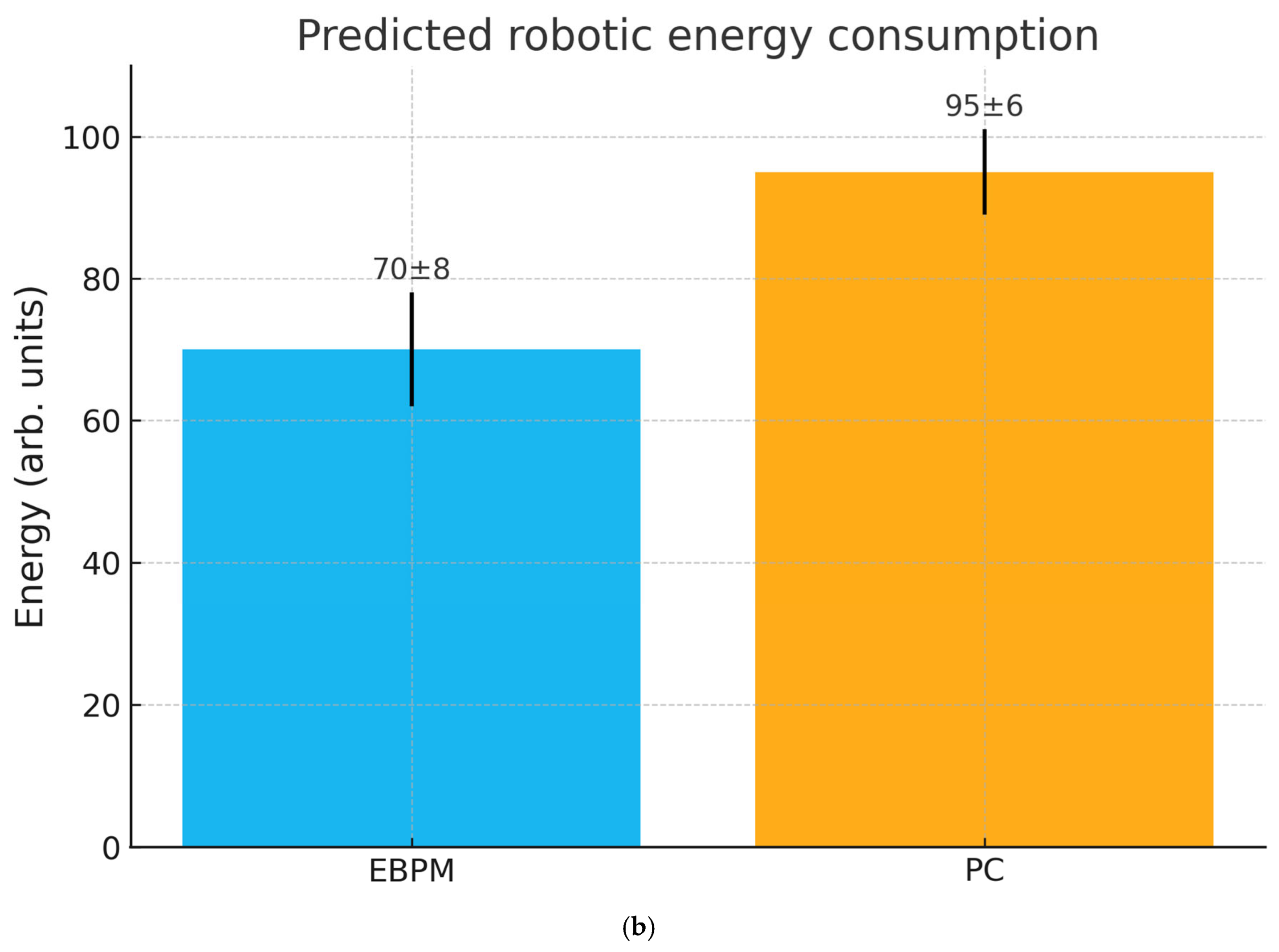
- H4 (Behavioral/robotic efficiency): Under stable familiarity, EBPM leads to lower inference time and energy cost than PC; under novelty/noise, DIME shifts toward PC to preserve robustness.
- H5 (NE-gain modulation): Pupil-indexed or physiological proxies of LC-NE correlate with novelty detection and proto-engram formation during EBPM-dominant novelty trials.
- Neuroimaging:
- fMRI (representational similarity analysis, RSA) → measures the overlap of patterns between learning and recognition.
- EEG/MEG → measures recognition latencies (EBPM ≈ shorter; PC ≈ longer).
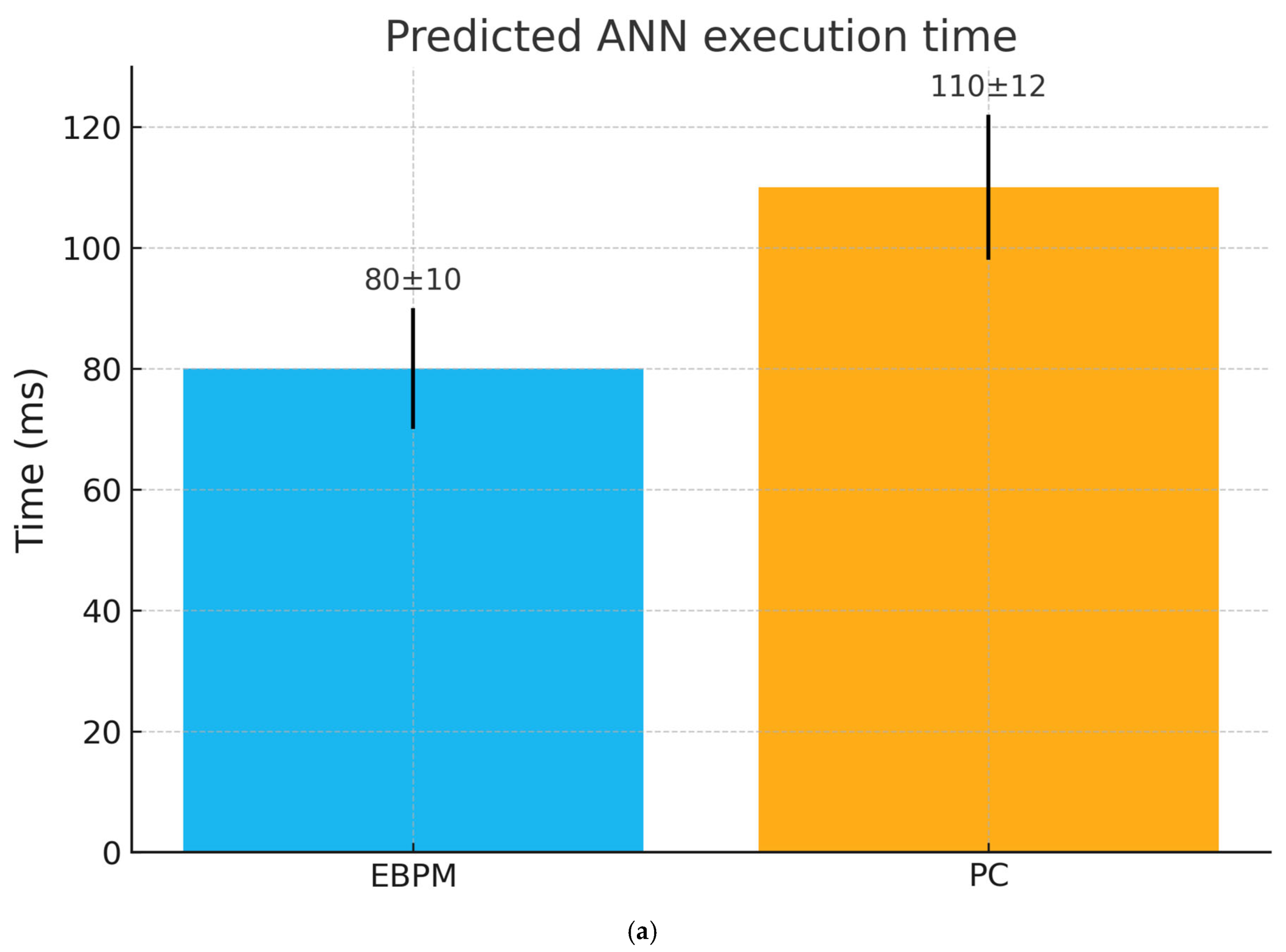
- Computational simulations:
- Artificial neural networks inspired by EBPM vs. PC.
- Comparison of inference times and computational cost.
- Robotic experiments:
- Implementation in visuomotor control.
- Measurement of reaction times and energy consumption in navigation tasks.
2.6. ANN Simulation Protocol
- (i)
- DIME-Prob (probability-level fusion): p = α·p_EBPM + (1 − α)·p_PC, with α driven by a familiarity score calibrated on familiar validation data. On CIFAR-10, we tune {gain = 4.0, thr_shift = 0.75, T_EBPM = 6.0, T_PC = 1.0}.
- (ii)
- DIME-Lazy (runtime-aware gating, used in robotics): δ = mean(|I_t − I_{t − 1}|). If δ ≤ 0.004 → EBPM-only; if δ ≥ 0.015 → PC-only; otherwise, fuse with fixed α = 0.65.
2.7. Intuitive Derivation of the Controller
3. Results
3.1. Preface—Scope of the Simulations (Proof-of-Concept)
3.2. ANN Simulations on Familiar vs. Novel Splits
- Metrics: Top-1 accuracy, latency (ms/ex.), and for DIME, the mean controller weight is where applicable.
- These results support the complementarity… (see Section 2.6).
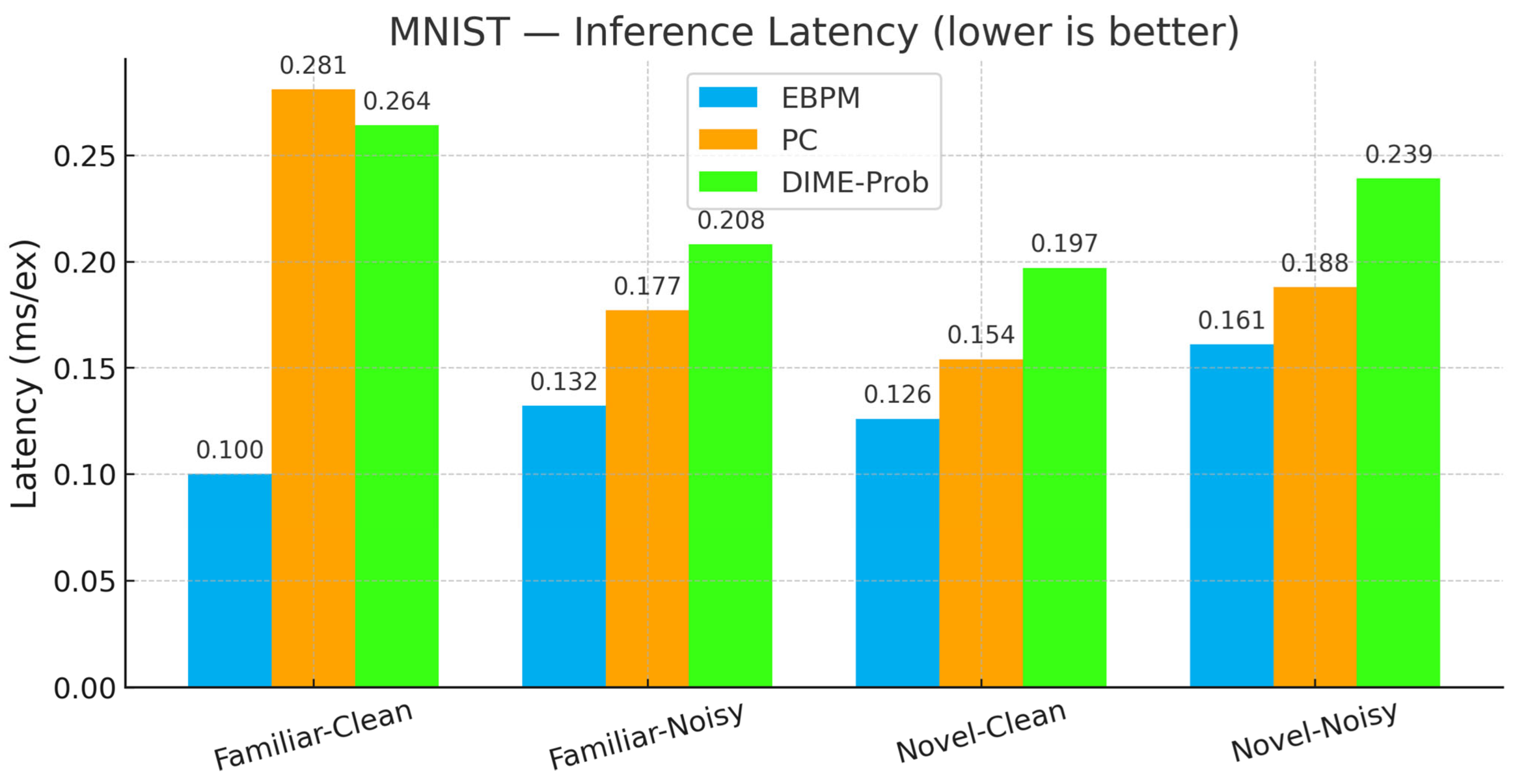
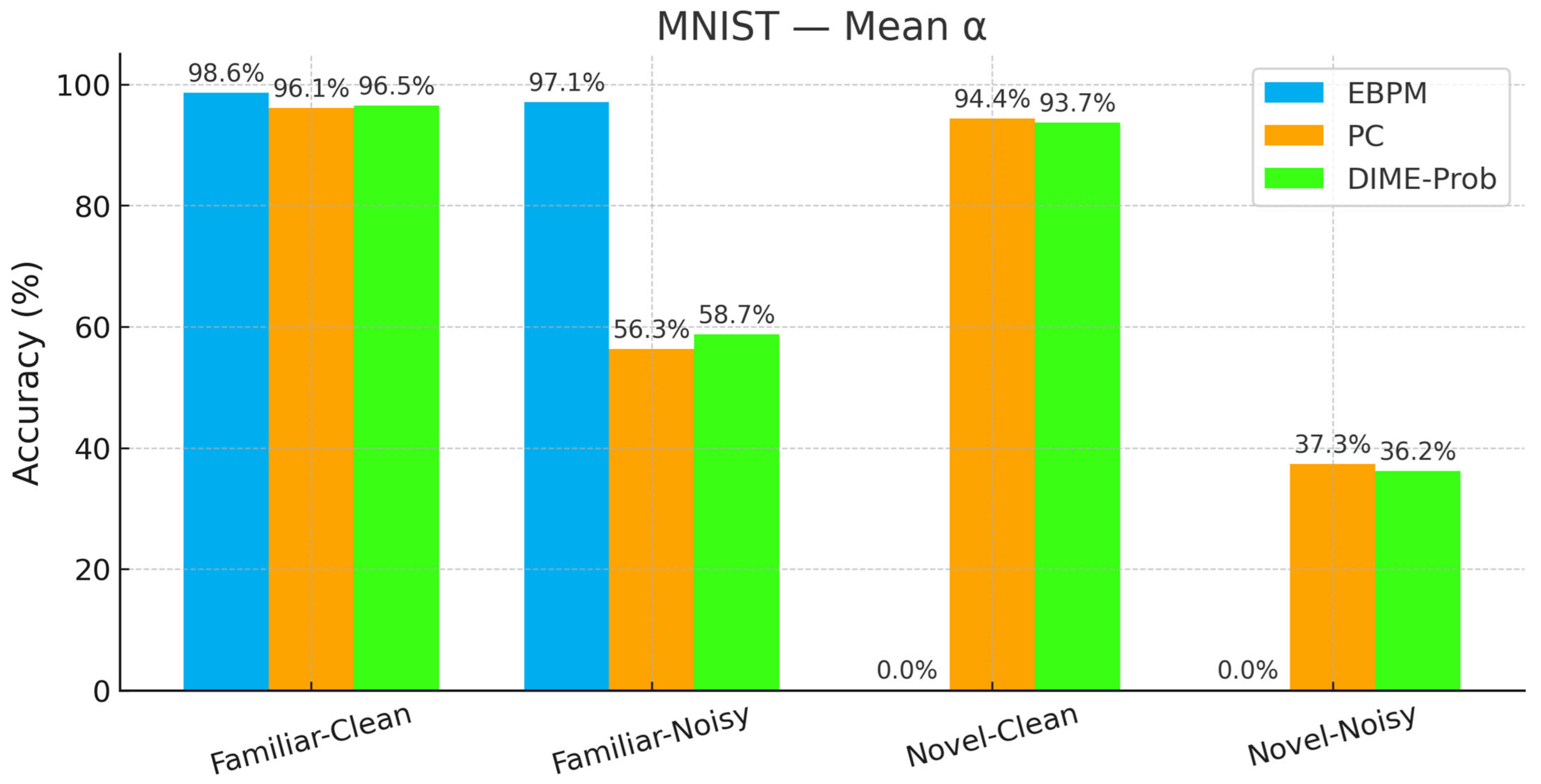
- EBPM—Familiar-Clean: 98.63%, 0.100 ms/ex; Familiar-Noisy: 97.13%, 0.132 ms/ex; Novel: 0.0%.
- PC—Familiar-Clean: 96.11%, 0.281 ms/ex; Familiar-Noisy: 56.28%, 0.177 ms/ex; Novel-Clean: 94.40%, 0.154 ms/ex; Novel-Noisy: 37.27%, 0.188 ms/ex.
- DIME (adaptive)—Familiar-Clean: 98.63%, 0.247 ms/ex, = 0.993; Familiar-Noisy: 96.93%, 0.188 ms/ex, = 0.974; Novel≈0% (as EBPM dominates unless fused).
- DIME-Prob (probability-level fusion)—Familiar-Clean: 96.47%, 0.264 ms; Familiar-Noisy: 58.68%, 0.208 ms; Novel-Clean: 93.65%, 0.197 ms; Novel-Noisy: 36.16%, 0.239 ms.
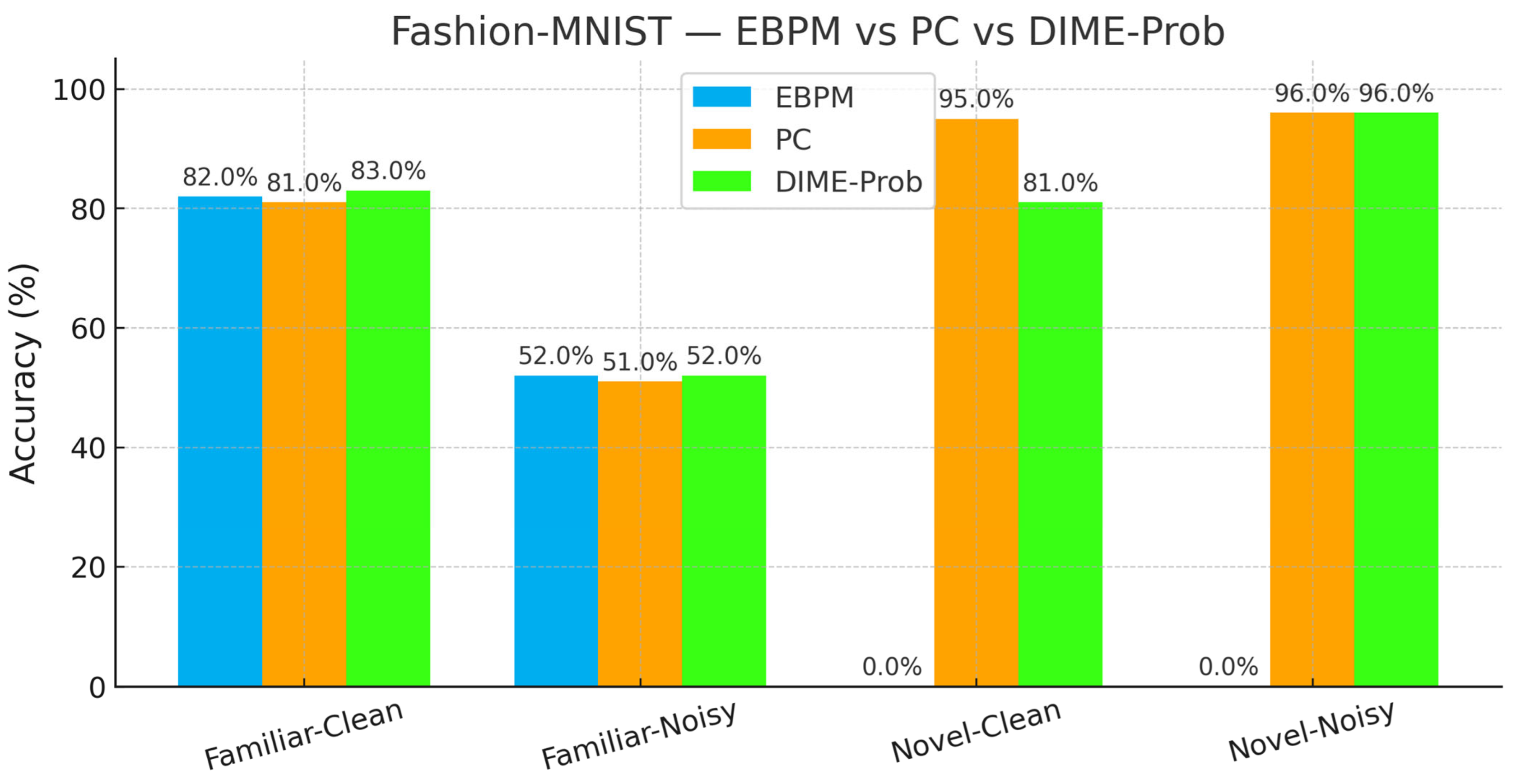
- EBPM—Familiar-Clean: 82.56%, 0.101 ms; Familiar-Noisy: 52.35%, 0.139 ms; EBPM reports ≈0% accuracy on novel inputs, consistent with its design as a novelty detector: sub-engrams activate but do not yield a full engram. This produces an explicit novelty signal, rather than a forced classification.
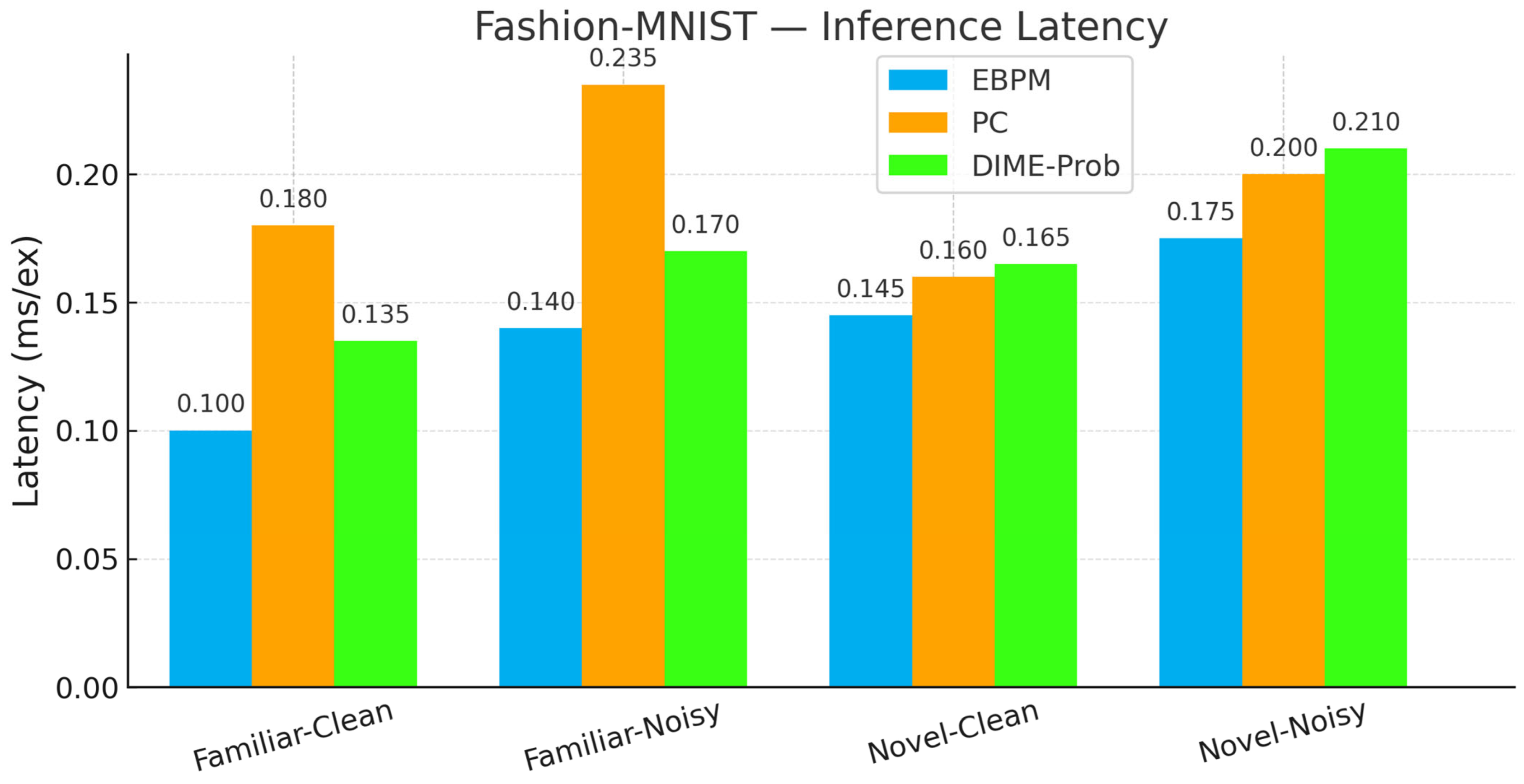
- PC—Familiar-Clean: 83.14%, 0.182 ms; Familiar-Noisy: 50.45%, 0.238 ms; Novel-Clean: 96.50%, 0.160 ms; Novel-Noisy: 97.00%, 0.203 ms.
- DIME (adaptive)—Familiar-Clean: 84.14%, 0.133 ms, = 0.536; Familiar-Noisy: 51.31%, 0.170 ms, = 0.221; Novel-Clean: 81.10%, 0.165 ms, = 0.506; Novel-Noisy: 97.10%, 0.213 ms, = 0.443.
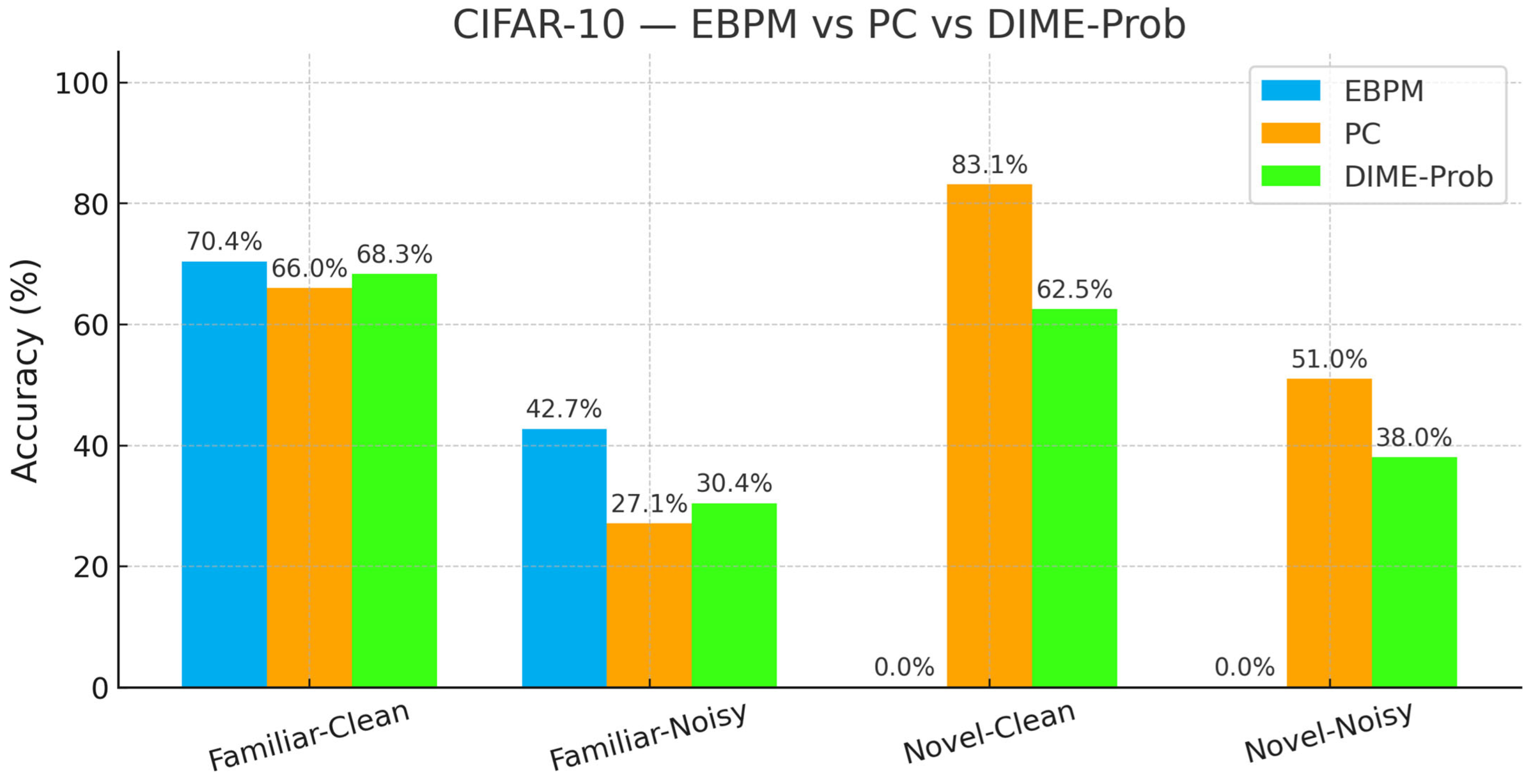
- EBPM—Familiar-Clean: 70.42%, 0.198 ms; Familiar-Noisy: 42.67%, 0.192 ms; Novel: 0%.
- PC—Familiar-Clean: 65.99%, 0.477 ms; Familiar-Noisy: 27.15%, 0.478 ms; Novel-Clean: 83.10%, 0.536 ms; Novel-Noisy: 50.95%, 0.548 ms.
- DIME-Prob (best tuned)—Familiar-Clean: 68.31%, 0.529 ms; Familiar-Noisy: 30.38%, 0.535 ms; Novel-Clean: 62.50%, 0.609 ms; Novel-Noisy: 38.05%, 0.675 ms.
3.3. Comparative Results and Simulations
- EBPM: Performs well in speed and efficiency but is limited in adaptation and robustness.
- PC: Flexible and robust but entails high costs.
- DIME: Integrates the advantages of both, providing an optimal balance between speed, efficiency, and flexibility.
3.4. General Information Flow in DIME
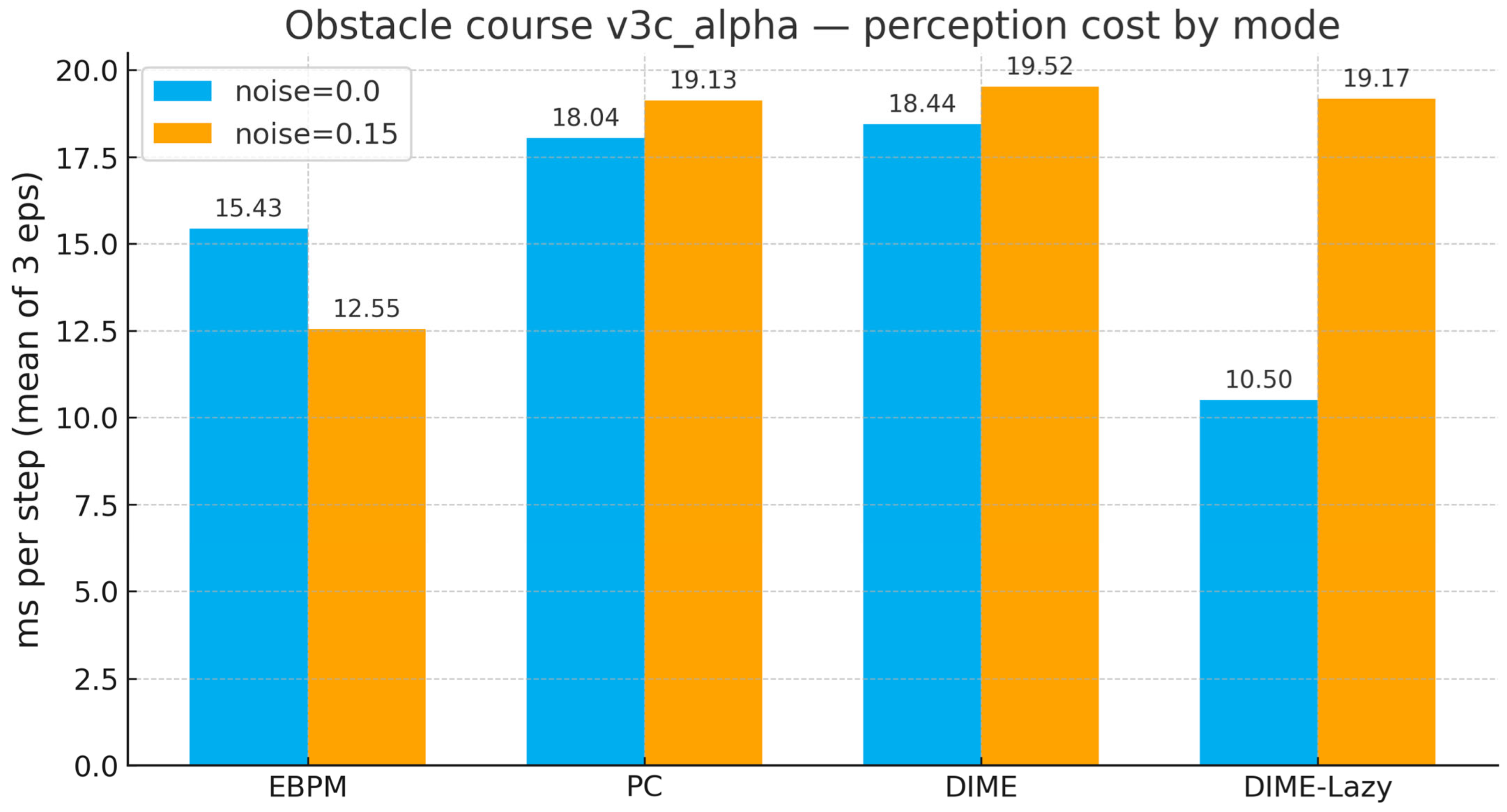
3.5. Virtual Robotics (Obstacle Course): Runtime-Aware DIME-Lazy (α Fixed)
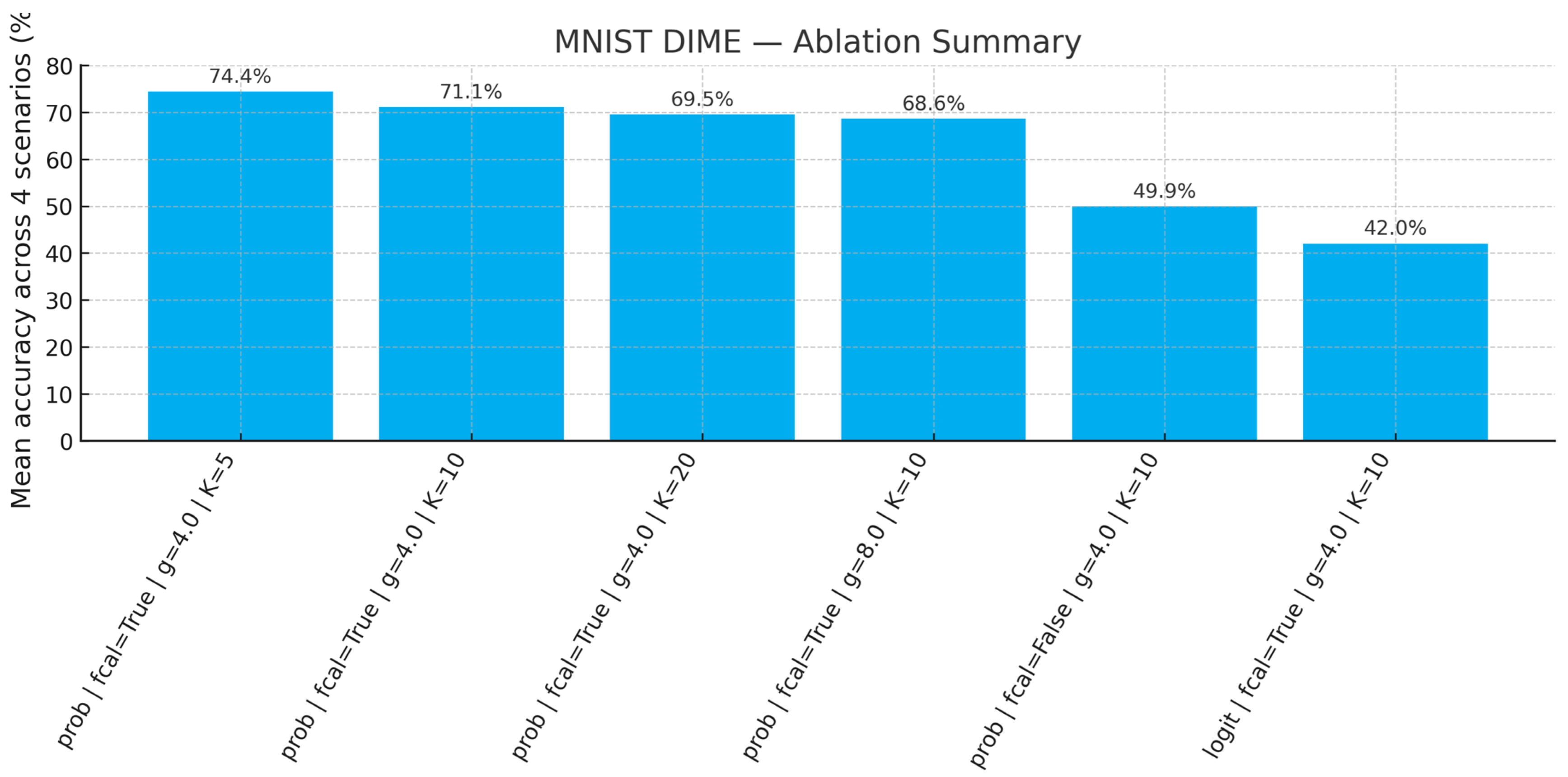
3.6. Ablation Studies
3.7. Statistical Significance
3.8. Complexity Analysis
3.9. Conclusions of Results
4. Discussion
4.1. Advantages of EBPM
4.2. Limitations of EBPM
4.3. Advantages of PC
4.4. Limitations of PC
4.5. Threats to Validity and Limitations
4.6. DIME as an Integrative Solution
- EBPM = fast, energy-efficient, but less flexible.
- PC = robust, adaptive, but computationally costly.
- DIME = hybrid integration, balancing both.
4.7. Interdisciplinary Implications
- Neuroscience: EBPM provides an alternative explanation for the phenomenon of memory replay, while DIME may serve as a more faithful framework for understanding the interaction between memory and prediction.
- Artificial Intelligence: EBPM-inspired architectures are more energy-efficient, and their integration with PC-type modules can enhance noise robustness.
5. Conclusions
- In neuroscience, it provides a more comprehensive explanation of the interaction between memory and prediction;
- In artificial intelligence, it suggests hybrid architectures that are more energy-efficient;
- In robotics, it paves the way for autonomous systems that can combine rapid recognition with adaptability to unfamiliar environments.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
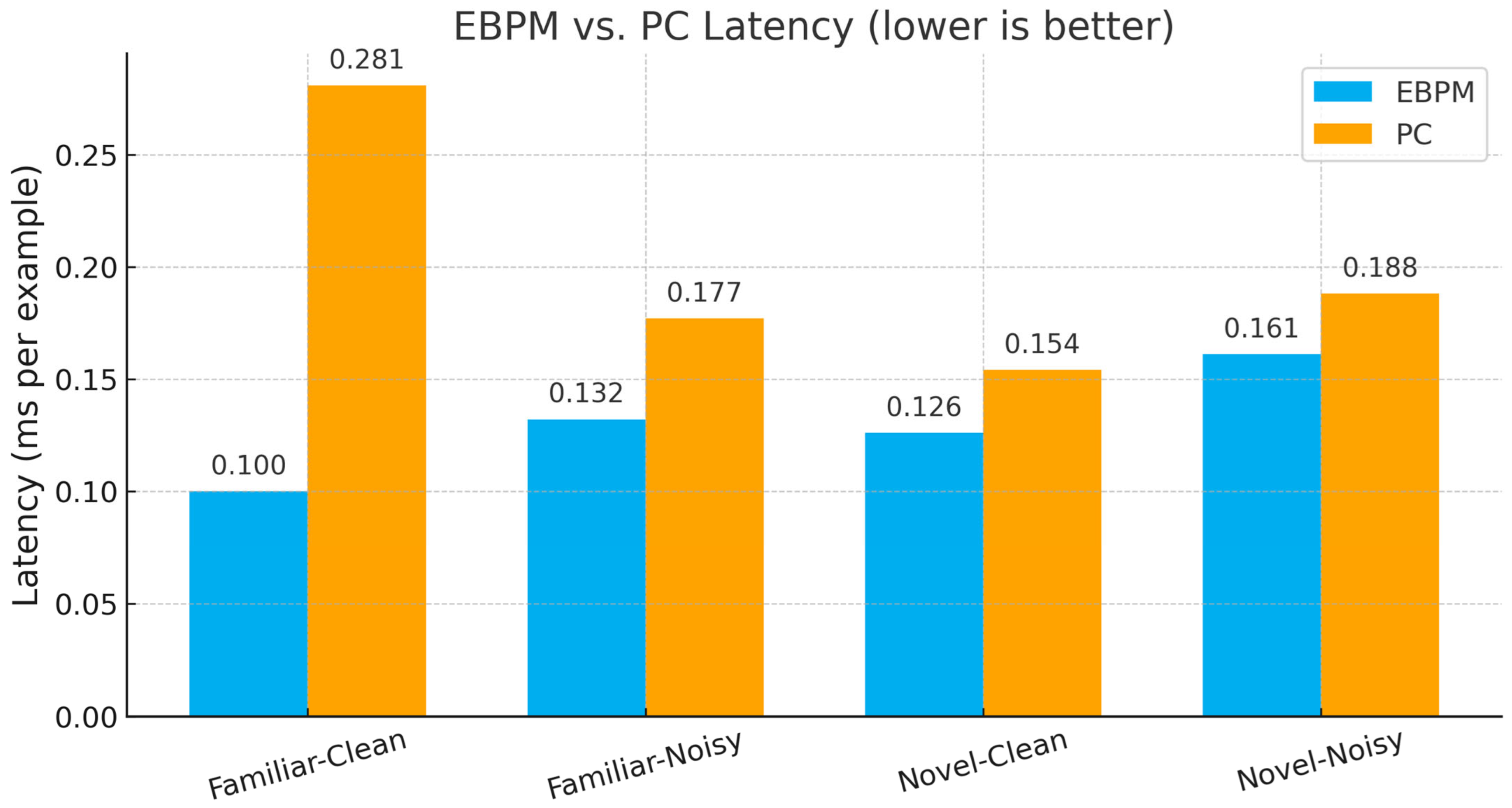

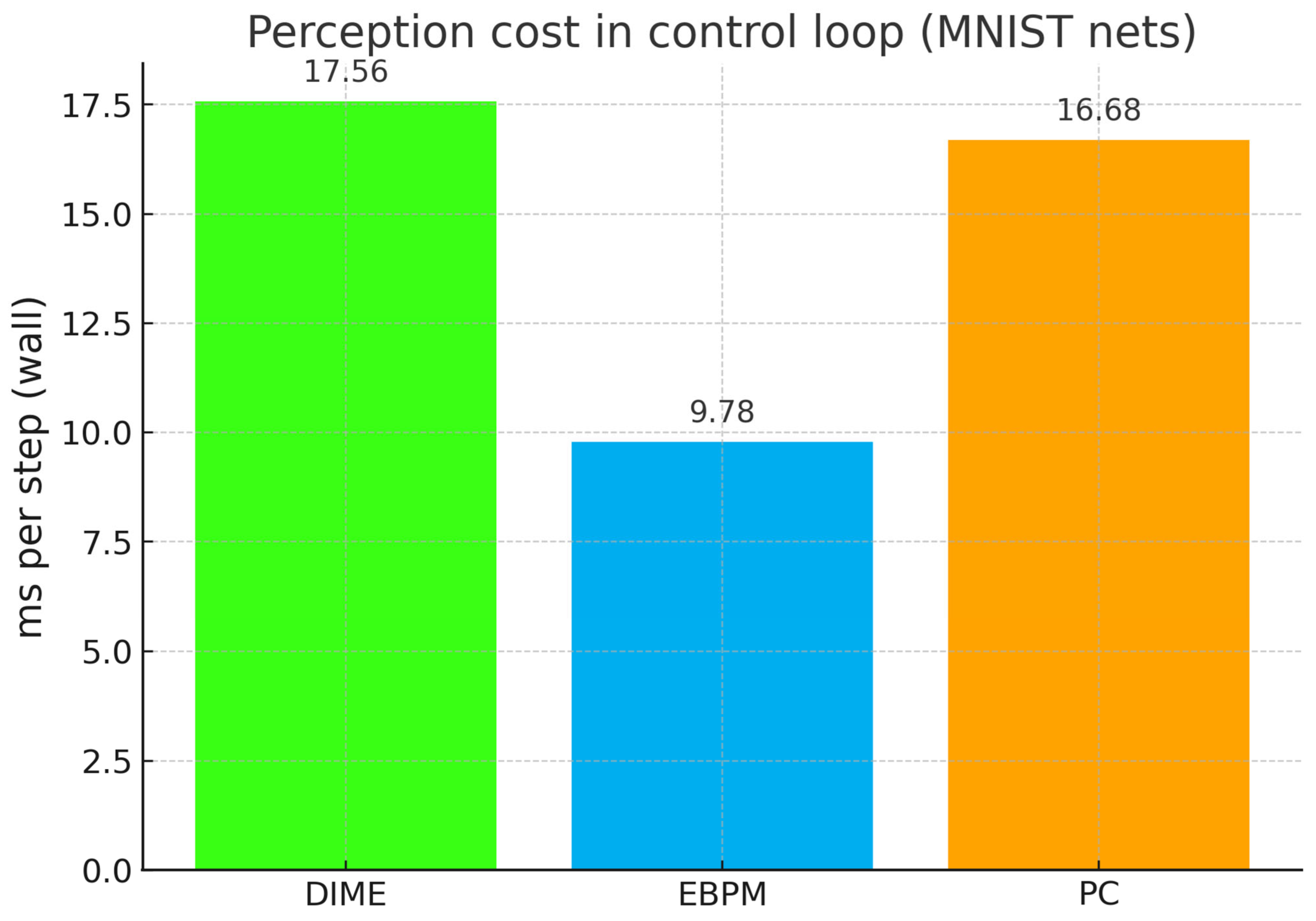
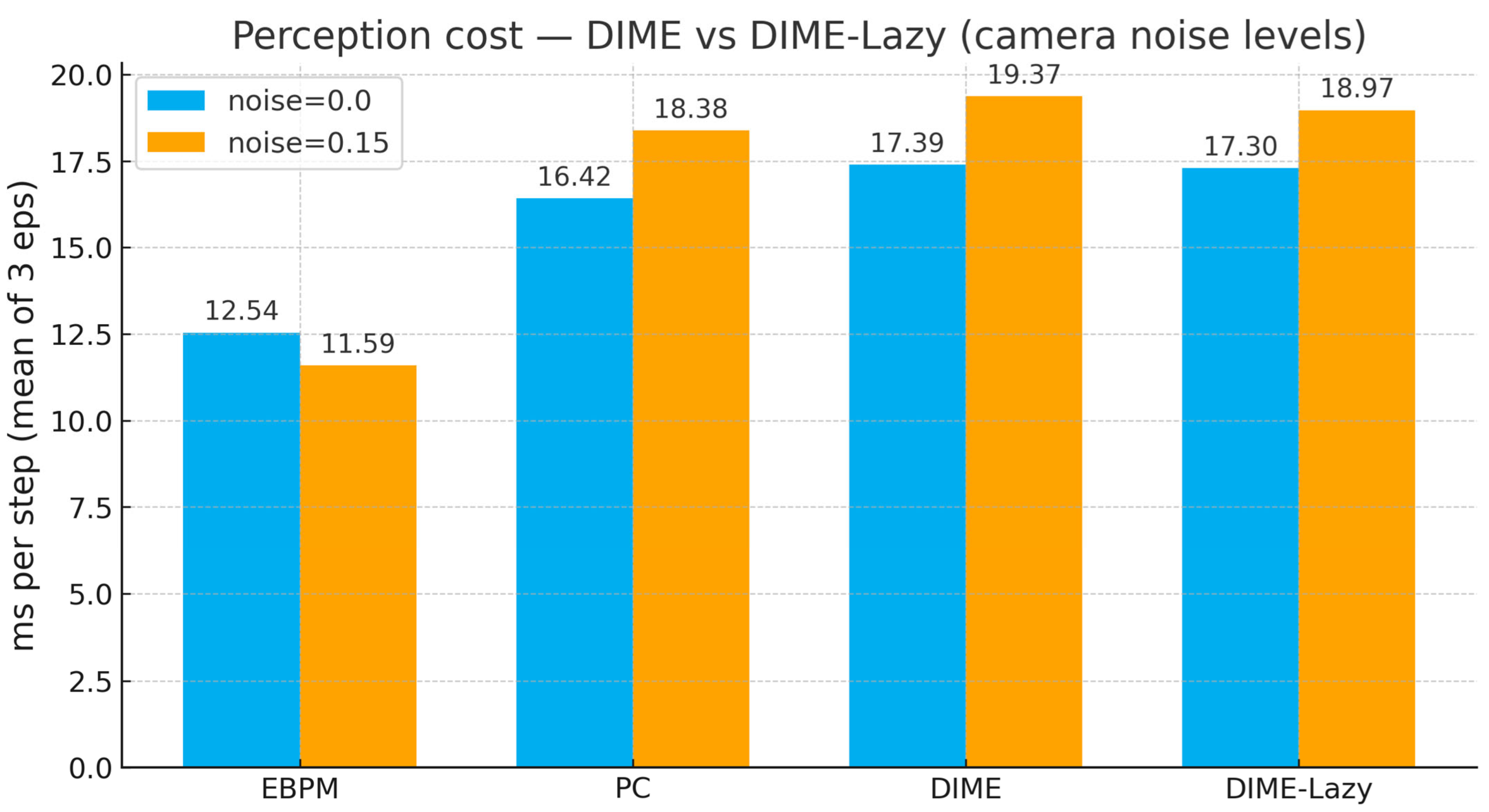
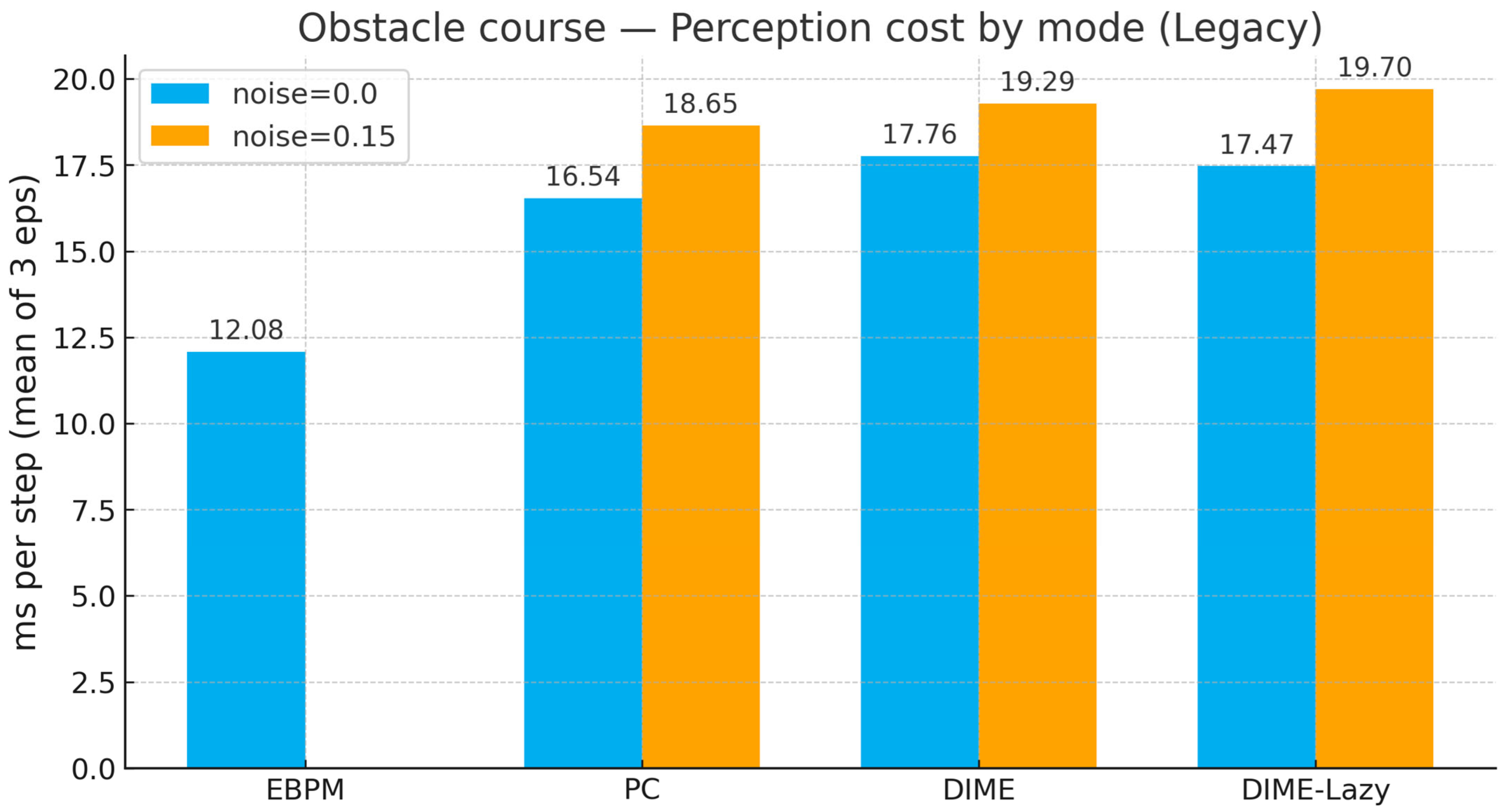
Appendix B
| File (Relative Path) | What It Contains |
|---|---|
| results_csv/pybullet_obstacles_metrics_v3c_alpha.csv | v3c_alpha (α = 0.65): ms/step mean, steps, success, collisions, avg PC calls per mode and noise |
| results_csv/pybullet_obstacles_metrics_v3c.csv | v3c (dyn gating, no fixed α): same fields |
| results_csv/pybullet_obstacles_metrics_v3b.csv | v3b: success and collisions breakdown |
| results_csv/pybullet_perception_metrics.csv | demo perception ms/step EBPM vs. PC vs. DIME |
References
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef]
- Rao, R.P.N.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef]
- Kanai, R.; Komura, Y.; Shipp, S.; Friston, K. Cerebral hierarchies: Predictive processing, precision and the pulvinar. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140169. [Google Scholar] [CrossRef]
- Buzsáki, G. Neural Syntax: Cell Assemblies, Synapsembles, and Readers. Neuron 2010, 68, 362–385. [Google Scholar] [CrossRef]
- Hawkins, J.; Ahmad, S. Why Neurons Have Thousands of Synapses, a Theory of Sequence Memory in Neocortex. Front. Neural Circuits 2016, 10, 23. [Google Scholar] [CrossRef]
- Xiang, Q.; Wang, X.; Song, Y.; Lei, L. ISONet: Reforming 1DCNN for aero-engine system inter-shaft bearing fault diagnosis via input spatial over-parameterization. Expert Syst. Appl. 2025, 277, 127248. [Google Scholar] [CrossRef]
- Xiang, Q.; Wang, X.; Lei, L.; Song, Y. Dynamic bound adaptive gradient methods with belief in observed gradients. Pattern Recognit. 2025, 168, 111819. [Google Scholar] [CrossRef]
- Markram, H.; Gerstner, W.; Sjöström, P.J. Spike-Timing-Dependent Plasticity: A Comprehensive Overview. Front. Synaptic Neurosci. 2012, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- McClelland, J.L.; McNaughton, B.L.; O’Reilly, R.C. Why there are complementary learning systems in the hippocampus and neocortex: Insights from the successes and failures of connectionist models of learning and memory. Psychol. Rev. 1995, 102, 419–457. [Google Scholar] [CrossRef]
- Teyler, T.J.; DiScenna, P. The hippocampal memory indexing theory. Behav. Neurosci. 1986, 100, 147–154. [Google Scholar] [CrossRef]
- Rolls, E.T. The mechanisms for pattern completion and pattern separation in the hippocampus. Front. Syst. Neurosci. 2013, 7, 74. [Google Scholar] [CrossRef] [PubMed]
- Nosofsky, R.M. Attention, similarity, and the identification–categorization relationship. J. Exp. Psychol. Gen. 1986, 115, 39–57. [Google Scholar] [CrossRef] [PubMed]
- Logan, G.D. Toward an instance theory of automatization. Psychol. Rev. 1988, 95, 492–527. [Google Scholar] [CrossRef]
- Biederman, I. Recognition-by-components: A theory of human image understanding. Psychol. Rev. 1987, 94, 115–147. [Google Scholar] [CrossRef] [PubMed]
- Kanerva, P. Sparse Distributed Memory; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Graves, A.; Wayne, G.; Danihelka, I. Neural Turing Machines. arXiv 2014, arXiv:1410.5401. [Google Scholar] [CrossRef]
- Graves, A.; Wayne, G.; Reynolds, M.; Harley, T.; Danihelka, I.; Grabska-Barwińska, A.; Colmenarejo, S.G.; Grefenstette, E.; Ramalho, T.; Agapiou, J.; et al. Hybrid computing using a neural network with dynamic external memory. Nature 2016, 538, 471–476. [Google Scholar] [CrossRef]
- Blundell, C.; Uria, B.; Pritzel, A.; Li, Y.; Ruderman, A.; Leibo, J.Z.; Rae, J.; Wierstra, D.; Hassabis, D. Model-Free Episodic Control. arXiv 2016, arXiv:1606.04460. [Google Scholar] [CrossRef]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical Networks for Few-shot Learning. arXiv 2017, arXiv:1703.05175. [Google Scholar] [CrossRef]
- Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 2013, 36, 181–204. [Google Scholar] [CrossRef]
- Bastos, A.M.; Usrey, W.M.; Adams, R.A.; Mangun, G.R.; Fries, P.; Friston, K.J. Canonical Microcircuits for Predictive Coding. Neuron 2012, 76, 695–711. [Google Scholar] [CrossRef]
- Olshausen, B.A.; Field, D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 1996, 381, 607–609. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C. Computational modelling of visual attention. Nat. Rev. Neurosci. 2001, 2, 194–203. [Google Scholar] [CrossRef]
- Aston-Jones, G.; Cohen, J.D. AN INTEGRATIVE THEORY OF LOCUS COERULEUS-NOREPINEPHRINE FUNCTION: Adaptive Gain and Optimal Performance. Annu. Rev. Neurosci. 2005, 28, 403–450. [Google Scholar] [CrossRef]
- Dehaene, S.; Meyniel, F.; Wacongne, C.; Wang, L.; Pallier, C. The Neural Representation of Sequences: From Transition Probabilities to Algebraic Patterns and Linguistic Trees. Neuron 2015, 88, 2–19. [Google Scholar] [CrossRef]
- Douglas, R.J.; Martin, K.A.C. Recurrent neuronal circuits in the neocortex. Curr. Biol. 2007, 17, R496–R500. [Google Scholar] [CrossRef] [PubMed]
- Ambrus, G.G. Shared neural codes of recognition memory. Sci. Rep. 2024, 14, 15846. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition, 1st ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Evans, J.S.B.T.; Stanovich, K.E. Dual-Process Theories of Higher Cognition: Advancing the Debate. Perspect. Psychol. Sci. 2013, 8, 223–241. [Google Scholar] [CrossRef]
- Hasson, U.; Chen, J.; Honey, C.J. Hierarchical process memory: Memory as an integral component of information processing. Trends Cogn. Sci. 2015, 19, 304–313. [Google Scholar] [CrossRef]
- Summerfield, C.; De Lange, F.P. Expectation in perceptual decision making: Neural and computational mechanisms. Nat. Rev. Neurosci. 2014, 15, 745–756. [Google Scholar] [CrossRef] [PubMed]
- Kok, P.; Jehee, J.F.M.; de Lange, F.P. Less Is More: Expectation Sharpens Representations in the Primary Visual Cortex. Neuron 2012, 75, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Kiebel, S.J.; Daunizeau, J.; Friston, K.J. A Hierarchy of Time-Scales and the Brain. PLoS Comput. Biol. 2008, 4, e1000209. [Google Scholar] [CrossRef] [PubMed]





| Aspect | Predictive Coding (PC) | Engram-Based Program Model (EBPM) |
|---|---|---|
| Basic principle | Predictions compared with input; error is propagated. | Recognition through engrams composed of reusable sub-engrams; full activation only for familiar stimuli. |
| Partial activation | - | Partial/similar stimuli → shared sub-engrams are activated; multiple engrams become partially active. |
| Selection | - | Lateral inhibition: the engram with the most complete activation prevails. |
| Novelty/unfamiliarity | Unclear how new representations are detected and formed. | If all engrams remain below the threshold: sub-engrams are active, but no parent engram is completed → novelty state. Attention is engaged. |
| Formation of new engrams (role of attention) | Does not specify a concrete biological mechanism. | Automatic (“fire together, wire together”): in the novelty state, attention increases neuronal gain and plasticity; co-active sub-engrams are bound into a proto-engram. Without repetition, the linkage fades/does not finalize. With repetition, it consolidates into a stable engram. |
| Signaling absence | Postulates “omission error” (biologically problematic). | No “negative spike.” Silence at the parent-engram level + fragmentary activation of sub-engrams defines novelty; attention manages exploration and learning. |
| Neuronal logic | Requires an internal comparator/explicit error signals. | Pure spike/silence + lateral inhibition + co-activation-dependent plasticity; attention sets the learning threshold. |
| (a) | |||
| Domain | EBPM | PC Prediction | |
| Central Mechanism | Direct activation of multimodal engrams | Continuous generation and updating of predictions | |
| The Role of Prediction | Non-existent; only goal-driven sensitization | Fundamental for processing | |
| Recognition Speed | Instantaneous for familiar stimuli | Slower, requires iterative computation | |
| Energy Efficiency | High (without generative simulation) | Lower (increased metabolic cost) | |
| Attention Control | Goal-driven (sensitization of relevant networks) | Through the magnitude of prediction errors | |
| Biological Plausibility | Supported by studies on engrams and inhibition | Supported by cortical predictive microcircuits | |
| Typical Application Domains | Rapid recognition, episodic memories, reflexes | Perception in ambiguous or noisy conditions | |
| (b) | |||
| Domain | EBPM | PC | Similar existing theories |
| Central Mechanism | Direct multimodal engram activation | Generative Predictive Coding | Hopfield attractors, episodic replay |
| Recognition Speed | Fast, one-step match | Iterative, slower | Fast (pattern completion) |
| Energy Efficiency | High, no generative loop | Low, high metabolic demand | Variable |
| Flexibility | Limited to stored engrams | High, reconstructive | Active inference |
| Biological Plausibility | Supported by engram studies | Supported by cortical microcircuits | Both partially supported |
| Domain | EBPM Prediction | PC Prediction | Testable Through |
|---|---|---|---|
| fMRI (similarity analysis) | Recognition = reactivation of storage networks | Anticipatory activation in higher cortical areas | fMRI + RSA |
| EEG/MEG (latency) | Rapid recognition of familiar patterns | Longer latencies due to generative processing | EEG/MEG |
| Cue-based recall | A partial cue reactivates the entire engram | The cue triggers generative reconstruction | Behavioral and neurophysiological studies |
| Robotic implementation | Faster execution of learned procedures | Better adaptive reconstruction with incomplete data | AI/Robotics benchmarks |
| Method/Framework | What the Method Does | Identical to EBPM | What It Adds vs. EBPM | What EBPM Adds |
|---|---|---|---|---|
| Hopfield/Attractor Networks [9] | Recurrent dynamics converge into stored patterns (content-addressable recall from partial cues). | Pattern completion from partial input; competition among states. | Explicit energy formalism; well-characterized attractor dynamics. | Explicit multimodality (sensory–motor–affective–cognitive) and engram units beyond binary patterns. |
| CLS—Complementary Learning Systems (hippocampus fast; neocortex slow) [10] | Episodic rapid learning + slow semantic consolidation. | Separation of “fast vs. slow” memory routes. | System-level transfer between stores. | EBPM is operational in real-time via direct matching; no mandatory inter-system consolidation for recognition. |
| Hippocampal indexing: pattern completion/separation [11,12] | Hippocampus index episodes; CA3 supports completion, and DG supports separation. | Fast episodic reactivation from indices; completion logic. | Fine neuro-anatomical mapping (CA3/DG) with predictions. | EBPM generalizes to neocortex and to multimodal action-oriented engrams, not only episodic replays. |
| Exemplar/Instance-Based (GCM; Instance Theory) [13,14] | Decisions by similarity to stored instances; latencies fall with instance accrual. | Direct “match to memory” with similarity score. | Quantitative psychophysics of categorization and automatization. | EBPM includes motor/interoceptive bindings and neuronal lateral inhibition/WTA selection. |
| Recognition-by-Components (RBC) [15] | Object recognition via geons and relations. | Sub-engrams akin to primitive features. | Explicit 3D structural geometry. | EBPM is not vision-limited; it covers sequences/skills and affective valence. |
| HTM/Sequence Memory (cortical columns) [5] | Sparse codes, sequence learning, local predictions. | Reuse of sparse distributed codes; sequence handling. | Continuous prediction emphasis. | EBPM does not require continuous generative prediction; for familiar inputs, it yields lower latency/energy via direct recall. |
| Sparse Distributed Memory (SDM) [16] | Approximate addressing in high-D sparse spaces; noise-tolerant recall. | Proximity-based matching in feature space. | Abstract memory addressing theory. | EBPM specifies engram units and novelty/attention gating with biological microcircuit motifs. |
| Memory-Augmented NNs (NTM/DNC) [17,18] | Neural controllers read/write an external memory differentiably. | Key-based recall from stored traces. | General algorithmic read/write; task-universal controllers. | EBPM is bio-plausible (engram units; STDP-like plasticity) without opaque external memory. |
| Episodic Control in RL [19] | Policies exploit episodic memory for rapid action. | Fast reuse of familiar episodes. | RL-specific credit assignment and returns. | EBPM operates for perception and action with multimodal bindings. |
| Prototypical/Metric-Learning (few-shot) [20] | Classify by distance to learned prototypes in embedding space. | Prototype-like matching ≈ EBPM encoder + similarity. | Episodic training protocols; few-shot guarantees. | EBPM grounds the embedding in neuro-plausible engrams + inhibition, not just vector spaces. |
| Predictive Coding/Active Inference [1,2,3,21,22] | Top-down generative predictions + iterative error minimization. | Shares attentional modulation and context use. | Robust reconstruction under missing data via generative loops. | EBPM delivers instant responses on familiar inputs (no iterative inference) with lower compute/energy; DIME then falls back to PC for novelty. |
| Model | Familiar-Clean (Acc/Ms) | Familiar-Noisy (Acc/Ms) | Novel-Clean (Acc/Ms) | Novel-Noisy (Acc/Ms) | |
|---|---|---|---|---|---|
| (a) | |||||
| EBPM | 98.63%/0.100 | 97.13%/0.132 | 0.00% */0.126 | 0.00% */0.161 | - |
| PC | 96.11%/0.281 | 56.28%/0.177 | 94.40%/0.154 | 37.27%/0.188 | - |
| DIME | 98.63%/0.247 | 96.93%/0.188 | 0.00%/0.135 | 0.00%/0.289 | 0.99/0.97/–/– |
| DIME-Prob | 96.47%/0.264 | 58.68%/0.208 | 93.65%/0.197 | 36.16%/0.239 | 0.61/0.38/0.41/0.23 |
| (b) | |||||
| EBPM | 82.56%/0.101 | 52.35%/0.139 | 0.00%/0.147 | 0.00%/0.174 | - |
| PC | 83.14%/0.182 | 50.45%/0.238 | 96.50%/0.160 | 97.00%/0.203 | - |
| DIME | 84.14%/0.133 | 51.31%/0.170 | 81.10%/0.165 | 97.10%/0.213 | 0.54/0.22/0.51/0.44 |
| (c) | |||||
| EBPM | 70.42%/0.198 | 42.67%/0.192 | 0.00%/0.201 | 0.00%/0.242 | |
| PC | 65.99%/0.477 | 27.15%/0.478 | 83.10%/0.536 | 50.95%/0.548 | |
| DIME-Prob ** | 68.31%/0.529 | 30.38%/0.535 | 62.50%/0.609 | 38.05%/0.675 | |
| Mode | Noise | Ms/Step (Mean) | Steps (Mean) | Success | Collisions (Mean) |
|---|---|---|---|---|---|
| EBPM | 0.00 | 15.43 | 381 | 1.00 | 113 |
| PC | 0.00 | 18.04 | 381 | 1.00 | 113 |
| DIME | 0.00 | 18.44 | 381 | 1.00 | 113 |
| DIME-Lazy | 0.00 | 10.50 | 381 | 1.00 | 113 |
| EBPM | 0.15 | 12.55 | 381 | 1.00 | 113 |
| PC | 0.15 | 19.13 | 381 | 1.00 | 113 |
| DIME | 0.15 | 19.52 | 381 | 1.00 | 113 |
| DIME-Lazy | 0.15 | 19.17 | 381 | 1.00 | 113 |
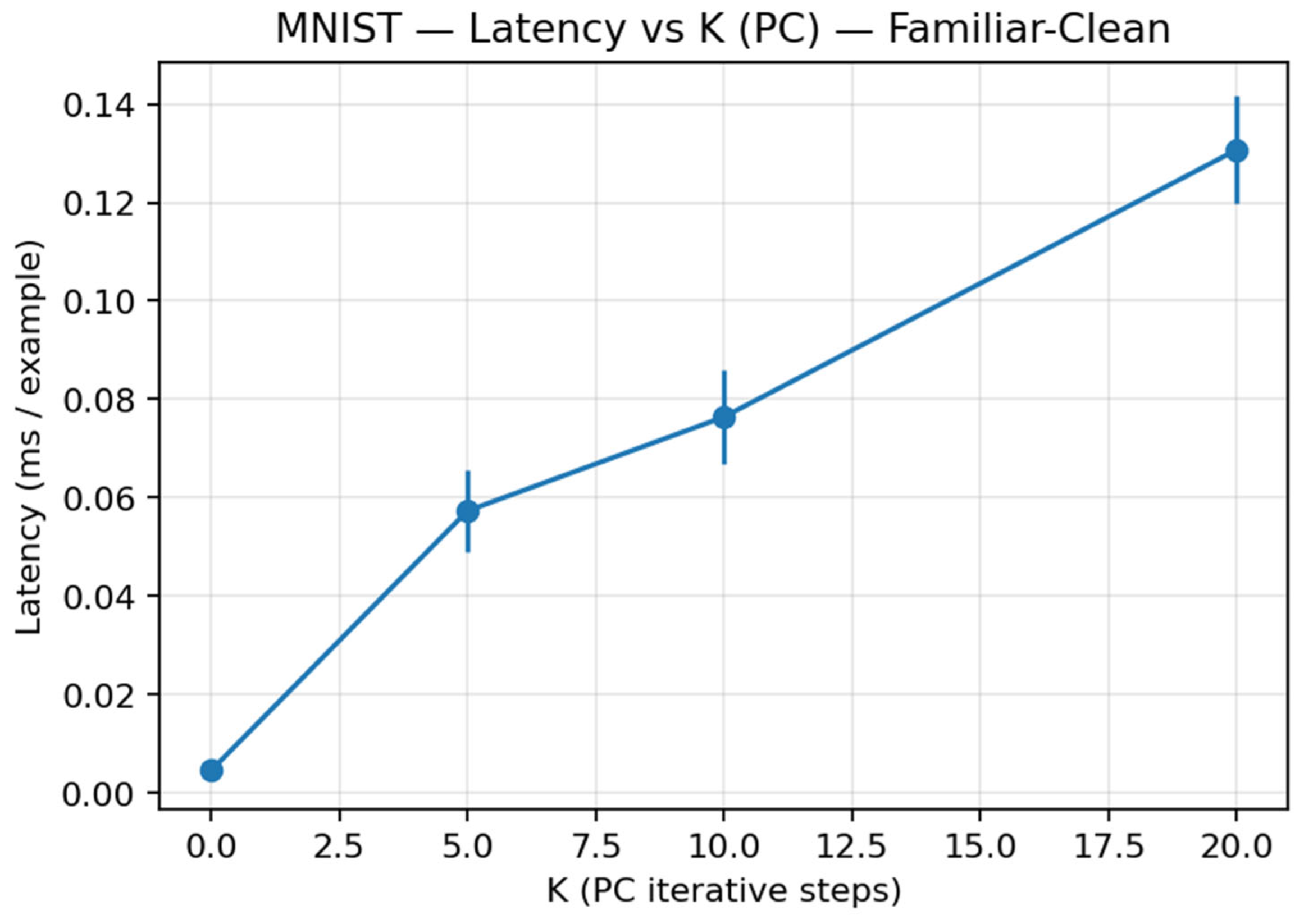
| Model | Accuracy (Mean ± Std) | Latency (Ms/Sample ± Std) |
|---|---|---|
| EBPM | 97.78 ± 0.12 | 0.0031 ± 0.0009 |
| PC (K = 0) | 96.97 ± 0.23 | 0.0034 ± 0.0009 |
| PC (K = 5) | 96.97 ± 0.23 | 0.0461 ± 0.0038 |
| PC (K = 10) | 96.97 ± 0.23 | 0.0694 ± 0.0108 |
| PC (K = 20) | 96.97 ± 0.23 | 0.1082 ± 0.0024 |
| DIME_ctrlOFF (α = 0.65) | 97.83 ± 0.08 | 0.0693 ± 0.0107 |
| DIME_ctrlON | 97.81 ± 0.09 | 0.0648 ± 0.0011 |
| Scenario | Comparison Pair | p-Value | Cohen’s d | CI Low | CI High | n |
|---|---|---|---|---|---|---|
| Familiar-Clean | EBPM vs. DIME_ctrlON | 0.000127 | −4.79 | −6.54 | −3.27 | 5 |
| Familiar-Clean | DIME_ctrlON vs. PC_K10 | 0.000807 | 4.07 | 2.59 | 4.86 | 5 |
| Familiar-Noisy | EBPM vs. PC_K10 | 0.004774 | −2.54 | −13.97 | −4.79 | 5 |
| Novel-Clean | EBPM vs. PC_K10 | 0.000022 | −10.23 | −66.36 | −51.99 | 5 |
| Novel-Clean | DIME_ctrlON vs. PC_K10 | 0.000016 | −11.12 | −60.48 | −48.32 | 5 |
| Mode | Latency (Ms/Step, Mean ± Std) | PC Calls (Mean ± Std) | Success Rate |
|---|---|---|---|
| EBPM | 0.026 ± 0.012 | 0.0 ± 0.0 | 1.0 |
| PC | 4.01 ± 1.31 | 5214 ± 1429 | 1.0 |
| DIME | 1.97 ± 1.08 | 2420 ± 1232 | 1.0 |
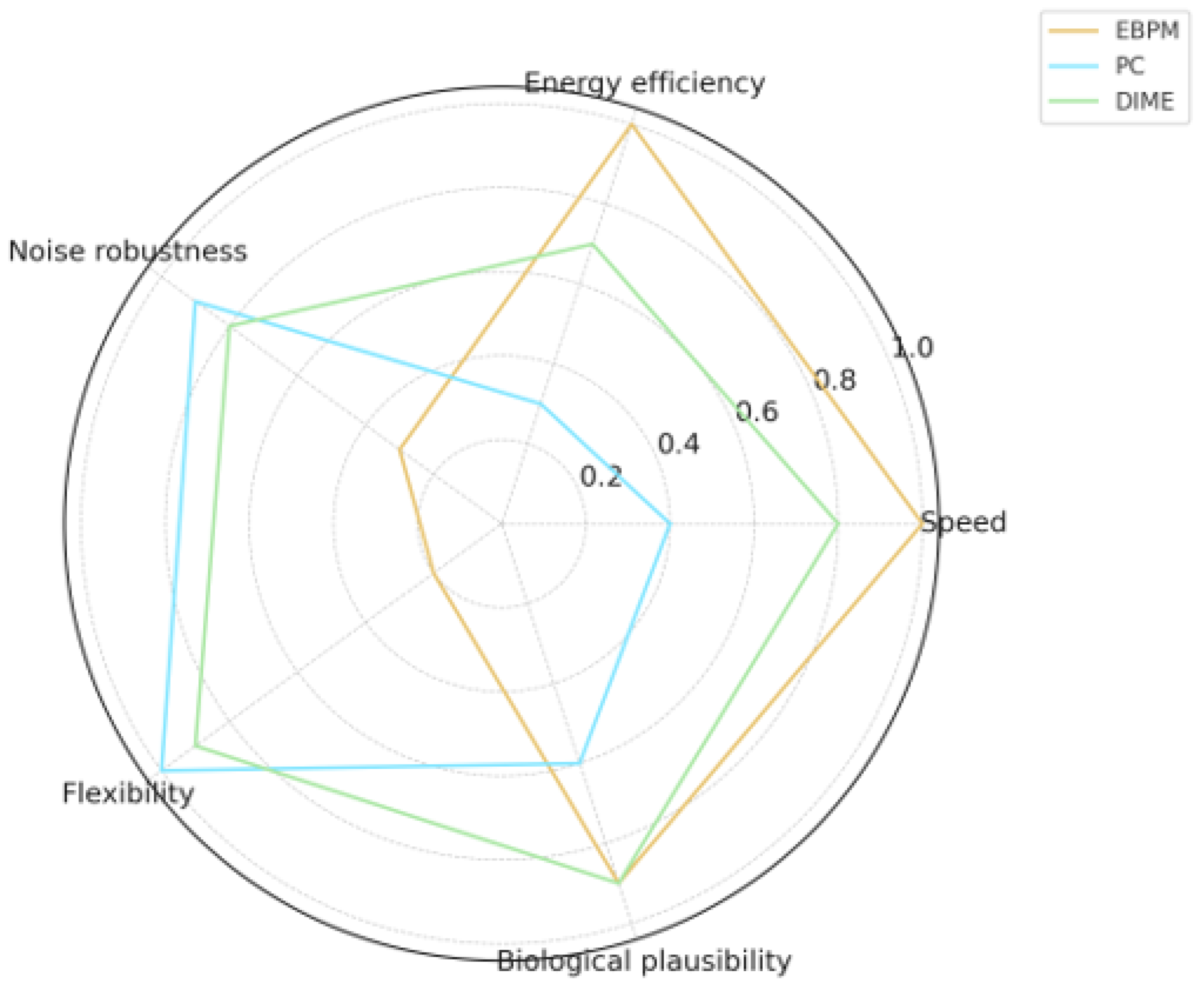
| Aspect | EBPM | PC | DIME |
|---|---|---|---|
| Speed | High | Medium | High |
| Energy Efficiency | High | Low | Medium–High |
| Noise Robustness | Medium–Low | High | High |
| Flexibility | Low | High | High |
| Biological Plausibility | High | Medium | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladu, I.C.; Bîzdoacă, N.G.; Pirici, I.; Cătălin, B. From Predictive Coding to EBPM: A Novel DIME Integrative Model for Recognition and Cognition. Appl. Sci. 2025, 15, 10904. https://doi.org/10.3390/app152010904
Vladu IC, Bîzdoacă NG, Pirici I, Cătălin B. From Predictive Coding to EBPM: A Novel DIME Integrative Model for Recognition and Cognition. Applied Sciences. 2025; 15(20):10904. https://doi.org/10.3390/app152010904
Chicago/Turabian StyleVladu, Ionel Cristian, Nicu George Bîzdoacă, Ionica Pirici, and Bogdan Cătălin. 2025. "From Predictive Coding to EBPM: A Novel DIME Integrative Model for Recognition and Cognition" Applied Sciences 15, no. 20: 10904. https://doi.org/10.3390/app152010904
APA StyleVladu, I. C., Bîzdoacă, N. G., Pirici, I., & Cătălin, B. (2025). From Predictive Coding to EBPM: A Novel DIME Integrative Model for Recognition and Cognition. Applied Sciences, 15(20), 10904. https://doi.org/10.3390/app152010904





