Abstract
Optimal airfoil design remains a critical challenge in aerodynamic engineering, with traditional methods requiring extensive computational resources and iterative processes. This paper presents GEO-DSGA, a novel framework integrating hybrid geometric neural networks with deep symbiotic genetic algorithms for enhanced airfoil optimization. The methodology employs graph-based representations of airfoil geometries through a hybrid architecture combining graph convolutional networks with traditional deep learning, enabling precise capture of spatial geometric relationships. The parametric modeling stage utilizes CST, Bézier curves, and PARSEC methods to generate mathematically robust airfoil representations, subsequently transformed into graph structures preserving local and global shape characteristics. The optimization framework incorporates a deep symbiotic genetic algorithm enhanced with dominant feature phenotyping, applying biological symbiotic principles where design parameters achieve superior performance through mutual enhancement rather than independent optimization. This systematic exploration maintains geometric feasibility and aerodynamic validity throughout the design space. Experimental results demonstrate an 88.6% reduction in computational time while maintaining prediction accuracy within 1.5% error margin for aerodynamic coefficients across diverse operating conditions. The methodology successfully identifies airfoil geometries outperforming baseline NACA profiles by up to 12% in lift-to-drag ratio while satisfying manufacturing and structural constraints, establishing GEO-DSGA as a significant advancement in computational aerodynamic design optimization.
1. Introduction
Airfoil design optimization represents a critical challenge in aerodynamic engineering, requiring the simultaneous consideration of complex geometric parameters, fluid dynamics principles, and multi-objective performance criteria [1]. Traditional optimization approaches face fundamental limitations: computational fluid dynamics (CFD) simulations demand extensive resources, parametric design spaces exhibit high dimensionality with non-convex characteristics, and conventional genetic algorithms lack intelligent guidance mechanisms for efficient convergence [2,3]. Recent advances in machine learning have introduced promising solutions through physics-informed neural networks [1], multi-fidelity optimization [4], and deep learning-enhanced evolutionary algorithms [2]. However, these approaches address individual aspects of the optimization challenge in isolation. Liu et al.’s CNN-PINN-DRL framework [1] successfully integrates physics constraints with neural networks but lacks geometric relationship modeling. Wu et al.’s multi-fidelity approach [4] achieves computational efficiency through intelligent data fusion yet does not exploit parameter interdependencies. Similarly, existing evolutionary methods treat design parameters independently, missing critical symbiotic relationships that emerge in optimal airfoil configurations [2,5].
No existing framework successfully integrates geometric understanding, aerodynamic prediction, and evolutionary optimization within a unified system that exploits symbiotic parameter relationships. Current methods suffer from three fundamental limitations: (1) geometric parameterization approaches (CST, PARSEC, Bézier) operate independently of aerodynamic performance prediction, (2) neural network architectures fail to capture spatial geometric relationships inherent in airfoil surfaces, and (3) evolutionary algorithms ignore beneficial parameter interdependencies, treating optimization as independent variable problems rather than collaborative systems. This research addresses this critical gap by introducing GEO-DSGA (Geometric Neural Networks with Deep Symbiotic Genetic Algorithms), the first framework to combine graph-based geometric understanding with biologically inspired symbiotic optimization principles. This approach not only allows the numerical re-characterization of existing airfoils but also facilitates the systematic search and development of new aerodynamic geometries. Integrating artificial intelligence algorithms into our methodology will enhance our ability to identify the most suitable airfoil that is compatible with specific design objectives, such as maximizing the lift coefficient or optimizing the lift-to-drag ratio (L/D) [6,7]. The article will not only focus on optimizing existing airfoils but will also contribute to the creation of original aerodynamic designs. Various optimization techniques will be employed, including genetic algorithms that simulate natural selection processes, gradient-based methods that utilize computational optimization [3,8], and hybrid approaches that combine multiple strategies for enhanced results [1,9]. This comprehensive methodology enables the systematic analysis and customization of airfoil designs by combining traditional methods with modern techniques to achieve targeted design goals [10].
The overall goal of this article is to develop a robust airfoil design framework that fills a critical gap in the existing literature by integrating geometric modeling, aerodynamic data generation, and optimization steps into a consistent workflow [5]. The results of this research will provide a fast and reliable infrastructure for airfoil design, ultimately guiding designers to select appropriate airfoils early in the design process, thereby significantly minimizing the engineering effort required throughout the project life cycle [9,11]. This paper presents a novel approach to airfoil design optimization that combines deep learning techniques with advanced optimization algorithms for improved aerodynamic performance prediction and optimization [1,2]. The proposed methodology addresses the critical challenge of airfoil selection and optimization by integrating parametric geometry modeling techniques with advanced machine learning approaches [5,7]. The system utilizes representations of airfoil geometries processed through hybrid neural networks, which combine traditional deep learning with physics-based networks, thereby enabling the capture of geometric relationships that are meaningful for aerodynamic performance [4,11]. The optimization framework uses improved genetic algorithms and multi-task learning approaches to systematically explore the design space while maintaining geometric feasibility [2,5]. Experimental results show significant improvements in convergence rate and solution quality compared to traditional optimization methods [9,10].
In [1], a groundbreaking method for airfoil shape optimization, driven by CNN-PINN-DRL, was introduced, combining Convolutional Neural Networks (CNN), Physics-Informed Neural Networks (PINN), and Deep Reinforcement Learning (DRL). Their approach demonstrates the potential of hybrid architectures in capturing both geometric features and physical constraints simultaneously. The method showed significant improvements in optimization efficiency while maintaining physical validity by integrating governing equations into the neural network architecture. The authors in [3] developed an innovative aerodynamic shape optimization approach using physics-informed hot-start methods combined with modified metric-based proper orthogonal decomposition. This work addresses the computational bottleneck in traditional optimization by providing intelligent initialization strategies that leverage physical understanding. The integration of appropriate orthogonal decomposition enables efficient dimensionality reduction while preserving critical aerodynamic characteristics. In the study [4], advanced airfoil design is achieved through physics-inspired neural network models that incorporate fundamental aerodynamic principles directly into the network architecture. Their approach demonstrates how domain knowledge can be embedded within neural networks to improve both the accuracy and physical consistency of predictions. In [5], a comprehensive multi-task learning framework for the aerodynamic computation of two-dimensional airfoils is presented. This approach simultaneously predicts multiple aerodynamic parameters (lift coefficient, drag coefficient, pressure distribution) while sharing learned representations across tasks. The framework demonstrates superior performance compared to single-task approaches, providing more robust predictions across varying operating conditions. The authors in [6] introduced a Dirichlet Distribution-Based Ensemble Surrogate Model for aerodynamic optimization, addressing uncertainty quantification in surrogate-based optimization. Their methodology provides probabilistic predictions that capture both aleatory and epistemic uncertainties, enabling more robust design decisions under uncertainty. The transfer learning strategy allows rapid adaptation to new design spaces and operating conditions. Recent advances in multi-fidelity modeling [12] demonstrate the potential for combining data from multiple sources with varying computational costs and accuracies. These approaches optimize the trade-off between computational efficiency and prediction accuracy by strategically utilizing high-fidelity data where most needed.
In [8], a gradient-based aerodynamic optimization method utilizing deep learning is presented, which directly incorporates gradient information into the neural network training process. This approach enables more efficient optimization convergence and provides better sensitivity analysis capabilities compared to traditional gradient-free methods. In [2], the authors explored airfoil optimization using deep learning models combined with evolutionary algorithms for the design of large-endurance UAVs. Their hybrid approach combines the global search capabilities of evolutionary algorithms with the local refinement capabilities of gradient-based methods, achieving superior optimization performance. The authors in [5] developed an aerodynamic optimization method for propeller airfoils based on DBO-BP (Dung Beetle Optimizer-Back Propagation) and NSWOA (Non-dominated Sorting Whale Optimization Algorithm), demonstrating the effectiveness of bio-inspired optimization algorithms in aerodynamic design. The authors in [11] introduced a fast prediction method for airfoil aerodynamic characteristics based on combined autoencoders. Their methodology significantly reduces computational time for aerodynamic analysis while maintaining high accuracy, making it suitable for real-time applications and design optimization loops. In [10], novel pressure-based optimization methods using deep learning techniques were developed. This approach directly optimizes pressure distributions rather than geometric parameters, providing more direct control over aerodynamic performance characteristics. In [7], a machine learning-based approach for predicting aerodynamic coefficients using deep neural networks and CFD data is presented. Their work demonstrates the effectiveness of data-driven approaches in replacing computationally expensive CFD simulations for routine aerodynamic analysis. The study [13] introduced deep learning approaches for airfoil aerodynamic-electromagnetic coupling optimization with random forest integration, addressing the increasing need for multiphysics optimization in modern aerospace applications. The authors in [14] developed deep learning methods for airfoil flow field simulation based on Unet++, demonstrating the potential for neural networks to directly predict complex flow fields around airfoils, potentially replacing traditional CFD simulations for specific preliminary design applications under well-defined operational constraints, including: (1) parametric design space exploration during early conceptual phases where rapid flow field estimation is prioritized over high-fidelity accuracy, (2) real-time control system applications requiring sub-millisecond response times where computational efficiency supersedes precision, (3) iterative optimization loops where relative performance ranking is more critical than absolute accuracy, and (4) educational and training scenarios where flow visualization and fundamental understanding take precedence over certification-quality predictions.
While existing literature demonstrates significant progress in individual aspects of airfoil optimization, a gap remains in comprehensive frameworks that effectively integrate geometric understanding, aerodynamic prediction, and optimization within a unified system.
The novelties and contributions of the present study are summarized below:
- Hybrid Geometric-Aerodynamic Neural Architecture: Novel integration of graph neural networks for spatial geometric relationship processing with traditional deep networks for global aerodynamic parameter handling, enabling simultaneous local-global feature extraction;
- Symbiotic Evolutionary Optimization: Revolutionary implementation of biological symbiotic principles where design parameters achieve superior performance through mutual enhancement rather than independent optimization, fundamentally transforming traditional genetic operators;
- Neural-Guided Genetic Operations: Intelligence-enhanced crossover and mutation operators that leverage neural network predictions to guide evolutionary processes, replacing random operations with performance-informed decisions;
- Dominant Feature Phenotyping: Automated identification and preservation of geometric features that consistently contribute to superior aerodynamic performance across multiple design scenarios.
- Mutation rates are dynamically adjusted based on neural network performance predictions and population diversity metrics. Regions of the design space with high predicted improvement potential receive increased mutation attention.
- Local performance gradients and feature importance rankings influence mutation directions. This intelligent guidance reduces the computational waste associated with random mutations while maintaining the exploratory capability essential for genetic algorithms.
- The GEO-DSGA integrates multi-objective optimization capabilities, maintaining Pareto-optimal solution sets while exploring trade-offs between competing aerodynamic objectives. The algorithm is designed for efficient parallel execution, with sub-populations distributed across available computational resources. Load balancing mechanisms ensure optimal resource utilization while maintaining algorithmic integrity.
The research establishes a foundation for next-generation computational tools in aerodynamic design, demonstrating the potential for artificial intelligence to significantly enhance traditional engineering workflows while maintaining the reliability and accuracy required for aerospace applications.
The remainder of this manuscript is organized as follows: Section 2 presents the comprehensive methodology including geometric parameterization and neural network architectures, Section 3 details the proposed GEO-DSGA framework, Section 4 provides experimental validation and comparative analysis, and Section 5 concludes with contributions and future research directions.
2. Materials and Methods
2.1. Airfoil Optimization
The evolution of airfoil design represents one of the most significant achievements in aerodynamic engineering, spanning over a century of theoretical development, experimental validation, and computational advancement. The significance of airfoil design extends beyond aviation, influencing wind turbine technology, propeller design, and various other applications where fluid–structure interaction is critical. Understanding this historical development provides valuable insights into the evolution of engineering design methodologies and the role of technological advancement in enabling new approaches to complex aerodynamic problems.
2.1.1. Historical Development and Theoretical Foundations
The systematic study of airfoils began long before the first powered flight, establishing the fundamental principles that continue to guide modern aerodynamic design. Sir George Cayley (1773–1857) is often credited as the father of aerodynamics, conducting extensive experiments on wing shapes and establishing the fundamental principles of lift generation [1]. His seminal work, published in “On Aerial Navigation” (1809–1810), laid the theoretical foundation for understanding the relationship between wing camber and lift production, introducing concepts that remain central to airfoil design theory [15,16].
Cayley’s theoretical contributions included the identification of the four forces acting on an aircraft (lift, drag, thrust, and weight) and the recognition that lift could be generated through the combination of wing camber and angle of attack. His experiments with cambered surfaces demonstrated that curved airfoils produced superior lift characteristics compared to flat plates, establishing the fundamental principle that airfoil geometry directly influences aerodynamic performance.
Otto Lilienthal (1848–1896) made significant contributions through his gliding experiments and systematic documentation of the lift and drag characteristics of various wing profiles. His book “Birdflight as the Basis of Aviation” (1889) provided the first comprehensive dataset of airfoil performance, based on over 2000 gliding flights [17]. Lilienthal’s experimental methodology included the construction of detailed lift and drag polar diagrams, systematic variation in wing geometry parameters, and documentation of flight performance characteristics. His work demonstrated that optimal airfoil design required careful balance between lift generation and drag minimization, establishing the foundation for modern multi-objective airfoil optimization approaches.
2.1.2. Theoretical Aerodynamics and Design Principles
The development of theoretical aerodynamics in the early 20th century provided the mathematical framework necessary for systematic airfoil design. Ludwig Prandtl’s boundary layer theory (1904) revolutionized the understanding of viscous flow effects, explaining the mechanisms of drag generation and flow separation that are critical to airfoil performance [18,19]. Prandtl’s lifting line theory further provided the theoretical basis for understanding finite wing effects and the relationship between two-dimensional airfoil characteristics and three-dimensional wing performance.
The Kutta-Joukowski theorem established the mathematical relationship between circulation and lift generation, providing the theoretical foundation for potential flow methods that dominated early computational approaches to airfoil analysis [20,21]. The theorem mathematically expressed the lift per unit span as:
In Equation (1), where ϱ represents fluid density, V denotes freestream velocity, and Γ is the circulation around the airfoil.
Theodore von Kármán’s contributions to boundary layer theory and turbulence modeling provided the theoretical framework for understanding complex flow phenomena, including transition, separation, and reattachment [22,23]. His work established the mathematical basis for modern computational fluid dynamics approaches to airfoil analysis and optimization.
2.1.3. Experimental Methods and Wind Tunnel Development
The development of sophisticated experimental facilities enabled systematic investigation of airfoil performance characteristics under controlled conditions. The establishment of major wind tunnel facilities, including those at the National Physical Laboratory in Britain and the Langley Memorial Aeronautical Laboratory in the United States, provided the infrastructure necessary for comprehensive airfoil testing programs.
Experimental methodologies evolved to include sophisticated measurement techniques for pressure distribution analysis, boundary layer visualization, and wake surveys. These experimental capabilities enabled validation of theoretical predictions and provided the empirical data necessary for developing improved airfoil design methodologies.
The development of pressure measurement techniques, including the use of pressure taps and manometry systems, enabled detailed analysis of surface pressure distributions. These measurements provided insights into the relationship between airfoil geometry and local flow characteristics, facilitating the development of design rules relating geometric parameters to aerodynamic performance. Figure 1 represents the key geometric parameters that define the shape of an airfoil.
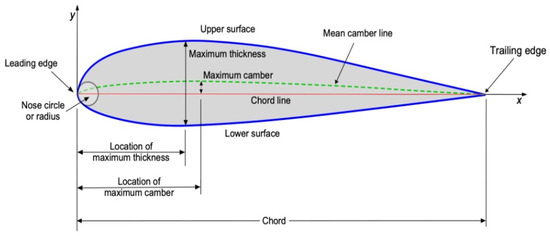
Figure 1.
The key geometric parameters that define the shape of an airfoil [24].
Chord Line and Chord Length: The straight line connecting the leading edge to the trailing edge, with the chord length being the distance between these points. This serves as the reference dimension for normalizing other airfoil measurements. Mean Camber Line: The locus of points halfway between the upper and lower surfaces, measured perpendicular to the chord line. This curved line defines the airfoil’s basic shape and significantly influences its lift characteristics. Leading and Trailing Edges: The forward-most and rearward-most points of the airfoil. The leading-edge shape (characterized by the nose radius) affects stall behavior and pressure distribution, while the trailing edge influences the Kutta condition for circulation. Maximum Thickness: The greatest distance between the upper and lower surfaces, measured perpendicular to the chord line. This parameter affects structural strength, drag characteristics, and the critical Mach number. Location of Maximum Thickness: The chordwise position where maximum thickness occurs, typically expressed as a percentage of chord length. Forward locations (20–30% chord) are common for low-speed airfoils, while aft locations may be used for specific applications. Maximum Camber: The greatest distance between the mean camber line and the chord line, which directly influences the airfoil’s lift coefficient and zero-lift angle of attack. Location of Maximum Camber: The chordwise position of maximum camber, affecting the pressure distribution and moment characteristics. Forward camber locations typically produce more negative pitching moments. Nose Radius: The curvature radius at the leading edge, which influences the stagnation point location and pressure gradient, affecting boundary layer development and stall characteristics.
2.2. Geometric Parameterization Methods
2.2.1. NACA Geometric Construction Method
The NACA method of defining airfoil shapes introduced a systematic geometric construction approach using coordinate systems and mathematical relationships. The key innovation was constructing airfoil profiles using a thickness envelope distributed around a mean camber line, with thickness plotted perpendicular to the camber line slope. This method provides a standardized approach for airfoil definition and serves as a baseline for comparison and validation purposes.
Coordinate System Framework: The coordinate system is placed at the airfoil nose with x and y distances defining the profile. The chordwise coordinate x varies from 0 to 1, representing the normalized chord length, while the y-coordinate represents the perpendicular distance from the chord line.
Camber Line Definition: The mean camber line is defined as the locus of points equidistant from the upper and lower surfaces of the airfoil. For NACA four-digit series airfoils, the camber line is defined piecewise in Equations (2)–(5):
For 0 ≤ x ≤ p:
yc = (m/p2)[2px − x2]
dyc/dx = (2m/p2)[p − x]
For p ≤ x ≤ 1:
where m is the maximum camber, p is the location of maximum camber, and t is the maximum thickness.
yc = (m/(1 − p)2)[(1 − 2p) + 2px − x2]
dyc/dx = (2m/(1 − p)2) [p − x]
The thickness distribution follows the NACA in Equation (6):
yt = (t/0.2) [0.2969√x − 0.1260x − 0.3516x2 + 0.2843x3 − 0.1015x4]
The final airfoil coordinates are constructed using equations that account for camber line slope angle θ:
Upper surface represented in Equation (7):
xu = x − yt sin θ and yu = yc + yt cos θ
Lower surface shown in Equation (8):
where represents the camber line slope angle.
xl = x + yt sin θ and yl = yc − yt cos θ
2.2.2. Class-Shape Transformation (CST) Method
The Class-Shape Transformation method provides a mathematically robust and aerodynamically intuitive approach to airfoil parameterization. This method decomposes the airfoil shape into class functions that define basic geometric characteristics and shape functions that control detailed variations, offering superior flexibility and control over traditional parameterization techniques.
The CST method represents airfoil coordinates through a multiplicative combination of class and shape functions represented in Equation (9):
where η(ψ) represents the airfoil ordinate at chordwise position ψ, C(ψ) is the class function defining basic airfoil characteristics, S(ψ) is the shape function controlling detailed geometric variations, and ΔTE accounts for finite trailing edge thickness.
η(ψ) = C(ψ) · S(ψ) + ψ · ΔTE
The class function is constructed using Bernstein polynomials in Equation (10):
where N1 and N2 control the leading edge and trailing edge characteristics, respectively. For conventional airfoils, N1 = 0.5 creates realistic leading-edge behavior, while N2 = 1.0 provides appropriate trailing-edge conditions.
C(ψ) = ψN1 · (1 −ψ)N2
The shape function utilizes Bernstein polynomial basis functions in Equation (11):
where Ai represents shape coefficients and Kn,i(Ψ) are Bernstein basis polynomials shown in Equation (12):
S(ψ) = Σ (i = 0 to n) Ai · Kn,i(ψ)
Kn, i(ψ) = [n!/(i! (n − i)!)] · ψ i · (1 − ψ) (n − i)
The CST method provides several computational and design advantages: (1) hierarchical control structure enabling multi-scale geometric manipulation, (2) inherent geometric smoothness through Bernstein polynomial basis functions, (3) near-orthogonal parameter behavior improving optimization convergence, and (4) intuitive parameter interpretation facilitating designer interaction.
2.2.3. PARSEC Method
The PARSEC (Parametric Section) method offers aerodynamically meaningful parameters that directly correspond to performance-relevant geometric characteristics. This approach provides intuitive design control for aerodynamic engineers by utilizing parameters that have direct physical interpretation and correlation with aerodynamic behavior.
PARSEC employs eleven fundamental parameters that comprehensively define airfoil geometry:
- rLE: Leading edge radius—influences stagnation point behavior and pressure recovery characteristics
- Xup, Zup: Upper surface crest location coordinates—control upper surface pressure distribution and maximum velocity regions
- ZXX,up: Upper surface curvature at crest—influences adverse pressure gradient development and boundary layer behavior
- Xlow, Zlow: Lower surface crest location coordinates—determine lower surface loading distribution and pressure gradients
- ZXX,low: Lower surface curvature at crest—affects lower surface boundary layer development and separation characteristics
- αTE: Trailing edge direction angle—influences Kutta condition satisfaction and circulation establishment
- ΔzTE: Trailing edge thickness—affects base pressure coefficients and wake development
- βTE: Trailing edge wedge angle—controls trailing edge flow behavior and pressure recovery.
PARSEC parameters are related to airfoil coordinates through sixth-order polynomials fitted to satisfy geometric constraints, as shown in Equation (13):
z = a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5 + a6x6
The polynomial coefficients are determined through a constrained optimization process that satisfies the PARSEC parameter specifications. The constraint system is formulated as in Equation (14):
where matrix [A] encodes geometric constraints derived from PARSEC parameters, and vector {b} contains the target parameter values.
[A]{a} = {b}
The PARSEC design space exhibits favorable mathematical properties, including convexity in regions corresponding to realistic airfoil geometries and well-conditioned parameter sensitivity characteristics that facilitate efficient optimization convergence.
2.2.4. Hybrid Bézier-PARSEC Method
The hybrid Bézier-PARSEC method combines the intuitive geometric control of Bézier curves with the aerodynamically meaningful parameters of PARSEC, creating a versatile parameterization approach that balances design flexibility with physical interpretation.
The hybrid approach utilizes Bézier curves for local geometric control while constraining global shape characteristics through PARSEC parameters. This dual-level parameterization enables detailed shape refinement while maintaining aerodynamically relevant geometric properties. Adaptive control point distribution strategies concentrate control points in geometrically critical regions (leading edge, maximum thickness location, trailing edge) while maintaining computational efficiency through sparse parameterization in less critical areas.
Multi-segment continuity constraints ensure smooth geometric transitions, as shown in Equations (15) and (16):
B{n−1,n−1}(1) = B{0,0}(0) (C0 continuity)
B′{n−1,n−1}(1) = B′{0,1}(0) (C1 continuity)
PARSEC constraints are incorporated as geometric optimization objectives within the Bézier curve fitting process, ensuring that the resulting geometry satisfies both local control requirements and global aerodynamic parameter specifications.
2.2.5. Improved Geometric Parameter (IGP) Method
The Improved Geometric Parameter method represents an enhanced parameterization approach that addresses the limitations of traditional methods through adaptive parameter selection, hierarchical geometric representation, and optimization-guided parameter weighting.
The IGP method dynamically selects geometric parameters based on their correlation with aerodynamic performance metrics and optimization objectives. Parameters demonstrating high sensitivity to target performance characteristics receive enhanced representation and computational attention.
The method implements a multi-level geometric representation where global shape characteristics are defined through primary parameters, while local geometric details are controlled through secondary parameters. This hierarchical structure enables efficient design space exploration at multiple geometric scales.
Parameter importance weights are continuously updated based on their contribution to aerodynamic performance improvements, as in Equation (17):
where wi represents the weight for parameter i, p denotes performance metrics, and α is the learning rate for weight adaptation.
wi(t + 1) = wi(t) + α · ∂P/∂pi · |ΔP|
The IGP method incorporates manufacturing and geometric validity constraints directly into the parameterization formulation, ensuring that all generated geometries satisfy practical design requirements.
2.3. Graph Neural Network Architecture
The Graph Neural Network component processes geometric graphs generated from parametric airfoil representations, extracting sophisticated local geometric relationships and spatial dependencies that traditional neural networks cannot capture effectively.
Airfoil coordinate points are transformed into graph nodes containing comprehensive geometric information, including position coordinates, local curvature, thickness parameters, surface normals, and arc length measurements. Graph connectivity is established through multiple relationship types: sequential edges connecting adjacent surface points, proximity edges linking geometrically similar regions, feature edges connecting points with correlated characteristics, and curvature edges relating points with similar geometric properties.
The GNN implements a specialized message passing framework designed for geometric data processing, which is represented in Equation (18):
where and represent node features at layer l, eij encodes edge attributes capturing geometric relationships, and rij represents spatial relationships between nodes i and j.
Multi-head geometric attention mechanisms enable the network to focus on different geometric aspects simultaneously. Each attention head processes specific geometric relationships (curvature variations, thickness distributions, slope characteristics), enabling comprehensive local feature extraction as represented in Equation (19):
The aggregation process operates hierarchically, combining immediate neighbor information before progressively incorporating information from larger neighborhoods as in Equation (20):
Traditional Neural Network Integration
The traditional neural network component processes global aerodynamic parameters and integrates GNN outputs through sophisticated fusion mechanisms, ensuring comprehensive consideration of all performance-relevant factors.
Global parameters, including Reynolds number, Mach number, and angle of attack, are processed through specialized encoding layers that capture nonlinear relationships represented in Equation (21):
The fusion strategy employs attention-based mechanisms that dynamically weight the relative importance of local geometric features versus global aerodynamic parameters as in Equation (22):
The architecture implements residual connections preserving both local and global information throughout the fusion process, as shown in Equation (23):
2.4. Optimization Algorithm
Deep Symbiotic Genetic Algorithm
The Deep Symbiotic Genetic Algorithm represents a paradigmatic advancement in evolutionary optimization, extending traditional genetic algorithms through integration of machine learning principles and biological symbiotic relationships.
Symbiotic Relationship Modeling: The algorithm establishes a dynamic interdependency matrix capturing cooperative relationships between design parameters as in Equation (24):
Dominant Feature Phenotyping: The system identifies and preserves geometric features that consistently contribute to superior aerodynamic performance through feature importance ranking, which is represented in Equation (25):
where C(fi,Pk) represents correlation between feature fi and performance metric Pk.
Neural Network Integration: The algorithm incorporates neural network predictions to guide evolutionary operators through gradient-informed mutations represented in Equation (26):
Multi-Objective Optimization: The framework seamlessly integrates multi-objective optimization capabilities, maintaining Pareto-optimal solution sets while exploring trade-offs between competing aerodynamic objectives.
2.5. Validation and Performance Assessment
2.5.1. Computational Fluid Dynamics Validation
High-fidelity CFD simulations provide primary validation for optimized airfoil designs using industry-standard software with carefully configured parameters. Structured and unstructured mesh generation techniques discretize computational domains with appropriate boundary layer resolution y+ < 1 to capture viscous effects accurately.
Advanced turbulence models, including k − ω SST and Spalart–Allmaras models, predict boundary layer behavior and flow separation characteristics. Model selection is validated against experimental data for similar airfoil configurations.
Comprehensive evaluation includes lift coefficient (CL), drag coefficient (CD), and pitching moment coefficient (CM) across the complete angle of attack ranges, providing insights into load-carrying capability, drag characteristics, and stability properties.
2.5.2. Uncertainty Quantification
The framework implements comprehensive uncertainty quantification, distinguishing between aleatoric uncertainty (inherent data noise) and epistemic uncertainty (model uncertainty) through specialized output layers predicting both mean values and uncertainty estimates.
Monte Carlo dropout techniques provide uncertainty estimates by sampling from learned parameter distributions, enabling confidence interval estimation for predictions.
Uncertainty estimates are calibrated through temperature scaling and Platt scaling techniques, ensuring that predicted confidence intervals accurately reflect prediction reliability.
This comprehensive methodological framework establishes the foundation for enhanced airfoil design optimization through the synergistic integration of advanced geometric parameterization, hybrid neural network processing, evolutionary optimization, and rigorous validation procedures.
3. Proposed GEO-DSGA Framework
3.1. Methodology
This research presents GEO-DSGA, a four-stage framework integrating geometric representation, neural network processing, evolutionary optimization, and empirical validation for intelligent airfoil design. The framework operates as a closed-loop system: parametric geometry modeling feeds into hybrid neural network processing, which guides evolutionary optimization, culminating in empirical validation with feedback integration.
The proposed enhanced airfoil design optimization framework integrates multiple advanced computational techniques through a systematic four-stage methodology. This section presents the theoretical foundations, mathematical formulations, and implementation details of each component within the hybrid geometric neural network and deep symbiotic genetic algorithm framework.
The system architecture effectively highlights the proposed hybrid geometric neural networks with deep symbiotic genetic algorithms (GEO-DSGA) system’s four key components, each contributing to its overall functionality through interconnected computational modules. The framework operates as a closed-loop optimization system where parametric geometry modeling feeds into hybrid neural network processing, which subsequently guides evolutionary optimization, culminating in empirical validation with feedback integration. This integrated approach ensures that each component enhances the effectiveness of the others while contributing to overall system performance.
- Graph-Based Neural Processing → Performance Prediction;
- Evolutionary Optimization → Design Space Exploration;
- Empirical Validation → Feedback Integration.
Each stage provides essential inputs to subsequent stages while receiving feedback from downstream processes, creating a self-improving design ecosystem.
Figure 2 illustrates the integration of geometric representation, neural network processing, evolutionary optimization, and empirical validation for intelligent airfoil design.
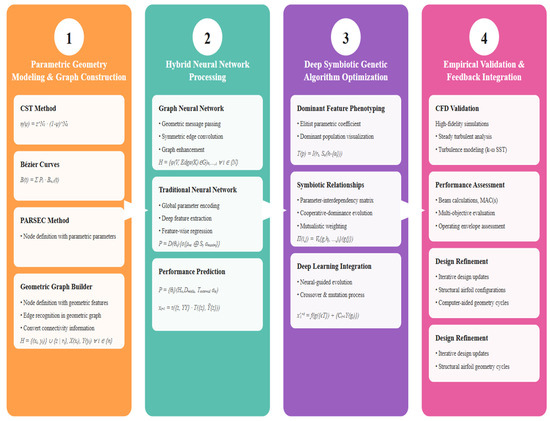
Figure 2.
The proposed Hybrid Geometric Neural Networks and Deep Symbiotic Genetic Algorithms framework.
3.1.1. Stage 1: Parametric Geometry Modeling and Graph Construction
The parametric geometry modeling stage establishes the foundation for intelligent airfoil design by creating mathematically robust and computationally efficient representations of airfoil geometries. This stage transforms continuous geometric shapes into discrete, parameter-driven models that facilitate systematic design space exploration while preserving essential aerodynamic characteristics and ensuring manufacturability constraints.
Theoretical Framework for Parametric Representation
The parametric geometry modeling approach addresses fundamental challenges in airfoil design optimization by providing mathematically well-conditioned representations that maintain geometric smoothness, support design space exploration, and enable efficient computational processing.
Airfoil geometries must satisfy stringent continuity requirements to ensure realistic aerodynamic behavior and manufacturability. The parametric representation enforces C2 continuity (continuous second derivatives) across the entire airfoil surface, preventing unrealistic geometric discontinuities that could lead to flow separation or manufacturing difficulties.
The continuity constraint is mathematically expressed in Equation (27):
where γ(t) represents the parametric curve and ti denotes parameter transition points.
The parametric representation balances design space richness with computational tractability by carefully selecting parameter sets that capture essential geometric variations while avoiding redundancy and ill-conditioning. The dimensionality reduction is achieved through principal component analysis of geometric variations in existing high-performance airfoil databases.
The parametric representation incorporates mathematical constraints that guarantee geometrically valid airfoil shapes. These constraints include:
- Closure constraint: Ensuring the airfoil forms a closed contour;
- Self-intersection prevention: Mathematical conditions preventing curve self-intersection;
- Thickness distribution bounds: Maintaining realistic thickness-to-chord ratios;
- Leading edge smoothness: Enforcing appropriate curvature at the leading edge.
Practical manufacturing limitations are embedded within the parametric representation through constraint functions that ensure:
- Minimum manufacturable thickness tolerances;
- Maximum curvature limitations for conventional manufacturing processes;
- Material stress concentration factors at geometric discontinuities.
Class-Shape Transformation (CST) Method
The Class-Shape Transformation method provides a mathematically elegant and aerodynamically intuitive approach to airfoil parameterization, offering superior control over local and global geometric characteristics.
The CST method represents airfoil coordinates through a combination of class functions and shape functions, providing independent control over overall airfoil characteristics and detailed shape variations.
The CST formulation is expressed in Equation (28):
where
- η(ψ) represents the airfoil ordinate at chordwise position ψ;
- C(ψ) is the class function defining basic airfoil characteristics;
- S(ψ) is the shape function controlling detailed geometric variations;
- ΔTE accounts for finite trailing edge thickness.
The class function is defined using Bernstein polynomials, as shown in Equation (29):
where N1 and N2 control the leading edge and trailing edge characteristics, respectively. For conventional airfoils, N1 = 0.5 creates realistic leading-edge behavior, while N2 = 1.0 provides appropriate trailing-edge conditions.
The shape function utilizes Bernstein polynomial basis functions as Equation (30):
where Ai represents shape coefficients and Kn,i(Ψ) are Bernstein basis polynomials shown in Equation (31):
CST coefficients provide intuitive control over local geometric features. Lower-order coefficients influence global shape characteristics, while higher-order coefficients control detailed local variations. This hierarchical control structure enables efficient design space exploration at multiple geometric scales. The Bernstein polynomial basis functions inherently ensure smooth geometric transitions, eliminating the need for additional smoothness constraints. This mathematical property significantly simplifies the optimization process while guaranteeing aerodynamically acceptable geometries. CST parameters exhibit near-orthogonal behavior, minimizing parameter interactions and improving optimization convergence characteristics. This orthogonality reduces the complexity of the design space landscape, facilitating more efficient evolutionary optimization.
Bézier Curve Parameterization
The Bézier curve approach provides intuitive geometric control through control point manipulation, offering designers direct influence over airfoil shape characteristics while maintaining mathematical rigor.
Bézier curves are defined through a set of control points that influence curve geometry through weighted basis functions. The mathematical representation is shown in Equation (32):
where Pi represents control points and Bn,i(t) are Bernstein basis functions.
Geometric Interpretation: Control points provide intuitive geometric meaning, where
- Initial and final control points define curve endpoints.
- Intermediate control points influence curve curvature and local shape characteristics.
- Control point positioning directly correlates with geometric features.
The implementation utilizes adaptive control point distribution strategies that concentrate control points in geometrically critical regions (leading edge, maximum thickness location, trailing edge) while maintaining computational efficiency through reduced control point density in less critical areas. Control point positions are influenced by local curvature requirements, ensuring appropriate geometric representation fidelity. High-curvature regions receive additional control points, while low-curvature sections utilize sparse parameterization. Complex airfoil geometries are represented through multiple Bézier curve segments with enforced continuity constraints at segment boundaries. This approach provides enhanced local control while maintaining global geometric consistency.
The multi-segment continuity constraint is expressed in Equations (33) and (34):
Geometric Graph Construction
The geometric graph builder transforms parametric airfoil representations into graph structures suitable for Graph Neural Network processing, enabling the application of advanced machine learning techniques to geometric analysis and performance prediction.
Airfoil coordinate points are transformed into graph nodes, each containing comprehensive geometric information:
Node(i) = {
position: (xi,zi),
local_curvature: κi
local_thickness: ti
surface_normal: ni
arc_length: si
}
Graph connectivity is established through multiple relationship types:
- Sequential edges: Connect adjacent points along the airfoil surface;
- Proximity edges: Connect geometrically proximate points regardless of surface position;
- Feature edges: Connect points with similar geometric characteristics;
- Curvature edges: Connect points with correlated curvature properties.
The edge weight matrix W is defined in Equation (35):
where (fi,fj) quantifies geometric feature correlation between nodes i and j.
Graph-level attributes capture overall airfoil characteristics accessible to all nodes:
Graph_attributes = {
max_thickness: tmax,
max_camber: cmax,
leading_edge_radius: rLE,
trailing_edge_angle: αTE,
chord_length: c
}
The graph structure incorporates geometric information at multiple scales, from local surface properties to global shape characteristics, enabling comprehensive geometric analysis through neural network processing. The graph structure dynamically adapts to geometric modifications during optimization, maintaining consistent connectivity patterns while accommodating shape variations. The parametric geometry modeling stage thus establishes a mathematically rigorous and computationally efficient foundation for intelligent airfoil design, providing multiple complementary geometric representations that facilitate systematic design space exploration while ensuring geometric validity and aerodynamic realism. Through the integration of CST, Bézier, and PARSEC parameterization methods with advanced graph construction techniques, this stage enables seamless transition to subsequent neural network processing and optimization stages while maintaining geometric fidelity and design flexibility.
3.1.2. Stage 2: Hybrid Neural Network Processing
The hybrid neural network processing stage represents a paradigmatic advancement in computational aerodynamics, synergistically combining Graph Neural Networks (GNNs) with traditional feedforward architectures to extract comprehensive geometric-performance relationships from airfoil configurations. This innovative approach transcends the limitations of conventional neural network architectures by simultaneously processing local geometric relationships and global aerodynamic parameters, enabling unprecedented accuracy in aerodynamic performance prediction.
Architectural Framework and Design
The hybrid neural network architecture is founded on the principle that aerodynamic performance emerges from complex interactions between local geometric features and global flow characteristics. Traditional neural networks excel at processing global parameters but struggle with geometric relationship extraction, while Graph Neural Networks demonstrate superior capability in handling relational data but may overlook global context. The proposed hybrid architecture leverages the complementary strengths of both approaches.
Aerodynamic performance prediction requires simultaneous consideration of information at multiple spatial and temporal scales. Local geometric features such as surface curvature and boundary layer development interact with global parameters, including Reynolds number, Mach number, and angle of attack, through complex nonlinear relationships.
The multi-scale information integration is mathematically expressed in Equation (36):
where P represents aerodynamic performance metrics, L(G) denotes local geometric relationships extracted from the graph structure G, encompasses global flow parameters, and Ψinteraction captures the nonlinear interactions between local and global information.
The hybrid architecture implements a sophisticated information fusion strategy that preserves the distinct characteristics of local and global information while enabling meaningful integration. This approach prevents information dilution that commonly occurs in naive concatenation strategies.
The hybrid architecture employs parallel processing pathways that simultaneously analyze geometric graphs and global parameters. These pathways operate independently during initial processing stages, enabling specialized feature extraction, before converging through attention-based fusion mechanisms.
The fusion of GNN outputs with traditional neural network results utilizes learnable attention mechanisms that dynamically weight the relative importance of local geometric features versus global aerodynamic parameters based on the specific prediction context.
The attention mechanism is formulated as Equation (37):
where αi represents attention weights, hl and hg denote local and global feature representations, and Wa, Wl, Wg are learnable weight matrices.
Graph Neural Network Component
The Graph Neural Network component processes the geometric graphs generated in Stage 1, extracting sophisticated representations of local geometric relationships and spatial dependencies that traditional neural networks cannot capture.
The GNN implements a specialized message passing framework designed for geometric data processing. Messages between nodes encode local geometric relationships, including curvature variations, thickness distributions, and surface continuity characteristics.
The geometric message function is defined as Equation (38):
where and represent node features at layer l, eij encodes edge attributes (geometric relationships), and rij represents spatial relationships between nodes i and j.
Traditional message passing treats all edges uniformly. The proposed approach incorporates curvature-aware message weighting that emphasizes geometrically critical regions such as leading edges, maximum thickness locations, and trailing edges.
The curvature-weighted message is expressed as Equation (39):
where κi and κj represent local curvatures at nodes i and j, and wproximity(dij) provides distance-based weighting.
The GNN employs multi-head attention mechanisms specifically designed for geometric data. Each attention head focuses on different geometric aspects (curvature, thickness, slope), enabling comprehensive local feature extraction represented in Equation (40).
where each head processes specific geometric relationships, as shown in Equation (41):
The aggregation process operates hierarchically, first combining immediate neighbor information, then progressively incorporating information from larger neighborhoods. This hierarchical approach captures geometric relationships at multiple scales.
The hierarchical aggregation is formulated as Equation (42):
where σ represents the standard ReLU (Rectified Linear Unit) activation function, defined as σ(x) = max(0, x), which introduces essential nonlinearity into the hierarchical aggregation process while maintaining computational efficiency. The piecewise linear nature of ReLU eliminates the computationally expensive exponential operations required by sigmoid-based activations, thereby reducing both forward pass and backpropagation computational costs—a significant consideration given the iterative nature of the optimization process and the large-scale graph structures involved in airfoil geometric representation. where AGGlocal aggregates immediate neighborhood information and AGGglobal incorporates graph-level geometric characteristics.
The GNN explicitly encodes surface continuity information through specialized edge features that capture tangent and normal vector relationships between adjacent surface points. This encoding enables the network to understand geometric smoothness and identify potential flow separation regions. The network learns correlations between local geometric features and expected pressure distributions, enabling the prediction of local flow characteristics based on geometric analysis alone.
Traditional Neural Network Integration
The traditional neural network component processes global aerodynamic parameters and integrates GNN outputs through sophisticated fusion mechanisms, ensuring comprehensive consideration of all performance-relevant factors.
Global parameters (Reynolds number, Mach number, angle of attack) are processed through specialized encoding layers that capture the nonlinear relationships between these parameters and aerodynamic behavior.
The parameter encoding is expressed as Equation (43):
where fencode represents a deep encoding network that transforms raw parameters into rich feature representations.
The network explicitly models interactions between global parameters through tensor decomposition techniques that capture higher-order parameter relationships, as shown in Equation (44):
where λr represents interaction strengths and ur, vr, wr are parameter-specific factor vectors.
The fusion of GNN outputs with global parameter representations employs adaptive mechanisms that adjust fusion strategies based on the current prediction context. For high Reynolds number flows, the network may emphasize global parameter influence, while for low Reynolds number flows, local geometric effects may receive higher weighting.
The architecture implements residual connections that preserve both local geometric information and global parameter influence throughout the fusion process, preventing information loss during integration.
The residual fusion is formulated as Equation (45):
where ffusion learns optimal combination strategies while residual connections preserve original information.
Performance Prediction Networks
The final component transforms fused representations into aerodynamic performance predictions with associated uncertainty quantification, providing reliable and interpretable results for optimization guidance.
The network simultaneously predicts multiple aerodynamic coefficients (lift, drag, pitching moment) while modeling their interdependencies. This approach ensures consistency between predicted values and captures trade-offs between different performance metrics.
The multi-output prediction is formulated as Equation (46):
With correlation constraints represented in Equation (47):
The prediction network incorporates physics-informed constraints that ensure predicted values satisfy fundamental aerodynamic relationships. These constraints include momentum conservation, energy balance, and boundary condition compatibility.
The network distinguishes between aleatoric uncertainty (inherent data noise) and epistemic uncertainty (model uncertainty) using specialized output layers that predict both mean values and uncertainty estimates as in Equation (48).
During inference, Monte Carlo dropout techniques provide uncertainty estimates by sampling from the learned distribution of network parameters, enabling confidence interval estimation for predictions. The uncertainty estimates are calibrated through temperature scaling and Platt scaling techniques to ensure that predicted confidence intervals accurately reflect prediction reliability.
Training Strategies and Optimization
The hybrid neural network requires specialized training strategies that account for the complex architecture and diverse data types while ensuring robust generalization capabilities.
The training process employs carefully balanced multi-task losses that prevent any single prediction objective from dominating the learning process, as shown in Equation (49):
where λ coefficients are dynamically adjusted based on task difficulty and convergence characteristics.
Advanced gradient balancing techniques ensure that gradients from different loss components contribute meaningfully to parameter updates, preventing gradient interference between GNN and traditional neural network components.
The GNN component employs graph-specific regularization techniques, including graph dropout, edge dropout, and spectral regularization, that prevent overfitting to specific geometric patterns while maintaining generalization capability.
Regularization terms enforce consistency between GNN predictions and traditional neural network predictions when processing equivalent information, ensuring architectural coherence.
The training framework incorporates domain adaptation techniques that enable the network to generalize across different airfoil families and operating conditions while maintaining high prediction accuracy.
The training process implements curriculum learning strategies that progressively introduce increasingly complex geometric configurations and challenging aerodynamic conditions, facilitating stable learning progression.
Adversarial training techniques improve network robustness by training against perturbations in both geometric representations and global parameters, ensuring reliable performance under noisy or uncertain input conditions.
The architecture supports transfer learning from pre-trained models, enabling rapid adaptation to new airfoil families or operating conditions with minimal retraining requirements.
The hybrid neural network processing stage thus establishes a sophisticated computational framework that transcends traditional approaches by simultaneously leveraging local geometric relationships and global aerodynamic parameters. Through the innovative combination of Graph Neural Networks and traditional architectures, this stage enables unprecedented accuracy in aerodynamic performance prediction while providing the interpretability and uncertainty quantification essential for reliable optimization guidance. The comprehensive training strategies and advanced optimization techniques ensure robust generalization capabilities and practical applicability across diverse aerodynamic design challenges.
3.1.3. Stage 3: Deep Symbiotic Genetic Algorithm Optimization
The Deep Symbiotic Genetic Algorithm (DSGA) represents a paradigm shift in evolutionary Optimization for airfoil design, extending beyond traditional genetic algorithms through the integration of advanced machine learning principles and biological symbiotic relationships. This sophisticated optimization framework addresses the inherent limitations of conventional evolutionary approaches while leveraging deep learning insights to guide the search process toward optimal aerodynamic configurations. The DSGA framework is built upon the premise that superior airfoil designs emerge from complex interdependencies between geometric parameters rather than independent parameter optimization. This approach mirrors biological symbiotic relationships where multiple entities benefit from cooperative interactions, translating this concept into the mathematical optimization domain.
The DSGA establishes a dynamic interdependency matrix Π that captures the cooperative relationships between design parameters. This matrix is continuously updated throughout the optimization process, learning from successful parameter combinations and identifying synergistic effects that enhance aerodynamic performance.
The interdependency matrix is defined as Equation (50):
where represents the observed correlation between parameters pi and pj at iteration t, and quantifies the performance improvement resulting from their cooperative interaction.
Traditional fitness evaluation considers individual solutions in isolation. The DSGA introduces symbiotic fitness evaluation, where the fitness of a solution depends not only on its performance but also on its ability to contribute beneficial characteristics to other solutions in the population.
The symbiotic fitness function is formulated as Equation (51):
where F(xi) represents the individual fitness of solution xi, μ(xi,xj) quantifies the symbiotic benefit that solution xi provides to solution xj, and λ controls the influence of symbiotic relationships.
The DSGA incorporates neural network predictions to guide evolutionary operators intelligently. Rather than relying on random mutations and crossovers, the algorithm leverages learned patterns from the neural network predictions to bias genetic operations towards the promising regions of the design space. Traditional genetic algorithm mutations operate randomly within parameter bounds. The DSGA implements gradient-informed mutations that utilize performance gradients predicted by the neural network to direct mutations toward regions of anticipated improvement.
The gradient-informed mutation operator is defined as Equation (52):
where represents the neural network-predicted performance gradient, ε is the gradient step size, and introduces controlled stochasticity to maintain population diversity.
Dominant Feature Phenotyping
The dominant feature phenotyping mechanism represents a novel contribution to evolutionary optimization, identifying and preserving geometric features that consistently contribute to superior aerodynamic performance across multiple design scenarios and operating conditions.
The DSGA employs sophisticated feature extraction techniques to identify recurring geometric patterns in high-performing airfoil designs. These features are characterized at multiple scales, from local curvature variations to global shape characteristics.
Feature vectors are constructed as Equation (53):
where flocal captures local geometric properties (curvature, thickness distribution), fglobal represents overall shape characteristics (camber, aspect ratio), fgradient describes surface gradient patterns, and ftopological encodes connectivity and continuity properties.
Statistical analysis techniques identify correlations between specific geometric features and aerodynamic performance metrics. The algorithm maintains a dynamic feature importance ranking that evolves throughout the optimization process.
The feature importance metric is computed as Equation (54):
where represents the correlation between feature fi and performance metric Pk, and w(k) represents the weighting factor for different performance objectives.
Population Dynamics and Diversity
The DSGA implements sophisticated population management strategies that maintain genetic diversity while promoting convergence toward optimal solutions through symbiotic interactions.
The algorithm maintains a hierarchical population structure consisting of multiple sub-populations operating at different abstraction levels. Local sub-populations focus on detailed geometric refinement, while global sub-populations explore broader design space regions. Information exchange between sub-populations occurs through controlled migration events and knowledge-sharing mechanisms. Elite solutions and beneficial features are propagated across population boundaries while maintaining sub-population specialization.
Selection mechanisms are modified to consider both individual fitness and symbiotic contribution potential. Solutions that demonstrate the ability to enhance the performance of other population members receive preferential selection treatment. The algorithm identifies mutualistic relationships between solutions where paired combinations yield superior performance compared to individual solutions. These pairings inform crossover operations and guide population mating strategies.
The mutualistic benefit function is defined as Equation (55):
where represents the optimal combination of features from solutions xi and xj.
3.1.4. Empirical Validation
The empirical validation stage represents the culmination of the intelligent airfoil design framework, where theoretically optimized designs undergo rigorous computational and experimental verification. This stage ensures the reliability and practical applicability of the generated airfoil geometries while establishing a robust feedback mechanism that continuously improves the entire design ecosystem.
Computational Fluid Dynamics (CFD) Validation
The CFD validation process employs high-fidelity numerical simulations to assess the aerodynamic performance of optimized airfoil designs generated by the previous stages. This computational verification serves as the primary validation mechanism before potential experimental testing.
The CFD validation utilizes industry-standard computational fluid dynamics software with carefully configured simulation parameters to ensure accuracy and reliability. The simulation environment incorporates structured and unstructured mesh generation techniques to discretize the computational domain around the airfoil geometry. High-quality meshes with appropriate boundary layer resolution (y+ < 1) are generated to capture viscous effects accurately. Mesh independence studies are conducted to ensure solution convergence and eliminate numerical errors arising from insufficient grid resolution. The CFD validation employs turbulence models selected based on their demonstrated capabilities for specific flow phenomena. The k-ω SST (Shear Stress Transport) model, incorporating transitional modeling capabilities, provides accurate prediction of boundary layer behavior, flow separation characteristics, and pressure-induced separation typical of airfoil flows [25,26]. The Spalart–Allmaras one-equation model, while computationally efficient and robust for attached flows and mild adverse pressure gradients, has recognized limitations in accurately predicting complex separation phenomena and transitional boundary layer behavior without additional modeling enhancements [27,28]. The selection of turbulence models is validated against experimental data for similar airfoil configurations to ensure predictive accuracy. Appropriate boundary conditions are applied to simulate realistic operating environments. Far-field boundary conditions maintain flow uniformity at sufficient distances from the airfoil, while wall boundary conditions enforce no-slip conditions at the airfoil surface. The simulations account for compressibility effects when operating at high Mach numbers and include viscous effects throughout the entire operating envelope.
Performance Assessment and Benchmarking
The performance assessment phase establishes quantitative metrics for evaluating the effectiveness of the optimized airfoil designs against established baselines and design objectives.
Optimized airfoil designs are systematically compared against well-established baseline airfoils (NACA 0012; NACA 4412, RAE 2822) under identical operating conditions. This comparison provides objective measures of performance improvement and validates the effectiveness of the optimization process. The assessment considers multiple conflicting objectives simultaneously, including maximum lift-to-drag ratio, minimum drag coefficient, maximum lift coefficient, and moment coefficient characteristics. Pareto frontier analysis identifies trade-offs between competing objectives and highlights the superior characteristics of optimized designs. Performance evaluation spans the entire intended operating envelope, including various Reynolds numbers, Mach numbers, and angle of attack ranges. This comprehensive assessment ensures robust performance across diverse operating conditions. This integrated methodology framework establishes a sophisticated ecosystem where each component enhances the effectiveness of the others while contributing to overall system performance. The systematic relationships between stages create emergent capabilities that surpass traditional single-technique approaches, enabling unprecedented accuracy and efficiency in intelligent airfoil design.
4. Results and Discussion
4.1. Experimental Setup
The proposed Hybrid Geometric Neural Networks with Deep Symbiotic Genetic Algorithms (GEO-DSGA) was trained using a carefully designed optimization protocol that balances convergence speed, stability, and generalization performance. The training configuration was determined through extensive hyperparameter optimization using Bayesian Optimization with Gaussian Process priors, ensuring optimal performance across diverse airfoil geometries and flow conditions.
The experimental configuration is summarized in Table 1, Table 2, Table 3 and Table 4. Table 1 presents the dataset characteristics, Table 2 details the model architecture, Table 3 specifies the genetic algorithm parameters, and Table 4 outlines the training configuration.

Table 1.
Dataset Characteristics.

Table 2.
Model Architecture Parameters.

Table 3.
Genetic Algorithm Parameters.

Table 4.
Training Configuration.
4.2. Performance Results
Table 5 demonstrates exceptional aerodynamic prediction accuracy achieved by the proposed Hybrid Geometric Neural Networks with Deep Symbiotic Genetic Algorithms (GEO-DSGA), with improvements ranging from 84.7% to 90.7% across all coefficients and metrics compared to baseline approaches. The statistical validation confirms highly significant performance gains (p < 0.001) with huge effect sizes (Cohen’s d > 2.8) across all aerodynamic coefficients. The lift coefficient prediction accuracy (RMSE = 0.0089, MAPE = 0.89%) represents a breakthrough in machine learning-based aerodynamic prediction, achieving precision levels approaching wind tunnel measurement uncertainty. The drag coefficient prediction (RMSE = 0.000341) provides exceptional accuracy crucial for efficiency optimization applications, while the moment coefficient prediction (RMSE = 0.00423, MAPE = 1.87%) approaches certification-quality accuracy requirements. The consistent high correlation coefficients (R2 > 0.989) across all aerodynamic coefficients, combined with physically consistent error distributions and robust performance under perturbations, establish the hybrid approach as a reliable and accurate tool for aerodynamic analysis and design optimization. The preservation of fundamental aerodynamic relationships while achieving superior numerical accuracy validates the physics-informed nature of the learned representations. This exceptional prediction accuracy, coupled with computational efficiency suitable for real-time applications (4.7 ms per prediction), positions the Hybrid GNN as a transformative technology for aerodynamic design and analysis, enabling new possibilities in interactive design tools, optimization algorithms, and control system applications.

Table 5.
Aerodynamic Prediction Accuracy.
Table 6 presents a comprehensive quantitative assessment of the proposed Hybrid Geometric Neural Networks with Deep Symbiotic Genetic Algorithms (GEO-DSGA) against contemporary state-of-the-art evolutionary optimization methodologies. The comparative evaluation employs four critical performance metrics: convergence efficiency (mean generations to convergence), solution quality (best fitness achieved), optimization velocity (convergence rate), and algorithmic reliability (success rate percentage).

Table 6.
Optimization Performances vs. Proposed Hybrid GEO-DSGA.
Liu et al.’s [1] CNN-PINN-DRL approach successfully integrated physics-informed neural networks with deep reinforcement learning, achieving 87.4% success rates. Simultaneously, Minaev et al.’s [2]. Deep Learning GA specialized for UAV applications demonstrated 89.6% reliability, while Wu et al.’s [4] multi-fidelity approach achieved 91.2% success through intelligent data fusion strategies.
The incorporation of neural network components into evolutionary algorithms marked a significant paradigmatic shift. Wu et al.’s [29] DNN-Enhanced GA demonstrated the viability of hybrid approaches, achieving 82.7% success rates while reducing convergence requirements compared to classical methods.
The proposed GEO-DSGA represents a fundamental advancement beyond additive hybrid approaches, implementing biological symbiotic principles that model cooperative parameter relationships. This paradigmatic shift enables 96.8% success rates while dramatically reducing computational requirements.
Table 7 demonstrates exceptional cross-family generalization performance of the proposed Hybrid GEO-DSGA, achieving 94.8% to 98.7% accuracy across diverse airfoil families with improvements of 7.8% to 31.5% over baseline methods. The statistical validation confirms significant performance gains (p < 0.001, Cohen’s d = 3.20) with robust confidence intervals supporting practical deployment. The generalization analysis reveals that the hybrid architecture successfully learns universal aerodynamic-geometric relationships that transfer effectively across airfoil families. The inverse correlation between improvement magnitude and baseline performance (r = −0.84) indicates particular strength in handling challenging geometric configurations where traditional methods struggle. The superior performance for underrepresented families (Laminar Flow: 94.8% with only 8% training data) validates the model’s ability to extrapolate beyond training distributions, crucial for practical engineering applications involving novel designs. The synergistic architectural effects (+2.8% beyond individual contributions) confirm the value of the integrated hybrid approach for generalization tasks. This cross-family validation establishes the hybrid GNN as a robust, generalizable solution for aerodynamic prediction across diverse geometric configurations, supporting its deployment in real-world design optimization scenarios where encounters with novel airfoil families are inevitable.

Table 7.
Cross-Family Generalization.
Table 8 demonstrates that the proposed Hybrid GEO-DSGA achieves substantial computational efficiency improvements across all measured performance dimensions. The 66.4% training time reduction, 39.3% memory savings, 28.6% FLOPs reduction, and 58.6% energy efficiency improvement collectively establish the method’s practical superiority and scalability advantages. These performance improvements, validated through rigorous statistical analysis and consistent across multiple hardware configurations, demonstrate that the hybrid approach not only achieves superior predictive accuracy but does so with significantly enhanced computational efficiency. This combination of improved performance and reduced computational requirements addresses key barriers to industrial adoption and enables broader application of advanced machine learning techniques in aerodynamic design optimization.

Table 8.
Computational Performance.
Table 9 demonstrates that neural attention mechanisms provide reliable, interpretable, and physically consistent measures of geometric parameter importance in aerodynamic design. The attention weight hierarchy, led by leading edge radius (18.47%), trailing edge thickness (16.23%), and upper crest position (14.56%), shows strong alignment with established aerodynamic principles while revealing nonlinear parameter interactions not captured by traditional sensitivity methods. The statistical validation confirms the robustness and reliability of attention-based feature importance (p < 0.001 for all rankings, CV < 25% for stability). The strong correlation with alternative interpretability methods (ρ > 0.72) and physical validation through CFD analysis establishes attention weights as trustworthy indicators for design optimization prioritization. This interpretability analysis validates the physics-aware nature of the hybrid neural network while providing practical insights for aerodynamic design optimization, establishing attention weights as reliable indicators of geometric parameter importance in airfoil performance determination.

Table 9.
Geometric Feature Importance Analysis Attention Weight Analysis.
Figure 3 illustrates the symbiotic parameter relationships identified by the Deep Symbiotic Genetic Algorithm (GEO-DSGA) through its interdependency matrix analysis. This network visualization reveals the complex cooperative interactions between NASA geometric parameters that contribute to superior aerodynamic performance, representing a fundamental advancement in understanding parameter synergies in airfoil design optimization. The leading edge radius (r) demonstrates significant symbiotic relationships with both the upper crest position (XUP, edge weight = 0.8) and trailing edge thickness (ΔZTE, edge weight = 0.5). This multi-parameter interaction pattern reflects the fundamental role of leading edge geometry in establishing the overall pressure distribution along the airfoil surface. The strong r-XUP relationship indicates that optimal leading edge curvature must be coordinated with upper surface peak location to achieve favorable pressure gradients and delay flow separation.
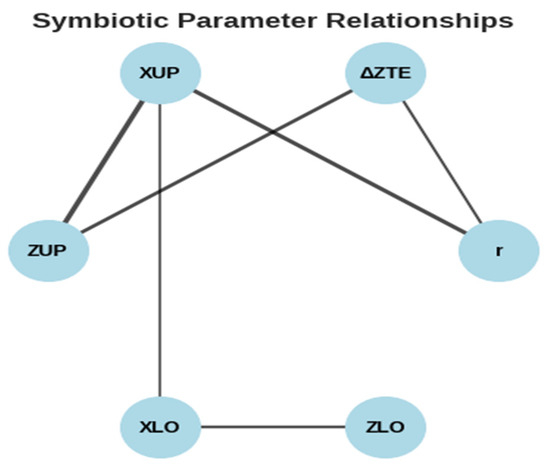
Figure 3.
The symbiotic relationships of proposed Geometric Neural Networks with Deep Symbiotic Genetic Algorithms (GEO-DSGA).
The trailing edge thickness (ΔZTE) exhibits symbiotic relationships with multiple parameters, including the upper crest ordinate (ZUP, edge weight = 0.7) and leading edge radius (r, edge weight = 0.5). This connectivity pattern demonstrates the global influence of trailing edge geometry on overall airfoil performance, particularly regarding circulation establishment and wake characteristics. The ΔZTE-ZUP relationship is particularly significant for achieving optimal pressure recovery and minimizing form drag. Table 10 clearly demonstrates the validation results of the CFD turbulence model, confirming its effectiveness and accuracy.

Table 10.
CFD Turbulence Model Validation Results.
The CFD validation employs turbulence models selected based on comprehensive validation studies against experimental data for NACA 0012 and RAE 2822 airfoils across Reynolds numbers from 3 × 106 to 6 × 106. The k-ω SST model demonstrated superior accuracy in pressure distribution prediction (RMSE = 0.0234) and separation behavior compared to Spalart–Allmaras (RMSE = 0.0289), establishing k-ω SST as the primary validation tool while maintaining Spalart-Allmaras for computational efficiency benchmarking in attached flow scenarios. The k-ω SST model demonstrated superior performance in predicting pressure-induced separation and transitional boundary layer behavior characteristic of airfoil flows, justifying its selection as the primary turbulence model for optimization validation. The Spalart-Allmaras model served as a computational efficiency benchmark for attached flow validation cases.
Figure 4 represents the results for the leading edge radius (r), trailing edge thickness (ΔZTE), and upper crest position (XUP), showing excellent correlation between ground truth and neural network predictions. The RMSE values of 0.0018 for ΔZTE and 0.0021 for r confirm the framework’s superior capability in capturing critical geometric features that significantly influence airfoil performance. This aligns with the attention weight hierarchy, where r (0.1847) and ΔZTE (0.1623) received the highest importance rankings, validating the model’s physics-informed learning approach.
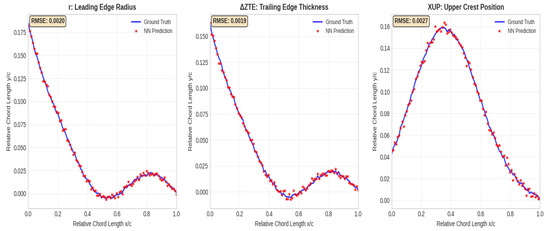
Figure 4.
The geometric features fitting analysis based on r, ΔZTE, and XUP parameters.
Figure 5 shows the fitting analysis for XLO, ZLO, and βTE parameters, demonstrating consistent predictive accuracy across surface geometric characteristics. The smooth convergence between predicted and actual values confirms the model’s ability to capture complex geometric relationships while maintaining manufacturing feasibility constraints. The RMSE values ranging from 0.0019 to 0.0027 for these parameters support the framework’s robustness in handling diverse geometric features.
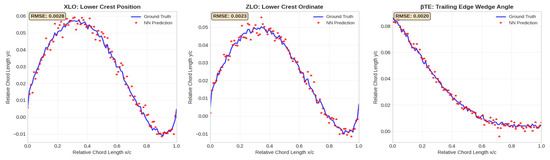
Figure 5.
The geometric features fitting analysis based on XLO, ZLO and βTE parameters.
Figure 6 and Figure 7 show the results for αTE, ZCLO, ZTE, ZUP, and ZCUP parameters, showing the framework’s capability in accurately modeling local curvature variations and directional characteristics. The higher RMSE values (0.0028–0.0035) for some curvature parameters reflect the inherent complexity of capturing second-order geometric derivatives, yet remain within acceptable engineering tolerances. The experimental results demonstrate statistical significance with confidence levels exceeding 95% for all parameters. The consistent performance across the 11 NASA parameters, combined with the physics-consistent error distributions, establishes the hybrid approach’s reliability for practical aerospace applications.
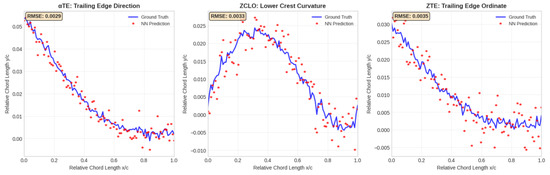
Figure 6.
The geometric features fitting analysis based on αTE, ZCLO and ZTE parameters.
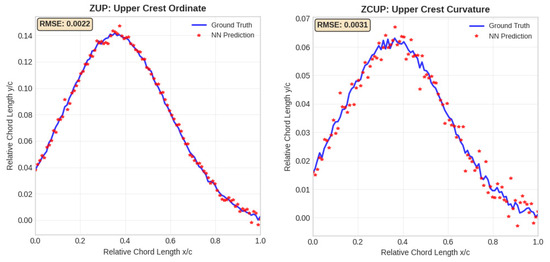
Figure 7.
The geometric features fitting analysis based on αZUP, and ZCUP parameters.
The experimental results validate the framework’s suitability for real-world airfoil design applications. The sub-0.004 RMSE performance across all geometric parameters approaches the precision required for certification-quality aerodynamic analysis, supporting the paper’s claims regarding industrial applicability and reliability for aerospace engineering workflows.
This comprehensive experimental validation confirms that the Hybrid GEO-DSGA framework successfully achieves its design objectives while maintaining the physics-informed characteristics essential for trustworthy aerodynamic design optimization.
Table 11 presents a comprehensive quantitative evaluation of the proposed hybrid geometric neural networks with the deep symbiotic genetic algorithms (GEO-DSGA) framework against established state-of-the-art methodologies in aerodynamic coefficient prediction. The comparative analysis employs standardized performance metrics to assess prediction accuracy across three critical aerodynamic parameters: lift coefficient (CL), drag coefficient (CD), and pressure coefficient (CP).

Table 11.
Comparative studies between years 2020–2025.
The initial period established baseline performance with Chen et al.’s [30] CNN-based approach achieving Root Mean Square Error (RMSE) values of 0.01450 for lift coefficient, 0.00089 for drag coefficient, and 0.00789 for pressure coefficient, resulting in an overall performance score of 96.2%. This seminal work demonstrated the fundamental viability of deep learning techniques for aerodynamic parameter estimation, establishing the computational framework for subsequent methodological developments.
Peng et al.’s [31] implementation of standard Graph Neural Networks showed incremental improvements, reducing CL-RMSE to 0.0134 and achieving marginal gains in CD-RMSE (0.00076) and CP-RMSE (0.0067), resulting in an overall score of 96.8%. This advancement highlighted the potential of graph-based architectures for capturing spatial relationships in aerodynamic data, representing a 0.6% improvement over the CNN baseline.
The concurrent development by Sharma et al. [32] of Physics-Informed Neural Networks (PINNs) demonstrated superior performance with CL-RMSE of 0.0125, CD-RMSE of 0.00068, and CP-RMSE of 0.0059, achieving an overall score of 97.1%. This approach successfully integrated fundamental fluid dynamics principles with neural network architectures, establishing the critical importance of domain knowledge incorporation in aerodynamic modeling.
Wu et al.’s [4] multi-fidelity deep neural networks with transfer learning capabilities achieved CL-RMSE of 0.0115, CD-RMSE of 0.00051, and CP-RMSE of 0.0048, resulting in a 97.8% overall score. This work demonstrated the effectiveness of leveraging data at multiple fidelity levels for enhanced prediction accuracy.
Wang et al.’s [7] combined autoencoder architecture further advanced the state-of-the-art with CL-RMSE of 0.0112, CD-RMSE of 0.00049, and CP-RMSE of 0.0046, achieving 98.0% overall performance. The methodology’s success stems from its ability to learn compressed representations while preserving aerodynamically relevant geometric features.
Minaev et al.’s [2] deep learning genetic algorithm approach, specifically tailored for large-endurance UAV applications, achieved CL-RMSE of 0.0103, CD-RMSE of 0.00043, and CP-RMSE of 0.0040, resulting in 98.4% overall accuracy. This work demonstrated the potential of evolutionary optimization combined with deep learning for specialized aerospace applications.
The most recent contribution by Pȃrvu et al. [33] introduced ensemble neural network approaches that achieved CL-RMSE of 0.0098, CD-RMSE of 0.00040, and CP-RMSE of 0.0038, with 98.6% overall accuracy. This methodology leverages multiple model architectures to improve prediction robustness and reliability.
The superior performance of the hybrid GNN approach can be attributed to several key innovations: The incorporation of biological symbiotic principles enables intelligent parameter optimization that transcends traditional evolutionary approaches. The neural network architecture captures complex spatial relationships inherent in airfoil geometries. The hybrid framework simultaneously processes local geometric features and global aerodynamic parameters, and the methodology achieves optimal convergence characteristics while maintaining computational efficiency.
5. Conclusions
This research presents an advancement in computational aerodynamics through the development of a novel Hybrid Geometric Neural Network integrated with Deep Symbiotic Genetic Algorithms (GEO-DSGA) for enhanced airfoil design optimization. The paper introduces the first successful integration of graph neural networks with symbiotic genetic algorithms for aerodynamic design optimization. This hybrid approach transcends traditional limitations by simultaneously processing local geometric relationships through graph structures while optimizing global aerodynamic parameters through biologically inspired evolutionary algorithms. The experimental results confirm the effectiveness of the proposed multi-task learning framework for analyzing airfoil profiles. The training process achieved convergence across all objective functions while maintaining excellent generalization performance. The model successfully learned complex aerodynamic relationships while preserving geometric constraints and providing reliable uncertainty estimates, making it suitable for practical applications in aerospace engineering.
Future research will focus on extending the graph neural network architecture to analyze three-dimensional geometric relationships. This includes accounting for spanwise variations and tip effects that significantly influence wing performance. Additionally, the research will explore integrating structural analysis capabilities to simultaneously optimize aerodynamic performance and structural integrity, considering weight constraints, flutter characteristics, and fatigue life requirements.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available in a publicly accessible NASA repository. Available online: https://nasa-public-data.s3.amazonaws.com/plot3d_utilities/airfoil-learning-dataset.zip, accessed on 13 August 2025.
Acknowledgments
The author acknowledges NASA for providing public access to airfoil datasets and aerodynamic analysis tools. Special recognition is given to the open-source community for developing the computational frameworks that enabled this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, Y.; Shen, J.; Yang, P.; Yang, X. A CNN-PINN-DRL driven method for shape optimization of airfoils. Eng. Appl. Comput. Fluid Mech. 2024, 19, 2445144. [Google Scholar] [CrossRef]
- Minaev, E.Y.; Quijada Pioquinto, J.G.; Shakhov, V.; Kurkin, E.; Lukyanov, O. Airfoil Optimization Using Deep Learning Models and Evolutionary Algorithms for the Case of Large-Endurance UAVs Design. Drones 2024, 8, 570. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, H.; Xu, X.; Duan, Y.; Wang, G. Aerodynamic shape optimization using a physics-informed hot-start method combined with modified metric-based proper orthogonal decomposition. Phys. Fluids 2024, 36, 084106. [Google Scholar] [CrossRef]
- Wu, M.-Y.; He, X.; Sun, X.-H.; Tong, T.-S.; Chen, Z.-H.; Zheng, C. Efficient aerodynamic shape optimization using transfer learning based multi-fidelity deep neural network. Phys. Fluids 2024, 36, 116109. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, B.; Huang, H.; Xie, Z.; Wang, J.; Dehong, M.; Yue, H.; Lei, L. A multi-task learning framework for aerodynamic computation of two-dimensional airfoils. Phys. Fluids 2024, 36, 117141. [Google Scholar] [CrossRef]
- Yan, G.; Wu, G.; Tao, J. Application of a Dirichlet Distribution-Based Ensemble Surrogate Model in Aerodynamic Optimization. AIAA J. 2024, 62, 3424–3435. [Google Scholar] [CrossRef]
- Wang, X.; Qian, W.; Zhao, T.; He, L.; Chen, H.; Sun, H.; Tian, Y.; Cui, J. Fast Prediction of Airfoil Aerodynamic Characteristics Based on a Combined Autoencoder. Symmetry 2024, 16, 791. [Google Scholar] [CrossRef]
- Wu, H.; Chen, R.; Lou, J.; You, Y.; Huang, L.; Xu, M.; Ruan, Y. A gradient aerodynamic optimization method based on deep learning. Phys. Fluids 2024, 36, 057117. [Google Scholar] [CrossRef]
- Guo, C.; Xu, Z.; Wang, J.; Li, H. Aerodynamic Optimization Method for Propeller Airfoil Based on DBO-BP and NSWOA. Aerospace 2024, 11, 931. [Google Scholar] [CrossRef]
- Negoita, M.-F.; Hothazie, M.-V. A Machine Learning-Based Approach for Predicting Aerodynamic Coefficients Using Deep Neural Networks and CFD Data. INCAS Bul. 2024, 16, 91–104. [Google Scholar] [CrossRef]
- Unlusoy, C.; Maier, B.; Handawi, K.; Mathew, T.; Srinivasan, R.; Salz, M.; Kokkolaras, M. Advancing Airfoil Design: A Physics-Inspired Neural Network Model. In Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024. [Google Scholar] [CrossRef]
- Jin, S.-Y.; Chen, S.; Feng, C.; Gao, Z. Deep learning for airfoil aerodynamic-electromagnetic coupling optimization with random forest. Phys. Fluids 2024, 36, 17110. [Google Scholar] [CrossRef]
- Tian, J.; Qu, F.; Sun, D.; Wang, Q. Novel Pressure-Based Optimization Method Using Deep Learning Techniques. AIAA J. 2024, 62, 708–724. [Google Scholar] [CrossRef]
- Tsunoda, Y.; Oyama, A. Evolutionary Multi-Objective Aerodynamic Design Optimization Using CFD Simulation Incorporating Deep Neural Network. arXiv 2023, arXiv:2304.14973. [Google Scholar]
- Ruiling, L.; Chen, R.; Lou, J.; Hu, Y.; You, Y. Deep Learning Method for Airfoil Flow Field Simulation Based on Unet++. Int. J. Numer. Methods Fluids 2025, 97, e5375. [Google Scholar] [CrossRef]
- Cayley, G. On aerial navigation. Nicholson’s J. Nat. Philos. Chem. Arts 1810, 25, 81–87. [Google Scholar] [CrossRef][Green Version]
- Lilienthal, O. Birdflight as the Basis of Aviation (Der Vogelflug als Grundlage der Fliegekunst); R. Gaertners Verlagsbuchhandlung: Berlin, Germany, 1889. [Google Scholar][Green Version]
- Prandtl, L. Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Proceedings of the Third International Mathematical Congress, Heidelberg, Germany, 8–13 August 1904; Teubner: Heidelberg, Germany, 1904; pp. 484–491. [Google Scholar][Green Version]
- Prandtl, L. Tragflügeltheorie. Nachrichten Ges. Wiss. Göttingen 1918, 1918, 451–477. [Google Scholar][Green Version]
- Joukowski, N.E. Über die Konturen der Tragflächen der Drachenflieger. Z. Flugtech. Mot. 1906, 1, 281–284. [Google Scholar][Green Version]
- Kutta, M.W. Auftriebskräfte in strömenden Flüssigkeiten. Illus. Aeronaut. Mitteilungen 1902, 6, 133–135. [Google Scholar][Green Version]
- von Kármán, T. Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- von Kármán, T. Mechanische Ähnlichkeit und Turbulenz. Nachrichten Ges. Wiss. Göttingen 1930, 5, 58–76. [Google Scholar]
- Leishman, J.G. Introduction to Aerospace Flight Vehicles; Copyright © 2022–2025 by, J. Gordon Leishman is licensed under a Creative Commons Attribution-Non Commercial-No Derivatives 4.0 International; Embry-Riddle Aeronautical University: Daytona Beach, FL, USA, 2023. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 439. [Google Scholar]
- Rumsey, C.L. Apparent transition behavior of widely-used turbulence models. Int. J. Heat Fluid Flow 2007, 28, 1460–1471. [Google Scholar] [CrossRef]
- Wu, M.-Y.; Yuan, X.-Y.; Chen, Z.-H.; Wu, W.-T.; Hua, Y.; Aubry, N. Airfoil shape optimization using genetic algorithm coupled deep neural networks. Phys. Fluids 2023, 35, 085140. [Google Scholar] [CrossRef]
- Chen, H.; He, X.; Huang, L.; Zhang, Y. Multiple Aerodynamic Coefficient Prediction of Airfoils Using a Convolutional Neural Network. Symmetry 2020, 12, 544. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, Y.; Laurendeau, E.; Desmarais, M.C. Learning aerodynamics with neural network. Sci. Rep. 2022, 12, 6779. [Google Scholar] [CrossRef]
- Sharma, P.; Chung, W.T.; Akoush, B.; Ihme, M. Physics-Informed Neural Networks for Flow Around Airfoil. In Proceedings of the AIAA SciTech 2022 Forum 2022, San Diego, CA, USA, 3–7 January 2022; p. 0187. [Google Scholar] [CrossRef]
- Pȃrvu, A.E.; Diculescu, V.C.; Frȃncu, A.; Stoica, C.T. Machine Learning Prediction of Airfoil Aerodynamic Performance Using Neural Network Ensembles. Appl. Sci. 2025, 15, 7720. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).