Optimization of Reasonable Finished State for Cable-Stayed Bridge with Steel Box Girder Based on Multiplier Path Following Method
Abstract
1. Introduction
2. Optimization Principles
- The cable forces should lie between the minimum force required by the cable sag considerations and the maximum force allowed by the material’s strength and should increase uniformly with an increasing cable length. Nevertheless, localized variations in the cable force are permissible in regions such as near the pylon, transition piers, or auxiliary piers.
- The internal forces and normal stresses in the main beam should be small and uniformly distributed to ensure that the normal stresses at the top and bottom edges of the cross-section do not exceed the allowable values specified in the code under the most adverse load combinations.
- The eccentricity of the pylon should be minimized to ensure a smaller bending moment in the pylon. Considering live loads and the most adverse load combinations, the pylon should be pre-eccentricated towards the outer span under the dead load of the completed bridge.
- The transition and auxiliary piers should possess an adequate upward vertical reaction capacity under a dead load to minimize the occurrence of negative reactions under a live load. Should negative reactions prove unavoidable, the counterweights or tension-type supports can be incorporated to satisfy the design requirements.
3. The Optimization Model
3.1. Design Variables
3.2. The Optimized Objective
3.3. Constraint Conditions
3.3.1. Constraint on the Cable Force
3.3.2. A Uniformity Constraint on the Cable Force
3.3.3. The Displacement Constraint on the Main Girder and the Pylons
3.3.4. Normal Stress Constraints on the Main Girder and the Pylons
3.3.5. Other Constraints
3.4. Establishment of the Optimization Model
4. Principles and Solving Steps of the Multiplier Path Following Method
4.1. Principles
4.1.1. Conversion of the Compound Constraints into Inequality Constraints Using the Multiplier Method
4.1.2. Introduction of the Relaxed KKT Condition
4.1.3. Solving Along the Direction of the Center Path
4.1.4. Determination of the Optimal Step Size
4.1.5. The Convergence Criterion
- Condition 1: If , the iteration converges, yielding the optimal solution that meets the requirements;
- Condition 2: If and , the penalty function , and the Lagrange multiplier vector is updated;
- Condition 3: If and , the penalty function remains unchanged, and the Lagrange multiplier vector is updated.
4.2. Solving Steps
- The initialization step involves setting the initial value , , , , the positive parameter , , the permissible error , and the iteration counter .
- Subsequently, these formulas , , , and are solved. If the resulting solution satisfies condition , we can determine , and the iterative process is terminated. Otherwise, the Lagrange multiplier vector is updated based on the convergence criterion, and the algorithm proceeds to the next iteration.
- The search direction is calculated from Formulas (23) and (24).
- The step size parameter is obtained for the search along the direction .
- Following the determination of the step size parameter , these formulas , , and are solved. Subsequently, the iteration counter k is incremented to k + 1, and the algorithm returns to step 2. Iteration proceeds until convergence is reached [40].
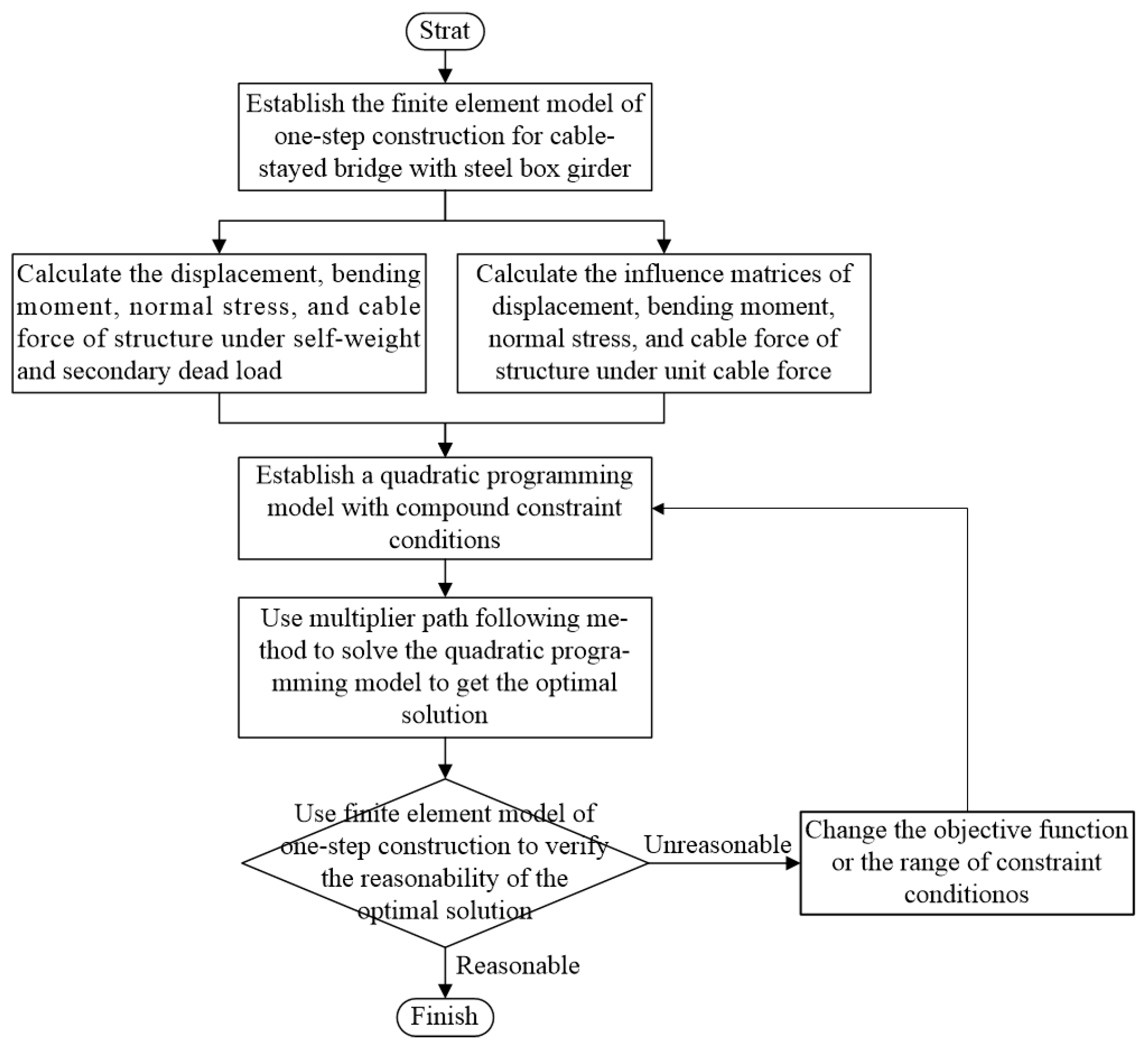
5. The Optimization Method for the Finished State
- A finite element analysis is conducted using a model of the cable-stayed bridge with steel box girders that accounts for the finished state. This analysis determines the influence matrices for the displacements, internal forces, normal stresses, and cable forces, as well as these same structural responses under self-weight and secondary dead load conditions.
- The finite element analysis results, in conjunction with Formulas (6) and (14), are used to determine the parameters , , , , and necessary for the formulation of the quadratic programming model.
- According to the objective function, the constraint conditions, and Formula (14), the quadratic programming model for optimizing the finished state of a cable-stayed bridge can be established.
- Given the initial iterative value for the iteration of the initial cable force and the convergence criterion , the MATLAB program [41] is developed based on the multiplier path following optimization algorithm. This program is then used to compute the optimal initial cable force , satisfying the constraint conditions.
- The reasonableness of is assessed by incorporating it into the finite element model and evaluating the results. A reasonable finished state is determined if the computed results satisfy the established constraints; otherwise, iterative refinement involves adjusting the constraint bounds or modifying the objective function, returning to step 3 for model re-optimization and resolution, a process depicted in Figure 2.
6. A Feasibility Analysis of the Optimization Method for the Finished State
6.1. Bridge Overview
6.2. The Finite Element Model
6.3. Calculation of the Influence Matrices
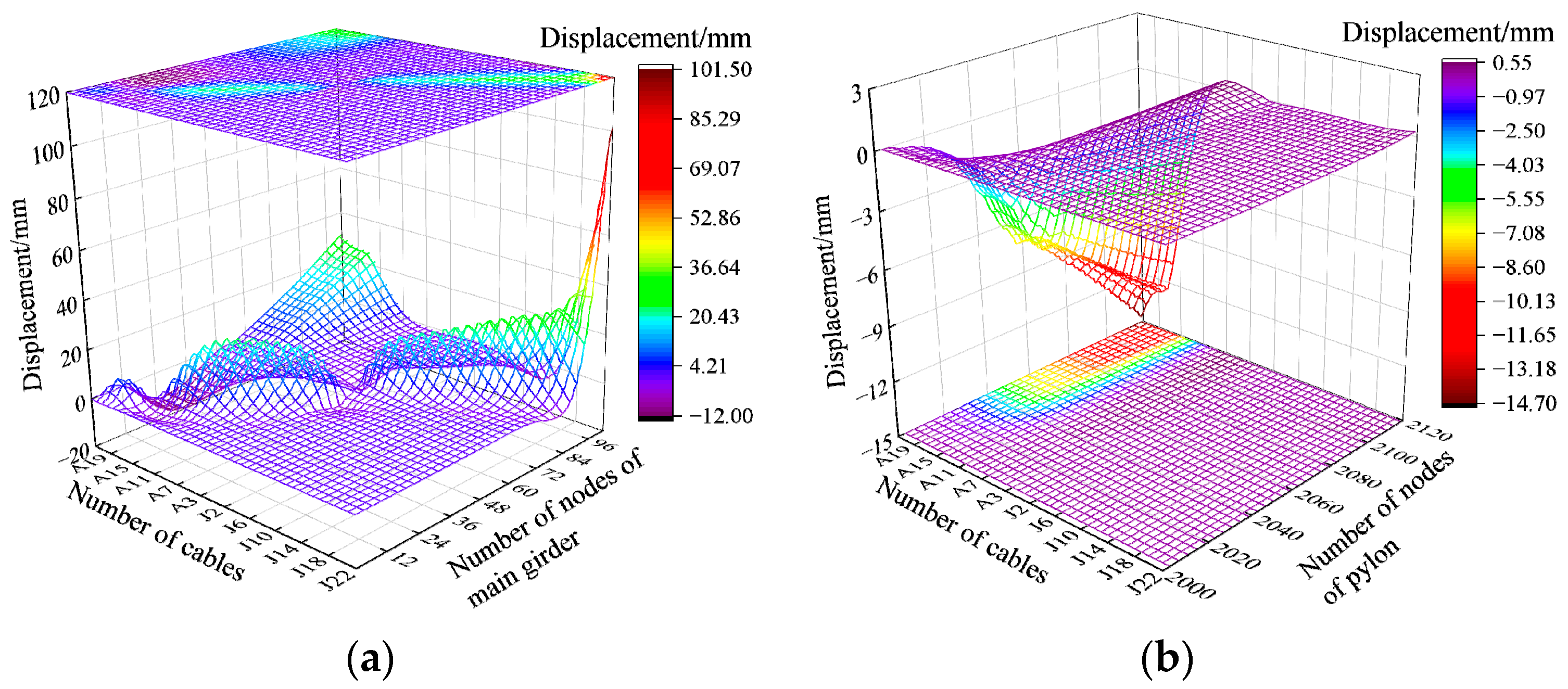
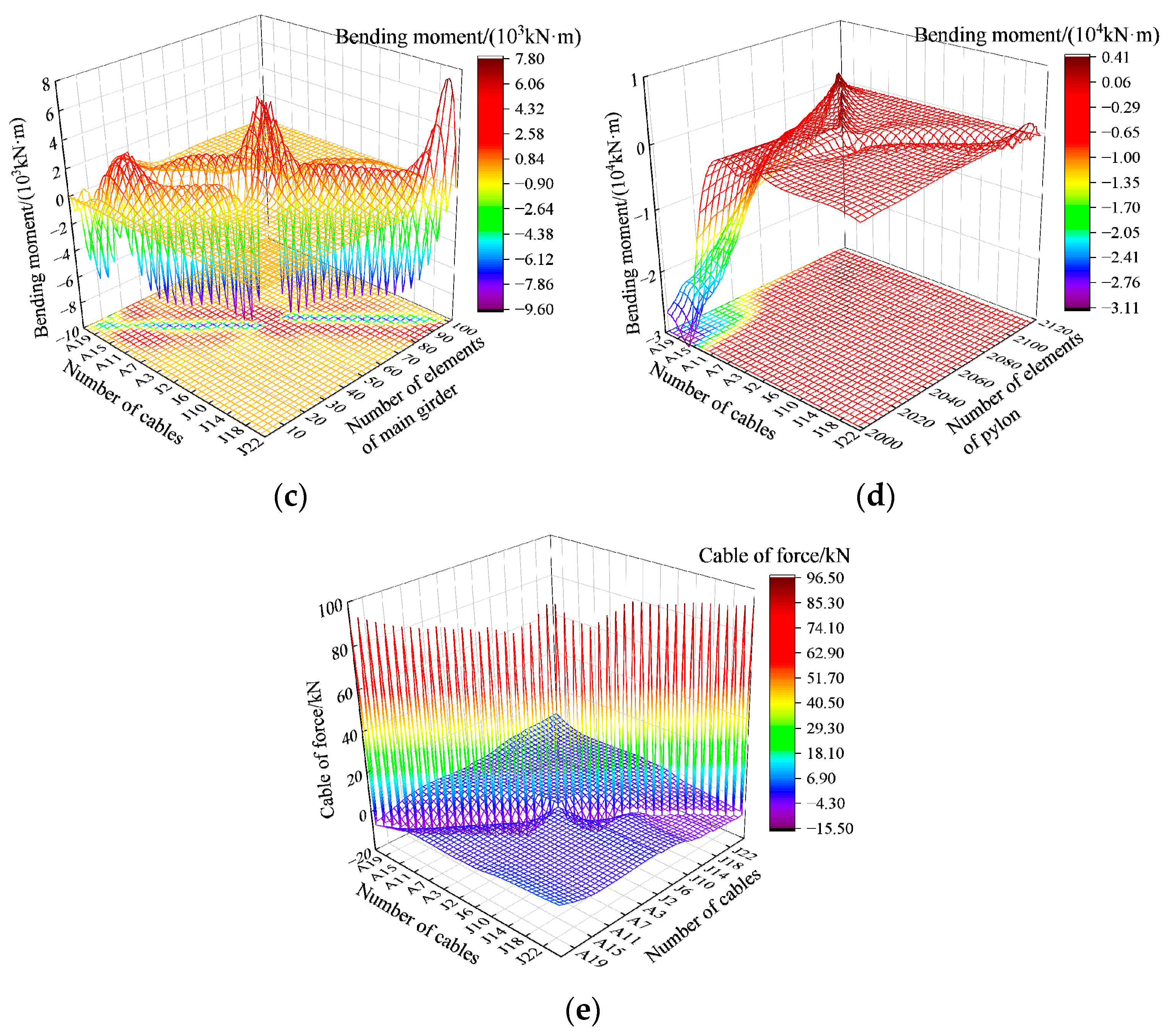
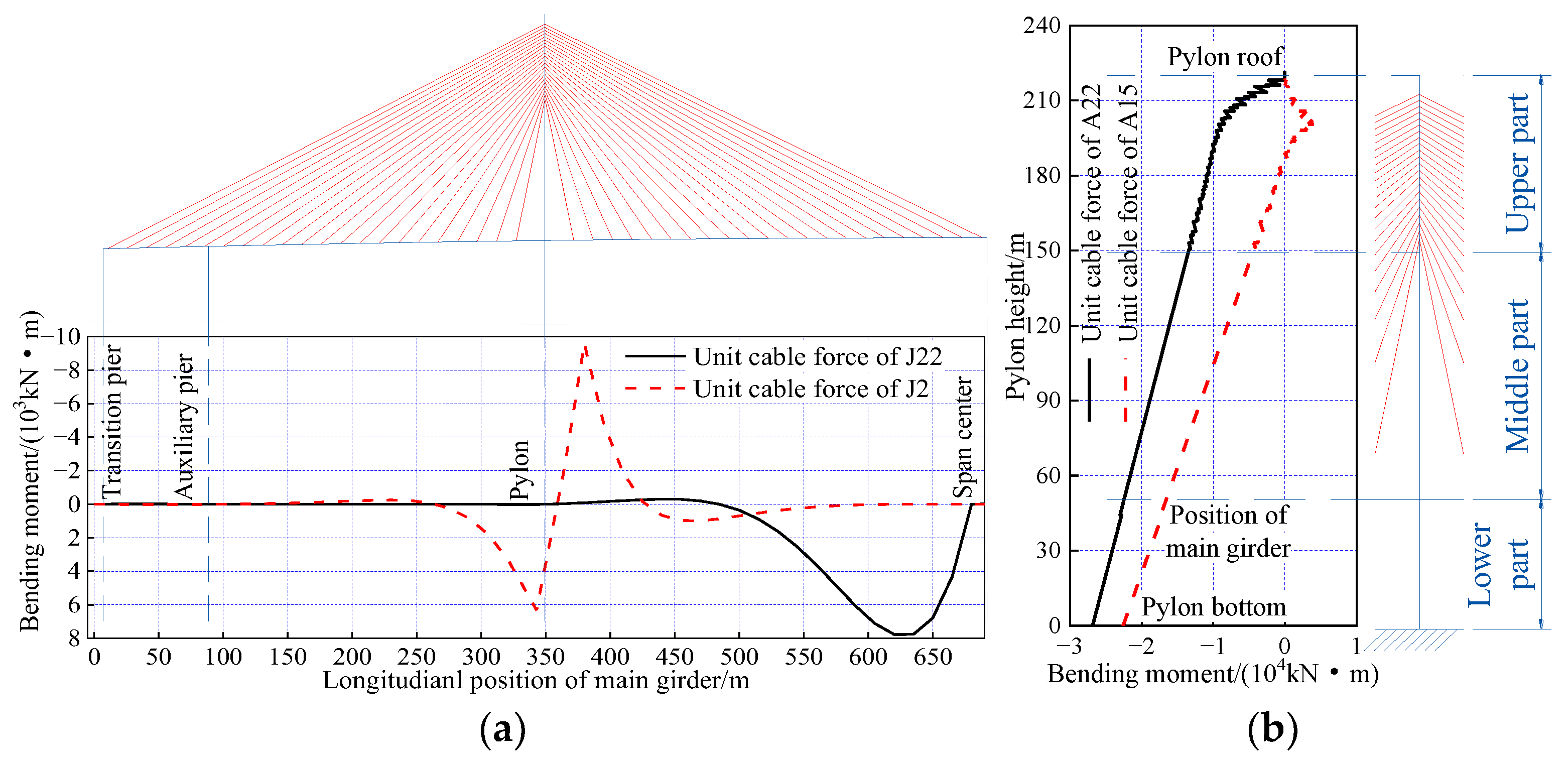
6.4. Calculation of the Structure’s State
6.5. Setting the Optimization Parameters
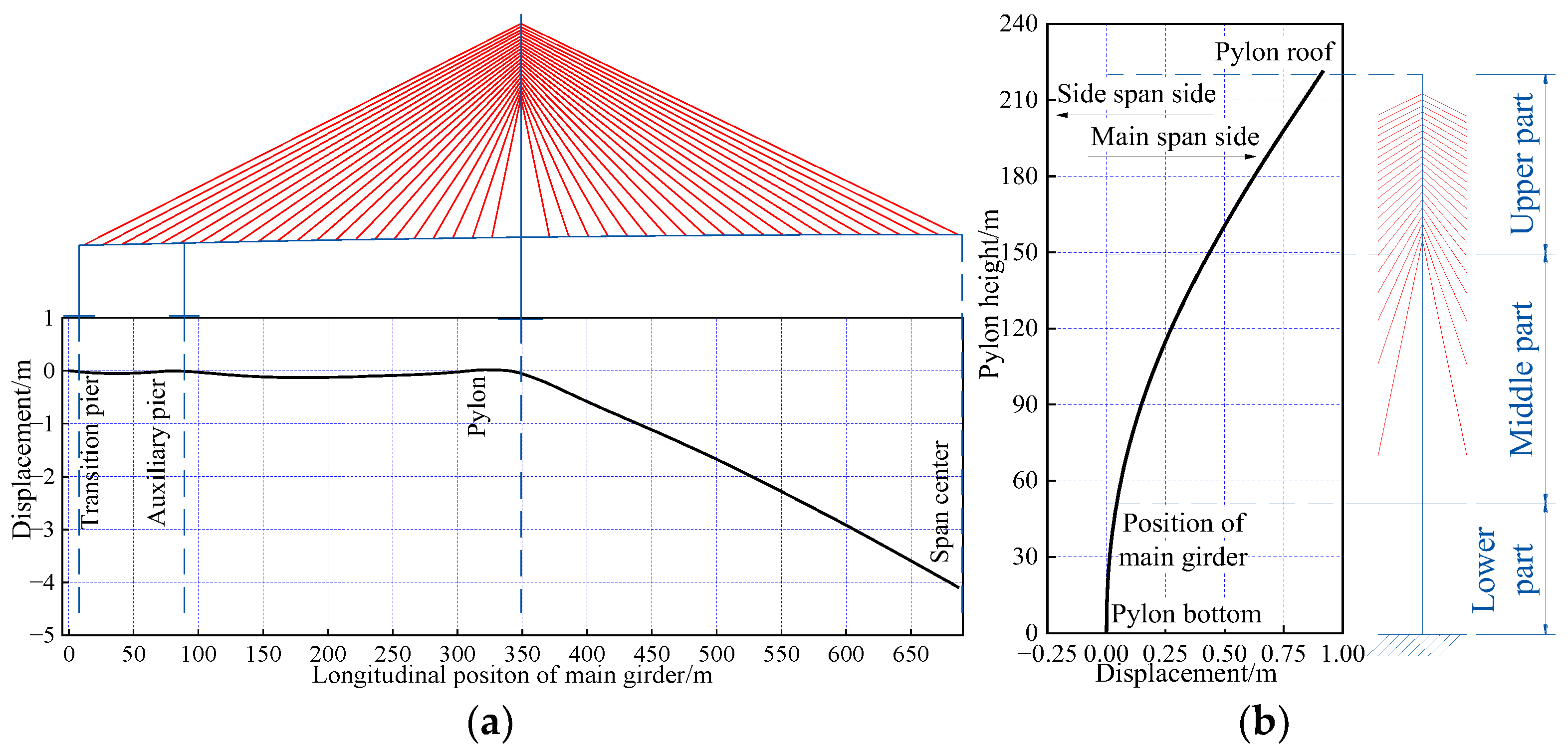
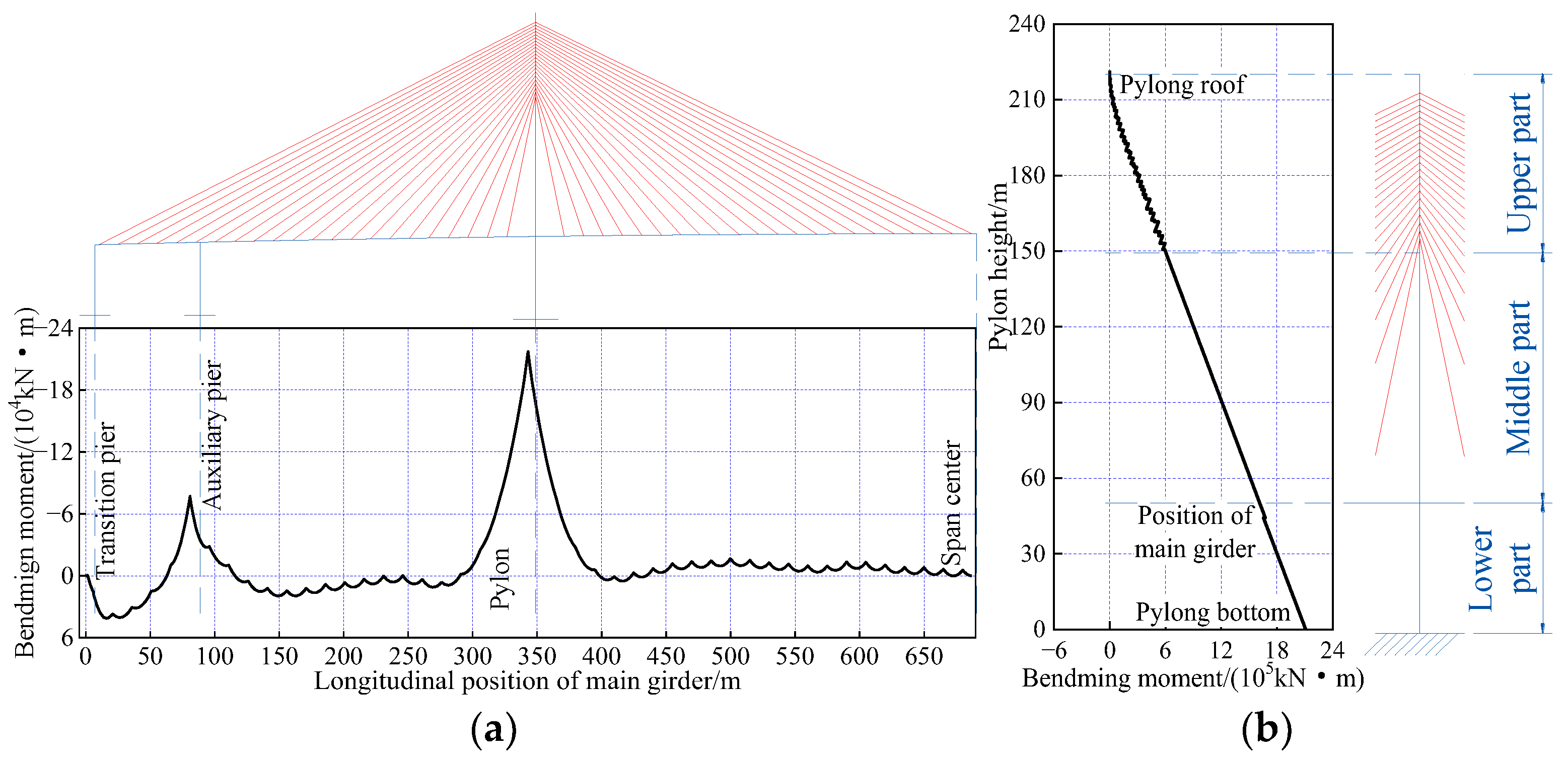
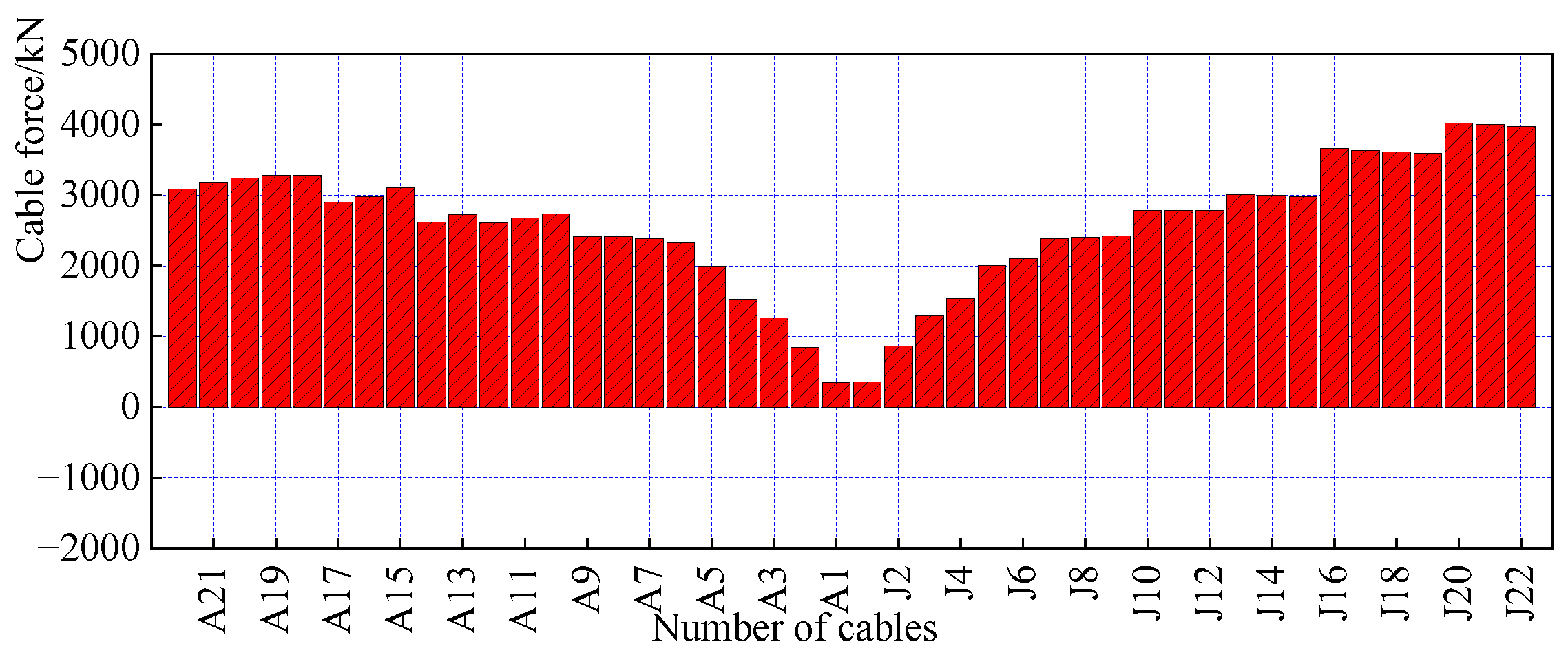
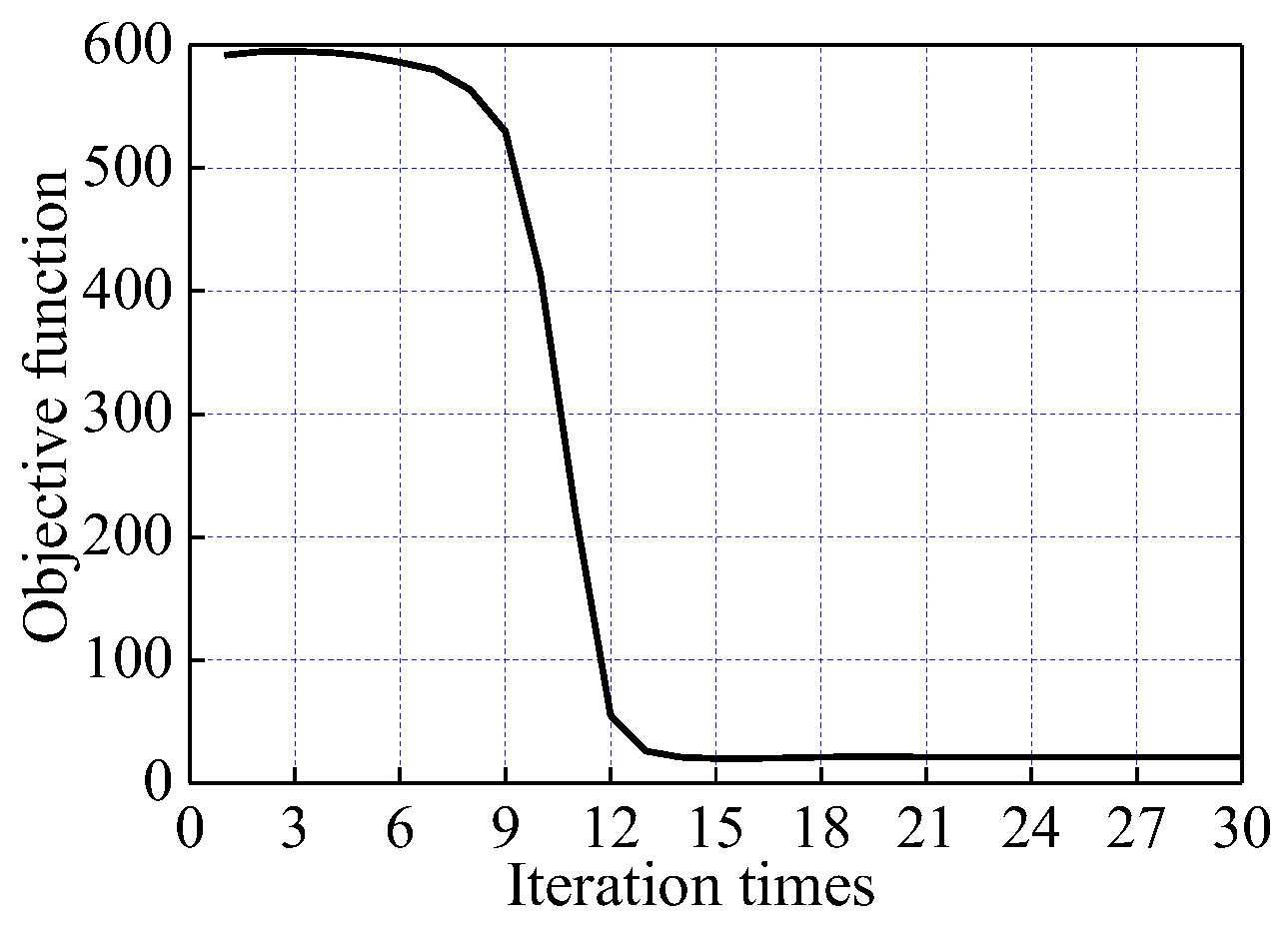
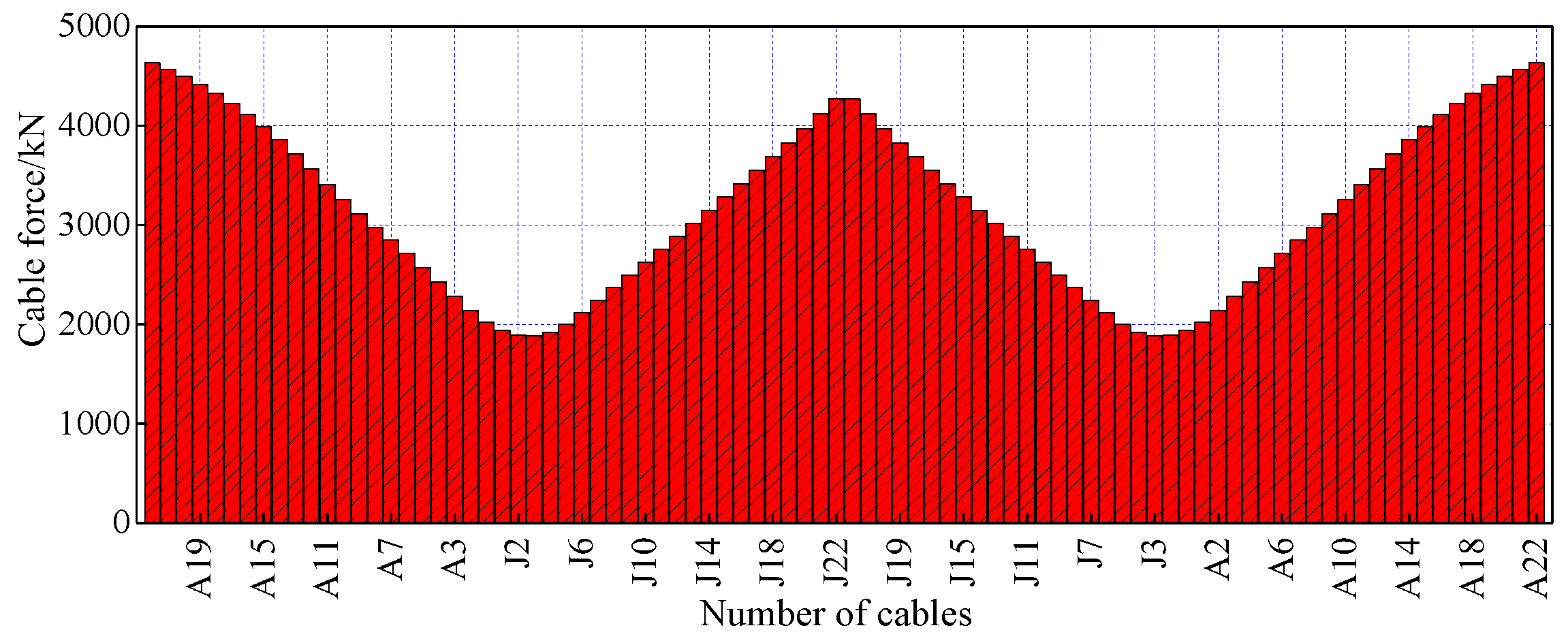
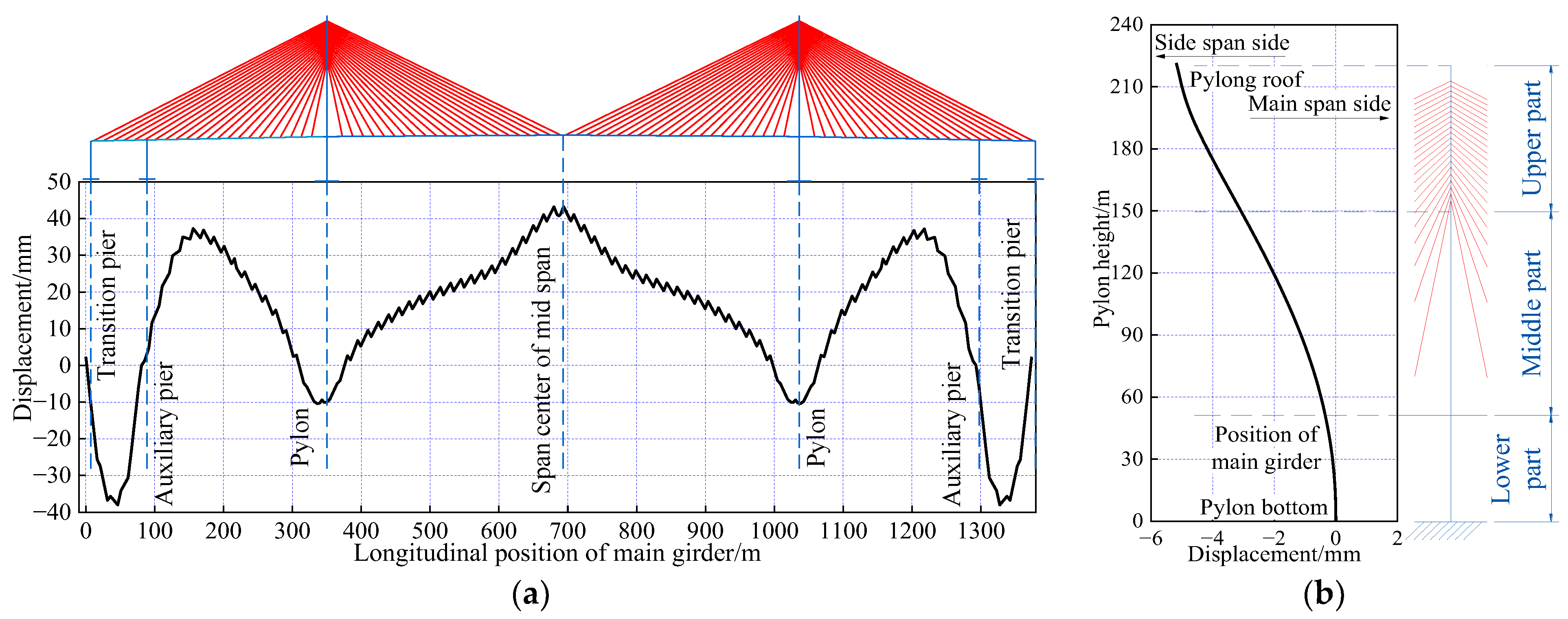
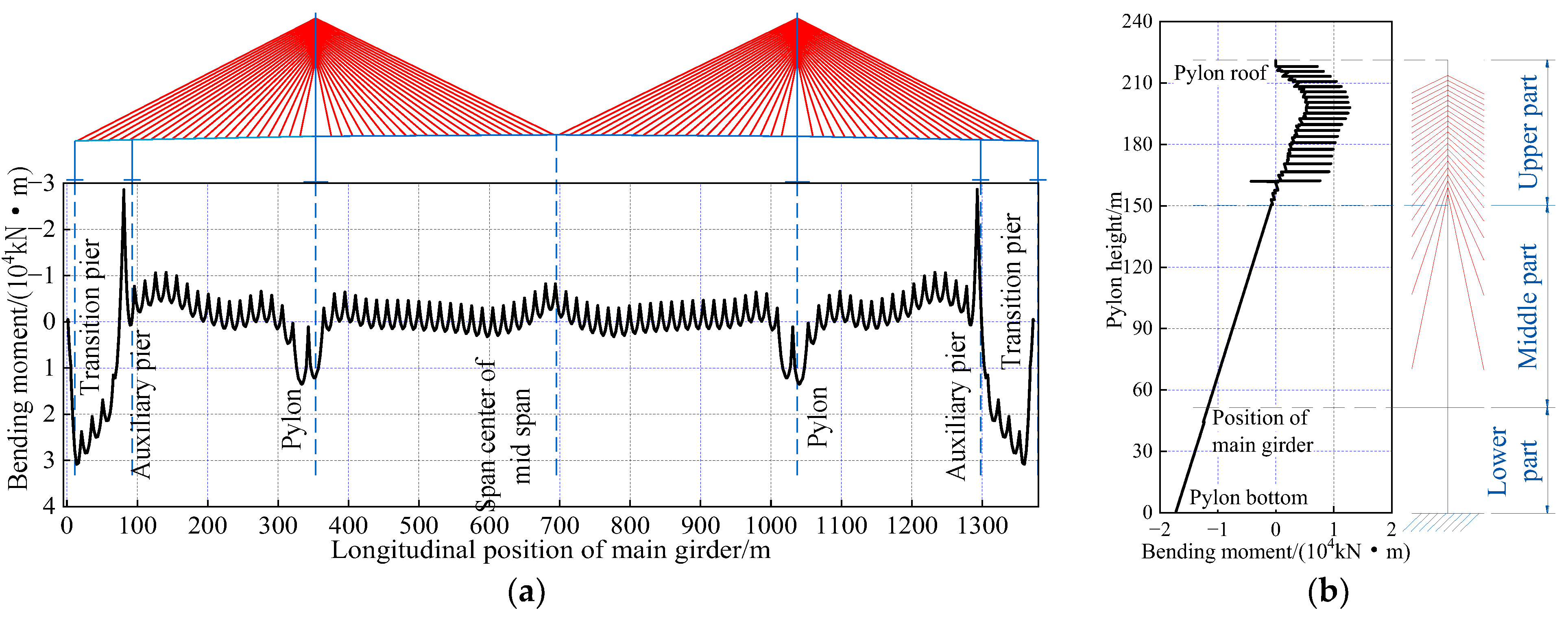
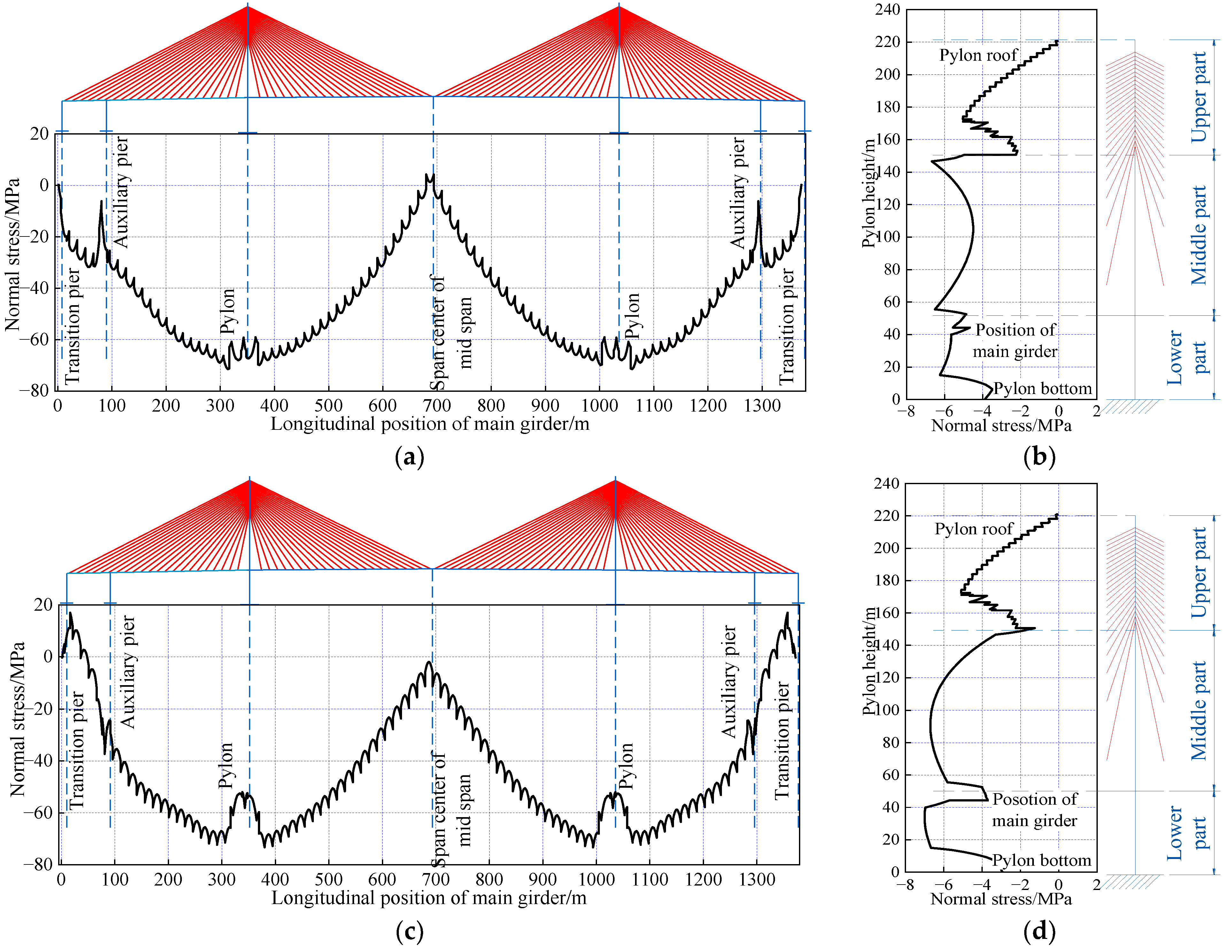
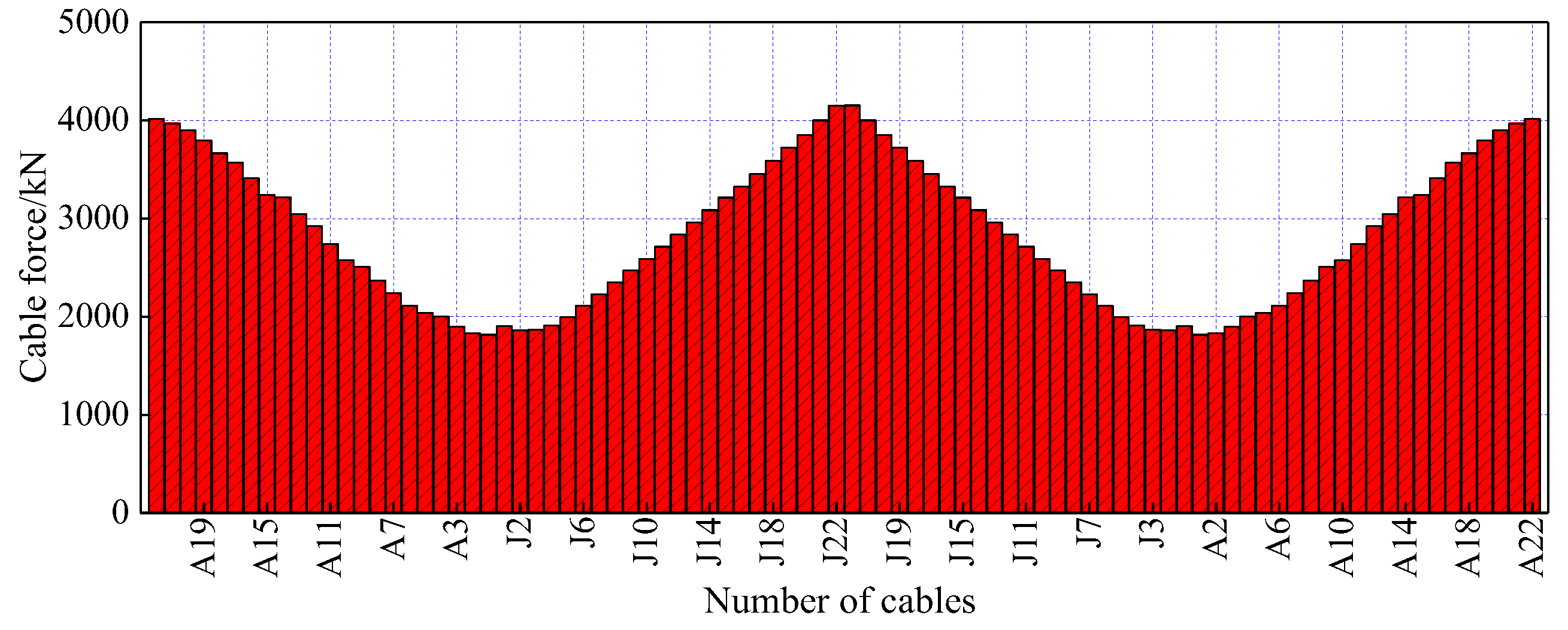
6.6. Optimization Results
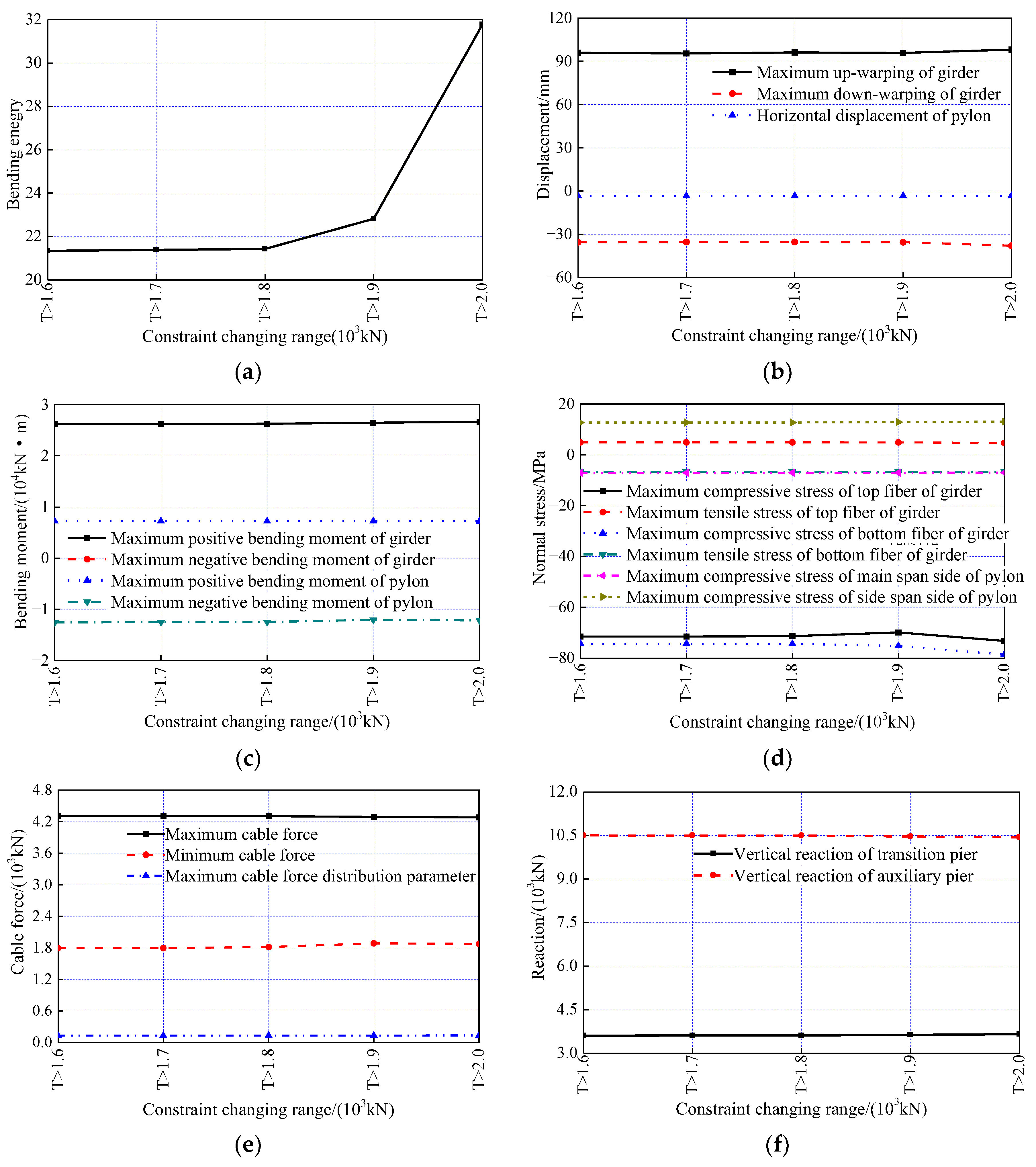
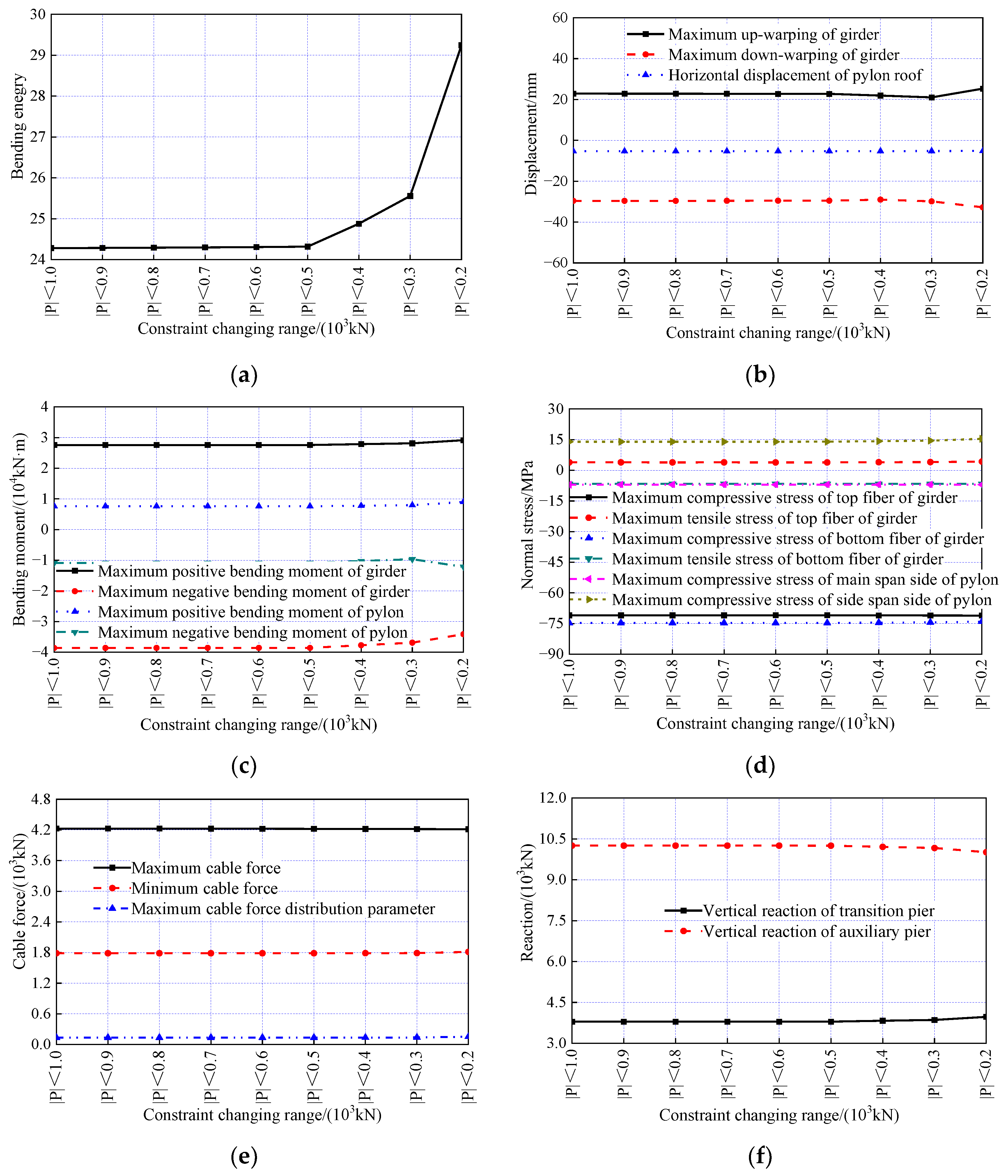
7. The Influence of the Constraint Range on the Optimization Results
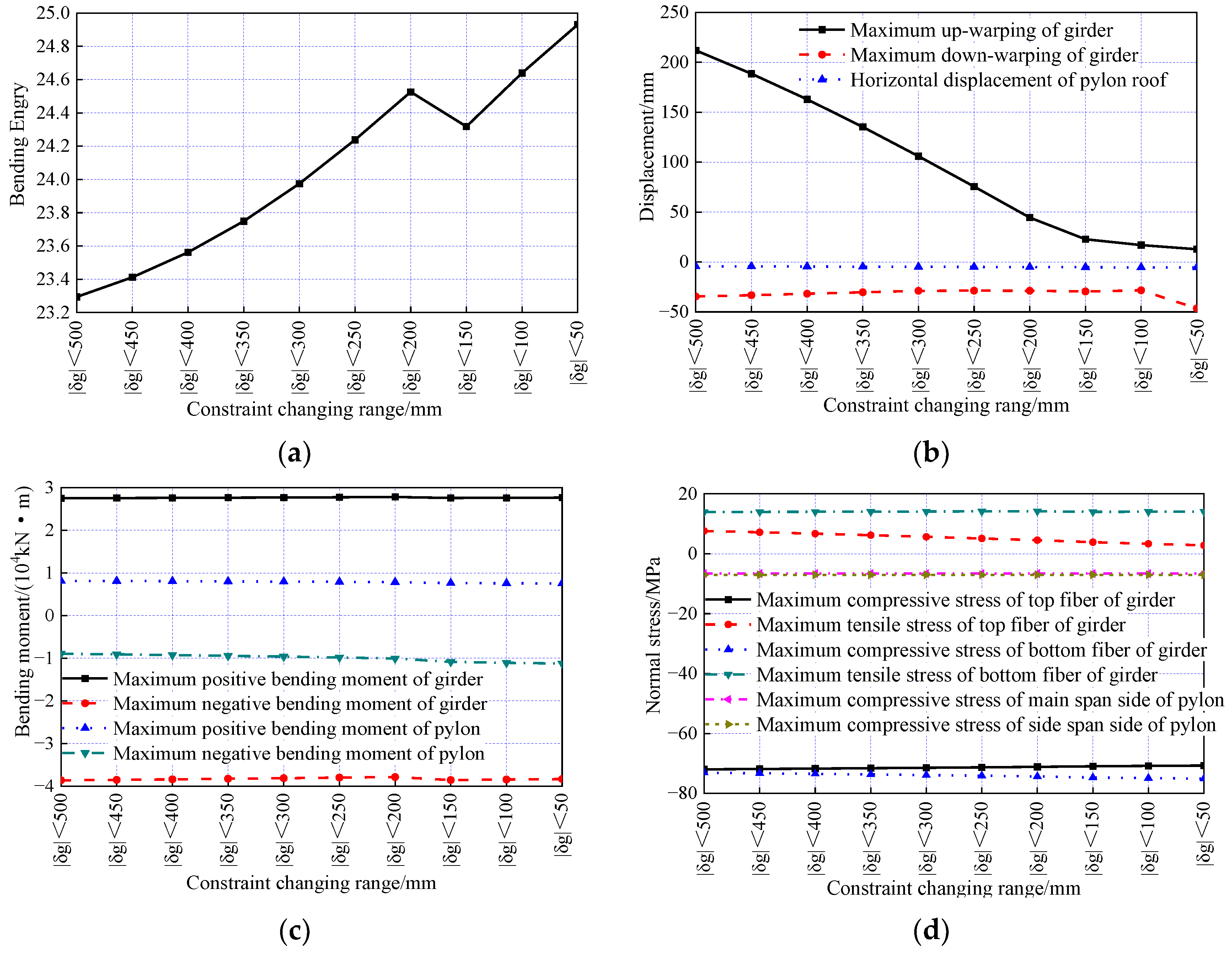
7.1. The Influence of the Constraint Range for the Main Girder’s Vertical Displacement on the Optimization Results
7.2. Influence of a Changing Range of Horizontal Displacements of the Pylon on the Optimization Results
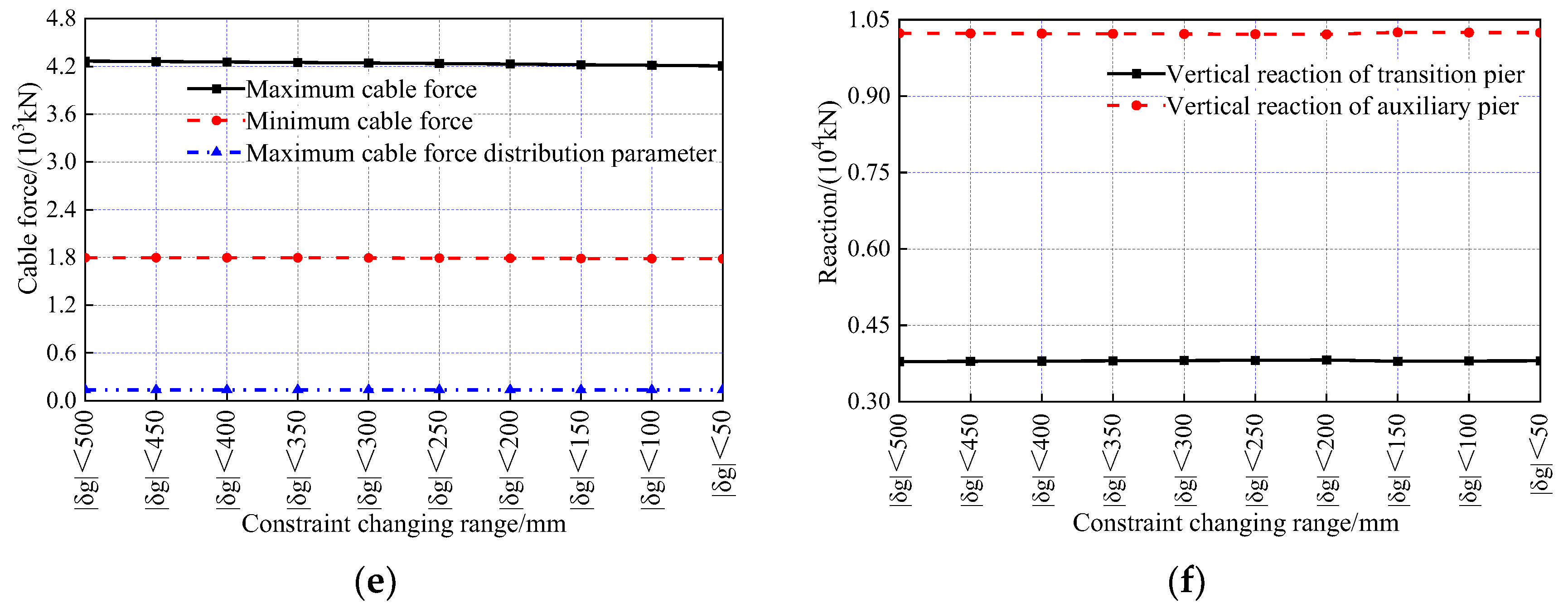
7.3. Influence of the Constraint Range for the Cable Force on the Optimization Results
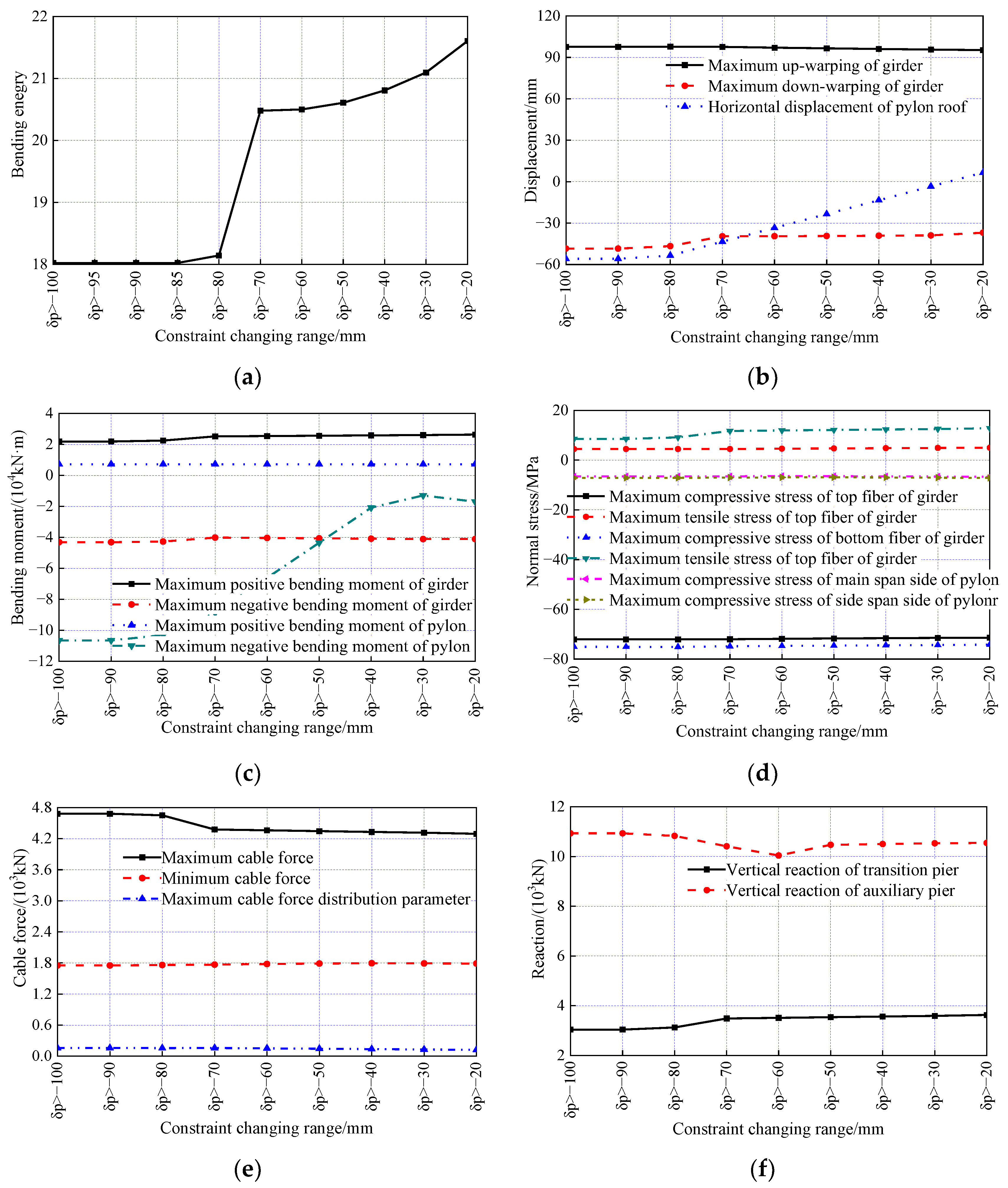
7.4. The Influence of the Constraint Range for Cable Force Uniformity on the Optimization Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Šurdilović, S.M.; Živković, S.; Turnić, D. Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges. Appl. Sci. 2024, 14, 5410. [Google Scholar] [CrossRef]
- Yao, Y.C.; Pu, H.Q.; Yao, D.Y. Mechanical Features of Cable-Girder Anchorage for Long-Span Railway Cable-Stayed Bridge with Steel Box Girders. Appl. Mech. Mater. 2014, 3308, 1391–1394. [Google Scholar] [CrossRef]
- Shi, J.; Chen, Z. Research on Reasonable Construction Plan for Cast-in-Place UHPC Bridge Deck Plate of Cable-Stayed Bridge. Appl. Sci. 2023, 13, 8615. [Google Scholar] [CrossRef]
- Martins, M.A.; Simões, M.L.; Negrão, H.J. Optimization of cable-stayed bridges: A literature survey. Adv. Eng. Softw. 2020, 149, 102829. [Google Scholar] [CrossRef]
- Ma, Y.; Song, C.; Wang, Z.P.; Jiang, Z.Q.; Sun, B.; Xiao, R.C. Efficient Design Optimization of Cable-Stayed Bridges: A Two-Layer Framework with Surrogate-Model-Assisted Prediction of Optimum Cable Forces. Appl. Sci. 2024, 14, 2007. [Google Scholar] [CrossRef]
- Podolny, W.; Fleming, J.F. Historical Development of Cable-Stayed Bridges. J. Struct. Div. 1972, 98, 2079–2095. [Google Scholar] [CrossRef]
- Chatterjee, S. The Design of Modern Steel Bridges, 2nd ed.; Blackwell Science Ltd.: Berlin, Germany, 2003. [Google Scholar]
- Lin, Y.P. Cable-Stayed Bridge; China Communications Press: Beijing, China, 2004. (In Chinese) [Google Scholar]
- Wang, P.H.; Tseng, T.C.; Yang, C.G. Initial shape of cable-stayed bridges. Comput. Struct. 1993, 47, 111–123. [Google Scholar] [CrossRef]
- Chen, D.W.; Au, F.T.K.; Tham, L.G.; Lee, P.K.K. Determination of initial cable forces in prestressed concrete cable-stayed bridges for given design deck profiles using the force equilibrium method. Comput. Struct. 2000, 74, 1–9. [Google Scholar] [CrossRef]
- Yan, D.H.; Li, X.W.; Liu, G.D.; Yi, W.J. Deciding the reasonable finished dead state of the main beam of cable-stayed bridges using stress balanced method. China J. Highw. Transp. 2000, 13, 49–52. (In Chinese) [Google Scholar]
- Janjinc, D.; Pircher, M.; Pircher, H. Optimization of cable tensioning in cable-stayed bridges. J. Bridge Eng. 2003, 8, 131–137. [Google Scholar] [CrossRef]
- Liang, P.; Xiao, R.C.; Zhang, X.S. Practical method of optimization of cable tensions for cable-stayed bridge. J. Tongji Univ. 2003, 31, 1270–1274. (In Chinese) [Google Scholar]
- Kasuga, A.; Arai, H.; Breen, J.E.; Furukawa, K. Optimum cable-force adjustments in concrete cable-stayed bridges. J. Struct. Eng. 1995, 121, 685–694. [Google Scholar] [CrossRef]
- Xiao, R.C.; Xiang, H.F. Influence matrix method of cable tension optimization for cable-stayed bridges. J. Tongji Univ. 1998, 26, 235–240. (In Chinese) [Google Scholar]
- Lute, V.; Upadhyay, A.; Singh, K.K. Genetic algorithms-based optimization of cable stayed bridges. J. Softw. Eng. Appl. 2011, 4, 571–578. [Google Scholar] [CrossRef]
- Hassan, M.M. Optimum Design of Cable-Stayed Bridges. Ph.D. Thesis, University of Western Ontario, London, ON, Canada, 2010. [Google Scholar]
- Hassan, M.M. Optimization of stay cables in cable-stayed bridges using finite element, genetic algorithm, and B-spline combined technique. Eng. Struct. 2013, 49, 643–654. [Google Scholar] [CrossRef]
- Sung, Y.C.; Chang, D.W.; Teo, E.H. Optimization post-tensioning cable forces of Mau-Lo Hsi cable-stayed bridge. Eng. Struct. 2006, 28, 1407–1417. [Google Scholar] [CrossRef]
- Wilson, R.B. A Simplicial Method for Concave Programming. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1963. [Google Scholar]
- Han, S.P. Superlinearly Convergent Variable Metric Algorithms for General Nonlinear Programming Problems. Math. Program. 1976, 11, 263–282. [Google Scholar] [CrossRef]
- Powell, M.J.D. A fast algorithm for nonlinearly constrained optimization calculations. In Numerical Analysis; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1978; p. 630. [Google Scholar]
- Powell, M.J.D. Algorithms for nonlinear constraints that use lagrangian functions. Math. Program. 1978, 14, 224–248. [Google Scholar] [CrossRef]
- Xiao, R.C.; Hai, F.X. Optimization Method of Cable Prestresses of Cable-Stayed Bridges and Its Engineering Applications. Chin. J. Comput. Mech. 1998, 15, 118–126. [Google Scholar]
- Lonetti, P.; Pascuzzo, A. Design Analysis of the Optimum Configuration of Self-Anchored Cable Stayed Suspension Bridges. Struct. Eng. Mech. 2014, 51, 847–866. [Google Scholar] [CrossRef]
- Lonetti, P.; Pascuzzo, A. Optimum Design Analysis of Hybrid Cable-Stayed Suspension Bridges. Adv. Eng. Softw. 2014, 73, 53–66. [Google Scholar] [CrossRef]
- Hassan, M.; Nassef, A.O.; El Damatty, A.A. Determination of Optimum Post-Tensioning Cable Forces of Cable Stayed Bridges. Eng. Struct. 2012, 44, 248–259. [Google Scholar] [CrossRef]
- Manh, H.H.; Quoc, A.V.; Viet, H.T. Optimum Design of Stay Cables of Steel Cable-stayed Bridges Using Nonlinear Inelastic Analysis and Genetic Algorithm. Structures 2018, 16, 288–302. [Google Scholar]
- Guo, J.J.; Yuan, W.C.; Dang, X.Z.; Alam, M.S. Cable force optimization of a curved cable-stayed bridge with combined simulated annealing method and cubic B-Spline interpolation curves. Eng. Struct. 2019, 201, 109813. [Google Scholar] [CrossRef]
- Sung, Y.C.; Wang, C.Y.; Teo, E.H. Application of particle swarm optimisation to construction planning for cable-stayed bridges by the cantilever erection method. Struct. Infrastruct. Eng. 2016, 12, 208–222. [Google Scholar] [CrossRef]
- Wang, L.F.; Xiao, Z.W.; Li, M.; Fu, N. Cable Force Optimization of Cable-Stayed Bridge Based on Multiobjective Particle Swarm Optimization Algorithm with Mutation Operation and the Influence Matrix. Appl. Sci. 2023, 13, 2611. [Google Scholar] [CrossRef]
- Lei, L.H. Exploration of optimization design for cable force of cable-stayed bridge. J. China Foreign Highw. 2006, 26, 77–80. (In Chinese) [Google Scholar]
- Powell, M.J.D. A Method for Nonlinear Constraints in Minimization Problems. In Optimization; Fletcher, R., Ed.; Academic Press: New York, NY, USA, 1969; pp. 283–298. [Google Scholar]
- Hestenes, M.R. Multiplier and gradient methods. J. Optim. Theory Appl. 1969, 4, 303–320. [Google Scholar] [CrossRef]
- Karmarkar, N. A new polynomial-time algorithm for linear programming. Combinatorica 1984, 4, 373–395. [Google Scholar] [CrossRef]
- Lu, Z.S.; Monteiro, R.D.C. An iterative solver-based long-step infeasible primal-dual path-following algorithm for convex QP based on a class of preconditioners. Optim. Methods Softw. 2009, 24, 123–143. [Google Scholar] [CrossRef]
- Goldfarb, D.; Liu, S. An O (n3L) primal Interior point algorithm for convex quadratic programming. Math. Program. 1991, 49, 325–340. [Google Scholar] [CrossRef]
- Monteiro, R.D.C.; Adler, I. Interior path following primal-dual algorithm. Part I: Linear programming. Math. Program. 1989, 44, 27–41. [Google Scholar] [CrossRef]
- Monteiro, R.D.C.; Adler, I. Interior path following primal-dual algorithm. Part II: Convex quadratic programming. Math. Program. 1989, 44, 43–66. [Google Scholar] [CrossRef]
- Chen, B.L. Optimization Theory and Algorithm, 2nd ed.; Tsinghua University Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Gong, C.; Wang, Z.L. Proficient in MATLAB Optimization Calculation, 2nd ed.; Publishing House of Electronics Industry: Beijing, China, 2012. (In Chinese) [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Tao, Y.; Xu, Q.; Dai, J.; Di, J.; Qin, F. Optimization of Reasonable Finished State for Cable-Stayed Bridge with Steel Box Girder Based on Multiplier Path Following Method. Appl. Sci. 2025, 15, 937. https://doi.org/10.3390/app15020937
Shi J, Tao Y, Xu Q, Dai J, Di J, Qin F. Optimization of Reasonable Finished State for Cable-Stayed Bridge with Steel Box Girder Based on Multiplier Path Following Method. Applied Sciences. 2025; 15(2):937. https://doi.org/10.3390/app15020937
Chicago/Turabian StyleShi, Jiapeng, Yu Tao, Qingyun Xu, Jie Dai, Jin Di, and Fengjiang Qin. 2025. "Optimization of Reasonable Finished State for Cable-Stayed Bridge with Steel Box Girder Based on Multiplier Path Following Method" Applied Sciences 15, no. 2: 937. https://doi.org/10.3390/app15020937
APA StyleShi, J., Tao, Y., Xu, Q., Dai, J., Di, J., & Qin, F. (2025). Optimization of Reasonable Finished State for Cable-Stayed Bridge with Steel Box Girder Based on Multiplier Path Following Method. Applied Sciences, 15(2), 937. https://doi.org/10.3390/app15020937







