Func-Bagging: An Ensemble Learning Strategy for Improving the Performance of Heterogeneous Anomaly Detection Models
Abstract
Featured Application
Abstract
1. Introduction
1.1. Background
1.2. Related Work
- For the final result fusion strategy of bagging, we propose an intuitive anomaly detection weight allocation strategy: when merging results, if the predicted score (predict probability, also known as prediction confidence) given by a classifier is closer to 0 or 1, it indicates that the classifier has higher confidence in its judgment, and therefore should be assigned higher weight.
- Based on the above weight allocation strategy, three weight generation functions with a “high at both ends, low in the middle” curve are designed, and better results than fixed weight allocation strategies are obtained on two datasets.
- To explore the relationship between the outputs of base learners and weight allocation, a special neural network and loss function are designed. The network’s input is the output of the base learners, and the output is the weight to be allocated. After sufficient training, the function curve drawn by this network is consistent with the proposed weight allocation strategy, proving the reasonableness of the strategy. Since this neural network is trained in a data-driven manner, it generalizes better compared to the weight generation functions with fixed expressions mentioned earlier.
2. Materials and Methods
2.1. Problem Definition
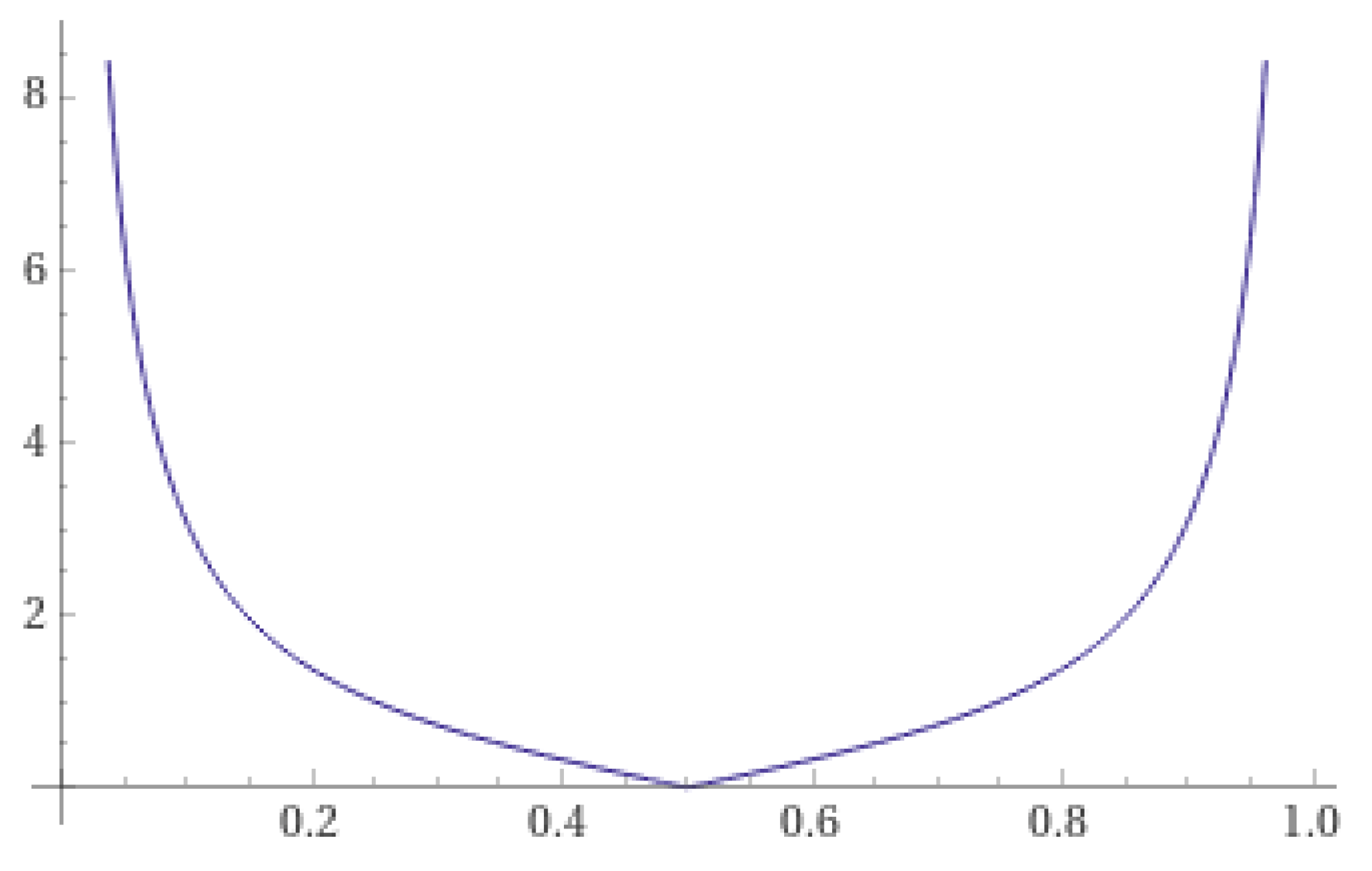
- If the range of is , thenThere exists a such that the function attains its minimum value at c, i.e.,The function exhibits the property of having high values at both ends and low values in the middle.
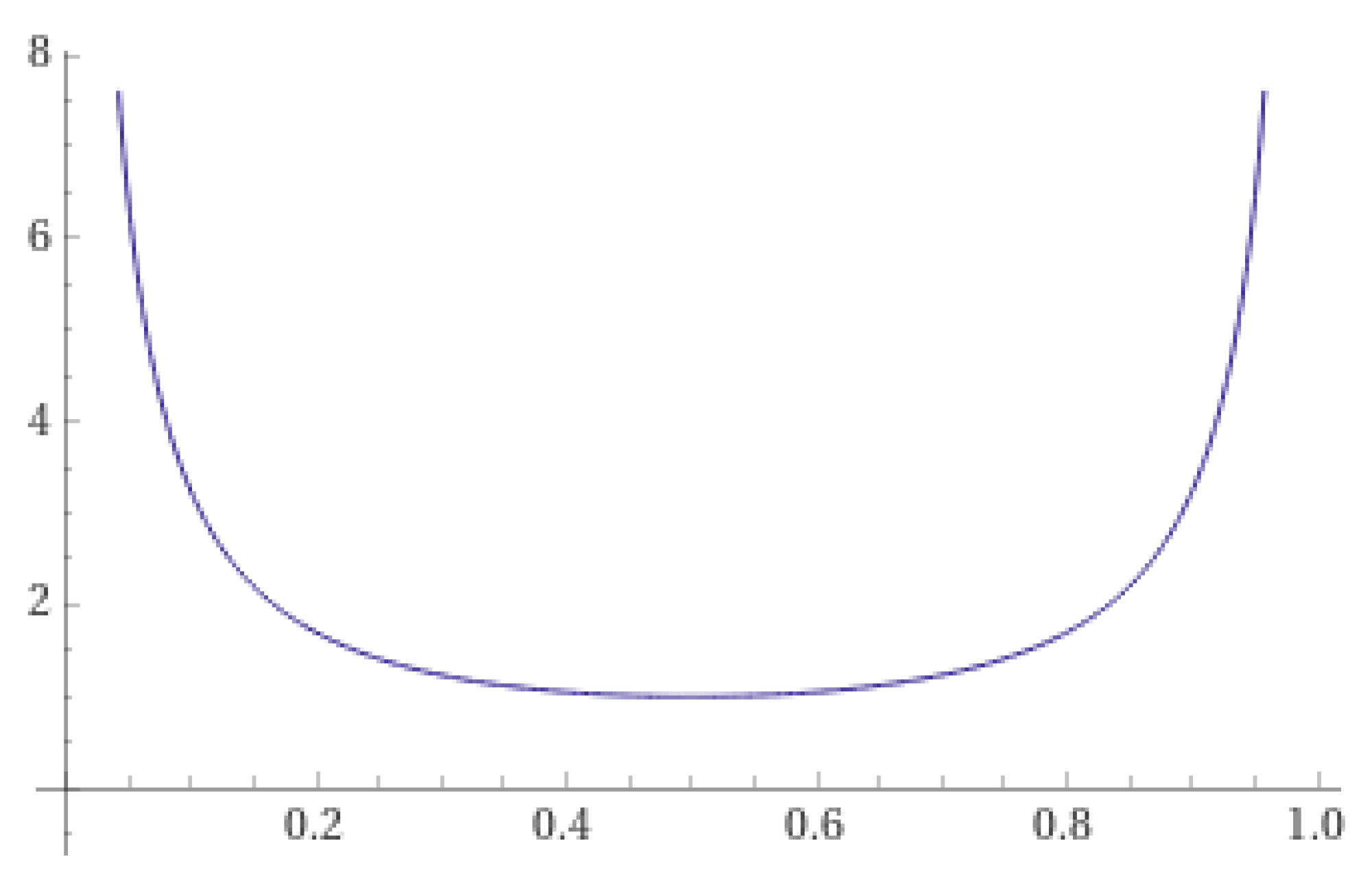
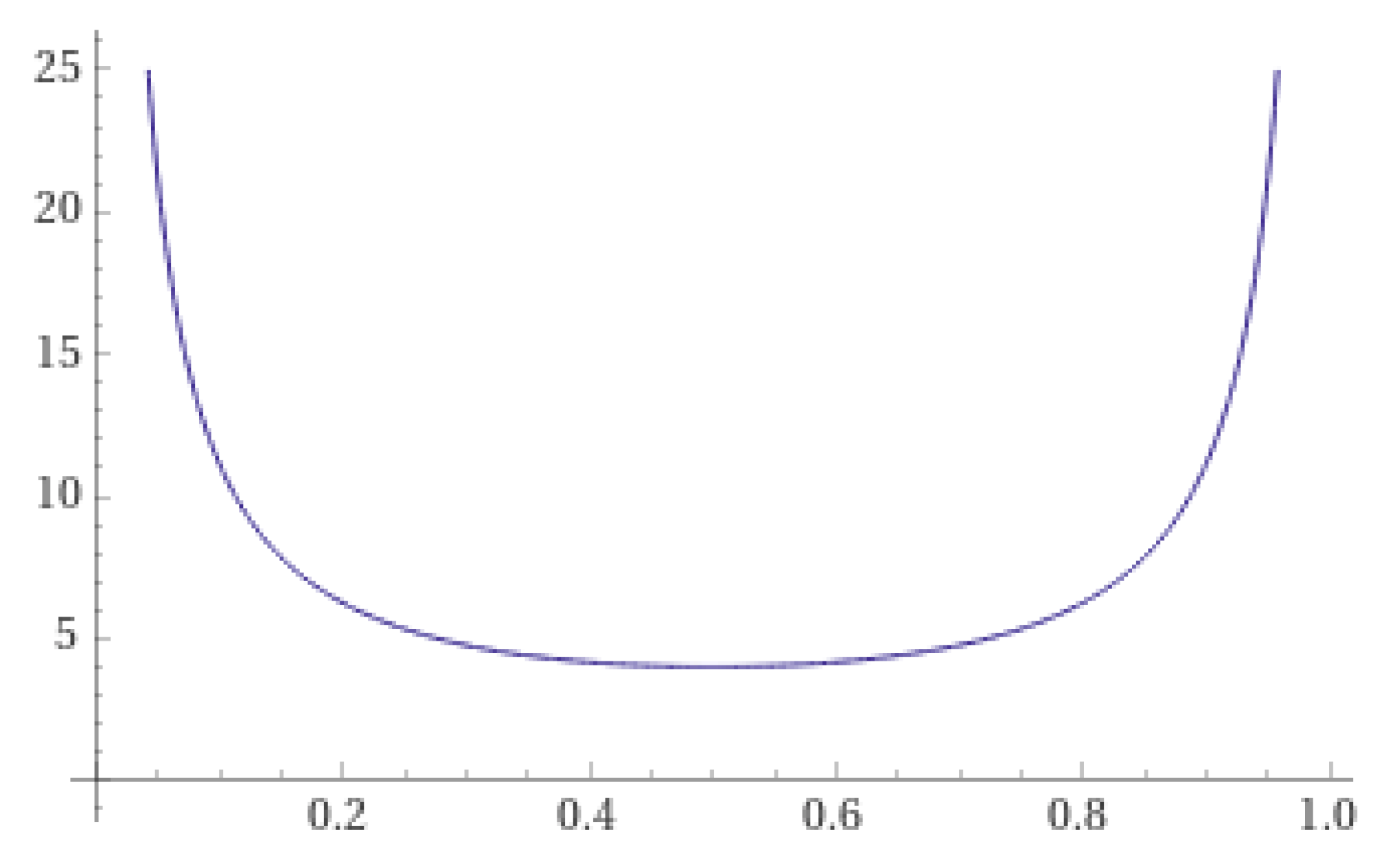
- If the range of is , thenThere exists a such that the function attains its minimum value at c, i.e.,The function exhibits the property of having low values at both ends and high values in the middle.
2.2. Three “High at Both Ends, Low in the Middle” Functions
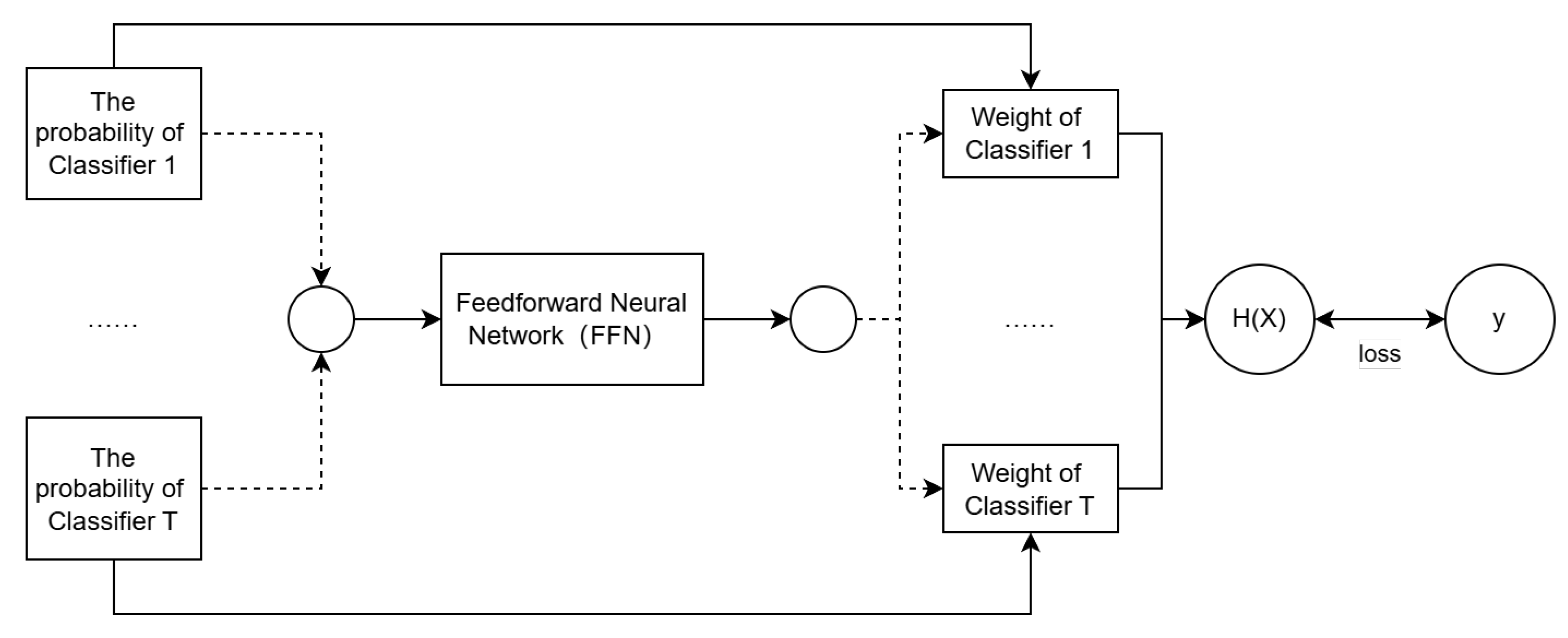
2.3. Neural Network-Based Weight Generation Function
2.4. Datasets and Evaluation Metrics
3. Results
3.1. Comparison of Fixed Expression Weight Generation Function and Fixed Weight Ensemble Results
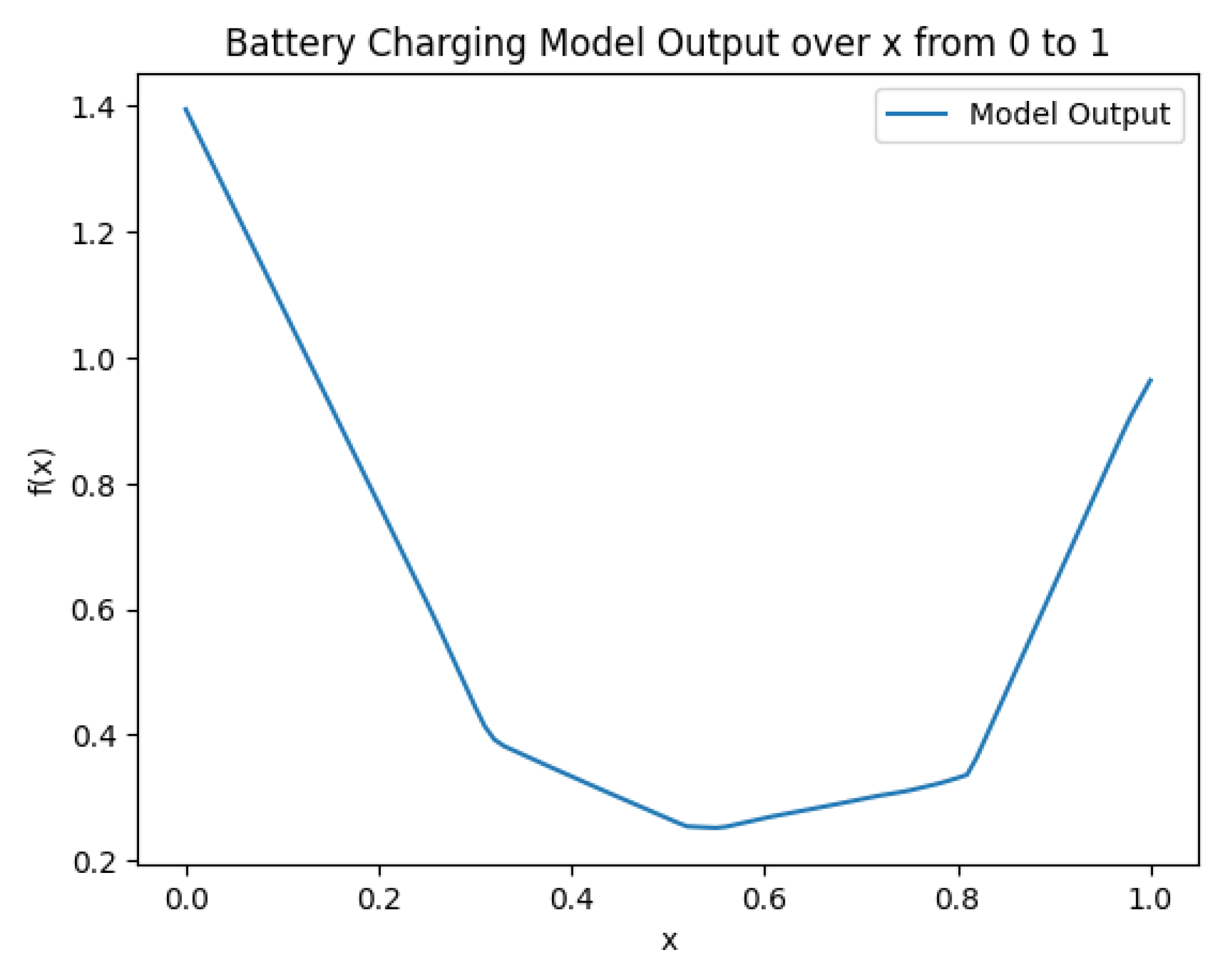
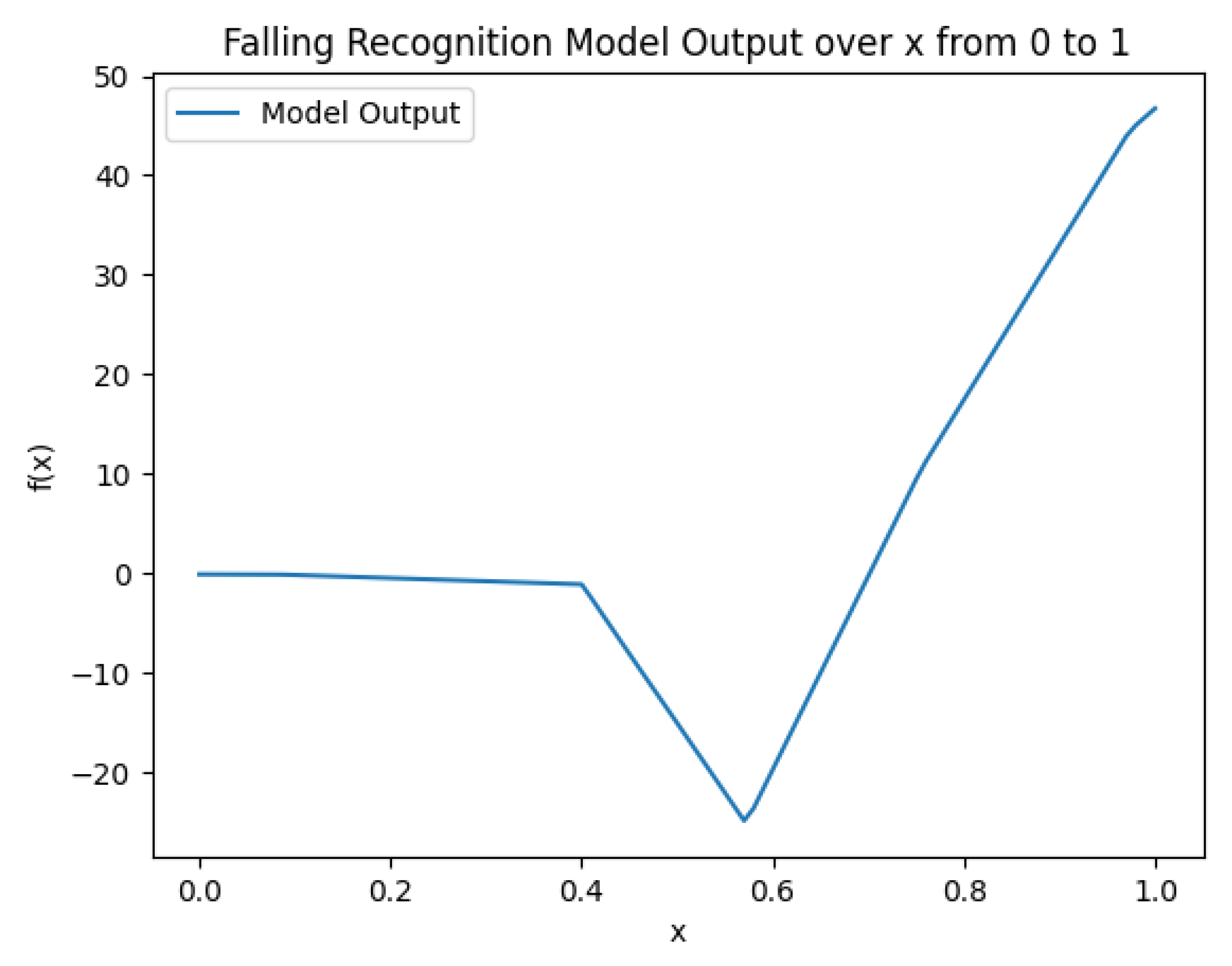
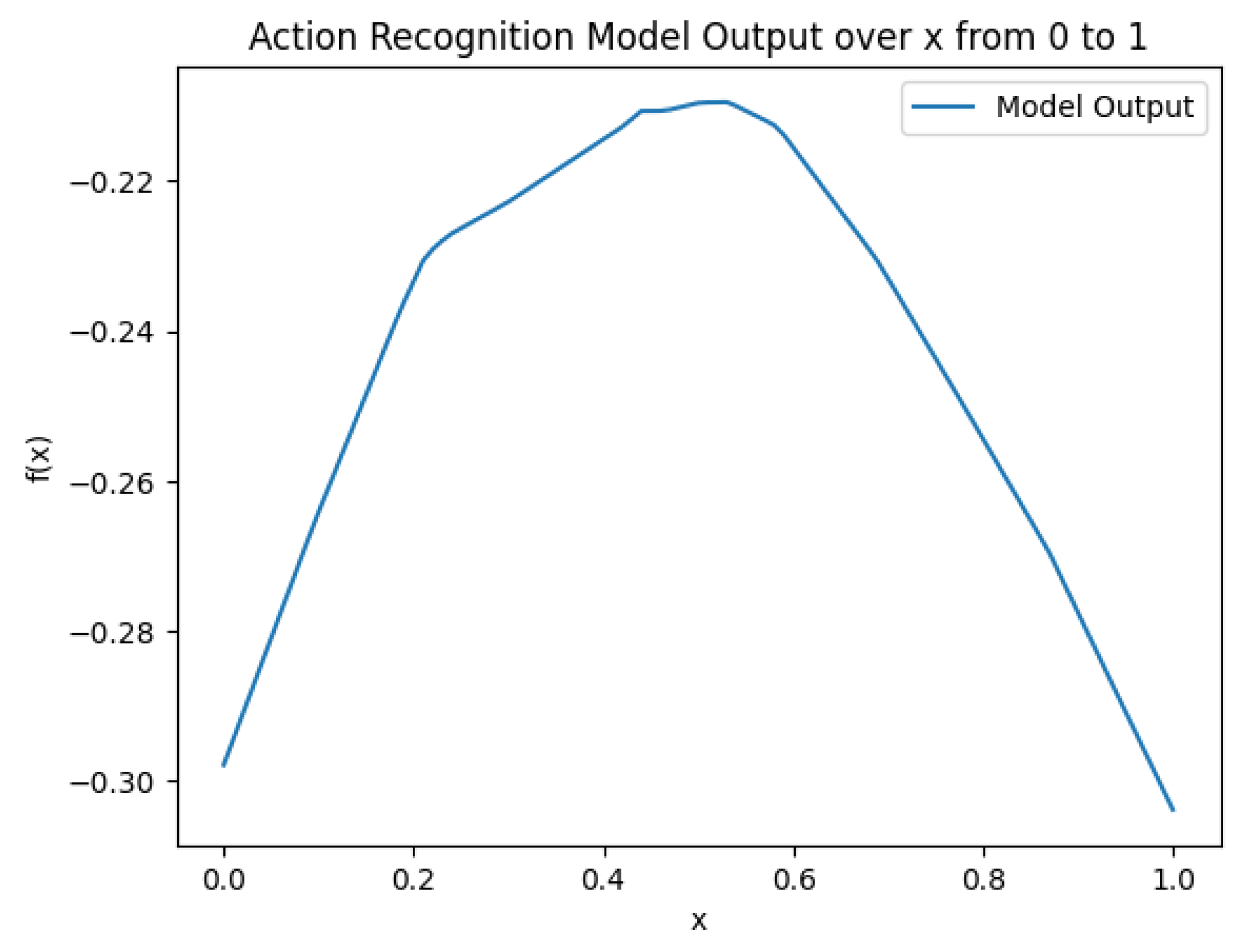
3.2. Neural Network-Based Weight Generation Function
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier chains: A review and perspectives. J. Artif. Intell. Res. 2021, 70, 683–718. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial neural networks based optimization techniques: A review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Costa, V.G.; Pedreira, C.E. Recent advances in decision trees: An updated survey. Artif. Intell. Rev. 2023, 56, 4765–4800. [Google Scholar] [CrossRef]
- Cropper, A.; Dumančić, S. Inductive logic programming at 30: A new introduction. J. Artif. Intell. Res. 2022, 74, 765–850. [Google Scholar] [CrossRef]
- Khan, M.E.; Rue, H. The bayesian learning rule. arXiv 2021, arXiv:2107.04562. [Google Scholar]
- Mienye, I.D.; Sun, Y. A survey of ensemble learning: Concepts, algorithms, applications, and prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Sesmero, M.P.; Ledezma, A.I.; Sanchis, A. Generating ensembles of heterogeneous classifiers using stacked generalization. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2015, 5, 21–34. [Google Scholar] [CrossRef]
- Odegua, R. An empirical study of ensemble techniques (bagging, boosting and stacking). In Proceedings of the Deep Learning Indaba, Sandton, South Africa, 25–30 August 2019. [Google Scholar]
- Wang, J.; Xu, H.; Liu, J.; Peng, X.; He, C. A bagging-strategy based heterogeneous ensemble deep neural networks approach for the multiple components fault diagnosis of hydraulic systems. Meas. Sci. Technol. 2023, 34, 065007. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, C.; Da, B.; Xie, F. A novel heterogeneous ensemble credit scoring model based on stacking approach. Expert Syst. Appl. 2018, 93, 182–199. [Google Scholar] [CrossRef]
- Sobanadevi, V.; Ravi, G. Handling data imbalance using a heterogeneous bagging-based stacked ensemble (HBSE) for credit card fraud detection. In Intelligence in Big Data Technologies—Beyond the Hype: Proceedings of ICBDCC 2019; Springer: Singapore, 2021; pp. 517–525. [Google Scholar]
- Skalak, D.B. Prototype Selection for Composite Nearest Neighbor Classifiers; University of Massachusetts Amherst: Amherst, MA, USA, 1997. [Google Scholar]
- Fan, W.; Stolfo, S.; Chan, P. Using conflicts among multiple base classifiers to measure the performance of stacking. In Proceedings of the ICML-99 Workshop on Recent Advances in Meta-Learning and Future Work; Stefan Institute Publisher: Ljubljana, Slovenia, 1999; pp. 10–17. [Google Scholar]
- Merz, C.J. Using correspondence analysis to combine classifiers. Mach. Learn. 1999, 36, 33–58. [Google Scholar] [CrossRef]
- Ting, K.M.; Witten, I.H. Issues in stacked generalization. J. Artif. Intell. Res. 1999, 10, 271–289. [Google Scholar] [CrossRef]
- Zefrehi, H.G.; Altınçay, H. Imbalance learning using heterogeneous ensembles. Expert Syst. Appl. 2020, 142, 113005. [Google Scholar] [CrossRef]
- Zhao, Q.L.; Jiang, Y.H.; Xu, M. Incremental learning by heterogeneous bagging ensemble. In Advanced Data Mining and Applications, Proceedings of the 6th International Conference, ADMA 2010, Chongqing, China, 19–21 November 2010, Proceedings, Part II; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–12. [Google Scholar]
- Hsu, K.W.; Srivastava, J. Improving bagging performance through multi-algorithm ensembles. In New Frontiers in Applied Data Mining, Proceedings of the PAKDD 2011 International Workshops, Shenzhen, China, 24–27 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 471–482. [Google Scholar]
- Nguyen, T.T.; Luong, A.V.; Dang, M.T.; Liew, A.W.C.; McCall, J. Ensemble selection based on classifier prediction confidence. Pattern Recognit. 2020, 100, 107104. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, M.P.; Pham, X.C.; Liew, A.W.-C. Heterogeneous classifier ensemble with fuzzy rule-based meta learner. Inf. Sci. 2018, 422, 144–160. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, M.P.; Pham, X.C.; Liew, A.W.-C.; Pedrycz, W. Combining heterogeneous classifiers via granular prototypes. Appl. Soft Comput. 2018, 73, 795–815. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 7132–7141. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Kaluza, B.; Mirchevska, V.; Dovgan, E.; Luštrek, M.; Gams, M. An agent-based approach to care in independent living. In Ambient Intelligence, Proceedings of the First International Joint Conference, AmI 2010, Malaga, Spain, 10–12 November 2010. Proceedings 1; Springer: Berlin/Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Heydarian, M.; Doyle, T.E.; Samavi, R. MLCM: Multi-label confusion matrix. IEEE Access 2022, 10, 19083–19095. [Google Scholar] [CrossRef]
- Narkhede, S. Understanding AUC-ROC Curve. Towards Data Sci. 2018, 26, 220–227. [Google Scholar]
- Yue, S.; Li, P.; Hao, P. SVM classification: Its contents and challenges. Appl.-Math.-J. Chin. Univ. 2003, 18, 332–342. [Google Scholar] [CrossRef]
- Singh, J.; Banerjee, R. A study on single and multi-layer perceptron neural network. In Proceedings of the 2019 3rd International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 27–29 March 2019; IEEE: New York, NY, USA, 2019; pp. 35–40. [Google Scholar]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN model-based approach in classification. In On The Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE, Proceedings of the OTM Confederated International Conferences, CoopIS, DOA, and ODBASE 2003 Catania, Sicily, Italy, 3–7 November 2003. Proceedings; Springer: Berlin/Heidelberg, Germany, 2003; pp. 986–996. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Harris, J.K. Primer on binary logistic regression. Fam. Med. Community Health 2021, 9 (Suppl. S1), e001290. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Sun, D. The improved AdaBoost algorithms for imbalanced data classification. Inf. Sci. 2021, 563, 358–374. [Google Scholar] [CrossRef]
- Reddy, E.M.K.; Gurrala, A.; Hasitha, V.B.; Kumar, K.V.R. Introduction to Naive Bayes and a review on its subtypes with applications. In Bayesian Reasoning and Gaussian Processes for Machine Learning Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022; pp. 1–14. [Google Scholar]


| Author(s) | Key Influence |
|---|---|
| Skalak (1997) [12] | Introduced instance-based learning classifiers as Level-0 base learners, using prototypes for classification instead of traditional models. |
| Merz (1999) [14] | Proposed Stacking with Correspondence Analysis and Nearest Neighbor (SCANN), using correspondence analysis to remove redundancy between base learners and a nearest neighbor method as the meta-learner, improving model diversity. |
| Fan et al. (1999) [13] | Evaluated stacking ensemble accuracy with conflict-based estimates, using tree-based and rule-based classifiers as base learners. |
| Qiang Li Zhao et al. (2010) [17] | Explored classifier ensemble methods in incremental learning, proposing Bagging++, which integrates new incremental base learners into the original ensemble model using a simple voting strategy. |
| Kuo-Wei Hsu et al. (2011) [18] | Demonstrated that higher divergence (heterogeneity) between base classifiers leads to stronger model performance, although they used the original bagging voting strategy without exploring a new fusion strategy. |
| M. Paz Sesmero et al. (2015) [7] | Enhanced understanding of stacking method variants and their applications. |
| Yufei Xia et al. (2018) [10] | Enhanced ensemble performance but lacked interpretability in base learner weight distribution. |
| Hossein Ghaderi Zefrehi et al. (2020) [16] | Addressed the class imbalance problem in binary classification tasks using heterogeneous ensembles and various sampling methods (undersampling and oversampling). |
| Nguyen et al. (2020) [19] | Proposed an ensemble selection method based on classifier prediction confidence and reliability, optimizing the empirical 0-1 loss to effectively combine static and dynamic ensemble selection, outperforming traditional strategies in experiments on 62 datasets. |
| V. Sobanadevi and G. Ravi (2021) [11] | Improved credit card fraud detection but lacked interpretability in base learner contributions. |
| Junlang Wang et al. (2023) [9] | Improved computational efficiency and diagnostic accuracy through feature selection, dimensionality reduction, and ensemble learning. |
| Feature Name | Meaning |
|---|---|
| volt | Overall voltage |
| current | Overall current |
| soc | State of Charge |
| max_single_volt | Maximum cell voltage |
| min_single_volt | Minimum cell voltage |
| max_temp | Maximum temperature |
| min_temp | Minimum temperature |
| timestamp | Timestamp |
| Feature Name | Meaning |
|---|---|
| x | x-coordinate of the sensor |
| y | y-coordinate of the sensor |
| z | z-coordinate of the sensor |
| 010-000-024-033 | Sensor 1 data |
| 010-000-030-096 | Sensor 2 data |
| 020-000-032-221 | Sensor 3 data |
| 020-000-033-111 anomaly | Sensor 4 data Anomaly label (whether a fall occurred) |
| Hyper Parameter | SVM | MLP | KNN | RF |
|---|---|---|---|---|
| C (Penalty coefficient) | 0.88 | * | * | * |
| kernel | RBF | * | * | * |
| gamma | * | * | * | |
| random_state | 42 | 1 | 0 | 42 |
| solver | * | lbfgs | * | * |
| learning_rate | * | 0.00001 | * | * |
| hidden_layer_sizes | * | (5, 2) | * | * |
| max_iter | * | 200 | * | * |
| n_neighbors | * | * | 200 | * |
| n_estimators | * | * | * | 3 |
| n_jobs | * | * | * | −1 |
| Dataset | SVM | MLP | KNN | RF | Fixed Weight Ensemble | Tan Function Ensemble | Sec Function Ensemble | Fractional Function Ensemble |
|---|---|---|---|---|---|---|---|---|
| Battery Data | 0.9366 | 0.9313 | * | * | 0.9441 | 0.9556 | 0.9558 | 0.9557 |
| Fall Data | * | 0.8168 | 0.8170 | * | 0.8353 | 0.8329 | 0.8375 | 0.8377 |
| Motion Data | * | 0.9806 | * | 0.9779 | 0.9883 | 0.9806 | 0.9855 | 0.9879 |
| Dataset | SVM | MLP | KNN | RF | Fixed Weight Ensemble | Fixed Function Ensemble | Neural Network Function Ensemble |
|---|---|---|---|---|---|---|---|
| Battery Data | 0.9364 | 0.9367 | * | * | 0.9504 | 0.9515 | 0.9508 |
| Fall Data | * | 0.8203 | 0.8170 | * | 0.8375 | 0.8407 | 0.8354 |
| Motion Data | * | 0.9809 | * | 0.9787 | 0.98879 | 0.9884 | 0.98881 |
| Model | AUC | Improvement over Base Classifier | Note |
|---|---|---|---|
| SVM | 0.9364 | * | Base classifier |
| MLP | 0.9367 | * | Base classifier |
| Fixed Weight Ensemble | 0.9504 | 1.479% | The weight ratio of the two base classifiers is 5:5 |
| Fixed Function Ensemble | 0.9515 | 1.596% | Frac function |
| Neural Network Function Ensemble | 0.9508 | 1.522% | * |
| Stacking | 0.9497 | 1.404% | * |
| Bagging (SVM) | 0.9374 | 0.107% | Bagging does not support integrating two heterogeneous models |
| Bagging (MLP) | 0.9445 | 0.833% | * |
| Logistic [31] | 0.8497 | * | Base classifier |
| AdaBoost [32] (Logistic) | 0.8471 | −0.306% | AdaBoost does not support models without the sample_weight parameter |
| Gaussian Naive Bayes [33] | 0.8201 | * | Base classifier |
| AdaBoost (Gaussian Naive Bayes) | 0.7077 | −13.706% | * |
| Model | AUC | Improvement over Base Classifier | Note |
|---|---|---|---|
| MLP | 0.8168 | * | One of the base classifiers |
| KNN | 0.8170 | * | One of the base classifiers |
| Fixed Weight Ensemble | 0.8375 | 2.522% | The weight ratio of the two base classifiers is 4:6 |
| Fixed Function Ensemble | 0.8407 | 2.913% | Sec function |
| Neural Network Function Ensemble | 0.8354 | 2.277% | * |
| Stacking | 0.8336 | 2.044% | * |
| Bagging (MLP) | 0.8345 | 2.167% | * |
| Bagging (KNN) | 0.8192 | 0.269% | * |
| Logistic | 0.8118 | * | Base classifier |
| Adaboost (Logistic) | 0.8123 | 0.062% | * |
| Gaussian Naive Bayes | 0.8001 | * | Base classifier |
| Adaboost (Gaussian Native Bayers) | 0.6538 | −18.285% | * |
| Model | AUC | Improvement over Base Classifier | Note |
|---|---|---|---|
| MLP | 0.9809 | * | One of the base classifiers |
| RF | 0.9787 | * | One of the base classifiers |
| Fixed Weight Ensemble | 0.98879 | 0.918% | The weight ratio of the two base classifiers is 6:4 |
| Fixed Function Ensemble | 0.9884 | 0.878% | Sec function |
| Neural Network Function Ensemble | 0.98881 | 0.920% | * |
| Stacking | 0.98879 | 0.918% | * |
| Bagging (MLP) | 0.9851 | 0.633% | * |
| Bagging (RF) | 0.98875 | 0.913% | * |
| Logistic | 0.5428 | * | Base classifier |
| Adaboost (Logistic) | 0.5419 | −0.166% | * |
| Gaussian Naive Bayes | 0.8077 | * | Base classifier |
| Adaboost (Gaussian Native Bayers) | 0.6817 | −15.600% | * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, R.; Yin, Y.; Su, Q.; Guan, T. Func-Bagging: An Ensemble Learning Strategy for Improving the Performance of Heterogeneous Anomaly Detection Models. Appl. Sci. 2025, 15, 905. https://doi.org/10.3390/app15020905
Qiu R, Yin Y, Su Q, Guan T. Func-Bagging: An Ensemble Learning Strategy for Improving the Performance of Heterogeneous Anomaly Detection Models. Applied Sciences. 2025; 15(2):905. https://doi.org/10.3390/app15020905
Chicago/Turabian StyleQiu, Ruinan, Yongfeng Yin, Qingran Su, and Tianyi Guan. 2025. "Func-Bagging: An Ensemble Learning Strategy for Improving the Performance of Heterogeneous Anomaly Detection Models" Applied Sciences 15, no. 2: 905. https://doi.org/10.3390/app15020905
APA StyleQiu, R., Yin, Y., Su, Q., & Guan, T. (2025). Func-Bagging: An Ensemble Learning Strategy for Improving the Performance of Heterogeneous Anomaly Detection Models. Applied Sciences, 15(2), 905. https://doi.org/10.3390/app15020905







