Abstract
Predictive maintenance in manufacturing industry applications is a challenging research field. Packaging machines are widely used in a large number of logistic companies’ warehouses and must be working uninterruptedly. Traditionally, preventive maintenance strategies have been carried out to improve the performance of these machines. However, these kinds of policies do not take into account the information provided by the sensors implemented in the machines. This paper presents an expert system for the automatic estimation of work orders to implement predictive maintenance policies for packaging machines. The central innovation lies in a two-stage process: a classifier generates a binary decision on whether a machine requires maintenance, and an unsupervised anomaly detection module subsequently audits the classifier’s probabilistic output to refine and interpret its predictions. By leveraging the classifier to condense sensor data and applying anomaly detection to its output, the system optimizes the decision reliability. Three anomaly detection methods were evaluated: One-Class Support Vector Machine (OCSVM), Minimum Covariance Determinant (MCD), and a majority (hard) voting ensemble of the two. All anomaly detection methods improved the baseline classifier’s performance, with the majority voting ensemble achieving the highest F1 score.
1. Introduction
Production lines in large companies rely on equipment to work properly. A failure in a device or component may cause a stop in the entire production line. Production stops are associated with huge costs, causing not only production loss due to downtime but also efforts to identify the cause of the failure and repair it []. In the new industrial era, predictive maintenance has been adopted by many companies to estimate when maintenance should be performed to avoid unnecessary losses [].
In recent years, industry has developed towards the fourth stage of industrialization [] (the so-called Industry 4.0). The connectivity of various devices, especially industrial ones, has experienced substantial growth, partly due to the advances and cost reduction of Ethernet-based buses. The current trend is that any industrial device, from a Programmable Logic Controller (PLC) to a complete manufacturing cell, is connected to a network. Usually, industrial devices send data related to the manufacturing process (performance, machine status, etc.). Thus, data analysis related to the improvement of industrial processes is a reality. A proof of this is the wide and prolific state of the art in this field [,]. The incorporation of advanced data-driven techniques and models enables analysis that goes beyond merely visualizing process parameters. These approaches provide valuable insights for optimizing maintenance and managing industrial manufacturing cells more effectively.
This paper addresses the problem of establishing predictive maintenance strategies in a group of packaging machines that operate in logistic centers. Packaging machines are devices used for applying sheets of plastic film on transport pallets. These machines are designed to wrap the load without having to turn around a platform in order to secure the load, protect it from dust or water, reduce its volume, strengthen the packaging, etc. An example of a fixed automatic packaging machine is shown in Figure 1. All these packaging machines are connected to an Ethernet network and periodically report a set of alarms associated with different types of anomalous behaviors. The status variables of each machine are received by a central server and are stored in a database. Despite the availability of the status variables of each machine in real time, several challenges arise when planning the development of an expert system to decide when the company must send a technician to take maintenance actions. These challenges are related to some main issues: (1) as in almost every predictive maintenance problem, there is a strong imbalance between the classes of the data set. This imbalance should be addressed before building a classifier to avoid the undesirable situation where the classifier consistently predicts the majority class, thereby neglecting all failure predictions []. The following steps are crucial: (1) extracting relevant alarms and constructing the dataset that will serve as input for the machine learning algorithms; (2) defining a strategy to assess the importance of past alarms in the classification system; (3) determining the frequency with which the models are updated; and (4) integrating the machine learning algorithms into the production lines of the manufacturing company.

Figure 1.
Automatic fixed wrapping machine F-2200 (Aranco, Valencia, Spain). Source: https://www.aranco.com/en/services/sie-wrappers/fixed-wrapping-machine-f-2200 (accessed on 16 December 2024).
The main contribution of this paper will be to introduce the framework and methodology to audit an expert system (a Random Forest-based classifier) for planning predictive maintenance actions (work orders) in the ERP (Enterprise Resource Planning) system of a packaging machine company by appending an unsupervised anomaly detection stage at its output that acts as a supervisor. The anomaly detection stage only uses the information given by the classifier during the first 30 days of run-time and is then applied sequentially to time windows of a determined duration to predict if the following day may be considered as an anomaly and would involve a maintenance action. We concluded that this auditing stage is useful to improve the precision and recall of the baseline classifier, which are measured globally as the F1 score.
The rest of the paper is organized as follows. Section 2 reviews the existing literature in the field. Section 3 formulates the objective of the work and provides a graphical description of the system. Materials and methods used are explained in Section 4, including the strategy to build the dataset and the anomaly detection methods and libraries used to fine-tune the expert system. Section 5 shows the obtained classification results and Section 6 discusses and analyzes those results.
2. Literature Review
Predictive maintenance has been gaining prominence in multidisciplinary research groups, proposing the creation and integration of lines of research related to data acquisition, infrastructure, storage, distribution, security, and intelligence []. The ability to predict the need for maintenance of assets at a specific future moment is one of the main challenges in Industry 4.0. New smart industrial facilities are focused on creating manufacturing intelligence from real-time data to support accurate and timely decision-making that can have a positive impact across the entire organization [,]. In particular, the possibility of performing predictive maintenance contributes to enhancing machine downtime, costs, control, and quality of production [,,].
Emerging technologies such as Internet of Things (IoT) and Cyber Physical Systems (CPSs) are being embedded in physical processes to measure and monitor real-time data from across a factory, which will ultimately give rise to unprecedented levels of data production. This obliges resorting to Big Data technologies to manage these massive amounts of data [,,].
Historically, preventive maintenance techniques have typically been used to minimize failures in manufacturing cells using maintenance strategies such as breakdown maintenance, preventive maintenance, and condition-based maintenance, including models and algorithms in manufacturing [,,]. However, nowadays, other kinds of strategies are also considered. Examples of these techniques are cloud-based predictive maintenance [] and mobile agent technologies []. According to [], maintenance approaches capable of monitoring equipment conditions for diagnostic and prognostic purposes can be grouped into three main categories: statistical approaches, artificial intelligence approaches and model-based approaches. As model-based approaches need mechanistic knowledge and theory of the equipment to be monitored, and statistical approaches require mathematical background, artificial intelligence approaches, and machine learning techniques in particular, have been increasingly applied in predictive maintenance applications [,].
Examples of these techniques are Multiple Classifiers [], Random Forests (RFs) [,] and Support Vector Machines (SVMs) [,,,], among many others []. These strategies take into account issues like real-time alarm monitoring in the manufacturing cell and the general status of the machine in order to determine the best timing to take maintenance actions. The acquired data collects and saves the machine state by means of communication interfaces connected between the machine and the computing servers that host the maintenance algorithms.
Anomaly detection refers to identifying data values that significantly deviate from typical behavior, which can be caused by various factors such as errors in the acquisition system or industrial equipment malfunction []. Anomaly detection can be approached through centralized or distributed solutions and using statistical or machine learning (ML) methods. Statistical approaches are based on the distribution of variables, while ML provides techniques for handling high-dimensional data and identifying hidden relationships in complex environments []. While previous works typically relied on fully labeled data, such scenarios are less common in practice, because labels are particularly difficult (or impossible) to obtain during the training stage. Furthermore, even when labeled data are available, there could be biases in the way samples are labeled, causing distribution differences. Such real-world data challenges limit the achievable accuracy of prior methods in detecting anomalies. In contrast, unsupervised methods perform their tasks without resorting to class labels. This framework aims at learning the steady state of a working machine and, from that knowledge, trying to predict anomalous behavior. One example of algorithm that follows this principle is the One-Class Classifier []. This framework makes it possible to work with very few training examples and to implement online anomaly detection solutions that are proven to complement a classifier in the task of detecting different types of anomalies [].
In real-time operating systems, the ability to detect anomalies promptly is critical to maintaining system stability, safety, and performance. One of the main challenges in such systems is the dynamic nature of the data, which can vary continuously over time. Anomalies often manifest as deviations from typical patterns, but their detection requires a method that adapts to this changing environment. This is where the sliding window technique proves invaluable. By using a sliding window, the system can continuously monitor a fixed-size subset of the most recent data points, allowing for real-time anomaly detection without needing to process the entire dataset. This method helps in capturing local variations in data, making it especially useful in environments where system behavior fluctuates rapidly. The sliding window enables timely detection of outliers or failures, ensuring that the system can respond to anomalies as they emerge without the delay of waiting for the entire history to be processed. In the fields of industry and predictive maintenance, sliding-window-based anomaly detection has been successfully implemented to detect outliers in hydrological time series [], to detect anomalous vibrations in robots [], and for abnormal network traffic detection []. To the best of our knowledge, no prior research in the field of industrial predictive maintenance has explored the integration of machine learning model auditing to enhance performance through unsupervised anomaly detection techniques. Notably, this approach eliminates the need for access to the entire historical dataset, making it uniquely suited for deployment in real-time operational environments within the production chain. This represents a novel contribution, bridging the gap between model auditing and the practical constraints of industrial settings.
3. Expert System Description and Objective of the Work
Figure 2 shows the global structure of the proposed expert system. Packaging machine sensors periodically report information about the status of the machine to the company’s ERP system through a TCP/IP connection and an SQL database. This information is read by the expert system module and is preprocessed by the filtering module of the expert system in order to prepare the data to be used by the classification algorithms. Then, the classifier module writes the information related to the timing when a maintenance action has to be taken in the ERP SQL database. The objective of this work will be the development of an anomaly detection stage, following the existing pretrained classifier, to optimize its precision and recall. The main novelty and contribution of this work is the development of dynamic unsupervised anomaly detection techniques that (a) avoid the tedious labeling process and (b) allow for rapid deployment in a complex industrial maintenance and scheduling system for packaging machines, without the need for a long training process. To achieve this goal, we developed and tested an online framework based on sliding windows in combination with several anomaly detection techniques.
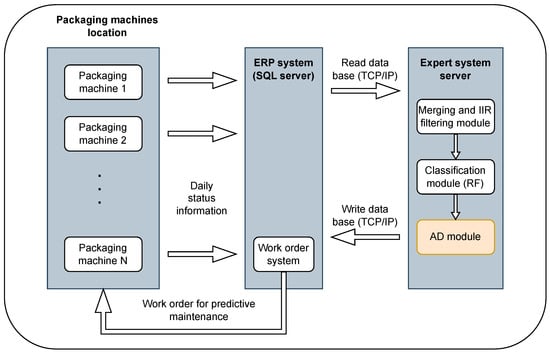
Figure 2.
Predictive maintenance expert system. The main contribution of this work is the improvement of the existing classification module by means of unsupervised AD techniques (AD module).
4. Methods
4.1. Data Preprocessing
The specification of the expert system imposed by the company was that it should provide a daily prediction to allow for programming of the daily schedule of work orders. Thus, the sampling period at which the patterns from each machine in the training set are acquired is one day. In order to build the dataset, daily information about all the events from a machine (alarm occurrence, counters, working orders, and tasks associated with these working orders) was collected, and then the information was organized in a vector containing all the information from that particular day. The alarm variables provided daily monitoring information that was used to train the classifier. An alarm event indicates some kind of machine malfunction. Table 1 shows the possible causes of an alarm event.

Table 1.
Set of alarms and their description.
Historical events from the previous working order are of paramount importance to the company. Therefore, a first-order Infinite Impulse Response (IIR) filter was applied to the sensor signals from the machines to account for historical information. This filter weighs past information in a decreasing way, that is, the more recent the event, the more relevant it is, as represented in Equation (1):
where is the current input, and is the previous output. The parameter () is a smoothing factor used to weigh the past information. This filtering provides a decreasing sum of the frequency of occurrence of each alarm from the date of the event to the last working order. The parameter was empirically set to 0.63 after tests conducted by company experts, resulting in an IIR low-pass filter.
The target (binary) output defines whether there was a maintenance action for that day. The classes in the data set were extremely imbalanced (1.3% positive (maintenance action required) and 98.7% negative (maintenance not required)). Therefore, the SMOTE method [] was employed to minimize the effect of class imbalance.
4.2. Classifier
The pretrained classifier used by the packaging company was also developed by the authors of this article and consists of a Random Forest (RF) used to classify the binary variable that encodes whether a maintenance action took place on a particular date for a specific machine. RFs are a popular machine learning algorithm that can be used for both classification and regression tasks. They work by creating multiple decision trees, each trained on a random subset of the data and a random subset of the features. The final prediction is then made by averaging the predictions of all individual trees []. Random forests are known for their high accuracy and robustness to overfitting. They have been successfully applied in various fields, such as finance, industry, and medicine.
In particular, a single RF was trained using the R caret package [] to predict maintenance actions for all machines. The selected model is composed of 500 trees (ntree parameter) and uses 17 randomly sampled predictors (mtry parameter). The resulting Area Under the ROC was 0.848 on the test set (50% of the data). Theoretically, this result is satisfactory, but due to the significant imbalance between classes, a large number of false positives occurred, resulting in very low F1 scores (approximately 0.2 on average).
4.3. Anomaly Detection Methods
Anomaly detection (AD) is the identification of observations that do not conform to an expected pattern or other items in a dataset. It is an important data mining tool for discovering induced errors, unexpected patterns, and more general anomalies.
There are various ways of performing AD, and the approach to take will depend on the nature of the data and the types of anomalies to detect. When labels are scarce or not available, unsupervised learning schemes may be considered. Basically, this model identifies outliers during the fitting process, where it learns a steady state and can then infer abnormal variations (or novelties) from it. It can be used when outliers are defined as points that exist in low-density regions of the dataset. Thus, any new observation which does not belong to high-density areas will be labeled as such automatically by the algorithm.
In the anomaly detection stage of the developed framework, two of the most successful AD methods were compared, while also creating an ensemble of them. These are the One-Class Support Vector Machine (OCSVM) and Minimum Covariance Determinant (MCD).
4.3.1. OCSVM
The OCSVM is a variant of the traditional Support Vector Machine (SVM) that is trained on only one class of data, i.e., the normal data. The algorithm learns the boundaries of the normal data and identifies any data points that fall outside these boundaries as anomalous []. This algorithm can be used both in a supervised or unsupervised manner. The OCSVM has been widely used in various fields such as finance, cybersecurity, medical diagnosis, and fault detection in industrial systems.
The OCSVM model used in this work is a wrapper of Python’s scikit-learn one-class SVM class with more functionalities, included in the pyOD package []. In particular, we used an OCSVM with a radial basis function (RBF) kernel. Given a dataset , where , the objective of the OCSVM with the RBF kernel is to find the optimal hyperplane that separates the data from the origin, capturing the regions with the majority of the data points.
The RBF kernel function is used for mapping the input data into a higher-dimensional feature space and is defined by the following:
where is a parameter that controls the width of the Gaussian function.
The primal problem of the OCSVM with the RBF kernel can be formulated as follows:
which is subject to the constraints
where we have the following definitions:
- is the weight vector in the feature space;
- are the slack variables representing margin violations;
- is the offset term (the decision function’s threshold);
- is the feature mapping function;
- controls the fraction of outliers and the margin (a value between 0 and 1).
The goal is to find , , and such that the margin is maximized while minimizing the slack variables . It is more common to solve the dual problem for the OCSVM. The dual problem involves introducing Lagrange multipliers for the constraints. After applying the Lagrangian, the dual problem is defined as follows:
which is subject to the constraints
where are the Lagrange multipliers that correspond to each data point.
The dual problem involves maximizing the Lagrange multipliers subject to the given constraints. After solving the dual problem, the decision function is used to classify new data points x as normal or anomalous:
The classification of a point based on is as follows:
- If , the point is classified as “normal”.
- If , the point is classified as an “anomaly”.
Unlike linear or polynomial kernels, the RBF is more complex and efficient at the same time that it can combine multiple polynomial kernels multiple times and using different degrees to project the non-linearly separable data into a higher dimensional space so that they can be separable using a hyperplane.
4.3.2. MCD
The MCD estimator is another popular robust method for estimating multivariate location and scatter. It finds the best fitting elliptical distribution by minimizing the determinant of the covariance matrix subject to a constraint on the number of observations. First, it fits a minimum covariance determinant model and then computes the Mahalanobis distance as the outlier degree of the data.
Supposing the data are stored in an matrix , the classical tolerance ellipse is defined as the set of p-dimensional points whose Mahalanobis distance is defined in terms of the statistical distance (d) as follows:
equals the cutoff value (We denote as the quantile of the distribution). Here, is the sample mean, and is the sample covariance matrix. The Mahalanobis distance should tell us how far away is from the center of the data cloud, relative to its size and shape, and consequently, it determines an outlier degree of the data point. On the other hand, the robust tolerance ellipse used by the MCD estimator is based on the robust distance:
where is the MCD estimate of location, and is the MCD covariance estimate.
The MCD estimator is resistant to outliers and can handle high-dimensional data. It can also be applied both in supervised or unsupervised learning. A study by Rousseeuw and Driessen [] showed that the MCD estimator outperformed other robust estimators in terms of efficiency and breakdown point. Another study by Croux and Haesbroeck [] demonstrated the effectiveness of the MCD estimator in real-world applications.
The MCD model used in this work is a wrapper of Python’s scikit-learn MinCovDet class function with more functionalities that is included in the pyOD package [].
4.3.3. AD Ensembles
Our initial findings when testing the aforementioned AD methods were that none of them obtained the best precision and recall in all scenarios. That is the reason why we proposed to combine their outputs using a model ensemble. Several types of model ensembles exist in the literature, like voting, averaging, weighted averaging, etc. In this work, a voting ensemble has been selected.
A voting ensemble works by combining the predictions from multiple models by returning the most voted result. It can be used for classification or regression. In the case of regression, this involves calculating the average of the predictions from the models. In the case of classification, the predictions for each label are summed, and the label with the majority vote is predicted. In the binary case (normal or abnormal observation), a majority voting with two models requires that both models must agree that the observation is abnormal in order to tag it as an anomaly.
Recent studies [] have shown that ensemble methods outperform individual models in complex and imbalanced settings like anomaly detection. The ensemble approach works by reducing variance and bias, improving stability, and making the detection process more adaptable to different anomaly types and data distributions.
4.4. Streaming Framework
Real-time AD is crucial in industrial environments, as it helps in promptly recognizing and resolving errors before they cause major failure or even the destruction of industrial equipment. It can also provide insight on the causes that lead to those failures based on the ongoing activities of a system in near real time, enabling better decisions by detecting anomalies as they occur [].
To enable a real-time implementation of the AD models in an industrial environment, we proposed a streaming framework based on sliding windows. For this purpose, this work profited from Python’s pySAD library []. This library is open-source and compatible with pyOD. The window scheme was based on the study by Manzoor et al. [] that addressed the outlier detection problem for feature-evolving streams using an algorithm called xStream. In our work, we used a similar window scheme but with different detectors (the OCSVM, MCD, and voting ensemble).
Essentially, the AD models observe the probabilistic output from the classifier for a particular machine and for a determined period of time. This initial window makes it possible to train the AD models in an unsupervised way. In this stage, the models extract information about the normal or abnormal status of the machine. This initial window size was set to 30, which corresponds to 30 daily data samples. During this training period, no output is given by the AD system.
Once the initial window frame has passed, the probabilistic output from the classifier is fed sequentially to the AD models, which are fitted to the new observation and provide an anomaly score. This score is then normalized to the range [0, 1] to provide a new probability value. The probability value is then compared with the same decision threshold used by the classifier (that was optimized during its training stage) to convert the returned probability to a binary value (whether a work order should be taken or not). The streaming dynamics of the proposed approach are shown in Figure 3, and the final architecture proposed for the AD module is summarized in Figure 4.
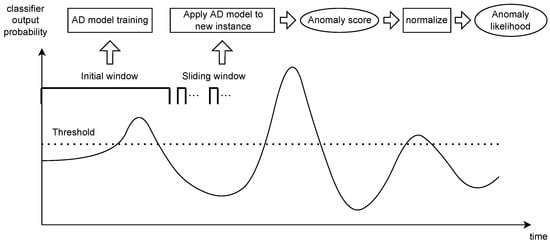
Figure 3.
Anomaly detection streaming procedure for online auditing of the classifier.
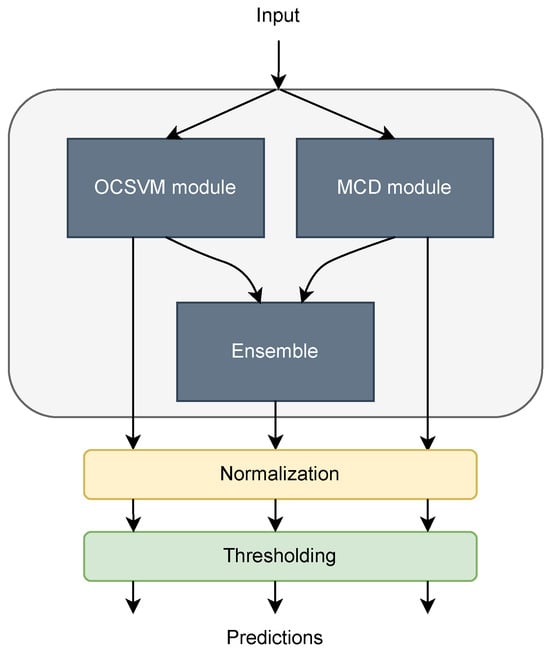
Figure 4.
Proposed architecture for the AD module.
4.5. Performance Metric
The performance metric used to compare the existing classifier (baseline) with the proposed methods was the F1 score, which is a robust metric that combines both precision and recall performance outcomes:
where precision and recall are defined as
and
where is the number of true positives, is the number of false positives, and is the number of false negatives.
All results refer to the test set, i.e., after the initial training window, to evaluate the generalization capabilities of the AD methods.
5. Results
We utilized machine records with the longest data history (more than 1000 days of run time) to test the proposed methodology. This approach ensured that the performance evaluation was realistic and reflective of long-term outcomes. This restriction reduced the number of machines to 23. The AD models were built and trained individually for each one of the machines. As an example, in Figure 5, we represent the classifier output probability and the anomaly likelihood obtained by the OCSVM for one of the machines. The true labels are also represented with a different line. The threshold applied was obtained during the classifier’s training to optimize the Area Under the Receiver Operating Characteristic Curve (AUROC) and determined the part of the signal where each method predicted a work order.
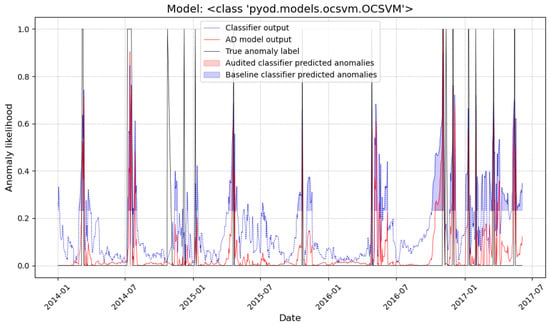
Figure 5.
Auditing example for one of the machines using OCSVM. The output from the classifier and the AD model output are represented as different lines, and the shaded part of each signal indicates if the threshold to call for a work order has been exceeded.
In this figure, we can observe that the proposed AD auditing stage started producing a non-null output after the first 30 samples used to train the model. After that period, it filtered the classifier output and made it more selective when predicting a maintenance action. This behavior was consistent with the rest of the machines. The effect of the AD stage was quantified by using a performance metric with respect to the true labels for each data point.
The data used to calculate the score were, in all cases, the inferred data after the initial training period of 30 days. The obtained F1 scores for the three AD methods are compared in Table 2. This table includes the baseline classifier F1 score to better assess the improvement offered by the AD methods.

Table 2.
Test set F1 score comparison between the three AD methods and the baseline classifier for 23 packaging machines. The best results for each machine have been highlighted in bold. The maximum relative percentage change is indicated in the rightmost column.
In quantitative terms, the voting ensemble was the best method tested, with a test F1 score of 0.48 ± 0.17 for the 23 machines. The OCSVM and MCD obtained F1 scores of 0.44 ± 0.17 and 0.44 ± 0.19, respectively. All methods significantly improved the baseline model that produced a test F1 of 0.21 ± 0.10. The maximum absolute F1 score improvement was obtained for machine 25ARE2200:2AB-0118. Using the ensemble model, the F1 score was increased to 0.784 from a baseline of 0.277. In relative terms, the highest increase in F1 was achieved for the machine 25ARE22V2: 2BC-0248, where the ensemble method reached a +933.3% improvement compared to the baseline. The minimum absolute variation in the F1 score was obtained by the MCD for machine 25ARF22V2:1AA-0108 (−5.0%). However, this decrease in the F1 score with respect to the baseline only occurred with one machine, so it can be considered a very unlikely scenario.
A statistical analysis was conducted to determine the statistical significance of the differences between the three proposed methods and the baseline. Figure 6 shows the differences between the F1 distributions for each method. From the visual inspection of the boxplots, the distributions of the OCSVM, MCD, and the voting ensemble differ significantly from the baseline (non-audited classifier). Specifically, the interquartile ranges (Q1–Q3) do not overlap. The voting ensemble was the superior method in terms of the median score, followed by the OCSVM. A Shapiro–Wilk test was used to demonstrate the normality of each group (p > 0.1), and the one-way ANOVA test was used to indicate significant differences between the means (p < 0.001).
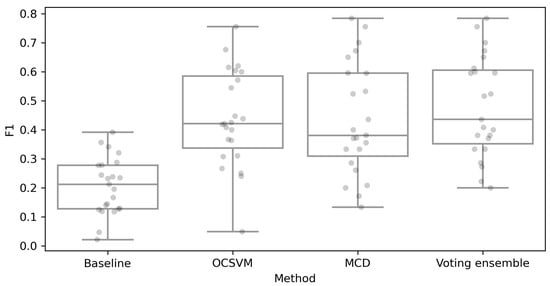
Figure 6.
Box plots illustrating the differences between the F1 scores distributions obtained by the compared methods.
The isolated recall and precision scores are also shown in Table 3 and Table 4, respectively. The results in Table 3 show that, in terms of recall alone, the baseline method often performed better than the AD techniques proposed for the 23 packaging machines, followed by the OCSVM. The maximum average percentage improvement of the AD methods was in this case negative (−15.5%). Alternatively, Table 4 reflects a much better performance of the proposed AD methods in terms of precision. The leading method was in this case the voting ensemble, and the maximum percentage change in the F1 score using the best method for each machine reached 675.9% This suggests that while the standard classifier captured most anomalies, it also generated a large number of false positives, which were corrected by the AD methods. The classifier’s threshold used in this study was set to optimize the F1 score, which balances precision and recall. This is evident from the observed improvements in F1 scores across the machines when using the AD module and the fact that the precision was markedly improved while maintaining competitive recall.

Table 3.
Recall performance comparison between baseline, OCSVM, MCD, and voting ensemble methods. The maximum relative percentage change is indicated in the rightmost column, with the values responsible for the maximum change highlighted in bold for each row.

Table 4.
Precision comparison between the three AD methods and the baseline classifier for 23 packaging machines. The maximum relative percentage change is indicated in the rightmost column, with the values responsible for the maximum change highlighted in bold for each row.
One of the key challenges in predictive maintenance within industry settings is the accurate identification of anomalous events or failures to prevent costly downtime. In this context, the OCSVM and MCD methods have emerged as effective techniques to audit and correct the output of classifiers. The OCSVM algorithm is widely used for anomaly detection tasks and has shown promising results in various industrial applications, including fault detection and diagnosis. On the other hand, the MCD estimator is a robust estimator of multivariate location and scatter, which makes it suitable for detecting outliers in datasets with high-dimensional features. Numerous studies have demonstrated the effectiveness of the OCSVM and MCD methods in auditing and correcting classifier outputs for predictive maintenance tasks, improving the overall accuracy and reliability of anomaly detection. These methods provide a valuable means of refining the results of classifiers, enhancing the decision-making process, and facilitating more efficient maintenance strategies in industrial settings. However, according to our findings, none of the aforementioned methods has absolute superiority over the other, so they need to be evaluated separately, and their performance outcomes need to be compared.
We also proposed an ensemble method that tags a sample as an outlier only if both methods are in agreement (voting). Ensemble methods have gained significant popularity in various fields due to their ability to improve the robustness and overall performance of predictive models compared to individual methods. One key advantage of ensemble methods is their capacity to reduce the risk of overfitting by combining multiple models. By aggregating the predictions of these models, ensemble methods can effectively smooth out errors and biases that may be present in individual models, leading to more accurate and robust predictions. Moreover, ensemble methods can handle complex relationships and capture non-linear patterns by combining different modeling techniques or incorporating diverse feature representations. This versatility allows ensembles to adapt to a wide range of data distributions and increase the generalization capability of the model. In addition, ensemble methods can provide better exploration of the feature space and overcome the limitations of individual models, thus enhancing the model’s ability to capture important and relevant patterns.
On paper, the high AUC obtained on the test set by the original classifier previously developed by our group is satisfactory. However, when the client company deployed it to predict work orders in the ERP system, due to the class imbalance, no decision threshold on the signal captured from each machine was found to be optimal: it either prioritizes false positive detection or true negative detection, which results in a low F1 score. The main advantage of adding the proposed AD stage is the significant increase in the F1 score without modifying the input information to the model. Since the model is in production, this aspect is of paramount importance.
From the results of our experiments, we observe that all AD techniques contribute to improve the classifier performance. In particular, the ensemble method has obtained the best results in terms of its F1 score, followed by the MCD and OCSVM in that order. Out of the 23 machines, the ensemble method obtained the best performance in 20 cases, proving its consistency, although it tied with the MCD estimator in 14 of those cases. In four cases (machines 25ARE22V2:2BC-0248, 25ARF2200:101-0027, 25ARF22V2:1AA-0098, and 25ARF22V2:1AA-0113 (Aranco, Valencia, Spain)) it improved the performance of the MCD or OCSVM alone. With regard to the OCSVM, despite not being the best method in many cases, it achieved a similar average F1 score to that of the MCD and showed potential to improve beyond the ensemble performance in three of the cases.
The percentage of improvement in the F1 score with respect to the baseline model was led by the ensemble method, with an average improvement of 192.5%, followed by the MCD with an improvement of 146.7% and the OCSVM with 140.1%. Taking the best of the three methods, the maximum average percentage increase in the F1 score reached 198%, as stated in Table 2.
Although the heterogeneous results reflect differences in the time series of each machine, they also highlight the adaptability of the proposed methods to varying data characteristics.
6. Conclusions and Future Work
This paper proposes a framework to audit the classifier implemented in an expert system used for planning predictive maintenance policies in the ERP (Enterprise Resource Planning) system of a packaging machine company.
The study was conducted on 23 time series with more than 1000 data points, corresponding to daily predictions of the degree of likelihood of a work order. An unsupervised AD module was cascaded at the pretrained classifier’s output so that, for every new sample, it produced three outputs (based on the OCSVM, MCD, and an ensemble of them). These predictions were used to audit and correct the classifier’s output. This new score was normalized and thresholded to determine if the sample actually corresponded to an anomaly.
By examining the results, we observe that all AD techniques contributed to improve the classifier performance. More specifically, the ensemble method obtained the best results in terms of the F1 score with an average increase in the F1 score of 192.5% on the test set, although the individual AD methods also produced an average increase above 140%.
The main contribution of the proposed methods lies in their integration that streams unsupervised anomaly detection with a sliding window, enabling real-time auditing of classifiers as new samples arrive. The implemented methods demonstrate their ability to enhance classifier performance while maintaining simplicity and adaptability. This strategy significantly improves precision and recall in an already optimized classifier, yielding notable improvements for this specific system. Moreover, the approach has the potential to be easily transferred to other similar predictive maintenance settings.
Future work will focus on improving the applicability of methods by incorporating domain-specific features, refining ensemble weighting mechanisms, exploring adaptive approaches to improve performance consistency across diverse scenarios, and conducting comprehensive comparisons with state-of-the-art deep learning techniques to evaluate their relative effectiveness and potential integration.
Author Contributions
Conceptualization, A.J.S.-L., J.G.-S. and J.V.-F.; methodology, F.M., A.J.S.-L. and M.M.-S.; software, F.M. and J.V.-F.; validation, E.S.-O., J.G.-S. and F.M.; formal analysis, F.M., E.S.-O. and M.M.-S.; investigation, F.M. and A.J.S.-L.; resources, E.S.-O. and J.V.-F.; data curation, J.G.-S., A.J.S.-L. and M.M.-S.; writing—original draft preparation, F.M.; writing—review and editing, A.J.S.-L., E.S.-O. and J.V.-F.; visualization, F.M.; supervision, A.J.S.-L. and J.V.-F.; project administration, A.J.S.-L. and J.V.-F.; funding acquisition, A.J.S.-L. and J.V.-F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MCIN/AEI/10.13039/501100011033 “ERDF A way of making Europe” through grant number PID2021-127946OB-I00.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author due to privacy restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ayvaz, S.; Alpay, K. Predictive Maintenance System for Production Lines in Manufacturing: A Machine Learning Approach Using IoT Data in Real-Time. Expert Syst. Appl. 2021, 173, 114598. [Google Scholar] [CrossRef]
- Froger, A.; Gendreau, M.; Mendoza, J.E.; Pinson, E.; Rousseau, L.M. Maintenance scheduling in the electricity industry: A literature review. Eur. J. Oper. Res. 2016, 251, 695–706. [Google Scholar] [CrossRef]
- Stock, T.; Seliger, G. Opportunities of sustainable manufacturing in industry 4.0. Procedia CIRP 2016, 40, 536–541. [Google Scholar] [CrossRef]
- Yin, S.; Li, X.; Gao, H.; Kaynak, O. Data-Based Techniques Focused on Modern Industry: An Overview. IEEE Trans. Ind. Electron. 2015, 62, 657–667. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Yu, Z.; Zeng, M. Incremental supervised locally linear embedding for machinery fault diagnosis. Eng. Appl. Artif. Intell. 2016, 50, 60–70. [Google Scholar] [CrossRef]
- Lee, S.S. Noisy replication in skewed binary classification. Comput. Stat. Data Anal. 2000, 34, 165–191. [Google Scholar] [CrossRef]
- Zonta, T.; da Costa, C.A.; da Rosa Righi, R.; de Lima, M.J.; da Trindade, E.S.; Li, G.P. Predictive maintenance in the Industry 4.0: A systematic literature review. Comput. Ind. Eng. 2020, 150, 106889. [Google Scholar] [CrossRef]
- O’Donovan, P.; Leahy, K.; Bruton, K.; O’Sullivan, D.T. Big data in manufacturing: A systematic mapping study. J. Big Data 2015, 2, 20. [Google Scholar] [CrossRef]
- Muhuri, P.K.; Shukla, A.K.; Abraham, A. Industry 4.0: A bibliometric analysis and detailed overview. Eng. Appl. Artif. Intell. 2019, 78, 218–235. [Google Scholar] [CrossRef]
- Lee, J.; Bagheri, B.; Kao, H.A. Recent advances and trends of cyber-physical systems and big data analytics in industrial informatics. In Proceedings of the International Conference on Industrial Informatics (INDIN), Porto Alegre, Brazil, 27–30 July 2014; pp. 1–6. [Google Scholar]
- Rodríguez-Mazahua, L.; Rodríguez-Enríquez, C.A.; Sánchez-Cervantes, J.L.; Cervantes, J.; García-Alcaraz, J.L.; Alor-Hernández, G. A general perspective of Big Data: Applications, tools, challenges and trends. J. Supercomput. 2016, 72, 3073–3113. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Lu, B.; Durocher, D.B.; Stemper, P. Predictive maintenance techniques. IEEE Ind. Appl. Mag. 2009, 15, 52–60. [Google Scholar] [CrossRef]
- Chouikhi, H.; Khatab, A.; Rezg, N. A condition-based maintenance policy for a production system under excessive environmental degradation. J. Intell. Manuf. 2014, 25, 727–737. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Duan, L.; Gao, R. A new paradigm of cloud-based predictive maintenance for intelligent manufacturing. J. Intell. Manuf. 2015, 28, 1125–1137. [Google Scholar] [CrossRef]
- Cucurull, J.; Martí, R.; Navarro-Arribas, G.; Robles, S.; Overeinder, B.; Borrell, J. Agent mobility architecture based on IEEE-FIPA standards. Comput. Commun. 2009, 32, 712–729. [Google Scholar] [CrossRef]
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco, R.d.P.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, D.; Wang, H. Data-driven methods for predictive maintenance of industrial equipment: A survey. IEEE Syst. J. 2019, 13, 2213–2227. [Google Scholar] [CrossRef]
- Susto, G.A.; Schirru, A.; Pampuri, S.; McLoone, S.; Beghi, A. Machine learning for predictive maintenance: A multiple classifier approach. IEEE Trans. Ind. Inform. 2014, 11, 812–820. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Prytz, R.; Nowaczyk, S.; Rögnvaldsson, T.; Byttner, S. Predicting the need for vehicle compressor repairs using maintenance records and logged vehicle data. Eng. Appl. Artif. Intell. 2015, 41, 139–150. [Google Scholar]
- Vapnik, V.N. Support Vector Machines. In Encyclopedia of Biometrics; Li, S.Z., Jain, A.K., Eds.; Springer: Boston, MA, USA, 2009; pp. 1365–1368. [Google Scholar] [CrossRef]
- Gryllias, K.; Antoniadis, I. A Support Vector Machine approach based on physical model training for rolling element bearing fault detection in industrial environments. Eng. Appl. Artif. Intell. 2012, 25, 326–344. [Google Scholar] [CrossRef]
- Li, H.; Parikh, D.; He, Q.; Qian, B.; Li, Z.; Fang, D.; Hampapur, A. Improving rail network velocity: A machine learning approach to predictive maintenance. Transp. Res. Part C Emerg. Technol. 2014, 45, 17–26. [Google Scholar] [CrossRef]
- Langone, R.; Alzate, C.; Ketelaere, B.D.; Vlasselaer, J.; Meert, W.; Suykens, J.A. LS-SVM based spectral clustering and regression for predicting maintenance of industrial machines. Eng. Appl. Artif. Intell. 2015, 37, 268–278. [Google Scholar] [CrossRef]
- Erhan, L.; Ndubuaku, M.; Di Mauro, M.; Song, W.; Chen, M.; Fortino, G.; Bagdasar, O.; Liotta, A. Smart anomaly detection in sensor systems: A multi-perspective review. Inf. Fusion 2021, 67, 64–79. [Google Scholar] [CrossRef]
- Nunes, P.; Santos, J.; Rocha, E. Challenges in predictive maintenance—A review. CIRP J. Manuf. Sci. Technol. 2023, 40, 53–67. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Learning from Imbalanced Data Sets; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10. [Google Scholar]
- Morselli, F.; Bedogni, L.; Mirani, U.; Fantoni, M.; Galasso, S. Anomaly Detection and Classification in Predictive Maintenance Tasks with Zero Initial Training. IoT 2021, 2, 590–609. [Google Scholar] [CrossRef]
- Kulanuwat, L.; Chantrapornchai, C.; Maleewong, M.; Wongchaisuwat, P.; Wimala, S.; Sarinnapakorn, K.; Boonya-aroonnet, S. Anomaly Detection Using a Sliding Window Technique and Data Imputation with Machine Learning for Hydrological Time Series. Water 2021, 13, 1862. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhao, Y.; Yang, A.; Zhang, H.; Qiao, D.; Zhang, Z. Industrial Robot Vibration Anomaly Detection Based on Sliding Window One-Dimensional Convolution Autoencoder. Shock Vib. 2022, 2022, 1179192. [Google Scholar] [CrossRef]
- Li, Z.; Li, G.; Liu, Y.; Li, Z.; Li, G.; Liu, Y. Network traffic anomaly detection based on sliding window. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 1820–1823. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Int. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. Artic. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Schölkopf, B.; Williamson, R.C.; Smola, A.; Shawe-Taylor, J.; Platt, J. Support vector method for novelty detection. Adv. Neural Inf. Process. Syst. 1999, 12, 582–588. [Google Scholar]
- Zhao, Y.; Nasrullah, Z.; Li, Z. PyOD: A Python Toolbox for Scalable Outlier Detection. J. Mach. Learn. Res. 2019, 20, 1–7. [Google Scholar]
- Rousseeuw, P.J.; Driessen, K.V. A fast algorithm for the minimum covariance determinant estimator. Technometrics 1999, 41, 212–223. [Google Scholar] [CrossRef]
- Croux, C.; Haesbroeck, G. Influence function and efficiency of the minimum covariance determinant scatter matrix estimator. J. Multivar. Anal. 1999, 71, 161–190. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Ding, L.; Huang, Z.; Sui, H.; Wang, S.; Song, Y. Selective ensemble method for anomaly detection based on parallel learning. Sci. Rep. 2024, 14, 1420. [Google Scholar] [CrossRef] [PubMed]
- Grunova, D.; Bakratsi, V.; Vrochidou, E.; Papakostas, G.A. Machine Learning for Anomaly Detection in Industrial Environments. Eng. Proc. 2024, 70, 25. [Google Scholar] [CrossRef]
- Yilmaz, S.F.; Kozat, S.S. PySAD: A Streaming Anomaly Detection Framework in Python. arXiv 2020, arXiv:2009.02572. [Google Scholar]
- Manzoor, E.; Lamba, H.; Akoglu, L. xstream: Outlier detection in feature-evolving data streams. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1963–1972. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).